Abstract

Defining the metric for synthesizability and predicting new compounds that can be experimentally realized in the realm of data-driven research is a pressing problem in contemporary materials science. The increasing computational power and advancements in machine learning (ML) algorithms provide a new avenue to solve the synthesizability challenge. In this work, using the Inorganic Crystal Structure Database (ICSD) and the Materials Project (MP) database, we represent crystal structures in Fourier-transformed crystal properties (FTCP) representation and use a deep learning model to predict synthesizability in the form of a synthesizability score (SC). Such an SC model, as a synthesizability filter for new materials, enables an efficient and accurate classification to identify promising material candidates. The SC prediction model achieved 82.6/80.6% (precision/recall) overall accuracy in predicting ternary crystal materials. We also trained the SC model by only considering compounds uploaded on the MP before 2015 as the training set and testing on multiple sets of materials uploaded after 2015. In the post-2019 test set, we obtain a high 88.60% true positive rate accuracy, coupled with 9.81% precision, indicating that newly added materials remain unexplored and have high synthesis potential. Further, we provide a list of 100 materials predicted to be synthesizable from this post-2019 dataset (highest SC) for future studies, and our SC model, as a validation filter, is beneficial for future material screening and discovery.
Introduction
The ability to predict if a material can be experimentally realized via synthesis is an important characteristic that is linked to its structure, phase, and composition. Such a prediction of the synthesizability of unexplored inorganic crystal materials is an important bridge connecting theoretical approaches to experimental synthesis and remains an unsolved and urgent challenge.1−5 Traditionally, researchers approach synthesizability by a trial-and-error search for material candidates, which typically combines empirical experience and theoretical calculations.6,7 Since there is a large variance in human experience and material choices, discovery and synthesis of new materials can be slow and unpredictable.8−10 Therefore, an accurate way to determine material synthesizability is needed to improve the efficiency and productivity of new material discovery.11 One necessary but insufficient step toward predicting synthesizability is the prediction of its ground state stability. As the availability of computational power increases, first-principles density functional theory (DFT) calculations have become the most widely used method to predict such thermodynamical stability, with relatively high efficiency and low cost.12−14 In DFT calculations, material properties can be determined through an investigation of the many-body electronic interactions, typically only in the material’s ground state.14−16
Thermodynamically, the stability of an inorganic crystal can be described by its Gibbs energy of formation, Gf(T), which combines the formation enthalpy and the temperature-scaled entropic effects (configurational and vibrational).17 However, an accurate calculation of the Gibbs energy for a large number of inorganic crystals is still a difficult task.5 The internal energy of any incompressible inorganic crystal structure can be calculated via DFT calculations performed at 0 K, which is representative of the enthalpy term. Using this, relative to nearby stable compositions in the relevant binary, ternary, or quaternary space, the formation energy (FE) of any new compositional structure can be determined.18−20 When the temperature-dependent entropic contributions are ignored, if the FE is positive, then the crystal is expected to be unstable, and if FE is negative, it can be stable. Typically, a lower FE value indicates higher stability and hence a higher chance of synthesizability. The difference between the formation energy of a new crystal and its expected decomposition products is defined as the energy above the hull surface (Ehull).21 Materials with DFT-calculated Ehull of zero are, by definition, on the hull surface and hence thermodynamically stable.
The formation energy and Ehull can therefore be used as a proxy for synthesizability. However, these are far from accurate because of deviations from ideality in the DFT calculations caused by the assumption of perfect crystals (ignoring defects and other real-world factors).14−16 To estimate synthesizability, even for those compounds that have a negative formation energy and Ehull close to zero, there are more screening criteria that need to be included, such as (1) no negative phonon energies,22 (2) multiple phases and polymorphs for the same composition,23,24 and (3) a weak tendency for phase decomposition.25 Explicitly, polymorphs with similar DFT-calculated energy values require extra considerations and calculations of other properties to determine if each phase is synthesizable or not. The computation of such properties is difficult and expensive. Practical considerations such as the availability of precursors, earth abundance and toxicity of starting materials, and accessibility of high temperatures and/or high pressures make this further complicated.26−28 In the absence of such contributions, a threshold for FE and Ehull values (for example, FE lower than 1 eV and Ehull lower than 0.08 eV) can be used as a simple estimate for synthesizability of a DFT-calculated material and has been shown to act as a good filter to determine whether one should proceed into experimental studies or not.29 In short, the likelihood of successful synthesis is affected not only by DFT-calculated thermodynamic parameters like the material formation energy or energy above the hull but also by phase transformation, experimental requirements, and reaction kinetics. As a result, the central problem of predicting synthesizability is to first define a clear metric for it, utilizing domain knowledge and information of existing materials.
In recently developed high-throughput (HT) databases, DFT calculations have been performed on a large number of inorganic materials to calculate their internal energies, formation energies, and more: as of this date, 126,335 materials in Materials Project (MP),20 1,022,603 materials in the Open Quantum Materials Database (OQMD),30 and 3,562,831 in Automatic FLOW for Materials Discovery (AFLOW).31 With data-driven approaches applied on these databases, especially machine learning (ML), many attempts have successfully reproduced the formation energy calculations.21,32,33 In fact, packing faster speed and lower computational cost compared to first-principles calculations, ML models are widely used in not only predicting the formation energy but also material properties such as the material’s band gap (Eg),34,35 mechanical and structural properties,36,37 and others. Similarly, ML models can be an alternative path to solve the demanding synthesizability problem. Unlike DFT calculations, which can only provide a rough guide for synthesis through FE and Ehull, ML models can output a direct prediction for synthesizability for any target material. Moreover, machine learning models can combine thermodynamic stability information, crystal structure information, and other stability-related material properties to make more accurate synthesizability predictions.
To build such a synthesizability model, multiple steps must be performed: (1) transforming crystal structures into computer-readable crystal representations; (2) constructing a machine learning model that can predict results from the crystal representation; and (3) training and validating to ensure the highest accuracy and prediction capability. The first and quite demanding task is that of finding a robust crystal representation, as it greatly affects the accuracy and efficiency of the predictive model; there have been various attempts at creating such representations including the atomistic line graph neural network (ALIGNN),38 compositionally restricted attention-based network (CrabNet),39 MegNet,40 crystal graph convolutional neural networks (CGCNN),33 and ElemNet.41 A frequently used crystal representation is using crystal graphs in CGCNN that encode both atomic properties and bonding of a crystal structure in unit cells and edges, which can describe periodicity by connecting multiple edges between nodes. On the other hand, a recently published Fourier-transformed crystal properties (FTCP) implementation includes a crystal representation in both real space and reciprocal space.42 The real-space crystal features are constructed using one-hot encoding, while the reciprocal-space features are formed using elemental property vectors and discrete Fourier transform of real-space features. The addition of reciprocal space allows FTCP to describe crystal periodicity and convoluted elemental properties, thereby capturing important information that is unexplored through other representations. In this work, we choose to use the FTCP representation and benchmark using the CGCNN approach.
The second component is the building of an ML model suitable for the selected crystal representation and can solve the classification problem. The CGCNN,33 which uses two-component convolutional neural networks (CNN) to process the crystal graph input, shows high accuracy in predicting crystal properties. CGCNN also shows good performance in predicting material stability. Jang et al. built a model to predict the synthesizability crystal-likeness score (CLscore)43 of new materials, which achieved 86.2% recall on experimentally synthesized and reported materials. Ren et al. built an ML model consisting of a CNN encoder to transform the FTCP input into latent vectors coupled with a target-learning branch structure to predict specific material properties such as the band gap and formation energy with a mean absolute error (MAE) of 0.204 and 0.051eV/atom, respectively.42 Saidi et al. built a hierarchical convolutional neural network (HCNN)34 that employs a combination of a CNN range classifier and regressor, achieving a root-mean-square error (RMSE) of 0.01 Å, 5°, and 0.02 eV on the lattice constant, octahedral angle, and band gap prediction, respectively. Wang et al. recently constructed CrabNet39 to predict material properties with only chemical compositions. CrabNet uses self-attention to capture the contribution of each element in the crystal and their interaction and obtained MAE of 0.077 eV/atom and 0.263 eV, respectively, when predicting the MP FE and MP band gap.
In this work, we represented inorganic crystal structures using the FTCP technique and used an ML classifier to predict the likelihood of a material being successfully synthesized. The complete synthesizability prediction model employs three components: (1) an inorganic crystal structure database (ICSD) tag in the MP database as the ground truth for model development; (2) FTCP that represents the crystal structure; and (3) a deep learning model that processes the FTCP input into a binary classification prediction output. Our model transforms all inorganic crystal structures in material databases into an FTCP representation and processes it into synthesizability score (SC) prediction with a precision higher than 82%. Our pretrained models enable fast, low computational cost, and high-fidelity synthesizability prediction of a newly generated material.
Methods
The training and validation datasets for our synthesizability prediction model are obtained from the MP20 and ICSD.44 The MP is a growing inorganic material database that contains DFT-relaxed crystal structures for materials and corresponding calculated properties such as the formation energy and band gap energy. This open-source database can be accessed through the open Materials Application Programming Interface (MAPI) and the Python Materials Genomics (pymatgen)45 materials analysis package. In our work, a total of 39,198 ternary compounds and 12,869 quaternary compounds were queried from the MP database (the database version we used is v2021.03.22). We frame the synthesizability challenge as a property estimation problem. The Inorganic Crystal Structure Database (ICSD)44 and MP database provide such structural information and properties for both experimentally synthesized and DFT-calculated crystal structures. In fact, the ICSD tag in MP, which identifies whether materials have already been experimentally synthesized, does exactly this, thereby providing a convenient route to process such labels for a classification model. If a material in MP has one or multiple ICSD IDs, it will be given the label “1”. Tag “0” will be assigned to materials without an ICSD ID.
The crystal structure representation features for training and validating the deep learning model are separated into two parts: real-space features and reciprocal-space features. The real-space features consist of both atomic (compositional) features and real-space crystal features, where atomic features are matrices constructed using the one-hot encoding method to describe the stoichiometry of compounds and corresponding elemental properties for each element in the compound. The real-space crystal features encode the site location and element occupation information in the unit cell. The reciprocal-space features are represented in the form of FTCP,42 where atomic properties of each element are projected onto crystal planes using the Fourier transform.
Based on different sets of crystal structure representations features, we next built the machine learning models for synthesizability. Here, we adopted the encoder in the inverse design generative model developed by Ren et al. to process the input feature sets.42 In this encoder, crystal representations are treated as one-dimensional (1D) arrays containing the atom and crystal structure information in channels and then are encoded using a 1D convolutional neural network (CNN) into a reduced material space (Figure 1). Then, we use a regression deep learning model, multilayer perceptron (MLP), to reduce the latent space into a specific SC, which represents the likelihood of a successful synthesis. The SC is a number ranging from 0 to 1, where a score of 1 or near 1 indicates that the material has a high probability of being synthesized; contrarily, 0 means not synthesizable. The final binary synthesizability prediction result is determined by an SC threshold: if the SC is larger than the threshold, materials are predicted to be synthesizable and not synthesizable if the SC is lower than the threshold. The choice of the threshold affects the model performance in the form of a precision/recall score, whose default value for binary classification is 0.5. The receiver operating characteristic (ROC) curve and precision versus recall curve (threshold set at default 0.5) for our ternary SC model using real-space crystal feature sets are plotted in Figures S3 and S4, Supporting Information. In the ROC curve, the area under the ROC curve (AUC) of 0.93 is achieved with this default threshold value, which proves that this threshold is good enough for our classifier, while the precision versus recall curve additionally shows that the 0.5 value maintains a good balance between the precision and recall performance (both higher than 0.8).
Figure 1.

Schematic of the full synthesizability score (SC) model. The full crystal representation is formed by three components: compositional features, real-space crystal features, and FTCP. After data processing and concatenation, the full representation is reduced into a smaller dimension by convolutional encoders. Then, the reduced material space is processed by a fully connected neural network into the SC. The detailed network structure can be found in Figures S5 and S6.
Data processing, model training, and validation process were performed using scikit-learn and TensorFlow in Python (version 3.7.4). To test the relevance of each crystal representation, three kinds of input feature combinations were used in model training/validation: atomic features, atomic features + real-space crystal features, and all crystal representations. For both ternary and quaternary compound models and three sets of features, data points were randomly divided into training (80%) and test sets (20%). The ratio of data points with ICSD label “1” (synthesized) to those with ICSD label “0” (not synthesized yet) was the same in the training and test sets. We assumed that the ratio of materials in the MP, which have already been synthesized, was higher before 2015, while a lot more “hypothetical” materials were computed but not yet synthesized. Hence, we also trained a model based on materials added to the MP before 2015 (pre-2015 training set) and tested the model on both the pre-2015 test set and materials added to the MP after 2015 (post-2015 test set). One can imagine the usefulness of such an exercise as a synthesizability score with the post-2015 data as a test set can provide strong support for materials synthesis given pre-2015 data. Moreover, the comparison of test results of pre-2015 and post-201X (X = 5–9 for materials added to the MP after a particular time) test sets provides a better view of materials in different time frames. Each model was trained for 200 epochs at a learning rate of 8 × 10–5 (ternary models) or 4 × 10–5 (quaternary models), and early stopping was used to prevent overfitting. Finally, we list several materials which have high SCs according to our prediction model but did not have an ICSD tag on the MP before 2015; furthermore, these materials have since been experimentally synthesized after 2015 and reported in the literature, thereby validating our study.
Results and Discussion
Ternary and Quaternary Compound Results
Table 1 shows the performance of SC prediction models, trained and tested based on different material types and crystal representation methods. Both the true positive rate (recall) and positive predictive value (precision) were used to evaluate the performance of our models: recall indicates the accuracy of predicting the SC when the data shows a truly synthesizable material, while precision focuses on the positive predictions and their reliability score. In the ternary dataset (with a threshold of SC = 0.5), the best-performing model achieved 82.6% precision using atomic features as well as real-space crystal features and the FTCP, meaning that 82.6% of predicted synthesizable compounds have an ICSD ID tag and 80.6% recall. The model based on the quaternary dataset also reached a similar level of performance, with 82.3% precision and 74.8% recall. The combination of high precision and recall shows that our crystal representation techniques, with the neural network model, have successfully learned the features related to material synthesizability during training. More importantly, tests on ternary and quaternary datasets show a similar level of performance. We also built a combination model with 82.5% precision and 81.2% recall, which can predict the SC for both ternary and quaternary compounds; however, this performance is not better than previous models due to the increased input size and model complexity. We compared this to the CGCNN model built on the same ternary dataset, which achieved 77.9 and 68.2% for precision and recall, accordingly. Our model has 4.7% higher performance in precision and 12.4% in recall than the result of the CGCNN model. The difference in performance shows that the combination of our feature sets and the neural network model is more efficient in finding and learning those features that link to synthesizability.
Table 1. SC Results for Different Datasets and Crystal Representation.
| material type | crystal representation | precision | recall | ||
|---|---|---|---|---|---|
| ternary | atomic | 68.9 | 64.0 | ||
| ternary | atomic | real-space crystal | 82.5 | 81.3 | |
| ternary | atomic | real-space crystal | FTCP | 82.6 | 80.6 |
| quaternary | atomic | real-space crystal | FTCP | 82.3 | 74.8 |
| ternary (baseline random model) | atomic | real-space crystal | FTCP | 48.6 | 44.5 |
| ternary | CGCNN (state-of-the-art graph-based model) | 77.9 | 68.2 | ||
To ensure our model indeed learned synthesizability-related crystal features, we built a baseline model using the ternary compound dataset, where we randomly assigned synthesizability labels to materials in the ternary dataset. The ternary compound dataset consists of 39 198 data points, where 13 816 data points are confirmed to be synthesizable. In the baseline model dataset, we randomly assigned an equivalent 13 816 data points with “1” as a synthesizable tag and gave the remaining data points “0” or a not synthesizable tag. With the same crystal representation and neural network, the baseline model had a performance of 48.6% precision and 44.5% recall. The results show that the baseline model failed to learn crystal features and related them to a randomly assigned synthesizability tag, resulting in a similar performance as a random guessing model. The performance difference between our ternary model and the baseline model illustrates that features in the crystal representation that are related to synthesizability have efficiently been learned by our deep learning model.
Crystal Representation and Its Effect on Model Performance
Figure 2 shows the performance of our SC prediction models trained and tested using different combinations of crystal representation in the form of confusion matrices when applied on the ternary compound dataset. The composition-only crystal representation model worked with 68.9% precision, where 1742 of 2529 positive predictions are confirmed to be synthesizable materials, and 64% recall with a threshold of SC = 0.5 (Figure 2a). Compared to the baseline model, the atomic-features-only model has higher performance under both evaluation matrices, but the sub-70% precision value indicates that material composition itself does not provide enough information for predicting synthesizability. In other words, atomic feature representation is not sufficient for the neural network model to learn and give correct SC predictions. Upon adding real space crystal features, the performance of the SC predictor improved to 82.5 and 81.3% for precision and recall, respectively (Figure 2b). This large performance difference demonstrates that our deep learning model can find the key features from the combination of atomic features and real space crystal features. Therefore, we can conclude that crystal structure information and atomic interactions encoded in real-space features are crucial to determine material synthesizability. However, after FTCP is added to the crystal representation feature set, the performance stayed at the same level as the previous model (Figure 2c and Table 1). That means the crystal structure factor information itself or its combination with previously used features does not provide new information to improve the learning of the deep learning model. In other words, the reciprocal-space representation does not have a strong correlation with material synthesizability, while compositional and structural information within a crystal unit cell is sufficient to train a great performing SC model. One could generalize this learning and determine if a hypothetical material can be synthesized with ∼70% accuracy when only its composition is known. However, if some information is known (via generative models, for example) for their atomic locations and unit cell structure, then the accuracy of prediction of synthesizability increases significantly to ∼82%. The periodicity of lattice and higher-order miller indices are presumably not as important in determining a material’s synthesizability.
Figure 2.
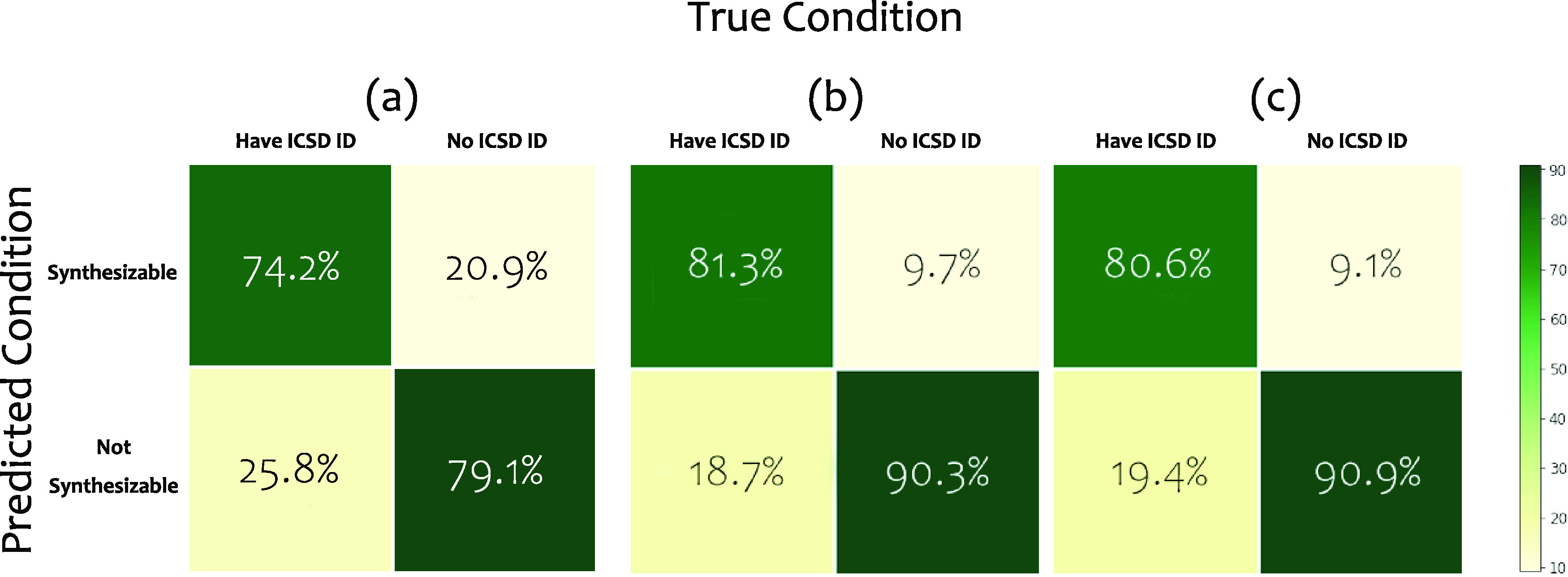
Confusion matrices showing the test set result of the ternary dataset using (a) atomic features only, (b) both atomic features and real space crystal features, and (c) the full crystal representation consisting of all three types of features. The color bar signifies the percent of true condition samples.
Time-Dependent Synthesizability Model and Validation
To further validate our approach and to get a better understanding of the predictive power of the MP and ICSD databases, we built several models based on when the stated material was uploaded onto the database. Figure 3a shows the performance of the SC model trained and tested based on data points uploaded to the MP database before 2015 (pre-2015 model). The model achieved over 90.3% precision and 90.2% recall, significantly better than all previous models (the train-test performance vs. epoch of our best pre-2015 model is provided in Figure S1). We also tested the same model on all materials uploaded after 2015. Interestingly, the test achieved 91.2% recall; however, the precision is as low as 31.73%. The high recall performance shows our model learned the features of truly synthesizable materials and can identify them efficiently. On the other hand, the high false positive rate (FPR) of 55.2% indicates that our model predicted a large amount of database tag “0” materials to be synthesizable. This is possibly due to what the “0” synthesizability tag in the MP database means: it does not mean that the material is not synthesizable; it just means that it does not have an ICSD tag. In our SC model, this indicates that a large portion of the newly added materials are predicted to be synthesizable (tag “1”) even though they do not have an ICSD ID tag.
Figure 3.

Confusion matrices showing results using the full crystal representation consisting of all three types of features (a) from the model trained and tested using materials uploaded to the MP before 2015 and (b) from the model trained using materials uploaded to the MP before 2015 but tested on materials uploaded after 2015. The color bar signifies the percent of true condition samples. (c) Performance of the SC model trained on materials uploaded before 2015 and tested on materials uploaded after 2015–2019.
Because the problem “a portion of the unsynthesizable materials could be synthesizable” also applies to the training data, we would also expect a correction in reality with higher-than-expected false negative rates (because some of the actual “0”s could be “1”s as they might, in reality, be synthesizable). To minimize this problem, the pre-2015 data is used as a training set, as this data is balanced with both scores (in 15582 pre-2015 training materials, 8660 entries have an ICSD tag and 6922 entries do not). Training with pre-2015 data will lower the amount of tagged “unsynthesizable” materials being actually synthesizable. Then, the effect of having a low false negative rate effect is minimal using this training strategy, while the high false positive rate has a more significant effect on the final result. We note that there is no way to solve this problem completely in the model but nevertheless is an important caveat to mention.
Figure 3c shows the performance of the pre-2015 model on data points added to the MP database after a particular time (2015–2019). Recall results for all tests are above 88%, while the precision values decrease over time from 31.73% for 2015 to 9.81% for 2019.
We hypothesize that one major cause of the decreasing precision results with progressing time in the test sets is that newly computationally evaluated materials added to the MP database have not yet been experimentally tested (due to their relatively more recent release date), and hence their ICSD IDs have not been updated. This highlights the strength of computational databases, where high-performance computing and access to supercomputers can allow for theoretical calculations of a much larger number of inorganic materials, while experiments generally tend to lag behind. Hence, it is not a surprise that materials uploaded to the MP database before 2015 have historically been well studied. To test this hypothesis, we searched and found several crystals that have a “0” tag in the MP database but were confirmed either experimentally or via careful DFT simulations to be stable and subsequently reported in the literature. Figure 4 shows the formula, MP ID, SC, year synthesized, and crystal structure of four such selected materials. These results indicate that in the post-2019 test set, a large portion of newly added materials remain unexplored and have high synthesis potential. To facilitate more effort toward this unexplored material space, we trained a SC model with the pre-2015 set to predict the SC of materials in the post-2019 set that do not have an ICSD ID. A full list of 100 materials predicted to be synthesizable from the post-2019 dataset (with the highest SC) is provided in the Supporting Information as Table S1.
Figure 4.

Validation via experimental post-synthesis of predicted compounds. Four materials with a negative tag (no ICSD ID) in the MP database are confirmed to be synthesizable or to be stable in DFT calculations. (a) Cs2AgSbBr6,46 (b) BaHfO3,47 and (c) Cs2InAgCl648 are synthesized and reported in the literature. (d) LaMoN3 is a stable compound according to DFT calculations.49 All four crystal structure figures are created using CIF files from the MP database20 and the Visualization of Electronic and Structural Analysis (VESTA) software package.50
Polymorphs and SC Model Validation
As mentioned in the previous section, DFT and DFT-calculated properties are not sufficient to determine the synthesizability of polymorphs with similar energy values. On the other hand, the SC model can distinguish polymorphs because it uses the crystal structure as part of the input to predict the SC. In this final validation section, we trained SC models on different training sets (excluding all targeted polymorphs) and tested different sets of targeted polymorphs. Table 2 shows the SC predictions of all AgClO2 polymorphs in the MP database. Formation energy values of each AgClO2 polymorph range between −0.2 and −0.4 eV/atom, which is not sufficient to determine the synthesizability of all polymorphs. On the other hand, our SC model correctly predicts both materials with ICSD IDs (column shaded green) while maintaining a large decision boundary between the synthesizable materials (higher than 0.4) and not synthesizable materials (all lower than 0.1). More material validation related to polymorphs can be found in the Supporting Information.
Table 2. SC Results of AgClO2 Polymorphs in the MP Database.
Conclusions
We used a combination of crystal representation and a deep learning-based machine learning technique to predict synthesizability by utilizing the existing databases computational and experimental inorganic compounds. The combination of real-space features and reciprocal-space features encodes the compositional information, crystal structure, and crystal periodicity. Our ML model learns synthesizability-related features from the crystal input and outputs high-accuracy synthesizability predictions: 82.6/80.6% precision/recall for ternary inorganic compounds and 82.3/74.8 precision/recall for quaternary compounds. The prediction model trained and tested on the pre-2015 dataset achieved an even better result of 90.3% precision and 90.2% recall, which indicates that the pre-2015 dataset is more balanced and well studied. The “0” synthesizability tag of materials from the MP database stands for the absence of an ICSD ID, but it does not mean these materials are not synthesizable. In the post-2015 dataset, 70% of all materials have tag “0,” but 55% of these materials are predicted to be synthesizable, which indicates there are a large amount of undiscovered synthesizable materials in the database without an ICSD ID. We validated this hypothesis by finding materials with tag “0” but experimentally synthesized and reported after 2015. With the flexibility of taking any inorganic crystal as input and fast calculation time, our SC model can be an accurate synthesizability filter for generative models for new materials discovery.
Acknowledgments
We acknowledge Shyue Ping Ong from UCSD for discussions and validation of our idea during the “Matminer” seminar series based in Singapore. K.H. acknowledges funding from the Accelerated Materials Development for Manufacturing Program at A*STAR via the AME Programmatic Fund by the Agency for Science, Technology and Research under Grant No. A1898b0043. K.H. also acknowledges funding from the NRF Fellowship NRF-NRFF13-2021-0011. T.B. and Z.R. acknowledge support by the National Research Foundation, Prime Minister’s Office, Singapore, under its Campus for Research Excellence and Technological Enterprise (CREATE) program through the Singapore–Massachusetts Institute of Technology (MIT) Alliance for Research and Technology’s Low Energy Electronic Systems research program.
Data Availability Statement
The train and test datasets were queried from the Materials Project20 in March 2021. Source codes, training data, and trained parameters are available at https://github.com/RaymondZhurm/SC_model.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c04856.
Test set performance (precision and recall) against the number of training epoch; training and validation set binary cross entropy loss against the number of training epoch; receiver operating characteristic (ROC) curve of ternary SC models; precision recall curve of ternary SC models; convolution neural network of ternary SC models; list of 100 materials (without ICSD ID) which have the highest SC prediction in the post-2019 dataset; SC results of TiCdO3 polymorphs in the MP database (PDF)
Author Contributions
K.H. conceived the research. R.Z. worked closely with S.I.P.T., Z.R., and J.L. and developed and tested the crystal representation and the variational autoencoder, with key intellectual contributions from T.B. and K.H. K.H. and R.Z. wrote the manuscript, with input from all co-authors.
The authors declare the following competing financial interest(s): Some of the authors hold equity in a start-up designed to accelerate the development of materials using machine learning methods.
Supplementary Material
References
- Ono S.; Satomi H. High-throughput computational search for two-dimensional binary compounds: Energetic stability versus synthesizability of three-dimensional counterparts. Phys. Rev. B 2021, 103, L121403 10.1103/PhysRevB.103.L121403. [DOI] [Google Scholar]
- Alberi K.; Nardelli M. B.; Zakutayev A.; et al. The 2019 materials by design roadmap. J. Phys. D: Appl. Phys. 2019, 52, 013001 10.1088/1361-6463/aad926. [DOI] [Google Scholar]
- Sun W.; Dacek S. T.; Ong S. P.; et al. The Thermodynamic Scale of Inorganic Crystalline Metastability. Sci. Adv. 2016, e1600225 10.1126/sciadv.1600225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aykol M.; Dwaraknath S. S.; Sun W.; Persson K. A. Thermodynamic Limit for Synthesis of Metastable Inorganic Materials. Sci. Adv. 2018, eaaq0148 10.1126/sciadv.aaq0148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartel C. J.; Millican S. L.; Deml A. M.; et al. Physical descriptor for the Gibbs energy of inorganic crystalline solids and temperature-dependent materials chemistry. Nat. Commun. 2018, 9, 4168 10.1038/s41467-018-06682-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athayde D. D.; Souza D. F.; Silva A. M. A.; et al. Review of perovskite ceramic synthesis and membrane preparation methods. Ceram. Int. 2016, 42, 6555–6571. 10.1016/j.ceramint.2016.01.130. [DOI] [Google Scholar]
- Rao C. N. R.; Ramakrishna Matte H. S. S.; Voggu R.; Govindaraj A. Recent progress in the synthesis of inorganic nanoparticles. Dalton Trans. 2012, 41, 5089–5120. 10.1039/c2dt12266a. [DOI] [PubMed] [Google Scholar]
- Davies D. W.; Butler K. T.; Jackson A. J.; et al. Computational Screening of All Stoichiometric Inorganic Materials. Chem. 2016, 1, 617–627. 10.1016/j.chempr.2016.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies D.; Butler K.; Jackson A.; Skelton J.; Morita K.; Walsh A. SMACT: Semiconducting Materials by Analogy and Chemical Theory. J. Open Source Software 2019, 4, 1361. 10.21105/joss.01361. [DOI] [Google Scholar]
- Sun S.; Hartono N. T. P.; Ren Z. D.; et al. Accelerated Development of Perovskite-Inspired Materials via High-Throughput Synthesis and Machine-Learning Diagnosis. Joule 2019, 3, 1437–1451. 10.1016/j.joule.2019.05.014. [DOI] [Google Scholar]
- Wei J.; Chu X.; Sun X.; et al. Machine learning in materials science. InfoMat 2019, 1, 338–358. 10.1002/inf2.12028. [DOI] [Google Scholar]
- Neugebauer J.; Hickel T. Density functional theory in materials science. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2013, 3, 438–448. 10.1002/wcms.1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schleder G. R.; Padilha A. C. M.; Acosta C. M.; Costa M.; Fazzio A. From DFT to machine learning: Recent approaches to materials science - A review. J. Phys. Mater. 2019, 2, 032001 10.1088/2515-7639/ab084b. [DOI] [Google Scholar]
- Hafner J. Materials simulations using VASP-a quantum perspective to materials science. Comput. Phys. Commun. 2007, 177, 6–13. 10.1016/j.cpc.2007.02.045. [DOI] [Google Scholar]
- Burke K.; Wagner L. O. DFT in a nutshell. Int. J. Quantum Chem. 2013, 113, 96–101. 10.1002/qua.24259. [DOI] [Google Scholar]
- Kohn W.; Becke A. D.; Parr R. G. Density Functional Theory of Electronic Structure. J. Phys. Chem. A 1996, 12974. 10.1021/jp960669l. [DOI] [Google Scholar]
- Jiang B.; Yu Y.; Cui J.; et al. High-entropy-stabilized chalcogenides with high thermoelectric performance. Science 2021, 371, 830–834. 10.1126/science.abe1292. [DOI] [PubMed] [Google Scholar]
- Kirklin S.; Saal J. E.; Meredig B.; et al. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015, 15010 10.1038/npjcompumats.2015.10. [DOI] [Google Scholar]
- Emery A. A.; Wolverton C. High-Throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO 3 perovskites. Sci. Data 2017, 4, 170153 10.1038/sdata.2017.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain A.; Ong S. P.; Hautier G.; et al. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002 10.1063/1.4812323. [DOI] [Google Scholar]
- Li W.; Jacobs R.; Morgan D. Predicting the thermodynamic stability of perovskite oxides using machine learning models. Comput. Mater. Sci. 2018, 150, 454–463. 10.1016/j.commatsci.2018.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malyi O. I.; Sopiha K. V.; Persson C. Energy, Phonon, and Dynamic Stability Criteria of Two-Dimensional Materials. ACS Appl. Mater. Interfaces 2019, 11, 24876–24884. 10.1021/acsami.9b01261. [DOI] [PubMed] [Google Scholar]
- Lai Z.; He Q.; Tran T. H.; et al. Metastable 1T′-phase group VIB transition metal dichalcogenide crystals. Nat. Mater. 2021, 20, 1113–1120. 10.1038/s41563-021-00971-y. [DOI] [PubMed] [Google Scholar]
- Satoh N.; Nakashima T.; Yamamoto K. Metastability of anatase: Size dependent and irreversible anatase-rutile phase transition in atomic-level precise titania. Sci. Rep. 2013, 3, 1959 10.1038/srep01959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu G.; Guo X.; Wang L. Review of recent progress in chemical stability of perovskite solar cells. J. Mater. Chem. A 2015, 3, 8970–8980. 10.1039/c4ta04994b. [DOI] [Google Scholar]
- Pickard C. J.; Errea I.; Eremets M. I. Superconducting Hydrides under Pressure. Annu. Rev. Condens. Matter Phys. 2020, 11, 57–76. 10.1146/annurev-conmatphys-031218-013413. [DOI] [Google Scholar]
- Dean C. R.; Young A. F.; Meric I.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. 10.1038/nnano.2010.172. [DOI] [PubMed] [Google Scholar]
- Taniguchi T.; Watanabe K. Synthesis of high-purity boron nitride single crystals under high pressure by using Ba-BN solvent. J. Cryst. Growth 2007, 303, 525–529. 10.1016/j.jcrysgro.2006.12.061. [DOI] [Google Scholar]
- Sun W.; Dacek S. T.; Ong S. P.; et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2016, 2, e1600225 10.1126/sciadv.1600225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saal J. E.; Kirklin S.; Aykol M.; Meredig B.; Wolverton C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. 10.1007/s11837-013-0755-4. [DOI] [Google Scholar]
- Curtarolo S.; Setyawan W.; Hart G. L. W.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 2012, 58, 218–226. 10.1016/j.commatsci.2012.02.005. [DOI] [Google Scholar]
- Lotfi S.; Zhang Z.; Viswanathan G.; Fortenberry K.; Mansouri Tehrani A.; Brgoch J. Targeting Productive Composition Space through Machine-Learning-Directed Inorganic Synthesis. Matter 2020, 3, 261–272. 10.1016/j.matt.2020.05.002. [DOI] [Google Scholar]
- Xie T.; Grossman J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 145301 10.1103/PhysRevLett.120.145301. [DOI] [PubMed] [Google Scholar]
- Saidi W. A.; Shadid W.; Castelli I. E. Machine-learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network. npj Comput. Mater. 2020, 6, 36 10.1038/s41524-020-0307-8. [DOI] [Google Scholar]
- Pilania G.; Mannodi-Kanakkithodi A.; Uberuaga B. P.; Ramprasad R.; Gubernatis J. E.; Lookman T. Machine learning bandgaps of double perovskites. Sci. Rep. 2016, 6, 19375 10.1038/srep19375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong J.; Zhang T. Y.; Shi S. Q. Machine learning of mechanical properties of steels. Sci. China Technol. Sci. 2020, 63, 1247–1255. 10.1007/s11431-020-1599-5. [DOI] [Google Scholar]
- Evans J. D.; Coudert F. X. Predicting the Mechanical Properties of Zeolite Frameworks by Machine Learning. Chem. Mater. 2017, 29, 7833–7839. 10.1021/acs.chemmater.7b02532. [DOI] [Google Scholar]
- Choudhary K.; DeCost B. Atomistic Line Graph Neural Network for improved materials property predictions. npj Comput. Mater. 2021, 7, 185 10.1038/s41524-021-00650-1. [DOI] [Google Scholar]
- Wang A.-T.; Kauwe S. K.; Murdock R. J.; Sparks T. D. Compositionally restricted attention-based network for materials property predictions. npj Comput. Mater. 2021, 7, 77 10.1038/s41524-021-00545-1. [DOI] [Google Scholar]
- Li H.; Lee S. R.; Luo M.; Sullivan C. R.; Chen Y.; Chen M. In MagNet: A Machine Learning Framework for Magnetic Core Loss Modeling, 2020 IEEE 21st Work Control Model Power Electron COMPEL 2020, 2020.
- Jha D.; Ward L.; Paul A.; et al. ElemNet: Deep Learning the Chemistry of Materials From Only Elemental Composition. Sci. Rep. 2018, 8, 17593 10.1038/s41598-018-35934-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren Z.; Tian S. I. P.; Noh J.; et al. An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 2022, 5, 314–335. 10.1016/j.matt.2021.11.032. [DOI] [Google Scholar]
- Jang J.; Gu G. H.; Noh J.; Kim J.; Jung Y. Structure-Based Synthesizability Prediction of Crystals Using Partially Supervised Learning. J. Am. Chem. Soc. 2020, 142, 18836–18843. 10.1021/jacs.0c07384. [DOI] [PubMed] [Google Scholar]
- Hellenbrandt M. The inorganic crystal structure database (ICSD) - Present and future. Crystallogr. Rev. 2004, 10, 17–22. 10.1080/08893110410001664882. [DOI] [Google Scholar]
- Ong S. P.; Richards W. D.; Jain A.; et al. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
- Wei F.; Deng Z.; Sun S.; et al. Enhanced visible light absorption for lead-free double perovskite Cs2AgSbBr6. Chem. Commun. 2019, 55, 3721–3724. 10.1039/c9cc01134j. [DOI] [PubMed] [Google Scholar]
- Kegler V. D.; Cristina F. S. Synthesis of BaHfO3 through with reduction of KOH. Int. J. Adv. Eng. Res. Sci. 2018, 5, 349–352. 10.22161/ijaers.5.5.47. [DOI] [Google Scholar]
- Volonakis G.; Haghighirad A. A.; Milot R. L.; et al. Cs2InAgCl6: A New Lead-Free Halide Double Perovskite with Direct Band Gap. J. Phys. Chem. Lett. 2017, 8, 772–778. 10.1021/acs.jpclett.6b02682. [DOI] [PubMed] [Google Scholar]
- Sarmiento-Pérez R.; Cerqueira T. F. T.; Körbel S.; Botti S.; Marques M. A. L. Prediction of Stable Nitride Perovskites. Chem. Mater. 2015, 27, 5957–5963. 10.1021/acs.chemmater.5b02026. [DOI] [Google Scholar]
- Momma K.; Izumi F.. VESTA: a Three-Dimensional Visualization System, Published online, 2013, pp 1–2.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The train and test datasets were queried from the Materials Project20 in March 2021. Source codes, training data, and trained parameters are available at https://github.com/RaymondZhurm/SC_model.



