NOSER: An Algorithm for Solving the Inverse Conductivity Problem

Abstract

The inverse conductivity problem is the mathematical problem that must be solved in order for electrical impedance tomography systems to be able to make images. Here we show how this inverse conductivity problem is related to a number of other inverse problems. We then explain the workings of an algorithm that we have used to make images from electrical impedance data measured on the boundary of a circle in two dimensions. This algorithm is based on the method of least squares. It takes one step of a Newton’s method, using a constant conductivity as an initial guess. Most of the calculations can therefore be done analytically. The resulting code is named NOSER, for Newton’s One-Step Error Reconstructor. It provides a reconstruction with 496 degrees of freedom. The code does not reproduce the conductivity accurately (unless it differs very little from a constant), but it yields useful images. This is illustrated by images reconstructed from numerical and experimental data, including data from a human chest.

THE PROBLEM AND ITS CONNECTION WITH OTHER INVERSE PROBLEMS

Electrical impedance imaging systems apply currents to the surface S of a body B, measure the induced voltages at the surface, and from this information reconstruct an approximation to the conductivity in the interior [1-3]. The reader interested in background literature is referred to Ref. 4. Mathematically, this can be formulated as follows [5]: If u is the electric potential and σ the conductivity, then u satisfies

$$\nabla \cdot \sigma (\overrightarrow{p})\nabla u(\overrightarrow{p})=0\text{for}\overrightarrow{p}\text{in}B$$ (1)

$$\sigma (\overrightarrow{p})\frac{\partial u(\overrightarrow{p})}{\partial \nu }=j(\overrightarrow{p})\text{for}\overrightarrow{p}\text{on}S,$$ (2)

where ν denotes the outward unit normal to the body and j denotes the current density applied to the surface of the body. The amount of current leaving the body must be the same as the amount entering, which implies

$${\int }_{s}j(\overrightarrow{p})d{S}_p=0.$$ (3)

Electrical impedance imaging systems not only apply current, but also measure voltages on the boundary

$$u(\overrightarrow{p})=V(\overrightarrow{p})\text{for}\overrightarrow{p}\text{on}S.$$ (4)

For convenience, we choose the ground or reference potential so that

$${\int }_{s}V(\overrightarrow{p})d{S}_p=0.$$ (5)

The idealized inverse conductivity problem is this: Given all possible current densities j and their corresponding voltage distributions V, find the conductivity σ in the interior of the body.

This problem is closely related to a number of other inverse problems. For example, if we make the change of variables u = σ ^−1/2ψ, then ψ satisfies the Schrödinger equation

$$-{\nabla }^2\psi (\overrightarrow{p})+q(\overrightarrow{p})\psi (\overrightarrow{p})=0\text{in}B,$$

where

$$q(\overrightarrow{p})=\frac{{\nabla }^2{\sigma }^{1∕2}(\overrightarrow{p})}{{\sigma }^{1∕2}(\overrightarrow{p})}.$$

The relations between the inverse conductivity problem and an inverse boundary value problem for the Schrödinger equation are studied in Refs. 6-10. This inverse boundary value problem is, in turn, related to inverse scattering problems [11].

If we now make the further change of variables w = ρ^1/2Ψ, then w satisfies the acoustic equation

$$\nabla \cdot \frac{1}{\rho (\overrightarrow{p})}\nabla w(\overrightarrow{p})+{\omega }^2\kappa (\overrightarrow{p})w(\overrightarrow{p})=0\text{in}B,$$

where ρ, κ, and ω are related to q by

$$q(\overrightarrow{p})={\rho }^{1∕2}(\overrightarrow{p}){\nabla }^2\frac{1}{{\rho }^{1∕2}(\overrightarrow{p})}-{\omega }^2\kappa (\overrightarrow{p})\rho (\overrightarrow{p}).$$

The acoustic equation governs the pressure w in a fluid with density ρ and compressibility κ when it is probed by a time-harmonic wave of frequency ω. Acoustic inverse boundary value problems are thus also closely related to the inverse conductivity problem [6].

THE ACTUAL PROBLEM

The above mathematical model is an idealization. In practice, we cannot specify current densities, but rather only currents, which are applied through electrodes attached to the surface. Similarly, we can measure voltages only on these electrodes. There are a number of ways of modeling this situation [5, 12], but here we use only the above model (1)-(4), which we call the continuum model, and a second model, which accounts for the discretization effects of the electrodes as follows.

The “gap” model uses the same differential equation (1)) inside B, but it replaces the boundary condition (2) with

$$\sigma (\overrightarrow{p})\frac{\partial u(\overrightarrow{p})}{\partial \nu }=\{\begin{array}{cc}{I}_l∕A_l\hfill & \text{for}\overrightarrow{p}\in e_l,l=1,2,\dots ,L\hfill \\ 0\hfill & \text{for}\overrightarrow{p}\notin \underset{l=1}{\overset{L}{U}}{e}_l.\hfill \end{array}\phantom{\}}$$ (6)

Here L denotes the number of electrodes; e_l the lth electrode; I_l, the current sent to the lth electrode; and A_l the area of the lth electrode. This model for the boundary condition assumes that the current density is zero in the gaps between electrodes and is constant over the surface of each electrode. The conservation of charge condition (3) is replaced by the corresponding condition on the currents themselves:

$$\sum _{l=1}^L{I}_l=0.$$ (7)

The voltages that we measure are assumed to have the values of the potential at the center of each electrode:

$$u(\text{center of}{e}_l)=V_l.$$ (8)

We choose the ground so that

$$\sum _{l=1}^L{V}_l=0.$$ (9)

In this more realistic gap model formulation, the inverse conductivity problem becomes the following: Given all possible current patterns $\overrightarrow{I}=(I_1,\dots ,I_L)$ and their corresponding voltage patterns $\overrightarrow{V}=(V_1,\dots ,V_L)$, find the conductivity σ inside the body.

Unfortunately, this is impossible, for the following reason: There are only L − 1 linearly independent current patterns [L degrees of freedom minus one for the constraint (7)]. Any other current pattern must be a linear combination of L − 1 “basis” patterns. Because the differential equation (1) is linear, any voltage pattern must be a linear combination of L − 1 basis voltage patterns. Thus, we have only a finite number of linearly independent measurements. From a finite number of measurements, we cannot hope to obtain σ at every point in the interior of the body. We can only hope for an approximation to σ that depends on a finite number of parameters.

A simple finite-parameter approximation is one that is piecewise constant, and this is the approximation that the NOSER [13] code uses. The reconstruction is done on a particular mesh described below. The conductivity is assumed to be constant on each mesh element. Mathematically, this can be expressed as

$$\sigma (\overrightarrow{p})=\sum _{n=1}^N{\sigma }_n{\chi }_n(\overrightarrow{p}),$$ (10)

where ${\chi }_n(\overrightarrow{p})$ is the characteristic function that is 1 for $\overrightarrow{p}$ contained in the nth mesh element and zero otherwise.

The inverse problem can thus be stated as follows: Choose a basis of current patterns ${\overrightarrow{I}}^1$, ${\overrightarrow{I}}^2$, … , ${\overrightarrow{I}}^{L-1}$. For each current pattern ${\overrightarrow{I}}^k$, suppose we know the corresponding voltage pattern ${\overrightarrow{V}}^k$. From this information, find σ of the form (10), where σ is connected to each $\overrightarrow{I}$ and $\overline{V}$ by (1) and (6)-(9). It will turn out to be more convenient to work with the resistivity ρ, which is the reciprocal of the conductivity σ. Assumption (10) in terms of resistivity is

$$\rho (\overrightarrow{p})=\sum _{n=1}^N{\rho }_n{\chi }_n(\overrightarrow{p}).$$ (10a)

(The resistivity ρ is not related to the density ρ that we mentioned earlier.)

Here we will consider only two-dimensional problems, in fact, problems in which the body B is a disk of radius r₀. We use an even number of electrodes, which we assume to be of equal sizes so that A_l = A for all l. We center the lth electrode at the angular position

$$\theta ={\theta }_l=2\pi l∕L,l=1,2,\dots ,L.$$ (11)

MESH DESIGN

The design of the mesh on which we represent the conductivity or resistivity deserves careful attention [14]. This is because the ill-conditioning of the reconstruction is affected by the number, size, and position of the mesh elements.

That the size and position are important can be seen by noting that the boundary measurements are most sensitive to the parts of the disk near the boundary [15]. We therefore expect to obtain better resolution there, which implies that we should take smaller mesh elements near the boundary. On the other hand, we should not take mesh elements too small: If a mesh element is significantly smaller than the size of the smallest object that can be distinguished at that location, then the inverse problem will be worse conditioned, because many conductivity distributions will produce the same data. The size of the smallest distinguishable object is, in turn, determined by the measurement precision [15].

The number of mesh elements is also important. If we try to do the reconstruction on a mesh with more elements than the number of independent measurements, then the reconstruction problem will be underdetermined. What is the number of independent measurements? Since the relation between the $\overrightarrow{I}$’s and $\overrightarrow{V}$’s is linear, we can think of this relation as being given by a matrix, which must have dimensions (L − 1) × (L − 1). This matrix, however, is self-adjoint [14], which implies that it contains only L(L − 1)/2 degrees of freedom. [To obtain this number, subtract the number of diagonal elements, L − 1, from (L − 1)². This gives the number of off-diagonal elements. Divide by two to obtain the number of off-diagonal degrees of freedom, and then add the L − 1 diagonal degrees of freedom.] Thus, in order to avoid making our problem underdetermined, we should take

$$N\le \frac{L(L-1)}{2},$$ (12)

where L is the number of electrodes and N the number of mesh elements.

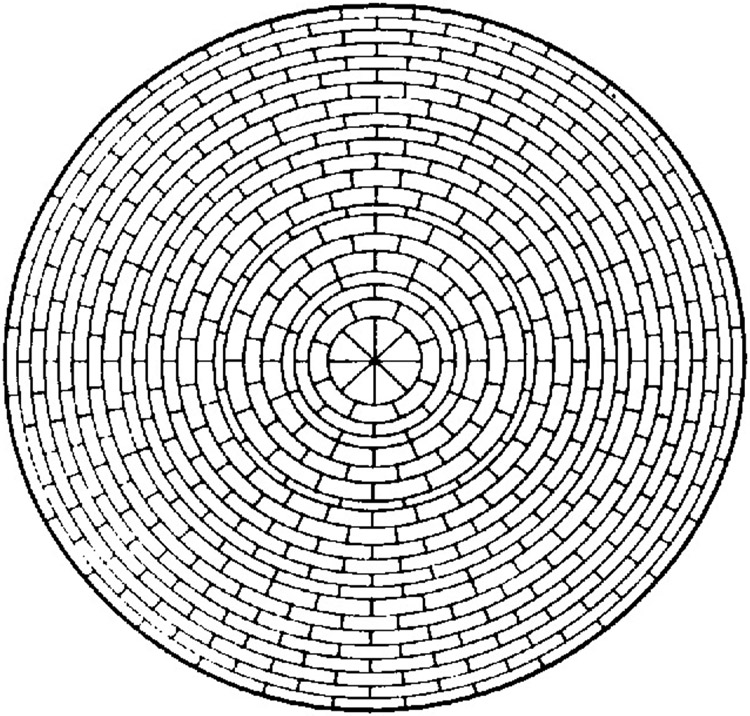
The mesh used by NOSER, dubbed the “Joshua tree” mesh, is shown in Figure 1. It has L = 32, N = 496, and can be specified by giving radial and angular subdivisions.

Figure 1.

The 496-element mesh used for the reconstructed resistivity distributions shown in Figures 2, 4, and 6.

THE PLAN: LEAST SQUARES

To get a full set of measurements, we apply a full set of basis current patterns ${\overrightarrow{I}}^1$, ${\overrightarrow{I}}^2$, … , ${\overrightarrow{I}}^{L-1}$. For simplicity, we use a basis of trigonometric patterns ${\overrightarrow{I}}^k=(I_1^k,I_2^k,\dots ,I_L^k)$, where

$$I_l^k=T_l^k=\{\begin{array}{c}\cos k{\theta }_l,k=1,2,\dots ,L∕2\hfill \\ \sin (k-L∕2){\theta }_l,k=(L∕2)+1,\dots ,L-1.\hfill \end{array}\phantom{\}}$$ (13)

(Any other basis of current patterns can be decomposed into linear combinations of these trigonometric ones.) We denote the measured voltage patterns corresponding to these trigonometric current patterns by ${\overrightarrow{V}}^1$, ${\overrightarrow{V}}^2$, … , ${\overrightarrow{V}}^{L-1}$. Note that if we knew a resistivity of the form (10a). we could compute the voltages that would be produced by the trigonometric current patterns. These voltage patterns we denote by ${\overrightarrow{U}}^1(\overrightarrow{\rho })$, ${\overrightarrow{U}}^2(\overrightarrow{\rho })$, … , ${\overrightarrow{U}}^{L-1}(\overrightarrow{\rho })$, where we have written $\overrightarrow{\rho }$ as a shorthand for the N constants ρ₁, ρ₂, … ρ_N appearing in (10a). Our goal is to find $\overrightarrow{\rho }$ so that

$${\overrightarrow{U}}^k(\overrightarrow{\rho })={\overrightarrow{V}}^k,k=1,2,\dots ,L-1.$$ (14)

Unfortunately, we cannot hope to do this, for two reasons. First, there is no reason to think that the true resistivity is of the form (10a). Since (10) is only an approximation to the true resistivity, we expect that the resulting voltage pattern ${\overrightarrow{U}}^k(\rho )$ should be only an approximation to the voltage pattern ${\overrightarrow{V}}^k$. Second, even if the true resistivity were of the form (10a), we could not hope to satisfy (14) because the $\overrightarrow{V}$’s, in general, contain measurement errors. Thus, a resistivity that produces the $\overrightarrow{V}$’s may not even exist.

For these reasons, we do not try to find a resistivity that reproduces the measured voltages. Instead, we look for a resistivity $\overrightarrow{\rho }$ that minimizes the errors ${\overrightarrow{V}}^k-{\overrightarrow{U}}^k(\overrightarrow{\rho })$, k = 1, 2, … , L − 1. A convenient way to measure the total error is to take the sum of the squares of these differences:

$$E(\overrightarrow{\rho })=\sum _{k=1}^{L-1}\Vert {\overrightarrow{V}}^k-{\overrightarrow{U}}^k(\overrightarrow{\rho }){\Vert }^2=\sum _{k=1}^{L-1}\sum _{l=1}^L(V_l^k-U_l^k(\overrightarrow{\rho }){)}^2.$$ (15)

Minimizing this particular error functional is called the method of least squares [16].

It is certainly possible to use other error functionals [17-21]. Here, however, we consider only least squares.

We consider the error (15) as a function of N variables ρ₁, … , ρ_N. To minimize this function, we differentiate with respect to each variable and set each derivative to zero. This gives us the system of N equations:

$$0=\frac{\partial E(\overrightarrow{\rho })}{\partial {\rho }_n}=-2\sum _{k=1}^{L-1}\sum _{l=\mathrm{I}}^L(V_l^k-U_l^k(\overrightarrow{\rho }))\frac{\partial U_l^k(\overrightarrow{\rho })}{\partial {\rho }_n}.$$ (16)

If we denote the right side of the nth equation of (16) by $F_n(\overrightarrow{\rho })$, i.e.,

$$F_n(\overrightarrow{\rho })=\frac{\partial E(\overrightarrow{\rho })}{\partial {\rho }_n}=-2\sum _{k=1}^{L-1}\sum _{l=\mathrm{I}}^L(V_l^k-U_l^k(\overrightarrow{\rho }))\frac{\partial U_l^k(\overrightarrow{\rho })}{\partial {\rho }_n},$$ (17)

then we can rewrite (16) as the system

$$0=F_n({\rho }_1,\dots ,{\rho }_N),n=1,2,\dots ,N.$$ (18)

This is a system of N nonlinear equations in N variables. A standard method for solving such systems is Newton’s method.

NEWTON’S METHOD

Newton’s method for the case of a system of N equations in N variables is [16, 22, 23]

$${\overrightarrow{\rho }}^{\text{new}}={\overrightarrow{\rho }}^{\text{old}}-[{\overrightarrow{F}}^{\prime }({\overrightarrow{\rho }}^{\text{old}}){]}^{-1}\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}}).$$ (19)

Here the derivative of the vector $\overrightarrow{F}(\overrightarrow{\rho })$ is the Jacobian matrix

$$\begin{gathered} F_{n,m}^{\prime }(\overrightarrow{\rho })=\frac{\partial }{\partial {\rho }_m}\frac{\partial E(\overrightarrow{\rho })}{\partial {\rho }_n} \\ =2\sum _{k=1}^{L-1}\sum _{l=1}^L\frac{\partial U_l^k(\overrightarrow{\rho })}{\partial {\rho }_n}\frac{\partial U_l^k(\overrightarrow{\rho })}{\partial {\rho }_m} \\ -2\sum _{k=1}^{L-1}\sum _{l=1}^L(V_l^k-U_l^k(\overrightarrow{\rho }))\frac{{\partial }^2{U}_l^k(\overrightarrow{\rho })}{\partial {\rho }_n\partial {\rho }_m}. \end{gathered}$$ (20)

The overall plan of the NOSER code is to do one step of Newton’s method, using the initial guess ${\overrightarrow{\rho }}^{old}=\text{constant}$. For the initial guess, the vector $\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}})$ and matrix ${\overrightarrow{F}}^{\prime }({\overrightarrow{\rho }}^{\text{old}})$ can be obtained analytically. Finding ${\overrightarrow{\rho }}^{\text{new}}$ from (19) therefore involves only inverting the known matrix ${\overrightarrow{F}}^{\prime }({\overrightarrow{\rho }}^{\text{old}})$, applying the inverse to the known vector $\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}})$, and subtracting it from the known vector ${\overrightarrow{\rho }}^{\text{old}}$.

Before we consider how to obtain the quantities appearing in (19) from the data, we discuss the matrix F’.

MODIFICATION OF ${\overrightarrow{\mathit{F}}}^{\prime }$

It turns out that the matrix F’ is ill-conditioned, which means that some of its eigenvalues are large and some are very small. These small eigenvalues prevent us from computing the inverse of ${\overrightarrow{F}}^{\prime }$ numerically. Even if we could invert ${\overrightarrow{F}}^{\prime }$, the inverse matrix would have very large eigenvalues. If we were to apply this inverse matrix to $\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}})$, these large eigenvalues would cause small errors in $\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}})$ to be magnified tremendously.

To get around this problem, we need to modify ${\overrightarrow{F}}^{\prime }$ to get rid of its small eigenvalues. There are many ways to do this. The modification used in the NOSER code is based on the meaning of the two terms in the definition (20) of ${\overrightarrow{F}}^{\prime }$.

The first term of (20), namely.

$${\mathbf{A}}_{n,m}=2\sum _{k=1}^{L-1}\sum _{l=1}^L\frac{\partial U_l^k}{\partial {\rho }_n}\frac{\partial U_l^k}{\partial {\rho }_m},$$ (21)

can be understood as follows: If we apply the kth current pattern and calculate the voltage on the lth electrode, then $\partial U_l^k∕\partial {\rho }_n$ is the change in this voltage when we change the resistivity in the nth mesh element. Similarly, $\partial U_l^k∕\partial {\rho }_m$ results from changing the mth mesh element. If the nth and mth mesh elements are near each other, then the changes in voltage they produce will be nearly the same, so the product $(\partial U_l^k∕\partial {\rho }_n)(\partial U_l^k∕\partial {\rho }_m)$ will be positive. In particular, this is true if n = m. Suppose, on the other hand, that the nth and mth mesh elements are far from each other. Suppose, further, that the nth mesh element is close to the lth electrode, so it has a big effect on the voltage $U_l^k$, which means that $\partial U_l^k∕\partial {\rho }_n$ is relatively large. But then the mth mesh element must be far away from electrode l, so its effect $\partial U_l^k∕\partial {\rho }_m$ is small. Thus, the product $(\partial U_l^k∕\partial {\rho }_n)(\partial U_l^k∕\partial {\rho }_m)$ is small relative to $(\partial U_l^k∕\partial {\rho }_n)(\partial U_l^k∕\partial {\rho }_n)$ if the nth and mth mesh elements are far from each other. If the mesh is numbered so that nearby elements have close indices, then the matrix A, whose (n, m)th element is given by (21), has its largest elements on and near the diagonal.

Moreover, these diagonal elements are all positive. The largest diagonal elements are those corresponding to mesh elements near the boundary, and the smallest correspond to mesh elements near the center. This variation, between the smallest and largest diagonal elements, is of a reasonable size. In other words, the diagonal of A would itself be a well-conditioned matrix.

The second term of (20), namely,

$$B_{n,m}=-2\sum _{k=1}^{L-1}\sum _{l=1}^L(V_l^k-U_l^k(\overrightarrow{\rho }))\frac{{\partial }^2{U}_l^k(\overrightarrow{\rho })}{\partial {\rho }_n\partial {\rho }_m},$$ (22)

is more complicated to interpret and to compute. However, if our guess ${\overrightarrow{\rho }}^{\text{old}}$ is close to the true ρ, then the predicted voltages $U_l^k({\overrightarrow{\rho }}^{\text{old}})$ will be close to the measured voltages $V_l^k$ and B_n,m will be small. The Levenberg–Marquardt approximation [16] used by NOSER is to neglect this term entirely, replacing it by a multiple of the diagonal of A. Thus, we replace B_n,m by

$$\gamma {\mathbf{A}}_{n,m}{\delta }_{n,m},$$ (23)

where δ_n,m is the Kroenecker delta, which equals one if n = m and zero otherwise. Here, the parameter γ is to be chosen as small as practically possible.

Explicitly, the modified version of F’ that we use is

$${\mathbf{A}}_{n,m}+\gamma {\mathbf{A}}_{n,m}{\delta }_{n,m}.$$ (24)

By taking γ large enough, we can force the modified ${\overrightarrow{F}}^{\prime }$ to be diagonally dominant and positive definite. Since the diagonal matrix A_n,mδ_n,m is well conditioned, by taking γ large enough, we improve the conditioning of the modified ${\overrightarrow{F}}^{\prime }$. Moreover, this modification allows us to avoid computing the second derivatives that appear in ${\overrightarrow{F}}^{\prime }$. Because we throw away these second derivatives, and because we take only one step of Newton’s method, our algorithm can also be thought of as finding an approximate solution to the linearized problem. In particular, this algorithm can be viewed as a regularized solution of the least-squares minimization of the linear problem.

The parameter γ was selected empirically to produce a suitable balance between stability on the one hand and image contrast and definition on the other. The choice was made by simulating analytically a data set representing a highly conductive disc of medium size centered in a circular homogeneous region. These data were then used to make conductivity reconstructions for different values of γ. When γ was less then about 0.005, the reconstructed conductivity overshot the discontinuity by more than 20%. At even lower values of γ, the instability made the reconstruction unusable. For values of γ more than about 0.02, the reconstruction smoothed the discontinuity excessively; in other words, the image was dull and blurred. The value 0.01 was therefore chosen for γ for all reconstructions reported here. The images would differ appreciably from those presented if γ were to vary by more than approximately 50% in either direction.

HOW TO DO THE COMPUTATIONS

We now turn to the matter of computing the quantities in (19) needed for one step of a Newton iteration. We need to understand the following:

1. How to pick ${\overrightarrow{\rho }}^{\text{old}}$.

2. How to compute $U_l^k({\overrightarrow{\rho }}^{\text{old}})$.

3. How to compute $\frac{\partial U_l^k({\overrightarrow{\rho }}^{\text{old}})}{\partial {\rho }_n}$.

Once we know how to do these three things, we can compute ${\overrightarrow{F}}^{\prime }({\overrightarrow{\rho }}^{\text{old}})$ from (17). We can then compute A from (21), and from A, we obtain the modified version of ${\overrightarrow{F}}^{\prime }$ from (24). It is this modified version of ${\overrightarrow{F}}^{\prime }$ that we invert and apply to $\overrightarrow{F}({\overrightarrow{\rho }}^{\text{old}})$ in (19).

1. How to Pick ${\overrightarrow{\rho }}^{\mathbf{old}}$.

We have decided to take ${\overrightarrow{\rho }}^{\text{old}}=c(1,1,\dots ,1)$ for some scalar c. How should we choose c?

To find c, we again use the method of least squares. We use the same functional as before, namely (15), with $\overrightarrow{\rho }=c\overrightarrow{1}$, where $\overrightarrow{1}=(1,1,\dots ,1)$. The expression on the right-hand side of (15) simplifies for this special resistivity: Because the differential equation (1) is linear, multiplying the resistivity 1 by the constant c causes the voltage to be multiplied by c. In symbols,

$$U_l^k(c\overrightarrow{1})=c{U}_l^k(\overrightarrow{1}).$$ (25)

Thus, the error functional (15) can be written

$$E(c\overrightarrow{1})=\sum _{k=1}^{L-1}\sum _{k=l}^L(V_l^k-c{U}_l^k(\overrightarrow{1}){)}^2.$$ (26)

Again, we minimize the error by differentiating and setting the derivative to zero. This time, however, the differentiation is with respect to c and can be done easily:

$$O=\frac{dE}{dc}=-2\sum _{k=1}^{L-1}\sum _{l=1}^L[V_l^k-c{U}_l^k(\overrightarrow{1})]U_l^k(\overrightarrow{1}).$$

Solving for c, we obtain

$$c=\sum _{k=1}^{L-1}\sum _{l=1}^L(V_l^k{U}_l^k(\overrightarrow{1}))/\sum _{k=1}^{L-1}\sum _{l=1}^L[U_l^k(\overrightarrow{1}){]}^2.$$ (27)

Thus, we see that we should choose our first guess ${\overrightarrow{\rho }}^{\text{old}}=c\overrightarrow{1}$, where c is given by (27). To compute the right-hand side of (27) from the data, we need to know how to find $U_l^k(\overrightarrow{1})$.

2. How to Find ${\mathit{U}}_{\mathit{l}}^{\mathit{k}}(\overrightarrow{1})$.

The voltage $U_l^k(\overrightarrow{1})$ is the voltage on the lth electrode due to the trigonometric current pattern (13) and the resistivity that is the constant 1. To find the voltage, we must first choose the mathematical model we wish to use. The more accurate models [5, 12] give better reconstructions with fewer boundary effects, but we do not discuss in this paper all the modifications to the algorithm necessary to incorporate these more accurate models. For example, if we use the gap model, then we use (6) to find the current density corresponding to the trigonometric current pattern (13). Here, for simplicity, we use only the continuum model, so that the corresponding current density is

$$\frac{\partial u^k}{\partial r}(r_0,\theta )=\{\begin{array}{c}\cos k\theta ,k=1,2,\dots ,L∕2\hfill \\ \sin [(k-L∕2)\theta ],k=L∕2+1,\dots ,L-1,\hfill \end{array}\phantom{\}}$$ (28)

on S.

In either case, once the current density on the boundary is known, the boundary value problem (1), (2) can be solved by separation of variables. This straightforward procedure (which we omit) gives the Fourier series for the potential u in terms of the Fourier series for the current density. In the case of the continuum model, the result is especially simple:

$$u^k(r,\theta )=r_0\{\begin{array}{c}\frac{\cos k\theta }{k}{\left(\frac{r}{r_0}\right)}^k,k=1,2,\dots ,L∕2\hfill \\ \frac{\sin [(k-L∕2)\theta ]}{k-L∕2}{\left(\frac{r}{r_0}\right)}^{k-L∕2},k=(L∕2)+1,\dots ,L-1.\hfill \end{array}\phantom{\}}$$ (29)

The voltage $U_l^k(\overrightarrow{1})$ on the lth electrode is taken to be the potential at the center of the electrode:

$$U_l^k(\overrightarrow{1})=u^k(r_0,{\theta }_l)=\{\begin{array}{c}\frac{r_0}{k}{T}_l^k,k=1,2,\dots ,L∕2\hfill \\ \frac{r_0}{k-L∕2}{T}_l^k,k=L∕2+1,\dots ,L-1.\hfill \end{array}\phantom{\}}$$ (30)

To obtain $U_l^k({\overrightarrow{\rho }}^{\text{old}})$, we merely use (25).

3. How to Find $[\partial {\mathit{U}}_{\mathit{l}}^{\mathit{k}}({\overrightarrow{\rho }}^{\mathbf{old}})]∕\partial {\rho }_{\mathit{n}}$.

We compute the vector $\partial {\overrightarrow{U}}^k({\overrightarrow{\rho }}^{\text{old}})∕\partial {\rho }_n$ by expanding it in the trigonometric basis (13):

$$\frac{\partial {\overrightarrow{U}}^k}{\partial {\rho }_n}=\sum _{s=1}^{L-1}\frac{\langle {\overrightarrow{T}}^s,\frac{\partial U^k}{\partial {\rho }_n}\rangle }{\langle {\overrightarrow{T}}^s,{\overrightarrow{T}}^s\rangle }{\overrightarrow{T}}^s,$$ (31)

where the brackets denote the usual inner product

$$\langle \overrightarrow{W},\overrightarrow{X}\rangle =\sum _{l=1}^L{W}_l{X}_l.$$

The inner products in the denominator of (31) are merely normalization factors:

$$\begin{gathered} \langle {\overrightarrow{T}}^s,{\overrightarrow{T}}^s\rangle \\ =\{\begin{array}{cc}L∕2\hfill & s=1,2,\dots ,(L∕2)-1,(L∕2)+1,\dots ,L-1\hfill \\ L\hfill & s=L∕2.\hfill \end{array}\phantom{\}} \end{gathered}$$ (32)

In the appendix, we show that for a conductivity of the form (10),

$$\langle {\overrightarrow{T}}^s,\frac{\partial {\overrightarrow{U}}^k(\overrightarrow{\rho })}{\partial {\rho }_n}\rangle \approx \frac{1}{{\rho }_n^2}{\int }_{M_n}\nabla u^k\cdot \nabla u^s,$$ (33)

where M_n is the nth mesh element and where u^k is the solution to the problem (1), (6), (13).

This solution u^k has been calculated analytically for the constant resistivity $\overrightarrow{\rho }=\overrightarrow{1}$. To obtain u^k for $\overrightarrow{\rho }=c\overrightarrow{1}$, we simply multiply (29) by c.

With u^k given in a form like (29), it is useful to write the derivatives in (33) in polar coordinates as well:

$$\langle {\overrightarrow{T}}^s,\frac{\partial U^k}{\partial {\rho }_n}({\overrightarrow{\rho }}^{\text{old}})\rangle \approx \frac{1}{{\rho }_n}{\int }_{M_n}\left(\frac{\partial u^k}{\partial r}\frac{\partial u^s}{\partial r}+\frac{1}{r^2}\frac{\partial u^k}{\partial \theta }\frac{\partial u^s}{\partial \theta }\right).$$ (34)

The differentiations in (34) result in an integrand that is a product of a function of r times a function of θ. For a mesh element determined by radial and angular subdivisions, the integration results in a simple expression. We omit these straightforward calculations, but caution that there are a number of different cases.

NOSER IMPLEMENTATION

In this section, we describe a portable fortran77 implementation of the NOSER algorithm and tabulate some typical results from these computations. In general, run times are dominated by computation of the Jacobian and Hessian matrices of the error functional E. These are F [Eq. 17] and F’ [Eq. (24)], respectively. As noted, however, we can expand these in the trigonometric basis (13) and manipulate the derivatives so that much of the computational effort is dependent only on the mesh geometry. These terms can be precomputed and stored. This has been done for the implementation whose results are reported here.

With this enhancement, the computation becomes dominated by the solution of the linear system. This is done conventionally, using the linpack routines dsifa and dsisl for factorization and solution, respectively. As expected, the reconstruction time for a single iteration behaves as O(L³), in L, the number of electrodes. Typical run times (in seconds) for several machines on a 32-electrode problem are displayed in Table I.

Table I.

Some Typical Run times for NOSER.

Machine	Operating system	CPU utilization
IBM 3090 w/VF	AIX	10.9
SUN 4/150	SunOs	181.3
Cray Y/MP	UNICOS	2.2

IMAGES MADE BY NOSER

In this section, we discuss some examples of reconstructions made by NOSER. The first set of examples are reconstructions made from analytically generated data. We began with an assumed conductivity distribution composed of a body of constant resistivity, in this case 500 Ω cm, containing a concentric “target,” a disk of resistivity 50 Ω cm. For this simple conductivity distribution, we solved the boundary value problem (1), (2) analytically. We then used this data as input to NOSER. This avoids problems of experimental error and effects of the electrodes and, thus, provides a good test of the algorithm itself.

The results are shown in Figure 2, which contains reconstructions of targets of diameters 2, 4, 8, and 16 cm, respectively, in a body of diameter 2r₀ = 30 cm. The top row in Figure 2 is a drawing of the tank and the targets studied. The bottom row is the reconstructed resistivity distribution. The reconstructions are exhibited on gray scales chosen so that the range from black to white represents a resistivity difference of 40 Ω cm. Each reconstruction, however, has its own gray scale, i.e., black represents a different resistivity on each picture.

Figure 2.

Reconstructed resistivity distributions for analytically derived data sets simulating targets of 1, 2-, 4-, and 8-cm radii in a field of 15-cm radius. Target resistivity was 50 Ω cm in a field of 500 Ω cm. The resistivity scale is from 460 Ω cm (black) to 500 Ω cm (white).

To see how the reconstructions compare with each other, one should look at Figure 3, which shows slices through the different reconstructions. The vertical bar on each curve shows the true size and location of the target. When the reconstruction algorithm is free to choose the best value of average resistivity, the presence of a large conductive target lowers the estimate of the background resistivity. For this reason, the algorithm was constrained to give a background resistivity of 500 Ω cm in figure 3. We do not show a picture of the reconstruction obtained when there is no target. For analytic data from a homogeneous disk, NOSER produces a reconstruction that is homogeneous to within a fraction of an Ω cm. One can also see from Figure 3 that a sufficiently small target will not be detectable. The oscillations appearing in the reconstruction of the largest target disappear if γ is increased to 0.05. For large targets, the maximum difference in reconstructed conductivity between the inhomogeneity and the background is about 35 Ω cm. However, the true difference in conductivity is 450 Ω cm. Clearly, the reconstructed conductivities are not accurate. Nevertheless, the images show approximately the size and location of the inhomogeneities.

Figure 3.

Profiles of the resistivity vs. radius of the reconstructions shown in Figure 2.

The next set of examples are from data collected experimentally with the Rensselaer ACT 2 system [2]. The tests were made using a cylindrical tank of diameter 30 cm with 32 metal electrodes attached around the periphery. The tank was filled with a saline solution of conductivity about 150 Ω cm. and cylindrical targets were placed in it (Fig. 4). Since the test tank has no vertical variation, the experimental setup simulates a two-dimensional system.

Figure 4.

Reconstructed resistivity distributions for 33-mm diameter insulating and conducting targets in a 300-mm diameter saline tank having a conductivity of about 150 Ω cm. The middle row of images are the conductivity distributions yielded by NOSER for a tank with no target, one centered insulator, two insulators, and a conductor/insulator pair as shown in the top row. The resistivity scale is from 142 Ω cm (blue) to 158 Ω cm (red). The bottom row of images are the difference in resistivity between the image above, with a target, and the upper left image, with no target present. The resistivity scale for the bottom row is from −8 Ω cm (blue) to 9 Ω cm (red).

The first image is a reconstruction of the homogeneous tank, with no targets in the middle. It shows that the ACT 2 system introduces errors, which are not compensated for in NOSER. The second image is a reconstruction of the tank with an insulating target of diameter 3.2 cm. Immediately below this picture is a difference image formed by subtracting the reconstruction of the homogeneous tank from the raw image above it. This has the effect of partially removing the errors due to improper modeling of the boundary and unmodeled errors in the instrumentation. The third image in Figure 4 is a reconstruction of the tank with two insulating targets, each of diameter 3.2 cm, and below it, its difference image (again formed by subtracting the homogeneous reconstruction). The last image is a reconstruction of the tank with an insulator and a conductor of the same dimensions as before, and below it, its difference image. In all four of the pictures in the middle row, the unmodeled presence of electrodes at the periphery appears as a ring of low resistivity (blue). Since the electrodes are present in all of these images, including the background, their effect is not seen in the difference images in the bottom row. Other artifactual inhomogeneities in the raw reconstructions also disappear in the subtractions. All the images in Figure 4 are displayed on the same color scale. Again we see that targets of higher or lower conductivity pull the background up or down.

To see what the colors in Figure 4 represent, one can look at Figure 5, which displays slices through the three difference images in Figure 4. Note that the maximum contrast for the single, centered insulator, about 4 Ω cm, is consistent with the results in Figure 3 for a similar-sized target.

Figure 5.

Profiles of resistivity vs. radius of the difference images shown in the bottom row of Figure 4.

The final set of examples we show here are reconstructions of the chest of a human volunteer. Thirty-two karaya-gum-faced foil electrodes were attached in a plane around the chest above the nipples (level T7). Data were collected using the Rensselaer ACT 2 system, which required about 30 s to acquire enough data for a reconstruction. Measured amounts of air were introduced into the lungs of the subject, who then held his breath for the 30 s of data collection.

The results are shown in Figure 6. First, we discuss the top row of pictures. The leftmost is a reconstruction of the chest with no air added to the lungs. The second corresponds to 500 ml of added air, the third to 1000 ml, and the fourth to 1500 ml. In each case, the front of the chest is at the bottom of the picture and the left side of the chest is at the right. In these images, one can see clearly a bright, low conductivity layer around the boundary, which might correspond to skin and fat. At the bottom of each image appear a number of bright spots whose locations do not change as air is added. These may be the ribs. Areas just to the left and right of center are probably lungs: These areas grow brighter or less conductive as more air is added to the lungs.

Figure 6.

Reconstructions at a section of the chest of a human subject at different lung volumes. Top row, left to right: 0, 500, 1000, and 1500 mL of air added above normal resting lung volume. Bottom row: Changes in resistivity from the levels seen at resting lung volume. In the top row, the scale is from 345 Ω cm (black) to 465 Ω cm (white). The difference images are on a scale of −12 Ω cm (black) to 38 Ω cm (white).

The second row of pictures in Figure 6 are difference images. These are obtained by subtracting the 0-ml image from the image directly above. The greatest conductivity change occurs in the region where the lungs should be located. These images may be useful even though the human volunteer is neither two-dimensional nor circular.

CONCLUSION

We have described a simple algorithm for producing qualitative impedance images. We have illustrated the performance of the algorithm on numerical and experimental data.

APPENDIX

Here we explain some tricks that allow us to compute $\langle {\overrightarrow{T}}^s,(\partial {\overrightarrow{U}}^k∕\partial {\rho }_n)(\rho )\rangle$, which we denote by $Y_{s,k}^n(\rho )$. First, we recall that the components of ${\overrightarrow{U}}^k(\rho )$ are the values, at the centers of the electrodes, of the solution u^k to the problem (1), (6), (13). The inner product $\langle {\tilde{T}}^s,{\overrightarrow{U}}^k(\rho )\rangle$ is thus a discrete approximation to the integral

$${\int }_S{u}^k\sigma \frac{\partial u^s}{\partial \nu }dS={\int }_B\sigma \nabla u^k\cdot \nabla u^s,$$ (A1)

where we have obtained the right side of (A1) by multiplying the equation for u^s by u^k and using the divergence theorem. We can therefore approximate $Y_{s,k}^n$ by differentiating the right side of (A1):

$$Y_{s,k}^n\equiv \langle {\overrightarrow{T}}^s,\frac{\partial {\overrightarrow{U}}^k}{\partial {\rho }_n}(\rho )\rangle \approx \frac{\partial }{\partial {\rho }_n}{\int }_B\sigma \nabla u^k\cdot \nabla u^s.$$ (A2)

The right side of (A2), however, can be reduced to a simple, easily calculated expression as follows:

Claim.

$$\frac{\partial }{\partial {\rho }_n}{\int }_B\sigma \nabla u^k\cdot \nabla u^s=-{\int }_B\frac{\partial \sigma }{\partial {\rho }_n}\nabla u^k\cdot \nabla u^s.$$ (A3)

Proof. We differentiate the left side of (A3) using the product rule:

$$\begin{gathered} \frac{\partial }{\partial {\rho }_n}{\int }_B\sigma \nabla u^k\cdot \nabla u^s={\int }_B\frac{\partial \sigma }{\partial {\rho }_n}\nabla u^k\cdot \nabla u^s+{\int }_B\sigma \nabla \frac{\partial u^k}{\partial {\rho }_n}\cdot \nabla u^s \\ +{\int }_B\sigma \nabla u^k\cdot \nabla \frac{\partial u^s}{\partial {\rho }_n}. \end{gathered}$$ (A4)

To simplify the last two terms on the right side of (A4), we differentiate problem (1), (6) with respect to ρ_n:

$$\nabla \cdot \sigma \nabla \frac{\partial u^k}{\partial {\rho }_n}=-\nabla \cdot \frac{\partial \sigma }{\partial {\rho }_n}\nabla u^k\text{in}B$$ (A5)

$$\sigma \frac{\partial }{\partial \nu }\frac{\partial u^k}{\partial {\rho }_n}=-\frac{\partial \sigma }{\partial {\rho }_n}\frac{\partial u^k}{\partial \nu }\text{on}S.$$ (A6)

We multiply (A5) by u^s, integrate over B, and use the divergence theorem, obtaining

$${\int }_B\sigma \nabla \frac{\partial u^k}{\partial {\rho }_n}\cdot \nabla u^s={\int }_S{u}^s\sigma \frac{\partial }{\partial \nu }\frac{\partial u^k}{\partial {\rho }_n}+{\int }_B{u}^s\nabla \cdot \frac{\partial \sigma }{\partial {\rho }_n}\nabla u^k.$$ (A7)

In the first term on the right side of (A7), we use (A6); in the second, we again apply the divergence theorem, making use of the fact that u^s also satisfies (A5). This gives us

$$\begin{gathered} {\int }_B\sigma \nabla \frac{\partial u^k}{\partial {\rho }_n}\cdot \nabla u^s=-{\int }_S{u}^s\frac{\partial \sigma }{\partial {\rho }_n}\frac{\partial u^k}{\partial \nu }+{\int }_S{u}^s\frac{\partial \sigma }{\partial {\rho }_n}\frac{\partial u^k}{\partial \nu } \\ -{\int }_B\frac{\partial \sigma }{\partial {\rho }_n}\nabla u^s\cdot \nabla u^k. \end{gathered}$$ (A8)

The first and second terms on the right side of (A8) cancel, giving us

$${\int }_B\sigma \nabla \frac{\partial u^k}{\partial {\rho }_n}\cdot \nabla u^s=-{\int }_B\frac{\partial \sigma }{\partial {\rho }_n}\nabla u^s\cdot \nabla u^k.$$ (A9)

Clearly, the same relation holds when s and k are interchanged. Using (A9) in the last two terms of (A4), we obtain the claimed result (A3). ■

The derivative on the right side of (A3) can be evaluated easily for a conductivity of the form (10):

$$\frac{\partial \sigma }{\partial {\rho }_n}(\overrightarrow{p})=-\frac{1}{{\rho }_n^2}{\chi }_n(\overrightarrow{p}).$$ (A10)

Combining this with (A2) and (A3), we obtain

$$Y_{s,k}^n\approx \frac{1}{{\rho }_n^2}{\int }_{M_n}\nabla u^k\cdot \nabla u^s,$$ (A11)

where M_n denotes the nth mesh element.