Abstract
Simulation techniques are crucial to establish a firm link between phenomena occurring at the atomic scale and macroscopic observations of functional materials. Importantly, extensive sampling of space and time scales is paramount to ensure good convergence of physically relevant quantities to describe ion transport in energy materials. Here, a number of simulation methods to address ion transport in energy materials are discussed, with the pros and cons of each methodology put forward. Emphasis is given to the stochastic nature of results produced by kinetic Monte Carlo, which can adequately account for compositional disorder across multiple sublattices in solids.
Keywords: Ion transport, Kinetic Monte Carlo, Ion conductors, Solid electrolytes, Density functional theory, First-principles calculations
1. Jump Diffusivity—An Important Quantity
Storing and distributing green energy is central to the process of modernization of our society. Rechargeable batteries, including lithium (Li)-ion batteries, contribute substantially to shifting away from oil and other petrochemicals. The 2019 Nobel prize in chemistry awarded to John Goodenough, Stanley Whittingham, and Akira Yoshino resulted in the introduction of the Li-ion battery as a mainstream technology powering millions of portable devices, electric vehicles, and stationary applications.1,2
In any rechargeable battery architecture, including the Li-ion battery, the active ions, Li+, Na+ etc., are discharged from the anode (negative electrode) into the positive electrode (the cathode) through an electrolyte in a reversible manner. The rapid transport of ions in electrode materials and between the electrodes by means of electrolytes enables the battery itself. The physical quantity characterizing ionic movement in materials (i.e., in solids) is the “jump” diffusivity (or diffusion coefficient), DJ of eq 1.
| 1 |
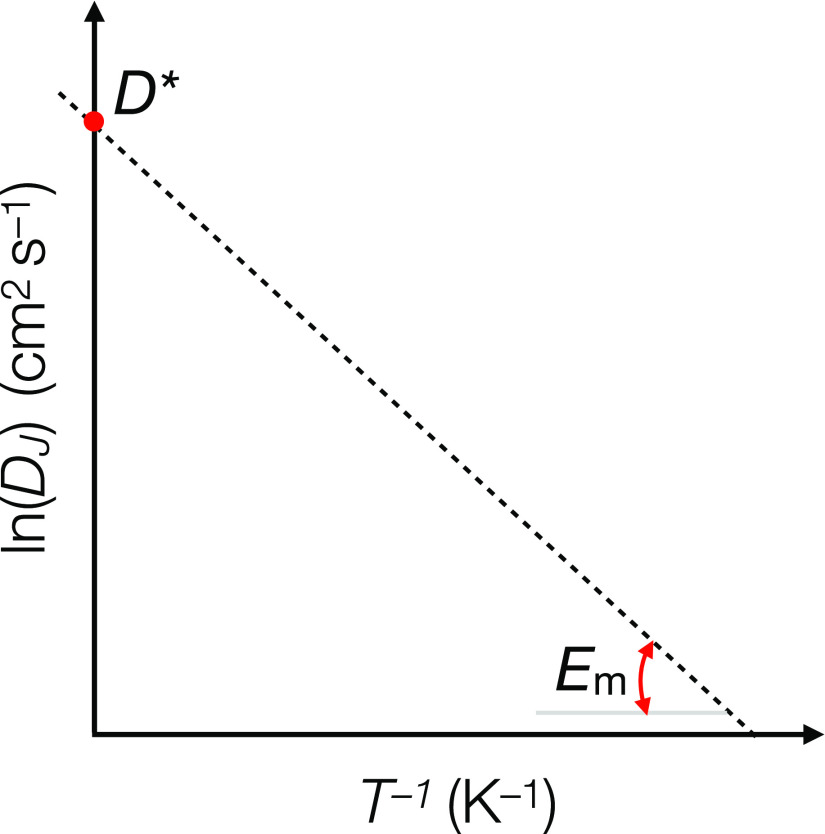
D* is a prefactor, Em is the energy of ionic migration, T is the temperature, and kB is the Boltzmann constant. The physical origins of DJ and D* and related physical quantities have been extensively reviewed elsewhere.3−12Figure 1 shows graphically the main elements enclosed by eq 1.
Figure 1.
Arrhenius plot of ion jump diffusivity DJ (in cm2 s–1) vs reciprocal of temperature (K–1). The slope of the line Em sets the migration barrier associated with ion motion, whereas the intercept with the y-axis is the prefactor D* of eq 1.
The migration energy Em and the prefactor D* depend intrinsically on the chemical composition and the specific polymorph (or phase) of a material. Going forward, this Perspective will focus on crystalline compounds, which display long-range order of atoms and will be referred to more generally as materials.
A number of experimental and computational techniques can be used to determine DJ in materials for energy storage. For example, the galvanostatic intermittent titration technique (GITT) is largely used to evaluate solid-state diffusion coefficients in electrode materials.13DJ in solid (and liquid) electrolytes can be inferred from ion conductivity measurements derived from electrochemical impedance spectroscopy (EIS). Spin–lattice solid-state nuclear magnetic resonance (SL-SS-NMR), quasi-elastic neutron scattering (QENS), secondary ion mass spectrometry (SIMS), and muon spectroscopy have been largely employed to indirectly probe diffusivities in materials (via estimation of Em).9 Altogether these techniques can sample wide space and time domains, and have enabled invaluable progress in our understanding of the physical phenomena of ion transport in electrode and solid-electrolyte materials.9,11
Alongside experimental techniques, computational methodologies have steadily progressed in the simulation of ion transport phenomena in materials. Computational methodologies set a firm link between macroscopic measurements of ion diffusivity (or conductivity) with the atomistic processes of ionic migration. The latter is inherently connected to the intrinsic chemical and structural properties of the materials investigated.10 Note that ionic diffusion happens through random walks, or random migration events, within a solid. Therefore, the jump-diffusion coefficient of eq 1 can also be defined in terms of the root-mean-square of the displacement of the center of mass of all random walkers, e.g. Li-ions:
| 2 |
where the numerator of eq 2 is the square of the sum of all random walk trajectories. In the denominator, d is the dimensionality of the diffusion network, N is the number of random walkers, and T is the temperature. Because DJ tracks the center of mass of ion transport, the jump diffusion incorporates all correlation effects between ions.4 The tracer diffusion coefficient, DT, when computed as if each random walker is treated as an individual diffusion center.
| 3 |
Equations 2 and 3 are connected by the Haven ratio, HR.
| 4 |
HR provides a measure of the correlation between migrating ions.
2. Computation to Predict Ion Transport in Materials
Existing computational methodologies to study ion transport in materials are arranged in Figure 2 according to their abilities in sampling the space and time domains. In sequence from left to right in Figure 2, we find
-
Ab initio Molecular Dynamics (AIMD) simulations integrate Newton’s equations of motion, by exploring the potential energy surfaces (PESs) of materials using first-principles methodologies, with the most popular method being density functional theory (DFT).14
pros: Because AIMD simulations rely on solving approximately the many-body Schrödinger equation, they provide one of the most accurate representations of PESs in materials15 and thus sample accurately forces and stresses acting on atoms. As AIMD simulations compute directly DT at different temperatures, D* and Em can be directly extracted by fitting eq 1 and using HR. Since DFT can adequately treat the electronic structure of insulators, semiconductors, and even metals, AIMDs can be automated (to a large extent).
cons: Albeit very accurate, AIMD are computationally expensive, limiting the propagation of MD simulations to materials systems with just a handful of atoms (<500 atoms) and short-production runs (lower than 1 ns, typically restricted to a hundred or so ps). As the statistic of rare events—ionic migration—provided by AIMDs remains rather limited, room (and low)-temperature ion diffusivities are often extrapolated by high-temperature AIMDs. Moreover, the convergence of DJ is slow with ionic displacements and usually requires extended sampling of rare events beyond the current capabilities of AIMD.16 Typically, AIMD simulations compute the tracer diffusivity DT, while HR are often fitted from experimental data, from which DJ is computed.
-
Nudged Elastic Band (NEB) simulations, developed by Jónsson and Henkelman,17−19 explore the PES of materials at a fixed temperature as ions (e.g., Li+ and Na+) migrate along specific “reaction coordinates”, identifying saddle points of the PES, which in turn correspond to Em. Typically, NEB estimates forces and stresses on atoms using DFT; thus, the temperature of calculation is 0 K. NEBs are direction dependent; to this end, the introduction of the kinetically resolved activation energies developed by Van der Ven et al. can be employed.3,10
pros: Given a specific crystal structure and composition, NEB calculations can identify all possible migration barriers. NEB establishes a direct structure–property relationship by linking migration trajectories in the host materials directly to Em values. In systems with sluggish kinetics of ion transport, primarily associated with large values of Em, NEB becomes extremely handy and perhaps the only methodology capable of providing accurate migration energies.20−23
cons: Depending on the structural complexities of the ionic conductor, NEB calculations can be time-consuming and in specific situations hard to converge.23 Within the framework of transition state theory,24 values of D* can be approximated indirectly through statistical thermodynamics from phonon calculations, but these are time-consuming too.
-
Classical Molecular Dynamics (CMD) simulations chart the PES of materials utilizing interatomic potentials (IPs), fitted on features of the chemical bonds of materials.
pros: Simulating ion transport in ion conductors with IPs enables large MDs for tens of nanoseconds (using models containing less than one million atoms). Therefore, CMD simulations can achieve longer sampling statistics even at low temperatures.7,25−29 For example, CMD simulations have been recently used to simulate grain boundaries in Li-ion conductors.29,30 IPs driving CMD simulations rely on combinations of Morse, Buckingham, Lennard–Jones, etc., potentials that are physically interpretable. Many of these IPs are available “off-the-shelf” for several materials and in various software packages.
cons: Parameters entering IPs are typically fitted from ab initio data or experimental observables, or a mixture of both. This aspect limits the extrapolative ability of IPs as their usability is limited only to chemical domains where these potentials have been fitted. Therefore, the transferability of IPs among slightly different chemical systems is one of the main limiting factors.
-
Machine-Learned Molecular Dynamics (ML-MD) simulations explore the PES of ion conductors using machine-learned interatomic potentials (MLIPs). Some of the MLIPs build upon the force-matching ideas developed by Ercolessi and Adams,31 where PESs from AIMD simulations are used to train surrogate models that are computationally more accessible.32,33 Shapeev34 proposed the moment tensor potentials, where PESs are developed as linear combinations of polynomial basis functions describing one-body, two-body, and three-body interactions. Another strategy is that of Behler and Parrinello,35 where PESs are represented by neural networks, but this method has been mostly confined to investigating the thermodynamic stability of energy materials.36,37 Mueller et al.38 have recently presented an exhaustive description of exiting MLIPs.
pros: ML-MD are orders of magnitude less expensive compared to AIMD, but provide comparable accuracies to AIMD.39−41 For this reason, ML-MDs can deal with larger supercell models (<100 000 atoms) and long simulations runs spanning tens of nanoseconds.
cons: The parametrization of MLIPs still requires extensive AIMD (or DFT) simulations, with thousands (even tens of thousands) of “force/stress calls”. The computation of forces and stresses in MLIPs is still contingent on numerical differentiation, making their MD simulations more expensive than the CMD. Albeit more accurate than classical IPs, current MLIPs are not physically interpretable and may suffer from overfitting. The transferability of MLIPs between similar chemical systems, e.g., polymorphs of the same material, appears contingent on the training set.42
-
Kinetic Monte Carlo (kMC) enables the evaluation of large stochastic ensemble of ion migration events.3,10 In kMC, the frequency Γ (eq 5) of ion migration event is evaluated through the transition state theory.3,10
where ν* (measured in Hz) is the attempt frequency, associated with the vibrational modes of atoms. Values of ν* can be derived from first-principles calculations as extensively discussed by Van der Ven et al.10 kMC simulations become only feasible once “auxiliary models“ to quickly estimate Em’s are available. One reliable strategy to develop systematically improvable “auxiliary models” is that of first-principles based local-lattice Hamiltonians, also known as local cluster expansions. A local cluster expansion can be used to estimate inexpensively migration barriers as the chemical compositions of the active ions are varied.3,10,16,43−49 If constructed correctly, local cluster expansions carry the accuracy of first-principles calculations. An example of local cluster expansion combined with kMC will be given in section 3. In principle, kMC simulations driven by IPs can be also used to assess Ems, but with a notable loss of accuracy and other limitations, as discussed in the previous paragraphs.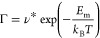
5 pros: Selecting viable migration events according to their frequency, Γ of eq 5, kMC can be easily propagated to perform long simulation runs in the realm of millisecond and on extended structures models (>1 000 000 atoms).3,10,16,46,49,50 Given the extremely long times sampled by kMC, the evaluation of DJ, DT, and HR is guaranteed to converge to representative values.3,10,16,43,44,46,49,50 An immediate advantage of this is that material systems operating in the regime of nondilute carriers can be treated seamlessly. If coupled with lattice Hamiltonian models, kMC can screen efficiently many compositions of ion conductors,3,10,16,49 thus addressing situations of compositional disorder—a commonality of the electrode and solid electrolyte materials. kMC simulations can be easily applied to systems with sluggish diffusivities.
cons: kMC relying on lattice models cannot provide meaningful trajectories of the moving ions. In contrast, trajectories of all moving and nonmoving ions are accessible via all MD methods. Although relaxation effects of structural models are typically captured implicitly in local cluster expansion models driving kMC simulations, this may turn out to be a limitation in ion conductors exhibiting significant ion mobility. In contrast to any MD method, in kMC, the pre-exponential factors ν*’s (and hence D*’s) are not derived directly from the simulations, but instead, the ν*’s must be provided as an input parameter.
Figure 2.
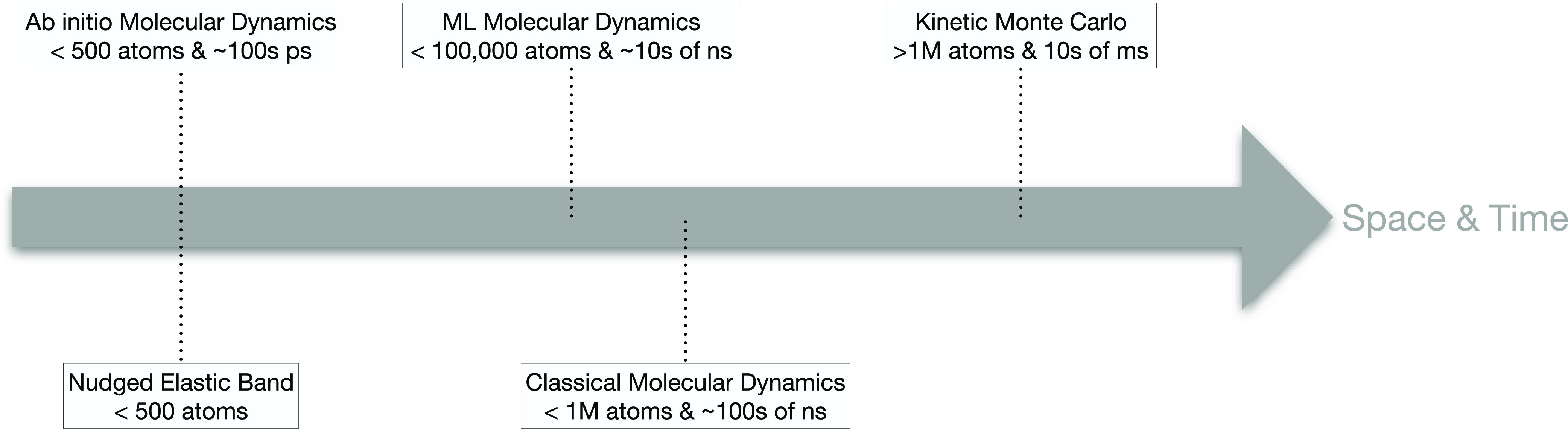
Computational methodologies to study ion transport in energy materials arranged left to right according to their abilities in sampling the space and time domains. Machine learning is abbreviated as ML.
In relation to the predicting capabilities and power of the simulation techniques discussed in the previous paragraphs, computer time is certainly a crucial variable that must be understood in depth when planning the application of specific methodologies and algorithms to study ion transport in materials. Indeed, the computer time required by specific methods highly depends on several variables, such as the specific hardware utilized for the simulation, the implementation and optimization of specific algorithms, the parallelization capability of codes and algorithms, and the simulation size targeted (often set by the number of atoms per “simulation box”).
3. Kinetic Monte Carlo Applied to Na1+xZr2SixP3–xO12 Ion-Conductors
In the field of energy storage, the development and application of lattice Hamiltonians in combination with kMC appears less common in comparison to molecular dynamic simulations. Van der Ven has pioneered the application of local cluster expansion and kMC to the study of Li+, Na+, and Mg+ mobility in electrode materials.3,43,44,47,50 Indeed just a handful of research groups globally have been pushing the development of this methodology.3,10,16,43,44,46−49 This section discusses an example of the application of kMC+local-cluster expansion in the study of ion transport phenomena in the Na1+xZr2SixP3–xO12 solid electrolyte. We refrain from discussing the application of kMC+local-cluster expansion to intercalation electrode materials, as it has been extensively covered by Van der Ven et al.10
The Natrium Super-Ionic CONdcutor (NaSICON)
with the composition
Na1+xZr2SixP3–xO12 is a
well-known ceramic solid-electrolyte for all-solid-state Na-ion batteries,49,51−56 with impressive ion-conductivities of ∼4 mS cm–1 at 298 K (for composition Na3.4Zr2Si2.4P0.6O12).49 NaSICON
provides a versatile framework, incorporating both cations (Na+ and Zr4+) and anion (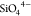 and
and 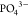 ) moieties, which enable the number of Na+ ions to vary between 1 and 4 per f.u. with the corresponding
variation in the P/Si ratio and Na-ion conductivity. In NaSICON, superionic
conductivity is driven by a Na-vacancy migration mechanism that links
directly to the occupational disorder of the Na sites. Variations
of sodium compositions in the range 1 < x <
3 control directly the mixing between
) moieties, which enable the number of Na+ ions to vary between 1 and 4 per f.u. with the corresponding
variation in the P/Si ratio and Na-ion conductivity. In NaSICON, superionic
conductivity is driven by a Na-vacancy migration mechanism that links
directly to the occupational disorder of the Na sites. Variations
of sodium compositions in the range 1 < x <
3 control directly the mixing between 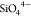 and
and 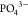 , which disorder in the NaSICON lattice.51−55 Thus, describing accurately the effects of Na+ and vacancy
disordering and polyanion disordering is crucial to rationalize the
Na-ion transport in NaSICON materials.
, which disorder in the NaSICON lattice.51−55 Thus, describing accurately the effects of Na+ and vacancy
disordering and polyanion disordering is crucial to rationalize the
Na-ion transport in NaSICON materials.
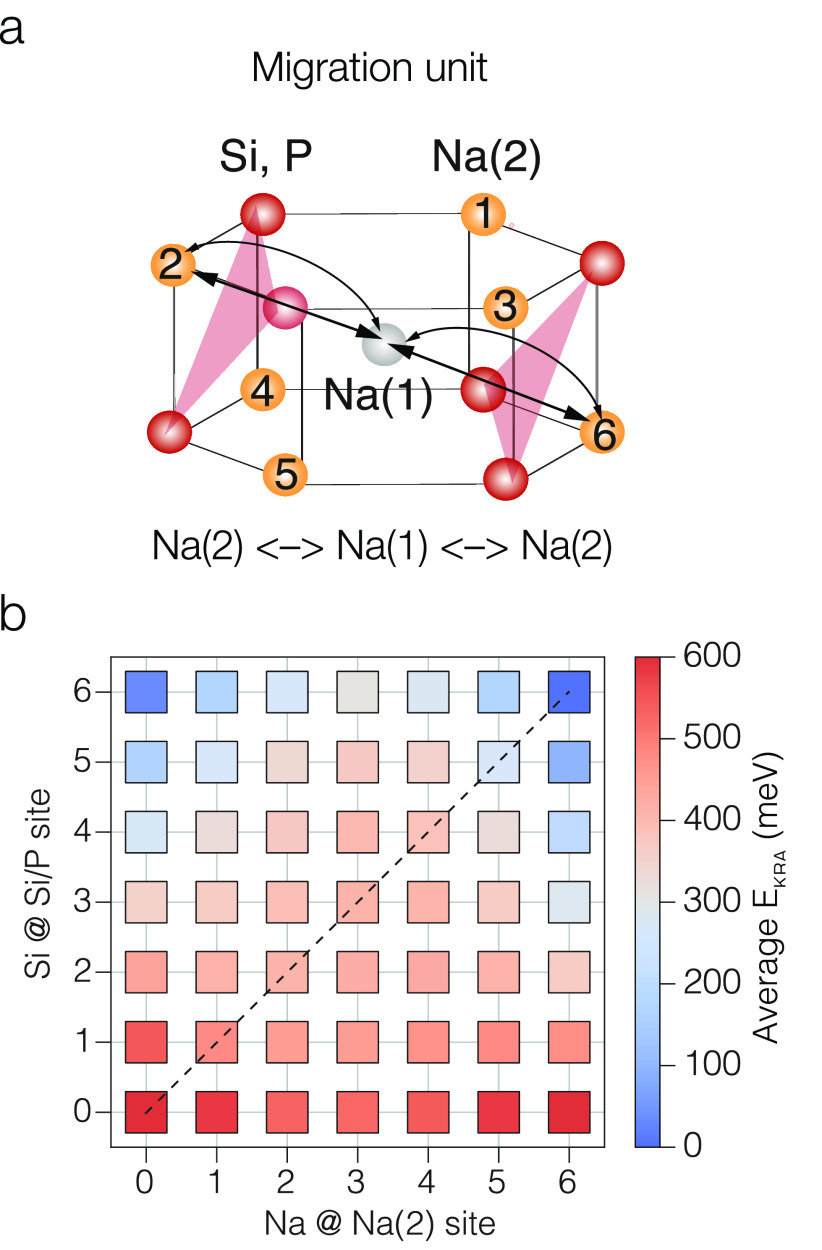
With two inequivalent Na crystallographic sites, i.e., Na(1) and Na(2), the Na+ transport in Na1+xZr2SixP3–xO12 follows a vacancy-mediated mechanism relying on the interplay on the population of Na(1) and Na(2) sites at different temperatures and Si/P compositions. As a result, Na-ion transport in Na1+xZr2SixP3–xO12 requires both Na(1) and Na(2) sites, and migration pathways of the kind Na(1) ↔ Na(2), as shown in Figure 3a.
Figure 3.
Na+ migration in Na1+xZr2SixP3–xO12.49 (a) Minimal migration unit describing Na-ion migration in Na1+xZr2SixP3–xO12, where Na follows a Na(2) ↔ Na(1) ↔ Na(2) hop. In (b) Na(1) sites are shown by silver spheres, Na(2) sites by orange spheres, and red triangles indicate the bottlenecks caused by PO4/SiO4 tetrahedra (where oxygen atoms are not shown). (b) Computed kinetically resolved activation barriers for Na(2) ↔ Na(1) hops, with varying Na(2) site occupation and Si/P content per migration unit. Adapted with permission under a Creative Commons Attribution 4.0 International License from ref (49). Copyright 2022 Springer Nature.
Figure 3a shows the so-called migration unit which can be used to derive a local cluster expansion, fitted on migration barriers computed with DFT-NEB calculations. In practice, in ref (49), a process of enumeration of all unique Na/Vacancy/PO4/SiO4 combinations of the migration unit (Figure 3a) was performed. Starting from these enumerated model structures, DFT-based NEB calculations of migration pathways, such as Na(2) → Na(1) → Na(2), were calculated, from which the kinetically resolved activation barriers (KRAs) were derived.3 The computed KRA barriers were used to train a local cluster expansion, whose details are given in ref (49). The local cluster expansion can effortlessly and efficiently generate any migration barrier at any Na/Vacancy (or equivalently PO4/SiO4) composition of the Na1+xZr2SixP3–xO12 material. Figure 3b shows the Na+ KRAs as obtained by the local cluster expansion for all Na1+xZr2SixP3–xO12 compositions identified in the migration unit of Figure 3a. Low values of KRAs are proportional to low values of migration barriers and vice versa.
By varying the Si/P environment of the migration
unit of Figure 3a,
two regions of
low and high KRA barriers could be isolated (Figure 3b). At low Si or high P content (bottom rows
of Figure 3b), high
KRAs (∼500 meV) were observed. On the contrary, low values
of KRA barriers were predicted as the Si amount was increased (see
top row of Figure 3b). A monotonic decrease in KRA values (and migration barriers) with
Si content was ascribed to lower 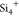 –Na+ electrostatic repulsions
compared to P5+–Na+ repulsion during
Na-ion migration.
–Na+ electrostatic repulsions
compared to P5+–Na+ repulsion during
Na-ion migration.
Indeed, the migration unit can be used to “tessellate” periodically the three-dimensional structure of Na1+xZr2SixP3–xO12 at selected Na/Vacancy (or PO4/SiO4) compositions. Having selected an input temperature and starting Na1+xZr2SixP3–xO12, which is an ensemble of migration units representing a desired Na1+xZr2SixP3–xO12 composition, the kMC can be started. Three major steps are done in the rejection-free kMC as proposed initial by Bortz–Kalos–Lebowitz:57 (i) Using eq 5, the probabilities Γs of Na+ migration in thousands of migration units are accurately computed. (ii) A kMC step is performed by choosing a random number, and a new Na+ migration event is selected. (iii) New Na+ migration events and trajectories are obtained, and the simulation time is advanced. Because computing migration energies within the local cluster expansion is a very efficient task (just algebraic summations),3,10 these three steps discussed above can be repeated at ease countless (million) times, for several temperatures and compositions.
Using the extensive sets of local migrations generated by kMC, properties of interest, such as DJ, DT and HR can be computed. Figure 4 shows the predicted jump diffusivities DJ of Na1+xZr2SixP3–xO12 at variable temperature and Na content by Deng et al.,49 as derived from the kMC approach implementing the local cluster expansion.3
Figure 4.
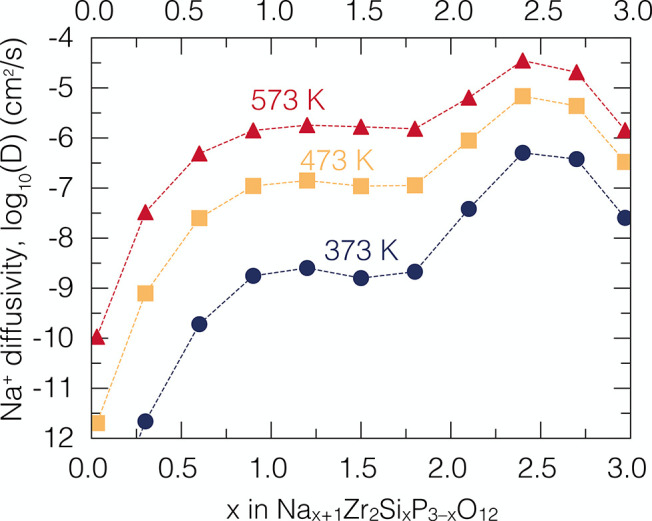
Predicted jump diffusivities DJ of Na1+xZr2SixP3–xO12 as a function of Na composition and temperature (373 K blue, 473 K yellow, and 573 K red shapes).49 Each kMC simulation included 2 048 000 equilibration steps, and 12 288 000 production steps at each temperature and Na composition, respectively. All points in Figure 4 stem form 1650 independent kMC simulations (11 compositions × 50 initial configurations × 3 temperatures) that is ∼14 million steps per configuration. Each diffusivity DJ value in Figure 4 is the arithmetic average of the diffusivities computed for 50 different starting equilibrium configurations generated from the compositional phase diagram of Na1+xZr2SixP3–xO12.55 Adapted with permission under a Creative Commons Attribution 4.0 International License from ref (49). Copyright 2022 Springer Nature.
As demonstrated by Deng et al.,49 the diffusivities of Figure 4 can be utilized to predict (via the Nernst–Einstein equation) the ionic conductivities as a function of Na composition and temperature in Na1+xZr2SixP3–xO12. The predicted composition-dependent conductivities were found to be in good agreement with experimental values of bulk conductivities of Na1+xZr2SixP3–xO12.49 Note that to capture adequately the statistical disorder of the PO4/SiO4 polyanion in NaSICON, each point of diffusivity in Figure 4 represents the arithmetic average of 50 distinct spatial arrangements of the silicate and phosphate units at a given Na composition.
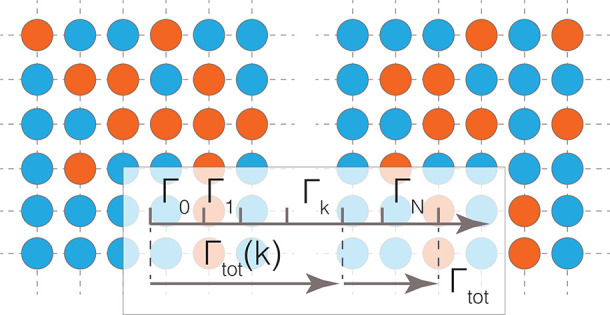
Figure 5 depicts the time scale accessible by kMC simulations coupled with the formalism of local-cluster expansion. Remarkably, within this computational framework, simulations can extend to regimes of milliseconds. These time scales are clearly not accessible by the current MD approaches discussed above.
Figure 5.
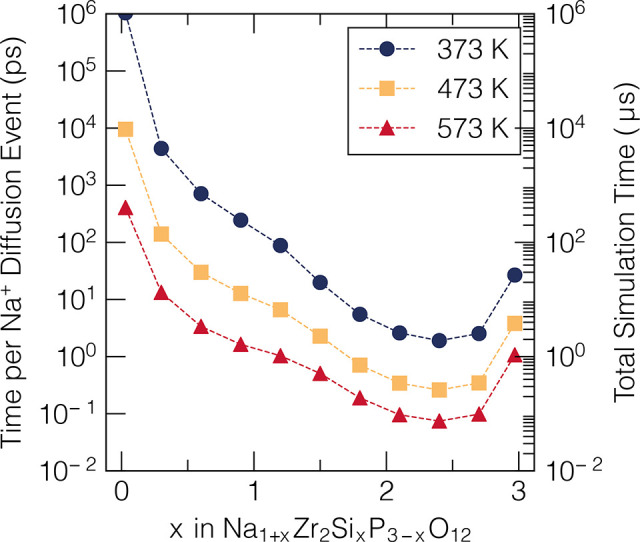
Average time for each Na+ diffusion event (in ps) and total simulation time at temperatures of 373, 473, and 573 K and different sodium compositions, respectively. The sum of the time of each kMC event (left y-axis) provides the total simulation time (right y-axis).49 Adapted with permission under a Creative Commons Attribution 4.0 International License from ref (49). Copyright 2022 Springer Nature.
Indeed, trends shown in Figure 5 are just manifestations of the transition state theory of eq 5, which favors migration processes accompanied by low migration barriers, which results in small times per diffusion event. In the specific case of Na1+xZr2SixP3–xO12, high P content materials (i.e., x ∼ 1) show consistently high Na+ migration barriers, which is directly reflected by large values on both y-axes.
4. Outlook and Final Remarks
We have elucidated the role of modern computational techniques, including ab initio molecular dynamics, machine learning-based molecular dynamics, and kinetic Monte Carlo (kMC) methods, to describe phenomena of ion transport in functional materials. The importance of kMC coupled with lattice Hamiltonians was emphasized. This combination can sample astoundingly large and long simulations while carrying the accuracy of first-principles calculations. By virtue of its construction, kMC incorporates statistical distributions of moving and nonmoving ions. In the example of Na1+xZr2SixP3–xO12 in the composition range 0 < x < 3, compositional disorder occurs both on the sub-Na/Vacancy lattice and the anion sublattice, i.e., PO4/SiO4. Compositional disorder on anion sublattice is a common feature of many fast-ion conductors (and electrode materials), such as the LiSiCON-type Li4±xSi1–xZxO4 (Z = P5+, Al3+, Sn4+ and/or Ge4+), Li10MP2S12 based on Li4MS4:Li3PS4 (M = Ge4+, Sn4+, and Si4+).
Because in the kMC approach combined with local-cluster expansion, a migration unit must be identified a priori. Hence, the generalizability of codes to different material systems is often a major obstacle. Researchers have designed specialized codes around topical materials of interest. Indeed, this limitation has curbed the distribution of general plug-and-play simulation packages.
Machine-learned interatomic potentials (MLIPs) for simulations of ion transport appear the right strategy bridging the accuracy of ab initio simulations and extended sampling capabilities of classical IPs. Efforts toward the generalization of MLIPs do exist, and currently, different research groups provide “plug-and-play” software (with or without active learning) to train and perform MD simulations. In the future, progress in this important area may bring physics-interpretable MLIPs. A main advantage of MLIP-MDs is that structural deformations occurring during ion transport are fully captured in the trajectories. In contrast, in lattice-Hamiltonian kMC, effects of local geometrical deformations resulting from ion migrations are only captured implicitly in the lattice Hamiltonian. This is another limitation of the kMC and local cluster expansion approach.
Given a set of materials, a general challenge is the reliable identification of good ionic conductors by surfacing all possible ion migration pathways giving rise to ion percolation and associated migration energies. This is a crucial aspect in kMC models, which become only effective for large data sets of migration events. Several strategies to identify migration energies and migration paths in materials have been proposed. For example, Adams and collaborators using the softBV method could screen large libraries of inorganic materials for the identification of good ionic conductors.25,26,58−60 While this methodology is certainly computationally efficient at screening thousands of compounds, it lacks the appropriate accuracy required to predict reliable migration energies. Transferability across different material chemistries remains another limitation of the softBV method. Pathfinder developed by Rong et al.61 can derive all possible migration paths in bulk materials from an analysis of their DFT electronic charge densities and electrostatic potentials. Building upon Pathfinder, AprroxNEB61 identifies viable ion-migration paths in materials as the minimum energy path through a static potential, derived from DFT charge densities. This method can decrease runtimes by ∼25% in NEBs.61 While this methodology performs well on compact host materials, it appears less accurate at identifying ion migration paths in more open anion frameworks, such as tunnel-like structures (Hollandite) or 2D conductors, e.g., LiCoO2 or LiNi0.8Mn0.1Co0.1O2. These strategies are implemented in powerful materials-screening workflows.62 The estimation of migration barriers displaying reflection symmetry can be accelerated using R-NEB by Mathiesen et al.63 More recently, Bölle et al.64 suggested that a Voronoi tessellation is sufficient to propose a reasonable guess of transition states in ion conductor and electrode materials. They also demonstrated that six geometrical descriptors combined with a principal component analysis are sufficient to identify migration pathways with similar topologies, thus limiting the overall number of calculations.64 By relaxing the chain of states in the field of the electrostatic potential averaged over a spherical volume using different finite-size ion models, Zimmermann et al.65 identified migration paths in materials at significantly lower computational costs. This methodology appears less robust when applied to open-framework materials. While all these strategies contribute toward autonomous workflows for screening large data sets of materials,66 all these methodologies eventually require time-consuming DFT calculations.
These examples demonstrate the urgent need for new general algorithms to assess ion transport in materials, with the accuracy of DFT but at reduced computational costs. In this context, MLIPs offer a degree of advantage. Combining databases of migration barriers from MLIPs with kMC models will provide a robust and powerful strategy to assess ion transport in materials.
Presently, both MLIP and kMC-type models remain confined to bulk systems.66 In this context, Dawson and collaborators have applied successfully classical interatomic potentials through molecular dynamics to study the effects of grain boundaries (homogeneous interfaces) on ion transport.29,30 Lately, Wang et al. have attempted the application of MLIP to the study of Li-ion transport in heterogeneous interfaces typically formed in batteries.42 The description of transport phenomena at homogeneous and heterogeneous interfaces, such as the electrode and electrolyte interfaces, remains an active area of research. Another area where these methods should see more development, is the description of amorphous systems, motifs that are recurrent in glassy ion-conductors, such as Li4MS4:Li3PS4 (M = Ge4+, Sn4+, and Si4+).
We hope that the technical advancements summarized in this Perspective foster new technical insights and developments in the field of computational materials science toward the investigation of ion transport in materials.
Acknowledgments
P.C. acknowledges funding from the National Research Foundation under his NRF Fellowship NRFF12-2020-0012 and support from the Singapore Ministry of Education Academic Fund Tier 1 (R-284-000-186-133). Prof. Gopalakrishnan Sai Gautam at the Indian Institute of Science, Bangalore is acknowledged for his critical insights while writing this Perspective. Naomi M. Henry is acknowledged for her critical reading of the early drafts of this Perspective and her continuous support.
Biography
Pieremanuele Canepa is an Asst. Prof. in the Department of Materials Science and Engineering at the National University of Singapore and has a joint appointment with the Department of Chemical and Biomolecular Engineering at the same institution. Pieremanuele is also part of the Singapore-MIT Alliance. Previously, he was a Postdoctoral fellow under the guidance of Prof. Ceder initially at the Massachusetts Institute of Technology and later at Lawrence Berkeley National Laboratory. Between November 2016 and August 2018, Pieremanuele was an independent Ramsay Memorial Fellow at the University of Bath (United Kingdom). He received his bachelor’s and master’s degrees in Chemistry from the University of Torino (Italy) and his PhD from the University of Kent (United Kingdom). His research contributes to the rational design of new materials for clean energy technologies, such as electrode materials for batteries, ionic conductors, and liquid electrolytes for sustainable energy storage devices. In March 2020, Piero was awarded the National Research Fellowship, the equivalent of the NSF CAREER in the US (or the ERC starting grant in Europe). In 2021 he was elected a Fellow of the Royal Society of Chemistry. In 2022 Pieremanuele was nominated as a Materials Au Rising Star by the American Chemical Society, which is the result of this perspective.
Author Contributions
CRediT: Pieremanuele Canepa conceptualization (lead), data curation (lead), formal analysis (lead), funding acquisition (lead), investigation (lead), methodology (lead), project administration (lead), resources (lead), visualization (lead), writing-original draft (lead), writing-review & editing (lead).
The author declares no competing financial interest.
References
- Press release: The Nobel Prize in Chemistry 2019, accessed on 09/27/2022. https://www.nobelprize.org/prizes/chemistry/2019/press-release/.
- Castelvecchi D.; Stoye E. Chemistry Nobel honours world-changing batteries. Nature 2019, 574, 308–308. 10.1038/d41586-019-02965-y. [DOI] [PubMed] [Google Scholar]
- Van der Ven A.; Ceder G.; Asta M.; Tepesch P. D. First-principles theory of ionic diffusion with nondilute carriers. Phys. Rev. B 2001, 64, 184307. 10.1103/PhysRevB.64.184307. [DOI] [Google Scholar]
- Balluffi R. W.; Allen S. M.; Carter W. C.. Kinetics of Materials; Wiley, 2005. [Google Scholar]
- He X.; Zhu Y.; Mo Y. Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 2017, 8, 15893. 10.1038/ncomms15893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcolongo A.; Marzari N. Ionic correlations and failure of Nernst-Einstein relation in solid-state electrolytes. Phys. Rev. Materials 2017, 1, 025402. 10.1103/PhysRevMaterials.1.025402. [DOI] [Google Scholar]
- He X.; Zhu Y.; Epstein A.; Mo Y. Statistical variances of diffusional properties from ab initio molecular dynamics simulations. npj Comput. Mater. 2018, 4, 18. 10.1038/s41524-018-0074-y. [DOI] [Google Scholar]
- Famprikis T.; Canepa P.; Dawson J. A.; Islam M. S.; Masquelier C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 2019, 18, 1278–1291. 10.1038/s41563-019-0431-3. [DOI] [PubMed] [Google Scholar]
- Gao Y.; Nolan A. M.; Du P.; Wu Y.; Yang C.; Chen Q.; Mo Y.; Bo S.-H. Classical and Emerging Characterization Techniques for Investigation of Ion Transport Mechanisms in Crystalline Fast Ionic Conductors. Chem. Rev. 2020, 120, 5954–6008. 10.1021/acs.chemrev.9b00747. [DOI] [PubMed] [Google Scholar]
- Van der Ven A.; Deng Z.; Banerjee S.; Ong S. P. Rechargeable Alkali-Ion Battery Materials: Theory and Computation. Chem. Rev. 2020, 120, 6977–7019. 10.1021/acs.chemrev.9b00601. [DOI] [PubMed] [Google Scholar]
- Gao Y.; Mishra T. P.; Bo S.-H.; Gautam G. S.; Canepa P. Design and Characterization of Host Frameworks for Facile Magnesium Transport. Annu. Rev. Mater. Res. 2022, 52, 129–158. 10.1146/annurev-matsci-081420-041617. [DOI] [Google Scholar]
- Iton Z. W. B.; See K. A. Multivalent Ion Conduction in Inorganic Solids. Chem. Mater. 2022, 34, 881–898. 10.1021/acs.chemmater.1c04178. [DOI] [Google Scholar]
- Kang S. D.; Chueh W. C. Galvanostatic Intermittent Titration Technique Reinvented: Part I. A Critical Review. J. Electrochem. Soc. 2021, 168, 120504. 10.1149/1945-7111/ac3940. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Urban A.; Seo D.-H.; Ceder G. Computational understanding of Li-ion batteries. npj Comput. Mater. 2016, 2, 16002. 10.1038/npjcompumats.2016.2. [DOI] [Google Scholar]
- Morgan B. J. Lattice-geometry effects in garnet solid electrolytes: a lattice-gas Monte Carlo simulation study. R. Soc. Open Sci. 2017, 4, 170824. 10.1098/rsos.170824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jónssson H.; Mills G.; Jacobsen K. W.. Nudged elastic band method for finding minimum energy paths of transitions. Chapter 16: Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific, 1998; pp 385–404. [Google Scholar]
- Henkelman G.; Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Sheppard D.; Terrell R.; Henkelman G. Optimization methods for finding minimum energy paths. J. Chem. Phys. 2008, 128, 134106. 10.1063/1.2841941. [DOI] [PubMed] [Google Scholar]
- Rong Z.; Malik R.; Canepa P.; Gautam G. S.; Liu M.; Jain A.; Persson K.; Ceder G. Materials Design Rules for Multivalent Ion Mobility in Intercalation Structures. Chem. Mater. 2015, 27, 6016–6021. 10.1021/acs.chemmater.5b02342. [DOI] [Google Scholar]
- Canepa P.; Bo S.-H.; Gautam G. S.; Key B.; Richards W. D.; Shi T.; Tian Y.; Wang Y.; Li J.; Ceder G. High magnesium mobility in ternary spinel chalcogenides. Nat. Commun. 2017, 8, 1759. 10.1038/s41467-017-01772-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T.; Gautam G. S.; Canepa P. Ionic Transport in Potential Coating Materials for Mg Batteries. Chem. Mater. 2019, 31, 8087–8099. 10.1021/acs.chemmater.9b02692. [DOI] [Google Scholar]
- Devi R.; Singh B.; Canepa P.; Gautam G. S. Effect of exchange-correlation functionals on the estimation of migration barriers in battery materials. npj Comput. Mater. 2022, 8, 160. 10.1038/s41524-022-00837-0. [DOI] [Google Scholar]
- Vineyard G. H. Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids 1957, 3, 121–127. 10.1016/0022-3697(57)90059-8. [DOI] [Google Scholar]
- Adams S. Relationship between bond valence and bond softness of alkali halides and chalcogenides. Acta Crystallogr. B: Struct. Sci. Cryst. Eng. Mater. 2001, 57, 278–287. 10.1107/S0108768101003068. [DOI] [PubMed] [Google Scholar]
- Adams S. From bond valence maps to energy landscapes for mobile ions in ion-conducting solids. Solid State Ion 2006, 177, 1625–1630. 10.1016/j.ssi.2006.03.054. [DOI] [Google Scholar]
- Islam M. S.; Fisher C. A. J. Lithium and sodium battery cathode materials: computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. 10.1039/C3CS60199D. [DOI] [PubMed] [Google Scholar]
- Burbano M.; Carlier D.; Boucher F.; Morgan B. J.; Salanne M. Sparse Cyclic Excitations Explain the Low Ionic Conductivity of Stoichiometric Li7La3Zr2O12. Phys. Rev. Lett. 2016, 116, 135901. 10.1103/PhysRevLett.116.135901. [DOI] [PubMed] [Google Scholar]
- Dawson J. A.; Canepa P.; Famprikis T.; Masquelier C.; Islam M. S. Atomic-Scale Influence of Grain Boundaries on Li-Ion Conduction in Solid Electrolytes for All-Solid-State Batteries. J. Am. Chem. Soc. 2018, 140, 362–368. 10.1021/jacs.7b10593. [DOI] [PubMed] [Google Scholar]
- Dawson J. A.; Canepa P.; Clarke M. J.; Famprikis T.; Ghosh D.; Islam M. S. Toward Understanding the Different Influences of Grain Boundaries on Ion Transport in Sulfide and Oxide Solid Electrolytes. Chem. Mater. 2019, 31, 5296–5304. 10.1021/acs.chemmater.9b01794. [DOI] [Google Scholar]
- Ercolessi F.; Adams J. B. Interatomic Potentials from First-Principles Calculations: The Force-Matching Method. Europhys. Lett. 1994, 26, 583–588. 10.1209/0295-5075/26/8/005. [DOI] [Google Scholar]
- Podryabinkin E. V.; Shapeev A. V. Active learning of linearly parametrized interatomic potentials. Comput. Mater. Sci. 2017, 140, 171–180. 10.1016/j.commatsci.2017.08.031. [DOI] [Google Scholar]
- Novoselov I.; Yanilkin A.; Shapeev A.; Podryabinkin E. Moment tensor potentials as a promising tool to study diffusion processes. Comput. Mater. Sci. 2019, 164, 46–56. 10.1016/j.commatsci.2019.03.049. [DOI] [Google Scholar]
- Shapeev A. V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. 10.1137/15M1054183. [DOI] [Google Scholar]
- Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
- Lacivita V.; Artrith N.; Ceder G. Structural and Compositional Factors That Control the Li-Ion Conductivity in LiPON Electrolytes. Chem. Mater. 2018, 30, 7077–7090. 10.1021/acs.chemmater.8b02812. [DOI] [Google Scholar]
- Guo H.; Wang Q.; Urban A.; Artrith N. Artificial Intelligence-Aided Mapping of the Structure–Composition–Conductivity Relationships of Glass–Ceramic Lithium Thiophosphate Electrolytes. Chem. Mater. 2022, 34, 6702–6712. 10.1021/acs.chemmater.2c00267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller T.; Hernandez A.; Wang C. Machine learning for interatomic potential models. J. Chem. Phys. 2020, 152, 050902. 10.1063/1.5126336. [DOI] [PubMed] [Google Scholar]
- Wang C.; Aoyagi K.; Wisesa P.; Mueller T. Lithium Ion Conduction in Cathode Coating Materials from On-the-Fly Machine Learning. Chem. Mater. 2020, 32, 3741–3752. 10.1021/acs.chemmater.9b04663. [DOI] [Google Scholar]
- Qi J.; Banerjee S.; Zuo Y.; Chen C.; Zhu Z.; Chandrappa M. H.; Li X.; Ong S. Bridging the gap between simulated and experimental ionic conductivities in lithium superionic conductors. Mater. Today Phys. 2021, 21, 100463. 10.1016/j.mtphys.2021.100463. [DOI] [Google Scholar]
- Wu E. A.; et al. A stable cathode-solid electrolyte composite for high-voltage, long-cycle-life solid-state sodium-ion batteries. Nat. Commun. 2021, 12, 1256. 10.1038/s41467-021-21488-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Panchal A. A.; Gautam G. S.; Canepa P. The resistive nature of decomposing interfaces of solid electrolytes with alkali metal electrodes. J. Mater. Chem. A 2022, 10, 19732–19742. 10.1039/D2TA02202H. [DOI] [Google Scholar]
- Van der Ven A.; Thomas J. C.; Xu Q.; Swoboda B.; Morgan D. Nondilute diffusion from first principles: Li diffusion in LixTiS2. Phys. Rev. B 2008, 78, 104306. 10.1103/PhysRevB.78.104306. [DOI] [Google Scholar]
- Bhattacharya J.; Van der Ven A. Phase stability and nondilute Li diffusion in spinel Li1+xTi2O4. Phys. Rev. B 2010, 81, 104304. 10.1103/PhysRevB.81.104304. [DOI] [Google Scholar]
- Puchala B.; Lee Y.-L.; Morgan D. A-Site Diffusion in La1–xSrxMnO3: Ab Initio and Kinetic Monte Carlo Calculations. ECS Trans 2013, 50, 97–110. 10.1149/05027.0097ecst. [DOI] [Google Scholar]
- Li C.; Nilson T.; Cao L.; Mueller T. Predicting activation energies for vacancy-mediated diffusion in alloys using a transition-state cluster expansion. Phys. Rev. Materials 2021, 5, 013803. 10.1103/PhysRevMaterials.5.013803. [DOI] [Google Scholar]
- Kolli S. K.; Van der Ven A. Elucidating the Factors That Cause Cation Diffusion Shutdown in Spinel-Based Electrodes. Chem. Mater. 2021, 33, 6421–6432. 10.1021/acs.chemmater.1c01668. [DOI] [Google Scholar]
- Kaufman J. L.; Van der Ven A. Cation Diffusion Facilitated by Antiphase Boundaries in Layered Intercalation Compounds. Chem. Mater. 2022, 34, 1889–1896. 10.1021/acs.chemmater.1c04152. [DOI] [Google Scholar]
- Deng Z.; Mishra T. P.; Mahayoni E.; Ma Q.; Tieu A. J. K.; Guillon O.; Chotard J.-N.; Seznec V.; Cheetham A. K.; Masquelier C.; Gautam G. S.; Canepa P. Fundamental investigations on the sodium-ion transport properties of mixed polyanion solid-state battery electrolytes. Nat. Commun. 2022, 13, 4470. 10.1038/s41467-022-32190-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Ven A.; Gerbrand C. Lithium Diffusion in Layered LixCoO2. Electrochem. Solid-State Lett. 1999, 3, 301. 10.1149/1.1391130. [DOI] [Google Scholar]
- Hong H.-P. Crystal structures and crystal chemistry in the system Na1+xZr2SixP3–xO12. Mater. Res. Bull. 1976, 11, 173–182. 10.1016/0025-5408(76)90073-8. [DOI] [Google Scholar]
- Goodenough J.; Hong H.-P.; Kafalas J. Fast Na+-ion transport in skeleton structures. Mater. Res. Bull. 1976, 11, 203–220. 10.1016/0025-5408(76)90077-5. [DOI] [Google Scholar]
- Boilot J.; Collin G.; Colomban P. Relation structure-fast ion conduction in the NASICON solid solution. J. Solid State Chem. 1988, 73, 160–171. 10.1016/0022-4596(88)90065-5. [DOI] [Google Scholar]
- Masquelier C.; Croguennec L. Polyanionic (Phosphates, Silicates, Sulfates) Frameworks as Electrode Materials for Rechargeable Li (or Na) Batteries. Chem. Rev. 2013, 113, 6552–6591. 10.1021/cr3001862. [DOI] [PubMed] [Google Scholar]
- Deng Z.; Gautam G. S.; Kolli S. K.; Chotard J.-N.; Cheetham A. K.; Masquelier C.; Canepa P. Phase Behavior in Rhombohedral NaSiCON Electrolytes and Electrodes. Chem. Mater. 2020, 32, 7908–7920. 10.1021/acs.chemmater.0c02695. [DOI] [Google Scholar]
- Deb D.; Gautam G. S. Critical overview of polyanionic frameworks as positive electrodes for Na-ion batteries. J. Mater. Res. 2022, 10.1557/s43578-022-00646-7. [DOI] [Google Scholar]
- Bortz A.; Kalos M.; Lebowitz J. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. 10.1016/0021-9991(75)90060-1. [DOI] [Google Scholar]
- He B.; Chi S.; Ye A.; Mi P.; Zhang L.; Pu B.; Zou Z.; Ran Y.; Zhao Q.; Wang D.; Zhang W.; Zhao J.; Adams S.; Avdeev M.; Shi S. High-throughput screening platform for solid electrolytes combining hierarchical ion-transport prediction algorithms. Sci. Data 2020, 7, 151. 10.1038/s41597-020-0474-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; He B.; Zhao Q.; Zou Z.; Chi S.; Mi P.; Ye A.; Li Y.; Wang D.; Avdeev M.; Adams S.; Shi S. A Database of Ionic Transport Characteristics for Over 29 000 Inorganic Compounds. Adv. Funct. Mater. 2020, 30, 2003087. 10.1002/adfm.202003087. [DOI] [Google Scholar]
- Wong L. L.; Phuah K. C.; Dai R.; Chen H.; Chew W. S.; Adams S. Bond Valence Pathway Analyzer—An Automatic Rapid Screening Tool for Fast Ion Conductors within softBV. Chem. Mater. 2021, 33, 625–641. 10.1021/acs.chemmater.0c03893. [DOI] [Google Scholar]
- Rong Z.; Kitchaev D.; Canepa P.; Huang W.; Ceder G. An efficient algorithm for finding the minimum energy path for cation migration in ionic materials. J. Chem. Phys. 2016, 145, 074112. 10.1063/1.4960790. [DOI] [PubMed] [Google Scholar]
- Bölle F. T.; Mathiesen N. R.; Nielsen A. J.; Vegge T.; Garcia-Lastra J. M.; Castelli I. E. Autonomous Discovery of Materials for Intercalation Electrodes. Batter. Supercaps 2020, 3, 488–498. 10.1002/batt.201900152. [DOI] [Google Scholar]
- Mathiesen N. R.; Jónsson H.; Vegge T.; Lastra J. M. G. R-NEB: Accelerated Nudged Elastic Band Calculations by Use of Reflection Symmetry. J. Chem. Theory Comput. 2019, 15, 3215–3222. 10.1021/acs.jctc.8b01229. [DOI] [PubMed] [Google Scholar]
- Bölle F. T.; Bhowmik A.; Vegge T.; Lastra J. M. G.; Castelli I. E. Automatic Migration Path Exploration for Multivalent Battery Cathodes using Geometrical Descriptors. Batter. Supercaps 2021, 4, 1516–1524. 10.1002/batt.202100086. [DOI] [Google Scholar]
- Zimmermann N. E. R.; Hannah D. C.; Rong Z.; Liu M.; Ceder G.; Haranczyk M.; Persson K. A. Electrostatic Estimation of Intercalant Jump-Diffusion Barriers Using Finite-Size Ion Models. J. Phys. Chem. Lett. 2018, 9, 628–634. 10.1021/acs.jpclett.7b03199. [DOI] [PubMed] [Google Scholar]
- Deng Z.; Kumar V.; Bölle F. T.; Caro F.; Franco A. A.; Castelli I. E.; Canepa P.; Seh Z. W. Towards autonomous high-throughput multiscale modelling of battery interfaces. Energy Environ. Sci. 2022, 15, 579–594. 10.1039/D1EE02324A. [DOI] [Google Scholar]