Fig. 6. Clustering of sensory and motorneurons and interneurons in an optimization of full network is different to actual clustering. (A) Average distance between neurons belonging to the same ganglion (diagonal elements) or different ganglia (nondiagonal elements) for sensory and motorneuron positions when the complete network is optimised and a= b = 1/29.3. Clustering error is e_c = 12.3%. (B) Same as A but for the actual nematode. (C) Same as A but for interneurons. Ganglion 7 has been omitted because it contains no interneurons. Clustering error is e_c = 25.2%. (D) Same as C but for the actual nematode.

Fig. 7. Method to dissect networks with noiseless optimal subnetwork and nonoptimal subnetworks with Gaussian noise. (A) Step 2 in the dissection method calculates the average position error in networks of decreasing size eliminating worst located neurons in the order determined in step 1 of the method. Position of somas for optimal subnetwork obtained from an optimization of that subnetwork. Soma positions for the nonoptimal subnetwork obtained from an optimization of the complete network and then adding Gaussian noise of std = 35% to the neurons selected as nonoptimal. Point with plus sign indicates the point that our algorithm finds separating optimal and nonoptimal subnetworks. (B) Estimated size of the nonoptimal subnetwork (blue) and correctly estimated nonoptimal neurons (green).

Fig. 8. Same as SI Fig. 7 but Step 1 in the dissection method does not classify neurons using an iterative method

Fig. 9. Method to dissect networks with near-optimal subnetwork with low Gaussian noise (std = 5.5%) and nonoptimal subnetworks with larger Gaussian noise (std = 35%). (A) Step 2 in the dissection method calculates the average position error in networks of decreasing size eliminating worst located neurons in the order determined in step 1 of the method. Blue line, case of network with near-optimal and nonoptimal subnetworks. Position of somas for near-optimal subnetwork obtained from an optimization of that subnetwork and adding Gaussian noise of std = 5.5% (as obtained in the elegans near-optimal subnetwork). Soma positions for the nonoptimal subnetwork obtained from an optimization of the complete network and then adding Gaussian noise of std = 35% to the neurons selected as nonoptimal. Red line, noisy network with neuron positions obtained adding Gaussian noise of std = 8% to the optimal position of all neurons. (B) Estimated size of the nonoptimal subnetwork (blue points) and correctly estimated nonoptimal neurons (green points) for networks formed by a near-optimal subnetwork and nonoptimal subnetworks of different sizes. (C) Same as B but for noisy networks of different std. (D) Deviation of neuron position from optimal position in actual nematode consistent with near-optimal subnetwork of Gaussian noise of std = 5.5% and nonoptimal subnetwork of std = 35%.

Fig. 10. Encephalization in actual network and optimal subnetwork and optimization of complete network. Histogram of number of neurons along the animal.

Fig. 11. Histogram of synapse location in the animal assuming that synapses are at midpoints between soma.

Fig. 12. Interaction matrices for nonoptimal and near-optimal neurons. (A) Change in position error in each of the near-optimal neurons (bottom) when removing one of the nonoptimal neurons (left) from the network. Neuron labels in the figure are positioned such that most damaging nonoptimal neurons are at the bottom and most damaged near-optimal neurons to the left. Only the 12 ´ 24 matrix at the bottom-left of the complete 34 ´ 184 matrix (SI Fig. 13) is shown here. (B) Same as A but for the change in position error of nonoptimal neurons. Shown are the 15 ´ 22 of most damaging and most damaged neurons (see SI Fig. 14 for the complete 34 ´ 34 matrix).

Fig. 13. Interaction matrix for nonoptimal and near-optimal neurons. Shown is the change in position error in the near-optimal neurons (bottom) when removing one of the nonoptimal neurons (left) from the complete network. Neuron labels in the figure are positioned such that most damaging nonoptimal neurons are at the bottom and most affected near-optimal neurons are to the left.

Fig. 14. Interaction matrix between nonoptimal neurons. Shown is the change in position error in the nonoptimal neurons (bottom) when removing one of the nonoptimal neurons (left). Neuron labels in the figure are positioned such that most damaging nonoptimal neurons are at the bottom and most affected nonoptimal neurons are to the left.

This function has a minimum where partial derivatives with respect to the positions of all neurons are zero, for all p = 1,...,N, with

,

and the Kronecker delta (=1 when i = j and 0 otherwise). Because of the Kronecker delta functions, most terms vanish. However, we keep most of them for later convenience. After regrouping terms and removing some of the vanishing terms, we get

As the matrix A is symmetric, the first and second terms are identical, giving

Regrouping terms we obtain

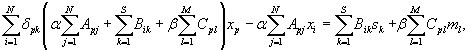
where we have eliminated vanishing terms in the second term. Renaming the summation index j for i in the second term, and using the definition of Q in Eq. 2b, we can write

This is a system of N equations with the soma positions x_i as the N unknowns. In matrix notation we can write it as , where , and are column vectors that store the positions of all neurons, sensors and muscles, respectively. Multiplying from the left by both members of the matrix equation, we obtain the solution , as given in Eq. 2a.

where is the number of sensory and motor neurons. The minimum is characterized by vanishing partial derivatives

Note that the neuron positions can be taken out from the sums and Eq. 4 in the main text is then obtained directly.

Robustness of Predictions Using the Center-of-Mass Formula, Eq. 4. First, the prediction is almost independent of any parameters. Although the parameter appears in Eq. 4, only 13 out of 199 neurons are both sensory and motorneurons, and for the remaining 186 neurons the equation further reduces to separate expressions for sensory and motorneurons, which are independent of . In practice, predictions improve for increasing b but, in any case, the maximum difference is for the mean error position and for the clustering error. For different powers for the wire cost in Eq. 3, we found differences in position and clustering errors to be and , respectively (see next section below). Even when changing the connectivity matrix B to a matrix of 1s and 0s, the difference was found to be for mean error position and for clustering error. The reason for this strong robustness is that, although some of the patches of sensors and muscles to which each ganglion is connected are relatively large, each neuron connects to a much smaller mini-patch of sensors or muscles. Fig. 2F in the main text gives the statistics of the size of the mini-patch a single neuron connects to, with a maximum at zero length (single connections) and another maximum at a length of 5% the total length of the animal. Any sensible wiring economy approach for this subnetwork would predict the location of each neuron somewhere within the length of the mini-patch it connects to. Therefore, any modification of the model's parameters should cause position differences below 5% the length of the animal. As mentioned above, on average, these differences are below 1%, and affect the clustering error less than 0.3% (adding up all the contributions listed above, due to changing parameters and and the detailed form of matrix B).

,

with the cost associated to neuron i. Therefore, the optimization problem reduces to numerically obtain the optimal position of each neuron separately by minimizing its individual cost. A Newton's minimization algorithm was used for these calculations. This algorithm starts at position 0.5, estimates the position of the minimum from the two first derivatives at that point, and iterates until convergence. As cost functions are convex for exponents greater than 1, convergence to the global minimum is guaranteed.

For the general optimization problem, we tested polynomial costs up to degree 4, restricted to be monotonically increasing and convex. Using a multidimensional Newton's algorithm and a multidimensional greatest-gradient algorithm, we obtained no relevant differences compared with quadratic cost. Therefore, predictions seem to be robust independently of the cost function as long as it is monotonically increasing and convex, and the quadratic case seems to be a good representative function.

Estimate derivative at the end, using the last 6 points.

Set Point of Separation = Number of Neurons

If derivative at the end > 0

Do

For c=1 to Point of Separation

Slopes(c)=(e_p(Point of Sep.) - e_p(c))/(Point of Sep. - c)
End for

If Max(Slopes) > Derivative at the end / n

Point of Separation=Index(Max(Slopes))

End if

Loop while Max(Slopes) > Derivative at the end / n

End if.

1. Hall K (1970) Management Sci 17:219-229

2. Chklovskii DB (2004) Neural Comput 16:2067-2078