Feedback and Feedforward Control of Frequency Tuning to Naturalistic Stimuli

Abstract

Sensory neurons must respond to a wide variety of natural stimuli that can have very different spatiotemporal characteristics. Optimal responsiveness to subsets of these stimuli can be achieved by devoting specialized neural circuitry to different stimulus categories, or, alternatively, this circuitry can be modulated or tuned to optimize responsiveness to current stimulus conditions. This study explores the mechanisms that enable neurons within the initial processing station of the electrosensory system of weakly electric fish to shift their tuning properties based on the spatial extent of the stimulus. These neurons are tuned to low frequencies when the stimulus is restricted to a small region within the receptive field center but are tuned to higher frequencies when the stimulus impinges on large regions of the sensory epithelium. Through a combination of modeling and in vivo electrophysiology, we reveal the respective contributions of the filtering characteristics of extended dendritic structures and feedback circuitry to this shift in tuning. Our results show that low-frequency tuning can result from the cable properties of an extended dendrite that conveys receptor-afferent information to the cell body. The shift from low- to high-frequency tuning, seen in response to spatially extensive stimuli, results from increased wide-band input attributable to activation of larger populations of receptor afferents, as well as the activation of parallel fiber feedback from the cerebellum. This feedback provides a cancellation signal with low-pass characteristics that selectively attenuates low-frequency responsiveness. Thus, with spatially extensive stimuli, these cells preferentially respond to the higher-frequency components of the receptor-afferent input.

Introduction

Animals must efficiently process sensory stimuli to successfully interact with their environment. Thus, sensory neuron tuning must match the spatiotemporal frequency content of naturalistic stimuli (Rieke et al., 1995; Machens et al., 2001). Anatomical studies in several systems have shown that feedback projections from higher centers often vastly outnumber feedforward projections from the periphery (Cajal, 1909; Hollander, 1970; Ostapoff et al., 1990; Sherman and Guillary, 2002). It is generally agreed that this feedback can modify the flow of sensory information from the periphery, thus mediating attention and facilitating the extraction of relevant information. Various operations such as selective gating (Sherman, 2001; Le Masson et al., 2002), gain control (Bastian, 1986a), modulation of receptive field (RF) properties (Wang, 2003), and control of bursting firing patterns (Krahe and Gabbiani, 2004) can be mediated by feedback pathways. The precise mechanisms by which feedback mediates these effects are, however, poorly understood.

This study concentrates on central sensory neurons, pyramidal cells, of the electrosensory lateral-line lobe (ELL) of weakly electric fish. These fish generate an electric field that surrounds their bodies, the electric organ discharge (EOD), which is continuously monitored by electroreceptors scattered over the fish’s surface (for review, see Turner et al., 1999). The electroreceptor afferents provide excitatory synaptic input to basilar pyramidal cells, also known as E cells, and provide disynaptic inhibitory input to nonbasilar pyramidal cells, or I cells (Maler, 1979; Maler et al., 1981; Saunders and Bastian, 1984). Pyramidal cells also receive massive projections from higher brain centers (Sas and Maler, 1983, 1987; Berman and Maler, 1999), and, as in other systems, this feedback is known to participate in gain control mechanisms as well as the selective attenuation of redundant stimulus patterns (Bastian, 1999; Bastian et al., 2004).

Behaviorally relevant electrosensory stimuli consist of amplitude modulations (AMs) of the ongoing EOD and can be broadly subdivided into two categories: electrolocation and electrocommunication stimuli. The former include stimuli generated by small aquatic invertebrate prey that cause spatially restricted AMs, which are dominated by frequencies <25 Hz. Electrocommunication signals, in contrast, impinge on large areas of the sensory surface and include signals such as “chirps,” which are dominated by higher frequencies with peak power at ~50 Hz (Zupanc and Maler, 1993). ELL pyramidal cells show vastly different responses to stimuli of differing spatial extent (Bastian et al., 2002, 2004; Chacron et al., 2003; Doiron et al., 2003). In particular, the frequency selectivity (i.e., tuning) of ELL pyramidal cells has been shown recently to change, contingent on the spatial characteristics of electrosensory stimuli, and this tuning shift ensures a near-optimal match between the AM frequency response of the cells and the spectral characteristics of prey-like versus communication-like stimuli (Chacron et al., 2003).

Here, we describe the neural mechanisms that are responsible for the control of pyramidal cell frequency tuning. Through a combination of modeling and in vivo recordings in normal, lesioned, and pharmacologically manipulated animals, we reveal the roles of pyramidal cell morphology (cable properties) and feedback input in determining their frequency tuning.

Materials and Methods

Experimental preparation

The weakly electric fish Apteronotus leptorhynchus was used in these studies. Fish were housed in groups of 3–10 in 150 L tanks, temperature was maintained at 26–28°C, and water resistivity varied from 2000 to 5000 Ω·cm. Experiments were performed in a 39 × 44 × 12-cm-deep Plexiglas aquarium with water recirculated from the animal’s home tank. Animals were artificially respirated with a continuous water flow of 10 ml/min. Surgical techniques were the same as those described previously (Bastian, 1996a,b); all procedures were in accordance with animal care and use guidelines of the University of Oklahoma.

Recording

Extracellular single-unit recordings from pyramidal cells were made with metal-filled micropipettes (Frank and Becker, 1964). Recording sites, determined from surface landmarks and recording depths, were limited to the lateral and centrolateral ELL segments. Intracellular recordings from receptor afferents were made with KCl-filled micropipettes, with electrode resistance ranging from 70 to 150 MΩ. Extracellularly recorded spikes were detected with window discriminators and were time stamped (resolution, 0.1 ms; CED 1401plus hardware and Spike2 software; Cambridge Electronic Design, Cambridge, UK). Intracellularly recorded spikes were detected in the same manner, and membrane potential was analog-to-digital converted at 10 kHz.

RAM stimulation

The stimulation protocol was described previously in detail (Bastian et al., 2002). The stimuli consisted of random AMs of an animal’s own EOD. Random AMs were produced by multiplying an EOD mimic with zero-mean band-limited Gaussian white noise with an upper cutoff frequency of 120 Hz. The EOD mimic consisted of a train of single sinusoids of a duration slightly less than that of a single EOD cycle synchronized to the zero-crossings of the animal’s own EOD. The resulting signal was presented to the animal with either global or local geometry via a World Precision Instruments (model A395; Sarasota, FL) linear stimulus-isolation unit. Global stimulation geometry was achieved via two silver chloride electrodes placed ~19 cm lateral to either side of the fish, creating relatively spatially homogeneous stimuli on both sides of the fish. Local stimuli were generated by positioning a small dipole (2 mm tip spacing) 2–3 mm lateral to the fish and positioned within the RF center. Global and local stimulus intensities were essentially identical to those used in a previous study (Bastian et al., 2002). Both were calibrated to cause similar electroreceptor-afferent responses. Overall, the mean contrast level averaged 11.7 ± 0.7% (n = 77). Contrast values were not significantly different for the different subpopulations of cells studied. Stimuli were applied for at least 100 s to obtain sufficient amounts of data.

Lesions and pharmacology

The connection between the ganglion of the anterior lateral-line nerve and the ELL on one side of the body was severed to remove electroreceptor-afferent input to the pyramidal cells recorded from. This removes all ipsilateral afferent input, but higher electrosensory centers continue to receive electrosensory information from the contralateral ELL. A portion of the descending electrosensory input to the ipsilateral ELL remains, because the major feedback pathways project bilaterally to the ELLs (Sas and Maler, 1983, 1987). Subsets of ELL pyramidal cells responded with either an increase or decrease in activity to increased receptor-afferent input from the contralateral side of the body. However, we cannot determine whether these subsets correspond to the E cell/I cell subsets of normal animals. Because responses of these subsets, other than response polarity, did not vary, these data were pooled. In separate experiments, descending pathways to the ELL were eliminated by microknife cuts, beginning at the lateralmost aspect of the brain at the level of the caudal optic tectum and continuing caudomedially to the midline at an angle of ~45° to the mediolateral axis. The knife was held in a micromanipulator, and the cut extended from the surface of the brain to the floor of the brain case. This procedure severs the descending electrosensory pathways, as well as the ipsilateral lateral lemniscus, which conveys ELL output to the contralateral midbrain. After these experiments, brains were fixed in situ and then subsequently dissected to verify the extent of the lesions.

Micropressure ejection techniques were used to apply the non-NMDA glutamate antagonist 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) to local regions of the ELL molecular layer containing the apical dendrites of a recorded cell. Multibarrel pipettes were pulled to a fine tip and broken back to a total tip diameter of ~10 μm. One barrel was filled with a 1 mM solution of disodium CNQX, and a second was filled with 1 mM glutamate. After a well isolated single-unit extracellular recording was established, the pressure pipette was slowly advanced into an appropriate region of the ELL molecular layer while periodically ejecting “puffs” of glutamate. Typically, ejection duration ranged from 50 to 100 ms, and ejection pressure was usually 40 psi. As described previously (Bastian, 1993), proximity to the recorded cell was indicated by short-latency increases in firing rate evoked by glutamate ejection. After correct placement, CNQX was delivered as a single dose or a series of pulses (e.g., 100 ms puffs at 0.5 Hz for 20 s), and this treatment typically resulted in alterations in pyramidal activity, lasting ~5 min.

Data analysis

All data analysis was performed using Matlab (Math-Works, Natick, MA). Two functional categories of electrosensory lateral-line lobe pyramidal cells exist: basilar pyramidal cells (E cells) and non-basilar pyramidal cells (I cells). The former receive direct excitatory receptor-afferent input, whereas the latter are driven disynaptically via inhibitory interneurons. Several morphological and physiological features vary continuously with pyramidal cell spontaneous-firing rate (Bastian and Courtright, 1991; Bastian and Nguyenkim, 2001; Bastian et al., 2004). To facilitate descriptions of differences among pyramidal cells, we compared subpopulations taken from the low- and high-frequency regions of the firing-rate continuum. Cells with spontaneous firing rates <15 spikes/s were categorized as superficial cells, and these reside in the uppermost regions of the ELL laminas. Cells residing deep within the ELL laminas have high-firing rates, and those with spontaneous rates ≥30 spikes/s were categorized as deep pyramidal cells. Cells between these limits (intermediate cells) were also studied and included in the analysis of the entire population.

The phase relationships between the firing times of a neuron and the EOD waveform were summarized as phase histograms, and the magnitude of phase locking was quantified by the vector strength (Mardia and Jupp, 1999). The coherence between the spike train of a neuron and the stimulus (EOD modulation waveform) was computed as C(f) ≡ P_sx(f) ²/[P_ss(f) P_xx(f)], where P_ss(f) and P_xx(f) are the power spectra of the stimulus and spike train, respectively, and P_sx(f) is the cross-spectrum between the stimulus and the spike train. In these analyses, frequency f refers to the temporal amplitude modulation frequency of the EOD and not to the spectral characteristics of the EOD itself. All of these quantities were estimated using multitaper techniques (Jarvis and Mitra, 2001). We obtained a lower bound on the mutual information (MI) rate per frequency: MI(f) = −log₂[1 − C(f)] (Rieke et al., 1996), and this is expressed in bits per second per hertz. The total mutual information rate in bits per second increases linearly as a function of the firing frequency of a cell (Borst and Haag, 2001). To facilitate comparisons among neurons with significantly different firing rates, we normalized the mutual information rate to the spike rate. This was done by dividing MI(f) by the mean firing rate of the cell during stimulation to obtain the mutual information rate in bits per spike per hertz. Nonlinearities could cause discrepancies between this lower bound and the true information rate of the system (Cooper et al., 2000). However, a previous study of the electrosensory system in a related species found that the addition of nonlinear terms made little difference (Metzner et al., 1998). We thus assume that this technique accurately measures the information transmission capabilities of the sensory neurons studied here. Spike-triggered averages (STAs) were obtained by averaging the EOD modulation waveform surrounding each spike. In cases in which STAs were pooled, the negative-going STAs of I cells, or I-like responses after afferent input removal, were inverted before analysis.

Modeling

Our model consists of n = 50 receptor afferents converging onto the basilar dendrite of a pyramidal cell; this is approximately the convergence estimated for the centrolateral segment of the ELL (L. Maler, unpublished observations). Each receptor afferent is modeled as a leaky integrate-and-fire neuron with dynamic threshold. This simple model reproduces the experimental data with surprising accuracy (Chacron et al., 2000, 2001). The voltage V_i and threshold θ_i of receptor afferent i obey the following differential equations over times between action potentials:

$${\stackrel{.}{V}}_i=-\frac{V_i}{{\tau }_V}+\frac{I_i}{{\tau }_V}$$

and θ_i = (θ₀ − Θ_i)/τ_θ, with I_i given by the following: I_i = [S(t) + A₀]sin(2πf_EODt) × Θ[sin(2πf_EODt)][1 + σξ_i(t)], where f_EOD is the EOD frequency, Θ(.) is the Heaviside function [Θ(x) = 0, if x < 0; otherwise, Θ(x) = 1], and ξ_i(t) is Gaussian white noise with zero mean and unit variance. S(t) is the stimulus, which we consider to be low-pass-filtered Gaussian white noise with the same cutoff (120 Hz) used in the experiments. When, V_i(t) = θ_i(t), V_i is reset to 0, θ_i is incremented by Δθ and an action potential is said to have occurred. Parameter values used were the same as those used by Chacron et al. (2001), except that σ = 0.2, f_EOD = 700 Hz, and A₀ = 0.2613 mV.

The pyramidal cell basilar dendrite is modeled by a cylindrical cable of length L. The voltage along the cable is described by the following cable equation:

$${\tau }_{\mathrm{m}}\frac{\partial V(x,t)}{\partial t}=-V(x,t)+E_{\text{leak}}+{\lambda }_{\mathrm{c}}^2\frac{{\partial }^{2}V(x,t)}{\partial x^2}+\rho \zeta (x,t)+G\delta (x-0)\sum _{i=1}^N\sum _{j=1}^{K_i(t)}\frac{t-t_{ij}}{{\tau }_{\alpha }}exp\left[-\frac{t-t_{ij}}{{\tau }_{\alpha }}\right]+\delta (x-L)G_{N}N(t),$$

where τ_m is the membrane time constant, E_leak is the leak reversal potential, λ_c is the space constant, ζ(x,t) is zero-mean Gaussian white noise with unit variance that is uncorrelated in both space and time, t_ij is the jth firing time of afferent i, K_i(t) is the spike count of afferent i, δ(x) is the δ function, and N(t) is a feedback signal originating in higher brain centers, whereas G_N is the feedback gain. We took the feedback signal to be a low-pass- (first-order Butterworth) filtered version of the stimulus S(t) with 40 Hz cutoff frequency and a delay of 15 ms to account for conduction delays to and from the higher centers. The synaptic EPSC is modeled as an α function with a short time constant τ_α, as observed in vitro (Berman and Maler, 1998), with G being the feedforward gain. Anatomical studies (Bastian and Courtright, 1991) show that pyramidal cells vary considerably in apical and basilar dendritic morphology. Deep pyramidal cells have shorter and thinner basilar dendrites than the most superficial types; therefore, we modeled two different basilar dendrites representing the extremes of their morphological variation (for cell morphologies, see Fig. 8A). In vitro studies have reported membrane time constants of ~18 ms (Berman and Maler, 1998), we took slightly lower values to account for in vivo conditions. Because we are interested in the effects of basilar dendritic dimensions on frequency response characteristics and because the membrane time constant is independent of surface area, we assumed that deep and superficial cells had similar time constants. The basilar dendrite of the deep cell was given a shorter length and smaller space constant (L = 50 μm; λ_c = 80 μm) than that of the superficial cell (L = 500 μm; λ_c = 120 μm). In vitro patch-clamp and imaging studies of several neuron types have reported space constants on the order of 200 μm (Magee and Cook, 2000; Williams and Stuart, 2002; Djurisic et al., 2004). Basilar dendrites of pyramidal cells are heavily invested with inhibitory synaptic terminals of ovoid cells (Maler and Mugnaini, 1994). Because these neurons display high rates of spontaneous activity (Bastian et al., 1993), the intense synaptic bombardment in vivo is expected to further reduce the space constant. The cable equation was solved numerically using M compartments and an integration time step of 0.01 ms. The last compartment (x = L) was endowed with a spiking mechanism: each time the voltage reached a threshold θ_pyr = −57.2 mV, it was reset to V_reset = −80 mV, and an action potential was said to have occurred. The spike trains from the model were analyzed in the same way as the in vivo data. Parameter values were chosen in accordance with existing data and to mimic the effects of local and global stimulation geometries. Table 1 summarizes the parameter values used for the different simulations. The increased G under global stimulation represents increased receptor-afferent input caused by spatial saturation of the RF center. Consistent with results of this study and previous findings (Bastian et al., 2004), the feedback input is only present during global stimulation for superficial cells. The increased G_N represents recruitment of a negative-image feedback input to superficial cells caused by activation of the antagonistic RF surround of the cell under global stimulation. Because global stimulation of the deepest cells results in essentially no change in tuning (see Figs. 3B, 8E), we assume that the feedback input to these cells is minimally effective. Therefore, we set G_N = 0 during both global and local deep cell simulations, as in previous modeling studies (Bastian et al., 2004). The decreased membrane time constant under global stimulation simulates increased ovoid cell synaptic input to the basilar dendrite.

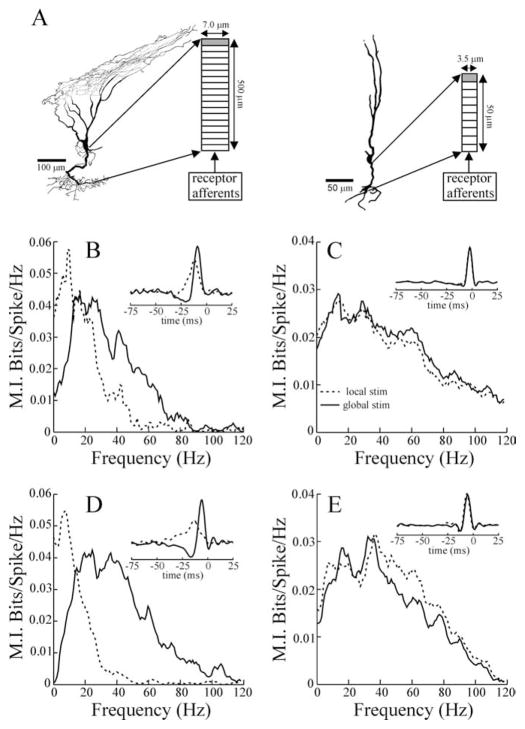
Figure 8.

A, Examples of superficial and deep E cells reconstructed from intracellular fills. The importance of the long basilar dendrite of the superficial E cells is highlighted by the anatomical characteristics of the reconstruction shown in A. This cell was found far laterally in the ELL, in which the distance between the pyramidal and deep fiber layers (site of receptor-afferent termination) is minimal, yet the dendrite followed a sinuous trajectory that substantially increased its length. The diagrams to the right of each cell illustrate the dimensions and compartmentalization of the basilar dendrite models. The shaded compartment contained a spike-generating mechanism. B, C, Mutual information curves and STAs (inset) resulting from the superficial and deep pyramidal cell models, respectively. Firing rates for the superficial and deep cell simulations were 14.7 and 36.5 spikes/s, respectively, with local stimulation (stim) and 13.4 and 34.3 spikes/s with global stimulation. D, E, Example MI curves and STAs (insets) from example single superficial (13.6 spikes/s spontaneous rate) and deep (32.9 spikes/s spontaneous rate) E cells. Dashed and solid lines indicate local and global stimulus geometries, respectively.

Table 1.

Parameter values used for the pyramidal cell dendrite compartmental model

	Deep local/global	Superficial local/global
M	10/10	18/18
L (μM)	50/50	500/500
ρ (mV)	2/2	4/4
G (mV μM)	20/21.28	63/83
GN (mV μM)	0/0	0/15
Eleak (mV)	−70/−70	−70/−70
λc (μM)	80/80	120/120
τα (ms)	0.2/0.2	0.2/0.2
τm (ms)	12/9	12/9

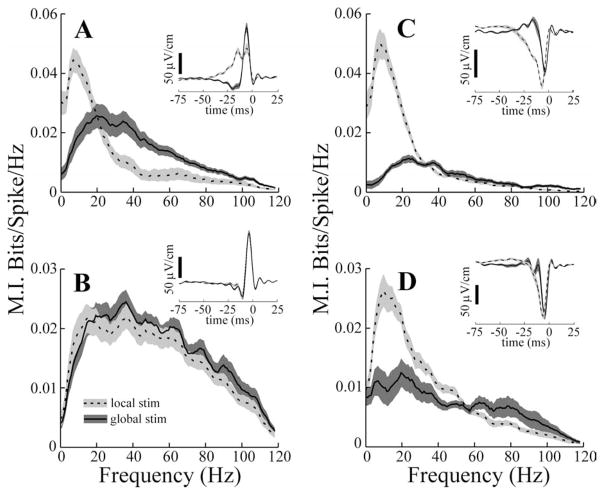
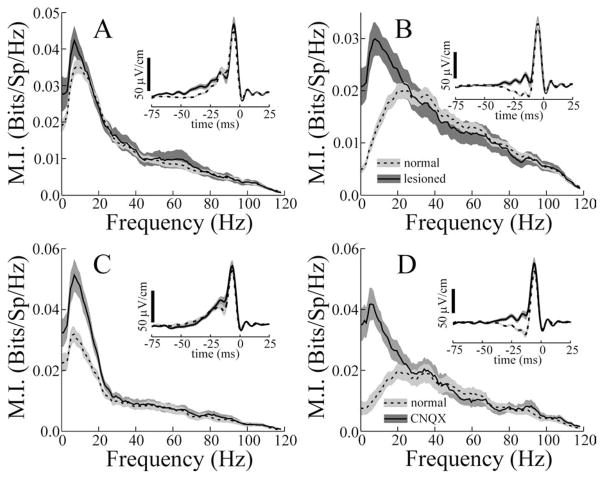
Figure 3.

Mutual information curves for subsets of ELL pyramidal cells. A, B, Mean responses of superficial (firing frequency ≤15 spikes/s) and deep (firing frequency ≥30 spikes/s) E cells, respectively, to locally applied (dashed line) and globally applied (solid line) 0–120 Hz RAM stimuli (stim). C, D, Responses of superficial and deep I cells, respectively. A–D, Insets, Mean spike-triggered averages for the same cell populations. Dashed and solid lines have the same meaning in all panels and insets. Gray areas indicate ± 1 SEM of the average curves.

Results

Effects of local and global stimulation on pyramidal cell frequency tuning

An example of the spatially induced pyramidal cell (P cell) frequency tuning shift is shown in Figure 1. Random amplitude modulations (RAMs) of the EOD were presented with both local and global geometries to mimic the spatial characteristics of electrolocation and electrocommunication stimuli, respectively. Responses to these were quantified as measures of MI, normalized by the mean firing frequency of the cell during the stimulus presentation. Local RAMs applied to the RF center of this cell evoke responses preferentially driven by low-frequency components (Fig. 1, dashed line). The same stimulus waveform applied via global geometry results in a shift of the peak responsiveness of the cell to higher frequencies (Fig. 1, solid line). Pyramidal cell frequency response properties measured in this manner closely parallel those determined from conventional tuning curves based on responses to sinusoidal AMs of different frequencies (Chacron et al., 2003).

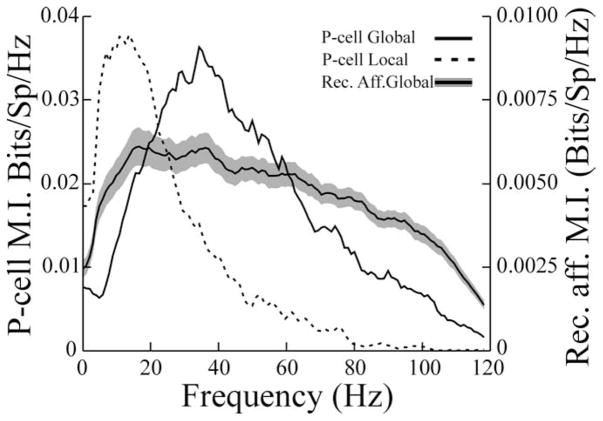
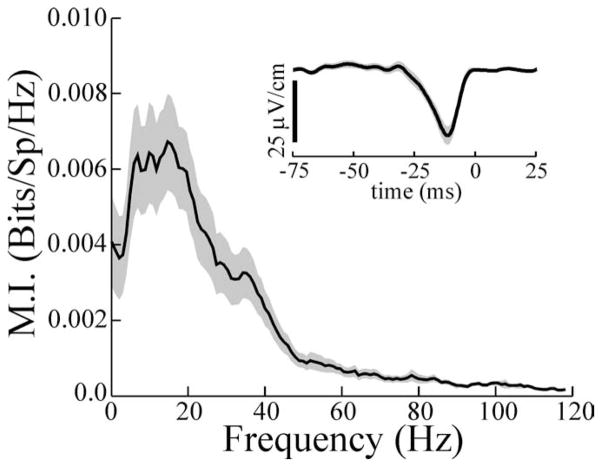
Figure 1.

Mutual information curves for a typical basilar pyramidal cell describing responses to local RAM stimulation (dashed line) and global RAM stimulation (solid line). The firing frequency of this cell averaged 24.7 and 25.3 spikes/s during local and global stimulation, respectively. Stimulus contrasts were 9 and 10% for local and global stimuli, respectively. The solid line bracketed by the gray area shows the average mutual information curve ± 1 SEM for 25 receptor afferents stimulated with the same RAM with similar contrasts. Note different ordinates for the P-cell and receptor afferents (Rec. Aff.). Bits/Sp/Hz, Bits per spike per hertz.

Seventy-seven pyramidal cells were studied with this stimulus paradigm, and changing the stimulus geometry from local to global resulted, on average, in a more than twofold increase in the frequency at which peak information rates occurred (F_p) (Table 2, all cells) (compare F_p global with F_p local; p ≪ 0.001; pairwise t test). In addition to measuring the frequency associated with peak MI rates, the widths of the MI curves at one-half of the peak rate were measured as an estimate of the response bandwidth (B_w). This measure was also larger for responses to global stimulation (Table 2, all cells) (B_w global versus B_w local; p ≪ 0.001). Averages of mutual information per spike were computed over frequency bands of 0–20 Hz (MI_low) and 40–60 Hz (MI_high) to assess the relative abilities of the cells to encode high- and low-frequency information under the two stimulus regimes (Chacron et al., 2003). The highest values of MI_low occurred in response to local stimuli, whereas the highest value for MI_high occurred with global stimulation (Table 2) (p values ≪ 10⁻³). The same stimulus was applied globally while recording was done from electroreceptor afferents (Fig. 1). In Figure 1, the solid line bracketed by the gray area shows the average MI rates ± 1 SEM, recorded from 25 receptor afferents. Receptor-afferent responses have, on average, a wide-band response when information-theoretic measures are used. We note that this differs from previous estimates of receptor-afferent tuning based on conventional measures (Bastian, 1981). Information tuning curves take into account the amount of noise present in the baseline activity of a neuron and are thus more realistic measures of tuning from the point of view of the postsynaptic cell (Chacron et al., 2005). This wide-band receptor-afferent response suggests that P cells selectively filter the electroreceptor input and that the filter characteristics are sensitive to the spatial aspects of the stimulus.

Table 2.

Summary of mutual information measures for pyramidal cells in normal animals

Cell type	All cells	Superficial E cells	Deep E cells	Superficial I cells	Deep I cells
Fp global (Hz)	33.3 ± 2.1	30.4 ± 4.0	38.3 ± 5.9 (NS)	28.9 ± 3.8	31.5 ± 9.4 (NS)
Fp local (Hz)	15.9 ± 1.8	9.0 ± 0.7	42.1 ± 6.2**	9.1 ± 0.6	12.2 ± 0.9*
Bw global (Hz)	56.5 ± 2.5	49.1 ± 4.3	78.8 ± 3.7**	44.4 ± 5.2	55.8 ± 7.5 (NS)
Bw local (Hz)	35.6 ± 2.8	21.4 ± 1.2	74.8 ± 6.9**	21.1 ± 1.2	31.4 ± 2.9*
MIlow global (bits/sp/Hz)	0.013 ± 0.001	0.017 ± 0.003	0.015 ± 0.002 (NS)	0.006 ± 0.001	0.010 ± 0.002 (NS)
MIlow local (bits/sp/Hz)	0.029 ± 0.001	0.036 ± 0.003	0.017 ± 0.002**	0.040 ± 0.003	0.021 ± 0.002**
MIhigh global (bits/sp/Hz)	0.014 ± 0.001	0.016 ± 0.002	0.021 ± 0.001 (NS)	0.006 ± 0.001	0.007 ± 0.001 (NS)
MIhigh local (bits/sp/Hz)	0.010 ± 0.001	0.006 ± 0.002	0.019 ± 0.002**	0.005 ± 0.0005	0.008 ± 0.001**
n	77	18	14	11	8

Comparisons of mean values for superficial and deep E and I cells were made with t tests.

^*p < 0.05;

^**p < 0.001.

bits/sp/Hz, Bits per spike per hertz; NS, not significant.

Pyramidal cell frequency tuning varies with cell type and morphology

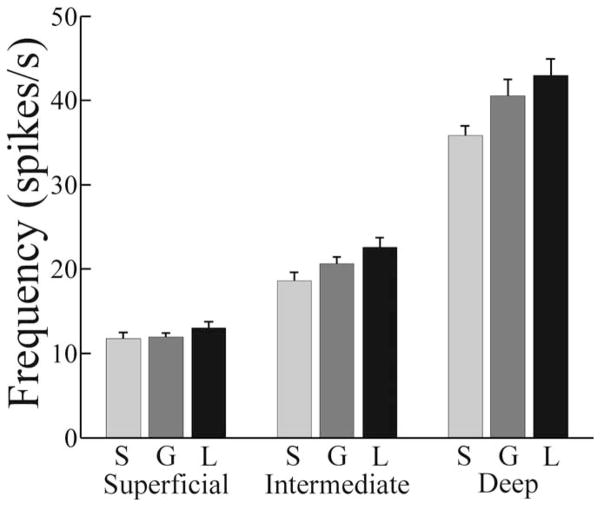
Two functional categories of ELL P cells exist. Basilar pyramidal cells, also known as E cells, receive direct excitatory receptor-afferent input; however, nonbasilar pyramidal cells, also known as I cells, are driven disynaptically via inhibitory interneurons. E cells are excited by increases in EOD amplitude, whereas I cells are inhibited (Maler et al., 1981; Saunders and Bastian, 1984). Intracellular recording and labeling studies showed that pyramidal cells within both categories vary markedly in morphology, particularly in apical dendritic size, and position within the ELL laminas (Bastian and Courtright, 1991; Bastian et al., 2004). In addition, the length of the basilar dendrites of E cells varies systematically, being shorter for the cells found deeper within the ELL pyramidal cell layer. These morphological features, as well as numerous physiological properties, including RF organization, adaptation time course, the presence or absence of specific neurotransmitter receptor subtypes, and intracellular signaling systems are each strongly correlated with the firing rate of a cell (Bastian and Courtright, 1991; Bastian and Nguyenkim, 2001; Bastian et al., 2002, 2004). Therefore, several morphological and functional characteristics can be inferred from the firing rate of a cell. In addition to describing the sensitivity of pyramidal cells to stimulus geometry across the firing rate continuum, we also compared subpopulations at the extremes of this continuum. Cells found most superficially within the ELL pyramidal cell lamina have the largest apical dendritic tree and, in the case of E cells, the longest basilar dendrites. These cells display the lowest firing rates, and we defined superficial cells as those having spontaneous rates of ≤15 spikes/s. Cells found deepest within this lamina have the smallest apical dendritic trees, the shortest basilar dendrites (E cells), and the highest firing rates. Cells with spontaneous rates of ≥30 spikes/s are categorized as deep cells. The remainder of the population is referred to as intermediate cells. Figure 2 summarizes the spontaneous firing frequencies as well as firing frequencies during global and local stimulation for these pyramidal cell subsets. The firing rates of superficial cells were not significantly different, contingent on the presence or absence of stimulation or stimulation geometry; however, the firing rates of intermediate and deep cells were significantly higher during stimulation, and local stimulation caused the greatest increases.

Figure 2.

Firing rates of pyramidal cell subcategories, with and without RAM stimulation. S, Spontaneous firing; G, firing during global stimulation; L, firing rates during local stimulation. The firing rate of superficial cells was insensitive to the presence or absence of stimulation (F = 1.17; df = 2.88; p = 0.32; one-way ANOVA; n = 29). The presence of RAM stimulation did significantly increase the firing rates of intermediate cells (F = 4.19; df = 2.75; p = 0.02; one-way ANOVA; n = 26). Firing frequency during local stimulation was significantly greater than spontaneous, but firing frequency during global stimulation was not. RAM stimulation also significantly increased the firing rates of deep cells (F = 4.42; df = 2.63; p = 0.02; one-way ANOVA; n = 22). Firing frequency during local stimulation was significantly greater than spontaneous, but firing frequency during global stimulation was not. Error bars indicate 1 SEM.

Figure 3 shows plots of means ± 1 SEM of the mutual information measure for the superficial and deep subsets of both E and I cells. Local stimulation of deep and superficial E cells resulted in mutual information curves that are obviously different (Fig. 3A, B, dashed lines). F_p was significantly higher for deep compared with superficial E cells (Table 2, compare superficial and deep E cells, F_p local). Mean F_p values were also significantly greater for deep versus superficial I cells; however, the magnitude of the increase for deep cells was far smaller (Table 2). The dependence of the F_p measure on cell type, inferred from firing frequency, is preserved over the entire population of cells studied. The high correlation between the F_p local measure and firing rate (r = 0.66; p < 0.001; n = 77) supports the idea that differences in cell morphology are related to frequency tuning for local stimuli. However, the lack of significant differences among F_p global values of the superficial versus deep subcategories of E and I cells (Table 2), as well as the lack of a significant correlation between F_p global and firing rate for the entire population (r = 0.2; p = 0.1; n = 77), indicates that factors in addition to cell morphology probably contribute to the tuning to global stimuli. In addition to the differences in F_p values seen with local stimulation, B_w, MI_low, and MI_high all differed significantly for superficial and deep P cells (Table 2). All of these measures were also significantly correlated with the firing rates of the cells.

MI curves resulting from global stimulation, however, were essentially independent of cell category. Neither F_p, MI_low, or MI_high values for deep and superficial cells differed significantly (Table 2), and none of these measures correlated with the firing rates of the cells. Only the B_w measure showed significant variation with cell category under global stimulation (Table 2).

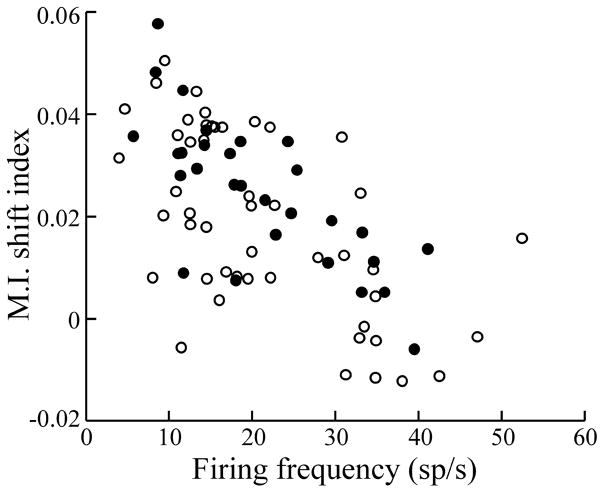
The overall shift in frequency tuning resulting from the transition from local to global geometry was quantified using a mutual information shift index, defined as ΔMI_low − ΔMI_high, where Δ represents the difference between the values obtained with local and global geometries. Figure 4 shows the MI shift index as a function of cell firing frequency. A negative correlation with firing rate (r = −0.64; p ≪ 10⁻³; n = 77) is observed. Therefore, superficial cells showed a much larger change in frequency tuning than deep (high firing rate) cells when stimulus geometry was changed from local to global.

Figure 4.

Plot of mutual information shift index (see Results) versus the firing rate of the cells. E cells and I cells are indicated by open and filled symbols, respectively. Correlation coefficient for pooled data, r = −0.64. n = 77; p ≪ 10⁻³. sp, Spikes.

STAs were also computed from the responses of each cell to the RAM stimuli to recover the temporal features of the EODAM that were most effective in driving the cells. The mean STAs for all P-cell subtypes are shown in the insets of Figure 3. With local stimulation, superficial firing of E cells is preferentially evoked by a slow rise in EOD amplitude, followed by a second, rapid rising phase (Fig. 3A, inset, dashed line). The same is seen for superficial I cells but with reversed polarity (i.e., the slow rise/fast rise is a slow fall/fast fall) (Fig. 3C, inset, dashed line). With global stimulation, there are major differences in the STAs of superficial cells. In the case of E cells, the initial slow rise is replaced by a slow dip followed by a fast rise, similar to the second STA phase seen with local stimulation (Fig. 3A, inset, solid line). Analogous changes occur for superficial I cells but with opposite polarity (Fig. 3C, inset, solid line). STAs with global stimulation are very similar to those described previously in a related fish (Eigenmannia) (Metzner et al., 1998); similar biphasic STAs have also been observed in other sensory neurons (Warland et al., 1997; Reinagel et al., 1999; Bair and Movshon, 2004; Svirskis et al., 2004). Deep cells, however, showed only minor changes in the STA as a function of stimulus geometry. With either local or global stimuli, deep E and I cells are preferentially driven by rapid EOD AM transients similar in time course to the STAs of superficial cells given global stimulation [Fig. 3, compare B, D (insets, solid and dashed lines) with A, C (solid lines)].

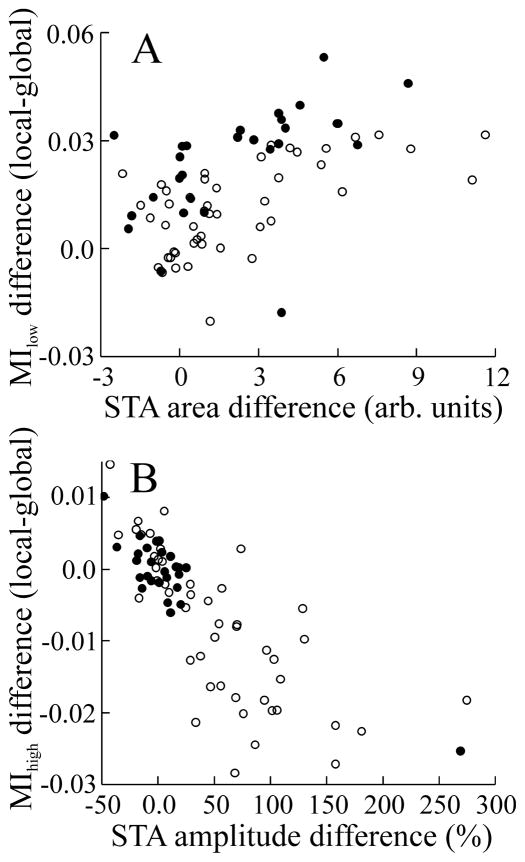
Changes in the STA as a function of stimulus geometry were quantified by two measures: the change in STA area, which was obtained by integrating STAs, and the change in STA peak-to-peak (p–p) amplitude. Both measures were correlated with firing rate (for area change, r = −0.56, p ≪ 0.001, n = 76; for p–p amplitude change, r = −0.30, p = 0.008, n = 76). Changes in the low- and high-frequency regions of the MI curves were also related to different specific STA features (Fig. 5A, B). The increase in MI_low for both E and I cells, attributable to the change from global to local geometry, is significantly correlated with the increase in STA area (Fig. 5A). Changes in MI_high were negatively correlated with changes in STA p–p amplitude (Fig. 5B). Changing from local to global stimulus geometry results in the replacement of the initial slow rise with a negative deflection, thereby reducing low-frequency responsiveness. Removal of the slow rise also unmasks the fast STA component, thereby enhancing high-frequency responsiveness. This effect is strongest for the superficial E cells and nearly absent in the deep E and I cells.

Figure 5.

Plots of changes in mutual information measures versus changes in STA features. A, Change in MI_low (local–global) as a function of change in STA area (r = 0.53; n = 76; p ≪ 10⁻³). B, Change in MI_high versus percentage change in STA p–p amplitude (r = −0.78; n = 76; p ≪ 10⁻³). Open symbols indicate data from E cells; filled symbols indicate data from I cells. arb. units, arbitrary units.

In summary, superficial P cells show more pronounced stimulus geometry-dependent changes in MI curves and STAs than do deep cells. P cells receive both feedforward input via electroreceptor afferents and massive feedback inputs from higher-order electrosensory processing stations. The strikingly different morphologies of deep and superficial cells could impact on their abilities to respond to such inputs. The following surgical and pharmacological manipulations were conducted to isolate the contributions of feedforward and feedback pathways in the control of P-cell frequency tuning.

Lesions of feedback inputs to ELL pyramidal cells

To assess the effects of descending inputs to pyramidal cells, we performed brain lesions to isolate the ELL from sources of feedback input (see Materials and Methods). These lesions disrupt direct input from the nucleus praeminentialis dorsalis to the ELL ventral molecular layer (direct feedback pathway) as well as input from nucleus praeminentialis dorsalis to the posterior eminentia granularis (EGp). Output of the EGp provides cerebellar parallel fiber input to the ELL dorsal molecular layer (indirect feedback pathway). In addition, these lesions section the lateral lemniscus, depriving higher electrosensory centers of ascending electrosensory inputs. Figure 6A compares the MI curves and STAs (inset) of P cells from intact animals to those (n = 21) of lesioned animals given local stimulus geometry (dashed and solid lines, respectively). Although firing frequencies still varied among P cells after these lesions, it is unknown whether firing frequencies are still correlated with cell morphology. Data from all cells were pooled and compared with the pooled data from normal animals. Both the MI curve and the STA seen in response to local stimulation were mostly unaffected by the removal of feedback to the ELL. Mean F_p, B_w, MI_low, or MI_high values were not significantly different in lesioned compared with normal animals (Fig. 6). Likewise, the STAs seen with local stimulation were similar in intact and lesioned animals, except for a very slow positive-going phase, from approximately −75 to −25 ms (Fig. 6, solid line), which was accentuated in lesioned fish. This change probably accounts for the higher average responsiveness of cells from lesioned fish to frequencies less than ~5 Hz (Fig. 6A, solid line). Removal of feedback did not significantly affect STA p–p amplitude, as expected given that this treatment did not change MI_high. This result suggests that local stimulation does not significantly activate ELL feedback circuitry and that the low-pass characteristic of pyramidal cells receiving stimuli restricted to their RF centers results from feedforward inputs and/or pyramidal cell intrinsic characteristics.

Figure 6.

A–D, The effects of surgical (A, B) and pharmacological (C, D) disruption of electrosensory feedback to the ELL. Data from E and I cells were pooled. A, Responses to local stimulation. Dashed line, Average MI curve from the population of normal cells studied (n = 77). Solid line, Average MI curves from experiments in which descending feedback was lesioned. F_p, B_w, MI_low, and MI_high values averaged 11.3 ± 2.7 and 33.1 ± 5.1 Hz and 0.033 ± 0.003 and 0.010 ± 0.002 bits/Sp/Hz, respectively (n = 21). sp, Spike. These values did not differ significantly from the mean values from the population of normal cells studied (Table 2). Inset, Mean STAs from these same data sets. B, Responses of the cell populations of A to global stimulation. Line types have the same meaning, and gray areas indicate ± 1 SEM. F_p, B_w, MI_low, and MI_high values averaged 13.6 ± 2.2 and 43.2 ± 6.0 Hz and 0.026 ± 0.003 and 0.013 ± 0.002 bits/Sp/Hz, respectively (n = 21). Inset, Mean STAs from the same data sets. C, Dashed and solid lines indicate mean mutual information curves during local stimulation from 23 pyramidal cells before and during CNQX blockade, respectively, of descending excitation to the ELL molecular layers. Frequencies of MI curve peak are F_p = 12.0 ± 2.7 and 12.6 ± 3.1 Hz before and during CNQX blockade, respectively (p = 0.61). Bandwidths at half maximum are B_w = 30.3≥5.0 and 25.0 ± 4.3 Hz before and during CNQX blockade, respectively (p = 0.98). MI_high values = 0.009 ± 0.0013 and 0.009 ± 0.0015, respectively (p = 0.47). MI_low values = 0.026 ± 0.002 and 0.041 ± 0.009, respectively (p ≪ 10⁻³). D, Dashed and solid lines indicate mean mutual information curves given global stimulation before and during CNQX blockade, respectively. F_p normal = 31.8 ± 4.9 Hz, F_p CNQX = 15.5 ± 3.2, p ≪ 10⁻³; B_w normal = 48.4 ± 4.0, B_w CNQX = 31.6 ± 4.7, p = 0.009; MI_low normal = 0.013 ± 0.002, MI_low CNQX = 0.034 ± 0.003, p ≪ 10⁻³; MI_high normal = 0.014 ± 0.002, MI_high CNQX = 0.013 ± 0.003, p = 0.37. All p values are from pairwise t tests.

Figure 6B compares MI curves and STAs (inset) from the same populations of cells but with global stimulation. Lesions of the feedback pathways caused large increases in the sensitivity of cells to low frequencies (Fig. 6B, solid line), without significantly altering the high-frequency responsiveness. Mean F_p was shifted to a significantly lower frequency, not different from the mean F_p value seen for cells from normal or lesioned animals with local stimulation. Likewise, with global stimulation, lesioning resulted in significant increases in mean MI_low values compared with that of cells from normal animals, and these increased MI_low values were not different from those from either normal or lesioned animals given local stimulation. However, MI_high remained unchanged compared with the average seen with global stimulation of cells from normal animals. Thus, lesioning alters the ability of the system to suppress low-frequency responsiveness as normally occurs when the stimulus geometry is shifted to global. However, lesioning does not alter high-frequency responsiveness.

The STA shape changed in a manner consistent with the improvement of low-frequency responsiveness to global stimuli after these lesions. The dip in the STA was replaced with a slow positive phase (Fig. 6B, inset, compare solid and dashed lines). This increased STA area to 300% of that seen for cells from normal animals and accounted for the improved low-frequency responsiveness. Peak-to-peak STA amplitude was also slightly increased by this treatment; however, this change was not statistically significant, as expected given the minimal changes in MI_high. These results indicate that the loss of low-frequency responsiveness seen when stimulus geometry is switched from local to global is a consequence of recruitment of descending or feedback inputs to the ELL. This increase in feedback input may cause the early dip in the STAs of normal animals receiving global stimulation.

Pharmacological blockade of electrosensory feedback

Focal interruption of descending inputs to the apical dendritic trees of pyramidal cells can be achieved by micropressure ejection of neurotransmitter antagonists into the ELL molecular layers. Parallel fibers of the ELL dorsal molecular layer provide excitatory input directly to P-cell apical dendrites and to inhibitory interneurons that are presynaptic to these same dendrites (Maler et al., 1981). This indirectly descending feedback is known to participate in an ELL gain-control mechanism (Bastian, 1986a) as well as a mechanism for the adaptive attenuation of expected or redundant electrosensory inputs (Bastian, 1999; Bastian et al., 2004). Previous studies showed that this technique blocks both the excitation and disynaptic inhibition within very small regions of the ELL (Bastian, 1993) and interferes with gain control as well as adaptive cancellation (Bastian, 1996a; Bastian et al., 2004). Micropressure ejection of the non-NMDA glutamate antagonist CNQX was used to determine the degree to which the indirect feedback pathway was involved in the spatially mediated frequency tuning shift. The effects of focal blockade of parallel fiber input were similar, but not identical, to the effects of lesions of descending pathways. Comparison of the means of MI curves obtained with local stimulation before and during CNQX treatment (Fig. 6C, dashed and solid lines, respectively) showed that neither F_p, B_w, or MI_high values differed significantly (Fig. 6). However, MI_low was increased 50% by this treatment (p ≪ 0.001; pairwise t test; n = 21), and this was paralleled by an ~20% increase in STA area, however, the STA area increase was not significant (p = 0.4; pairwise t test; n = 21). This increase in MI_low very likely results from the fact that CNQX blockade reduces firing frequency for all P-cell subtypes. On average, spontaneous firing frequency was decreased to 54% of its initial value, and firing rates during local and global stimulation were depressed by similar amounts. Therefore, the increased MI_low values (bits per spike per hertz) indicate that pyramidal cell coding efficiency actually increases because mutual information rates do not fall in proportion to the reduction in spike rate.

As with the brain lesion experiments, CNQX blockade of molecular layer excitation caused large changes in the low-frequency responsiveness of P cells stimulated with global geometry but no change in their high-frequency responsiveness (Fig. 6D). Overall, this treatment shifted the peak of the MI curves to frequencies typical for local stimulation and increased MI_low by nearly 300% on average. The STA waveform also changed in a manner similar to that caused by lesioning descending pathways (Fig. 6D, inset). The initial dip in the STA was replaced by a positive phase, resulting in a mean increase in STA area of >600%. Data from all cell types were also pooled for these analyses.

Spatially extensive or global electrosensory stimuli not only activate electroreceptor afferents contributing to the RF center and surround but also activate a nonclassical RF (Chacron et al., 2003). This nonclassical RF participates in an adaptive mechanism, which attenuates pyramidal cell responses to various patterns of predictable electrosensory inputs, including those resulting from the animal’s own body movements (Bastian, 1995; Bastian et al., 2004). This adaptive cancellation mechanism is based on the generation of a negative image of the predictable input, which is then subtracted from the afferent pattern at the level of the pyramidal cells, and this mechanism has low-pass frequency-response characteristics (Bastian, 1996a). Thus, a simple explanation for the loss of low-frequency sensitivity of pyramidal cells as a result of changing stimulus geometry to global is the activation of a descending negative-image input, which cancels the low-frequency components of the responses of a cell to receptor-afferent input. Both lesions, as well as pharmacological blockade, remove this negative-image input, thereby restoring low-frequency responsiveness during global stimulation.

Lesions of feedforward ELL input

Receptor-afferent input was removed from pyramidal cells by sectioning the connection between the anterior lateral-line ganglion and ELL from which recordings were made. Although this treatment removes all receptor-afferent input to the pyramidal cells within the ipsilateral ELL, feedback input ultimately driven by the contralateral ELL remains intact. Because the feedback projections are bilateral, at least a portion of the normal descending electrosensory feedback to the ipsilateral ELL remains functional. Thus, assuming that the feedback pathways driven by ipsilateral and contralateral ELLs are approximately equivalent, this treatment can reveal the characteristics of the feedback inputs in isolation. However, only responses to global stimulation can be studied, because input to the RF centers of the cells is removed. Of the 29 cells studied in this experiment, 17 showed E-like responses and 12 showed I-like responses. Because the characteristics of the MI curves and those of the STAs did not differ among these populations, results were pooled. Although responses to global RAM stimuli were much weaker overall, these did show clear-cut frequency preferences, and the peak of the MI curve occurred at 15.0 ± 1.6 Hz (Fig. 7). This was significantly lower than the mean F_p value of 33.3 Hz seen for the population of normal cells given global stimuli (p ≪ 0.001; t test; df = 104) but was not different from the F_p of 15.9 Hz for normal cells given local stimuli (p = 0.77; df = 104; t test). The average STA waveform most closely resembled the initial negative-going phase or dip region of the STAs seen in response to global stimulation of normal pyramidal cells (Fig. 7, inset). The average latency between the minima of the STAs from cells with afferent input removed and spike time (time 0) was not significantly different from the mean latency between the minima of STAs from normal cells and spike time. However, this latency was significantly longer than the latency from the principal peak of the STAs of normal cells to spike time. Likewise, the mean width of the STAs from cells after afferent input removal was more similar to the mean width of the STA dips from normal cells but much greater than the mean width of the principal STA peak of the normal cells (Fig. 7).

Figure 7.

Mean MI curve and STA resulting from global stimulation of pyramidal cells with ipsilateral receptor-afferent input removed. Latency from STA minimum to spike time averaged 13.0 ± 1.7 ms. The latency of normal cells from STA minimum to spike time was not different, averaging 13.7 ± 1.1 ms (p = 0.73; t test; df = 101). The latency of normal cells from STA principal peak to spike time was significantly shorter, averaging 4.5 ± 0.2 ms (p < 0.001; t test; df = 102). The width of the STA averaged 14.3 ± 1.8 ms and was slightly greater than the width of the dip of STAs from normal cells, which averaged 10.2 ± 0.9 ms (p = 0.03; t test; df = 103), but was far greater than the width of the principal STA peak of normal cells, which averaged 5.8 ± 0.1 ms (p < 0.001; t test; df = 103). Gray areas indicate ± 1 SEM. bits/Sp/Hz, Bits per spike per hertz.

MI curve shape, as well as STA width and latency seen after removal of ipsilateral afferent input, supports the idea that a major component of the electrosensory feedback is a negative-image input with low-pass characteristics. When stimulus geometry is switched from local to global, the low-frequency responsiveness of pyramidal cells is attenuated by this negative-image input. However, none of the manipulations of feedback altered the frequency tuning of pyramidal cells seen with local stimulation. This suggests that the low-pass characteristics of pyramidal cells results from a feedforward mechanism. Furthermore, this feedforward mechanism must have different characteristics for superficial versus deep cells given the large differences that we see in the MI curves and STAs of these P-cell subtypes [compare Fig. 3A, B (dashed lines) with Table 2 (local values)].

Low-pass filtering by pyramidal cell basilar dendrites

E-type pyramidal cells not only show pronounced differences in their apical dendritic morphology (Bastian and Courtright, 1991; Bastian et al., 2004) but also vary in their basilar dendrite morphology. Basilar dendrites of deep E cells can be as short as 50 μm and have diameters of 3–4 μm, whereas the basilar dendrites of the superficial E cell are as much as 10-fold longer and twofold larger in diameter (Fig. 8A) (Maler, unpublished data). We built models of superficial and deep E-cell dendrites to determine whether, with realistic parameter selection, the filter characteristics of these dendrites could explain the different frequency-response properties of these cells seen with local stimulation. The model incorporated a population of receptor afferents driven by and phase locked to a randomly amplitude-modulated (0–120 Hz) EOD signal. These receptor afferents provided a sequence of postsynaptic potentials that converged on models of P-cell basilar dendrites typical of superficial and deep cells (Fig. 8A) (see Materials and Methods). To model responses to global stimulus geometry, we increased the gain of the receptor-afferent input to simulate the increased area of the RF center that is activated with global stimulation (RF center saturation). This has been demonstrated previously to increase the high-frequency responsiveness of these cells without compromising responses to low frequencies (Chacron et al., 2003). In addition, in the case of the superficial cell simulation, a simple feedback input was included in the model to mimic the negative-image input driven by P-cell receptive-field antagonistic surround and recruited under global stimulation. The addition of this input allowed us to test whether a simple low-pass negative-image input could mimic the change in frequency response and STA shape seen when stimulus geometry was switched from local to global. The feedback signal was not included in the simulations of deep cell responses to global stimulation, because previous studies, as well as the results presented above, showed that, for these cells, minimum changes in response occurred because of the transition from local to global geometry (Bastian et al., 2004). The compartment of the dendritic models most distal to the receptor-afferent input, closest to the cell body, included a spike-generating mechanism. Thus, the model produced spike time data that could be directly compared with those of the in vivo experiments.

Figure 8, B and C, shows the mutual information curves from the simulations of superficial and deep cells, respectively. Close agreement with the in vivo data are seen, in that the simulated superficial cell shows an improvement in low-frequency sensitivity, along with reduced sensitivity to high frequencies attributable to local versus global stimulation (Fig. 8B, dashed and solid lines, respectively). The superficial cell simulation agrees well with the single-example superficial cell (Fig. 8D) as well as the mean MI curves of the population of superficial E cells studied (Fig. 3A). Likewise, the simulated mutual information curves of the deep E cell (Fig. 8C) agree well with the MI curves of the single example (Fig. 8E) and with the population-averaged deep E-cell responses (Fig. 3B). In all cases, MI curves are wide-band and similar to the MI curves for receptor afferents (Fig. 1). Minimal changes occur, contingent on local versus global stimulation. These differences in simulated responses of superficial versus deep E cells to local versus global stimulation cannot be attributable to the membrane time constants of the cells, because these were the same for both models. Instead, the more robust low-pass filtering of local stimuli by the superficial cells is a result of a stronger frequency-dependent attenuation attributable to the increased length of the basilar dendrites of these cells. Similar patterns of frequency-dependent attenuation have been described previously in both experimental (Callaway and Ross, 1995) and modeling (Henze et al., 1996) studies. This is a property of the passive cable equation (Weiss, 1996).

Figure 8, B and C (insets), shows the STAs obtained for the responses of the model cells. Again, close agreement with experimental data was observed (Figs. 3A, B, 8D, E, insets). For the superficial cell simulation, local stimulation (Fig. 8B, dashed line) produced a wider and lower STA, whereas global stimulation decreased the width of the STA and increased its p–p amplitude (Fig. 8B, solid line). Furthermore, as with the in vivo results, an early dip occurred with global stimulation, which contributed to reducing the STA area and further increasing its p–p amplitude. For the simulated deep cell, local and global stimulation produced similar STAs (Fig. 8C, dashed and solid lines, respectively).

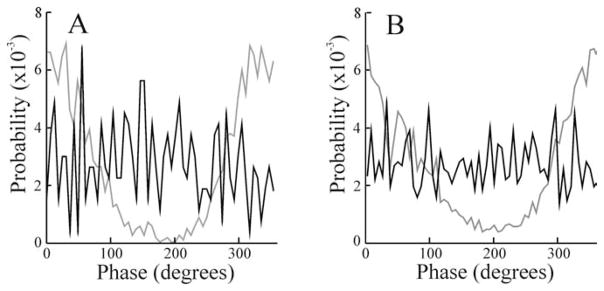
Electroreceptor afferents fire action potentials that are strongly phase locked to the EOD waveform (Bastian, 1981). Previous work (Bastian and Nguyenkim, 2001) showed that the spontaneous activity of deep basilar pyramidal cells is also phase coupled to the EOD but the firing of superficial cells is not. We analyzed the phase relationships between times of spike occurrence and EOD input of the model deep and superficial cells to see whether the differential low-pass filtering of deep and superficial cell basilar dendrites could also explain these differences in phase locking to the EOD. Figure 9A shows phase histograms with respect to the EOD for both the simulated superficial (black line) and the deep (gray line) cells under local stimulation. The simulated deep cell showed significant phase locking to the EOD (vector strength, 0.59), but the simulated superficial cell did not (vector strength, 0.04), in good agreement with previous results based on spontaneous pyramidal cell activity (Bastian and Nguyenkim, 2001). Phase histograms for an actual superficial (black line) and a deep basilar pyramidal (gray line) cell during local RAM stimulation are shown in Figure 9B for comparison (vector strengths, 0.02 and 0.50, respectively). Vector strengths for the samples of superficial and deep cells studied averaged 0.10 ± 0.02 and 0.43 ± 0.05, respectively, during local simulation. Thus, the differential low-pass filtering, resulting from morphological variation of superficial versus deep E-type pyramidal cell basilar dendrites, is correlated with both the variation in frequency tuning given local stimuli and the differences in phase coupling to the EOD waveform.

Figure 9.

A, Phase histograms summarizing the phase relationships between simulated superficial (black line) and deep (gray line) cells and the EOD waveform during local stimulation. B, Phase histograms for an actual superficial (black line) and deep (gray line) basilar pyramidal cell during local stimulation. Firing rates for these cells were 12.2 and 37.6 spikes/s, respectively.

Discussion

Shifts in spatial or temporal tuning occur in numerous sensory systems. However, these shifts are often observed in higher centers of the nervous system and typically involve developmental, experience-dependent, or hormonal changes, and develop over time scales of minutes to months (Kilgard and Merzenich, 1998; Sisneros and Tricas, 2000; Xiao and Suga, 2002; Sisneros and Bass, 2003; Sisneros et al., 2004; Tsodyks and Gilbert, 2004). Changes in tuning described here are rapid or switch like, appear immediately after altered stimulus geometry, and are more similar to changes in temporal response properties of retinal ganglion cells or V1 neurons seen, contingent on changes in stimulus spatial characteristics (Kuffler, 1951; Vinje and Gallant, 2000, 2002). However, unlike retinal processing, changes in ELL pyramidal cell tuning cannot be attributable to feedforward or lateral inhibitory processes alone, because the shift requires electrosensory feedback. Instead, the tuning shift involves the interaction of feedback from higher centers with the intrinsic filtering properties of pyramidal cells.

The frequency response characteristics of receptor afferents, measured as information tuning curves, are best described as weakly low pass or broadband (Fig. 1). Pyramidal cell responses to stimuli delivered to their RF center are expected to be principally driven by these afferents, and the responses of deep basilar pyramidal cells most closely approximate receptor-afferent tuning (Fig. 3B). Superficial E cells, however, respond to local stimuli in a distinctly low-pass manner. The modeling component of this study, which was constrained by the well known anatomy of pyramidal cell basilar dendrite, verifies that their long basilar dendrite can provide a low-pass filter sufficient for accounting for this low-frequency tuning. Furthermore, the enhanced low-pass filtering by the longer basilar dendrite of superficial versus deep cells can explain the observation that superficial E-cell action potentials lack phase coupling to the EOD waveform, whereas deep E-cell action potentials preserve this phase coupling (Bastian and Nguyenkim, 2001). Dendritic cable properties have been shown to impose frequency-selective attenuation of synaptic inputs or action potentials (Callaway and Ross, 1995; Henze et al., 1996; Weiss, 1996). Low-pass filtering by E-cell basilar dendrites provides the simplest explanation for the correlation of E-cell tuning to local stimuli with cellular morphology.

However, I cells displayed poor responses to high-frequency components of the stimulus, independent of stimulus geometry or morphological subtype (Table 2). Because I cells lack basilar dendrites, it is likely that ELL inhibitory interneurons provide the required low-pass filtering. In vitro results, showing that these generate slow IPSPs (Berman and Maler, 1998), support this hypothesis. Furthermore, the same interneurons contribute to the E-cell antagonistic surround (Maler et al., 1981; Maler and Mugnaini, 1994), and responses to E-cell surround stimulation show low-pass characteristics in vivo (J. Bastian, unpublished results).

Changing stimulus geometry from local to global attenuates low-frequency responsiveness and, in the case of E cells, increases high-frequency sensitivity. This effect, summarized as an MI shift index, was most pronounced for the superficial cells (Fig. 4, low-frequency cells), was negatively correlated with increased firing frequency, and was minimal for the deep cells. Global stimulation alters the constellation of synaptic inputs to pyramidal cells in at least three ways.

First, although local stimulation activates only a subset of the receptor afferents that drive the RF center of a pyramidal cell (Bastian et al., 2002), the transition to global stimulation increases the feedforward input to the cell via activation of the entire center (RF center saturation). Increasing the proportion of the RF center simultaneously stimulated was shown previously to improve the high-frequency responsiveness of E cells (Chacron et al., 2003). The effect of RF saturation is expected to vary, depending on the size of the RF center of a cell; that is, greater effects are expected for cells with large RF centers, because the local stimulus activates a smaller fraction of the total center area. Thus, cells with smaller RF centers should display better high-frequency responsiveness to local stimuli, as well as smaller improvements in high-frequency responsiveness to global stimuli. Superficial E cells have the largest RF center areas, whereas deep E cells have the smallest (Bastian et al., 2002), and the MI_high values shown in Table 2 for E cells vary in accordance with these predictions. Average MI_high in response to local stimulation is smaller for superficial E cells compared with deep E cells, and the increase in MI_high for global versus local stimuli is much greater for the superficial E cells. Thus, the shorter basilar dendrites and smaller RF centers of deep E cells could account for their relatively robust high-frequency responses to both local and global stimuli.

A second consequence of global stimulation is activation of commissural electrosensory neurons, including the ovoid cells that have large RFs (Bastian and Courtright, 1991), and provide a dense plexus of GABAergic terminals surrounding the basilar dendrites of E cells (Maler and Mugnaini, 1994). Ovoid cells do not contact I cells. In vivo (Bastian et al., 1993) and in vitro (Berman and Maler, 1998) studies of ovoid cells verified that they inhibit basilar pyramidal cells and that they produce long-duration IPSPs with a GABA_B component. Therefore, spatially extended stimuli should enhance this inhibition, thereby increasing the conductance of the E-cell basilar dendrite. Our model predicts that this increased conductance allows an improved response to higher frequencies, as seen with globally stimulated superficial E cells.

A third consequence of global stimulation involves the activation of pyramidal-cell receptive-field antagonistic surround as well as a powerful nonclassical RF component. Previous work showed that nonclassical RF stimulation combined with RF center stimulation attenuated low-frequency responses (Chacron et al., 2003). Blockade of descending electrosensory inputs by lesions or glutamate antagonists, and the subsequent loss of globally induced attenuation of low-frequency responsiveness, verifies that the nonclassical RF effects are mediated by descending input from cerebellar granule cells. Furthermore, the same feedback pathways are involved in an adaptive mechanism that attenuates predictable patterns of electrosensory input (Bell et al., 1997; Bastian, 1999). This adaptive mechanism functions by supplying a negative image of expected input to the apical dendrites of the pyramidal cells. It displays low-pass properties (Bastian, 1996a), is most effective for the superficial cells, and is virtually ineffective for the deep cells (Bastian et al., 2004). Removal of ipsilateral afferent input by cutting the anterior lateral-line nerve ganglion revealed effects of the descending feedback in isolation; the resulting low-pass responses to global stimuli were expected given the low-frequency negative image driven by the nonclassical receptive field. Vinje and Gallant (2000) showed that nonclassical RF stimulation of V1 neurons increased their ability to detect high-frequency transients and sparsened their responses. Furthermore, anatomical studies showed that the nonclassical RF of V1 cells originates, at least in part, from feedback connections (Angelucci et al., 2002). Mechanisms similar to those described here may exist in the visual system.

The large tuning shift of the superficial E cells with global versus local stimulation results from attenuation of low-frequency responsiveness via feedback of a negative-image response plus an increase in high-frequency responsiveness attributable to RF center saturation and increased conductance of the basilar dendrite. I cells show a comparable loss of low-frequency sensitivity contingent on global stimulation. This is consistent with the fact that E and I cells have similar apical dendrites (Maler, 1979; Saunders and Bastian, 1984) and that the negative-image input function is the same (Bastian et al., 2004).

Changes in the mutual information curves were paralleled by changes in the spike-triggered averages of the AM stimulus envelope. The loss of low-frequency responsiveness and the associated improvement of high-frequency responsiveness are correlated with reduced STA area and increased p–p STA amplitude, respectively. In E cells, both of these changes stem from replacement of the initial low-frequency positive-going phase of the locally evoked STA with a dip. Thus, with global stimulation, E cells show the highest firing probability after a positive-going EOD AM, preceded by a negative-going phase or dip, as described previously for a related species (Gabbiani et al., 1996; Metzner et al., 1998). A similar sequence of AMs, but of opposite polarity, triggers I-cell firing. STAs seen with global stimulation are similar to those seen in other systems (Warland et al., 1997; Reinagel et al., 1999; Bair and Movshon, 2004; Svirskis et al., 2004). Lesions or pharmacological block of the feedback to the ELL abolished this early dip. Furthermore, responses to global stimuli after removal of ipsilateral afferent input yielded STAs having properties similar to this dip. Thus, the STA dip is a correlate of the negative-image input that attenuates low-frequency responses and originates from the cerebellar parallel fiber input to both E- and I-cell apical dendrites. Cerebellar granule cells/parallel fibers are involved in descending control of several lateral-line and eighth-nerve sensory systems including auditory processing in the dorsal cochlear nucleus. It has been suggested that granule cells in these systems may also be involved in the cancellation of redundant inputs as well as in other forms of regulation (Bell et al., 1997; Oertel and Young, 2004). It will be interesting to learn whether the granule cell/parallel fibers of these systems also contribute to nonclassical RFs capable of modulating spatial or temporal response characteristics as observed here.