Automatic Detection of Synaptic Partners in a Whole-Brain Drosophila EM Dataset

Abstract

We developed an automatic method for synaptic partner identification in insect brains and use it to predict synaptic partners in a whole-brain electron microscopy dataset of the fruit fly. Those predictions can be used to infer a connectivity graph with high accuracy, thus allowing fast identification of neural pathways. To facilitate circuit reconstruction using our results, we developed CircuitMap, a user interface add-on for the circuit annotation tool Catmaid.

A neuron-level wiring diagram (connectome) is a valuable resource for neuroscience [1]. Currently, high-resolution electron microscopy (EM) is the only scalable method to comprehensively resolve individual synaptic connections. EM at nanometer scale provides enough detail to identify pre-synaptic sites, synaptic clefts, and post-synaptic partners. A challenging and currently limiting step is the extraction of the connectome from EM volumes, as manual analysis is prohibitively slow and unfeasible for large datasets.

Connectome analysis of the fruit fly is of particular interest on a whole-brain scale. So far, the “full adult fly brain” (FAFB) EM volume [2] is the only available dataset comprising a complete adult fly brain. The automatic segmentation of neurons in this volume has recently allowed speeding-up tracing efforts [3], but the reconstruction of synapses has remained a purely manual task. This step now represents a major bottleneck towards the whole-brain fruit fly connectome, as annotating all estimated 250 million synaptic partners by hand would take 40 years, assuming an annotation time of 5 s per synaptic partner.

Several approaches have been developed for the automatic detection of synapses in EM volumes, tailored towards the model organism of interest. In vertebrates, recent methods have been shown to infer synaptic connectivity reliably [4, 5]. In insect brains, however, the task of identifying synaptic connections is more challenging, since the size of synapses is generally smaller than in vertebrates and many synapses are polyadic (i.e., one pre-synaptic site connects to several post-synaptic sites). Most methods for synaptic partner prediction deal with those challenges in two steps: The first step consists of identifying and localizing synaptic features such as T-bars or synaptic clefts, whereas in the second step neuron segments in physical contact are classified as synaptically “connected” or “not-connected”. For the first step, convolutional neural networks (CNNs) were used to detect synaptic clefts [6] or T-bars [7]. For the second step, a graphical model was developed to solve synaptic partner assignment given a neuron segmentation and candidate synapse detections [8]. More recently, CNNs have been used to infer synaptic connectivity directly, either to predict pre- and post-synaptic neuron masks from synaptic cleft segmentations [9] or to classify neuron pair candidates extracted from a neuron segmentation as “connected” or “not-connected” [10]. Similarly, multilayer perceptrons have been applied to local context features [7]. In contrast to these two-step approaches, our method jointly detects pre- and post-synaptic sites and infers their connectivity, thus building on previous work, which leveraged long-range affinities [11].

However, few methods have been applied so far to large-scale Drosophila datasets: synaptic clefts have been predicted densely in the whole FAFB dataset, albeit without extraction of synaptic partners [6]. To the best of our knowledge, only one method has been used to predict synaptic partners [7] in a large dataset of the central brain of Drosophila [12].

Here, we present a method for synaptic partner identification, which we used to process the FAFB dataset, and a user interface to make predicted synaptic partners accessible in current circuit mapping workflows.

Our method uses a 3D U-Net CNN [13] to predict for each voxel in a volume whether it is part of a post-synaptic site and, if it is, an offset vector pointing from this voxel to the corresponding pre-synaptic site (Figure 1a and Methods). The method is similar to our previous work [11] in that it does not require explicit annotation of synapse features (such as T-bars or clefts) by a human annotator, but instead learns to make use of those features by its own, if they are helpful to predicting synaptic partners. The method presented here uses a different target representation (Methods), which eliminates potential blind spots for synaptic partner prediction and alleviates the need for a high quality neuron segmentation. Furthermore, the post-processing is 15 times more efficient, which we consider crucial for the processing of large volumes.

Figure 1. Method overview for synaptic partner prediction, application to the “full adult fly brain” (FAFB) dataset and usage of CircuitMap for circuit reconstruction and analysis in Catmaid.

a CNN predictions of post-synaptic sites (m) and direction vectors pointing to the pre-synaptic site ($\widehat{d}$, 3D vectors shown as RGB-color) together with final detections after post-processing. Arrows show synaptic cleft (red), T-bar (white), and vesicles (black). b Sample section of the FAFB dataset with predicted synaptic partners (pre-synaptic site purple, post-synaptic site turquoise). c Using CircuitMap (left image), predicted synaptic partners are available in Catmaid to allow exploration of automatically reconstructed neural circuits. The example shows five automatically segmented neurons from [3] (middle image) together with their predicted number of synaptic connections (right image, node colors match the segmentation). See also Supplementary Video.

In particular, our method can be trained from pre- and post-synaptic point annotations alone, which reduces the effort needed to annotate future training datasets. Similarly, the prediction of synaptic partner sites does not rely on the availability of a neuron segmentation. Only the mapping of sites to neurons requires a segmentation, which facilitates replacing neuron segmentations and incorporation of our results into proof-reading workflows where changes to the segmentation occur frequently: an updated neuron segmentation changes only the mapping of already found synaptic partners onto neurons, synaptic partner sites do not have to be detected again. Furthermore, errors in the neuron segmentation do not propagate to the synaptic partner detection (Supplementary Discussion).

We train and validate our method using the publicly available training dataset of the Cremi challenge (https://cremi.org). This dataset consists of three 5 × 5 × 5 μm cubes, cropped from the calyx (part of the mushroom body) of the FAFB volume, in which synaptic partners were fully annotated (1965 synapses in total, Supplementary Figure 1). We performed a grid search on the Cremi dataset to find the best performing configuration amongst different architecture choices, network sizes, training losses and balancing strategies (Methods, Supplementary Figure 2). We further explore the possibility to improve accuracy by making use of a neuron segmentation during post-processing. A neuron segmentation allows us to filter two types of false positives: false positives connecting the same neurite and duplicate close-by detections of a single synaptic partner pair with the same connectivity. We find that when using a large network (192 million parameters) our model achieves good results even in the absence of a neuron segmentation (f-score 0.74 without neuron segmentation versus 0.76 with neuron segmentation). In the presence of an accurate neuron segmentation, smaller, more efficient architectures with ∼90% less parameters are on par with larger ones: small and large networks both achieve f-scores of 0.76 (Supplementary Note 2).

Following the insights gained from validation on the Cremi datasets, we chose a small network (22 million parameters) with a cross-entropy loss to process the whole FAFB volume. To limit extraction to areas containing synapses we ignore regions not part of the neuropil using a previously described mask [6]. The remaining volume consists of ∼50 teravoxels or equivalently ∼32 million μm³, which we process in 3 days on 80 GPUs obtaining 244 million putative synaptic partners (Figure 1b, Methods).

Predicted synapses in FAFB can be analyzed with the query library Synful-Circuit [14]. Additionally, we implemented CircuitMap [15], an extension for the tracing tool Catmaid currently used for connectome annotation in FAFB (Supplementary Video). CircuitMap allows identification of partner neurons with a given number of synaptic connections and thus quick discovery of neural pathways in the Drosophila brain (Figure 1c).

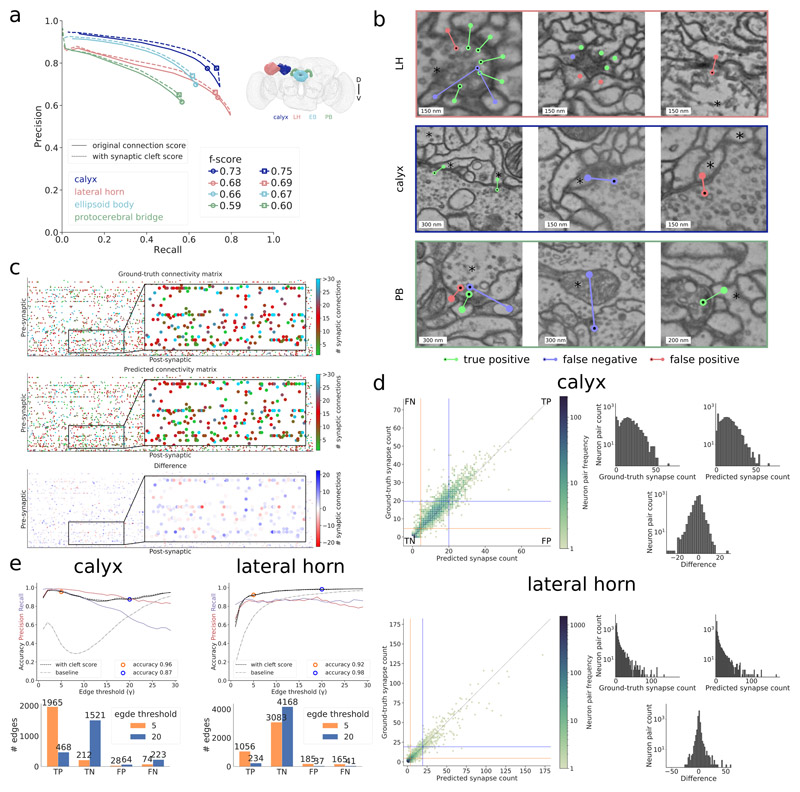
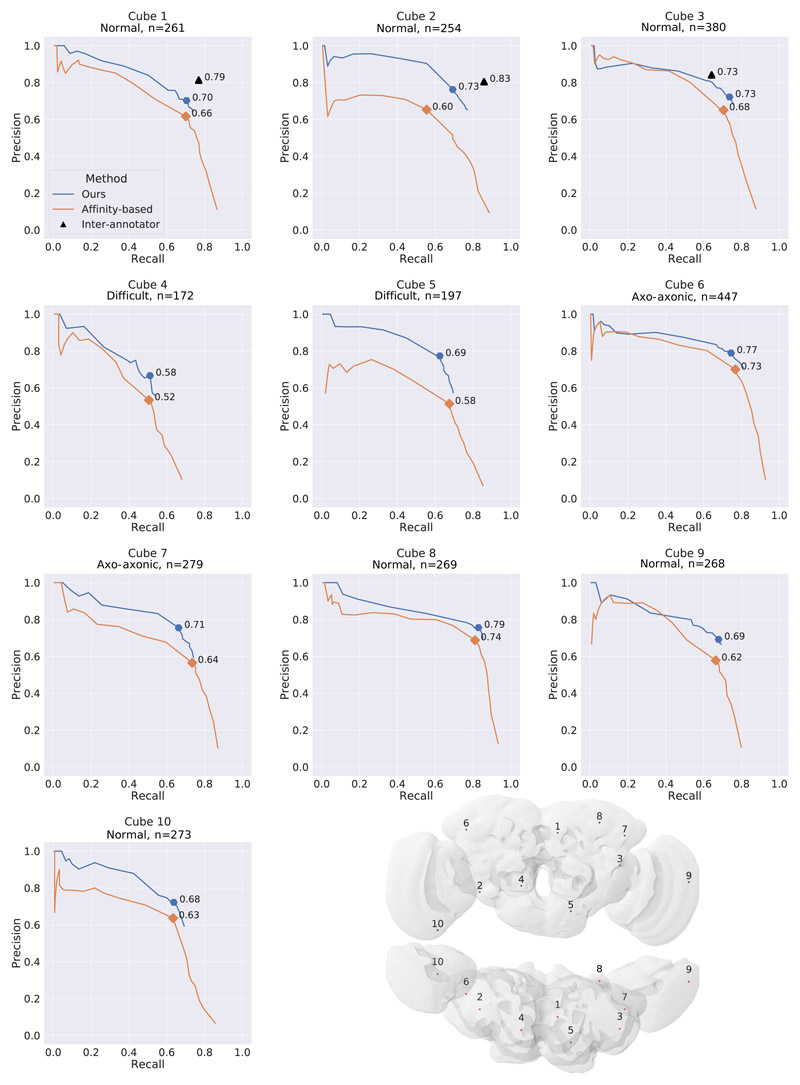
We evaluate the quality of the whole-brain predictions on six datasets with manually placed skeleton and synapse annotations created with Catmaid [16] in the four brain regions calyx (∼60,000 connections), lateral horn (∼25,000 connections), ellipsoid body (∼60,000), and protocerebral bridge (∼15,000 connections) (Figure 2, Supplementary Figure 1, Supplementary Note 1). When measuring performance at an individual synaptic connection level using the CREMI metric (Supplementary Note 2), we obtain f-scores of 0.73, 0.68, 0.66 and 0.59 for the four different brain areas calyx, lateral horn, ellipsoid body, and protocerebral bridge, respectively (Figure 2a and Supplementary Note 2). Examples of identified synapses representing true positives, false positives and false negatives are shown in Figure 2b. We observe a decrease in f-score in regions farther away from the training datasets, suggesting that more diverse training datasets are needed to improve overall accuracy. Some errors in the reconstruction can be attributed to data ambiguities. On three densely reconstructed cubes (9 μm³ each), we observed inter-human differences that correspond to f-scores of 0.79, 0.83, and 0.73. On the same cubes, our predictions reach f-scores of 0.70, 0.73, and 0.73 (Extended Data Figure 1 and Supplementary Note 2).

Figure 2. Results in whole-brain FAFB dataset.

a Precision-recall curves using the Cremi metric for the four different brain regions calyx (dark blue), lateral horn (peach), ellipsoid body (light blue) and protocerebral bridge (green) over different prediction score thresholds, with (solid) and without (dashed) filtering via synaptic cleft predictions [6] (Supplementary Note 2). Markers highlight validation best score threshold (f-score with cleft predictions: 0.75, 0.69, 0.67, 0.60 for calyx, lateral horn, ellipsoid body, and protocerebral bridge, respectively). b Examples of identified true positives, false positives, false negatives in lateral horn (top row), calyx (middle row), and protocerebral bridge (bottom row) on ground-truth neurons (marked with an asterisk). False positive in top row left, false positives and false negative in top row middle are examples of ambiguous cases, false negative in bottom row middle is an example of a missed axo-axonic connection. c Ground-truth, predicted, and difference of number of synaptic connections between 138 projection neurons (pre-synaptic) and 528 Kenyon cells (post-synaptic) in calyx. d For calyx, same data as in (c), shown as ground-truth versus predicted count of number of synaptic connections between pairs of neurons and equivalent plot for lateral horn. Pairs with both zero connections in ground-truth and prediction are omitted. Orange/blue line quadrants highlight false negative (FN), true positive (TP), false positive (FP), and true negative (TN) edges for two connectivity criteria, i.e., number of synapses equal or greater than γ = 5 (orange) and γ = 20 (blue). Histograms on the right show the respective frequency distributions of number of synaptic connections per edge. e Edge accuracy, precision, and recall over different connectivity thresholds γ for calyx (left) and lateral horn (right). Accuracy results for thresholds γ = 5 and γ = 20 are highlighted and their absolute numbers of TPs, TNs, FPs, FNs are provided in the bar plots below. Connectivity derived from neuron-proximity is shown as “baseline” (Supplementary Note 2).

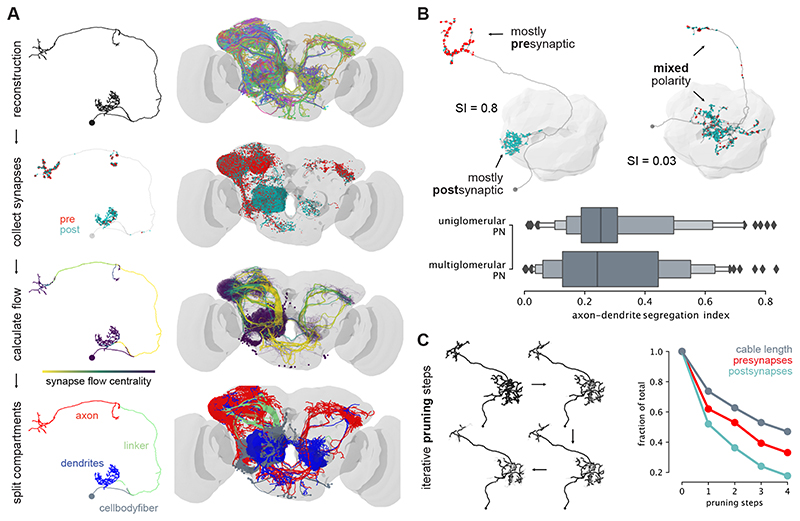
The predicted synaptic connections can be used to automatically infer the presence of a connectome edge with high accuracy (Figure 2c–e). We say that a pair of neurons is connected by an edge, if and only if the true number of synaptic connections is larger or equal to a given threshold γ (Supplementary Note 2). For γ = 5, between 92% and 96% of edges are correctly identified. We compare our method to a neuron-proximity baseline using neuron contact area as a proxy for synaptic weight and find substantial differences in accuracy: 39% and 69% for the baseline versus 96% and 92% for our method for calyx and lateral horn respectively. We further demonstrate that the predictions are conducive to supplement morphological studies of neuron types. Concretely, we study the polarization (i.e., distribution of synaptic inputs and outputs) of uni- and multiglomerular olfactory projection neurons (Extended Data Figure 2 and Supplementary Note 3).

Although our model is well-suited to detect the typical one-to-many synapse in Drosophila (one pre-synaptic site targeting many post-synaptic sites), we observe limitations with regards to rare synapse types. Conceptually, our model is less-suited to detect many-to-one synapses, as we extract only a single synaptic connection for a detected post-synaptic site. We also observe problems with the detection of axo-axonic links (Figure 2b), indicating that more representative training datasets are needed.

Methods

Synapse Representation

Due to the polyadic nature of synapses in Drosophila, we represent synapses as sets of connections C ⊂ Ω² between pairs of voxels (s,t) ∈ Ω², where s and t denote pre- and post-synaptic locations, respectively, and Ω the set of all voxels in a volume. In this representation, pre-synaptic locations do not have to be shared for connections that involve the same T-bar or synaptic cleft (Supplementary Figure 1a). This is in constrast to the convention followed in annotation tools like Catmaid or NEUTU, where one pre-synaptic connector node serves as a hub for all post-synaptic partners (Supplementary Figure 1e). Although this convention might be beneficial for manual annotation, the representation proposed here is potentially better suited for automatic methods, as it does not require the localization of a unique pre-synaptic site per synapse. Instead, automatic methods can learn to identify synaptic partners independently from each other. Furthermore, this representation is also the one used by the CREMI challenge, which allows us to use the provided training data and evaluation metrics.

Connection Prediction

Given ground-truth annotations C and raw intensity values x : Ω ↦ ℝ, we train a neural network to produce two voxel-wise outputs: a mask $\widehat{m}$: Ω ↦ [0,1] to indicate post-synaptic sites and a field of 3D vectors $\widehat{d}$: Ω ↦ ℝ³ that point from post-synaptic sites to their corresponding pre-synaptic site (see Supplementary Figure 3 for an illustration). Both outputs are trained on ground-truth m and d, extracted from C in the following way: m(i) is equal to 1 if voxel i is within a threshold distance r_m to any post-synaptic site t over all pairs (s, t) ∈ C, and 0 otherwise (resulting in a sphere). Similarly, d(i) = s – i for every voxel i within a threshold distance r_d to the closest t over all pairs (s, t) ∈ C, and left undefined otherwise (during training, gradients on $\widehat{d}$ are only evaluated where d is defined). To obtain a set Ĉ of putative synaptic connections from predictions $\widehat{m}$ and $\widehat{d}$, we find connected components in $\widehat{m}$ ≥ θ _CC, where θ _CC is a parameter of our method to threshold the real-valued output $\widehat{m}$. For each component, we sum up the underlying predicted values of $\widehat{m}$, which we refer to as the connection score. Each component with a score larger than a threshold θ _CS is considered to represent a post-synaptic site, from which we extract a location $\widehat{t}$ as the maximum of an Euclidean distance transform of the component. The corresponding pre-synaptic site location $\widehat{s}$ is then found by querying the predicted direction vectors $\widehat{d}$, i.e., $\widehat{s}=\widehat{t}$+ $\widehat{d}$($\widehat{t}$).

Network Architectures

We use a 3D U-Net [17] as our core architecture, following the design used by [18] and [6], i.e., we use four resolution levels with downsample factors in xyz of (3, 3, 1), (3, 3, 1), and (3, 3, 3) and a five-fold feature map increase between levels. Convolutional passes are comprised of two convolutions with kernel sizes of (3, 3, 3) followed by a RELU activation. Final activation functions for $\widehat{m}$ and $\widehat{d}$ are sigmoid and linear, respectively. The initial number of feature maps f is left as a free hyper-parameter. In order to train the two outputs $\widehat{m}$ and $\widehat{d}$ required by our method, we explore three specific architectures: Architecture ST (single-task) refers to two separate U-Nets trained individually for either $\widehat{m}$ and $\widehat{d}$, and thus does not benefit from weight sharing. Architectures MT₁ and MT₂ refer to multi-task networks that use weight sharing to jointly predict $\widehat{m}$ and $\widehat{d}$. MT₁ is a default U-Net with four output feature maps (one feature map for $\widehat{m}$ and three feature maps for $\widehat{d}$). MT₂ is a U-Net with two independent upsampling paths (as independently proposed by [19]), each one predicting either $\widehat{m}$ and $\widehat{d}$, i.e., weights are only shared during the downsampling path between the two outputs. Supplementary Figure 3d summarizes the architecture choices.

Training

Our training loss L_d for (d, $\widehat{d}$) is based on mean squared error (MSE). For the post-synaptic mask loss L_m(m, m), we explore both error functions MSE and cross-entropy (CE). In the multi-task context (MT₁, MT₂), we simply sum the two losses to obtain the total loss: L _total = L _d + L _m.

We train all investigated networks (ST, MT₁, and MT₂) on randomly sampled volumes of size (430, 430, 42) voxels, which we refer to as mini-batches. Each mini-batch is randomly augmented with xy-transpositions, xy-flips, continuous rotations around the z-axis, and section-wise elastic deformations and intensity changes. We use the GUNPOWDER library (https://github.com/funkey/gunpowder) for data loading, preprocessing, and all augmentations mentioned above. Training using TENSORFLOW on an NVIDIA Titan X GPU takes 6-11 days to reach 700,000 iterations.

Due to the sparseness of post-synaptic sites, the training signal m is heavily unbalanced: ∼65% of randomly sampled mini-batches do not contain post-synaptic sites at all, the remaining mini-batches have a ratio of foreground- to background-voxels of ∼1:4000 on average. We mitigate this imbalance with two balancing strategies: First, we reject empty mini-batches during training with probability p _rej. Second, we scale the loss for $\widehat{m}$ voxel-wise with the inverse class frequency ratio of foreground- and background-voxels, clipping at 0.0007^-1. In practice, the loss for a foreground voxel is scaled on average with a factor of ∼1400.

Model Validation

We realign and split the Cremi cubes into a training dataset (75% of the volume of each cube, resulting in a total of 1402 synapses) and a validation dataset (25%, 540 synapses).

We use the Cremi evaluation procedure to assess performance. In short, we match a predicted connection to a ground-truth connection if the underlying neuron segmentation IDs are the same and if the synaptic sites are in close distance (smaller than 400 nm). Matched connections are counted as true positives, unmatched ground-truth connections are considered false negatives, unmatched predicted connections are considered false positives. We obtain precision and recall values by adding up true positives, false positives, and false negatives of all three Cremi samples before computing precision and recall values. This is different from the original proposed Cremi score, where precision and recall is computed for each sample individually and then averaged, which effectively weights samples based on the inverse of the number of synaptic connections they contain.

We performed a grid search on the validation dataset to find the best performing configuration amongst different architecture choices (ST, MT₁, and MT₂), number of initial feature maps (small: f = 4, big: f = 12), training loss for $\widehat{m}$ (CE: cross entropy, MSE: mean squared error), and two sample balancing strategies (standard: p _rej = 0.95 throughout training, curriculum: p _rej = 0.95 until 90,000 training iterations, then p _rej = 0). The resulting numbers of trainable parameters for the investigated small networks are 22 million (ST), 11 million (MT₁), 12 million (MT₂) and for the big networks 192 million (ST), 96 million (MT₁), 115 million (MT₂).

Supplementary Figure 2 summarizes the grid search results in terms of best f-score obtained over all connection thresholds θ _CS. Best validation results are obtained using big networks with curriculum learning (f-score 0.74, precision 0.72, recall 0.77). Differences between training losses (CE and MSE) as well as architectures ST and MT₂ are marginal, however, architecture MT₁ consistently failed to jointly predict $\widehat{d}$ and $\widehat{m}$, also when trained with a product loss (L_total = L_d · L_m).

Synapse prediction on the complete FAFB dataset

We chose a small ST architecture with curriculum learning and a cross-entropy loss to process the whole FAFB volume. To limit prediction and synaptic partner extraction to areas containing synapses we ignore regions not part of the neuropil using a previously described mask [6]. The remaining volume consists of ∼50 teravoxels or equivalently ∼32 million μm³, which we process in blocks. For each block, we read in raw data with size (1132, 1132, 90) voxels to produce predictions of size (864, 864, 48) voxels (size difference due to valid convolutions in the U-Net). From those predictions we extract synaptic partners on the fly with a θ _CC ≥ 0.95 and store only their coordinates and associated connectivity scores if this score exceeds a very conservative threshold (θ _CS ≥ 5). To ensure sufficient context for partner extraction, we discard detections close (∼100 nm) to the boundary of the prediction (≤28 voxels in xy, ≤2 sections in z). With a connected component radius of ∼40 nm, this provides enough context to avoid duplicated connections at the boundary. A final block output size of (810, 810, 42) voxels per block or (3.2,3.2,1.6) μm results in a total of ∼1.8 million blocks to cover the whole neuropil.

Using Daisy (https://github.com/funkelab/daisy), we parallelized processing with 80 workers, each having access to one RTX 2080Ti GPU for continuous prediction and five CPUs for simultaneous, parallel data pre-fetching and synaptic partner extraction. Processing all ∼1.8 million blocks took three days, with a raw throughput of 1.53 μm³/s per worker, yielding a total of 244 million putative connections.

Given a neuron segmentation l : Ω ↦ N, a straight-forward mapping results from assigning each synaptic site to the neuron skeleton that shares the same segment. However, false merges in the segmentation and misplaced skeleton nodes can lead to ambiguous situations where the segment containing a synaptic site contains several skeletons. Therefore, we assign synaptic sites to the closest skeleton node in the same segment, limited to nodes that are within a distance of 2 μm. The latter threshold was found empirically to confine the influence of wrong merges in the segmentation that otherwise could spread into neurites without skeleton traces. Wrong splits in the segmentation can lead to situations where no neuron skeleton shares the same segment as a synaptic site. In these cases, we leave the synaptic site unmapped.

According to the validation results on the Cremi dataset (Supplementary Notes 2), we further filter connections inside a neuron. Analogous to the Cremi dataset, where we filter connections inside the same segment (l($\widehat{s}$) = l($\widehat{t}$)), we filter connections mapped to the same neuron (n($\widehat{s}$) = n($\widehat{t}$)). Thus, we remove putative false positives, at the expense of potentially losing the ability to detect autapses (synapses connecting the identical neuron). We further cluster synaptic partners that connect the same neurons within a distance threshold of 250 nm, in order to avoid counting a single synaptic connection between two neurons multiple times. We remove all connections except the one with the highest score (θ _CS) in each identified cluster.

Extended Data

Extended Data Fig. 1.

Extended Data Fig. 2.

Data Availability

The datasets generated during and/or analysed during the current study are available in the “synful_fafb” repository [20] and “synful_experiments” [21]. The following Figures and Tables use this data:

• Figure 1: partner predictions (link to SQL dump in “synful_fafb”)

• Figure 2: evaluation results (datasets an code in “synful_fafb” and “synful_experiments”)

• Extended Data Figure 1: datasets and code in “syn-ful_experiments”

• Extended Data Figure 2: polarity analysis based on partner predictions, code in “syn-ful_experiments”

• Supplementary Figure 2: gridsearch code in “syn-ful_experiments”

Code Availability

The code used to train networks and predict synaptic partners is available in the “synful” repository, https://github.com/funkelab/synful [22]. Code used to evaluate the results is available in the “synful_fafb” repository, https://github.com/funkelab/synful_fafb [20]. A python library to query circuits in the FAFB volume using the predicted synaptic partners is available in the “Syn-fulCircuit” repository, https://github.com/funkelab/synfulcircuit [14]. The Catmaid widget used to interactively query circuits is available in the “CircuitMap” repository, https://github.com/catmaid/circuitmap [15].