Abstract
Background and Aims
Quantifying relationships between snow cover duration and plant community properties remains an important challenge in alpine ecology. We developed a method to estimate spatial variation in energy availability in the context of a topographically complex, high-elevation watershed, which we used to test the explanatory power of environmental gradients both with and without snow cover in relation to taxonomic and functional plant diversity.
Methods
We mapped snow cover at 15 m resolution using Landsat imagery for five recent years and fitted a generalized additive model (GAM) for each year linking snow to time and topography. Predicted snow cover maps were combined with air temperature and solar radiation at daily resolution, summed for each year and averaged across years. Equivalent growing season energy gradients were also estimated without accounting for snow cover duration. Relationships were tested between environmental gradients and diversity metrics measured for 100 plots (including species richness, community weighted mean traits, functional diversity and hyperspectral estimates of canopy chlorophyll content).
Key Results
Accounting for snow cover in environmental variables consistently led to improved predictive power as well as more ecologically meaningful characterizations of plant diversity. Model parameters differed significantly when fitted with and without snow cover. Filtering solar radiation with snow as compared to without led to an average gain in R2 of 0.26 and also reversed slope direction to more intuitive relationships for several diversity metrics.
Conclusions
We show that in alpine environments, high-resolution data on snow cover duration are pivotal for capturing the spatial heterogeneity of both taxonomic and functional diversity. The use of climate variables without consideration of snow cover can lead to erroneous predictions of plant diversity. Our results further indicate that studies seeking to predict the response of alpine plant communities to climate change need to consider shifts in both temperature and nival regimes.
Keywords: Alpine grasslands, French Alps, growing season length, mesotopography, community structure, remote sensing, snow cover
INTRODUCTION
In alpine landscapes, variation in snow cover duration along elevation and mesotographic gradients has long been recognized as a key environmental filter structuring patterns of plant distribution and community composition (Billings, 1973; Evans et al. 1989). Snowpack affects the functioning of alpine ecosystems by exerting strong regulatory control on near-surface soil temperature (Edwards and Cresser, 1992), water and nutrient availability (Freppaz et al., 2007; Weingartner et al., 2007), plant growth and phenology (Kudo et al., 2006; Wipf et al., 2009), growing season length and gross primary production (Baptist and Choler, 2008). Snowmelt timing has also been related to consistent shifts in alpine plant functional traits (Choler, 2005; Venn et al., 2011). Certain late-melting sites, for example, while limited by a short growing season, benefit from decreased exposure to frigid air temperatures in the winter and spring as well as increased water and nitrogen availability at the time of snowmelt (Björk and Molau, 2007), and are identified as taxonomically distinct snow bed communities with particular functional traits including low stature, high nitrogen leaf content per unit of mass and high specific leaf area (Choler, 2005). In the Alps, altered snow cover regimes in the form of earlier melt dates and rising snow lines have been observed during recent decades, and are anticipated to be an important on going consequence of climate change in alpine environments (Beniston, 2012). Collectively, this evidence highlights the importance of better understanding the linkages between snow cover regimes and plant diversity in order to improve models of alpine biodiversity in response to climate change.
Recognizing the importance of snow in alpine systems and building upon a naturalist tradition of field observations and descriptive studies (e.g. Walker et al., 1993), several authors have incorporated snow as an explanatory variable with the goal of improving species distribution models (Heegaard, 2002; Odland and Munkejord, 2008; Randin et al., 2009; Schöb et al., 2009). Previous studies connecting plant occurrence or traits to snowmelt gradients have quantified snow cover duration by snowmelt rank (e.g. Heegaard, 2002), or by the first snow free Julian day (e.g. Choler, 2005). Additionally, species distribution modelling studies focused on alpine plants have routinely estimated growing season length-related energy variables (e.g. solar radiation and growing degree days), without considering the mediating effect of snow cover duration on incoming solar radiation or near-surface air temperature (e.g. Zimmermann and Kienast, 2001; Randin et al., 2009; Carlson et al., 2014), which may lead unrealistic estimates of energy availability for plants (Scherrer and Körner, 2011; Ford et al., 2013).
One consistent difficulty shared by plant ecologists seeking to take snow into account involves mapping and quantifying snow cover duration at sufficiently fine grain to represent mesotopographic heterogeneity (<50 m). Approaches used thus far have been based on manual field surveys (Heegaard, 2002; Choler, 2005; Odland and Munkejord, 2008; Schöb et al., 2009), in-situ repeat photography (Scherrer and Körner, 2011) and at least one application of a mechanistic model of snow redistribution by wind (Randin et al., 2009). Process-based models accounting for meteorological forcing, topography and land cover have been developed and applied to forecast the effect of anticipated climate change on water budgets in mountainous environments (Liston and Elder, 2006; Viviroli et al., 2009; Vionnet et al., 2014). Validation of snow cover maps generated by two state of the art hydrological models (Liston and Elder, 2006; Viviroli et al., 2009) relative to classified high-resolution imagery, however, showed fairly weak spatial agreement of snow-covered pixels during the snowmelt period (Randin et al., 2014; Table E.1), which is of critical interest to plant ecologists. Classification routines applied to Landsat imagery have long existed as tools for generating high-resolution snow cover maps at the regional scale (Dozier, 1989; Rosenthal and Dozier, 1996). Landsat images are freely available and have the added advantage of providing multiple scenes during the spring and summer months.
Here, we implement a remote sensing-based framework for high-resolution mapping of snow cover duration that can be applied to larger extents than would be feasible with a field-mapping approach. While acknowledging the merits of a physical model of snow distribution (Randin et al., 2009), we present our approach as an empirical alternative for snow distribution modeling at the mesotopographic scale. In this study, our goal was to investigate the importance of snow cover duration for predicting multiple facets of plant community structure, including both trait-based and taxonomic diversity. At the scale of a 6.7 km2 alpine basin, we mapped snow cover at 15 m resolution for five snowmelt cycles using Landsat imagery, modelled daily snow melt relative to time and mesotopography and combined snow cover maps with air temperature and solar radiation maps at a daily time step and for all five years. Assuming that the presence of snow cancelled incoming solar radiation and maintained near surface air temperature at 0° C, we averaged the sum of snow-free growing season days, frost days and solar radiation across years. Comparable energy budgets were also estimated without taking snow cover into account. We then analysed the statistical and ecological implications of snow for predicting taxonomic and functional diversity metrics for 100 vegetation plots, including species richness, Simpson index, species composition as measured by NMDS dissimilarity (Faith et al., 1987), community weighted mean plant height, specific leaf area (SLA), hyperspectral-derived estimates of leaf chlorophyll content and functional diversity. While we focus here on predicting current patterns of alpine plant community structure, a secondary aim is to elucidate which predictive variable(s) may be the most ecologically meaningful for forecasting the response of alpine plant communities to climate change.
MATERIALS AND METHODS
Study area and floristic data
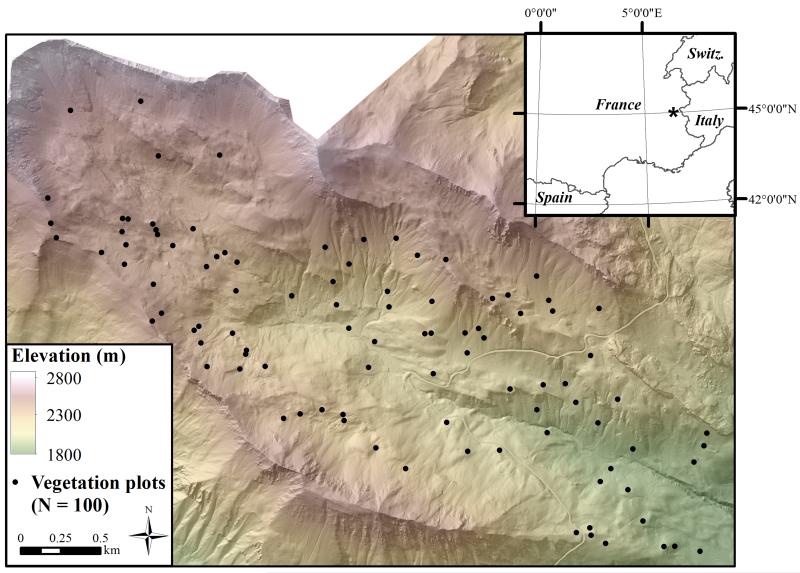
The study area consists of a 6.7 km2 watershed, spanning an elevation range from 1980 to 3114 m a.s.l., situated in the Grand Galibier Massif of the south-western French Alps (Fig. 1). This area, referred to as the Vallon de Roche Noire, is located in the commune of Le Monêtier-les-Bains within the Ecrins National Park. Vegetation consists of a mosaic of heath, sub-alpine and alpine forb and graminoid communities. Summer grazing is limited to sheep and cattle presence from late July to mid-September. Comprehensive botanical relevés, including visual estimates of species’ relative abundance (Braun-Blanquet, 1957), were carried out for ninety 2-5 m radius plots in July, 2007. Ten additional relevés were completed in July, 2011, making for a total of 100 plots available for this analysis (Fig. 1).
Figure 1.
Locator map for the study area displaying elevation and the location of vegetation plots. * Shows the location of the study area in the inset map.
Measuring alpine plant community diversity
For each plot, species richness and Simpson diversity were quantified based on the community relevé. Non-Metric Multidimensional Scaling (NMDS; Kruskal, 1964) was applied in order to estimate turnover in species composition across plots. Bray-Curtis dissimilarity was calculated between plots and the resulting dissimilarity matrix as an input for NMDS ordination (Stress = 0.2). Twenty-five per cent quantiles of scores from the first axis were used to class plots into four distinct groups, based on their taxonomic dissimilarity.
Morphological plant functional traits, including plant height, specific leaf area (SLA), leaf dry matter content (LDMC) and leaf nitrogen content (LNC) were collected from several field campaigns carried out in the study area (Choler, 2005; Chalmandrier et al., 2014). In order to reduce the pervasive effects of intra-specific trait variability on diversity estimates (Albert et al., 2012), we only used trait measurements sampled above 1800 m a.s.l. Community-weighted mean (CWM; Garnier et al., 2007) trait values for each plot were calculated for specific leaf area (SLA) and plant height by summing species-level trait values, weighted by the abundance of species in the community. Plots for which we lacked trait data for 20% or more of relative community composition were excluded from the analysis, as recommended by Pakeman and Quested (2007), resulting in the exclusion of thirty-one plots. For each of the sixty-nine remaining plots, functional diversity was estimated by (1) calculating Gower’s distance between all species relative to plant height, SLA, LDMC and LNC and (2) calculating the abundance-weighted mean pairwise distance between all species of each plot using the mpd function in the picante R-package. Lastly, a community re-shuffling routine that randomized species composition within plots while maintaining species richness was used to test whether convergence of functional diversity differed significantly from a null distribution following 1000 repetitions.
In order to complement field-based measures of plant diversity, leaf chlorophyll content (a + b; μg/cm2) was extracted from a hyperspectral image (AISA; Specim Ltd., Finland) obtained for the study area in 2008. Leaf chlorophyll content estimated from reflectance values of hyperspectral imagery has been shown to be a reliable proxy for leaf nitrogen content (Haboudane et al., 2002). Details concerning image acquisition and processing can be found in Pottier et al. (2014). The initial 0.8 m resolution image was resampled to 5 m using a mean function and values were extracted for each of the 100 vegetation plots.
Quantifying energy gradients
Daily solar radiation values for 2013 were calculated with the area solar radiation tool in ArcGIS [version 10.2 (2013) Redlands, CA, USA] using a 2 m LiDAR digital elevation model and the clear sky model set to a sky size of 2800 pixels. Output solar radiation maps (Watts/m2) for 2013 were used for corresponding calendar days in all other years, given that the underlying model did not account for inter-annual variation caused by nebulosity.
One-minute interval air temperature data for the Grand Galibier Massif was obtained by 300 m elevation class from the SAFRAN–Crocus–MEPRA model chain developed by Météo France. Details on data description, methodology, and validation of this regional climate model for the French Alps are provided in Durand et al. (2009). Time series of air temperature for the years 2000-2014 were aggregated to daily minimum (Tmin) and mean (Tmean) values. Daily Tmean values averaged across years were used to assess the potential length of the growing season, which was defined by the number of consecutive days with a mean temperature above 0° C. The threshold of 0° C was selected based on the minimum required temperature for alpine plant growth, as in Zimmermann and Kienast (1999). In order to add spatial grain, temperature values associated with a given elevation class (e.g. 2100 – 2400 m a.s.l.) were assigned to the median elevation (e.g. 2250 m a.s.l.) and elevation-dependent linear regression was used to downscale temperature values across the study area. Daily Tmean and Tmin rasters were reclassified into binary maps, where growing season days were defined as grid cells above 0° C and frost days were defined as grid cells less than 0° C. For each day falling within the potential estimated growing season and for five years (2000, 2001, 2002, 2013 and 2014), daily frost and growing season day maps were exported for the study area at 2 m resolution.
Snow cover mapping and modelling
Landsat 7 (ETM+ sensor) imagery was obtained for five dates in 2000, five dates in 2001, and four dates in 2002. Landsat 8 (OLI sensor) was obtained for six dates in 2013 (Fig. S1) and four dates in 2014. All retained images had less than 30% cloud cover and were acquired between late March and mid-August. Adequate imagery between 2003 and the commissioning of the Landsat 8 satellite in April, 2013, was unavailable due to irreparable sensor damage to the Landsat 7 satellite occurring in the spring of 2003 (www.landsat.gsfc.nasa.gov). The panchromatic band 8 at 15 m resolution was selected for this analysis in order to maximize the resolution of snow cover maps. Scenes were re-projected to Lambert 93 and cropped to the study area prior to classification in eCognition Developper [version 8.0 (2012) Munich, Germany]. Binary snow cover maps were generated first by segmenting the grey scale image according to the spectral values of the pixels and second by applying an object based classification to the segmented image based on a nearest neighbour algorithm. Assignment of objects to snow or no snow classes took into account spectral signal values, as well as topographic context (slope and aspect). Given that available Landsat scenes did not always cover the end of the snowmelt cycle, a snow cover map derived from a 50 cm aerial photograph obtained on August 6, 2003, was aggregated to 15 m resolution using the majority parameter in ArcGIS and subsequently added to each annual Landsat time series. This additional step ensured that late summer snow patches, which occur in consistent locations in the study area from one year to the next (Choler, personal observation), were consistently documented.
Following data exploration, for each Landsat year, a binomial generalized additive model (GAM; Wood 2006) in the mgcv R-package was used to relate the presence/absence of snow cover to temporal and topographic variables at 15 m resolution (N=654,858 grid cells). Restricted maximum likelihood was used to estimate penalized regression splines without a fixed number of degrees of freedom. Explanatory variables included: (1) calendar day; (2) solar radiation (estimated by calendar day); (3) normalized topographic position index (TPI; Wilson and Gallant, 2000) multiplied by slope for a 45m moving window; (4) normalized TPI multiplied by slope for a 225m moving window and (5) mean annual temperature. Solar radiation was calculated using the same approach detailed above with a 15 m DEM as the input. TPI was calculated as a proxy for convexity and concavity relative to a neighbourhood of surrounding cells. Normalizing TPI values between 0 and 1 and multiplying this term by slope angle was intended to account for the expected increased likelihood of snow accumulation and persistence in low-angle, convex areas (Fig. S2). The use of two different window sizes is supported by previous works (e.g. Revuelto et al., 2014) and was intended to quantify local topographic heterogeneity both in a local 3×3 (45 m2) grid cell neighbourhood and at the scale of a slope in a 15×15 (225 m2) neighbourhood. Mean annual temperature was estimated across the study area by (1) calculating mean annual temperature by elevation class from 2000 to 2013; (2) averaging mean annual temperature across years and (3) applying elevation-dependent regression in order to provide continuous temperature predictions. In the GAM, mean annual temperature values were grouped by slope orientation category (N, NE, E, SE, S, SW, W and NW) and a response curve was fit for each aspect class.
Fitted GAMs for each year were used to generate daily snow cover maps for five Landsat years (2000, 2001, 2002, 2013 and 2014). Although topographic variables remained constant, date and corresponding solar radiation varied by time step. Continuous probability of snow cover maps were converted to binary snow cover maps using the optimal threshold as determined by the true skill statistic (TSS) calculated between probability maps and observed snow cover maps (Allouche et al., 2006; Thuiller et al., 2009). Daily snow cover maps were exported for the five years at 15 m resolution.
Snow cover model validation
SPOT 4 images were obtained for four additional dates in 2013 (www.cnes.fr). After correcting reflectance values for topography (Shepherd and Diamond, 2003), snow cover maps were generated at 20 m resolution by applying a threshold to the normalized difference snow index (NDSI; Dozier, 1989). SPOT 4 and Landsat-derived snow cover maps were resampled to a common 15 m resolution and compared to predicted GAM snow cover maps both (1) non-spatially, i.e. comparing estimates of percent snow cover for the study area and (2) spatially, by applying the true skill statistic (TSS; Allouche et al., 2006).
Combining snow cover with energy gradients
For the length of the estimated growing season and for the five years considered, snow cover maps were combined with daily maps of air temperature and solar radiation. Snow cover maps were disaggregated to 2 m resolution to align with high resolution maps and applied as a mask, e.g. if a grid cell contained snow, frost days, solar radiation and growing season days were set to zero. Temperature and solar radiation rasters were not upscaled to 15 m (the resolution of snow cover maps) in order to preserve variation in energy variables linked to finer topographic heterogeneity. Snow-free growing season days, frost days and solar radiation were summed for each grid cell and for each year, averaged across years and exported as 2 m raster layers. The sum of snow free growing season days from now on will be referred to as growing season length (GSL). In addition to calculating average GSL across years, the variability in GSL was also estimated by extracting the range (max-min) of GSL from all five years and for each grid cell. This metric will be referred to as GSL variability. Solar radiation (for one year) and growing season length (for all five years, and then averaged) were also calculated by summing daily radiation and growing season day maps in the absence of snow cover.
Relating energy gradients to community properties
Values for GSL and solar radiation with and without snow, GSL variability and snow-free frost days were extracted for each of the 100 vegetation plots and integrated into a common data table. Additionally, the percentage of bare ground at 5 m resolution was derived from a high-resolution aerial photograph using image segmentation and this information was extracted for each vegetation plot. We considered the percentage of bare ground to be a proxy for geomorphic disturbance related to slope and possible cryoturbation (Le Roux et al., 2013) and also for biotic disturbance linked primarily to Alpine marmot activity, Marmota marmota (Choler, 2005).
In order to simplify parameter comparison across models, ordinary least squares linear regression was used to relate GSL and solar radiation with and without snow to taxonomic and functional diversity metrics. Model performance was measured by adjusted R2 and mean absolute error (MAE). In the case of GSL and solar radiation filtered by snow cover, GSL variability, frost days and the percentage of bare ground were tested as explanatory variables against linear model residuals. Predictors explaining a significant portion of model residuals were retained and the best multivariate model (taking into account possible interaction effects) was fit to each of the seven biodiversity metrics tested (species richness, Simpson index, NMDS dissimilarity, CWM plant height, CWM SLA, functional diversity and hyperspectral-based leaf chlorophyll content). Finally, in order to test for spatial patterns in diversity metrics not explained by selected input variables, Moran’s I was systematically used to test for spatial autocorrelation among residuals of the best-fitting model.
RESULTS
Snow cover model validation
Model performance for snow cover GAMs was consistent across years, with adjusted R2 varying from 0.75 to 0.81, and explained deviance varying from 71% to 81%. Comparison of estimates of relative snow cover area across the study site for seven dates in 2013 showed strong agreement between observed snow cover maps derived from Landsat 8 and SPOT imagery with GAM model outputs (MAE = 6.02%, R2 = 0.94, P < 0.001, Fig. S3A-B). Agreement estimated by TSS between observed and predicted snow cover maps was especially elevated through mid-July (>0.50), followed by a decline in agreement after this date (mean TSS = 0.54; Fig. S3C). Sensitivity exhibited a similar pattern, with close to 100% of true positives detected through July 15 followed by decreasing precision during the second half of the snowmelt period (mean sensitivity = 0.68).
Quantifying energy gradients
The maximum length of the potential alpine growing season based on inter-annual daily mean air temperatures was found to occur from April 22 to November 7 (Fig. S4). Here, we summed growing degree days and solar radiation from April 22 to August 15 as the length of the initial period of growth has been shown to be a primary factor driving plant phenology and growth in alpine systems (Wipf et al., 2009). Growing season length in this case is defined by relative differences in snowmelt timing prior to August 15 and therefore does not represent total energy received during the potential summer growing season.
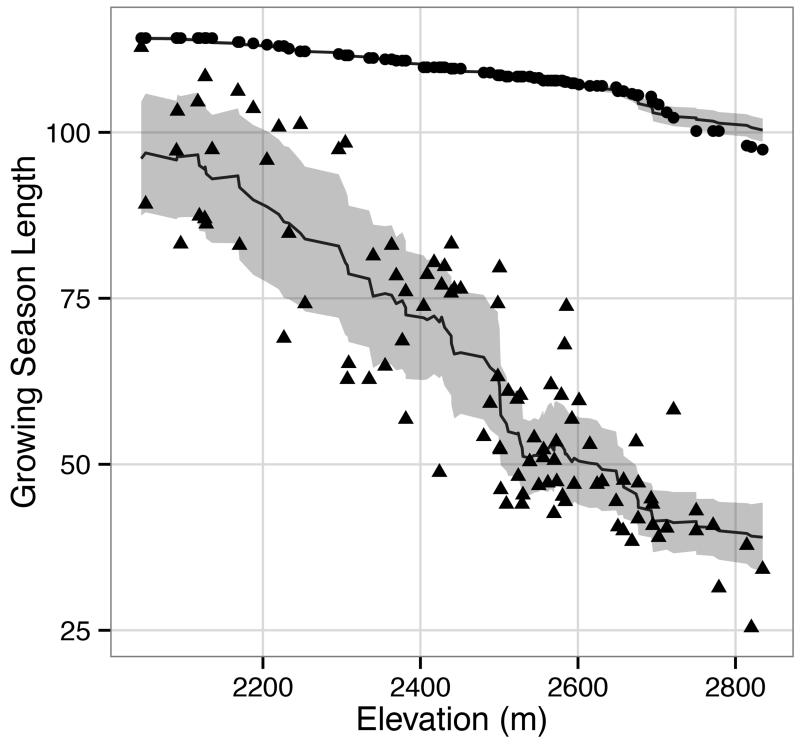
Median differences in growing season length (GSL) and in the sum of solar radiation with and without snow cover duration were significant (P < 0.001). When GSL was plotted against elevation, standard error was substantially higher when snow cover was integrated (2.12 days as compared 0.38 days without snow), which was also the case for solar radiation (14,173 Watts/m2 with snow as compared to 6,569 Watts/m2 without). For a given elevation, the range of GSL with snow varied up to forty days, whereas without snow fluctuation in GSL relative to elevation was almost non-existent and could be attributed to inter-annual variability in daily air temperatures (Fig. 2). Within supplementary information, a video file illustrates the combination of daily snow cover and solar radiation maps for 2013.
Figure 2.
Variation in growing season length relative to elevation estimated with snow cover (triangles) and without snow cover (circles). Trend lines represent the running mean (k=20), while the shaded ribbon represents the running mean +/− the running mean absolute error (k=20)
Relating energy gradients to community properties
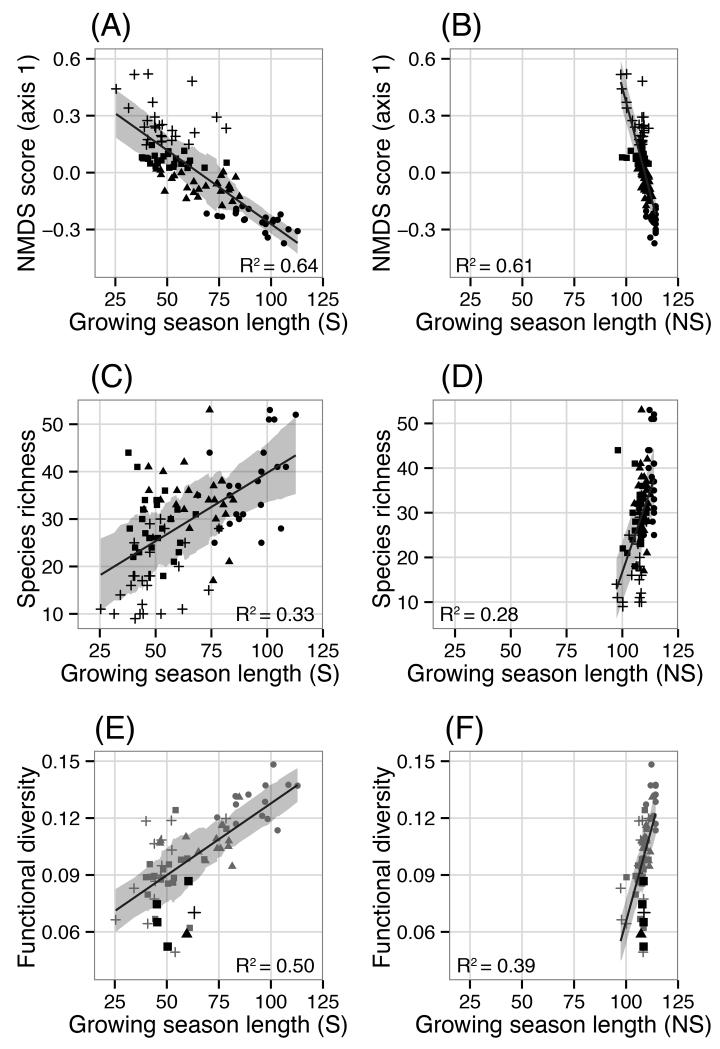
Due to strong co-linearity between solar radiation and GSL estimated with snow cover (Pearson’s r = 0.96), energy gradients were analysed separately in relation to plant community properties. Pearson’s r estimated between GSL and solar radiation without snow was substantially weaker (r = −0.32). For GSL estimated with snow cover, adjusted R2 increased and mean absolute error decreased for all taxonomic and functional diversity metrics, with the exception of leaf chlorophyll content (Table 1). While average gain in explanatory power when snow cover was taken into account was 3-4%, increase in R2 was particularly pronounced for community weighted mean plant height (+ 0.20) and for functional diversity (+ 0.10; Table 1). Slope estimates were consistently lower and intercept values were consistently higher for GSL with snow cover as compared to without (Table 1; Fig. 3). For the seven diversity metrics considered, 95% confidence intervals for parameter estimates (slope and intercept) did not overlap across models fit to gradients with and without snow cover (Table 1).
Table 1.
Linear model parameters, including 95% confidence intervals and performance measures (adjusted R2 and Mean Absolute Error, MAE) for gradients estimated with (S) and without (NS) snow.
|
|
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Taxonomic (N=100) | Functional | |||||||
|
|
|
|||||||
| Richness | Simpson | NMDS | Height (N=98) | SLA (N=95) | FD (N=67) | Chlorophyll (N=74) | ||
|
|
|
|
||||||
| GSL | Intercept estim. | 10.933 | 0.760 | 0.507 | −1.933 | 11.712 | 0.052 | 17.952 |
| Intercept lower | 5.529 | 0.730 | 0.429 | −4.373 | 10.169 | 0.040 | 4.562 | |
| Intercept upper | 16.337 | 0.791 | 0.585 | 0.507 | 13.255 | 0.065 | 31.342 | |
| Slope estim. | 0.288 | 0.001 | −7.78 × 10−3 | 0.196 | 0.035 | 7.56 × 10−4 | 0.296 | |
| Slope lower | 0.208 | 0.001 | −8.94 × 10−3 | 0.160 | 0.012 | 5.70 × 10−4 | 0.113 | |
| Slope upper | 0.368 | 0.002 | −6.62 × 10−3 | 0.231 | 0.057 | 9.43 × 10−4 | 0.478 | |
| MAE | 6.673 | 0.035 | 0.096 | 2.804 | 1.784 | 0.012 | 11.008 | |
| R2 (adj.) | 0.334*** | 0.292*** | 0.641*** | 0.543*** | 0.080** | 0.495*** | 0.114** | |
|
|
|
|
||||||
| GSL (NS) | Intercept estim. | −128.947 | −0.056 | 4.523 | −84.062 | −4.082 | −0.335 | −336.700 |
| Intercept lower | −178.584 | −0.316 | 3.804 | −110.305 | −17.904 | −0.467 | −472.083 | |
| Intercept upper | −79.311 | 0.205 | 5.243 | −57.820 | 9.741 | −0.202 | −201.309 | |
| Slope estim. | 1.147 | 8.37 × 10−3 | −0.042 | 0.871 | 0.166 | 4.0 × 10−3 | 3.410 | |
| Slope lower | 1.000 | 5.97 × 10−3 | −0.048 | 0.630 | 0.039 | 2.79 × 10−3 | 2.181 | |
| Slope upper | 1.913 | 10.8 × 10−3 | −0.035 | 1.112 | 0.293 | 5.22 × 10−3 | 4.640 | |
| MAE | 7.787 | 0.035 | 0.096 | 3.530 | 1.801 | 0.013 | 9.914 | |
| R2 (adj.) | 0.283*** | 0.324*** | 0.609*** | 0.342*** | 0.057* | 0.390*** | 0.288*** | |
|
|
|
|
||||||
| Solar | Intercept estim. | 13.549 | 0.771 | 0.438 | −0.763 | 11.137 | 0.056 | 25.270 |
| Intercept lower | 8.174 | 0.741 | 0.353 | −3.164 | 9.731 | 0.044 | 12.040 | |
| Intercept upper | 18.924 | 0.800 | 0.523 | 1.639 | 12.543 | 0.068 | 38.500 | |
| Slope estim. | 3.88 × 10−5 | 2.03 × 10−7 | −1.05 × 10−6 | 2.79 × 10−5 | 6.817 × 10−6 | 1.073 × 10−7 | 3.00 × 10−5 | |
| Slope lower | 2.63 × 10−5 | 1.35 × 10−7 | −1.25 × 10−6 | 2.23 × 10−5 | 3.596 × 10−6 | 7.96 × 10−8 | 1.848 × 10−6 | |
| Slope upper | 5.13 × 10−5 | 2.71 × 10−7 | −8.57 × 10−7 | 3.41 × 10−5 | 1.004 × 10−5 | 1.35 × 10−7 | 5.810 × 10−5 | |
| MAE | 6.953 | 0.036 | 0.107 | 2.941 | 1.705 | 0.012 | 10.894 | |
| R2 (adj.) | 0.273*** | 0.257*** | 0.531*** | 0.505*** | 0.151*** | 0.471*** | 0.046* | |
|
|
|
|
||||||
| Solar (NS) | Intercept estim. | 60.842 | 0.941 | −0.617 | 13.897 | 2.696 | 0.099 | 113.500 |
| Intercept lower | 38.285 | 0.816 | −1.059 | 1.357 | −2.328 | 0.025 | 69.508 | |
| Intercept upper | 83.399 | 1.066 | −0.174 | 26.438 | 7.721 | 0.174 | 157.568 | |
| Slope estim. | −4.28 × 10−5 | −1.19 × 10−7 | 8.50 × 10−7 | −4.37 × 10−6 | 1.531 × 10−5 | 1.62 × 10−9 | −1.02 × 10−4 | |
| Slope lower | −7.33 × 10−5 | −2.88 × 10−7 | 2.51 × 10−7 | −4.37 × 10−6 | 8.504 × 10−6 | −9.80 × 10−8 | −1.61 × 10−4 | |
| Slope upper | −1.22 × 10−5 | 5.066 × 10−8 | 1.45 × 10−7 | −4.37 × 10−6 | 2.211 × 10−5 | 1.01 × 10−7 | −4.19 × 10−6 | |
| MAE | 7.745 | 0.041 | 0.160 | 4.132 | 1.572 | 0.018 | 10.418 | |
| R2 (adj.) | 0.064** | 0.009 | 0.065** | −0.008 | 0.168*** | −0.015 | 0.126** | |
|
|
|
|
||||||
P-values are expressed as follows:
0>0.001
0.001>0.01
0.01>0.05.
NMDS = scores from the first axis of Non-Metric Multidimensional Scaling ordination; SLA = community weighted mean Specific Leaf Area; FD = Functional Diversity.
Figure 3.
First axis Non-Metric Multidimensional Scaling (NMDS) score (A-B), species richness (C-D) and functional diversity (E-F) plotted relative to growing season length estimated with (S) and without (NS) snow cover. Point symbols correspond to quartiles of the NMDS score. Black points in (E) and (F) represent significant functional convergence. Shadded ribbons correspond to the linear model +/− the running mean absolute error (k=25).
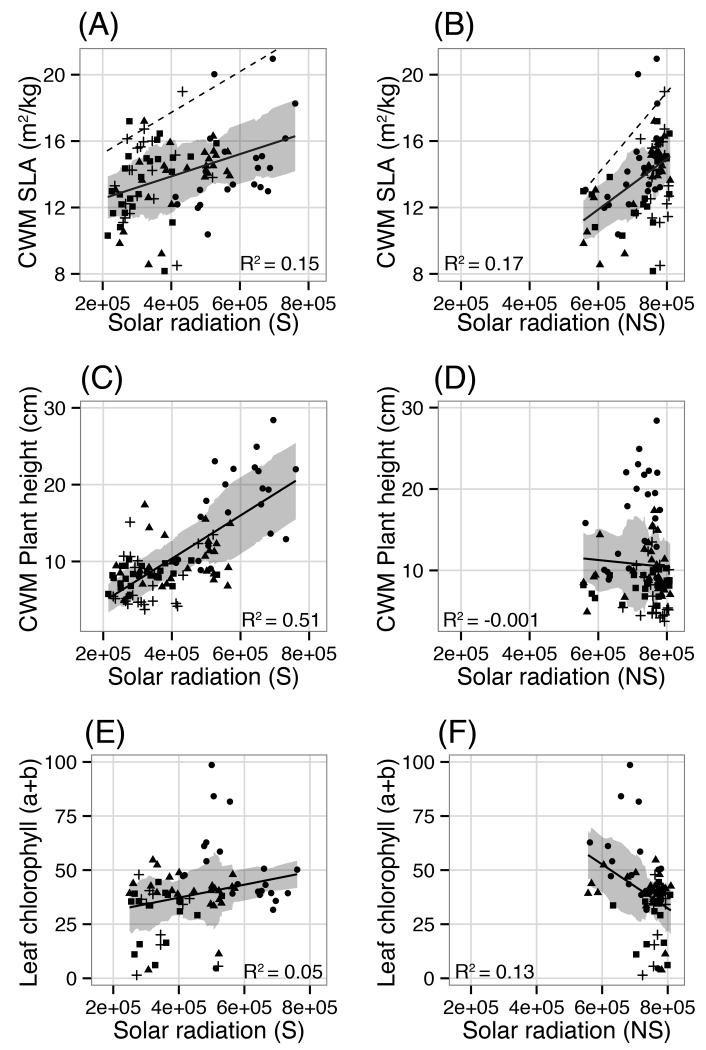
For solar radiation, pronounced shifts in both explanatory power and the direction of relationships occurred. Whereas solar radiation exhibited no significant relationship with the Simpson index, plant height or functional diversity, these relationships became highly significant when snow cover was added (Table 1; Fig. 4C-D). Although the direction of relationships remained positive both with and without snow, substantial gains in R2 occurred when snow was included with respect to species richness (+0.21) and relative to first axis non-metric multi-dimensional scaling (NMDS) scores (+ 0.51). Shifts in R2 corresponded with similar magnitude changes in mean absolute error (Table 1). Negative slope values estimated without snow for species richness, Simpson, plant height and leaf chlorophyll content switched to being positive with snow, whereas the relationship between solar radiation and NMDS taxonomic dissimilarity changed from being positive to negative when snow was taken into account (Table 1; Fig. 4C-F). Explanatory power was slightly higher for specific leaf area (SLA) without snow (+ 0.02), however mean absolute error was the same for both models. Within the 95% quantile of SLA, snow bed plots expected to receive low solar radiation and exhibit high SLA were differentiated with snow (Fig. 4A), while these plots were scattered and poorly characterized when solar radiation was summed without snow cover (Fig. 4B). As was the case for GSL, 95% confidence intervals for slope and intercept estimates for models with and without snow cover did not overlap (Table 1).
Figure 4.
Specific Leaf Area (SLA, A-B), plant height (C-D) and per cent leaf chlorophyll content (μg/cm2; E-F) plotted relative to the sum of solar radiation (Watts/m2) estimated with (S) and without (NS) snow cover. Point symbols correspond to quartiles of the NMDS score. Shadded ribbons correspond to the linear model +/− the running mean absolute error (k=25). CWM = community weighted mean. In (A) and (B), dashed lines represent the best fit regression applied to the 95% quantile of CWM SLA values.
Analysis of residuals
Overall, model residuals for solar and GSL responded in an equivalent manner with respect to other estimated environmental gradients (physical disturbance, frost stress and inter annual variability in GSL), although R2 was slightly higher for predictors applied to solar radiation residuals (Table 2). Accordingly, results for the two will be reported simultaneously. Physical disturbance explained a significant portion of residual variation for all taxonomic diversity metrics (Table 2). To a lesser degree, physical disturbance also captured variation in residuals for SLA and leaf chlorophyll content, but not for height or functional diversity. The estimated number of snow free frost days was not a significant predictor of residual error for diversity metrics, with the exception of a weak relationship with plant height residuals in the case of solar radiation. Inter-annual variability in GSL was a significant predictor of model residuals in the case of species richness, NMDS dissimilarity, plant height, SLA and leaf chlorophyll content, but not for Simpson or functional diversity (Table 2). GSL variability was greatest for high-elevation, south-facing scree communities, characterized by R. glacialis and O. dignya.
Table 2.
Residual variance explained (adjusted R2) by disturbance (% bare ground), frost (number of snow-free frost days) and inter-annual growing season length (GSL) variation. Model performance (adjusted R2) and results from Moran’s I test are reported for the best model. Significant predictors of model residuals were included in the best model
| Taxonomic |
Functional |
|||||||
|---|---|---|---|---|---|---|---|---|
| Richness | Simpson | NMDS | Height | SLA | Functional diversity | Chlorophyll | ||
| GSL | Residual R2 (disturbance) | 0·098*** | 0·211*** | 0·240*** | −0·002 | 0·055* | 0·005 | 0·054* |
| Residual R2 (frost) | −0·01 | 0·009 | −0·001 | 0·024 | −0·002 | −0·015 | 0·026 | |
| Residual R2 (variation) | 0·079** | −0·009 | 0·069* | 0·079* | 0·060** | −0·013 | 0·041* | |
| Moran’s I (P value) | 0·305 | 0·901 | 0·116 | 0·725 | 0·359 | 0·121 | 0·95 | |
| R2 (best model) | 0·434*** | 0·467*** | 0·768*** | 0·534*** | 0·291*** (x) | 0·495*** | 0·213*** | |
| Solar | Residual R2 (disturbance) | 0·123*** | 0·236*** | 0·257*** | −0·008 | 0·047* | 0·009 | 0·065* |
| Residual R2 (frost) | −0·004 | 0·002 | −0·009 | 0·030* | −0·011 | −0·014 | −0·005 | |
| Residual R2 (variation) | 0·158*** | 0·008 | 0·197*** | 0·037* | 0·053* | 0·012 | 0·086** | |
| Moran’s I (P value) | 0·333 | 0·917 | 0·131 | 0·462 | 0·453 | 0·131 | 0·709 | |
| R2 (best model) | 0·434*** | 0·456*** | 0·744*** | 0·525*** | 0·332*** (x) | 0·471*** | 0·195*** | |
P values:
P < 0·05
P < 0·01
P < 0·001.
(x) denotes an interaction effect between solar/GSL and GSL variation (all other multivariate combinations are additive).
NMDS, scores from the first axis of NMDS ordination; SLA, community-weighted mean SLA.
Model residuals were not found to be spatially auto-correlated for gradients estimated with snow cover (Table 2). When snow cover was not taken into account, however, residuals were spatially auto-correlated for both GSL and solar radiation in the case of NMDS dissimilarity and plant height (results not shown), even when other predictors were incorporated in the model (bare ground and GSL variability). The lack of spatial autocorrelation when snow was included indicates that remaining unexplained variance in diversity metrics was due to local heterogeneity not accounted for in the model rather than systematic error in the estimation of energy availability. Finally, adjusted R2 for the best fitting multivariate model was equivalent or slightly higher in the case of GSL as compared to solar radiation, with the exception of SLA for which the solar radiation model captured 4% more variation (Table 2). Averaging R2 across diversity metrics, the multivariate GSL model was able to explain 56% of variation in taxonomic diversity and 38% of variation in functional diversity. In comparison, the solar radiation model captured slightly less (51%) of variation in taxonomic diversity and an equivalent amount (37%) of variation in functional diversity.
DISCUSSION
Although previous studies have examined relationships between snow cover and alpine plant distribution patterns (Heegaard, 2002; Odland and Munkejord, 2008; Randin et al., 2009; Schöb et al., 2009) and functional traits (Choler, 2005; Venn et al., 2011), to the best of our knowledge, this study is the first to quantitatively assess the importance of snow cover duration for predicting multiple facets of alpine plant diversity and structure along environmental gradients at the community level. Methodologically, we used a combination of high-resolution remote sensing products, a digital elevation model and coarse-resolution gridded climate data to implement an empirical snow distribution model (see Appendix for further discussion of our method relative to other approaches). Conceptually, we show the enhanced ecological relevance and statistical predictive power of bio-climatic variables that combine energy inputs (temperature and solar radiation) with snow cover duration. Our findings furthermore indicate that in addition to energy gradients, inter-annual variability in growing season length, as well as physical disturbance, have strong effects on alpine plant community properties. Despite the small extent (~7 km2) of our study area, given the ubiquitous nature of snow cover throughout high-elevation systems (Billings, 1973), we are confident that our findings are applicable to alpine areas in other geographic contexts.
Ecological and statistical contributions of integrating snow cover
High variability in estimated growing season length for plots located at similar elevations but within contrasting mesotopographic contexts (Fig. 2) is in agreement with previous studies applying field-mapping techniques to differentiate environmental conditions for alpine plant communities (Walker et al., 1993; Choler, 2005). Our remote-sensing approach thus provides a spatially continuous method for estimating energy availability, which field measurements have shown is a strong driver of both community type and of aboveground phytomass production (Walker et al., 1994). Ideally, our estimate of growing season days would have been conducted using plot-level measures from in situ soil data loggers in order to better approximate thermal conditions found in micro-habitats (Scherrer and Körner, 2011; Slavich et al., 2014). These data were not available for all Landsat years, however. Furthermore, and particularly given the remote-sensing approach used here, we argue that it is worthwhile to test the utility of variables that are widely available and that can be applied more readily at broader spatial scales, such as regional or in this case massif-scale air temperature. The local meteorological model we used (Durand et al., 2009) is based on continuous measurements from multiple local weather stations, and the outputs by 300 m elevation class that we downscaled are finer than standard macroclimatic variables, such as WorldClim (Hijmans et al., 2005). In the case of solar radiation, simulating daily clear sky gain in a GIS appears to be the best approach, given the difficulty and cost of instrumentation and the impracticality of interpolating point measurements. In summary, we consider that both GSL and solar radiation filtered by snow cover duration represent good proxies of energy availability, providing a more realistic estimate of conditions experienced by plant communities as compared to thermal gradients estimated independently of snow cover duration. Furthermore, our selection of environmental variables based on ecological significance, e.g. plants only receiving radiation in the absence of snow, represents an important change in approach relative to modelling studies that frequently select predictors strictly on a statistical basis.
The comparatively strong statistical performance of GSL estimated without snow can be attributed to the underlying elevation gradient resulting from temperature downscaling. Despite the modest gain in explanatory power conferred by estimating GSL with snow cover (+ 3-4%), the shift in model parameters (slope and intercept) emphasizes that snow cover had a strong effect on model fit. Furthermore, the more substantial 20% gain in R2 in the case of plant height suggests that energy availability estimated with snow better captures the environmental filter controlling variation in community weighted mean plant height. By extension, the 10% increase in R2 relative to functional diversity is a strong indicator that functional convergence around an optimal trait in stressful conditions is better predicted when snow cover is taken into account (Table 1; Fig. 3E-F). As found in another study measuring leaf chlorophyll in the North American Rockies, we observed a decrease in leaf chlorophyll content with elevation (Spasojevic and Suding, 2012). However, high measured chlorophyll values for both Vaccinium sp.-dominated and F. paniculata-dominated communities, which are found at similar elevations but in opposite mesotopographic contexts, led to a decrease in R2 for GSL with snow as compared to without (Table 1). This finding indicates that there may be a broad range of community-aggregated leaf trait values for a given level of snow cover duration.
Our findings strongly caution against the use of incident solar radiation summed without consideration of snow cover duration as a predictive variable for modelling studies in alpine environments. We found summer solar radiation estimated without snow to be a weak and at times misleading predictor of both functional and taxonomic diversity. The pronounced rise in R2 for species richness, Simpson index, taxonomic dissimilarity (NMDS), plant height and functional diversity when snow was taken into account highlights the statistical gain afforded by summing snow-free incoming radiation during the growing season. Additionally, we found solar radiation summed without snow cover to be a significant negative predictor of species richness and leaf chlorophyll content. The switch to a more intuitive positive relationship between energy availability, photosynthetic activity and species richness points to the enhanced ecological significance gained by summing snow-free solar radiation.
While it has been demonstrated that community weighted mean specific leaf area (SLA) declines with elevation (Bello et al., 2013), and that SLA increases in late-melting sites along a mesotopographic gradient (Choler, 2005), a third study shows that variation in community weighted mean SLA measured in the context of a combined mesotopographic and elevation gradient exhibits no clear trend (Spasojevic and Suding, 2012). Although we found a significant relationship between SLA and solar radiation with and without snow (Table 1; Figure 4A-B), consistently elevated mean absolute error points to the high range of SLA values for a given value of radiation throughout the gradient. We do not consider the R2 value to be particularly meaningful in the case of SLA, given that previous studies have documented a wide range of community-weighted mean SLA values at high-elevation in relation to snow cover duration (Choler, 2005). Diverging functional strategies, linked to fellfield and snowbed communities, are apparent at upper elevations when solar radiation is filtered by snow cover, however this variation in the cold portion of the gradient is absent when received solar radiation is calculated in the absence of snow (Fig 4A-B).
Despite the documented importance of frost events as a stress factor affecting the growth and survival of alpine plants (Körner 2003; Wipf et al., 2006, 2009), our approach to summing snow-free frost days during the growing season did not constitute a significant predictor of model residuals (Table 2). We attribute this absence of explanatory power largely to a lack of measurement of sub-surface soil temperature, during the winter months but also in spring when plants are the most sensitive to snow-free frost damage (Banister et al., 2005). Significant residual variance explained by physical disturbance, particularly in the case of taxonomic diversity (Table 1), however, confirms that the percentage of bare ground estimated from high-resolution imagery is a meaningful proxy for biotic and geomorphic disturbances affecting community composition.
Finally, while it is difficult to classify inter-annual variability in snow cover duration and air temperature as stress or disturbance (Grime, 1977), the amplitude of variation in GSL was a significant predictor for model residuals for the majority of diversity metrics considered (Table 2). A study conducted in Japan documents highly variable phenology of snowbed species relative to inter-annual variation in snow melt, whereas fellfield species initiated flowering and seed-set at consistent times regardless of melt date (Kudo et al., 2006). In addition to phenology, our findings support the conclusion that the taxonomic and functional characteristics of alpine grasslands are sensitive to the inter-annual consistency of snow cover duration, which has implications for ecosystem functioning (Baptist and Choler, 2008). Evidence from long-term monitoring of alpine plant communities’ response to environmental change in the Colorado Rockies furthermore indicates that directional shifts in plant diversity are accompanied by fine-scale oscillations in community composition linked to inter-annual variability in environmental conditions, including snow cover duration (Spasojevic et al., 2013).
Implications for predicting community responses to climate change
Our study, while focused on current patterns of alpine plant community properties, has strong implications for forecasting the response of alpine plants to global change. We view the shift in model parameters with and without snow as being of equivalent importance to the gain in explanatory power conferred by taking snow cover duration into account. More specifically, slope values were consistently higher when GSL was estimated without snow, which could lead to potentially extreme predictions of community responses to incremental climate change if snow cover is not taken into account.
As a next step emerging from this work, geared toward linking energy availability to alpine plant diversity and functioning (phenology and productivity), we recommend summing received snow-free solar radiation when air temperature is above a physiologically meaningful threshold, such as 0° C. Ecologically, this metric of energy availability would aim to quantify the amount of incoming solar radiation available for photosynthesis, as mediated by snow cover duration. Statistically, it would be possible to integrate available air temperature scenarios for the coming decades in order to define the potential growing season length (IPCC, 2007), even if clear sky solar radiation remained constant for the prediction period. An ongoing challenge involves the procuration of future, climate-driven snow cover maps at appropriate spatial and temporal scales. Despite difficulties predicting persistent snow patches, recent studies demonstrate that forecasting the response of snow regimes to climate change is becoming increasingly feasible due to advances in hydrological modelling in mountainous study areas (Kobierska et al., 2013; Randin et al., 2014).
Conclusion
While other studies have examined current patterns in order to imply the relevance of snow cover for predicting responses of alpine plants to global change (Bannister et al., 2005; Wipf et al., 2009; Kudo et al., 2010; Venn et al., 2011), to the best of our knowledge ours is the first to demonstrate the utility of high-resolution imagery for mapping snow cover patterns in complex alpine terrain, and furthermore to provide a methodological framework for quantifying relationships between snow-mediated energy budgets and the multiple facets of taxonomic and functional diversity. The findings reported here underscore the importance of considering spatial heterogeneity in both thermal and nival regimes in order to link alpine plant community properties to environmental gradients, both for the present and in the context of global change.
Supplementary Material
ACKNOWLEDGEMENTS
We thank D. Georges, F. Mazel, L. Chalmandrier and C. Dentant for technical assistance and helpful discussions. Thanks are also due to T. Cavallo, who contributed results from the SPOT 4 – TAKE 5 Program.
FUNDING
This research was conducted on the Long-Term Ecosystem Research (LTER) Zone Atelier Alpes, a member of the ILTER-Europe network. Data were provided in the context of the SPOT4-TAKE5 Program, initiated by the Centre d’Etudes Spatiales de la Biosphère (CESBIO) and which received additional funding from the Zone Atelier Alpes. The research leading to this paper received funding from the European Research Council under the European Community’s Seven Framework Programme FP7/2007-2013 Grant Agreement no. 281422 (TEEMBIO).
APPENDIX
Strengths and limitations of the snow distribution model
Predicting snow height, snow water equivalent and snow distribution at spatial resolutions pertinent to mesotopographic variation in an alpine context (<50 m) constitutes an on-going challenge in the realm of process-based climate and hydrological modelling (Vionnet et al., 2014). Mechanistic models have been developed for this purpose, taking into account meteorological forcing, land cover and topography (PREVAH – Viviroli et al., 2009) and also snow redistribution by wind (SnowModel - Liston and Elder, 2006; Crocus - Vionnet et al. 2014). Such models are well-suited to forecasting the effect of climate change on snow cover regimes (Kobierska et al., 2013), and have already been applied successfully to improve predictive variables in a species distribution modelling context (Randin et al., 2009). For the time being and from the standpoint of plant ecologists, however, we are not convinced that existing process-based models are superior to a remote sensing-based approach at <20 m resolution, particularly when the critical period of interest is the snowmelt cycle. A recent study comparing snow cover maps at 20 m resolution generated by SnowModel and PREVAH in the Austrian Alps to observed snow cover maps classified from SPOT imagery found low agreement during the melting period (5.4% of true positives were detected in the case of PREVAH, and 10.1% for SnowModel; Randin et al., 2014). Comparison of predicted snow cover maps with 2013 Landsat and SPOT imagery in this study, in contrast, yielded an average detection of 68% of true positives during the melting period, although this rate did fall below 50% after July 15 (Fig. S3D). In short, while a process-based approach to snow modelling is ultimately the most desirable, we argue that the approach used here is viable for two principal reasons: (1) the spatial patchwork generated by snowmelt patterns is well captured by high-resolution imagery (Fig. S1), allowing for simplistic modelling of a highly complex phenomenon and (2) our approach is applicable by ecologists with access to high-resolution digital elevation data and Landsat imagery.
Despite a number of advantages, we are aware that our empirical approach to snow modelling falls short for precisely predicting end of season snow patches persisting through early August. Late-melting sites largely independent of elevation caused by snow accumulation due to avalanches, for example, were not captured by our model. While model performance remained high for the majority of the melt period from the end of April to mid July (Fig. S3A-B), the decline in spatial agreement at the end of summer as compared to observed snow cover maps can be attributed to an increasing relative importance of mesotopographic context and a decreasing relative importance of date and elevation over the course of the melt cycle. Failure to account for this tendency in the model explains at least in part why the predicted ranking of snowmelt by site differed for certain high-elevation plots from field observations. Although late July snow patches can affect the growing season length for certain nival species such as D. grandiflorum and G. reptans, the first snow free day for snow bed communities dominated by S. herbacea., A. pentaphyllea and C. foetida typically occurs before the beginning of July within the study area (Choler 2005). The strong spatial agreement between observed and predicted snow cover maps through July 15 therefore justifies the approach adopted here for modelling snowmelt patterns (Fig. S3), and suggests that our method can be expected to perform well in the context of other alpine environments.
LITERATURE CITED
- Albert CH, de Bello F, Boulangeat I, Pellet G, Lavorel S, Thuiller W. On the importance of intraspecific variability for the quantification of functional diversity. Oikos. 2012;121:116–126. [Google Scholar]
- Allouche O, Tsoar A, Kadmon R. Assessing the accuracy of species distribution models: prevalence, kappa and the true skill statistic (TSS) Journal of applied ecology. 2006;43:1223–1232. [Google Scholar]
- Bannister P, Maegli T, Dickinson KJ, Halloy SR, Knight A, Lord JM, Alan MF, Spencer KL. Will loss of snow cover during climatic warming expose New Zealand alpine plants to increased frost damage? Oecologia. 2005;144:245–256. doi: 10.1007/s00442-005-0087-3. [DOI] [PubMed] [Google Scholar]
- Baptist F, Choler P. A simulation of the importance of length of growing season and canopy functional properties on the seasonal gross primary production of temperate alpine meadows. Annals of botany. 2008;101:549–559. doi: 10.1093/aob/mcm318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bello FD, Lavorel S, Lavergne S, Albert CH, Boulangeat I, Mazel F, Thuiller W. Hierarchical effects of environmental filters on the functional structure of plant communities: a case study in the French Alps. Ecography. 2013;36:393–402. [Google Scholar]
- Beniston M. Is snow in the Alps receding or disappearing? Wiley Interdisciplinary Reviews: Climate Change. 2012;3:349–358. [Google Scholar]
- Billings WD. Arctic and Alpine Vegetations: Similarities, Differences, and Susceptibility to Disturbance. BioScience. 1973;23:697–704. [Google Scholar]
- Björk RG, Molau U. Ecology of alpine snowbeds and the impact of global change. Arctic, Antarctic, and Alpine Research. 2007;39:34–43. [Google Scholar]
- Braun-Blanquet J. Ein Jahrhunder Florenwandel am Piz Linard (3414 m) Bulletin du Jardin Botanique de l’Etat a Bruxelles. 1957:221–232. volume jubilaire Walter Robyns. [Google Scholar]
- Carlson BZ, Georges D, Rabatel A, Randin CF, Renaud J, Delestrade A, Choler P, Thuiller W. Accounting for tree line shift, glacier retreat and primary succession in mountain plant distribution models. Diversity and Distributions. 2014;20:1379–1391. [Google Scholar]
- Chalmandrier L, Münkemüller T, Lavergne S, Thuiller W. Effects of species’ similarity and dominance on the functional and phylogenetic structure of a plant meta-community. Ecology. 2014 doi: 10.1890/13-2153.1. doi: 10.1890/13-2153.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choler P. Consistent shifts in alpine plant traits along a mesotopographical gradient. Arctic, Antarctic, and Alpine Research. 2005;37:444–453. [Google Scholar]
- Dozier J. Spectral signature of alpine snow cover from the Landsat Thematic Mapper. Remote sensing of Environment. 1989;28:9–22. [Google Scholar]
- Durand Y, Laternser M, Giraud G, Etchevers P, Lesaffre B, Merindol L. Reanalysis of 44 Yr of Climate in the French Alps (1958-2002): Methodology, Model Validation, Climatology, and Trends for Air Temperature and Precipitation. Journal of Applied Meteorology and Climatology. 2009;48:429–449. [Google Scholar]
- Edwards AC, Cresser MS. Advances in Soil Science. Springer; New York: 1992. Freezing and its effect on chemical and biological properties of soil; pp. 59–79. [Google Scholar]
- Evans BM, Walker DA, Benson CS, Nordstrand EA, Petersen GW. Spatial interrelationships between terrain, snow distribution and vegetation patterns at an arctic foothills site in Alaska. Ecography. 1989;12:270–278. [Google Scholar]
- Faith DP, Minchin PR, Belbin L. Compositional dissimilarity as a robust measure of ecological distance. Vegetatio. 1987;69:57–68. [Google Scholar]
- Ford KR, Ettinger AK, Lundquist JD, Raleigh MS, Lambers JHR. Spatial Heterogeneity in Ecologically Important Climate Variables at Coarse and Fine Scales in a High-Snow Mountain Landscape. PloS one. 2013;8:e65008. doi: 10.1371/journal.pone.0065008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freppaz M, Williams BL, Edwards AC, Scalenghe R, Zanini E. Simulating soil freeze/thaw cycles typical of winter alpine conditions: implications for N and P availability. Applied Soil Ecology. 2007;35:247–255. [Google Scholar]
- Garnier E, Lavorel S, Ansquer P, Castro H, Cruz P, Dolezal J, Zarovali MP. Assessing the effects of land-use change on plant traits, communities and ecosystem functioning in grasslands: a standardized methodology and lessons from an application to 11 European sites. Annals of Botany. 2007;99:967–985. doi: 10.1093/aob/mcl215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grime JP. Evidence for the existence of three primary strategies in plants and its relevance to ecological and evolutionary theory. American Naturalist. 1977;111:1169–1194. [Google Scholar]
- Haboudane D, Miller JR, Tremblay N, Zarco-Tejada PJ, Dextraze L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sensing of Environment. 2002;81:416–426. [Google Scholar]
- Heegaard E. A model of alpine species distribution in relation to snowmelt time and altitude. Journal of Vegetation Science. 2002;13:493–504. [Google Scholar]
- Hijmans RJ, Cameron SE, Parra JL, Jones PG, Jarvis A. Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology. 2005;25:1965–1978. [Google Scholar]
- IPCC . Climate change 2007: the physical science basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge: 2007. [Google Scholar]
- Kobierska F, Jonas T, Zappa M, Bavay M, Magnusson J, Bernasconi SM. Future runoff from a partly glacierized watershed in Central Switzerland: a 2 model approach. Advances in Water Resources. 2013;55:204–214. [Google Scholar]
- Körner C. Alpine plant life: functional plant ecology of high mountain ecosystems. Springer; 2003. [Google Scholar]
- Kruskal JB. Nonmetric multidimensional scaling: a numerical method. Psychometrika. 1964;29:115–129. [Google Scholar]
- Kudo G, Hirao AS. Habitat-specific responses in the flowering phenology and seed set of alpine plants to climate variation: implications for global-change impacts. Population Ecology. 2006;48:49–58. [Google Scholar]
- Le Roux PC, Virtanen R, Luoto M. Geomorphological disturbance is necessary for predicting fine-scale species distributions. Ecography. 2013;36:800–808. [Google Scholar]
- Liston GE, Elder K. A distributed snow-evolution modeling system (SnowModel) Journal of Hydrometeorology. 2006;7:1259–1276. [Google Scholar]
- Odland A, Munkejord HK. Plants as indicators of snow layer duration in southern Norwegian mountains. Ecological Indicators. 2008;8:57–68. [Google Scholar]
- Pakeman RJ, Quested HM. Sampling plant functional traits: What proportion of the species need to be measured? Applied Vegetation Science. 2007;10:91–96. [Google Scholar]
- Pottier J, Malenovský Z, Psomas A, Homolová L, Schaepman ME, Choler P, Thuiller W, Guisan A, Zimmermann NE. Modelling plant species distribution in alpine grasslands using airborne imaging spectroscopy. Biology Letters. 2014;10:20140347. doi: 10.1098/rsbl.2014.0347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randin CF, Dedieu JP, Zappa M, Long L, Dullinger S. Validation of and comparison between a semidistributed rainfall–runoff hydrological model (PREVAH) and a spatially distributed snow-evolution model (SnowModel) for snow cover prediction in mountain ecosystems. Ecohydrology. 2014 doi: 10.1002/eco.1570. [Google Scholar]
- Randin CF, Vuissoz G, Liston GE, Vittoz P, Guisan A. Introduction of snow and geomorphic disturbance variables into predictive models of alpine plant distribution in the Western Swiss Alps. Arctic, Antarctic, and Alpine Research. 2009;41:347–361. [Google Scholar]
- Revuelto J, López-Moreno JI, Azorín-Molina C, Vicente Serrano SM. Topographic control of snowpack distribution in a small catchment in the central Spanish Pyrenees: intra-and inter-annual persistence. The Cryosphere. 2014;8:1989–2006. [Google Scholar]
- Rosenthal W, Dozier J. Automated mapping of montane snow cover at subpixel resolution from the Landsat Thematic Mapper. Water Resources Research. 1996;32:115–130. [Google Scholar]
- Scherrer D, Körner C. Topographically controlled thermal-habitat differentiation buffers alpine plant diversity against climate warming. Journal of Biogeography. 2011;38:406–416. [Google Scholar]
- Schöb C, Kammer PM, Choler P, Veit H. Small-scale plant species distribution in snowbeds and its sensitivity to climate change. Plant Ecology. 2009;200:91–104. [Google Scholar]
- Shepherd JD, Dymond JR. Correcting satellite imagery for the variance of reflectance and illumination with topography. International Journal of Remote Sensing. 2003;24:3503–3514. [Google Scholar]
- Slavich E, Warton DI, Ashcroft MB, Gollan JR, Ramp D. Topoclimate versus macroclimate: how does climate mapping methodology affect species distrifbution models and climate change projections? Diversity and Distributions. 2014;20:952–963. [Google Scholar]
- Spasojevic MJ, Suding KN. Inferring community assembly mechanisms from functional diversity patterns: the importance of multiple assembly processes. Journal of Ecology. 2012;100:652–661. [Google Scholar]
- Spasojevic MJ, Bowman WD, Humphries HC, Seastedt TR, Suding KN. Changes in alpine vegetation over 21 years: Are patterns across a heterogeneous landscape consistent with predictions? Ecosphere. 2013;4:art17. [Google Scholar]
- Thuiller W, Lafourcade B, Engler R, Araujo MB. BIOMOD – A platform for ensemble forecasting of species distributions. Ecography. 2009;32:369–373. [Google Scholar]
- Venn SE, Green K, Pickering CM, Morgan JW. Using plant functional traits to explain community composition across a strong environmental filter in Australian alpine snowpatches. Plant Ecology. 2011;212:1491–1499. [Google Scholar]
- Vionnet V, Martin E, Masson V, Guyomarc’h G, Bouvet FN, Prokop A, Durand Y, Lac C. Simulation of wind-induced snow transport and sublimation in alpine terrain using a fully coupled snowpack/atmosphere model. Cryosphere. 2014;8:395–415. [Google Scholar]
- Viviroli D, Zappa M, Gurtz J, Weingartner R. An introduction to the hydrological modelling system PREVAH and its pre-and post-processing-tools. Environmental Modelling & Software. 2009;24:1209–1222. [Google Scholar]
- Walker DA, Halfpenny JC, Walker MD, Wessman CA. Long-term studies of snow-vegetation interactions. BioScience. 1993;43:287–301. [Google Scholar]
- Walker MD, Webber PJ, Arnold EH, Ebert-May D. Effects of interannual climate variation on aboveground phytomass in alpine vegetation. Ecology. 1994:393–408. [Google Scholar]
- Weingartner R, Viviroli D, Schaedler B. Water resources in mountain regions: a methodological approach to assess the water balance in a highland-lowland-system. Hydrological processes. 2007;21:578–585. [Google Scholar]
- Wilson JP, Gallant JC. Terrain analysis: principles and applications. John Wiley & Sons; 2000. [Google Scholar]
- Wipf S, Rixen C, Mulder CP. Advanced snowmelt causes shift towards positive neighbour interactions in a subarctic tundra community. Global Change Biology. 2006;12:1496–1506. [Google Scholar]
- Wipf S, Stoeckli V, Bebi P. Winter climate change in alpine tundra: plant responses to changes in snow depth and snowmelt timing. Climatic Change. 2009;94:105–121. [Google Scholar]
- Wood S. Generalized additive models: an introduction with R. CRC press; 2006. [Google Scholar]
- Zimmermann NE, Kienast F. Predictive mapping of alpine grasslands in Switzerland: species versus community approach. Journal of Vegetation Science. 1999;10:469–482. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.