Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2017 Feb 8.
Published in final edited form as: Circ Cardiovasc Imaging. 2017 Jan;10(1):e005207. doi: 10.1161/CIRCIMAGING.116.005207

Beyond Bernoulli: Improving the Accuracy and Precision of Non-Invasive Estimation of Peak Pressure Drops

Fabrizio Donati 1, Saul Myerson 2, Malenka M Bissell 2, Nicolas P Smith 1,3, Stefan Neubauer 2, Mark J Monaghan 4, David A Nordsletten 1,#, Pablo Lamata 1,#
PMCID: PMC5265685  EMSID: EMS70690  PMID: 28093412

Abstract

Background

Transvalvular peak pressure drops are routinely assessed non-invasively by echocardiography using the Bernoulli principle. However, the Bernoulli principle relies on a number of approximations, that may not be appropriate, including that the majority of the pressure drop is due to the spatial acceleration of the blood flow, and the ejection jet is a single streamline (single peak velocity value).

Methods and Results

We assessed the accuracy of Bernoulli principle to estimate the peak pressure drop at the aortic valve using three-dimensional cardiovascular magnetic resonance flow data in 32 subjects. Reference pressure drops were computed from the flow field accounting for the principles of physics (i.e. the Navier-Stokes equations). Analysis of the pressure components confirmed that the spatial acceleration of the blood jet through the valve is most significant (accounting for 99% of the total drop in stenotic subjects). However, the Bernoulli formulation demonstrated a consistent overestimation of the transvalvular pressure (average of 54%, range 5-136%) resulting from the use of a single peak velocity value, which neglects the velocity distribution across the aortic valve plane. This assumption was a source of uncontrolled variability.

Conclusions

The application of the Bernoulli formulation results in a clinically significant overestimation of peak pressure drops due to approximation of blood flow as a single streamline. A corrected formulation that accounts for the cross sectional profile of the blood flow is proposed and adapted to both CMR and echocardiographic data.

Subject codes: Stenosis, Hemodynamics, Blood pressure, Diagnostic testing, Valvular Heart Disease

Keywords: stenosis, hemodynamics, blood pressure, biomarker, valve, Bernoulli principle

In the presence of aortic stenosis (AS), obstruction of the aortic outflow tract results in increased work of the left ventricle (LV), and eventually leads to heart failure if symptomatic severe AS is left untreated 1. The transvalvular pressure drop (TPD), also referred to as ‘gradient’ in clinical guidelines, is the recommended measure of severity that best correlates with clinical outcomes2,3. Continuous wave Doppler echocardiography and invasive catheterization measurements are the two main methodologies to assess the TPD, and despite underlying discrepancies between the approaches4,5, clinical guidelines recommend the use of both methodologies interchangeably2,3. Doppler-based pressure drops are typically evaluated non-invasively using the simplified Bernoulli formulation6, which requires the assessment of the maximum velocity to estimate the peak instantaneous pressure drop at the point of maximum constriction, or the mean drop during ejection. Catheter-based methodology provides two recordings of pressure before and after the obstruction, and therefore estimates not the peak but the net pressure drop, by either the peak to peak difference (since synchronous acquisitions are not common) or by the mean drop of systolic pressure4,5.

Despite its widespread use, the Bernoulli principle provides an over-simplification of human hemodynamics. The complete behavior of flow hemodynamics is described by the Navier-Stokes equations: the pressure drop is the result of the temporal acceleration of blood velocity (unsteady pressure component), the spatial transport of momentum of the blood (advective pressure component) and the deceleration due to friction losses (viscous pressure component). The Bernoulli principle is a simplification of the Navier-Stokes equations that estimates pressure drops between two locations across a cardiovascular compartment by applying two significant assumptions. The first is that the entire pressure drop is due to advective acceleration/deceleration of the blood flow, neglecting the impact of the unsteady and viscous components6,7. The second is that blood flow is considered as a single streamline – or a column of flow with uniform velocity distribution - therefore ignoring the complex hemodynamics8. In an extended version of the Bernoulli principle used in hydraulics, the non-uniform velocity spatial distribution is handled by multiplying the estimated pressure drop by a correction factor α when the full profile is available9. Nevertheless, the strict requirement of a complete acquisition of the velocity profile to evaluate this factor in the vasculature has hampered its clinical applicability so far.

In consideration of these aspects, a more accurate description of the intra-vascular pressure fields is now feasible through recent advances in medical imaging10 and computational methods11,12. Using a combination of comprehensive velocity fields available via four-dimensional (3D+time) flow phase-contrast Cardiovascular Magnetic Resonance (4D flow CMR), and the Work-Energy Relative Pressure (WERP) estimation method13, a more robust and accurate computation of pressure drops can be achieved. This formulation uses an energy principle derived directly from the Navier-Stokes equations, with a reduced number of simplifications, and enables the separate evaluation of each component of the pressure drop14 accounting for the full 3D nature of the blood flow.

The aim of this work was to use the WERP approach to evaluate the two fundamental assumptions in the Bernoulli calculation for the assessment of the TPD, and determine its accuracy in-vivo. Accounting for the proximal velocity (as in a modified Bernoulli formulation) will not be a question visited in this work.

Methods

Patient data

Thirty-two subjects with a bicuspid aortic valve were selected for this study from subjects undergoing CMR scans for another research study15. The study protocol was approved by the West Berkshire ethics committee and all participants or their guardians gave written informed consent. Each subject underwent a CMR scan on a 3T system (Trio, Siemens, Erlangen, Germany) for 4D flow CMR assessment using a 32-channel cardiac coil. Flow-sensitive gradient-echo pulse sequence CMR datasets were acquired with prospective ECG-gating during free-breathing, using a respiratory navigator. The image acquisition volume was in an oblique sagittal plane encompassing the whole thoracic aorta, with voxel size 1.9-2.0×1.5-1.7×2.0-2.2 mm3, and temporal resolution 40ms. The velocity encoding range was determined using the lowest non-aliasing velocity on scout measurements (up to 4.5m/s in the most stenotic subject).

Subjects were divided between those with no significant AS (Group I [n=20], mean TPD<20mmHg) and those with AS (Group II [n=12]), mean TPD>20mmHg) following current clinical guidelines2. The Bernoulli method using the mean drop across the valve during systole was used for the computation of these pressure values. Aortic dimensions and hemodynamics data are shown in Table 1.

Table 1.

Aortic dimensions and flow hemodynamics in n=32 patients divided in two groups based on the mean systolic pressure drop by Bernoulli (last row): Group I (Δp¯ ≤ 20 mmHg, n=20) and Group II (Δp¯ > 20 mmHg, n=12). Body Surface Index (BSA) computed following the DuBois formula16. Effective Orifice Area computed by EOA = SV/VTImax (SV: Stroke Volume; VTI: Velocity Time Integral).

Group I Group II
Male 35% 91%
Age 28.2±14.1 38.8±20.2
Aortic Diameters/BSA [mm/m2]
     Left ventricle outflow tract 13.4±2.6 15.4±3.8
     Aortic valve 14.5±1.7 17.6±4.0
     Brachiocephalic artery 14.5±1.5 20.7±3.9
     Left subclavian artery 12.2±1.2 13.8±1.8
     Mid descending aorta 11.1±1.1 12.0±1.4
Cardiac output [L/min] 4.65±1.14 6.19±2.04
Effective Orifice Area [mm2] 2.29±0.61 1.18±0.51
Pressure drop [mmHg] 4.95±3.28 32.45±9.26
Open in a new tab

Values are mean ± std. BSA indicates body surface area.

Pre-processing and definition of anatomical regions

4D flow CMR images had field inhomogeneities and eddy currents corrected using available pre-processing tools17. The lumen of LV and aorta were identified, using a thresholding criterion calibrated by the peak velocity magnitude, to remove the impact of noise at the near-wall vascular regions. A skeletonization algorithm is then used to extract the centerline of the aorta and its perpendicular planes, as required for the WERP computations.

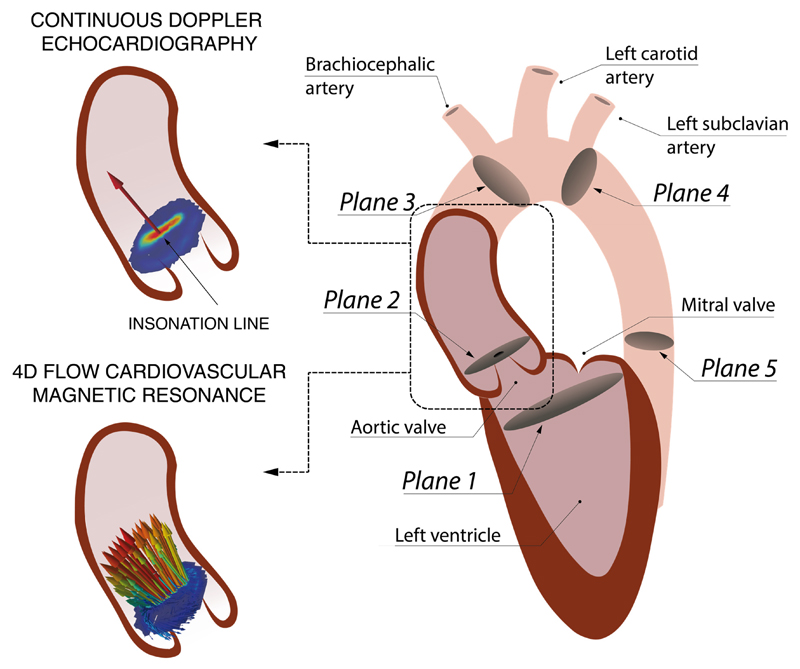
TPD were calculated over the transvalvular region (TVR), between the left ventricular outflow tract (LVOT) (Plane 1, see Figure 1) and the vena contracta (VC) (Plane 2). The LVOT plane was located 12mm before the VC, following the definition used by Garcia et al.18, and the VC is detected from the image as the plane containing the peak velocity magnitude, i.e. the plane of maximum narrowing of the aortic valve jet.

Figure 1.

Figure 1

Open in a new tab

Left: Schematics of the velocity field at the VC acquired during systole with continuous Doppler (1D encoded velocity value, top) and 4D flow CMR (3D encoded two-dimensional velocity field, bottom). Right: Definition of the anatomical regions to compute the RPD from the LVOT (Plane 1) to the VC (Plane 2). Two other anatomical regions are defined for the Supplemental Material B, the ascending aorta (AA) from the VC to the brachiocephalic artery (Plane 3), and the descending aorta (DA) from the left subclavian artery (Plane 4) to a plane at the same height of the aortic valve plane (Plane 5).

Simulated Doppler echocardiography

In order to avoid inter-modality variability in the interpretation of results, simulated echocardiographic velocity data were derived by sampling the 4D flow CMR data. Idealized conditions were taken: a perfect alignment between the direction of the blood jet and the ultrasound probe orientation, and no acoustic shadowing. Simulated echocardiographic data was then simply the peak velocity value in Plane 2 at the VC (see Figure 1), which was constructed through linear interpolation of the original 3D velocity field onto a grid of 1mmx1mm sample points in the perpendicular plane to the centerline of the aorta.

Non-invasive pressure drop estimates

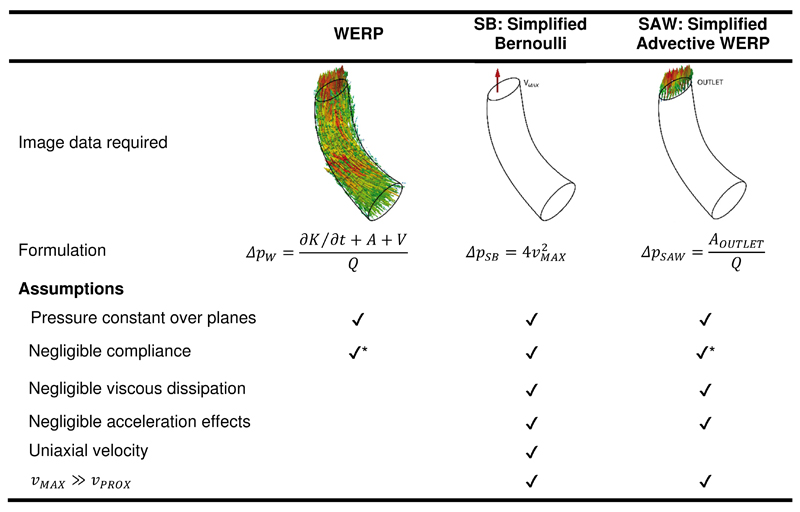
The Simplified Bernoulli (SB) formulation6 only accounts for the advective pressure drop, assumes that the flow jet is a single streamline, and neglects the proximal velocity at the LVOT, approximating the pressure drop in mmHg as,

ΔpSB=4vMAX2 (Equation 1)

where vMAX is the peak velocity at the VC, and the factor 4 comes from the conversion of pressure units from Pascals to mmHg, taking a blood density of ρ = 1060 kg/m3.

SB formulation neglects the unsteady and viscous terms of the Navier-Stokes equation, thus we evaluated the magnitude of all the components of the pressure drop to determine if the assumption holds true. We used the WERP method, due to its accuracy and robustness13, that computes the total pressure drop accounting for the complete fluid dynamics, i.e. the unsteady, advective and viscous components:

ΔpW=−1Q(∂K∂t+A+V), (Equation 2)

where Q is the flow rate computed at the outlet, ∂K/∂t is the temporal derivative of the kinetic energy within the vascular region, A is the advective energy rate describing the energy transfer due to the physical movement of a fluid in and out of the domain, and V is the rate of viscous dissipation describing energy losses due to friction.

The assumption of spatially uniform velocity distribution was evaluated by a comparison of the pressure drop computed by SB to one accounting for the complete velocity profile at the VC, the Simplified Advective WERP (SAW) pressure drop (ΔpSAW) - see Supplemental Material A for the derivation of SAW. SB, SAW and WERP methods are schematically presented in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Mathematical formulations to compute a pressure drop. Compliant models can be added in the formulations labeled with (*), but this is not applied in this work.

Within this work we focus on instantaneous peak pressure drops at the VC, and not on the net pressure drop downstream of the constriction. Results also include the temporal mean of this drop Δp¯ that is estimated averaging the 8 or 9 systolic frames of each subject.

Statistical analysis

Differences between Groups I and II are evaluated by an unpaired T-test.

Results

Analysis of the components of the pressure drop

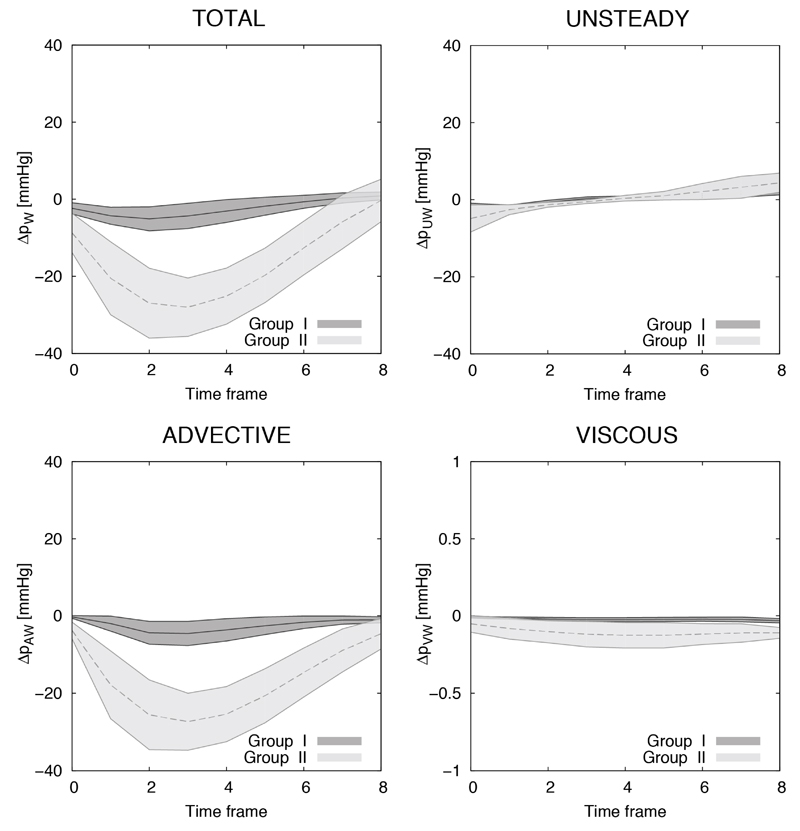
The advective pressure component is the main contributor to the TPD, especially in higher degrees of stenosis (Group II), as illustrated in Figure 3 and quantified in Table 2. Subjects in Group II had a mean advective drop of 16.33±4.02 mmHg, which reflected 99% of the mean total TPD on average (range 96-101%), and was dominant over the unsteady component by almost one order of magnitude (2.09±1.44 mmHg during acceleration) and over the viscous component by two orders of magnitude (0.10±0.06 mmHg). Prevalence of the advective component is also shown in Group I although to a lesser extent (2.55±1.80, 1.49±0.57 and 0.02±0.01 mmHg for the advective, unsteady and viscous components, respectively).

Figure 3.

Figure 3

Open in a new tab

Instantaneous TPD and its components computed for Group I (n=20) and Group II (n=12) using WERP formulation. Each line with range illustrates the mean±std of the distribution.

Table 2.

Average of the instantaneous TPD during systole Δp¯, in mmHg, in Group I and Group II (Mean±std) by WERP. Unsteady pressure drops are reported on acceleration (A) and deceleration (D) systolic events separately because otherwise they will greatly cancel each other. Negative values represent pressure increases. Note that the pressure components averaged during systole reported here do not add up into the total drop: only the instantaneous drop is the result of the addition of its components.

Component Group I Group II p-value
Total 2.55 ± 1.80 16.33 ± 4.02 < 0.001
Unsteady A 1.49 ± 0.57 A 2.09 ± 1.44 A 0.105
D -0.92 ± 0.39 D -2.20 ± 1.52 D 0.001
Advective 2.52 ± 1.79 16.29 ± 3.98 < 0.001
Viscous 0.02 ± 0.01 0.10 ± 0.06 < 0.001
Open in a new tab

Results in Table 2 highlight a clear differentiation in the TVR between groups for the advective and viscous drops (p<0.001) and for the unsteady component during deceleration (p=0.001), while showing non-significant differences during acceleration (p=0.105). To contextualize these results, Supplemental Material B provides the pressure drops along the ascending and descending part of the aorta in the two experimental groups.

Analysis of the impact of the velocity profile in the pressure drop

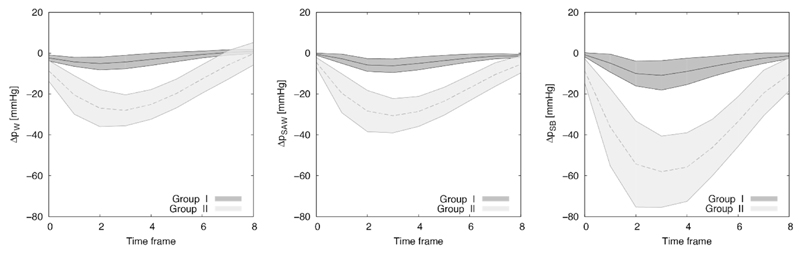
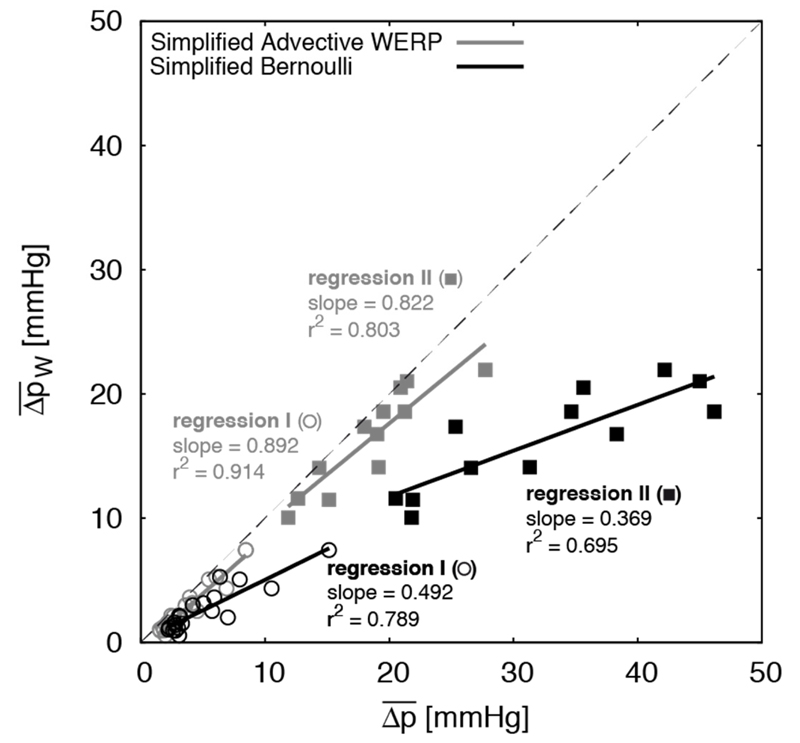
The impact of the assumption of a flat velocity profile is assessed by comparing TPD computed using SB and SAW formulations, finding an SB overestimation of 54% in the 32 subjects (range 5-136%), being smaller in the non-stenotic group (41% vs. 76% for Groups I and II, respectively).

Accounting for all the assumptions, Figure 4 illustrates the SB overestimation compared to the reference by WERP (average of 99% in stenotic subjects, range 49-145%). SAW had a milder overestimation, averaging 14% (range 1-35%) in the same group. Figure 5 reveals a poorer agreement with the reference pressure drops for SB when compared to SAW. SB also shows a lower precision (larger variability of the error) compared to SAW after correction for the linear regression observed in the 32 cases reported in Figure 5, with standard deviations observed for the two formulations of 0.8 and 0.5 mmHg in Group I and of 2.4 and 0.9 mmHg in Group II, respectively.

Figure 4.

Figure 4

Open in a new tab

Instantaneous TPD (mean±std values during systolic frames) estimated for Group I and II using WERP (left), SAW (center) and SB (right) formulations.

Figure 5.

Figure 5

Open in a new tab

Linear regression between the reference mean TPD from 4D flow CMR data using the WERP formulation against the mean TPD estimated using the SB (black) and SAW (grey) formulations in the two groups of patients. Case-specific values for subjects in Group I (circles) and Group II (squares), regressions for the estimation methods (solid lines) and identity line (dashed grey line).

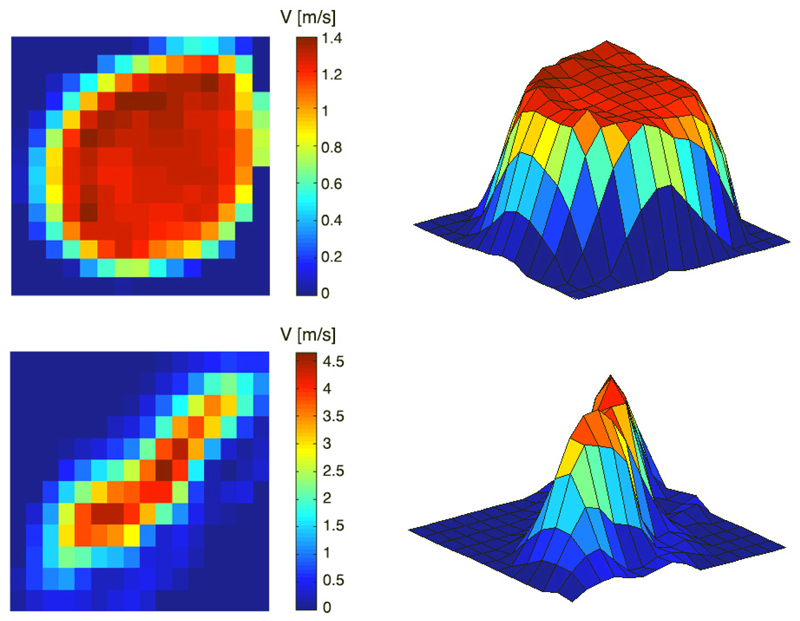
To contextualize the impact of the velocity profile on the estimated pressure drops, two representative cases for patients in both groups are presented in Figure 6. For completeness, Supplemental Material C provides a comprehensive description of the velocity profiles at the VC in all 32 subjects demonstrating their wide variability. Supplemental Material D provides an analysis of velocity profiles in three idealized stenosis, demonstrating that the SB overestimation as compared to SAW is uniquely caused by the velocity profile, and illustrates that a paraboloid distribution introduces an overestimation of the advective drop of ~100% (i.e. double) by SB.

Figure 6.

Figure 6

Open in a new tab

Velocity magnitude distribution from 4D flow data: in plane visualization (left) and 3D surface plot (right) in representative control (top) and stenotic (bottom) patients. The deviation from a flat profile in these two examples causes a SB overestimation of a 20% and 136%, respectively.

Discussion

The non-invasive assessment of the peak TPD at the VC can be simplified to the computation of its advective component, consistent with the SB formulation. Nevertheless, our results report that this formulation introduces a variable overestimation (range of 5-136% in 32 subjects) because velocity profiles at the VC are not uniform.

Analysis of pressure components

We experimentally verified in-vivo that the TPD is primarily driven by the spatial acceleration of the flow. This confirms the sensible choice of the SB formulation to quantify the maximal pressure drop from continuous Doppler recordings, since the Bernoulli principle simplifies the flow through a pipe by only accounting for the advective forces. This result agrees with the seminal work by Hatle et al.6 that established a landmark piece of evidence to justify the adoption of the SB formulation to stratify vascular constrictions.

However, the simplification of the pressure drop into only the advective component is not generalizable to all anatomical regions. We demonstrated that in the descending aorta - without any obstruction – the pressure drop is dominated by the unsteady component (see Supplemental Material B), in agreement with results reported in the human healthy aorta14. The trans-mitral pressure drop has been shown, contradicting the initial evidence6, to require the unsteady component to complement the SB formulation in order to find a good agreement with catheterization recordings19. The unsteady component also plays a significant role in the TPD in the pulmonary valve, and neglecting it with the SB formulation leads to a significant underestimation of the pressure drop20.

The ability to analyze the contributors of a pressure drop also opens the possibility for an improved understanding of the impact of the valve dysfunction, and to eventually define biomarkers with enhanced risk stratification and predictive power. Bernoulli based metrics from clinical guidelines2,3 only capture the advective drop in the TVR, and our analysis reveals the presence of additional contributors to the functional differences between a stenotic and healthy valve. First, a stenotic valve introduces a significant increment of the laminar viscous losses in all vascular segments analyzed (Table 2 and Supplemental Material B). Viscous drops capture the inefficiency of the aorta as a conduit, an additional burden to the heart in every heartbeat, and therefore could be a more specific prognostic marker for heart failure. It is nevertheless important to highlight that current spatial resolution of phase-contrast CMR provides an underestimated and resolution-dependent viscous dissipation, up to only a 9% of the real magnitude with isotropic resolution of 2mm21. We speculate that, by using similar CMR protocols across studies, viscous dissipation can be estimated with sufficient precision to enable the extraction of a clinically diagnostic value. The differences found in this study, together with previous findings of the analysis of viscous laminar losses22, support this claim.

Results also reveal that the narrow jet produced by a stenotic valve introduces a significantly larger unsteady pressure drop in the AA (Supplemental Material B). The heart requires more energy to create the flow momentum of the narrow blood jet caused by a stenotic valve, to accelerate it in time, and this functional difference might be a specific prognostic marker for heart failure. It is relevant to note that this increment in unsteady pressure cannot be captured by the peak or the average pressure drop value: an average during systolic events will cancel the acceleration and deceleration events, and the peak unsteady effects are not synchronous with the peak advective effects14, therefore not contributing to the peak TPD value in the stenotic group that is dominated by advective effects. Further studies are thus required to identify which pressure component holds the largest prognostic value.

Impact of the velocity profile

The most interesting finding of this study is that the SB simplification of blood flow as a single streamline8,23 produces a significant overestimation of the estimated pressure drop. The study in Supplemental Material D demonstrates that SB would only be accurate if the velocity distribution was uniform, with all particles at the cross-section of a vessel having the same velocity.

Analysis of our 32 subjects reveals a large variability in the morphology of the velocity profiles, as illustrated in Supplemental Material C. The non-stenotic group shows flatter velocity profiles, and had a reduced overestimation by SB as compared to the stenotic group. This finding agrees with previous works that already describe the over-amplification of the assumption of a non-uniform velocity profile24,25, and that attributed the variability of the measurements to the different flow profile characteristics from patient to patient.

The cause of this variability could be initially attributed to the shape of the valve orifice: the more circular shape, the blunter the velocity profile. This was the justification in the early studies that tested and verified the validity of Bernoulli principle despite very irregular orifice shapes tested26,27. Nevertheless, it is the blood velocity distribution, and not the shape of the orifice, that should be analyzed. In these preliminary works the abrupt transition from a wide cavity into a small orifice is not fully representative of the cardiac valve mechanics. We speculate that the interaction between a pulsatile flow and the deformable and compliant valve leaflets that create the gradual transition from the ventricular chamber to the blood jet is the main cause of the non-flat velocity profiles in valve stenosis.

The core of the question then is to interrogate the velocity profile at the point of the VC: any deviation from a flat shape is a cause of overestimation of SB. And the existence of non-flat velocity profiles at the VC has been reported using a variety of technologies, such as advanced laser particle tracking technologies28, Doppler ultrasound29,30 and Phase-contrast CMR31. Nevertheless, it should be noted that the point-spread function of a CMR system causes a spatial averaging of the velocity data. As a consequence, our results contain a spurious source of amplification of the deviation from a flat velocity profile. This factor alone cannot explain the anisotropic velocity distribution highlighted at the VC of the representative stenotic case illustrated in Figure 6, nor the wide range of shapes in the velocity profiles observed in Supplemental Material C. Previous experimental findings in bioprosthetic valves comparing peak drops at the VC between manometers and Bernoulli-based continuous Doppler assessment reported an average overestimation of a 24% with the latter (average slope of 0.809 in all explanted valves in Table 5 in Stewart et al.32), which is approximately half of the 54% in our findings. Future work is thus needed to fully characterize the overestimation of the advective pressure drop at the VC through the acquisition of more accurate velocity profiles.

The simplification of the transvalvular jet as a flow field with uniform velocity distribution therefore introduces a loss, not only in accuracy, but also in precision. Average bias correction of SB (our results suggest a factor of 0.65 to compensate the average 54% of overestimation) will not be enough to account for the fact that the increment of work, or energy, to push blood through the valve does depend on the morphology of the blood jet.

Potential correction of the Bernoulli method

Proposed method (SAW formulation), by correctly accounting for the factor of the velocity profile, can improve the risk stratification of any condition that currently relies on Bernoulli’s simplification. Aortic stenosis is the condition exemplified and analyzed in this work, and an immediate extension is the functional characterization of the narrow left ventricular outflow tract in hypertrophic cardiomyopathy.

The SAW formulation (see details in Supplemental material A) is conceptually an extension of SB into a cross section of the vessel. As such, it can also be extended to account for the proximal velocity, as detailed in Supplemental material A. SAW can be used with both 4D and 2D flow CMR, since data is only required in one plane, thus enabling the possibility of high frame rates of 2D acquisitions. The adoption of the correct formulation is therefore straightforward in future clinical research studies using CMR flow.

SAW introduces further requirements in the spatio-temporal resolution of velocity data compared to SB. A previous study with in-silico data reports that a very coarse temporal resolution of 8 frames per heartbeat (125ms of temporal resolution), and with a reasonable 2 mm of spatial resolution and SNR=20dB, the relative error of the total pressure drop was below 12%13. Note that the technique used in this work has higher frame rates (40 ms of temporal resolution). Further research is nevertheless needed to identify the optimal CMR acquisition protocol (resolution and noise) for SAW.

Access to 4D flow CMR sequences is mainly restricted to specialized research centers, and translation to our findings to echocardiographic imaging is strongly desirable. A CMR technique may help to develop an echo protocol to address this area better, potentially with newer techniques in 3-dimensional echo flow, based on the positive feasibility results reported in this manuscript. In this direction, supplemental material A describes how to adapt SAW to the characteristics of the velocity data obtained by echocardiography. Furthermore, Supplemental material E illustrates that simulated 3D echocardiographic data, offering a complete velocity profile at the VC with artefacts from the funneling effect and from the projection of the velocity along the echocardiographic probe insonation line, will introduce a tolerable bias. Access to one line of insonation as with a 2D echo probe will only partially correct SB overestimation and will suffer from an additional variability caused by a partial view of the complete profile, justifying the need of improved acquisition strategies that render a more complete picture of the velocity profile. Besides these theoretical considerations, practical considerations such as the limited access to the valve anatomy by shadowing effects caused by a calcified valve, or the presence of aliasing, will be additional challenges that need to be addressed for the successful adoption of a correct estimation of the advective pressure drop at the VC.

The adoption of the improved formulation is thus feasible to a wide range of imaging acquisition protocols and modalities, and further research is needed to define the optimal strategy to control the location of the VC to be imaged, to identify the direction of the jet, and to maximize the amount and quality of velocity data.

Peak vs. net pressure drops

Our work focused on the analysis of the peak pressure drop at the point of the VC, and not on the net pressure drop after the VC, which has been proposed as a more efficient biomarker for the degree of constriction experienced by the blood flow, i.e. the additional burden that the LV has to overcome27,33,34. The net pressure drop is lower than the peak pressure drop estimated at the TVR, and it better correlates with catheter measurements4,5. It accounts for the partial recovery of pressure downstream of the VC18,33,34 caused by the full recovery of the advective pressure (i.e. the transition from a narrow jet to a wide velocity profile across the complete aortic cross-section) and by the losses due to viscous dissipation.

The net drop can be estimated non-invasively from the peak drop (peak velocity) and an assessment of the amount of the energy loss as a function of the valve effective orifice area and the size of the ascending aorta33. Here we speculate that a more accurate and robust estimation of the peak drop, as demonstrated in this work, will also improve the prediction of the net pressure drop from velocity and geometrical data.

The net drop quantifies pressure differences between LVOT and end of the AA, and our results provide further insights about the choice of the anatomical point after the VC where to estimate the net drop. In our cohort the advective pressure drop in the TVR was fully recovered along the AA in both groups (Supplemental Material B). The length of the AA may thus be enough to make the transition from a narrow jet of the VC to a fully developed flow profile, but further investigation in more severe stenotic subjects is needed to confirm this finding. On the contrary, results report that the length of the vascular domain that is affected by additional viscous losses caused by the constriction is larger than the AA: losses in the DA are doubled in the stenotic group compared to the control group (0.15 vs 0.07 mmHg, p<0.001, Supplemental Material B), accounting for approximately a quarter of the cumulative viscous pressure drop in the three regions under study. Quantification of the total additional burden caused to the heart by a stenotic valve might thus require the study of the complete aortic anatomy, and not only the AA.

Limitations

The main limitation is the lack of catheterization recordings of pressure, and is justified by the experimental difficulty to get the instantaneous pressure drop between the LVOT and the VC in-vivo. This requires a stable and accurate placement of the catheterized sensor at the VC to avoid the spurious effect of the pressure recovery, and the verification that the sensor is not introducing an artifact in the pressure data, as it is expected in the very narrow jets35.

Current spatio-temporal resolution of phase-contrast CMR data is not suitable for the estimation of the net pressure drop because it misses the energy loss caused by laminar viscous or turbulent dissipation21,36. An attenuated and resolution-dependent version of the real dissipation due to laminar friction effects, and a surrogate of the turbulent viscous dissipation, are the metrics that can be extracted from this data21,36.

Supplementary Material

Supplemental Material

Clinical Perspective.

A more accurate and precise noninvasive estimation of the peak pressure drop, beyond Bernoulli’s principle, is now possible by a more comprehensive examination of blood velocity. This work illustrates the large variability in the shape of the velocity profile at the vena contracta after a stenosed valve, and how this introduces an uncontrolled source of error in current practice based on Bernoulli’s formulation. Errors are larger and more variable in stenotic cases, where the narrow and irregular opening of the impaired valve produces anisotropic, non-axisymmetric and skewed blood flow jets. Controlling this factor through the formulation proposed in this work will improve risk stratification and clinical decision-making in valve stenosis, and potentially in any other conditions that experience flow constriction, such as a narrowed left ventricular outflow tract in hypertrophic cardiomyopathy. More precise and accurate values of pressure drop can already be obtained clinically from CMR, also removing the difficulty of aligning an echo probe with the flow jet. Widespread clinical adoption using echo probes is feasible, direct for 3D echo with a good anatomical window, although further efforts to define the optimal acquisition strategy are needed for 2D echo. Avenues of further research are now open to establish the new cut-off values of pressure drop to risk stratify flow constrictions, to improve the prediction of the net pressure drop, and to determine which pressure biomarker (peak, net, or any of its components) holds the largest prognostic value to predict clinical outcomes.

Acknowledgments

Sources of Funding

Wellcome Trust and Royal Society (Grants no. 099973/Z/12/Z, WT088641), EPSRC (EP/N011554/1), British Heart Foundation Centres of Research Excelence (KCL and Oxford), and UK NIHR (Guy's and St Thomas' & Oxford NIHR Biomedical Research Centres, Healthcare Technology Co-operative for Cardiovascular Disease).

Footnotes

Disclosures

None.

References

  • 1.Cioffi G, Faggiano P, Vizzardi E, Tarantini L, Cramariuc D, Gerdts E, de Simone G. Prognostic effect of inappropriately high left ventricular mass in asymptomatic severe aortic stenosis. Heart. 2011;97:301–307. doi: 10.1136/hrt.2010.192997. [DOI] [PubMed] [Google Scholar]
  • 2.Baumgartner H, Hung J, Bermejo J, Chambers B, Evangelista A, Griffin BP, Iung B, Otto CM, Pellikka PA, Quinones M. Echocardiographic assessment of valve stenosis: EAE/ASE recommendations for clinical practice. J Am Soc Echocardiogr. 2009;22:1–23. doi: 10.1016/j.echo.2008.11.029. [DOI] [PubMed] [Google Scholar]
  • 3.Nishimura RA, Otto CM, Bonow RO, Carabello BA, Erwin JP, Guyton RA, O'Gara PT, Ruiz CE, Skubas NJ, Sorajja P, Sundt TM, et al. 2014 AHA/ACC guideline for the management of patients with valvular heart disease: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J Am Coll Cardiol. 2014;63:e57–185. doi: 10.1016/j.jacc.2014.02.536. [DOI] [PubMed] [Google Scholar]
  • 4.Baumgartner H, Stefenelli T, Niederberger J, Schima H, Maurer G. “Overestimation” of catheter gradients by Doppler ultrasound in patients with aortic stenosis: A predictable manifestation of pressure recovery. J Am Coll Cardiol. 1999;33:1655–1661. doi: 10.1016/s0735-1097(99)00066-2. [DOI] [PubMed] [Google Scholar]
  • 5.Garcia D, Dumesnil JG, Durand L-G, Kadem L, Pibarot P. Discrepancies between catheter and Doppler estimates of valve effective orifice area can be predicted from the pressure recovery phenomenon: practical implications with regard to quantification of aortic stenosis severity. J Am Coll Cardiol. 2003;41:435–42. doi: 10.1016/s0735-1097(02)02764-x. [DOI] [PubMed] [Google Scholar]
  • 6.Hatle L, Brubakk A, Tromsdal A, Angelsen B. Noninvasive assessment of pressure drop in mitral stenosis by Doppler ultrasound. Br Heart J. 1978;40:131–40. doi: 10.1136/hrt.40.2.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Yoganathan AP, Cape EG, Sung HW, Williams FP, Jimoh A. Review of hydrodynamic principles for the cardiologist: Applications to the study of blood flow and jets by imaging techniques. J Am Coll Cardiol. 1988;12:1344–1353. doi: 10.1016/0735-1097(88)92620-4. [DOI] [PubMed] [Google Scholar]
  • 8.Garcia D, Pibarot P, Durand LG. Analytical modeling of the instantaneous pressure gradient across the aortic valve. J Biomech. 2005;38:1303–1311. doi: 10.1016/j.jbiomech.2004.06.018. [DOI] [PubMed] [Google Scholar]
  • 9.Marriott M. Civil Engineering Hydraulics. John Wiley & Sons; 2009. [Google Scholar]
  • 10.Markl M, Kilner PJ, Ebbers T. Comprehensive 4D velocity mapping of the heart and great vessels by cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2011;13:7. doi: 10.1186/1532-429X-13-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Krittian SBS, Lamata P, Michler C, Nordsletten DA, Bock J, Bradley CP, Pitcher A, Kilner PJ, Markl M, Smith NP. A finite-element approach to the direct computation of relative cardiovascular pressure from time-resolved MR velocity data. Med Image Anal. 2012;16:1029–1037. doi: 10.1016/j.media.2012.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Meier S, Hennemuth A, Friman O, Bock J, Markl M, Preusser T. Non-invasive 4D blood flow and pressure quantification in central blood vessels via PC-MRI BT. Computing in Cardiology. 2010;37:903–906. [Google Scholar]
  • 13.Donati F, Figueroa CA, Smith NP, Lamata P, Nordsletten DA. Non-Invasive Pressure Difference Estimation from PC-MRI Using the Work-Energy Equation. Med Image Anal. 2015;26:159–72. doi: 10.1016/j.media.2015.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Lamata P, Pitcher A, Krittian S, Nordsletten DA, Bissell MM, Cassar T, Barker AJ, Markl M, Neubauer S, Smith NP. Aortic relative pressure components derived from four-dimensional flow cardiovascular magnetic resonance. Magn Reson Med. 2014;72:1162–9. doi: 10.1002/mrm.25015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Bissell MM, Hess AT, Biasiolli L, Glaze SJ, Loudon M, Pitcher A, Davis A, Prendergast B, Markl M, Barker AJ, Neubauer S, et al. Aortic dilation in bicuspid aortic valve disease: flow pattern is a major contributor and differs with valve fusion type. Circ Cardiovasc Imaging. 2013;6:499–507. doi: 10.1161/CIRCIMAGING.113.000528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Du Bois D, Du Bois EF. A formula to estimate the approximate surface area if height and weight be known. Nutrition. 1916;5:303–11. [PubMed] [Google Scholar]
  • 17.Bock J, Frydrychowicz A, Lorenz R, Hirtler D, Barker AJ, Johnson KM, Arnold R, Burkhardt H, Hennig J, Markl M. In vivo noninvasive 4D pressure difference mapping in the human aorta: Phantom comparison and application in healthy volunteers and patients. Magn Reson Med. 2011;66:1079–88. doi: 10.1002/mrm.22907. [DOI] [PubMed] [Google Scholar]
  • 18.Garcia J, Capoulade R, Le Ven F, Gaillard E, Kadem L, Pibarot P, Larose E. Discrepancies between cardiovascular magnetic resonance and Doppler echocardiography in the measurement of transvalvular gradient in aortic stenosis: the effect of flow vorticity. J Cardiovasc Magn Reson. 2013;15:84. doi: 10.1186/1532-429X-15-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Firstenberg MS, Vandervoort PM, Greenberg NL, Smedira NG, McCarthy PM, Garcia MJ, Thomas JD. Noninvasive estimation of transmitral pressure drop across the normal mitral valve in humans: Importance of convective and inertial forces during left ventricular filling. J Am Coll Cardiol. 2000;36:1942–1949. doi: 10.1016/s0735-1097(00)00963-3. [DOI] [PubMed] [Google Scholar]
  • 20.Falahatpisheh A, Rickers C, Gabbert D, Heng EL, Stalder A, Kramer HH, Kilner PJ, Kheradvar A. Simplified Bernoulli’s method significantly underestimates pulmonary transvalvular pressure drop. J Magn Reson Imaging. 2016;43:1313–9. doi: 10.1002/jmri.25097. [DOI] [PubMed] [Google Scholar]
  • 21.Casas B, Lantz J, Dyverfeldt P, Ebbers T. 4D flow MRI-Based pressure loss estimation in stenotic flows: Evaluation using numerical simulations. Magn Reson Med. 2015;000(4):1808–21. doi: 10.1002/mrm.25772. [DOI] [PubMed] [Google Scholar]
  • 22.Barker AJ, van Ooij P, Bandi K, Garcia D, Albaghdadi M, McCarthy P, Bonow RO, Carr J, Collins J, Malaisrie SC, Markl M. Viscous energy loss in the presence of abnormal aortic flow. Magn Reson Med. 2014;72:620–8. doi: 10.1002/mrm.24962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Heys JJ, Holyoak N, Calleja AM, Belohlavek M, Chaliki HP. Revisiting the simplified bernoulli equation. Open Biomed Eng J. 2010;4:123–128. doi: 10.2174/1874120701004010123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Requarth JA, Goldberg SJ, Vasko SD, Allen HD. In vitro verification of Doppler prediction of transvalve pressure gradient and orifice area in stenosis. Am J Cardiol. 1984;53:1369–73. doi: 10.1016/0002-9149(84)90096-1. [DOI] [PubMed] [Google Scholar]
  • 25.Rijsterborgh H, Roelandt J. Doppler assessment of aortic stenosis: Bernoulli revisited. Ultrasound Med Biol. 1987;13:241–8. doi: 10.1016/0301-5629(87)90096-2. [DOI] [PubMed] [Google Scholar]
  • 26.Teirstein PS, Yock PG, Popp RL. The accuracy of Doppler ultrasound measurement of pressure gradients across irregular, dual, and tunnellike obstructions to blood flow. Circulation. 1985;72:577–84. doi: 10.1161/01.cir.72.3.577. [DOI] [PubMed] [Google Scholar]
  • 27.Voelker W, Reul H, Stelzer T, Schmidt A, Karsch KR. Pressure recovery in aortic stenosis: an in vitro study in a pulsatile flow model. J Am Coll Cardiol. 1992;20:1585–93. doi: 10.1016/0735-1097(92)90454-u. [DOI] [PubMed] [Google Scholar]
  • 28.Raghav V, Okafor I, Quach M, Dang L, Marquez S, Yoganathan AP. Long-Term Durability of Carpentier-Edwards Magna Ease Valve: A One Billion Cycle In Vitro Study. Ann Thorac Surg. 2016;101:1759–65. doi: 10.1016/j.athoracsur.2015.10.069. [DOI] [PubMed] [Google Scholar]
  • 29.Haugen BO, Berg S, Brecke KM, Torp H, Slørdahl SA, Skjærpe T, Samstad SO. Blood flow velocity profiles in the aortic annulus: a 3-dimensional freehand color flow Doppler imaging study. J Am Soc Echocardiogr. 2002;15:328–33. doi: 10.1067/mje.2002.117292. [DOI] [PubMed] [Google Scholar]
  • 30.Mathison M, Furuse A, Asano K. Doppler analysis of flow velocity profile at the aortic root. J Am Coll Cardiol. 1988;12:947–54. doi: 10.1016/0735-1097(88)90460-3. [DOI] [PubMed] [Google Scholar]
  • 31.Kozerke S, Hasenkam JM, Nygaard H, Paulsen PK, Pedersen EM, Boesiger P. Heart motion-adapted MR velocity mapping of blood velocity distribution downstream of aortic valve prostheses: initial experience. Radiology. 2001;218:548–55. doi: 10.1148/radiology.218.2.r01ja07548. [DOI] [PubMed] [Google Scholar]
  • 32.Stewart SFC, Nast EP, Arabia FA, Talbot TL, Proschan M, Clark RE. Errors in pressure gradient measurement by continuous wave Doppler ultrasound: Type, size and age effects in bioprosthetic aortic valves. J Am Coll Cardiol. 1991;18:769–779. doi: 10.1016/0735-1097(91)90801-f. [DOI] [PubMed] [Google Scholar]
  • 33.Garcia D, Pibarot P, Dumesnil JG, Sakr F, Durand L-GGLG. Assessment of aortic valve stenosis severity: A new index based on the energy loss concept. Circulation. 2000;101:765–771. doi: 10.1161/01.cir.101.7.765. [DOI] [PubMed] [Google Scholar]
  • 34.Pibarot P, Dumesnil JG. Improving assessment of aortic stenosis. J Am Coll Cardiol. 2012;60:169–80. doi: 10.1016/j.jacc.2011.11.078. [DOI] [PubMed] [Google Scholar]
  • 35.de Vecchi A, Clough RE, Gaddum NR, Rutten MC, Lamata P, Schaeffter T, Nordsletten DA, Smith NP. Catheter-Induced Errors in Pressure Measurements in Vessels: An In-Vitro and Numerical Study. IEEE Trans Biomed Eng. 2014;61:1844–1850. doi: 10.1109/TBME.2014.2308594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Binter C, Gülan U, Holzner M, Kozerke S. On the accuracy of viscous and turbulent loss quantification in stenotic aortic flow using phase-contrast MRI. Magn Reson Med. 2016;76:191–6. doi: 10.1002/mrm.25862. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
NIHMS70690-supplement-Supplemental_Material.pdf (1.4MB, pdf)

RESOURCES