Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2017 Jan 6.
Published in final edited form as: Wellcome Open Res. 2016 Dec 14;1:27. doi: 10.12688/wellcomeopenres.10284.1

Quantification and determinants of the amount of respiratory syncytial virus (RSV) shed using real time PCR data from a longitudinal household study

Miriam Wathuo 1, Graham F Medley 2, D James Nokes 1,3,a, Patrick K Munywoki 1,4
PMCID: PMC5218551  EMSID: EMS70985  PMID: 28066826

Abstract

Background

A better understanding of respiratory syncytial virus (RSV) epidemiology requires realistic estimates of RSV shedding patterns, quantities shed, and identification of the related underlying factors.

Methods

RSV infection data arise from a cohort study of 47 households with 493 occupants, in coastal Kenya, during the 2009/2010 RSV season. Nasopharyngeal swabs were taken every 3 to 4 days and screened for RSV using a real time polymerase chain reaction (PCR) assay. The amount of virus shed was quantified by calculating the ‘area under the curve’ using the trapezoidal rule applied to rescaled PCR cycle threshold output. Multivariable linear regression was used to identify correlates of amount of virus shed.

Results

The median quantity of virus shed per infection episode was 29.4 (95% CI: 15.2, 54.2) log10 ribonucleic acid (RNA) copies. Young age (<1 year), presence of upper respiratory symptoms, intra-household acquisition of infection, an individual’s first infection episode in the RSV season, and having a co-infection of RSV group A and B were associated with increased amount of virus shed.

Conclusions

The findings provide insight into which groups of individuals have higher potential for transmission, information which may be useful in designing RSV prevention strategies.

Keywords: RSV, viral density, shedding, household, PCR, cycle threshold

Introduction

Respiratory syncytial virus (RSV) is the most common viral cause of severe lower respiratory tract infection (LRTI) among infants and children under 5 years old worldwide, with the greatest burden occurring in developing countries 1. Most children experience an RSV infection episode by the age of two years, with peak rates of infection occurring in the first year of life 2. Re-infections occur throughout life 3 as RSV infections provide incomplete or waning immunity. There are no licensed RSV vaccines but there is heightened activity in vaccine development 4–8.

Vaccine delivery strategies should be informed by detailed understanding of RSV transmission dynamics. To reduce the circulation of RSV, identifying which groups are responsible for majority of the infections is critical. Transmission potential can be estimated by a combination of mixing patterns 9 and virus shedding (viral density and duration). Human experimental infection with RSV reported that volunteers inoculated with a higher dose of virus (4.7 log10 tissue culture infectious dose (TCID)50 of RSV A2) were more likely to be infected than those given low doses of the inoculum (3.7 log10 TCID50 of RSV A2) 10, suggesting that individuals who shed more virus are likely to be more infectious. Determining quantities shed and the related underlying factors, will help in predicting the spread of infection in a population and identify key groups to target for infection control. Previous studies have used the duration of shedding to identify individuals with the greatest potential for infection spread11, based on the assumption that they have a higher number of infectious contacts. Several studies report on the duration of RSV shedding with mean values ranging from 4.5 to 11.2 days 12, 13. In addition to variation in assay type, determinants included history of RSV infection 12, age, infection severity, detection of other viruses before and during the RSV infection, and presence of concurrent RSV infections in the same household13. These studies and others 14, 15 do not account for the temporal changes in quantity of virus shed. Experimental RSV infection studies indicate that an individual infection episode begins with low viral shedding, which rises with time as the virus continues to replicate within epithelial cells and finally declines as the infection clears 16.

The current analysis aims to include temporal changes in viral excretion in estimating the total amount of virus shed during an individual RSV infection episode. Relative to the duration of shedding, this may provide an improved correlate of infectiousness and help in identifying the key factors influencing RSV shedding patterns. Such data are informative in formulating vaccine product profiles and designing prevention strategies for RSV.

Methods

Data

The RSV infection data arise from an intensively followed cohort of 47 households with 493 occupants in rural coastal Kenya. The details of the study have been described elsewhere 13, 17, 18. In summary, throughout an RSV season spanning 26 weeks (December 2009–June 2010), nasopharyngeal swabs (NPS) were collected by trained field assistants every 3–4 days, irrespective of symptoms, from 47 RSV naïve infants and their household members. Households were selected through the Kilifi Health and Demographic Surveillance System (KHDSS) and local community health workers and were considered eligible if they had a child born after 1 st April 2009. The infants were assumed to be RSV naïve because they were born after the 2008/2009 RSV season. A total of 16928 NPS collections were tested for RSV (groups A and B) and other prevalent respiratory viruses (adenoviruses, rhinoviruses and human coronaviruses (NL63, 229E and OC43)) using multiplex real time polymerase chain reaction (PCR) assay as previously described 19. As PCR cycles proceed the quantity of product detected rises and at some point passes through a user assigned threshold for detection (set at the point of observable exponential rise in product), known as the cycle threshold (Ct). The earlier (lower) the Ct value the higher the starting concentration of target sequence (equated with viral density). As a cut-off, samples with Ct values of 35.0 and below were considered positive. An RSV infection episode was defined as the period within which an individual provided specimens which were PCR positive for the same infecting RSV group with no more than 14 days separating any two positive samples. A household outbreak was defined as a period in which a household experienced more than one individual infection episode, without there being more than 14 days between any two infection episodes. A primary/index case was a person first identified to have an RSV infection leading to a household outbreak. A first episode was the first episode in that season that an individual had while a subsequent episode was a second or third episode that a person may have had during the follow up. Virus test results, recorded in Ct values, were converted to log10 ribonucleic acid (RNA) copy numbers (direct measure of viral density) to enable plotting of the time – concentration curve. The equation y = -3.308x + 42.9 was used to convert Ct values (y), to their log10 RNA equivalents (x), as a way of quantifying RNA 20. The converted values are hereafter referred to as viral densities. Amount of virus shed during an infection episode was estimated by calculating the area under the time-concentration curve (AUC) using the trapezoidal rule 21. The peak viral density for each episode was identified as the highest measured viral density in an infection episode.

Calculation of area under curve

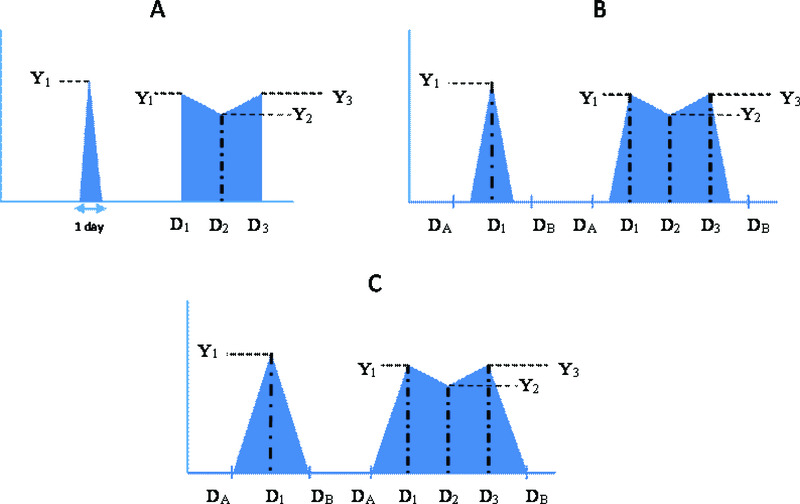
For every episode, calculation of the area under the curve involved plotting a time concentration (viral density) curve of the different viral densities over the duration of shedding of the episode (Figure 1). Three scenarios were explored which take account of uncertainty arising from the sampling intervals, estimating a minimum, midpoint and maximum AUC, for which calculations are described below, aided by illustrations in Figure 1A – C). For each scenario, two examples are described: the first with one positive observation, and the second with three positive observations (Figure 1). This analogy can be extended to episodes with a different number of positive observations. The number of positive observations in an episode ranged from 1 to 11.

Figure 1.

Figure 1.

Open in a new tab

Schema depicting the patterns of virus shedding for three possible scenarios, A, B and C, graphically representing the minimum, midpoint and maximum AUC calculations, respectively, defined in the Methods text. For each scenario two example episodes are shown, the first with only one virus positive sample, and the second with three virus positive samples. Yi - Viral density values; DA – Day of last negative sample before start of episode; DB – Day of first negative sample after end of episode; D1 – Day of first positive sample; D2 – Day of second positive sample; D3 – Day of third positive sample.

a) Minimum area under curve. The minimum AUC estimate assumed that an individual started shedding on the day of the first positive sample in an infection episode, and stopped shedding on the day of the last positive sample of the episode, in the form shown in Figure 1A, with viral density Y1, and hence calculated as,

AUC = 0.5 * Y1 * 1 day.

If an episode had two or more consecutive positive observations, AUC was calculated by including all days in which they were assumed to be shedding. Thus, for an example episode with three positive observations, with viral density Yi, i=1,3, respectively, then:

AUC = (0.5 *((D2 – D1) +1) * (Y1+ Y2)) + (0.5 * (D3– D2) * (Y2+ Y3))…………….….. (i).

Note the addition of one day to the calculation such that shedding on day 1 is included. Days with zero Ct values in between samples with positive viral densities were taken to have zero viral density. Therefore, AUC was calculated as in (i) above including both zero and non-zero observations. For left and right censored episodes, calculation of the amount of virus remained as in (i) above.

b) Midpoint area under curve. The midpoint AUC estimate assumed that an individual began shedding midway between the day of the first positive sample of an infection episode and the day of the last negative sample before the start of the episode. An individual was assumed to have stopped shedding midway between the day of the last positive sample of an episode and the day of the first negative sample after the episode (Figure 1B).

Hence to calculate the AUC for an episode with one positive observation:

Let the midpoint days be: x = (DA + D1)/2, and y = (DB + D1)/2, where DA, DB and D1 are, respectively, the day of the last negative sample before the start of the episode; day of the first negative sample after the end of the episode; day of the first positive sample, hence

AUC = 0.5 *((y – x) + 1) * Y1.

To calculate the AUC for an episode with three positive observations:

Let the midpoint days be: x = (DA + D1)/2, and y = (DB + D3)/2, where D2 and D3 are the days of the second and third positive samples, respectively, so

AUC = (0.5 * Y1 * ((D1- x) +1)) + (0.5 * (D2 – D1) * (Y1 + Y2)) + (0.5 * (D3– D2) * (Y2 + Y3)) + (0.5 * Y3 * (y - D3)) …………. (ii).

Days with zero Ct values in between samples with positive viral densities were taken to have a Ct value of 40, and the AUC calculated as in (ii) above.

For left and right censored episodes, with unknown DA and DB, respectively, shedding was assumed to start 1.85 days (ie half the mean sampling interval) before the first observed day of shedding, D1, and to finish 1.85 days after the last positive (D3 in the example of (ii) above). Hence, in (ii) above, (D1-x) and (y-D3) were replaced with the value 1.85 days, for left and right censored data, respectively.

Maximum area under curve. To calculate the maximum AUC, individuals were assumed to have begun shedding immediately after the last negative sample before the start of an episode, and stopped shedding immediately before the first negative sample after the episode (Figure 1C). The viral densities for the days when individuals were considered to have begun and stopped shedding were assumed to be zero. Zero Ct values in between samples with positive viral densities were substituted with the average of the two immediate positive values.

Hence, to calculate the AUC for an episode with one positive observation:

AUC = 0.5 *(DB – DA) * Y1,

and to calculate the AUC for an episode with three positive observations:

AUC = (0.5 * Y1 * (D1- DA)) + (0.5 * (D2– D1) * (Y1+ Y2)) + (0.5 * (D3– D2) * (Y2 + Y3)) + (0.5 * Y3 * (DB - D3)) ……………………(iii).

Left and right censored episodes were treated similarly to that for midpoint AUC, but assuming shedding began and ended 3.7 days (i.e. the mean sampling interval) before the first positive sample of an episode and after the last positive sample of an episode. Hence in (iii) above, (D1-DA) and (DB-D3) were replaced with the value 3.7 days, for left and right censored data, respectively.

Statistical analysis

Data were analysed using Stata version 13.1 (StataCorp. College Station, TX: StataCorp LP. RRID:SCR_012763) and RStudio version 0.99.489 (RStudio Team. RStudio, Inc., Boston, MA. RRID:SCR_000432). The differences in the distribution of amount of virus by various characteristics was tested using the Wilcoxon rank-sum test and Kruskal Wallis rank test as appropriate. Spearman's rank correlation coefficient was used to find the association between the different measures of viral quantity calculated. Linear regression was used to identify the main factors associated with the amount of virus shed, i.e. AUC. Possible covariates were chosen from the dataset by selecting those that could plausibly be associated with AUC. A univariable analysis was carried out to identify factors independently associated with AUC. All variables with a p-value of <0.1 in the univariable analysis were included in the multivariable regression analysis. The final multivariable regression model was developed by a backward stepwise procedure, rejecting variables with a p-value >0.05 in likelihood ratio tests. Risk factors were removed in descending order of strength of association determined from the multivariable analysis. Two interactions were tested in the multivariable model. An interaction between age and symptom status was tested to determine if the effect of age on the amount of virus shed varied by symptom status. An interaction between age and primary/secondary case status was also tested because it was suspected that the effect of age on the amount of virus shed could vary by primary/secondary case status. The final model was adjusted for sex, even though it was not statistically significant.

Ethics

The household study was approved by the KEMRI Ethical Review Committee in Kenya, SSC No. 1651, and the Biomedical Research Ethics Committee at the University of Warwick in the United Kingdom. Data was anonymised by using identification IDs for each participant and household.

Consent

Written informed consent was obtained from all participants and/or their parents or guardians.

Results

Infection episodes

The mean (SD) sampling interval was 3.7 (2.3) days. The median number of swabs collected for an individual was 41, with the minimum being 1 swab and the maximum 48 swabs. There were 537 (3.2%) samples from 179 individuals that were positive for RSV. RSV group A only, group B only, and group A/B co-infections were detected in 231 (1.5%), 287 (1.8%), and 19 (0.1%) NPS collections, respectively (Table 1). From the 179 infected individuals, a total of 208 infection episodes were observed during the six-month study period; 180 were fully observed episodes while 13 and 17 were left and right censored episodes respectively. Two episodes were both left and right censored. Eighty three (39.9%), 111 (53.4%), and 14 (6.7%) episodes were associated with RSV group A, group B and a co-infection respectively. One hundred and fifty two (84.9%) individuals had one episode, while 25 (14.0%) and 2 (1.1%) had two and three episodes respectively (Table 1). In addition, 24 (60.0%) households had one outbreak, while 5 (12.5%) had two outbreaks.

Table 1. Distribution of RSV infection episodes among 179 infected individuals during the 2009/2010 RSV season in a household cohort, coastal Kenya.

Characteristic Categories Infected a
(n=179)		 Episodes b
(n=208)		 Total AUC c
(n=7875.47)
n % n % n %
Age at infection <1y 31 17.3 35 16.8 2424.1 30.7
1-<5y 41 22.9 51 24.5 2011.8 25.5
5-<15y 64 35.8 73 35.1 2241.7 28.4
15-<40y 35 19.6 40 19.2 854 10.8
> = 40y 8 4.5 9 4.3 366.9 4.6
Sex Female 96 53.6 118 56.7 4392.4 55.6
Male 83 46.4 90 43.3 3506.2 44.4
Symptomatic No 71 39.7 90 43.3 2145.2 27.2
Yes 108 60.3 118 56.7 5753.3 72.8
Participant in school d No 101 56.4 119 57.2 5184.2 65.6
Yes 78 43.6 89 42.8 2714.4 34.4
Infecting RSV group RSV A 88 49.2 83 39.9 2838.1 35.9
RSV B 113 63.1 111 53.4 4170 52.8
Co-infection 14 7.8 14 6.7 890.5 11.3
Order of the episode
in individual 		First 152 84.9 179 86.1 7130.3 90.3
Subsequent 27 15.1 29 13.9 768.3 9.7
Introducer of RSV
infection in household 		Primary case 57 31.8 70 33.7 2372.7 30
Others 131 73.2 138 66.4 5525.9 70
Living with smoker in
household 		No 155 86.6 181 87 7081.2 89.7
Yes 24 13.4 27 13 817.3 10.3
Household size < = 5 22 12.3 25 12 992.6 12.6
6 to 10 52 29.1 61 29.3 2605.3 33
11 to 15 35 19.6 40 19.2 1360.5 17.2
>15 70 39.1 82 39.4 2940.1 37.2
Infection with other
viruses 		Yes 96 53.6 110 52.9 5054.6 64
No 93 46.4 98 47.1 2844 36
During Household
outbreak 		Yes 165 92.2 192 92.3 7460.6 94.5
No 14 7.8 16 7.7 438 5.5
Open in a new tab

aNumber of infected individuals; bNumber of infection episodes; cTotal amount of virus shed (midpoint AUC). dIncludes some participants in the age groups 1-<5 years, 5-<15 years, and 15-<40 years only.

Overall amount of RSV shed

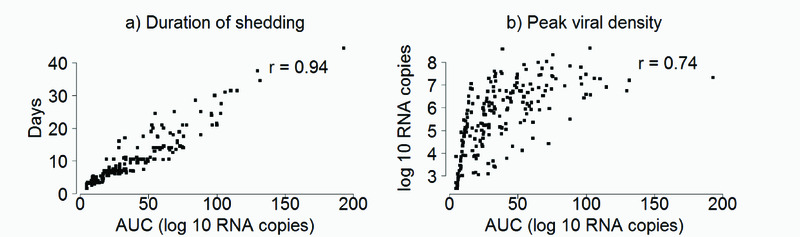
The median (interquartile range) of the amount of virus shed estimated by the minimum, midpoint and maximum AUC approaches was 31.1 (15.4, 57.9), 41.7 (24.3, 68.0), and 50.7 (31.0, 79.6) log10 RNA copies per infection episode, respectively. The minimum and maximum AUC estimates were strongly correlated with the midpoint AUC estimates (r=0.97 P < 0.001 and r=0.96 P < 0.001, respectively) (Supplementary Material Figure S1). The alternative measures of RSV shedding, (shedding duration and peak viral density), were also strongly correlated to the midpoint AUC estimates; 0.94 (P < 0.001) and 0.74 (P < 0.001) (Figure 2). Note, however, that within a narrow range of AUC the range of peak virus can be wide. The distribution of the amount of RSV shed by the various characteristics explored were similar regardless of the estimation method (i.e. minimum, midpoint, or maximum AUC) (See Supplementary Material Table S1) and hereafter only the midpoint estimates are reported. Viral densities by time over the study period did not change for RSV B, but showed a slight trend for decrease over time for RSV A (see Supplementary Material Figure S2).

Figure 2.

Figure 2.

Open in a new tab

Scatter plots showing the correlation between (a) duration of shedding (days) and (b) peak viral density (log10 RNA) and midpoint AUC estimates.

Amount of RSV shed by various characteristics

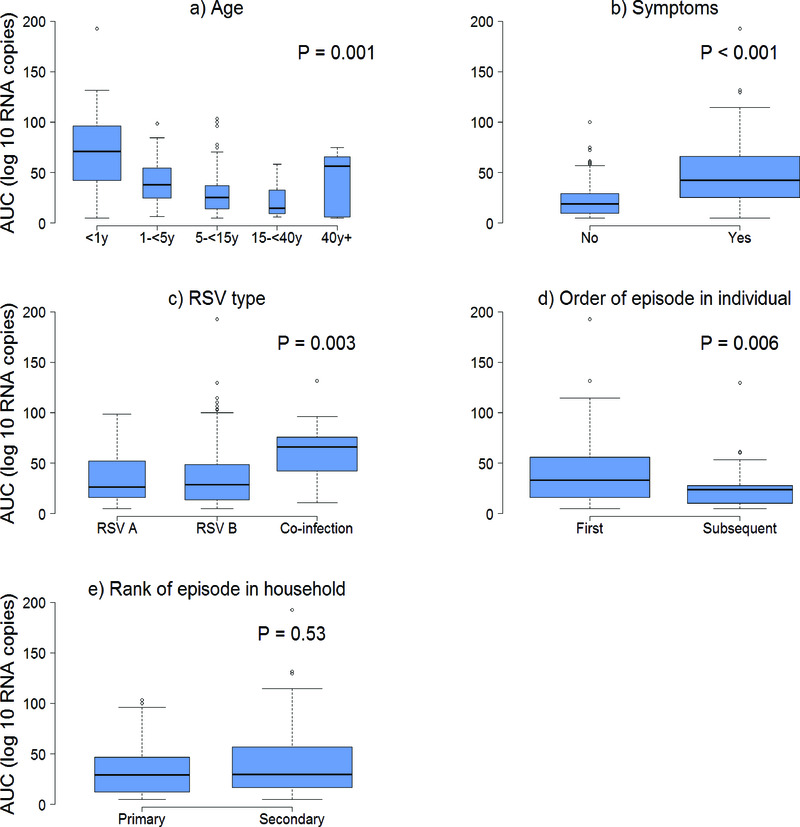
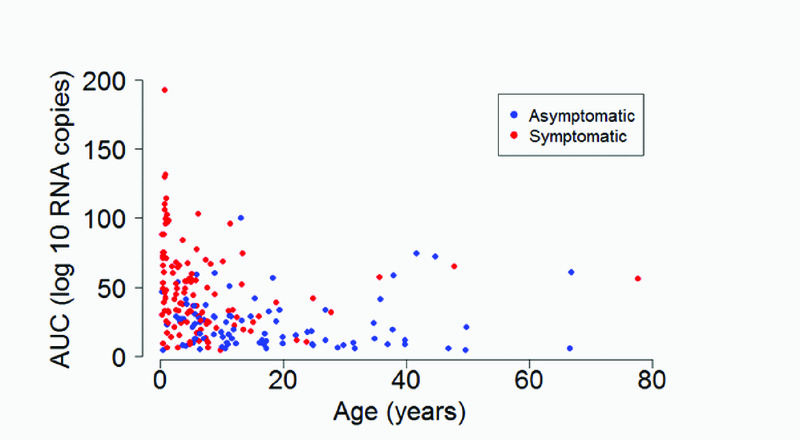
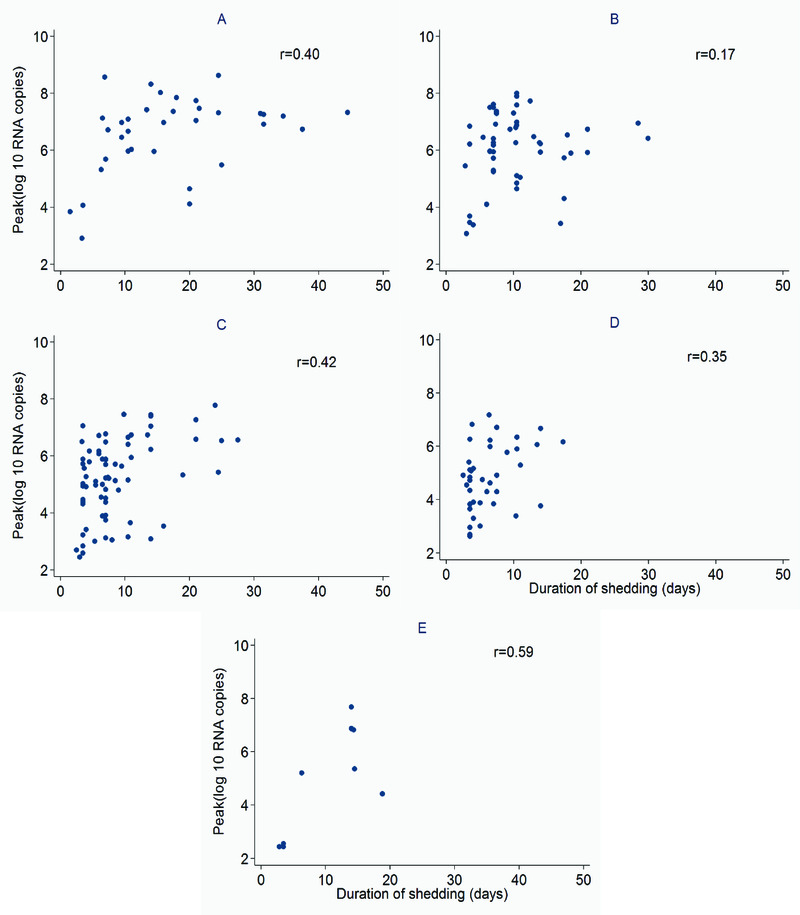
The median (interquartile range) amount of virus shed was 71.0 (IQR: 42.3, 96.7), 37.7 (IQR: 24.6, 54.4), 25.0 (IQR: 14.1, 36.7), 14.6 (IQR: 9.4, 32.4), and 56.3 (IQR: 5.7, 65.3) log10 RNA copies for individuals aged <1y, 1-<5y, 5-<15y, 15-<40y and >=40y respectively (Figure 3a) based on the midpoint approach, and there was strong evidence of a difference in distribution of AUC in different age groups (P = 0.001). Infection episodes associated with symptoms had a higher median amount of virus shed than those without symptoms (42.5 (IQR: 25.1, 66.0) vs 19.0 (IQR: 9.8, 29.0) log10 RNA copies; P < 0.001) (Figure 3b). Most symptomatic episodes were experienced by younger individuals (<20 years), while older individuals above 20 years mostly had asymptomatic episodes (Figure 4). Episodes associated with RSV A only, RSV B only, and RSV group A/B co-infection had a median amount of virus of 26.4 (IQR: 15.1, 52.4), 28.8 (IQR: 13.2, 48.9), and 66.1 (IQR: 42.1, 75.5) log10 RNA copies respectively (P = 0.003) (Figure 3c). Co-infection (associated with adenoviruses, rhinovirus, or coronaviruses) episodes had a median amount of virus of 38.7 (IQR: 19.6, 65.3) log10 RNA copies, while episodes not associated with any other infection had a median of 25.0 (IQR: 11.1, 37.0) log10 RNA copies, and there was strong evidence (P = 0.003) of a difference in the distribution of AUC in these two groups of episodes. Episodes that occurred during a household outbreak had a median amount of virus of 31.6 (IQR: 15.9, 54.8) log10 RNA copies, compared to a median of 20.3 (IQR: 10.2, 35.4) log10 RNA copies for episodes that were not associated with household outbreaks, though there was weak evidence of a difference in medians (see Supplementary Material Table S1). Infants had the highest peak viral density, and longest duration of shedding (Figure 5). Lowering the threshold below 35 Ct did not greatly change the results but reduced the total number of infections (see Supplementary Material Figure S3).

Figure 3.

Figure 3.

Open in a new tab

Box and whisker plots showing the distribution of amount of virus shed using the midpoint estimates by a) age b) symptoms c) RSV type d) order of episode in individual, and e) primary or secondary episode in household.

Figure 4. Scatter plot showing the relationship between midpoint AUC and age stratified by symptom status.

Figure 4.

Open in a new tab

Figure 5. Scatter plots showing the relationship between duration of shedding and peak viral density stratified by age.

Figure 5.

Open in a new tab

Factors associated with the amount of virus shed

The final regression model identified age, sex, symptom status, RSV infecting group, order of episode in an individual, and primary/secondary infection in the household as the main factors associated with the amount of virus shed. The effect of age on the amount of virus shed seemed to vary with primary/secondary case status (Table 2). The results reported here are, therefore, adjusted for the above covariates. The difference in mean amount of virus in secondary case episodes for age groups 1-<5y, 5-<15y, 15-<40y, and >=40y when compared to infants <1y was; -41.6 (95% CI: -53.7, -29.6), -43.1 (-55.5, -30.7), -50.6 (95% CI: -64.9, -36.3), and -29.4 (95% CI: -50.8, -8.1) log10 RNA copies respectively (P < 0.001). There was no evidence (p=0.594) of a difference in amount of virus by age for primary cases. There was an increase in mean amount of virus for symptomatic episodes compared to asymptomatic episodes by 14.1 (95% CI: 6.3, 21.9) log10 RNA copies, and strong evidence of a difference in means (P < 0.001). Mean amount of virus shed for subsequent episodes of individuals in the study RSV season compared to first infections was -10.4 (95% CI: -20.0, -0.8) log10 RNA copies (P = 0.03). The difference in mean amount of virus for episodes of RSV B only and RSV A/B co-infections when compared to episodes of RSV group A only was 3.7 (95% CI: -3.1, 10.5) log10 RNA copies, and 21.3 (95% CI: 7.3, 35.3) log10 RNA copies (P = 0.012) respectively (Table 2). For all age groups, there was no evidence of a difference in amount of virus for primary and secondary episodes. There was no evidence that the effect of age on amount of virus varied by symptom status.

Table 2. Factors influencing amount of virus shed in rural coastal Kenya during the 2009/2010 RSV season: Multiple linear regression analysis.

Factors Categories Beta a (log 10 RNA copies) 95% CI P-value
Primary cases:
Age in years 		<1y Ref*
1-<5y -0.21 -18.4, 17.9 0.594
5-<15y -7.3 -23.0, 8.4
15-<40y -12.7 -30.7, 5.2
> = 40y -9.4 -39.3, 20.5
Secondary cases:
Age in years 		<1y Ref*
1-<5y -41.6 -53.7, -29.6 <0.001
15-<15y -43.1 -55.5, -30.7
15-<40y -50.6 -64.9, -36.3
>=40y -29.4 -50.8, -8.1
Symptomatic No Ref*
Yes 14.1 6.3, 21.9 <0.001
Order of infection
in individual 		First Ref*
Subsequent -10.4 -20.0, -0.8 0.03
RSV group RSV A Ref* 0.012
RSV B 3.7 -3.1, 10.5
Co-infection 21.3 7.3, 35.3
Sex Female Ref* 0.287
Male -4.0 -10.2, 3.0
Open in a new tab

aDifference in mean AUC in comparison to reference category using midpoint estimates. * Reference category.

Discussion

We report a detailed analysis of RSV shedding patterns in which the amount of virus shed during the course of an infection was quantified, and factors associated with the quantity shed were identified. Young age at infection, presence of respiratory symptoms, intra-household acquisition of infection, being a first infection episode in the season for an individual, and having a co-infection were associated with increased amounts of RSV shed. The majority of virus available for transmission during an RSV epidemic appears to arise from individuals in their first year of life and therefore undergoing their first RSV infection episode (since all were born after the preceding RSV epidemic). Household size did not influence the per person amount of virus shed, and neither did the presence of a smoker in the household. The apparent effect of school going status on amount of virus shed was confounded by age, as school was attended by young individuals, who in turn shed more virus. RSV viral densities appeared to be low for most individuals in the beginning of the season but increased well into the season. This was a reflection of the occurrence of the RSV epidemic. Viral densities for RSV B were first to increase followed by viral densities for RSV A. RSV B infections spread to more individuals probably due to earlier onset by chance compared to RSV A infections.

Of particular importance is the finding that 90.3% of virus shed was from individuals experiencing their first episode in the RSV season (Table 1). Modelling studies have been unable to determine to what extent reinfections contribute to transmission 11, 22, which has a big influence on predictions of the effect of vaccination on transmission dynamics 11. Whilst these results do not include the opportunities to transmit, which will be generally higher for school-going children undergoing their second or third infection 9, they suggest that people with their first episode in the season are the most likely to transmit infection when they contact susceptible individuals. Peak viral density and duration of infection episodes were highly correlated with the amount of virus shed. Infants had the highest peak viral density, and longest duration of shedding (Figure 5).

Infants shed the highest median amount of virus followed by individuals aged 40 and above. The adults (15 to 39 years) shed the lowest amounts (Figure 3a). Acquired immunity (following exposure to RSV) and physiological development of the airways with age have been linked with reduced risk of severe RSV disease 12, 13. We speculate that elderly individuals are more prone to infection because of their deteriorating immune response which could explain the higher amount of virus in individuals over 40 years, compared to other adults. However, this study cannot discriminate between the two factors of young age and a first infection as the dominant factors associated with shedding (infants all had first infections, and we do not know the history of previous infection in all other ages). Individuals with a co-infection of RSV group A and B shed twice the amount of virus compared to those infected with either RSV A or B only, suggesting that the physiological infection processes for two viruses might be independent (rather than competitive or synergistic). Similar patterns of shedding were reported based on shedding duration estimates using this dataset 13 and others 12, 15. These findings can provide a hint to pathogenesis of RSV disease 6. A recent experimental study has reported disease severity to be closely related to viral load16 even though another shows contrasting observations on disease severity and viral load link 10. Our study showed a strong positive association between virus shedding and presence of respiratory symptoms. Symptomatic individuals shed higher amounts of virus than asymptomatic individuals irrespective of age. Overall those who were both young (<5 years) and symptomatic contributed to the highest amount of virus shed (51.8%). Using amount of virus as a correlate of infectiousness, these two factors are associated with virus spread within the community and in families and thus have direct implications in design and delivery of transmission-blocking interventions such as vaccines.

This analysis had some limitations. First, the nasal samples were collected with intervals of 3 to 4 days hence a complete profile of the viral density changes over time could not be captured. This has implications on the accuracy of our AUC estimates. However we minimize this by using a conservative approach providing three possible estimates i.e. minimum, midpoint and maximum estimates as detailed in the Supplementary Material. Furthermore, the three measures were strongly correlated and their variations by various characteristics such as age and symptoms, were comparable. Second, Ct values were converted to RNA copies using published associations 20 hence providing only a relative measure of virus density in the sample taken rather than absolute values of the amount of virus shed. Using the inverse of the Ct values as a measure of viral load did not change the distribution of AUC by various characteristics or any conclusions made from the results. There are no published studies using our approach in a community setting to facilitate comparison. Our approach takes into account both changing viral load and the duration of shedding making it more robust. However, its accuracy also relies on user selected thresholds for measures of viral load, and this could result in some differences in findings across studies. A quantitative PCR would be preferable. Third, there is inherent variability in estimated viral load due to variation (both biological and methodological) in the amount of virus collected using a nasopharyngeal swab. Deep NPS collections might have a higher density than perinasal swabs but events prior to sampling, e.g. sneezing, might introduce variations in sample quality. However this is likely to be non-systematic hence only conservatively affects our final conclusions. Finally, the assumption is made that virus density as measured by PCR is a measure of infectious virus. The most likely limitation of this assumption is over-estimating the duration of and peak shedding of viable virus.

In conclusion, long shedders tend to shed more virus and are likely to be more infectious. However, it is also evident that individuals with similar durations of shedding may shed different amounts of virus. Individuals with a combination of high viral density and long shedding durations are likely to shed the most virus. This improves on existing literature that measures infectiousness using the duration of shedding only. The groups that are most likely to spread infection are individuals with a first infection episode, the symptomatic, and most predominantly, the young, which has implications on which groups to target for vaccination in RSV prevention strategies.

Data availability

The data referenced by this article are under copyright with the following copyright statement: Copyright: © 2016 Wathuo M et al.

The dataset used in this study, together with associated analysis code (.do), graphics code (.R), variable codebook (.pdf), and summary file (.txt) are available from Harvard Dataverse: doi: 10.7910/DVN/MOTEJH 23. The dataset has restricted access, retaining Personal Identifiable Information (specifically dates) for analysis duplication. Please request access as instructed in the Readme.txt file. Other files are open access.

Acknowledgement

We would like to thank the Virus Epidemiology and Control Research Group at KEMRI-Wellcome Trust Research Programme in Kilifi, Kenya for their contribution towards the development of this manuscript, and the Data Management Group for their support during the analysis. Special thanks also goes to the field workers for their hard work in sample collection, and the laboratory team for their dedication in sample testing. This article was published with permission from the Director of KEMRI.

Grant Information

This work was supported by the Wellcome Trust [102975], [090853].

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

[version 1; referees: 2 approved, 1 approved with reservations]

Supplementary material

This file provides (a) Scatter plots showing the association between minimum, midpoint and maximum AUC (Figure S1), (b) graphical presentation of the relationship between amount of virus and duration of shedding for different thresholds of positivity (Figure S2), and temporal patterns of virus load (Figure S3), and (c) descriptive analysis tables for virus shedding (Table S1 and Table S2).

References

  • 1. Nair H, Nokes DJ, Gessner BD, et al. : Global burden of acute lower respiratory infections due to respiratory syncytial virus in young children: a systematic review and meta-analysis. Lancet. 2010;375(9725):1545–1555. 10.1016/S0140-6736(10)60206-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2. Glezen WP, Taber LH, Frank AL, et al. : Risk of primary infection and reinfection with respiratory syncytial virus. Am J Dis Child.[electronic article].1986;140(6):543–6. 10.1001/archpedi.1986.02140200053026 [DOI] [PubMed] [Google Scholar]
  • 3. Henderson FW, Collier AM, Clyde WA, Jr, et al. : Respiratory-syncytial-virus infections, reinfections and immunity. A prospective, longitudinal study in young children. N Engl J Med. 1979;300(10):530–4. 10.1056/NEJM197903083001004 [DOI] [PubMed] [Google Scholar]
  • 4. Modjarrad K, Giersing B, Kaslow DC, et al. : WHO consultation on Respiratory Syncytial Virus Vaccine Development Report from a World Health Organization Meeting held on 23–24 March 2015. Vaccine. 2016.34(2):190–7. 10.1016/j.vaccine.2015.05.093 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5. Karron RA, Wright PF, Belshe RB, et al. : Identification of a recombinant live attenuated respiratory syncytial virus vaccine candidate that is highly attenuated in infants. J Infect Dis. 2005;191(7):1093–104. 10.1086/427813 [DOI] [PubMed] [Google Scholar]
  • 6. Wright PF, Karron RA, Belshe RB, et al. : The absence of enhanced disease with wild type respiratory syncytial virus infection occurring after receipt of live, attenuated, respiratory syncytial virus vaccines. Vaccine. 2007;25(42):7372–7378. 10.1016/j.vaccine.2007.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. Anderson LJ, Dormitzer PR, Nokes DJ, et al. : Strategic priorities for respiratory syncytial virus (RSV) vaccine development. Vaccine. 2013;31(SUPPL 2):B209–15. 10.1016/j.vaccine.2012.11.106 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8. Guvenel AK, Chiu C, Openshaw PJ: Current concepts and progress in RSV vaccine development. Expert Rev Vaccines.[electronic article].2014;13(3):333–44. 10.1586/14760584.2014.878653 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9. Chapa Kiti M, Kinyanjui TM, Koech DC, et al. : Quantifying Age-Related Rates of Social Contact Using Diaries in a Rural Coastal Population of Kenya. PLoS One. 2014;9(8):e104786. 10.1371/journal.pone.0104786 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Lee FE, Walsh EE, Falsey AR, et al. : Experimental infection of humans with A2 respiratory syncytial virus. Antiviral Res. 2004;63(3):191–196. 10.1016/j.antiviral.2004.04.005 [DOI] [PubMed] [Google Scholar]
  • 11. Kinyanjui TM, House TA, Kiti MC, et al. : Vaccine Induced Herd Immunity for Control of Respiratory Syncytial Virus Disease in a Low-Income Country Setting. PLoS One. 2015;10(9):e0138018. 10.1371/journal.pone.0138018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12. Okiro EA, White LJ, Ngama M, et al. : Duration of shedding of respiratory syncytial virus in a community study of Kenyan children. BMC Infect Dis. 2010;10:15. 10.1186/1471-2334-10-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13. Munywoki PK, Koech DC, Agoti CN, et al. : Influence of age, severity of infection, and co-infection on the duration of respiratory syncytial virus (RSV) shedding. Epidemiol Infect. 2015;143(4):804–12. 10.1017/S0950268814001393 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Hall CB, Geiman JM, Biggar R, et al. : Respiratory syncytial virus infections within families. N Engl J Med.[electronic article].1976;294(8):414–9. 10.1056/NEJM197602192940803 [DOI] [PubMed] [Google Scholar]
  • 15. Frank AL, Taber LH, Wells CR, et al. : Patterns of shedding of myxoviruses and paramyxoviruses in children. J Infect Dis.[electronic article].1981;144(5):433–41. 10.1093/infdis/144.5.433 [DOI] [PubMed] [Google Scholar]
  • 16. DeVincenzo JP, Wilkinson T, Vaishnaw A, et al. : Viral load drives disease in humans experimentally infected with respiratory syncytial virus. Am J Respir Crit Care Med. 2010;182(10):1305–1314. 10.1164/rccm.201002-0221OC [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. Munywoki PK, Koech DC, Agoti CN, et al. : Frequent Asymptomatic Respiratory Syncytial Virus Infections During an Epidemic in a Rural Kenyan Household Cohort. J Infect Dis. 2015;212(11):1711–8. 10.1093/infdis/jiv263 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18. Munywoki PK, Koech DC, Agoti CN, et al. : The source of respiratory syncytial virus infection in infants: a household cohort study in rural Kenya. J Infect Dis.[electronic article].2014;209(11):1685–92. 10.1093/infdis/jit828 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19. Agoti CN, Mwihuri AG, Sande CJ, et al. : Genetic relatedness of infecting and reinfecting respiratory syncytial virus strains identified in a birth cohort from rural Kenya. J Infect Dis. 2012;206(10):1532–1541. 10.1093/infdis/jis570 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Nolan T, Hands RE, Bustin SA: Quantification of mRNA using real-time RT-PCR. Nat Protoc. 2006;1(3):1559–1582. 10.1038/nprot.2006.236 [DOI] [PubMed] [Google Scholar]
  • 21. Dassios G: Integration techniques.2012;109–123. Reference Source [Google Scholar]
  • 22. White LJ, Waris M, Cane PA, et al. : The transmission dynamics of groups A and B human respiratory syncytial virus (hRSV) in England & Wales and Finland: seasonality and cross-protection. Epidemiol Infect. 2005;133(2):279–289. 10.1017/S0950268804003450 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23. Munywoki PK, Nokes DJ: Replication Data for: Quantification and determinants of the amount of respiratory syncytial virus (RSV) shed using real time PCR data from a longitudinal household study. Harvard Dataverse, V5. 2016. Data Source [DOI] [PMC free article] [PubMed]
Wellcome Open Res. 2017 Jan 3.

Referee response for version 1

Peter F Wright 1

The report by the KEMRI team builds on a cohort of 47 households followed through an RSV season in coastal Kenya with frequent nasopharyngeal swabs for detection of RSV. The introduction and rationale for the study are very clearly provided.

More complicated is the analysis to determine minimum and maximum areas under the curve representing estimates of the total amount of virus shed based on a PCR cycle to detection of virus. Once this is accepted the analysis of factors influencing the amount of virus detected is straightforward and indicates age, symptoms, RSV type B, and whether infection is the initial infection during the sampling period. Each of these observations remained significant in a multiple linear regression analysis. None of these observations are surprising but all are of interest in this locale and within a community based study design. Might the large number of asymptomatic individuals include some who subsequently became symptomatic and were at the time of sampling in the incubation period of their illness?

The authors address some limitations of the study. Other things that might be considered include an analysis based gradation of symptoms in terms of virus recovered, whether frequency of sampling was influenced by symptoms, and patterns of spread within families. The latter is of particular interest in that I suspect that with many viral infections the peak titre will influence spread more than the total amount shed. The number of days to detection of secondary infections in the household might give a clue to the validity of this hypothesis.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Wellcome Open Res. 2016 Dec 30.

Referee response for version 1

H Rogier van Doorn 1, Lien Anh Ha Do 2

This is an interesting paper using area under curve (AUC), derived from non-quantitative PCR data using three different estimates, as a unit to measure viral shedding during an RSV season 8 years ago for a prospective cohort of 47 households in rural coastal Kenya. AUC can take variability of viral load due to different factors (technical, biological) into account and reflects the overall temporal changes of virus shed.

The authors use three models for calculating the AUC. While this is not my expertise, I cannot comment on these models, but I strongly believe that choosing an appropriate model is one of the most crucial parts of this study, any wrong assumption/ formula of these models will affect the results and its interpretations. Hence, the introduction of AUC as a measurement unit for transmission studies is an interesting concept, however, it may need a validation step using data from animal models, human challenge models, or clinical data monitoring RSV load.

Below are some points requiring more clarification:

  1. The interval between samples is 3-4 day, why did the author choose this big interval, while previous human challenge studies have suggested daily sampling or every 2 days could be the best follow-up (1). This is a major limitation as samples are taken only every 3-4 days and amounts of shed virus are therefore modelled based on little data and many assumptions, which may or may not equal out. The authors should definitely include more information on how their semi-quantitative data was calibrated.

  2. As authors didn’t use qPCR and use of a standard curve is not described, authors should clarify how they ensured PCR efficiency was stable between runs and what was used to calibrate runs and Ct values. This is a crucial thing to add, as all results in this paper are based on (semi)quantitative measurements and therefore, proper quantification is absolutely key.

  3. At the beginning of the Methods section, the authors specified that the AUC was calculated using viral load in log scale, but later for the midpoint AUC, they used Ct-value, please clarify.

  4. Reference 21 and 23 are not accessible

  5. Without baseline demographics about the sampled cohort I find some of this information hard to interpret. Symptomatic infections would also be interesting to see by age group.

  6. In Table 1, it is not clear how the total AUC was calculated. Surprisingly, the number of RSV infection episodes in the young age group (less than 1 year old and less than 5 years old) is much lower (denominator?) than those in the age group of 5-15 years old, while many epidemiological data have shown the re-infection rates are higher in the young age group. There is no comment/discussion on this result.

    In addition, the number of RSV infection episodes and the AUC in “living with smokers” group were lower and similar, respectively, compared to those who do not live with smokers. This result is controversial with the common observations from many epidemiological studies on RSV susceptibility and there is no comment/discussion regarding this.

Specific minor comments: 

  1. P3c1p2: The comparison with human volunteer studies to suggest load / inoculum may be associated with infection is not very strong, this may only be true in the background of a well-developed immune history against RSV whereas the main burden of disease of RSV is in infants who will not have this history yet.

  2. P3c1p3: I don’t think excretion is proper terminology for the process of virus shedding (nor is viral density – which is used later on, p6).

  3. P3c1p4: the number of sampled household members and the inclusion criteria should be added here.

  4. P3c2p1: why were only adeno, corona and rhino targeted with the diagnostic PCR and not the influenzas, parainfluenzas and hMPV? This is a very limited definition of co-infection.         

      

  5. P6: Please clarify why data are presented as median (IQR) amounts of virus shed in one paragraph but then as mean amounts (95%CI) of virus shed in the other.

  6. P8c1p2: In Table 2 sex is not significant, but its mentioned here as an associated factor.

  7. P8c2p3: the result that timing within the season was (appeared?) associated with the amount of virus shed is presented in the discussion section, shouldn’t this also be presented as a result, with data and a p-value?

  8. P8c2p3: why is it of particular importance that 90.3% of virus shed is from individuals experiencing their first episode? Also, 179/208 episodes studied were first episodes.

  9. Table 2: the number of primary and secondary cases per age group would be informative here

In summary, this paper reports important data on RSV transmission in a community setting; data on this subject is still scarce. This data is relevant for RSV vaccine and treatment development and can help suggest target groups for vaccination and implications of infection control measurement.

We have read this submission. We believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

References

  • 1. DeVincenzo JP, Wilkinson T, Vaishnaw A, Cehelsky J, Meyers R, Nochur S, Harrison L, Meeking P, Mann A, Moane E, Oxford J, Pareek R, Moore R, Walsh E, Studholme R, Dorsett P, Alvarez R, Lambkin-Williams R: Viral load drives disease in humans experimentally infected with respiratory syncytial virus. Am J Respir Crit Care Med.2010;182(10) : 1305-14 10.1164/rccm.201002-0221OC [DOI] [PMC free article] [PubMed] [Google Scholar]
Wellcome Open Res. 2016 Dec 23.

Referee response for version 1

Benjamin J Cowling 1

This is an interesting manuscript about RSV shedding, in the context of household transmission. There are few data on this topic in the literature and this is a valuable contribution. I thought the manuscript was clear and well written and should be indexed. I only had one comment:

  1. Please comment on the choice of log viral load in analyses

In Figure 1 please clarify the y-axis metric and you might like to explain this choice as well.

Is it viral density (copies), or log_10 copies ?

It seems as if you are calculating the AUC based on log_10 viral copies but what is the biological interpretation of that? I was wondering whether the number of viruses could be a better correlate of transmission, not their log?

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Data Citations

    1. Munywoki PK, Nokes DJ: Replication Data for: Quantification and determinants of the amount of respiratory syncytial virus (RSV) shed using real time PCR data from a longitudinal household study. Harvard Dataverse, V5. 2016. Data Source [DOI] [PMC free article] [PubMed]

    Supplementary Materials

    This file provides (a) Scatter plots showing the association between minimum, midpoint and maximum AUC (Figure S1), (b) graphical presentation of the relationship between amount of virus and duration of shedding for different thresholds of positivity (Figure S2), and temporal patterns of virus load (Figure S3), and (c) descriptive analysis tables for virus shedding (Table S1 and Table S2).

    NIHMS70985-supplement-Supplementary_Table_3.tgz (1.1MB, tgz)

    Data Availability Statement

    The data referenced by this article are under copyright with the following copyright statement: Copyright: © 2016 Wathuo M et al.

    The dataset used in this study, together with associated analysis code (.do), graphics code (.R), variable codebook (.pdf), and summary file (.txt) are available from Harvard Dataverse: doi: 10.7910/DVN/MOTEJH 23. The dataset has restricted access, retaining Personal Identifiable Information (specifically dates) for analysis duplication. Please request access as instructed in the Readme.txt file. Other files are open access.

    RESOURCES