Variation graph toolkit improves read mapping by representing genetic variation in the reference

Abstract

Reference genomes guide our interpretation of DNA sequence data. However, conventional linear references represent only one version of each locus, ignoring variation in the population. Poor representation of an individual's genome sequence impacts read mapping and introduces bias. Variation graphs are bidirected DNA sequence graphs that compactly represent genetic variation across a population, including large scale structural variation such as inversions and duplications¹. Previous graph genome software implementations^2–4 have been limited by scalability or topological constraints. Here we present vg, a toolkit of computational methods for creating, manipulating, and utilizing these structures as references at the scale of the human genome. vg provides an efficient approach to mapping reads onto arbitrary variation graphs using generalised compressed suffix arrays⁵, with improved accuracy over alignment to a linear reference, and effectively removing reference bias. These capabilities make using variation graphs as references for DNA sequencing practical at gigabase scale, or at the topological complexity of de novo assemblies.

For small genomes, it is possible to study genetic variation by assembling whole genomes and then comparing them via whole-genome comparison^6,7. For large genomes, such as the human genome, complete and accurate de novo genome assembly is impractical because of repeat complexity and scale. Therefore prior information is used to interpret new sequence data in its correct genomic context. The current practice is to align sequence reads to a single high-quality reference genome sequence that represents one haplotype at each location in the genome. Although much faster than de novo assembly, and simplifying discovery and reporting of genetic variants, this approach leads to mapping biases towards variants matching the reference sequence and away from alternative variants. There will even be some sequence in each new sample that is entirely absent in the reference⁸.

To avoid these biases, data would need to be aligned to a “personalized” reference sequence that already incorporates the individual’s variants⁹, but in general it is not known what variants are present in a sample before aligning data from it. However, most differences between any one genome and the reference are segregating in the population. Thus, a reference structure that represents known shared variation will contain most of the correct personalised sequence for any individual.

The natural computational structure for doing this is the sequence graph¹. Sequence graphs or equivalent structures have been used previously to represent multiple sequences that contain shared differences or ambiguities in a single structure. For example, multiple sequence alignments have a natural representation as partially ordered sequence graphs¹⁰. The variant call format¹¹ (VCF), which is a common data format for describing sets of genome sequences can be understood as defining a partially ordered graph similar to those implied by a multiple sequence alignment. Related structures frequently used in genome assembly include the De Bruijn graph¹² and string graph¹³, which collapse long repeated sequences, so the same nodes are used for different regions of the genome. Graphs to represent genetic variation have previously been used for microbial genomes and localized regions of the human genome such as the Major Histocompatibility Complex².

We define a variation graph as a sequence graph together with a set of paths representing possible sequences from a population (Figure 1). Recently, software packages have been introduced that support a subset of variation graphs that reflect local variation away from a linear reference^2,3, formalising approaches introduced in FreeBayes and the GATK HaplotypeCaller for the 1000 Genomes Project analysis^14–16. Our model goes beyond these in that it does not require the graph to be based on an initial linear reference, or indeed directionally ordered, and thus supports cycles and inversions. vg is the first openly available tool with these properties to scale practically to the multi-gigabase scale required for whole vertebrate genomes.

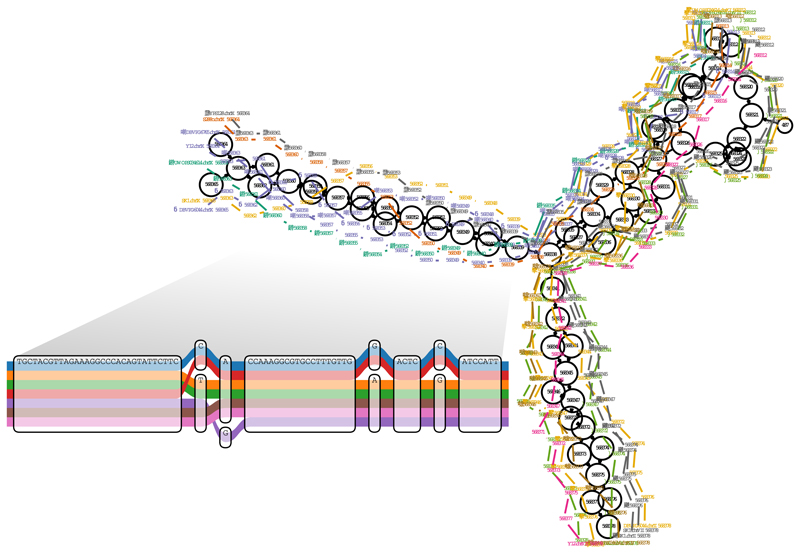
Figure 1.

A region of a yeast genome variation graph. This displays the start of the subtelomeric region on the left arm of chromosome 9 in a multiple alignment of the strains sequenced by Yue et al.22, built using vg from a full genome multiple alignment generated with the Cactus alignment package6. The inset shows a subregion of the alignment at single base level. The colored paths correspond to separate contiguous chromosomal segments of these strains. This illustrates the ability of vg to represent paths corresponding to both colinear (inset) and structurally rearranged (main figure) regions of genomic variation.

The core data model, data structures and algorithms, and implementation of vg are described in the Online Methods. Indicative memory and compute run time requirements are given in Supplementary Table 1. Below we present results demonstrating the functionality of vg. Variant calling using vg against a variety of different human genome variation graphs is described elsewhere¹⁷.

For a species such as human, with only 0.1% nucleotide divergence on average between individual genome sequences, over 90% of 100bp reads will derive from sequence exactly matching the reference. Therefore new mappers should perform at least as well for linear reference mapping as the current standard, which we take to be bwa mem¹⁸ with default parameters. We show that vg does this, and then that around divergent sites vg maps more informatively.

The final phase of the 1000 Genomes Project (1000GP) produced a data set of approximately 80 million variants in 2504 humans¹⁶. We made a series of vg graphs containing all variants or those with minor allele frequency thresholds at 0.1%, 1% or 10%, as well as a graph corresponding to the standard GRCh37 linear reference sequence without any variation. The full vg graph uses 3.92 GB when serialized to disk, and contains 3.181 Gbp of sequence, which is exactly equivalent to the length of the input reference plus the length of the novel alleles in the VCF file. Complete file sizes including indices vary from 25GB to 63GB, with details including build and mapping times given in Supplementary Table 1.

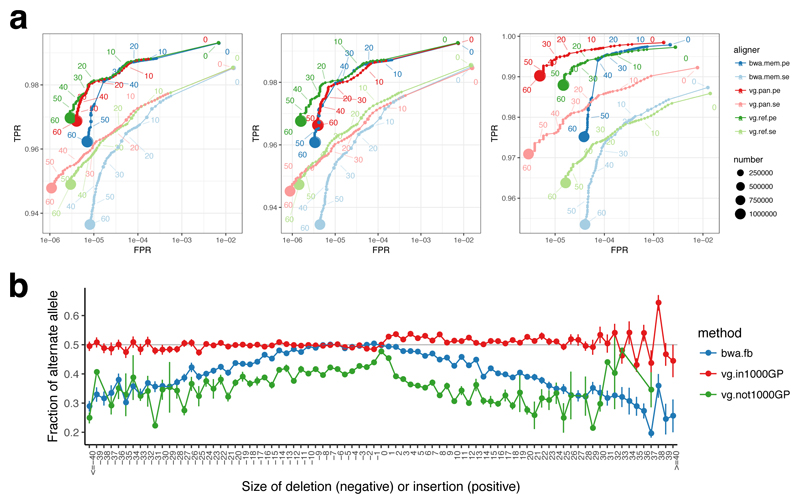
We next aligned ten million 150 bp paired end reads simulated with errors from the parentally phased haplotypes of an Ashkenazi Jewish male NA24385, sequenced by the Genome in a Bottle (GIAB) Consortium¹⁹ and not included in the 1000GP sample set, to each of these graphs as well as to the linear reference using bwa mem. Figure 2a shows the accuracy of these alignments compared with bwa mem for the 1% allele frequency threshold graph, in terms of Receiver Operating Characteristic (ROC) curves. Comparable plots for other data are given in Supplementary Figure 1.

Figure 2.

Mapping accuracy for vg against the human genome. (a) ROC curves parameterised by mapping quality for 10M read pairs simulated from NA24385 as mapped by bwa mem, vg with the 1000GP 1% allele frequency threshold pangenome reference, and vg with a linear reference, using single end (se) or paired end (pe) mapping. Left: all reads, middle: reads simulated from segments matching the linear reference, Right: reads simulated from segments different from the linear reference. (b) the mean alternate allele fraction at heterozygous variants previously called19 in NA24385 as a function of deletion or insertion size (SNPs at 0). Error bars are +/- one standard error.

Reads that come from parts of the sequence without differences from the reference (middle panel of Fig. 2a) map slightly better to the reference sequence (green) than to the 1000GP graph (red), which we attribute to a combination of the increase in options for alternative places to map reads provided by the variation graph, and the fact that we needed to prune some search index k-mers in the most complex regions of the graph. As expected this difference increases as the allele frequency threshold is lowered and more variants are included in the graph (Supplementary Figure 1).

For reads that were simulated from segments containing non-reference alleles (approximately 10% of reads), which are the reads relevant to variant calling, vg mapping to the 1000GP graph (red) gives better performance than either vg (green) or bwa mem (blue) mapping to the linear reference (Figure 2b), because many variants present in NA24385 are already represented in the 1000GP graph. This is particularly clear for single end mapping, since many paired end reads are rescued by the mate read mapping. Overall vg performs at least as well as bwa mem even on reference-derived reads, and substantially better on reads containing non-reference variants.

We also mapped a real human genome read set with approximately 50X coverage of Illumina 150bp paired end reads from the NA24385 sample to the 1000GP graph. vg produced mappings for 98.7% of the reads, 88.7% with reported mapping quality score 30 on the Phred scale, and 76.8% with perfect, full-length sequence identity to the reported path on the graph. For comparison, we also used vg to map these reads to the linear reference. Similar proportions of reads mapped (98.7%) and with reported quality 30 (88.8%), but considerably fewer with perfect identity (67.6%). Markedly different mappings were found for 1.0% of reads (0.9% mapping to widely separated positions on the two graphs, and 0.1% mapping to one graph but not the other). The reads mapping to widely separated positions were strongly enriched for repetitive DNA. For example, the linear reference mappings for 27.5% of these read pairs overlap various types of satellite DNA identified by RepeatMasker, compared to 3.0% of all read pairs.

To illustrate the consequences of mapping to a reference graph rather than a linear reference, we stratified the sites independently called as heterozygous in NA24385 by deletion or insertion length (0 for single nucleotide variants) and by whether the site was present in 1000GP, and measured the fraction of reads mapped to the alternate allele for each category. The results show that mapping with vg to the population graph when the variant is present in 1000GP (95.4% of sites) gives nearly balanced coverage of alternate and reference alleles independent of variant size, whereas mapping to the linear reference either with vg or bwa mem leads to a progressively increasing bias with increasing deletion and (especially) insertion length (Figure 2b), so that for insertions around 30bp a majority of insertion containing reads are missing (there are over twice as many reference reads as alternate reads).

This removal of bias is important when mapping functional genomics data such as ChIP-seq data, where allele specific expression analysis can reveal genetic variation that affects function but is confounded by reference mapping bias²⁰, especially given that read lengths are typically shorter for these experiments. We compared mapping with bwa or vg for data set ENCFF000ATK from the ENCODE project²¹, which contains 14.9 million 51bp ChIP-seq reads for the H3K4me1 histone methylation mark from the NA12878 cell line. When mapping with bwa the ratio of reference to alternate allele matches at heterozygous sites was 1.20, whereas with vg to the 1000GP graph the ratio was 1.01, effectively eliminating reference bias.

We also explored integration of vg with the recently published GraphTyper¹² method, which calls genotypes by remapping reads to a local partially ordered variation graph built from a VCF file, relying on initial global assignment to a region of the genome by mapping with bwa to a linear reference. Therefore, although GraphTyper also scales to the whole human genome because it is essentially a local method, its functionality is complementary to that of vg, which maps to a global variation graph and does not directly call genotypes. In experiments where we used vg rather than bwa as the primary mapper for GraphTyper, true positives increased marginally (0.02% for SNPs and 0.06% for indels) while false positives increased for SNPs by 0.15% and decreased for indels by 0.03%. We note, however that GraphTyper was developed by its authors for bwa mapping.

The graphs that we have used so far were constructed from variation data obtained from mapping to a linear reference, and so are directed acyclic graphs. We next demonstrate the ability of vg to work with arbitrary graphs that include duplications, inversions, and translocations, by showing its use with multiple yeast strains independently assembled de novo using long read data²². These assemblies manifest large scale structural variation and novel sequence not detected in reference-based sequencing, including extensive rearrangement and reordering in subtelomeric regions²² as illustrated in Figure 1.

We compared four vg graphs: a linear reference graph from the standard S288c strain, a linear reference from the SK1 strain, a pangenome graph of all seven strains, and a “drop SK1” variation graph in which all sequence private to the strain SK1 was removed from the pangenome graph. The multiple genome graphs were constructed with the Cactus progressive aligner⁶, which generates graphs that typically contain cycles and are not partially ordered.

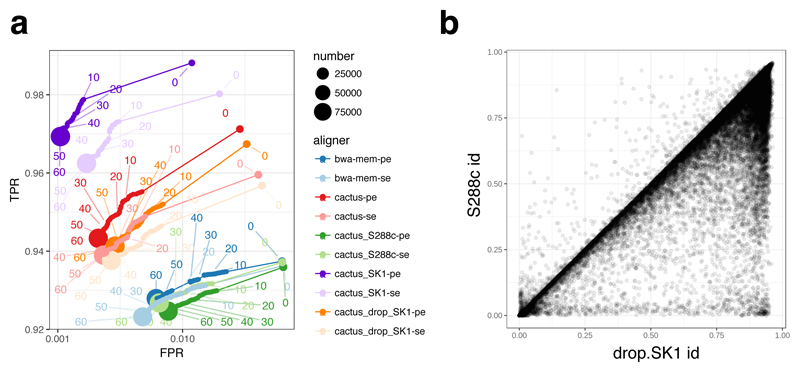
Similarly to the human experiments, we simulated 100,000 150bp paired reads from the SK1 reference, modelling sequencing errors, and mapped them to the four references. The resulting ROC curves are shown in Figure 3a. Not surprisingly, the best performance is obtained by mapping to a linear reference of the SK1 strain from which the data were simulated, with substantially higher sensitivity and specificity compared to mapping to the standard linear reference from the strain S288c with either vg or bwa mem. Mapping to the variation graphs gives intermediate performance, with over one percent more sensitivity and lower false positive rates than to the standard reference. There is surprisingly little difference between mapping to graphs with and without the SK1 private variation, probably because much of what is novel in SK1 compared to the reference is also seen in other strains. We see lower sensitivity compared to mapping just to the SK1 sequence, likely because of suppression of GCSA2 index kmers in complex or duplicated regions. In Figure 3b we show the benefit of aligning long reads to a pangenome graph compared to the S288c reference, using a set of 43,337 Pacific Biosciences SK1 reads (mean length 4.7kb) from Ref. 22.

Figure 3.

Mapping short and long reads with vg to yeast genome references. (a) ROC curves obtained by mapping 100,000 simulated SK1 yeast strain 150bp paired reads against a variety of references described in the text; (b) a density plot of identity fraction when mapping 43,337 Pacific Biosciences long reads from the SK1 strain to the drop.SK1 reference or the S288c reference.

Finally, to further demonstrate the ability of vg to map to arbitrary sequence graphs, we constructed a vg graph from a metagenomic assembly of a polar freshwater viral DNA community²³ that was constructed with the minia3²⁴ assembler. We then aligned a held-out subset of 100,000 reads to this assembly graph using vg, and to the linear contigs using bwa. Although both methods map approximately 96% of the reads, vg has an average identity score of 95% compared to 87% for bwa, reflecting that the bwa alignments in many cases are not full length (Supplementary Figure 2).

In conclusion, vg implements a suite of tools for genomic sequence data analysis using general variation graph references. Using the vg toolkit, we can construct or import a graph, modify it, visualize it, and use it as a reference. vg can accurately map new sequence reads to the reference using succinct indexes of the graph and its sequence space, and can describe variation between a new sample and an arbitrary reference embedded as a path in the graph. Elsewhere¹⁷ we discuss the use of vg to map read sets and call variants against a number of alternative human reference graphs built from multiple regions of the human genome with different properties.

There are many areas for potential future development and application of vg. These include further improvements in the mapping and variant calling algorithms, potentially using long range statistical haplotype structure information, stored in a graph extension of the PBWT haplotype compression and search data structure²⁵, as proposed by Novak²⁶. Beyond variant calling, the ability to map in an unbiased way to both reference and alternate alleles is potentially important when quantitating allele-specific protein binding as shown with ChIP-seq data above or allele-specific expression²⁷. We note that graphs can also naturally represent the relationships between transcribed, spliced and edited RNA sequences and the genome from which they are transcribed, so the vg software can potentially be used for splice-aware RNAseq mapping²⁸.

We believe that genome variation graphs will underpin a new paradigm for genome sequence data analysis¹. They support the representation of structural variation using the same components (edges, nodes and paths) that are used to represent single base changes. For human, they allow more accurate and complete read mapping (Figure 2). The benefits will only be greater for other organisms with higher levels of genetic variation, or for which uncertainties remain in the reference assembly. For the biological research community to exploit these advantages, it needs software for variation graphs that scales to the genomes of humans and other complex organisms. vg is a robust and openly available platform to fulfil this need.

A life sciences reporting summary is available.

Online Methods

Model

We define a variation graph to be a graph with embedded paths G = (N, E, P) comprised of a set of nodes N = n₁ … n_M, a set of edges E = e₁ … e_L, and a set of paths P = p₁ … p_Q, each of which describes the embedding of a sequence into the graph.

Each node n_i represents a sequence seq(n_i) which is built from an alphabet A = {A,C,G,T}. Nodes may be traversed in either the forward or reverse direction, with the sequence being reverse-complemented in the reverse direction. We write n*_Ifor the reverse-complement of node n_i, so that seq(n_i) = revcomp(seq(n*_i)); note that n_i = n**_i. For convenience, we refer to both n_i and n*_i as “nodes”. Edges represent adjacencies between the sequences of the nodes they connect. Thus, the graph implicitly encodes longer sequences as the concatenation of node sequences along walks through the graph. Edges can be identified with the ordered pairs of oriented nodes that they link, so we can write e_ij = (n_i,n_j). Edges also can be traversed in either the forward or the reverse direction, with the reverse traversal defined as e*_ij = (n*_j,n*_i). Note that graphs in vg can contain ordinary cycles (in which n_i is reachable from n_i), reversing cycles (in which n_i is reachable from n*_i), and non-cyclic instances of reversal (in which both n_i and n*_i are reachable from n_j). We implement paths as an edit string with respect to the concatenation of node sequences along a directed walk through the graph. We do not require the alignment described by the edit string to start at the beginning of the sequence of the initial node, nor to terminate at the end of the sequence of the terminal node.

Implementation

The vg implementation is multithreaded and written in C++11, and is available from https://github.com/vgteam/vg (version v1.6.0 for code used in the mapping experiments) under the MIT open source software license. It provides both a primary application to support the operations we describe here, and a library libvg which applications can use to access the data structures, indexes and low level operations.

Our core representation of the graph uses Google's open source protobuf system, which directly supports serialisation onto disk for storage. We also provide a protobuf alignment format, GAM (for “Graph Alignment Map”), with analogous functionality to BAM²⁹, but can also export mappings with respect to embedded references in BAM format. To enable read mapping and other random access operations against large sequence graphs we have implemented a succinct representation of a vg variation graph (xg) that is static but very memory and time efficient, using rank/select dictionaries and other data structures from the Succinct Data Structures Library (SDSL)³⁰. Graphs can be imported from and exported to a variety of formats, including the assembly format GFA and the W3C graph exchange format RDF. Further details about the implementation and features are available in the supplement and at the Github website.

Alignment

A key requirement for a reference genome is the ability to efficiently and accurately find an optimal alignment for a new DNA sequence such as a sequencing read. Analogous to the way that read mappers to linear references work, our approach to this problem is to find seed matches by an indexed search process, cluster them if there are multiple seeds close together, and then perform a local constrained dynamic programming alignment of the read against a region of the graph around each cluster. A brief description of the key steps in this process is given here, with further details in the supplement.

The GCSA2 library⁴ that vg uses for seeding can perform linear time exact match queries independent of the graph size to find super-maximal exact match (SMEM) seeds, subject to a maximum query length, in time comparable to the corresponding operations in bwa mem. SMEMs are exact matches between a query substring and a reference substring that cannot be extended in either direction, and for which there is no extension of the query substring that matches elsewhere in the graph.

After obtaining SMEMs for a query sequence using GCSA2, we cluster them using a global approximate distance metric and distance estimates provided by any nearby paths. For paired reads, we cluster all the SMEMs for both reads in the pair to preferentially support mappings where the SMEMs match a fragment model that we establish online during the alignment of the read set.

We next chain the SMEMs within each cluster by selecting the maximum likelihood path through a Markov model that rewards long SMEMs and short colinear gaps between SMEMs. In many cases there is just one SMEM in the sequence, but there are complex cases where the best SMEM sequence is not correct, and to catch these we recursively mask out the SMEMs in paths found so far and re-run the algorithm to obtain additional disjoint SMEM sequences if available.

For each consistent sequence of SMEMs, we then obtain the subgraph containing the cluster. To avoid the complications introduced by cycles and inversions³¹, we transform the local graph region into a directed acyclic graph (DAG) while maintaining an embedding in the original, potentially cyclic bidirected graph (Supplementary figures S3, S4). We can then perform partial order alignment to the DAG⁹, using banded dynamic programming and an extension of Farrar's SIMD-accelerated striped Smith Waterman algorithm³².

When mapping long sequences, we split them into overlapping “chunks” (default 256bp with 32bp overlap), map those as above, then chain them using the same colinear Markov model method as described for SMEMs within a chunk. This scales effectively linearly in sequence length up to multiple megabases.

The vg alignment tool also uses base qualities in alignment scores and calculates adjusted mapping quality scores. Base qualities are probabilistic estimates of the condence of each base call in a read provided by the sequencing technology. vg combines these with a probabilistic interpretation of alignment³³ to adjust the scoring function for alignments, which has previously been shown to improve variant calling accuracy³⁴. Mapping qualities³⁵ are a probability-based measure of the confidence in the localisation of a read on the reference that is important for variant calling and other downstream analyses. vg computes mapping qualities by comparing the scores of optimal and suboptimal alignments under the probabilistic alignment model, in a similar fashion to bwa mem.

Graph editing and construction

We can build a graph either by direct construction from external graphs such as from de novo assemblies, or by a series of editing operations applied to simple starting graphs such as standard linear reference genomes. To support editing of existing graphs, vg supports operations that can split a node where sequences diverge and insert additional edges and nodes. While doing this it keeps track of the relationship to the previous graph in a translation object, which supports projection of coordinates from one version of the graph to another.

We make use of the editing operations to construct graphs from Variant Call Format (VCF) files¹⁰ as produced by population sequencing projects such as the 1000 Genomes Project¹⁶, inserting a cluster of nodes and edges into a linear reference for each overlapping subset of VCF records. Edit operations also allow progressive construction of a vg graph from a set of sequences by repeated alignment and editing, so that all the initial sequences are embedded in the graph as paths. Last but not least, edit operations allow new variants to be added to an existing vg reference graph to support use cases such as incorporating novel variants from new individuals mapped and called against the graph, while retaining a coordinate mapping to the existing reference. These actions are also invertible, in that vg can generate VCF to describe the graph as a set of variants, using an arbitrarily chosen embedded path as a reference.

Experiments

Experiments were carried out on a dedicated compute node with 256 gigabytes of RAM and two 2.4GHz AMD Opteron 6378 processors with a total of 32 CPU cores. Mapping comparisons were to bwa version 0.7.15-r1142.

GraphTyper comparisons

To test how vg map complements genotyping in Graphtyper, we mapped reads from the Genome In A Bottle (GIAB) Ashkenazi Jewish Trio benchmark sample HG002 readset, and analyzed variant calling performance on chromosome 21 against the HG002_GRCh37_GIAB_highconf_CG-IllFB-IllGATKHC-Ion-10X-SOLID_CHROM1-22_v.3.3.2_highconf_triophased.vcf.gz calls using Illumina’s Haplotype Comparison Toolset available from https://github.com/Illumina/hap.py. Bwa mem mappings were against the GRCh37d5 reference, and vg mappings against the 1000GP graph then projected onto the GRCh37d5 reference, which is embedded in the 1000GP graph. GraphTyper version 1.3 was run using the dbSNP “common variant” chromosome 21 VCF from NCBI (ftp://ftp.ncbi.nlm.nih.gov/snp/organisms/human_9606_b150_GRCh37p13/VCF/common_all_20170710.vcf.gz). Code used for the analysis is available on request.