Reduced efficacy of the KCC2 cotransporter promotes epileptic oscillations in a subiculum network model

Abstract

Pharmacoresistant epilepsy is a chronic neurological condition in which a basal brain hyper excitability results in paroxysmal hyper synchronous neuronal discharges. Human temporal lobe epilepsy has been associated with dysfunction or loss of the potassium-chloride co-transporter KCC2 in a subset of pyramidal cells in the subiculum, a key structure generating epileptic activities. KCC2 regulates intra-neuronal chloride and extracellular potassium levels by extruding both ions. Absence of effective KCC2 may alter dynamics of chloride and potassium levels during repeated activation of GABAergic synapses due to interneuron activity. In turn such GABAergic stress may itself affect Cl^- regulation. Such changes in ionic homeostasis may switch GABAergic signaling from inhibitory to excitatory in affected pyramidal cells and also increase neuronal excitability. Possibly they contribute to periodic bursting in pyramidal cells, an essential component in the onset of ictal epileptic events. We tested this hypothesis with a computational model of a subicular network with realistic connectivity. The pyramidal cell model explicitly incorporated the cotransporter KCC2 and its effects on the internal/external chloride and potassium levels. Our network model suggested the loss of KCC2 in a critical number of pyramidal cells increased external potassium and intracellular chloride concentrations leading to seizure-like field potential oscillations. These oscillations included transient discharges leading to ictal-like field events with frequency spectra as in vitro. Restoration of KCC2 function suppressed seizure activity and thus may present a useful therapeutic option. These simulations therefore suggest that a reduced KCC2 cotransporter activity alone may underlie the generation of ictal discharges.

Introduction

Epilepsy is a chronic neurological disorder characterized by recurring seizures (Beghi et al., 2005, Fisher et al., 2005, Ullah and Schiff, 2009). GABAergic signaling is the main inhibitory system in the brain and its integrity is compromised in epilepsy. Intracellular chloride is maintained low so that when the GABA A receptor channel opens, chloride flows into neurons under the control of favorable concentration gradients despite unfavorable forces dictated by negative intracellular charges. Such accumulation results in an inhibitory hyperpolarization. Defects in chloride homeostasis may contribute to the epileptic activities generated in tissue of patients with pharmacoresistant temporal lobe epilepsy associated with hippocampal sclerosis (Huberfeld et al., 2007) and in the cortical tissue surrounding tumors (Pallud et al., 2014). The expression or function of potassium-chloride transport proteins is altered in both these syndromes. The KCC2 cotransporter maintains basal chloride levels using ionic gradients created by the sodium-potassium pump to extrude intracellular chloride and potassium ions to the extracellular space (Payne et al., 2003). An absence of KCC2 has been correlated with a depolarizing shift in the resting reversal potential of GABAergic synaptic events in a minority of human subicular pyramidal cells (Huberfeld et al., 2007). In addition to basal effects experimental (Alger and Nicoll, 1982; Kaila and Voipio, 1987; Staley and Proctor 1999) and theoretical studies (Jedlicka et al., 2011; Doyon et al., 2011) shows that intense GABAergic stimulation leads to progressive chloride accumulation and therefore shifts the reversal potential to depolarized values. Thus, intensive activation of GABA synapses combined with impaired KCC2 cotransporter function may produce an aberrant pro-epileptic excitation.

In addition to chloride homeostasis, changes in extracellular potassium levels mediated via KCC2 may increase neuronal excitability and contribute to seizure generation (Fröhlich et al., 2008b). Potassium accumulation in the extracellular space is associated with seizures (Fertziger 1970) and spreading depression (Grafstein, 1956; Kraig and Nicholson, 1978). Intense neuronal firing should increase extracellular potassium further increasing neuronal excitability in a positive feedback that promotes seizure generation. Recent computational models suggest changes in extracellular potassium may suffice to induce seizure-like firing in single neurons (Barreto et al., 2009; Hübel and Dahlem 2014; Wei et al., 2014) or recurrent neural networks (Bazhenov et al., 2004; Ullah et al., 2009; Krishnan and Bazhenov 2011).

However, relations between potassium-chloride transporters and dynamic changes in chloride and potassium levels during the transition to seizure are not completely understood. In this work we therefore construct and validate a computational model incorporating realistic data on how KCC2 activity controls basal levels of chloride as a function of external potassium (Payne 1997; Doyon et al., 2011). We use this model to explore how KCC2 controls dynamic changes in chloride levels due to GABAergic synaptic stimulation (Fujiwara-Tsukamoto et al., 2007; Fujiwara-Tsukamoto et al., 2010; Isomura et al., 2003) and the effects of an absence of KCC2 actions. The model let us ask two questions. Might normal KCC2 activity in some pyramidal cells have pro-epileptic actions mediated via an increase in extracellular potassium (Viitanen et al., 2010; Hamidi and Avoli 2015)? Might an absence of KCC2 in other cells be pro-epileptic due to intracellular chloride accumulation with resulting depolarizing effects of GABA (Cohen et al., 2002; Huberfeld et al., 2007)?

We incorporated models of bursting pyramidal cells and interneurons of the subiculum into a neuronal network with realistic synaptic connectivity. Transport kinetics and exchange of both chloride and potassium between intra-neuronal and extracellular space were explicitly modeled. Neuronal voltages were used to derive values for a local field potential (LFP) generated during normal and epileptic activity. Incorporating KCC2-deficient cells into this network reproduced ictal-like extracellular field potentials as in slices of human subiculum. Thus, our results support the hypothesis that a reduction in the effects of KCC2 in the pyramidal cells may contribute to ictal activity and provide the basis for further experimental studies on the homeostasis of chloride in an epileptic context by pyramidal cells.

Materials and Methods

Epileptic tissue

Temporal lobe tissue blocks containing the hippocampus, subiculum and part of the entorhinal cortex were obtained from 45 people of either sex with pharmacoresistant mesial temporal lobe epilepsies associated with hippocampal sclerosis (age 18–52 years, seizures for 3–35 years) undergoing resection of the amygdala, the hippocampus, and the anterior parahippocampal gyrus. All of the individuals gave their written informed consent and the study was approved by the Comité Consultatif d’Ethique.

Tissue preparation

The post-surgical tissue was transported in a cold, oxygenated solution containing 248 mM d-sucrose, 26 mM NaHCO₃, 1 mM KCl, 1 mM CaCl₂, 10 mM MgCl₂ and 10 mM d-glucose, equilibrated with 5% CO₂ in 95% O₂. Hippocampal-subicular-entorhinal cortical slices or isolated subicular slices (400 µm thickness, 3x12 mm length and width) were cut with a vibratome (HM650 V, Microm). They were maintained at 37 °C, and equilibrated with 5% CO₂ in 95% O₂ in an interface chamber perfused with a solution containing 124 mM NaCl, 26 mM NaHCO₃, 4 mM KCl, 2 mM MgCl₂, 2 mM CaCl₂ and 10 mM d-glucose. NBQX and d,l-AP5 were used to block glutamatergic signaling, and bicuculline or picrotoxin was used to block GABA A receptors. Ictal-like activity was induced by increasing the external K⁺ concentration to 8 mM and reducing the Mg²⁺ concentration to 0.25 mM.

Recordings

Up to four tungsten electrodes etched to a tip diameter of ~5 µm were used for the extracellular recordings. The signals were amplified 1,000-fold and filtered to pass frequencies of 0.1 Hz to 10 kHz (AM systems, 1700). The intracellular recordings were made with glass microelectrodes containing 2 M potassium acetate and beveled to a resistance of 50–100 MΩ. The signals were amplified with an Axoclamp 2B amplifier in current-clamp mode. The intracellular and extracellular signals were digitized at 10 kHz with a 12–bit, 16-channel A-D converter (Digidata 1200A, Axon Instruments), and monitored and saved to a PC with Axoscope (Axon Instruments).

Data analysis

Records were analyzed with Clampfit 10 software and scripts written in Matlab 2015a.

Simulations

Single neuron and neural network simulations were performed in Matlab 2015a using the direct Euler method of integration, with a time step of 0.05 ms. We checked that smaller time steps provided substantially similar results. Bifurcation analysis was performed in XPPAUT 7.0 and the AUTO package. In all simulations, initial conditions were systematically varied to check stability of numerical results. The model code is available on Model DB (https://senselab.med.yale.edu/modeldb/).

Neuron intrinsic properties

Single neuron activity was modeled using the conductances derived from previous studies (Mainen and Sejnowski 1996; Krishnan and Bazhenov 2011). The intrinsic currents selected represent the major currents needed to reproduce the firing patterns of subicular pyramidal cells (Jung et al., 2001; Staff et al., 2000). We used a model of a regular spiking neuron for the pyramidal cells and a fast spiking neuron for the interneurons (Mainen and Sejnowski 1996; Bazhenov et al., 2004). To take into account the activation of bursting properties of pyramidal cells due to increased extracellular potassium (Jensen et al., 1994), the intrinsic potassium currents were modulated by its concentration similar to (Fröhlich and Bazhenov, 2006).

The following equations describe the evolution of voltage over time for somatic and dendritic compartments:

$$C_{m}d{V}_d/dt=-I_d^{Int}-g_c^d\left(V_d-V_s\right)-I_d^{leak}-I_d^{pump}$$

$$g_c^S\left(V_d-V_s\right)=-I_s^{Int}-I_s^{leak}-I_s^{pump}$$

V_d is the voltage of the dendritic compartment, $I_d^{leak}$ includes sodium, potassium, and chloride leak currents (PY: g_K = 0.044, g_Na = 0.02, g_Cl = 0.01 mS / cm²; IN: g_K = 0.035, g_Na = 0.02, g_Cl = 0.01 mS / cm²) and $I_s^{leak}$ includes sodium and potassium leak currents (PY: g_Na = 0.019, g_K = 0.042 mS / cm²; IN: g_Na = 0.019, g_K = 0.042 mS /cm²). $I_d^{Int}$ and $I_s^{Int}$ are the sums of intrinsic currents for axo-somatic and dendritic compartments, respectively. $I_d^{pump}$ and $I_s^{pump}$ are the sums of the Na⁺ and K⁺ ion currents $(I_{Na}^{pump},I_K^{pump})$ carried by the Na⁺-K⁺ pump for somatic and dendritic compartments. The compartments were coupled by an axial current (PY: g_C = 1.65 μS ; IN: g_C = 0.5 μS). Axosomatic currents were assumed to be sufficiently strong to change the somatic membrane voltage instantaneously, so the axosomatic compartment has no capacitance current. Current carried by the sodium-potassium pump was dependent on intracellular $(N{a}_{IN}^{+})$ and extracellular sodium $(N{a}_{OUT}^{+})$ as well as intracellular $(K_{IN}^{+})$ and extracellular potassium $(K_{OUT}^{+})$ concentrations given by the following equations (Kager et al., 2000):

$$A=1/{\left(1+K_{o\alpha }/K_{OUT}^{+}\right)}^2/{\left(1+N{a}_{i\alpha }/N{a}_{IN}^{+}\right)}^3$$

$$I_{Na-K}^{pump}=-2I_{Na-K}^{\text{max}}A+3I_{Na-K}^{\text{max}}A$$

where K_oα = 3.5 mM, Na_iα = 20 mM, $N{a}_{IN}^{+}=20,$ and $I_{Na-K}^{\text{max}}=25mA/c{m}^2.$

The sum of intrinsic currents for the dendritic compartment was given by $I_d^{Int}=I_{HVA}+I_{KCa}+I_{Km}+I_{Nap}+I_{Na}^d+I_{Ca}+I_d^{pump}+I_d^c+I_d^{leak}$ currents for the pyramidal cells and by $I_d^{Int}=I_d^{pump}+I_d^c+I_d^{leak}$ currents for interneuron. Intrinsic currents for the somatic compartment are described as $I_d^{Int}=I_d^{pump}+I_d^c+I_d^{leak}$ for both pyramidal cells and interneurons, where $I_s^{Int}$ consists of the voltage-gated sodium (PY and IN: G_Na = 3450 mS / cm²) and delayed-rectifier potassium (G_Kv = 200 mS / cm²) currents. The dendritic compartment for pyramidal cells had a high-threshold calcium current (I_HVA), a calcium-activated potassium current (I_KCa), a calcium current (I_Ca), a slowly activating potassium current (I_Km), voltage-gated and persistent-sodium currents (I_Na and I_Nap, respectively) (Jung et al., 2001), and leak conductances (PY: G_K = 0.044, g_Na = 0.02, g_Cl = 0.01 mS / cm² ; IN: G_K = 0.035, G_Na = 0.02, G_Cl = 0.035 mS / cm²). Full approximations of these currents have been described (Mainen and Sejnowski, 1996; Krishnan and Bazhenov 2011).

Ion concentration dynamics

We modeled variations in $C{a}_{IN}^{2+},$ $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ levels, leak currents, intrinsic currents, pump-mediated currents, extracellular diffusion, and glial activities, which affected ionic homeostasis. The Nernst equation was used to determine reversal potentials for potassium and chloride from internal and external concentrations for each ion. These ionic levels were calculated from active currents, activities of the sodium-potassium pump and the KCC2 cotransporter (Doyon et al., 2011) as well as ion flow between pyramidal cells and through extracellular space (Wei et al., 2014). We followed the assumption that the activity of the Na-K pump is regulated by extracellular potassium in neurons (Kager et al., 2000) and glia (Grisar, 1984). External potassium, $K_{OUT}^{+},$ was modeled as in (Krishnan and Bazhenov, 2011), and a 2-dimensional network was used to model extracellular diffusion taking into account the cortical structure of subiculum. The intracellular potassium was set at $K_{IN}^{+}=150mM.$

$$d{K}_{OUT}^{+}/dt=(k_K/Fd)(\text{Σ}{I}_K^{\mathrm{int}}+I_{Na-K}^{pump}-I_{KCC2})+G+{\displaystyle \sum _{i=1}^4{D}_{ij}/\text{Δ}{x}^2(K_{OUT}^{+}}-K_{OUT}^{+(i)})+d_{bath}/\text{Δ}{l}^2(K_{OUT}^{+}-K_{bath})$$

where the glial uptake G was modeled as in (Kager et al., 2007):

$$G=k_{ON}/k_{1N}(B_{\max }-B)-k_{OFF}{K}_{OUT}^{+}B$$

$$dB/dt=k_{OFF}(B_{\max }-B)-k_{ON}{K}_{OUT}^{+}B,$$

where the conversion factor k=10 10³ cm³, F=96489 C/mol, and the ratio between the cell volume and extracellular volume d=0.15. D_ij is an element of diffusion matrix d, and D_ij = 4 × 10⁻⁶ cm²/s for neighboring neurons (cat neocortex data (Fisher et al., 1976) and D_ij = 0 otherwise. Since subiculum pyramidal cells are organized in layers of few millimeters depth, we have chosen a 2-dimensional diffusion model, which allowed to save significantly on computational requirements without jeopardizing the main results of the paper. The first order diffusion approximation efficiently takes into account the spread of potassium in the cortical layer from 0.8 up to 3mm depth (Fisher et al., 1975). Each subicular pyramidal cell has 4 neighboring cells with a mean distance of Δx = 50 μm between their somata (Huberfeld et al., 2007), d_bath = 4 × 10⁻⁷ Hz is the coefficient for diffusion from the bath (Cressman et al., 2009; Barreto and Cressman 2011; Florence et al., 2009) and Δl = 200 μm is the depth of the neurons in the slice. The bath $K_{OUT}^{+}$ concentration was assumed to be uniform in the network and to equilibrate very rapidly (Bazhenov et al., 2004). Glial $K_{OUT}^{+}$ uptake was modeled by free buffer (with total capacity B_max = 500 mM) with a concentration B, which bound and unbound from $K_{OUT}^{+}$ with first-order kinetics, and the rates k_ON and k_OFF were given by k_ON = 0.008 and $k_{OFF}=k_{ON}/(1+\exp (-(K_{OUT}^{+}-K_{oth}^{+})/1.15))$ (Kager et al., 2007; Volman et al., 2007). The spatial buffering via gap-junctions was not modeled since it has been found that $K_{OUT}^{+}$ clearance does not strongly depend on connections between the astrocytes (Wallraff et al., 2006). Changes in $K_{OUT}^{+}$ due to the interneurons were assumed to be negligible compared to the $K_{OUT}^{+}$ produced by the pyramidal cells. Changes in $K_{OUT}^{+}$ due to extrusion from pyramidal cells were assumed to affect both pyramidal cells and interneurons. In some simulations, extracellular diffusion from the bath to neurons was set to zero to mimic in vivo conditions. In simulations without KCC2 contribution to $K_{OUT}^{+}$ (I_KCC2(−) cells) parameter $I_{KCC2}^{\text{max}}$ was set to zero in $K_{OUT}^{+}$ equation but was still present for ${\mathit{Cl}}_{IN}^{-}.$

Extracellular chloride concentration is assumed to be constant: ${\mathit{Cl}}_{OUT}^{-}=130mM.$ Intracellular chloride ${\mathit{Cl}}_{IN}^{-}$ concentration was calculated from the following equations:

$$dC{l}_{IN}/dt=(k_{Cl}/F)(I_D^{Cl}+I_{GABA}+I_{KCC2})$$

$$I_{KCC2}=I_{KCC2}^{\text{max}}(V_K-V_{Cl})/((V_K-V_{Cl})+V_{1/2}),$$

where $I_D^{Cl}$ is the chloride leak current on the dendrite, I_KCC2 = 2μA / cm² is the maximal current through the KCC2 cotransporter, V_K and V_Cl are the reversal potentials of potassium and chloride, and V_1/2 = 40 mV is the voltage difference when the chloride-potassium current reaches half maximum velocity, $I_{GABA}={\displaystyle \sum _i{g}_{GABA}^i{s}_{GABA}^i(V-V_{GABA})}$ is the sum of GABAergic currents received by a neuron. Using the conductance-based GABA synapse model and chloride leak current allows us to take into account the depolarization-driven uptake of intracellular chloride.

The outgoing flux via KCC2 was modeled according to (Doyon et al., 2011; Doyon et al., 2016) and (Staley et al., 1995; Staley and Proctor, 1999). The current via KCC2 describes the flow of potassium and chloride ions from the intracellular to the extracellular space. Both these currents are assumed to be equal in the absolute value, but opposite in polarity so that the net current is zero. I_KCC2 describes the currents of potassium and chloride ions via the KCC2, which could flow in either direction, depending on the sign of free energy proportional the voltage difference (V_K − V_Cl) (Staley and Proctor, 1999). The value of half maximum velocity V_1/2 of the KCC2 pump corresponds to the assumption that ${\mathit{Cl}}_{IN}^{-}$ increased up to 15mM and ${\mathit{Cl}}_{OUT}^{-}$ decreased up to 120mM, while V_K = −95mV (Doyon et al., 2011).

Intracellular calcium dynamics was modeled with the following equation:

$$dC{a}_{IN}^{2+}/dt=-(5.18\times {10}^{-5})/D_{Ca}{I}_{HVA}+(2.4\times {10}^{-4}-C{a}_{IN}^{2+})/{\tau }_{Ca},$$

where τ_Ca = 800 ms and D_Ca = 0.85 cm²mM / μA.

Reversal potentials for each current were calculated from the Nernst equation and continuously updated with internal and external ion concentrations on every time step:

$$V_K=\frac{RT}{F}\ln (\frac{K_{OUT}^{+}}{K_{IN}^{+}}),V_{Cl}=\frac{RT}{F}\ln (\frac{{\mathit{Cl}}_{IN}^{-}}{{\mathit{Cl}}_{OUT}^{-}})\text{and}{V}_{GABA}=\frac{RT}{F}\ln (\frac{{\mathit{Cl}}_{IN}^{-}+4{\mathit{HCO}}_{3IN}^{-}}{{\mathit{Cl}}_o^{-}+4{\mathit{HCO}}_{3OUT}^{-}}),$$

where ${\mathit{HCO}}_{3IN}^{-}$ = 16 mM and ${\mathit{HCO}}_{3OUT}^{-}$ = 26 mM (Doyon et al., 2011).

Network and synaptic model

The subiculum network was modeled with 841 pyramidal cells and 225 interneurons, to give a ratio close to 80% excitatory and 20% inhibitory cells. Increasing the size of the network had a minimal effect on the network dynamics. Synaptic connectivity between cells was made at random at levels based on estimates from the mouse subiculum measured at standard potassium concentrations (Böhm et al., 2015): P_PY-PY = 0.05, P_IN-PY = 0 65, P_PY-IN = 0.3, P_IN-IN = 0.4. Peak conductances at simulated synapses varied according to the normal distribution with the following means PY-PY: 1.5 nS / cm² for AMPA and 0.02 nS / cm² for NMDA; PY-IN: 1 nS / cm² for AMPA; IN-PY: 0.7 nS / cm² for GABA; and IN-IN: 0.5 nS / cm² for GABA and a variances at 10% of the corresponding mean. Synaptic parameters were systematically varied to ensure stability of network activity. Both pyramidal cells and interneurons also received a noisy excitatory synaptic input (AMPA) to induce spontaneous firing. Additional AMPA synaptic currents were modeled by an Ornstein-Uhlenbeck process (Renart et al., 2007): ${\tau }_{AMPA}\frac{d{I}_{AMPA}}{dt}=-I_{AMPA}+{\sigma }_{E/I}\eta (t),$ where τ_AMPA = 5.4 ms, σ_E = 0.50 μA / cm² and σ_I = 0.60 μA / cm². The time course of currents at simulated AMPA, NMDA and GABA synapses followed first-order kinetics, similar to those used in (Brunel et al., 2001).

LFP model

We computed a local field potential (LFP) from the summed activity of neurons of the simulated network. Pyramidal cells were assumed to provide the largest component of the LFP signal (Buzsáki et al., 2012). Each pyramidal cell i generated a dipole ${\phi }_i=-k\left(V_d^i-V_s^i\right)$ (Chizhov et al., 2015) as in (Demont-Guignard et al., 2012; Wendling et al., 2012), where k = 0.02 is the proportionality coefficient for the pyramidal cell layer. A global LFP signal was computed as a superposition assuming all pyramidal cells contribute equally: $LFP={\displaystyle \sum _i{\phi }_i}.$

Seizure detection algorithm

Seizure-like events in the simulated field activity were detected with an algorithm, which estimated the total power spectrum over a time window of 5 seconds. Events exceeding an amplitude threshold were classified as seizures.

Results

Absence of KCC2 leads to a depolarizing GABA reversal potential

Pyramidal cells with associated intrinsic and synaptic conductances of somatic and dendritic compartments were modeled (Fig. 1A). Active currents include the calcium-dependent potassium conductances that contribute to burst firing in subicular pyramidal cells (Jung et al., 2001; Stanford et al., 1998). Random synaptic currents mediated by AMPA and NMDA receptors initiate firing in the model cell and each action potential induces an increase in extracellular potassium. Major ion pathways associated with potassium and chloride homeostasis are shown in Fig. 1B. $K_{OUT}^{+}$ affects the reversal potential of all potassium currents and so modulates the excitability of the neuron model. The sodium-potassium pump, glial buffering and extracellular diffusion to the neighboring cells restore potassium levels towards the original value of ~3.35 mM. With these homeostatic mechanisms, we found ion concentrations in the model reached a stable equilibrium at physiological levels.

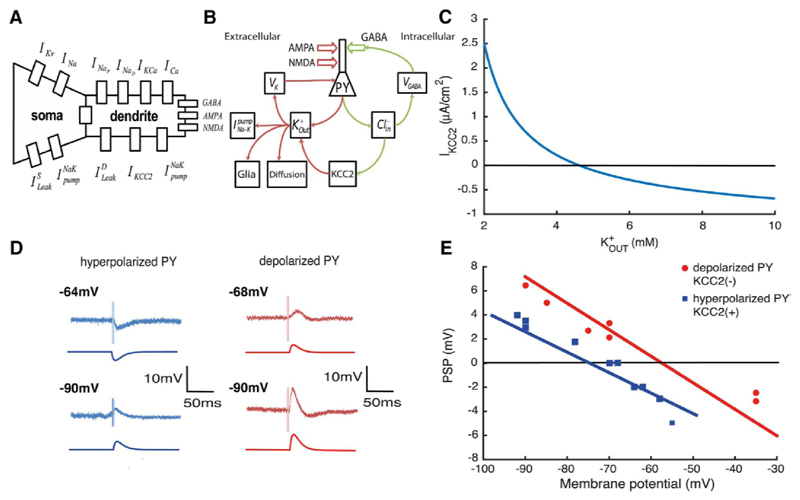
Figure 1. Absence of KCC2 leads to a depolarizing GABA reversal potential.

A, scheme of the PY model with intrinsic currents. B, ionic pathways in the single cell model. C, current via KCC2 cotransporter I_KCC2 as function of extracellular potassium $K_{OUT}^{+}$ when ${\mathit{Cl}}_{IN}^{-}=4mM$ and $I_{KCC2}^{\max }=2\mu A/c{m}^2.$ D, experimental and model voltage traces during GABAergic stimulation. E, amplitude of post-synaptic potential (PSP) during experimental stimulation (red and blue dots) and in the model (red and blue lines). Experimental traces of D and E are taken from (Cohen et al., 2002).

Activation of GABAergic synapses increases intracellular chloride concentrations ${\mathit{Cl}}_{IN}^{-}$ in the model (Fig. 1B). Intracellular chloride levels are then restored by activity of the KCC2 cotransporter, which extrudes chloride and potassium ions into extracellular space. The KCC2 cotransporter current depends on $K_{OUT}^{+}$, Fig. 1C. At large values of $K_{OUT}^{+}$ it could reverse the direction and load neurons with chloride (Payne, 1997). The increase in internal chloride levels leads to higher V_GABA values and so decreases the efficacy of inhibition.

Baseline intracellular chloride levels in the model cell depend on KCC2 activity. In KCC2(+) cells, they tend to return to ~3.5 mM, corresponding to a GABA reversal potential of V_GABA = −78mV, with an associated neuronal resting potential of -70 mV. In model cells with no KCC2 actions, KCC2(-), internal chloride stabilizes at 11.3 mM, corresponding to V_GABA = −56mV, with an associated resting potential of -65 mV. The absence of KCC2 thus results in a depolarizing GABA reversal potential and an depolarized resting membrane potential due to the chloride leak currents (Jedlicka et al., 2011; Krishnan and Bazhenov, 2011).

According to our model the value of V_GABA in KCC2(-) and KCC2(+) cells is the result of intracellular chloride concentration levels ${\mathit{Cl}}_{IN}^{-}.$ V_GABA is determined by joint concentration of chloride Cl⁻ and bicarbonate ${\mathit{HCO}}_3^{-}$ ions inside and outside of the cell, see Materials and Methods. Thus the presence of ${\mathit{HCO}}_3^{-}$ component makes V_GABA significantly higher than V_Cl (Payne et al., 2003), while the value of V_Cl is equal to the membrane potential.

The pyramidal cell model was stimulated with a GABA conductance to ask how internal chloride levels affect GABAergic signaling (Fig. 1D). The GABAergic synaptic current was modeled with second order synaptic kinetics (Chizhov 2002) and no excitatory input was modeled (Cohen et al., 2002). The dependence of GABA currents on KCC2 actions is shown by plotting the amplitude of the postsynaptic potential (PSP) as a function of membrane potential (experimental and model traces in Fig. 1E). The same GABAergic stimulus induces a hyperpolarization in the KCC2(+) pyramidal cell, but depolarizes the KCC2(-) cell. The blue and red lines are predictions of PSP amplitude from the model. The absence of the KCC2 cotransporter results in a difference of ~20 mV in the reversal potential of the response to GABA.

Single cell consequences of KCC2(-) pathology

We next asked how KCC2 influences excitability by exploring responses of the model cell to synaptic stimuli. The stimulation protocol was developed to reproduce seizure-like events in rat hippocampal slices (Fujiwara-Tsukamoto et al., 2007; Fujiwara-Tsukamoto et al., 2010) and epileptic human hippocampal slices (Huberfeld et al., 2011). AMPA, GABA and NMDA conductances in KCC2(+) or KCC2(-) neurons were activated for 5 seconds at 5Hz (Fig. 2 A,B). This simulated synaptic stimulation provoked a sustained bursting afterdischarge activity, which was prolonged after the stimulus stopped. Bursting activity in the KCC2(+) cell, was short lasting (Fig. 2A), while that of the KCC2(-) cell lasted for several hundred milliseconds (Fig. 2B). A slow depolarization after stimulation in both cells resulted from the excitatory effect of extracellular potassium accumulation.

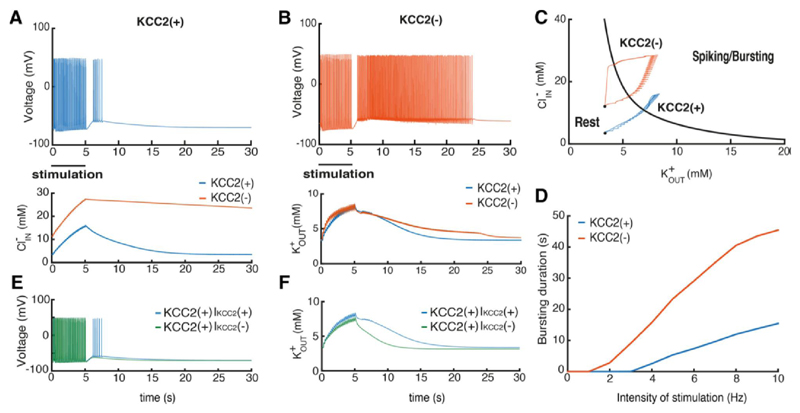
Figure 2. Consequences of the KCC2(-) pathology in single pyramidal cells.

A, B, voltage trajectories of the KCC2(-) and KCC2(+) PY neurons after stimulation with periodic AMPA, GABA and NMDA synaptic input for 5 seconds. Lower panels show changes in K⁺ and Cl^- levels. C, state diagram of the model and changes in ionic concentrations. Red and blue trajectories correspond to the KCC2(-) and KCC2(+) cells, respectively. D, Relations between stimulus intensity and firing after stimulation for KCC2(-), red, and KCC2(+), blue, cells. E - voltage trajectories of the KCC2(+) with and without KCC2 contribution to the extracellular potassium after the same synaptic stimulation as in A and B, I_KCC2(+) and I_KCC2(–). F - the corresponding extracellular potassium concentration changes.

We explored how changes in potassium and chloride levels contribute to sustained afterdischarges in model neurons in a bifurcation analysis using levels of these ions as control parameters. The resulting state diagram (Fig. 2C) shows how the intracellular chloride ${\mathit{Cl}}_{IN}^{-}$ and extracellular potassium $K_{OUT}^{+}$ concentrations affect neuron behavior. The black line figures the border between regions of firing or silence in the model neuron. It corresponds to a line of saddle-node bifurcations in the two-parameter diagram. Thus, high levels of $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ move the neuron into the burst firing regime. In KCC2(-) cells elevated internal chloride ${\mathit{Cl}}_{IN}^{-}$ provides an additional depolarization via effects on chloride leak current reversal potential (Krishnan and Bazhenov, 2011). Thus an absence of KCC2 increases excitability by moving neuronal potential towards the firing region of the state diagram (Fig. 2C).

The enhanced excitability of the KCC2(-) neuron affects how it respond to synaptic stimulation. $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ increase due to spiking and GABAergic stimulation and when ionic concentrations increase sufficiently, the cell moves into the region of spiking/bursting (Fig. 2C). When KCC2 is active however, the accumulation of intracellular chloride was much reduced. The same synaptic stimulation moved the cell KCC2(+) less far into the spiking/bursting region of the state plot. The time to restore baseline ionic homeostasis in the KCC2(-) cell was longer than in the control neuron resulting in a long afterdischarge before return to baseline (Fig. 2C black dots).

We then explored how the absence of KCC2 affects responses to different intensities of synaptic stimulation. The minimal stimulation intensity needed to evoke spiking during slow depolarization was less and that the duration of the afterdischarge was longer in KCC2(-) than in KCC2(+) cells for all frequencies. In summary when KCC2 actions are suppressed, pyramidal cell generate bursting activity more easily due to larger amount of depolarization provided by chloride leak current because of increased ${\mathit{Cl}}_{IN}^{-}$ concentration.

Since KCC2 affects both $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-},$ it is important to separate these two contributions for single neuron excitability. For this purpose we performed simulations with KCC2(+) cell when the $K_{OUT}^{+}$ level depends on KCC2 activity, I_KCC2(+), and does not depend on I_KCC2(−), see Materials and Methods. We found that in the I_KCC2(+) case the synaptic stimulation similar to Fig. 2A leads to the substantial depolarization triggering the spiking activity, Fig. 2E, while in the I_KCC2(−) case the depolarization is smaller. Analysis of ion concentration changes after the stimulation showed that I_KCC2(+) cells provide substantially higher amount of $K_{OUT}^{+}$ compared to I_KCC2(−), Fig. 2F. The difference between these curves corresponds to the amount of $K_{OUT}^{+}$ released uniquely by KCC2 co-transporter after synaptic stimulation. This additional $K_{OUT}^{+}$ increase caused larger depolarization leading to the spiking activity in the I_KCC2(+) cell, Fig. 2E.

We found that the amount of excessive $K_{OUT}^{+}$ released by KCC2 could trigger spiking activity in the KCC2(+) case after application of the synaptic stimulation, while in the stationary case the presence of the co-transporter in KCC2(+) cells does not provide the substantial increase of $K_{OUT}^{+}$ concentration, Fig. 2C. The paradoxical effect of KCC2 is observed because the cotransporter operates close to the thermodynamic equilibrium where V_K is close to V_Cl (Payne et al., 2003) thus making the current passing via KCC2 very small. Therefore, there is no substantial difference between KCC2(-) and KCC2(+) cells in terms of $K_{OUT}^{+}$ concentration. Yet the situation changes dramatically once the ion concentrations of $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ and the corresponding reversal potentials are increased, Fig. 2F. In this case the additional amount of $K_{OUT}^{+}$ passing through KCC2 provides substantial depolarization leading to spiking, Fig. 2E, similar to the experiments in (Viitanen et al., 2010).

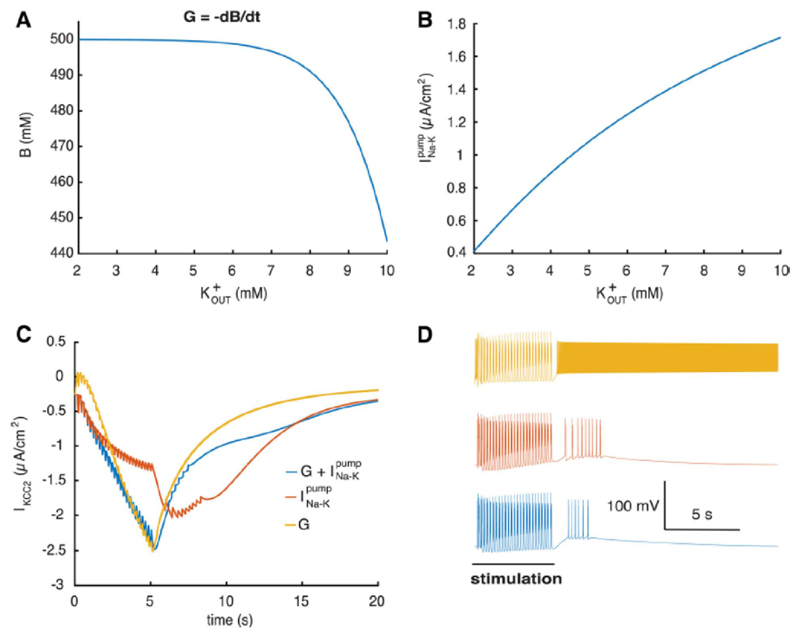
Since the interaction between $K_{OUT}^{+}$ and neural excitability depends on multiple mechanisms we performed simulations to clarify each specific contribution. Glial buffer and $I_{Na-K}^{pump}$ have different dependence on $K_{OUT}^{+},$ Fig. 3A, B, and therefore should have different effect on ion regulation. To clarify their contribution we stimulated the KCC2(+) cell with a burst induction stimulus (same stimuli as in Fig. 2A). Blocking the various $K_{OUT}^{+}$ mechanisms lead to changes in the I_KCC2 current, during the $K_{OUT}^{+}$ increase induced by stimulation, Fig. 2B. Fig. 3C. We found that removal of the glial buffer substantially increases neural excitability leading to longer after-depolarization and more after-discharges, Fig. 3D. Removing the sodium-potassium pump contribution, at constant sodium concentration, has even more dramatic effects on single neuron dynamics. At the end of the stimulation the KCC2(+) neuron fires continuously due to extracellular potassium accumulation, Fig. 3D, Fig. 2B, while the glial buffer is not fast enough to compensate. Based on these simulations we conclude that both $I_{Na-K}^{pump}$ and glial buffer have large effect on $K_{OUT}^{+}$ regulation and corresponding excitability changes, yet $I_{Na-K}^{pump}$ provides the major contribution.

Figure 3. Mechanisms of extracellular potassium regulation.

A, capacity of the glial buffer depending on $K_{OUT}^{+}.$ B, current via $I_{Na-K}^{pump}$ depending on $K_{OUT}^{+}.$ C, current via KCC2 when different $K_{OUT}^{+}$ regulation mechanisms are present in the KCC2(+) cell. D, corresponding voltage traces (same stimulus as in Fig. 2 A, B).

Gamma oscillations in KCC2(+) subiculum network model

We next asked how these KCC2-dependent changes in potassium and chloride homeostasis and the resulting alterations in neuronal excitability affect network behavior. Network oscillations were examined in a subiculum network consisting of GABAergic two-compartment interneurons (IN) and pyramidal cells (PY) as described in the Material and Methods section. PY and IN neurons were sparsely connected by conductance-based synapses with realistic subiculum connectivity (Böhm et al., 2015). Parameters used at these synapses were adjusted to physiologically realistic values. All neurons in the network were exposed to the same $K_{OUT}^{+}$ ion concentration, which affected both the PYs and INs, and the dynamics of chloride concentrations ${\mathit{Cl}}_{IN}^{-}$ in pyramidal cells were identical.

We examined responses of the network to protocols similar to those used experimentally to evoke pathological bursting discharges (cf. Huberfeld et al., 2011). With an excitation equivalent to that provided by 8 mM potassium and 0.5 mM magnesium in the external solution (Huberfeld et al., 2011), activity of network model became organized into stable oscillations (Fig. 4A) at a peak frequency of ~36 Hz. This gamma frequency oscillation is similar to recorded from the subiculum in vitro (Colling et al., 1998; Huchzermeyer et al., 2008; LeBeau et al., 2002; Jackson et al., 2011; Stanford et al., 1998). The increased potassium concentrations provide significant excitation to both PY and IN cells so contributing to the population oscillations. At levels equivalent to 4 mM potassium, the network activity organizes into sparse random firing. We ensured that stable gamma oscillations exist in the network in the absence of the additional extracellular potassium from the bath, when PY and IN populations receive sufficient amount of external excitation (simulations not shown).

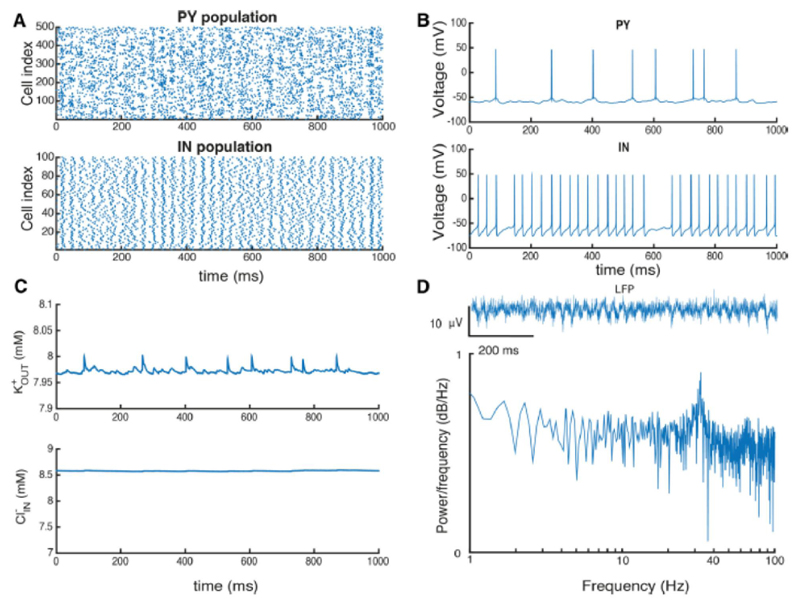
Figure 4. Ion concentrations during gamma oscillations in the PY-IN network in the presence of 8 mM potassium in the bath solution.

A, raster plot showing activity for a representative part of the pyramidal cell (PY) and interneuron (IN) populations. B, voltage traces from representative PY and IN cells. C, $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ concentrations during network activity. D, local field potential (LFP) computed from pyramidal cell activity and, below, power spectrum of LFP signal.

Both extracellular potassium and intracellular chloride levels increase during simulated gamma oscillations. At a steady state after 1-2 minutes of simulated oscillations, $K_{OUT}^{+}$ reached an equilibrium at 7.9 mM and ${\mathit{Cl}}_{IN}^{-}$ was 8.6 mM (Fig. 4C). We note local increases in $K_{OUT}^{+}$ during spiking which tend to equilibrate quickly after each spike, and also small oscillations during each cycle of network activity. Thus, the oscillations generated by the PY-IN network led to quasistationary ion levels and a physiological type of population activity.

Synchronous pyramidal cell firing during the gamma oscillations led to oscillations of our computed LFP (Fig. 4D). While single pyramidal cells did not fire on each cycle of the oscillation, the overall PY population activity fluctuated with the LFP oscillations (Fig. 4B). In contrast inhibitory cells tended to fire a spike on every oscillation cycle with a strong peak at ~36 Hz (Fig. 4D). Such PY-IN interplay has been described as a PING mechanism (Whittington et al., 2000).

KCC2(-) pathology in the subiculum circuit

We studied how KCC2(-) cells might contribute to seizure initiation by constructing networks with a varying proportion of KCC2-deficient PY cells. All neurons in simulated networks were excited by an equivalent external potassium level of 8 mM to reflect previous work (Huberfeld et al., 2011). Effective extracellular potassium levels were dependent on this excitation and also on the potassium extruded by neuronal firing. We assumed KCC2(-) pyramidal cells were not clustered in simulated network space and performed additional simulations to check that such clusters did not affect results (simulations not shown). The initial conditions were set at baseline ionic levels for KCC2(-) and KCC2(+) cells, calculated from the single neuron model (Fig. 2C).

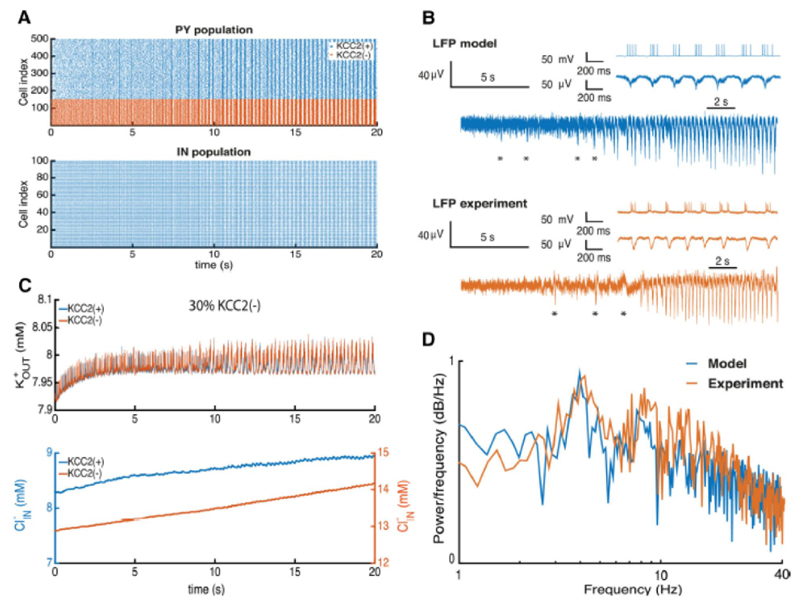
The addition of 30% of KCC2(-) PY cells to the simulated network provoked synchronous population bursting similar to ictal discharges (Fig. 5A). PY cell firing due to elevated chloride levels in these KCC2(-) cells led to a substantial activation of IN cells and a strong recurrent GABAergic input to PY cells. With a depolarized GABAergic reversal potential, KCC2(-) cells did not receive an effective inhibition, and tended to discharge more strongly than KCC2(+) cells.

Figure 5. KCC2(-) pathology in the subiculum circuit.

A, raster plot of firing in pyramidal cells (PY) and interneurons (IN) during seizure initiation. B, extracellular potassium, $K_{OUT}^{+},$ and intracellular chloride, ${\mathit{Cl}}_{IN}^{-},$ changes during seizure initiation. C, LFP computed from the network and experimental LFP recordings. D, power spectrum of the LFP from the model and experimental records.

We next compared LFPs generated by the simulated network with those recorded from human subicular tissue during the transition to ictal activity (Fig. 5B). As in experimental records, the model initially generated a weakly synchronous activity that gradually shifted into a more synchronous periodic population bursting (Fig. 5A). Initial fast oscillations in the simulated LFP result from strong pyramidal cell firing and are then transformed into population burst firing at ~4 Hz (Fig. 5A) as experimentally (see insets in Fig. 5B). We noted a number of non-periodic synchronous population bursts being generated by the model before the onset of the seizure (Fig. 5B, asterix). These irregular discharges occurred as the network approached an ictal state characterized by periodic bursting.

In the network these discharges were initiated by recurrent AMPA-mediated synaptic events and terminated by cellular Ca²⁺-dependent potassium currents. A close analysis of simulated activity revealed the following sequence of events. Random excitatory inputs in the KCC2(-) group of PY cells initiate firing in other neurons via recurrent excitatory synapses, which tends to trigger Ca²⁺-dependent potassium currents and so stop firing in PY cells that participate in the initial aperiodic population bursts (Fig. 5B, asterix). With a random initiation, the irregular character of these discharges (Jirsa et al., 2014) gradually transforms into the periodic bursting activity specific for ictal discharges.

During transition to the ictal state an enhanced excitation from KCC2(-) PY cells activated IN cells leading to a strong repetitive activation of GABAergic synapses. Consequences include an increase of intracellular chloride levels ${\mathit{Cl}}_{IN}^{-}$ in pyramidal cells and of $K_{OUT}^{+}$ levels in the extracellular space due to the increased firing (Fig. 5C). While the increase in extracellular potassium during the transition was buffered by rapid diffusion, the intracellular chloride in both KCC2(-) and KCC2(+) cells increased significantly. The GABAergic reversal potential was considerably depolarized and an effective positive feedback loop between $K_{OUT}^{+},$ ${\mathit{Cl}}_{IN}^{-}$ and neuronal firing resulted in a continued increase in neuronal firing and synchrony. We note that changes in internal chloride levels in PY cells were relatively small, consisting in a 1 mM increase induced a depolarizing shift of 2-3 mV in the GABAergic reversal potential (Fig. 5C). Indeed the resulting decrease of inhibitory processes in the network induced pathologically synchronous bursting in both PY and IN populations.

We compared seizure dynamics in the model and experiment by analyzing normalized power spectra of the corresponding LFPs during the epileptic oscillations (Fig. 5D). A strong peak at 4 Hz in both cases corresponds to the principal frequency with several harmonic peaks. The LFP spectrum of the model capture the main frequency peak and 1/f behavior (Buzsáki et al., 2012). Oscillations at frequencies above 40 Hz were not prominent. While our model did not capture all aspects of experimental traces (Fig. 5B insets), many aspects of the LFP signal and power spectrum during the seizure were well matched (Fig. 5D). Thus accumulation of $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ in the subicular PY-IN network with ~30% or more KCC2(-) cells produces a pattern of activity similar to that recorded experimentally from human epileptic subiculum.

Analysis of epileptiform oscillations

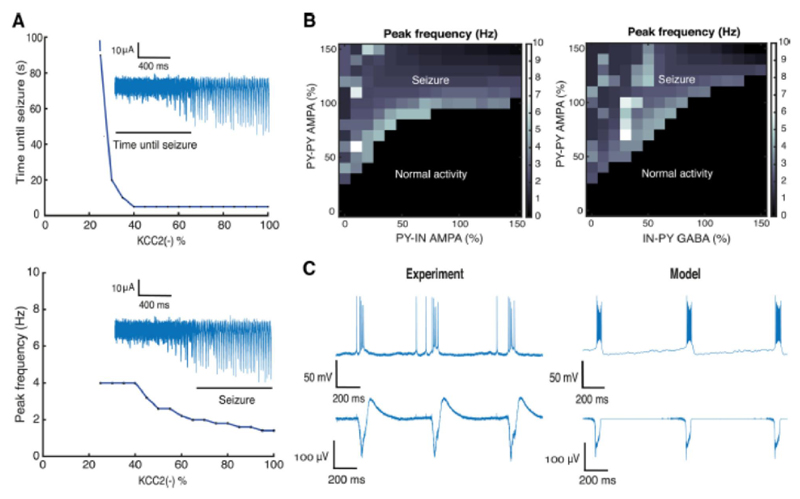
The stability of epileptic network oscillations was assessed over a range of model parameters in simulations with 30% KCC2(-) pyramidal cells in the network. A seizure detection algorithm was applied to the model LFP to capture the moment of seizure initiation. Since the frequency of population bursts may change during the course of seizure, we used the initial oscillation frequency at seizure onset, corresponding to the peak of the power spectrum (Fig. 5D). We found that this frequency decreases with the number of KCC2(-) cells (Fig. 6A). Bursting became slower as the duration of population bursts decreased, resulting in an increased inter-burst interval. This effect does not conform to a decrease in seizure activity since the prominence of population bursts increases with their duration.

Figure 6. Analysis of epileptic oscillations.

A, relations between the number of KCC2(-) cells in the network, and time until seizure initiation and peak frequency of LFP spectrum. The insets show characteristic LFP traces. B, LFP peak frequency as a function of the mean strength of AMPA and GABA conductances in the network. C, population bursts generated after blocking inhibition in the model and experimental records (block with bicuculline). Synaptic conductances were varied from 0 to 150%: PY-PY 0 – 2.25 nS / cm²; PY-IN 0 – 1.5 nS / cm²; IN-PY 0 – 1.05 nS / cm².

With a stimulus equivalent to 8 mM extracellular potassium, the network tolerates up to 25% KCC2(-) cells before epileptic bursting emerges (Fig. 6A). At these lower levels, gamma frequency oscillations are generated (Fig. 4). Epileptic oscillations were produced as the proportion of KCC2(-) cells exceeded a critical threshold (dashed line in Fig. 6A). Higher proportions resulted in a faster transition to epileptic activity. For instance with more than 40% of KCC2(-) cells, activity became pathological in less than 5 seconds (Fig. 6A).

The strength of synaptic conductances may be an especially important factor in the initiation of seizure-like activity. We examined the effect of varying these parameters in a network with a suprathreshold proportion of 30% KCC2(-) cells (cf. (Marder and Taylor, 2011). Mean values of synaptic parameters were altered and expressed as a percentage of the initial mean (Fig. 6, caption). We found large regions of parameter space corresponding to both resting state and epileptic oscillations (Fig. 6B). In the black region, the network generated oscillations at various frequencies, while in the white region epileptic oscillations were generated, at 1-10 Hz for different synaptic parameter combinations. In general, the mean strength of AMPA-mediated recurrent PY-PY synapses governed seizure initiation threshold (Fig. 6B). In contrast, increasing the mean strength of excitatory synapses made with IN inhibitory cells tended to suppress ictal-like discharges. Similarly, increasing the strength of inhibitory synapses (GABA IN-PY) tended to reduce epileptic activity (Fig. 6B).

We also examined the effects of reducing the inhibitory synaptic parameters to zero for comparison with experiments using GABA-A receptor antagonists bicuculine (Fig. 6C, left panel). Suppressing GABAergic signaling in the model caused the network to generate periodic population bursts at ~1 Hz (Traub et al., 1987, de la Prida et al., 2006, Huberfeld et al., 2011). LFP oscillations became phase locked with pyramidal cell activity (Fig. 6C, right). The simulated network oscillation resulted from an interplay between recurrent excitation within the PY population and intrinsic neuronal currents $I_{Ca}^K$ and I_Ca (Traub et al., 1987, Jung et al., 2001), which depend on intracellular Ca²⁺ dynamics. While the shape of the LFP differed to some extent, these data reflected the characteristic frequency of population events.

Thus the presence of a threshold proportion of KCC2(-) cells has robust pro-ictal effects evident over a range of excitatory and inhibitory synaptic strengths. Increasing synaptic inhibition reduces ictal-like activity and increasing recurrent excitation favors seizure-like events.

KCC2(-) pathology in the subiculum circuit with endogenous potassium

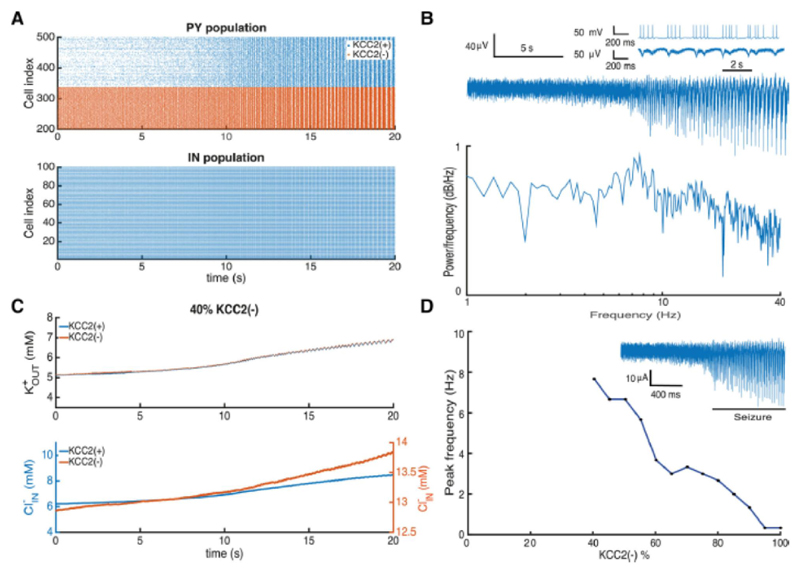
Using our model we were able to separate the $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ contributions to seizure initiation. In the intact brain extracellular potassium level depend on network activity, and potassium is effectively controlled by glial cells, diffusion and Na-K pump (Bazhenov et al., 2004). To recreate this scenario in our computational model, we simulated this condition by eliminating the extracellular potassium in the bath with a compensatory increase in the input to PY and IN cells at an intensity that generated sustained activity at physiological firing frequencies (Fig. 4). In these conditions, the presence of 40% of KCC2(-) PY cells sufficed to generate epileptic oscillations (Fig. 7A). As in simulations using extracellular potassium as a stimulus (Fig. 5) a high frequency PY cell activity led to the gradual emergence of synchronicity in the network with population bursts as during ictal discharges.

Figure 7. Adding KCC2(-) cells to the network with endogenous ion concentrations leads to the development of pathological oscillations.

A, activity of pyramidal cells (PY) and interneurons (IN) during seizure initiation. B, LFP trace computed from neuronal activity and corresponding power spectrum, the inset shows pyramidal cell activity during the seizure. C, changes in the extracellular potassium $K_{OUT}^{+}$ and intracellular chloride ${\mathit{Cl}}_{IN}^{-}$ concentrations during seizure initiation. D, seizure frequency plotted against the proportion of KCC2(-) cells. The inset shows a typical LFP signal.

Ictal activity emerges after an increase in firing of both PY and IN cells induces a progressive increase in $K_{OUT}^{+}$ and ${\mathit{Cl}}_{IN}^{-}$ levels (Fig. 7C). The resulting excitation-inhibition imbalance induced the emergence of synchronous bursting activity after 12 seconds. Extracellular potassium $K_{OUT}^{+}$ levels then rose rapidly due to high frequency firing in PY cells. The positive feedback between firing and potassium levels continue to increase neuronal excitability and synchrony. Intracellular chloride levels ${\mathit{Cl}}_{IN}^{-}$ also increased with IN cell firing, repetitive activation of inhibitory synapses and a depolarizing shift in the GABA reversal potential in PY cells.

Simulated LFP activity reflected firing in PY cells (Fig. 7B) as with the elevated potassium stimulus (cf. Fig. 5B). The power spectrum of LFP signals showed a maximum near 8 Hz, corresponding to the inter-burst interval (see inset) with more peaks than in the elevated potassium simulations (Fig. 5B) but with a comparable general shape. As previously, we found that a threshold proportion of at least 40% of KCC2(-) PY cells was needed for seizure initiation (Fig. 7D). Oscillation frequency decreased as the proportion increased (Fig. 6A) and with more than 90% of KCC2(-) cells longer duration epileptic bursts were generated at frequencies of ~0.4 Hz.

Thus, accumulation of extracellular potassium and intracellular chloride induced seizure-like oscillations at endogenous potassium levels when the network contains a supra-threshold proportion of KCC2(-) PY cells. Reducing the extracellular potassium preserved synchrony and oscillations were shifted to a higher frequency.

Dynamic elimination of the KCC2(-) pathology prevents seizure

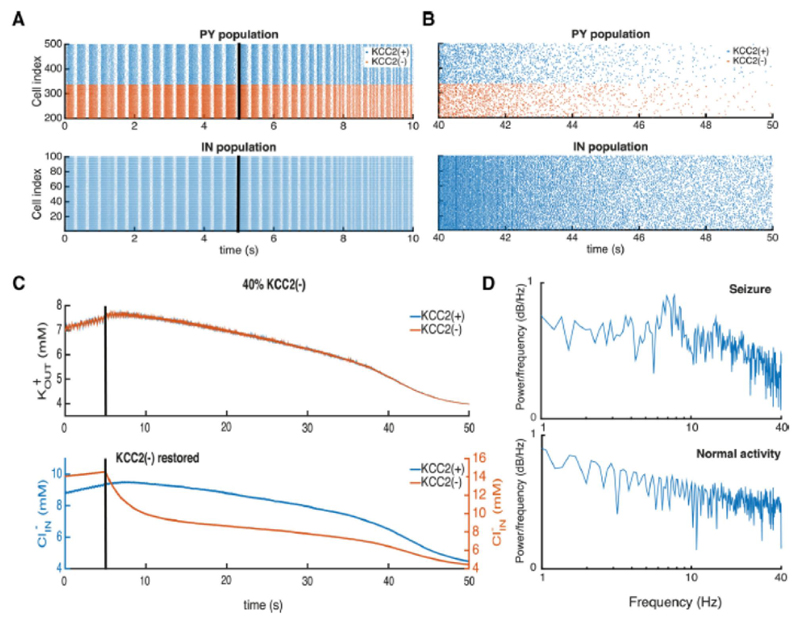
As a final test, we asked whether restoring chloride homeostasis in an epileptic network at endogenous potassium concentrations could suppress epileptic synchrony. The network was initialized in conditions where epileptic oscillations were generated (cf. Fig. 8) and after 5 seconds KCC2 function was restored in all KCC2(-) cells. The return to full KCC2 function slowly decreased synchrony in the PY and IN populations (Fig. 8A) transforming network activity. after 45 seconds into stable, asynchronous firing corresponding to normal activity (Fig. 8B).

Figure 8. Restoring KCC2(-) function with realistic ionic levels prevents seizure.

A, B, raster plots of pyramidal cell (PY) and interneuron (IN) activities during seizure oscillations are shown on the left. Those during the transition to normal activity after restoring KCC2 function (black line at 5 sec) are shown on the right. C, changes in the extracellular potassium $K_{OUT}^{+}$ and intracellular chloride ${\mathit{Cl}}_{IN}^{-}$ concentrations after restoring KCC2 function, at the black line. D, LFP power spectra during epileptic oscillations and after KKC2 function was restored in KCC2(-) cells.

Restoring KCC2 function, restored potassium and chloride homeostasis. Internal chloride ${\mathit{Cl}}_{IN}^{-}$ was reduced to 4.1 mM and external potassium $K_{OUT}^{+}$ fell to 4 mM (Fig. 8C). A reduction in internal PY cell chloride levels reduced the excitatory drive to IN cells, and so reduced release from GABAergic synapses further decreasing internal chloride in KCC2(+) as well as KCC2(-) PY cells. Excitation-inhibition balance in the network was restored and neuronal synchrony reduced. Lower rates of PY cell firing led to reduced levels of extracellular potassium (Fig. 8A, B). We noted a biphasic decay in extracellular potassium and internal chloride levels (at ~40 s in Fig. 8C). It reflects the time point at which synchronous burst firing ceased. Ion concentrations were rapidly reestablished after this point. Restoring KCC2 function reverses epileptic oscillations in networks with up to 100% of KCC2(-) PY cells and is equally effective in simulations with fixed $K_{OUT}^{+}$ up to 8mM (results not shown).

The recovery of network function after KCC2 restoration is evident in LFP power spectra (Fig. 8D). A characteristic peak in the LFP spectrum during seizure activity (cf.. Fig. 7A) is suppressed and the spectrum transformed to a 1/f type (Bédard and Destexhe, 2009) when asynchronous firing re-emerges.

Discussion

In this modeling study, we asked how the absence of KCC2 in some pyramidal cells might contribute to the generation of ictal-like activity in human epileptic subiculum. The absence of KCC2 in simulated neurons results in a depolarizing shift of the reversal potential for responses to GABA. KCC2(-) neurons displayed an exaggerated persistent burst firing in response to elevated external potassium. In network model with realistic subicular synaptic connectivity, epileptic oscillations developed when a critical proportion of KCC2(-) neurons were included. Simulated field potentials possessed a similar time course and frequency components to experimental data. Ictal-like activity was stable over a range of values for excitatory and inhibitory synaptic conductances, was generated with either fixed or endogenous levels of external potassium and was blocked by restoring KCC2 activity. These data suggest that a defect in KCC2 expression or function in a minority of pyramidal cells could suffice to generate seizures.

Intracellular chloride homeostasis in pyramidal cells

The cotransporter KCC2 controls both chloride and potassium levels in neurons and is suggested to contribute to seizure initiation (Huberfeld et al., 2011, Zhang et al., 2011). There are several animal models incorporating the KCC2 deficiency (Hübner et al., 2005; Woo et la 2002; Hekmat-Scafe et al. 2006), but their application for human studies is not straightforward. KCC2 is especially significant for synaptic responses to GABA, which may depolarize neurons during early development (Ben-Ari, 2002). At this stage, chloride homeostasis depends largely on the NKCC1 cotransporter, but later as KCC2 is expressed, responses to GABA become hyperpolarizing (Khalilov et al., 1999; Rivera et al., 1999; Payne et al., 2003). Multiple other factors including pH, HCO₃ and CO₂ control responses to GABA (Dulla et al., 2005) and may be modified during epileptic activities, including febrile seizures (Schuchmann et al., 2009; Tolner et al., 2011). Local impermeant anions may also contribute to basal intracellular chloride (Glykys et al., 2014). Chloride levels also increase as inhibitory synapses are repetitively activated due to interneuron activity before and during ictal behaviors in hippocampus (Isomura et al., 2003; Fujiwara-Tsukamoto et al., 2007; Lillis et al., 2012) and neocortex (Dietzel and Heinemann, 1986; Dietzel et al., 1989).

Our model did not include several factors contributing to chloride homeostasis that may be significant. The NKCC1 cotransporter has been shown to be involved in focal epilepsies (Huberfeld et al., 2007; Huberfeld et al., 2011; Pallud et al., 2014). It appears to be upregulated and its blockade controls both interictal and ictal epileptic activities. The upregulation of NKCC1 results in the increase of GABA reversal potential level (results not shown) so as the downregulation of KCC2. The absence of NKCC1 in the present model highlights the crucial effect of reduced KCC2 function or expression on ictogenesis. The anion exchangers and NKCC1 undoubtedly contribute to the intracellular chloride homeostasis (Doyon et al., 2016), while in our study we concentrate on the crucial role of KCC2 with respect to K and Cl. Concentration changes of bicarbonate ions via anion exchangers such as AE3 (Hentschke et al., 2006) and EAAT 3-4 (Deisz et al., 2014) could significantly affect the chloride extrusion rate. However the reversal potential of GABAergic currents in neurons of diseased human neocortex tends to be depolarized from rest (Deisz et al., 2011; Pallud et al., 2014; Deisz et al., 2014). KCC2 activity is consistently reduced but some degree of Cl^- extrusion may persist due to AE3 or EAAT3-4 (Deisz et al., 2011; Deisz et al., 2014). However, currently there is little data on residual anion exchangers function in the subiculum and the contribution of these mechanisms together with intracellular chloride should be evaluated in the future studies.

The present KCC2 model used in this study (Doyon et al., 2011) is based on the assumption that chloride clearance is proportional to the free energy available for ion transport that could be estimated as potential difference between V_K and V_Cl (Staley and Proctor, 1999). More complex KCC2 models (Chang and Fujita, 1999) describe chloride clearance in more details, yet they would provide substantially similar results if they are based on the same data (Staley and Proctor, 1999), see (Lewin et al., 2012).

Extracellular potassium contribution to epileptiform activity

Elevated extracellular potassium levels were initially associated with seizure initiation (Fertziger and Ranck 1970, Ranck 1970, Dietzel and Heinemann, 1986; Dietzel et al., 1989). External potassium increases not only at a seizure onset site but also along pathways of seizure spread. Although it may be difficult to measure timing of potassium kinetics precisely due to slow response of ion sensitive electrodes. Seizure threshold potassium levels have been defined in hippocampus but are less clear in neocortex (Antonio et al., 2015). After more recent studies (Bazhenov et al., 2004; Fröhlich et al., 2008a; Ullah et al., 2009; D'Antuono 2004; Wei et al., 2014) it still remains unclear whether an accumulation of extracellular potassium is a cause or a consequence of ictal behavior.

Our simulations suggest that an increase in extracellular potassium alone did not lead to seizure activity, at least at 8 mM. Even so the KCC2 transporter clearly increases external potassium and contributes to the enhanced, self-sustained firing of pyramidal cells. In this context it is interesting that the KCC2 pathology in epileptic human tissue affects only a minority of pyramidal cells (Huberfeld et al., 2007). In certain conditions potassium extrusion from KCC2(+) neurons may be equally important in the generation of ictal events (Hamidi and Avoli, 2015). Our results therefore suggest that the increase of extracellular potassium (Antonio et al., 2015) and intracellular chloride in subiculum contribute to seizure initiation. These predictions should be tested by simultaneously measuring these parameters in slice experiments during seizure initiation.

Extracellular levels of potassium also affect GABAergic signaling. Since the KCC2 cotransporter operates close to a thermodynamic equilibrium (Payne, 1997) external potassium levels are closely linked to basal levels of intracellular chloride thus defining the efficacy of GABAergic signaling (Khalilov et al., 1999). Even small increases in external potassium induce significant neuronal chloride accumulation (Payne et al., 2003) thus reducing the efficacy of GABAergic synapses.

The role of the KCC2(-) cells

Our data show that including a minority of KCC2(-) cells in a simulated subicular network induced ictal-like epileptic oscillations (Fig. 4, 6). Restoring function in these neurons blocked the activity. The presence of KCC2(-) cells stimulated interneuron firing, so provoking a feedback increase in intracellular chloride in KCC2(-) pyramidal cells. The resulting imbalance in excitation and inhibition led to generation of epileptic oscillations by the network. These data mirror the experimental finding of strong interneuron firing at seizure initiation (Gnatkovsky et al., 2008). Thus an activity-dependent chloride accumulation in pyramidal cells due to intensive interneuron firing (Lillis et al., 2012) contributes to a gradual failure of an inhibitory restraint as seizures propagate (Trevelyan et al., 2007; Schevon et al., 2012).

Elevated internal chloride levels in KCC2(-) pyramidal cells resulted in a depolarized resting potential and GABAergic reversal potential as compared to KCC2(+) cells. The resulting persistent increase in the excitability of KCC2(-) may induce plasticity in the strength or number of recurrent excitatory connections made by these neurons. Further work should address possible differences in synaptic function and connectivity between KCC2(-) and KCC2(+) pyramidal cells.

Our data showed that restoring KCC2 function in pyramidal cells effectively blocked seizure activity in the network (Fig. 7) Thus pharmaceutical strategies to restore or strengthen chloride homeostasis (Gagnon et al., 2013) may be a useful therapeutic tool in certain epileptic syndromes.

It has been recently found that addition of the specific KCC2 blocker VU0463271 to the mouse hippocampal slices provokes generation of epileptic activity (Sivakumaran et al., 2015). This study is consistent with our model and conclusions based on human hippocampal sclerotic tissue (Huberfeld et al., 2007). In contrast to this the authors another work (Hamidi and Avoli, 2015) showed that the blockade of KCC2 with another compound VU0240551 prevents generation of ictal discharges in similar experimental conditions. Nonetheless we found that downregulation of the KCC2 in the network provides larger increase of excitability due to ${\mathit{Cl}}_{IN}^{-}$ accumulation leading to ictal discharge generation, Fig. 4, 6. Therefore we predict that the epileptogenic effect of KCC2 is mostly due to failure of chloride regulation, while the increase of excitability due to extracellular potassium released by KCC2 (Viitanen et al., 2010) has smaller effect for seizure initiation. We believe that further development of more specific KCC2 blockers would allow to resolve this controversial issue.

Conclusions

Epilepsy is a complex disease involving dynamic interactions between many different elements of an epileptic brain (Lytton, 2009; Jirsa et al., 2014; Proix et al., 2014; Naze et al., 2015). In this work we have characterized one pathological pathway associated with chloride and potassium homeostasis in the human subiculum. Recent work on epileptic peritumoral cortex (Pallud et al., 2014), cortical dysplasias and tuberous sclerosis (Talos et al., 2012) suggests that changes in chloride-potassium co-transport contribute to epileptic syndromes beyond the sclerotic hippocampal formation. Further modeling and experimental work may lead to a deeper understanding of the mechanisms involved and help define new therapeutic targets.

Significance statement.

Ion regulation in the brain is a major determinant of neural excitability. Intracellular chloride in neurons, partial determinant of the resting potential and the inhibitory reversal potentials, is regulated together with extracellular potassium via kation chloride cotransporters. During temporal lobe epilepsy the homeostatic regulation of intracellular chloride is impaired in pyramidal cells, yet how this dysregulation may lead to seizures has been unexplored. Using realistic neural network model describing ion mechanisms we show that chloride homeostasis pathology provokes seizure activity analogous to recordings from epileptogenic brain tissue. We show that there is a critical percentage of pathological cells required for seizure initiation. Our model predicts that restoration of the chloride homeostasis in pyramidal cells could be a viable anti-epileptic strategy.