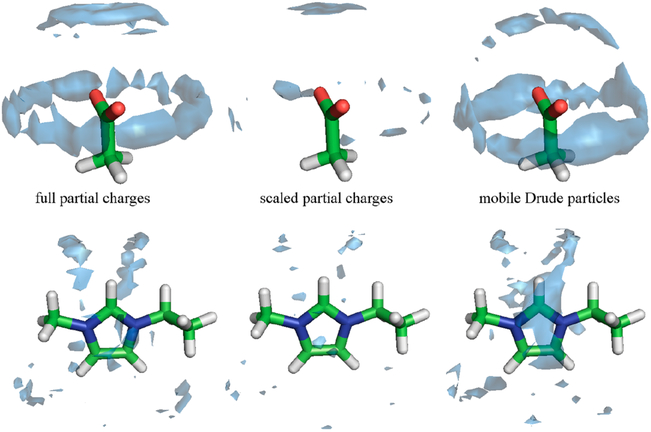
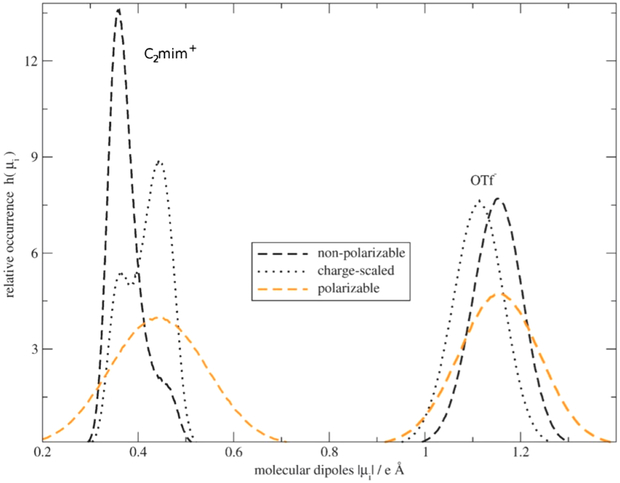
Abstract
Many applications in chemistry, biology, and energy storage/conversion research rely on molecular simulations to provide fundamental insight into structural and transport properties of materials with high ionic concentrations. Whether the system is comprised entirely of ions, like ionic liquids, or is a mixture of a polar solvent with a salt, e.g., liquid electrolytes for battery applications, the presence of ions in these materials results in strong local electric fields polarizing solvent molecules and large ions. To predict properties of such systems from molecular simulations often requires either explicit or mean-field inclusion of the influence of polarization on electrostatic interactions. In this manuscript, we review the pros and cons of different treatments of polarization ranging from the mean-field approaches to the most popular explicit polarization models in molecular dynamics simulations of ionic materials. For each method, we discuss their advantages and disadvantages and emphasize key assumptions as well as their adjustable parameters. Strategies for the development of polarizable models are presented with a specific focus on extracting atomic polarizabilities. Finally, we compare simulations using polarizable and nonpolarizable models for several classes of ionic systems, discussing the underlying physics that each approach includes or ignores, implications for implementation and computational efficiency, and the accuracy of properties predicted by these methods compared to experiments.
Graphical Abstract
1. INTRODUCTION
The increase in computational power and accessibility of massively parallel architectures combined with the maturation of advanced modeling techniques and force fields allowed atomistic molecular dynamics (MD) simulations to transform into an essential tool for providing molecular scale insight into the structure–property relationships and virtual design of novel materials. Condensed phase ionic systems have attracted attention of the modeling and simulation community due to their applications in chemistry, biology, and energy storage research.1,2 Room temperature ionic liquids (ILs) and solvent-in-salt concentrated electrolytes are particularly interesting due to their potential applications in batteries, nanoreactors, and separation mediums. 1,2 Examples of typical ionic liquid cations and anions are depicted in Figure 1, including their commonly accepted abbreviations.
Figure 1.
Typical ionic liquid cations and anions and their abbreviations used in this review. In the IL research community, NTf2 is the common reference for this anion, while in the electrochemical community working with battery electrolytes, TFSI is the more common notation. Taking this into account, throughout the paper we will use both notations to be consistent with the most common usage in the discussed corresponding application.
High ionic concentration in these materials results in local electric fields polarizing solvent and large ions that often requires either explicit or mean-field inclusion of polarization effects in order for molecular models to be accurate and predictive, especially for sampling far-from-equilibrium structures such as electric double layers or nanoconfinement.
1.1. Nonpolarizable Simulations of Ionic Systems
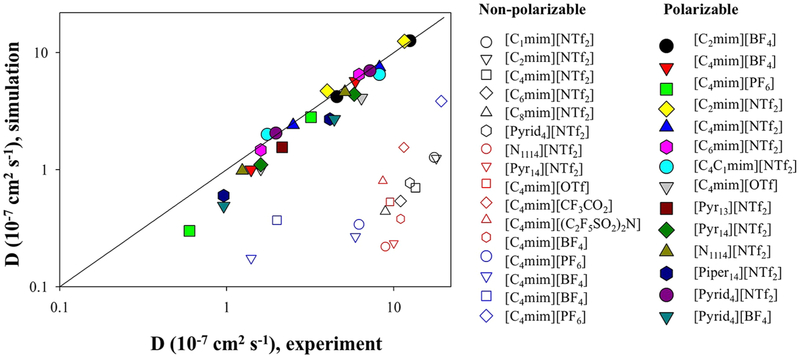
Initial attempts to model these ionic systems using traditional nonpolarizable potential energy functions or force fields, which successfully worked for a variety of nonpolar and polar systems with low salt concentrations, uncovered challenges for the accurate prediction of transport and thermodynamic properties. Numerous studies indicated that additional attention should be paid to polarization treatment in systems with high ionic concentrations.3-41 While simulations using nonpolarizable models provided important insight into molecular level correlations and structure in ionic systems,42,43 they also demonstrated that thermodynamic and transport properties predicted from MD simulations are often inconsistent with experiments showing much slower dynamics, with the agreement becoming worse at higher salt concentrations.43-46 For example, recent simulations by Rajupt et al. of 3 M lithium bis(trifluoro-methanesulfonyl)imide (referred as NTf2 or TFSI or TFSA) solution in 1,3-dioxolane and 1,2-dimethoxyethane (DOL:DME) mixture predicted Li+ and NTf2 ion diffusion coefficients more than 100 times slower than experiments.43 The self-diffusion coefficients obtained from simulations using the Canongia-Lopes et al. force field16,18-21 were an order of magnitude smaller than experimental values29 for 1-ethyl-3-methylimidazolium bis(trifluoro-methanesulfonyl)imide [C2mim][NTf2] and significantly slower than in experiment for 1,3-dimethylimidazolium chloride [C1mim][Cl] and 1-butyl-3-methyl-imidazolium hexafluorophosphate [C4mim]-[PF6].27 Similarly, a sluggish ion transport has been found in simulations of [C2mim][PF6], [C4mim][PF6], and [C4mim]-[BF4] by Picálek et al. utilizing five different force fields.30 MD simulations of alkylpyridinium-based ILs predicted apparent self-diffusivities that are roughly 10 times lower than experimental values.33 In simulations of 13 different ionic liquids by Tsuzuki et al.47 using a modified OPLS force field, self-diffusion coefficients with deviations from experiments ranging from a factor of almost 10 up to as much as a factor of 40 were obtained. This trend is illustrated in Figure 2, where a correlation between ion self-diffusion coefficients (average for cation and anion) gained from MD simulations using nonpolarizable force fields and experiments is summarized for various ILs. Similarly, large deviations were observed for ionic conductivity and viscosity indicating sluggish dynamics from simulations using the nonpolarizable force fields without charge scaling.
Figure 2.
Correlation between averaged (for cation and anion) self-diffusion coefficients obtained from fully atomistic MD simulations and experimental data for several ionic liquids. Data for nonpolarizable force field are shown as open symbols and were compiled from several works where generic force fields were used without extended adjustments or modifications. For comparison, filled symbols show predictions of the generic polarizable force field. Data are compiled from refs 30, 47, and 44 and references therein.
The systematic trend observed for a variety of ILs, as well as concentrated organic solvent electrolytes clearly indicates that these discrepancies are not a problem of a particular force field or a specific system, but rather that the important physics or interactions are missing in the nonpolarizable simulations. Not surprisingly, these interactions are related to the induced polarization which plays a crucial role in molecular ionic systems as expected. The inclusion of induced atomic polarization, where in addition to fixed partial atomic charges each atom/molecule has a fluctuating induced dipole responding to the local environment, noticeably improved the description of transport and thermodynamic properties of ionic systems. For example, Figure 2 shows a significantly enhanced correlation between simulation vs. experiment data for the self-diffusion coefficients obtained from simulations using a transferable many-body polarizable force field (APPLE&P).44
1.2. Mean-Field Treatment of Polarization Effects
While the concept of polarizable molecular models existed since the late 1970s, the practical application of this approach was not straightforward due to the lack of generic polarizable force fields, limited availability in popular simulation packages, and a substantial (factor of 3–10) increase in computational costs. Therefore, while simulations using polarizable models were regarded as more accurate compared to those with non-polarizable models, alternative approaches were investigated to bypass the complexity of explicit induced polarization in MD simulations, aiming at a reduction in the computational cost and ensuring the stability of numerical integration.48
One of the approaches is to account for polarization implicitly by modifying the parameters of van der Waals dispersion interactions. For example, KÖddermann et al.29 modified the Lennard-Jones parameters from the original Canongia-Lopes et al. force field16,18-21 to match the description of dynamical and thermodynamic properties of the [Cnmim][NTf2] series with n = 1, 2, 4, 6, and 8. Taking into account that the interaction between two induced dipoles separated by distance r scales as r−6, i.e., the same scaling as the dispersion term in the Lennard-Jones potential, such an approach represents an effective mean-field approximation of induced polarization effects. However, it does not take into account the directionality of interactions with and between induced dipoles and requires a significant modification of the Lennard-Jones parameters, which makes such a force field system specific and less transferable. In another approach, the effective repulsion–dispersion parameters of nonpolarizable models with united atom representation of sp3 carbons were adjusted to reproduce the data (density, heat of vaporization, and self-diffusion coefficients) predicted from fully atomistic polarizable MD simulations of ILs or electrolytes.49-51 Unlike the original atomistic polarizable force field that utilized essentially a universal set of repulsion–dispersion parameters for most of the atom types (i.e., only one oxygen type of interaction for all ether compounds, carbonate solvent molecules, and anions), therefore ensuring transferability and predictive capabilities for novel materials, the effective two-body non-polarizable force field had to introduce numerous chemistry-specific additional repulsion–dispersion parameters leading to limited transferability. The approach of adjusting the van der Waals interactions in nonpolarizable models was taken even further by using the force matching approach to fit numerical, system-specific two-body potential functions based on instantaneous atomic forces predicted from polarizable simulations in the condensed phase.52 While such approximations of polarization by the two-body terms noticeably improved the description of structural properties (compared to just omitting polarization), it was not possible to completely reproduce the ion transport, highlighting the challenges with incorporating the many-body terms into effective two-body interactions.
Another mean-field approach to effectively take into account induced polarization is to scale ionic charges. This approach is one of the most popular in application to ILs and electrolytes. It was motivated by several ab initio calculations on ion pairs and clusters, which suggested that the net charges on ions have to be reduced due to charge transfer or/and polarization effects.6,53-58 To define an atomic or molecular charge, a specific approximation for correlating the electron density or wave function distributions obtained from DFT or ab initio calculations with the point charge assignments must be employed (e.g., restrained electrostatic potential (RESP), charge from electrostatic potential (CHELPG), natural population analysis (NPA), etc.). Taking into account that strong polarization effects can lead to significant spatial overlap of electron orbitals, it is expected that without considering polarization explicitly (i.e., imposing the constraint of non-polarizable models) the partial atomic charge distribution and molecular charges extracted from such calculations will be effectively reduced. However, if the same data from DFT or ab initio calculations are approximated assuming a polarizable model, the effective ionic charges can be kept close to unity while the weakening of interactions between ionic species is captured by explicit induced polarization interactions.45 Chaban and Voroshylova reported that the cluster size of 1-ethyl-1-methylpyrrolidinium chloride and dicyanamide had no significant impact on the charge scaling factor.59 In contrast, Dommert et al. showed that the charge distributions obtained from fitting gas-phase first-principles data are significantly (qualitatively) different from those obtained from fitting the data from condensed phase DFT calculations.48
In the absence of explicit polarization, the scaling of ionic charges is the most effective option which has been employed for the adjustment of various force fields for a wide range of ionic systems. Below we list several popular strategies for including polarization in a mean-field sense by modifying Coulomb interactions. The exact strategies for how to implement the scaling also vary:
Chaban has uniformly scaled the atomic charges by different factors to match various experimental thermodynamic properties60 such as density, viscosity, conductivity, and heat of vaporization. Although these properties have no obvious correlation, a uniform charge scaling factor of 0.7–0.8 was sufficient to reproduce these properties in nonpolarizable simulations. Interestingly, this scaling factor is quite close to the inverse of the refractive index.
SchrÖder reported on a linear correlation between the charge scaling factor of 1-ethyl-3-methylimidazolium trifluoromethanesulfonate [C2mim][OTf] and the polarizability on the basis of the effective Coulomb energy.45
Müller-Plathe and co-workers used an effective dielectric constant ϵ∞ of 1.8 to scale down the Coulomb interaction.61 This ansatz corresponds to an electronic continuum correction (ECC) or dielectric continuum model to reproduce the effect of the induced dipoles.45,62,63 Following this model, one may use the inverse of the refractive index as a charge scaling factor (i.e., yielding a scaling factor of 0.75).45 In addition to the ECC correction that weakens the ion–solvent interaction, one needs to decrease the ion–solvent repulsion parameters to avoid unrealistically high solvent–cation coordination numbers and overestimation of the ion–solvent packing.64-66 Examination of 29 combinations of nonpolarizable ion–water force fields based on SPC/E, TIP4P, and TIP4Pew water models for the LiCl/water system at four different salt concentrations showed that none of the investigated models yield satisfactory results for all tested properties such as density, static dielectric constants, self-diffusion coefficients, and structure factor, but the force field using the ECC correction resulted in by far better prediction of transport properties.46
Unlike the ECC correction that often results in a weaker (compared to the full charge model) ion–solvent binding for solvent molecules in the first coordination shell of the ion, a mean-field polarizable model was proposed. This model added an effective polarizable term to enhance the ion–solvent attraction at short distances for solvent molecules within the first ion solvation shell. The effective polarization term was scaled to zero beyond the first coordination shell using a distance dependent dielectric constant approach. Thus, it effectively accounted for the increased dipole for the solvents directly coordinating small ions (e.g., Li+) as has been observed in DFT-based MD simulations.67 It roughly took into account the ion–solvent polarization screening due to electronic polarizability within the first solvation shell and due to dipole (and multipole) contributions beyond the first coordination shell.68,69 Such an approach, however, overestimated the size of the first ion solvation shell and resulted in the slower ion dynamics compared to MD simulations with an explicit inclusion of polarization.70
Fileti and Chaban recommended that prior to the determination of partial charges the structure should be derived from DFT functionals including dispersion, e.g., ωB97XD,71,72 followed by partial charge assignment via the electrostatic potential and MØller–Plesset second-order perturbation theory to be more compatible with CHARMM force fields.
Schmidt et al. used the BlÖchl method to fit ionic charge distributions based on DFT data for the condensed phase (bulk) conditions.58 Similarly, Mondal and Balasubramanian used crystalline and liquid phase DFT data to extract reduced charges for imidazolium-based ILs, thus implicitly accounting for polarization.73,74 They also pointed out that utilization of different charge fitting schemes does not result in a consistent set of charges.
A more extended discussion of earlier charge scaling strategies and approaches can be found in ref 48. However, such an approach might be to some extent counterintuitive for organic solvent electrolytes because DFT calculations revealed that the solvent dipole moment is higher for the molecules coordinating small cations than in a bulk solvent. Thus, the solvent–cation interactions in the first solvation shell should be stronger and not weaker due to polarization effects.67
Chen et al.75 compared three different nonpolarizable force fields commonly used for ILs for simulations of [C4mim][Cl] and its mixtures with ethanol. For neat IL with nonscaled charges, i.e., ion q = ±1.0e, the self-diffusion coefficients, conductivity, and viscosity were about 2 orders of magnitude off from experimental values. Simulations of [C4mim][Cl] with scaled charges (ion q = ±0.85e) showed noticeable improvement of transport property predictions; however, they were still a factor of 5–20 off from experiments. For the [C4mim][Cl] mixtures with ethanol the accuracy of predicted thermodynamic properties, such as the ethanol activity coefficient was found to be even more complicated. At dilute ethanol concentrations, the force fields with full ionic charges yielded values in reasonable agreement with experimental correlations, while simulations with scaled charges increased the activity coefficient by about a factor of 2. On the other hand, at high ethanol concentrations the trend reversed, showing a better description from simulations using the scaled charges while simulations with full charges overestimated the solubility of ethanol compared to experiments. Therefore, if someone is interested in investigating this IL/solvent mixture in the entire composition range, the selection of an appropriate force field/model becomes a taunting task.
The lack of transferability of nonpolarizable force fields with scaled charges specifically tuned to describe one system (e.g., pure IL) to mixtures of several ILs, IL with solvents or polymers, or organic solvent electrolytes, is one of the major disadvantages and limitations of the scaled charge approach. For example, if one mixes two ionic liquids sharing the same cationic species but with different charge scaling factors for the pure systems, the question arises which charge scaling factor should be applied to the cations? If one sticks to the factors for the pure systems, cations of the very same type may have different total charges which may lead to spurious artifacts in the simulations. Similarly, the alternate possibility to determine the uniform cationic scaling factor as a function of the mole fraction is not satisfactory as cations and the two anionic species can have different scaling factors. Furthermore, although the anionic scaling factors can be kept constant when changing the mixture composition, the cationic scaling factor has to be re-evaluated.
Choi and Yethiraj76 reported that the scaled charge model for [C4mim] [BF4] failed to predict the phase separation of this IL with poly(ethylene oxide) chains at any temperatures, which is in disagreement with experiments. It was argued that this failure is a generic phenomenon, primarily due to significant and artificial underestimation of IL cohesive energy in simulations with scaled charges, therefore leading to poor predictions of phase behavior in IL mixtures.77 This conclusion is further supported by recent work of McDaniel that states “Due to the important contribution of polarization, we find that non-polarizable force fields qualitatively fail to predict mixing of ionic liquids with low dielectric solvents, predicting phase-separation instead!” after investigating the phase behavior of [C4mim] [BF4] mixtures with 1,2-dichloroethane, acetone, acetonitrile, and water using polarizable and nonpolarizable force fields.78 McDaniel and Yethiraj also found that scaling of charges cannot remedy the artificially enhanced long-range ion–ion correlations in ionic liquids.79 They demonstrated that this artifact is apparent to simulations with any nonpolarizable force field due to inability to capture the infinite frequency dielectric response ε∞ (and hence electrostatic screening) by nonpolarizable models. The authors showed that the long-range electrostatic interactions, usually handled by one of the Ewald-type summation techniques, are fundamentally altered by electronic polarization. Polarizable simulations predict ε∞ ≈ 2, while all nonpolarizable models (whether with scaled ionic charges or not) give ε∞ = 1, therefore leading to overestimation of electrostatic interactions in the small wavevector limit. This work clearly illustrates the fundamental difference between polarizable and nonpolarizable models that attempt to approximate the influence of polarization.
In this review, we discuss the pros and cons of different treatments of polarization ranging from the mean-field approaches to the most popular explicit polarization models in MD simulations of highly ionic materials. Most of molecular simulation softwares now have an option to include induced polarization interactions. Therefore, each user (whether a modeling expert or a novice user) has to make choices deciding which model to select for his/her particular system of interest. We believe this review will serve as a practical guide both to expert and nonexpert users of molecular simulations.
The goal of this review is, first, to briefly introduce the basic concepts of induced polarization interactions in molecular systems and to describe several strategies for implementing these effects into molecular simulations such as fluctuating charge models, classical Drude oscillator, and point dipoles. For each method, we discuss the advantages and disadvantages as well as key assumptions and adjustable parameters (the latter are often taken as default universal parameters, which is not always the case). Furthermore, we compare the outcomes using one or the other polarizable model and discuss the origin of the observed discrepancies.
Then, we review the methods/strategies for the parametrization of polarizable models, specifically focusing on extracting atomic polarizabilities (the key adjustable parameter in polarizable force fields) and universal scaling behavior that has been discovered recently. Next, we compare simulation predictions obtained using polarizable and nonpolarizable models. We discuss the underlying physics that each approach includes or ignores, implications for implementation and computational efficiency, accuracy, and transferability. These comparisons are made for several classes of bulk systems that include: dilute and concentrated electrolytes with the focus on emerging battery applications, bulk ILs, and electrolytes at charged surfaces, where the isotropic approximations are no longer valid and explicit inclusion of polarization of electrolyte and the electrode can be important.
2. TREATMENT OF INDUCED POLARIZATION IN MD SIMULATIONS
2.1. Fluctuating Charge Model
Polarizability refers to the response of the electron density due to a local electric field. In classical MD simulations, the electron density is accounted by the partial charges qiβ of atom β in molecule i of the system, allowing them to change during the simulation, i.e., qiβ(t), mimicking polarizability effects.80-82 This approach has a big advantage that no new interaction types have to be implemented as polarizable and permanent electrostatic interactions are handled using Coulomb’s law with the same monopoles. This method is referred to as the fluctuating charge, charge equilibration, or chemical potential equilibration model. While it has been successfully implemented in a number of programs, one has to be careful because a possible overestimation of the polarizability as significant charge flows within the molecule (or even between them) may happen at small energetic costs.81
The energy U(qiβ(t)) required to create a charge qiβ(t) on an isolated atom β of molecule i can be described by a Taylor series
| (2.1.1) |
with the amount of charge flow based on the Mulliken electronegativity and the hardness . Going beyond the quadratic term possibly increases the accuracy of the model but causes problems for treating the charge dynamics as discussed below. However, in molecules, this electrostatic energy is augmented by the interaction with the partial charges of the other atoms γ of the same molecule i or another molecule j:
| (2.1.2) |
Here, {q(t)} and {} represent the sets of partial charges and coordinates of all atoms at time t. The second-order coefficient depends on the distance between the atoms iβ and jγ and should become at very long distances. At shorter distances, the screening of the electrostatic interaction between the atoms due to delocalized charge distributions can be computed by the integral
| (2.1.3) |
or can be obtained by a mixing rule:80,83
| (2.1.4) |
Using these mixed hardness parameters ensures the correct limiting behavior as 1/riβjγ in (t) in eq 2.1.2 for separations greater than 2.5 Å. Consequently, eq 2.1.4 applies to induced charge interaction of atoms connected by bonds, angles, and dihedrals.
The molecular polarizability 3 × 3 tensor can be evaluated from the inverse of the n × n hardness matrix containing the elements Jiβjγ(t):
| (2.1.5) |
where are the atomic coordinates relative to the center of geometry of the n atoms under investigation.
2.1.1. Charge Flux and Electronegativity Equalization.
The current partial charges qiβ(t) on each atom β of molecule i are obtained by minimizing the electrostatic energy
| (2.1.6) |
using the Lagrange multiplier method with one of the following charge restraining conditions f(q):
-
Bond charges bβγ between atoms β and γ connected by a covalent bond cancel each other:84-87
(2.1.7) (2.1.8) The unambiguous assignment of bond charges bβγ is always possible for neutral molecules but needs additional rules for distributing the net charge in the case of ions. This has the considerable advantage that partial charges cannot be accumulated at a particular site of the molecule. This might happen in ionic systems as the redistribution stops once the charge has arrived at the site with the closest distance to the counterion, as the electrostatic potential between unlike charges is very steep at short distances.
-
The molecular charge qi is constant:
(2.1.9) The molecular charge can be set to zero for neutral species, +1e and −1e for the monovalent ionic liquid cations and anions, respectively, or to subinteger values as inspired by the work of Morrow and Maginn.6 This way, intermolecular charge transfer processes are prevented. This is the most common option, in particular if only one ionic species is made polarizable.88,89
-
Charge transfer is allowed between an ion pair:90
(2.1.10) However, the complete assignment which cation i belongs to which anion j is ambiguous as a particular anion may have the shortest distance from several cations. Nevertheless, temporary charge transfer between cations and anions can be realized this way.
-
The total charge of the system is zero
(2.1.11) which should always be the case, even if the charge flow is restricted otherwise. This option guarantees free charge flow in the system. In the case of pure ionic liquids, this may jeopardize the stability of the polarizable MD simulation.
The energy gradients are electronegativities χiβ(t) of the corresponding atoms by Mulliken’s definition91
| (2.1.12) |
and result in
| (2.1.13) |
Because eq 2.1.13 equals a constant λ for all atoms sharing the respective charge condition described above, their electronegativities are equal as well. In other words, the electronegativity χiβ(t) of each atom β in molecule i equals the average value χi(t) of the molecule i if the molecular charge is constant (see second charge condition eq 2.1.9). If the charge flow is allowed between all atoms in a system, i.e., only the total charge of the system is zero, all atomic electronegativities χiβ(t) at a particular time have the very same value. The fluctuating charge model is often also called electronegativity equalization method or chemical potential equalization method because the chemical potential μiβ(t) equals the negative electronegativity χiβ(t):
| (2.1.14) |
Using the Taylor expansion of the electrostatic energy up to the second term (see eq 2.1.1) and the minimization condition in eq 2.1.13 results in a coupled set of (n − 1) linear independent equations of charges and the charge condition f(q). Solving these coupled equations by Cramer’s rule yields all partial charges qiβ(t).
The partial charge solution can also be obtained by means of an extended Lagrangian dynamics method. Here, a fictitious uniform mass, mq, is assigned to each charge. Time evolution of the charges are computed by Newton’s equation of motion
| (2.1.15) |
with the average electronegativity χi(t) of the molecule i in case of second charge condition eq 2.1.9
| (2.1.16) |
As a consequence, eq 2.1.15 describes forces experienced by each atom β driving the atomic electronegativity χiβ(t) toward the molecular average χi(t). In this view, this approach mimics the process of moving electrons from atoms with low electronegativity (= high chemical potential) to highly electronegative atoms having a lower chemical potential.
2.1.2. Fluctuating Charge Simulations of Simple Molten Salts and Ionic Liquids.
The fluctuating charge model has been applied to aqueous electrolytes,92,93 molten salts,89,94-99 and ionic liquids.88,90 However, most of these simulations are performed with self-written MD codes as only LAMMPS, earlier versions of CHARMM83, and nonofficial versions of GROMACS have implemented a fluctuating charge algorithm. This explains the far less common use of these polarizable method compared to Drude oscillators or induced point dipoles.
Of course, the atomic electronegativity χiβ(t) of atom β in a molecule i differs from the value of the isolated atom as the chemical environment and, in particular, neighboring atoms directly bonded to atom β influence the behavior of the charge flow. Hence, the parameter values and for an atom type in eq 2.1.2 are usually not computed from the ionization potential and electron affinity as proposed by Mulliken91 but are subject to optimization routines.82,100 However, they may reveal some insights in the electronic structure of that atom, e.g., the oxidation state.
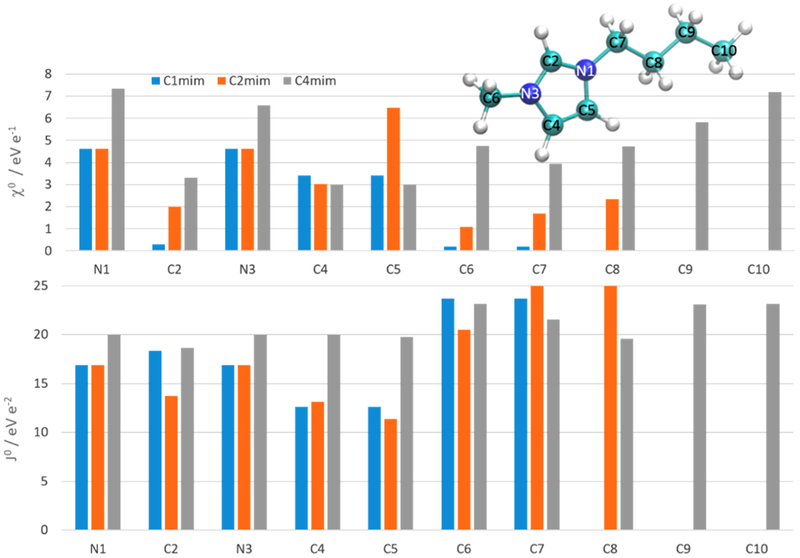
In Figure 3, the fluctuating charge parameters for methyl-imidazolium Cnmim from ref 88 are displayed. The anions were made nonpolarizable in the reported systems and the charge flow was restricted to each cation corresponding to the molecular charge restraining condition (eq 2.1.9). Using these parameters, the partial charges of the cations resemble the Mulliken charges of these molecules.88 However, the parameters do not seem to be transferable as prolonging the alkyl chain has a significant impact on χ0 and J0. In particular, the electronegativity of the imidazolium nitrogens jumps to higher values from C2mim to C4mim. The values for the acidic ring carbon C2 increases with increasing alkyl chain length. This is also true for the carbon adjacent to the nitrogens. Interestingly, the electronegativity of the C5 carbon for C2mim is much higher than for C1mim and C4mim. The charge flow within the molecules seems to be strong as the electronegativity of the terminal methyl carbon C6 changes by a factor of 25 between C1mim and C4mim. The electronegativity of the alkyl carbons increases with the distance from the imidazolium ring. Quite counterintuitively, the fluctuating charge electronegativities do not correlate with the acidity of the atoms because the alkyl carbons possess higher values than the ring carbons. The acidity of the C2 carbon should be highest, but the corresponding electronegativity has the lowest value. The reported hardness values J0 show less variation among the atom types.
Figure 3.
Fluctuating charge force field parameters of Cnmim with the alkyl chain length n =1, 2, and 4.88
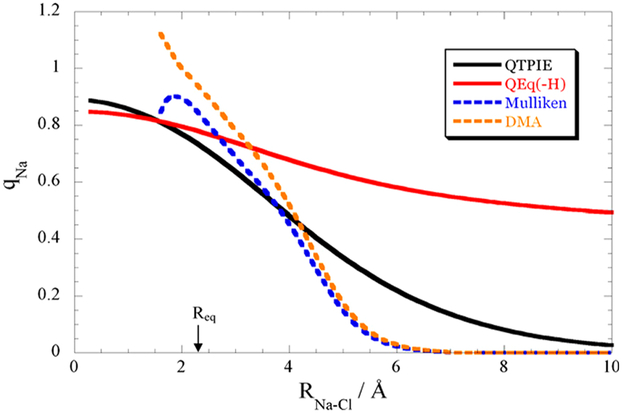
Standard charge equalization schemes work reasonably well for structures of neutral molecules close to equilibrium but may have problems for nonequilibrium situations or charged systems,81,82,99 resulting in nonphysical charge flows. For example, increasing the bond length of a sodium chloride ion pair should result in a vanishing partial charge of the participating atoms at infinite distance. However, as visible in Figure 4, the partial charge of the sodium as a function of the distance to the chlorine does not approach zero (red line) for the standard equalization scheme although Mulliken charges of CAS(8,5)/3-21G calculations (blue dashed line) went to zero for distances longer than 6 Å. However, Martinez and coworkers99 developed a distance-dependent penalty function for long-range charge transfer (black solid line), which pushes the partial charges closer to the values obtained from a Mulliken (blue dashed line) or a distributed multipole analysis (orange dashed line).
Figure 4.
Partial charges (in elementary charge) on dissociating NaCl. The blue and orange dashed curves show the quantum mechanical results from a Mulliken population (blue) and a distributed multipole analysis (DMA, orange), respectively. Qeq refers to the standard charge equilibration scheme101 without charge depending radius for hydrogens. The fluctuating charge model QTPIE developed by Chen and Martinez99 particularly takes the charge transfer between atoms into account and hence is more appropriate for the dissociating ion pair. Reproduced with permission from ref 99. Copyright 2007 Elsevier.
The fluctuating charge formalism could also be used in conjunction with the Drude or atom polarizable models to describe the intermolecular charge transfer (CT).102 It is a complementary approach to account for CT via the explicit introduction of additional terms in the potential energy function,103 like it is done in the sum of intermolecular fragment ab initio (SIBFA) model.104,105 In the fluctuating charge model of CT, parameters in eq 2.1.12 model only the CT part. The negative sign of the Mulliken electronegativity, , represents the tendency of an atom to attract electrons in intermolecular CT. The hardness represents the atoms’ resistance to losing electrons in intermolecular CT. There is also a maximum amount of CT for each pair that is dependent on the distance and decays to zero at large separations in order to limit the unphysical low-energy long-range transfer.102,106
2.1.3. ReaxFF Simulations.
ReaxFF is a reactive force field technique for modeling the interactions on the basis of bond orders 107-109 to allow for bond forming and breaking in MD simulations:
| (2.1.17) |
Here, the first, second, and third exponential term determines the single, double, and triple bond order, respectively. The parameters c1…6 and the equilibrium distance rσ, rπ, and rππ have been modeled to agree with corresponding quantum-chemical results at a distance of riβiγ(t) between the atoms β and γ. Angle and torsional potentials depend on the respective bond orders. The Coulomb interaction between two atoms is shielded at shorter distances
| (2.1.18) |
with the shielding parameter siβjγ, which is the arithmetic110 or geometric mean111 of the respective atomic contributions. The time-dependent partial charges qiβ(t) and qjγ(t) are obtained by an electronegativity equilibration scheme as described in section 2.1.1. When the charge flow between molecules is not restricted, the spurious long-range charge transfer occurs in the standard ReaxFF. To minimize this artifact, the atom-condensed Kohn–Sham density functional (ACKS2) charge calculation scheme was developed by adding quadratic energy terms to eq 2.1.2 in order to control the range over which the charge is allowed to delocalize.112 The reference charges were introduced in ACKS2 in order to distinguish between ions, neutral molecules, and to correctly describe limiting charge transfer. In the ACKS2, every atom must have a reference charge and the total charge of an isolated molecule is always equal to the sum of these reference charges. These rules are essential for the correct dissociation limits and linear response properties of ACKS2. In addition, the hardness parameters are dependent on the interatomic distance controlling the change of charge transfer, similar in spirit to the approach by Martinez and co-workers discussed above and shown in Figure 4.
2.2. Classical Drude Oscillator Model
Another technique to allow for a polarizable response of molecules to an electric field is the classical Drude oscillator model, which is also known as the “charge-on-a-spring” or “shell” model.113-115 In contrast to the fluctuating charge model,82,115 the Drude oscillator model does not modify partial charges due to changes in the local electric field during the simulation, but adds additional particles (the oscillators) that mimic physical dipoles on each polarizable atom to model the corresponding distortion of the electron density.
The first particle comprising the dipole is located at the position of the nuclei of the polarizable atom β of molecule i and usually its partial charge, –qD that contributes to the dipole of the atom is merged with the corresponding partial atomic charge qiβ of the polarizable atom. The second, mobile Drude particle or oscillator carries a partial charge of qD and is tethered by a harmonic spring to the atomic nuclei and moves around the polarizable atom as depicted in Figure 5. Because the Drude charges qD are set to negative values, the mobile Drude particle is interpreted as a representation of the electron cloud of the polarizable atom. This picture should not be taken literally because the Drude pair is a simple method to introduce a dipole on each atom that can be handled with the same or similar algorithms for atoms in molecular dynamics simulations, e.g., reaction fields, Ewald summations, and particle mesh Ewald techniques114-117 as only additional charged particles are introduced. Furthermore, QM/MM with polarizable forces are easier to implement with Drude oscillators118 than induced point dipoles. As the Drude particles may point in any direction in three-dimensional space, they are not restricted to the dimensionality of the underlying molecule. For example, the polarizability of a fluctuating charge model of imidazole is more or less restricted to the two-dimensional plane in which the atoms lie. However, as the Drude oscillators may point below and above the imidazole plane, the polarizability is truly three-dimensional. In addition, while recent studies have shown that the Drude oscillator model may be considered equivalent to the induced dipole model,119 it has the advantage that a van der Waals term may be included on the oscillator, thereby offering steric effects associated with distortion of the electron cloud82,120,121
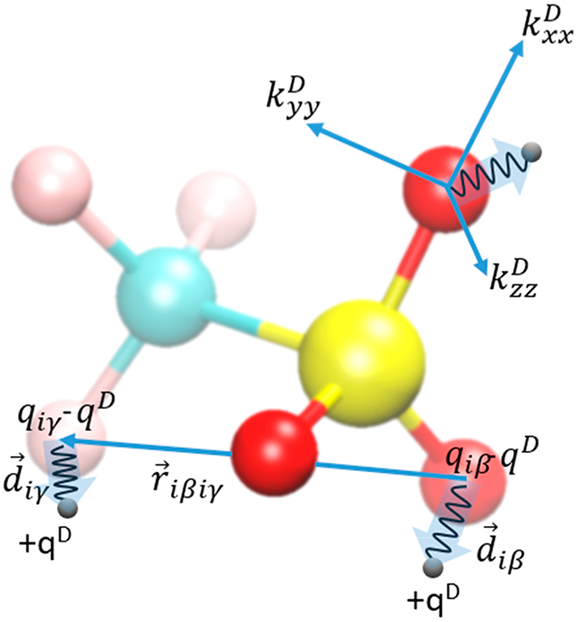
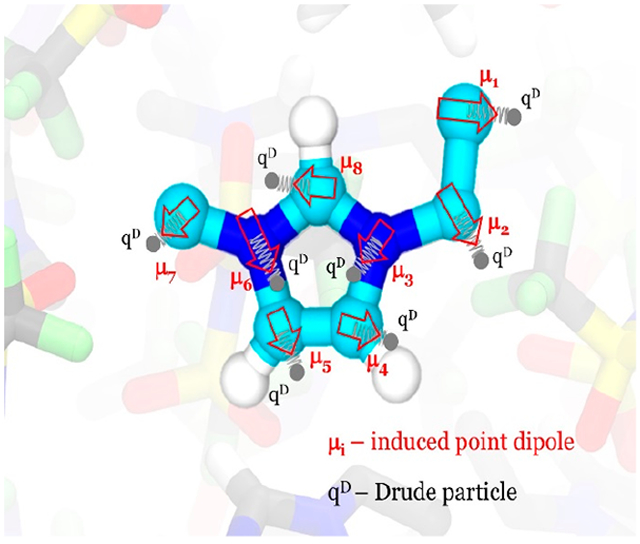
Figure 5.
Sketch of several Drude interactions in OTf. The atomic induced dipole is realized by the atomic nuclei and Drude particle (black circles) having a charge of qD and −qD, respectively. The Drude particle moves around the nucleus tethered by a harmonic spring. The vectors and point in the direction of the respective induced dipoles and . Anisotropic polarization can be introduced by three force constants , , and based on a local coordinate frame.
Each Drude pair results in a physical atomic dipole shown as transparent arrows in Figure 5:
| (2.2.1) |
The displacement of the mobile Drude particle from the position of the polarizable nucleus
| (2.2.2) |
originates from the balance of electrostatic forces characterized by the local electric field and forces of the harmonic spring between the nucleus and Drude particle with the force constant . Usually, these displacements are quite short; in fact, they are largely exaggerated in Figure 5, with typical lengths of less than 0.1 Å.122 A hardwall restraint has been introduced to enforce an upper limit for this distance, e.g., < 0.2 Å,123,124 to prevent instabilities in the simulation from overpolarization of the Drude particles.
In practice, increasing the Drude charge while greatly increasing the force constant lowers the average displacement of the mobile Drude particle to keep the induced dipole almost constant. However, this holds only true for Drude charges > 1.0e as visible in Figure 6 for 1-ethyl-3-methylimidazolium C2mim+.122 Van Gunsteren and co-workers used qD = −8.0e to yield a high force constant on the nucleus–Drude pair, thereby keeping the displacement at a minimum.117 This approach, versus smaller Drude charges and associated force constants, yields physical dipoles that more closely mimic a pure induced dipole model. However, very high values for the Drude charge may cause problems for the dynamics of the mobile Drude particle as discussed below.
Figure 6.
Induced atomic dipoles of several atoms in 1-ethyl-3-methylimidazolium as a function of the Drude charge qD. Blue, orange, gray, and yellow represent −0.5e, −1.0e, −2.0e, and −4.0e, respectively.122
The energy Upol(t) due to polarizable forces consists of three contributions:45,122 The harmonic potentials of the Drude springs
| (2.2.3) |
the Coulombic interaction between the nucleus and Drude particle charges associated with the dipoles on the polarizable atoms (see Figure 5)
| (2.2.4) |
| (2.2.5) |
and the interaction of the Drude pairs with the permanent charges of the nonadjacent atoms jγ
| (2.2.6) |
| (2.2.7) |
The prefactor 4πϵ0 includes the vacuum permittivity of 8.85 × 10−12 As/Vm. The dipole–dipole tensor
| (2.2.8) |
depends on distance vector from the atom β of molecule i to atom γ of molecule j.125 Equations 2.2.5 and (2.2.7) are obtained via Taylor series at small Drude distances and and show that the electrostatic interactions of the Drude pair model resembles those of mathematical induced dipoles described in the next chapter concerning induced point dipoles. Although the last equations suggest a more or less complete analogy between Drude oscillators and induced-point dipoles differing only in technical details, the polarizable model of Drude particles is based on charge–charge interactions and offers additional features, e.g., modeling steric effects of the distortion of the electron cloud by introducing van der Waals interactions with the mobile Drude particle120 or QM/MM mixed approaches126-129
2.2.1. Basic Implementation.
To date, the polarizable classical Drude oscillator model has been implemented in multiple simulation packages including CHARMM,130 DLPOLY,131 ESPResSo,132 GROMACS,123 LAMMPS,133 OPenMM,134 and NAMD.116 These implementations may be performed in various fashions, as described below.
-
All Drude charges are set to a uniform value, i.e., .45,122,135-139 Consequently, the harmonic force constant depends on the isotropic polarizability αiβ of the respective atom β of molecule i:
(2.2.9) High polarizabilities weaken the spring of the respective mobile Drude particle allowing for larger displacements and consequently higher induced dipoles. Figure 6 shows that uniform polarizabilities αiβ and hence uniform for carbons do not necessarily result in comparable induced dipole moment as these dipole depends on the local field which is stronger for C2 and C8 because the anions approach the imidazolium cations from this direction.
-
All force constants for the harmonic Drude spring are set to a uniform value, i.e., .140-142 This implementation offers better control on the simulation time step compared to the first implementation because small polarizabilities in eq 2.2.9 result in huge force constants requiring a smaller time step. Furthermore, in atom-type based force fields, e.g., in CHARMM topology files, all harmonic Drude potentials can be declared by a single line in the force field file. Typical values for kD are 500–1000 kcal mol−1 Å−2.114,140-142 With the force constant fixed, the value of the Drude charges of polarizable atoms dictate the corresponding polarizability
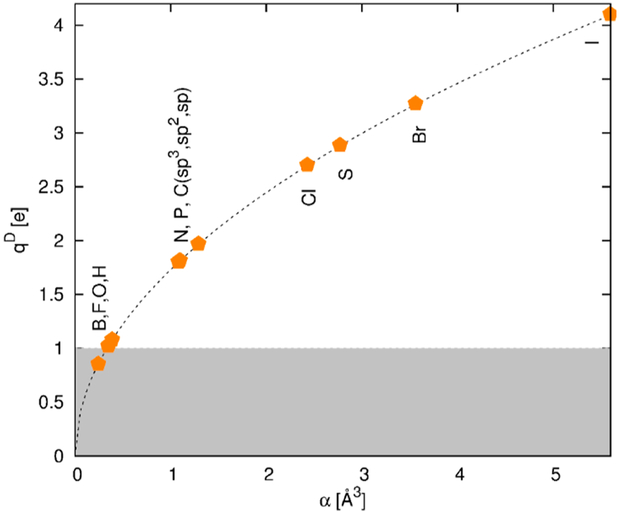
(2.2.10) and are depicted in Figure 7 for common atoms in ionic liquids. A harmonic force constant kD of 1000 kcal mol−1 Å−2 ensures that the Drude charges are above the limit to yield induced dipoles independent of the actual value of . For example, for nitrogens and carbons is approximately 2.0e and hence the induced dipole of those atoms should not vary in the simulations if one increases kD.
In the polarizable, coarse-grained MARTINI force field143,144 two mobile Drude particles carrying opposite charges (q ≅ ±0.46e) are attached to the polarizable atom. The bond length of each mobile Drude particle to the atom is fixed to l = 1.4 Å and the angle between the two bonds is modeled by an harmonic potential (kθ = 4.2 kJ mol−1 rad−2,θeq = 0°). The Coulomb and Lennard-Jones interaction between the two Drude particles are disregarded. Consequently, a zero angle represents the nonpolarized situation. The maximum induced dipole is μind = 2 l qD.
Figure 7.
Drude charge of several polarizable atoms using a harmonic force constant kD of 1000 kcal mol−1 Å−2. Polarizabilities are taken from ref 145.
2.2.2. Dynamics of Drude Particles.
After the movement of all atoms in the simulation at each MD step according to the potentials given in the force field, the positions of the mobile Drude particles are determined by the electric field generated by the remaining atomic dipoles and the permanent charges of the atoms. This corresponds to a relaxation of the electronic degrees of freedom immediately upon any change in the nuclear configuration in analogy to the Born–Oppenheimer approximation. A self-consistent field approach may be applied to find the minimum total electrostatic energy for the Drude particles according to
| (2.2.11) |
for all mobile Drude particles of polarizable atoms β of molecules i.146,147 However, this procedure is computationally demanding due to multiple force evaluations at each minimization step.
As a Car–Parrinello alternative to the SCF minimization, an extended Lagrangian approach was developed by Lamoureux and Roux based on a dual-thermostat approach. The method has been implemented in CHARMM,130 GROMACS,123 LAMMPS,133 OpenMM,134 and NAMD.116 Because of the speedup of computational demands over the SCF methods, the dual-thermostat extended Lagrangian is the standard for MD simulations using the Drude force field.114,123
In the extended Lagrangian approach, the first thermostat keeps the atoms at the desired simulation temperature T. The thermostated forces 114,123,133
| (2.2.12) |
act on the center-of-mass of the atomic nucleus iβ and its corresponding mobile Drude particle. Here, and are the positions of the atomic nucleus and the mobile Drude particle, respectively.
The second thermostat serves to dynamically maintain the nucleus–Drude oscillator at a very low temperature TD ⪡ T
| (2.2.13) |
to a polarization energy Upol(t) close to the SCF value “on the fly”. In practice, each mobile Drude particle is assigned a small mass mD that is subtracted from the mass of the polarizable atom to keep the total atomic mass of the polarizable atom constant. The implementation of the model using a mass mD of 0.4 amu and a force constant on the nucleus–Drude pairs of 500 kcal mol−1 A−2 allows for an integration time step of 1.0 fs in MD simulations.114,124,130,141,148-152 Polarizable simulations of ionic liquids have been carried out with a Drude mass mD of 0.1 amu,45,122,138,139 although using too small values for Drude mass might also affect the integration time step that can be used. Because of the finite mass ascribed to the mobile Drude particles, treating the polarizability of light atoms such as hydrogens using an extended Lagrangian may also encounter some challenges, although this is not an issue if the model is propagated via a SCF approach.
2.3. Induced Point Dipoles
The polarization response of a molecule to an electric field can also be modeled via the induction of atomic point dipoles. In contrast to the Drude oscillators, these induced point dipoles are mathematical dipoles without additional particles having a mass. Hence, in principle, they can be placed anywhere in the molecule. Typically, induced point dipoles are placed at the center of atoms but can also be added to the massless force centers situated off the atomic sites in order to better represent anisotropy and spatial distribution of the polarization response. In the latter case, the forces then are transferred to the basis of three atoms defining the position of the massless center using chain rule differentiation. Induced point dipoles are implemented in AMBER,153 Tinker (Tinker 8, Tinker-OpenMM, and Tinker-HP),154-156 OpenMM,157 CP2K,158 and WMI-MD159 codes.
2.3.1. Interaction of Induced Dipoles with Permanent Charges and Other Dipoles.
In the atomic point dipole model, an induced dipol at the force center i is proportional to the total electric field at this point that is composed of the electric field due to permanent charges and multipoles and a field due to induced dipoles
| (2.3.1) |
The prefactor is a 3 × 3 atomic polarizability tensor. If the polarizability tensor is isotropic (i.e., diagonal and ), it can be replaced by a scalar value αiβ which is one-third of the trace of . Atomic polarizability terms can be straightforwardly included in polarization at both atom and off-atom massless force centers. Anisotropic polarizabilities lead to a torque on the force center that needs to be distributed among the bonded atoms. In practice, models mostly use isotropic polarizabilities but some force fields that actually embody anisotropic dipole polarizabilities enable a more detailed representation of the polarization response. Here we only give an illustration of the polarization equations based on models limited to point charge electrostatics, but it can be extended to the more general case of multipole interactions, leading to more complex equations that have been shown to be fully extended up to periodic boundary conditions in Ewald summations.160,161.
The polarization energy Upol = Uμq + Uμμ + Uself can be decomposed into contributions from the interaction of the induced dipoles with permanent charges (dipole–field interaction, cf Uq,D(t) in eq 2.2.7)
| (2.3.2) |
with other induced dipoles (cf UDD(t) in eq 2.2.5)
| (2.3.3) |
and the self-polarization energy (see eq 2.2.3)
| (2.3.4) |
The interaction energies Uμq(t) and Uμμ(t) stem from the interaction with the external electric field, whereas the last contribution represents the required work to create the induced dipoles82,147,162
Equation 2.3.5 defines a many-body problem for finding the induced dipoles
| (2.3.5) |
as the strength and orientation of the induced dipoles strongly depend on the neighboring induced dipoles connected via the dipole–dipole tensor defined in eq 2.2.8. Consequently, a self-consistent field approach of eq 2.3.5 which minimizes the energy Upol yields the induced dipoles at a given configuration of the system. Equation 2.3.5 can be recast in a matrix form 163
| (2.3.6) |
using the 3N×3N relay matrix R to correlate the induced dipoles with the corresponding electric fields
| (2.3.7) |
of the N atoms. Consequently, the polarization energy Upol is
| (2.3.8) |
Using a variational method, e.g. the iterative atomic multipole optimized energetics for biomolecular simulation (AMOEBA) approach,164 the induced dipoles are obtained by minimizing the residual
| (2.3.9) |
The dominant computational cost is the repeated evaluation of during the self-consistent field computation.
Of course, one way to reduce the computational cost is to use a direct polarization method (iAMOEBA),165 where the coupling (= off diagonal) terms are neglected. This can be rationalized by the fact that the interaction between close induced dipoles will be damped (see section 2.4.3). If the interacting induced dipoles are more distant, the corresponding interaction approaches zero as a function of r−3, making the respective off-diagonal elements in R very small. Hence, the computational bottleneck of the direct method is shifted to the evaluation of the electric fields and their derivatives with respect to the coordinates.165 However, despite the speed gain, for most systems including ionic ones, inclusion of fully converged induced dipoles matter and one would like to stick to the full resolution of the polarization equations. Fortunately, such problems are mathematically well-defined and various high-performance strategies can be then employed to speed up the process. We will discuss these advanced techniques in section 2.4.
To conclude, it is also important to highlight that due to its self-consistent nature, the point dipole model is well-suited for hybrid QM/MM simulations166 where the induced dipoles can be fully coupled to the electronic density, i.e., a full self-consistent relaxation of both the AMOEBA induced dipoles and the DFT electron density at each MD step is then possible allowing for embedded DFT Born–Oppenheimer/AMOEBA simulations.167 In the same spirit, force fields such as AMOEBA can be self-consistently coupled to polarizable solvation methods to perform MD simulations.168
2.3.2. Comparison to Drude Oscillator Model.
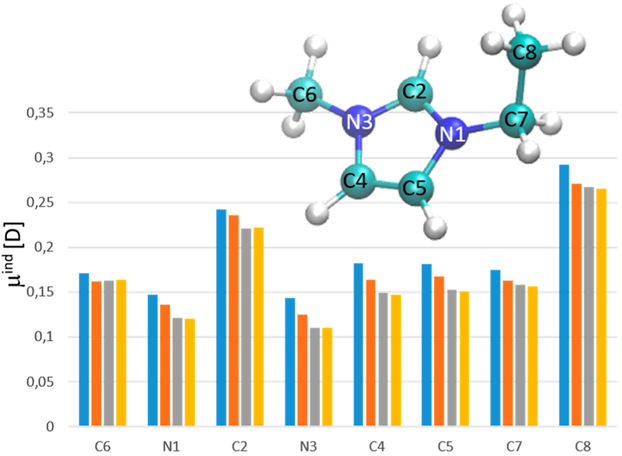
Both the induced point dipole and the Drude oscillator approaches try to model the electronic degrees of freedom by an induced dipole. In a recent publication,135 Schroder and co-workers checked in the case of 1-ethyl-3-methylimidazolium trifluoromethylsulfonate [C2mim][OTf] if both approaches result in similar dynamic properties. This is particularly important as the Drude oscillator approach using the extended Lagrangian does not allow for polarizable hydrogens. Consequently, the effect of merging hydrogen polarizabilities with the polarizability of the atom to which they are attached (implicit H) versus the full atomistic polarizable representation (explicit H) was tested and compared to the induced point dipoles in AMBER.153
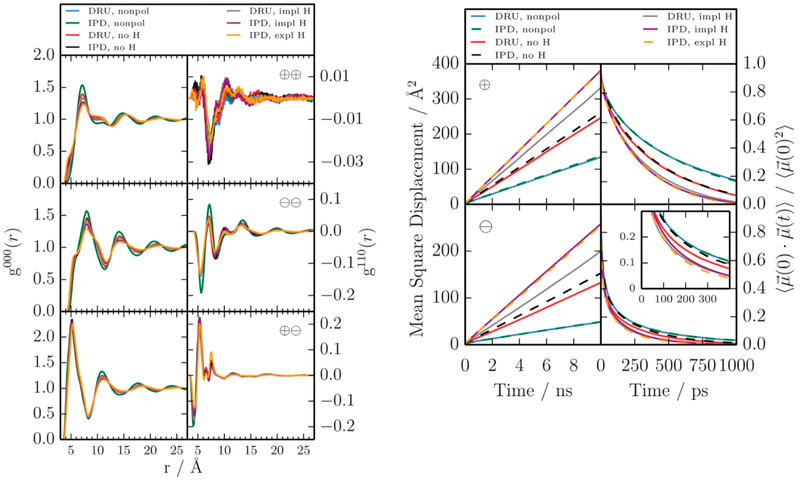
As visible in Figure 8, the radial distribution functions g000(r) and g110(r) for cation–cation, cation–anion, and anion–anion of the implicit (violet) and explicit (orange) hydrogen polarization are in excellent agreement. The radial distribution function g110(r) weights the respective g000(r) with the cosine of the angle between the total molecular dipoles of the species. Negative values (e.g., for the cation–cation orientation) indicate that antiparallel alignment of the dipoles is preferred. However, also for dynamic properties such as the rotational relaxation constant (via the relaxation of the dipole–dipole autocorrelation function) as well as the diffusion coefficients (via the meansquare displacement), the perfect agreement between implicit and explicit hydrogen polarizability using induced point dipoles (IPD) holds. Neglecting the hydrogen polarizability (IPD no H (dashed black line)) in Figure 8 results in lower molecular polarizabilities and hence lower translational and rotational mobility of the ions. Nonpolarizable simulations yield much lower diffusion coefficients and longer rotational relaxation times. Because the force field used in CHARMM (DRU) and in AMBER (IPD) is the same, results from the nonpolarizable simulations coincide (blue and green lines). However, small discrepancies are observed between the polarizable Drude oscillators in CHARMM (DRU no H (red lines)) and induced point dipoles in AMBER (IPD no H (black dashed line)) for the transport properties. This becomes more obvious for the implicit hydrogen polarization (gray and violet lines in Figure 8). This can be due to the different thermostats applied to the polarizable model. In CHARMM, the temperature of the mobile Drude particles was close to 1 K, whereas the induced point dipoles in AMBER showed higher temperatures up to 40 K. The discrepancies between DRU and IPD is more pronounced for the anions which possess atoms with higher polarizabilities, in particular, the sulfur atoms are highly polarizable. For these highly polarizable atoms, the representation of the induced dipole by a pair of charged Drude particles may not be accurate anymore. However, the biggest drawback of nonpolarizable hydrogens in polarizable simulations using Drude oscillators and Lagrangian thermostats can be solved by adding hydrogen polarizabilities to the atoms they are attached to.
Figure 8.
Structure and dynamics of [C2mim][OTf] from nonpolarizable and polarizable simulations using CHARMM (DRU) and AMBER (IPD). Reproduced with permission from ref 135. Copyright 2015 RCS Publishing.
To conclude on such model comparisons, it is worth noting that an automatic strategy allowing mapping of the Drude polarizable force field onto a multipole and induced dipoles model is currently developed to enable the direct use of Drude models into induced dipoles codes.119
2.4. Beyond Induced Dipoles
At this point, the following question can then be raised: are induced dipole models enough to deal with many-body interactions in complex systems? Indeed, one can always try to compare the induction energy values extracted from modern ab initio energy decomposition analysis such as symmetry adapted perturbation theory (SAPT)169 to force field estimates, and as a matter of fact, usually they do not match. This comes from various reasons, the first one being the definition itself of the polarization energy. In ab initio theory, the induction energy is more general than the classical polarization energy obtained from a point dipole approximation. Indeed, such a term appears at second order in a Rayleigh–Schrodinger perturbation expansion of the total intermolecular interactions.125,169 Physically, the induction contribution is the energy of interaction of the permanent multipole moments of one molecule interacting with the induced multipole moments of another. Force field models do approximate the long-range behavior of the induction energy (i.e., the polarization) but usually fail to give a good approximation at the short-range which embodies both charge transfer and other nonclassical effects. Various solutions can be found to overcome such difficulties.
2.4.1. Higher-Order Induced Moments.
As a matter of fact, the long-range, i.e., classical, part of the induction could be modeled by expanding electrostatics to high-rank multipoles to compute accurately permanent electric fields and by using higher-order polarizabilities. Higher-order terms for the polarization computation appear as the induced point dipole model is only the truncation of the total response. Indeed, in practice, if a dipole moment is by far the largest contribution to the response, it is induced along a long series of higher-order electric induced moments by introducing dependence not only to the electric field but also to the field gradients and so on.125 Effects of the higher-order electric induced moments are discussed since the 1960s170 and include dipole–quadrupole, quadrupole–quadrupole polarizabilities as well as the first hyperpolarizability. They have competing effects but lead to a modulation of the final induced dipoles values.170 Over all of these higher-order induced moments, the induced quadrupoles were reported to have the most noticeable effects171 and lead to a non-negligible polarization contribution in the case of metal and heavy metal cations.172 Net benefits of a generalized inclusion of higher-order polarizabilities are yet to be demonstrated in real-life simulations, but accurate approaches offering direct evaluation of such quantities are now available.170,173-175 However, the corresponding quantities are not available in common MD programs.
As a first, cheap remedy to implement anisotropic field gradients in the Drude model, anisotropic polarizabilities can be defined in CHARMM,113,114,176,177 i.e., the induced dipole may point in a different direction than the local electric field :
| (2.4.1) |
| (2.4.2) |
The isotropic force constant is expanded to a 3 × 3 tensor, with zero off-diagonal and the diagonal elements , , and allowing for anisotropic displacement with respect to an intramolecular reference frame located at that atom (see Figure 5). This feature was introduced in CHARMMs Drude 2013 force field to more accurately describe hydrogen-bond acceptors177 and may be in particular valuable for protic ionic liquids. Furthermore, mobile Drude particles are allowed to have Lennard-Jones parameters in CHARMM120 to model the anisotropic van der Waals surface of atoms.
Anisotropic distributed polarizabilities are, by definition, also used in point induced polarizable force field such as the sum of interaction between fragment ab initio (SIBFA).175 When distributed on nonatomic centers such as lone pairs, anisotropic polarizabilities were shown to provide a closer agreement with the ab initio reference data, both in terms of polarization energy and in terms of dipole moment.178
2.4.2. Modeling Short-Range Induction.
As we discussed, point dipole models usually encounter difficulties to model the short-range contribution of induction. Indeed, when molecules overlap, an electron of a donor molecule can be excited into the molecular orbital of another molecule, i.e. the acceptor creates a charge delocalization. Short-range induction effects are easily accessible in the fluctuating charge model (see section 2.1), but are not included in point dipole models. Since the relative importance of short-range inductions differs between variational energy decomposition analysis179,180 and perturbation approaches181,182 such as SAPT, its exact magnitude is still a matter of debate.125 It was furthermore shown that the short-range induction should not be included within classical polarization contribution and should preferably be either incorporated into the pairwise van der Waals contribution or treated explicitly.183 If explicitly taken into account, charge transfer is usually modeled by a simple exponential function184 according to its known exponential decay.125 However, as part of the induction, charge transfer exhibits a many-body behavior105,125 and many-body force field approximations exist in the framework of SIBFA104,105,175 or effective fragment potential (EFP)185 polarizable force fields and are particularly useful for the modeling of metal ions where donation and back-donation become non-negligible contributions175,185
The absence of the Pauli repulsion in the induced dipole model leads to potential polarization catastrophe at the short range. The earlier Drude oscillators and induced dipole models for water tended to overpolarize if the gas phase polarizability was used. This was due to lack of screening resulting in too high dielectric permittivity. A typical solution was to reduce the water model polarizability from 1.44 to 1.04 Å and scaling polarizabilities for other solvents as done in CHARMM. Such adjustments limit overpolarization and allow for the correct treatment of the dielectric constant in the liquid.
2.4.3. Thole Screening Functions.
When molecules closely approach each other, the molecular orbitals overlap and atom-based charge models no longer describe the electrostatic potential adequately.186,187 Quite often, the point-charge model predicts that the electrostatic potential continues to increase/decrease in the immediate vicinity of atoms, while QM calculations clearly indicate that the interaction should taper off or be damped. As a consequence, such inadequate electrostatic potentials often lead to overestimation of the manybody polarization energy at short distances (see eq 2.3.5). This shortcoming could be partially corrected by increasing repulsive interactions between force centers. However, this leads to shifting the energy from the many-body nonadditive polarization response to the two-body additive repulsion terms, thus degrading the description of the potential energy. Four approaches can be applied to improve the modeling of the electrostatic potential and field around a molecule or ion:
Simply add additional charges on off-atom force centers.
Introduce a screening function sk(r) to correct for the penetration energy.163
Add atomic or bond centered dipoles, quadrupoles, etc.
Combine the first two approaches and use screened multipoles such as Gaussian multipoles.186
Bearing analogy to the screening of partial charges, the screening functions between induced dipoles at short distances do not only improve the description of the interaction energies but are necessary to obtain convergence of the self-consistent interative process under certain conditions. The most popular approaches for damping the induced dipole–induced dipole interactions is
to either utilize the screened induced dipoles in conjunction to the distributed charges using Gaussian, Slater charge density distributions,188 or point charges or
to combine Thole screening163,189 with point charges and multipoles. While Thole originally examined numerous scaling functions, the exponential screening of the induced dipoles became the most widely adopted perhaps due to the similarity with Slater orbitals.
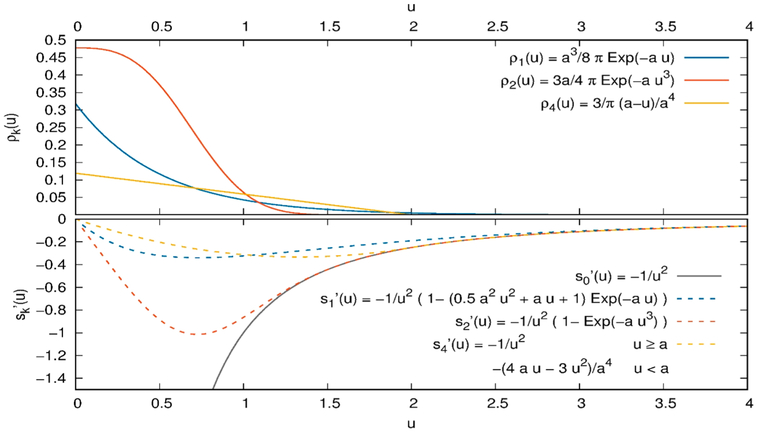
In 1981, Thole163 developed screening functions on the basis of smeared charges of atom iβ
| (2.4.3) |
instead of point charges qiβ using a dimensionless distance and the smearing function ρk(u) (see Figure 9). The first derivative with respect to u of the screening function sk′(u) is
| (2.4.4) |
as depicted in Figure 9. In the following, the vector is defined by . This charge smearing has consequences for the local fields emerging from the charges (see eq 2.3.2)
| (2.4.5) |
and from other induced dipoles (see eq 2.3.3)
| (2.4.6) |
as the corresponding electrostatic interaction tensors115,162
| (2.4.7) |
| (2.4.8) |
are screened by the first and second derivative of the damping function sk(r(t)). Here, is a 3 × 3 unity matrix
Figure 9.
Smearing functions ρk(u) of partial charges and the first derivative of the corresponding damping functions sk′(u). For further details, the reader is referred to refs 163 and 190.
The moderate effect of these functions on structure and dynamics of [C2mim][OTf] was reported in ref 190. The exponential Thole functions s1 and s2 seem to slightly reduce the molecular polarizability by shifting the distances between the ions but keeping mutual positions and orientations. This effect can be reduced for s1 by using a higher default radius a. In fact, the default value is increased from 2.089 in AMBER to 2.600 in CHARMM. More recent versions of the CHARMM Drude model apply an atom-specific s1 value making the term a parameter that my be optimized as part of the parametrization process.191 As not all screening functions sk are available in standard MD programs like TINKER, CHARMM, DLPOLY, GROMACS, and LAMMPS, one may replace them by 1–2, 1–3 exclusions for the interaction of induced dipoles like already used for Coulomb and Lennard-Jones interactions. Here, the induced interaction between atoms connected by bonds and angles are not computed. This prevents an intramolecular “polarization catastrophe,” and the effective molecular polarizability gets close to the sum of all atomic polarizabilities which might not be the case using the shape functions. However, intermolecular induced dipole interactions are not damped by the exclusions. Therefore, one has to be careful during the force field parametrization process as only large enough Lennard-Jones spheres prevent the intermolecular “polarization catastrophe”. However, polarizing the Canongia-Lopes and Padua force field192 as reported in refs 45, 122, 135-138, 190, and 193 caused no problem using the exclusions instead of the Thole screening functions.
2.4.4. Other Polarizability Damping Approaches.
Nonlinear short-range induction effects are linked to orbital overlap, and can be modeled by damping models such as Thole-type models, or can be traced back to the value of the electric field as obtained from point charges or multipole classical approximations. Kunz and van Gunsteren194 suggested an alternative approach by introducing nonlinear effects that would limit the maximum electric field in either Drude or induced dipole models as given by
| (2.4.9) |
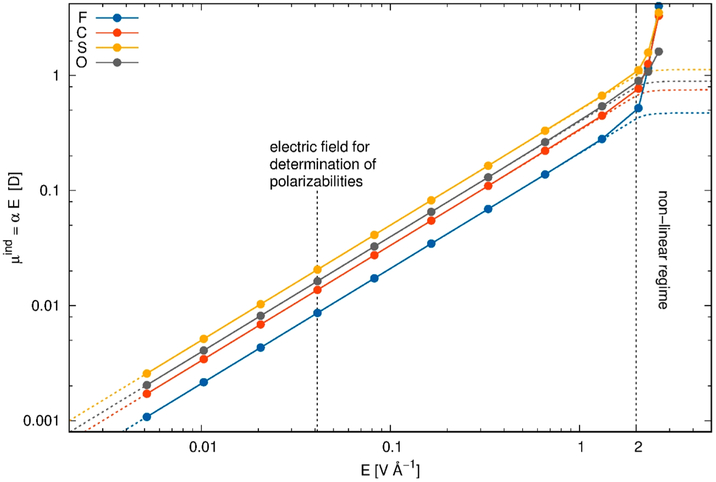
with the adjustable parameters p and E0. Here, α and E are the original polarizability and the electric field, respectively. The corresponding induced dipole of triflate [OTf] as a function of the electric field E is depicted in Figure 10 as dashed lines with p = 8 and E0 = 2 V/Å. At this strong electric field, nonlinear effects are expected.194 AIM (= atoms in molecules) calculations of Schröder and co-workers also show nonlinear behavior beyond 2 V/Å but instead of leveling off with increasing field strength, the polarizabilities diverge. However, the underlying QM calculations start to have convergence problems and hence the actual values at these high field strengths should not be trusted too much. On the other hand, the evaluation of the polarizability αiβ is constant over a large electric field regime. In practice, they determine their polarizabilities at an electric field strength of 0.0008 au = 0.041 V/Å as indicated by the dashed line in Figure 10.195-197
Figure 10.
Atomic polarizabilities of OTf atoms as a function of the applied field. The values were determined via the AIM approach described in the next chapter. Additional details can be found in refs 195, 196.
Discrepancies from the linear behavior can also be modeled by the hyperpolarizability
| (2.4.10) |
In CHARMM,176 additional potentials Uhyper = khyper(d – d0)n may be applied to account for the nonlinear hyperpolarizability effects. Here, d is the distance of the Drude particle from the corresponding polarizable atom. The default value of the “equilibrium distance” d0 is 0.2 Å The potential is only calculated at distances larger than d0. Consequently, the force resulting from this potential is reducing the distance d and thereby weakening the induced dipole μind. The default value for the exponent n is four.
Models such as SIBFA175 or EFP198 also used damping functions of the electric field to maintain a linear regime in the polarization evaluation. Indeed, classical/multipolar electric fields clearly differ from their ab initio counterpart missing some screening effects.199 Such behavior was noticed by Chelli et al.200 They showed that nonlinear effects cannot be simply linked to the lack of hyperpolarization in the polarizable models but depend on the strength of the electric field. In contrast to the linear response at weak fields, strong fields enforce an intramolecular charge redistribution resulting in a nonlinear response. In other words, having some QM description of the fields is important and another strategy evolved starting with the replacement of point charges by Gaussian charges,201 followed by an inclusion of polarizability via atomic dipoles or Drude particles and finally damping electrostatics via Gaussian distributed dipoles and polarizabilities.202,203 Some remarkable manifestation of the importance of screening of the short-range electrostatic and polarization response was that the polarizable model with the Gaussian charges was able to accurately reproduce not only properties of water at ambient temperature but also at liquid vapor equilibrium, while previous attempt to achieve this proved unsuccessful. The developed water model satisfied the water monomer and dimer properties and simultaneously yielded very accurate predictions of dielectric, structural, vapor–liquid equilibria, and transport properties over the entire fluid range.201 Beyond this first-generation Gaussian model, more evolved models fitting the electron density itself appeared. On the basis of Hermite Gaussians204,205 (or Slater-type functions206) that are closely related to distributed multipoles, they reproduce very accurately reference ab initio surfaces by enabling an extremely precise density-based evaluation of other contributions such as electrostatic (including penetration effects) exchange repulsion. The extension to particle Mesh Ewald of Hermite Gaussian treatment205 make such models available in molecular dynamics.207 Although still in development,208 such methods are able to reproduce quasi-exact quantum permanent electric fields in standard QM quality.199 They recently allowed to understand a little bit further the dual level of nonlinear effects discussed by Chelli et al.200 It was reported by Piquemal and co-workers,199 that in the case of high electric fields generated by metal cations, high-level Gaussian models were not able to fully recover the ab initio polarization but still required some damping function. In other words, Gaussian electrostatics (exact electric fields) can deal with the linear regime discussed by Chelli but necessitates damping or Gaussian dipole screening to recover the second intramolecular nonlinear effect which can be traced back to exchange-polarization effects199 due to the neglect of Pauli repulsion. Such observations led recently to simple modifications of the Thole model.209 In the new framework, the Thole parameter for the direct (permanent) field was chosen to be different from the current Thole damping value used for the mutual induction, which leads to a significant improvement of results by separating the two nonlinear effects.
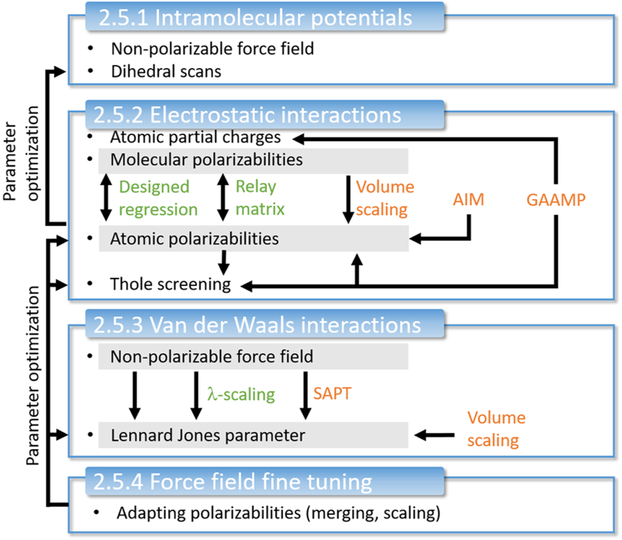
2.5. Parametrization of Polarizable Force Fields
A suitable force field model balances the needed accuracy, computational costs, transferability of parameters, and available software supporting particular potentials. Simple models that are readily available in simulation packages often dominate until the community learns about their drawbacks promoting more accurate but often computationally more expensive models to be implemented in common MD codes. For example, water models progressed from simple three site to 4, 5, and 6 sites and/or multipoles,210 or Gaussian screened charges211 in order to improve the description of the electrostatic potential followed by the inclusion of polarizability via induced point dipoles or Drude particles. Further improvements included damped electrostatics using Gaussian distributed dipoles and polarizabilities.202,203 More sophisticated polarizable models such as SIBFA or EFP are now fast enough to be applied to ionic liquids.212 Also, multipolar models originating from the biological applications, such as AMOEBA, propose new parametrizations.213-215 An extended discussion on force field parametrization is out of the scope of this review. Hence, we will focus primarily on the parametrization of electrostatic interaction parameters, e.g., partial charges and polarizabilities, which should be most important for modeling ions, and their balance with the corresponding van der Waals parameters.
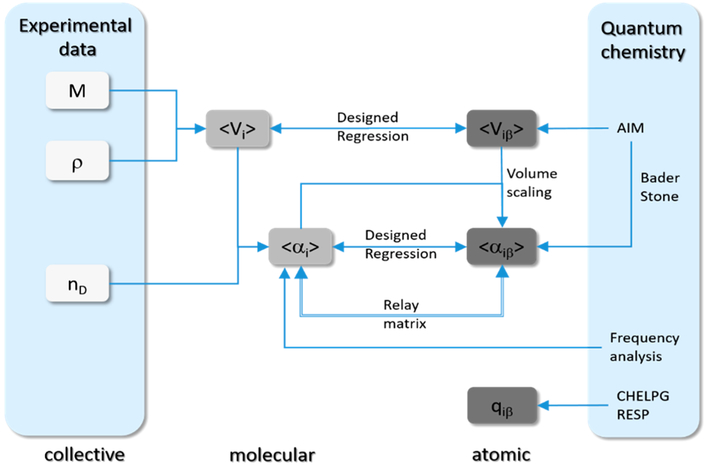
One approach to develop polarizable force fields (e.g., for ILs) is to use the existing nonpolarizable force fields as a starting point for the parametrization as depicted in Figure 11. Molecular polarizabilities αi can be deduced from experimental refractive indices nD or calculated quantum mechanically. However, the decomposition into atomic polarizabilities αiβ is not straightforward. Section 2.5.2 describes statistical approaches (shown in green in Figure 11) as well as QM procedures (shown in orange) to get atomic αiβ values. Some of these methods (relay matrix optimizations and the electrostatic grid-based approach216) already include the Thole screening functions (see section 2.4.3).163,189,190,217,218 After addition of the atomic polarizabilities, the intramolecular potentials have to be readjusted because the induced dipoles may affect internal torsions as well as the intramolecular geometries and general vibrational properties.
Figure 11.
Schematic illustration of the protocol for polarizable force field parametrization for ionic liquids.
Importantly, induced polarization has a direct impact on intermolecular interactions. Because nonpolarizable force fields already include average dispersion between the molecules, existing Lennard-Jones parameters need to be reparametrized. The protocol for this optimization is described in section 2.5.3. Finally, condensed phase MD simulations are performed to fine-tune and validate the parameters of the force field assembled according to the above procedure. Depending on the agreement with experimental data and the computational setup, a number of parameters may be slightly adjusted to fine-tune the force field following the protocol summarized in section 2.5.4. Please note that the approach illustrated in Figure 11 practically relies on the assumption that an existing nonpolarizable force field is a good starting point, which is not necessarily the case, even if the simulations using a nonpolarizable force field were tuned to accurately describe some specific properties of the system of interest. There is no guarantee that in the original empirical adjustment of the nonpolarizable force field the approximation of average polarization effects has been uniformly distributed into van der Waals interactions and no artificial imbalance of repulsion–dispersion interactions has been introduced. Thus, it is generally better to start development of the repulsion–dispersion interactions for the polarizable force field from scratch by fitting quantum chemistry data and experimental measurement for density, heats of vaporization, and solvation energies to improve the force field transferability.
2.5.1. Intramolecular Potentials.
In contrast to simple atomic ions like halides, ILs are charged molecules. Consequently, care must be taken to optimize the intramolecular parameters to accurately treat the geometries, vibrational properties, and relative conformational energies. The geometries are strongly influenced by the bond and angle equilibrium parameters and dihedral multiplicities and phase shifts, while the vibrations are governed by the force constants. The conformational energies are dominated by the dihedral parameters. Importantly, it must be remembered that the intramolecular parameters, especially the dihedral force constants, are coupled with the nonbonded parameters. Accordingly, when any parameter of a force field is changed, it is necessary to check all aspects of the model with respect to reproduction of the target data, with additional optimizations performed as required. Generally, such an approach requires only one to two iterations, especially when the initial guess parameters are of high quality such as those from the Canongia-Lopes et al. force field (from OPLS),192 CGenFF,219,220 or APPLE&P.44
As intramolecular parameter optimization procedures have been described in detail elsewhere,114,221 we only present them briefly here. Equilibrium, multiplicity, and phase term optimization typically targets QM geometries obtained at the MP2/6-31G(d) or higher level chemistry. When available, information from experimental data, such as microwave spectra and crystal structures, may be used as target data. When using crystal structures, ideally the geometries are obtained from MD simulations of the molecule in the crystal environment at the experimental temperature. A nice alternative is the use of crystal survey data that can be taken advantage of when large numbers of structures containing the molecular connectivity of interest are available. Force constants are optimized by targeting QM vibrational spectra, although experimental spectra may be used when available. When performing such optimizations, it is important to reproduce the contribution of the intramolecular degrees of freedom to the individual frequencies (i.e., the potential energy distribution) and apply the appropriate scale factor for the QM frequencies associated with the model chemistry used.222,223 Targeting of the vibrations is used to optimize the bond and angle force constants as well as those of nonrotatable dihedrals and dihedrals terminated with hydrogens, excluding those terminated by hydroxyl or sulfhydryl groups. Optimization of dihedral force constants along with the determination of correct multiplicities are usually performed on the basis of QM potential energy scans. QM potential energy surfaces are typically calculated using electron correlation (e.g., MP2/6-31G(d) optimized geometries with single point energies at the MP2/aug-cc-pVTZ or MP2/cc-pVQZ model chemistry). Accurate treatment of the dihedral parameters of rotatable bonds is quite important for obtaining the correct conformational energies, although all the intramolecular terms contribute. Indeed, accurate optimization of the intramolecular parameters is essential to ensure proper treatment of the intramolecular distortions molecules undergo during MD simulations.
2.5.2. Electrostatic Interactions.
In addition to the permanent charges qiβ already present in nonpolarizable MD force fields (an excellent review is given by Holm and co-workers48), atomic polarizabilities αiβ are responsible for the strength of the induced dipoles emerging from the local electric fields at the position of the atom β of molecule i. In a first attempt to optimize these parameters, one may use the corresponding polarizabilities αiβ reported for neutral molecules.189,224-227 However, it is typically preferable to derive new parameters for both neutral and ionic species, either from experimental data or QM calculations as depicted in Figure 12.
Figure 12.
Schematic illustration of pathways from experimental data or quantum chemical calculations to atomic polarizabilities and volumes.
Further optimization and validation of electrostatic parameters can take advantage of a range of condensed phase experimental data. This general philosophy of exploiting experimental data to empirically improve the model has been applied successfully to optimize the van der Waals parameters in the case of additive nonpolarizable force fields.228 On the basis of a large database of experimental densities ρ and refractive indices nD of a range of structurally diverse ILs averaged molecular volumes 〈Vi〉 and molecular polarizabilities 〈αi〉 of the cations and anions can be determined assuming no particular correlation between the molecules (see Figure 12).145,229 As the molecular composition of the ion pairs is known, a “designed regression”-analysis yields atomic volumes 〈Viβ〉 and polarizabilities 〈αiβ〉 of each chemical element involved, assuming again that there is no particular correlation between the atoms with respect to these properties. These atomic values can be used to predict molecular polarizabilities of ion pairs which were not part of the initial database. Notably, these predictions match QM calculations at the MP2/aug-cc-pVTZ level229,230 despite the crude approximations made. Furthermore, the predicted density can be used as a starting point for the simulation box length in a constant pressure equilibration run. In addition, this approach is superior compared to classical quantitative structure–property relationship models231 as physically meaningful descriptors are used in the designed regression approach without losing accuracy in the predicted refractive indices.
As each chemical element was assigned an averaged atomic polarizability and volume, it does not matter if this atom is part of the anion or cation. Also, the position of methyl groups within the cations depicted in Figure 13 does not change the predicted results as the composition stays the same. However, the predicted refractive indices nD and mass densities ρ agree very well with all experimental values with a maximum deviation of 0.2% and 2%, respectively.
Figure 13.
Prediction of the density and refractive index based on the designed regression values for atomic polarizabilities and volumes229 matches quite well the experimental values of various imidazolium NTf2 based ionic liquids with the same molecular formula.
The biggest discrepancy to experimental refractive indices is found for dicyanamide based ILs.229 This is due to the sp hybridization state of the carbon and nitrogen of the cyano-groups. During the designed regression analysis in ref 229, all carbons were treated the same way irrespective of the hybridization state. Because in ionic liquids most nitrogens are sp2 hybridized in the imidazolium rings and carbons are sp2 for the aromatic rings or sp3 for the aliphatic chains, the different electronic environments for triple bonded carbons and nitrogens are not well represented. In a subsequent paper,145 the hybridization state of the carbons was explicitly taken into account, resulting in much better predictions for dicyanamide based ILs. Originally, the hybridization state of nitrogens and oxygens was also incorporated. The results did not improve very much, and it was very difficult to assign the correct hybridization state based on the chemical formula for some compounds. For example, sp2 and sp3 hybridization state of nitrogen had to be detected sometimes by planar or tetrahedral configurations obtained from QM calculations. However, if one has to perform these calculations, the additional effort to determine the atomic polarizabilities, e.g., by means of AIM models (see below), is negligible.
The resulting atomic polarizabilities of ref 145 do not differ substantially from values derived from noncharged species189,218,224,225 and are depicted in Table 1. The polarizability of bromine and iodine in Table 1 was obtained from the refractive index and density of imidazolium-based ionic liquids containing mixed polyhalides using the atomic polarizabilities of ref 145 for the nonhalide atoms.
Table 1.
Designed Regression, Relay Matrix, and AIM Values for Atomic Polarizabilities and Volumes of Atoms in Ionic Liquid145,195,196,218,a
| designed regression |
relay matrix |
AIM |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| ⟨αiβ⟩ |
αiβ(s1) |
αiβ(s2) |
⟨αiβ⟩ |
||||||
| atom | ⟨Viβ⟩ | cation | anion | cation | anion | cation | anion | cation | anion |
| H | 5.91 | 0.389 | 0.389 | 0.257 | 0.641 | 0.444 | 0.829 | 0.323 | 0.323 |
| B | 18.15 | 0.243 | 1.461 | 0.666 | 1.085 | 0.434 | 0.578 | ||
| C(sp3) | 15.84 | 1.081 | 1.081 | 1.427 | 1.461 | 1.152 | 1.126 | 1.016 | 1.016 |
| C(sp2) | 15.27 | 1.290 | 1.290 | 1.427 | 1.461 | 1.152 | 1.126 | 1.122 | 1.432 |
| C(sp) | 20.04 | 1.192 | 1.192 | 1.427 | 1.461 | 1.152 | 1.126 | 1.587 | 1.587 |
| N | 14.35 | 1.085 | 1.085 | 1.051 | 1.749 | 0.917 | 2.305 | 1.208 | 1.698 |
| O | 9.28 | 0.354 | 0.354 | 0.372 | 0.597 | 0.331 | 0.669 | 1.144 | 1.144 |
| P | 22.99 | 1.098 | 1.098 | 2.660 | 1.772 | 1.750 | 0.965 | 1.237 | 1.237 |
| S | 37.28 | 2.771 | 3.223 | 2.863 | 2.703 | 2.380 | 1.553 | ||
| F | 13.26 | 0.346 | 0.163 | 0.142 | 0.256 | 0.247 | 0.625 | ||
| Cl | 40.00 | 2.424 | 2.231 | 3.241 | 2.138 | 2.903 | 2.43 | ||
| Br | 32.84 | 3.441 | 3.334 | 4.471 | 3.096 | 4.161 | 4.03 | ||
| I | 58.38 | 5.596 | 3.80 | 7.95 | |||||
All values are in Å3. The Thole screening functions s1 and s2 are discussed in section 2.4.3.
On the basis of the 〈αiβ〉 in Table 1, molecular polarizabilities αi and volumes Vi for several classes of ionic liquids can be computed. The resulting values agree quite well with the corresponding experimental values as shown in Figure 14. The lines represent the prediction from the designed regression with different alkyl chain length n. The symbols correspond to the respective experimental values.
Figure 14.
Juxtaposition of experimental (symbols) and designed regression (lines) of molecular polarizabilities and molecular volumes.
Strictly speaking, the designed regression analysis is performed for an ion pair and not the individual molecular ions. The molecular polarizabilities of the cations and anions obtained from the designed regression analysis show a shift with respect to those obtained from MP2/aug-cc-pVDZ calculations. Regardless of the chemical nature of the respective ion, designed regression molecular polarizabilities have an average shift of +1.82 Å3 and – 1.92 Å3 for the cations and anions, respectively, which can be explained by the model of the polarizability of the excess electron αe = 1.87 Å3:145
| (2.5.1) |
In a first attempt, this excess polarizability or its lack is distributed equally over the corresponding atoms of the molecule
| (2.5.2) |
Taking αe into account, the atomic polarizability of sp3 carbons differs if they are part of an anion or cation. In the latter case, the polarizability is slightly less. The polarizability of sp3 carbon also decreases comparing C8mim and C2mim due to the respective number of atoms.
As observed in Figure 14, the polarizability seems to be a linear function of the respective volume. Consequently, Uhlig et al.232,233 decomposed the molecular polarizability αi into bead contributions αiβ
| (2.5.3) |
of a coarse-grained model of [Cnmim][PF6]. The bead volumes were obtained from a Bader’s atoms-in-molecules (AIM) analysis234,235 of single ions or ion pairs. These AIM volumes differ from those Viβ computed by designed regression as only intramolecular space is attributed to the atoms. In contrast, the designed regression values contain also space between the ions in the liquid phase. As a consequence, the linear correlation between the atomic polarizability and atomic volume in eq 2.5.3 may be violated.196
So far, no interaction between the induced dipoles is assumed. However, the local electric field of atom iβ also contains a contribution from all other atoms jγ as shown in eq 2.3.5 connected via the distant-dependent dipole–dipole tensor . The inverse of the relay matrix R in eq 2.3.6 consists of N2 3 × 3 submatrices, which have to be summed up to get the molecular polarizability tensor αi
| (2.5.4) |
using the index a and b for the corresponding x-, y-, and z-components. A third of the trace of the polarizability tensor in eq 2.5.4 yields the molecular polarizability which can be compared to the experimental values. Gu and Yan218 used the geometries of 158 different cations and 75 different ionic liquids anions to determine averaged atomic polarizabilities for the chemical elements depicted in Table 1. Again, the net charge of the molecule has an impact on the atomic polarizabilities αiβ. Hydrogens, nitrogens, oxygens, chlorines, and bromines follow the expected trend and have higher average polarizabilities in the anions. However, boron and phosphorus show the opposite behavior.
The statistical approaches described so far rely on experimental data (see Figure 12). In principle, QM calculations of the molecular polarizability are readily performed230,236 and use Stark’s relation
| (2.5.5) |
which links the energy U to an applied external electric field . The subscripts a and b denote the x-, y-, and z-directions. Either the second derivative of U or the first derivative of the dipole moment μ with respect to the electric field yields the components of the polarizability tensor
| (2.5.6) |
The average molecular polarizability αi is defined as the third of the trace of the polarizability tensor. The total molecular dipole moment μ can be evaluated relative to an arbitrary reference point. However, for charged molecules i, it turned out that the center of mass is an appropriate choice as a reference site.237,238 Hence, the molecular dipole moment reads
| (2.5.7) |
where Ziβ is the nuclear charge of the atom β at the nuclear position and ρ(r) is the electron density. Following an AIM approach,195,234,239 nonoverlapping atomic integration basins Ωiβ can be defined for each atom iβ as shown in Figure 15. The decomposition of the molecular dipole moment into atomic contributions is then realized via atomic charges qiβ and atomic dipoles:
| (2.5.8) |
Figure 15.
(left) AIM analysis of local dipole moments and to compute atomic polarizabilities αiβ. (right) Bond charge model of 1,1-dimethylimidazolium. The transparent spheres sketch the atomic integration basins Ω of the corresponding atoms. The bond charges are located midway between the respective atoms where the bond changes its color.
The atomic charge qiβ includes the nuclear charge and some localized surrounding electron density. Consequently, describes the charge contribution to the dipole moment. Within the atomic basin Ωiβ, the electron density can polarize and contribute to an atomic polarizable dipole moment . Applying an external electric field E perturbs the charge distribution of the molecule. The electron density can be transferred from one atom to another, giving rise to . The electron density around an atomic site also responds to changing the polarization within the atomic basins ΔΩiβ and giving rise to .195,234,239
To make the calculation of the polarizability (see eq 2.5.6) independent of the origin, the charge distribution contributing to the dipole moment can be converted to a sum of surrounding bond charges bβγ
| (2.5.9) |
For example, the partial charge of the C2 atom in Figure 15 equals the sum of the bond charges qC2 = bC2,H2 + bC2,N1 + bC2,N3. Because these bond charges describe directed contributions, the reversal of β and γ leads to a change in the sign of the bond charge
| (2.5.10) |
which resembles the charge restraining condition in eq 2.1.7. Furthermore, bond charges within ring structures add up to zero, bC2,N1 + bN1,C5 + bC5,C4 + bC4,N3 + bN3,C2 = 0 in Figure 15. To determine the bβγ values, a nonunique set is chosen where γ > β fulfill eq 2.5.9 for each atom in the molecule.195 As hydrogens are connected to other atoms via a single bond, the respective bond charges are set to the value of the partial charge of the hydrogen, bH,γ = qH. Finding the best solution for the bond charges yields atomic contributions to the charge term in eq 2.5.8
| (2.5.11) |
with the position of the bond charge midway between the atoms, . The partial charges qiβ and polarizable part of the atomic dipole moment can be obtained from the GDMA code of Misquitta and Stone.173,240 Applying a small external electric field in +a and −a direction with a ∈ {x,y,z} yields the corresponding element of the polarizability tensor 195,241
| (2.5.12) |
| (2.5.13) |
The average atomic polarizability for [C2mim][OTf] and [C2mim][N(CN)2] is depicted in Table 2 using M06-2X/Sadlej pVTZ for the QM calculation and an electric field strength of 0.0008 au = 0.041 V/Å. The agreement with the corresponding designed regression values is quite reasonable (taking into account that different functionals/basis sets alter the results slightly) for the sulfur and oxygen in the triflate and the carbons in the dicyanamide, with an exception being the acidic H2 of the imidazolium ring. This indicates that the averaged designed regression values do not completely resemble the current situation of the ionic liquid. In the case of imidazolium H2, the acidity and hydrogen bond capability are known to be enhanced compared to H4 or H5. The electron density of triflate in the bond charge model and consequently its ease to be distorted shifts from the sulfur to the oxygens. In the case of the dicyanamide, the shift is from the carbons to the nitrogens.
Table 2.
Atomic Polarizabilities from Designed Regression,145 AIM,196 and GAAMP140,216 Calculations for [C2mim][OTf] and [C2mim][N(CN2)2]
| AIM |
GAAMP |
||||||
|---|---|---|---|---|---|---|---|
| atom | designed regression |
[C2mim] [OTf] |
[C2mim] [N(CN)2] |
[C2mim] [OTf] |
[C2mim] [N(CN)2] |
||
| ⟨αiβ⟩ [Å3] | αiβ from eq 2.5.2 [Å3] | ⟨αiβ⟩ [Å3] | ⟨αiβ⟩ [Å3] | ⟨αiβ⟩ [Å3] | ⟨αiβ⟩ [Å3] | ||
| C2mim | C6 | 1.08 | 0.98 | 0.82 | 0.86 | 2.03 | 2.03 |
| H61 | 0.39 | 0.29 | 0.26 | 0.27 | |||
| H62 | 0.39 | 0.29 | 0.26 | 0.27 | |||
| H63 | 0.39 | 0.29 | 0.26 | 0.27 | |||
| N1 | 1.09 | 0.99 | 1.20 | 1.17 | 0.90 | 0.90 | |
| C2 | 1.29 | 1.19 | 1.03 | 1.06 | 1.53 | 1.53 | |
| H2 | 0.39 | 0.29 | 0.66 | 0.76 | |||
| N3 | 1.09 | 0.99 | 1.04 | 1.07 | 0.90 | 0.90 | |
| C4 | 1.29 | 1.19 | 1.11 | 1.08 | 1.56 | 1.56 | |
| H4 | 0.39 | 0.29 | 0.31 | 0.29 | |||
| C5 | 1.29 | 1.19 | 1.06 | 1.29 | 1.56 | 1.56 | |
| H5 | 0.39 | 0.29 | 0.31 | 0.29 | |||
| C7 | 1.08 | 0.98 | 1.02 | 1.03 | 1.68 | 1.68 | |
| H71 | 0.39 | 0.29 | 0.31 | 0.39 | |||
| H72 | 0.39 | 0.29 | 0.31 | 0.39 | |||
| C8 | 1.08 | 0.98 | 0.83 | 0.89 | 2.05 | 2.05 | |
| H81 | 0.39 | 0.29 | 0.27 | 0.30 | |||
| H82 | 0.39 | 0.29 | 0.27 | 0.30 | |||
| H83 | 0.39 | 0.29 | 0.27 | 0.30 | |||
| OTf | C1 | 1.08 | 1.31 | 0.97 | 1.23 | ||
| F11 | 0.35 | 0.58 | 0.56 | 0.3 | |||
| F12 | 0.35 | 0.58 | 0.56 | 0.3 | |||
| F13 | 0.35 | 0.58 | 0.56 | 0.3 | |||
| S2 | 2.77 | 3.00 | 2.36 | 2.66 | |||
| O21 | 0.35 | 0.59 | 1.03 | 0.27 | |||
| O22 | 0.35 | 0.59 | 1.03 | 0.27 | |||
| O23 | 0.35 | 0.59 | 1.03 | 0.27 | |||
| N(CN)2− | N1 | 1.09 | 1.46 | 1.69 | 0.98 | ||
| C2 | 1.19 | 1.56 | 1.37 | 1.04 | |||
| N3 | 1.09 | 1.46 | 1.69 | 1.79 | |||
| C4 | 1.19 | 1.56 | 1.37 | 1.04 | |||
| N5 | 1.09 | 1.46 | 1.69 | 0.98 | |||
Atomic polarizabilities αiβ (gained by the AIM approach described above) and partial charges qiβ derived from RESP calculations of several thousand molecules were also used to train a linear increment scheme as well as a neural net.242 On the basis of these data, fast prediction of qiβ and αiβ with average errors of <0.02e/0.03 Å3 and <0.07e/0.07 Å3 are possible using the neural net and linear increment system, respectively. This method to determine the electrostatic parameters may be handy for large molecules where QM calculations might be too expensive computationally.
However, for small molecules, atomic polarizabilities αiβ, corresponding Thole screening parameters and atomic charges qiβ can be optimized in the standard CHARMM procedure on the basis of a QM calculation of the electrostatic potential (ESP). To determine αiβ, a test charge was placed on various positions of a grid and a series of perturbed ESPs is generated for each charge location around the molecule and the electrostatic parameters were optimized to reproduce the perturbed ESPs.243 This procedure was implemented by Roux and co-worker216,244 in a general force field generation tool general automated atomic model parametrization (GAAMP) and was used during APPLE&P force field parametrization for battery electrolytes.44,245,246 Here, this procedure was followed to determine qiβ, polarizabilities αiβ, and the corresponding Thole screening parameters (s2) to reproduce the perturbed ESPs, with the restraints included to prevent nonphysical values. The resulting atomic polarizabilities are depicted in Table 1 and differ slightly from those values obtained from designed regression145 and the AIM196 analysis in the case of the cations. However, terminal oxygens and fluorine in trifluoromethylsulfonate have significant lower polarizabilities as well as the terminal nitrogens of the dicyanamide anion.
2.5.3. van der Waals Interactions.
Nonpolarizable force fields already contain Lennard-Jones parameters characterizing the exchange repulsion and dispersion of the molecules. Simply adding induced dipoles to these force fields results in an overestimation of the attraction between the molecules.122,136-138,190 This leads to a significant increase in density for polar neutral solvents, like methanol and N-methylacetamide (NMA), and a moderate increase for various ionic liquids as visible in Figure 16. This was also observed for other ionic liquids.52
Figure 16.
Increase in simulation predicted density when switching on induced dipoles in various solvents using the Canongia-Lopes force field.192
Apolar liquids, e.g., hydrocarbons, do not show an increase in density because the partial charges on the atoms of hydrocarbons are low and consequently the local electric field is negligible. Hence, the induced dipoles in these systems are weak (see eq 2.5.5). In contrast to polar, neutral liquids, the attraction in ionic liquid is dominated by Coulomb interactions between the cations and anions. Although the strong induced dipoles increase the density in these ionic liquid systems, the effect is counteracted by a reduction of the electrostatic interactions as the partial charges are now immersed in an “inner solvent”45,61,62,190 of the induced dipoles with an effective dielectric constant ϵ∞
| (2.5.14) |
This reduction in Coulomb interaction is stronger for the ionic liquids compared to the neutral polar solvents and consequently the increase in density is weaker.
For the design of a polarizable force field, several strategies have evolved:
All Lennard-Jones parameters are reparametrized after adding the polarizable forces to the simulation.
The ratio between the interaction of the induced dipoles and dispersion can be determined by DFT calculations using symmetry-adapted perturbation theory.247 As shown in Table 3, dispersion entirely dominates the interaction between hydrocarbons,248 whereas the contribution of the induced dipoles become almost an equal partner in case of the interaction between the ions. The two values for the NTf2-anion discriminate between the oxygens or the fluorine of the NTf2 being closest to the hydrocarbon.
-
The Lennard-Jones parameter are not reparametrized individually but scaled according to the polarizability of the corresponding atom iβ:140,233,249
(2.5.15) Here, αmax is the highest atomic polarizability in the system and Δα is the difference between αmax and the polarizability of the current atom αiβ. The scaling parameter λ varies between zero (disregarding εiβ for the atom with the highest polarizability) and one (no scaling at all). It can be determined by comparison of computational and experimental data of the mass density and conductivity.140
-
The molecular dispersion coefficients C6 can also be determined via the isotropic dynamic polarizabilities232,250
(2.5.16) and then scaled to the atomic property by the respective volumes:232,251,252
Table 3.
Ratio Udisp/(Udisp + Uind) between Dispersion and Interaction of Induced Dipoles247
| C4H10 | C2C1im | Pyr11 | |
|---|---|---|---|
| C4H10 | 0.94 | ||
| C2C1im | 0.76 | ||
| Pyr11 | 0.67 | ||
| N(CN)2 | 0.69 | 0.61 | |
| NTf2 | 0.71/0.77 | 0.65 | 0.54 |
| (2.5.17) |
Another possibility to obtain C6 coefficients is from maximally localized Wannier functions.253
A choice of combining rules for the repulsion–dispersion interactions is also important but is often hard to assess due to the presence of electrostatic and polarizable interactions in polar or charged molecules. Therefore, simulations of noble gases and mixtures of relatively uncharged hydrocarbon molecules can be good candidates for the evaluation of combining rules. In noble gases, standard arithmetic and geometric combining rules perform poorly.254 Combining rules used in the OPLS-AA force field fail to predict the enthalpy and volume of mixing for n-alkanes and fluoroalkanes while modified Waldman–Hagler combining rules for the repulsion–dispersion parameters used in APPLE&P accurately predict these mixing properties. Therefore, the application of the Waldman–Hagler combining rules in simulations of ionic system should provide an accurate description of the fluorinated and nonfluorinated parts of solvents and anions that are of high interest in battery electrolytes.255 The repulsion–dispersion parameters in polarizable force fields are quite transferable. For example, in the APPLE&P,47 only one set of oxygen, hydrogen, and carbon repulsion–dispersion parameters is used with a minor exception of slightly different parameters for the terminal methyl group. Yet the densities and heat of vaporization were accurately predicted for more than 30 common ILs, a wide range of solvents (alkanes, fluoroalkanes, ethers, carbonates, sulfones, phosphates), and a wide range of electrolytes from low to high salt concentrations indicating good transferability of a selected set of repulsion–dispersion parameters and combining rules44,256-261
2.5.4. Fine Tuning.
To improve the computational efficiency, polarizable Drude MD simulations are propagated using a dual-thermostat extended Lagrangian approach to approximate the time-consuming self-consistent field calculations of the induced dipoles.130 The approach involves assigning all Drude particles a mass of 0.4 amu which is subtracted from the mass of the respective polarizable atom. Hydrogens are not polarizable in these Drude-MD simulations to reduce the number of Drude particles. In principle, it is possible to polarize the hydrogens as well using Drudes, although this requires a recalibration of the Drude mass within the extended Lagrangian approach. Alternatively, it could be propagated via slow self-consistent field optimization of the Drude particles.146
As the dynamics of the ionic liquids depend on the molecular polarizability,45,135 neglecting all hydrogen polarizability can be disadvantageous, in particular for cations with long alkyl chains. A possible byway is the merging of the hydrogen polarizability with the polarizability of the atom to which they are attached to.45,122,135,137,138,140,190 Alternatively, the GAAMP procedure216,243 is able to assign an Åiβ to these non-hydrogen atoms to reproduce the ESPs without the need to polarize the hydrogens as well. As a result, the molecular polarizability is preserved. In contrast to the Drude model, induced point dipoles are mathematical dipoles having no additional particle with an artificial mass. As a result, polarizable hydrogens pose no problems using Lagrangian thermostats. In practice, induced point dipole simulations of [C2mim][OTf] showed very similar dynamics if all atoms were made polarizable or the hydrogen polarizabilities merged to the corresponding carbons.135
In case of the polarizable, coarse-grained MARTINI force field for monovalent ions262 in aqueous solution143,144 the ion beads carry two Drude particles (see section 2.2.1). The partial charges and van der Waals parameters were determined by running a manifold of coarse-grained simulations with incremental changes in these parameters to reproduce the density and the dielectric constant as a function of the ion concentration as close as possible.
2.6. Computational Efficiency and Benchmarking
One key aspect of polarizable force fields in term of efficiency compared to classical simulations is the mandatory additional computational cost associated with the evaluation of polarization energy. Over the years, considerable work has been performed to overcome this computational bottleneck without compromising the accuracy. Solving the polarization equations using point dipoles usually costs more than half the total cost of an MD step (depending on the force field and simulation setup). To reduce that cost and to keep accuracy, various strategies are possible. Nevertheless, some limitations exist due to the imperfect time reversibility and volume preservation that they may imply. Furthermore, the ability to parallelize the method efficiently also influences the choice of the optimal method and therefore the final efficiency.
2.6.1. The Speed versus Accuracy Dilemma.
In practice, the evaluation of the polarization equations for point dipole models can be seen as the resolution of a large set of linear equations therefore requiring a matrix inversion.263,264 Usually polarizable simulations deal with thousands to hundred of thousands of atoms, consequently, as the polarization matrix size depends on such a large number of polarizable sites, “exact” direct matrix inversion approaches such as LU or Cholesky factorization are unfeasible. Therefore, one has to resort to state-of-the-art mathematical iterative methods.265 Iterative methods used in molecular dynamics264,265 can be grouped in two main families: stationary methods, like Jacobi Iterations, or the Jacobi over-relaxation method, and Krylov subspace methods, such as the conjugate gradient (CG) or the Jacobi/direct inversion of the iterative subspace (JI/DIIS). Historically the first set of methods was used in the community. For example, the Jacobi over-relaxation approach was used in the context of the AMOEBA force field.164 Gradually, as convergence issues were known in the mathematics community and because they cannot be recovered by adding more iterations,147 they were abandoned and replaced by Krylov approaches.147,263,264 Efficiency of CG and JI/DIIS are similar and only potentially differ when a large number of cores is used within massively parallel implementaions147
By definition, iterative techniques are nonexact inversion approaches, so they have to embody two qualities: a low computational cost and a high accuracy on both energy and forces. Of course, the devil being hidden in the details, the standard way of computing the forces assumes that the dipoles are fully converged. Unfortunately, to enforce the quality of the nonanalytical forces, a very tight convergence threshold of 10−5 −10−8 D on the dipoles is mandatory but also associated with a lot more iterations leading to a slowdown of the simulation.147,263,264 In practice, such setup being rarely chosen, the dipoles are not fully converged and thus the forces are not the exact opposite of the gradient of the polarization energy, generating errors that accumulate leading to energy drifts. This degrades the computational efficiency of the solvers and limits the use of molecular dynamics with point dipole polarizable force fields, however several strategies have recently been developed to solve this issue.
2.6.2. Fast and Accurate Algorithms for Point Dipole Models.
As we just discussed, the more advanced Krylov solvers are the most suited to be employed to solve the polarization equations being ensured of a guaranteed mathematical convergence.265 To reduce the computational cost associated with reached convergence, several techniques have been developed and aim at reducing the number of necessary iterations to do so. For example, in the context of the conjugate gradient approach, it is possible to use a preconditioner.263,264 It consists in choosing a matrix P such that P−1 is close to the inverse relay matrix R−1 (see eq 2.3.6), and in applying the iterative method to the modified linear system where the matrix and the right-hand side are multiplied by P−1. The convergence of the solver is then accelerated because of the clustering of the eigenvalues of the matrix P−1⋅R.
Efficient preconditioners exist with various associated complexities,263,264 and some of them have been designed for the polarization problem, such as the ones proposed by Wang and Skeel.263 All provide a reduction in the number of iterations required to reach convergence up to 10–20%, depending on the nature of the chemical system which, of course, impacts the condition number of the matrix that one needs to invert. If preconditioning is not suitable for Jacobi/Direct Inversion of the Iterative Subspace (JI/DIIS) solvers, solutions also exist for this approach. For example, Nocito and Beran recently introduced the faster Divide and Conquer Block-Jacobi/DIIS method266,267 that solves the polarization equations by partitioning the molecular system into a set of smaller clusters treated at the JI/DIIS level, leading to a 10–20% speedup compared to the standard approach.
Another solution that can be added on top of the CG and JI/DIIS strategies is to choose an initial “predictor” guess as close as possible to the actual solution of the linear equations. This guess can be constructed using information from one or a few of the past values of the dipoles. The simplest choice is therefore to take the “previous guess”, i.e., the value of the dipoles at the previous time step, but one can go for more elaborate and efficient strategies such as Kolafa’s Always Stable Predictor Corrector (ASPC)268 or Skeel’s Least Square Predictor Corrector (LSPC).263 These two advanced predictor/corrector approaches reduce the number of iterations by a factor two in a standard production simulation context. One should note that these techniques lose their efficiency when one uses larger time steps. In the case of the Reversible Reference System Propagator Algorithm (RESPA) multiple time step269 integrator instabilities occur when such predictors are used with time steps larger than 2 fs.
Close in spirit, the last strategy, derived from ab initio MD, has been shown to be successful, leading to convergence acceleration through the addition of an extended Lagrangian scheme to propagate a set of dipoles that are used as an initial guess to standard iterative solvers (iEL/SCF or Extended Lagrangian Self Consistent Field).270 This approach offers comparable performances and time step capability as the ASPC predictor but requires an additional thermostat in order to prevent energy flows between the degrees of freedom.
At this point of the discussion, the presented acceleration strategies do speed up the computations, but all ultimately suffer from the drawback of the presence of nonanalytical forces which lead to accumulating errors. Therefore, to ensure stability of very long time scale simulations toward microseconds, they should all employ a tighter dipole convergence criterion leading to a higher number of iterations than usually discussed in benchmarks for short “10−5 D-like” simulations. This uncomfortable diagnostic led the community to consider approaches offering analytical formulas for the polarization energy.
Analogous to the iEl-SCF approach,270 one can consider the actual induced dipoles as new degrees of freedom and build an extended Lagrangian. It has been shown that such an approach could be extended by defining the way to propagate the dipoles during the dynamics without any SCF cycles. The first results using this nonempirical strategy are promising, and the resulting method named iEl/0-SCF271 does not require any iteration, therefore offering higher energy conservation compared to standard iterative approach. On the performance side, the method does presently offer performance in line with iterative techniques but appears limited to standard time steps due to its use of extended Lagrangian.
Another family of methods, closer to the mathematical ideas governing the matrix inversion techniques, were introduced by Wang and Skeel.263,272 Indeed, they introduced 13 years ago the initial idea of “analytical forces” for polarizable forces and proposed a method relying on Chebyshev polynomials enabling the simultaneous analytical expression of both the energy and of its derivatives. Despite this conceptual advance removing any source of energy drifts, the approach was not applicable to production simulation as the resulting final energies were too degraded compared to fully converged reference ones. However, a few years ago, Simmonett et al. revisited the concept and improved it by proposing the extrapolated perturbation theory (ExPT).273 ExPT can be seen as a truncation of the Jacobi iterative method at a predetermined order combined with the use of a few parameters. Initially, as the empirical and difficult choice of parameters limited the full applicability of the approach to all kinds of systems, the authors proposed an evolution of the method. Now denoted as OPT3 (OPT = orders of perturbation theory),274 the strategy is pushed to a higher order of perturbation, and although it still involves parameters, OPT3 provides a systematic way for the parametrization, extending the applicability of the method. On the computational point of view, the analytical aspect of the evaluation of derivatives also reduces the cost of the method compared to the best iterative approaches by roughly a factor 2, making it attractive.
To overcome the EXPT/OPT3 limitations, a nonempirical and noniterative strategy denoted the truncated conjugate gradient (TCG) has been proposed.275,276 It is derived by explicitly writing down all numerical operations of a finite number of CG cycles of iteration. The level of TCG can be user-chosen: TCG-n, n = 1,3. For a chosen TCG level, the number of operations is fixed once and for all, and it is then possible to derive an exact analytical expression of the gradient of the energy exactly in the same spirit as in the Skeel or ExPT/OPT3 approaches. By construction, it avoids any energy drift in microcanonical simulations. TCG remains a Krylov CG approach, therefore its error is monotonically reduced at each cycle: the higher the TCG level is, the higher its accuracy is. Other advantages exist as the CG-method being mathematically optimal at each iteration provides “on the fly” optimal coefficients that do not need to be parametrized as in ExpT/OPT and therefore guarantees that the number of the required matrix-vector products (1 per iteration in any iterative approach) is reduced to a minimum compared to any other methods. In practice, the TCG accuracy can be improved at negligible costs:
by using preconditioners as previously introduced leading to the truncated preconditioned conjugate gradient (TPCG);
by using the residue of the final CG step, available without any additional cost, to perform an additional “peek” pseudoiteration, equivalent to one step of Jacobi Over Relaxation with a relaxation parameter which can be found adaptively. As TPGC3 is virtually exact, TPCG2 can be used coupled to a peek step as a production method for any type of systems ranging from biological systems to ionic liquids at a cost comparable to OPT3. Finally, being analytical, TCG does not rely on history (no predictor-corrector) and can be applied to larger time-steps for the same fixed computational cost.
It can be coupled to efficient multi-timestep integrators to provide a very fast evaluation of short-range polarization. In practice, an integrator such as BAOAB-RESPA1435 uses TCG-1 at short-range and provides up to a 7-fold acceleration of polarizable point dipole simulations compared to standard 1fs approaches without loss of accuracy of the dynamics.
2.6.3. Evaluation of Polarization: Other Sources of Acceleration.
All discussed polarization solvers have the advantage to ensure convergence and to be compatible with massively parallel implementations (see for example ref 154), but in practice, to be able to achieve scalable performance on modern supercomputers, they need to be coupled to two categories of algorithms. The first category is a linear scaling algorithm that will enable the fast evaluation of electric fields that are required to evaluate the polarizable energy and forces. The most common choice is the Smooth Particle Mesh Ewald (SPME) that is a well suited (n log(n)) fast periodic boundary conditions approach that was extended to the use of point dipole models as well as the alternative P3 M (particle–particle particle–mesh). If one wants to use distributed multipoles, especially at high angular momenta, specific recursions or tree code techniques should be used to ensure a fast evaluation of electric fields.160,277,278 Finally, to tackle very large systems, one should rely on techniques such as fast multipoles279,280 or limit communications using 3D decomposition techniques such as the midpoint approach that is at the heart of the Tinker-HP code.154,281
3. COMPARATIVE CASE STUDIES
In this section, we focus on the discussion of influence of polarization (or the lack of thereof) on the prediction of properties for several prominent classes of ionic systems. Taking into account that each application emphasizes the importance of a specific subset of properties, this discussion is organized based on different applications and the corresponding key physical phenomena. Specifically, first we discuss aqueous solutions focusing on the properties related to biological and biomedical systems. Then, we review MD simulations of electrolytes for rechargeable battery applications, which primarily focus on the ability of polarizable and nonpolarizable models to adequately predict small metal cation solvation and transport. Bulk ILs are another class of ionic systems where interactions due to induced polarization impact important structural and dynamic characteristics. Finally, electrolytes near charged surfaces represent another challenging case, where polarization of both electrolyte and electrodes can influence the mechanisms of charge separation and storage.
3.1. Pure Solvents and Dilute Aqueous Solutions
An important quality of a force field is its ability to accurately model pure solvents and dilute aqueous solutions as these are representative of the conditions typically present in biological systems. For example, the interior of lipid bilayers or certain domains of proteins have characteristics of pure solvents, while the environments around biological molecules are dilute aqueous solutions. In addition, such systems have often been subjected to extensive experimental analysis from which thermodynamics parameters are available that may be used to optimize or validate force fields.282-284 In this section, we will briefly summarize the various types of pure solvents and dilute aqueous solutions used in the polarizable force field development with the emphasis on Drude oscillators and the AMOEBA induced point dipole force field.
3.1.1. Polarizable Water Models.
Pure solvents played a central role in the development of force fields designed for condensed phase simulations. The most widely studied pure solvent is water, and there have been numerous comprehensive reviews of this topic.285-287
Drude Model.
When the development of the Drude force field was initiated, the initial focus was on a water model. Given the success of the TIP4P288 and related additive four-point water models,289 an analogous four-point model was developed in which the charge sites were the “MW” (see Figure 17) or fourth off-center site and the hydrogens while the Lennard-Jones parameters and polarizability were placed on the oxygen.148
Figure 17.
Schematic representation of a water molecule: the oxygen (OW) and the two hydrogen (HW1, HW2) sites are present in all water models, the virtual site (MW) is present in TIP4P, TIP4P-2005, SWM4-DP, SWM6, and COS/G3 models, whereas the lone pair charges (LP1,LP2) are present only in TIP5P, TIP5P-E, and SWM6 models.290 Reproduced from ref 290. Copyright 2015 American Chemical Society.
Target data included high level QM data of the water dimer and a range of experimental pure solvent water properties. A systematic search of parameter space in which the polarizability was fixed to the gas experiment value, yielded a number of models that produced good agreement with a range of target data at room temperature, such as density and heat of vaporization, but yielded a dielectric constant systematically larger than the experimental value. This led to reconsideration of the approximation of the fixed polarizability, with subsequent optimization allowing the polarizability to vary as part of the fitting process, yielding a model with the experimental gas phase polarizability scaled by 0.72 that was in good agreement with the dielectric constant as well as a range of other properties. The model was named SWM4-DP, standing for “simple water model with four sites and Drude polarizability”. The physical justification for the need for scaling the polarizability is still a point of debate, although a decreased ability of the electron cloud to distort in the condensed phase and the approximation that the polarization of the water model (or of a polarizable atom) is based on the electric field at the nucleus rather than being integrated over the entire volume291 appear to be an important factor.114 A modified version of SWM4-AD,292 where AD stands for isotropic atomic dipole polarizability was also developed and showed an equivalent performance to SWM4-DP. However, while the SWM4-DP model did reproduce a range of experimental data, the model was developed with the Drude oscillator carrying a positive charge. As the Drude particle is meant to represent the electronic degrees of freedom, a second water model was developed, SWM4-NDP, where NDP stands for negative Drude polarizability.149 This model was optimized in a manner similar to that used for the SWM4-DP model, yielding good agreement with a range of experimental data. However, because the impact of system size on the calculated diffusion coefficient,293 (an issue that was not identified until the period during which SWM4 models were being developed) was not considered during the optimization process, both models actually overestimate the self-diffusion constant. This is due to the fact that the apparent self-diffusion constant was in good agreement with experiment while the size correction leads to a value that is too high. More recently, the SWM6 water model included two lone pairs along with the atomic and MW sites as depicted in Figure 17. During the development of this model, it was determined that six rather than just five sites (MW-site omitted) were required to model the full range of gas phase (e.g., quadrupole moment) as well as condensed phase properties.294 The SWM6 model yielded improved agreement with respect to water clusters and for the diffusion constant relative to the SWM4-NDP model, although at an additional computational cost. Finally, it should be noted that the temperature-density profile of the SWM4 and SWM6 water models are not in good agreement with experiment, a problem that ongoing optimization efforts are addressing.
As an alternative to the polarizable water models in CHARMM (SWM4-NDP, SWM6), several other Drude-like models exist in literature, for example, the COS/G3 model295 developed by van Gunsteren and co-workers or the polarizable model of Dang and Chang297 used by Salanne and co-workers for aqueous electrolytes.298-300 The COS/G3 water model is the oldest and uses a tetrahedral angle of 109.47° as shown in Table 4, leading to a distorted water structure. POL3 is the standard polarizable water model for AMBER force fields.301 The polarizable water model of Dang and Chang297 is parametrized to reproduce structure and thermodynamic data of aqueous clusters, bulk phase, and liquid/vapor interface of water. However, a frequency-dependent dielectric analysis of several nonpolarizable and polarizable water models290 showed that SWM4-DP does not only reproduce the static permittivity ε but also comes closest to the experimental relaxation time. The various nonpolarizable and polarizable water models and their properties are reviewed in refs 290 and 291.
Table 4.
Force Field Parameters for Polarizable Water Models
| COS/G3a | POL3b | Dang/Changc | SWM4-DPd | SWM6e | |
|---|---|---|---|---|---|
| qO [e] | 0.000000 | −0.7300 | 0.0000 | 0.00000 | 0.28800 |
| qH [e] | 0.450672 | 0.3650 | 0.5190 | 0.55733 | 0.53070 |
| qMW [e] | −0.901344 | −1.0380 | −1.11466 | −1.13340 | |
| qLP [e] | −0.10800 | ||||
| rOH [Å] | 1.0000 | 1.0000 | 0.9572 | 0.9572 | 0.9572 |
| θHOH [deg] | 109.47 | 109.47 | 104.52 | 104.52 | 104.52 |
| σO [Å] | 3.1746 | 3.204 | 3.2340 | 3.1803 | 3.1984 |
| εO [kJ/mol] | 0.9445 | 0.653 | 0.7636 | 0.8600 | 0.6778 |
| αO [Å3] | 1.250 | 0.528f | 1.444 | 0.978 | 1.043 |
| ε | 107.5 ± 1.8h | 78.9 ± 1.0h | 71.9 ± 1.3h |
AMOEBA Model.
The AMOEBA water model uses distributed multipoles and is based on the induced dipole model for polarization. The AMOEBA energy function is the following:
| (3.1.1) |
In AMOEBA, the short-range valence interactions are described by five terms, namely: bond stretching, angle bending, bond-angle cross term, out-of-plane bending, and torsional rotation. Such terms are complemented by the nonbonded van der Waals interactions, permanent multipolar electrostatics (up to quadrupoles), and explicit point dipole polarization that couples isotropic polarizability to Thole damping. Particularities of AMOEBA for the short-range interactions include the use of bond-angle cross terms, a decomposition of angle bending into in-plane and out-of-plane components using a Wilson–Decius– Cross form as well as the use of the buffered 14–7 “Halgren” function254 to deal with van der Waals interactions. Bond stretching, angle bending, and stretching–bending coupling, are identical to those of the MM3 force field.302 Anharmonicity is taken into account using higher-order deviations from ideal bond lengths and angles. Accuracy of electrostatic interactions is ensured by expansion of the multipolar development beyond point charges and up to quadrupoles, allowing for a better representation of directional effects such as those, for example, found in hydrogen bond interaction networks. These distributed multipoles are extracted form ab initio computations using Stone’s Distributed Multipoles Analysis (DMA).303 The original 2003 AMOEBA model164 exhibited a good agreement for water properties304 including: density, heat of vaporization, radial distribution functions, magnetic shielding, self-diffusion, as well as the static dielectric constant. Since 2003, various reparametrizations occurred. The first noticeable model was i-AMOEBA (i = inexpensive) based on the use of as simplified “direct field” polarization model. Despite being found extremely accurate for bulk water simulations and computationally cheaper, the model was found to be poorly transferable compared to the 2003 model. Despite these problems, such studies demonstrated the advantage of using the ForceBalance (https://simtk.org/home/forcebalance) automated procedure. Another reparametrization attempt based this time on the full initial AMOEBA energy function was performed using ForceBalance in order to enforce AMOEBA’s agreement with reference gas phase ab initio results for water clusters and condensed phase experimental data. This led to the AMOEBA 14 potential305 which was exhibiting a net improvement over the previous 2003 model, keeping its transferability over ranges of systems. Since that date, optimization work is still in progress and other reparametrizations occurred.306 Recently, the AMOEBA methodology has been extended to the AMOEBA+ model436 which embodies more physics (i.e. electrostatic short-range charge penetration, 2-body charge transfer). The water model exhibits superior agreement with experiment and ab initio reference results.
3.1.2. Other Polarizable Solvents.
Beyond water, additional pure solvents or neat liquids have played a central role in development of the additive CHARMM force field and the Drude polarizable model, not to mention their central role as target data for development of OPLS,307 AMBER,307 GROMOS,308 APPLE&P,44,309 and other force fields.310 The advantage of pure solvents is the availability of accurate experimental data on properties including the density (or molecular volume), the heat of vaporization, the isothermal compressibility, and the dielectric permittivity, among others. This offers data that allows for, in particular, Lennard-Jones parameters to be systematically optimized, especially in the context of a hierarchical optimization approach. For example, following optimization of the Drude SWM4-NDP water model, optimization of the alkane parameters was undertaken, from which CH3─, ─CH2─, and ─CH─ parameters were optimized.244 Subsequently, alcohol parameters were optimized with the aliphatic parameters initially being transferred from the alkanes, such that optimization focused on the hydroxyl.311 This was also undertaken for amides and sulfur containing species,177,312 although in specific cases adjustments of the parameters on the aliphatic carbon covalently linked to heteroatoms was undertaken. A similar hierarchical approach was performed for benzene leading to heterocycles,313 including nucleic acid bases.314 A specific advantage for the use of pure solvents with the Drude force field was the ability to systematically scale the polarizabilities from the experimental gas phase values.217 As the physical justification for this was not clear, as discussed above, an empirical approach was used in which the scaling factor was empirically optimized targeting the pure solvent dielectric constants. This approach leads to scaling factors ranging from 0.6 with some sulfur containing species, 0.7 with amides and alcohols, 0.85 with amides and heterocycles, and 1.0 with aliphatics and halogens.114 Moving forward, a scaling factor of 0.85 is typically applied in cases where access to experimental dielectric permittivities is not available. During fitting, the APPLE&P force field for alkanes, fluoroalkanes, ethers, carbonates, nitriles, ionic liquids, and battery electrolytes, the polarizabilities of solvents and especially anions were also reduced from the gas-phase values or were fit to QM calculations with a smaller basis set that effectively scales the magnitude of polarizability.309,315
Visscher et al. recommended to reparametrize not only the Lennard-Jones interactions when considering polarizable forces for alcohols but also the partial charges of the atoms.310 These were scaled to improve the description of ΔHvap and ΔGhyd. Furthermore, the polarizabilities were determined in gas phase and liquid phase using a QM/MM approach. It turned out that the polarizabilities in the liquid phase of the investigated alcohols are significantly lower than the corresponding values in the gas phase which legitimates the scaling factor of the other approaches mentioned above in some way.
Of course, in the same spirit, various polarizable solvents have been derived for AMOEBA and are available for the general public.213
3.1.3. Polarizable Ions in Aqueous Solutions.
In contrast to simple atomic ions, water interactions with ionic liquids are more complex due to the anisotropic and bulky nature of the molecular ions.316 Furthermore, multiple possibilities for (bifurcated) hydrogen bonding exist and are in competition with the interionic interactions. Hence, the need for polarizable ion models in aqueous solution has been argued several times.317-319 Consequently, the preliminary set of Drude and AMOEBA force fields was applied in dilute aqueous solution simulations, typically in the context of estimations of free energies of aqueous solvation (or hydration free energies ΔGhyd). These efforts include the various neutral species, monoatomic and molecular ions. For Drude, concerning neutral species, the initial hope with the polarizable model was that the pure solvent Lennard-Jones parameters in conjunction with the more sophisticated electrostatic model would yield good agreement with experiment when used to calculate ΔGhyd values. However, this was found not to be the case, leading to the use of atom-pair specific Lennard-Jones parameters for selected solute atoms with water (e.g. use of the NBFIX term in CHARMM that applies specific Lennard-Jones parameters to specific atom pairs rather than assigning them based on combination rules).320 In retrospect, the need for atom-pair specific Lennard-Jones parameters intuitively makes sense as the variation of the electronic distribution of atoms and molecules associated with the explicit treatment of electron polarizability will be accompanied by variations in the van der Waals features of the system, such that different Lennard-Jones parameters are required for specific environments. Thus, in the absence of a model that allows the van der Waals term to vary as a function of environment the approximation of parameters for specific interacting pairs has been applied. This successfully led to good agreement for the ΔGhyd values for a range of neutral species with experimental data.320 Moreover, a particular advantage of the Drude polarizable model over other methods to treat polarizability is the use of an explicit particle for the electronic degrees of freedom. This allows for Lennard-Jones parameters to be applied to the electronic degrees of freedom thereby modeling steric effects associated with perturbation of the electron cloud as well as electronic effects in the context of an empirical force field.82 In the case of Drude halogens, this approach accurately treats both halogen bonds and halogen–hydrogen bond donor interactions as well as reproduces both pure solvent and ΔGhyd experimental data.120 It has also been applied to more accurately model Mg2+, allowing for accurate reproduction of the ΔGhyd and of the energetics of specific water–ion interactions.121
A central aspect of the Drude ion parameter optimization to yield a set of models that is internally consistent was the adoption of a global free energy scale based on experimental data for neutral salts. One cannot simply rely on absolute experimental values because there is no unambiguous reference scale for charged species; all experiments have to utilize some reference scale. The significance of a global solvation scale is important in force field development because the absolute hydration free energies of the different ions must be internally consistent, for example, to accurately account for the relative binding and ion-pairing affinities. As described in detail elsewhere, handling this issue properly requires that the target ΔGhyd values extracted from different experimental studies be adjusted such that the values are effectively offset to the same counterion.149,321 Doing this assures that all the ΔGhyd values are constrained to lie on the same consistent scale, such that their relative ΔGhyd values are representative of the experimental regime. Using this approach, in combination with QM calculations, yielded a set of parameters for monoatomic ions including both mono- and divalent cationic species and monoanions.322 More recently, these efforts have been extended to molecular ions representative of charged moieties in biological macromolecules.321 An interesting observation from the latter study are differences in the three-dimensional probability of water around the molecule in the Drude versus the CHARMM36 additive model, indicating differences in the nature of the atomic details of the interaction of the ions with the aqueous environment.
A systematic optimization of atomic ions and subsequently molecular ions has also been reported in the context of the AMOEBA induced dipole-based polarizable force field. First, AMOEBA was tested for monovalent ions such as K+ and Na+.323 Absolute solvation free energies were accurately described for such cations as well as for the chloride ions in liquid water and formamide. Such results clearly demonstrated the ability of AMOEBA to capture the thermodynamics and free energies of solvated ions. Extension to divalent cations came later as AMOEBA was extended to Ca2+ and Mg2+.324 Such an addition required the introduction of a cation specific parametrization of the Thole polarization damping model which was required to be different in cation–water over water–water interactions and adjusted on ab initio polarization energies computed using energy decomposition analysis. This opened the door to hydration free energy for the cations which were found, again, in good agreement with experiment.183,325 The same ab initio bottom-up strategy coupled to higher-level quantum chemistry was used to enable AMOEBA simulations of tetravalent actinides such as Th4+ in water.326 The first polarizable force field estimate of Th(IV) solvation free energy was then predicted. On the basis of these encouraging results, more difficult heavy metal cations were modeled more recently and hydration free energies, structures, and dynamics of open- and closed-shell trivalent lanthanide and actinide metal cations were computed. AMOEBA simulations of six cations solvated in bulk water predicted first-and second shell hydration numbers, water residence times, and free energies of hydration are fully consistent with experiment (as illustrated in Figure 18) offering a predictive modeling of f-elements compounds.327
Figure 18.
Solvation free energy (in kJ mol−1 of the actinide (III) and lanthanide (III) cations in water: AMOEBA vs reference data. Reproduced with permission from ref 327. Copyright 2014 Springer.
Such parameters were later used in polarizable simulations of water and an aqueous mixture of 1-ethyl-3-methylimidazolium ethylsulfate [C2mim][EtSO4] using the AMOEBA force field and revealed different mechanisms of water exchange processes around the lanthanides Gd3+, Dy3+, and Ho3+.328 In pure water, the exchange of water molecules in the first solvation shell of the lanthanides can be explained by an associative process. In contrast, in the aqueous mixture of the ionic liquid, the mechanism is of dissociative nature. Here, the interaction of the lanthanide with the polarizable anion plays an important role.
3.1.4. Experimental Data for Optimizing Pair Specific Interactions.
The studies discussed in the previous section yielded Drude parameters that are in quite good agreement with the experimental ΔGhyd data. However, accurate simulations of heterogeneous systems require that the interactions of the different solutes in the system to be balanced with those with water as pointed out within the AMOEBA results. An efficient approach to address this is using osmotic pressure calculations.329,330 Such calculations are computational tractable and yield high precision data that can be directly compared to experimental data and may be used to optimize atom-pair specific (NBFIX) parameters between the individual solutes, including ions. In the context of polarizable force fields scaling of the atomic dipole–dipole interactions may also be performed using the through-space Thole scaling term (NBTHOLE).163 This approach has been used to improve a number of ion–ion parameters in the context of both the additive CHARMM36 and Drude polarizable force fields121,331 as well as for other force fields.330
An alternative utilization for dilute aqueous solution and pure solvent data is based on the availability of X-ray or neutron scattering data.332,333 These experiments yield atomic resolution data on the distribution between molecules and, when isotopic replacement can be performed, between specific atoms in those molecules. The utilization of scattering data for the optimization of water models has a long history and the approach can be used to gain insights into the structure of salt solutions.334 In the context of the Drude force field neutron scattering data on methanol (MeOH) and tetrahydrofuran (THF), along with water, was used to validate the associated force field parameters.335 Comparison of simulated and experimental partial structure factors yielded improved agreement with the Drude model for both MeOH and THF over the additive CHARMM36 force field.
The Kirkwood–Buff theory represents another approach to obtain atomistic details from condensed phase simulations that may be directly compared to experimental data.336 The Kirkwood–Buff theory has been used for a number of years as a guide for force field development337 and can be used to understand the interactions of solutes with macromolecules.338 In the context of the Drude force field, the Kirkwood–Buff theory was used to validate the amide and alcohol parameters. Results with the Drude model for amides in aqueous solution led to improved interactions over the additive force field for selected molecular interactions, although deficiencies in both models are evident.339 Studies on methanol solutions showed some properties being better modeled by the Drude force field (e.g., solution densities and dielectric constants, among others) while better performance for the additive force field was obtained with activity derivative, the excess molar Gibbs energy, and the excess molar enthalpy of mixing.340 Thus, the Kirkwood–Buff analysis clearly indicates the need for improvement in the Drude force field for the balance of the solute–solute, solute–solvent, and solvent–solvent interactions.
Dielectric spectra of aqueous ionic liquid mixtures can already be reproduced with reasonable agreement using classical nonpolarizable force fields of Canongia-Lopes et al.18 and TIP3P as the most important feature is the breaking of the cation—anion interaction by the interstitial water molecules, accelerating the overall dynamics of the system. However, if one is also interested in conductivities of the various mixtures, nonpolarizable simulations fail for aqueous ionic liquid systems and polarizable MD simulations140 are mandatory to get closer to the experimental values.
3.1.5. Ionic Solutions at Interfaces.
Aqueous solutions of ILs at the solution/water interface were studied by Jungwirth and co-workers using a nonpolarizable and polarizable force field.341 The water was modeled by TIP4P/2005 and POL3.296 At low IL concentration, the nonpolarizable and polarizable force fields of the electrolyte yielded reasonable agreement with the experimental surface tension. However, at higher ion concentrations, only the polarizable force field was able to reproduce the experimental increase in surface tension. Voth and co-workers also detected an enhanced concentration of C2mim at the vacuum interface, going along with a reduced charge density at the surface to the vacuum.342 Due to the reduced repulsion, the average distance between the ions is less compared to the nonpolarizable force field, which also favors anions at the vacuum interface. The surface tension of the polarizable force field was lower compared to the nonpolarizable and hence closer to experiment. Wick et al. investigated the different CO2 and SO2 uptake at the air/liquid interface of [C4mim][BF4].343 The potential of mean force for both gases showed a preferred position at the air/liquid interface close to the cations pointing their tails toward the air phase. However, transitioning into the bulk liquid phase, the oscillatory behavior of the potential of mean force indicated that CO2 and SO2 interact stronger with the anions.
Interesting application studies on dilute aqueous simulations with the Drude ion parameters in contact with DNA have been reported: The osmotic pressure calculations and QM interactions of the ions with model compounds representative of the phosphate backbone and nucleic acid bases improve the balance of the ion–macromolecule vs. ion–water interactions via the use of atom-pair specific parameters,344 analogous to the use of the osmotic pressure calculations discussed above. This optimization in conjunction with the optimized Drude DNA and ion parameters was shown to yield a model that gave improved agreement with counterion condensation theory345 with respect to the neutralization of the DNA charge by the ions.344 Significantly improved agreement over the additive CHARMM36 force field was also obtained on the competition of counterions (e.g., Na+ competition with Li+, K+, or Rb+) for the ion environment around DNA, yielding improved agreement with buffer exchange-atomic emission spectroscopy experiments.346 Results from that study also reinforced the need for large simulation systems (e.g. solvation for 25 Å beyond the DNA) for proper sampling of the ion environment of the DNA. Another interesting observation was that the presence of different counterions in DNA simulations leads to changes in the calculated scattering spectra of the DNA with the Drude force field.347 This effect, which is associated with cooperative base-water–ion hydrogen bond interactions in the grooves of the DNA, is not present with the additive CHARMM36 force field, showing that the DNA conformational properties are sensitive to ion type in the polarizable model, a property that is not present in additive force fields. Similarly to these studies, ion interactions with nucleic acids were very recently studied in a paper published during the completion of this review and concerning the extension of AMOEBA to nucleic acids that now enable full polarizable AMOEBA simulations of complex DNA and RNA systems with various ions.348
3.2. Modeling of Battery Electrolytes
Rapid development of batteries for portable electronic and automotive applications highlighted the need for fundamental understanding of transport mechanisms in battery electrolytes at molecular scale. Seven major classes of electrolyte systems are attracting the attention of the modeling community:
Liquid aprotic electrolytes that are widely used in current lithium ion batteries. These simulations are mostly focused on the traditional baseline chemistries comprised of aprotic solvents such as ethylene carbonate (EC) and dimethyl carbonate (DMC). EC has the ability to efficiently dissociate Li-salts as well as its reduction products passivate and stabilize graphite electrode surfaces, while DMC or other linear carbonate or ester solvates decrease electrolyte viscosity and improve ion transport at low temperatures.
Liquid aprotic electrolytes for the “beyond Li” chemistry with an emphasis on Mg, Na, and Zn.
Aqueous electrolytes due to their intrinsic nonflammability, ease of processing, fast bulk, and interfacial ion transport.
Solid polymer electrolytes that are investigated with the aim to eliminate volatile organic components, to increase mechanical stability and flexibility, and to decrease the dendrite growth, therefore allowing usage of Li metal anodes. Poly(ethylene oxide) and other polyethers doped with lithium salts such as Li[TFSI] are considered as baseline systems for this electrolyte class.
IL electrolytes doped with the Li, Na, Mg, or Zn salts are investigated due to their low volatility that leads to safety advantages such as delayed thermal runaway and a large variation of available cation and anion combinations that provide an opportunity to tailor electrolyte properties.
Solid state conductors that form interphases at the electrodes due to electrolyte reduction and oxidation.
Hybrid electrolytes combining multiple classes of electrolytes.
3.2.1. Solvent Polarization and Cation Coordination.
Accurate prediction of the structure and transport in battery electrolytes requires accurate representation of the binding energy of small cations such as Li+, Mg2+, or Zn2+ with solvents and anions. Because of the small size of the Li+ cation, about 30% of its binding energy with ether, carbonate, or water comes from the induced polarization interactions, indicating a strong need to include these interactions either in a mean-field sense through the two-body terms or explicitly through the atom dipole polarization or Drude model.245,246,349 The analysis of the distribution of dipole moments extracted from DFT calculations clearly revealed that molecular dipole moments for typical battery solvents such as EC or propylene carbonate (PC) near Li+ are about 50% larger than the gas-phase values and 20% larger than the average dipoles in neat liquid as shown in Figure 19. An increased dipole moment of solvent molecules near Li+ observed in DFT calculations is in stark contrast with the scaled-charge mean-field approach that yields smaller dipole moments due to charge reduction. Yet, counterintuitively the charge scaling was empirically found to improve the ion transport often at the expense of predicting a larger coordination number around metal cations.
Figure 19.
Combined density distribution of the ethylene carbonate (EC) dipole moment as a function of radial distance from the ion from the PBE periodic DFT calculations of the simulation cell containing 31 EC and one Li+ by Pollard et al.67 Dipoles measured from Wannier centers (grayscale) and GAFF point charges (color). Solid, horizontal lines highlight average gas and condensed phase dipole moments. Reproduced with permission from ref 67. Copyright 2017 American Institute of Physics.
Another interesting observation made by Pollard et al.67 is that unlike the increased dipole moment of EC and PC molecules coordinating Li+ ion, no increase in the dipole moment of water molecules coordinating halide anions was observed.349,350 This is likely due to the larger size of anions compared to Li+ cation, weaker anion–solvent binding energy and the difference in the hydrogen bonding network formed near anions. The larger size of anions that are of interest for battery electrolytes results in even weaker anion–solvent interactions compared to halide–water. Thus, the solvent dipole is significantly enhanced near small cations such as Li+ and unchanged near anions. This consideration is often overlooked during parametrization of the scaled charge (or other mean-field polarizability) models. For the large size cations, e.g., the Drude Mg2+ model and the SWM4-NDP water,121 the inner shell waters around Mg2+ have a dipole of 2.94 ± 0.11 D on average versus 2.48 ± 0.18 D for the water model in bulk solution. In the development of the Drude Mg2+ ion parameters, the Lennard-Jones potential was applied to the SWM4-NDP water Drude particle–Mg2+ atom pair interaction that effectively buffered the polarization response of water when coordinated with the ion. This was shown to be essential for the accurate treatment of both the hydration free energy of Mg2+ and the kinetics of water–ion binding.
Scaled charge force field molecular dynamics (FFMD) simulations were reported for the dilute and low concentration electrolytes based upon LiPF6 in EC and PC solvents by Chaudhari et al.351 and are compared with the results from ab initio molecular dynamics (AIMD) simulations. A comparison of the full charge FFMD with AIMD revealed that the Li+ first coordination shell is significantly more structured in the FFMD as illustrated in Figure 20, where the magnitude of the first peak in the Li-O(carbonyl) radial distribution function gLi-O(r) is about twice of that observed in AIMD. The overstructuring of the Li+ first coordination shell leads to a slower exchange of solvent molecules around Li+ and a lower Li+ diffusion coefficient. Unlike in ether solvents, such as tetraglyme and longer glymes, where Li+ ions are primarily coordinated by one solvent molecule for a very long time,352,353 the exchange of solvent molecules in the Li+ coordination shell in carbonate-based solvents, where four to five molecules participate in cation coordination, significantly contributes to the Li+ transport mechanism.354 As the partial charges of atoms in the solvent molecules decrease, i.e., reducing the molecular dipole moment, the first solvation shell of Li+ becomes less structured and shifts to larger separations. This leads to an improved agreement of the magnitude of the gLi-O(r) first peak from FFMD with the AIMD results. While with the reduction of partial charges the magnitude of the gLi-O(r) peak decreased, the peak becomes broader and the Li+ coordination by EC and PC is effectively increasing as the Li+ first solvation shell becomes more diffuse. Thus, the resulting coordination numbers from FFMD with reduced solvent dipoles are larger than AIMD results.351 Authors recommended a scaling factor of 0.8. Using Bader charge analysis that indicated that the Li+ cation charge is reduced by 0.1e, one can partially justify the scaling of charges351 in these electrolytes, but that is inconsistent with the increased dipole from the condensed phase DFT shown in Figure 19. A similar scaling factor of 0.75 was obtained for water using the ECC64-66 where scaling the charges of all ions by the inverse of the square root of the electronic part of solvent dielectric constant was applied. It is clear from Figure 20 that it is necessary to decrease the ion–solvent repulsion parameters to avoid the unrealistically high solvent–cation coordination numbers. This correction was made for aqueous electrolytes64-66 but not in simulations of LiPF6 in EC and PC by Chaudhari et al.351 The AIMD simulations of more concentrated EC:DMC electrolytes with LiPF6 at solvent:Li ratios of 10:1 reported a slightly higher magnitude (35) for the gLi-O(r) of EC peak.355 MD simulations employing many-body polarizable force fields such as APPLE&P and using full charges for ions (and no rescaling for solvents) reported the first peak of the gLi–O(r) around 30 for EC:LiPF6 and EC: Li[TFSI] and EC:LiPF6 electrolytes, which is in good agreement with AIMD results.260,309 Importantly, the electrolyte conductivity and the extent of ion aggregation were also accurately predicted using the APPLE&P force field for a variety of electrolytes comprised of carbonates,309,354 glymes,246,354,356 sulfones (SL),257 acetonitrile (AN),357-360 and water258,259 doped with LiPF6, LiFSI, LiTFSI, NaTFSI, LiDFOB, and NaOTf salts.259
Figure 20.
Radial distribution (g(r)) of carbonyl oxygens (Oc) in (top) EC and (bottom) PC around Li+ using (left) FFMD and (right) AIMD simulations by Chaudhari et al.351 In the FFMD case, the partial charges on EC and PC molecules were reduced from 100 to 90% and subsequently to 80%. Corresponding running coordination numbers (⟨n(r)⟩) are also plotted to show how the number of solvent molecules changes with a change in partial charges. Reproduced with permission from ref 351. Copyright 2016 American Chemical Society.
3.2.2. Ion Transport.
In dilute and moderately concentrated electrolytes such as traditional 1 M, the Li+ often moves primarily with its solvation shell with minimal contribution from exchange of solvent molecules in the shell. Thus, an overestimation of the Li-solvent residence time leads only to moderate errors. As the salt concentration increases and the exchange of solvents and anions in Li+ coordination becomes increasingly important for Li+ transport,360,361 the full charge nonpolarizable force fields become increasingly inadequate. For example, Takeuchi et al.362 reported good predictions of structural properties for PC doped with one molar LiBF4 or LiPF6 using nonpolarizable force field while the predicted conductivity was about one order of magnitude lower than in experiment. Another recent MD simulation study from the LBNL group by Rajput et al.43 clearly demonstrated that ion and solvent diffusion coefficients predicted from MD simulations increasingly deviated from experiments as the LiTFSI concentration increases as shown in Figure 21a. In fact, the predicted Li+ and TFSI diffusion coefficients were more than 100 times slower at 3 M salt concentration. In contrast, MD simulations using the polarizable APPLE&P force field yielded an excellent prediction for dimethoxy ethane (DME):LiTFSI and PC:LiTFSI solutions over a wide concentration range as shown in Figure 21b.246 MD simulations employing a modified polarizable APPLE&P force field also predicted self-diffusion coefficients for the Li+ and Na+ cations, TFSI anion, and the same DME solvent in excellent agreement with experiments as reported by Liyana-Arachchi et al.356 and shown in Figure 22.
Figure 21.
(a) Self-diffusion coefficients of solvents and ions in the 1,3-dioxalane (DOL): dimethoxy ethane (DME) electrolytes with 0.25 M, 1 M, or 3 M LiTFSI, 0.25 M Li2Sx (x = 4, 6, 8), and 0.25 M Li2Sx (x = 4, 6, 8) + 1 M LiTFSI salts computed from MD simulations and PFG-NMR.43 Reproduced with permission from ref 43. Copyright 2017 American Chemical Society. (b) Conductivity of DME:LiTFSI and PC:LiTFSI electrolytes as a function of salt concentration expressed in mol per kg solvent (m) as obtained from experiments and from MD simulations using a many-body polarizable force field.246 Reproduced with permission from ref 246. Copyright 2006 American Chemical Society.
Figure 22.
Diffusion coefficients of LiTFSI in DME (circles) and NaTFSI in DME (squares) as a function of salt concentration from MD simulations by Liyana-Arachchi et al.356 for (a) DME, (b) Li+ or Na+, and (c) TFSI. Computational results are given as filled symbols, while experimental values are shown as open symbols. Reproduced with permission from ref 356. Copyright 2018 American Chemical Society.
While the polarizable force fields usually do not require charge rescaling, a slight charge scaling by a factor of 0.94 for the Li+ and anion oxygen charges was reported to be important in order to obtain excellent agreement with experimental conductivities at low temperatures over a wide concentration range in H2O:LiTFSI and sulfolane(SL):LiFSI electrolytes as shown in Figure 23a,b. This scaling also improved the ability of polarizable force fields to predict ion and water self-diffusion coefficients over a wide concentration range for H2O:LiTFSI as shown in Figure 23c. Without scaling, the ion dynamics was up to two times slower compared to experiment at the highest concentration but quite similar at moderate concentrations.363 On the other hand, the conductivity of concentrated acetonitrile(AN):LiTFSI (AN:Li = 3) predicted from simulations using the same force field agreed well with experiments without charge scaling for a wide temperature range as shown in Figure 23b.
Figure 23.
(a) Temperature dependence of ionic conductivity in SL-based electrolyte doped with 1 m and 3.25 m of LiFSI salt obtained from experiments (shown as lines) and MD simulation predictions using the polarizable APPLE&P force field (large triangle symbols) from Alvarado et al.257 Reprinted with permission from ref 257. Copyright 2018 Elsevier. (b) Temperature dependence of conductivity from MD simulations and experiments for AN:LiTFSI electrolyte with AN:Li = 3 from Seo et al.360 and H2O:LiTFSI electrolyte with H2O:Li = 2.67 from Borodin et al.258 (c) Self-diffusion coefficients of Li+, TFSI, and H2O as a function of salt concentration in H2O:LiTFSI electrolytes from MD simulations and PFG-NMR experiments.258 Reprinted from ref 258. Copyright 2017 American Chemical Society.
The scaling of the partial charges is rather motivated by mimicking the polarizability than an actual charge transfer.45, 61-63,145 Consequently, one should use a scaling factor f for the partial charges during trajectory production but full charges for analysis. Although the dynamics increases very strongly with decreasing scaling factor and hence an agreement between experimental and computational conductivity is also possible when using scaled charges for its evaluation, the actual values of these scaling factors are quite low (), much lower than values (≅f) obtained by quantum-mechanical calculations of an ion pair. In addition, these very low scaling factors also have to be applied to the computation of the dipole moment. As a result, the corresponding dipoles vanish and their correlation functions cannot contribute to the dielectric spectrum. On the other hand, if full charges are used for the analysis, dielectric spectra of charge-scaled using the factor f and polarizable MD simulations almost coincide.45
A more rigorous strategy for designing liquid electrolytes and solid electrolyte force fields was implemented by Jorn et al.,364 who used force matching to fit a nonpolarizable force field to PBE-based AIMD results on a smaller cell. A very good agreement between the two-body and APPLE&P polarizable force field was reported for both Li+ solvation and diffusion coefficients in EC-LiPF6 electrolytes, therefore indicating a great promise of such numerical force matched force fields for bulk electrolytes. Despite the great ability of this effective two-body force field to predict bulk properties of EC-LiPF6 electrolyte and dilithium ethylene dicarbonate (Li2EDC) model solid electrolyte interphase in a good agreement with predictions from polarizable force field-based simulations,365 the interfacial kinetics of Li+ transfer between electrolyte and SEI phases is quite different in the nonpolarizable and polarizable force fields. This indicates a potential limitation of the effective two-body polarization treatment when it is extended to simulations of interfacial properties while being parametrized using bulk properties.366
MD simulations also investigated ILs doped with Li+, Na+, and Mg2+ ion-based salts as alternatives for battery electrolytes. Polarizable force fields generally yielded accurate predictions of the transport and structural properties with the representative temperature dependent conductivity and ion self-diffusion predictions shown in Figure 24. Importantly, self-diffusion coefficients of organic and metal salts were accurately predicted. Special attention had to be paid to the inclusion or exclusion of the intramolecular polarization. For example, inclusion of full induced dipole-induced dipole interaction between oxygen atoms on the same TFSI anion (see Figure 24c for structure) penalizes the bidendate orientation of TSFI near the cation in which Li+ complexes with two oxygens from the same TFSI. As a result, simulations predict a lower fraction of the Li+–bidentate complexes.36,367 Decreasing oxygen polarization or exclusion of the induced dipole-induced dipole interactions between oxygens on the same molecule stabilizes the bidentate complex and improves agreement with experimental data.
Figure 24.
(a) Conductivity from the MD simulations (symbols) and experimental data (lines) of [Pyr14][TFSI] doped with LiTFSI, NaTFSI, Mg(TFSI)2, and Zn(TFSI)2 salts at metal:Pyr14 = 1:4 ratio.367 Reprinted from ref 367. Copyright 2018 American Chemical Society. (b) Diffusion coefficients for [C2mim][TFSI] + LiTFSI with C2mim:Li = 10.6 ratio from MD simulations368 shown as black symbols, lines represent the Vogel–Tamman–Fulcher fit to experimental data,368 the colored symbols show the diffusion coefficients determined by Hayamizu et al.369 for m = 0.32 mol kg−1. Reprinted from ref 368. Copyright 2014 American Chemical Society. (c) Ionic conductivity of [C2mim][BF4] and [Pyr14][TFSI] ILs doped with Li salts and snapshots of representative solvates from MD simulations using APPLE&P force field.370 Reprinted from ref 370. Copyright 2014 American Chemical Society.
The charge scaling approach was extensively discussed on the basis of MD simulations of ILs doped with Li+ and other salts. The Maginn group371 noted that “some authors have proposed the use of scaled charge models, in which the charges are uniformly scaled by a factor of 0.8 to represent the charge transfer and the polarization. The use of this kind of model provides better results to dynamical properties such as self-diffusion coefficients, viscosity, and conductivity without the high cost of the polarizable force fields. On the other hand, some works have shown that the use of full charge models (total ion charge 1.0) provides better results for structure and density, sometimes comparable to polarizable force fields.” A compromise between structural and dynamic properties is typically found on a case by case basis371 with a typical range of scaling factors from 0.6 to 0.8. In another example, in the MD simulation study of Li+ containing a dual-cation ionomer, the charge scaling decreased the ion–ion interaction distance and increased the size of ion aggregates together with speeding up dynamics.371
Another attempt to incorporate polarization involves an additional short-range two-body function that sharply decays to zero beyond the first Li+ solvation shell.69,70 It was supposed to account for the increased dipole in the first coordination shell but not beyond it. This effective two-body approach also overestimated the size of the Li+ coordination shell and predicted a slower Li+–ligand exchange and transport,70 while MD simulations using polarizable force fields accurately predicted transport and ion aggregation in poly(ethylene oxide)-based electrolytes and molten salts.261,372
3.3. Ionic Liquids
Numerous MD simulation studies of room temperature ionic liquids comprised of various cation/anion combinations have been investigated using polarizable and nonpolarizable force fields and reported thermodynamic, structural, and dynamic properties. These data provide a good opportunity for assessing the importance of inclusion of polarization in systems with chemically diverse sets of cations and anions. Despite an extensive amount of literature on modeling ILs, the direct comparison of simulation predictions using polarizable and nonpolarizable has to be made with caution. The existing nonpolarizable and polarizable force fields usually have different legacy and history of parametrization and empirical adjustments.29,44,48,192,233,262,373 This leads to variations not only in parameters related to electrostatic interactions48 but also the parameters for valence and van der Waals interactions.24,29 For example, when the parameters for the latter are fitted to match ab initio/DFT binding energies or are empirically adjusted to match certain experimental data (e.g., density ρ, heat of vaporization ΔHvap, etc.) they will most likely be quite different depending on whether a polarizable or nonpolarizable model was assumed for the force field. The dispersion term (~1/r6) describing the van der Waals interactions in a nonpolarizable model might already include some effective (mean field) approximation of the induced polarization effects.60 Therefore, it is hard to find a consistent set of polarizable and nonpolarizable models for comparison. Even when simulations do report the results for the same system using both polarizable and nonpolarizable force fields, the latter is usually reduced to simulations with a polarizable force field but the polarizability being “turned off” without any adjustment of the nonpolarizable model to effectively match the polarizable one. In such cases, while one can get a good measure of contribution of induced polarization interactions in defining a particular property of interest, it is not necessarily a fair comparison of reliability and predictability for the nonpolarizable model.
Nevertheless, a couple of studies reported data where polarizable and nonpolarizable models had the same origin and extra efforts were made to make the two types of models as consistent as possible with each other. For example, Bedrov et al.52 used the force matching approach to derive a non-polarizable version of the force field that provides the best description of atomic forces acting on atoms during simulations of ILs using a corresponding polarizable model. In this approach, first, the simulations of IL were conducted using a polarizable model. Then a nonpolarizable model that preserves parameters for van der Waals and valence interactions and partial atomic charges, but has additional two-body interaction terms that are supposed to effectively capture all induced polarization interactions, was fitted to match as close as possible the atomic forces from polarizable simulations. Taking into account that additional terms which effectively approximate polarization interactions did not have any constraints on their functional form (i.e., they were fitted as numerical functions for each possible type of atom–atom interaction) and the fitting of forces was done for the environments corresponding to the condensed state of interest, this nonpolarizable model can be considered as consistent as possible with the polarizable model it was derived from. The comparison of IL properties predicted from this consistent set of polarizable and nonpolarizable force fields facilitates the head-to-head comparison of two types of models as discussed below. However, polarizable parameters are usually transferable, making them superior to fixed charge models as the latter assume a particular environment during the parametrization process. The resulting parameters will not always function well if those assumptions are violated.323
Also, we look at more generic trends in correlations and properties of ILs predicted from simulations employing various polarizable and nonpolarizable force fields.
3.3.1. Thermodynamics.
Chaban and Prezhdo374 analyzed the impact of temperature on the ionic charges of LiCl, NaCl, and KCl clusters of 10 ionic pairs. Depending on the charge partitioning scheme, the partial charges of the atomic ions varied from ±0.34e to ±0.55e (Hirshfeld method) and from ±0.75e to ±0.87e (ESP charges). Furthermore, the temperature effect on the atomic charges was only visible for those derived by the Hirshfeld method. However, impact of the cations on the respective charges of chloride was more pronounced. The authors pointed out that the Hirshfeld charges measure the electron density localization within a certain radius and is therefore adequate to provide information on nonpolar, polar, ionic, and other types of chemical bonding between the atoms. In contrast, ESP charges reflect the electrostatic potential at the surface of the molecules and are consequently used for the intermolecular interactions. Chaban and Prezhdo also argued for the nonadditivity of the electronic interactions, leading to electronic polarization and charge transfer. The same authors also showed from ab initio MD simulations that in pyridinium-based ionic liquids the influence of the temperature on the electron delocalization was minor. However, the molecular dipole moments increased as a function of temperature due to growing thermal fluctuations.375
While the rescaling of ionic charges in nonpolarizable classical MD simulations improved the prediction of cohesive energy density, heat capacity,33,60,376 and dynamic properties,45,60 it can hardly be considered as a reliable approximation of induced polarization effects:
In MD simulations, usually no explicit hydrogen bonding potential is used. Instead, hydrogen bonding is realized via the Coulomb interaction between the positively charged hydrogen and the negatively charged, electronegative atom. In case of charge scaling, this interaction is drastically weakened, resulting in wiping out all hydrogen bonds as depicted in Figure 25.
-
For some ionic systems, the reduction of charges still did not provide a satisfactory description as visible for the molecular dipole moments in Figure 26. Although the distribution of dipoles is broadened a little bit due to the charge scaling (compare black dashed and dotted lines in Figure 26), polarizable simulations lead to much broader distributions similar to the QM results.45 However, shifts to higher dipole moments for the cations and slightly lower dipole moments for the anions are already visible from the charge scaling approach.
The impact of the induced dipoles on the molecular dipole is even more pronounced in the gas phase.52 In the case of N-methyl-N-propyl-pyrrolidinium bis-(fluorosulfonyl)imide [Pyr13][FSI], the cationic dipole moment in the nonpolarizable force field does not change very much between liquid and gas phase. The changes for the anion were a little bit more pronounced. However, in the case of the polarizable force field, the molecular dipole moments increased for both cations and anions. In addition, the discrepancy between liquid and gas phase values were much more pronounced, e.g., the dipole moment of FSI increased from 1.34 D in the liquid phase to 3.12 D in the gas phase.
-
These drastic changes for the gas phase compared to the liquid phase naturally have an impact on the heat of vaporization ΔHvap as the difference of the averaged interaction energy in liquid and gas phases is a major component. However, this effect is usually hidden by the fact that ΔHvap is part of the force field parametrization process. As such, other parameters compensate for this effect resulting in reasonable ΔHvap for nonpolarizable force fields. For example, ΔHvap of [C2mim][NTf2] is 134–136 kJ/mol. The polarizable APPLE&P force field predicts 127.7 kJ/mol, which is as fine as the values 130.629 and 143 kJ/mol377 obtained from nonpolarizable force fields. The standard nonpolarizable force field from Canongia-Lopes and Pádua29,44,60 overestimates ΔHvap = 159 kJ/mol, whereas the GAFF force field from AMBER and a charge scaling factor of 0.8 underestimates ΔHvap = 117 kJ/mol.
To analyze the impact of polarizability on ΔHvap, Bedrov et al.52 turned off the polarizable interactions in their simulations. In contrast to observations in neutral liquids, ΔHvap increased by 20–30%. It is important to keep in mind that ΔHvap for ILs is calculated relative to ion pairs in the gas phase, where polarization energy per ion is larger than in the bulk. Hence, turning off polarization reduces the cation–anion gas-phase energy more than the bulk energy per ion, therefore resulting in the increased ΔHvap, which is the opposite trend from neutral molecules.
The modeling of thermal conductivity λT of molten salts at high temperatures (1200–1300 K) with a polarizable force field378 is superior compared to switching off the induced forces or other standard nonpolarizable force fields (Fumi–Tosi potentials) as depicted in Table 5. The nonpolarizable force fields for all three molten salts tend to overestimate the thermal conductivity. Another interesting fact is that the contribution from permanent charges is counteracted by the induced contribution. As we will see, this is also true for other properties.
Figure 25.
Hydrogen bonding in various MD simulations of aqueous [C2mim][acetate] mixtures using full and scaled partial charges as well as a polarizable force field. The blue areas depict favorable positions of the water hydrogens.
Figure 26.
Histogram of molecular dipole moments of C2mim and OTf for a nonpolarizable, charge-scaled, and polarizable simulation. Except for the charges and polarizabilities all other force field parameters were kept fixed. Reproduced with permission from ref 45. Copyright 2012 RSC Publishing.
Table 5.
Thermal Conductivities of Molten Salts with Nonpolarizable and Polarizable Force Fields
| λT [W m−1 K−1] | LiCl (1200 K) |
NaCl (1300 K) |
KC1 (1300 K) |
|---|---|---|---|
| polarizable force field | 0.643 | 0.509 | 0.343 |
| polarizable force field (only nonpolarizable contributions) | 1.321 | 0.763 | 0.499 |
| nonpolarizable force field | 0.841 | 0.581 | 0.387 |
| nonpolarizable Fumi–Tosi potentials | 0.862 | 0.558 | 0.407 |
| experiment | 0.534 | 0.478 | 0.345 |
3.3.2. Structural Correlations.
The comparison between polarizable and nonpolarizable models for the description of IL structure has been discussed in several works. Quite generally, charge scaling reduces the density ρ of the ionic liquid,60 whereas polarizability increases ρ44,52 In particular, the polarizability of the cations seems to be important for the density. Turning off the anionic polarizability does not change ρ so much.44
Bedrov et al.52 compared the center-of-mass radial distribution functions g(r) for bulk [C2mim][BF4], [C2mim][FSI], and [Pyr13][FSI] ILs at 393 K as obtained from simulations using a polarizable force field (POL), a nonpolarizable force field where polarization was simply turned off (NP), and two versions of the force-matched nonpolarizable force field (NP-FMp and NP-FMe) where polarization interactions were effectively approximated by two-body interactions. Figure 27 shows the comparison of cation–cation g++(r), cation–anion g+−(r), and anion–anion g−−(r) radial distribution functions. In all three systems, the largest deviation between POL and NP force fields is observed for anion–anion correlation. Moreover, in case of cation–cation and cation–anion, the mean field adjustment to the nonpolarizable model (NP-FMp and NP-FMe models) leads to almost a complete recovery of g(r)s predicted from the POL model. In contrast, for the anion–anion correlation this provides only minor improvement. The anion–anion g−−(r)s with any nonpolarizable model showed stronger ordering compared to predictions using the POL model.
Figure 27.
Ion center-of-mass radial distribution functions g(r) obtained from simulations using different force fields for [C2mim][BF4], [C2mim][FSI], and [Pyr13][FSI] ILs at atmospheric pressure and 393 K.52 Reproduced from ref 52. Copyright 2010 American Chemical Society.
Because of the screening of the electrostatic interactions by the induced dipoles, the repulsion between like charges and the attraction between ions of opposite charges is reduced.45 Consequently, the structural order is less.122,135 At short distances, the energy barriers to escape the ion cage are lower.48,138 At longer distances, the oscillations in the radial distribution functions and hence the charge ordering function Q(r) are flattened,122,135 which can be fitted beyond 5 Å by
| (3.3.1) |
and is depicted in Figure 28. Negative values of Q(r) indicate ions of opposite charge, whereas positive values depict an accumulation of like charge ions. As visible in the inset, the flattening parameter 1/σ increases linearly with the amount of molecular polarizability.
Figure 28.
Charge ordering function Q(r) (see eq 3.3.1) of [C2mim][OTf] using a polarizable and nonpolarizable force field.135
The same trend was observed by Yan et al.,63 who compared ion–ion correlations in [C2mim][NO3] and also found significantly more ordered and longer-range anion–anion correlations predicted by a nonpolarizable model compared to the polarizable one. A very recent study by McDaniel and Yethiraj79 further confirmed that this phenomenon is quite generic by studying bulk [C4mim][BF4] and demonstrating that even charge rescaling does not eliminate the overestimated long-range ordering in the anion–anion correlation. These authors also provided a mechanistic explanation why this effect has to be generic to all ionic liquids with asymmetric cation/anion pairs. McDaniel and Yethiraj suggested that the observed structural deviations are the consequence of a qualitatively different electronic dielectric response at infinite frequency by polarizable and nonpolarizable models. The average reciprocal space Coulomb interactions are plotted in Figure 29 as a function of wavevectors k. In the long-range limit (small wavevector) the Coulomb interactions are approaching unity for nonpolarizable models (independently whether the ionic charges were scaled or not), indicating an infinite frequency dielectric response of ϵ∞ ≈ 1.0. For the polarizable model, the Coulomb interactions are approaching 0.5 value, which corresponds to ϵ≈ ≈ 2.0. The difference in screening conditions is the primary reason for enhanced ion structuring at 6–7 Å distances, which is independent of the strength of ion–ion interactions (as demonstrated by results from scaled and nonscaled simulations with nonpolarizable force fields). Therefore, McDaniel and Yethiraj suggest that any simulations using pairwise-additive potentials (i.e., nonpolarizable electrostatic interactions) will contain some artifacts in the predicted liquid structure.
Figure 29.
Reciprocal-space Coulomb interaction in [C2mim][BF4] computed with (black curve) and without (red curve) polarization and with scaled charges (blue curve). The dashed lines correspond to the long-range limit (k = 0). Reproduced from ref 79. Copyright 2018 American Chemical Society.
3.3.3. Ion Dynamics.
It is well documented that for all ionic liquids, polarizable models consistently predict faster relaxations (including translational and rotational motions), higher selfdiffusion and ionic conductivity, and lower shear viscosity than the nonpolarizable models.45,60,77,122,379-381 Bedrov et al.52 showed that even if a nonpolarizable model is fitted (using the force matching approach, NP-FMe and NP-FMp models discussed above) to reproduce (as far as possible) the forces acting on atoms in the simulations using a polarizable model, the self-diffusion coefficients are still a factor of two to three lower than what was predicted by simulations with the polarizable force field. The authors associated such behavior with the inability of the fitted nonbonded force field to capture directionality of instantaneous atomic forces and as a consequence the correct distribution/fluctuations of those forces. Yan et al.382 suggested that the faster dynamics observed in simulations of ILs with polarizable models is the consequence of attenuated long-range electrostatic interactions caused by enhanced screening from the induced dipoles, implying that simulations using polarizable models are analogous to simulations with the nonpolarizable model but at higher temperatures. The influence of polarization on the ion transport increases with decreasing temperature indicating that a nonpolarizable force field will have a higher activation energy for transport properties.44 Interestingly, a temperature effect on the charge scaling factor derived by ESP charges could not be observed for simple molten salts374 and pyridinium-based ionic liquids.375
Yan et al. also suggested that polarization affects the vibrational spectrum and hence can influence the hydrogen bond dynamics in ILs.382 McDaniel and Yethiraj suggested that enhanced dynamics in simulations with polarizable force fields is due to the influence of long-range screening conditions on modulated ion structuring.79 The enhanced dynamics in ILs also could be obtained by reducing ion charges (through uniform rescaling). Chaban et al.60 reported that scaling factors ranging between 0.64 and 0.78 (depending on IL and property of interest) can reproduce experimental dynamic and thermodynamic properties. Effectively, by scaling ionic charges, the effective ion–ion interactions are weakened resulting in a higher mobility. The damping of electrostatic interactions can also be explained by a continuum model depicted in Figure 30. Here, the charged particles are immersed in an “inner solvent” of the induced dipoles, represented by a dielectric continuum with a dielectric constant ϵ∞. Choosing the correct boundary conditions for the electrostatic potential inside the spheres Φsp and in the dielectric continuum Φcon,
| (3.3.2) |
| (3.3.3) |
| (3.3.4) |
using the general solution
| (3.3.5) |
of the Laplace equation ∇2Φ = 0. The interaction of the point charge in Figure 30 with charges outside its sphere is given by (see appendix of ref 45 for details).
Figure 30.
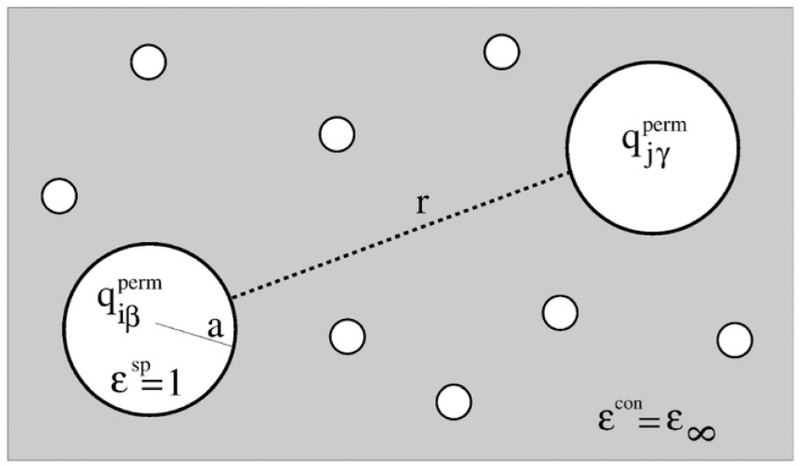
Continuum model of charged particles. Each atom β of molecule i or atom γ of molecule j is approximated by sphere with a dielectric constant of ϵsp = 1 and a radius a. The dielectric continuum between two charges has a dielectric constant of ϵ∞. Reproduced with permission from ref 45. Copyright 2012 RSC Publishing.
| (3.3.6) |
In eq 3.3.6, the radius a of the sphere does not play a role as the distance r between the two charges is much larger than a. (Although this assumption might not be valid in dense liquids and solid stets where r can be comparable to a). The screening of the electrostatic interaction by a factor of 1/ϵ∞ in eq 3.3.6 corresponds to a screening factor of for each partial charge,45,62 which is basically the reciprocal value of the refractive index and is in the range of 0.7–0.8, which was already obtained by quantum-mechanical calculations of molecular charges of ion pairs.6,48,61 The corresponding calculation for the interaction inside the cavity yields
| (3.3.7) |
The acceleration of the ionic diffusion coefficients due to the damping of the electrostatic interactions can be fitted to60
| (3.3.8) |
The constant exponent c2 is similar for cations and anions45,60 in charge scaled simulations. If one correlates the scaling factor f with a molecular polarizability α on the basis of the effective Coulomb energy as reported in ref 45, eq 3.3.8 also holds true for the molecular polarizability.45,135 Again, c2 values for cations and anions are similar but less compared to the respective scaling factor f. So far, the molecular polarizabilities were scaled in a uniform way.
Chaban et al. used a pseudofluctuating charge model to describe the charge transfer in NaCl and KCl using classical MD simulations of 1000 ion pairs and switching a certain number of atomic charges to zero or ±1e for neighboring pairs.383 At a fraction of roughly 90% of fully ionic species, the computational diffusion coefficients agree with experimental data. As average scaling factors of 0.80 or even lower for each ion are needed to reproduce experimental diffusion coefficients, the nonlinearity of the scaling factor becomes evident. This further argues for using the factor f scaled charges only for trajectory production to mimic the average effect of polarizable forces and the full charges should be used for the computation of conductivity as much lower charge scaling factors would be required to reproduce conductivity if the scaled charges are also applied for the conductivity computation.
However, the cationic polarizability seems to have a bigger impact on the diffusion coefficients than the anionic α. Turning off the respective induced dipoles for cations resulted in much lower diffusion coefficients, whereas nonpolarizable anions but polarizable cations yielded diffusion coefficients comparable to the full polarizable system. To some extent, this can be explained by the significantly higher molecular polarizability of the cations compared to the anions.
Depending on the ionic liquid, polarizability effects on the rotation are comparable45 or less pronounced.52 The rotational relaxation of the dipole moment may change drastically for small changes of the charge scaling factor as visible in Figure 31. For [C2mim][OTf], this turning point appears around a scaling factor of 0.85, which is most common for the scaling. Consequently, one has to be very careful for the evaluation of a meaningful scaling factor as several properties may be quite insensitive and others very sensitive for the variation of the scaling factor. As a consequence, an analogous equation to (3.3.8) does not exist for the scaling factor f but for the molecular polarizability α. Flowever, the corresponding c2-value of the cations is higher than for the anions.
Figure 31.
Rotational relaxation constants of (a) C2mim and (b) OTf of a charge-scaled and polarizable simulation. Reproduced with permission from ref 45. Copyright 2012 RSC Publishing.
3.3.4. Collective Dynamics.
Because many dynamic properties scale with the viscosity of the system, the reproduction of this physicochemical property is highly desirable. Both the nonpolarizable GAFF-force field using a charge scaling factor f = 0.8376 as well as the polarizable APPLE&P force field44 yield reasonable agreement with experiment for many ILs. The latter force field is also capable of reproducing the corresponding conductivities. Only for some NTf2-based ILs the polarizable force field has to be optimized to show less discrepancy with the experimental values.
Polarizable force fields for ionic liquids are also suitable to compute frequency-dependent spectra, e.g., the conductivity spectrum,382 OKE spectrum,382 and dielectric spectrum.45,136,138 Interestingly, charge scaled simulations are also capable of reproducing the frequency-dependent dielectric spectrum over a broad frequency regime.45 Generally, the dielectric spectrum can be decomposed into a dielectric permittivity ϵ(ω) and a dielectric conductivity ϑ0(ω). The latter is only present in the case of charged species. Ionic liquids are an interesting solvent class as the molecular ions possess a net charge and dipole moment.138 Consequently, these ions contribute to both ϵ(ω) describing the relaxation of the collective dipole rotations and ϑ0(ω) characterizing the mutual motions of the ions. In simple electrolyte solutions, the neutral solvent, e.g., water, is responsible for ϵ(ω) and the atomic ions, e.g., NaCl, yield a small ϑ0(ω) usually at higher frequencies ω. In ionic liquids ϵ(ω) and ϑ0(ω) are not separated in frequency space but overlap making an interpretation on the sole basis of the experimental spectrum difficult. In MD simulations, the collective dipole moment can be split into several contributions:
| (3.3.9) |
| (3.3.10) |
| (3.3.11) |
Because the ionic liquid ions are charged species with a molecular charge qi, a molecular dipole moment is not-well-defined. Consequently, one has to choose a reference site. The center of mass of that molecule i turned out to be useful, as it is also the reference site for rotation and translation.138,316 Autocorrelation functions of the collective rotational dipole moment and the collective induced dipole moment contribute to the dielectric permittivity ϵ(ω)
| (3.3.12) |
and the autocorrelation function of the time derivative of the collective translational dipole moment to the dielectric conductivity ϑ0(ω). Interestingly, the relaxation constants for the latter autocorrelation function are very similar to those obtained from the autocorrelation function of neighborhood residency.138 In other words, the stability of the ion cage and the exchange of its members directly influences the jittering of the central ion and consequently the high-frequency regime of ϑ0(ω).
The summations in eqs 3.3.9-3.3.11 can also be split into contributions from the cations and anions. A corresponding decomposition is given in Table 6. The static permittivity ϵ(0) is governed by the relaxation of the permanent dipoles of the anions. Pure induced contributions are negligible for the static value. The cross-correlations between permanent anionic and induced cationic dipoles enhances ϵ(0), whereas the interaction of permanent anionic dipoles with induced anionic dipole moments decreases ϵ(0). The influence of the induced dipoles is more of subtle nature and becomes visible in the frequency-dependent dielectric spectrum as it shifts ϵ(ω) contributions of the cations and anions to higher frequencies (as expected from the increased dynamics of polarizable systems). Furthermore, at high frequencies an additional small peak arises from the autocorrelation of the induced cationic dipole moments.
Table 6.
Contributions of , , and to the Static Dielectric Permittivity ϵ(0) Obtained from a Polarizable MD Simulation of [C2mim][OTf]138,a
| C2mim |
OTf |
||||
|---|---|---|---|---|---|
| permanent | induced | permanent | induced | ||
| C2mim | permanent | 0.82 (0.69) | 0.03 | 0.18 (0.30) | 0.04 |
| induced | 0.03 | 0.11 | 0.36 | 0.00 | |
| OTf | permanent | 0.18 (0.30) | 0.36 | 6.53 (6.46) | −0.15 |
| induced | 0.04 | 0.00 | −0.15 | 0.03 | |
The number in brackets represent the contributions in a non-polarizable simulation of the otherwise same force field.
Optical Kerr effect (OKE) spectroscopy yields complementary information to dielectric spectra. First, computational OKE spectra were calculated by Margulis and co-workers384 using molecular polarizabilities due to the immense computational effort. They showed that the ionic cage is important for the longtime decay of the OKE spectrum in agreement with experiment.385 Ishida et al.386 also used molecular polarizabilities to compare vibrational density of state spectra to OKE spectra for [C4mim][XF6] with X = (P,As,Sb). They also reported that the OKE spectra are dominated by the molecular reorientation of the cations and anions indicating weak interionic interactions.
In principle, the collective polarizability Π(t) is given by
| (3.3.13) |
The nonlinear response of the liquid probed by OKE is composed of a zero-time electronic response (containing no information on molecular dynamics) and the nuclear response characterized by the anisotropic polarizability response function
| (3.3.14) |
using the off-diagonal Cartesian components a ≠ b ∈ (x,y,z) and the Heaviside function θ(t). Its Laplace transform yields the OKE response function χ(ω) depicted in Figure 32 for [C2mim][NO3].382
Figure 32.
Anisotropic response function R(3)(t) and OKE response function χ(ω) of polarizable and nonpolarizable [C2mim][NO3] simulations.382 Reproduced from ref 382. Copyright 2010 American Chemical Society.
In the first approximation, χ(ω) can be calculated from nonpolarizable simulations using the time-dependent dipole–dipole tensor and molecular polarizabilities from a QM frequency calculation. The initial response in Figure 32 at 10 fs is attributed to intramolecular vibrational motion. The following underdamped oscillations with a period of 0.037 ps (~900 cm–1) on top of the damped collective response are assigned to bending motions. The collective response itself is mainly due to librational dynamics. As intramolecular bonding and angle vibrations are similar in the polarizable and nonpolarizable simulation, the corresponding R(3)(t) looks alike. However, at longer times the polarizable R(3)(t) of a stronger signal is visible, indicating faster relaxation of rotational dynamics which is already expected because of the overall faster dynamics in polarizable systems. The OKE response function χ(ω) shows a broad peak up to 300 cm−1. Here, the discrepancy between polarizable and nonpolarizable response is most prominent and be attributed to diffusive reorientation.
Another THz spectroscopy is solvation dynamics spectroscopy387 probing the solvent response due to an instantaneous change of the local electric field. This solvent response is coupled to the dielectric spectrum,136 which is expected because dielectric spectroscopy applies an external electric field, whereas solvation dynamics spectroscopy creates a strong local electric field and both probe the solvent response. Polarizable simulations of the ionic liquids [C2mim][BF4], [C2mim][OTf], and [C4mim][BF4] improved the agreement with experimental data significantly, in particular in the initial time regime and the long-time limit.137 Only the induced dipoles of first-shell solvent molecules around the excited solute are affected by the solute dipole change, although the electrostatic interactions are visible up to 40 Å. Interestingly, the pure induced contribution to the solvent response function is weak, but the cross-correlation between permanent charges and induced dipoles is strong and counteracting the contribution from the permanent charges only.
Furthermore, polarizable forces in [C2mim][OTf] and [C2mim][N(CN)2] are responsible for the hidden breakdown of linear response theory in the computation of the Stokes shift.388,140 Using a corresponding nonpolarizable force field nonlinear effects (slowing down the Stokes shift relaxation function) could not be detected.388,389 Consequently, this fact emphasizes again that induced dipoles do not only affect the dynamics of the liquid system but may also change the fundamental response mechanism to a nonequilibrium event changing the local electric field.
3.4. Electrolyte–Electrode Interfaces
Development of electrochemical devices such as batteries and supercapacitors critically depends on understanding of the charge transport, charge storage, and interfacial chemistry at the electrolyte–electrode interfaces.390-393 Atomistic MD simulations have been extensively applied to study various correlations of electrolytes at charged surfaces, including the structure of electric double layers (EDL) of pure ILs and ionic solutions on flat electrodes,394-398 dependence of EDL capacitance on electrode voltage and temperature,50,399,400,401 as well as electrode surface topography, curvature, and porosity.396,402-410 A more comprehensive discussion of these simulations can be found in several recent review papers.411-415 In such simulations, the influence of polarization effects is even more complex and can be divided into two issues:
Electrodepolarization;
Influence of electrolyte polarization on EDL structure and properties.
In this section, we briefly discuss these specific issues.
3.4.1. Electrode Polarization.
The first issue is related to how the charged surface is represented in MD simulation methodology and is coupled to the electrolyte. The most straightforward approach is to confine the electrolyte between two solid surfaces and then apply fixed charges +Q and −Q on the electrodes. The total electrode charge Q is usually homogeneously distributed between N atoms on the electrode surface, with each atom being assigned a charge value of q = Q/N. As the simulation progresses, the electrolyte will rearrange near each charged surface forming the corresponding EDLs. The electrode potentials as well as the potential difference between electrodes are not known a priori and have to be determined by post analysis of simulation average charge density profiles established in the electrolyte in the direction perpendicular to the electrode surfaces. Because of its simplicity, this approach has been employed in the overwhelming majority of simulations of various ILs and other electrolytes on charged surfaces. However, there is an important drawback in the underlying physical assumption of this approach. In real charge storage devices, the control parameter is the electrostatic potential difference between electrodes, while the charge magnitude and distribution on the electrode surface must reflect the electrode polarization associated with the restructuring of EDL near the electrode surface.
A more natural simulation set up is to confine the electrolyte between two electrodes with a specified applied potential difference between them. This method does not assume a priori any charge distribution on the electrode surface. Instead, the potential difference between two electrodes is constrained while the charges on electrode surfaces are allowed to equilibrate to minimize the electrostatic energy of the system. In this constant potential technique, the electrode charges are assigned either by imposing a fixed electrostatic potential on the electrode surface416-418 or by constraining the total electrode charge to a desired value and computing the electrode chemical potential as a Lagrange multiplier associated with such a constraint.419 To reflect a semiconducting character of the electrode, one can introduce an additional energy term approximating the density of states dependence on electrode charge. However, in most simulations using a constant potential approach, the electrodes are treated as conductors and the distribution of charges on such electrodes can be effectively captured using Gaussian smeared charges assigned on electrode atoms.417,420 The distribution of each charge is controlled by a single parameter, the width of the Gaussian, that in turn can be tuned to quantitatively reproduce the expected behavior of a conductor upon the approach of an external charge.418 It was shown that the width of the Gaussian distribution of about 0.5 Å is optimal for most cases.418,421 The electrode charges can also be assigned on a finer grid than the locations of atoms representing the electrode, resulting in a better stability and convergence of the method.422 The choice of the width of Gaussian distribution is often ambiguous, therefore raising an important question regarding the sensitivity of EDL properties predicted from simulations on the choice of this simulation parameter. Moreover, most MD simulation codes treat electrostatic charges as point distributed and hence utilization of Gaussian distributed charges requires modification of the energy, force, and stress functions. However, Vatamanu et al.423 recently showed that constant electrode potential simulations that employ Gaussian distributed charges can be modified by adding an energy term proportional to the electrode charge squared while keeping other electrostatic interactions similar to those of point charges (i.e., excluding calculations of Gaussian cross terms of the electrode–electrode and electrode–electrolyte electrostatic interactions). The scheme can be straightforwardly implemented in most MD simulation codes, as it requires no modifications of the standard energy and force evaluation routines and has demonstrated accurate prediction of EDL structure, electrode charge density, and differential capacitance.
Holm and co-workers proposed other efficient methods to handle electrostatic interactions in systems with 2D periodicity and dielectric interfaces. They demonstrated that linear scaling with number of charges can be obtained for electrostatic interactions that include image charges (ICMMM2D and ELCIC methods).424,425 Subsequently, the induced charge computation (ICC) approach426 was introduced and which can treat arbitrary curved surfaces and calculate the induced polarization charge located on point charges (instead of Gaussian charges discussed above). It can be applied for systems with arbitrary dielectric contrasts, including metallic electrodes, and any point charge Poisson solver can be used for efficient calculation of Coulomb interactions. The method can be straightforwardly applied to constrain a desired potential difference between electrodes427 and has been employed in recent studies of charging/discharging kinetics of IL electrolyte in charged nanopores.428,429
In the constant electrode potential approach, the charges on the surface can
evolve in response to EDL restructuring, i.e., due to electrode electronic polarization from electrolyte rearrangement near the surface, and
have a heterogeneous distribution in accordance with the structural heterogeneities (surface roughness or defects) inherent to a given electrode surface structure.
It is clear that in this case, the electrode polarization and electrolyte restructuring in the EDL are coupled, which is physically a more realistic representation. The question is, how important is the inclusion of this additional physics into simulations for prediction of different properties? Figure 33 compares charge distributions on the basal and prismatic plane graphite surfaces as obtained from MD simulations using a constant applied potential approach.394 In the constant charge method, the charge distribution would correspond to the delta function. In the constant potential method, a relatively broad distribution of charges for the electrode surface atoms is observed. Note that on atomically flat basal plane graphite, the distributions are relatively symmetric and have a single peak, therefore approximating such distribution with a single average value (as in the constant charge approach) might be a reasonable approximation. However, for an atomically more corrugated prismatic graphite electrode, multiple peaks in the charge distribution are visible, indicating that approximating such distributions with a single charge value cannot be adequate. Taking into account that in many energy storage devices, various chemical modifications of electrode surfaces are considered as one of the routes to design more efficient electrode materials, the ability of MD simulations to capture the details of charge distribution on electrode surfaces is crucial for the accurate prediction of EDL properties.
Figure 33.
Distribution of instantaneous charges induced on electrode surface atoms as obtained from simulations using the constant applied potential for two ILs on atomically flat basal plane graphite (top) and atomically corrugated prismatic graphite (bottom). Reprinted with permission from ref 394. Copyright 2015 Elsevier.
There have been several works that compared properties predicted from simulations using constant charge and constant potential approaches. One of the most comprehensive discussions and comparisons were presented by Haskins and Lawson,430 where they systematically investigated properties of [C2mim][BF4] at charged surfaces using different methods. Figure 34 shows the differential capacitance obtained for this IL at the graphite electrode. Both, constant charge and constant potential approaches result in very similar average capacitance of ~4.8 μF/cm2. However, the dependence of differential capacitance on the electrode potential is different. The constant charge method produces a well-defined camel-shape dependence, while constant potential approach results in more shallow dependence with less pronounced peaks. At larger magnitudes of electrode potential (>∣1∣V), the constant electrode potential predicts higher values of the capacitance and weaker dependence on the electrode potential. An analysis of rearrangements in the EDL structure with changes of the electrode potential allowed the authors to make the following conclusions: In the constant electrode potential method, more cations and anions are allowed to pack in the surface ion layer compared to a constant charge method. Thus, the energetic favorability to have both ions in the surface layer makes their separation more difficult and hence higher electrode potentials are required to expel the co-ion from the surface layer. This leads to higher values of differential capacitance for the constant charge potential at low voltages and lower values at higher voltages compared to the constant potential method. Because the average capacitance in both methods is the same, Figure 34 illustrates that in the constant electrode method the EDL restructuring responsible for the charge storage is spread out over a larger potential window compared to the constant charge method. Interestingly, in coarse-grained simulation of IL on a smooth electrode surface or atomistically detailed graphene surface, the choice of electrode treatment (constant charge or constant potential approach) did not show a significant effect on electric double layer structure or differential capacitance.431 In another work, Wang et al.432 showed that if the electrode charge distribution is restricted to the locations of atoms representing the electrode surface, then it does not provide a uniformly constant electrostatic potential on the electrode surface leading to both spatial and temporal deviations from the target value of the potential. While in the constant potential method these deviations are relatively minor, for the constant charge method they can be up to 20%, particularly at higher voltages. Finally, Merlet et al.433 and Vatamanu et al.50 showed that utilization of the constant charge approach can significantly change the relaxation times in the EDL and lead to orders of magnitude faster charging/discharging kinetics compared to the constant potential method.
Figure 34.
Differential capacitance as a function of electrode potential as obtained from MD simulations of [C2mim][BF4] on atomically flat basal plane graphite using constant charge and constant potential methods. Adapted with permission from ref 430. Copyright 2016 American Institute of Physics.
The inclusion of electrode polarization becomes even more important for the accurate modeling of aqueous electrolytes with small ions such as Li+ that have a compact solvation shell and strongly polarize the electrode upon their close approach.434 Figure 35a compares the distribution of the surface charges from constant potential simulations of the water-in-salt electrolyte (WiSE) with the surface charges for the electrodes in contact with traditional ILs. A much stronger polarization of the surface by small Li+ compared to polarization by the bulky C2mim, C4mim, and NTf2 ions of IL leads to a much broader charge distribution with higher probability of more negative charges due to close approach of the Li+ to the negative electrode. A positive electrode has a narrower charge distribution because the inner Helmholtz layer primarily consists of the bulky NTf2 anions, leading to weaker electrolyte polarization similar to the IL double layers as seen in Figure 35b. Thus, the constant electrode approaches are expected to become even less accurate for the WiSE electrolytes than for ILs.
Figure 35.
(a) The distribution of fluctuant charges for the graphite electrode top layer in contact to the electrolyte at a potential difference between electrodes of ΔU = 2 V for the water-in-salt (WiSE) (21m LiNTf2 + 7m LiOTf) electrolyte from MD simulations using a constant electrode potential methodology.434 Solid black line compared electrode charges in contact with WiSE electrolyte and IL at similar surface voltage φ. A comparison of the fluctuant charge distribution for WiSE electrolyte studied here at the positive and negative electrode of a system at ΔU = 2 V as a function of the positive part of the charge.434 Reproduced from ref 434. Copyright 2017 American Chemical Society.
3.4.2. Electrolyte Polarization.
Another question is, how important is the electrolyte polarizability near charged surfaces? Besides the already discussed influence of induced polarization on bulk properties of ILs and electrolytes, polarizability of electrolytes can also affect the EDL properties. Haskins and Lawson430 compared the average magnitude of induced dipoles on [C2mim][BF4] ions as a function of their separation from the electrode surface (Figure 36a). They found that surface cations have induced dipoles directed away from the surface, while surface anions have their induced dipoles toward the surface. This alters the interaction of these ions with the corresponding surfaces and between ions in the surface layer(s) and hence creates additional energetic barriers to EDL formation. To quantify how much this affects the differential capacitance, Haskins and Lawson430 conducted two simulations of the same electrolyte at charged surfaces using a constant potential approach: in the first case, they used a fully polarizable force field to represent [C2mim][BF4], while in the second, they turned off all polarization effects in the electrolyte (i.e., set atomic polarizabilities to zero). Figure 36b shows the resulting difference of differential capacitance (ΔCD = CD(pol) – CD(nonpol)). They reported that at lower voltages, electrolyte polarizability tends to reduce the differential capacitance values, while at higher voltages it leads to a slight increase. This behavior can be understood by realizing that induced dipoles oppose the electric field imposed by the electrode surface and hence soften the interactions between ions near the surface.
Figure 36.
(a) The average induced dipole normal to the electrode surface in simulation [C2mim][BF4] using a polarizable force field on atomically flat basal plane graphite using constant potential method. (b) Difference of differential capacitances obtained from simulations using polarizable nonpolarizable force fields for [C2mim][BF4] in simulations with constant potential method. Adapted with permission from ref 430. Copyright 2016 American Institute of Physics.
4. CONCLUSIONS
Nowadays, polarizable MD simulations of electrolytes, ionic liquids, their mixtures with cosolvents like water as well as at interfaces with gases or solids start to become routine as the corresponding computational power is available. For many applications, in particular for structural investigations, non-polarizable simulations may yield satisfactory agreement with experimental results. Here, system sizes and simulation trajectory length can be extended due to the cheaper computational costs compared to polarizable simulations, leading to statistically more reliable computational results. On the other hand, local interactions in a fluctuating environment cannot be easily modeled by static electrostatic parameters, i.e., fixed charges, and induced dipoles may be inevitable to make simulation predictions close to experimental data. However, there is an unjustified belief that reliability problems disappear once the induced dipoles are switched on.
The dilemma is depicted in Figure 37. Nonpolarizable MD simulations are usually three to ten times faster than corresponding polarizable simulations depending on the exact computational conditions, e.g., the MD program, its algorithm to compute the induced dipoles at a given configuration, the time step, etc. Nonpolarizable MD simulations have proven to reproduce structural features for a plethora of ionic liquids. However, they usually fail to capture the dynamics of various systems by a significant factor. Possible byways in non-polarizable simulations, e.g., scaling charges or reparametrizing Lennard-Jones interactions, come at a cost as they only model an averaged effect of the induced dipoles. The collective dynamics and sometimes even the molecular dynamics may be reproduced by these methods, but local interactions like hydrogen bonds suffer from downscaling the charges. Spontaneous, nonequilibrium events, e.g., turning on an electric field or exciting a molecule by a laser beam require an instantaneous response of the ions and solvent molecules which may only be given by their induced dipoles. Furthermore, the local environment may also influence the interactions of the ions. For example, the repulsion between ionic liquid cations is reduced at the interface between liquid and air or at a negative electrode. Because many building blocks of the ionic liquid cations and anions are rather rigid (with the exception of the alkyl tails), fixed partial charge distributions may not be able to capture this effect.
Figure 37.
Comparison of polarizable and nonpolarizable MD simulations of ionic liquids for various applications. Nonpolarizable simulations with particularly modified Lennard-Jones interactions to accelerate dynamics as well as fluctuating charge simulations in case of polarizable MD simulations are less popular and hence grayed in this figure.
Interestingly, the physicochemical properties, which are generally more time-consuming to compute, are usually those which are better described with polarizable force fields as visible in Figure 37. MD simulations of mixtures are more computationally demanding compared to bulk simulations of pure liquids. Here, the interactions of the ions with cosolvents or solutes profit from a polarizable description which is especially profound for the concentrated electrolytes containing small cations such as Li+, Mg2+, or Zn2+ that are of interest to battery applications. As described above, interfaces are even more complicated and also often require induced dipoles. In the case of dynamics, the very large number of nonequilibrium simulations, e.g., in solvation dynamics spectroscopy, to get reliable statistics is often a computational issue. As a result, the total simulation period of these nonequilibrium simulations is longer compared to a single equilibrium run. Nonequilibrium events may necessitate induced dipoles for nonlinear effects.142,388
The most common algorithms to model induced dipoles are Drude oscillators and induced point dipoles, which are physical and mathematical approximations of induced polarization, result in similar predictions of structure and dynamics for ionic liquids and electrolytes. The computational cost of these two approaches is comparable and significant progress has been made to reduce it in the past decades. Atomic polarizabilities are available from various sources, but only a few complete polarizable force fields (e.g., APPLE&P) of ionic liquids exists. Using atomic polarizabilities in combination with existing nonpolarizable force fields, e.g., the ionic liquids force field from Canongia-Lopes and Padua, requires a reparametrization of the Lennard-Jones interactions which can be done individually for the atoms or by scaling the Lennard-Jones ϵ as a function of the atomic polarizabilities. However, polarizable force fields for ionic liquids from various groups are currently under development and will be available soon to the computational community, enabling large scale simulations with high performance packages such as NAMD116 for Drude approaches or Tinker-HP154 for AMOEBA and other point dipole induced models up to Gaussian-based electrostatics ones.
ACKNOWLEDGMENTS
We acknowledge support from the following grants: C.S. from the Austrian Science Fund (FWF P28556-N34), D.B. from the Army Research Laboratory under cooperative agreement number (W911NF-12-2-0023), and A.D.M. and B.R. from National Institutes of Health (GM131710 and GM072558). O.B. was supported as part of the Joint Center for Energy Storage Research, an Energy Innovations Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences through IAA SN2020957.
Biography
Dmitry Bedrov received his Ph.D. in Chemical & Fuels Engineering in 1999 and has been working in the area of multiscale modeling of materials for more than 20 years. He has been involved in several interdisciplinary multiscale modeling centers in academia and industry. Currently, Prof. Bedrov is an Associate Professor in the Materials Science & Engineering Department at the University of Utah. He is the Associate Director of the Collaborative Research Alliance with the Army Research Laboratory for Multiscale Modeling of Electronic Materials, leading the Electrochemical Devices area. He has over 150 publications in peer-reviewed journals and four book chapters. His awards include Humboldt Foundation Fellowship for Experienced Researchers and recognition by the University of Utah for Extraordinary Research Accomplishments.
Jean-Philip Piquemal completed his Ph.D. in Theoretical Chemistry at Université Pierre et Marie Curie (UPMC) in Paris (2004). He then moved to the theory group of Thomas Darden at the National Institute of Environmental Health Sciences (NIEHS, NC, USA) for a NIH postdoctoral fellowship. In 2006, he was appointed as an Assistant Professor at UPMC and came back to Paris, where he defended his Research Habilitation (2009). Since 2011, he is Professor of Theoretical Chemistry at Sorbonne Université. He is currently junior member of the Institut Universitaire de France and Director of the Laboratoire de Chimie Théorique (UMR 7616, Sorbonne Université-CNRS). He is specialized in the fields of Quantum Chemistry and Molecular Simulation. In 2018, he was awarded an ERC Synergy grant to develop new High-Performance Computing strategies for multiscale modeling.
Oleg Borodin is a scientist at the Electrochemistry Branch of the Army Research Laboratory (ARL), Adelphi, MD, working on multiscale modeling of materials for energy storage applications with a focus on advancing battery technology. His expertise includes quantum chemistry calculations and high throughput screening of electrochemical reactions in electrolytes and electrode–electrolyte interfaces including solid electrolyte interphases (SEIs), atomistic molecular dynamics simulations of liquid, ionic liquid, polymeric, and solid electrolytes for battery applications, solid electrolyte interphase components, and electric double layer structures. Dr. Borodin published more than 170 peer-reviewed papers and coauthored six book chapters.
Alex MacKerell received a Ph.D. in Biochemistry in 1985 from Rutgers University, which was followed by postdoctoral fellowships in the Department of Medical Biophysics, Karolinska Institutet, Stockholm, Sweden, and the Department of Chemistry, Harvard University. In 1992, he assumed his faculty position in the School of Pharmacy, University of Maryland, where he is currently the Grollman–Glick Professor of Pharmaceutical Sciences and the Director of University of Maryland Computer-Aided Drug Design Center. MacKerell is also cofounder and CSO of SilcsBio LLC, a biotech company in the area of computer-aided drug design and development.
Benoit Roux was born in the city of Montreal, Canada, in 1958. In 1981, he received a B.Sc. in Physics from the University of Montreal, followed by a M.Sc. in Biophysics in 1985 under the supervision of Remy Sauvé. In 1990, he obtained a Ph.D. in Biophysics from Harvard University under the direction of Martin Karplus. In the past decade, he has held positions at the University of Montreal and the Weill Medical College of Cornell University. Since 2005, he is at the University of Chicago, where he is the Amgen Professor of Biochemistry and Molecular Biology and Professor in the Chemistry Department. He also has a joint appointment at Argonne National Laboratory, where he is Senior Computational Biologist. His laboratory mostly uses theoretical techniques, such as classical molecular dynamics and free energy computations, to understand the function of biological macromolecular systems such as ion channels, receptors, and protein kinases.
Christian Schröder studied Chemistry at the Justus-Liebig University in Giessen and at the Georg-August University in Göttingen (Germany). After receiving his Ph.D. at the Max Planck Institute for Biophysical Chemistry in Göttingen in 2003, he accepted a position as postdoctoral research fellow at the University of Vienna (Austria) to study biomolecular solvation via MD simulations. In 2006, Christian Schröder started his independent research career at the University of Vienna, focusing on the evaluation of the bulk behavior of ionic liquids and on the development of polarizable force fields to reproduce experimental spectroscopy data from MHz to THz. In 2012, he finished his habilitation thesis on “Computational Studies of Molecular Ionic Liquids” and was awarded the venia docendi in “Theoretical Chemistry”. From 2013 to 2017, he was appointed as working group leader of European COST action CM1206 responsible for “Physicochemical Properties of Ionic Liquids and Their Modelling”. Christian Schröder’s current research interests are based on computational spectroscopy including NMR, dielectric, and THz spectroscopy to study solvation behavior with a particular focus on neoteric solvents such as ionic liquids or their solutions.
Footnotes
Notes
The authors declare the following competing financial interest(s): DB is one of the co-owners of Wasatch Molecular Inc. which distributes the APPLE&P database.
REFERENCES
- (1).Azov VA; Egorova KS; Seitkalieva MM; Kashin AS; Ananikov VP “Solvent-in-salt” Systems for Design of New Materials in Chemistry, Biology and Energy Research. Chem. Soc. Rev 2018, 47, 1250–1284. [DOI] [PubMed] [Google Scholar]
- (2).Armand M; Endres F; MacFarlane DR; Ohno H; Scrosati B Ionic-liquid Materials for the Electrochemical Challenges of the Future. Nat. Mater 2009, 8, 621–629. [DOI] [PubMed] [Google Scholar]
- (3).Wang L; Huang Y; Jia D Triethyl Orthoformate as a New Film-Forming Electrolytes Solvent for Lithium Ion-Batteries with Graphite Anodes. Electrochim. Acta 2006, 51, 4950–4955. [Google Scholar]
- (4).Bhargava BL; Balasubramanian S Dynamics in a Room-Temperature Ionic Liquid: A Computer Simulation Study of 1,3-Dimethylimidazolium Chloride. J. Chem. Phys 2005, 123, 144505. [DOI] [PubMed] [Google Scholar]
- (5).Shah JK; Maginn EJ Monte Carlo Simulations of Gas Solubility in the Ionic Liquid 1-n-Butyl-3-methylimidazolium Hexafluorophosphate. J. Phys. Chem. B 2005, 109, 10395–10405. [DOI] [PubMed] [Google Scholar]
- (6).Morrow TI; Maginn EJ Molecular Dynamics Study of the Ionic Liquid 1-n-Butyl-3-methylimidazolium Hexafluorophosphate. J. Phys. Chem. B 2002, 106, 12807–12813. [Google Scholar]
- (7).Shah JK; Brennecke JF; Maginn EJ Thermodynamic Properties of the Ionic Liquid 1-n-Butyl-3-methylimidazolium Hexafluorophosphate from Monte Carlo Simulations. Green Chem. 2002, 4, 112–118. [Google Scholar]
- (8).Cadena C; Anthony JL; Shah JK; Morrow TI; Brennecke JF; Maginn EJ Why is CO2 So Soluble in Imidazolium-Based Ionic Liquids? J. Am. Chem. Soc 2004, 126, 5300–5308. [DOI] [PubMed] [Google Scholar]
- (9).Del Popolo MG; Lynden-Bell RM; Kohanoff J Ab Initio Molecular Dynamics Simulation of a Room Temperature Ionic Liquid. J. Phys. Chem. B 2005, 109, 5895–5902. [DOI] [PubMed] [Google Scholar]
- (10).Del Popolo MG; Voth GA On the Structure and Dynamics of Ionic Liquids. J. Phys. Chem. B 2004, 108, 1744–1752. [Google Scholar]
- (11).Lynden-Bell RM; Kohanoff J; Del Popolo MG Simulation of Interfaces Between Room Temperature Ionic Liquids and Other Liquids. Faraday Discuss. 2005, 129, 57–67. [DOI] [PubMed] [Google Scholar]
- (12).Yan TY; Burnham CJ; Del Popolo MG; Voth GA Molecular Dynamics Simulation of Ionic Liquids: The Effect of Electronic Polarizability. J. Phys. Chem. B 2004, 108, 11877–11881. [Google Scholar]
- (13).Kunsági-Máté S; Lemli B; Nagy G; Kollár L Conformational Change of the Cation-Anion Pair of an Ionic Liquid Related to Its Low-Temperature Solid-State Phase Transitions. J. Phys. Chem. B 2004, 108, 9246–9250. [Google Scholar]
- (14).Antony JH; Mertens D; Breitenstein T; Dölle A; Wasserscheid P; Carper WR Molecular Structure, Reorientational Dynamics, and Intermolecular Interactions in the Neat Ionic Liquid 1-Butyl-3-Methylimidazolium Hexafluorophosphate. Pure Appl. Chem 2004, 76, 255–261. [Google Scholar]
- (15).de Andrade J; Böes ES; Stassen H Computational Study of Room Temperature Molten Salts Composed by 1-Alkyl-3-methyl-imidazolium Cations-Force-Field Proposal and Validation. J. Phys. Chem. B 2002, 106, 13344–13351. [Google Scholar]
- (16).Rogers RD; Seddon KR Ionic Liquids III A: Fundamentals, Progress, Challenges, and Opportunities: Properties and Structure; ACS Symposium Series; American Chemical Society, 2005; Vol. 901. [Google Scholar]
- (17).Jensen MP; Neuefeind J; Beitz JV; Skanthakumar S; Soderholm L Mechanisms of Metal Ion Transfer into Room-Temperature Ionic Liquids: The Role of Anion Exchange. J. Am. Chem. Soc 2003, 125, 15466–15473. [DOI] [PubMed] [Google Scholar]
- (18).Canongia-Lopes JN; Deschamps J; Pádua AAH Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar]
- (19).Canongia-Lopes JNA; Pádua AAH Using Spectroscopic Data on Imidazolium Cation Conformations To Test a Molecular Force Field for Ionic Liquids. J. Phys. Chem. B 2006, 110, 7485–7489. [DOI] [PubMed] [Google Scholar]
- (20).Deetlefs M; Hardacre C; Nieuwenhuyzen M; Padua AAH; Sheppard O; Soper AK Liquid Structure of the Ionic Liquid 1,3-Dimethylimidazolium Bis{(trifluoromethyl)sulfononyl}amide. J. Phys. Chem. B 2006, 110, 12055–12061. [DOI] [PubMed] [Google Scholar]
- (21).Canongia-Lopes JN; Costa Gomes MF; Pádua AAH Nonpolar, Polar, and Associating Solutes in Ionic Liquids. J. Phys. Chem. B 2006, 110, 16816–16816. [DOI] [PubMed] [Google Scholar]
- (22).Wu XP; Liu ZP; Huang SP; Wang W Molecular Dynamics Simulation of Room-Temperature Ionic Liquid Mixture of [Bmim][BF4] and Acetonitrile by a Refined Force Field. Phys. Chem. Chem. Phys 2005, 7, 2771–2779. [DOI] [PubMed] [Google Scholar]
- (23).Hunt PA The Simulation of Imidazolium-Based Ionic Liquids. Mol. Simul 2006, 32, 1–10. [Google Scholar]
- (24).Micaelo NM; Baptista AM; Soares CM Parametrization of 1-Butyl-3-methylimidazolium Hexafluorophosphate/Nitrate Ionic Liquid for the GROMOS Force Field. J. Phys. Chem. B 2006, 110, 14444–14451. [DOI] [PubMed] [Google Scholar]
- (25).Rey-Castro C; Vega LF Transport Properties of the Ionic Liquid 1-Ethyl-3-Methylimidazolium Chloride from Equilibrium Molecular Dynamics Simulation. The Effect of Temperature. J. Phys. Chem. B 2006, 110, 14426–14435. [DOI] [PubMed] [Google Scholar]
- (26).Siqueira LJA; Ribeiro MCC Molecular Dynamics Simulation of the Ionic Liquid N-Ethyl-N,N-dimethyl-N-(2-methoxyethyl)ammonium Bis(trifluoromethanesulfonyl)imide. J. Phys. Chem. B 2007, 111, 11776–11785. [DOI] [PubMed] [Google Scholar]
- (27).Bhargava BL; Balasubramanian S Refined Potential Model for Atomistic Simulations of Ionic Liquid [Bmim][PF6]. J. Chem. Phys 2007, 127, 114510. [DOI] [PubMed] [Google Scholar]
- (28).Bhargava BL; Balasubramanian S; Klein ML Modelling Room Temperature Ionic Liquids. Chem. Commun 2008, 0, 3339–3351. [DOI] [PubMed] [Google Scholar]
- (29).Köddermann T; Paschek D; Ludwig R Molecular Dynamic Simulations of Ionic Liquids: A Reliable Description of Structure, Thermodynamics and Dynamics. ChemPhysChem 2007, 8, 2464–2470. [DOI] [PubMed] [Google Scholar]
- (30).Picálek J; Kolafa J Molecular Dynamics Study of Conductivity of Ionic Liquids: The Kohlrausch Law. J. Mol. Liq 2007, 134, 29–33. [Google Scholar]
- (31).Borodin O; Smith GD; Kim H Viscosity of a Room Temperature Ionic Liquid: Predictions from Nonequilibrium and Equilibrium Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 4771–4774. [DOI] [PubMed] [Google Scholar]
- (32).Smith GD; Borodin O; Li L; Kim H; Liu Q; Bara JE; Gin DL; Nobel R A Comparison of Ether- and Alkyl-Derivatized Imidazolium-Based Room-Temperature Ionic Liquids: A Molecular Dynamics Simulation Study. Phys. Chem. Chem. Phys 2008, 10, 6301–6312. [DOI] [PubMed] [Google Scholar]
- (33).Cadena C; Zhao Q; Snurr RQ; Maginn EJ Molecular Modeling and Experimental Studies of the Thermodynamic and Transport Properties of Pyridinium-Based Ionic Liquids. J. Phys. Chem. B 2006, 110, 2821–2832. [DOI] [PubMed] [Google Scholar]
- (34).Canongia-Lopes JN; Pádua AAH Molecular Force Field for Ionic Liquids Composed of Triflate or Bistriflylimide Anions. J. Phys. Chem. B 2004, 108, 16893–16898. [Google Scholar]
- (35).Borodin O; Smith GD Structure and Dynamics of N-Methyl-N-propylpyrrolidinium Bis(trifluoromethanesulfonyl)imide Ionic Liquid from Molecular Dynamics Simulations. J. Phys. Chem. B 2006, 110, 11481–11490. [DOI] [PubMed] [Google Scholar]
- (36).Borodin O; Smith GD; Henderson W Li+ Cation Environment, Transport, and Mechanical Properties of the LiTFSI Doped N-Methyl-N-alkylpyrrolidinium+TFSI− Ionic Liquids. J. Phys. Chem. B 2006, 110, 16879–16886. [DOI] [PubMed] [Google Scholar]
- (37).Cadena C; Maginn EJ Molecular Simulation Study of Some Thermophysical and Transport Properties of Triazolium-Based Ionic Liquids. J. Phys. Chem. B 2006, 110, 18026–18039. [DOI] [PubMed] [Google Scholar]
- (38).Jiang W; Yan T; Wang Y; Voth GA Molecular Dynamics Simulation of the Energetic Room-Temperature Ionic Liquid, 1-Hydroxyethyl-4-amino-1,2,4-triazolium Nitrate (HEATN). J. Phys. Chem. B 2008, 112, 3121–3131. [DOI] [PubMed] [Google Scholar]
- (39).Zhou G; Liu X; Zhang S; Yu G; He H A Force Field for Molecular Simulation of Tetrabutylphosphonium Amino Acid Ionic Liquids. J. Phys. Chem. B 2007, 111, 7078–7084. [DOI] [PubMed] [Google Scholar]
- (40).Adebahr J; Grozema FC; deLeeuw SW; MacFarlane DR; Forsyth M Structure and Dynamics of the Plastic Crystal Tetramethylammonium Dicyanamide - A Molecular Dynamics Study. Solid State Ionics 2006, 177, 2845–2850. [Google Scholar]
- (41).Schurhammer R; Wipff G Solvation of Uranium Hexychloro Complexes in Room-Temperature Ionic Liquids. A Molecular Dynamics Investigation in Two Liquids. J. Phys. Chem. B 2007, 111, 4659–4668. [DOI] [PubMed] [Google Scholar]
- (42).Canongia-Lopes JN; Padua AA Nanostructural Organization in Ionic Liquids. J. Phys. Chem. B 2006, 110, 3330–3335. [DOI] [PubMed] [Google Scholar]
- (43).Rajput NN; Murugesan V; Shin Y; Han KS; Lau KC; Chen JZ; Liu J; Curtiss LA; Mueller KT; Persson KA Elucidating the Solvation Structure and Dynamics of Lithium Polysulfides Resulting from Competitive Salt and Solvent Interactions. Chem. Mater 2017, 29, 3375–3379. [Google Scholar]
- (44).Borodin O Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. [DOI] [PubMed] [Google Scholar]
- (45).Schröder C Comparing Reduced Partial Charge Models with Polarizable Simulations of Ionic Liquids. Phys. Chem. Chem. Phys 2012, 14, 3089–3102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Pethes I A Comparison of Classical Interatomic Potentials Applied to Highly Concentrated Aqueous Lithium Chloride Solutions. J. Mol. Liq 2017, 242, 845–858. [Google Scholar]
- (47).Tsuzuki S; Shinoda W; Saito H; Mikami M; Tokuda H; Watanabe M Molecular Dynamics Simulations of Ionic Liquids: Cation and Anion Dependence of Self-Diffusion Coefficients of Ions. J. Phys. Chem. B 2009, 113, 10641–10649. [DOI] [PubMed] [Google Scholar]
- (48).Dommert F; Wendler K; Berger R; Delle Site L; Holm C Force Fields for Studying the Structure and Dynamics of Ionic Liquids: A Critical Review of Recent Developments. ChemPhysChem 2012, 13, 1625–1637. [DOI] [PubMed] [Google Scholar]
- (49).Vatamanu J; Borodin O; Smith GD Molecular Insights into the Potential and Temperature Dependences of the Differential Capacitance of a Room-Temperature Ionic Liquid at Graphite Electrodes. J. Am. Chem. Soc 2010, 132, 14825–14833. [DOI] [PubMed] [Google Scholar]
- (50).Vatamanu J; Borodin O; Smith GD Molecular Simulations of the Electric Double Layer Structure, Differential Capacitance, and Charging Kinetics for N-Methyl-N-propylpyrrolidinium Bis-(fluorosulfonyl)imide at Graphite Electrodes. J. Phys. Chem. B 2011, 115, 3073–3084. [DOI] [PubMed] [Google Scholar]
- (51).Vatamanu J; Vatamanu M; Borodin O; Bedrov D A Comparative Study of Room Temperature Ionic Liquids and Their Organic Solvent Mixtures Near Charged Electrodes. J. Phys.: Condens. Matter 2016, 28, 464002. [DOI] [PubMed] [Google Scholar]
- (52).Bedrov D; Borodin O; Li Z; Smith GD Influence of Polarization on Structural, Thermodynamic, and Dynamic Properties of Ionic Liquids Obtained from Molecular Dynamics Simulations. J. Phys. Chem. B 2010, 114, 4984–4997. [DOI] [PubMed] [Google Scholar]
- (53).Wendler K; Zahn S; Dommert F; Berger R; Holm C; Kirchner B; Delle Site L Locality and Fluctuations: Trends in Imidazolium-Based Ionic Liquids and Beyond. J. Chem. Theory Comput 2011, 7, 3040–3044. [DOI] [PubMed] [Google Scholar]
- (54).Koßmann S; Thar J; Kirchner B; Hunt PA; Welton T Cooperativity in Ionic Liquids. J. Chem. Phys 2006, 124, 174506. [DOI] [PubMed] [Google Scholar]
- (55).Bühl M; Chaumont A; Schurhammer R; Wipff G Ab Initio Molecular Dynamics of Liquids 1,3-Dimethylimidazolium Chloride. J. Phys. Chem. B 2005, 109, 18591–18599. [DOI] [PubMed] [Google Scholar]
- (56).Kohagen M; Brehm M; Thar J; Zhao W; Müller-Plathe F; Kirchner B Performance of Quantum Chemically Derived Charges and Persistence of Ion Cages in Ionic Liquids. A Molecular Dynamics Simulations Study of 1-n-Butyl-3-methylimidazolium Bromide. J. Phys. Chem. B 2011, 115, 693–702. [DOI] [PubMed] [Google Scholar]
- (57).Youngs TGA; Hardacre C Application of Static Charge Transfer within an Ionic-Liquid Force Field and Its Effect on Structure and Dynamics. ChemPhysChem 2008, 9, 1548–1558. [DOI] [PubMed] [Google Scholar]
- (58).Schmidt J; Krekeler C; Dommert F; Zhao Y; Berger R; Delle Site L; Holm C Ion Charge Reduction and Atomic Partial Charges from First-Principles Calculations of 1,3-Dimethylimidazolium Chloride. J. Phys. Chem. B 2010, 114, 6150–6155. [DOI] [PubMed] [Google Scholar]
- (59).Chaban VV; Voroshylova IV Systematic refinement of Canongia-Lopes–Padua force field for pyrrolidinium-based ionic liquids. J. Phys. Chem. B 2015, 119, 6242–6249. [DOI] [PubMed] [Google Scholar]
- (60).Chaban V Polarizability Versus Mobility: Atomistic Force Field for Ionic Liquids. Phys. Chem. Chem. Phys 2011, 13, 16055–16062. [DOI] [PubMed] [Google Scholar]
- (61).Zhao W; Eslami H; Cavalcanti WL; Müller-Plathe F A Refined All-Atom Model for the Ionic Liquid 1-n-Butyl 3-Methylimidazolium bis(Trifluoromethylsulfonyl)imide [bmim]-[Tf2N]. Z. Phys. Chem 2007, 221, 1647–1662. [Google Scholar]
- (62).Leontyev IV; Stuchebrukhov AA Electronic Continuum Model for Molecular Dynamics Simulations. J. Chem. Phys 2009, 130, 085102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Yan T; Wang Y; Knox C On the Structure of Ionic Liquids: Comparisons Between Electronically Polarizable and Nonpolarizable Models I. J. Phys. Chem. B 2010, 114, 6905–6921. [DOI] [PubMed] [Google Scholar]
- (64).Pluhařová E; Mason PE; Jungwirth P Ion Pairing in Aqueous Lithium Salt Solutions with Monovalent and Divalent Counter-Anions. J. Phys. Chem. A 2013, 117, 11766–11773. [DOI] [PubMed] [Google Scholar]
- (65).Duboué-Dijon E; Mason PE; Fischer HE; Jungwirth P Hydration and Ion Pairing in Aqueous Mg2+ and Zn2+ Solutions: Force-Field Description Aided by Neutron Scattering Experiments and Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 3296–3306. [DOI] [PubMed] [Google Scholar]
- (66).Kohagen M; Mason PE; Jungwirth P Accounting for Electronic Polarization Effects in Aqueous Sodium Chloride via Molecular Dynamics Aided by Neutron Scattering. J. Phys. Chem. B 2016, 120, 1454–1460. [DOI] [PubMed] [Google Scholar]
- (67).Pollard TP; Beck TL Structure and Polarization Near the Li+ Ion in Ethylene and Propylene Carbonates. J. Chem. Phys 2017, 147, 161710. [DOI] [PubMed] [Google Scholar]
- (68).Smith GD; Borodin O; Pekny M; Annis B; Londono D; Jaffe RL Polymer Force Fields from Ab Initio Studies of Small Model Molecules: Can We Achieve Chemical Accuracy? Spectrochim. Acta, Part A 1997, 53, 1273–1283. [Google Scholar]
- (69).Borodin O; Smith GD; Jaffe RL Ab Initio Quantum Chemistry and Molecular Dynamics Simulations Studies of LiPF6/Poly(Ethylene Oxide) Interactions. J. Comput. Chem 2001, 22, 641–654. [Google Scholar]
- (70).Borodin O; Smith GD; Douglas R Force Field Development and MD Simulations of Poly(Ethylene Oxide)/LiBF4 Polymer Electrolytes. J. Phys. Chem. B 2003, 107, 6824–6837. [Google Scholar]
- (71).Fileti EE; Chaban VV The scaled-charge additive force field for amino acid based ionic liquids. Chem. Phys. Lett 2014, 616–617, 205–211. [Google Scholar]
- (72).Fileti EE; Chaban VV The Force Field for Imidazolium-Based Ionic Liquids: Novel Anions with Polar Residues. Chem. Phys. Lett 2015, 633, 132–138. [Google Scholar]
- (73).Mondal A; Balasubramanian S Quantitative Prediction of Physical Properties of Imidazolium Based Room Temperature Ionic Liquids throuhg Determination of Condensed Phase Site Charges: A Refined Force Field. J. Phys. Chem. B 2014, 118, 3409–3422. [DOI] [PubMed] [Google Scholar]
- (74).Mondal A; Balasubramanian S A Refined All-Atom Potential for Imidazolium-Based Room Temperature Ionic Liquids: Acetate, Dicyanamide, and Thiocyanate Anions. J. Phys. Chem. B 2015, 119, 11041–11051. [DOI] [PubMed] [Google Scholar]
- (75).Chen M; Pendrill R; Widmalm G; Brady JW; Wohlert J Molecular Dynamics Simulations of the Ionic Liquid 1-n-Butyl-3-Methylimidazolium Chloride and Its Binary Mixtures with Ethanol. J. Chem. Theory Comput 2014, 10, 4465–4479. [DOI] [PubMed] [Google Scholar]
- (76).Choi E; Yethiraj A Entropic Mechanism for the Lower Critical Solution Temperature of Poly(ethylene oxide) in a Room Temperature Ionic Liquid. ACS Macro Lett. 2015, 4, 799–803. [DOI] [PubMed] [Google Scholar]
- (77).Son CY; McDaniel JG; Schmidt JR; Cui Q; Yethiraj A First-Principles United Atom Force Field for the Ionic Liquid BMIM+BF4−: An Alternative to Charge Scaling. J. Phys. Chem. B 2016, 120, 3560–3568. [DOI] [PubMed] [Google Scholar]
- (78).McDaniel JG Polarization Effects in Binary [BMIM+][BF4−]/1,2-Dichloroethane, Acetone, Acetonitrile, and Water Electrolytes. J. Phys. Chem. B 2018, 122, 4345–4355. [DOI] [PubMed] [Google Scholar]
- (79).McDaniel JG; Yethiraj A The Influence of Electronic Polarization on the Structure of Ionic Liquids. J. Phys. Chem. Lett 2018, 9, 4765–4770. [DOI] [PubMed] [Google Scholar]
- (80).Patel S; Brooks CL Fluctuating Charge Force Fields: Recent Developments and Applications from Small Molecules to Macro-molecular Biological Systems. Mol. Simul 2006, 32, 231–249. [Google Scholar]
- (81).Olano LR; Rick SW Fluctuating Charge Normal Modes: An Algorithm for Implementing Molecular Dynamics Simulations with Polarizable Potentials. J. Comput. Chem 2005, 26, 699–707. [DOI] [PubMed] [Google Scholar]
- (82).Rick SW; Stuart SJ Potentials and Algorithms for Incorporating Polarizability in Computer Simulations. Rev. Comput. Chem 2002, 18, 89–146. [Google Scholar]
- (83).Patel S; Mackerell AD Jr.; Brooks CL CHARMM Fluctuating Charge Force Field for Proteins: II Protein/Solvent Properties from Molecular Dynamics Simulations Using a Nonadditive Electrostatic Model. J. Comput. Chem 2004, 25, 1504–1514. [DOI] [PubMed] [Google Scholar]
- (84).Zhao DX; Liu C; Wang FF; Yu CY; Gong LD; Liu SB; Yang ZZ Development of a Polarizable Force Field Using Multiple Fluctuating Charges per Atom. J. Chem. Theory Comput 2010, 6, 795–804. [DOI] [PubMed] [Google Scholar]
- (85).Banks JL; Kaminski GA; Zhou R; Mainz DT; Berne BJ; Friesner RA Parametrizing a Polarizable Force Field from Ab Initio Data. I. The Fluctuating Point Charge Model. J. Chem. Phys 1999, 110, 741–754. [Google Scholar]
- (86).Chelli R; Procacci P; Righini R; Califano S Electrical Response in Chemical Potential Equalization Schemes. J. Chem. Phys 1999, 111, 8569–8575. [Google Scholar]
- (87).Chen J; Hundertmark D; Martinez TJ A Unified Theoretical Framework for Fluctuating-Charge Models in Atom-Space and in Bond-Space. J. Chem. Phys 2008, 129, 214113. [DOI] [PubMed] [Google Scholar]
- (88).de Oliveira Cavalcante Ade A; Ribeiro MCC; Skaf MS Polarizability Effects on the Structure and Dynamics of Ionic Liquids. J. Chem. Phys 2014, 140, 144108. [DOI] [PubMed] [Google Scholar]
- (89).Urahata SM; Ribeiro MCC Molecular Dynamics Simulation of Molten LiNO3 with Flexible and Polarizable Anions. Phys. Chem. Chem. Phys 2003, 5, 2619–2624. [Google Scholar]
- (90).Wu Y; Li Y; Hu N; Hong M The Electronegativity Equalization Method Fused with Molecular Mechanics: A Fluctuating Charge and Flexible Body Potential Function for [Emim][Gly] Ionic Liquids. Phys. Chem. Chem. Phys 2014, 16, 2674–2685. [DOI] [PubMed] [Google Scholar]
- (91).Mulliken RS A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities. J. Chem. Phys 1934, 2, 782–793. [Google Scholar]
- (92).Stuart SJ; Berne BJ Surface Curvature Effects in the Aqueous Ionic Solvation of the Chloride Ion. J. Phys. Chem. A 1999, 103, 10300–10307. [Google Scholar]
- (93).Stuart SJ; Berne BJ Effects of Polarizability on the Hydration of the Chloride Ion. J. Phys. Chem 1996, 100, 11934–11943. [Google Scholar]
- (94).Ribeiro MCC Polarization Effects in Molecular Dynamics Simulations of Glass-Formers Ca(NO3)2 × H2O, n = 4, 6, and 8. J. Chem. Phys 2010, 132, 134512. [DOI] [PubMed] [Google Scholar]
- (95).Ribeiro MCC Ionic Dynamics in the Glass-Forming Liquid Ca0.4K0.6(NO3)(1.4): A Molecular Dynamics Study with a Polarizable Model. Phys. Rev. B: Condens. Matter Mater. Phys 2001, 63, 094205. [Google Scholar]
- (96).Ribeiro MCC Molecular Dynamics Study on the Glass Transition in Ca0.4K0.6(NO3)(1.4). J. Phys. Chem. B 2003, 107, 9520–9527. [Google Scholar]
- (97).Ribeiro MCC; Almeida LCJ Validating a Polarizable Model for the Glass-Forming Liquid Ca0.4K0.6(NO3)1.4 by Ab Initio Calculations. J. Chem. Phys 2000, 113, 4722–4731. [Google Scholar]
- (98).Ribeiro MCC; Almeida LCJ Fluctuating Charge Model for Polyatomic Ionic Systems: A Test Case with Diatomic Anions. J. Chem. Phys 1999, 110, 11445–11448. [Google Scholar]
- (99).Chen J; Martínez TJ QTPIE: Charge Transfer with Polarization Current Equalization. A Fluctuating Charge Model with Correct Asymptotics. Chem. Phys. Lett 2007, 438, 315–320. [Google Scholar]
- (100).Tanaka M; Siehl H-U An Application of the Consistent Charge Equilibration (CQEq) Method to Guanidinium Ionic Liquid Systems. Chem. Phys. Lett 2008, 457, 263–266. [Google Scholar]
- (101).Rappe AK; Goddard WA Charge Equilibration for Molecular Dynamics Simulations. J. Phys. Chem 1991, 95, 3358–3363. [Google Scholar]
- (102).Soniat M; Rick SW The Effects of Charge Transfer on the Aqueous Solvation of Ions. J. Chem. Phys 2012, 137, 044511. [DOI] [PubMed] [Google Scholar]
- (103).Kumar R; Wang FF; Jenness GR; Jordan KD A Second Generation Distributed Point Polarizable Water Model. J. Chem. Phys 2010, 132, 014309. [DOI] [PubMed] [Google Scholar]
- (104).Gresh N; Claverie P; Pullman A Intermolecular Interactions- Elaboration on an Additive Procedure Including an Explicit Charge-Transfer Contribution. Int. J. Quantum Chem 1986, 29, 101–118. [Google Scholar]
- (105).Piquemal J-P; Chevreau H; Gresh N Towards a Separate Reproduction of the Contributions to the Hartree-Fock and DFT Intermolecular Interaction Energies by Polarizable Molecular Mechanics with the SIBFA Potential. J. Chem. Theory Comput 2007, 3, 824–837. [DOI] [PubMed] [Google Scholar]
- (106).Nguyen M; Rick SW The Influence of Polarizability and Charge Transfer on Specific Ion Effects in the Dynamics of Aqueous Salt Solutions. J. Chem. Phys 2018, 148, 222803. [DOI] [PubMed] [Google Scholar]
- (107).Russo MF; van Duin ACT Atomistic-Scale Simulations of Chemical Reactions: Bridging from Quantum Chemistry to Engineering. Nucl. Instrum. Methods Phys. Res., Sect. B 2011, 269, 1549–1554. [Google Scholar]
- (108).Senftle TP; Hong S; Islam MM; Kylasa SB; Zheng Y; Shin YK; Junkermeier C; Engel-Herbert R; Janik MJ; Aktulga HM; Verstraelen T; Grama A; van Duin ACT The ReaxFF Reactive Force-Field: Development, Applications and Future Directions. npj Comput. Mater 2016, 2, 15011. [Google Scholar]
- (109).van Duin ACT; Dasgupta S; Lorant F; Goddard WA ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar]
- (110).Clavaguera C; Calvo F; Dognon J-P Theoretical Study of the Hydrated Gd3+ Ion: Structure, Dynamics, and Charge Transfer. J. Chem. Phys 2006, 124, 074505. [DOI] [PubMed] [Google Scholar]
- (111).Gale JD; Raiteri P; van Duin AC AReactive Force Field for Aqueous-Calcium Carbonate Systems. Phys. Chem. Chem. Phys 2011, 13, 16666–16679. [DOI] [PubMed] [Google Scholar]
- (112).Verstraelen T; Ayers PW; Van Speybroeck V; Waroquier M ACKS2: Atom-Condensed Kohn-Sham DFT Approximated to Second Order. J. Chem. Phys 2013, 138, 074108. [DOI] [PubMed] [Google Scholar]
- (113).Yu H; van Gunsteren WF Accounting for Polarization in Molecular Simulation. Comput. Phys. Commun 2005, 172, 69–85. [Google Scholar]
- (114).Lemkul JA; Huang J; Roux B; MacKerell AD Jr., An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev 2016, 116, 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (115).Cieplak P; Dupradeau FY; Duan Y; Wang J Polarization Effects in Molecular Mechanical Force Fields. J. Phys.: Condens. Matter 2009, 21, 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (116).Jiang W; Hardy DJ; Phillips JC; Mackerell AD Jr.; Schulten K; Roux B High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett 2011, 2, 87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (117).Geerke DP; van Gunsteren WF On the Calculation of Atomic Forces in Classical Simulation Using the Charge-on-Spring Method To Explicitly Treat Electronic Polarization. J. Chem. Theory Comput 2007, 3, 2128–2137. [DOI] [PubMed] [Google Scholar]
- (118).Lu Z; Zhang Y Interfacing ab Initio Quantum Mechanical Method with Classical Drude Osillator Polarizable Model for Molecular Dynamics Simulation of Chemical Reactions. J. Chem. Theory Comput 2008, 4, 1237–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (119).Huang J; Simmonett AC; Pickard F. C. t.; MacKerell AD Jr.; Brooks BR Mapping the Drude Polarizable Force Field Onto a Multipole and Induced Dipole Model. J. Chem. Phys 2017, 147, 161702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (120).Lin F-Y; MacKerell AD Jr. Polarizable Empirical Force Field for Halogen-Containing Compounds Based on the Classical Drude Oscillator. J. Chem. Theory Comput 2018, 14, 1083–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (121).Lemkul JA; MacKerell AD Jr. Balancingthe Interactions of Mg2+ in Aqueous Solution and with Nucleic Acid Moieties For a Polarizable Force Field Based on the Classical Drude Oscillator Model. J. Phys. Chem. B 2016, 120, 11436–11448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (122).Schröder C; Steinhauser O Simulating Polarizable Molecular Ionic Liquids with Drude Oscillators. J. Chem. Phys 2010, 133, 154511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (123).Lemkul JA; Roux B; van der Spoel D; MacKerell AD Jr. Implementation of Extended Lagrangian Dynamics in GROMACS for Polarizable Simulations Using the Classical Drude Oscillator Model. J. Comput. Chem 2015, 36, 1473–1479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (124).Chowdhary J; Harder E; Lopes PE; Huang L; MacKerell AD Jr.; Roux B A Polarizable Force Field of Dipalmitoylphospha-tidylcholine Based on the Classical Drude Model for Molecular Dynamics Simulations of Lipids. J. Phys. Chem. B 2013, 117, 9142–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (125).Stone AJ The Theory of Intermolecular Forces; Oxford University Press, 1996. [Google Scholar]
- (126).Boulanger E; Thiel W Solvent Boundary Potentials for Hybrid QM/MM Computations Using Classical Drude Oscillators: A Fully Polarizable Model. J. Chem. Theory Comput 2012, 8, 4527–4538. [DOI] [PubMed] [Google Scholar]
- (127).Ganguly A; Boulanger E; Thiel W Importance of MM Polarization in QM/MM Studies of Enzymatic Reactions: Assessment of the QM/MM Drude Oscillator Model. J. Chem. Theory Comput 2017, 13, 2954–2961. [DOI] [PubMed] [Google Scholar]
- (128).Metz S; Kästner J; Sokol AA; Keal TW; Sherwood P ChemShell-A Modular Software Package for QM/MM Simulations. Wiley Interdiscip. Rev.: Comput. Mol. Sci 2014, 4, 101–110. [Google Scholar]
- (129).Lev B; Zhang R; de la Lande A; Salahub D; Noskov SY The QM-MM Interface for CHARMM-deMon. J. Comput. Chem 2009, 31, 1015–1023. [DOI] [PubMed] [Google Scholar]
- (130).Lamoureux G; Roux B Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys 2003, 119, 3025–3039. [Google Scholar]
- (131).Smith W; Yong CW; Rodger PM DL_POLY: Application to molecular simulation. Mol. Simul 2002, 28, 385–471. [Google Scholar]
- (132).Weik F; Weeber R; Szuttor K; Breitsprecher K; de Graaf J; Kuron M; Landsgesell J; Menke H; Sean D; Holm C ESPResSo 4.0—An Extensible Software Package for Simulating Soft Matter Systems. Eur. Phys. J.: Spec. Top 2019, 227, 1789–1816. [Google Scholar]
- (133).Dequidt A; Devemy J; Padua AA Thermalized Drude Oscillators with the LAMMPS Molecular Dynamics Simulator. J. Chem. Inf. Model 2016, 56, 260–268. [DOI] [PubMed] [Google Scholar]
- (134).Huang J; Lemkul JA; Eastman PK; MacKerell AD Jr. Molecular Dynamics Simulations Using the Drude Polarizable Force Field on GPUs with OpenMM: Implementation, Validation, and Benchmarks. J. Comput. Chem 2018, 39, 1682–1689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (135).Schmollngruber M; Lesch V; Schröder C; Heuer A; Steinhauser O Comparing Induced Point-Dipoles and Drude Oscillators. Phys. Chem. Chem. Phys 2015, 17, 14297–14306. [DOI] [PubMed] [Google Scholar]
- (136).Schmollngruber M; Schröder C; Steinhauser O Dielectric Spectra of Ionic Liquids and Their Conversion to Solvation Dynamics: A Detailed Computational Analysis of Polarizable Systems. Phys. Chem. Chem. Phys 2014, 16, 10999–11009. [DOI] [PubMed] [Google Scholar]
- (137).Schmollngruber M; Schröder C; Steinhauser O Polarization Effects on the Solvation Dynamics of Coumarin C153 in Ionic Liquids: Components and Their Cross-Correlations. J. Chem. Phys 2013, 138, 204504. [DOI] [PubMed] [Google Scholar]
- (138).Schröder C Collective Translational Motions and Cage Relaxations in Molecular Ionic Liquids. J. Chem. Phys 2011, 135, 024502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (139).Schröder C; Sonnleitner T; Buchner R; Steinhauser O The Influence of Polarizability on the Dielectric Spectrum of the Ionic Liquid 1-Ethyl-3-methylimidazolium Triflate. Phys. Chem. Chem. Phys 2011, 13, 12240–12248. [DOI] [PubMed] [Google Scholar]
- (140).Heid E; Docampo-Alvarez B; Varela LM; Prosenz K; Steinhauser O; Schröder C Langevin Behavior of the Dielectric Decrement in Ionic Liquid Water Mixtures. Phys. Chem. Chem. Phys 2018, 20, 15106–15117. [DOI] [PubMed] [Google Scholar]
- (141).Yu H; Whitfield TW; Harder E; Lamoureux G; Vorobyov I ; Anisimov VM; MacKerell ADJ; Roux B Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J. Chem. Theory Comput 2010, 6, 774–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (142).Heid E; Schröder C Solvation Dynamics in Polar Solvents and Imidazolium Ionic Liquids: Failure of Linear Response Approximations. Phys. Chem. Chem. Phys 2018, 20, 5246–5255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (143).Yesylevskyy SO; Schäfer LV; Sengupta D; Marrink SJ Polarizable Water Model for the Coarse-Grained MARTINI Force Field. PLoS Comput. Biol 2010, 6, No. e1000810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (144).Michalowsky J; Schäfer LV; Holm C; Smiatek J A Refined Polarizable Water Model for the Coarse-Grained MARTINI Force Field with Long-Range Electrostatic Interactions. J. Chem. Phys 2017, 146, 054501. [DOI] [PubMed] [Google Scholar]
- (145).Bernardes CE; Shimizu K; Lopes JN; Marquetand P; Heid E; Steinhauser O; Schröder C Additive Polarizabilities in Ionic Liquids. Phys. Chem. Chem. Phys 2016, 18, 1665–1670. [DOI] [PubMed] [Google Scholar]
- (146).van Maaren PJ; van der Spoel D Molecular Dynamics Simulation of Water with Novel Shell-Model Potentials. J. Phys. Chem. B 2001, 105, 2618–2626. [Google Scholar]
- (147).Lagardère L; Lipparini F; Polack E; Stamm B; Cances E; Schnieders M; Ren P; Maday Y; Piquemal JP Scalable Evaluation of Polarization Energy and Associated Forces in Polarizable Molecular Dynamics: II.Towards Massively Parallel Computations using Smooth Particle Mesh Ewald. J. Chem. Theory Comput 2015, 11, 2589–2599. [DOI] [PubMed] [Google Scholar]
- (148).Lamoureux G; MacKerell AD Jr.; Roux B A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J. Chem. Phys 2003, 119, 5185–5197. [Google Scholar]
- (149).Lamoureux G; Roux B Absolute Hydration Free Energy Scale for Alkali and Halide Ions Established from Simulations with a Polarizable Force Field. J. Phys. Chem. B 2006, 110, 3308–3322. [DOI] [PubMed] [Google Scholar]
- (150).Lopes PE; Huang J; Shim J; Luo Y; Li H; Roux B; Mackerell AD Jr. Force Field for Peptides and Proteins based on the Classical Drude Oscillator. J. Chem. Theory Comput 2013, 9, 5430–5449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (151).Huang J; Lopes PE; Roux B; MacKerell AD Jr. Recent Advances in Polarizable Force Fields for Macromolecules: Microsecond Simulations of Proteins Using the Classical Drude Oscillator Model. J. Phys. Chem. Lett 2014, 5, 3144–3150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (152).Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD Jr. A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules. Chem. Phys. Lett 2006, 418, 245–249. [Google Scholar]
- (153).Salomon-Ferrer R; Case DA; Walker RC An Overview of the AMBER Biomolecular Simulation Package. WIREs: Comput. Mol. ScI 2013, 3, 198–210. [Google Scholar]
- (154).Rackers JA; Wang Z; Lu C; Laury ML; Lagardère L; Schnieders MJ; Piquemal J-P; Ren P; Ponder J Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput 2018, 14, 5273–5289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (155).Lagardère L; Jolly LH; Lipparini F; Aviat F; Stamm B; Jing ZF; Harger M; Torabifard H; Cisneros GA; Schnieders MJ; Gresh N; Maday Y; Ren PY; Ponder JW; Piquemal JP Tinker-HP: A Massively Parallel Molecular Dynamics Package for Multiscale Simulations of Large Complex Systems with Advanced Point Dipole Polarizable Force Fields. Chem. Sci 2018, 9, 956–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (156).Harger M; Li D; Wang Z; Dalby K; Lagardère L; Piquemal J-P; Ponder J; Ren P Tinker-OpenMM: Absolute and Relative Alchemical Free Energies using AMOEBA on GPUs. J. Comput. Chem 2017, 38, 2047–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (157).Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang L-P; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol 2017, 13, No. e1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (158).Tazi S; Molina JJ; Rotenberg B; Turq P; Vuilleumier R; Salanne M A Transferable Ab Initio Based Force Field for Aqueous Ions. J. Chem. Phys 2012, 136, 114507. [DOI] [PubMed] [Google Scholar]
- (159).WMI-MD Molecular Simulation Toolkit, 2019; http://www.wasatchmolecular.com/wmimd.html (accessed April 28, 2019).
- (160).Sagui C; Pedersen LG; Darden TA Towards an Accurate Representation of Electrostatics in Classical Force Fields: Efficient Implementation of Multipolar Interactions in Biomolecular Simulations. J. Chem. Phys 2004, 120, 73–87. [DOI] [PubMed] [Google Scholar]
- (161).Stamm B; Lagardère L; Polack É; Maday Y; Piquemal J-P A Coherent Derivation of the Ewald Summation for Arbitrary Orders of Multipoles: The Self-Terms. J. Chem. Phys 2018, 149, 124103. [DOI] [PubMed] [Google Scholar]
- (162).Sala J; Guardia E; Masia M The Polarizable Point Dipoles Method with Electrostatic Damping: Implementation on a Model System. J. Chem. Phys 2010, 133, 234101. [DOI] [PubMed] [Google Scholar]
- (163).Thole BT Molecular Polarizabilities Calculated with a Modified Dipole Interaction. Chem. Phys 1981, 59, 341–350. [Google Scholar]
- (164).Ren P; Ponder JW Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar]
- (165).Wang LP; Head-Gordon T; Ponder JW; Ren P; Chodera JD; Eastman PK; Martinez TJ; Pande VS Systematic Improvement of a Classical Molecular Model of Water. J. Phys. Chem. B 2013, 117, 9956–9972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (166).Loco D; Polack E; Caprasecca S; Lagardère L; Lipparini F; Piquemal J-P; Mennucci B A QM/MM Approach Using the AMOEBA Polarizable Embedding: From Ground State Energies to Electronic Excitations. J. Chem. Theory Comput 2016, 12, 3654–3661. [DOI] [PubMed] [Google Scholar]
- (167).Loco D; Lagardère L; Caprasecca S; Lipparini F; Mennucci B; Piquemal J-P Hybrid QM/MM Molecular Dynamics with AMOEBA Polarizable Embedding. J. Chem. Theory Comput 2017, 13, 4025–4033. [DOI] [PubMed] [Google Scholar]
- (168).Lipparini F; Lagardère L; Raynaud C; Stamm B; Cances E; Schnieders M; Ren PY; Mennucci B; Maday Y; Piquemal J-P Polarizable Molecular Dynamics in a Polarizable Continuum Solvent. J. Chem. Theory Comput 2015, 11, 623–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (169).Jeziorski B; Moszynski R; Szalewicz K Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev 1994, 94, 1887–1930. [Google Scholar]
- (170).Coulson CA; Eisenberg D Interactions of H2O Molecules in Ice I. The Dipole Moment of an H2O Molecule in Ice. Proc. R. Soc. A 1966, 291, 445–453. [Google Scholar]
- (171).Holt A; Karlström G Inclusion of the Quadrupole Moment when Describing Polarization. The Effect of the Dipole-Quadrupole Polarizabilit. J. Comput. Chem 2008, 29, 2033–2038. [DOI] [PubMed] [Google Scholar]
- (172).Devereux M; van Severen M-C; Parisel O; Piquemal J-P; Gresh N The Role of Cation Polarization in holo- and hemi-Directed [Pb(H2O)n]2+ Complexes and Development of a Pb2+ Polarizable Force Field. J. Chem. Theory Comput 2011, 7, 138–147. [DOI] [PubMed] [Google Scholar]
- (173).Misquitta AJ; Stone AJ Distributed Polarizabilities Obtained Using a Constrained Density-Fitting Algorithm. J. Chem. Phys 2006, 124, 024111. [DOI] [PubMed] [Google Scholar]
- (174).Lillestolen TC; Wheatley RJ First-Principles Calculation of Local Atomic Polarizabilities. J. Phys. Chem. A 2007, 111, 11141–11146. [DOI] [PubMed] [Google Scholar]
- (175).Gresh N; Cisneros GA; Darden TA; Piquemal J-P Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and Ligand-Macromolecule Complexes. A Bottom-Up Strategy. J. Chem. Theory Comput 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (176).Zhu X; Lopes PE; MacKerell AD Jr. Recent Developments and Applications of the CHARMM force fields. WIRs Comput. Mol. Sci 2012, 2, 167–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (177).Harder E; Anisimov VM; Vorobyov IV; Lopes PEM; Noskov SY; MacKerell ADJ; Roux B Atomic Level Anisotropy in the Electrostatic Modeling of Lone Pairs for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory Comput 2006, 2, 1587–1597. [DOI] [PubMed] [Google Scholar]
- (178).Piquemal J-P; Chelli R; Procacci P; Gresh N Key Role of the Polarization Anisotropy of Water in Modeling Classical Polarizable Force Fields. J. Phys. Chem. A 2007, 111, 8170–8176. [DOI] [PubMed] [Google Scholar]
- (179).Piquemal J-P; Marquez A; Parisel O; Giessner-Prettre C A CSOV Study of the Difference Between HF and DFT Intermolecular Interaction Energy Value: The Importance of the Charge Transfer Contribution. J. Comput. Chem 2005, 26, 1052–1062. [DOI] [PubMed] [Google Scholar]
- (180).Khaliullin RZ; Cobar EA; Lochan RC; Bell AT; Head-Gordon M Unravelling the Origin of Intermolecular Interactions Using Absolutely Localized Molecular Orbitals. J. Phys. Chem. A 2007, 111, 8753–8765. [DOI] [PubMed] [Google Scholar]
- (181).Stone AJ; Misquitta AJ Charge-Transfer in Symmetry-Adapted Perturbation Theory. Chem. Phys. Lett 2009, 473, 201–205. [Google Scholar]
- (182).Misquitta AJ Charge Transfer from Regularized Symmetry-Adapted Perturbation Theory. J. Chem. Theory Comput 2013, 9, 5313–5326. [DOI] [PubMed] [Google Scholar]
- (183).Wu J; Piquemal J-P; Chaudret R; Reinhardt P; Ren P Polarizable Molecular Dynamics Simulation of Zn(II) in Water Using the Polarizable AMOEBA Force Field. J. Chem. Theory Comput 2010, 6, 2059–2070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (184).Hagberg D; Karlstrom G; Roos BO; Gagliardi L The Coordination of Uranyl in Water: A Combined Quantum Chemical and Molecular Simulation Study. J. Am. Chem. Soc 2005, 127, 14250–14256. [DOI] [PubMed] [Google Scholar]
- (185).Li H; Gordon MS; Jensen JH Charge transfer interaction in the effective fragment potential method. J. Chem. Phys 2006, 124, 214108. [DOI] [PubMed] [Google Scholar]
- (186).Stone AJ Electrostatic Damping Functions and the Penetration Energy. J. Phys. Chem. A 2011, 115, 7017–7027. [DOI] [PubMed] [Google Scholar]
- (187).Borodin O; Smith GD, Molecular Modeling of Poly-(ethylene oxide) Melts and Poly(ethylene oxide) Based Polymer Electrolytes In Computational Materials Chemistry, Methods and Applications; Curtiss LA, Gordon MS, Eds.; Kluwer Academic Publishers, 2004. [Google Scholar]
- (188).Ghahremanpour MM; van Maaren PJ; Caleman C; Hutchison GR; van der Spoel D Polarizable Drude Model with s-Type Gaussian or Slater Charge Density for General Molecular Mechanics Force Fields. J. Chem. Theory Comput 2018, 14, 5553–5566. [DOI] [PubMed] [Google Scholar]
- (189).van Duijnen PT; Swart M Molecular and Atomic Polarizabilities: Thole’s Model Revisited. J. Phys. Chem. A 1998, 102, 2399–2407. [Google Scholar]
- (190).Taylor T; Schmollngruber M; Schröder C; Steinhauser O The Effect of Thole Functions on the Simulation of Ionic Liquids with Point Induced Dipoles at Various Densities. J. Chem. Phys 2013, 138, 204119. [DOI] [PubMed] [Google Scholar]
- (191).Harder E; Anisimov VM; Whitfield T; MacKerell AD Jr.; Roux B Understanding the Dielectric Properties of Liquid Amides from a Polarizable Force Field. J. Phys. Chem. B 2008, 112, 3509–3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (192).Canongia-Lopes JN; Pádua AAH CL&P: A Generic and Systematic Force Field for Ionic Liquids Modeling. Theor. Chem. Acc 2012, 131, 1129. [Google Scholar]
- (193).Lesch V; Montes-Campos H; Mendez-Morales T; Gallego LJ; Heuer A; Schröder C; Varela LM Molecular Dynamics Analysis of the Effect of Electronic Polarization on the Structure and Single-Particle Dynamics of Mixtures of Ionic Liquids and Lithium Salts. J. Chem. Phys 2016, 145, 204507. [DOI] [PubMed] [Google Scholar]
- (194).Kunz AP; van Gunsteren WF Development of a Nonlinear Classical Polarization Model for Liquid Water and Aqueous Solutions: COS/D. J. Phys. Chem.A 2009, 113, 11570–11579. [DOI] [PubMed] [Google Scholar]
- (195).Heid E; Heindl M; Dienstl P; Schröder C Additive Polarizabilities of Halides in Ionic Liquids and Organic Solvents. J. Chem. Phys 2018, 149, 044302. [DOI] [PubMed] [Google Scholar]
- (196).Heid E; Szabadi A; Schröder C Quantum Mechanical Determination of Atomic Polarizabilities of Ionic Liquids. Phys. Chem. Chem. Phys 2018, 20, 10992–10996. [DOI] [PubMed] [Google Scholar]
- (197).Heid E; Hunt P; Schröder C Evaluating Excited State Atomic Polarizabilities of Chromophores. Phys. Chem. Chem. Phys 2018, 20, 8554–8563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (198).Slipchenko LV; Gordon MS Damping Functions in the Effective Fragment Potential Method. Mol. Phys 2009, 107, 999–1016. [Google Scholar]
- (199).Chaudret R; Gresh N; Narth C; Lagardère L; Darden TA; Cisneros GA; Piquemal J-P S/G-1: An Ab Initio Force-field Blending Frozen Hermite Gaussian Densities and Distributed Multipoles. Proof of Concept and First Applications to Metal Cations. J. Phys. Chem.A 2014, 118, 7598–7612. [DOI] [PubMed] [Google Scholar]
- (200).Chelli R; Barducci A; Bellucci L; Schettino V; Procacci P Behavior of Polarizable Models in Presence of Strong Electric Fields. I. Origin of Nonlinear Effects in Water Point-Charge Systems. J. Chem. Phys 2005, 123, 194109. [DOI] [PubMed] [Google Scholar]
- (201).Paricaud P; Predota M; Chialvo AA; Cummings PT From Dimer to Condensed Phases at Extreme Conditions: Accurate Predictions of the Properties of Water by a Gaussian Charge Polarizable Model. J. Chem. Phys 2005, 122, 244511. [DOI] [PubMed] [Google Scholar]
- (202).Schwörer M; Wichmann C; Tavan P A Polarizable QM/MM Approach to the Molecular Dynamics of Amide Groups Solvated in Water. J. Chem. Phys 2016, 144, 114504. [DOI] [PubMed] [Google Scholar]
- (203).Tröster P; Lorenzen K; Tavan P Polarizable Six-Point Water Models from Computational and Empirical Optimization. J. Phys. Chem. B 2014, 118, 1589–1602. [DOI] [PubMed] [Google Scholar]
- (204).Piquemal J-P; Cisneros GA; Reinhardt P; Gresh N; Darden TA Towards a Force Field Based on Density Fitting. J. Chem. Phys 2006, 124, 104101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (205).Cisneros GA; Piquemal J-P; Darden TA Generalization of the Gaussian Electrostatic Model: Extension to Arbitrary Angular Momentum, Distributed Multipoles and Speedup with Reciprocal Space Methods. J. Chem. Phys 2006, 125, 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (206).Elking DM; Cisneros GA; Piquemal J-P; Darden TA; Pedersen LG Gaussian Multipole Model. J. Chem. Theory Comput 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (207).Duke R; Starovoytov O; Piquemal J-P; Cisneros GA GEM*: A Molecular Electronic Density–Based Force Field for Classical Molecular Dynamics Simulations. J. Chem. Theory Comput 2014, 10, 1361–1365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (208).Piquemal JP; Cisneros GA Status of the Gaussian Electrostatic Model a Density-Based Polarizable Force Field In Many-Body Effects and Electrostatics in Biomolecules; Pan Stanford Publishing, 2016; Chapter 8. [Google Scholar]
- (209).Liu C; Qi R; Wang Q; Piquemal J-P; Ren P Capturing Many-body Interactions with Classical Dipole Induction Models. J. Chem. Theory Comput 2017, 13, 2751–2761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (210).Tan ML; Tran KN; Pickard F. C. t.; Simmonett AC; Brooks BR; Ichiye T Molecular Multipole Potential Energy Functions for Water. J. Phys. Chem. B 2016, 120, 1833–1842. [DOI] [PubMed] [Google Scholar]
- (211).Kiss PT; Baranyai A A Systematic Development of a Polarizable Potential of Water. J. Chem. Phys 2013, 138, 204507. [DOI] [PubMed] [Google Scholar]
- (212).Tan SYS; Izgorodina EI Comparison of the Effective Fragment Potential Method with Symmetry-Adapted Perturbation Theory in the Calculation of Intermolecular Energies for Ionic Liquids. J. Chem. Theory Comput 2016, 12, 2553–2568. [DOI] [PubMed] [Google Scholar]
- (213).Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA; Head-Gordon M; Clark GNI; Johnson ME; Head-Gordon T Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (214).Torabifard H; Reed L; Berry MT; Hein JE; Menke E; Cisneros GA Computational and Experimental Characterization of a Pyrrolidinium-Based Ionic Liquid for Electrolyte Applications. J. Chem. Phys 2017, 147, 161731. [DOI] [PubMed] [Google Scholar]
- (215).Starovoytov ON; Torabifard H; Cisneros GA Development of AMOEBA Force Field for 1, 3-Dimethylimidazolium Based Ionic Liquids. J. Phys. Chem. B 2014, 118, 7156–7166. [DOI] [PubMed] [Google Scholar]
- (216).Huang L; Roux B Automated Force Field Parameterization for Non-Polarizable and Polarizable Atomic Models Based on Ab Initio Target Data. J. Chem. Theory Comput 2013, 9, 3543–3556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (217).Baker CM; Mackerell AD Jr. Polarizability Rescaling and Atom-Based Thole Scaling in the CHARMM Drude Polarizable Force FIeld for Ethers. J. Mol. Model 2010, 16, 567–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (218).Gu Y; Yan T Thole Model for Ionic Liquid Polarizability. J. Phys. Chem.A 2013, 117, 219–227.23214431 [Google Scholar]
- (219).Vanommeslaeghe K; MacKerell AD Jr. Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (220).Vanommeslaeghe K; Raman EP; MacKerell AD Jr. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model 2012, 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (221).Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell AD Jr. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem 2009, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (222).Pulay P; Fogarasi G; Pongor G; Boggs JE; Vargha A Combination of Theoretical Ab Initio and Experimental Information to Obtain Reliable Harmonic Force Constants. Scaled Quantum Mechanical (QM) Force Fields for Glyoxal, Acrolein, Butadiene, Formaldehyde, and Ethylene. J. Am. Chem. Soc 1983, 105, 7037–7047. [Google Scholar]
- (223).Merrick JP; Moran D; Radom L An Evaluation of Harmonic Vibrational Frequency Scale Factors. J. Phys. Chem. A 2007, 111, 11683–11700. [DOI] [PubMed] [Google Scholar]
- (224).Miller KJ Additivity Methods in Molecular Polarizability. J. Am. Chem. Soc 1990, 112, 8533–8542. [Google Scholar]
- (225).Kang YK; Jhon MS Additivity of Atomic Static Polarizabilities and Dispersion Coefficients. Theor. Chim. Acta 1982, 61, 41–48. [Google Scholar]
- (226).Bosque R; Sales J Polarizabilities of Solvents from the Chemical Composition. J. Chem. Inf. Comp. Sci 2002, 42, 1154–1163. [DOI] [PubMed] [Google Scholar]
- (227).Jensen L; Astrand P-O; Osted A; Kongsted J; Mikkelsen KV Polarizability of Molecular Clusters as Calculated by a Dipole Interaction Model. J. Chem. Phys 2002, 116, 4001–4010. [Google Scholar]
- (228).Boulanger E; Huang L; Rupakheti C; MacKerell AD Jr.; Roux B Optimized Lennard-Jones Parameters for Druglike Small Molecules. J. Chem. Theory Comput 2018, 14, 3121–3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (229).Bica K; Deetlefs M; Schröder C; Seddon KR Polarisabilities of Alkylimidazolium Ionic Liquids. Phys. Chem. Chem. Phys 2013, 15, 2703–2711. [DOI] [PubMed] [Google Scholar]
- (230).Izgorodina EI; Forsyth M; Macfarlane DR On the Components of the Dielectric Constants of Ionic Liquids: Ionic Polarization? Phys. Chem. Chem. Phys 2009, 11, 2452–2458. [DOI] [PubMed] [Google Scholar]
- (231).Sattari M; Kamari A; Mohammadi AH; Ramjugernath D Prediction of Refractive Indices of Ionic Liquids – A Quantitative Structure-Property Relationship Based Model. J. Taiwan Inst. Chem. Eng. 2015, 52, 165–180. [Google Scholar]
- (232).Uhlig F; Zeman J; Smiatek J; Holm C First-Principles Parameterization of Polarizable Coarse-Grained Force Fields for Ionic Liquids. J. Chem. Theory Comput 2018, 14, 1471–1486. [DOI] [PubMed] [Google Scholar]
- (233).Zeman J; Uhlig F; Smiatek J; Holm C A Coarse-Grained Polarizable Force Field for the Ionic Liquid 1-Butyl-3-methylimidazolium Hexafluorophosphate. J. Phys.: Condens. Matter 2017, 29, 504004. [DOI] [PubMed] [Google Scholar]
- (234).Laidig KE; Bader RFW Properties of Atoms in Molecules: Atomic Polarizabilities. J. Chem. Phys 1990, 93, 7213–7224. [Google Scholar]
- (235).Matta CF; Boyd RJ, An Introduction to the Quantum Theory of Atoms in Molecules In The Quantum Theory of Atoms in Molecules; Matta CF. Ed.; Wiley, 2007. [Google Scholar]
- (236).Millot C; Chaumont A; Engler E; Wipff G Distributed Polarizability Models for Imidazolium-Based Ionic Liquids. J. Phys. Chem.A 2014, 118, 8842–8851. [DOI] [PubMed] [Google Scholar]
- (237).Schröder C; Rudas T; Neumayr G; Gansterer W; Steinhauser O Impact of Anisotropy on the Structure and Dynamics of Ionic Liquids: A Computational Study of 1-Butyl-3-methyl-imidazolium Trifluoroacetate. J. Chem. Phys 2007, 127, 044505. [DOI] [PubMed] [Google Scholar]
- (238).Schröder C; Wakai C; Weingartner H; Steinhauser O Collective Rotational Dynamics in Ionic Liquids: A Computational and Experimental Study of 1-Butyl-3-methyl-imidazolium Tetrafluoroborate. J. Chem. Phys 2007, 126, 084511. [DOI] [PubMed] [Google Scholar]
- (239).Gross L; Herrmann C Local Electric Dipole Moments: A Generalized Approach. J. Comput. Chem 2016, 37, 2260–2265. [DOI] [PubMed] [Google Scholar]
- (240).Stone AJ Distributed Multipole Analysis: Stability for Large Basis Sets. J. Chem. Theory Comput 2005, 1, 1128–1132. [DOI] [PubMed] [Google Scholar]
- (241).Marenich AV; Cramer CJ; Truhlar DG Reduced and Quenched Polarizabilities of Interior Atoms in Molecules. Chem. Sci. 2013, 4, 2349–2356. [Google Scholar]
- (242).Heid E; Fleck M; Chatterjee P; Schröder C; MacKerell AD Jr. Toward Prediction of Electrostatic Parameters for Force Fields That Explicitly Treat Electronic Polarization. J. Chem. Theory Comput 2019, 15, 2460–2469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (243).Anisimov VM; Lamoureux G; Vorobyov IV; Huang N; Roux B; MacKerell AD Determination of Electrostatic Parameters for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory Comput 2005, 1, 153–168. [DOI] [PubMed] [Google Scholar]
- (244).Vorobyov IV; Anisimov VM; MacKerell AD Jr. Polarizable Empirical Force Field for Alkanes Based on the Classical Drude Oscillator Model. J. Phys. Chem. B 2005, 109, 18988–18999. [DOI] [PubMed] [Google Scholar]
- (245).Borodin O; Smith GD Development of Many-Body Polarizable Force Fields for Li-Battery Components: 1. Ether, Alkane, and Carbonate-Based Solvents. J. Phys. Chem. B 2006, 110, 6279–6292. [DOI] [PubMed] [Google Scholar]
- (246).Borodin O; Smith GD Development of Many-Body Polarizable Force Fields for Li-Battery Applications: 2. LiTFSI-Doped Oligoether, Polyether, and Carbonate-Based Electrolytes. J. Phys. Chem. B 2006, 110, 6293–6299. [DOI] [PubMed] [Google Scholar]
- (247).Padua AAH Resolving Dispersion and Induction Components for Polarisable Molecular Simulations of Ionic Liquids. J. Chem. Phys 2017, 146, 204501. [DOI] [PubMed] [Google Scholar]
- (248).MacKerell AD; Karplus M Importance of Attractive van der Waals Contribution in Empirical Energy Function Models for the Heat of Vaporization of Polar Liquids. J. Phys. Chem. 1991, 95, 10559–10560. [Google Scholar]
- (249).Becker TM; Dubbeldam D; Lin L-C; Vlugt TJH Investigating Polarization Effects of CO2 Adsorption in MgMOF-74. J. Comput. Sci 2016, 15, 86–94. [Google Scholar]
- (250).Hamaker HC The London—van der Waals Attraction Between Spherical Particles. Physica 1937, 4, 1058–1072. [Google Scholar]
- (251).Gould T How Polarizabilities and C6 Coefficients Actually Vary with Atomic Volume. J. Chem. Phys 2016, 145, 084308. [DOI] [PubMed] [Google Scholar]
- (252).Gould T; Bucko T C6 Coefficients and Dipole Polarizabilities for All Atoms and Many Ions in Rows 1–6 of the Periodic Table. J. Chem. Theory Comput 2016, 12, 3603–3613. [DOI] [PubMed] [Google Scholar]
- (253).Salanne M; Rotenberg B; Jahn S; Vuilleumier R; Simon C; Madden PA Including Many-Body Effects in Models for Ionic Liquids. Theor. Chem. Acc. 2012, 131, 1143. [Google Scholar]
- (254).Halgren TA Representation of van der Waals (vdW) Interactions in Molecular Mechanics Force Fields: Potential Form,Combination Rules, and vdW Parameters. J. Am. Chem. Soc 1992, 114, 7827–7843. [Google Scholar]
- (255).Pierce F; Tsige M; Borodin O; Perahia D; Grest GS Interfacial Properties of Semifluorinated Alkane Diblock Copolymers. J. Chem. Phys 2008, 128, 214903. [DOI] [PubMed] [Google Scholar]
- (256).Borodin O; Gorecki W; Smith GD; Armand M Molecular Dynamics Simulation and Pulsed-Field Gradient NMR Studies of Bis(fluorosulfonyl)imide (FSI) and Bis[(trifluoromethyl)sulfonyl]-imide (TFSI)-Based Ionic Liquids. J. Phys. Chem. B 2010, 114, 6786–6798. [DOI] [PubMed] [Google Scholar]
- (257).Alvarado J; Schroeder MA; Zhang M; Borodin O; Gobrogge E; Olguin M; Ding MS; Gobet M; Greenbaum S; Meng YS; Xu K A Carbonate-free, Sulfone-based Electrolyte for High-voltage Li-ion Batteries. Mater. Today 2018, 21, 341–353. [Google Scholar]
- (258).Borodin O; Suo L; Gobet M; Ren X; Wang F; Faraone A; Peng J; Olguin M; Schroeder M; Ding MS; Gobrogge E; von Wald Cresce A; Munoz S; Dura JA; Greenbaum S; Wang C; Xu K Liquid Structure with Nano-Heterogeneity Promotes Cationic Transport in Concentrated Electrolytes. ACS Nano 2017, 11, 10462–10471. [DOI] [PubMed] [Google Scholar]
- (259).Suo L; Borodin O; Wang Y; Rong X; Sun W; Fan X; Xu S; Schroeder MA; Cresce AV; Wang F; Yang C; Hu Y-S; Xu K; Wang C “Water-in-Salt” Electrolyte Makes Aqueous Sodium-Ion Battery Safe, Green, and Long-Lasting. Adv. Energy Mater. 2017, 7, 1701189. [Google Scholar]
- (260).Borodin O; Smith GD LiTFSI Structure and Transport in Ethylene Carbonate from Molecular Dynamics Simulations. J. Phys. Chem. B 2006, 110, 4971–4977. [DOI] [PubMed] [Google Scholar]
- (261).Borodin O; Smith GD; Geiculescu O; Creager SE; Hallac B; DesMarteau D Li+ Transport in Lithium Sulfonylimide-Oligo(ethylene oxide) Ionic Liquids and Oligo(ethylene oxide) Doped with LiTFSI. J. Phys. Chem. B 2006, 110, 24266–24274. [DOI] [PubMed] [Google Scholar]
- (262).Michalowsky J; Zeman J; Holm C; Smiatek J A Polarizable MARTINI Model for Monovalent Ions in Aqueous Solution. J. Chem. Phys 2018, 149, 163319. [DOI] [PubMed] [Google Scholar]
- (263).Wang W; Skeel RD Fast Evaluation of Polarizable Forces. J. Chem. Phys 2005, 123, 164107. [DOI] [PubMed] [Google Scholar]
- (264).Lipparini F; Lagardère L; Stamm B; Cances E; Schnieders M; Ren P; Maday Y; Piquemal J-P Scalable Evaluation of the Polarization Energy and Associated Forces in Polarizable Molecular Dynamics: I. Towards Massively Parallel Direct Space Computations. J. Chem. Theory Comput 2014, 10, 1638–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (265).Saad Y Iterative Methods for Sparse Linear Systems; SIAM, 2003. [Google Scholar]
- (266).Nocito D; Beran G Fast Divide-and-Conquer Scheme for Evaluating Polarization in Classical Force Fields. J. Chem. Phys 2017, 146, 114103. [DOI] [PubMed] [Google Scholar]
- (267).Nocito D; Beran G Massively Parallel Implementation of Divide-and-Conquer Jacobi Iterations Using Particle-Mesh Ewald for Force Field Polarization. J. Chem. Theory Comput 2018, 14, 3633–3642. [DOI] [PubMed] [Google Scholar]
- (268).Kolafa J Time-Reversible Always Stable Predictor–Corrector Method for Molecular Dynamics of Polarizable Molecules. J. Comput. Chem 2004, 25, 335–342. [DOI] [PubMed] [Google Scholar]
- (269).Tuckerman M; Berne BJ; Martyna G Reversible Multiple Time Scale Molecular Dynamics. J. Chem. Phys 1992, 97, 1990–2001. [Google Scholar]
- (270).Albaugh A; Demerdash ON; Head-Gordon T An Efficient and Stable Hybrid Extended Lagrangian/Self-consistent Field Scheme for Solving Classical Mutual Induction. J. Chem. Phys 2015, 143, 174104. [DOI] [PubMed] [Google Scholar]
- (271).Albaugh A; Niklasson A; Head-Gordon T Accurate Classical Polarization Solution With No Self-consistent Field Iterations. J. Phys. Chem. Lett 2017, 8, 1714–1723. [DOI] [PubMed] [Google Scholar]
- (272).Wang W Fast Polarizable Force Field Computation in Biomolecular Simulations; University of Illinois at Urbana—Champaign, 2005. [Google Scholar]
- (273).Simmonett AC; Pickard FC IV; Shao Y; Cheatham TE III; Brooks BR Efficient Treatment of Induced Dipoles. J. Chem. Phys 2015, 143, 074115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (274).Simmonett AC; Pickard FC IV; Ponder JW; Brooks BR An Empirical Extrapolation Scheme for Efficient Treatment of Induced Dipoles. J. Chem. Phys 2016, 145, 164101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (275).Aviat F; Lagardère L; Piquemal J-P The Truncated Conjugate Gradient (TCG), a Non-iterative/Fixed-cost Strategy for Computing Polarization in Molecular Dynamics: Fast Evaluation of Analytical Forces. J. Chem. Phys 2017, 147, 161724. [DOI] [PubMed] [Google Scholar]
- (276).Aviat F; Levitt A; Maday Y; Stamm B; Ren PY; Ponder JW; Lagardère L; Piquemal J-P Truncated Conjugate Gradient (TCG): An Optimal Strategy for the Analytical Evaluation of the Many-Body Polarization Energy and Forces in Molecular Simulations. J. Chem. Theory Comput 2017, 13, 180–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (277).Simmonett AC; Pickard FC IV; Schaefer HF III; Brooks BR An Efficient Algorithm for Multipole Energies and Derivatives Based on Spherical Harmonics and Extensions to Particle Mesh Ewald. J. Chem. Phys 2014, 140, 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (278).Boateng H Mesh-Free Hierarchical Clustering Methods for Fast Evaluation of Electrostatic Interactions of Point Multipoles. J. Chem. Phys 2017, 147, 164104. [DOI] [PubMed] [Google Scholar]
- (279).Greengard L; Rokhlin V A Fast Algorithm for Particle Simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar]
- (280).Coles JP; Masella M The Fast Multipole Method and Point Dipole Moment Polarizable Forces. J. Chem. Phys 2015, 142, 024109. [DOI] [PubMed] [Google Scholar]
- (281).Bowers KJ; Dror RO; Shaw DE The Midpoint Method for Parallelization of Particle Simulations. J. Chem. Phys 2006, 124, 184109. [DOI] [PubMed] [Google Scholar]
- (282).Jorgensen WL; Madura JD; Swenson CJ Optimized Intermolecular Potential Functions for Lipuid Hydrocarbons. J. Am. Chem. Soc 1984, 106, 6638–6646. [Google Scholar]
- (283).Jorgensen WL Optimized Intermolecular Potential Functions for Liquid Alcohols. J. Phys. Chem. 1986, 90, 1276–1284. [Google Scholar]
- (284).MacKerell AD Jr. Empirical Force Fields for Biological Macromolecules: Overview and Issues. J. Comput. Chem 2004, 25, 1584–1604. [DOI] [PubMed] [Google Scholar]
- (285).Head-Gordon T; Hura G Water Structure from Scattering Experiments and Simulation. Chem. Rev 2002, 102, 2651–2670. [DOI] [PubMed] [Google Scholar]
- (286).Nilsson A; Pettersson LGM The Structural Origin of Anomalous Properties of Liquid Water. Nat. Commun. 2015, 6, 8998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (287).Foroutan M; Fatemi SM; Esmaeilian F A Review of the Structure and Dynamics of Nanoconfined Water and Ionic Liquids via Molecular Dynamics Simulation. Eur. Phys. J. E: Soft Matter Biol. Phys. 2017, 40, 19. [DOI] [PubMed] [Google Scholar]
- (288).Jorgensen WL; Madura JD Temperature and Size Dependence for Monte Carlo Simulations of TIP4P Water. Mol. Phys 1985, 56, 1381–1392. [Google Scholar]
- (289).Huggins DJ Correlations in Liquid Water for the TIP3P-Ewald, TIP4P-2005, TIP5P-Ewald, and SWM4-NDP Models. J. Chem. Phys 2012, 136, 064518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (290).Sega M; Schröder C Dielectric and Terahertz Spectroscopy of Polarizable and Nonpolarizable Water Models: A Comparative Study. J. Phys. Chem.A 2015, 119, 1539–1547. [DOI] [PubMed] [Google Scholar]
- (291).Schropp B; Tavan P The Polarizability of Point-Polarizable Water Models: Density Functional Theory/Molecular Mechanics Results. J. Phys. Chem. B 2008, 112, 6233–6240. [DOI] [PubMed] [Google Scholar]
- (292).Starovoytov ON; Borodin O; Bedrov D; Smith GD Development of a Polarizable Force Field for Molecular Dynamics Simulations of Poly (Ethylene Oxide) in Aqueous Solution. J. Chem. Theory Comput 2011, 7, 1902–1915. [DOI] [PubMed] [Google Scholar]
- (293).Yeh IC; Hummer G System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. [Google Scholar]
- (294).Yu W; Lopes PE; Roux B; MacKerell AD Jr. Six-Site Polarizable Model of Water Based on the Classical Drude Oscillator. J. Chem. Phys 2013, 138, 034508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (295).Yu H; van Gunsteren WF Charge-on-Spring Polarizable Water Models Revisited: From Water Clusters to Liquid Water to Ice. J. Chem. Phys 2004, 121, 9549–9564. [DOI] [PubMed] [Google Scholar]
- (296).Caldwell JW; Kollman PA Structure and Properties of Neat Liquids Using Nonadditive Molecular Dynamics: Water, Methanol, and N-Methylacetamide. J. Phys. Chem. 1995, 99, 6208–6219. [Google Scholar]
- (297).Dang LX; Chang T-M Molecular Dynamics Study of Water Clusters, Liquid, and Liquid–Vapor Interface of Water with Many-Body Potentials. J. Chem. Phys 1997, 106, 8149–8159. [Google Scholar]
- (298).Molina JJ; Lectez S; Tazi S; Salanne M; Dufreche JF; Roques J; Simoni E; Madden PA; Turq P Ions in Solutions: Determining Their Polarizabilities from First-Principles. J. Chem. Phys 2011, 134, 014511. [DOI] [PubMed] [Google Scholar]
- (299).Carof A; Salanne M; Charpentier T; Rotenberg B On the Microscopic Fluctuations Driving the NMR Relaxation of Quadrupolar Ions in Water. J. Chem. Phys 2015, 143, 194504. [DOI] [PubMed] [Google Scholar]
- (300).Carof A; Salanne M; Charpentier T; Rotenberg B Collective Water Dynamics in the First Solvation Shell Drive the NMR Relaxation of Aqueous Quadrupolar Cations. J. Chem. Phys 2016, 145, 124508. [DOI] [PubMed] [Google Scholar]
- (301).Wang J; Cieplak P; Cai Q; Hsieh MJ; Wang J; Duan Y; Luo R Development of Polarizable Models for Molecular Mechanical Calculations. 3. Polarizable Water Models Conforming to Thole Polarization Screening Schemes. J. Phys. Chem. B 2012, 116, 7999–8008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (302).Allinger NL; Yuh YH; Lii J-H Molecular Mechanics. The MM3 Force Field for Hydrocarbons. 1. J. Am. Chem. Soc 1989, 111, 8551–8566. [Google Scholar]
- (303).Stone AJ Distributed Multipole Analysis, or How to Describe a Molecular Charge Distribution. Chem. Phys. Lett 1981, 83, 233–239. [Google Scholar]
- (304).Ren P; Ponder JW Temperature and Pressure Dependence of the AMOEBA Water Model. J. Phys. Chem. B 2004, 108, 13427–13437. [Google Scholar]
- (305).Laury ML; Wang L-P; Pande VS; Head-Gordon T; Ponder JW Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model. J. Phys. Chem. B 2015, 119, 9423–9437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (306).Torabifard H; Starovoytov ON; Ren P; Cisneros GA Development of an AMOEBA Water Model Using GEM Distributed Multipoles. Theor. Chem.Acc. 2015, 134, 101. [Google Scholar]
- (307).Harder E; Damm W; Maple J; Wu C; Reboul M; Xiang JY; Wang L; Lupyan D; Dahlgren MK; Knight JL; Kaus JW; Cerutti DS; Krilov G; Jorgensen WL; Abel R; Friesner RA OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput 2016, 12, 281–296. [DOI] [PubMed] [Google Scholar]
- (308).Horta BA; Merz PT; Fuchs PF; Dolenc J; Riniker S; Hunenberger PH A GROMOS-Compatible Force Field for Small Organic Molecules in the Condensed Phase: The 2016H66 Parameter Set. J. Chem. Theory Comput 2016, 12, 3825–3850. [DOI] [PubMed] [Google Scholar]
- (309).Borodin O; Smith GD Quantum Chemistry and Molecular Dynamics Simulation Study of Dimethyl Carbonate: Ethylene Carbonate Electrolytes Doped with LiPF6. J. Phys. Chem. B 2009, 113, 1763–1776. [DOI] [PubMed] [Google Scholar]
- (310).Visscher KM; Vosmeer CR; Luirink RA; Geerke DP A Systematic Approach to Calibrate a Transferable Polarizable Force Field Parameter Set for Primary Alcohols. J. Comput. Chem 2017, 38, 508–517. [DOI] [PubMed] [Google Scholar]
- (311).Anisimov VM; Vorobyov IV; Roux B; MacKerell AD Jr. Polarizable Empirical Force Field for the Primary and Secondary Alcohol Series Based on the Classical Drude Model. J. Chem. Theory Comput 2007, 3, 1927–1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (312).Zhu X; MacKerell AD Jr. Polarizable Empirical Force Field for Sulfur-Containing Compounds Based on the Classical Drude Oscillator Model. J. Comput. Chem 2010, 31, 2330–2341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (313).Lopes PEM; Lamoureux G; Roux B; MacKerell AD Jr. Polarizable Empirical Force Field for Aromatic Compounds Based on the Classical Drude Oscillator. J. Phys. Chem. B 2007, 111, 2873–2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (314).Baker CM; Anisimov VM; MacKerell AD Jr. Development of CHARMM Polarizable Force Field for Nucleic Acid Bases Based on the Classical Drude Oscillator Model. J. Phys. Chem. B 2011, 115, 580–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (315).Borodin O Relation between Heat of Vaporization, Ion Transport, Molar Volume, and Cation and Anion Binding Energy for Ionic Liquids. J. Phys. Chem. B 2009, 113, 12353–12357. [DOI] [PubMed] [Google Scholar]
- (316).Schröder C; Hunger J; Stoppa A; Buchner R; Steinhauser O On the Collective Network of Ionic Liquid/Water Mixtures. II. Decomposition and Interpretation of Dielectric Spectra. J. Chem. Phys 2008, 129, 184501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (317).Chang TM; Dang LX Recent Advances in Molecular Simulations of Ion Solvation at Liquid Interfaces. Chem. Rev 2006, 106, 1305–1322. [DOI] [PubMed] [Google Scholar]
- (318).Wernersson E; Jungwirth P Effect of Water Polarizability on the Properties of Solutions of Polyvalent Ions: Simulations of Aqueous Sodium Sulfate with Different Force Fields. J. Chem. Theory Comput 2010, 6, 3233–3240. [DOI] [PubMed] [Google Scholar]
- (319).Bordin JR; Podgornik R; Holm C Static Polarizability Effects on Counterion Distributions Near Charged Dielectric Surfaces: A Coarse-Grained Molecular Dynamics Study Employing the Drude Model. Eur. Phys. J.: Spec. Top. 2016, 225, 1693–1705. [Google Scholar]
- (320).Baker CM; Lopes PE; Zhu X; Roux B; Mackerell AD Jr. Accurate Calculation of Hydration Free Energies using Pair-Specific Lennard-Jones Parameters in the CHARMM Drude Polarizable Force Field. J. Chem. Theory Comput 2010, 6, 1181–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (321).Lin F-Y; Lopes PEM; Harder E; Roux B; MacKerell AD Jr. Polarizable Force Field for Molecular Ions Based on the Classical Drude Oscillator. J. Chem. Inf. Model. 2018, 58, 993–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (322).Yu H; Whitfield TW; Harder E; Lamoureux G; Vorobyov I ; Anisimov VM; MacKerell AD Jr.; Roux B Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J. Chem. Theory Comput 2010, 6, 774–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (323).Grossfield A; Ren P; Ponder JW Ion Solvation Thermodynamics from Dimulation with a Polarizable Force Field. J. Am. Chem. Soc 2003, 125, 15671–15682. [DOI] [PubMed] [Google Scholar]
- (324).Piquemal J-P; Perera L; Cisneros GA; Ren P; Pedersen LG; Darden TA Towards Accurate Solvation Dynamics of Divalent Cations in Water Using the Polarizable AMOEBA Force Field: From Energetics to Structure. J. Chem. Phys 2006, 125, 054511. [DOI] [PubMed] [Google Scholar]
- (325).Jiao D; King C; Grossfield A; Darden TA; Ren P Simulation of Ca2+ and Mg2+ Solvation Using Polarizable Atomic Multipole Potential. J. Phys. Chem. B 2006, 110, 18553–18559. [DOI] [PubMed] [Google Scholar]
- (326).Marjolin A; Gourlaouen C; Clavaguera C; Gresh N; Ren PY; Wu J; Dognon J-P; Piquemal J-P Towards Accurate Solvation Dynamics of Lanthanides and Actinides in Water Using Polarizable Force Fields: From Gas Phase Energetics to Hydration Free Energies. Theor. Chem.Acc. 2012, 131, 1198. [Google Scholar]
- (327).Marjolin A; Gourlaouen C; Clavaguera C; Ren PY; Piquemal J-P; Dognon J-P Hydration Gibbs Free Energies of Open and Closed Shell Trivalent Lanthanide and Actinide Cations from Polarizable Molecular Dynamics. J. Mol. Model. 2014, 20, 2471. [DOI] [PubMed] [Google Scholar]
- (328).Tu YJ; Allen MJ; Cisneros GA Simulations of the Water Exchange Dynamics of Lanthanide Ions in 1-Ethyl-3-methylimidazolium Ethyl Sulfate ([EMIm][EtSO4]) and Water. Phys. Chem. Chem. Phys 2016, 18, 30323–30333. [DOI] [PubMed] [Google Scholar]
- (329).Luo Y; Roux B Simulation of Osmotic Pressure in Concentrated Aqueous Salt Solutions. J. Phys. Chem. Lett 2010, 1, 183–189. [Google Scholar]
- (330).Yoo J; Aksimentiev A New Tricks for Old Dogs: Improving the Accuracy of Biomolecular Force Fields by Pair-Specific Corrections to Non-bonded Interactions. Phys. Chem. Chem. Phys 2018, 20, 8432–8449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (331).Luo Y; Jiang W; Yu H; MacKerell AD Jr.; Roux B Simulation Study of Ion Pairing in Concentrated Aqueous Salt Solutions with a Polarizable Force Field. Faraday Discuss. 2013, 160, 135–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (332).Kohagen M; Pluharova E; Mason PE; Jungwirth P Exploring Ion-Ion Interactions in Aqueous Solutions by a Combination of Molecular Dynamics and Neutron Scattering. J. Phys. Chem. Lett 2015, 6, 1563–1567. [DOI] [PubMed] [Google Scholar]
- (333).Borreguero JM; Lynch VE Molecular Dynamics Force-Field Refinement against Quasi-Elastic Neutron Scattering Data. J. Chem. Theory Comput 2016, 12, 9–17. [DOI] [PubMed] [Google Scholar]
- (334).Bouazizi S; Nasr S; Jaidane N; Bellissent-Funel MC Local Order in Aqueous NaCl Solutions and Pure Water: X-ray Scattering and Molecular Dynamics Simulations Study. J. Phys. Chem. B 2006, 110, 23515–23523. [DOI] [PubMed] [Google Scholar]
- (335).Thomas JL; Tobias DJ; Mackerell AD Jr. Direct Comparisons of Experimental and Calculated Neutron Structure Factors of Pure Solvents as a Method for Force Field Validation. J. Phys. Chem. B 2007, 111, 12941–12944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (336).Kirkwood JG; Buff FP The Statistical Mechanical Theory of Solutions. I. J. Chem. Phys 1951, 19, 774. [Google Scholar]
- (337).Kang M; Smith PE A Kirkwood-Buff Derived Force Field for Amides. J. Comput. Chem 2006, 27, 1477–1485. [DOI] [PubMed] [Google Scholar]
- (338).Smith PE Equilibrium Dialysis Data and the Relationships Between Preferential Interaction Parameters for Biological Systems in Terms of Kirkwood-Buff Integrals. J. Phys. Chem. B 2006, 110, 2862–2868. [DOI] [PubMed] [Google Scholar]
- (339).Lin B; Lopes PEM; Roux B; MacKerell AD Jr. Kirkwood-Buff Analysis of Aqueous N-Methylacetamide and Acet-amide Solutions Modeled by the CHARMM Additive and Drude Polarizable Force Fields. J. Chem. Phys 2013, 139, 084509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (340).Lin B; He X; MacKerell AD Jr. A Comparative Kirkwood-Buff Study of Aqueous Methanol Solutions Modeled by the CHARMM Additive and Drude Polarizable Force Fields. J. Phys. Chem. B 2013, 117, 10572–10580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (341).Picalek J; Minofar B; Kolafa J; Jungwirth P Aqueous Solutions of Ionic Liquids: Study of the Solution/Vapor Interface Using Molecular Dynamics Simulations. Phys. Chem. Chem. Phys 2008, 10, 5765–5775. [DOI] [PubMed] [Google Scholar]
- (342).Yan T; Li S; Jiang W; Gao X; Xiang B; Voth GA Structure of the Liquid-Vacuum Interface of Room-Temperature Ionic Liquids: A Molecular Dynamics Study. J. Phys. Chem. B 2006, 110, 1800–1806. [DOI] [PubMed] [Google Scholar]
- (343).Wick CD; Chang TM; Dang LX Molecular Mechanism of CO2 and SO2 Molecules Binding to the Air/Liquid Interface of 1-Butyl-3-methylimidazolium Tetrafluoroborate Ionic Liquid: A Molecular Dynamics Study with Polarizable Potential Models. J. Phys. Chem. B 2010, 114, 14965–14971. [DOI] [PubMed] [Google Scholar]
- (344).Savelyev A; MacKerell AD Jr. Balancing the Interactions of Ions, Water and DNA in the Drude Polarizable Force Field. J. Phys. Chem. B 2014, 118, 6742–6757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (345).Manning GS The Molecular Theory of Polyelectrolyte Solutions with Applications to the Electrostatic Properties of Polynucleotides. Q. Rev. Biophys. 1978, 11, 179–246. [DOI] [PubMed] [Google Scholar]
- (346).Savelyev A; MacKerell AD Jr. Competition among Li, Na, K and Rb Monovalent Ions for DNA in Molecular Dynamics Simulations using the Additive CHARMM36 and Drude Polarizable Force Fields. J. Phys. Chem. B 2015, 119, 4428–4440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (347).Savelyev A; MacKerell AD Jr. Differential Impact of the Monovalent Ions Li, Na, K, and Rb on DNA Conformational Properties. J. Phys. Chem. Lett 2015, 6, 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (348).Zhang C; Lu C; Jing Z; Wu C; Piquemal J-P; Ponder JW; Ren P AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput 2018, 14, 2084–2108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (349).Pollard TP; Beck TL Toward a Quantitative Theory of Hofmeister Phenomena: From Quantum Effects to Thermodynamics. Curr. Opin. Colloid Interface Sci. 2016, 23, 110–118. [Google Scholar]
- (350).Raugei S; Klein ML An Ab Initio Study of Water Molecules in the Bromide Ion Solvation Shell. J. Chem. Phys 2002, 116, 196–202. [Google Scholar]
- (351).Chaudhari MI; Nair JR; Pratt LR; Soto FA; Balbuena PB; Rempe SB Scaling Atomic Partial Charges of Carbonate Solvents for Lithium Ion Solvation and Diffusion. J. Chem. Theory Comput 2016, 12, 5709–5718. [DOI] [PubMed] [Google Scholar]
- (352).Dong D; Bedrov D Charge Transport in [Li(tetraglyme)]-[bis(trifluoromethane) sulfonimide] Solvate Ionic Liquids: Insight from Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 9994–10004. [DOI] [PubMed] [Google Scholar]
- (353).Shinoda W; Hatanaka Y; Hirakawa M; Okazaki S; Tsuzuki S; Ueno K; Watanabe M Molecular Dynamics Study of Thermodynamic Stability and Dynamics of [Li(glyme)]+ Complex in Lithium-glyme Solvate Ionic Liquids. J. Chem. Phys 2018, 148, 193809. [DOI] [PubMed] [Google Scholar]
- (354).Borodin O; Smith GD Li+ Transport Mechanism in Oligo(Ethylene Oxide)s Compared to Carbonates. J. Solution Chem. 2007, 36, 803–813. [Google Scholar]
- (355).Borodin O; Olguin M; Ganesh P; Kent PRC; Allen JL; Henderson WA Competitive Lithium Solvation of Linear and Cyclic Carbonates from Quantum Chemistry. Phys. Chem. Chem. Phys 2016, 18, 164–175. [DOI] [PubMed] [Google Scholar]
- (356).Liyana-Arachchi TP; Haskins JB; Burke CM; Diederichsen KM; McCloskey BD; Lawson JW Polarizable Molecular Dynamics and Experiments of 1,2-Dimethoxyethane Electrolytes with Lithium and Sodium Salts: Structure and Transport Properties. J. Phys. Chem. B 2018, 122, 8548–8559. [DOI] [PubMed] [Google Scholar]
- (357).Seo DM; Borodin O; Han S-D; Boyle PD; Henderson WA Electrolyte Solvation and Ionic Association II. Acetonitrile-Lithium Salt Mixtures: Highly Dissociated Salts. J. Electrochem. Soc. 2012, 159, A1489–A1500. [Google Scholar]
- (358).Seo DM; Borodin O; Han S-D; Ly Q; Boyle PD; Henderson WA Electrolyte Solvation and Ionic Association. I. Acetonitrile-Lithium Salt Mixtures: Intermediate and Highly Associated Salts. J. Electrochem. Soc. 2012, 159, A553–A565. [Google Scholar]
- (359).Han S-D; Borodin O; Allen JL; Seo DM; McOwen DW; Yun S-H; Henderson WA Electrolyte Solvation and Ionic Association: IV. Acetonitrile-Lithium Difluoro(oxalato)borate (LiDFOB) Mixtures. J. Electrochem. Soc. 2013, 160, A2100–A2110. [Google Scholar]
- (360).Seo DM; Borodin O; Balogh D; O’Connell M; Ly Q; Han S-D; Passerini S; Henderson WA Electrolyte Solvation and Ionic Association III. Acetonitrile-Lithium Salt Mixtures–Transport Properties. J. Electrochem. Soc. 2013, 160, A1061–A1070. [Google Scholar]
- (361).Chen FF; Kerr R; Forsyth M Cation Effect on Small Phosphonium Based Ionic Liquid Electrolytes with High Concentrations of Lithium Salt. J. Chem. Phys 2018, 148, 193813. [DOI] [PubMed] [Google Scholar]
- (362).Takeuchi M; Kameda Y; Umebayashi Y; Ogawa S; Sonoda T; Ishiguro SI; Fujita M; Sano M Ion-Ion Interactions of LiPF6 and LiBF4 in Propylene Carbonate Solutions. J. Mol. Liq. 2009, 148, 99–108. [Google Scholar]
- (363).Suo L; Borodin O; Gao T; Olguin M; Ho J; Fan X; Luo C; Wang C; Xu K “Water-in-salt” Electrolyte Enables High-Voltage Aqueous Lithium-Ion Chemistries. Science 2015, 350, 938–943. [DOI] [PubMed] [Google Scholar]
- (364).Jorn R; Kumar R; Abraham DP; Voth GA Atomistic Modeling of the Electrode–Electrolyte Interface in Li-Ion Energy Storage Systems: Electrolyte Structuring. J. Phys. Chem. C 2013, 117, 3747–3761. [Google Scholar]
- (365).Borodin O; Zhuang GV; Ross PN; Xu K Molecular Dynamics Simulations and Experimental Study of Lithium Ion Transport in Dilithium Ethylene Dicarbonate. J. Phys. Chem. C 2013, 117, 7433–7444. [Google Scholar]
- (366).Borodin O; Bedrov D Interfacial Structure and Dynamics of the Lithium Alkyl Dicarbonate SEI Components in Contact with the Lithium Battery Electrolyte. J. Phys. Chem. C 2014, 118, 18362–18371. [Google Scholar]
- (367).Borodin O; Giffin GA; Moretti A; Haskins JB; Lawson JW; Henderson WA; Passerini S Insights into the Structure and Transport of the Lithium, Sodium, Magnesium, and Zinc Bis-(trifluoromethansulfonyl)imide Salts in Ionic Liquids. J. Phys. Chem. C 2018, 122, 20108–20121. [Google Scholar]
- (368).Lesch V; Jeremias S; Moretti A; Passerini S; Heuer A; Borodin O A Combined Theoretical and Experimental Study of the Influence of Different Anion Ratios on Lithium Ion Dynamics in Ionic Liquids. J. Phys. Chem. B 2014, 118, 7367–7375. [DOI] [PubMed] [Google Scholar]
- (369).Hayamizu K; Tsuzuki S; Seki S; Umebayashi Y Nuclear Magnetic Resonance Studies on the Rotational and Translational Motions of Ionic Liquids Composed of 1-Ethyl-3-methylimidazolium Cation and Bis(trifluoromethanesulfonyl)amide and Bis-(fluorosulfonyl)amide Anions and Their Binary Systems Including Lithium Salts. J. Chem. Phys 2011, 135, 084505. [DOI] [PubMed] [Google Scholar]
- (370).Haskins JB; Bennett WR; Wu JJ; Hernández DM; Borodin O; Monk JD; Bauschlicher CW; Lawson JW Computational and Experimental Investigation of Li-Doped Ionic Liquid Electrolytes: [pyr14][TFSI], [pyr13][FSI], and [EMIM][BF4]. J. Phys. Chem. B 2014, 118, 11295–11309. [DOI] [PubMed] [Google Scholar]
- (371).Lourenço TC; Zhang Y; Costa LT; Maginn EJ A Molecular Dynamics Study of Lithium-Containing Aprotic Hetero-cyclic Ionic Liquid Electrolytes. J. Chem. Phys 2018, 148, 193834. [DOI] [PubMed] [Google Scholar]
- (372).Borodin O; Smith GD Mechanism of Ion Transport in Amorphous Poly(Ethylene Oxide)/LiTFSI from Molecular Dynamics Simulations. Macromolecules 2006, 39, 1620–1629. [Google Scholar]
- (373).Voroshylova IV; Chaban VV Atomistic Force Field for Pyridinium-Based Ionic Liquids: Reliable Transport Properties. J. Phys. Chem. B 2014, 118, 10716–10724. [DOI] [PubMed] [Google Scholar]
- (374).Chaban VV; Prezhdo OV Nonadditivity of Temperature Dependent Interactions in Inorganic Ionic Clusters. J. Phys. Chem. C 2015, 119, 8974–8979. [Google Scholar]
- (375).Chaban VV; Prezhdo OV Polarization versus Temperature in Pyridinium Ionic Liquids. J. Phys. Chem. B 2014, 118, 13940–13945. [DOI] [PubMed] [Google Scholar]
- (376).Sprenger KG; Jaeger VW; Pfaendtner J The General AMBER Force fFeld (GAFF) Can Accurately Predict Thermodynamic and Transport Properties of Many Ionic Liquids. J. Phys. Chem. B 2015, 119, 5882–5895. [DOI] [PubMed] [Google Scholar]
- (377).Kelkar MS; Maginn EJ Calculating the Enthalpy of Vaporization for Ionic Liquid Clusters. J. Phys. Chem. B 2007, 111, 9424–9427. [DOI] [PubMed] [Google Scholar]
- (378).Ohtori N; Salanne M; Madden PA Calculations of the Thermal Conductivities of Ionic Materials by Simulation with Polarizable Interaction Potentials. J. Chem. Phys 2009, 130, 104507. [DOI] [PubMed] [Google Scholar]
- (379).Salanne M; Madden PA Polarization Effects in Ionic Solids and Melts. Mol. Phys 2011, 109, 2299–2315. [Google Scholar]
- (380).Chaban VV; Prezhdo OV A New Force Field Model of 1-Butyl-3-methylimidazolium Tetrafluoroborate Ionic Liquid and Acetonitrile Mixtures. Phys. Chem. Chem. Phys 2011, 13, 19345–19354. [DOI] [PubMed] [Google Scholar]
- (381).Choi E; McDaniel JG; Schmidt JR; Yethiraj A First-Principles, Physically Motivated Force Field for the Ionic Liquid [BMIM][BF4]. J. Phys. Chem. Lett 2014, 5, 2670–2674. [DOI] [PubMed] [Google Scholar]
- (382).Yan T; Wang Y; Knox C On the Dynamics of Ionic Liquids: Comparisons between Electronically Polarizable and Nonpolarizable Models II. J. Phys. Chem. B 2010, 114, 6886–6904. [DOI] [PubMed] [Google Scholar]
- (383).Chaban VV; Pereverzev YV; Prezhdo OV A New Model of Chemical Bonding in Ionic Melts. J. Chem. Phys 2012, 136, 164112. [DOI] [PubMed] [Google Scholar]
- (384).Hu Z; Huang X; Annapureddy HV; Margulis CJ Molecular Dynamics Study of the Temperature-Dependent Optical Kerr Effect Spectra and Intermolecular Dynamics of Room Temperature Ionic Liquid 1-Methoxyethylpyridinium Dicyanoamide. J. Phys. Chem. B 2008, 112, 7837–7849. [DOI] [PubMed] [Google Scholar]
- (385).Shirota H; Castner EW Jr. Physical Properties and Intermolecular Dynamics of an Ionic Liquid Compared with Its Isoelectronic Neutral Binary Solution. J. Phys. Chem. A 2005, 109, 9388–9392. [DOI] [PubMed] [Google Scholar]
- (386).Ishida T; Nishikawa K; Shirota H Atom Substitution Effects of [XF6]- in Ionic Liquids. 2. Theoretical Study. J. Phys. Chem. B 2009, 113, 9840–9851. [DOI] [PubMed] [Google Scholar]
- (387).Maroncelli M; Zhang X-X; Liang M; Roy D; Ernsting NP Measurements of the Complete Solvation Response of Coumarin 153 in Ionic Liquids and the Accuracy of Simple Dielectric Continuum Predictions. Faraday Discuss. 2012, 154, 409–424. [DOI] [PubMed] [Google Scholar]
- (388).Heid E; Schröder C Polarizability in Ionic Liquid Simulations Causes Hidden Breakdown of Linear Response Theory. Phys. Chem. Chem. Phys 2019, 21, 1023–1028. [DOI] [PubMed] [Google Scholar]
- (389).Terranova ZL; Corcelli SA Decompositions of Solvent Response Functions in Ionic Liquids: A Direct Comparison of Equilibrium and Nonequilibrium Methodologies. J. Phys. Chem. B 2018, 122, 6823–6828. [DOI] [PubMed] [Google Scholar]
- (390).McOwen DW; Seo DM; Borodin O; Vatamanu J; Boyle PD; Henderson WA Concentrated Electrolytes: Decrypting Electrolyte Properties and Reassessing Al Corrosion Mechanisms. Energy Environ. Sci 2014, 7, 416–426. [Google Scholar]
- (391).Borodin O; Ren X; Vatamanu J; von Wald Cresce A; Knap J; Xu K Modeling Insight into Battery Electrolyte Electrochemical Stability and Interfacial Structure. Acc. Chem. Res. 2017, 50, 2886–2894. [DOI] [PubMed] [Google Scholar]
- (392).Yang C; Chen J; Qing T; Fan X; Sun W; von Cresce A; Ding MS; Borodin O; Vatamanu J; Schroeder MA; Eidson N; Wang C; Xu K 4.0 V Aqueous Li-Ion Batteries. Joule 2017, 1, 122–132. [Google Scholar]
- (393).Groß A; Sakong S Modelling the Electric Double Layer at Electrode/Electrolyte Interfaces. Curr. Opin. Electrochem. 2019, 14, 1–6. [Google Scholar]
- (394).Bedrov D; Vatamanu J; Hu Z Ionic Liquids at Charged Surfaces: Insight from Molecular Simulations. J. Non-Cryst. Solids 2015, 407, 339–348. [Google Scholar]
- (395).Xing L; Vatamanu J; Borodin O; Smith GD; Bedrov D Electrode/Electrolyte Interface in Sulfolane-Based Electrolytes for Li Ion Batteries: A Molecular Dynamics Simulation Study. J. Phys. Chem. C 2012, 116, 23871–23881. [Google Scholar]
- (396).Feng G; Cummings PT Supercapacitor Capacitance Exhibits Oscillatory Behavior as a Function of Nanopore Size. J. Phys. Chem. Lett 2011, 2, 2859–2864. [Google Scholar]
- (397).Xu S; Xing S; Pei S-S; Ivaništšev V; Lynden-Bell R; Baldelli S Molecular Response of 1-Butyl-3-Methylimidazolium Dicyanamide Ionic Liquid at the Graphene Electrode Interface Investigated by Sum Frequency Generation Spectroscopy and Molecular Dynamics Simulations. J. Phys. Chem. C 2015, 119, 26009–26019. [Google Scholar]
- (398).Rotenberg B; Salanne M Structural Transitions at Ionic Liquid Interfaces. J. Phys. Chem. Lett 2015, 6, 4978–4985. [DOI] [PubMed] [Google Scholar]
- (399).Feng G; Li S; Atchison JS; Presser V; Cummings PT Molecular Insights into Carbon Nanotube Supercapacitors: Capacitance Independent of Voltage and Temperature. J. Phys. Chem. C 2013, 117, 9178–9186. [Google Scholar]
- (400).Vatamanu J; Xing L; Li W; Bedrov D Influence of Temperature on the Capacitance of Ionic Liquid Electrolytes on Charged Surfaces. Phys. Chem. Chem. Phys 2014, 16, 5174–5182. [DOI] [PubMed] [Google Scholar]
- (401).Feng G; Huang J; Sumpter BG; Meunier V; Qiao R Structure and Dynamics of Electrical Double Layers in Organic Electrolytes. Phys. Chem. Chem. Phys 2010, 12, 5468–5479. [DOI] [PubMed] [Google Scholar]
- (402).Feng G; Qiao R; Huang J; Dai S; Sumpter BG; Meunier V The Importance of Ion Size and Electrode Curvature on Electrical Double Layers in Ionic Liquids. Phys. Chem. Chem. Phys 2011, 13, 1152–1161. [DOI] [PubMed] [Google Scholar]
- (403).Xing L; Vatamanu J; Smith GD; Bedrov D Nano-patterning of Electrode Surfaces as a Potential Route to Improve the Energy Density of Electric Double-Layer Capacitors: Insight from Molecular Simulations. J. Phys. Chem. Lett 2012, 3, 1124–1129. [DOI] [PubMed] [Google Scholar]
- (404).Vatamanu J; Cao L; Borodin O; Bedrov D; Smith GD On the Influence of Surface Topography on the Electric Double Layer Structure and Differential Capacitance of Graphite/Ionic Liquid Interfaces. J. Phys. Chem. Lett 2011, 2, 2267–2272. [Google Scholar]
- (405).Tazi S; Salanne M; Simon C; Turq P; Pounds M; Madden PA Potential-Induced Ordering Transition of the Adsorbed Layer at the Ionic Liquid/Electrified Metal Interface. J. Phys. Chem. B 2010, 114, 8453–8459. [DOI] [PubMed] [Google Scholar]
- (406).Vatamanu J; Hu Z; Bedrov D; Perez C; Gogotsi Y Increasing Energy Storage in Electrochemical Capacitors with Ionic Liquid Electrolytes and Nanostructured Carbon Electrodes. J. Phys. Chem. Lett 2013, 4, 2829–2837. [Google Scholar]
- (407).Vatamanu J; Vatamanu M; Bedrov D Non-Faradaic Energy Storage by Room Temperature Ionic Liquids in Nanoporous Electrodes. ACS Nano 2015, 9, 5999–6017. [DOI] [PubMed] [Google Scholar]
- (408).Kondrat S; Georgi N; Fedorov MV; Kornyshev AA A Superionic State in Nano-Porous Double-Layer Capacitors: Insights from Monte Carlo Simulations. Phys. Chem. Chem. Phys 2011, 13, 11359–11366. [DOI] [PubMed] [Google Scholar]
- (409).Merlet C; Péan C; Rotenberg B; Madden PA; Daffos B; Taberna PL; Simon P; Salanne M Highly Confined Ions Store Charge More Efficiently in Supercapacitors. Nat. Commun. 2013, 4, 2701. [DOI] [PubMed] [Google Scholar]
- (410).Merlet C; Rotenberg B; Madden PA; Taberna P-L; Simon P; Gogotsi Y; Salanne M On the Molecular Origin of Supercapacitance in Nanoporous Carbon Electrodes. Nat. Mater. 2012, 11, 306–310. [DOI] [PubMed] [Google Scholar]
- (411).Fedorov MV; Kornyshev AA Ionic Liquids at Electrified Interfaces. Chem. Rev 2014, 114, 2978–3036. [DOI] [PubMed] [Google Scholar]
- (412).Hayes R; Warr GG; Atkin R Structure and Nanostructure in Ionic Liquids. Chem. Rev 2015, 115, 6357–6426. [DOI] [PubMed] [Google Scholar]
- (413).Merlet C; Rotenberg B; Madden PA; Salanne M Computer Simulations of Ionic Liquids at Electrochemical Interfaces. Phys. Chem. Chem. Phys 2013, 15, 15781–15792. [DOI] [PubMed] [Google Scholar]
- (414).Vatamanu J; Bedrov D Capacitive Energy Storage: Current and Future Challenges. J. Phys. Chem. Lett 2015, 6, 3594–3609. [DOI] [PubMed] [Google Scholar]
- (415).Vatamanu J; Borodin O; Olguin M; Yushin G; Bedrov D Charge Storage at the Nanoscale: Understanding the Trends from the Molecular Scale Prospective. J. Mater. Chem. A 2017, 5, 21049–21076. [Google Scholar]
- (416).Vatamanu J; Borodin OS; Smith GD Molecular Dynamics Simulations of Atomically Flat and Nanoporous Electrodes with a Molten Salt Electrolyte. Phys. Chem. Chem. Phys 2010, 12, 170–182. [DOI] [PubMed] [Google Scholar]
- (417).Siepmann JI; Sprik M Influence of Surface Topology and Electrostatic Potential on Water/Electrode Systems. J. Chem. Phys 1995, 102, 511. [Google Scholar]
- (418).Reed SK; Lanning OJ; Madden PA Electrochemical Interface Between an Ionic Liquid and a Model Metallic Electrode. J. Chem. Phys 2007, 126, 084704. [DOI] [PubMed] [Google Scholar]
- (419).Pastewka L; Jarvi TT; Mayrhofer L; Moseler M Charge-Transfer Model for Carbonaceous Electrodes in Polar Environments. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 165418. [Google Scholar]
- (420).Kiss PT; Sega M; Baranyai A Efficient Handling of Gaussian Charge Distributions: An Application to Polarizable Molecular Models. J. Chem. Theory Comput 2014, 10, 5513–5519. [DOI] [PubMed] [Google Scholar]
- (421).Reed SK; Madden PA; Papadopoulos A Electrochemical Charge Transfer at a Metallic Electrode: A Simulation Study. J. Chem. Phys 2008, 128, 124701. [DOI] [PubMed] [Google Scholar]
- (422).Golze D; Iannuzzi M; Nguyen M-T; Passerone D; Hutter J Simulation of Adsorption Processes at Metallic Interfaces: An Image Charge Augmented QM/MM Approach. J. Chem. Theory Comput 2013, 9, 5086–5097. [DOI] [PubMed] [Google Scholar]
- (423).Vatamanu J; Bedrov D; Borodin O On the Application of Constant Electrode Potential Simulation Techniques in Atomistic Modeling of Electric Double Layers. Mol. Simul. 2017, 43, 838–849. [Google Scholar]
- (424).Tyagi S; Arnold A; Holm C ICMMM2D: An Accurate Method to Include Planar Dielectric Interfaces via Image Charge Summation. J. Chem. Phys 2007, 127, 154723. [DOI] [PubMed] [Google Scholar]
- (425).Tyagi S; Arnold A; Holm C Electrostatic Layer Correction with Image Charges: A Linear Scaling Method to Treat Slab 2D+h Systems with Dielectric Interfaces. J. Chem. Phys 2008, 129, 204102. [DOI] [PubMed] [Google Scholar]
- (426).Tyagi S; Suzen M; Sega M; Barbosa M; Kantorovich SS; Holm C An Iterative, Fast, Linear-scaling Method for Computing Induced Charges on Arbitrary Dielectric Boundaries. J. Chem. Phys 2010, 132, 154112. [DOI] [PubMed] [Google Scholar]
- (427).Arnold A; Breitsprecher K; Fahrenberger F; Kesselheim S; Lenz O; Holm C Efficient Algorithms for Electrostatic INteractions Including Dielectric Contrasts. Entropy 2013, 15, 4569–4588. [Google Scholar]
- (428).Breitsprecher K; Holm C; Kondrat S Charge Me Slowly, I Am in a Hurry: Optimizing Charge–Discharge Cycles in Nanoporous Supercapacitors. ACS Nano 2018, 12, 9733–9741. [DOI] [PubMed] [Google Scholar]
- (429).Breitsprecher K; Abele M; Kondrat S; Holm C The Effect of Finite Pore Length on On Structure and Charging. J. Chem. Phys 2017, 147, 104708. [DOI] [PubMed] [Google Scholar]
- (430).Haskins JB; Lawson JW Evaluation of Molecular Dynamics Simulation Methods for Ionic Liquid Electric Double Layers. J. Chem. Phys 2016, 144, 184707. [DOI] [PubMed] [Google Scholar]
- (431).Breitsprecher K; Szuttor K; Holm C Electrode Models for Ionic Liquid-Based Capacitors. J. Phys. Chem. C 2015, 119, 22445–22451. [Google Scholar]
- (432).Wang Z; Olmsted DL; Asta M; Laird BB Electric Potential Calculation in Molecular Simulation of Electric Double Layer Capacitors. J. Phys.: Condens. Matter 2016, 28, 464006. [DOI] [PubMed] [Google Scholar]
- (433).Merlet C; Pean C; Rotenberg B; Madden PA; Simon P; Salanne M Simulating Supercapacitors: Can We Model Electrodes As Constant Charge Surfaces? J. Phys. Chem. Lett 2013, 4, 264–268. [DOI] [PubMed] [Google Scholar]
- (434).Vatamanu J; Borodin O Ramifications of Water-in-Salt Interfacial Structure at Charged Electrodes for Electrolyte Electrochemical Stability. J. Phys. Chem. Lett 2017, 8, 4362–4367. [DOI] [PubMed] [Google Scholar]
- (435).Lagardère L; Aviat F; Piquemal J-P Pushing the Limits of Multiple-Time-Step Strategies for Polarizable Point Dipole Molecular Dynamics. J. Phys. Chem. Lett 2019, 10, 2593–2599. [DOI] [PubMed] [Google Scholar]
- (436).Liu C; Piquemal J-P; Ren P AMOEBA+ Classical Potential for Modeling Molecular Interactions. J. Chem. Theory. Comput 2019, DOI: 10.26434/chemrxiv.7904450.v2. [DOI] [PMC free article] [PubMed] [Google Scholar]