Abstract
Multiparameteric imaging is a critical tool in the non-invasive study and assessment of cancer. Imaging methods have evolved over the past several decades to provide quantitative measures of tumor and healthy tissue characteristics related to (for example) cell number, blood volume fraction, blood flow, hypoxia, and metabolism. Mechanistic models of tumor growth have also matured to a point where the incorporation of patient-specific measures could provide clinically relevant predictions of tumor growth and response. In this review, we identify and discuss approaches that utilize multiparametric imaging data including diffusion-weighted magnetic resonance imaging (DW-MRI), dynamic contrast enhanced MRI (DCE-MRI), diffusion tensor imaging (DTI), contrast enhanced computed tomography (CE-CT), 18F-fludeoxyglucose (18FDG) positron emission tomography (PET), and 18F-fluoromisonidazole (18FMISO) PET to initialize and calibrate mechanistic models of tumor growth and response. We focus our discussion on brain and breast cancer; however, we also identify three emerging areas of application in kidney, pancreatic, and lung cancers. We conclude this review, with a discussion of the future directions for incorporating multiparameteric imaging data and mechanistic modeling into clinical decision making for cancer patients.
Keywords: DW-MRI, DCE-MRI, FDG-PET, FMISO-PET, Proliferation, Diffusion, Calibration
1. Introduction
Medical imaging serves a critical role in the assessment and diagnosis of solid tumors. Following diagnosis, a series of imaging data is collected to evaluate tumor size, invasion into adjacent structures, and metastatic spread. These data are used in conjuction with a clinical staging model to help guide treatment decisions and provide a crude prognosis for the disease course. A current challenge in clinical oncology is to predict the response of the individual patient to a specified therapeutic approach. While the above measures can provide a general prognosis based on the stage of the disease and historical data, the specific response of the patient population to standard therapies is heterogenous. A potential approach to this challenge is to leverage radiographic changes, which can readily be acquired at multiple time points before and during therapy, to enable patient-specific predictions of treatment response.
The radiographic assessment of changes in tumor size following treatment has been standardized to objectively categorize treatment response. One commonly employed technique is the response criteria in solid tumors (RECIST1, 2). RECIST primarily rely on morphological changes to identify patient response. However, the predictive utility of these measures is fundamentally limited as the morphological changes that form the basis of RECIST are temporally downstream of the underlying biochemical responses to therapy. Developments in imaging technologies have moved well-beyond morphological characterization and can provide non-invasive characterization of the tumor microenvironment3. Post-treatment changes in magnetic resonance imaging (MRI) or positron emission tomography (PET) measures of hypoxia4, cellularity5, 6, blood volume7, and perfusion8, 9 may be predictive of response. Incorporating these advanced imaging measures into mechanism-based models presents an opportunity to fundamentally shift cancer care through the development of individually optimized therapies10, 11. It is important to note that mechanism-based mathematical models of disease is a fundamentally different approach to relying only on statistical data analysis (“big data”). This is not to dispute the fact that statistical inference in itself is not of critical importance, but rather, by its very nature it is based on statistical properties of large populations of patients in which conditions that prevail in specific individuals are hard to detect. That is, the “big data-only” approach captures the general trends but cannot account for subtle changes in the individual patient—indeed, the very characteristics that make us individuals—over an extended time. Imaging based mechanistic models are designed to predict the spatio-temporal changes associated with disease onset, progression, and response to therapy. Such a validated mathematical framework enables the generation of testable, patient-specific hypotheses in silico, thereby allowing optimization of interventions for the individual patient using the specific characteristics of their own unique situation.
Mechanism based models are built on the assumption that behavior of a complex system can be predicted with mathematical descriptions of the interactions of individual system components. Only recently have these models begun to incorporate non-invasive imaging measurements12, 13 as a means to parameterize these models on a patient-specific basis. Non-invasive imaging techniques are well suited for model initialization and calibration as they can provide repeatable, reproducible, and evenly discretized measures of tumor properties before, during, and after therapy. Initializing and calibrating mechanism based models of tumor growth on an individual basis facilitates the generation of individual “forecasts” of response to chemotherapies14, 15, radiation therapy (RT)11, 16, 17, and resection18 that could be used for therapeutic planning. One potential (clinical) utility of mechanism based models is in the application of optimized and adaptive RT plans. RT is a central component of the standard of care for many cancers, with medical imaging playing a critical role in the positioning and guidance of RT19. Adaptive RT is a strategy to alter treatment plans and delivery to control for variations in patient radiosensivity20. One potential scenario for mechanistic modeling is to use patient data before and during therapy to calibrate predictive models of tumor growth and response to determine a patient’s response to therapy. Guided by model predictions, clinicians could simulate alternative treatment plans and select a treatment plan that improves the patient’s outcome. This modeling scenario could then repeated every time new data is collected, providing a means to continuously adapt therapy for individual patients. Recent developments in MRI guided linear accelerators21 could be used to provide the necessary quantitative multiparametric data to update model calibrations and adapt patient therapy.
Two barriers to implementing imaging-based mechanistic modeling are the access to proper data and the validity of current mathematical descriptions of tumor growth and response. In this review, we will identify the type of data imaging measures can provide, before proceeding to the numerical methods, considerations required for implementation and validation. We will then present current modeling approaches with examples from cancer of the brain, breast, pancreas, kidney, and lung. Finally, we identify future opportunies in this emerging sub-field of oncology, frequently referred to as Mathematical Oncology22.
2. Imaging Measurements and Patient Data
2.1. Multiparametric Imaging Measures of Tumor and Tissue Properties
In this section, we will identify some of the imaging techniques that are currently being used in mechanstic models of tumor growth. Tumor cellularity (or the number of cells within an imaging voxel) can be estimated using diffusion-weighted MRI23 (DW-MRI), dynamic contrast enhanced MRI24, 25 (DCE-MRI), and contrast enhanced computed tomography (CT)26, 27 (CE-CT). A variant of DW-MRI called diffusion tensor imaging28 (DTI) can also be used to assess the magnitude and direction of water diffusion in tissue, thereby providing an estimate of the preferred direction of tumor cell movement. Properties of the tumor vasculature such as blood volume and perfusion can be estimated using constrast based techniques such as DCE-MRI24and dynamic CE-CT26.
Several PET tracers have been developed which can provide estimates of glucose uptake, tumor hypoxia, and cell proliferation. 18F-fludeoxyglucose PET29 (18FDG-PET) is a glucose analog that is taken up by cells, phosphorylated, and then trapped within the cell; thus FDG preferentially accumulates within metabolically active cells. 18F-fluoromisonidazole PET30 (18F-MISO) is a PET tracer that is commonly used to assess the level of hypoxia in tumors. A summary of the measurable quantities discussed in this section is provided in Table 1, while Figure 1 provides an example of quantitative PET and MRI data acquired in a breast cancer patient before and following the start of therapy.
Table 1:
Summary of tumor properties available from common medical imaging techniques
Figure 1:
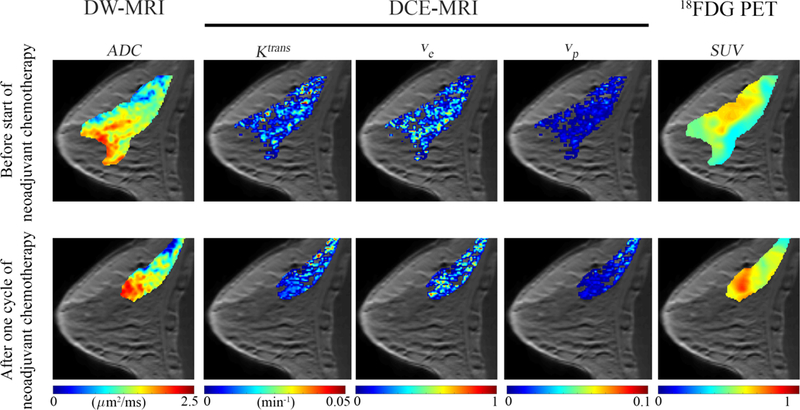
Example multi-parameteric data acquired in a breast cancer patient before treatment (top row) and after (bottom row) one cycle of neoadjuvant chemotherapy. DW-MRI (first column) returns estimates of the ADC which can be used to provide estimates of cellularity. DCE-MRI (second through fourth columns) provides estimates of tissue blood flow and permeability (Ktrans), extracellular-extravascular volume fraction (ve), and the plasma volume fraction (vp). 18FDG-PET provides estimates of glucose uptake (SUV). These imaging measurements can be acquired non- invasivley before, during, and after the start of therapy to characterize functional changes in tumor properties.
2.2. Challenges in the Acquistion, Processing, and Sharing of Patient Image Data
While multi-parametric imaging data is the focus of this review, there are many pieces of information needed to provide informative model predictions to clinicians. In this section, we highlight challenges and concerns regarding imaging metadata, medical records, instrument types and variability, and data sharing. A more comprehensive review on these challenges can be found in Yankeelov et al31 and Shaikh et al32.
Imaging metadata (e.g., observations and tissue annotations) and medical records are essential for proper utilization of imaging datasets. These data are often stored separately from the image data itself, requiring database management33 to connect metadata and medical records to the appropriate image series. Modelers should be aware of medical details (e.g., patient’s individual history, disease subtype(s), treatment schedules, and response) to accurately model treatment response. When sharing data, researchers should utilize consistent file types, naming procedures, and deidentification procedures to ease the interpretation and use of imaging data. Curated repositories34 can provide a mechanism for archived data to meet consistent standards and improve the utilitiy of shared data.
Site to site variation in image acquisition and analysis may also effect the interpretation of imaging data. Researchers should establish the repeatability and reproducibility of the imaging techniques employed in their study31. Additionally, post-processing (e.g., tissue segmentation, image analysis) procedures should be reproducible within and outside a site, to provide consistent analysis of the imaging data. These analyses are particularly important when working with data acquired from multiple-institutions with different instruments and different post-processing routines36–40.
3. Numerical Methods
In this section we review the calibration, selection, and validation of models, the sensitivity analysis of the parameters, and how to address uncertainties in data, model selection, parameter estimation, and predictions. Figure 2 shows a schematic of a framework for model calibration, selection, and validation.
Figure 2:

Schematic of model calibration, selection, and validation framework. A determistic or statistical (panel a) approach to model calibration is used to minimize the error between the model and the measurement of a specific quantity of interest (e.g., tumor volume, cell density distribution). In this example, the model is initialized at time point 1 (t1) and the error is calculated at time point 2 (t2) Model selection (panel b) criterion are used to select the most appropriate model that accurately describes the data. The selected model is then evaluated in a validation stage (panel c) by simulating tumor growth at t3 and comparing it to the measured tumor growth. If the model error is within a prescribed error threshold for a quanity of interest the model is then considered valid.
3.1. Model Calibration, Selection, Validation
For a given problem (e.g., predicting tumor growth41), different mathematical models can be developed based on the hypotheses that are to be tested. This will lead to different sets of parameters within the model that need to be estimated. The process of determing the values of the free paraemeters within a model is called calibration, and it frequently involves solving an inverse problem for the parameters based on experimental observations. More specifically for a given a model M(Ψ), where Ψ are the model parameters, calibration consists of minimizing the residual R = y - M(Ψ), where y is the measured data 44, 45. If the parameters are properly calibrated R = 0 assuming that there is no experimental error or model inadequacies46. This minimization process can be done in a deterministic or statistical framework. The deterministic framework searches for the set of parameter values that minimize the residual error. In the statistical framework, the parameters are assumed to have a prior distribution that contains the true parameter. The statistical model is the probability distribution image of the mechanistic model applied to the prior distribution. The data is just one realization of this model44. Through Bayes’ theorem, the data is used to improve the knowledge regarding the parameter distribution. Among the enormous number of possible calibrated models, it is crucial to select which model is the “best” for predicting the quantities of interest. Two common methods are based on information theory, such as the Akaike Information Criterion47 and the Bayesian Information Criterion48 that penalizes the number of parameters from the model. Once the best model is selected, it must be determined if the model is capable of predicting the quantities of interest with sufficient accuracy. This process is called validation and it involves experimental observations, obtained from more complex scenarios than those involved in the calibration process, or an independent subset of the data not used during the calibration step. The model is tested at this new scenario with the calibrated parameters, and if the differences between the values of quantities of interest is less than the (user-defined) tolerance, the model is ‘valid’, but technically, one can only say that with this metric and with this tolerance, the model is ‘not invalid’ because additional information could always falsify a model. Thus, a not informative or inaccurate model is ‘invalid’ as it does not satisfy the validation metric that compares the model prediction with experimental data46.
3.2. Sensitivity Analysis
Sensitivity analysis refers to quantitatively understanding how variation in a model’s parameters influences the output of the model. (This is not to be confused with “uncertainty analysis,” which generally refers to a lack of knowledge about parameter values.)The goal of a sensitivity analysis is to rank parameters by their importance based upon how their prescribed variations affect the output measures when compared to the results from other parameters’ changes. This provides a means to identify the driving interactions of the system and narrow the scope for which parameters should be targeted for experimental estimation—particularly useful for complex systems—or identify parameters that could be eliminated or set to a nominal value. There are a broad range of methods for calculating sensitivity measures that can be divided into to two major groups: local and global. For local sensitivity measures, each parameter is varied individually, whereas for global sensitivity measures, individual parameter sensitivity is determined while all parameters are varied. While global methods are more computationally expensive, they are less likely to miscategorize an important parameter as insignificant. Within these two groups, the types of analyses range from derivatives determining local dependence49, 50, statistical methods using correlations51–53, popular variance-based methods54–58, and even methods that consider the shape of output distributions59, 60. Careful examination of individual sensitivity methods should be performed before choosing a sensitivity index to rank parameters in a model because different methods can give differing rankings of parameters or can even disagree on the importance of particular parameters overall.
3.3. Uncertainty Quantification
The construction of models to represent most phenomena are subject to uncertainties in the observational data parameters, and in the mathematical and computational models (e.g., model structure, modeling assumptions, constitutive laws, boundary conditions). The models can be subject to epistemic uncertainties, due to our lack of knowledge about the parameters, or aleatoric uncertainties, due to the parameter variability61. Disregarding such uncertainties would lead to biased predictions of the quantities of interest. In particular, for the tumor growth models, this can lead to under or over estimation of the tumor size/position, incorrect treatment protocols, and it might select an inadequate model62. To have a way to quantify these uncertainties and quantify their propagation through the several steps leading to the model prediction is of fundamental importance. One way is through Bayesian approaches, where the parameters, the data, and the model are not assumed to be deterministic, instead, they are considered as random variables characterized by probability density functions 63. These characterizations lead to a stochastic model that is able to propagate uncertainty from model inputs to outputs.
4. Examples from the literature
4.1. Brain Cancer
Mathematical modeling of glioblastoma growth has a well-developed literature16–18, 64–71 that utilizes advanced imaging techniques to initialize and calibrate subject-specific models of growth and response to therapy. Tumor growth in general, and glioblastoma growth in particular, has commonly been modeled using a reaction-diffusion type model which describes the proliferation (reaction) and movement (diffusion) of tumor cells as shown in Eq. (1):
| (1) |
where N() is the number of tumor cells at a given 3D position and time t, D is the tumor cell diffusion coefficient, k is their proliferation rate, and θ is the carrying capacity or the maximum number of cells that can be fit within a volume of interest (e.g., a voxel)). Swanson et al 65 pionereed image based model calibration for glioblastoma by introducing the use of anatomical T1- and T2-weighted MRI to provide estimates of the detectable tumor and the infiltrative non- detectable tumor margins, respectively. Model parameters calibrated from individual patients using this approach correlated with tumor grade72, overal patient survival73, and predicting response to therapy16, 18. Swanson et al’s approach has been expanded by many groups to include multi-parameteric imaging measures from MRI17, 70, 74–76 and PET66. Incorporating DTI data has been investigated as a means to introduce anisotropic movement of tumor cells67–70, 74, 76, 77 It has been suggested70 that the direction of cell movement is aligned with the diffusion tensor direction, potentially introducing anisotropic cell diffusion within the brain. DTI data is often incorporated in mechanistic models using data acquired in the individual subject68, 74, 76 or supplied from a common brain atlas67, 69, 70, 77 In Swan et al, incorporating anisotropic diffusion (using DTI data) compared to isotropic diffusion has showed promising results where a higher level of overlap between the model and measured tumor volumes was observed for the anisotropic diffusion model for 9 of the 10 patients74. This approach could potentially be used to identify infiltrative regions or define treatment volumes that incorporate areas where tumor cells are likely to migrate. 18FMISO-PET data has also been incorporated into a reaction-diffusion type model of response to RT66. The level of hypoxia as assessed from 18FMISO uptake was used to assign an oxygen enhancing ratio to spatially vary the radiosensitivity of tumor cells to the delivered therapy. Rockne et al observed in one patient dataset that incorporating 18FMISO data in their mechanistic model relative to the model not including 18FMISO decreased the error in tumor volume predictions from 14.6% to 1.1%. Several efforts have proposed incorporating DW-MRI estimates of cellularity17, 64, 75, fluid attenuated inversion recovery MRI estimates of edema78, DCE-MRI estimates of perfusion78, and DCE-MRI estimates of blood volume fraction79.
4.2. Breast Cancer
Imaging based models for breast cancer have been quickly developing over the past decade, beginning with first DW-MRI measures used to approximate tumor cell number and initialize a simple logistic growth model (i.e., tumor cell proliferation slows as it reaches a carrying capacity)to predict tumor growth80. Using DW-MRI data for individual patients, the tumor cell number within the tumor region of interest was estimated from the ADC value. For each patient, one pre-treatment and one early post-treatment scans were used to calibrate the parameters of the model, which were then used to simulate the tumor forward to be compared to the third imaging time point. Using this patient specific data, the mathematical model’s prediction for tumor cell numbers in the patients’ third scan was found to be statistically correlated to the corresponding experimental data. Later, DW-MRI data was used to initialize a partial differential equation model that included a mathematical diffusion term to simulate the outward movement of cells as the tumor mass grows (mass effect) based on similar modeling efforts for glioblastomas81. The mechanical properties of these different tissues were incorporated by modulating the diffusive effect of the tumor cells. Briefly, this coupled model describes tumor growth changes that can cause deformations in the surrounding healthy tissues, potentially increasing stress and therefore reducing the outward expansion of tumor growth14, 15, 82. When compared to RECIST measures of response, Weis et al’s approach had increased specificity, and equal sensitivity to RECIST results. The most recent work in this effort utilized DCE-MRI data to estimate the delivery of chemotherapy to the tumor. Using parameters derived from the extended Kety-Tofts24 model built to determine the concentration of contrast agent in tissues for DCE-MRI, the concentration of drug in the tissue is approximated for each individual patient per voxel. The system of equations in Eq. (2) are thus extended as follows:
| (2) |
| (3) |
| (4) |
| (5) |
where N (x̅, t) is the number of tumor cells at time t, D the diffusion coefficient, k(x̅) is a spatially resolved proliferation rate map for tumor cells, θ the carrying capacity, and is the approximate amount of drug therapy in the tissue at time t with effectiveness α. Ktrans is the volume transfer constant from the plasma space to the tissue space, vp is the volume fraction of the plasma space, ve is the volume fraction of the extravascular extracellular space24, and is the concentration of the drug in the plasma. D0 is the tumor cell diffusion constant in the absence of stress, γ an empirical coupling constant for the von Mises stress, σvm, G the shear modulus, where for the Young’s modulus (E) and Poisson’s ratio ( v) material properties; is the displacement due to tumor cell growth, and λ is another empirical coupling constant. (σvm reflects the experienced stress, and is often used within failure criterion strategies in materials.) Preliminary results using a cohort of five patients show reductions in the error between the model’s predictions of tumor cellularity and size when compared to when drug therapy is not incorporated explicitly. This approach demonstrates the plausibility of using DCE-MRI to characterize drug delivery and representes a step toward the goal of achieving a patient-specific model for predicting tumor response to neoadjuvant chemotherapy in breast cancer83.
4.3. Other disease sites
The mathematical modeling frameworks developed for glioblastoma and breast cancer described above have, in principle, application to any solid tumor type. Recently, image based models have also been developed for kidney84, lung85, and pancreatic86 tumors. For example, Chen et al leveraged CE-CT images to develop a reaction-diffusion equation to predict kidney tumor growth on a longitudinal image series84, 87 which expanded Eq. (1) to include a biomechanical model which related tumor cell density to a force applied on the surrounding tissue. In this effort, Chen et al observed an average error in tumor volume predictions of 5.1% in 5 patients. Mi et al developed an advection-reaction model of lung tumor growth during RT leveraging PET/CT imaging. Tumor cell diffusion was assumed to be neglible within the lung and any motion (the advection term) was assumed to be the result of cells migrating towards increased concentrations of oxygen, nutrients, and space. The group assumed cell density to be proportional to 18FDG-PET SUV, and the model provided a means to estimate the effect of radiotherapy. The approach demonstrated promising results in a cohort of seven non-small cell lung carcinoma patients with an average concordance of 76% between measured and predicted tumor volumes85. The group extended this approach to improve tumor segmentation on subsequent imaging data, providing a method to more accurately estimate tumor changes (and thus model parameters), and thereby improve model predictions of tumor volumes 88. Liu et al developed a reaction-advection-diffusion model describing the proliferation of tumor cells (reaction), the movement of tumor cells to displacement (advection), and the movement of tumor cells due to diffusion to predict the growth of pancreatic tumors 86. The model was parameterized using 18FDG-PET and dual phase CT to estimate the proliferation rate and cellular volume fraction, respectively. Liu et al s model was expanded recently by modeling tumor mass effects with elastic growth decomposition, which separates the continuous deformation field of a growing tumor into its elastic and growth components to more accurately describe pancreatic tumor behavior27. These examples demonstrate the broad application areas for image based models of cancer growth and treatment response.
5. Future Directions
There are two fundamental barriers to the field of imaging based, mechanistic modeling of tumor growth and response to treatment being able to reach its promise: access to proper data, and model validity. Mechanism based models require a level of quantification that is not typically available in the standard of care setting. The majority of imaging data types acquired as standard of care are limited to qualitative decriptions of tissue morphology. Such data types fundmentally limit the calibration and prediction fidelity that can be achieved with mechanism based models. Thus, specialized clinical studies must be designed and executed to provide the data types needed to initialize and constrain these models. With such data available, it then becomes possible to systematically test the validity of a range of mathematical models that account for a wide range of biological and physical factors, leading to an entire family of potentially predictive models. Model selection algorithms can then be employed to select the optimal model and then validate its ability to accurately predict the spatiotemporal development of an individual patient’s tumor41, 42.
If the above two limitations can be overcome or, even, partially addressed, then it may be possible to build, calibrate, and apply realistic mathematical models for use in patient care; Figure 3 provides a schematic for how such an approach could be realized. Initially, a mathematical formulation is defined to model the desired quantity of interest. In vitro experiments can be used to acquire knowledge on parameter values43 (panel a). Imaging data is then acquired during prior to and early in the course of therapy (panel b). The images are spatially co-registered (or aligned) across time, discretized, and segmented according to the important features to be captured by the model. The values of the parameters are updated on this patient-specific scenario. With the optimized parameter values, the model passes through the validation step (panel c). If it is deemed valid, the model can be used with some confidence to make a prediction. This prediction will provide additional ‘scores’ or model based biomarkers to be used to improve current clinical staging models and response assessment criteria or to define new therapy protocols. Success in this program would represent, without question, an enormous improvement in the human condition.
Figure 3:
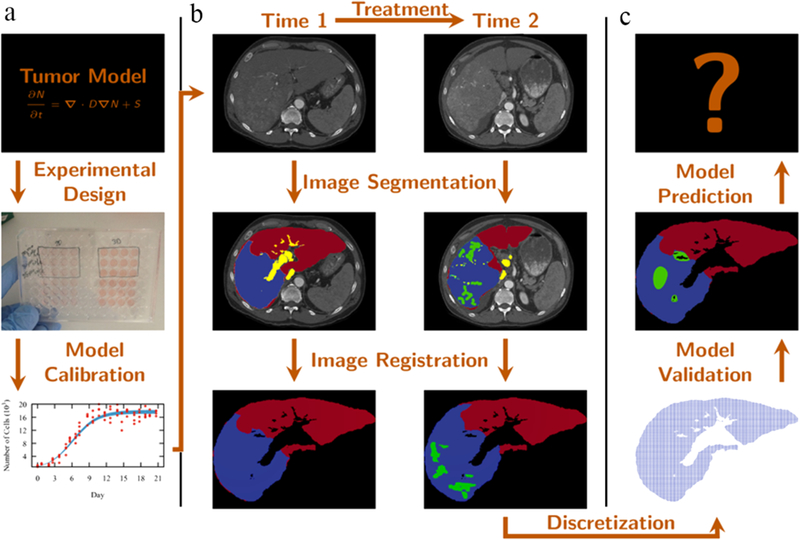
Modeling framework describing how a mathematical model can be developed and implemented. In vitro experiments (panel a) are designed to provide data to calibrate a particular tumor model. Tri-phase CT data is acquired (before and after the treatment), segmented,and registered (panel b). The domain is discretized (panel c) so the model can be calibrated and validated to patient data. If the model meets validation criterion it can be used to predict the tumor evolution.
6. Summary
The integration of mechanism based, mathematical modeling with quantitative, multiparametric imaging data that captures the unique characteristics of the individual patient, promises to generate accurate and actionable predictions that can optimally guide the care of the patient. This would fundamentally shift existing paradigms of therapy monitoring and selection in cancer, and hasten personalized cancer medicine.
7. Acknowledgements
We thank the National Cancer Institute for U01 CA174706, U01 CA154602, and R01 CA186193. We thank the Cancer Prevention Research Institute of Texas for CPRIT RR160005.
Grant Sponsor: NCI U01 CA174706, NCI U01 CA154602, and CPRIT RR160005
Footnotes
Journal: JCO Clinical Cancer Informatics
8. References
- 1.Therasse P, Arbuck SG, Eisenhauer EA, et al. : New Guidelines to Evaluate the Response to Treatment in Solid Tumors. J Natl Cancer Inst 92:205–216, 2000 [DOI] [PubMed] [Google Scholar]
- 2.Eisenhauer EA, Therasse P, Bogaerts J, et al. : New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer 45:228–247, 2009 [DOI] [PubMed] [Google Scholar]
- 3.Yankeelov TE, Abramson RG, Quarles CC: Quantitative multimodality imaging in cancer research and therapy. Nat Rev Clin Oncol 11:670–680, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sorace AG, Syed AK, Barnes SL, et al. : Quantitative [18F]FMISO PET Imaging Shows Reduction of Hypoxia Following Trastuzumab in a Murine Model of HER2+ Breast Cancer. Mol Imaging Biol 19:130–137, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schmainda KM: Diffusion-weighted MRI as a biomarker for treatment response in glioma. CNS Oncol 1:169–180, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Padhani AR, Liu G, Mu-Koh D, et al. : Diffusion-Weighted Magnetic Resonance Imaging as a Cancer Biomarker: Consensus and Recommendations. Neoplasia 11:102–125, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Galban CJ, Chenevert TL, Meyer CR, et al. : Prospective Analysis of Parametric Response Map-Derived MRI Biomarkers: Identification of Early and Distinct Glioma Response Patterns Not Predicted by Standard Radiographic Assessment. Clin Cancer Res 17:4751 LP–4760, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Virostko J, Hainline A, Kang H, et al. : Dynamic contrast-enhanced magnetic resonance imaging and diffusion-weighted magnetic resonance imaging for predicting the response of locally advanced breast cancer to neoadjuvant therapy: a meta-analysis. J Med Imaging 5:11011–11013, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barnes SL, Sorace AG, Whisenant JG, et al. : DCE- and DW-MRI as early imaging biomarkers of treatment response in a preclinical model of triple negative breast cancer. NMR Biomed 30:e3799-n/a, 2017 [DOI] [PubMed] [Google Scholar]
- 10.Yankeelov TE, Quaranta V, Evans KJ, et al. : Toward a Science of Tumor Forecasting for Clinical Oncology. Cancer Res 75:918–923, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Corwin D, Holdsworth C, Rockne RC, et al. : Toward Patient-Specific, Biologically Optimized Radiation Therapy Plans for the Treatment of Glioblastoma. PLoS One 8:e79115, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yankeelov TE, Atuegwu N, Hormuth DA, et al. : Clinically Relevant Modeling of Tumor Growth and Treatment Response. Sci Transl Med 5:187ps9–187ps9, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Atuegwu NC, Gore JC, Yankeelov TE: The integration of quantitative multi-modality imaging data into mathematical models of tumors. Phys Med Biol 55:2429–49, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Weis JA, Miga MI, Arlinghaus LR, et al. : Predicting the Response of Breast Cancer to Neoadjuvant Therapy Using a Mechanically Coupled Reaction-Diffusion Model. Cancer Res , 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weis JA, Miga MI, Arlinghaus LR, et al. : A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy. Phys Med Biol 58:5851–66, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rockne R, Rockhill JK, Mrugala M, et al. : Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach. Phys Med Biol 55:3271–3285, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hormuth D II, Weis J, Barnes S, et al. : Biophysical modeling of in vivo glioma response following whole brain radiotherapy in a murine model of brain cancer. Int J Radiat Oncol Biol Phys In Press, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Swanson KR, Rostomily RC, Alvord EC: A mathematical modelling tool for predicting survival of individual patients following resection of glioblastoma: a proof of principle. Br J Cancer 98:113–9, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jaffray DA: Image-guided radiotherapy: from current concept to future perspectives. Nat Rev Clin Oncol 9:688–99, 2012 [DOI] [PubMed] [Google Scholar]
- 20.Yan D: Adaptive Radiotherapy: Merging Principle Into Clinical Practice. Semin Radiat Oncol 20:79–83, 2010 [DOI] [PubMed] [Google Scholar]
- 21.Lagendijk JJW, Raaymakers BW, Raaijmakers AJE, et al. : MRI/linac integration. Radiother Oncol 86:25–29, 2008 [DOI] [PubMed] [Google Scholar]
- 22.Anderson ARA, Quaranta V: Integrative mathematical oncology. Nat Rev Cancer 8:227–234, 2008 [DOI] [PubMed] [Google Scholar]
- 23.Koh DM, Collins DJ: Diffusion-Weighted MRI in the Body: Applications and Challenges in Oncology. Am J Roentgenol 188:1622–1635, 2007 [DOI] [PubMed] [Google Scholar]
- 24.Yankeelov TE, Gore JC: Dynamic Contrast Enhanced Magnetic Resonance Imaging in Oncology: Theory, Data Acquisition, Analysis, and Examples. Curr Med Imaging Rev 3:91–107, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Atuegwu NC, Arlinghaus LR, Li X, et al. : Parameterizing the Logistic Model of Tumor Growth by DW-MRI and DCE-MRI Data to Predict Treatment Response and Changes in Breast Cancer Cellularity during Neoadjuvant Chemotherapy. Transl Oncol 6:256–264, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.O’Connor JPB, Tofts PS, Miles KA, et al. : Dynamic contrast-enhanced imaging techniques: CT and MRI. Br J Radiol 84:S112–S120, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wong KCL, Summers RM, Kebebew E, et al. : Pancreatic Tumor Growth Prediction With Elastic-Growth Decomposition, Image-Derived Motion, and FDM-FEM Coupling. IEEE Trans Med Imaging 36:111–123, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sundgren PC, Dong Q, Gomez-Hassan D, et al. : Diffusion tensor imaging of the brain: review of clinical applications. Neuroradiology 46:339–350, 2004 [DOI] [PubMed] [Google Scholar]
- 29.Kubota K: From tumor biology to clinical Pet: a review of positron emission tomography (PET) in oncology. Ann Nucl Med 15:471–86, 2001 [DOI] [PubMed] [Google Scholar]
- 30.Eschmann SM, Paulsen F, Bedeshem C, et al. : Hypoxia-imaging with 18F-Misonidazole and PET: Changes of kinetics during radiotherapy of head-and-neck cancer. Radiother Oncol 83:406–410, 2007 [DOI] [PubMed] [Google Scholar]
- 31.Yankeelov TE, Mankoff DA, Schwartz LH, et al. : Quantitative Imaging in Cancer Clinical Trials. Clin Cancer Res 22:284 LP–290, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shaikh FA, Kolowitz BJ, Awan O, et al. : Technical Challenges in the Clinical Application of Radiomics. JCO Clin Cancer Informatics 1–8, 2017 [DOI] [PubMed] [Google Scholar]
- 33.Korenblum D, Rubin D, Napel S, et al. : Managing biomedical image metadata for search and retrieval of similar images. J Digit Imaging 24:739–748, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Prior F, Smith K, Sharma A, et al. : The public cancer radiology imaging collections of The Cancer Imaging Archive. Sci Data 4:170124, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kaufmann M, Hortobagyi GN, Goldhirsch A, et al. : Recommendations from an international expert panel on the use of neoadjuvant (primary) systemic treatment of operable breast cancer: an update. J Clin Oncol 24:1940–1949, 2006 [DOI] [PubMed] [Google Scholar]
- 36.Grech-Sollars M, Hales PW, Miyazaki K, et al. : Multi-centre reproducibility of diffusion MRI parameters for clinical sequences in the brain. Nmr Biomed 28:468–485, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chenevert TL, Malyarenko DI, Newitt D, et al. : Errors in Quantitative Image Analysis due to Platform-Dependent Image Scaling. Transl Oncol 7:65–71, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Malyarenko DI, Wilmes LJ, Arlinghaus LR, et al. : QIN DAWG Validation of Gradient Nonlinearity Bias Correction Workflow for Quantitative Diffusion-Weighted Imaging in Multicenter Trials. Tomogr a J imaging Res 2:396–405, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sorace AG, Wu C, Barnes SL, et al. : Repeatability, reproducibility, and accuracy of quantitative mri of the breast in the community radiology setting. J Magn Reson Imaging 0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ger RB, Mohamed ASR, Awan MJ, et al. : A Multi-Institutional Comparison of Dynamic Contrast-Enhanced Magnetic Resonance Imaging Parameter Calculations. Sci Rep 7:11185, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lima EABF Oden JT, Hormuth DA, et al. : Selection, calibration, and validation of models of tumor growth. Math Model Methods Appl Sci 26:2341–2368, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lima EABF Oden JT, Wohlmuth B, et al. : Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data. Comput Methods Appl Mech Eng 327:277–305, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stein S, Zhao R, Haeno H, et al. : Mathematical modeling identifies optimum lapatinib dosing schedules for the treatment of glioblastoma patients. PLoS Comput Biol 14:e1005924, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Aster R, Borchers B, Thurber C: Parameter Estimation and Inverse Provlems. Elsevier Science, 2011 [Google Scholar]
- 45.Sun N, Sun A: Model calibration and parameter estimation: for environmental and water resource systems. Springer-Verlag, 2015 [Google Scholar]
- 46.Oden JT, Lima EABF, Almeida RC, et al. : Toward Predictive Multiscale Modeling of Vascular Tumor Growth. Arch Comput Methods Eng 23:735–779, 2016 [Google Scholar]
- 47.Akaike H: A new look at the statistical model identification. Autom Control IEEE Trans 19:716–723, 1974 [Google Scholar]
- 48.Schwarz G: Estimating the Dimension of a Model. Ann Stat 6:461–464, 1978 [Google Scholar]
- 49.Kucherenko S, Rodriguez-Fernandez M, Pantelides C, et al. : Monte Carlo evaluation of derivative-based global sensitivity measures. Reliab Eng Syst Saf 94:1135–1148, 2009 [Google Scholar]
- 50.Sobol’ IM, Kucherenko S: A new derivative based importance criterion for groups of variables and its link with the global sensitivity indices. Comput Phys Commun 181:1212–1217, 2010 [Google Scholar]
- 51.Bianca C, Chiacchio F, Pappalardo F, et al. : Mathematical modeling of the immune system recognition to mammary carcinoma antigen. BMC Bioinformatics 13: S21–S21, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Blower SM, Dowlatabadi H: Sensitivity and Uncertainty Analysis of Complex Models of Disease Transmission: An HIV Model, as an Example. Int Stat Rev / Rev Int Stat 62:229–243, 1994 [Google Scholar]
- 53.Jarrett AM, Cogan NG, Shirtliff ME: Modelling the interaction between the host immune response, bacterial dynamics and inflammatory damage in comparison with immunomodulation and vaccination experiments. Math Med Biol 32:285–306, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cukier RI, Fortuin CM, Shuler KE, et al. : Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J Chem Phys 59:3873–3878, 1973 [Google Scholar]
- 55.Sobol’ I: Sensitivity estimates for non-linear mathematical models. Math Model Comput Exp 1:407–414, 1993 [Google Scholar]
- 56.Sobol’ IM: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math Comput Simul 55:271–280, 2001 [Google Scholar]
- 57.Jarrett AM, Liu Y, Cogan NG, et al. : Global sensitivity analysis used to interpret biological experimental results. J Math Biol 71:151–170, 2015 [DOI] [PubMed] [Google Scholar]
- 58.Jarrett AM, Cogan NG, Hussaini MY: Combining Two Methods of Global Sensitivity Analysis to Investigate MRSA Nasal Carriage Model. Bull Math Biol 79:2258–2272, 2017 [DOI] [PubMed] [Google Scholar]
- 59.Borgonovo E: A new uncertainty importance measure. Reliab Eng Syst Saf 92:771–784, 2007 [Google Scholar]
- 60.Liu Q, Homma T: A new computational method of a moment-independent uncertainty importance measure. Reliab Eng Syst Saf 94:1205–1211, 2009 [Google Scholar]
- 61.Najm HN: Uncertainty Quantification and Polynomial Chaos Techniques in Computational Fluid Dynamics. Annu Rev Fluid Mech 41:35–52, 2008 [Google Scholar]
- 62.Lima EABF, Almeida RC, Oden JT: Analysis and numerical solution of stochastic phase- field models of tumor growth. Numer Methods Partial Differ Equ 31:552–574, 2015 [Google Scholar]
- 63.Jaynes E: Probability Theory: The Logic of Science. Cambridge University Press, 2003 [Google Scholar]
- 64.Hormuth DA II, Weis JA, Barnes SL, et al. : Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data. Phys Biol 12:46006, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Baldock A, Rockne R, Boone A, et al. : From Patient-Specific Mathematical Neuro-Oncology to Precision Medicine. Front Oncol 3, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rockne RC, Trister AD, Jacobs J, et al. : A patient-specific computational model of hypoxia- modulated radiation resistance in glioblastoma using (18)F-FMISO-PET. J R Soc Interface 12:20141174, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hogea C, Davatzikos C, Biros G: An image-driven parameter estimation problem for a reaction-diffusion glioma growth model with mass effects. J Math Biol 56:793–825, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Konukoglu E, Clatz O, Menze BH, et al. : Image Guided Personalization of Reaction- Diffusion Type Tumor Growth Models Using Modified Anisotropic Eikonal Equations. Med Imaging, IEEE Trans 29:77–95, 2010 [DOI] [PubMed] [Google Scholar]
- 69.Bondiau P-Y, Clatz O, Sermesant M, et al. : Biocomputing: numerical simulation of glioblastoma growth using diffusion tensor imaging. Phys Med Biol 53:879–93, 2008 [DOI] [PubMed] [Google Scholar]
- 70.Jbabdi S, Mandonnet E, Duffau H, et al. : Simulation of anisotropic growth of low-grade gliomas using diffusion tensor imaging. Magn Reson Med 54:616–24, 2005 [DOI] [PubMed] [Google Scholar]
- 71.Hormuth DA II, Weis JA, Barnes SL, et al. : A mechanically-coupled reaction-diffusion model that incorporates intra-tumoral heterogeneity to predict in vivo glioma growth. J R Soc Interface 14, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Harpold HLP, Alvord ECJ, Swanson KR: The Evolution of Mathematical Modeling of Glioma Proliferation and Invasion. J Neuropathol Exp Neurol 66, 2007 [DOI] [PubMed] [Google Scholar]
- 73.Wang CH, Rockhill JK, Mrugala M, et al. : Prognostic significance of growth kinetics in newly diagnosed glioblastomas revealed by combining serial imaging with a novel biomathematical model. Cancer Res 69:9133–40, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Swan A, Hillen T, Bowman JC, et al. : A Patient-Specific Anisotropic Diffusion Model for Brain Tumour Spread. Bull Math Biol 1–33, 2017 [DOI] [PubMed] [Google Scholar]
- 75.Hormuth DA II, Weis JA, Barnes SL, et al. : A mechanically coupled reaction-diffusion model that incorporates intra-tumoural heterogeneity to predict in vivo glioma growth. J R Soc Interface 14, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mosayebi P, Cobzas D, Murtha A, et al. : Tumor invasion margin on the Riemannian space of brain fibers. Med Image Anal 16:361–373, 2012 [DOI] [PubMed] [Google Scholar]
- 77.Clatz O, Sermesant M, Bondiau P-Y, et al. : Realistic simulation of the 3-D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. Med Imaging, IEEE Trans 24:1334–1346, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Hawkins-Daarud A, Rockne RC, Anderson ARA, et al. : Modeling tumor-associated edema in gliomas during anti-angiogenic therapy and its impact on imageable tumor. Front Oncol 3, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Hormuth D, Jarrett A, Feng X, et al. : Angi-08. Predicting in vivo tumor growth and angiogenesis with an MRI calibrated biophysical model. Neuro Oncol 19:vi23–vi23, 2017 [Google Scholar]
- 80.Atuegwu NC, Arlinghaus LR, Li X, et al. : Integration of diffusion-weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy.Magn Reson Med 66:1689–1696, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Garg I, Miga MI: Preliminary investigation of the inhibitory effects of mechanical stress in tumor growth, in Proc. SPIE. Proc. SPIE, 2008, p 69182L-69182L-11 [Google Scholar]
- 82.Weis JA, Miga MI, Yankeelov TE: Three-dimensional image-based mechanical modeling for predicting the response of breast cancer to neoadjuvant therapy. Comput Methods Appl Mech Eng 314:494–512, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Jarrett A, Hormuth D II, Barnes S, et al. : Incorporating drug delivery into an imaging-driven, mechanics-coupled reaction diffusion model for predicting the response of breast cancer to neoadjuvant chemotherapy: theory and preliminary clinical results. Phys Med Biol Accepted/I, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Chen X, Summers R, Jianhua Yao J: FEM-Based 3-D Tumor Growth Prediction for Kidney Tumor. IEEE Trans Biomed Eng 58:463–467, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Mi H, Petitjean C, Dubray B, et al. : Prediction of Lung Tumor Evolution During Radiotherapy in Individual Patients With PET. IEEE Trans Med Imaging 33:995–1003, 2014 [DOI] [PubMed] [Google Scholar]
- 86.Liu Y, Sadowski SM, Weisbrod AB, et al. : Patient specific tumor growth prediction using multimodal images. Med Image Anal 18:555–566, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Chen X, Summers RM, Yao J: Kidney Tumor Growth Prediction by Coupling Reaction- Diffusion and Biomechanical Model. Biomed Eng IEEE Trans 60:169–173, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Mi H, Petitjean C, Vera P, et al. : Joint tumor growth prediction and tumor segmentation on therapeutic follow-up PET images. Med Image Anal 23:84–91, 2015 [DOI] [PubMed] [Google Scholar]


