MRI-Only Based Synthetic CT Generation Using Dense Cycle Consistent Generative Adversarial Networks

Abstract

Purpose:

Automated synthetic CT (sCT) generation based on magnetic resonance imaging (MRI) images would allow for MRI-only based treatment planning in radiation therapy, eliminating the need for CT simulation and simplifying the patient treatment workflow. In this work, the authors propose a novel method for generation of sCT based on dense cycle-consistent generative adversarial networks (cycle GAN), a deep-learning based model that trains two transformation mappings (MRI to CT and CT to MRI) simultaneously.

Methods and materials:

The cycle GAN-based model was developed to generate sCT images in a patch-based framework. Cycle GAN was applied to this problem because it includes an inverse transformation from CT to MRI, which helps constrain the model to learn a one-to-one mapping. Dense block-based networks were used to construct generator of cycle GAN. The network weights and variables were optimized via a gradient difference loss and a novel distance loss metric between sCT and original CT.

Results:

Leave-one-out cross-validation was performed to validate the proposed model. The mean absolute error (MAE), peak signal-to-noise ratio (PSNR) and normalized cross correlation (NCC) indexes were used to quantify the differences between the sCT and original planning CT images. For the proposed method, the mean MAE between sCT and CT were 55.7 Hounsfield units (HU) for 24 brain cancer patients and 50.8 HU for 20 prostate cancer patients. The mean PSNR and NCC were 26.6 dB and 0.963 in the brain cases, and 24.5 dB and 0.929 in the pelvis.

Conclusion:

We developed and validated a novel learning-based approach to generate CT images from routine MRIs based on dense cycle GAN model to effectively capture the relationship between the CT and MRIs. The proposed method can generate robust, high-quality sCT in minutes. The proposed method offers strong potential for supporting near real-time MRI-only treatment planning in the brain and pelvis.

1. INTRODUCTION

Magnetic resonance imaging (MRI) has superior soft tissue contrast over computed tomography (CT), allowing for improved organ-at-risk segmentation and target delineation for radiation therapy treatment planning.^1–3 Since dose calculation algorithms rely on electron density maps generated from CT images for calculating dose, MRIs are typically registered to CT images and used alongside the CT image for treatment planning.^4,5 However, the CT/MRI registration process has inherent errors, for example, a geometrical uncertainty of approximately 2 mm is present in cranial MRI.^6–8 A potential treatment planning process with MRI as a sole imaging modality could eliminate systematic CT/MRI co-registration errors, reduce medical cost, minimize patient radiation exposure, and streamline clinical workflow.^2,9 However, the main challenge in substituting CT with MRI is that MRI cannot provide the key electron density information that is needed for accurate dose calculation. Additionally, daily patient setup for radiotherapy is based on either cone-beam CT or orthogonal planar x-ray images which are then compared to planning CTs or digitally reconstructed radiographs (DRRs) generated from the planning CT. This setup process inherently relies on a CT image taken at the beginning of the treatment planning process.

Since electron density information and CT images are vital to the treatment-planning workflow, methods which generate electron density and CT image from MRIs, called synthetic CT (sCT) generation, have been investigated recently.^10–12. Atlas-based methods are typically used to generate sCT images. These rely on a deformable image registration to bring the sCT atlas to the current MRI.^13–16 These methods are inherently limited by the performance of deformable registration. Another approach relies on specialized MRI sequences, such as ultra-short echo time (UTE) sequences, that allow for enhanced bony anatomy visualization.^17,18 sCT images can then be generated via post-processing. However, the current image quality of UTE sequences is inadequate for accurate delineation of blood vessels from the bone.^19,20 Moreover, the use of non-standard MRI sequences may introduce additional scanning time to the existing MRI scanning workflow and may increase the patient discomfort, leading to motion artifacts.

With the development of machine learning in the medical imaging field, more sophisticated methods for sCT generation have been proposed. The machine learning-based model relies on learning the relationship between MRI and CT images for several representative sets of CT/MRI pairs, called a training set. After training, sCT images can be generated by feeding new MRIs into the model. Such sCT images will share the same structural information with MRI, but the intensity values will be scaled to typical Hounsfield units (HU) seen on a CT scan. The electron density can then be derived from this sCT image. Based on different training models, these methods can be broadly classified into three categories: dictionary learning-based methods,^21–24 random forest-based methods,^25–29 and deep learning-based methods.^30–37 Dictionary learning-based methods rely on the similarity between different MRIs. When a new patient’s MRI is put into the model, the similarity between the new MRI and training MRIs in the dictionary is calculated. An sCT image is then synthesized from a linear combination of the most similar paired CT images, with the weights calculated based on the MRI similarity. These methods are sensitive to MRI intensities which can vary as a function of scanning parameters for a given tissue. They also rely on a large base dataset, and the accuracy of the method is inherently dependent on the representing accuracy of an overcomplete dictionary. Random forest-based methods train a set of decision trees. Each decision tree learns the optimal way to separate a set of training paired MRI and CT patches into smaller and smaller subsets to predict the CT intensity. When a new MRI patch is put into the model, the sCT intensity is estimated as the combination of the predicted results of all decision trees. However, these methods can lead to ambiguous results when the decision trees do not learn a one-to-one mapping from the source image to the target image.

Since deep learning-based methods can provide a more complex non-linear mapping from input to output image through a multi-layer and fully trainable model, these methods are becoming popular for the task of image synthesis.^30–37 In contrast with dictionary learning-based and random forest-based methods, whose accuracy and robustness are sensitive to hand-crafted features extracted from MRI patches, deep learning-based methods have potential to learn which features are the best representation of the MRI patch. Li et al first applied a convolutional neural network (CNN), a deep learning-based method to generate PET attenuation correction map from the MRI of the same subject.³⁰ Nie et al. proposed to train a patch-to-patch relationship from an MRI to a CT image by using 3D fully convolutional neural network (FCN), a variation of the conventional CNN.³¹ Different from patch-based deep learning, Han apply the FCN to learn a direct image-to-image mapping between MRIs and their corresponding CTs.³² A limitation of the CNN-based methods is that slight voxel-wise misalignment of MRI and CT images may lead to blurred synthesis.³⁴ Generative adversarial networks (GAN) have been used in the generation of sCT by introducing an additional discriminator to distinguish the sCT from real CT, improving the final sCT imaging qualities in comparison to the previously deep learning-based methods.³⁵ These models incorporate an adversarial loss term in addition to the conventional synthesis error, with the objective of producing more realistic CT data.^33,35,36 GAN-based methods still require the training pairs of MRI and CT images to be perfectly registered, which can be difficult to carry out with the high levels of accuracy needed for image synthesis.³⁴ If the registration has some local mismatch between the MRI and CT training data, i.e. soft tissue misalignment after bone-based rigid registration, GAN-based methods would produce a degenerative network, decreasing their accuracy. Wolterink et al. show that training with pairs of spatially aligned MRI and CT images of the same patients is not necessary for cycle GAN-based sCT generation method.³⁴ However, due to computational limitations, the cycle GAN-based method images in a slice-by-slice fashion, i.e., the cycle GAN-based method is applied to 2D images. This approach is limited because it relies on a 2D model to generate 3D images, leading to discontinuous output signals over a continuous input space. To solve this challenge, we propose a dense cycle GAN-based method to train patch-to-patch translation CNNs. In this framework, a CNN is trained to translate an MRI patch to an sCT patch. We also train an additional CNN to translate the sCT patch back to the MRI patch. The difference between this reconstructed sCT image and the original CT image is added to help regularize the training.

The purpose of this work is to develop a deep learning-based method to generate patient-specific sCT from routine anatomical MRI for MRI-only radiotherapy treatment planning. The method is applied to both the brain and pelvic regions. The contributions of the paper are as follows: (1) In order to cope with local mismatches between MRI and CT after rigid registration as well as to capture more useful information for MRI patch representation, a dense cycle GAN is applied. Unlike traditional cycle GAN, where the generator is composed of residual blocks, dense blocks are used to capture multi-scale information to solve the significant differences in image property between the MRI and CT modalities. (2) A novel distance loss function is proposed to optimize the dense cycle GAN to overcome the blur and misclassification issues that occur when applying more commonly used distance functions, such as mean absolute distance and mean squared distance.

The paper is organized as follows: We first provide an overview of the proposed deep learning-based sCT generation framework, followed by a detailed description of the 3D cycle GAN, dense block, and then loss function. We evaluated the method’s sCT synthesis accuracy via comparison to random forest-based,²⁷, GAN-based,³⁵ and 2D cycle GAN-based³⁴ synthesis methods. Finally, we discuss the limitations and future applications of the proposed method.

2. MATERIALS AND METHODS

2.A. Overview

The proposed sCT generation algorithm consists of a training stage and a synthesizing stage. For a given pair of MRI and CT images, the CT image is used as a deep learning-based target of the MRI. Intra-subject registration is performed to align each image pair. Because local mismatches between MRI and CT remain even after rigid registration and the images have fundamentally different properties, training an MRI-to-CT transformation model is difficult. To cope with this challenge, a novel dense cycle GAN is introduced to capture the relationship between CT to MRIs while supervising an inverse MRI-to-CT transformation model. A 3D image patch (with voxel size [64, 64, 64]) is input to the proposed model to contain more spatial information. Unlike residual blocks used in Wolterink’s cycle GAN architecture³⁴ dense blocks³⁸ are used to construct our proposed dense cycle GAN (DCG) architecture. Fig. 1 outlines the workflow schematic of our proposed method.

Fig.1.

Schematic flow chart of the proposed algorithm for MRI-based sCT generation. The upper part of this figure shows the training stage of our proposed method, which consists of 4 generators and 2 discriminators. The middle part (yellow) shows the synthesizing stage. In synthesizing stage, a new MRI is fed into the well-trained DCG model to get an sCT image. The lower part shows the detailed structures for each network.

In the training stage, extracted patches of training MRI are fed into the generator (MRI-to-CT) to get equal-sized synthetic CT, which is called the sCT. The sCT is then fed into another generator (CT-to-MRI), creating a synthetic MRI which we term the cycle MRI. Similarly, in order to enforce forward-backward consistency, extracted patches of training CT are fed into the two generators in the opposite order first to create a synthetic MRI and cycle CT. Then two discriminators are used to judge the realistic of synthetic and cycle images.

Typically, the l₂-norm or l₁-norm distance, i.e., the mean absolute distance (MAD) or mean squared distance (MSD), are used as generator loss function between the synthetic image and the original image. However, the use of an MSD loss function in the network tends to produce images with blurry regions.³⁹ In order to solve this problem, we introduce a l_p-norm (p = 15) distance, termed mean p distance (MPD), to measure the distance between synthetic and original images. We also integrate an image gradient difference (GD) loss term into the loss function, with the aim of retaining the sharpness in the synthetic images.³⁵ A weighted summation of these two metrics forms the compound loss function for the proposed method. The generator loss is computed by the combination of compound loss between synthetic and real images, called adversarial loss, and compound loss between cycle and real images, called cycle loss. The discriminator loss is computed by MAD between the discriminator results of input synthetic and real images. To update all the hidden layers’ kernels, the Adam gradient descent method was applied to minimize both generator loss and discriminator loss.

In synthesizing stage, the patches of the new MRI are fed into the MRI-to-CT generator to obtain the sCT. Then, the final sCT was obtained by patch fusion.

2.B. Image acquisition and pre-process

We retrospectively analyzed the MRI and CT data acquired during treatment planning for 24 brain patients and 20 pelvis patients who received radiation therapy. For the brain images, standard T1-weighted MRI was captured using a GE MRI scanner with Brain Volume Imaging sequence (BRAVO) and 1.0×1.0×1.4 mm³ voxel size (TR/TE: 950/13 ms, flip angle: 90°) and CT was captured with a Siemens CT scanner with 1.0×1.0×1.0 mm³ voxel size with 120 kVp and 220 mAs. For the pelvis images, MRI was acquired using a Siemens standard T2-weighted MRI scanner with 3D T2-SPACE sequence and 1.0×1.0×2.0 mm³ voxel size (TR/TE: 1000/123 ms, flip angle: 95°) and CT was captured with a Siemens CT scanner with 1.0×1.0×2.0mm³ voxel size with 120 kVp and 299 mAs. MRI data were first resampled to match the resolution of CT data. For each patient, all training MRI and CT images were first rigidly registered by an intra-subject registration using a commercial software Velocity AI 3.2.1 (Varian Medical Systems, Palo Alto, CA).

2.C. Dense cycle GAN

MRI and CT images may have some local mismatches after the above registration process. Inspired by recent cycle GAN study,³⁴ we introduced a dense cycle GAN in our sCT generation algorithm because of its ability to mimic target data distribution by incorporating an inverse transformation that converts CT to MRI (CT-to-MRI transformation). Traditional GAN-based methods use loss functions that depend solely on the quality of the synthesized image. In the context of image synthesis, this may lead to CT images that look real but do not reflect patient anatomy. The proposed method employs a cycle GAN which eliminates this problem by incorporating an inverse transformation to enforce a one-to-one mapping.³⁴ The sCT is generated by a network that maps from a source domain (MRI) to target domain (CT) such that the distribution of sCT is indistinguishable from the CT image using an adversarial loss (called an MRI-to-CT generator). Then, we couple the mapping network with an inverse mapping network (CT-to-MRI generator), and introduce a cycle consistency loss such that the distribution of the cycle MRI is indistinguishable from the original MRI (and vice versa). By introducing MRI- and CT-discriminators that work in opposition to the generators, the whole network’s performance is enhanced through additional evaluations of real and synthetic CT and MRI. Typically, the generator’s training objective is to increase the judgement error of the discriminative network (i.e., “fool” the discriminator network by generating synthetic or cycle image that was very similar to the input training images). The discriminator’s training objective is to decrease the judge error of the discriminator network and encourage generator to produce synthetic images that share similar features with real images. Back-propagation is applied in both networks so that the generator performs better, while the discriminator becomes more skilled at determining whether an image is synthetic or real.

The major difficulty in modeling the MRI-to-CT transformation is the location, structure, and shape of the MRI and CT image can vary significantly among different patients. In order to accurately predict each voxel in the anatomic region (air, bone, and soft-tissue), inspired by densely connected CNN,³⁸ we introduced several dense blocks to capture multi-scale information (including low-frequency and high-frequency) by extracting features from previous hidden layers and deeper hidden layers. As is shown in generator architecture of Fig. 1, after two down-sampling convolutional layers to reduce the feature map sizes, the feature map goes through 9 dense blocks, and then two deconvolutional layers and a tanh layer to perform the end-to-end mapping. The end-to-end mapping denotes the mapping which has equal size input and output. The tanh layer works as a nonlinear activation function and makes it easy for the model to generalize or adapt to a variety of data and to differentiate between outputs, such as determining whether a voxel on a boundary is bony tissue or air. The dense block is implemented by 5 convolution layers, a concatenation operator, and a convolutional layer to shorten the feature map size.

2.D. MPD loss function

During training, all the networks are trained simultaneously with discriminators trying to correctly differentiate between real and synthetic data, while generators are trying to generate synthetic images that are very similar to real images to confuse discriminators. Supposing we use the discriminators D_MR and D_CT to discriminate the real and synthetic MRI and CT image patch, the discriminators should be optimized subjected to:

$$\left(D_{\text{MR}},D_{\text{CT}}\right)=\text{arg}\underset{D_{\text{MR}},D_{\text{CT}}}{\text{min}}\left\{\begin{array}{l}\text{MAD}\left(D_{\text{MRI}}\left(G_{\text{CT-MRI}}(I_{\text{CT}})\right),0\right)+\text{MAD}\left(D_{\text{MRI}}\left(I_{\text{MRI}}\right),1\right)\\ +\text{MAD}\left(D_{\text{CT}}\left(G_{\text{MRI-CT}}(I_{\text{MR}})\right),0\right)+\text{MAD}\left(D_{\text{CT}}\left(I_{\text{CT}}\right),1\right)\end{array}\right\}$$ (1)

where G_CT-MR and G_MR-CT denotes the generator trained from CT to MRI domain and from MRI to CT domain, respectively, 0 is a same-shape patch with all elements set to zero, 1 is a same-shape patch with all elements set to one. MAD(·) denotes the MAD calculating operator.

The loss function of each generator is composed of 2 losses: 1) the adversarial loss used for distinguishing real images from synthetic images; 2) the distance loss measured between real images and synthesis image.³⁵ The accuracy of the generator directly depends on how suitable the loss function is designed. Supposing we use the generator G to obtain a synthetic image G(X) = Z from original image X to target image Y. The generator G is optimized subjected to $G=\text{arg }\underset{G}{\text{min}}\left\{{\lambda }_{\text{adv}}{L}_{\text{adv}}(Z)+{\lambda }_{\text{distance}}{L}_{\text{distance}}(Z,Y)\right\}$. λ_adv and λ_distance are balancing parameter. Normally, the adversarial loss function is defined as L_adv(Z) = MAD(D(Z),1) in cycle GAN-based method.⁴⁰

For distance loss L_distance(Z,Y), in order to not only solve the blur and misclassification issues mentioned previously, but also maintain the sharpness of synthetic images, we use a compound loss function composed of MPD and GD. This GD loss function minimizes the difference of the magnitude of the gradient between the synthetic image and the original planning CT. In this way, the sCT will try to keep zones with strong gradients, such as edges, effectively compensating for the distance loss term. The generators are optimized as follows:

$$\left(G_{\text{CT-MRI}},G_{\text{MRI-CT}}\right)=\text{arg}\underset{G_{\text{CT-MRI}},G_{\text{MRI-CT}}}{\text{min}}\left\{\begin{array}{l}{\lambda }_{\text{adv}}\text{MAD}\left(D_{\text{MRI}}\left(G_{\text{CT-MRI}}(I_{\text{CT}})\right),1\right)+{\lambda }_{\text{MPD}}^{\text{cycle}}{\Vert G_{\text{MRI-CT}}\left(G_{\text{CT-MRI}}(I_{\text{CT}})\right),I_{\text{CT}}\Vert }_p^p\\ +{\lambda }_{\text{GDL}}^{\text{cycle}}\text{GD}\left(G_{\text{MRI-CT}}\left(G_{\text{CT-MRI}}(I_{\text{CT}})\right),I_{\text{CT}}\right)\\ +{\lambda }_{\text{MPD}}^{\text{fake}}{\Vert G_{\text{CT-MRI}}(I_{\text{CT}}),I_{\text{MRI}}\Vert }_p^p+{\lambda }_{\text{GDL}}^{\text{fake}}\text{GD}\left(G_{\text{CT-MRI}}(I_{\text{CT}}),I_{\text{MR}}\right)\\ +{\lambda }_{\text{adv}}\text{MAD}\left(D_{\text{CT}}\left(G_{\text{MRI-CT}}(I_{\text{MR}})\right),1\right)+{\lambda }_{\text{MPD}}^{\text{cycle}}{\Vert G_{\text{CT-MRI}}\left(G_{\text{MR-CT}}(I_{\text{MR}})\right),I_{\text{MR}}\Vert }_p^p\\ +{\lambda }_{\text{GDL}}^{\text{cycle}}\text{GD}\left(G_{\text{CT-MRI}}\left(G_{\text{MRI-CT}}(I_{\text{MR}})\right),I_{\text{MRI}}\right)\\ +{\lambda }_{\text{MPD}}^{\text{fake}}{\Vert G_{\text{MRI-CT}}(I_{\text{MRI}}),I_{\text{CT}}\Vert }_p^p+{\lambda }_{\text{GDL}}^{\text{fake}}\text{GD}\left(G_{\text{MRI-CT}}(I_{\text{MRI}}),I_{\text{CT}}\right)\end{array}\right\}$$ (2)

$$\text{GD}\left(Z,Y\right)=\sum _{i,j,k}\left\{\begin{array}{l}{\Vert \left|Z_{i,j,k}-Z_{i-1,j,k}\right|-\left|Y_{i,j,k}-Y_{i-1,j,k}\right|\Vert }_2^2+{\Vert \left|Z_{i,j,k}-Z_{i,j-1,k}\right|-\left|Y_{i,j,k}-Y_{i,j-1,k}\right|\Vert }_2^2\\ +{\Vert \left|Z_{i,j,k}-Z_{i,j,k-1}\right|-\left|Y_{i,j,k}-Y_{i,j,k-1}\right|\Vert }_2^2\end{array}\right\}$$ (3)

where ${\Vert \cdot \Vert }_p^p$ denotes the l_p-norm, and GD(·) denotes the gradient difference loss function.³⁵ ${\lambda }_{\text{MPD}}^{\text{cycle}}$, ${\lambda }_{\text{GD}}^{\text{cycle}}$, ${\lambda }_{\text{MPD}}^{\text{fake}}$, ${\lambda }_{\text{GD}}^{\text{fake}}$, ${\lambda }_{\text{MPD}}^{\text{cycle}}$, ${\lambda }_{\text{GD}}^{\text{cycle}}$, ${\lambda }_{\text{MPD}}^{\text{fake}}$, ${\lambda }_{\text{GD}}^{\text{fake}}$ are regularization parameters for different regularization.

As is known that the l_p-norm regularization has fewer solutions than l₂-norm optimization, which means some over-smoothing results (i.e. blur region in MSE loss optimization) are reduced. Going the other way, we can also see that the optimization solution under l_p-norm regularization has more solutions than l₁-norm optimization. This means some misclassification situations (the solution on ±1) are minimized by averaging several solutions obtained by similar MRI/CT patches (the solution around ±1).

2.E. Validation and evaluations

We performed leave-one-out cross validation to evaluate the proposed method. We chose one of the patients from the patient dataset as the test, or new arrival patient. The proposed method was trained on the other patients, and the test patient was used to generate an sCT. This procedure was repeated on all patients’ datasets. These sCT images were then compared with the original planning CT images, which served as ground truth for validation. The mean absolute error (MAE), peak signal-to-noise ratio (PSNR) and normalized cross correlation (NCC) indexes were used to quantify the absolute difference, relative difference, and image similarity within the body outline, respectively.

2.F. Comparison with existing methods

To demonstrate the advantages of the proposed method, we compare it to a random forest (RF)-based method previously published by our group.²⁹ We also compare it to a GAN-based method, a recent deep learning-based method proposed by Nie et al.,³³ and a recent cycle GAN-based method.³⁴ GAN-based methods incorporate an adversarial learning strategy into an end-to-end FCN to train nonlinear mapping from MRI patches to CT image patches. Considering the tradeoff between computational cost and spatial information, the patch size in the RF-based method was set to 15×15×15, the patch size in the GAN-based method was set to 32×32×32. All the comparing algorithms were performed using their optimal parameter settings. Paired two-tailed t-tests between the proposed method and comparison methods were performed to quantify the statistical difference between each of the evaluated metrics above. All the deep learning-based algorithms were implemented in Tensorflow with Adam optimizer, and were trained and tested on 2 NVIDIA Tesla V100 with 32 GB of memory for each GPU. The RF-based method was implemented in python Scikit-learn toolbox and was trained and tested on Intel Xeon(R) CPU E5–2623 v3 @ 3.00GHz × 8.

3. RESULTS

3.A. Comparison between the dense block and the residual block

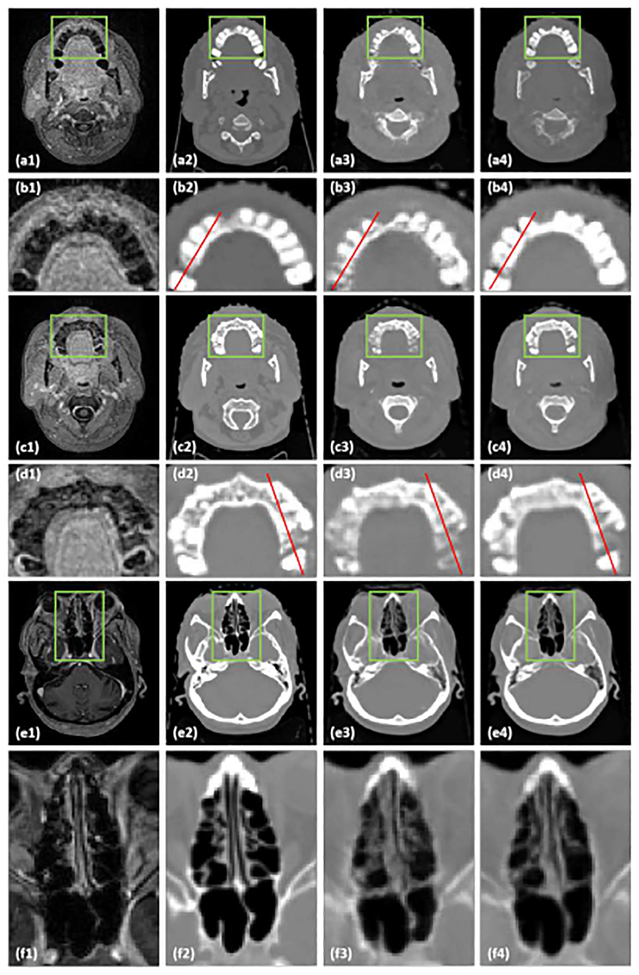
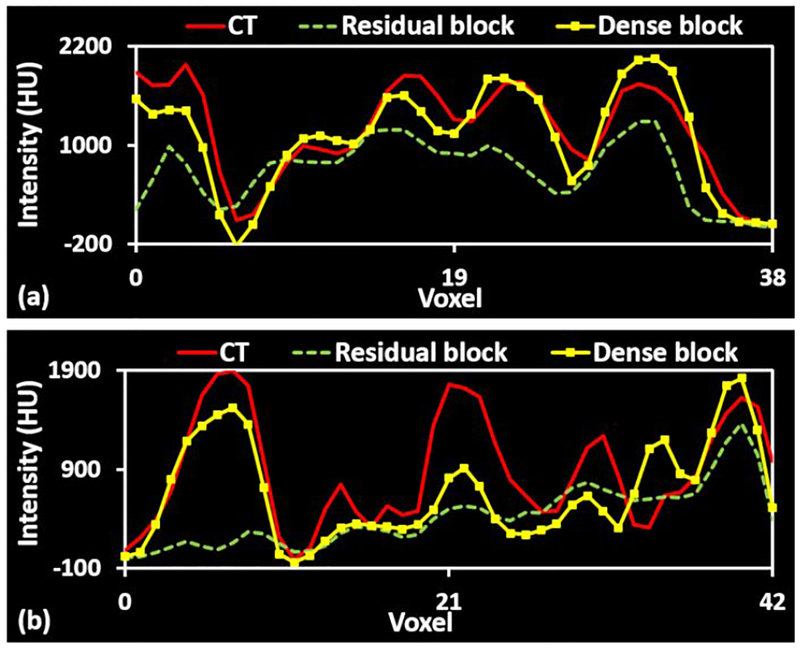
In order to test the influence of the dense block, we compared sCT results generated by a 3D cycle GAN-based method with 9 residual blocks method as recommended in³⁴ to the proposed method, in which 9 dense blocks are used. Fig. 2 shows axial views of MRI (a1-f1), corresponding CT (a2-f2), sCT (a3-f3) images generated by cycle GAN with 9 residual blocks, and sCT images generated by the proposed method. The inserts (b1-b4), (d1-d4), and (f1-f4) show zoomed-in views of the region of interests (ROIs) outlined in inserts (a1-a4). (c1-c4), and (e1-e4), respectively. These ROIs are highlighted because they contain large anatomic variations between air, soft tissue, and bone, and because there are some local mismatches between MRI and CT images within these ROIs. The cycle GAN with 9 residual blocks method captures the gross anatomy and preserves the structural details in soft tissue. However, it distorts structural details in regions with large anatomical variation, especially in the ROIs marked by the highlighted rectangles in Fig. 2 (a3, c3, e3). By introducing dense blocks, which combine both structural and textural information, the proposed method improves the estimation of sCT intensity and better preserves the tissue structural details. The zoomed-in views in Fig. 2 (b4, d4) demonstrate the superior accuracy of the proposed method with less bias around bony anatomy. The zoomed-in views in insert (f4) demonstrate the superior accuracy of the proposed method with less bias around soft tissue anatomy in nasal cavity, further shown by the line profiles in Fig. 3. It is important to note that bony anatomy has a larger effect on radiation dose calculations than other tissue types, so accurate bone intensity estimation in sCT images can have significant clinical impact.

Fig.2.

A comparison between the cycle GAN with residual blocks and the proposed method. (a1, c1, e1) are MRI shown in axial planes, the zoomed in insets below each image (b1, d1, f1) highlight regions of interest. (a2, c2, e2) are corresponding original CT images, and (b2, d2, f2) show the highlighted regions in greater detail. (a3, c3, e3) are sCT images generated by cycle GAN with 9 residual blocks method. (b3, d3, f3) show the highlighted region in greater detail. (a4, c4, e4) are sCT images generated by the proposed method. (b4, d4, f4) show the highlighted region in greater detail. The red lines on each image correspond to the line profiles shown in Fig. 3. The display windows are [0, 500] for MRI and [−1000 1000] for CT images.

Fig.3.

Line profile comparison between cycle-GAN with residual blocks and the proposed method. (a) and (b) are plot profiles of red lines in Fig. 4 (b2-b4) and (d2-d4).

3.B. Comparison of the loss function

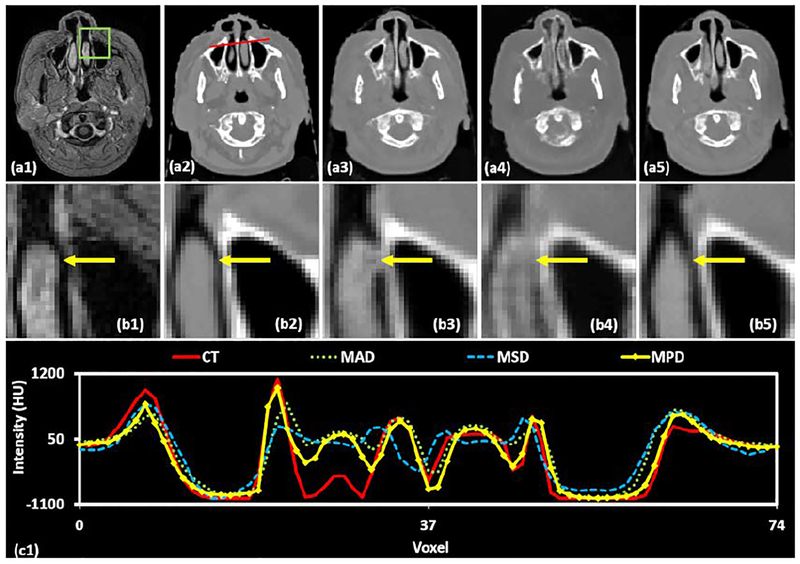
MPD was added to the compound loss function Eq. (2) to deal with blur and misclassification issues. We demonstrate the benefit of incorporating this loss function into the proposed method by comparing with networks optimized using traditional loss functions such as MAD and MSD. Fig. 5 and 6 depict the brain and pelvis sCT images generated by applying MAD, MSD and the proposed MPD loss functions.

Fig.5.

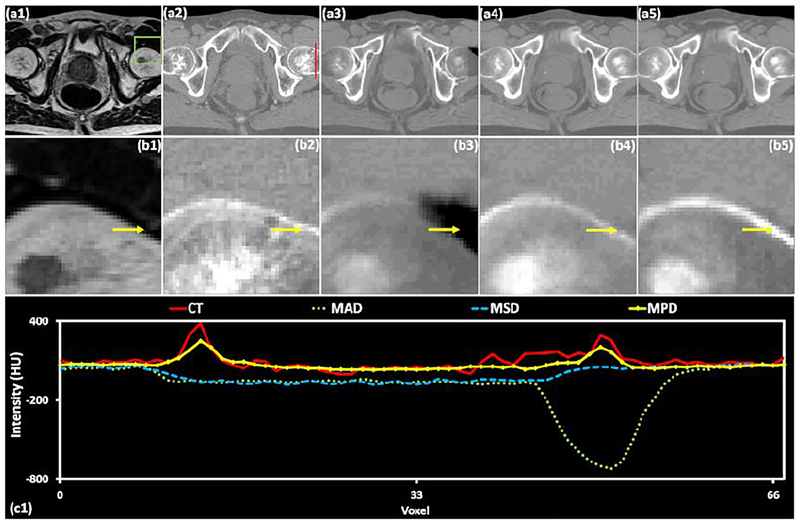
A comparison of different loss functions for a pelvis case. (a1) is MRI shown in the axial plane and (b1) shows the highlighted region in greater detail. (a2) is the corresponding original CT image and (b2) shows the highlighted region in greater detail. (a3-a5) are sCT images generated by using MAD, MSD, and MPD loss functions, respectively, and (b3-b5) are their corresponding zoomed-in insets. (c1) shows the line profile drawn in red on each CT image. The display windows for (a1-b1) are [0, 500]. The display windows are [0, 500] for MRIs and [−500 500] for CT images.

Fig.6.

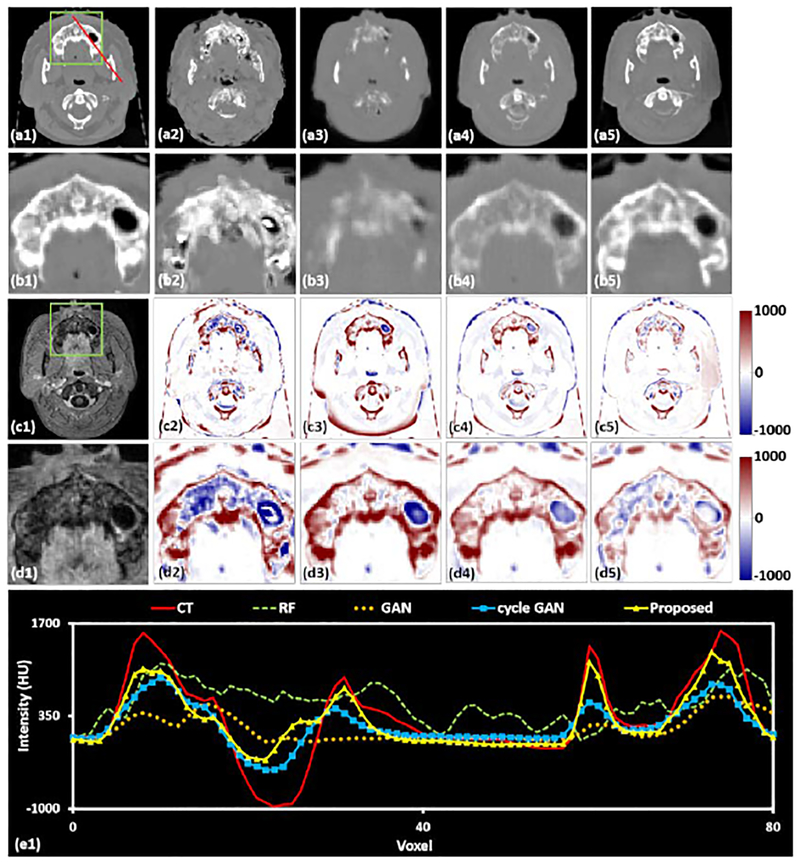
A comparison of different sCT generation methods in the brain in the axial plane. The first row shows the original CT (a1) and the sCT images produced by the RF-method (a2), the GAN method (a3), the cycle GAN method (a4), and the proposed method (a5). The second row (b1-b5) highlights the region of interest outlined by the green box on each corresponding CT. The corresponding MRI and ROI are shown in (c1) and (d1), respectively. Insets (c2-c5) show the error image, with the planning CT taken as the ground truth, for each sCT, and their ROIs are shown below (d2-d5). The line profile corresponding to the red line drawn on the CT images is plotted in (e1). The display windows are [0, 500] for MRIs and [−1000 1000] for CT images.

Fig. 5 shows axial views of brain MRI (a1), corresponding CT image (a2), and sCT (a3-a5) images generated by using MAD, MSD and MPD loss functions, respectively. The insets (b1-b5) show zoomed-in views of the ROIs outlined in insets (a1-a5). The ROI as shown in Fig. 4 (b1) was chosen at the site of rapid anatomic changes from soft tissue to air and then to the bone. Thus, the ROIs are challenging for sCT generation. By using the MAD loss function, some air voxels in the sCT image (b3) were misclassified as soft tissue voxels, some bone voxels were misclassified as soft tissue voxels. With the MSD loss function, some regions within the ROI in the sCT image (b4) were blurry and smooth. In contrast, the sCT image generated by the MPD loss function has more definitive tissue boundaries. The inset (c1) shows the line profile corresponding to the red lines in the CT images. As shown in (c1), the generated sCT intensities using MPD loss function outperform the intensities estimated by using other comparing loss functions.

Fig.4.

A comparison of different loss functions in brain images. (a1) is MRI shown in axial plane, (b1) shows the highlighted region in greater detail. (a2) is the corresponding original CT image, (b2) shows the highlighted region in greater detail. (a3-a5) are sCT images generated by using MAD, MSD, and MPD loss functions, respectively, and (b3-b5) show the highlighted region in greater detail. The line profile corresponding to the red line drawn on the CT images is shown in (c1). The display windows are [0, 500] for MRIs and [−1000 1000] for CT images.

Fig. 5 depicts axial views of pelvis MRI (a1), corresponding CT image (a2), and sCT (a3-a5) images generated by using MAD, MSD and MPD loss functions, respectively. The insets (b1-b5) show zoomed-in views of the ROIs outlined in insets (a1-a5), where bony structure varies in CT and MRIs. For sCT images generated by using MAD loss function (b3), the soft tissue voxels were misclassified as air as marked by yellow arrows. In inset (b4), the sCT image within the ROI was smooth and the bone intensity appears to lower as compared to the original CT. In contrast, the sCT generation based on MPD loss function (b5) outperforms the results from MAD (b3) and MSD (b4) by more accurately predicting bony intensities. Inset (c1) shows the line profile drawn on each CT image. The MPD-generated sCT nearly reflects the original CT along the entire profile, while the other two methods produce more intensity errors.

We also perform numerical comparisons of sCT images generated by using MAD, MSD, and the proposed MPD on both sites. The quantitative results are listed in Table 1, indicating that the proposed MPD significantly outperforms other comparing loss functions on MAE metric. Specifically, our MPD gives an average MAE of 57.5 and 49.4 HU on the brain and pelvic site, which are smaller than the MAE obtained by MAD and MSD loss functions.

Table 1.

Numerical results of using the three loss functions on brain and pelvic sCT images.

Loss function	Brain			Pelvis
	MAE (HU)	PSNR (dB)	NCC	MAE (HU)	PSNR (dB)	NCC
MAD	59.3±4.7	25.05±1.13	0.959±0.005	55.1±7.8	24.31±1.32	0.919±0.014
MSD	64.8±5.0	24.77±1.17	0.946±0.005	65.0±8.1	24.34±1.33	0.899±0.015
MPD	57.5±4.6	25.79±1.11	0.965±0.05	49.4±7.4	24.49±1.31	0.926±0.013
P-value MPD vs. MAD	0.048	0.633	0.812	0.05	0.243	0.713
P-value MPD vs. MSD	0.036	0.338	0.766	<0.001	0.598	0.301

3.C. Comparison with state-of-art methods

Fig. 6–8 show the axial, sagittal, and coronal views of an exemplary patient for comparing different methods of generating sCT images. These specific slices were selected because they represent some of the most challenging sites of accurate sCT generation in the brain.

Fig.8.

A comparison of different sCT generation methods in the brain in the coronal plane. The first row shows the original CT (a1) and the sCT images produced by the RF-method (a2), the GAN method (a3), the cycle GAN method (a4), and the proposed method (a5). The second row (b1-b5) highlights the region of interest outlined by the green box on each corresponding CT. The corresponding MRI and ROI are shown in (c1) and (d1), respectively. Insets (c2-c5) show the error image, with the planning CT taken as the ground truth, for each sCT, and their ROIs are shown below (d2-d5). The line profile corresponding to the red line drawn on the CT images is plotted in (e1). The display windows are [0, 500] for MRIs and [−1000 1000] for CT images.

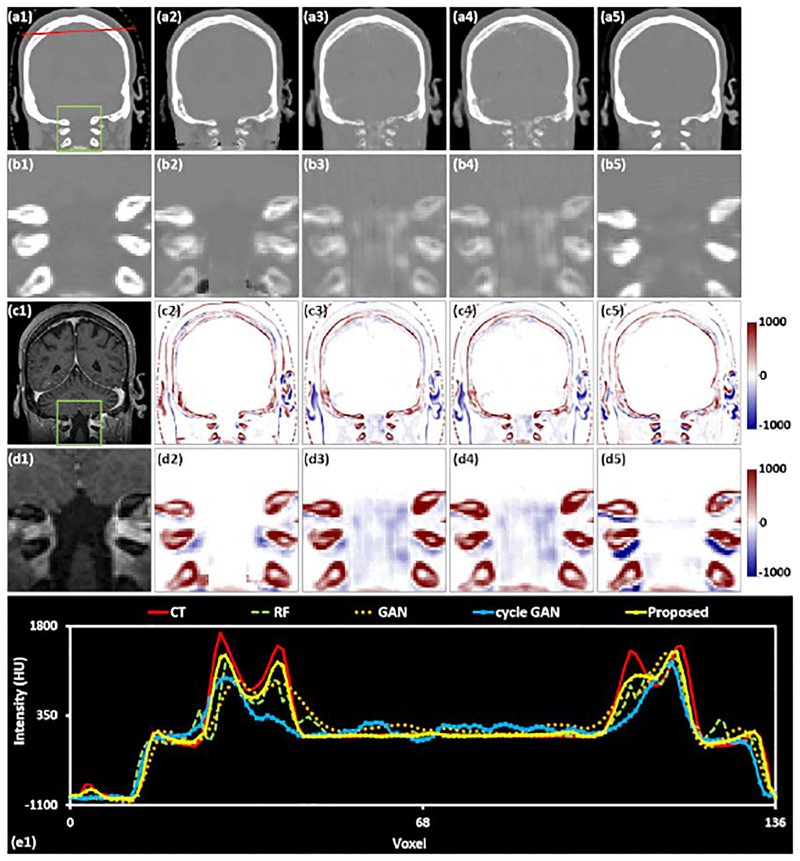
Fig.6 shows the axial plane containing the mandible, which can have large geometric variation and HU variation between patients. Inset (a1) shows an original CT image in the axial plane, (b1) shows the highlighted region in greater detail CT image, (c1) is the corresponding MRI, and (d1) shows the highlighted region of the MRI in greater detail. Insets (a2-a5) are sCT images generated by RF-, GAN-, and cycle GAN-based methods, and the proposed method, respectively, (b2-b5) show the highlighted ROIs in greater detail. Insets (c2-c5) are difference images between original CT images and sCT images, and (d2-d5) show the highlighted ROIs in greater detail. This specific region is challenging for generation of accurate sCT images owing to the local misalignment between MRI and CT images. In addition, many patients have dental fillings which create artifacts in the training CT images. The presence of image artifacts will degenerate sCT estimation performance in this region. As is shown in inset (b3-b5), the image quality of the sCT generated by our method is better than the other techniques in terms of fine structural details and contrast. Specifically, while the RF-based method (b3) has good contrast between the teeth and the surrounding soft tissue, it fails to predict the fine structures within the teeth. The GAN-based method (b4) has limited prediction capability in dental regions. The cycle GAN-based method underestimates the dental intensities. The insets in row (d) show that within the ROI, the proposed method generates the most accurate sCT image, both in terms of HU number and in structural shape. For further evaluation, the line profiles corresponding to the red lines drawn on insets (a1)-(a5) are shown in inset (e1). Although no methods perfectly match the original CT, the proposed method most closely reflects the shape and magnitude of the original CT.

Fig. 7 shows a sagittal view of the same patient shown in Fig. 6, containing various complex head and neck structures of the nasopharynx and oropharynx. The layout of Fig. 8 is the same as Fig. 6, with the first row showing CT or sCT images, the second row showing their corresponding ROIs, the third row showing the MRI and error images, and the fourth row showing their ROIs. Finally, the line profile corresponding to the red line on the CT or sCT images is shown in (e1). As is shown by the insets (b2-b5), the zoomed-in sCT image generated by RF-based method has some noisy regions. Fig. 8 shows a coronal view of the same patient shown in Fig. 6. The sCT images generated by GAN-, and cycle GAN-based method is closer to the original CT image, but still are blurry. The image quality of the sCT generated by the proposed method is superior to the other techniques in terms of fine structural details and contrast.

Fig.7.

A comparison of different sCT generation methods in the brain in the sagittal plane. The first row shows the original CT (a1) and the sCT images produced by the RF-method (a2), the GAN method (a3), the cycle GAN method (a4), and the proposed method (a5). The second row (b1-b5) highlights the region of interest outlined by the green box on each corresponding CT. The corresponding MRI and ROI are shown in (c1) and (d1), respectively. Insets (c2-c5) show the error image, with the planning CT taken as the ground truth, for each sCT, and their ROIs are shown below (d2-d5). The line profile corresponding to the red line drawn on the CT images is plotted in (e1). The display windows are [0, 500] for MRIs and [−1000 1000] for CT images.

Fig. 9 shows a comparison between the proposed method with the RF-based, GAN-based, and cycle GAN-based methods in the pelvis. Inserts (a1-b1) show MRIs shown in axial and coronal planes. Inserts (a2-b2) show the corresponding CT image. Inserts (a3-b3), (a4-b4), and (a5-b5) show the generated sCT images of RF-based, GAN-based, and cycle GAN-based methods, and the proposed method, respectively. As can be seen from this figure, the proposed method shows sharper tissue boundaries than the comparing methods. In addition, the bone shape is closest to the original CT image.

Fig.9.

A comparison of different methods on pelvic site. (a1-b1) are MRIs shown in axial and coronal planes. (a2-b2) are corresponding CT image. (a3-b3) show the corresponding sCT images generated by RF-based method. (a4-b4) show the corresponding sCT images generated by GAN-based method. (a5-b5) show the corresponding sCT images generated by 2D cycle GAN-based method. (a6-b6) show the corresponding sCT images generated by the proposed method. The display windows are [0, 500] for MRIs and [−1000 1000] for CT images.

We also conduct a numerical comparison of sCT image generated by all methods described above for each brain and pelvis case. The quantitative results are listed in Table 2, indicating that the proposed method outperforms the other methods. Specifically, our method gives an average MAE of 55.7 and 50.8 HU on the brain and pelvic site, which is lower than the average MAE of 69.8 and 69.7 HU, 66.9 and 74.7 HU, and 59.0 and 65.4 HU obtained by RF-based method, GAN-based method, and cycle GAN-based method, respectively. We further performed two-tail paired t-test to validate whether the improvement of our proposed method compared to the previous methods is significant or not. The experimental results in Table 3 show the statistically significant improvement (p-value <0.05).

Table 2.

Numerical results of different methods on brain and pelvis sCT images.

Method	Brain			Pelvis
	MAE (HU)	PSNR (dB)	NCC	MAE (HU)	PSNR (dB)	NCC
RF-based	69.8±15.2	24.41±1.71	0.955±0.002	69.7±19.7	24.25±2.20	0.893±0.026
GAN-based	66.9±15.6	25.10±2.02	0.937±0.021	74.7±20.0	22.08±2.7	0.877±0.053
2D Cycle GAN-based	59.0±11.9	25.75±1.81	0.953±0.009	65.4±18.6	23.45±2.97	0.903±0.037
The proposed	55.7±9.4	26.59±2.27	0.963±0.008	50.8±15.5	24.45±2.64	0.929±0.028

Table 3.

P-values by performing T-test between our proposed method and all the comparing methods for MAE, PSNR, and NCC on the brain and pelvic data.

Method	Brain			Pelvis
	MAE	PSNR	NCC	MAE	PSNR	NCC
RF-based	0.008	<0.001	0.011	0.008	0.009	0.014
GAN-based	0.002	0.009	<0.001	<0.001	0.002	0.002
2D Cycle GAN-based	0.009	0.011	0.001	0.002	0.005	0.007

We also used the other 10 brain and 10 pelvic data as independent testing data to evaluate the performance. The training data for the 10 brain MRIs was the previous 24 brain patient images. The training data for the 10 pelvic MRIs was the previous 20 pelvic MRIs. The MAE, PSNR, and NCC of our proposed method on the additional 10 brain images were 57.7±8.4 HU, 27.00±2.77 dB, and 0.963±0.007, respectively. The MAE, PSRN, and NCC of our proposed method on the additional 10 pelvic images were 42.3±8.4 HU, 23.89±2.01 dB, and 0.930±0.026, respectively. These metrics demonstrate the consistent performance on other data. For all test data, we also evaluated the Dice similarity coefficient (DSC) for air and bone region. The air and bone regions were defined within body outline and were dictated by CT HU values: [−∞, −400) corresponds to air and [300, +∞] is bone. The DSC of air region was 0.90±0.12 for brain site and 0.75±0.06 for pelvic site, respectively. The DSC of bony structure was 0.83±0.06 for brain site and 0.81±0.05 for pelvic site, respectively.

We evaluated the surface distance of body outline and bone for all test brain and pelvic data. For body outline, we first used threshold −500 HU to get the binary mask of CT and sCT images, and then we used dilate, fill holes and erode operation to get the CT and sCT body outlines. For bony structure, we regarded intensities of CT and sCT which are larger than 300 as bone intensities. For body outline, the 95% Hausdoff distance, mean surface distance and residual mean-square error were 3.55±1.38 mm, 0.28±0.07 mm and 1.71±0.93 mm for brain site and were 5.64±3.92 mm, 0.72±0.37 mm and 1.78±1.36 mm for pelvic site, respectively. For bony structure, the 95% Hausdoff distance, mean surface distance and residual mean-square error were 2.43±1.69 mm, 0.25±0.11 mm and 1.35±0.65 mm for brain site and were 5.74±4.35 mm, 0.74±0.42 mm and 2.65±1.81 mm for pelvic site, respectively. The mainly impact of local misalignment on accuracy of sCT is it enlarge the MAE around bone region. We evaluated the MAE within intersection set of sCT and CT bone region, and the union set of sCT and CT bone region. It is shown that the MAE within intersection set of sCT and CT bone region was 97.1±38.3 HU for brain site and 85.6±36.8 HU for pelvic site. However, the MAE within union set of sCT and CT bone region reached 259.9±68.7 HU for brain site and 268.1±73.2 HU for pelvic site. This means even if our sCT bone intensity can reach the similar level with CT bone intensity, the misregistration can enhance the MAE.

4. DISCUSSION

The proposed dense cycle GAN-based method is novel in two aspects. First and foremost, several dense blocks are engaged in constructing the network architecture of the generator of cycle GAN. Training the mapping between two different image modalities relies on the deep feature’s capability to not only capture the structural information but also to capture the textural information. The more informative and multi-scale features the generator acquires, the better one-to-one mapping the cycle GAN-based model learns. This significantly enhances the proposed method’s ability to generate distinctive tissue boundaries when local mismatches and misalignment occur. Second, MAD loss functions have the potential to misclassify image tissues, prediction bone as air or vice versa. This is especially problematic in the task of MRI-only based radiation treatment planning because local dose calculation is sensitive at tissue boundaries.⁴¹ An MPD loss function is used to overcome the blur and misclassification issues that occur when using traditional distance loss functions.

The whole image is first divided into multiple small patches, each of which has overlap with neighboring patches. Most of the patch pairs between MRI and CT match very well. Moreover, any mismatched pairs are not likely to be in the similar anatomic regions from patient to patient, meaning that each erroneous contribution can be effectively averaged out. Additionally, the dense blocks implemented by the proposed method can capture both structural information and textural information, which more tightly enforces the network to learn a one-to-one mapping.

Traditional cycle GAN methods use residual blocks to capture image features.⁴² A residual block is a fundamental network block that merges feature maps by adding previous layers to future layers. Incorporating these additive features forces the network to learn the residuals, i.e., the difference between previous convolutional layers and the current one. This approach can be easily applied for the synthesis of images between similar modalities, such as image quality enhancement for low-dose CT,⁴³ and image quality improvement for cone beam CT.⁴⁴ In contrast, dense block concatenate outputs from the previous layers instead of using the summation, connecting each layer to every other layer in a feed-forward fashion.³⁸ The dense block approach has several compelling advantages: they alleviate the vanishing-gradient problem, strengthen feature propagation, encourage feature reuse, and substantially reduce the number of parameters.³⁸ In our work, the dense blocks aim to combine the low frequency and high frequency information together to well represent the image patch and then map them to produce a synthetic image patch. The low frequency data, which often contains textural information, is obtained from previous convolutional layers. The high frequency data, which often contains structural information, is obtained from the current layer. Since the shape of the source image (MRI) varies significantly among different patients, the dense-block, which captures multi-scale information (low frequency and high frequency) better captures the relationship between MRI and CT images, and thus increases the accuracy of the generator. Even if there are some mismatches in pair-wise MRI and CT patches, the one-to-one mapping can avoid most potential bias. However, even though these effects will not affect image quality, they will affect our MAE, PSNR and NCC accuracy. Large mismatches may happen around the rectum and bladder due to different filling between CT and MR, which may confuse the training model. For clinical use, it is essential to establish the training database with standard clinical workflow to acquire CT and MR on the same day.

The MRI imaging acquisition parameters as well as magnetic field inhomogeneity and patient-specific distortion may influence the performance of the proposed method, with implications on dosimetry calculations and patient setup. In our study, all MRIs were pre-processed using an N3 Algorithm⁴⁵ to correct bias field before training or synthesis. The intensity normalization for these MRIs was also needed to bring the intensities to a common scale across patients.⁴⁶ Other novel methods such as a real-time image distortion correction method⁴⁷ have been reported to have excellent performance, and combining these preprocessing methods with our method could increase the accuracy of the sCTs. Due to the high volume of air, large motion, and distortion, the lung with poor resolution and low intensity in MRI is a very unique and difficult site for our MRI-based radiotherapy. Future research will include applying the proposed method to the lung.

In this study, we demonstrated the accuracy of sCT in HU numbers because dose calculation in MRI-only radiation therapy treatment planning relies solely on HU.⁴¹ In MRIs, bony tissues pose a significant susceptibility artifact, which can lead to an ambiguous boundary with air, introducing shifting errors in sCT images. Such an effect on dose calculation accuracy especially for surrounding tissues needs further evaluation. A combination of T1 MRI with ultrashort echo time (UTE) sequence provides much better signal for bones, which would help differentiate the bone-air boundary in sCT.

Our previous studies show that even an RF-based sCT, which has inferior image quality to our results, has very good dose calculation accuracy (<1% error) for brain stereotactic radiosurgery and pelvis radiation therapy for photon.^41,48 It is because that photon dose calculation are quite forgiving to pixel intensity errors, and dose calculation errors tend to be averaged and cancelled each other in a rapid arc plan. However, proton plans may benefit more from image quality improvement since the calculation on proton energy deposition is more sensitive to HU errors, especially the pixels along the beam path of limited beam angles. Moreover, better image quality of our results would still help patient setup in providing better DRR images. In the future, we plan to conduct studies to investigate the effects that various MRI artifacts and sCT errors will have on both photon and proton dose calculation and patient setup during MRI-only based radiotherapy.

Different scanners may have different intensity range and image quality. It is unclear how it would affect the results if the training datasets from one scanner and testing datasets from another one. Future study would involve a comprehensive evaluation with a larger cohort of patients acquired on different scanners with different protocols. These studies are necessary for testing the clinical utility of the proposed method.

As an emerging field in radiation therapy, currently there is no task group report or consensus of recommendation on quality assurance/commissioning on synthetic CT. However, we think it reasonable to refer to the current guidance of CT simulator QA (TG 66) and treatment planning system QA (TG 53) for both nondosimetric and dosimetric accuracy.^49,50 For machine learning-based method, special attention should be given to patient specific error because training datasets would not include all possible features and may produce unpredictable results when untrained features are presented in MR images. Possible solutions can be a CBCT scan as an independent verification.^11,51

Recently, Han proposed a deep CNN method for sCT synthesis.³² The MAE was 84.8±17.3 HU for all test brain data. Nie et al. reported that the MAE was 92.5±13.9 HU for the brain data by using GAN-based method.³⁵ Emami et al. also used GAN for brain cancer patients’ sCT synthesis.⁵² The mean MAE between sCT and CT were 89.3 HU across the entire field of view. Chen et al. applied U-net to generate sCT images for MRI-only prostate intensity-modulated radiation therapy treatment planning.⁵³ They reported the MAE value within body outline was 29.96±4.87 HU. The MAE from our proposed method was 54.2 HU for the brain data. Compared with the deep learning-based method proposed by Han, Emami et al. and Nie et al., our method obtained a much smaller MAE for the brain sites, which further demonstrates the performance of our sCT synthesis method. In comparison with state-of-the-art methods in the brain and pelvis, our method significantly outperforms the comparison methods. As is shown in Fig. 6–9, the sCT images generated by using RF-based method are often noisy. This may be caused by the RF-based method training a collection of weak learners by using handcrafted texture features.²⁹ However, structural features are also needed to train a one-to-one mapping from MRI to CT. The sCT image generated by using GAN-based method has some misclassification of tissue and some blurry estimation regions. This is because the GAN-based method uses deep features only from MRI and loses the information of CT during training.³⁵ In addition, the 3D patch size of GAN-based method is limited to 32×32×32 due to memory limitations, possibly contributing to a loss of global information, and making the GAN-based method more susceptible to local mismatches between the MRI and CT. The cycle GAN-based method³⁴ outperforms RF- and GAN-based methods by adding an additional generator. However, its performance may be limited by two reasons. First, its network consists of several residual blocks. The residual blocks focus on the difference between two images. If the MRI and CT images are accurately registered, and the ROIs of these two images are well registered, the residual blocks can learn the accurate mapping from MRI to CT within these ROIs. But if the two images have some local mismatches within these ROIs, the difference or residual between MRI and CT images modality will not only contain the voxel value difference between the two image modalities, but also contain the difference caused by the mismatch. This ambiguous difference will disturb the learning process for sCT generation, as is shown in the comparison of sCT images in Fig. 2. Second, cycle GAN-based methods used MSE loss as distance loss function to optimize the training model. However, the MSE loss often leads to blurring and over-smoothing as is shown in Fig. 4 and 5. Additionally, the cycle GAN-based method does not use the loss of GD, which can sharpen the tissue boundaries in the sCT.

One limitation of the proposed method is our MAE metric is affected by the misalignment between MRI and CT. Another limitation of this study is the small data set. However, rather than using whole image as training and testing data, we used 3D patch extracted by sliding with a window from MRI and CT images. By setting overlap between the two neighboring patches, for each patient’s image, we can get more than 6000 patches. Data augmentation such as image rotation, flipping, and as well as random elastic deformation were used to introduce more such training data diversity. Thus, although we trained on small data set, the diversity of training patches may be sufficient to train a robust sCT generation model.

Additionally, we did not use robust pre-processing methods, especially with regards to geometric artifact correction. However, the majority of the examples shown in this work are from the regions most affected by geometric artifacts, e.g., Fig. 2, 4, 6, 7. Wang et al. investigated the nature and magnitude of the subject-induced susceptibility effect on geometric distortions in clinical brain MRI, which are unneglectable, and showed the feasibility of in vivo quality control using field inhomogeneity mapping.⁵⁴ Therefore, without correcting geometric distortion around the nasal cavity region, contour plots in the paper are less robust. Effectively correcting these artifacts with additional short-scan sequences, for example, field-map based correction,⁵⁵ will be our future work.

Although we have tested our algorithm on 24 brain patients and 20 pelvis patients and added other 10 cases each from the brain and pelvis for separate testing. In the future, we plan to enroll more patients to further study the robustness of our algorithm. In addition, in this study we only used routine T1-weighted (brain) or T2-weighted (pelvis) MRIs to synthesize our sCTs. However, it is possible for our method to generate sCTs using other sequence-based MRIs. In future studies, we plan to combine several types of MRIs based on widely-used sequences into our training database to generate sCTs using multi-sequence MRIs.

5. CONCLUSIONS

We propose a novel deep learning-based approach to synthesize an sCT image from a routine MRI for potential MRI-based treatment planning in radiation therapy. The proposed method incorporates dense blocks into a cycle GAN-based framework using a novel MPD loss function. We demonstrated that the proposed method is capable of reliably generating a CT image from its MRI counterpart on brain and pelvis image data. This sCT synthesis technique could be a useful tool for MRI-based radiation treatment planning.