Automated mammographic breast density estimation using a fully convolutional network

Abstract

Purpose:

The purpose of this study was to develop a fully automated algorithm for mammographic breast density estimation using deep learning.

Method:

Our algorithm used a fully convolutional network, which is a deep learning framework for image segmentation, to segment both the breast and the dense fibroglandular areas on mammographic images. Using the segmented breast and dense areas, our algorithm computed the breast percent density (PD), which is the faction of dense area in a breast. Our dataset included full-field digital screening mammograms of 604 women, which included 1208 mediolateral-oblique (MLO) and 1208 Cranial-Caudal (CC) views. We allocated 455, 58, and 91 of 604 women’s exams into training, testing, and validation datasets, respectively. We established ground truth for the breast and the dense fibroglandular areas via manual segmentation and segmentation using a simple thresholding based on BI-RADS density assessments by radiologists, respectively. Using the mammograms and ground truth, we fine-tuned a pre-trained deep learning network to train the network to segment both the breast and the fibroglandular areas. Using the validation dataset, we evaluated the performance of the proposed algorithm against radiologists’ BI-RADS density assessments. Specifically, we conducted a correlation analysis between a BI-RADS density assessment of a given breast and its corresponding PD estimate by the proposed algorithm. In addition, we evaluated our algorithm in terms of its ability to classify the BI-RADS density using PD estimates, and its ability to provide consistent PD estimates for the left and the right breast and the MLO and CC views of the same women. To show the effectiveness of our algorithm, we compared the performance of our algorithm against a state of the art algorithm, LIBRA.

Result:

The PD estimated by our algorithm correlated well with BI-RADS density ratings by radiologists. Pearson’s rho values of our algorithm for CC view, MLO view, and CC-MLO averaged were 0.81, 0.79, and 0.85, respectively, while those of LIBRA were 0.58, 0.71, and 0.69, respectively. For CC view and CC-MLO averaged cases, the difference in rho values between the proposed algorithm and LIBRA showed statistical significance (p-value < 0.006). In addition, our algorithm provided reliable PD estimates for the left and the right breast (Pearson’s rho > 0.87) and for the MLO and CC views (Pearson’s rho = 0.76). However, LIBRA showed lower Pearson’s rho value (0.66) for left and right breast for CC view. In addition, our algorithm showed excellent ability to separate each sub BI-RADS breast density class (statistically significant, p-values = 0.0001 or less); only one comparison pair, density 1 and density 2 in CC view, was not statistically significant (p-value = 0.54). However, LIBRA failed to separate breasts in density 1 and 2 for both CC and MLO views (p-values > 0.64).

Conclusion:

We have developed a new deep learning based algorithm for breast density segmentation and estimation. We showed that the proposed algorithm correlated well with BI-RADS density assessments by radiologists and outperformed an existing state of the art algorithm.

1. Introduction

For over 30 years clinicians have used mammography for breast cancer screening. Research has shown that screening with mammography reduces breast cancer related deaths significantly, as noted with a 63% reduction among women who performed regular screening¹. However, mammography is not perfect, as it suffers from lower sensitivity for women with dense breast tissue than for women with fatty breast tissue², because of the potential masking of breast lesions by dense fibroglandular tissue. Women with dense breasts are often recommended to undergo additional screening procedures, such as magnetic resonance imaging (MRI) or ultrasound, which are more sensitive than screening mammography, but have lower specificity. In addition, research has shown that women with dense breasts are at higher risk for breast cancer than women with fatty breasts^{3, 4}. Assessing breast density from screening mammograms is an active area of research.

Among the various methods assessing breast density of women, the Breast Imaging Reporting and Data System (BI-RADS)⁵ by the American College of Radiology (ACR) is the most widely accepted classification method. Radiologists use the BI-RADS density classification to assign women to one of four categories. The BI-RADS (5^th edition) breast density categories are: 1) entirely fatty, 2) scattered, 3) heterogeneously dense, and 4) extremely dense.

However, BI-RADS breast density classification is subjective and coarse, and therefore, different radiologists can assign a different BI-RADS density level to the same breast, especially for moderately dense breasts, which can be categorized as either scattered or heterogeneously dense. Thus, many previous studies (to name a few^{6, 7}) have established a relative proportion of dense fibroglandular tissue in a breast, referred to as breast percent density (PD), as an alternative to the four BI-RADS categories.

To facilitate the process of estimating PD from a given FFDM, researchers have developed various automated algorithms. We can assign those algorithms into one of two categories: 1) area-based or two-dimensional methods^6–9 and 2) volumetric methods^10–12. Area-based or two-dimensional methods estimate PD from the proportion between the segmented breast area and the segmented dense fibroglandular areas in mammograms. Volumetric methods utilize the physics of x-ray attenuations in breast tissue to estimate how much dense fibroglandular tissue exists in each given x-ray path length. The area-based PD is the most validated measure and researchers are actively using this measure, as indicated in recent studies^13–15. Among the above algorithms, Cumulus, a semi-automatic area-based method for estimating PD from the University of Toronto⁶, is considered the gold standard for segmenting dense areas of the breast and estimating PD from given mammograms. However, Cumulus requires considerable human input and time to create the breast segmentation.

Laboratory for Individualized Breast Radiodensity Assessment (LIBRA), developed by Keller et al.⁷ at the University of Pennsylvania, is a fully automated algorithm for segmenting dense areas of the breast and estimating PD. LIBRA is a publicly available automated software that estimates area-based PD by utilizing multiclass fuzzy C means to locate and segment dense fibroglandular areas. The software was validated against the area-based PD from the mediolateral oblique (MLO) view of a mammogram estimated by radiologists using Cumulus. However, it may not always accurately segment the breast area, which can affect the PD estimate. Specifically, LIBRA uses a few connected straight lines to remove the pectoral muscle from the segmented breast area in the MLO view of a mammogram. However, the line between the pectoral muscle and the breast is not linear. Further, LIBRA cannot remove non-breast tissues, e.g., belly tissue, imaged in the mammogram. These factors can hinder the accurate estimation of PD. These limitations are coming from the fact that humans set a list of rules for algorithms to follow. The algorithm fails if it encounters an event that is out of the predefined rules. This is a universal issue for automated algorithms built from human defined rules.

To overcome such limitations, researchers in computer vision and machine learning communities introduced deep learning, where the machine learns and determines the rules to solve given problems. Deep learning is a branch of machine learning, where multiple layers of artificial neural networks are trained using millions of (labeled) data to solve various data analysis problems, such as image classification and speech recognition, with the help of massive computing power via GPU. Since its first successful appearance in classifying natural scenes¹⁶, deep learning has shown its effectiveness in various image analysis problems and it is now considered state of the art for various tasks in computer vision and machine learning fields. Researchers in the medical imaging field are now actively adopting deep learning to solve medical image analysis problems. Although there exists some areas of applications that deep learning outperforms medical professionals, e.g., detecting diabetic retinopathy¹⁷, deep learning in the medical imaging field is still in its infancy.

Previous studies for density segmentation using deep learning are very limited; Kallenberg et al., developed a convolutional sparse autoencoder (CSAE)¹⁸ to learn features in mammograms in an unsupervised fashion, and followed by a classifier on the learned features to solve a problem of interest, i.e., mammographic density segmentation. They used manual segmentations of dense areas on mammograms by a radiologist as ground truth and evaluated the segmentation performance of their algorithm against the manual segmentations. They showed a good correlation (Pearson’s rho of 0.85) between the PD computed from the manual segmentations and that from their algorithm’s outputs. However, the dense area segmentation performance by their algorithm against that of the radiologist was suboptimal; the image wise averaged Dice coefficient¹⁹ was 0.63 with a wide confidence interval of 0.19.

In this study, we developed a new fully automated algorithm for mammographic breast density estimation using deep learning. Specifically, we used a deep learning framework developed for image segmentation, i.e., Fully Convolutional Network (FCN), which shows successful performance in segmenting objects in natural scenes²⁰, to segment both the breast and the dense fibroglandular tissue areas from mammograms. We used manual segmentations of the breast area as ground truth. For dense area segmentation, we used a simple thresholding method based on BI-RADS density assessments as ground truth. Then, we trained, tested, and validated our algorithm on FFDM exams of 604 women. As the size of our dataset is small compared to a typical dataset for deep learning, e.g., ImageNet with over a million images with 1000 categories²¹, we used a transfer-learning method, i.e., fine-tuning, to train our algorithm. Then, we computed the PD using the segmented breast and dense area outcomes.

We compared the PD estimates of our algorithm against the BI-RADS density assessments of radiologists to evaluate the segmentation performance of our algorithm. Specifically, we conducted a correlation analysis between the PD estimates of the proposed algorithm and radiologists’ BI-RADS density assessments. In addition to the correlation analysis, we evaluated our algorithm’s ability to classify BI-RADS density levels using PD estimates, and the ability to provide consistent PD estimates for the left and the right breast, and for the MLO and CC views from the same women. To show effectiveness of our algorithm, we compared the performance of our algorithm to that of a state of the art and publicly available algorithm, LIBRA.

2. Methods

2.1. Dataset

Under an approved exempt institutional review board (IRB) protocol, we used screening mammography exams of 604 women who underwent breast screening within the University of Pittsburgh Medical Center (UPMC) network during 2007 to 2013. The UPMC network uses the Hologic Selenia system (Hologic Inc, MA, USA) to obtain screening mammograms. All exams consisted of at least four views: left and right mediolateral-oblique (MLO) views, and left and right Cranial-Caudal (CC) views. We utilized those four views and the “for presentation” version of the mammograms for this study. Although the most current BI-RADS version is the 5^th edition, our data were acquired before it was introduced, and therefore, radiologists reviewed the FFDM data of this study following the previous BI-RADS edition (4th edition). Thus, we used the previous BI-RADS edition for breast density assessments.

To develop and evaluate the proposed algorithm, of the 604 women’s mammography exams, we allocated the mammography exams of mutually exclusive 455, 58, and 91 women into training, test, and validation datasets (75%, 10%, and 15% of the entire exams), respectively. We grouped MLO and CC views together, but treated left and right mammograms as independent samples. Thus, the resulting mammogram images per view for each dataset were 910, 116, and 182, respectively. Table 1 summarizes the number of mammography images used for training, testing, and validating the proposed algorithm. We stratified the table in terms of BI-RADS density level to show the breast density distribution of our dataset. We allocated similar number of cases for each density level for the validation set to increase the statistical power for classifying density level with low prevalence, i.e., density level 1 and density level 4.

Table 1.

Characteristics of screening mammogram dataset

BI-RADS Density Level (4th edition)	Training (N = 455)		Test (N = 58)		Validation (N = 91)
	MLO	CC	MLO	CC	MLO	CC
Density 1	60	60	8	8	30	30
Density 2	366	366	46	46	44	44
Density 3	454	454	58	58	56	56
Density 4	30	30	4	4	52	52
Total (# of mammogram images)	910	910	116	116	182	182

2.2. Establishing ground truth

To train a deep learning network to segment the breast and the dense fibroglandular areas, we first established ground truth for both the breast and the dense fibroglandular areas.

This study utilized manually segmented breast areas as the ground truth. Using a computer Graphic User Interface (GUI) tool in MATLAB (Mathworks, MA), two undergraduate student research assistants delineated the breast areas on mammograms in the dataset of this study (Figure 1). We removed any non-breast areas, such as the pectoral muscle and/or belly tissue, from the resulting ground truth mask for the breast area.

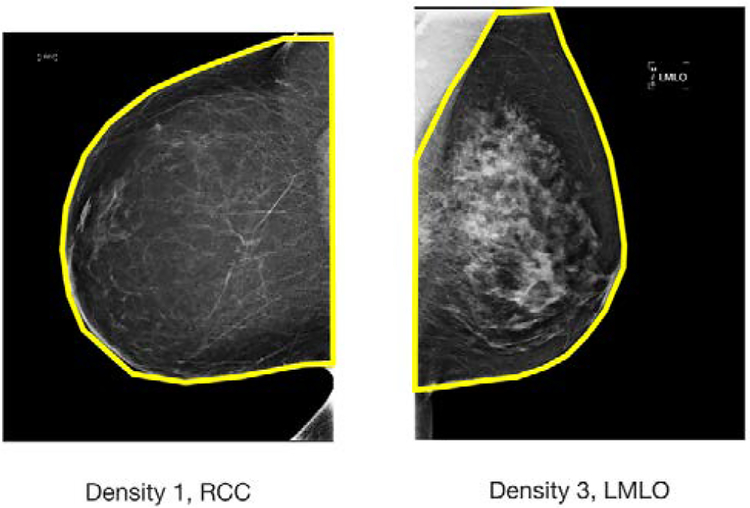
Figure 1.

Two undergrad research assistants delineated the breast area on mammograms using a GUI program in MATLAB. Created breast ground truth masks include only the breast area, removing the pectoral muscle, as shown in the right image, and/or belly tissue, as shown in the left image.

Then, within the manually segmented breast area from the above, we established the ground truth for the dense fibroglandular area per image as follows:

1. Remove breast skin by applying a binary image erosion filter with a square structure with an edge length of 1 cm.

2. Create a histogram of the given breast area in terms of its gray-level intensity.

3. Place a threshold in the histogram based on the BI-RADS density of a given mammogram:

   1. Density 1: threshold at 87.5 percentile of the histogram
   2. Density 2: threshold at 62.5 percentile of the histogram
   3. Density 3: threshold at 37.5 percentile of the histogram
   4. Density 4: threshold at 12.5 percentile of the histogram

4. Assign any pixels with an intensity level higher than the given threshold as fibroglandular tissue.

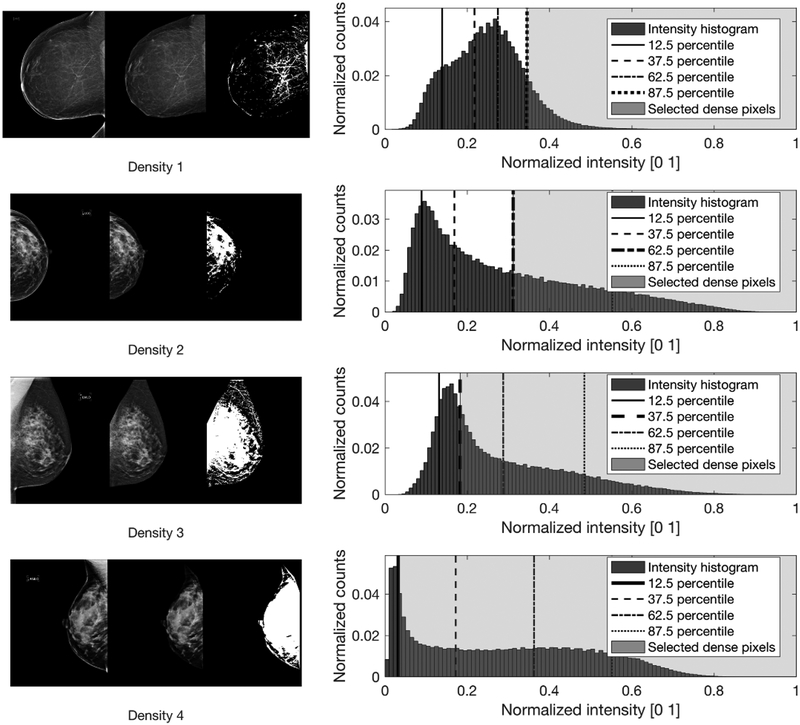
We used the definition of the BI-RADS density classification to create the above criteria. Note that radiologists reviewed the FFDM data of this study following the previous BI-RADS edition (4^th edition). According to the version of BI-RADS density classification relevant to our data²², the proportion of fibroglandular area in a mammogram increases every quartile (25%) as density level increases. Thus, the proportion of fibroglandular area in a histogram should increase as the BI-RADS density level increases. That is, for breast with a BI-RADS density level 1, we can expect that pixels in the last quartile in the intensity histogram would indicate dense fibroglandular area, while pixels in the last three quartiles would indicate dense fibroglandular area for a breast with BI-RADS density level 3. Using this rationale, we assigned the midpoint of each quartile, i.e., 12.5%, 37.5%, 62.5%, and 87.5 % as the threshold value for each density category. Figure 2 shows examples how we set up the ground truth for dense breast tissue. Note that we used the midpoint of each quartile instead of the minimum or the maximum as the minimum or the maximum threshold will produce less meaningful dense area segmentation outputs for either density level 1 or 4 for training. For example, for density level 1, if we used 100% (i.e., maximum) as the threshold, it will segment nothing from the given breast area.

Figure 2.

This figure shows a few examples from each density level and mammographic view on how we established the ground truth mask for dense fibroglandular area. Images on the left side of the panel show the original mammograms. Images in the middle show the results after applying manually delineated breast area mask and skin removal using a binary image erosion technique. Then, we applied a thresholding method to get ground truth mask for dense fibroglandular area. We used the mid-point of quartiles, i.e., 12.5, 37.5, 62.5, and 87.5 percentiles, of pixel intensity distribution as thresholds. Then, we assigned any pixels higher than a given threshold as dense fibroglandular area. Note that we selected thresholds in descending order based on each case’s BI-RADS density level. For example, we selected the 87.5 percentile as the threshold for BI-RADS density level 1 cases. Images on the right side of the panel show the results after applying the thresholding method. Also shown are the pixel intensity histograms inside the breast area.

2.3. Fully convolutional network for breast and dense area segmentation

This study used an existing deep learning framework for segmentation, called Fully Convolutional Network (FCN)²⁰, to segment the breast and the dense fibroglandular areas of the given breasts.

We used the VGG16 network²³ as our basic network structure and fine-tuned the network for segmenting breast and dense areas using our dataset. As described in²⁰, we removed the final classification layer of the VGG16 network and transformed the last two remaining fully connected layers to convolutional layers. Then, we added a 1 × 1 convolution layer with two channels to match our objective, which is assigning a pixel into either a foreground or background class. The resulting network provides a coarse score map for being a foreground or a background, since the original VGG16 network before fully connected layer has five pooling layers with a stride of two, with a padding option for convolution to keep image resolution same after convolution, which resulted in reducing the image size by a factor of 32. The resulting coarse-score map then was upsampled with a transposed convolution layer with a stride of 32 to provide the segmentation score map for a given image. As the resulting output is too coarse to provide meaningful segmentation results, we utilized skip architecture to extract lower layer information to obtain high-resolution segmentation outputs. We used the FCN-8s²⁰, which is a fused version of the output score map using the output of the final, pool4, and pool3 layers, as our final segmentation score map for a given image. To match the size of the output of the above three layers, we fused them in cascaded fashion; the final layer output is first upsampled with stride two and fused with the output of pool4, and then the resulting output upsampled with stride two again and fused with the output of pool3. At last, the resulting fused output is upsampled with stride 4. Note that each upsampling involves applying different transposed convolution layers. Following original FCN paper²⁰, we initialized the upsample layers to bilinear upsampling and then let their weights be learned during fine-tuning. Table 2 shows the FCN network architecture used for this study.

Table 2.

VGG16 based FCN network structure

Layer Type	Kernel Size	Stride	# Repetition	# Upsampling	Output
Output prediction FCN-8s					A + B + C
Conv7	3 × 3	1 × 1		×4	A
Conv6	3 × 3	1 × 1
Max pool5	2 × 2	2 × 2		×2	B
Conv5	3 × 3	1 × 1	×3
Max pool4	2 × 2	2 × 2
Conv4	3 × 3	1 × 1
Max pool3	2 × 2	2 × 2		×1	C
Conv3	3 × 3	1 × 1	×3
Max pool2	2 × 2	2 × 2
Conv2	3 × 3	1 × 1	×2
Max pool1	2 × 2	2 × 2
Conv1	3 × 3	1 × 1	×2
Input image

2.4. Training (fine-tuning) setup

The typical size of a mammogram is around 3000 by 4000 pixels. The purpose of this study is to segment breast area and dense area in the breast, which do not require the full resolution of mammogram. Thus, we conducted the following preprocessing step to make the mammogram images suitable to train FCN networks:

1. Convert an image I with 16 bit intensity [0, 65535] to an image $\widehat{I}$ with 8 bit intensity [0, 255] by using the following equation: $\widehat{I}=255*\tilde{I}$, where $\tilde{I}=\left(I-\text{min}\left(I\right)\right)/\text{max}\left(I\right).$

2. Convert $\widehat{I}$ to RGB image $\overline{I}$ by repeating $\widehat{I}$ in red, blue, and green channel.

1. Subsample images (original, breast area mask, and dense area mask) to 227 by 227 pixels.

The expected input image sizes for popular deep learning networks are ranged from 224 by 224 to 299 by 299. For example, AlexNet¹⁶ expects to have 227 by 227 as input image size, while VGG16²³ expects 224 by 224 and Google’s Inception model²⁴ expects 299 by 299 as input image resolution. Among these choices, we set 227 by 227 as input image resolution as it is enough to visualize the required information (e.g., dense area has higher pixel intensity than non-dense area) for the segmentation of breast and dense area. However, it should be noted that one can choose other higher resolutions (e.g., 299 by 299 or higher) as input image size to train FCN networks.

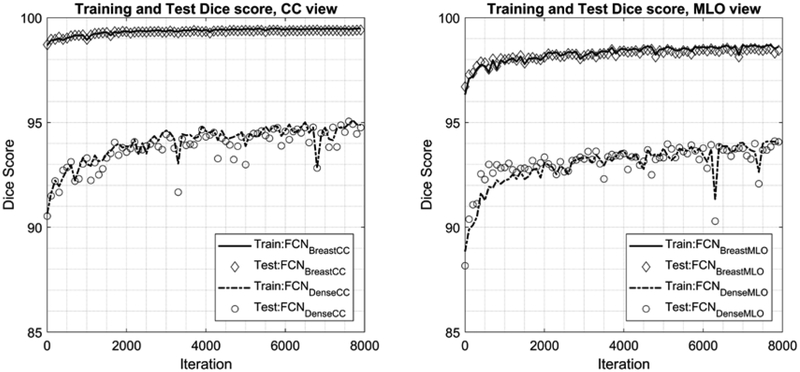
We then trained four FCN networks, two (MLO and CC) for segmenting the breast area and two (MLO and CC) for segmenting the dense fibroglandular area. We refer to the two FCN networks for segmenting the breast area as FCN_BreastMLO and FCN_BreastCC, and the other two for segmenting the dense area as FCN_DenseMLO and FCN_DenseMLO. Note that we trained separate FCN networks for the MLO and CC views, as they contain anatomically different body parts. For example, MLO view contains a pectoral muscle, which show high intensity comparing to other breast tissues, while CC view typically contains breast area only. We trained all networks using the Adaptive Moment Estimation (Adam) optimizer²⁵ with a learning rate of 0.00001. We used a weight decay of 0.0005 for all layers and a dropout probability of 0.5 for the convolution layers 6 and 7. We set the batch size as 1 and augmented the training data by applying a random cropping by randomly moving a window up to 32 pixels in both x and y axes. We followed the choice of the learning rate, weight decay, batch size, and dropout probability from a previous study²⁶, which showed the excellent result on a related but different task, i.e., the segmentation of roads for Kitti Road Detection Benchmark²⁷. We used cross-entropy as a loss function and set the maximum iteration as 8000 for all networks. Every 100 iterations, we evaluated each FCN using the test dataset. Specifically, we tested each FCN by computing the Dice coefficient between the FCN outputs and corresponding ground truth. We found that both FCNs for breast area and FCNs for dense area converged and were steady when they were at the maximum iteration for the both training and test datasets (Figure 3). FCN_BreastMLO and FCN_BreastCC converged 98 – 99 after 1000 iterations. FCN_DenseMLO and FCN_DenseMLO, relatively slow to converge compared to FCN networks for breast areas, with the maximum Dice score for 94 – 95 after 4000 or 6000 iterations. Thus, we used the version of FCN networks at 4000 iterations for FCN_BreastMLO and FCN_BreastCC, while we used the version of FCN networks at 8000 iterations for FCN_DenseMLO and FCN_DenseMLO.

Figure 3.

This figure shows the testing scores, i.e., Dice coefficient ranged [0, 100], for four FCN networks during the courses of training. Using the test dataset (N = 58 exams, i.e., 116 MLO and CC view mammograms) we tested each network every 100 iterations of training. The plots include the Dice coefficient values for training dataset (N = 455 exams, i.e., 910 MLO and CC view mammograms). FCN networks for breast areas quickly converges to 98 – 99 after 1000 iterations for both training and test datasets. FCN networks for dense areas relatively slow to converge compared to FCN networks for breast areas, with the maximum Dice score for 94 – 95 after 4000 or 6000 iterations for both training and test datasets. We used the version of FCN networks for breast areas at iteration 4000, and the version of FCN networks for dense areas at iteration 8000 for this study.

2.5. Computing percent density from segmentation outcomes

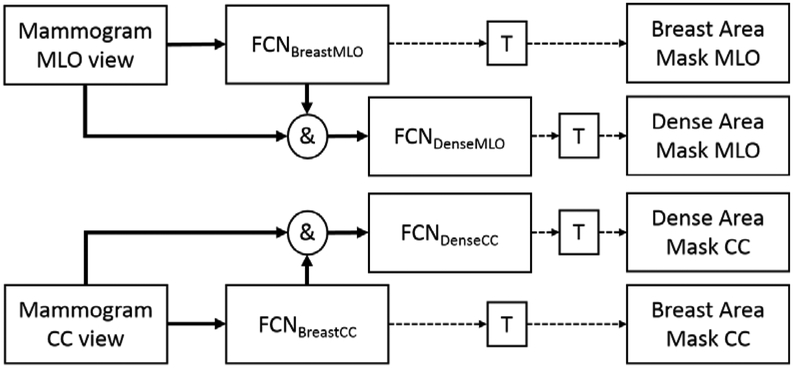
The output of the trained FCN networks is the probability map or score for each pixel being a foreground or a background. To convert the score map (ranged from 0 to 1) to a binary segmentation mask, we applied the threshold at 0.5. Note that one may see small blobs that are not the breast area in the output of FCN_BreastMLO and FCN_BreastCC. Thus, we selected the largest blob among all blobs in the output image as the breast area, and removed other smaller blobs from the output image. Figure 4 shows the flowchart of the proposed density segmentation algorithm of this study.

Figure 4.

This diagram summarizes the entire process of training, denoted as bold arrow lines, for the proposed algorithms, and how they create estimated breast area and dense area segmentations, denoted as dashed arrow lines. T refers to the thresholding to convert an estimated segmentation outcome in probability to binary masks. We used 0.5 for T. For breast area segmentation, we selected the largest blob in the resulting binary mask as breast area mask.

Using the segmented outcomes, i.e., breast and dense area masks, we then computed the percentage density (PD) for each mammogram using the following equation:

$$PD=\frac{Area\left(Dense Mask\right)}{Area\left(Breast Mask\right)}.$$ (Eq. 1)

2.6. Evaluation

We used the independent validation dataset, 182 MLO and CC view mammograms of 91 women, to evaluate the proposed algorithm.

We used BI-RADS density assessments by radiologists as ground truth, and calculated the Pearson’s correlation rho between it and the corresponding PD estimates by the algorithm. We computed the 95% confidence interval of the correlation coefficient using a bootstrapping over cases (N = 1000) in the validation set.

In addition, we evaluated whether the proposed algorithm has ability to separate given breasts into one of four BI-RADS density categories. To do so, we first conducted one-way analysis of variance (ANOVA) on both the proposed algorithm and LIBRA on PD estimates of all four BI-RADS density categories, and then conducted a post hoc analysis using a multiple comparison test (multcompare function in MATLAB) using the one-way ANOVA test statistics. In the multiple comparison test, we estimated the 95% confidence interval of the difference between the means of the two groups.

We also evaluated the algorithm’s ability to provide consistent PD estimates for the same women, by comparing left and right, and MLO and CC views. We used Pearson’s correlation analysis and Bland Altman plot to evaluate the consistency of the algorithm.

In addition, we compared our algorithm against the state of the art and publicly available breast density segmentation algorithm, LIBRA, in terms of the above three evaluation criteria.

3. Results

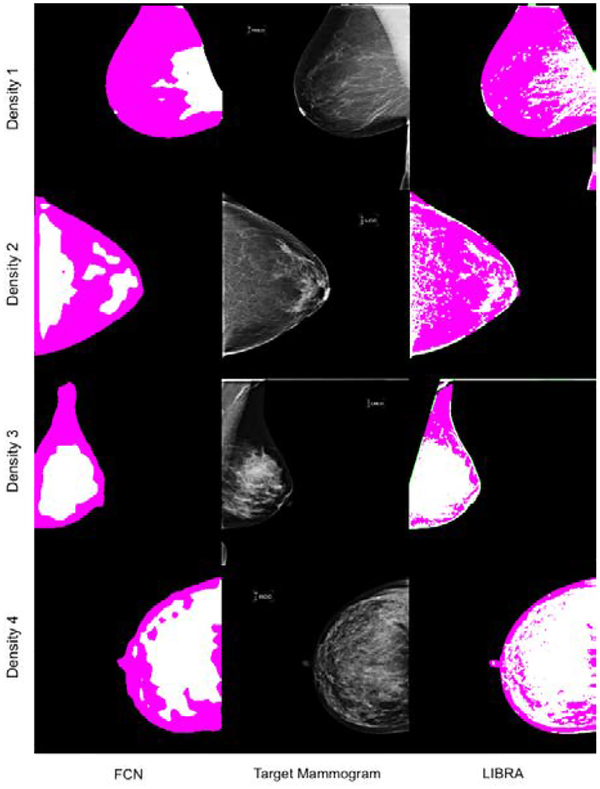
Figure 5 shows four examples of breast and dense area segmentation outcomes from our proposed algorithm and LIBRA. Compared to LIBRA, the proposed algorithms delineated breast and dense areas better than LIBRA. For example, the proposed algorithm provided a smoother contour between the pectoral muscle and the breast than LIBRA, and it removed the skin effectively, while LIBRA assigned the skin area as the dense part of the breast.

Figure 5.

This figure shows some examples of breast area and dense area segmentation for the proposed algorithm and LIBRA. Images in 1^st and 3^rd columns show the outcomes of the proposed algorithm and those of LIBRA, respectively. Images in the center show the target mammograms.

Table 3 shows the summary statistics of the PD estimates from the proposed algorithm and LIBRA. The proposed algorithm computed similar PD estimates for the CC and MLO views (p-value for mean difference was 0.2). However, LIBRA computed higher PD estimates for CC view cases, compared to those for the corresponding MLO view cases (p-value < 0.0001). In addition, we found that the PD estimates for the CC view from LIBRA was higher than those from the proposed algorithm (p-value < 0.0001). The above results indicate that the proposed algorithm estimated similar PD values for the CC and MLO views of the same breast, while LIBRA over-estimated CC view cases over MLO view cases.

Table 3.

Summary statistics for PD estimates by the proposed algorithm and LIBRA

N = 91 exams (182 mammograms)	CC, Mean [95% CI] ± SD	MLO, Mean [95% CI] ± SD	CC – MLO Mean [95% CI]
Proposed	0.42 [0.4, 0.44] ± 0.14	0.41 [0.39, 0.44] ± 0.15	0.01 [−0.005, 0.03]
LIBRA	0.52 [0.49, 0.56] ± 0.21	0.44 [0.41, 0.47] ± 0.22	0.08 [0.06, 0.11]*
LIBRA – Proposed	0.1 [0.08, 0.13]*	0.03 [0.01, 0.06]

^*Statistically significant with significance level was 0.0125 after Bonferroni correction.

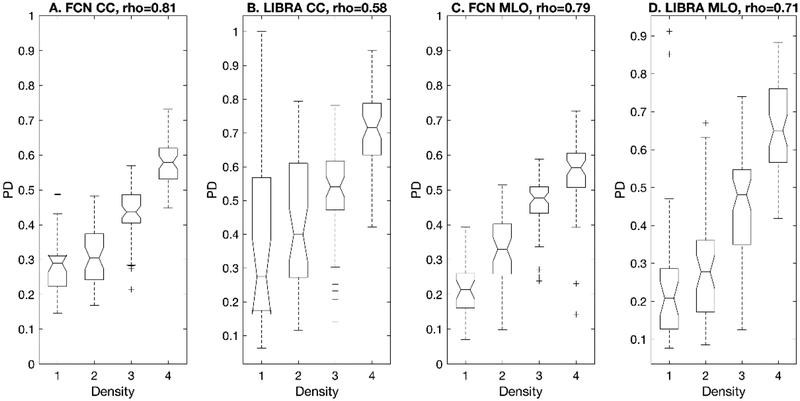
Then, we compared the PD values computed from each algorithm’s output against radiologists’ BI-RADS density assessments (Figure 6). We observed high correlations²⁸ between the proposed algorithm’s estimated PD values and the BI-RADS density levels for CC and MLO views, respectively, while the correlations between LIBRA’s estimates and the BI-RADS density levels were only moderate for the same cases. In fact, LIBRA showed a low correlation coefficient for the CC view. Further, the differences between the correlation values of the proposed algorithm and LIBRA for CC views were significantly different (Table 4).

Figure 6.

This figure shows the box plots of the proposed algorithm and LIBRA for the estimated PD values verses the BI-RADS breast densities. The number of exams in each breast density category (density 1 – 4) are 15, 22, 28, and 26, respectively. The two extreme values on the box plots indicate the 25 and 75 percentile of the data. The two extreme values of the dash lines refer to the minimum and the maximum of the data that are not considered outliers. The plus (+) marker indicates a possible outlier within the data (which is more than 2.7 standard deviations above or below the mean of a normal distribution). The notches indicate the 95% confidence interval of the median.

Table 4.

Comparison of correlation values of the proposed algorithm and LIBRA. The correlation is between the PD estimates and radiologists’ BI-RADS assessments

N = 91 exams (182 mammograms)	Proposed	LIBRA	Difference	p-value
CC	0.81 [0.74, 0.85]	0.58 [0.43, 0.68]	0.24 [0.12, 0.41]	<0.0001*
MLO	0.79 [0.7, 0.85]	0.71 [0.57, 0.79]	0.08 [−0.02, 0.24]	0.18
CC-MLO averaged	0.85 [0.8, 0.89]	0.69 [0.55, 0.77]	0.17 [0.08, 0.3]	0.006*

^*Statistically significant with significance level was 0.0167 after Bonferroni correction.

Both the proposed algorithm and LIBRA showed their ability to separate at least one BI-RADS density class from other classes using their PD estimates (Table 5, all p-values from one-way ANOVA were approximately 0). However, the post-hoc analysis results showed that the proposed algorithm had excellent ability to separate each sub BI-RADS breast density class (Table 6); only one comparison pair, density 1 and density 2 in CC view, was not statistically significant. However, LIBRA failed to separate breasts in density 1 and 2 for both CC and MLO views. We found that LIBRA tended to overestimate the PD values for density level 1 and 2. In addition, we found that LIBRA was more susceptible for incorrect dense area segmentation than our algorithm for CC views with a BI-RADS density level 1 (Figure 6.B). We also observed the cases that LIBRA failed to segment dense area correctly for CC views with a BI-RADS density level 1, resulting in a wide box plot for the corresponding density group.

Table 5.

One-way ANOVA Statistics for PD estimates by the algorithms

View		Proposed algorithm					LIBRA
		SS*	df	MS	F	p-value	SS	df	MS	F	p-value
CC	Groups	2.41	3	0.8	141.38	7e-47	2.99	3	0.996	32.97	5e-17
	Error	1.01	178	0.006			5.38	178	0.03
	Total	3.42	181				8.37	181
MLO	Groups	2.63	3	0.88	104.7	4e-39	4.78	3	1.59	72.47	1e-30
	Error	1.49	178	0.008			3.91	178	0.22
	Total	4.12	181				8.69	181
Averaged	Groups	2.45	3	0.82	168.04	1e-51	3.83	3	1.28	61.57	2e-27
	Error	0.87	178	0.005			3.69	178	0.021
	Total	3.32	181				7.52	181

^*SS, df, and MS refer to sum of squares, degree of freedom, and mean square error.

Table 6.

Evaluation of the algorithm’s ability to separate BI-RADS density levels

View	BI-RADS density level pairs	Proposed algorithm		LIBRA
		Mean difference and 95% CI	p-value	Mean difference and 95% CI	p-value
CC	1 – 2	−0.02 [−0.07, 0.02]	0.54	−0.05 [−0.15, 0.05]	0.64
	2 – 3	−0.12 [−0.16, −0.09]	<0.0001*	−0.11 [−0.2, −0.02]	0.0067
	3 – 4	−0.14 [−0.18, −0.11]	<0.0001*	−0.17 [−0.26, −0.09]	<0.0001*
MLO	1 – 2	−0.12 [−0.17, −0.06]	<0.0001*	−0.04 [−0.13, 0.05]	0.72
	2 – 3	−0.13 [−0.18, −0.09]	<0.0001*	−0.16 [−0.23, −0.08]	<0.0001*
	3 – 4	−0.08 [−0.13, −0.04]	<0.0001*	−0.22 [−0.29, −0.14]	<0.0001*
Averaged	1 – 2	−0.07 [−0.11, −0.03]	0.0001*	−0.04 [−0.13, 0.04]	0.59
	2 – 3	−0.13 [−0.17, −0.09]	<0.0001*	−0.14 [−0.21, −0.06]	<0.0001*
	3 – 4	−0.11 [−0.15, −0.08]	<0.0001*	−0.2 [−0.27, −0.12]	<0.0001*

^*Statistically significant with significance level of 0.0014 with Bonferroni correction. The mean difference for all other pairs, 1 – 3, 1 – 4, and 2 – 4 were statistically significant with p-value < 0.0001.

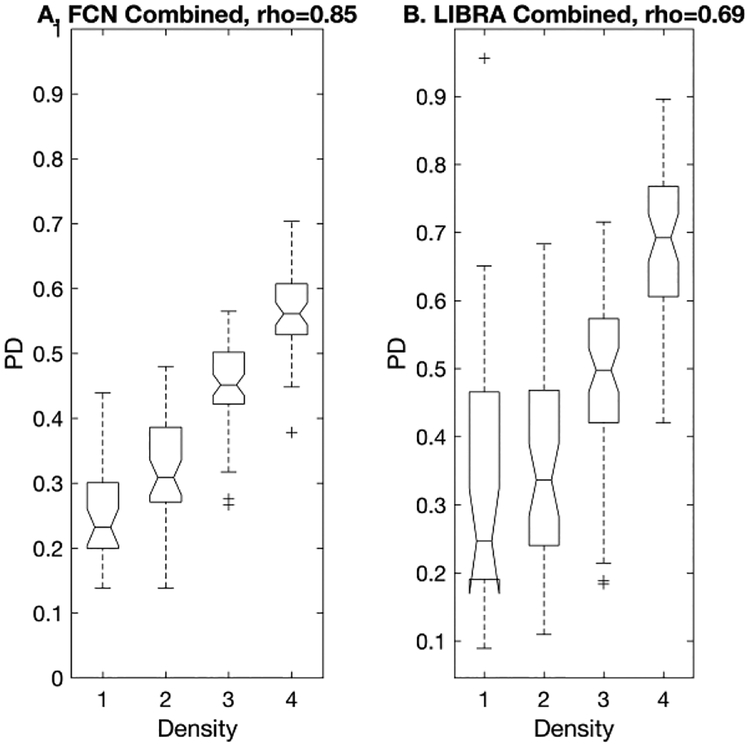
In addition, we averaged MLO and CC view PD estimates of both the proposed algorithm and LIBRA to obtain case-based PDs (Figure 7). The proposed algorithm showed high correlation with a Pearson’s correlation rho = 0.85 between the estimated PD values and the BI-RADS density levels, while LIBRA only showed moderate correlation with a Pearson’s correlation rho = 0.69. The difference between the above two correlations were statistically significant (Table 4). We found that the proposed algorithm showed excellent ability to assess the BI-RADS density level of the segmented dense area (Table 6). However, for LIBRA, the mean difference between BI-RADS density 1 and 2 was not statistically different (Table 6).

Figure 7.

This figure shows the box plots of the proposed algorithm and LIBRA for the case-based PD value, i.e., MLO and CC view averaged, verses BI-RADS breast density. The number of exams in each breast density category (density 1 – 4) are 15, 22, 28, and 26, respectively. The proposed algorithm showed higher correlation between the PD estimates and the BI-RADS density levels than LIBRA.

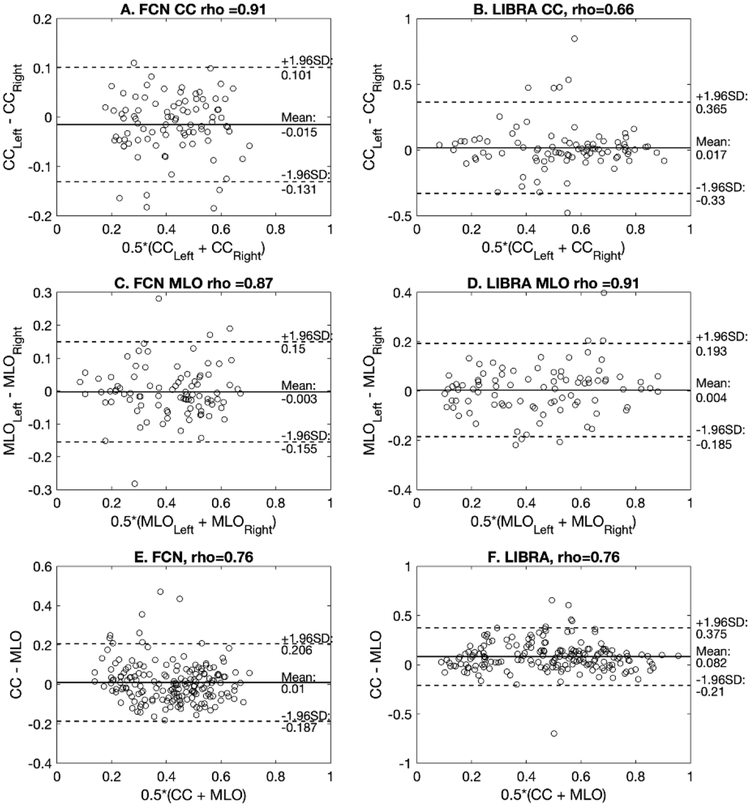
Figure 8. A-D shows the Bland Altman plot of the PD values for the left and right breasts estimated by the proposed algorithm and LIBRA. Both proposed algorithm and LIBRA showed no systematical bias (mean difference < 0.02) between measures, except LIBRA for the PD estimates between CC and MLO view (mean difference = −0.082), that is, LIBRA over-estimated PD estimates of CC view compared to that of PD view. However, LIBRA showed wider variations in PD estimate differences than the proposed algorithm for all comparisons (i.e., for subplots A vs. B, C vs. D, and E vs. F in Figure 8). The correlation between the PD values of the left and right breasts for the proposed algorithm were high with a Pearson’s correlation coefficient of 0.87 for the MLO view and 0.91 for the CC view. LIBRA showed a similar correlation level for the MLO view with a Pearson’s correlation coefficient of 0.91. However, we found that LIBRA showed only a moderate level of correlation in the PD values between the left and right breasts for CC view, and the difference between the correlation coefficients of the proposed and LIBRA algorithms was statistically different (Table 7).

Figure 8.

A and C show the Bland Altman plot between the PD values of the left and right breasts for the proposed algorithm on MLO and CC views, respectively. Similarly, B and D show the Bland Altman plots for LIBRA. E and F show the Bland Altman plot between the PD estimates of CC and MLO views for the proposed algorithm and LIBRA, respectively. Note that the validation dataset (N = 91 exams, i.e., 182 CC and MLO view mammograms) was used for this analysis. Both proposed and LIBRA showed no systematical bias (mean difference < 0.02) between measures, except LIBRA for the PD estimates between CC and MLO view (mean difference = −0.082), that is, LIBRA over-estimated PD estimates of CC view compared to that of MLO view. However, LIBRA showed wider variations in PD estimate differences than the proposed algorithm for all comparisons. The proposed algorithm showed high correlation (rho > 0.87) between left and right PD value estimates for both MLO and CC views, while LIBRA showed only moderate correlation (rho = 0.66) between left and right PD value estimates for CC views.

Table 7.

Comparison of the proposed algorithm and LIBRA for correlation in PD estimates between left and right, and MLO and CC view of same woman

Correlation (N = 91 exams, 182 mammograms)	Proposed	LIBRA	Difference	p-value
PDLeft – PDRight, CC	0.91 [0.87, 0.94]	0.66 [0.4, 0.8]	0.25 [0.1, 0.49]	0.014*
PDLeft – PDRight, MLO	0.87 [0.78, 0.92]	0.91 [0.84, 0.94]	−0.04 [−0.12, 0.02]	0.73
PDCC – PDMLO	0.76 [0.66, 0.83]	0.75 [0.63, 0.83]	0.01 [−0.11, 0.13]	0.9

^*Statistically significant with significance level of 0.0167 with Bonferroni correction.

In addition, we found that both the proposed algorithm and LIBRA showed similar correlation level for their PD estimates from the CC and MLO views, with Pearson’s correlation coefficient of 0.75 – 0.76. However, we found the difference in PD estimates between MLO and CC view from the proposed algorithm is smaller, with mean 0.07 ± 0.07, than those of LIBRA, with mean 0.12 ± 0.12. In fact, one can observe that PD estimates by our algorithm is closer to the mean than those of LIBRA (Figure 8.E–F).

4. Discussion

We have shown that compared to LIBRA, our proposed algorithm can estimate PD consistently with radiologists’ BI-RADS breast density categorization. It also has less variability and more consistency between views of the same breast and between views of the left and right breasts. In addition, LIBRA tended to have higher estimates of PD for dense breasts than those of the proposed algorithm (Figure 6 – 7). The possible reason for the difference is the inclusion of skin for PD estimates. We specifically trained our algorithm to remove skin for dense area segmentation, while LIBRA did not enforce such a restriction. Previous research showed that including skin for PD in mammograms can increase the estimated PD by 3.8% to 4.9%²⁹.

Both our algorithm and LIBRA showed similar correlation in PD estimates between the MLO and CC views of the same breast. Although correlation coefficient values of 0.75 – 0.76 indicate strong correlation, the correlation amount is lower than that of a previous study, which ranged from 0.86 – 0.96³⁰. For the case of our algorithm, some PD estimates for the CC view were higher than the corresponding MLO view, where the difference in PD estimates between them were higher than 0.25 (Figure 8.E). These cases were part of the outliers. Specifically, two of these outliers were from BI-RADS density level 1 cases and the remaining two were from BI-RADS density level 4 cases. For those outliers with a BI-RADS density 1 category, the proposed algorithm over-segmented the dense area in the CC view, while the proposed algorithm under-segmented the dense area in the MLO view for the outliers with a BI-RADS density 4 category (Figure 9). After removing the above four outliers, Pearson’s correlation between PD estimates of the MLO and CC views were increased to 0.83, which is the upper bound of the 95% CI of Pearson’s rho in Table 7.

Figure 9.

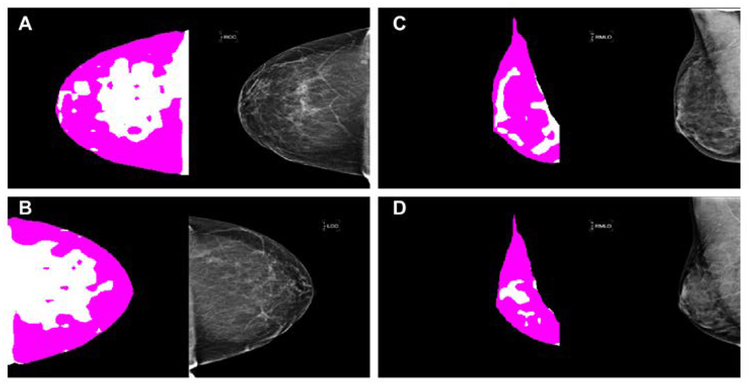
This figure shows outliers that the proposed algorithm either over-segmented (A-B) or under-segmented (C-D) dense fibroglandular areas of the breast. A and B are the right and left CC mammogram views from the same woman with a BI-RADS density level 1. C and D are the right MLO mammogram views of two different women with a BI-RADS density level 4.

LIBRA showed poor performance on the CC view, while it showed compatible performance to the proposed algorithm on the MLO view. One possible reason is that LIBRA was optimized for the MLO view. In the original publication and its follow-up research of LIBRA, the developers of LIBRA utilized the MLO view only^{7, 31} to segment dense area and estimate PD. Thus, one may need to avoid LIBRA to segment dense area and estimate PD from the CC view, as its performance on the CC view can be sub-optimal.

We developed the proposed algorithm using “for presentation” version of mammography exams from a single vendor (Hologic Inc), which can be a limitation of the proposed algorithm as each vendor uses different image processing algorithms for presentation of mammography exams. We expect that the pre-processing step to convert 16-bit mammograms to 8-bit grayscale images would reduce the image quality difference due to different imaging system from different vendors. However, it is required to test the proposed algorithm for mammography exams from other vendors such as GE to check the robustness of the proposed algorithm. Such testing can be a possible future study of this paper.

One may consider using BI-RADS density ratings as ground truth as a potential limitation of this paper. This is because BI-RADS density rating is an ‘indirect truth’ for breast dense fibroglandular area segmentation. In fact, many previous studies^{7, 10–12} on breast density segmentation typically used manual segmentation of dense fibroglandular areas by radiologists as ground truth. However, it is well known that each radiologist is different from each other for segmenting dense breast area³². In addition, most previous studies used segmentation outcomes from a very limited number of radiologists, typically one or two, as manual segmentation is time consuming and labor intense. Thus, it is possible that the density segmentation algorithms based on one or two radiologists are difficult to generalize for other radiologists and new cases. In this respect, the fact that we used indirect truth (i.e., BI-RADS density rating by radiologists) to train our algorithm can be an advantage, not a limitation, over other previous algorithms using manual segmentations by one or two radiologists. We used BI-RADS density ratings from a pool of radiologists, not just one or two radiologists, to create ground truth for dense fibroglandular area. As the PD estimates by our algorithm were highly correlated with BI-RADS density ratings by a pool of radiologists, we concluded that our algorithm was able to locate and learn a common area or feature that a pool of radiologists would assess as the dense portion of the breast.

Another possible limitation of this study is that we used the fixed threshold value based on the BI-RADS density ratings, e.g., 12.5 percentile for BI-RADS density 4, to obtain the ground truth segmentation for dense area. Thus, the resulting dense segmentation outcome can include error, either missing dense area or including non-dense area, which can degrade the segmentation performance of the algorithm. However, we showed that deep learning could learn essential information to segment dense fibroglandular area, despite these possible errors on the ground truth for dense area. This is an important finding, especially for developing deep learning algorithms for image segmentation, as this may indicate that rough outlines for the region of interest may be enough to train deep learning algorithms for image segmentation. Thus, researchers may spend less time on establishing ground truth by trading off its precision. Of course, the required precision for image segmentation is different from one application to another. Future research is therefore required on the effect on the precision of ground truth for developing deep learning algorithms for image segmentation.

We used the VGG16 network as a basis deep learning architecture for this study. There are other deep learning architectures such as ResNet³³. Although a previous study²⁶ reported that both VGG16 and ResNet showed similar performances on road segmentation benchmarks, there could be differences when applied to dense breast area segmentation. In addition, training parameters used for this study such as learning rate, and the threshold value to convert a score map to binary segmentation (i.e., T in Figure 4) can be further optimized. Evaluating other network architectures, finding the optimal training parameters and the threshold value can be a follow-up study of this paper.

In conclusion, we introduced a new deep learning based algorithm for breast density segmentation. We showed that the proposed algorithm can provide segmentation outcomes that its corresponding PD estimates are well correlated with radiologists’ BI-RADS density assessments. In addition, we showed that the proposed algorithm outperformed the existing state of art algorithm, LIBRA.