Construction of 4D infant cortical surface atlases with sharp folding patterns via spherical patch-based group-wise sparse representation

Abstract

4D (spatial + temporal) infant cortical surface atlases covering dense time points are highly needed for understanding dynamic early brain development. In this article, we construct a set of 4D infant cortical surface atlases with longitudinally consistent and sharp cortical attribute patterns at 11 time points in the first six postnatal years, that is, at 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months of age, which is targeted for better normalization of the dynamic changing early brain cortical surfaces. To ensure longitudinal consistency and unbiasedness, we adopt a two-stage group-wise surface registration. To preserve sharp cortical attribute patterns on the atlas, instead of simply averaging over the coregistered cortical surfaces, we leverage a spherical patch-based sparse representation using the augmented dictionary to overcome the potential registration errors. Our atlases provide not only geometric attributes of the cortical folding, but also cortical thickness and myelin content. Therefore, to address the consistency across different cortical attributes on the atlas, instead of sparsely representing each attribute independently, we jointly represent all cortical attributes with a group-wise sparsity constraint. In addition, to further facilitate region-based analysis using our atlases, we have also provided two widely used parcellations, that is, FreeSurfer parcellation and multimodal parcellation, on our 4D infant cortical surface atlases. Compared to cortical surface atlases constructed with other methods, our cortical surface atlases preserve sharper cortical folding attribute patterns, thus leading to better accuracy in registration of individual infant cortical surfaces to the atlas.

1 |. INTRODUCTION

The brain atlas plays an important role in brain-related research, since it provides a common space for normalizing, comparing, and analyzing brain structures and functions across different individuals and studies (Evans, Janke, Collins, & Baillet, 2012). The first brain atlas could date back to 1900s, when researchers used the cell stain method on ex vivo brains to label and map brain cytoarchitecture and myeloarchitecture, forming the earliest cerebral cortex parcellation (Brodmann, 1909, 1914). Due in part to the invention of the MRI, researchers can now construct brain atlas from in vivo brain images, which has greatly enriched the understanding and analysis on brains. Generally, there are two types of brain atlases: (a) volumetric atlases (Dickie, Shenkin, Anblagan, et al., 2017; Shi et al., 2011; Tzourio-Mazoyer et al., 2002) (which are directly constructed from volumetric brain MR images), and (b) cortical surface atlases (which are constructed based on the reconstructed cortical surfaces from volumetric MR images) (Fischl, Sereno, Tootell, et al., 1999; Lyttelton, Boucher, Robbins, & Evans, 2007; Toro & Burnod, 2003; Van Essen & Dierker, 2007). Compared to volumetric atlases, cortical surface atlases provide more valuable and accurate references for brain studies by respecting the topology of the highly convoluted cerebral cortex (Glasser et al., 2016; Li, Nie, Wang, Shi, Lyall, et al., 2013; Li et al., 2014; Li, Lin, Gilmore, & Shen, 2015; Van Essen, Drury, Joshi, et al., 1998, 2000; Van Essen, Smith, Barch, et al., 2013; Van Essen, Snyder, Raichle, et al., 2004).

Many cortical surface atlases have been constructed to facilitate adult brain studies. For example, FreeSurfer cortical surface atlas was constructed by landmark-free coregistration of cortical folding patterns of 40 adult brains (Fischl, Sereno, Tootell, et al., 1999). Population-Average, Landmark and Surface-based (PALS) cortical surface atlas was constructed by a sulcal – gyral landmark-constrained registration of 12 adult brains (Van Essen, 2005; Van Essen & Dierker, 2007). International Consortium for Brain Mapping cortical surface atlas was constructed by unbiased coregistration of curvature patterns of 222 adult brains (Lyttelton et al., 2007). More recently, the Human Connectome Project (HCP) cortical surface atlas (Glasser et al., 2016) was constructed by cortical surface registration driven by multimodal information in a common framework (Robinson et al.,(2014). These cortical surface atlases, encoding the geometric cortical folding attributes (e.g., average convexity, sulcal depth, curvature, etc.) as well as other informative cortical attributes (e.g., cortical thickness, myelin content, and functional connectivity), have been widely applied in understanding the adult brain. However, these adult cortical surface atlases are not suitable for characterizing the dynamic developing infant brains, due to the dramatic differences in brain size, appearance, shape, and folding between adults and infants. Therefore, infant-dedicated cortical surface atlases are highly needed for early brain development studies.

Few works have been dedicated to infant cortical surface atlas construction. Hill et al. (2010) constructed the first neonatal cortical surface atlas, PALS-term 12 atlas, by coregistration of 12 term-born neonatal cortical surfaces. In particular, the coregistration was driven by the manually delineated sulcal-gyral landmark curves (Van Essen et al., 2004; Van Essen, Drury, Dickson, et al., 2001). Kim et al. (2016) constructed a spatiotemporal cortical surface atlas for the preterm-born neonates from 26 to 40 postmenstrual weeks, based on surface registration framework (Lyttelton et al., 2007; Robbins, Evans, Collins, & Whitesides, 2004) from the CIVET¹ pipeline. Specifically, they used 231 scans from 158 preterm-born neonates, and constructed atlases at four postmenstrual age ranges, that is, 26–30, 31–33, 34–36, and 37–40 weeks. Bozek, Fitzgibbon, Wright, et al. (2016) and Bozek et al. (2018) created a spatiotemporal neonatal cortical surface atlas at each week from 36 to 44 weeks of postmenstrual age, based on 270 full-term subjects. The Multimodal Surface Matching registration (Robinson et al., 2014) was adopted to coregister spherical cortical surfaces in each week group.

However, these infant cortical surface atlases cover only the neonatal stage, which is not sufficient to accurately characterize the dynamic, regionally heterogeneous, and nonlinear postnatal development of infant brains (Li, Nie, Wang, Shi, Lin, et al., 2013). To address this issue, Li et al. (2015) constructed the first 4D infant cortical surface atlases at seven densely sampled time points, including 1, 3, 6, 9, 12, 18, and 24 months of age, based on 202 serial MRI scans from 35 healthy term-born infants, with each infant scanned longitudinally from birth. To ensure longitudinal consistency and unbiasedness to any specific subject and age, they first computed the within-subject mean by averaging the group-wise coregistered longitudinal cortical surfaces from an individual subject. Then, they further established longitudinally consistent and unbiased intersubject cortical surface correspondence by group-wise coregistration of the within-subject means from different subjects. Thus, these 4D surface atlases can capture dynamic population-average shape changes during early brain development. However, due to potential registration errors and considerable intersubject cortical attribute variations, the population-average cortical attributes were often oversmoothed on the constructed 4D atlases, which potentially degrades the registration performance when aligning new subjects to these 4D atlases.

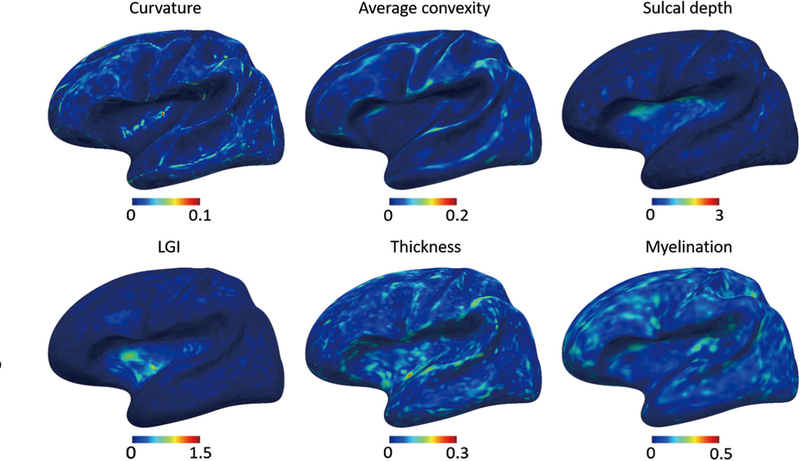
To address this issue, we propose to leverage a spherical patch-based sparse representation method to construct a set of 4D infant cortical surface atlases, which preserves sharper cortical attribute pattern and increases the registration performance. The spherical patch-based analysis has been shown as an elegant way for exploring the cerebral cortex, for example, for the Alzheimer’s disease diagnosis (Zhang, Fan, Li, et al., 2017). In this work, our central idea is (a) for each spherical patch in the atlas space, we build a dictionary which includes corresponding patches and their spatially neighboring patches from all coregistered cortical surfaces, and (b) for each cortical attribute on the atlas patch, we sparsely represent it using the dictionary patches. The advantages of this method include (a) by augmenting the patch dictionary with the neighboring patches, the potential registration errors can be tolerated, and (b) sparse representation is substantially robust to noisy cortical attributes, where the noisy cortical attribute refers to the cortical attribute that has least agreement with the population’s attribute. These two advantages made the proposed atlas construction framework more robust to noise in cortical attributes, and thus preserve the continuous attribute patterns on our atlases. In this work, we capitalize on six cortical attributes, that is, four geometric cortical folding attributes such as sulcal depth, average convexity, mean curvature, and local gyrification index (LGI), as well as the cortical thickness and myelin content. Note that, since different cortical attributes can be regarded as different views of the cortical folds, they are highly correlated and thus required to be consistent on the constructed 4D atlas. Therefore, instead of sparsely representing each cortical attribute independently, we jointly represent all attributes with a group-wise sparsity constraint. Our constructed 4D infant cortical surface atlases have three merits: (a) it covers the longest time range in the densest manner (i.e., the first six postnatal years with 11 time points at 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months of age) for characterizing the dynamic early postnatal brain development, based on 339 longitudinal MR scans from 50 healthy infants; (b) it provides comprehensive views for describing cerebral cortex development by introducing multiple longitudinal corresponding and consistent cortical attributes; and (c) it preserves sharp cortical attribute patterns for representing the population cortical attribute, which leads to better registration accuracy when used to align individual infant cortical surfaces. To further facilitate region-based analysis, we have also provided the constructed 4D infant cortical surface atlases with two widely used parcellations, that is, FreeSurfer parcellation (Desikan et al., 2006) and the HCP multimodality parcellation (MMP) (Glasser et al., 2016).

This article significantly extends our previous conference paper (Wu, Li, Meng, et al., 2017) in the following three aspects: (a) we have provided more cortical attributes to better characterize infant cerebral cortex development; (b) we have addressed the issue of consistency across different cortical attributes using the group-wise sparse representation; and (c) we have provided more details and experiments for explaining and validating our constructed 4D infant cortical surface atlases.

The rest of this article is organized as follows. In Section 2, we briefly introduce the dataset and related MR image processing steps involved in the atlas construction. In Section 3, we present the whole framework in detail. In Section 4, we evaluate our constructed 4D atlases qualitatively and quantitatively. In Section 5, we discuss some components in our framework and analyze their influences. Finally, we conclude this paper in the last section.

2 |. MATERIALS AND IMAGE PROCESSING

2.1 |. Materials

Serial T1-weighted (T1w) and T2-weighted (T2w) MR images from 50 healthy infants were acquired using a Siemens 3T head-only scanner with a 32-channel head coil. Each subject was scheduled to be scanned at 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months of age. At each scheduled scan, both T1w and T2w MR images were collected. All images were quality controlled by neuroradiologists, and images with insufficient quality were removed from the study. In total, 339 images were collected. The subject number and gender information (with M indicating male, and F indicating female) at each time point are reported in Table 1. The imaging parameters for T1w MR image are: Time of Repetition (TR) = 1,900 ms, Time of Echo (TE) = 4.38 ms, flip angle = 7, and the resolution = 1 × 1 × 1 mm³. The imaging parameters for T2w MR image are: TR = 7,380 ms, TE = 119 ms, flip angle = 150, and the resolution = 1.25 × 1.25 × 1.95 mm³. More detailed information on imaging protocol in this work can be found in Li, Wang, et al. (2015), Nie et al. (2011), and Wang et al. (2012).

TABLE 1.

Subjects for constructing the 4D infant cortical surface atlases

Scan age (months)	1	3	6	9	12	18	24	36	48	60	72	Total
Subject number	39	36	41	36	36	40	23	14	26	28	20	339
Gender	M:23	M:20	M:21	M:19	M:21	M:22	M:10	M:5	M:11	M:12	M:8	M:172
	F:16	F:16	F:20	F:17	F:15	F:18	F:13	F:9	F:15	F:16	F:12	F:167

2.2 |. Image processing

All infant T1w and T2w MR images were processed by the UNC Infant Cortical Surface Pipeline (Li, Nie, Wang, Shi, Lin, et al., 2013; Li et al., 2014; Li, Nie, et al., 2014; Li, Wang, et al., 2015). Briefly, it included the following major preprocessing steps: (a) intensity inho-mogeneity correction by N3 (Sled, Zijdenbos, & Evans, 1998); (b) rigid alignment of the T2w image to the corresponding T1w image and further resampling to 1 × 1 × 1 mm³ using FSL (Smith et al., 2004); (c) skull stripping by a learning-based method (Shi et al., 2012); (d) cerebellum and brain stem removal by registration (Shen & Davatzikos, 2002) with a volumetric atlas (Shi et al., 2011); (e) rigid alignment of all longitudinal images of the same subject; (f) longitudinally consistent tissue segmentation using learning-based multisource integration framework (Wang et al., 2012; Wang et al., 2015); and (g) masking and filling noncortical structures, and separation of each brain into left and right hemispheres (Li, Nie, Wang, Shi, Lin, et al., 2013; Li, Nie, Wang, Shi, Lyall, et al., 2013).

For each hemisphere of each subject brain, the topologically correct and geometrically accurate inner (white/gray matter interface) and outer (gray matter/cerebrospinal fluid interface) cortical surfaces were reconstructed using a topology-preserving deformable surface method based on tissue segmentation results (Li et al., 2012; Li, Nie, et al., 2014). Specifically, to reconstruct the inner cortical surface, firstly, topological defects were corrected on the white matter volume based on a learning-based method (Hao, Li, Wang, et al., 2016), ensuring a 2D topology for each hemisphere. Then, the corrected white matter volume was tessellated as a triangular mesh. Next, the triangular surface mesh was deformed by preserving its initial topology to reconstruct the inner and outer cortical surfaces (Li et al., 2012; Li, Nie, et al., 2014). To simplify cortical surface registration, the inner cortical surface was further smoothed, inflated, and mapped to a sphere by minimizing the metric distortion between the original cortical surface and its spherical representation (Fischl, Sereno, & Dale, 1999). Notably, the inner surface, outer surface, inflated surface, and the mapped spherical surface are all represented as triangular meshes, which can be uniformly denoted as Sτ = (Vτ,Fτ), with Vτ indicating the vertices, and Fτ indicating the triangular faces, where τϵ {Inner, Outer, Inflate, Sphere} indicates the surface type. Note that V_Inner, V_Outer, V_Inflate, and V_Sphere have one-to-one vertex correspondence.

The cortical attributes M are provided along with the cortical surface atlases. In this work, we mainly focus on six typical cortical attributes, that is, four geometric cortical folding attributes that include average convexity (denoted as M_A) (Fischl, Sereno, Tootell, et al., 1999), mean curvature (M_C) (Fischl, Sereno, Tootell, et al., 1999), sulcal depth (M_D) (Li, Wang, et al., 2014), and LGI (M_G) (Li, Wang, et al., 2014), and two other attributes that include cortical thickness (M_T) (Li, Lin, et al., 2015) and myelin content (M_L) (Glasser & Van Essen, 2011). These cortical attributes were computed from the reconstructed cortical surfaces using the UNC Infant Cortical Surface Pipeline (Li, Nie, Wang, Shi, Lin, et al., 2013; Li, Nie, et al., 2014; Li, Wang, et al., 2014; Li, Wang, et al., 2015). Once the cortical attributes are computed, they can be attached to any cortical surface (inner, outer, inflate, and sphere) for visualization or analysis. For a local vertex v_i ϵ V, i = 1,.., |V|, we use M_j(v_i) (j ϵ {A,C,D,G,T,L}) to denote a certain cortical attribute of this vertex.

3 |. METHODS

3.1 |. Main framework

After preprocessing, we obtain cortical surfaces and corresponding cortical attributes for each subject at each age. The atlas at each age, with specific cortical attribute, should be representative of the population from that age. Therefore, we can formulate the construction of a 4D infant cortical surface atlas for each cortical attribute as a sparse representation (Tibshirani, 1996) of cortical attributes of individual subjects. To maintain the consistency across different cortical attributes on the atlas, we further require that the representation for different cortical attributes should share similar sparsity structure, which can be achieved by introducing a group-wise sparsity constraint (Argyriou, Evgeniou, & Pontil, 2007, 2008; Liu, Ji, & Ye, 2009; Nie, Huang, Cai, et al., 2010).

The main framework for 4D infant cortical surface atlas construction includes the following three steps. First, we establish the unbiased spatio-temporal cortical correspondence across different subjects and different time points using a two-stage group-wise registration. Then, for each local patch in the atlas space, we build a dictionary for sparse representation. Of note, the dictionary includes not only the corresponding patches from the age-matched coregistered cortical surfaces, but also the neighboring patches to account for the possible registration errors. Finally, we jointly represent all cortical attributes of the atlas patch by the cortical attributes of patches in the dictionary, through a group-wise sparsity constraint. This joint representation is formulated as a multitask sparse representation problem, that is, the dirty model (Jalali, Sanghavi, Ruan, et al., 2010), with each task corresponding to sparsely representing a specific cortical attribute. The reason of choosing the dirty model is that it enables us to impose the group-wise sparse constraint and address potential noises in the obtained cortical attributes. By using these described steps, we can not only preserve sharp patterns of the cortical attributes, but also maintain consistency across different attributes on the constructed 4D cortical surface atlas. In the following section, we will explain each step in detail.

3.2 |. Establishing spatio-temporal cortical correspondences

Establishing correspondence across different individual cortical surfaces is the first step for atlas construction. To further assist longitudinal analysis, we require the 4D infant cortical surface atlases to have longitudinal (temporal) cortical correspondences across all ages. That means, for the same location in the atlas space, its cortical attributes from different ages are corresponded.

A straightforward solution is to directly align all individual cortical surfaces at different ages into a common space, using the group-wise registration. However, this will result in poor longitudinal correspondence across different time points because we have two kinds of cortical attribute variations that need to be normalized during the registration: (a) within-subject changes due to each subject’s own brain development and (b) intersubject variations due to interindividual differences. As the primary and secondary cortical folds are present at term birth and preserved during postnatal development (Hill et al., 2010; Li, Nie, Wang, Shi, Lin, et al., 2013), the within-subject changes of cortical attributes are much smaller than the intersubject variations. Thus, the registration will be dominated by the intersubject variations, whereas the within-subject (longitudinal) changes will be less addressed, causing inconsistent longitudinal correspondence.

To avoid this issue, we adopt a two-stage (intrasubject and intersubject) group-wise cortical surface registration strategy, to not only ensure the spatio-temporal correspondences, but also preserve the within-subject longitudinal consistency. The registration framework is illustrated in Figure 1.

FIGURE 1.

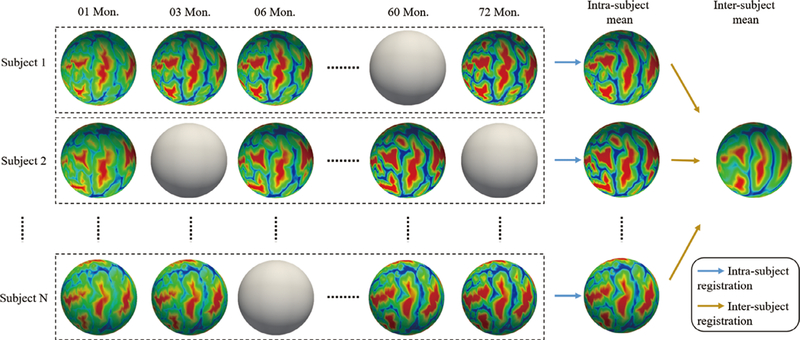
Illustration of two-stage registration for establishing intrasubject and intersubject cortical correspondences. The spheres without color indicate missing data at those time points

The first stage is to establish the unbiased intrasubject longitudinal cortical correspondences for each subject. To this end, all longitudinal cortical surfaces of the same subject are group-wise coregistered, and then the intrasubject mean is obtained. Note that, considering that all primary and secondary cortical folds preserve stably during postnatal development, accurate intrasubject registration can be obtained, which leads to sharp intrasubject mean for capturing subject-specific representative cortical attribute patterns.

The second stage is to establish intersubject cortical correspondences across all subjects. Specifically, the intrasubject mean surfaces of all subjects are group-wise coregistered into a common space, that is, the intersubject mean space. Then, the longitudinally consistent intersubject cortical correspondences are also established based on the sharp cortical attribute patterns in each intrasubject mean, and thus each cortical surface of each subject at each time point can be warped into the intersubject mean space.

The group-wise cortical surface registration method used in the above two stages is the spherical demons (Yeo, Sabuncu, Vercauteren, et al., 2009), which has been shown to have similar registration accuracy as FreeSurfer, but is much more efficient. It can group-wise align cortical surfaces based on the geometric cortical attribute patterns mapped on the spherical surface.

The spherical demons extends the traditional diffeomorphic demons algorithm (Cachier, Bardinet, Dormont, Pennec, & Ayache, 2003; Vercauteren, Pennec, Perchant, & Ayache, 2009) from the Euclidean space to the spherical space. The objective function of the traditional diffeomorphic demons in Euclidean space is:

$$\left({\Upsilon }^{*},{\Gamma }^{*}\right)=\arg \underset{\Upsilon ,\Gamma }{\min }{\Vert {\Sigma }^{-1}\left(\mathbb{F}-{\mathbb{M}}_0\Gamma \right)\Vert }^2+\frac{1}{{\sigma }_x^2}\mathrm{dist}(\Gamma ,\Upsilon )+\frac{1}{{\sigma }_T^2}\mathrm{Reg}(\Upsilon )$$

where F and M are the fixed image and moving image, respectively; Γ and ϒ are both deformation fields; dist( ) indicates the distance between Γ and ϒ; and Reg() denotes the regularization which generally penalizes the Jacobian of the deformation field. Matrix Ʃ models the variance of the voxel-wise attribute (intensity) across the images; σ_x and σ_T provide a balance across the data fitting term and the regularization term. The reasons for introducing two displacement fields Γ and ϒ are: (a) by introducing ϒ, the objective function could be more efficiently solved through iterative updating of Γ and ϒ; and (b) by modeling the process of updating Γ as a diffeomorphic velocity field evolution, the diffeomorphism of the transformation can be preserved. To extend it to the spherical surface space, the F and M are now regarded as the fixed and moving spherical surfaces with certain cortical attribute, for example, the average convexity or curvature (Yeo et al., 2009). The dist(Γ, ϒ) is defined as the distance of the tangent vectors of Γ and ϒ on the sphere; while Reg(ϒ) is defined as the energetic inner product with the Laplacian operator, which can preserve a smaller deformation field with a small Reg(ϒ). By introducing these new definitions, the spherical demons successfully extended the traditional demons registration to the spherical space. The advantages of the spherical demons registration are: (a) the registration is very efficient, that is, a pair-wise registration can be done in a few minutes; (b) the registration can be extended to involve multiple cortical attributes hierarchically, for example, the functional attributes or myelin content. In this work, we adopted the commonly used average convexity and curvature for driving the cortical surface registration.

Once the pair-wise surface registration is defined, the group-wise surface registration can be achieved by iteratively aligning each individual cortical surface into the same common space. Specifically, it first aligns each individual cortical surface into the mean surface of all cortical surfaces; second, given with the registered surfaces, the mean surface can be updated and all the individual cortical surfaces are then aligned to the updated mean surface. This procedure is iterated until convergence.

After aligning all individual cortical surfaces at different ages into the intersubject common space, we further resample all the registered surfaces and their cortical attributes with a standard mesh tessellation, which has 163,842 vertices and is sufficient to preserve the spatial detailed information of the convoluted cortical surface for infant brains (typically with less than 110,000 vertices).

3.3 |. Building spherical patch dictionary

After registration and resampling, all subjects are now sitting in the intersubject mean space and all spherical cortical surfaces from different subjects are sharing the same mesh structure. Although a direct average operation over all subjects at each age (time point) could be conducted to obtain age-specific population-average atlases (Li, Wang, et al., 2015), this will lead to oversmoothed cortical attribute patterns due to potential registration errors and large intersubject variations. As illustrated in Figure 2, the cortical attribute patterns on the population-average atlas are oversmoothed, and many detailed cortical attribute patterns are lost. Therefore, when using the population-average 4D atlases as the reference to spatially normalize the individual infant cortical surfaces with sharp cortical attribute patterns, the registration accuracy is often degraded due to the oversmoothed cortical attribute patterns.

FIGURE 2.

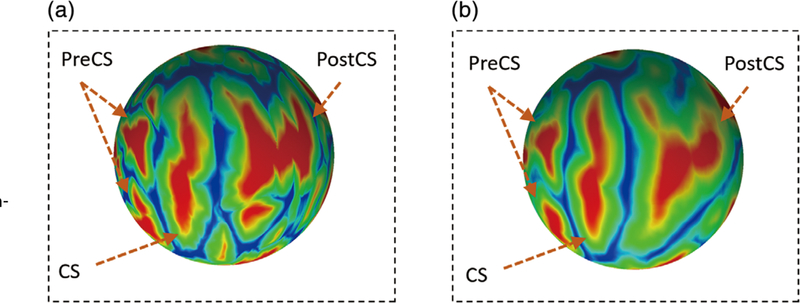
(a) The cortical attribute (i.e., average convexity) of an individual subject. (b) The same cortical attribute (i.e., average convexity) of the population-average 4D atlas. CS, central sulcus; PostCS, postcentral sulcus; PreCS, precentral sulcus

To address this oversmoothing issue, we formulate atlas construction as a problem of spherical patch-based sparse representation. That is, the cortical attribute on the atlas is sparsely represented by the underlying cortical attribute in the dictionary that is built from all the coregistered cortical surfaces. Specially, compared to the case of using the vertex-wise cortical attributes, the atlas constructed using patch-wise cortical attributes can be more robust by introducing the neighborhood context information (i.e., the local cortical attribute pattern). Moreover, with a properly designed dictionary building strategy (as illustrated in paragraph building dictionary), the effect of potential registration errors could also be minimized. Thus, the sharpness and representativeness of the cortical attribute patterns on the cortical surface atlas can be improved.

3.3.1 |. Building comparable neighboring spherical patches

To build a representation dictionary, we need to obtain comparable patches for neighboring vertices. As aforementioned, each spherical cortical surface is a triangular mesh, composed of the vertices set and their respective connections. There are two reasons that we need to do the patch rotation. The first reason is that, on the original spherical surface, different points may have different numbers of neighboring points. As illustrated in Figure 3a, vertex v₁ has 15 neighbors on its two-ring patch (the red patch), while vertex v₂ has 18 two-ring neighbors (the green patch). Therefore, we cannot directly augment the neighboring patches on the original spherical surfaces into the dictionary, since they are not comparable. The second reason is that we need consistent vertices orders on the patches. As illustrated in Figure 3a, we may regard the vertex inside the red circle as the first neighbor of local patch at v₁; however, if we need to augment the patch at v₂, which is one of the three-ring neighbors (the green vertices) of v₁, we need to make their vertices orders consistent. To solve these issues, we rotate the patch from v₁ to v₂, as illustrated in Figure 3b. Of note, both v₁ and v₂ are on the sphere, so we can rotate the patch at v₁ along the axis v₁ x v₂ with the angle of $\theta =\frac{\langle v_1,v_2\rangle }{\Vert v_1\Vert \cdot \Vert v_2\Vert }$. Then, the rotated patch at v₂ has the same vertex number and also consistent vertices order as the local patch at v₁. During the atlas construction, we use the local patch as the template, rotate it to its neighbors and then use the rotated patch after resampling as its neighboring patch.

FIGURE 3.

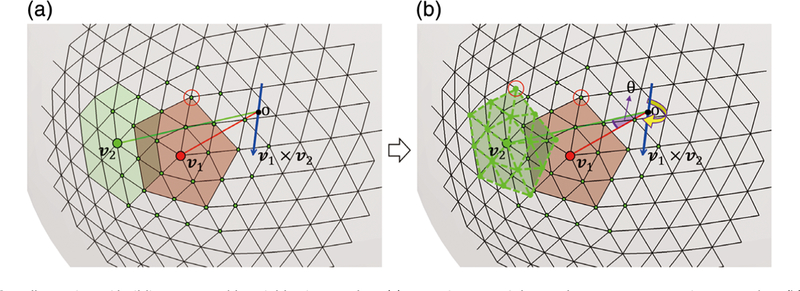
Illustration of building comparable neighboring patches. (a) Inconsistency of the mesh structures at vertices v₁ and v₂. (b) Rotation of the patch at ₁ to the patch of v₂ to 875 build the two comparable neighboring patches

3.3.2 |. Building dictionary

With the built comparable neighboring patches, for each atlas patch with a certain cortical attribute, we can now build a representation dictionary. Herein, we select one of the six cortical attributes M_j (j ϵ {A, C, D, G, T, L}), with j = A (i.e., average convexity) as an example, and build its corresponding representation dictionary. Other cortical attributes’ representation dictionaries at the same local patch can be built similarly. Specifically, for a local patch centered at vertex v₁, we extract all corresponding patches from N coregistered cortical surfaces and then include them into the dictionary, denoted as $p_{M_A}^{(n)}\left(v_i\right)$ (v_i), where n = 1,…, N denotes a subject index while M_A indicates that the elements in this patch are the average convexity. To increase the robustness to potential registration errors, all patches near to the current local patch are also extracted and augmented into the dictionary, denoted as $p_{M_A}^{(n)}\left(v_i^k\right)$, where $v_i^k$ is the kth vertex near to the vertex v_i; (i.e.,$v_i^k$ ,k =1,.,K, is the two-ring neighbor of v as illustrated in Figure 4). By including all these corresponding patches and their spatially neighboring patches, the dictionary D_Ma (v_i) can be well built to represent average convexity on the atlas patch centered at v_i Using the same method, we can also build dictionaries of other cortical attributes, DM_C(V_i), DM_D (V_i), DM_G(V_i), DM_T(V_i), and DM_L (V_i), for this local patch, as also illustrated in Figure 4.

FIGURE 4.

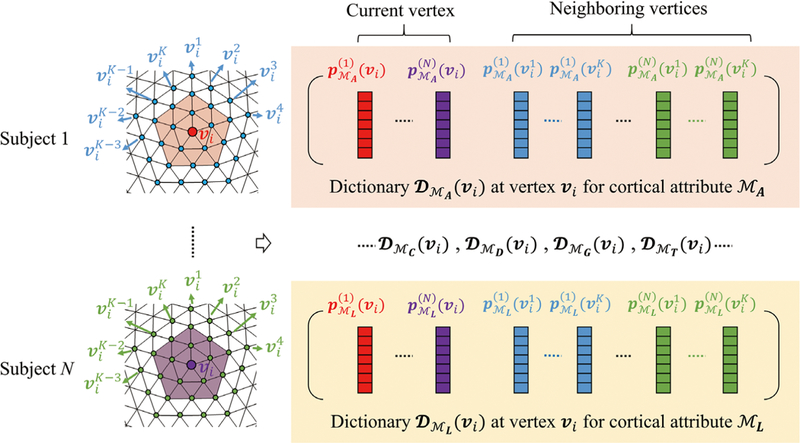
Construction of six cortical attribute dictionaries D_MA(v_i), D_MC(v_i), D_MD(v_i), D_MG(v_i), D_MT(v_i), and D_ML(v_i) for a local patch centered at vertex v_i. $v_i^k$, k = 1,…K, is the three-ring neighbor of v_i. Each dictionary includes not only the local two-ring patch from all subjects, but also the augmented three-ring neighbors’ patches from all subjects, thus improving robustness to potential registration errors

3.4 |. Constructing atlas by spherical patch-based group-wise sparse representation

Once the dictionaries are built, acquiring the certain cortical attribute on the atlas becomes finding the best sparse representation using the respective dictionary. For example, for a cortical attribute (e.g., M_A), given an atlas patch at v_i the N corresponding local patches from N coregistered surfaces can be obtained. However, due to potential registration errors and substantial intersubject variations, patches from certain subjects may have less agreement with patches from the rest of the subjects in representing the population-level cortical attribute.

An effective way to deal with this is to filter out these atypical patches in atlas construction with the following three steps. (a) the group center patch is first computed as the average over the N patches; (b) the correlation coefficient between each patch and the group center patch is then computed; (c) Finally, the top M (M ≤ N) patches corresponding to the top M correlation coefficients are selected, denoted as ${\widehat{p}}_{M_A}^{(m)}$(v_i), with m = 1,…, M. In the following, we will use our built dictionary to represent these top M patches.

Since there are three cortical attributes and each attribute can be regarded as a specific view of the cerebral cortex, these six different cortical attributes estimated for each atlas location should be consistent to each other. To this end, instead of independently estimating them, we estimate them jointly using a multi-task sparse representation with group-wise sparsity constraint, where each task corresponds to the estimation of a specific cortical attribute. We use the dirty model (Jalali et al., 2010; Zou & Hastie, 2005) for modeling this multi-task sparse representation with group-wise sparsity constraint.

The multitask sparse representation using the dirty model for the atlas construction can be formulated as the following minimization problem:

$$\underset{W}{\mathrm{argmin}}\left[\sum _i\sum _{m=1}^M{\Vert D_{M_j}\left(v_i\right){\omega }_j\left(v_i\right)-{\widehat{p}}_{M_j}^{(m)}\left(v_i\right)\Vert }_2^2+{\rho }_1\Vert P{\Vert }_{\infty ,1}+{\rho }_2\Vert Q{\Vert }_1\right]$$ (1)

$$\text{st}.W=P+Q$$ (2)

where $p_{M_j}^{(m)}$ (v_i) denotes the m-th extracted patch from the top M patches with the cortical attribute M_j, j ϵ {A, C, D, G, T, L}. D_Mj (v_i) is the dictionary of M_j for the local patch centered at v_i and ω_j is the sparse representation (column) vector for the jth cortical attribute. W= [ω_A(v_i), ω_C(V_i), ω_D(v_i;), ω_G(v_i;), ω_T(v_i;), ω_L(v_i;)] is the matrix containing all six sparse representation vectors for all six cortical attributes, and it is composed of two matrices, P and Q. The first term in Equation 1 is a fitting error for multitask representation of all cortical attributes. It encourages each constructed attribute D_Mj(v_i,) ω_j to be similar to each respective ${\widehat{p}}_{M_j}^{(m)}$ (v_i). The second term is the group-wise sparsity regularization term. ||P||∞, ₁ is a combination of both L_∞ and L₁ norms, while L_∞ is first imposed on each row vector of P and then L₁ is for getting sparse rows. This regularization term encourages similar sparse patterns across different cortical attribute representations. For different cortical attributes, this regularization term will lead the matrix P to having sparsely nonzero rows. Therefore, the consistent columns from different cortical attribute dictionaries are selected for representing the atlas. The third term is the element-wise sparsity component, to handle the potential noise included in the data that cannot be group-wise represented. Equation 2 constrains the relationship of W with P and Q. With this modeling, we can impose group-wise sparsity through P to preserve the consistency across six cortical attributes and handle the potential noises in cortical attributes through Q. ρ₁ and ρ ₂ are the two nonnegative parameters used to balance different terms.

By solving the above optimization problem using the multitask learning via structural regularization (Zhou, Chen, & Ye, 2011) package, all the cortical attributes on the atlas patch centered at vertex v_i; are jointly represented via the estimated representation coefficient matrix W, as illustrated in Figure 5. Using the above group-wise sparsity constraint, different cortical attributes at the same location of the atlas can share similar sparsity structure in their respective representations. Thus, the consistency across six cortical attributes can be preserved.

FIGURE 5.

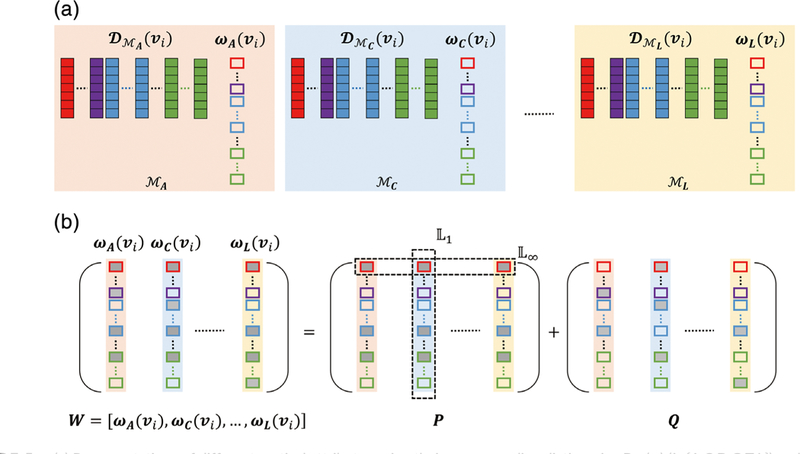
(a) Representations of different cortical attributes using their corresponding dictionaries D_Mj(v_i) (jϵ{A,C,D,G,T,L}) and sparse representation vectors ω_j (jϵ{A,C,D,G,T,L}). (b) Multitask sparse representation using the dirty model. W contains all sparse representation vectors [ω_j] for all cortical attributes, and it is composed of two matrices, P and Q. The matrix P is imposed with group-wise sparsity, to ensure sharing of similar sparsity structure for different cortical attributes. The matrix Q is imposed with element-wise sparsity

Notably, the use of nonoverlapping patches could lead to steep gradient changes along patch boundaries and also cause spatially inconsistent cortical attributes across nearby patches. To alleviate this issue, patches are overlapped during the atlas construction. Therefore, each vertex on the atlas will be covered by multiple patches, and thus have multiple representation results. To fuse these representation results, we simply average them to obtain the final cortical attribute for the atlas.

It is worth noting that during the implementation, we update the selection of top M typical highly correlated patches in an iterative manner. At the first iteration, we use the mean patch of all corresponding patches after registration to select the top M highly correlated patches at a certain age. However, the mean patch may not be the optimal one. Therefore, after the atlas is constructed, we replace the mean patch with the patch on the constructed atlas to further select another group of top M highly correlated patches. This could further increase the reliability of the highly correlated patches selection.

3.5 |. Parcellations on 4D cortical surface atlases

After constructing the 4D infant cortical surface atlas, we provide it with parcellations to facilitate region-based analysis. In particular, we have warped the FreeSurfer parcellations (Desikan et al., 2006) and the recent HCP MMP parcellations (Glasser et al., 2016) onto the last time point (age) of our atlas, that is, 72-month-old atlas. The main motivation is that the 72-month-old surface atlas is more similar to those adult cortical surface atlases and thus can be well aligned. After this warping, we propagate the parcellations at 72-month-old to all other time points according to the established temporal correspondences across different time points (ages). Note that the FreeSurfer Desikan parcellation protocol partitions the cerebral cortex into 72 (36 for each hemisphere, including subcortical regions) regions based on the major cortical folds, where each of the parcellation regions is relatively large. Since the major and secondary cortical folds have been largely established at term birth (Hill et al., 2010), it is rational to apply the FreeSurfer parcellation protocol for infant brains. The MMP parcellation protocol parcellates the brain into 360 (180 for each hemisphere, not including subcortical regions) regions based on multimodality data (especially the functional connectivity and myelin content), and the parcellations are defined in the FreeSurfer space. This parcellation provides a more detailed reference for inspecting the brains. Therefore, we also warped it to our atlas to provide more detailed cortical region references. Since we also construct our atlas in the FreeSurfer space, the respective warpings have relatively high accuracy. Figure S5 in the Supporting Information shows the MMP parcellation on the original HCP atlas and also the warped MMP parcellation on our atlas. It can be seen that the region of interest (ROI) regions are quite consistently overlaid on the corresponding cortical surfaces.

4 |. EXPERIMENTAL RESULTS

To assess the quality of the constructed 4D cortical surface atlases, we have performed evaluations both visually and quantitatively (i.e., when applied for spatial normalization). For evaluating each cortical surface atlas at each age, besides comparing with the FreeSurfer adult atlas (Fischl, Sereno, Tootell, et al., 1999), we have also introduced the following five atlases for extensive comparison: (a) the one-step registration atlas, which is constructed by first coregistering all infant cortical surfaces (of all subjects at all ages) into the common space, and then averaging the cortical attributes of age-matched coregistered surfaces and (b) the two-step registration atlas, which is constructed by first coregistering cortical surfaces using the two-step registration strategy in Section 3.2. After that, we obtain two deformation fields for each surface and use them to bring each individual surface to a common space. Finally, we average the cortical attributes of all registered subjects at this specific age to generate the age-specific atlas. (c) the top M patch-based atlas, which is constructed by averaging the top M highly correlated patches extracted from the age-matched two-step co-registered cortical surfaces; (d) the independent sparse atlas, which is constructed by independent sparse representation of each cortical attribute and thus ignores the relationship across different cortical attributes; (e) the group-wise sparse atlas (our atlas), which is constructed by imposing the group-wise sparsity constraint when jointly representing different cortical attributes on the atlas.

When performing visual inspection, we mainly compare cortical attribute patterns in different atlases, and the atlases with sharp and clear attribute patterns are regarded as better atlases. When performing quantitative evaluation, we use different atlases as templates for spatial normalization of individual cortical surfaces. The atlases with sharp and clear cortical attribute patterns will lead to better spatial normalization performance. We have evaluated the spatial normalization performance in both cross-sectional and longitudinal settings. Also, based on the spatial normalization performance, we have chosen the best parameter setting for constructing our atlases. Note that the LGI computation is relevant to the neighborhood size on the cortical surface, so in this work we use the 20-ring neighborhood to compute the LGI, which can well characterize the local folding.

4.1 |. Visual inspection

4.1.1 |. Overall inspection

The left hemisphere of our constructed 4D infant cortical surface atlases at all ages are presented in Figures 6–7, and 8. Specifically, Figure 6 shows the sulcal depth, average convexity, curvature, and LGI of the constructed 4D atlases at all ages using the spherical representation surface. For better inspection of these cortical attributes, we have also mapped them on the average inner cortical surface as shown in Figure 7. Of note, the average inner cortical surface is obtained by averaging the corresponding 3D coordinates of each vertex from the coregistered cortical surfaces, which is more suitable for inspecting the local cortical folding. From Figures 6 and 7, at each age, we can see consistent cortical attributes, which provide different detailed views for inspecting infant cortical surfaces and their developments. In addition, longitudinally, we can see that the major cortical attribute patterns in terms of these four geometric cortical folding attributes are established at term birth and well preserved during the postnatal development. Specifically, the magnitudes of the average convexity, sulcal depth, and LGI increase considerably, whereas the magnitude of curvature decreases gradually. In Figure 8, we present cortical thickness and myelin content in both spherical surfaces and average inner surfaces, respectively. Meanwhile, we also present the equipped parcellations on the average inner surface. From Figure 8, it can be seen that the cortical thickness has a dramatic increase in the first postnatal year, while the myelin content increases gradually with the maturing of the brain.

FIGURE 6.

The constructed 4D infant cortical surface atlases of the left hemisphere, with different cortical attributes shown on the spherical surface. Numbers on the left denote the month(s) of age and the subjects number, with M indicating male, and F indicating female. (a) Sulcal depth. (b) Average convexity. (c) Curvature. (d) Local gyrification index (LGI)

FIGURE 7.

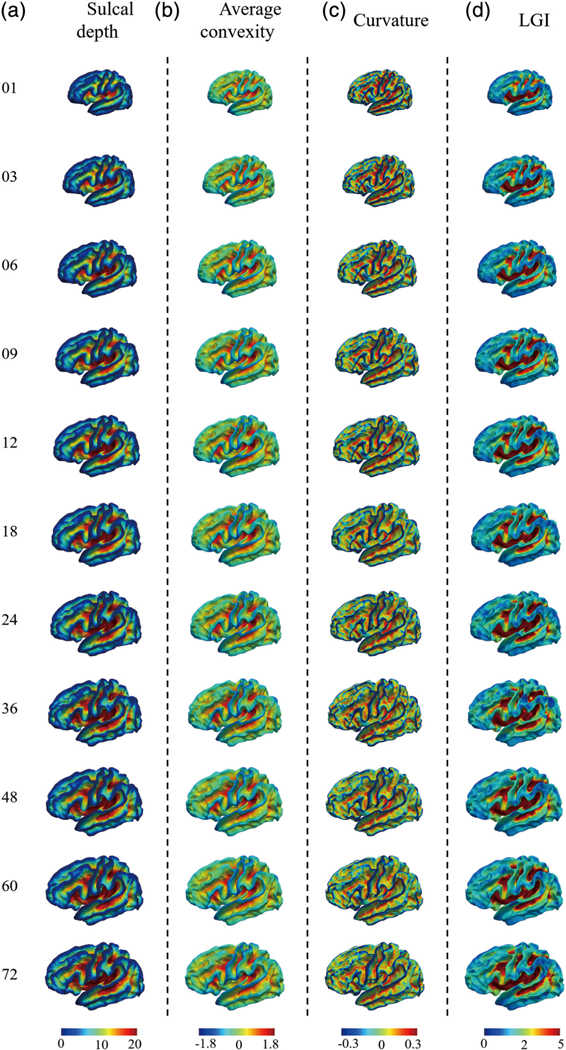
The constructed 4D infant cortical surface atlases of the left hemisphere, with different cortical attributes shown on the average inner cortical surface. Numbers on the left denote the month(s) of age. (a) Sulcal depth. (b) Average convexity. (c) Curvature. (d) Local gyrification index (LGI)

FIGURE 8.

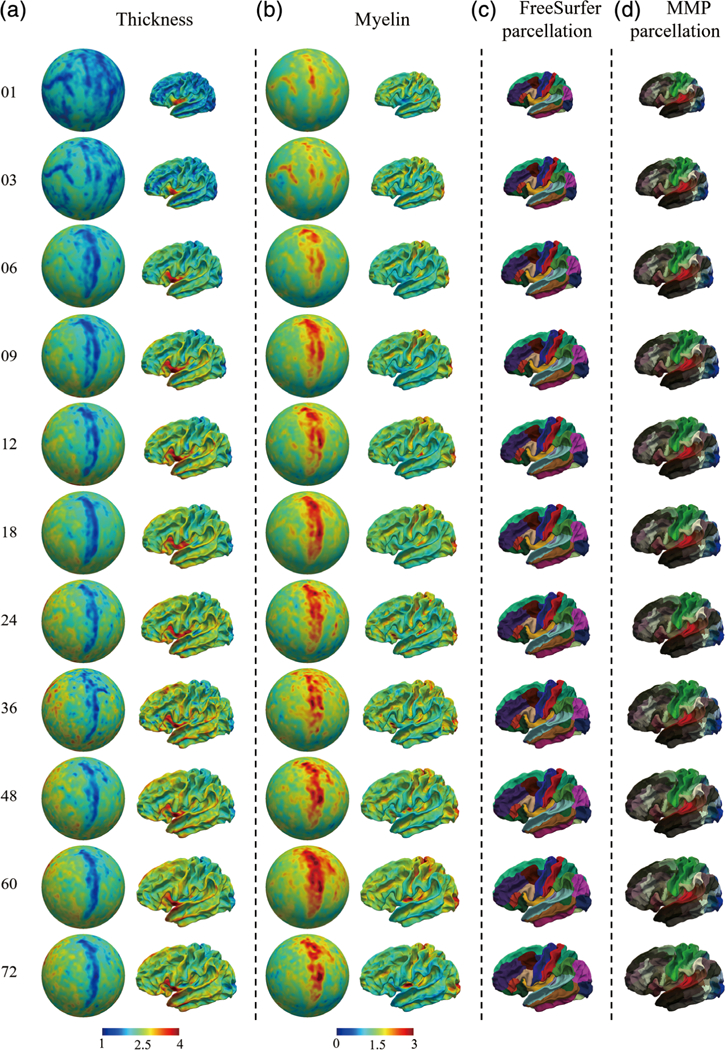
The constructed 4D infant cortical surface atlases of the left hemisphere, with thickness, myelin content, and equipped parcellations. Numbers on the left denote the month(s) of age. (a) Cortical thickness on spherical surfaces and average inner surfaces. (b) Myelin content on spherical surfaces and average inner surfaces. (c,d) The equipped FreeSurfer parcellations and Human Connectome Project multimodality parcellation parcellations, respectively

4.1.2 |. Cortical attribute pattern inspection

Generally, the cortical attribute patterns on the cortical surface atlases are mainly used for driving the spatial normalization of individual cortical surfaces. Since different cortical attributes differ from each other in their spatial scales, for example, the sulcal depth and average convexity can be regarded as a coarse scale for characterizing the cortical folding, while the curvature can be regarded as a fine scale. The cortical surface registration algorithm generally uses these cortical attributes in a coarse to fine manner. For example, the spherical demons uses the average convexity for a coarse alignment and then uses the curvature for a fine alignment. Therefore, the smooth cortical attribute pattern will generally degrade the registration accuracy and sharp cortical attribute pattern on the atlases is required. We have visually compared the sharpness of the registration related cortical attribute patterns on four atlases, that is, the two-step registration atlas, the top M patch-based atlas, the independent sparse atlas, and the group-wise sparse atlas. The reason we select these atlases for comparison is that they all adopted more appropriate cortical surface registration strategies, which helps preserve the longitudinal consistency of cortical attributes. In Figure 9, we show the zoomed-in cortical attribute patterns from two regions on the left hemispherical atlas at 12 months of age. The original region location in the inflated cortical surface is indicated by the red rectangle in the top. For better inspection, we use the inflated cortical surface since it can provide better geometric inspection. From the figures, it can be seen that the two-step registration atlas has the most ambiguous cortical attribute patterns, as indicated by the arrows, due to potential registration errors and substantial individual cortical attribute variations. Then, the top M patch-based atlas improves the sharpness of the cortical attribute pattern by filtering out the underlying atypical patches. However, the cortical attribute pattern is still unclear. Comparably, both the independent sparse atlas and the group-wise sparse atlas have better preserved cortical attribute patterns. This is benefited from two factors: (a) our dictionary construction strategy enables better tolerance to potential registration errors, and (b) sparse representation is relatively robust to outlier patches. By further comparing the cortical attribute patterns on the independent sparse atlas and the group-wise sparse atlas, it can be seen that patterns appear clearer on the group-wise sparse atlas, because the group-wise sparse constraint enables to take advantage of the implicit relationships among different cortical attributes. Moreover, for the group-wise sparse atlas, since the atlas patch is consistently represented by the patches from different cortical attribute dictionaries, it is less influenced by a certain cortical attribute once the attributes are obtained.

FIGURE 9.

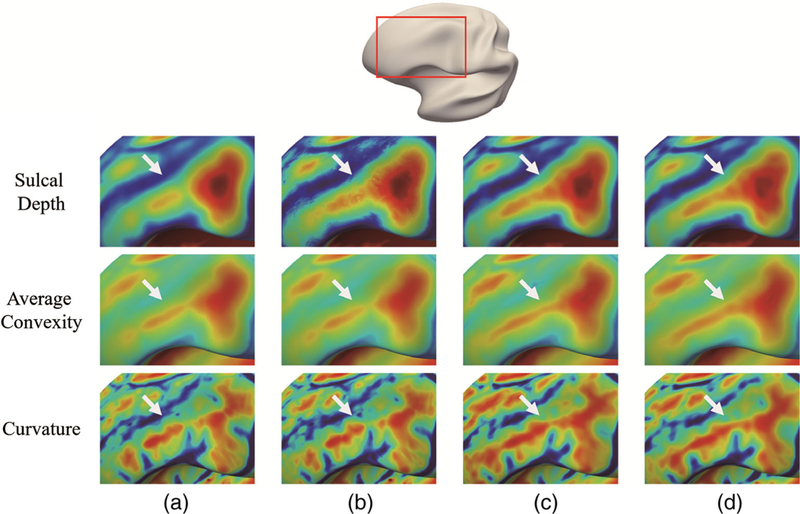
Comparison of zoomed cortical attribute patterns at one cortical region of 4 (12-month atlas, left hemispherical) comparison atlases. In the top of this figure, the original region location in the inflated cortical surface is indicated by the red rectangle. Each row shows the specific cortical attribute on different atlases. (a) Two-step registration atlas. (b) Top M patch-based atlas. (c) Independent sparse atlas.(d) Group-wise sparse atlas (our atlas)

4.1.3 |. Effectiveness of fusing representations of the overlapping patches representation

During the atlas construction, we use overlapped patches to capture local cortical attribute patterns. Therefore, for a local position on the atlas, there are multiple representation results that need to be fused. Two fusion strategies have been considered: (a) only use the local patch center’s representation without fusing the neighbors’ representation and (b) fuse the representations from all overlapping patches. To demonstrate the effectiveness of the fusion strategy in cortical surface atlas construction, we have compared the atlases with and without fusion strategies. For better investigation, we have mapped all six cortical attributes on both the inflated cortical surface and the average inner cortical surface. Note that, the inflated cortical surface can provide an overall inspection of the cortical surfaces, whereas the average inner cortical surface enables the detailed inspection of cortical attributes patterns. Figure 10 shows differences on one region of the cortical surface, as indicated by the red box in the top of Figure 10. Note that the two boxes on the inflated surface and the inner cortical surface indicate the same region. In Figure 10, each row corresponds to a specific cortical attribute; columns (a) and (c) show cortical attribute patterns with fusing the representations from overlapping patches on the inflated cortical surface and the average inner cortical surface, respectively, while Columns (b) and (d) show the corresponding cortical attribute patterns without fusing. From this figure, it can be seen that with the fusion strategy, we can get clearer and sharper cortical attributes patterns, compared to the cluttered patterns obtained without the fusion strategy.

FIGURE 10.

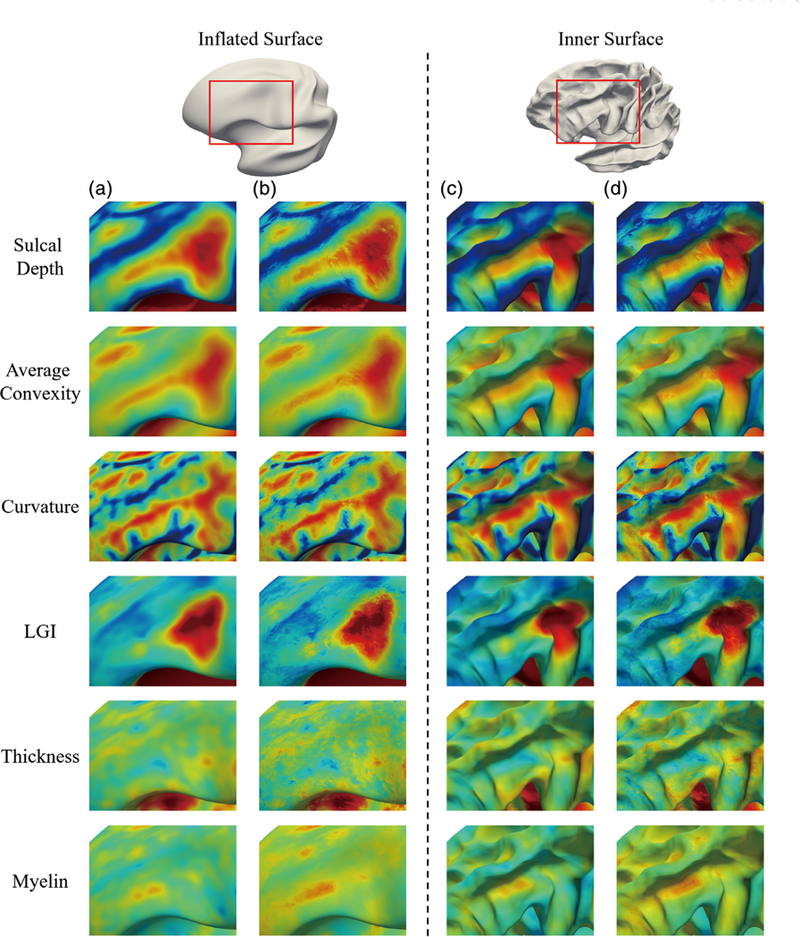
Comparison of the cortical attribute patterns with two different fusion strategies. The comparisons of patterns are demonstrated on the inflated and the average inner cortical surface, respectively. The red rectangles on the inflated and average inner cortical surfaces indicate the same zoomed region location. Each row corresponds to a specific cortical attribute. Columns (a) and (c) show the results with the second fusion strategy (proposed method), while (b) and (d) show results with the first fusion strategy (i.e., without fusion)

4.2 |. Quantitative evaluation of accuracy in cortical surface normalization

To quantitatively assess the constructed atlases, we have used them for spatial normalization of individual cortical surfaces. For evaluation, we uniformly divide all the cortical surfaces into three subgroups in a random manner at each age. Two subgroups are used as the training set for constructing the comparison atlases, while the third subgroup is used as the testing set (named as testing set 1) for evaluating the accuracy of spatial normalization. For more extensive validation, we also adopt an extra independent dataset (named as testing set 2), which has no subjects involved in the atlas construction; testing set 2 includes three time points, that is, 1, 12, and 24 months of age, and has images of 80 healthy subjects at each time point. The same pipe-line is used to generate the cortical surface for each (training/testing) subject at each age. For any individual cortical surface in the two testing sets, we register it onto the age-matched atlas using the spherical demons. If an atlas can better encode the cortical attributes and has sharper patterns, then the registration from each individual cortical surface to that atlas surface (driven by cortical attributes average convexity and curvature) is expected to be better. We have compared spatial normalization accuracy of six atlases, that is, the FreeSurfer adult atlas, the one-step registration atlas, the two-step registration atlas, the top M patch-based atlas, the independent sparse atlas, and the group-wise sparse atlas (our atlas).

Since there is no ground truth for the cortical surface registration, to quantitatively evaluate the accuracy of the spatial normalization at each age, we use the following four measurements: (a) the average information entropy of the sulcal and gyral regions of all aligned cortical surfaces; (b) the pairwise overlap of sulcal and gyral regions between each pair of subjects at each age (i.e., using Dice ratio [Dice, 1945]); (c) the average correlation coefficient of the average convexity maps between each pair of subjects; and (d) the average correlation coefficient of the curvature maps between each pair of subjects. Notably, the sulcal and gyral regions are determined by the signs of the average convexity attributes (Fischl, Sereno, & Dale, 1999) of the cortical surface. The sulcal region corresponds to the vertices with positive average convexity value, whereas the gyral region corresponds to the vertices with negative average convexity value. Therefore, for any cortical surface, we can easily obtain its sulcal and gyral regions. Then, for all the aligned cortical surfaces, at each local vertex v, we can compute the ratio of subjects belonging to the gyral or sulcal region. Finally, the average information entropy can be calculated as:

$$H=\frac{1}{\left|V\right|}\sum _{v\in V}\left(-p_{\text{sulci}}(v){\log }_2{p}_{\text{sulci}}(v)-p_{\text{gyri}}(v){\log }_2{p}_{\text{gri}}(v)\right)$$

where | V | is the vertex number, and p_sulci(v) and p_gyri(v) are the ratios of subjects belonging to the sulcal or gyral region at the given vertex v, respectively. Previously, this measurement has been used for evaluating the cortical surface registration performance (Lyttelton et al., 2007). Meanwhile, once the sulcal and gyral regions are determined, the Dice ratio for measuring the overlap of sulcal and gyral regions for any two aligned cortical surfaces in the testing set can be obtained. The correlation coefficient of the average convexity (or curvature) maps can be computed as the Pearson correlation coefficient for any pair of the aligned cortical surfaces in the testing set, and then the average of all pair-wise correlation coefficients can be used as the correlation coefficient for the whole testing set. Based on these four measurements, the atlas with sharp cortical attributes patterns is expected to have lower average information entropy value, higher Dice ratio for sulcal/gyral region, and higher correlation coefficient.

Table 2 reports the average information entropy of the sulcal and gyral regions after aligning the individual cortical surfaces of the two testing sets onto each of the comparison atlases. As can be seen, the FreeSurfer adult atlas gets the highest average information entropy for the two testing sets (i.e., 0.466 for the testing set 1 and 0.489 for the testing set 2), indicating the inappropriateness of using it for infant cortical surface normalization. The one-step registration atlas achieves better results (i.e., 0.428 for the testing set 1 and 0.473 for the testing set 2) than the FreeSurfer adult atlas, mainly due to the use of the infant data for the atlas construction. However, as we mentioned, the one-step registration atlas ignores the within-subject cortical attributes constraints during the registration, and, as can be seen from Table 2, the performance is inferior to the two-step registration atlas (i.e., 0.391 for the testing set 1 and 0.445 for the testing set 2). Since the top M patch-based atlases filtered out the patches with poor agreement to the population, it can achieve slightly better performance (i.e., 0.389 for the testing set 1 and 0.443 for the testing set 2) than the two-step registration atlas. While due to the better preservation of the cortical attribute patterns on the atlas, the registration accuracies of the independent sparse atlas (i.e., 0.378 for the testing set 1 and 0.433 for the testing set 2) and the group-wise sparse atlas (i.e., 0.378 for the testing set 1 and 0.432 for the testing set 2) are further improved. This indicates that the cortical attribute patterns of the infant population can be better captured by the use of sparse representation. Comparing the independent sparse atlas with the group-wise sparse atlas (our atlas), they achieve similar average information entropy, while the group-wise sparse atlas achieves a slightly better performance. Using the pairwise t test, we have further validated whether the atlas constructed by the group-wise sparse representation had statistically significant registration performance improvement over the other comparison atlases when aligning new subjects. Our group-wise sparse atlas achieves statistically significant improvement over the atlases constructed by the FreeSurfer, one-step registration, two-step registration, and also the top M patch-based method (with all p values smaller than .05). While comparing to the atlas constructed by the independent sparse representation, the registration performance improvement is not statistically significant.

TABLE 2.

The average information entropy on two testing sets

Data set Age (months)	Testing set 1											Testing set 2
	01	03	06	09	12	18	24	36	48	60	72	01	12	24
FreeSurfer	0.421	0.416	0.47	0.487	0.495	0.494	0.479	0.441	0.477	0.505	0.445	0.472	0.504	0.49
One-step registration	0.451	0.413	0.436	0.489	0.491	0.428	0.371	0.364	0.425	0.437	0.401	0.459	0.498	0.463
Two-step registration	0.405	0.397	0.394	0.397	0.389	0.401	0.368	0.342	0.409	0.415	0.38	0.431	0.445	0.458
Top M patch-based	0.403	0.394	0.394	0.396	0.386	0.398	0.363	0.341	0.408	0.413	0.378	0.432	0.441	0.455
Independent sparse	0.401	0.391	0.39	0.393	0.381	0.398	0.356	0.297	0.408	0.402	0.344	0.419	0.439	0.442
Group-wise sparse	0.401	0.39	0.39	0.393	0.381	0.398	0.356	0.297	0.407	0.402	0.344	0.419	0.439	0.441

Figure 11 presents the Dice ratios of the sulcal and gyral regions between each pair of subjects at each age on the two testing sets. It can be seen that, at each age of the two testing sets, the independent sparse atlas and the group-wise sparse atlas consistently achieved higher Dice scores for both sulcal and gyral regions than the other comparison atlases. For the sulcal regions, the independent sparse atlas and the group-wise sparse atlas achieve statistically significant higher Dice scores than the two-step registration atlas (i.e., p = .0002 for the independent sparse atlas, and p = .0001 for the group-wise sparse atlas) and the top M patch-based atlas (i.e., p = .0012 for independent sparse atlas, and p = .0006 for the group-wise sparse atlas). For the gyral regions, they also achieved statistically significant improvement in Dice score, compared to the two-step registration atlas (i.e., p = 2e-5 for the independent sparse atlas, and p = 7e-6 for the group-wise sparse atlas) and top M patch-based atlas (i.e., p = 1e-5 for the independent sparse atlas, and p = 5e-6 for the group-wise sparse atlas). Compared to the independent sparse atlas, the group-wise sparse atlas has slightly higher average Dice scores in both sulcal (0.812 vs. 0.810) and gyral regions (0.825 vs. 0.824), but not statistically significant.

FIGURE 11.

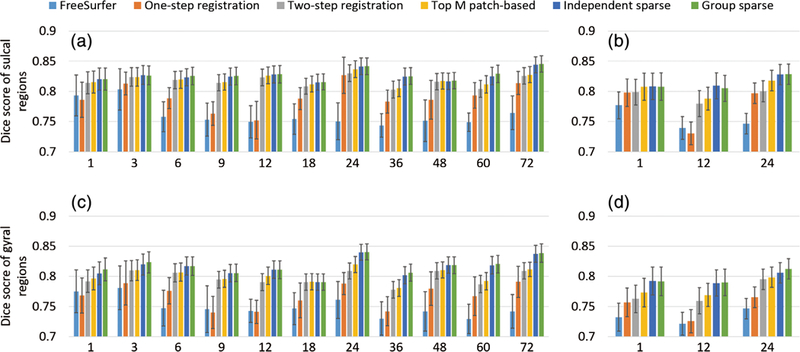
Comparison of Dice scores in the sulcal and gyral regions for the six comparison atlases at different ages, using two testing sets. (a,c) The sulcal and gyral Dice scores on the testing set 1, respectively. (b,d) The sulcal and gyral Dice scores on the testing set 2, respectively

In addition, Figure 12 presents the correlation coefficients of the average convexity maps between each pair of the normalized subjects at each age, using the two testing sets. Similarly, Figure 13 presents the correlation coefficients of the curvature maps, using the two testing sets. Larger correlation coefficients indicate better spatial normalization accuracy. From these two figures, it can be seen again that the independent sparse atlas and the group-wise sparse atlas clearly outperform other atlases. Also, compared to the independent sparse atlas, the group-wise sparse atlas achieves slightly better average convexity correlation (0.792 vs. 0.791) and average curvature correlation (0.357 vs. 0.356), while not statistically significant.

FIGURE 12.

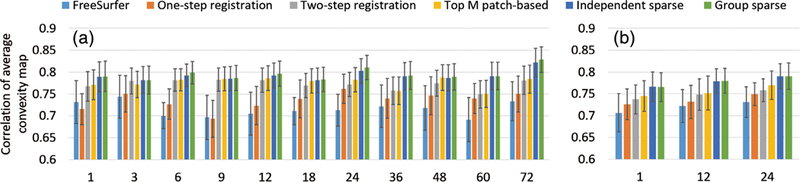
Comparison of correlation coefficients of the average convexity maps for the six comparison atlases at different ages, using (a) testing set 1 and (b) testing set 2

FIGURE 13.

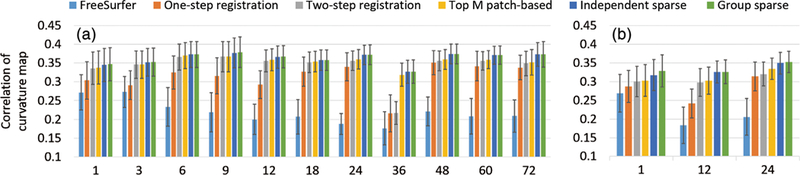
Comparison of correlation coefficients of the curvature maps for the six comparison atlases at different ages, using (a) testing set 1 and (b) testing set 2

From the above comparisons, we can see that the sparse representation can better preserve cortical attribute patterns on the atlas, since it is more robust to the cortical attribute noises, which leads to better spatial normalization accuracy compared to other atlas construction methods. The group-wise sparse representation achieves slightly better but not statistically significant performance improvement than the independent sparse representation. The main advantage is the group-wise representation helps to provide multiple different detailed views for inspecting the infant cortical surfaces and their development.

4.3 |. Quantitative evaluation of temporal consistency of cortical surface normalization

Besides evaluating the spatial normalization accuracy, we also quantitatively evaluate the temporal consistency when aligning the longitudinal cortical surfaces onto the age-matched atlas. To this end, we use multiple measurements, including the aforementioned Dice ratio of the sulcal and gyral regions, correlation coefficients of the average convexity maps, and correlation coefficients of the curvature maps. We define the following longitudinal consistency degree of sulcal and gyral regions for the normalized longitudinal cortical surfaces:

$$C=\frac{1}{\left|V\right|}\sum _{v\in V}\left(1-\frac{\alpha (v)}{T-1}\right)T>1$$

where α(v) is the accumulated time that the vertex label (sulcal or gyral vertex) changes between each pair of neighboring time points, and T is the available longitudinal scan number for a certain subject. Of note, for this measurement, we need at least two time points, that is, T >1. Ideally, after registration, C should be close to 1. Larger C value indicates better temporal consistency of the normalized cortical surfaces. In this evaluation, we did not use the testing set 2 because it is not a longitudinal testing set.

Table 3 reports the mean and SD of each temporal consistency measurement for the six comparison atlases. From this table, it can be seen that the atlases constructed using the infant data achieves better temporal consistency than the FreeSurfer adult atlas. Also, the atlases constructed using the two-step registration (including the two-step registration atlas, the top M patch-based atlas, the independent sparse atlas, and the group-wise sparse atlas [our atlas]) achieve better consistency than the one-step registration atlas. The reason is that they adopt more suitable registration strategies, which help preserve temporal consistency for the constructed 4D atlases.

TABLE 3.

Temporal consistency measurements on testing set 1

Measurement	Consistency	Sulcal Dice score	Gyral Dice score	Average convexity correlation	Curvature correlation
FreeSurfer	0.878 ± 0.016	0.857 ± 0.023	0.852 ± 0.022	0.884 ± 0.041	0.641 ± 0.076
One-step registration	0.908 ± 0.017	0.889 ± 0.023	0.884 ± 0.023	0.916 ± 0.039	0.675 ± 0.074
Two-step registration	0.921 ± 0.015	0.899 ± 0.022	0.895 ± 0.021	0.928 ± 0.037	0.694 ± 0.071
Top M patch-based	0.921 ± 0.014	0.900 ± 0.022	0.896 ± 0.021	0.926 ± 0.038	0.697 ± 0.069
Independent sparse	0.922 ± 0.014	0.901 ± 0.021	0.897 ± 0.020	0.929 ± 0.036	0.701 ± 0.067
Group-wise sparse	0.922 ± 0.014	0.901 ± 0.021	0.898 ± 0.020	0.930 ± 0.035	0.703 ± 0.066

5 |. DISCUSSION

5.1 |. Cortical surface registration

Cortical surface registration plays an important role in the cortical surface atlas generation. It normalizes the variation across individual cortical surfaces and establishes the correspondence among them. However, the cortical surface variations exist in two aspects, that is, structural variation and functional variation. Ideally, the registration successfully normalizes both variations. Unfortunately, although they are highly correlated (Fischl et al., 2007; Van Essen et al., 1998), the structural variation and the functional variation are heterogeneous, that is, good structural normalization does not necessarily indicate good functional normalization (Frost & Goebel, 2012; Glasser & Van Essen, 2011). Most existing cortical surface registration methods (Charon & Trouvé, 2013; Durrleman, Pennec, Trouvé, & Ayache, 2009; Fischl, Sereno, Tootell, et al., 1999; Lombaert, Grady, Polimeni, et al., 2011; Lombaert, Sporring, & Siddiqi, 2013; Robbins et al., 2004; Tardif et al., 2015; Vaillant & Glaunès, 2005; Yeo et al., 2009) mainly normalize structural variation. One recent method (Robinson et al., 2014) tried to consider both variations in a uniform framework by incorporating the fMRI data to drive the functional normalization.

In this work, we mainly focus on the structural atlas construction. Therefore, we adopt the cortical folding attributes, mainly the average convexity map and the mean curvature map, to drive the spherical Demons registration in a hierarchical manner (Yeo et al., 2009). The average convexity map is used to roughly align the cortical folding, and then the mean curvature map is used to finely align the cortical folding. When constructing the atlases, we did not specify any new cost function or optimization method for the registration. Instead, we use the conventional cost, optimization, and parameters in spherical Demons to make the registration accuracy less reliant on the specific cost function or optimization method when aligning new cortical surfaces onto our atlas. However, it is worth noting that more advanced registration could lead to further improved atlas construction. In addition, we also need to point out that the good alignment of the cortical folding attributes does not necessarily mean the good alignment of the noncortical folding attributes, for example, the myelin content. For the noncortical folding attributes, incorporating them into registration would improve their alignment. Since the focus of our atlas is mainly on the folding alignment, we have not incorporated nonfolding attributes into the current registration method. This will be done in our future work, since our atlas construction framework can be directly extended by using registration methods driven by multimodal data, such as myelin content or functional cortical attributes.

5.2 |. Robustness to missing data

There are missing data in our dataset because not all subjects are able to be scanned at each scheduled time point. Although various methods have been proposed to handle the missing data (Meng et al., 2017), the missing data itself is not the focus of this work. Our atlas construction framework is less influenced by the missing data due to two main reasons:

1. The registration is less influenced by missing data. Note that, in our method, all cortical surfaces of different time points of the same subject are group-wise registered into the within-subject common space, followed by group cross-subject registration among all within-subject mean images of all subjects. During the within-subject registration, the bias has been greatly suppressed, and the estimation of the within-subject mean does not rely on certain cortical surface at specific time point. Therefore, the final registration is less influenced by the missing data.

2. The dictionary construction is less influenced by missing data since it does not rely on specific subjects. Therefore, the final representation will also not rely on specific subjects at certain time points, which preserves the unbiasedness on subjects.

We have adopted the 6-month-old cortical surfaces to validate the robustness of the constructed atlas, since we have the most (total of 41) subjects at this time point. We first randomly separate these subjects into two groups. For each group, we can use the proposed method to construct the atlas. Then, we can compute the difference between these constructed atlases. We repeated the experiments 10 times. Figure 14 shows the visualized vertex-wise SD of these constructed atlases. From the figure, it can be seen that the constructed atlas is stable in the aspect of a low SD.

FIGURE 14.

Vertex-wise SD of the atlases with different groups of subjects

5.3 |. Applications

One assumption of our atlas construction method is that the cortical attributes from all registered cortical surfaces follow a single Gaussian-like distribution, and therefore the mean of the cortical attributes is meaningful for representing the population attributes. To verify this assumption, for a certain cortical attribute (e.g., average convexity, curvature, sulcal depth, and LGI) at a local position, we use the Anderson–Darling test (Stephens, 1974) to check whether the cortical attribute at this local position follows a single variate Gaussian distribution, especially for the top M highly correlated patches. Of note, we care about these attributes since the cortical surface registration is driven by them. We reported the vertex-wise hypothesis testing result in Table 4 for these cortical attributes from the typical patches at each time point, with each entry indicates the ratio of vertices that follows the normal distribution. From this table, we can see that cortical attributes at majority vertices can be regarded as following the Gaussian distribution. Therefore, it is rational to get the representation target (the population cortical attributes) through the mean operation. However, as more data are available for a certain time point, a single atlas may not be enough for representing the entire population for that time point due to the substantial cortical attribute variation. Therefore, we will try to build multiple cortical surface atlases with bigger datasets in the future.

TABLE 4.

The ratio of vertices that follows the Gaussian distribution for different cortical attributes at different time points

Months of age	01	03	06	09	12	18	24	36	48	60	72
Average convexity	0.93	0.93	0.91	0.93	0.93	0.91	0.96	0.97	0.95	0.95	0.96
Curvature	0.91	0.91	0.89	0.9	0.9	0.89	0.94	0.96	0.93	0.93	0.95
Sulcal depth	0.88	0.91	0.89	0.93	0.93	0.91	0.93	0.93	0.9	0.91	0.93
LGI	0.89	0.89	0.89	0.91	0.9	0.89	0.94	0.95	0.93	0.93	0.94

Abbreviation: LGI, local gyrification index.

The infant cortical surface atlases constructed in this work are different from the traditional volumetric infant atlases (Evans et al., 2012), since they respect and leverage the inherent 2D topology of the highly convoluted and geometrically complex cortical surfaces. Comparing to the analysis directly using the volumetric atlas, the cortical surface atlas is more suitable for the highly folded cerebral cortex with a sheet-like structure (Fischl, Sereno, Tootell, et al., 1999; Glasser et al., 2016; Hill et al., 2010; Li, Wang, Yap, et al., 2019; Van Essen & Dierker, 2007), especially for cortical thickness, myelination, and functional connectivity.

Our infant dedicated longitudinal 4D cortical surface atlases has two main advantages: (1) it preserves sharper cortical attribute pattern on the atlas, which leads to better spatial normalization for the infant cortical surfaces and (2) it contains a set of densely sampled atlases along with temporal correspondence from neonates to 6-year-olds, thus facilitating the infant brain development analysis. Specifically, aligning individual infant cortical surfaces to our age-matched atlas, rather than adult or infant atlases that neglect dynamic brain growth, would achieve better registration accuracy, as shown in experimental results. In addition, with two commonly used parcellations, that is, the FreeSurfer and the MMP parcellation, our atlases are usable for the ROI-based analysis. It is worth noting that our current parcellations are based on the adult brain parcellation protocol. As more infant data are available, it is desired to develop infant dedicated parcellation protocols to better characterize infant cortical surface anatomy.

5.4 |. Conclusion and future works

In this article, we have constructed a set of 4D infant cortical surface atlases based on 339 longitudinal MRI scans (covering 11 time points at 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months of age) from 50 healthy infants, for characterizing dynamic early postnatal brain development. By using a dedicated two-stage cortical surface registration strategy, we can better establish longitudinal correspondences across both time and subjects. By formulating the atlas construction as a sparse representation problem, we can preserve sharp cortical attributes patterns on our atlas. By jointly representing all cortical attributes with group-wise sparsity constraint, we can further achieve the consistency across different cortical attributes on the constructed atlas. With all these strategies, we constructed 4D infant cortical surface atlases which can provide comprehensive views for describing the cerebral cortex development over the first 72 months of life. To further facilitate ROI-based analysis, we have also equipped our constructed 4D infant cortical surface atlases with the two widely used parcellations, that is, the FreeSurfer parcellations and the HCP MMP parcellations. In the future, we will incorporate multimodal data to improve registration accuracy and model the atlas construction in a way that is more robust to registration errors, such as the Wasserstein barycenter modeling. Meanwhile, we will also develop infant dedicated parcellation protocols with the help of expert neurologists as more data becomes available. Our 4D infant cortical surface atlases will be released to the public to further research in this field.