Abstract
The auditory hair cell resting potential is critical for proper translation of acoustic signals to the CNS, because it determines their filtering properties, their ability to respond to stimuli of both polarities, and, because the hair cell drives afferent firing rates, the resting potential dictates spontaneous transmitter release. In turtle auditory hair cells, the filtering properties are established by the interactions between BK calcium-activated potassium channels and an L-type calcium channel (electrical resonance). However, both theoretical and in vitro recordings indicate that a third conductance is required to set the resting potential to a point on the ICa and IBK activation curves in which filtering is optimized like that found in vivo. Present data elucidate a novel mechanism, likely universal among hair cells, in which mechanoelectric transduction (MET) and its calcium-dependent adaptation provide the depolarizing current to establish the hair cell resting potential. First, mechanical block of the MET current hyperpolarized the membrane potential, resulting in broadband asymmetrical resonance. Second, altering steady-state adaptation by altering the [Ca2+] bathing the hair bundle changed the MET current at rest, the magnitude of which resulted in membrane potential changes that encompassed the best resonant voltage. The Ca2+ sensitivity of adaptation allowed for the first physiological estimate of endolymphatic Ca2+ near the MET channel (56 ±11μM), a value similar to bulk endolymph levels. These effects of MET current on resting potential were independently confirmed using a theoretical model of electrical resonance that included the steady-state MET conductance.
Keywords: resting potential, mechanoelectric transduction, auditory hair cells, calcium, adaptation, electrical resonance
Introduction
Spontaneous activity in auditory primary afferent neurons enables nonrectified stimulus coding. Because spontaneous activity results from continuous hair cell transmitter release, it requires that the hair cell resting potential be depolarized to activate the voltage-dependent calcium current that drives exocytosis (Robertson and Paki, 2002; Schnee et al., 2005). Maintaining a depolarized resting potential requires overcoming the outward conductances of the basolateral membrane (Hudspeth and Lewis, 1988a; Holt and Eatock, 1995; Jorgensen and Kroese, 2005). One source of depolarization comes from deflection of the sensory hair bundle, which regulates the open probability of mechanically gated channels and therefore the amount of depolarizing mechanoelectric transduction (MET) current (Ohmori, 1985; Crawford et al., 1989). For nonrectified representation of both positive and negative bundle deflections, critical for processing periodic stimuli, the resting open probability of the MET channels must be more than zero. It has been proposed that the inward MET current associated with a nonzero resting open probability should depolarize the hair cell resting potential (Hudspeth and Lewis, 1988b; Wu et al., 1995; Jorgensen and Kroese, 2005). The resting open probability of the channel is established by Ca2+- dependent adaptation of the MET machinery (Eatock et al., 1987; Crawford et al., 1991; Assad and Corey, 1992; Ricci and Fetti-place, 1998). Present data test the hypothesis that Ca2+- dependent adaptation is capable of generating a steady-state MET current that appropriately depolarizes the hair cell resting potential.
The endolymph solution bathing the sensory hair bundle contains potassium as the monovalent charge carrier with divalent ions maintained very low: magnesium being undetectable and [Ca2+ ranging in mammalian taxa (and cochlear position) from 17 to 41 μM (Sterkers et al., 1988; Salt et al., 1989). In turtle, measures of bulk endolymph [Ca2+] are ∼65 μM (Crawford et al., 1991). However, because the ionic composition of endolymph affects transduction [e.g., by maximizing MET current and Ca2+ permeation of the channel; (Ricci and Fettiplace, 1998)], understanding the function of endolymph requires estimates of the [Ca2+] near the channel. Knowing the [Ca2+] near the MET channel is particularly important because of its multiple functions in MET. Calcium blocks the channel with a half blocking dose of 1 mM (Ricci and Fettiplace, 1998). Calcium also permeates the channel in which it modulates at least two forms of MET adaptation (Ohmori, 1985; Crawford et al., 1989, 1991; Lumpkin et al., 1997; Ricci et al., 1998; Wu et al., 1999). Complicating interpretation of bulk endolymph Ca2+ concentrations is the high density of Ca2+ ATPases in the stereocilia, which may create an increasing [Ca2+] gradient near the MET channel and thus make a more localized [Ca2+] estimate essential (Lumpkin and Hudspeth, 1998; Yamoah et al., 1998). To this end, present work provides a functional assay of endolymph [Ca2+] by examining the response of Ca2+-sensitive mechanisms near the channel. Using voltage- and current-clamp recordings in turtle auditory hair cells, endolymphatic [Ca2+] was estimated by identifying the concentration that sets the resting potential to the voltage at which hair cell filtering and sensitivity are best. The data show that a low (56 ± 11 μM) concentration of endolymphatic Ca2+ is required to maintain a depolarized resting potential, a value comparable with previous estimates of bulk endolymph [Ca2+].
Materials and Methods
Tissue preparation
The turtle (Trachemys scripta elegans) auditory papilla preparation, stimulation, and recording procedures have been described in detail previously (Crawford and Fettiplace, 1985; Ricci and Fettiplace, 1997). All surgical procedures were approved by the Animal Care and Use Committee at Louisiana State University Health Sciences Center. One of two procedures was used to dissect individual auditory papilla from the turtle half head. The first dissection procedure used a solution containing the following (in mm): 126 NaCl, 0.5 KCl, 2.8 CaCl2, 2.2 MgCl2, 2 Na pyruvate, 2 ascorbate, 6 glucose, and 10 NaHEPES, pH 7.6 (275 mOsm). To expose the hair bundles, the tectorial membrane was removed using an etched tungsten wire after treatment with protease type XXIV (Sigma, St. Louis, MO) at 0.02– 0.04 mg/ml for 5–20 min. Rather than enzyme, the second procedure used high divalent 10 mm [Mg+2], 10 mm [Ca2+] (275 mOsm), and high osmolarity (375 mOsm, high divalent increased with sucrose) solutions to loosen the tectorial membrane (Shah et al., 1995). Tissue was incubated in the high divalent solution for 10 min, followed by 5 min in a high divalent, high osmolarity solution. No differences in responses were observed between methods. The trimmed papilla was mounted in a Plexiglas recording chamber on an upright fixed stage microscope (BX51; Olympus Optical, Tokyo, Japan). The chamber was perfused with a solution containing the following (in mm): 126 NaCl, 0.5 KCl, 2.8 CaCl2, 2.2 MgCl2, 2 Na pyruvate, 2 ascorbate, 6 glucose, and 10 Na HEPES, pH 7.6. To adjust apical [Ca2+], a perfusion pipette (∼15 μm tip diameter) coupled to a Parker Picospritzer II was placed within 20 μm of the hair bundle, perpendicular to its axis of sensitivity, allowing for rapid solution exchange around the bundle (<1 s) (see Fig. 2). Because of a change in diffraction, the perfusion flow could be observed, ensuring its position encompassed the bundle. To more closely mimic physiological conditions, the apical perfusion contained the following (in mm): 130 KCl, 2 Na pyruvate, 2 ascorbate, 6 glucose, and 10 HEPES (and varying [CaCl2] from 20 to 200 μm). The Ca2+ concentration was measured using a calibrated (standards of World Precision Instruments, Sarasota, FL) Microelectrode MI-600 Ca2+ electrode (Bedford, NH). Measurements of the steady-state MET with 2.8 mm Ca2+ were made when the bundles were bathed with the standard chamber solution.
Figure 2.
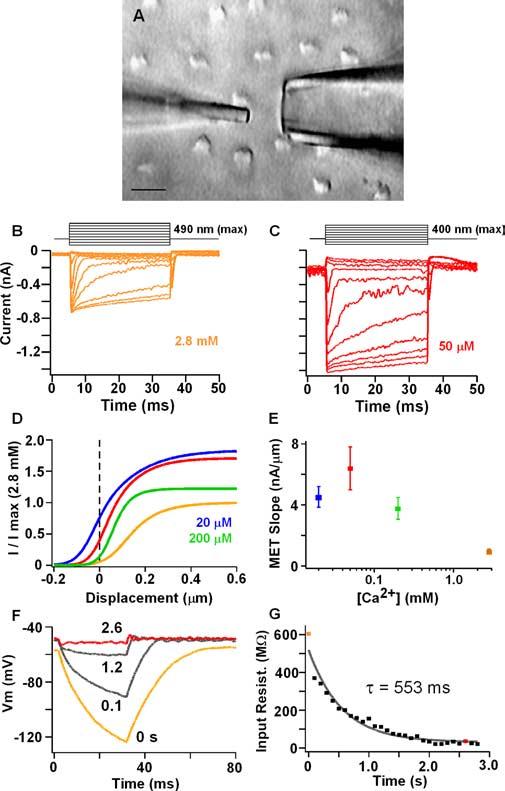
A, Apical view of hair bundles along reticular lamina. Tectorial membrane removed. Bottom is neural edge. Tip of stiff glass probe (left) rests on the side of the hair bundle opposite the kinocilium. Perfusion pipette is to the right at 90° to the axis of bundle sensitivity. Scale bar, 10 μm. B, C, Activation of MET current in 2.8 mm and 50 μm apical Ca2+ for a series of mechanical steps; stimuli are shown at the top (upward stimuli toward kinocilium). D, Mechanical activation curves calculated from mean Boltzmann fits for four apical [Ca2+]. Curves are scaled to that for 2.8 mm apical Ca2+. Low Ca2+ reduced channel block (increased peak current) and shifted the curve to the left, which increased the amount of current at rest. Boltzmann parameters (a1, a2, x1) are as follows: 2.8 mm,16 ± 11, 10 ± 3, and 0.54 ± 1; 200 μm, 20 ± 22, 21 ± 15, and 0.3 ± 0.5; 50μm,24 ± 21, 10 ± 4, and 0.2 ± 0.4; and 20μm,21 ± 5, 8 ± 0.5, and −0.03 ± 0.5. Units for a1 and a2 are in nanoamperes per nanometers; x1 is in nanometers. Peak MET current near resting potential in 2.8 mm was 692 ± 224 pA. E, Mean ± SE linear slopes of MET current– displacement response around 0 displacement (±25 nm). F, Membrane response to −110 pA current step injection during change in apical Ca2+ from 2.8 mm to 50 μm. Time after perfusion start noted near each trace. G, Change in input resistance versus time after perfusion start. Colored points represent different [Ca2+] as above.
Mechanical stimulation
Hair bundles were mechanically stimulated with a stiff glass fiber, shaped to a 1 μm diameter (MF 830 polisher; Narishige, Tokyo, Japan) and fixed to a piezoelectric bimorph. The fiber tip was placed on the hair bundle just above the row of shortest stereo-cilia. Deflections toward and away from the kinocilium opened and closed MET channels, respectively. The movements of the fiber was driven with voltage steps from Signal Software using a power CED 1401 analog-to-digital interface (Cambridge Electronics Design, Cambridge UK) and filtered at 1–5 kHz giving rise times of ∼200 μs. The system captured MET current and membrane potential recordings (20 kHz sample rate). Movement was calibrated with a dual photodiode system as described previously (Crawford and Fettiplace, 1985).
Recording
Whole-cell voltage- and current-clamp recordings were made using a Heka Elektronik (Lambrecht/Pfalz, Germany) EPC 8 amplifier attached to borosilicate patch electrodes (1.5 mm outer diameter) filled with the following (in mm): 101 KCl, 2.5 MgCl2, 3 MgATP, 5 creatine phosphate, 10 NaHEPES, 1 Na pyruvate, 2 ascorbate, and 5 EGTA, pH 7.2. Based on perforated-patch recordings of MET and BK currents in high-frequency turtle auditory hair cells, endogenous buffering is equivalent to 4.6 –7.1 mm EGTA (Ricci et al., 1998, 2000). Series resistance averaged 6.9 ± 2.7 MΩ (n = 46 cells) after compensation. Cell capacitance was 13 ± 2 pF, giving voltage-clamp speeds of <100 μs. A junction potential of −4 mV was corrected off-line. Leak currents were measured near resting potential in 2.8 mm CaCl2 while MET channels were mechanically closed. Cells with >44 pA leak were excluded. The mean leak was 14 ± 13 pA (n = 46). At a −80 mV holding potential, the maximum MET current (i.e., for saturating bundle displacement in 2.8 mm apical Ca2+) was 798 ± 157 pA (n = 46).
Responses shown are averages of at least four repetitions. Measurements were made at a similar papilla position of 0.59 ± 0.04 (n = 46) from the apex, corresponding to a resonant frequency near 310 Hz (Crawford and Fettiplace, 1980). Experiments were performed between 19 and 22°C. Data are presented as means ± SD except when noted. Student's t tests were used to compare means, with pairwise t tests noted. For tests using multiple comparisons, significance was adjusted (Bonferroni's test).
Experimental procedure
To determine whether the steady-state MET current sets hair cell resting potential, MET current amplitudes (voltage clamp) and the corresponding changes in membrane potential (current clamp) for varying concentrations of Ca2+ surrounding the hair bundle were measured. Voltage-clamp measures of MET currents were performed at a holding potential 2–3 mV negative from the 0 current potential (−52 ± 17 mV in 2.8 mm apical Ca2+;n = 46) to avoid erroneous activation of BK currents via series resistance artifacts (Farris and Ricci, 2005). Based on the current–voltage relationship for the MET current, a 3 mV change in holding potential corresponds to ∼36 pA change in maximum MET current (Farris et al., 2004). For each cell, two apical Ca2+ concentrations, 2.8 mm and either 20, 50, or 200 μm, were applied. The duration of low Ca2+ application to the hair bundle lasted between 10 and 60 s. While in current clamp, the current–voltage relationship was measured by mechanically blocking transduction and injecting direct current (DC) using a custom-built summing amplifier. This procedure facilitated measurement of current magnitudes required to depolarize hair cells to their best resonant voltage. Best resonant voltage is defined as the membrane potential that exhibits symmetrical oscillations in response to positive and negative 135 ± 48 pA, 30 ms steps. This step size was chosen because it elicited a response that was discernable above the resting membrane oscillations and because the stimulus was well below saturation on the displacement–voltage curve in turtle hair cells (Crawford and Fettiplace, 1985). Saturating MET current–displacement functions (I–X) were analyzed using a double Boltzmann equation of the following form:
| (1) |
where a1 and a2 determine the steepness (i.e., nanoamperes per nanometer), and x1 and x2 determine the positions of the functions on the displacement axis (x). For simplicity, x1 = x2 (Ricci and Fettiplace, 1997). I–X curves were measured with apical 2.8 mm and one concentration of low Ca2+. Current– displacement slopes near 0 displacement (± 25 nm or 3 dB with regard to threshold) (Crawford and Fettiplace, 1983) were analyzed using linear regression (minimum r2 = 0.904). Only cells in which complete I–X curves were generated are included in the analysis.
Spectral analysis and filter function
Previously, electrical resonance in turtle auditory hair cells was modeled using an equivalent circuit that allowed for calculation of the quality factor of the filter (Q) or bandwidth from the decay in amplitude of oscillations during a current step (Crawford and Fettiplace, 1981). This method was difficult to apply to cells that were not responding from the appropriate resting potential. Thus, the filter characteristics of electrical resonance were calculated by analyzing the spectrum of the unstimulated resting membrane potential (Patterson et al., 1982). First, the amplitude spectra of the membrane potentials (100 ms sweeps during DC injection) were calculated using a complex fast Fourier transform (FFT) function in Mathcad (Math-soft, Cambridge, MA); the spectra had a 10 Hz resolution and a bandwidth of 1 kHz. Each flank of the spectrum [i.e., on either side of the center frequency (CF)] was fit with the rounded exponential function roex(p,r):
| (2) |
where g is the normalized deviation of frequency from the center frequency, cf, g = (f−cf ) /cf, p is a dimensionless parameter determining the slope of the flanks of the resonant band, and r is a constant that sets the range limitation of the roex filter. Spectra were assumed asymmetrical around the center frequency, and separate slopes (p) were calculated for the upper and lower frequency flanks; r was limited to be ≥0.001 [60 dB, the maximum dynamic range of acoustic sensitivity in turtle hair cells (Crawford and Fettiplace, 1980)]. The model was fit using a least-squares method to solve for the slope parameter (p) and dynamic range (r) of each side of the peak frequency. The roex model facilitates calculation of the equivalent rectangular bandwidth (ERB), defined as the size of a rectangular filter that passes an equivalent amount of power for a white-noise input (Hartmann, 1998). This metric is useful when comparing the filtering properties of cells in conditions that generate different shaped responses. Because the FFT may not generate points at frequencies that are −10 dB (with regard to the peak) and in some cases the membrane response did not show damped resonance, Q10 dB values are calculated from the roex filter fits to the spectra. The filter parameters of a cell were only included if the roex model explained a significant portion of the variance of the spectrum (p < 0.002 for each curve).
Model
The effect of steady-state MET current on resting potential and electrical resonance was independently tested by mathematically simulating the membrane potential as the sum of the ionic and capacitive membrane currents (Hudspeth and Lewis, 1988a,b):
| (3) |
where gCa is the L-type Ca2+ conductance, gK(Ca) is the BK Ca2+ -activated potassium conductance, Cm is the membrane capacitance, and Icom is the step size of the externally injected current. To model the steady-state MET current at rest, the simulation varied gL. The temporal-, voltage-, and ionic-dependent properties of gCa (Schnee and Ricci, 2003) and gk(ca) (see Figs. 1, 6) were determined from activation curves and tail currents using a least-squares method and a quasi-Newton gradient fitting algorithm used by the Microsoft (Seattle, WA) Excel addin Premium Solver Platform version 6.5 (Frontline Systems, Incline Village, NV) (see Appendix). Initial parameter values used by the fitting algorithm were those for electrical resonance in frog saccular hair cells (Hudspeth and Lewis, 1988a,b).
Figure 1.
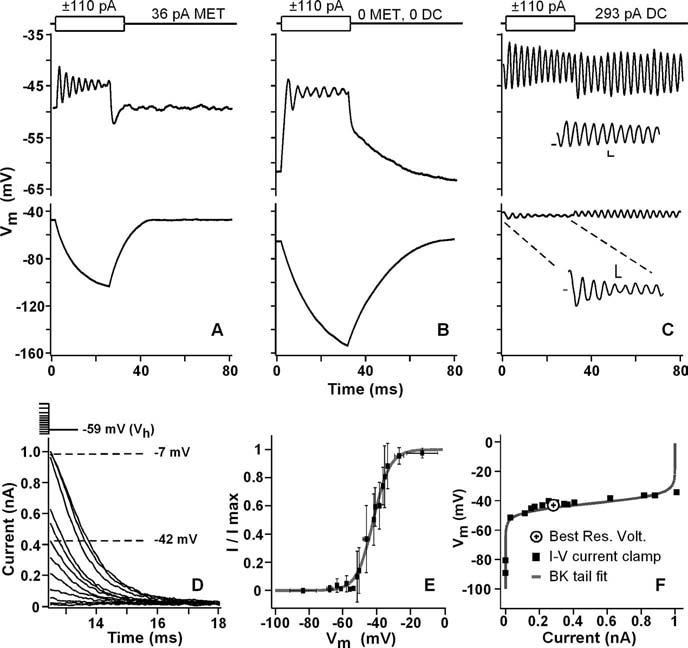
A–C, Membrane voltage responses to ±110 pA step injections; stimulus is shown at the top. A, Hair bundle exposed to 2.8 mm Ca2+ endolymph, generating 36 pA steady-state MET current. B, MET is mechanically blocked with a stiff probe, hyperpolarizing the cell and making it more nonlinear. C, MET is mechanically blocked and the cell is depolarized to best resonant voltage with 293 pA DC injection. Insets are first 30 ms. Calibration: 2 mV, 2 ms. D, Whole-cell voltage-clamp recording of a family of BK tail currents in response to a series of 10 ms voltage steps to various potentials; stimuli are shown at the top. E, Mean tail current activation curve (n = 17) and fit using a Boltzmann equation (V½ of −43 ± 2 mV; slope of 3 ± 1 mV). F, Comparison of the BK activation (gray) and the current–voltage relationship for a single cell: squares represent the resting potential for varying amounts of injected current. The axis is reversed from E.
Figure 6.
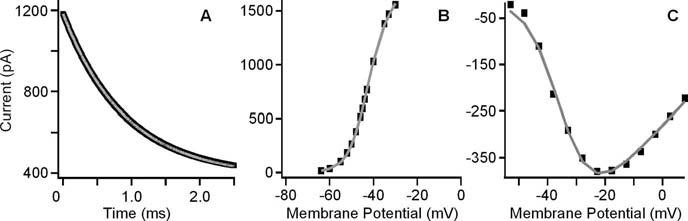
Panels show simulations (gray) of the BK tail current (A), BK voltage activation curve (B), and L-type Ca2+ voltage activation curve (C) in black. The BK tail current was generated after a voltage step from −35 mV to a holding potential of −47.7 mV, the resting potential of the cell.
Results
Turtle auditory hair cells are an excellent model for identifying factors involved in establishing hair cell resting potential, because their physiological resting potential can be identified by the proper functioning of their major tuning mechanism, electrical resonance (Art et al., 1985; Wu et al., 1995). Electrical resonance is generated by the interaction of BK potassium and L-type calcium channels (Crawford and Fettiplace, 1981; Hudspeth and Lewis, 1988a,b; Wu et al., 1995). Although hair cell recordings from the intact papilla reveal resting potential responses appropriately depolarized for evoking resonant behavior (Crawford and Fettiplace, 1981), recordings from dissociated hair cells or those from a semi-intact preparation require application of a DC to depolarize the resting potential to a voltage at which the sharpness, sensitivity, and linearity of the resonant filter are optimal (Fuchs et al., 1988; Wu et al., 1995; Ricci et al., 2000). A major goal of the present experiments was to determine whether MET channels provide this depolarizing current.
Illustrating the requirement for a DC to set the resting potential to the best voltage for filtering, Figure 1A-C shows the response of the hair cell membrane to positive and negative current steps with different sources of DC. Free-standing hair bundles bathed in 2.8 mM Ca2+ produced 32 ± 25 pA (n = 46) of steady-state MET current. This generated a resting potential of −49 mV (−56 ± 17 mV; n = 46), in which only the positive current step produced oscillations and the negative step elicited a passive response (Fig. 1A). Holding the sensory hair bundle in a position that closes all MET channels hyperpolarized the resting potential to −61 mV (−70 ± 9 mV; n = 42). Similar to Figure 1A, only the positive current step elicited membrane oscillations at the plateau, and the negative step again revealed the passive characteristics of the membrane with response amplitudes to positive and negative steps being different (29 ± 8 vs 89 ± 19 mV; p < 0.0001, t test, pairwise). The importance of sufficient DC is illustrated in Figure 1C, in which the cell is depolarized to its best resonant voltage, −41 mV (−45 ± 4 mV; n = 45) by injecting 293 pA (243 ± 77 pA; n = 45) of DC. At this potential, the membrane voltage change was linear as indicated by the comparable voltage change to positive and negative current injections (5 ± 1vs5 ± 2 mV; p > 0.8, t test, pairwise). The bandwidth of the membrane filter reached its narrowest point as estimated by evaluating the equivalent rectangular bandwidth of the spectra of the oscillations (51 ± 24 Hz; n = 45) or the Q10 dB (4.5 ± 2.4; n = 45). The peak resonant frequency at the best resonant voltage (318 ± 71 Hz; n = 45) is not different from that predicted from in vivo recordings (312 Hz; t = 0.7; p < 0.2) (Crawford and Fettiplace, 1980). Finally, there is resonance to both positive and negative current steps.
At the best resonant voltage, the membrane potential of the hair cell was sharply rectified because of the steepness of the BK potassium current (Fig. 1E). The BK activation curve was measured from tail currents (Fig. 1D) and analyzed using a single Boltzmann equation of the following form:
| (4) |
where V1/2 is the half-activating voltage, and K is the limiting slope (voltage dependence). Activation was steep (slope of 3.6 ± 1.0 mV) and showed a half-activation voltage of −43.0 ± 4.5 mV (Fig. 1E)(n = 17), which is not different from perforated-patch recordings or the best resonant voltage (p > 0.3) (Ricci et al., 2000). Maximal BK conductance was 12 ± 6 nS (using −135 mV EK because BK is K+ selective), similar to previous recordings (9.6 nS) (Ricci et al., 2000). The BK effect on membrane potential is illustrated in Figure 1F, in which the current–voltage relationship from a single cell was superimposed with its BK activation curve. Inward current sharply depolarized the membrane until the BK conductance activated and rectified the response. The best resonant voltage lay within the linear portion of this plot. The BK conductance served to buffer the membrane potential, preventing additional depolarization and maintaining the membrane potential within this linear range. The question remains as to what conductances provide the depolarizing (DC) current required to put the potential into the linear portion of the BK activation curve.
MET current at rest depolarized the membrane potential (Fig. 1), promoting the hypothesis that, under physiological conditions, steady-state MET current will depolarize the membrane potential to its best resonant voltage. The magnitude of MET current at rest is dictated by the MET channel resting open probability and the maximum MET conductance, both of which are regulated by Ca2+ (Eatock et al., 1987; Crawford et al., 1989; Ricci and Fettiplace, 1998; Wu et al., 1999). Ca2+ acts as a permeable blocker limiting MET conductance magnitude, whereas Ca2+ permeation controls the set point of the MET activation curve via adaptation (Crawford et al., 1991; Ricci and Fettiplace, 1998). These effects of Ca2+ are illustrated in Figure 2, B and C. For a series of mechanical steps to the hair bundle, the size of the MET current, the rate of adaptation, and the position of the I–X plot changed when apical [Ca2+] was varied from 2.8 mm to 50 μm. Plotting the mean Boltzmann fits to the peak (I–X) curves (Fig. 2D) quantified the effect of Ca2 on these processes. First, for free-standing bundles (i.e., 0 μm displacement) the amount of current at rest increased with decreasing apical [Ca2+ ] (Fig. 2D) (see Fig. 4A). Second, the current–displacement slope around 0 displacement was greatest for 50 μm apical [Ca2+] (Fig. 2E). These changes in MET with external Ca2+ were investigated next to determine its effect on membrane potential and resonance. Here, it was critical to maintain separation between apical perfusion and basolateral perfusion. To this end, a small pipette was placed near to the sensory hair bundle along its axis of least sensitivity (Fig. 2A). Perfusion of a solution with a lower [Ca2+] and high [K+] (130 mm) depolarized the membrane potential, reduced the input resistance, and elicited electrical resonance (Fig. 2F,G). Because resonance would not occur if the basolateral conductances were exposed to apical endolymph (i.e., K+ reversal potential would go to 0 mV), this result confirmed separation of apical and basolateral perfusions.
Figure 4.
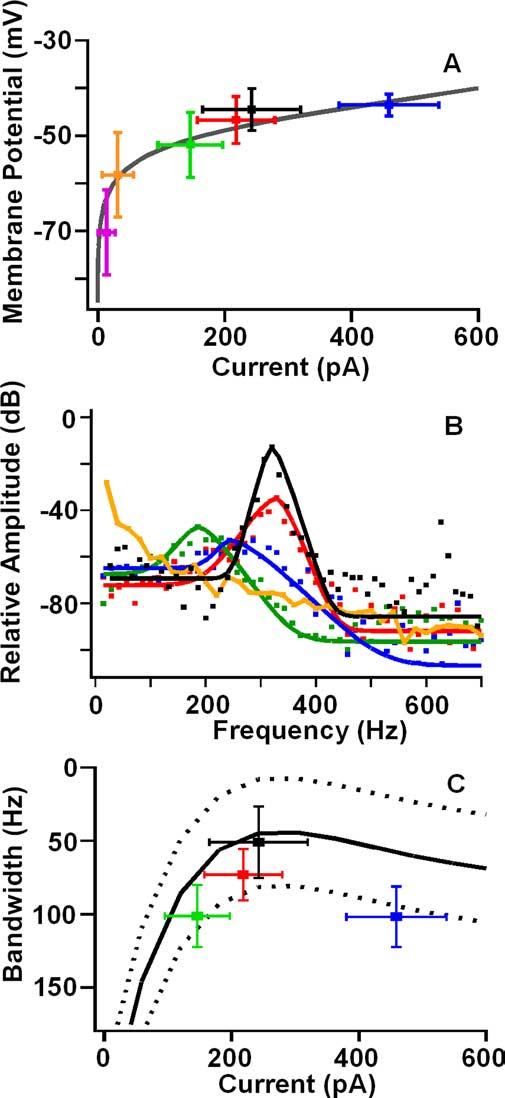
A, Resting potential as a function of inward current for different apical conditions. Colors are the same as Figure 3 showing steady-state MET for four apical [Ca2+] with free-standing bundles; purple is mechanical block of MET, and black is current injected to best resonant voltage.Gray curve is the BK activation curve in Figure 1, E and F,scaled to the maximum BK current. B, Points (squares) are the amplitude spectra of the baseline membrane potential for the four Ca2+ concentrations shown in Figure 3. Curves represent the least-squares fit of the roex filter functions to the amplitude spectra. Black represents response at the best resonant voltage. Response at 2.8 mm Ca2+ exhibitedalow-passresponse. C,Equivalent rectangular bandwidth of roex filters as a function of current at rest. Curve represents a polynomial fit (±SD) to the ERB when injecting current and mechanically blocking the MET (n = 6). Colors are the same as used previously, representing apical [Ca2+] and the response at the best resonant voltage (black). ERB for 50μm is smaller than those at 200μm (p < 0.0004) and 20μm (p < 0.00005). ERB at the best resonant voltage is smaller than that for each apical [Ca2+] (200 μm, p < 0.0025; 50 μm, p < 0.0002; 20 μm, p < 0.01; t test, pairwise). Q10 dB for the roex filters are as follows: 20 μm, 2.0 ± 1.1; 50 μm, 3.1 ± 0.8; 200 μm, 1.2 ± 0.9; DC, 4.5 ± 2.4.
The resting potential and electrical resonance varied with the change in apical Ca2+ (Fig. 3). As with injected current (Fig. 1C), changes in MET current with apical [Ca2+] caused the resting potential to depolarize along the BK voltage activation curve (Fig. 4A). Perfusion of different external [Ca2+] demonstrates that steady-state MET current can provide all of the required current to depolarize the hair cell to its best resonant voltage (Fig. 3C) and beyond (Fig. 3D). However, is the observed response simply a function of hair cell electrical properties in response to an increased conductance at rest or are other biochemical factors involved [e.g., cAMP (Ricci and Fettiplace, 1997)]? A comparison of the effects of apical perfusion of low Ca2+, high K+ solutions with injected DC suggests that electrical properties are dictating the response (Fig. 4). Plotting the steady-state MET current against membrane potential demonstrates that the potential change falls exactly along the voltage–current plot elicited with DC injections (Fig. 4A), supporting the conclusion that the response was driven electrically. A Fourier analysis of the baseline membrane potential (Fig. 4B) from data in Figure 3 demonstrated that, as the resting potential approached the best resonant voltage, a resonant peak was observed, similar to that obtained by DC injection. When MET was blocked (data not shown) or exposed to 2.8 mm Ca2+, there was no resonance in the baseline, and the filter exhibited only low-pass characteristics (Fig. 4B, orange trace).
Figure 3.
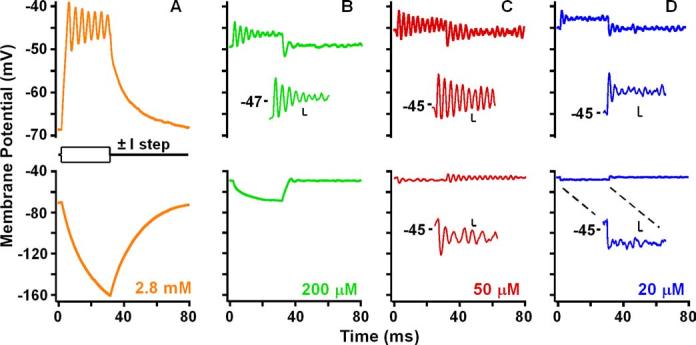
Membrane potential for four concentrations of apical Ca2+ (±110 pA, 30 ms steps). Responses in A and C are from the same cell. Colors are the same as in Figure 2. Inset calibration: 1 mV, 2 ms.
The resonant bandwidth (i.e., sharpness of tuning) varied with the resting MET current generated by each apical Ca2+ treatment. For example, baseline resonance was exhibited for 200 μm Ca2+. Although the input resistance for 200 μm Ca2+ (60 ± 19 MΩ) was still relatively high, presumably creating a narrow bandwidth [i.e., 1/(time constant = RC)], the resting potential (−52 ± 7 mV) was hyperpolarized from the activation range for the BK and L-type Ca2+ conductances, reducing resonance. Best resonance was exhibited when the bundle was exposed to 50 μm Ca2+ (Fig. 4C). The equivalent rectangular bandwidth (CF, 327 ± 81 Hz; ERB, 73 ± 17 Hz) was significantly smaller than that for 200 μm (CF, 293 ± 35 Hz; ERB, 101 ± 21 Hz; p < 0.001) and 20 μm (CF, 345 ± 46 Hz; ERB, 102 ± 21 Hz; p < 0.0001) Ca2+. Although the membrane potential was depolarized into a resonant range with 20 μm Ca2+, the wide spectrum was determined by the low input resistance (28 ± 9 MΩ), which increased the membrane time constant, broadening the bandwidth. The low input resistance was presumably the result of both the large MET current and the large BK current at such depolarized membrane potentials. Although for each apical Ca2+ treatment the bandwidth was still significantly wider than that measured using injected current (ERB, 51 ± 24 Hz), the effects of various external [Ca2] gave results similar to that when varying amplitudes of DC were injected directly (Fig. 4C). That the effects of the varying [Ca2+] never quite matched the best filter achieved by the DC may be a result of less than optimal MET, but it is more likely a result of the difference in input resistance between artificially injecting current into the hair cell versus directly reducing the input resistance by turning on the MET current.
Finally, the effect of the steady-state MET current on resting potential was independently confirmed with a model of electrical resonance (Hudspeth and Lewis, 1988b) that incorporated the steady-state MET conductance to reproduce all of the illustrated effects (Fig. 5). The model used activation properties for the BK and L-type Ca2+ conductances (Figs. 1, 6; Table 1) from this frequency location, with changes in leak conductance simulating the MET current. The ability of the model to reproduce the results obtained by bathing the hair bundle in low Ca2+ endolymph confirmed that the measured changes were electrically driven. Moreover, the model also provided independent evidence of apical–basolateral fluid separation, because partial mixing of baso-lateral K+ during apical perfusion would depolarize resting potential beyond that predicted from the voltage–current plot (Fig. 4A). Thus, it is concluded that steady-state MET current was capable of providing the DC needed to set the hair cell resting potential to its best resonant voltage.
Figure 5.
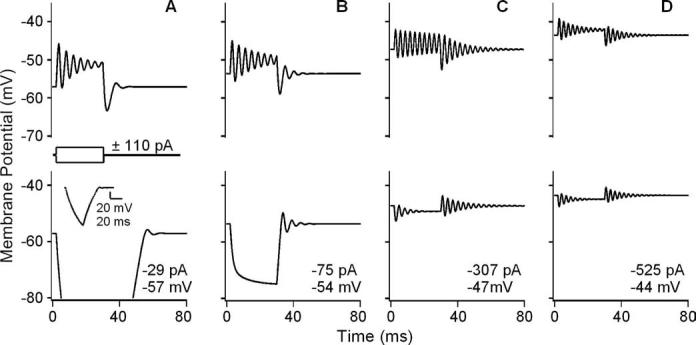
Membrane potential calculated using a model of electrical resonance (Hudspeth and Lewis, 1988a, b).Responses are to ± 110 pA current steps and varying amounts of MET (leak) current (A–D; leak values shown in each panel with the resting potential). The responses simulate the following conditions: A, 2.8 mm Ca2+; B, 200μm Ca2+; C,50 μm Ca2+; D, 20 μm Ca2+ (Fig. 3). Inset in bottom of A shows complete passive response to negative step, which extends off-scale. Spectral filtering is sharpest for simulation of 50 μm Ca2+ condition in C. ERBs of electrical resonance during the depolarizing step are as follows: A, 99 Hz; B, 71 Hz; C, 54 Hz; D, 82 Hz.
Table 1.
Parameter values for model of electrical resonance
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 6.7 nS | EK | −130 mV | |
| ECa | 100 mV | k1(0) | 1.004 μm/ms−1 |
| α0 | 23.18 ms−1 | k−1(0) | 0.346 ms−1 |
| V0 | 99.94 mV | δ1 | 1.00 |
| VA | 29.91 mV | k2(0) | 0.269 μm/ms−1 |
| KA | 6.74 × 10−4 ms−1 | k−2(0) | 2.16 ms−1 |
| β0 | 1.44 × 10−3 ms−1 | δ2 | 1.00 |
| VB | 7.55 mV | k3(0) | 1.25 μm/ms−1 |
| KB | 2.19 ms−1 | k−3(0) | 1.09 ms−1 |
| U | 0.02 | δ3 | 0.076 |
| ξ | 5.89 × 10−5 | αC(0) | 2.11 ms−1 |
| Cvol | 1.25 pl | Va | 10.10 mV |
| Ks | 4.91 ms−1 | βC(0) | 2.13 ms−1 |
| 17.06 nS | Vb | 520 mV | |
| EL | 0 mV |
Given the above conclusion regarding steady-state MET current dictating the hair cell resting potential, it was possible to use the voltage response of the hair cell in the presence of various apical Ca2+ solutions to titrate the physiological level of endolymphatic Ca2+ near the MET channel. For these interpolations, several response parameters were incorporated, including a direct comparison of MET current amplitude with the DC injected for best resonance, changes in filtering properties, response linearity, input resistance, and sensitivity.
When compared with the DC required to reach the best resonant voltage (243 ± 77 pA; n = 43), only the MET current generated by the 50 μm treatment did not differ significantly (2.8 mm, p < 0.00001; 200 μm, p < 0.05; 50 μm, p > 0.5; 20 μm, p < 0.00001; t test, pairwise). A plot of steady-state MET current against external [Ca2] allowed for interpolation of the [Ca2] required to reach the best resonant voltage (Fig. 7A). The data were fit with a simple power function, and interpolation of the mean DC to best resonant voltage suggests a concentration of 50 ± 5 μm. As a measure of response linearity, the relative change in membrane potential in response to positive and negative current step injections was plotted against apical [Ca2+] (Fig. 7B). Here, interpolating the value obtained from DC injection results in an endolymph [Ca2+] of 45 ± 1 μm. A similar value was also interpolated from a plot of the input resistance, measured from the membrane response to negative current injections, verses apical Ca2+ (48 ± 9 μm) (Fig. 7C). Membrane sensitivity to mechanical stimuli at the resonant frequency was estimated as the product of the mean linear slope of the MET activation curves near 0 displacement (Fig. 2E), the filter Q10 dB, and the input resistance for each cell. Membrane sensitivity was greatest in 50 μm [Ca2+] and comparable with that measured in intact preparations by Crawford and Fettiplace (1985) (1 mV/nm) (Fig. 7D). Such a value was also interpolated from the variance in resonant frequency with apical [Ca2+], 79 ± 30 μm (data not shown). Thus, multiple measurements indicate that endolymph [Ca2+] near to the MET channel is low, 56 ± 11 μm (mean ± SD interpolation) and not significantly different from the mean estimate (65 μm) for bulk endolymph (Crawford et al., 1991).
Figure 7.
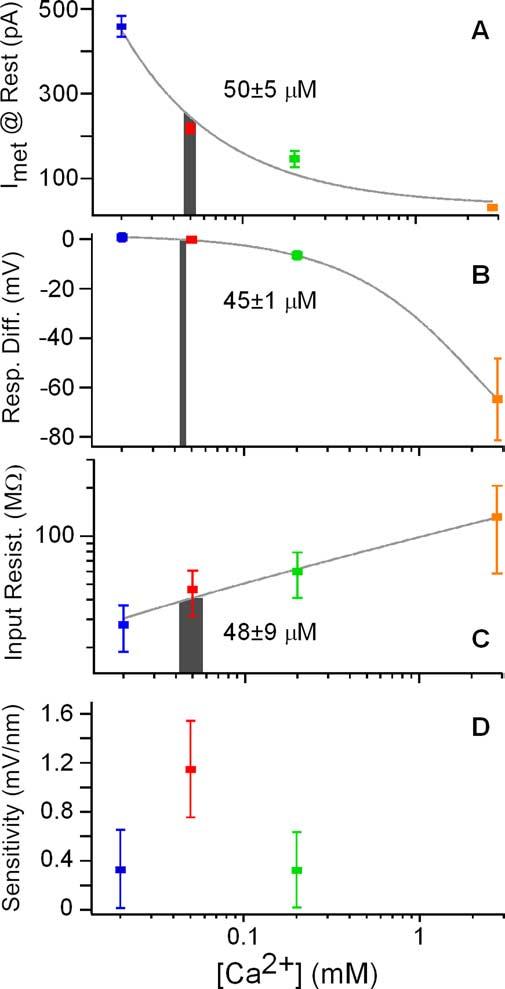
Characteristics of electrical resonance as a function of apical [Ca 2+]. A–C, Gray curves are polynomial fits to the data. Gray bars represent interpolation of the endolymphatic [Ca 2+] from the control condition at the best resonant voltage. Bar widths are generated from interpolation of the mean ± SE for each y-axis variable at the best resonant voltage: A, steady-state current; B, membrane response difference to positive and negative current; C, input resistance.D, Membrane sensitivity (±SE) to mechanical input at the resonant frequency calculated as the product of the linear slope of the current – displacement curves near 0 displacement (Fig. 2 D, E), the input resistance for positive current injections, and the Q10 dB of the roex filters.
Discussion
Data presented demonstrate a novel role for steady-state adaptation of mechanically gated channels: to provide depolarizing current needed to maintain the hair cell resting potential at a voltage that ensures sharpest tuning, greatest sensitivity, and the most linear response. Because adaptation is calcium dependent (Eatock et al., 1987; Crawford et al., 1991; Ricci and Fettiplace, 1997, 1998), the concentration of Ca2+ bathing the hair bundle is critical for establishing the hair cell resting potential. This Ca2+ sensitivity allowed for the resting potential of the hair cell to be used to estimate the endolymphatic [Ca2+] near the MET channel.
There are two effects of endolymphatic Ca2+ that together produce the appropriate current at steady state. Ca2+ is a permeable blocker of the MET current, such that a change in concentration from 2.8 mm (i.e., perilymph) to 20 μm results in MET currents increasing 1.6-fold. Alone, this effect would increase resting MET current from 32 ± 25 to 93 pA (maximum), a value insufficient to depolarize the cell to its best resonant voltage (Fig. 4A). Thus, an additional change in MET current is required, which is provided by the Ca2+-dependent shift in the mechanical activation curve produced by adaptation. Reduced Ca2+ shifts the curve leftward, increasing the amount of MET current at rest (Fig. 2).
Although it is possible that Ca2+ affects other hair cell processes aside from the electrical properties and that these serve to depolarize the cell more appropriately to its resting potential [e.g., intracellular effects of Ca2+ on cAMP adjusting MET current (Ricci and Fettiplace, 1997)], several lines of evidence suggest that this is not the case. First, the time course of the response was fast and comparable with that required for the shift in the MET activation curve induced by adaptation (Fig. 2). Second, the model reproduced the effects observed with varying [Ca2+] simply by varying the leak. Third, the effect of a hyperpolarized resting potential on resonance, attributable to reduced resting MET current (Figs. 1, 3), was also shown in studies examining efferent modulation of hair cell responses. Art et al. (1985) hyperpolarized hair cells by stimulating auditory efferents, which modulated resonant tuning by converting responses from sharply tuned bandpass filters to broad low-pass filters, very similar to data presented here when apical [Ca2+] was too high.
MET and resting potential in other hair cells
The general criteria used here to identify the appropriate resting potential can be extrapolated to hair cell types that do not exhibit electrical resonance. For example, mammalian outer hair cells (OHCs) change length (measured as capacitance change) in response to changes in membrane voltage (Brownell et al., 1985; Liberman et al., 2002). It is predicted that the electro-motile response should be most symmetrical and sensitive when resting potentials are set where the nonlinear capacitance shows steepest voltage sensitivity, −37 mV (Santos-Sacchi, 1991). However, recordings in OHCs often show relatively hyperpolarized resting potentials (approximately −65 mV) (Dallos, 1985), at which motility would be asymmetrical in response to different stimulus phases (Santos-Sacchi, 1989). Data presented here suggest that hyperpolarized resting potentials could be attributable in part to insufficient depolarizing current from MET channels, biasing the resting potential hyperpolarized attributable to KCNQ conductance (Oliver et al., 2003). Recent recordings in OHCs suggest that large MET currents are present, which could depolarize resting potentials. For example, Kennedy et al. (2003) showed that 15% of the MET current is on at rest in low apical Ca2+ (50 μm; 1.6 nA peak current), which, when combined with the increased driving force of the endocochlear potential (1.9 x values) and the increased conductance attributable to temperature (Q10 = 1.3; for 37°, 2.2 x values current at 20°), should produce ∼1.0 nA of resting MET current (1.9 × 2.2 × 1.6 nA = 6.6 nA maximum MET current). This steady-state current would require 33 MΩ input resistance to depolarize the cell ∼33 mV to the resting potential with best electromotility. Input resistance values for OHCs range from 156 to 12 MΩ (Dallos, 1985), suggesting that MET currents can provide the appropriate depolarizing current. Like OHCs, inner hair cells (IHCs) exposed to perilymph show hyperpolarized resting potentials near −60 mV, with depolarization limited by the KCNQ conductance (Kros and Crawford, 1990; Oliver et al., 2003). Whereas IHCs do not exhibit motility, steepest voltage sensitivity of the L-type Ca2+ conductance (Zhang et al., 1999), critical to nonrectified, graded transmitter release, starts at potentials depolarized from −40 mV (Marcotti et al., 2003). As with turtles, spontaneous activity in mammalian type 1 auditory afferents suggest that IHC resting potential is sufficiently depolarized for Ca2+ current activation and thus spontaneous transmitter release (Dallos, 1985; Cody and Russell, 1987; Robertson and Paki, 2002). Based on parameters from various IHC recordings (Kros et al., 1992), Zeddies and Siegel (2004) calculated that the MET conductance at rest needs to be ∼8 nS (∼312 pA) to maintain such a depolarized resting potential. Recent recordings in adult IHCs reveal MET current sizes comparable with those recorded here in turtle and the OHCs described above (D. He, personal communication); the effects of the endocochlear potential and temperature yield peak MET currents of >4 nA (615 pA at rest) at −40 mV, enough to provide depolarization that offsets known outward K+ conductances.
What is [Ca2+] of turtle endolymph?
The consequences of an endolymph solution containing a high K+ and low Ca2+ are multifold. MET current amplitude is increased because of high permeability of K+ through transduction channels relative to other monovalent ions (Ohmori, 1985; Ricci and Fettiplace, 1998; Farris et al., 2004). K+ promotes Ca2+ permeation through the channel, likely through anomalous mole fraction behavior (Lumpkin et al., 1997; Ricci and Fettiplace, 1998). A significant portion of MET current, 10–20%, is carried by Ca2+ when the bundle is exposed to [Ca2+] < 100 μm (Lumpkin et al., 1997; Ricci and Fettiplace, 1998). Ca2+ influx plays a role in numerous components of transduction: Ca2+ modulates channel block (Ricci and Fettiplace, 1998), regulates fast and slow adaptation (Eatock et al., 1987; Crawford et al., 1991; Ricci et al., 1998), affects the lipid environment of the channel (Hirono et al., 2004), affects the mechanical compliance of the hair bundle (Marquis and Hudspeth, 1997), and alters activation kinetics (Ricci et al., 2005). Accurate measures of endolymphatic [Ca2+] are thus critical to evaluating the functional significance of MET and endolymph. Understanding the functional role of the endolymph in MET is complicated by problems in directly measuring its composition, because of its small volume and difficult access (Sterkers et al., 1988). Furthermore, microdomains of Ca2+ may exist surrounding the hair bundle such that bulk [Ca2+] could be significantly lower than the effective concentration at the hair bundle (Yamoah et al., 1998). A functional assay using the response of the cell to [Ca2+] near the MET channel is thus useful. A previous bioassay measured endolymphatic [Ca2+] by adjusting Ca2+ to concentrations that produce oto-acoustic emissions comparable with those measured under control conditions. The assay was limited to changing [Ca2+] across the entire papilla, however, and was unable to control the concentration in the bundle microdomain. The high value obtained (>1mm) was unusual in that it suggested that >50% of the MET current would be blocked by Ca2+ under physiological conditions. Here, the well characterized electrical resonance was used to estimate endolymphatic [Ca2+] near individual hair bundles. Estimates presented were not different from bulk estimates (56 ± 11 vs 65 μm) (Crawford et al., 1991), suggesting that (at least in turtle) microdomains of Ca2+ near the MET channels do not play a significant role in regulating steady-state MET current. Given the high density of CaATPases found in the stereocilia and measured Ca2+ extrusion into endolymph (Yamoah et al., 1998), the predicted gradient may be dissipated rapidly by buffering or diffusion, because extruded Ca2+ is shown to mix with and equilibrate in the entire fluid (Wood et al., 2004). Additionally, a gradient produced by extruded Ca2+ may not have access to the MET channel or be large enough to have a significant effect.
The effects of Ca2+ on adaptation and thus the set point of the MET activation curve can be quite variable. Early reports suggested that hair bundles in low (50 μm) Ca2+ could abolish adaptation, reduce sensitivity, and leave a standing current insensitive to mechanical stimulation (Crawford et al., 1991). Additional characterizations, however, demonstrated that the sensitivity of adaptation to Ca2+ was related to the size of the MET current, and the loss of adaptation in low [Ca2+] was likely because of small or damaged MET currents (Ricci and Fettiplace, 1997; Ricci et al., 1998). Whereas initial results may have supported the hypothesis that microdomains of elevated Ca2+ are needed to ensure that adaptation can operate under physiological conditions, more recent data (Ricci and Fetti-place, 1998) and cells presented here demonstrate that adaptation can be maintained in low [Ca2+] and suggest that these low [Ca2+] are critical to establishing the appropriate response properties of hair cells. In fact, if MET currents presented in this study were partially damaged either mechanically or biochemically, then the estimates of Ca2+ are higher than would be required in vivo.
Appendix
Description of the kinetic model of electrical resonance
The model of electrical resonance (Hudspeth and Lewis, 1988a,b) is based on the following equation that describes the time-dependent change of voltage Vm as a function of Ca2+ current, K+ current, an externally injected current Icom, and a leak current that is hypothesized in this report to be the MET current:
| (A1) |
where gCa is the Ca2+ conductance through Ca2+ channels, ECa is the reversal potential of Ca2+, g K(Ca) is the K+ conductance through BK potassium channels, EK is the reversal potential of K+, gL is the leak conductance and assigned a constant value, and EL is the reversal potential of the leak current.
The following equations summarize how gCa is described based on a third-order Hodgkin–Huxley model (Hille, 2001, their pages 45–51):
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
where ICa is the Ca2+ current, is the maximum Ca2+ conductance when all Ca2+ channels are open, m is the activation probability of the Hodgkin–Huxley model, αm is the voltage-dependent closing rate of m, βm is the voltage-dependent opening rate of m, α0, KA, β0, and KB are rate constants, and V0, VA, and VB are potentials.
IK(Ca), the Ca2+-dependent K+ current through BK channels, is derived from the following five-state kinetic mechanism: 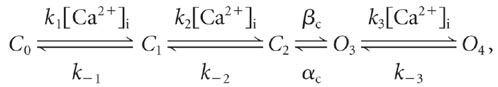 where C0, C1, and C2 are closed channel states, O3 and O4 are open states, and [Ca2+]i is the effective submembrane concentration of Ca2+ in a submembrane compartment containing Ca2+ for BK channels. The time-dependent changes in fractional state populations are described by the following set of differential equations:
where C0, C1, and C2 are closed channel states, O3 and O4 are open states, and [Ca2+]i is the effective submembrane concentration of Ca2+ in a submembrane compartment containing Ca2+ for BK channels. The time-dependent changes in fractional state populations are described by the following set of differential equations:
| (A7) |
| (A8) |
| (A9) |
| (A10) |
| (A11) |
Given these fractional state populations, IK(Ca) equals gK(Ca) (Vm − EK), where
| (A12) |
and is a constant conductance. The rate constants at the three Ca2+-dependent steps in the five-state kinetic mechanism are the following functions of voltage:
| (A13) |
| (A14) |
where kj(0) and k−j(0) are constants, and δj is the fraction of electric field at the jth Ca2+ binding site. The closing rate αC and opening rate βC are
| (A15) |
| (A16) |
where αC(0), βC(0), Va, and Vb are constants.
To compute the fractional state populations for BK channels, the time-dependent change of [Ca 2+] i is modeled as follows:
| (A17) |
where U is the fraction of free Ca 2+, Cvol is the total cell volume, z is the valence of Ca 2+, F is the Faraday constant, ξ is fraction of cell volume in the submembrane compartment containing Ca2+ for BK channels, and Ks is the rate constant describing exiting of Ca2+ from this submembrane compartment. The first term on the left side of Equation A17 describes the increase of [Ca2+]i in the submembrane compartment attributable to inward Ca2+ current; the second term describes the exit of Ca 2+ from this compartment.
To determine parameter values in Table 1 by least-squares fitting of the model output to tail current data and voltage–current data (Figs. 1, 6), the system of time-dependent Equations A7-A11 and A17 was solved numerically in Microsoft Excel with ODE_RK4, a fourth-order Runge–Kutta formula in Xnumbers, an Excel addin (http://digilander.libero.it/foxes/index.htm); fractional populations of BK channel states at time-independent voltages were solved in Microsoft Excel with xSYSLIN, a Gauss–Jordan diagonalization algorithm with partial pivoting method in Xnumbers, and Equation A4 was solved analytically. To simulate the voltage resonance for a given set of parameter values, Equation A1 was integrated numerically with the dsolve function in Maple (Maplesoft, Waterloo, Ontario, Canada) using a Runge–Kutta–Fehlberg method producing a fifth-order accurate solution.
Parameters ECa, U, Cvol, and EK were fixed at values shown in Table 1. For a specific value of , all other parameters in Table 1 were varied by the gradient optimization algorithm to obtain the best fit to tail current, voltage–current, or current-clamp data. The value of was adjusted manually to obtain simulated voltage resonance behavior in current clamp that best reproduced the observed resonance behavior.
Footnotes
H.E.F. is supported by a National Institute on Deafness and Other Communication Disorders (NIDCD)–National Research Service Award fellowship. A.J.R. is supported by National Institutes of Health (NIH) Grant RO1-DC03896. We thank R. Fettiplace, D. He, M. Schnee, and J. Santos-Sacchi for comments on this project. B. Kachar and the NIDCD at NIH and R. Raspet at the University of Mississippi graciously supplied space and support during hurricane evacuation.
A. J. Ricci's present address: Department of Otolaryngology, Stanford University, Stanford, CA 94305
References
- Art JJ, Crawford AC, Fettiplace R, Fuchs PA. Efferent modulation of hair cell tuning in the cochlea of the turtle. J Physiol (Lond) 1985;360:397–421. doi: 10.1113/jphysiol.1985.sp015624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assad JA, Corey DP. An active motor model for adaptation by vertebrate hair cells. J Neurosci. 1992;12:3291–3309. doi: 10.1523/JNEUROSCI.12-09-03291.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownell WE, Bader CR, Bertrand D, de Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- Cody AR, Russell IJ. The response of hair cells in the basal turn of the guinea-pig cochlea to tones. J Physiol (Lond) 1987;383:551–569. doi: 10.1113/jphysiol.1987.sp016428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford AC, Fettiplace R. The frequency selectivity of auditory nerve fibres and hair cells in the cochlea of the turtle. J Physiol (Lond) 1980;306:79–125. doi: 10.1113/jphysiol.1980.sp013387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford AC, Fettiplace R. An electrical tuning mechanism in turtle cochlear hair cells. J Physiol (Lond) 1981;312:377–412. doi: 10.1113/jphysiol.1981.sp013634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford AC, Fettiplace R. Auditory nerve responses to imposed displacements of the turtle basilar membrane. Hear Res. 1983;12:199–208. doi: 10.1016/0378-5955(83)90106-5. [DOI] [PubMed] [Google Scholar]
- Crawford AC, Fettiplace R. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J Physiol (Lond) 1985;364:359–379. doi: 10.1113/jphysiol.1985.sp015750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford AC, Evans MG, Fettiplace R. Activation and adaptation of transducer currents in turtle hair cells. J Physiol (Lond) 1989;419:405–434. doi: 10.1113/jphysiol.1989.sp017878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford AC, Evans MG, Fettiplace R. The actions of calcium on the mechano-electrical transducer current of turtle hair cells. J Physiol (Lond) 1991;434:369–398. doi: 10.1113/jphysiol.1991.sp018475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dallos P. Response characteristics of mammalian cochlear hair cells. J Neurosci. 1985;5:1591–1608. doi: 10.1523/JNEUROSCI.05-06-01591.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eatock RA, Corey DP, Hudspeth AJ. Adaptation of mechanoelectrical transduction in hair cells of the bullfrog's sacculus. J Neurosci. 1987;7:2821–2836. doi: 10.1523/JNEUROSCI.07-09-02821.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farris HE, Ricci AJ. Voltage-clamp errors cause anomalous interaction between independent ion channels. NeuroReport. 2005;16:943–947. doi: 10.1097/00001756-200506210-00013. [DOI] [PubMed] [Google Scholar]
- Farris HE, LeBlanc CL, Goswami J, Ricci AJ. Probing the pore of the auditory hair cell mechanotransducer channel in turtle. J Physiol (Lond) 2004;558:769–792. doi: 10.1113/jphysiol.2004.061267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs PA, Nagai T, Evans MG. Electrical tuning in hair cells isolated from the chick cochlea. J Neurosci. 1988;8:2460–2467. doi: 10.1523/JNEUROSCI.08-07-02460.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann WM. Signals, sound, and sensation. AIP/Springer; New York: 1998. [Google Scholar]
- Hille B. Ionic channels of excitable membranes. Sinauer; Sunderland, MA: 2001. [Google Scholar]
- Hirono M, Denis CS, Richardson GP, Gillespie PG. Hair cells require phosphatidylinositol 4,5-bisphosphate for mechanical transduction and adaptation. Neuron. 2004;44:309–320. doi: 10.1016/j.neuron.2004.09.020. [DOI] [PubMed] [Google Scholar]
- Holt JR, Eatock RA. Inwardly rectifying currents of saccular hair cells from the leopard frog. J Neurophysiol. 1995;73:1484–1502. doi: 10.1152/jn.1995.73.4.1484. [DOI] [PubMed] [Google Scholar]
- Hudspeth AJ, Lewis RS. Kinetic analysis of voltage- and ion-dependent conductances in saccular hair cells of the bull-frog, Rana catesbeiana. J Physiol (Lond) 1988a;400:237–274. doi: 10.1113/jphysiol.1988.sp017119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudspeth AJ, Lewis RS. A model for electrical resonance and frequency tuning in saccular hair cells of the bull-frog, Rana catesbeiana. J Physiol (Lond) 1988b;400:275–297. doi: 10.1113/jphysiol.1988.sp017120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen F, Kroese AB. Ion channel regulation of the dynamical instability of the resting membrane potential in saccular hair cells of the green frog (Rana esculenta) Acta Physiol Scand. 2005;185:271–290. doi: 10.1111/j.1365-201X.2005.01495.x. [DOI] [PubMed] [Google Scholar]
- Kennedy HJ, Evans MG, Crawford AC, Fettiplace R. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat Neurosci. 2003;6:832–836. doi: 10.1038/nn1089. [DOI] [PubMed] [Google Scholar]
- Kros CJ, Crawford AC. Potassium currents in inner hair cells isolated from the guinea-pig cochlea. J Physiol (Lond) 1990;421:263–291. doi: 10.1113/jphysiol.1990.sp017944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kros CJ, Rusch A, Richardson GP. Mechano-electrical transducer currents in hair cells of the cultured neonatal mouse cochlea. Proc R Soc Lond B Biol Sci. 1992;249:185–193. doi: 10.1098/rspb.1992.0102. [DOI] [PubMed] [Google Scholar]
- Liberman MC, Gao J, He DZ, Wu X, Jia S, Zuo J. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 2002;419:300–304. doi: 10.1038/nature01059. [DOI] [PubMed] [Google Scholar]
- Lumpkin EA, Hudspeth AJ. Regulation of free Ca2+ concentration in hair-cell stereocilia. J Neurosci. 1998;18:6300–6318. doi: 10.1523/JNEUROSCI.18-16-06300.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lumpkin EA, Marquis RE, Hudspeth AJ. The selectivity of the hair cell's mechanoelectrical-transduction channel promotes Ca2+ flux at low Ca2+ concentrations. Proc Natl Acad Sci USA. 1997;94:10997–11002. doi: 10.1073/pnas.94.20.10997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcotti W, Johnson SL, Rusch A, Kros CJ. Sodium and calcium currents shape action potentials in immature mouse inner hair cells. J Physiol (Lond) 2003;552:743–761. doi: 10.1113/jphysiol.2003.043612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquis RE, Hudspeth AJ. Effects of extracellular Ca2+ concentration on hair-bundle stiffness and gating-spring integrity in hair cells. Proc Natl Acad Sci USA. 1997;94:11923–11928. doi: 10.1073/pnas.94.22.11923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohmori H. Mechano-electrical transduction currents in isolated vestibular hair cells of the chick. J Physiol (Lond) 1985;359:189–217. doi: 10.1113/jphysiol.1985.sp015581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliver D, Knipper M, Derst C, Fakler B. Resting potential and sub-membrane calcium concentration of inner hair cells in the isolated mouse cochlea are set by KCNQ-type potassium channels. J Neurosci. 2003;23:2141–2149. doi: 10.1523/JNEUROSCI.23-06-02141.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson RD, Nimmo-Smith I, Weber DL, Milroy R. The deterioration of hearing with age: frequency selectivity, the critical ratio, the audiogram, and speech threshold. J Acoust Soc Am. 1982;72:1788–1803. doi: 10.1121/1.388652. [DOI] [PubMed] [Google Scholar]
- Ricci AJ, Fettiplace R. The effects of calcium buffering and cyclic AMP on mechano-electrical transduction in turtle auditory hair cells. J Physiol (Lond) 1997;501:111–124. doi: 10.1111/j.1469-7793.1997.111bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci AJ, Fettiplace R. Calcium permeation of the turtle hair cell mechanotransducer channel and its relation to the composition of endolymph. J Physiol (Lond) 1998;506:159–173. doi: 10.1111/j.1469-7793.1998.159bx.x. [Erratum (1998) 507:939] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci AJ, Wu YC, Fettiplace R. The endogenous calcium buffer and the time course of transducer adaptation in auditory hair cells. J Neurosci. 1998;18:8261–8277. doi: 10.1523/JNEUROSCI.18-20-08261.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci AJ, Gray-Keller M, Fettiplace R. Tonotopic variations of calcium signalling in turtle auditory hair cells. J Physiol (Lond) 2000;524:423–436. doi: 10.1111/j.1469-7793.2000.00423.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci AJ, Kennedy HJ, Crawford AC, Fettiplace R. The transduction channel filter in auditory hair cells. J Neurosci. 2005;25:7831–7839. doi: 10.1523/JNEUROSCI.1127-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson D, Paki B. Role of L-type Ca2+ channels in transmitter release from mammalian inner hair cells. II. Single-neuron activity. J Neurophysiol. 2002;87:2734–2740. doi: 10.1152/jn.2002.87.6.2734. [DOI] [PubMed] [Google Scholar]
- Salt AN, Inamura N, Thalmann R, Vora A. Calcium gradients in inner ear endolymph. Am J Otolaryngol. 1989;10:371–375. doi: 10.1016/0196-0709(89)90030-6. [DOI] [PubMed] [Google Scholar]
- Santos-Sacchi J. Asymmetry in voltage-dependent movements of isolated outer hair cells from the organ of Corti. J Neurosci. 1989;9:2954–2962. doi: 10.1523/JNEUROSCI.09-08-02954.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santos-Sacchi J. Reversible inhibition of voltage-dependent outer hair cell motility and capacitance. J Neurosci. 1991;11:3096–3110. doi: 10.1523/JNEUROSCI.11-10-03096.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnee ME, Ricci AJ. Biophysical and pharmacological characterization of voltage-gated calcium currents in turtle auditory hair cells. J Physiol (Lond) 2003;549:697–717. doi: 10.1113/jphysiol.2002.037481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnee ME, Lawton DM, Furness DN, Benke TA, Ricci AJ. Auditory hair cell-afferent fiber synapses are specialized to operate at their best frequencies. Neuron. 2005;47:243–254. doi: 10.1016/j.neuron.2005.06.004. [DOI] [PubMed] [Google Scholar]
- Shah DM, Freeman DM, Weiss TF. The osmotic response of the isolated, unfixed mouse tectorial membrane to isosmotic solutions: effect of Na+, K+, and Ca2+ concentration. Hear Res. 1995;87:187–207. doi: 10.1016/0378-5955(95)00089-m. [DOI] [PubMed] [Google Scholar]
- Sterkers O, Ferrary E, Amiel C. Production of inner ear fluids. Physiol Rev. 1988;68:1083–1128. doi: 10.1152/physrev.1988.68.4.1083. [DOI] [PubMed] [Google Scholar]
- Wood JD, Muchinsky SJ, Filoteo AG, Penniston JT, Tempel BL. Low endolymph calcium concentrations in deafwaddler2J mice suggest that PMCA2 contributes to endolymph calcium maintenance. J Assoc Res Otolaryngol. 2004;5:99–110. doi: 10.1007/s10162-003-4022-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu YC, Art JJ, Goodman MB, Fettiplace R. A kinetic description of the calcium-activated potassium channel and its application to electrical tuning of hair cells. Prog Biophys Mol Biol. 1995;63:131–158. doi: 10.1016/0079-6107(95)00002-5. [DOI] [PubMed] [Google Scholar]
- Wu YC, Ricci AJ, Fettiplace R. Two components of transducer adaptation in auditory hair cells. J Neurophysiol. 1999;82:2171–2181. doi: 10.1152/jn.1999.82.5.2171. [DOI] [PubMed] [Google Scholar]
- Yamoah EN, Lumpkin EA, Dumont RA, Smith PJ, Hudspeth AJ, Gillespie PG. Plasma membrane Ca2+-ATPase extrudes Ca2+ from hair cell stereocilia. J Neurosci. 1998;18:610–624. doi: 10.1523/JNEUROSCI.18-02-00610.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeddies DG, Siegel JH. A biophysical model of an inner hair cell. J Acoust Soc Am. 2004;116:426–441. doi: 10.1121/1.1755237. [DOI] [PubMed] [Google Scholar]
- Zhang SY, Robertson D, Yates G, Everett A. Role of L-type Ca2+ channels in transmitter release from mammalian inner hair cells. I. Gross sound-evoked potentials. J Neurophysiol. 1999;82:3307–3315. doi: 10.1152/jn.1999.82.6.3307. [DOI] [PubMed] [Google Scholar]


