On the evolution of the quality of macromolecular models in the PDB

Abstract

Crystallographic models of biological macromolecules have been ranked using the quality criteria associated with them in the Protein Data Bank (PDB). The outcomes of this quality analysis have been correlated with time and with the journals that published papers based on those models. The results show that the overall quality of PDB structures has substantially improved over the last ten years, but this period of progress was preceded by several years of stagnation or even depression. Moreover, the study shows that the historically observed negative correlation between journal impact and the quality of structural models presented therein seems to disappear as time progresses.

Graphical Abstract

Quality criteria are proposed to rank the macromolecular models in the Protein Data Bank (PDB) and the results are correlated with time and with the journals that published papers based on those models. The overall quality of PDB structures has substantially improved over the last decade and the negative correlation between journal impact factor and the quality of structural models presented therein seems to disappear as time progresses.

Introduction

Structural biology has fulfilled a history changing mission in science at the interface of physics, chemistry and biology when for over six decades it has maintained its leading role in providing the structural basis for our understanding of life [1–4]. Its results were always regarded as exceptionally solid, and created a gold standard in biological research, almost unattainable in many other areas of life sciences. This view has largely persisted until today, in part even fortified by the incredible technical advances in the generation and detection of X-rays, progress in computer software development, revolution in biotechnology, and innovations in crystallogenesis. However, with the expansion of the Protein Data Bank (PDB) [5] from merely seven structures at its inception in 1971 to ~160,000 today, it is inevitable that some of the macromolecular models will be subpar and sometimes even incorrect. Unfortunately, suboptimal structures have a tangible negative impact on biomedical research that relies on structural data [6]. However, crystallographers, who have always been in the forefront of structural biology, also in this regard seem to be setting example of how to deal with suboptimal or irreproducible science. The protein crystallographic community has been made painfully aware of these problems [7–10], partly in the rising wave of concern about irreproducibility of scientific research and of biomedical research in particular [11]. This awareness has led to positive outcomes, such as, for example, development of structure validation criteria and protocols, or development of tools for the detection and correction of model errors [12].

The PDB itself, who is the chief custodian of the structural treasury amassed by structural biologists, has been developing tools and standards for the assessment of the quality of the structural models deposited in its archives [13,14]. Similarly, more and more journals are starting to require structural validation reports generated by the PDB upon manuscript submission. However, in some opinions these actions are still insufficient and many problems could be better checked at source rather than being tracked in time-delayed model-correction actions [15,16], when the ripple effect of structural errors may have already taken its toll. Objectively speaking, however, in view of the immense scale of the PDB, one should be in fact grateful for all the effort already taken and the plans proposed for the future of the data bank. In particular, the PDB has been developing a consistent and informative set of quality indicators, which now accompany each new crystal structure deposition. These indicators have been recently used to assess the evolution of the quality of the PDB deposits with time [17].

However, it is not only the PDB that has the responsibility for maintaining high standard of the structural information generated by structural biology. The prime burden is of course on the authors, but this is usually the weakest link: rarely because of ill-intention or fraud and more frequently because of haste, lack of training, lack of supervision, or the delusive belief that the incredible recent progress has converted crystallography to a very easy and almost completely automatic analytical method. An important deal of responsibility rests with the referees and editors of the journals that publish those results, as the ripple effect of error and fatal contamination of science is most efficiently propagated through cited literature [18]. More than a decade ago Brown & Ramaswamy (hereinafter B&R) published a survey of the quality of crystallographic models of biological macromolecules [19], and correlated the results with the journals in which those models had been published. The results came as a bit of a shock to many because it turned out that the journals usually regarded as the most prestigious were found to publish worse than average structures when compared with other journals. The FEBS Journal was one of the first requesting structure validity reports and thus in the ranking list of B&R was among the top journals. Similar questions have been raised by Read & Kleywegt (hereinafter R&K), albeit using different statistical tools [20]. In contrast to the B&R study, R&K reported very small quality differences between structures published in high-impact journals and in other venues.

Nearly 13 years after the B&R study and with the PDB expanded nearly four times we decided to conduct a similar analysis to see if the community at large, or at least its journals, have improved. In our approach, we used the statistical methods of data imputation and Principal Component Analysis (PCA) of the model quality indicators recommended by the PDB. In contrast to previous studies, which focused on protein structures only, our analysis comprises all crystallographic structures in the PDB, i.e. also includes nucleic acids. Moreover, we also consider models marked as To be published, which were not analyzed by B&R or R&K. Although the scope of data and the statistical tools we are using are different from those used by B&R in 2007, we are still able to compare the journal rankings of the two surveys because our approach may be easily adapted to a retrospective analysis of data from past versions of the PDB. It is important to clarify that omission of NMR and Cryo-EM structures was intentional. Considering the difficulties connected with estimation of quality of NMR and Cryo-EM structural models, and also the very small contribution of both these methods to the characterization of structures that contain ligands (and are thus most interesting and important), we decided to focus on models provided by X-ray crystallography, which represent 89% of all models currently deposited in the PDB.

Our results show that the overall quality of PDB structures has substantially improved over the last ten years. However, our study also shows that this period of improvement was preceded by several years of stagnation or, if one considers the improvement of software and hardware over time, even depression. Finally, the observation made by B&R that journal impact factor (reputation) is frequently negatively correlated with structure quality is no longer true.

Results

Measure of Overall Model Quality and Missing Data Imputation

The analysis included all X-ray structures available in the PDB as of December 10, 2019, totaling 141,154 deposits dating back as far as 1972. To assess the quality of structures published in particular journals, we initially attempted to use the Q1_p measure proposed by Shao et al. [17]. Q1_p is a measure of overall protein structure quality that combines into one number five different indicators: R_free, RSRZ (normalized Real Space R-factor) outliers, Ramachandran outliers, Rotamer outliers, and Clashscore [21] using the following formula:

$$Q{1}_p=\frac{P_{\mathit{\text{Rfree}}}+P_{\%\mathit{\text{RSRZ}}}+P_{PC1\left(\mathit{\text{geometry}}\right)}}{3}$$ (1)

where P_Rfree, P_%RSRZ, and P_{PC1(geometry)} are ranking percentiles (the higher the better), characterizing for a given structural model, respectively, its R_free, percentage of RSRZ outliers, and the first principal component of the PCA of Ramachandran outliers, Rotamer outliers and Clashscore (see Methods section for details). Once Q1_p is calculated, each PDB deposit is ranked within the population to obtain its final ranking percentile P_Q1p, with the lowest (worst) value of Q1_p at 0% and highest (best) at 100% [17]. We note, that in this paper we took an averaging approach to percentiles, i.e., a group of tied Q1_p values was assigned the same percentile rank, one that is the average rank of the group. By combining five distinct quality measures, P_Q1p provides a simple way of comprehensive comparison and ranking of many structural models.

The P_Q1p metric was originally designed to assess protein structures only. For nucleic acid structures, which are also present in the PDB, Q1_p cannot be used directly because the notions of Ramachandran and Rotamer outliers are not applicable to those structures. However, for proteins both missing elements are implicitly contained in P_{PC1(geometry)}. Therefore, for nucleic acids we calculated analogous Q1_n without the use of PCA, but applying the following simplified formula:

$$Q{1}_n=\frac{P_{\mathit{\text{Rfree}}}+P_{\%\mathit{\text{RSRZ}}}+P_{\mathit{\text{Clashscore}}}}{3}$$ (2)

where P_Clashscore is the ranking percentile of Clashscore. In the following analysis, Q1_p and Q1_n (and, consequently, P_Q1p and P_Q1n) were computed separately for proteins and nucleic acids, respectively. This way, the percentiles used for Q1_p and Q1_n rank structures of the respective type. Protein-nucleic acid complexes were assigned to the protein group, since it is possible to calculate all quality metrics for such structures.

Since averaging of multiple quality metrics might potentially blur the spotlight on models with serious problems, an alternative aggregation method could involve taking only the minimum percentile of all the metrics used. In this approach, a structure is considered as good as its weakest feature, according to the following formulas:

$$Q{1}_{p_{min}}=\text{min}\left(P_{\mathit{\text{Rfree}}},P_{\%\mathit{\text{RSRZ}}},P_{PC1\left(\mathit{\text{geometry}}\right)}\right)$$ (3)

$$Q{1}_{n_{min}}=\text{min}\left(P_{\mathit{\text{Rfree}}},P_{\%\mathit{\text{RSRZ}}},P_{\mathit{\text{Clashscore}}}\right)$$ (4)

In the remainder of the paper, we will focus mainly on the averaging approach using Eq. 1 and 2, but will also compare it with the minimum approach based on Eq. 3 and 4.

It must be emphasized that P_Q1p can be computed only for those PDB structures that have all five (or in the case of P_Q1n all three) component measures attached to them. The PDB has done an excellent job of calculating these metrics for most of the deposits, but not all structures have all the necessary data to perform these calculations. Overall, 12.7% of all considered deposits are missing at least one quality metric, with RSRZ being the dominating missing value (Table 1). Leaving this situation as is would effectively limit the analysis to structures published after 1992, i.e., to the time after R_free was introduced [22]. To circumvent this dilemma and to perform a study encompassing the entire timespan of the PDB, we have developed a protocol for the estimation of the missing values based on a machine learning data imputation method.

Table 1.

Quality metric means, standard deviations, and fractions of missing values in the PDB.

Metric	Mean	Standard deviation	Missing values [%]
Clashscore	8.05	9.11	0.10
Ramachandran outliers [%]	0.49	1.26	1.69
Rotamer outliers [%]	3.26	3.65	1.72
RSRZ outliers [%]	4.05	4.06	9.56
Rfree [%]	23.35	3.82	4.29
Supporting metrics
R [%]	19.31	3.25	2.39
Resolution [Å]	2.13	0.56	0
Year of deposition	-	-	0

The validity of the data imputation procedure was assessed on the complete portion of the PDB, to which artificially missing (i.e. deliberately removed) values were introduced at random following the missing data proportions of each metric. The missing values were then replaced using either the metric’s mean, median or by an iterative method called Multiple Imputation by Chained Equations (MICE) [23,24] with Bayesian linear regression [25]. MICE builds regression functions for subsequent metrics based on non-missing values from other variables. The variables used to aid imputation involved all the metrics in question, plus three supporting variables, not used in the assessment protocol: the R factor, data resolution (d_min), and year of deposition (Table 1). The results of 100 random experiments testing the imputation methods are presented in Table 2.

Table 2. Evaluation of data imputation methods.

Mean results of 100 random experiments with standard deviations given in parentheses, in units of the last significant digit of the mean. MAD: Median Absolute Deviation, MAE: Mean Absolute Error, RMSE: Root-Mean-Square Error.

Error	Method	Clashscore	RSRZ outliers [%]	Ramachandran outliers [%]	Rotamer outliers [%]	R free [%]
MAD	MICE	2.5(3)	2.01(2)	0.21(1)	1.23(3)	1.02(2)
	Mean	4.4(3)	2.30(2)	0.49(1)	2.11(4)	2.50(4)
	Median	2.9(3)	1.86(2)	0.04(1)	1.39(4)	2.50(4)
MAE	MICE	3.7(4)	2.54(3)	0.41(2)	1.77(4)	1.31(2)
	Mean	5.7(6)	2.74(3)	0.61(2)	2.56(6)	3.00(3)
	Median	5.1(7)	2.60(3)	0.49(3)	2.34(7)	3.00(3)
RMSE	MICE	5.7(15)	3.84(15)	0.84(11)	2.64(10)	1.77(3)
	Mean	8.9(23)	4.04(14)	1.24(16)	3.65(14)	3.82(4)
	Median	9.3(24)	4.17(14)	1.32(16)	3.85(15)	3.82(4)

It can be seen that MICE is superior to mean/median replacement for all metrics according to the Mean Absolute Error (MAE) and Root-Mean-Square Error (RMSE), and for all but two metrics according to the Median Absolute Deviation (MAD). All the differences between MICE and the remaining methods are statistically significant according to the Friedman and Nemenyi post-hoc tests [26] (p < 0.001). In terms of absolute values, the mean absolute error of MICE is usually two to four times smaller than the standard deviation of a given quality metric (Table 1, Supplementary Fig. S1¹). The results are particularly good for Clashscore and R_free, owing to the small number of missing values and high correlation with R, respectively. In the remaining part of the paper, we discuss results obtained for the full PDB dataset with missing values imputed using the MICE method. We want to stress that in doing so our goal is to give an approximate overview of the average quality of structures in the early years of the PDB, and not to provide a way to assess individual deposits with missing quality metrics or to create nonexistent data.

Model quality at the Time of Deposition

Fig. 1 shows that P_Q1p and P_Q1n tend to gradually improve over the years. Almost identical trends can be noticed when looking at deposits without imputed data (Supplementary Fig. S2) and when using the minimum approach (Supplementary Fig. S3). Obviously, this trend is correlated with the advances in the generation of X-rays and in data collection procedures, with better computer hardware and software, with heightened structure validation standards, and with progress in crystallogenesis. If one were to use P_Q1 (i.e., P_Q1p or P_Q1n depending on structure type) calculated over all the analyzed years to rank journals, then journals with longer history would be at a disadvantage because they contain old, quality-wise inferior structures. Thus, even though a structure might have been refined to an impressively high standard in its time, today it might be treated as a poorly refined case. One could, of course, recalculate the percentiles separately for each decade or even shorter time periods, but this might not be enough to cure this problem (see the rapid improvement in quality over the last 10 years) or could drastically reduce the data volume and effectively make journal comparisons impossible. Therefore, we introduce here a new, time (t)-dependent P_Q1(t) parameter, which corresponds to P_Q1 calculated at the time of structure deposition. For example, the 1990 PDB deposition 2RSP [27] achieves an overall quality percentile P_Q1 of 36%, meaning that it is better than only 36% protein deposits that are currently held in the archive. Should the structure be ranked against the 416 structures deposited prior to 2RSP, it achieves P_Q1(t) of 69%, meaning that it was significantly above-average at the time of its deposition.

Figure 1. P_Q1 analysis.

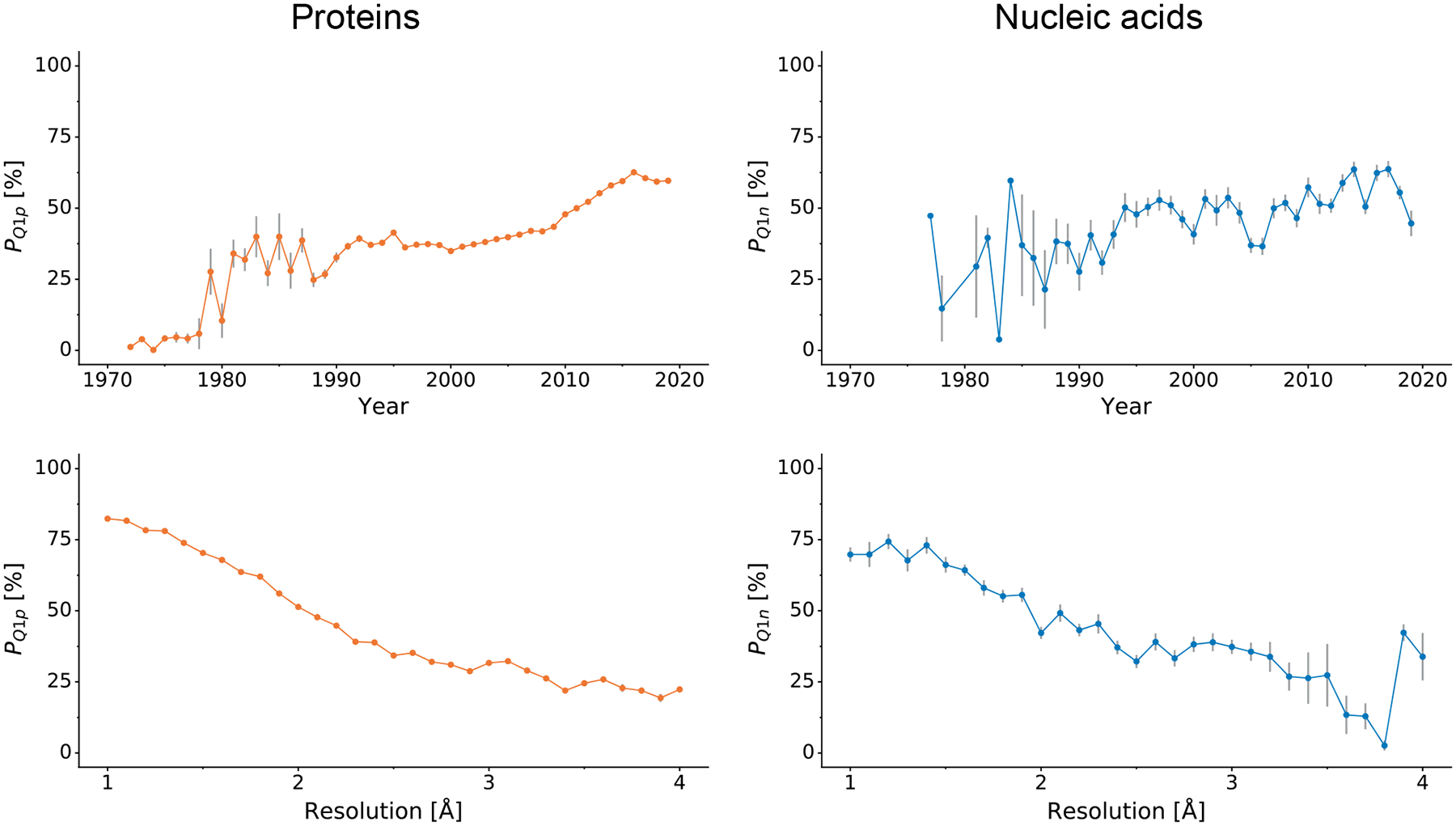
Variation in the mean P_Q1 percentile (higher is better) over time (top) and as a function of resolution (bottom) for proteins (left) and nucleic acids (right). Error bars indicate estimated unbiased standard errors of the mean.

Moreover, in view of the very high correlation between quality and resolution (Fig. 1, Supplementary Fig. S2 and S3), we propose yet another measure, called P_Q1(t,d). P_Q1(t,d) is the Q1 percentile calculated at the time of structure deposition (t) for a given resolution interval (d), where the resolution is rounded to the nearest 0.1 Å and capped at 1 Å and 4 Å. The 2RSP structure from the previous example scores a P_Q1(t,d) of 75%. The advantage of using P_Q1(t,d) is that data resolution will not affect the journal ranking list.

Using P_Q1p(t,d) and P_Q1n(t,d) one can assess the quality of protein and nucleic acid models over time. The average P_Q1p(t,d) for proteins in the PDB is 58.7%, whereas nucleic acids have the average P_Q1n(t,d) of 59.9%. Fig. 2 shows how the model quality at the time of deposition of these two types of macromolecules has evolved over the years. For many years in the past, newly deposited nucleic acid models were usually of better quality than newly deposited protein models, especially between 1993 and 2004. However, the steady improvement of the quality of protein models in the last decade has made them currently to be on a par, if not better, than currently deposited nucleic acids models. Similar trends were observed using P_Q1pmin(t,d) and P_Q1nmin(t,d), i.e. the minimum approach (Supplementary Fig. S4).

Figure 2. Comparison of P_Q1(t,d) of protein and nucleic acid structures over time.

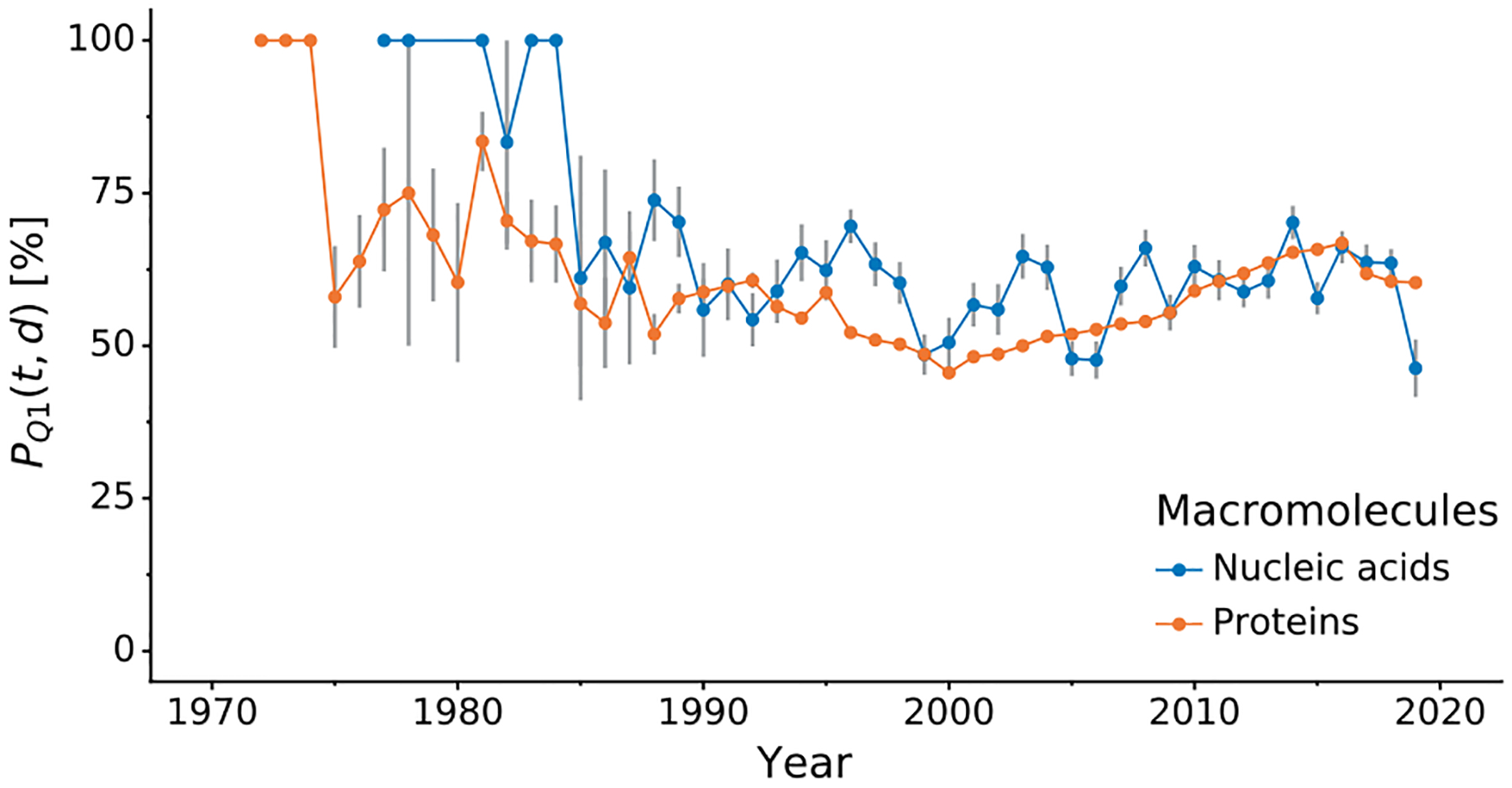
Variation in mean P_Q1(t,d) quality percentile (y-axis, higher is better), comparing nucleic acid and protein structures (color) over time (x-axis). Error bars indicate estimated unbiased standard errors of the mean.

In the following subsections, we will focus on ranking structures and their corresponding journals according to P_Q1(t,d). The rankings associated with P_Q1(t), P_Q1min(t,d) and P_Q1min(t) are available in the online supplementary materials for this publication. For the purposes of ranking journals, the percentiles for proteins and nucleic acids will be combined, and denoted jointly as P_Q1(t,d) or P_Q1(t).

All-time Journal Ranking

Out of 800 unique journals being the primary citations for the 141,154 deposits found in the PDB, we selected those that published papers presenting at least 100 macromolecular structures. We decided to limit the list of journals to such a subset, as we believe that it may be too early to assess journals with less than 100 described structures. The resulting 91 journals were ranked according to average P_Q1(t,d) (Table 3) as well as P_Q1(t), P_Q1min(t,d) and P_Q1min(t) (Supplementary Tables S1–S3).

Table 3. All-time journal ranking according to P_Q1(t,d).

The ranking includes all the journals that had at least 100 primary citations of structures in the PDB. P_Q1(t,d) higher than 50% means that the structures published in a given journal were, on average, better than 50% of structures of similar resolution present in the PDB at the time of deposition. Journals with more than 1000 structures are highlighted in gray. The most frequent venue (To be published) is highlighted in bold.

Rank	Journal	Mean PQ1(t,d) [%]	Mean resolution [Å]	G-Mean resolution [Å]	V-Mean resolution [Å]	Structure count
1	TUBERCULOSIS (EDINB)*	87.38	2.02	2.00	1.92	132
2	EUR J MED CHEM*	71.05	2.03	1.97	1.81	418
3	ACS CATAL*	69.25	1.94	1.88	1.70	241
4	ACS INFECT DIS*	68.32	1.95	1.90	1.78	153
5	CHEMBIOCHEM*	68.30	1.92	1.87	1.71	527
6	IUCRJ*	67.76	1.95	1.88	1.69	281
7	ORG BIOMOL CHEM	67.42	1.88	1.82	1.64	167
8	MBIO	66.72	2.24	2.15	1.91	169
9	ARCH BIOCHEM BIOPHYS*	66.13	2.08	2.03	1.89	276
10	INT J MOL SCI	65.77	2.12	2.04	1.81	103
11	CHEMISTRY	65.66	1.82	1.77	1.62	242
12	BIOCHEM J*	65.42	2.11	2.06	1.89	1,033
13	FEBS J*	65.11	2.02	1.97	1.81	1,539
14	CELL HOST MICROBE	64.85	2.50	2.43	2.20	107
15	PLOS PATHOG*	64.72	2.25	2.17	1.96	656
16	NAT MICROBIOL	64.69	2.32	2.25	2.04	111
17	CHEM COMMUN	64.58	1.81	1.75	1.59	280
18	VIROLOGY	64.38	2.44	2.37	2.18	126
19	NAT CHEM BIOL*	64.12	2.19	2.12	1.92	1,013
20	APPL ENVIRON MICROBIOL	64.00	2.01	1.96	1.83	112
21	ACS CHEM BIOL*	63.83	2.04	1.98	1.83	1,104
22	ACTA CRYST F*	63.59	2.09	2.02	1.81	1,466
23	SCI REP*	63.39	2.16	2.09	1.88	1,847
24	ANGEW CHEM*	63.25	1.92	1.85	1.64	1,065
25	J INORG BIOCHEM	62.82	1.78	1.73	1.57	171
26	J BIOL INORG CHEM	62.61	1.88	1.82	1.64	265
27	ACS OMEGA	62.60	1.81	1.77	1.64	102
28	J COMPUT AIDED MOL DES	62.39	1.88	1.86	1.77	115
29	CHEM SCI	61.98	1.87	1.83	1.68	268
30	MABS	61.91	2.35	2.29	2.14	115
31	J SYNCHROTRON RADIAT	61.75	1.79	1.73	1.56	147
32	PLOS ONE*	61.57	2.15	2.09	1.92	2,057
33	GLYCOBIOLOGY	61.48	1.96	1.90	1.74	188
34	CHEMMEDCHEM	61.40	1.94	1.88	1.69	556
35	TO BE PUBLISHED*	61.39	2.03	1.98	1.81	22,421
36	NAT COMMUN*	61.37	2.21	2.11	1.86	3,538
37	FEBS LETT	61.30	2.10	2.04	1.85	814
38	NAT CHEM	61.11	1.95	1.85	1.65	173
39	ANTIMICROB AGENTS CHEMOTHER	61.10	1.96	1.88	1.65	309
40	ACS MED CHEM LETT	61.01	2.12	2.06	1.88	1,062
41	RNA	60.95	2.44	2.32	1.97	245
42	J AM CHEM SOC	60.89	2.00	1.93	1.74	2,369
43	PROTEIN ENG DES SEL	60.59	2.05	2.00	1.84	294
44	CELL CHEM BIOL	60.17	2.08	2.03	1.88	902
45	ACTA CRYST D	60.06	1.99	1.91	1.70	4,952
46	MOL PHARMACOL	59.99	2.35	2.27	2.02	129
47	BMC STRUCT BIOL	59.56	2.08	2.02	1.84	228
48	BIOCHEMISTRY	59.45	2.05	2.00	1.84	8,896
49	MOL MICROBIOL	59.41	2.16	2.09	1.87	412
50	BIOCHIMIE	59.04	2.07	2.02	1.81	128
51	J BIOCHEM	59.01	2.05	2.01	1.88	279
52	FASEB J	58.88	2.03	1.98	1.86	161
53	NUCLEIC ACIDS RES	58.77	2.28	2.21	1.98	2,127
54	STRUCTURE	58.53	2.20	2.11	1.86	5,348
55	PROTEIN SCI	58.46	2.07	2.02	1.85	2,235
56	J MED CHEM	58.29	2.07	2.02	1.86	5,525
57	J VIROL	58.24	2.34	2.26	2.06	957
58	PLANT CELL	58.00	2.21	2.17	2.05	138
59	BIOCHIM BIOPHYS ACTA	57.99	2.09	2.04	1.87	600
60	SCI ADV	57.95	2.33	2.22	1.85	182
61	J BIOL CHEM	57.91	2.12	2.06	1.89	11,055
62	J STRUCT BIOL	57.49	2.15	2.08	1.90	1,038
63	J BACTERIOL	57.37	2.22	2.16	2.01	371
64	BIOORG MED CHEM	57.28	2.10	2.04	1.88	659
65	PROTEINS	57.09	2.07	2.01	1.84	1,999
66	CELL REP	56.55	2.52	2.42	2.16	399
67	J EXP MED	56.35	2.34	2.28	2.08	121
68	BIOCHEM BIOPHYS RES COMMUN	56.28	2.18	2.11	1.92	976
69	PNAS*	55.79	2.27	2.19	1.94	7,376
70	INT J BIOL MACROMOL	55.51	2.05	2.00	1.80	168
71	PLOS BIOL	55.43	2.35	2.25	2.01	336
72	ELIFE	55.40	2.41	2.30	2.03	869
73	BIOPHYS J	55.36	1.92	1.85	1.66	199
74	J MOL BIOL*	55.25	2.13	2.06	1.88	9,507
75	CELL RES	54.60	2.42	2.36	2.20	189
76	J STRUCT FUNCT GENOM	54.30	2.07	2.03	1.92	168
77	NATURE*	53.84	2.52	2.42	2.12	3,060
78	PROTEIN CELL	53.44	2.26	2.21	2.04	178
79	GENES DEV	53.44	2.41	2.33	2.11	279
80	SCIENCE*	53.15	2.50	2.39	2.10	1,949
81	NAT IMMUNOL	52.94	2.52	2.45	2.22	119
82	EMBO REP	52.92	2.35	2.28	2.09	211
83	J IMMUNOL	52.10	2.26	2.19	2.02	296
84	NEURON	51.35	2.63	2.41	2.08	149
85	IMMUNITY	51.10	2.44	2.37	2.18	265
86	COMMUN BIOL	51.01	2.39	2.31	2.00	104
87	MOL CELL*	50.38	2.45	2.37	2.14	1,599
88	BIOORG MED CHEM LETT*	50.19	2.19	2.16	2.05	1,590
89	NAT STRUCT MOL BIOL*	49.78	2.40	2.31	2.07	2,915
90	CELL*	49.38	2.54	2.45	2.20	1,563
91	EMBO J*	49.15	2.37	2.30	2.10	1,910

^*Denotes journals that have average P_Q1(t,d) significantly different than the average P_Q1(t,d) of the entire PDB, according to Welch’s t-test with Bonferroni correction at significance level α=0.001. Mean denotes the arithmetic mean, G-mean denotes the geometric mean (log-average), V-mean denotes the mean in Å⁻³.

Surprisingly, the first place in all versions of the ranking is occupied by Tuberculosis, a venue that is not well known as a structural journal. However, this place is well earned since Tubeculosis has over 16 percentage points of advantage over the second ranked journal in terms of P_Q1(t,d) and 12 percentage points of advantage in the P_Q1(t) ranking. A closer inspection of the structures published in Tuberculosis reveals that the vast majority of structures refer to one publication titled “Increasing the structural coverage of tuberculosis drug targets” [28]. The publication and its corresponding structures are the result of the joint effort of various departments working in the Seattle Structural Genomics Center for Infectious Disease. This finding is in accordance with the conclusions of B&R [19] that structural genomics initiatives usually deposit structures of above-average quality [29,30]. Indeed, taking into account all 12,494 deposits attributed to structural genomics projects, they achieve a mean P_Q1(t,d) of 63.7% and P_Q1(t) of 64.3%, substantially above the average of the entire PDB (58.6% and 57.7%, respectively). These differences are statistically significant according to Welch’s t-test (p < 0.001) and are much more prominent than those reported in the R&K study [20]. This discrepancy most probably stems from the fact that in our study we used a relative measure that combines several quality metrics, and had 2.3 times more structural genomics deposits at our disposal and 6.1 times more structures overall.

When looking at the most popular journals, i.e. those with more than 1000 structures (Table 3, gray rows), the top three spots are occupied by Biochemical Journal, FEBS Journal, and Nature Chemical Biology. At the other end of the spectrum, we have EMBO Journal, Cell, and Nature Structural & Molecular Biology, which were ranked last according to P_Q1(t,d). It is worth noting that the latter three journals are the only journals that have average P_Q1(t,d) below 50%. This means that, on average, at the time of deposition, the structures presented in these journals were already worse than over 50% of PDB structures of similar resolution. A similar ranking was obtained using P_Q1(t) (Supplementary Table S1), the main difference being that journals publishing structures at superior resolution, such Chemistry or Acta Crystallographica D, achieved much higher positions in the journal ranking. Table 3 and Supplementary Table S1–S3 also identify journals whose average P_Q1(t,d), P_Q1(t), P_Q1min(t,d), and P_Q1min(t) are significantly different from the expected values of the entire PDB population.

It should be noted that the ranking presented in Table 3 takes into account over 45 years of structural data. This means that the ranking averages the entire lifespans of journals, which in their own individual history might have evolved over time. That is why in the following section we analyze how the ranking of the most popular journals has changed over the years.

Quality of Journals’ Structures Over Time

Owing to the fact that P_Q1(t,d) assesses structures at the time of deposition, we also analyzed rankings of journals as a function of time. Fig. 3 presents the ranking of 25 all-time most popular journals in periods of five years. To minimize the effect of noise on the ranking, journals were assigned to a given five-year period only when they contained primary citations to at least 30 structures within that period.

Figure 3. Journal ranking over time according to P_Q1(t,d).

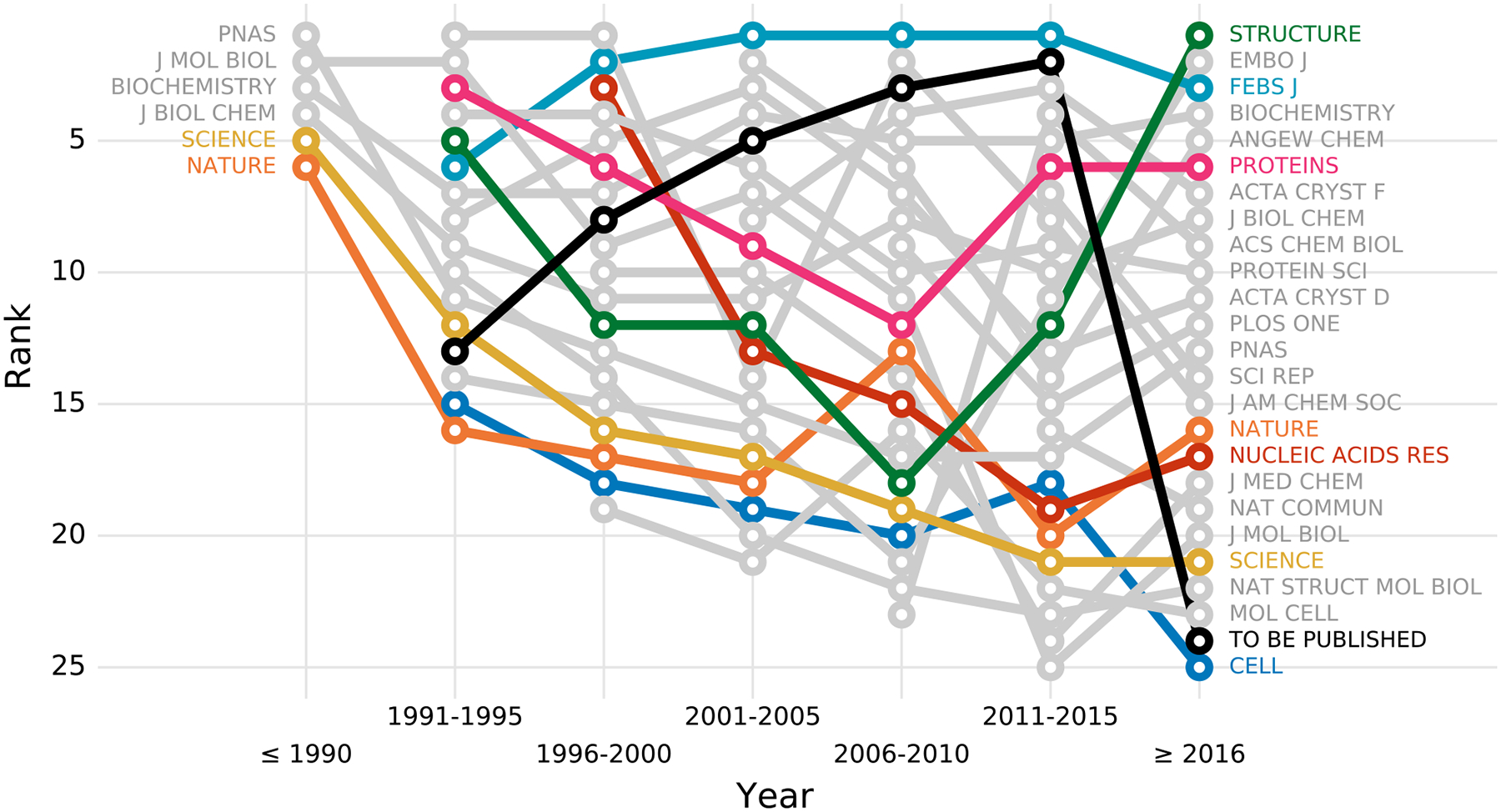
The plot shows the journal’s rank (y-axis) in a given time period (x-axis). The ranking includes 25 most popular journals, i.e. journals with most structures, ranked based on structures deposited within 5-year windows. A point appears only if a journal published at least 30 structures in a given 5-year interval.

As Fig. 3 shows, only six of the 25 journals published at least 30 structures before 1991, however, these six journals were the primary reference for 482 out of 666 PDB deposits from this period. Biochemistry remains one of the top journals in terms of structure quality to date, PNAS and J. Biol. Chem. are in the middle of the ranking, whereas Nature, Science, and J. Mol. Biol. occupy the bottom half of the ranking. A journal that has steadily remained at the top of the ranking list for most of the years is FEBS Journal. Apart from Biochemistry and FEBS Journal, Proteins can also pride itself with a solid presence in the top 10 of the ranking throughout the years. It is worth noting that these three journals were also highly ranked in the study of B&R [19].

Disappointingly, the relatively poor ranks of highly reputable venues are not a new concern, but rather have been a steady trend for many years. It must be noted, however, that the overall structure quality of practically all 25 of the most popular journals has greatly improved in the last ten years, with Science and Nature noting the most positive trends (Supplementary Fig. S5). Similar observations were made when the journals were ranked according to P_Q1(t) (Supplementary Fig. S6, S7).

A separate comment is required for the “venue” To be published, most frequently found in PDB deposits. This category of PDB entries, omitted in the studies of B&R [19] and R&K [20], presents a very interesting pattern over the years. For several decades, unpublished structures (because staying in the “to be published” state for several years in practice means “unpublished”) noted a steady upward trend, coming as far as the second place among the most popular venues between 2011 and 2015. The low position in the latest ranking period (2016-today) may stem from the fact that many of the recently deposited To be published structures from this time range still have a chance of being published and are under peer review. The retrospective pattern is that structures in the To be published category have higher P_Q1(t,d) (61.4%) than structures that are presented in concrete journals (58.0%) (Welch’s t-test, p < 0.001). Moreover, 8,543 out of 12,494 structural genomics structures remain unpublished even as structure notes, constituting over 66% and 33% of all unpublished structures in the 2005–2010 and 2011–2015 periods, respectively. With fewer structural genomics depositions in the last four years (only 15% of all unpublished structures for this period), the To be published category currently has a lower ratio of high-quality structures. This, combined with the observed constant improvement of published structures, may further contribute to the drop of the To be published category in the ranking.

Retrospective comparison with the results of Brown & Ramaswamy

The journal rankings presented in this work were inspired by the study of Brown and Ramaswamy (B&R) [19]. Although the methodologies used in these two analyses are different (most notably because of incorporation of nucleic acids and the use of data imputation in the present work), it is worth verifying how the two approaches compare, and what has changed since the original B&R study. To help answer these questions, Table 4 presents the journal ranking reported by B&R in 2007 together with two lists of the same journals ranked according to P_Q1(t,d): based on PDB deposits available in 2007, and based on all currently available data.

Table 4. Comparison of journal ranking by Brown and Ramaswamy [19] with rankings of the same journals created using P_Q1(t,d).

Numbers of structures considered from a given journal are shown in parentheses. The top three journals according to B&R are highlighted in green, the bottom three journals are highlighted in red.

B&R ranking [19] (Year < 2007)	Ranking according to PQ1(t,d) (Year < 2007)	Ranking according to PQ1(t,d) (current)
FEBS J*(159)	J BIOL INORG CHEM (114)	BIOCHEM J* (1033)
PROTEIN ENG DES SEL (96)	FEBS J*(356)	FEBS J*(1539)
BIOCHEMISTRY*(3346)	PROTEIN ENG DES SEL (173)	J BIOL INORG CHEM (265)
CELL CHEM BIOL (154)	ACTA CRYST D* (1766)	FEBS LETT* (814)
PROTEINS (398)	BIOCHEM J (165)	J AM CHEM SOC* (2369)
J MOL BIOL (3855)	FEBS LETT (232)	PROTEIN ENG DES SEL (294)
ACTA CRYST D (1074)	CELL CHEM BIOL (204)	CELL CHEM BIOL (902)
PROTEIN SCI (771)	PROTEIN SCI* (1104)	ACTA CRYST D* (4952)
BIOORG MED CHEM LETT (195)	BIOCHEMISTRY*(4564)	BIOCHEMISTRY*(8896)
J STRUCT BIOL (83)	J MOL BIOL* (5497)	NUCLEIC ACIDS RES (2127)
BIOPHYS J (71)	BIOPHYS J (95)	STRUCTURE (5348)
J BIOL INORG CHEM (81)	PROTEINS (993)	PROTEIN SCI (2235)
BIOCHEM J (67)	J AM CHEM SOC (459)	J MED CHEM (5525)
J BIOL CHEM (2849)	BIOCHEM BIOPHYS RES COMMUN (167)	J VIROL (957)
J AM CHEM SOC (324)	NUCLEIC ACIDS RES (288)	J BIOL CHEM (11055)
STRUCTURE (1412)	J BACTERIOL (141)	J STRUCT BIOL (1038)
FEBS LETT (173)	BIOORG MED CHEM (59)	J BACTERIOL (371)
J BACTERIOL (111)	J BIOL CHEM (4090)	BIOORG MED CHEM (659)
BIOORG MED CHEM (53)	J STRUCT BIOL (117)	PROTEINS (1999)
J MED CHEM (450)	J MED CHEM (605)	BIOCHEM BIOPHYS RES COMMUN (976)
NAT STRUCT MOL BIOL (768)	STRUCTURE (2017)	PNAS (7376)
PNAS (1324)	PNAS* (1839)	BIOPHYS J (199)
J VIROL (86)	J VIROL (141)	J MOL BIOL* (9507)
BIOCHEM BIOPHYS RES COMMUN (103)	SCIENCE*(712)	NATURE* (3060)
EMBO J* (768)	EMBO J* (1135)	SCIENCE*(1949)
NUCLEIC ACIDS RES (199)	NAT STRUCT MOL BIOL* (1342)	MOL CELL*(1599)
NATURE* (807)	NATURE* (976)	BIOORG MED CHEM LETT* (1590)
MOL CELL*(422)	BIOORG MED CHEM LETT* (323)	NAT STRUCT MOL BIOL* (2915)
SCIENCE*(571)	CELL*(647)	CELL*(1563)
CELL*(488)	MOL CELL*(571)	EMBO J* (1910)

^*Denotes journals whose quality was determined to be significantly different from the average quality of structures the entire PDB, at significance level α=0.001.

It can be noticed that the rankings bare several similarities, although they are not identical. Journals that were at the top of the B&R ranking generally remain highly ranked according to P_Q1(t,d). Similarly, the bottom regions of the rankings are occupied by the same group of journals. However, there are some notable differences. For example, Bioorg. Med. Chem. Lett. is ranked 19 places lower according to P_Q1(t,d), whereas J. Biol. Inorg. Chem., FEBS Lett. and Nucleic Acids Res. are ranked 11 places higher. These differences may be the result of the number of structures taken into account by each ranking. Compared to the time of the B&R study, significantly more precomputed quality metrics are now available, even for older PDB deposits. Moreover, the methodology proposed in this work imputes missing values, allowing for inclusion of 12.7% additional structures. As a result, the rankings based on P_Q1(t,d) were compiled using much more data, occasionally changing a journal’s rank substantially.

Correlation between structure quality and journal impact

The low-ranking of high impact journals in the current study raises the question of whether structure quality is negatively correlated with journal impact. The study of B&R [19] strongly suggested that this was the case, whereas the slightly more recent work of R&K [20] showed that the differences in structure quality between high-impact and other venues were relatively small. However, both studies manually categorized journals as high- or low-impact venues rather than investigating actual impact metrics for a large set of journal titles.

In this study, we decided to measure journal impact quantitatively and correlate it with our quantitative measure of structure quality. For this purpose, we used two metrics: Impact Per Publication (IPP) and Source Normalized Impact per Paper (SNIP) [31]. IPP is calculated the same way as 3-year impact factor (IF3) but using only publications that are classified as articles, conference papers, or reviews in Scopus. SNIP is a modification of IPP that corrects for differences in citation practices between scientific fields [31]. Both journal metrics have 20 years (1999–2018) of publicly available statistics and are based on the same source data.

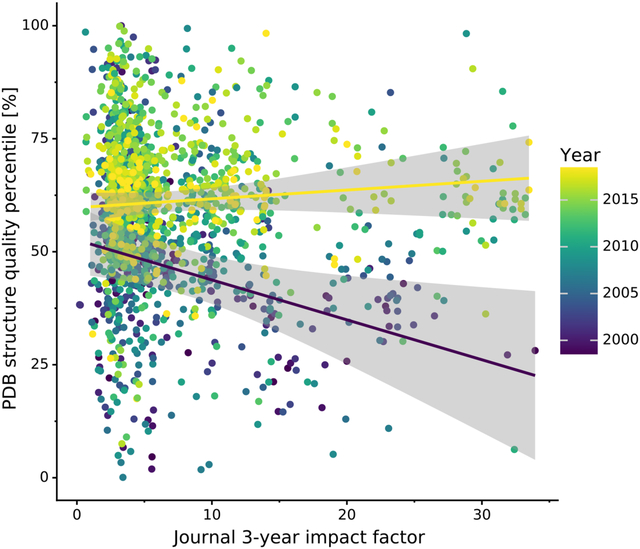
Fig. 4 shows the relation between P_Q1(t,d) and the journal impact over time (separate plots for each year are presented in Supplementary Fig. S8). It is evident that structure quality has substantially improved over the last decade and that the negative correlation between journal impact and the quality of structural models presented therein seems to disappear as time progresses. This observation is confirmed when the relation between journal impact (IPP, SNIP) and structure quality (P_Q1(t,d)) is gauged using Spearman’s rank correlation coefficient. Fig. 5 shows that even though structure quality and journal impact were indeed negatively correlated 20 years ago, currently there is no correlation between these two criteria.

Figure 4. Scatterplot of mean journal P_Q1(t,d) and the journal’s impact over time.

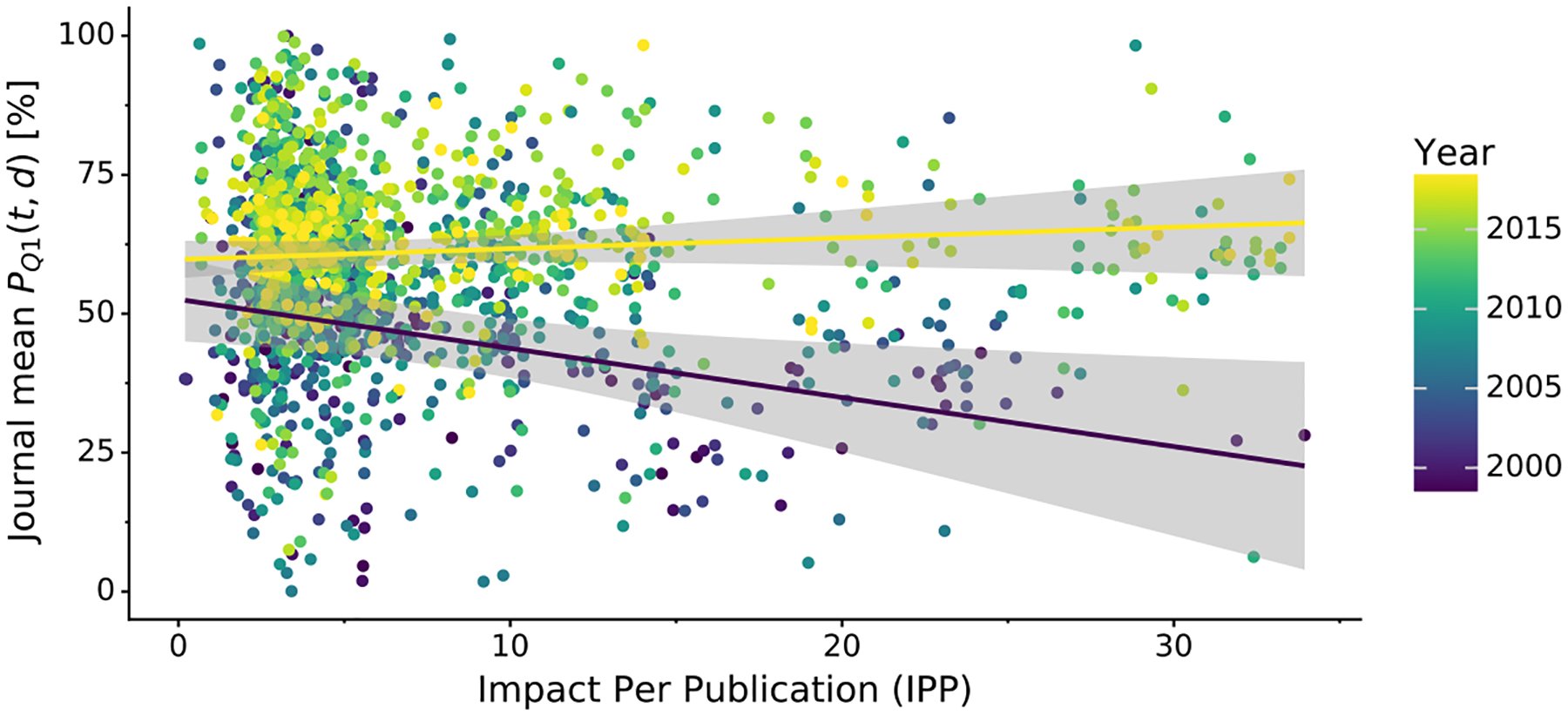
Variation in mean journal P_Q1(t,d) (y-axis) in a given year (color) plotted against the journals Impact Per Publication (IPP). IPP uses the same formula as the 3-year Impact Factor, but is based on publicly available Scopus data. The two regression lines show linear trends for 1999 (indigo) and 2018 (yellow) along with 95% confidence intervals (gray areas).

Figure 5. Correlation between structure quality and journal impact.

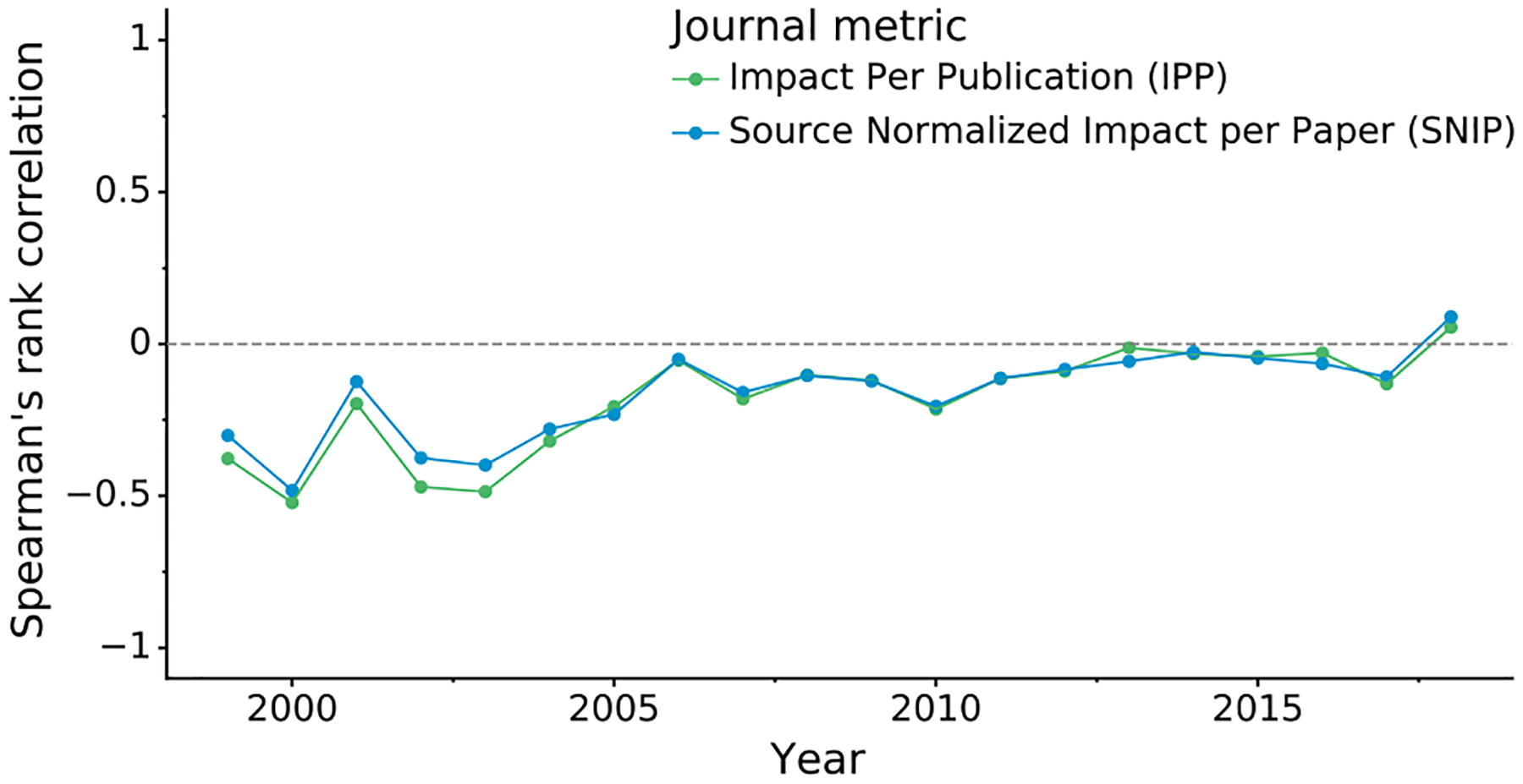
The plot shows Spearman’s rank correlation (y-axis) over time (x-axis) between structure quality measured by P_Q1(t,d) and journal impact measured using the IPP and SNIP metrics. IPP uses the same formula as the 3-year Impact Factor but is based on Scopus data, whereas SNIP additionally takes into account the scientific field.

Fig. 4 also shows a very interesting situation in the low-IF range, namely that low-IF journals publish just about anything: the most fantastic work as well as structures beneath contempt. On the other hand, medium-IF journals used to be primary citations of mostly poor structures in the past. At present, however, they are doing a much better job, publishing mostly better-than-average structures.

Discussion

Our analysis confirms recent reports that the quality of crystallographic macromolecular structures has improved over the last years [17]. However, we also found out that at the time of the B&R analysis the quality of PDB structures temporarily stopped improving, and that this is most likely why B&R did not report any correlation between quality and time [19]. In addition to confirming earlier findings, by using a data imputation algorithm we were able to put into context the quality of structural models going back in time as far as 1972. As convincingly illustrated by Figs. 1 and 2, the quality of PDB structures had rapidly improved over the first two decades of the database.

The ability to analyze quality over time using the proposed P_Q1(t,d) measure (Fig. 3) shows that there is tight competition among journals as their number increases. Quite interestingly, it is also evident that the PDB treasures many good quality structures that do not have primary citations. The fact that a structure remains To be published indicates that it is getting more and more difficult to publish papers based solely on crystallographic results, even if they are of high quality. Indeed, our study shows that structures without primary citations are on average of higher quality than structures published in many popular journals. Therefore, although many structures do not have any accompanying journal publications, they present a substantial value in their own right. As each PDB deposit has its own digital object identifier (DOI), citation of structures should be acknowledged not only by PDB IDs but also by DOIs. Full implementation of this mechanism would allow for easy estimation of the impact of To be published structures.

The proposed P_Q1(t,d) and P_Q1(t) measures manifest the overall attitude of authors towards the quality of the PDB: each next deposited structure should be better than the average previous deposit. Each new quality metric [21], visualization technique [32], set of restraints [33], validation algorithm [34], hardware improvement [35] or software update [36], make it easier to produce good quality structures and to avoid simple mistakes. In an effort to promote constant improvement of overall PDB quality it would be a desirable ideal to expect that newly added models are above the current average. However, such a recommendation should be applied judiciously as each case is different and should be always judged in a context-dependent manner. It is gratifying to see that almost all journals publish structures that are, on average, better than most of the previous ones while those that are not at that level yet, seem to be heading in the right direction.

Methods

Data collection and cleaning

To provide a comprehensive analysis of structure quality over time, we examined all X-ray structures available in the PDB that included 141,154 deposits between 1972 and 2019. The data were downloaded by performing an SQL query on PDBj [37,38] as of December 10, 2019.

In order to perform an analysis of structure quality in correlation with the primary citations, journal names had to be extracted from PDB files, cleaned and unified. Initially, the dataset contained 1,342 unique values describing the primary citation journal. After eliminating typos, unifying punctuation and ISSNs, and taking into account that some journals have changed their titles over time, the number of unique journal names dropped down to 800.

Bibliometric indicators of journals (IPP, SNIP) were downloaded from the Leiden University CWTS website (https://www.journalindicators.com/) and joined with the PDB data using ISSNs. Both indicators were calculated based on the Scopus bibliographic database produced by Elsevier.

Missing data imputation

To fill in missing data, three approaches were tested: filling missing values with the metric’s mean value, the metric’s median, and using the Multiple Imputation by Chained Equations algorithm (MICE) [23,24] with Bayesian ridge regression [25] as the predictor.

To see how well each of the three methods performed, the non-missing (i.e. complete) portion of the PDB data was used as the basis for creating a test set. We randomly introduced missing values to the complete portion of the data in the same proportions as those present in the actual dataset. As a result, the test dataset had the same proportion of deposits with at least one missing value and the same percentage of missing values per metric as the original (full) dataset. Next, these randomly introduced missing values were imputed and compared against the values originally present in the dataset. To quantify the imputation error we used the median absolute deviation (MAD), mean absolute error (MAE), and root-mean-square error (RMSE) [39]. The procedure was repeated 100 times with different subsets of values randomly eliminated from the complete dataset in each run. Imputed missing values were clipped when they were outside the range of possible values of a given metric.

Principal component analysis

The principal component analysis (PCA) required to calculate Q1_p was performed as described by Shao et al. [17]. The PCA was performed on three quality metrics: Clashscore, Ramachandran outliers, and Rotamer outliers. Since Ramachandran outliers and Rotamer outliers are meaningful only for proteins, the PCA analysis was performed for protein structures only. In the assessment of the quality of nucleic acid structures, the PCA step was not needed, as Clashscore was the only geometry-related quality index.

Upon visual inspection of the metrics’ values (Fig. S9), structures were marked as outliers and removed when the following criteria were reached: Rotamer outliers > 50% or Ramachandran outliers > 45% or Clashscore > 250. In total, 16 structures were marked as outliers: 1C4D, 1DH3, 1G3X, 1HDS, 1HKG, 1HPB, 1PYP, 1SM1, 2ABX, 2GN5, 2OGM, 2Y3J, 3ZS2, 4BM5, 4HIV, 5M2K. These structures were temporarily removed prior to PCA to decrease the effect of outlying values on the principal components, but they were not removed from the quality analysis. After removal of outstanding outliers, the input data for PCA were standardized by setting the mean to be 0 and standard deviation to 1. Running PCA on the standardized data resulted in three principal components: PC1, PC2 and PC3, explaining 78%, 14% and 8% variance, respectively. The coefficients of PC1 were: 0.60, 0.58, 0.56, indicating nearly equal contribution of Clashscore, Ramachandran outliers and Rotamer outliers. The explained variance of each principal component and the coefficients of PC1, were practically identical to those reported by Shao et al. [17].

As noted by one of the reviewers, the PC1 coefficients (0.60, 0.58, 0.56) are almost identical and roughly equal $\frac{1}{\sqrt{3}}$, making the respective weights of these contributions near equal for all three of them. This means that approximately the Q1_p measure could be presented as:

$$Q{1}_p=\frac{P_{\mathit{\text{Rfree}}}+P_{\%\mathit{\text{RSRZ}}}+\frac{1}{\sqrt{3}}\left(P_{\mathit{\text{Clashscore}}}+P_{\mathit{\text{Ramachandran}}}+P_{\mathit{\text{Rotamers}}}\right)}{3}$$ (5)

The above formula provides a simple metric that can be used without performing PCA. However, this approximate formula assumes that the relations between Clashscore, Ramachandran outliers and Rotamer outliers are fixed and will not change. For this reason, we chose to use the exact formula (1) as proposed by Shao et al. [17]. Nevertheless, the approximate formula (5) may be considered a simpler solution for less technical studies.

Computation

Data were extracted directly from PDBj using its SQL interface. All computations were performed with Python 3.7 using the scipy [40] and scikit-learn [41] libraries. The SQL query used, the resulting dataset, and fully reproducible analysis scripts in the form of a Jupyter notebook are available at https://github.com/dabrze/pdb_structure_quality.

Supplementary Material

sup info

Table S1. All-time journal ranking according to P_Q1(t). The ranking includes all the journals that had at least 100 primary citations of structures in the PDB. P_Q1(t) higher than 50% means that the structures published in a given journal were, on average, better than 50% of structures present in the PDB at the time of deposition (in this case regardless of resolution). Journals with more than 1000 structures are highlighted in gray.

Table S2. All-time journal ranking according to P_Q1min(t,d). The ranking includes all the journals that had at least 100 primary citations of structures in the PDB. P_Q1min(t,d) higher than 50% means that the structures published in a given journal were, on average, better than 50% of structures present in the PDB at the time of deposition. Journals with more than 1000 structures are highlighted in gray.

Table S3. All-time journal ranking according to P_Q1min(t). The ranking includes all the journals that had at least 100 primary citations of structures in the PDB. P_Q1min(t) higher than 50% means that the structures published in a given journal were, on average, better than 50% of structures present in the PDB at the time of deposition (in this case regardless of resolution). Journals with more than 1000 structures are highlighted in gray.

Figure S1. Histograms of quality metric values of structures found in the PDB. The histograms show the distribution of Clashscore, percent of Ramachandran outliers, percentage of rotamer outliers, percentage of RSRZ outliers and R_free values. The y-axis shows the number of depositions with a given metric value displayed on the x-axis.

Figure S2. P_Q1 analysis without imputed values. Variation in the mean P_Q1 percentile (higher is better) for deposits with all quality metrics over time (top) and resolution (bottom) for proteins (left) and nucleic acids (right). Error bars indicate the estimated unbiased standard error of the mean.

Figure S3. P_Q1min analysis (minimum approach). Variation in the mean P_Q1min percentile (higher is better) over time (top) and resolution (bottom) for proteins (left) and nucleic acids (right). Error bars indicate the estimated unbiased standard error of the mean.

Figure S4. Comparison of P_Q1min(t,d) of protein and nucleic acid structures over time. Variation in mean P_Q1min(t,d) quality percentile (y-axis, higher is better), comparing nucleic acid and protein structures (color) over time (x-axis). Error bars indicate estimated unbiased standard errors of the mean.

Figure S5. Average P_Q1(t,d) of popular journals for each year. The plot shows yearly (x-axis) means of P_Q1(t,d) values (y-axis) for each of the 25 most popular journals (panels). Regression lines computed using the locally estimated scatterplot smoothing (LOESS) method.

Figure S6. Journal ranking over time according to P_Q1(t). The plot shows the journal’s rank (y-axis) in a given time period (x-axis). Only the 25 most popular journals with at least 30 deposits in a given period were plotted.

Figure S7. Journal quality over time according to P_Q1(t). The plot shows yearly (x-axis) means of P_Q1(t) values (y-axis) for each of the 25 most popular journals (panels). Regression lines computed using the locally estimated scatterplot smoothing (LOESS) method.

Figure S8. Scatterplots of mean journal P_Q1(t,d) and the journal’s impact. Variation in mean journal P_Q1(t,d) (y-axis) in a given year (panel, color) plotted against the journals Impact Per Publication (IPP). IPP uses the same formula as the 3-year Impact Factor, but is based on publicly available Scopus data. The two regression lines show linear trends with 95% confidence intervals (gray areas).

Figure S9. Scatterplots of the values of Clashscore, Ramachandran outliers, and Rotamer outliers found in the PDB. Each point represents a PDB deposit.

Abbreviations:

PDB

Protein Data Bank

RSRZ

Real-Space R-value Z-score

MICE

Multiple Imputation by Chained Equations

MAE

Mean Absolute Error

RMSE

Root-Mean-Square Error

MAD

Median Absolute Deviation

IPP

Impact Per Publication

SNIP

Source Normalized Impact per Paper