A semiparametric method for the analysis of outcomes during a gap in HIV care under incomplete outcome ascertainment

Abstract

Objectives:

Estimation of the cascade of HIV care is essential for evaluating care and treatment programs, informing policy makers and assessing targets such as 90-90-90. A challenge to estimating the cascade based on electronic health record concerns patients “churning” in and out of care. Correctly estimating this dynamic phenomenon in resource-limited settings, such as those found in sub-Saharan Africa, is challenging because of the significant death under-reporting. An approach to partially recover information on the unobserved deaths is a double-sampling design, where a small subset of individuals with a missed clinic visit is intensively outreached in the community to actively ascertain their vital status. This approach has been adopted in several programs within the East Africa regional IeDEA consortium, the context of our motivating study. The objective of this paper is to propose a semiparametric method for the analysis of competing risks data with incomplete outcome ascertainment.

Methods:

Based on data from double-sampling designs, we propose a semiparametric inverse probability weighted estimator of key outcomes during a gap in care, which are crucial pieces of the care cascade puzzle.

Results:

Simulation studies suggest that the proposed estimators provide valid estimates in settings with incomplete outcome ascertainment under a set of realistic assumptions. These studies also illustrate that a naïve complete-case analysis can provide seriously biased estimates. The methodology is applied to electronic health record data from the East Africa IeDEA Consortium to estimate death and return to care during a gap in care.

Conclusions:

The proposed methodology provides a robust approach for valid inferences about return to care and death during a gap in care, in settings with death under-reporting. Ultimately, the resulting estimates will have significant consequences on program construction, resource allocation, policy and decision making at the highest levels.

Background

Since 2003 there has been a progressive expansion of the eligibility criteria for antiretroviral therapy (ART). This has culminated in the current universal test and treats guidance (Granich, Gilks, and Dye 2009; World Health Organization 2015). These efforts are embedded in the 90-90-90 targets, which advocate that, by the year 2020, 90% of all people living with HIV/AIDS (PLWH) will know their status, 90% of those will be receiving ART and 90% of those on ART be virally suppressed (UNAIDS 2014). 90-90-90 emanates from a conceptual framework that views HIV infection and subsequent engagement in care as a “cascade” of states, from prior to diagnosis through viral suppression (Gardner, McLees, and Steiner 2011). The HIV care cascade, in addition to being a useful model to convey the sequential nature of these states, readily lends itself to mathematical modeling. Mathematical modeling of this cascade is an important tool in our efforts to both design optimal models of care and to assess the effectiveness of these models in the real world.

The cascade of care can be naturally conceived as a multi-state model (Andersen and Keiding 2002; Gentleman et al. 1994; Lee et al. 2018; Meira-Machado, de Uña Álvarez, and Cadarso-Suárez 2009). Multi-state models can be used to describe the probability of transition between various states, based on characteristics of each individual. Gardner and colleagues, in their landmark study that ushered in the concept of the HIV care cascade, observed that not everyone remains engaged in the care cascade (Gardner, McLees, and Steiner 2011). The term “disengagement from care” has been used to describe the situation where a patient is alive but not in HIV care, after enrolling in care. The state “disengagement from care” has been typically considered an “absorbing” state in the literature, i.e., a terminal state from which there is no transition to other states (Bakoyannis and Yiannoutsos 2015; Bakoyannis, Zhang, and Yiannoutsos 2019; Graham et al. 2013; Rachlis et al. 2016; Schöni-Affolter et al. 2011). In addition, PLWH may also die of their disease at any point in the cascade. Figure 1 shows a simple competing risks model (for a review on competing risks see Bakoyannis and Touloumi 2012), which is a special case of a multi-state model with single initial state and several absorbing states, of the two aforementioned states.

Figure 1:

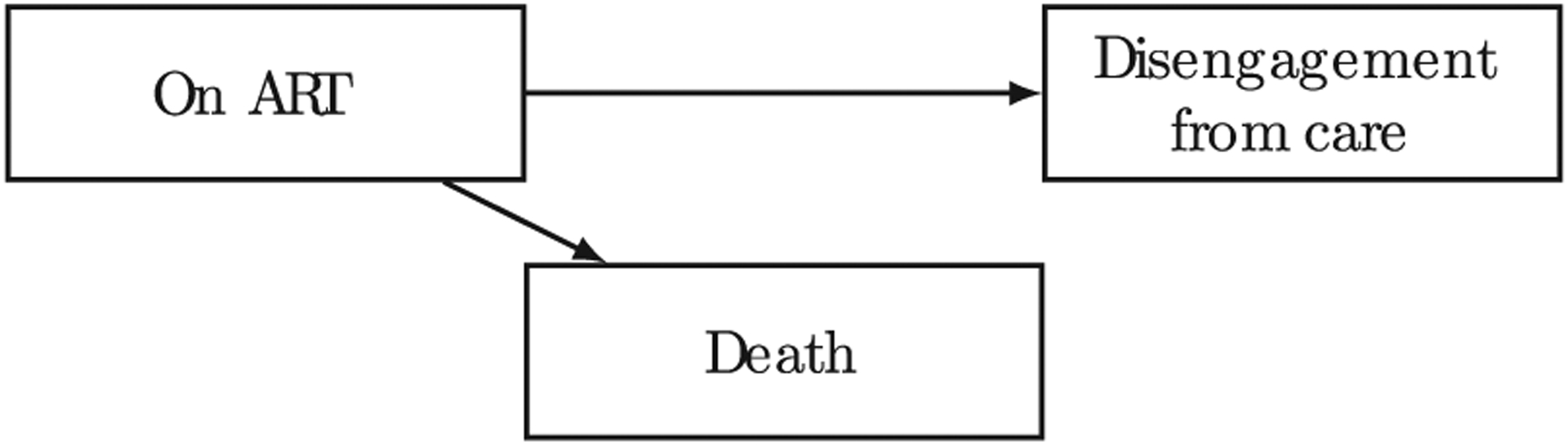
Competing risks model of disengagement from care and death after ART initiation.

More recently, a number of research papers have started to look at disengagement from care as a transient state, with a proportion of patients who have disengaged from care at one program re-engaging in care either in the same program or elsewhere (Geng, Odeny, and Lyamuya 2015, 2016; Lee et al. 2018; Rebeiro, Bakoyannis, and Musick 2017). This idea of patient “churn” (Gill and Krentz 2009) and the consequent rehashing of disengagement from care as just a “gap in care”, acknowledges the complex manner by which care is accessed within a mature ART delivery environment (Nsanzimana et al. 2014). Figure 2 presents a multi-state model of patient churning in an out of care after ART initiation.

Figure 2:

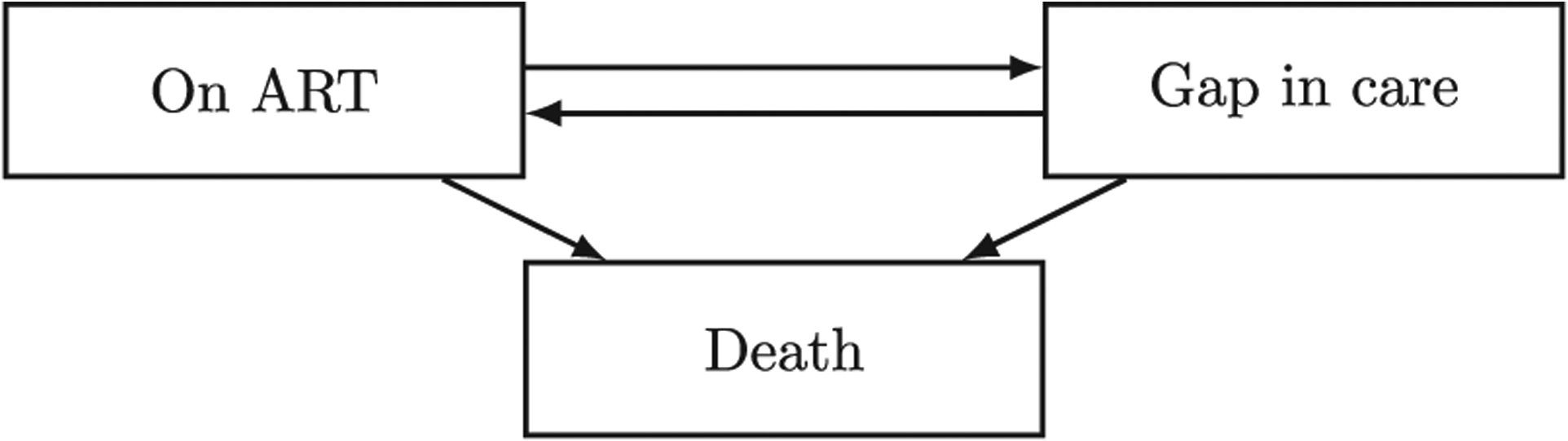
Multi-state model of patient churning in an out of care after ART initiation.

Estimation of the transition rates between the states of the multi-state model depicted in Figure 2 can be based on data from HIV care and treatment programs. Analysis of the data produced by these programs, in combination with the multi-state modeling framework provides an opportunity to perform principled monitoring and evaluation in an unprecedented scale. However, the methodological challenges to using programmatic data to estimate patient churn are formidable, especially in resource-constrained settings. A major issue is death under-reporting, which leads to a misclassification problem, since unreported deaths are typically classified as losses to care. This means that a patient who has been identified as “lost to care” can be either alive and without care (i.e. gap in care) or deceased, whose death was undocumented. A cost-efficient way to obtain additional information which can be used for adjusting such biases is a double-sampling study design (An et al. 2009). Under this design, a small sample of patients who have missed a scheduled clinic visit is intensively outreached in the community and, subsequently, their vital status is actively ascertained by outreach workers. Double sampling is also known as two-phase sampling.

The methodological work to date has focused on utilizing data from double-sampling to overcome biases arising from death under-reporting in situations such as the one depicted in the model in Figure 1 (An et al. 2009; Bakoyannis and Yiannoutsos 2015; Bakoyannis, Zhang, and Yiannoutsos 2019, 2020; Brinkhof, Spycher, and Yiannoutsos 2010). However, the previously proposed approaches cannot be used to adjust for the biases arising from death under-reporting when estimating more complex models, such as that depicted in Figure 2, where “gap in care” is not treated as an absorbing state. Nevertheless, unbiased estimates of the rates of patient churn is crucial for making valid inferences about the cascade of HIV care, as well as for mathematical modeling purposes.

In the present paper we address the issue of flexible semiparametric estimation of the rates of return to care and death after a gap in care, adjusting for death under-reporting. To achieve this adjustment, we leverage data on the true vital status and engagement in HIV care drawn from a double-sampling design. Our proposal relies on a partial pseudolikelihood-based approach which utilizes a flexible semiparametric inverse probability weighing approach. Estimation of the latter weights is achieved via B-spline-based sieve maximum likelihood estimation. The proposed approach does not rely on strong and restrictive parametric assumptions, which are typically violated in practice. Therefore, it provides a robust method for valid analyses of return to care and death after a gap in care based on programmatic data. The validity of the proposed approach is evaluated through simulation experiments. The method is also illustrated using routine programmatic data from sub-Saharan Africa to analyze return to care and death after a gap in HIV care.

The rest of the paper is organized as follows. The research context, population, data and statistical methodology are introduced in Section 2. Next, a number of simulation experiments is presented in Section 3, where both the extent of bias from naïve analytical approaches is quantified and the validity of the proposed methodology is assessed. An illustrative analysis of death and return to care after a gap in care is presented in Section 4, concluding with a discussion in Section 5. For completeness, the analysis of death while in care and gap in care after ART initiation (the remaining transitions in Figure 2) using previously proposed methods is provided in Appendix. R code that implements our simulation studies is available as an Online Supplementary Material with this paper. This code can be easily modified for implementing the proposed SIPW approach in practice.

Methods

Study population and setting

We use data from an HIV care and treatment program in western Kenya, the Academic Model Providing Access to Healthcare (AMPATH). In addition to providing care and treatment services to tens of thousands of PLWH, AMPATH has robust data collection and an extensive electronic medical record system. Moreover, and of direct relevance to this work, AMPATH has an intensive patient outreach program (a special case of a double-sampling design), as part of efforts to reach patients who are lost to care (i.e. have missed a clinic visit and have not return to clinic for a certain time period) and attempt to re-engage them. As part of the outreach process, data on vital status are collected. We will use this information, in conjunction to the clinical data routinely collected on all AMPATH patients, in order to adjust estimates of return to care and death after a gap in care. A schematic of the double-sampling strategy in AMPATH is shown in Figure 3.

Figure 3:

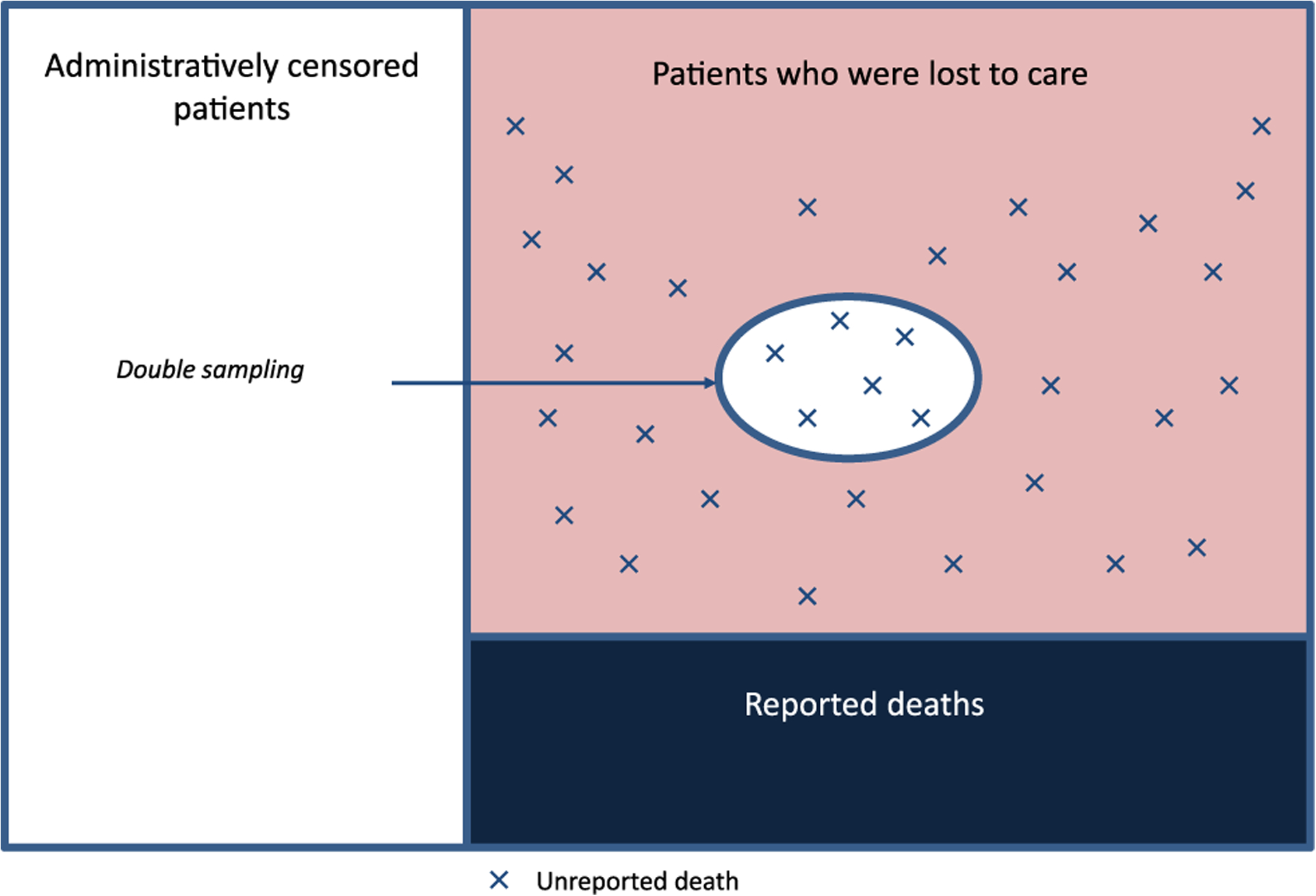
Double-sampling in AMPATH.

The statistical problem

Recently, we presented a methodology to nonparametrically estimate the transitions in a multi-state model with missing data on the absorbing states (Bakoyannis, Zhang, and Yiannoutsos 2019). This methodology is based on a nonparametric maximum pseudolikelihood estimator (NPMPLE) of the transition rates. Furthermore, we proposed a maximum partial pseudolikelihood estimator (MPPLE) for semiparametric regression analysis of competing risks data with missing event types (Bakoyannis, Zhang, and Yiannoutsos 2020). These methods can be used to analyze the transition hazards from the “on ART” state to the “gap in care” and “death” states in the model depicted in Figure 2 using the data up to the first gap in care or death (or right censoring), under a double-sampling design such as that implemented in AMPATH. However, these previous methods cannot be used to analyze the transition hazards from the “gap in care” state to the back to care and “on ART” or the “death” state. In this work we address the issue of analyzing this missing piece in the model, which is depicted in Figure 2. More precisely, we focus on the analysis of the hazard of return to care and death after the first true gap in care (Figure 2). To accomplish this we have to overcome a number of significant challenges:

• Not all lost patients have the same probability of being successfully traced. For this reason, a complete-case analysis is expected to lead to biased estimates.

• Among those lost to care, the non-traced patients have a missing “true gap-in-care” status. The immediate consequence of this fact is that there is uncertainty about whether these patients should be included in the analysis of return to care.

• In addition, these non-traced patients have missing vital status as well as missing death times. This in turn hampers defining events and calculating the risk sets in statistical analyses (e.g., in Cox’s partial likelihood for the semiparametric proportional hazards model).

Notation, assumption and model

Here, we assume the observation of n lost to care patients over the observation interval [0, τ], with τ < ∞. Also, let X_i be the first occurring event or right censoring time, and Δ_ij, j = 1, 2, denote the death before returing to care (Δ_i1) and return to care indicator (Δ_i2) for the ith patient. Note that trivially Δ_i1 + Δ_i2 ≤ 1 and, therefore, the problem under consideration can be treated as a competing risks problem. Based on these quantities we can define the event-specific counting process as N_ij(t) = I(X_i ≤ t, Δ_ij = 1), j = 1, 2, and the at-risk process as Y_i(t) = I(X_i ≥ t). Also, let R_i be the successful patient outreach indicator, with R_i = 1 if the ith patient has been successfully outreached, and R_i = 0 otherwise. Moreover, let G_i = 1 if the ith patient has a true gap in care, and G_i = 0 otherwise. Note that patients who have a missed visit due to an unreported death have G_i = 0. Finally, let $W_i={\left(Z_i^T,A_i^T\right)}^T$, with Z_i being a vector of covariates of scientific interest, and A_i a vector of auxiliary variables that are not of direct scientific interest but may be related to the probability of successful outreach (e.g. number of outreach workers in a particular clinic).

In this work we are interested in making inferences under the semiparametric proportional cause-specific hazards model

$${\lambda }_{0,j}\left(t;Z_i\right)={\lambda }_{0,j}\left(t\right)\text{exp}\left({\beta }_{0,j}^T{Z}_i\right),j=1,2,t\in \left[0,\tau \right],$$

where, λ_0,j(t), j=1, 2 are the unspecified baseline cause-specific hazards. This model is popular because it does not impose restrictive and, in some cases, unrealistic distributional assumptions. Estimation of the model parameters with incomplete programmatic data requires the key Missing at Random (MAR) assumption, which governs all statistical inference in the context of missing data. MAR means that, conditional on observed data, the probability of missingness (i.e. of non-outreach) is independent of the incompletely observed variables. In this work, we assume MAR conditional on both variables of interest Z_i and auxiliary variables A_i.

Definition:

MAR assumption:

The probability of missingness is independent of the incompletely observed (G_i, X_i, Δ_i1, Δ_i2) conditionally on the covariates of interest and auxiliary variables W_i

That is,

$$\begin{gathered} \text{Pr}\left(R_i=1\mid G_i,X_i,{\Delta }_{i1},{\Delta }_{i2},W_i\right)=\text{Pr}\left(R_i=1\mid W_i\right) \\ \equiv \pi \left(W_i\right). \end{gathered}$$

The incorporation of auxiliary variables makes the MAR assumption more plausible in practice (Bakoyannis, Zhang, and Yiannoutsos 2019; Lu and Tsiatis 2001).

A standard approach to deal with missingness is Rubin’s multiple imputation (Rubin 1996; Schafer 1999). However, this approach is not appropriate for the problem under consideration in this paper due to two main reasons. First, in our setting we have three incomplete variables, G_i, X_i, and Δ_i1, and this means that three parametric imputation models (one for each incomplete variable) need to be specified (White, Royston, and Wood 2011). Specifying multiple parametric models increases the risk of model misspecification in at least one of the imputation models, and this can lead to inconsistent estimates (Robins and Wang 2000). Second, since we introduce auxiliary variables to make the MAR assumption more plausible, the imputation models will be uncongenial with the main analysis model (i.e. the semiparametric proportional cause-specific hazards model). This will lead to biased Rubin’s variance estimates and, therefore, to invalid inferences (Meng 1994; Robins and Wang 2000). To deal with these issues we propose the use of inverse probability weighting (IPW) techniques (Li et al. 2013) along with bootstrap for variance estimation. Under the IPW approach, one needs to only specify a single model for the probability of non-missingness, i.e. π(W_i). Since specifying a parametric model for π(W_i) can lead to model misspecification, we consider the more flexible semiparametric generalized additive model (Hastie and Tibshirani 1986) of the form

$$\text{logit}\left[\pi \left(W\right)\right]={\varphi }_0+\sum _{k=1}^p{\varphi }_k\left(W_k\right),$$ (1)

where, for k = 1, …, p, ϕ_k(·) is an unspecified smooth function if W_k is a continuous variable, or ϕ_k(W_k) = ϕ_kW_k, with ${\varphi }_k\in ℝ$, if W_k is binary or indicator variable. This model admits also parametric interaction terms. The likelihood function under this semiparametric generalized additive model involves a number of unspecified smooth functions ϕ_k(·) (infinite-dimensional parameters). In general, maximization of a likelihood function with an infinite-dimensional parameter ϕ ∈ Φ over the whole space Φ may lead to inconsistent estimates (Shen and Wong 1994) and can also be very computationally burdensome. To circumvent these problems we use sieve maximum likelihood estimation (Shen and Wong 1994; Zhang, Hua, and Huang 2010). A “sieve” is a sequence of finite-dimensional parameter spaces {Φ_n}_n≥1 that approximates Φ, and the approximation error tends to 0 as n → ∞ (Shen and Wong 1994). A sieve maximum likelihood estimate is the maximizer of likelihood function over Φ_n. In this work, we use B-spline sieve spaces of the form

$${\Phi }_{k,n}=\left\{{\varphi }_k:{\varphi }_k\left(w\right)=\sum _{s=1}^{N_k+m_k}{\gamma }_{k,s}{B}_{s,m_k}\left(w\right),w\in \left[a_k,b_k\right],{\gamma }_k\in {ℝ}^{N_k+m_k}\right\},$$

for all subscripts k which correspond to a continuous W_k, where N_j and m_j are the number of internal knots and the order of the B-spline for the continuous variable W_k, and [a_k, b_k] the corresponding support. Following previous work on B-spline based sieve maximum likelihood estimation (Zhang, Hua, and Huang 2010), we allow the number of internal knots to increase with the total sample size n, satisfying

$$N_k=O\left(n^{\frac{1}{1+2s_k}}\right).$$

Here s_k is related to the smoothness of the underlying true function ϕ_k(·). Maximization of the resulting sieve maximum likelihood function leads to the sieve maximum likelihood estimate of π(W_i), denoted by $\widehat{\pi }\left(W_i\right)$. Based on this estimate, we can perform semiparametric estimation based on the following pseudo-score function:

$${\Psi }_{n,j}\left({\beta }_j;\widehat{\pi }\right)=\frac{1}{n}\sum _{i=1}^n\frac{R_i}{\widehat{\pi }\left(W_i\right)}{G}_i{\int }_0^{\tau }\left[Z_i-\frac{{\sum }_{l=1}^n\frac{R_l}{\widehat{\pi }\left(W_l\right)}{G}_l{Z}_l{Y}_l(t)e^{{\beta }_j^T{Z}_l}}{{\sum }_{l=1}^n\frac{R_l}{\widehat{\pi }\left(W_l\right)}{G}_l{Y}_l(t)e^{{\beta }_j^T{Z}_l}}\right]d{N}_{ij}\left(t\right),$$

for the events j=1, 2 (return to care and death). An estimator for β_0,j, j = 1, 2 is ${\widehat{\beta }}_{n,j}$ such that

$${\Psi }_{n,j}\left({\widehat{\beta }}_{n,j};{\widehat{\pi }}_n\right)=0.$$

We call the estimator ${\widehat{\beta }}_{n,j}$ a sieve inverse probability weighting (SIPW) estimator. Having obtained the SIPW estimator for β_0,j, it is possible to obtain an SIPW estimator of the cumulative baseline cause-specific hazard as follows:

$${\widehat{\Lambda }}_{n,j}\left(t\right)={\int }_0^t\frac{{\sum }_{i=1}^n\frac{R_i}{\widehat{\pi }\left(W_i\right)}{G}_{i}d{N}_{ij}\left(s\right)}{{\sum }_{i=1}^n\frac{R_i}{\widehat{\pi }\left(W_i\right)}{G}_i{Y}_i\left(s\right)e^{{\widehat{\beta }}_{n,j}^T{Z}_i}},j=1,2,t\in \left[0,\tau \right].$$

Finally, a plug-in estimator of the cumulative incidence function given the covariate pattern Z = z is

$${\widehat{F}}_{n,j}\left(t;z\right)={\int }_0^t\text{exp}\left[-\sum _{l=1}^2{\widehat{\Lambda }}_{n,l}\left(u-;z\right)\right]d{\widehat{\Lambda }}_{n,j}\left(u;z\right),j=1,2,t\in [0,\tau ],$$

where, ${\widehat{\Lambda }}_{n,j}\left(t;z\right)={\widehat{\Lambda }}_{n,j}\left(t\right)\text{exp}\left({\widehat{\beta }}_{n,j}^{T}z\right)$. For standard error estimation we suggest the use of bootstrap. The bootstrap has been shown to be consistent for the asymptotic distribution of Euclidean parameter estimators in general semiparametric M-estimation problems (Cheng and Huang 2010).

Computation of the estimators ${\widehat{\beta }}_{n,j}$, j = 1, 2, can be easily performed using the R package survival, by utilizing the weights option in the coxph function. The function coxph is particularly fast and using bootstrap with 100 (or more) replications for standard error estimation is not a computationally burdensome task. Computation of ${\widehat{\Lambda }}_{n,j}\left(t\right)$, j = 1, 2, can be performed in a straightforward manner, using the function basehaz with the option centered=FALSE, after running the coxph function.

Simulation studies

We performed a number of simulations studies in support of the validity of the SIPW estimator. We simulated two covariates of interest Z₁ ~ N(0, 1) and Z₂ ~ Bernoulli(0.4). The true gap in care status G was simulated from the Bernoulli distribution with probability equal to expit(2 − 0.5Z₁ + 0.5Z₂). For the observations with G_i = 1 (i.e. true gap in care), the two events of interest (death and return to care) were simulated based on the proportional cause-specific hazards models

$${\lambda }_1\left(t;Z\right)=\text{exp}\left({\beta }_{01}+{\beta }_{11}{Z}_1+{\beta }_{21}{Z}_2\right),$$

where, (β₀₁, β₁₁, β₂₁) (1, −0.5, 1), and

$${\lambda }_2\left(t;Z\right)=\frac{e^{{\beta }_{02}}}{2}{\left(e^{{\beta }_{02}}t\right)}^{-\frac{1}{2}}\text{exp}\left({\beta }_{12}{Z}_1+{\beta }_{22}{Z}_2\right),$$

where, (β₀₂, β₁₂, β₂₂) = (0.7, 0.5, −0.5). The first model is an exponential model while the second is a Weibull model. We also simulated an independent right-censoring time from Exp(1.5). In the simulation studies we considered scenarios with large percent of missingness. In order to simulate a more complex missingness pattern, we considered an auxiliary covariate A = −1 − X + 2Δ₁ + ϵ, where ϵ ~ N(0, 1), which was associated with the incomplete variables X and Δ₁. The true model for the probability of missingness was a nonlinear model of the form

$$\text{logit}\left[\pi \left(W\right)\right]=\theta -\text{cos}\left(Z_1\right)+Z_2-\frac{2}{1+\text{exp}\left(2A\right)},$$

where, θ depended on the scenario and controlled the proportion of missingness. Note that the MAR assumption is violated if the auxiliary variable A is not taken into account. For each of the three scenarios we simulated 1000 data sets, and in each data set we applied the naïve complete-case analysis, which ignores the auxiliary variable A, a flexible multiple imputation by chained equations (MICE) approach with five imputations, and the proposed SIPW method. For the MICE approach we assumed the following flexible imputation models:

$$\text{logit}\left[\text{Pr}\left(G=1\mid W\right)\right]={\eta }_0+{\eta }_1\left(Z_1\right)+{\eta }_2{Z}_2+{\eta }_3\left(A\right),$$

where, η₁ (·) and η₃ (·) were unspecified smooth functions,

$$\text{log}\left(X\right)\mid \left(G=1,W\right)~N\left({\gamma }_0+{\gamma }_1\left(Z_1\right)+{\gamma }_2{Z}_2+{\gamma }_3\left(A\right),{\sigma }^2\right),$$

where, γ₁ (·) and γ₃ (·) were unspecified smooth functions, and

$$\text{logit}\left[\text{Pr}\left({\Delta }_j=1\mid G=1,W,X\right)\right]={\psi }_{0,j}+{\psi }_{1,j}\left(Z_1\right)+{\psi }_{2,j}{Z}_2+{\psi }_{3,j}\left(A\right)+{\psi }_{4,j}X+{\psi }_{4,j}{X}^2,$$

for j = 1, 2, were ψ₁ (·) and ψ₃ (·) where unspecified smooth functions. We an assumed a quadratic effect of X in the last model for simplicity, because X contains missing values which need to be simulated in each imputation. Assuming an unspecified smooth effect of X in this model would require the calculation of the basis functions for the simulated Xs at every imputation, which could potentially lead to B-splines with different domains. For the SIPW approach we assumed the following model

$$\text{logit}\left[\text{Pr}\left(R=1\mid W\right)\right]={\varphi }_0+{\varphi }_1\left(Z_1\right)+{\varphi }_2{Z}_2+{\varphi }_3\left(A\right),$$

where, ϕ₁ (·) and ϕ₃ (·) were unspecified smooth functions. It is important to note that the MICE approach imposes additivity assumptions in all three imputation models, and it additionally imposes a distributional assumption for the event or censoring time X. In contrast, the SIPW approach imposes only an additivity assumption in a single model. In both MICE and SIPW approaches, estimation of the unspecified smooth functions was based on cubic B-spline sieve spaces. For the SIPW approach, the number of internal knots was set equal to the largest integer that is less than or equal to 0.5n^1/3, which is consistent with O(n^1/3). For MICE, we use the same rule but we replaced the total number of observations n with the number of non-missing observations (i.e. the size of the dataset to be used to fit the imputation models). We used Rubin’s rules to conduct inference based on the MICE approach. Standard error estimation for the SIPW estimator was based on the nonparametric bootstrap with 100 replications.

In this simulation study we considered three scenarios according to the sample size and the probability of missingness. For Scenarios 1 and 2, these figures were chosen in an effort to evaluate the performance of the method under less extreme settings compared to the data example presented in Section 4. The sample size and percent of missingness in Scenario 3 (n=20,000 and 87% missingness) were chosen to mimic the data example. We must note that there were many cases where the MICE estimators could not be calculated for event 1 (17.8% of the datasets in Scenario 1, 28.6% in Scenario 2, and 24.0% in Scenario 3), because of non-convergence issues in at least one of the imputation models. Such issues in MICE were minimal for event 2 (less than 0.8% of the datasets in all scenarios). These problematic estimates were not considered further in the simulation study. In many cases, both the logistic imputation models for MICE and the missingness model for SIPW exhibited perfect prediction issues as a result of their flexibility. The resulting estimates were not discarded from this simulation study.

Scenario 1: n=2,000 and ~51% missingness

Results regarding the covariate effect estimators from this scenario are shown in Table 1. The complete-case, MICE and SIPW estimates are shown for the two events along with the percent bias, the Monte Carlo standard deviation (MCSD) and the average of the bootstrap standard error (ASE) estimates. The attainment of a nominal coverage probability (CP) of 95% is also assessed.

Table 1:

Results from Scenario 1 (n=2,000 and about 51% missingness) based on the naïve complete case analysis (CC), the multiple imputation by chained equations approach (MICE), and the proposed sieve inverse probability weighting approach (SIPW).

Analysis		Event 1		Event 2
		${\widehat{\beta }}_{11}$	${\widehat{\beta }}_{21}$	${\widehat{\beta }}_{12}$	${\widehat{\beta }}_{22}$
CC	% Bias	−14.330	−17.478	23.845	3.144
	MCSDa	0.056	0.106	0.071	0.125
	ASEb	0.055	0.105	0.069	0.130
	CPc	0.740	0.621	0.604	0.959
MICE	% Bias	−6.876	−8.080	−15.471	−15.429
	MCSDa	0.055	0.100	0.050	0.091
	ASEb	0.065	0.120	0.055	0.097
	CPc	0.963	0.936	0.721	0.882
SIPW	% Bias	0.565	0.695	0.685	0.448
	MCSDa	0.062	0.119	0.070	0.125
	ASEb	0.063	0.122	0.070	0.129
	CPc	0.944	0.961	0.954	0.960

^aMonte Carlo standard deviation of the estimates.

^bAverage of the standard error estimates.

^cEmpirical coverage probability.

These simulation results indicate that the complete-case analysis is associated with significant levels of bias and suffers from lower than desired coverage probability. Its slightly lower MCSD and ASE, compared to the SIPW, in some cases, is attributed to the additional variability of the estimated weights in the SIPW approach. The MICE estimator for the regression parameter of the event two is biased, and the corresponding coverage probabilities are lower than the nominal level. This can be attributed to a misspecification of the imputation models for X and Δ₂, since the true structure of these models is quite complicated in competing risks situations. In contrast, the SIPW estimator is virtually unbiased and the corresponding coverage probabilities close to the nominal level.

Average estimates of the cumulative baseline cause-specific hazard functions along with the corresponding true values are shown in Figure 4.

Figure 4:

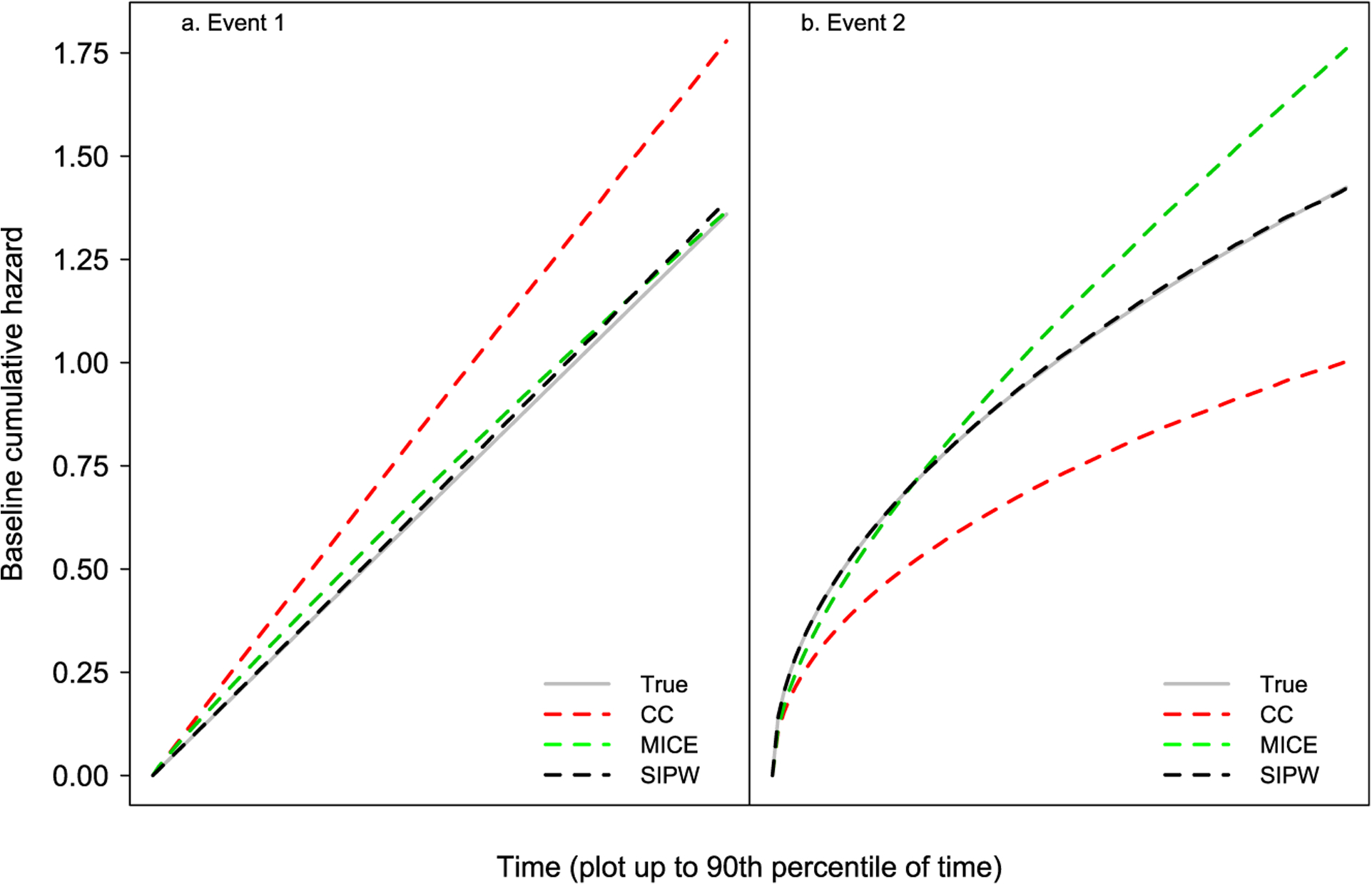
Simulation results corresponding to Scenario 1.

Similarly to the results for the covariate effect estimators, the estimate of the cumulative baseline cause-specific hazard from the complete case analysis is quite biased. Additionally, this estimate from the MICE approach is biased for the event 2. On the contrary, the corresponding estimate from the SIPW method exhibits negligible bias.

Scenario 2: n=5,000 and ~74% missingness

The results from this scenario are presented in Table 2 and Figure 5.

Table 2:

Results from Scenario 2 (n=5,000 and and ~74% missingness) based on the naïve complete case analysis (CC), the multiple imputation by chained equations approach (MICE), and the proposed sieve inverse probability weighting approach (SIPW).

Analysis		Event 1		Event 2
		${\widehat{\beta }}_{11}$	${\widehat{\beta }}_{21}$	${\widehat{\beta }}_{12}$	${\widehat{\beta }}_{22}$
CC	% Bias	−19.870	−20.374	32.168	20.748
	MCSDa	0.045	0.093	0.064	0.122
	ASEb	0.043	0.090	0.063	0.122
	CPc	0.375	0.388	0.279	0.875
MICE	% Bias	−9.884	−11.248	−26.093	−26.087
	MCSDa	0.044	0.083	0.041	0.074
	ASEb	0.057	0.105	0.042	0.076
	CPc	0.931	0.866	0.216	0.647
SIPW	% Bias	0.408	0.256	0.405	−0.656
	MCSDa	0.058	0.118	0.068	0.126
	ASEb	0.056	0.117	0.068	0.125
	CPc	0.937	0.941	0.949	0.950

^aMonte Carlo standard deviation of the estimates.

^bAverage of the standard error estimates.

^cEmpirical coverage probability.

Figure 5:

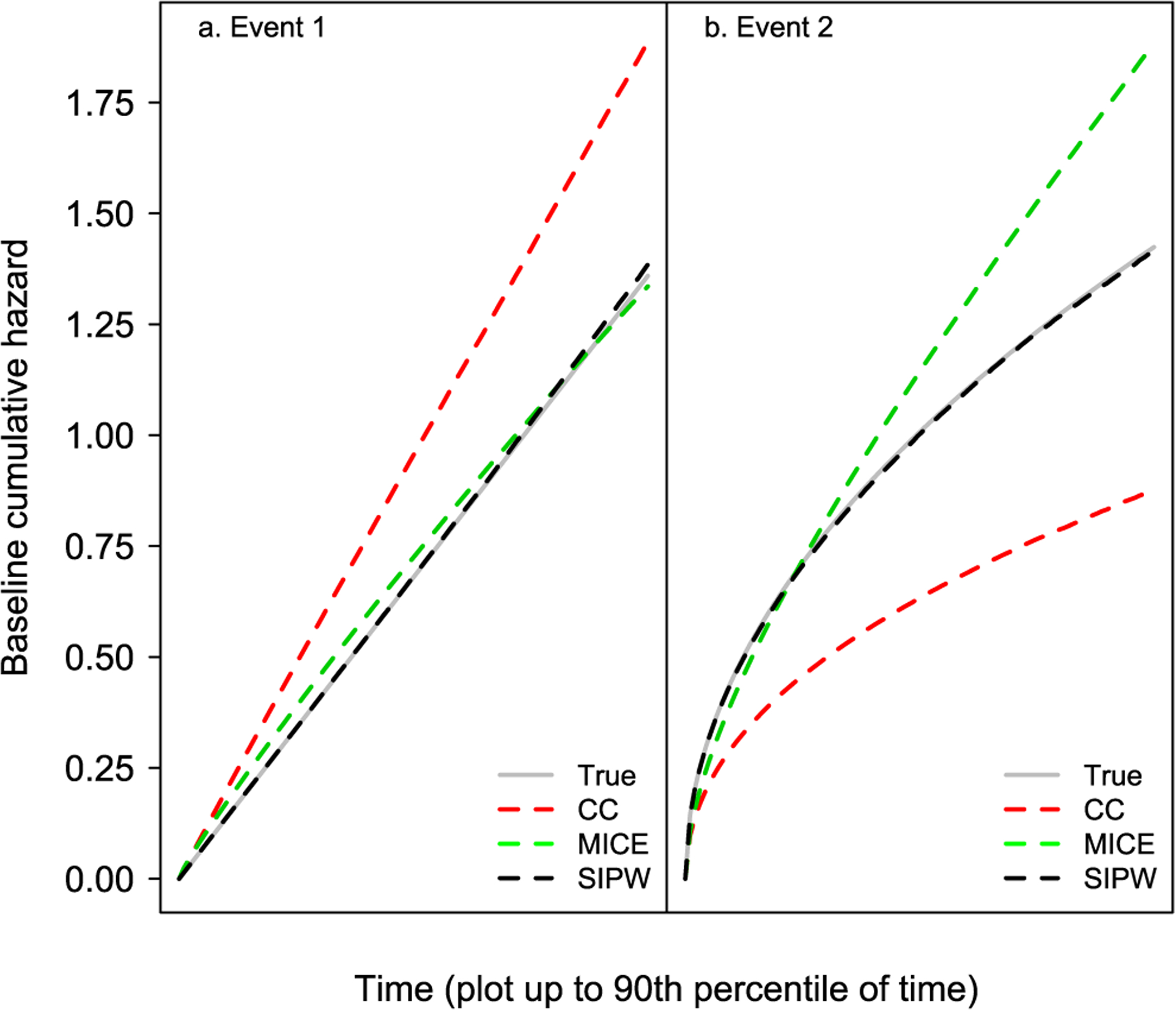
Simulation results corresponding to Scenario 2.

The results shown in Table 2 are similar as in Scenario 1 (Table 1). The complete-case analysis is associated with substantial levels of bias and small coverage probabilities in all cases as opposed to the proposed SIPW estimator. The MICE estimators for event two are also biased and the corresponding coverage probabilities have a poor coverage rate. The biases of the complete-case and MICE analyses are more pronounced in Scenario 2, as a result of the larger percent of missingness. Also, the MICE estimator for event one exhibits a somewhat larger bias in Scenario 2, and the coverage probability for β₂1 is quite low. A similar pattern in bias is observed with respect to the estimation of the baseline cumulative cause-specific hazard (Figure 5).

Scenario 3: n=20,000 and ~87% missingness

The results from this scenario are presented in Table 3 and Figure 6.

Table 3:

Results from Scenario 3 (n=20,000 and and ~87% missingness) based on the naïve complete case analysis (CC), the multiple imputation by chained equations approach (MICE), and the proposed sieve inverse probability weighting approach (SIPW).

Analysis		Event 1		Event 2
		${\widehat{\beta }}_{11}$	${\widehat{\beta }}_{21}$	${\widehat{\beta }}_{12}$	${\widehat{\beta }}_{22}$
CC	% Bias	−22.842	−21.349	36.646	37.663
	MCSDa	0.030	0.064	0.047	0.092
	ASEb	0.029	0.064	0.046	0.092
	CPc	0.028	0.091	0.019	0.473
MICE	% Bias	−9.713	−11.929	−30.823	−31.537
	MCSDa	0.032	0.063	0.027	0.050
	ASEb	0.042	0.077	0.028	0.050
	CPc	0.873	0.780	0.011	0.276
SIPW	% Bias	−0.376	−0.546	0.467	0.269
	MCSDa	0.043	0.092	0.052	0.098
	ASEb	0.042	0.090	0.053	0.097
	CPc	0.947	0.938	0.949	0.942

^aMonte Carlo standard deviation of the estimates.

^bAverage of the standard error estimates.

^cEmpirical coverage probability.

Figure 6:

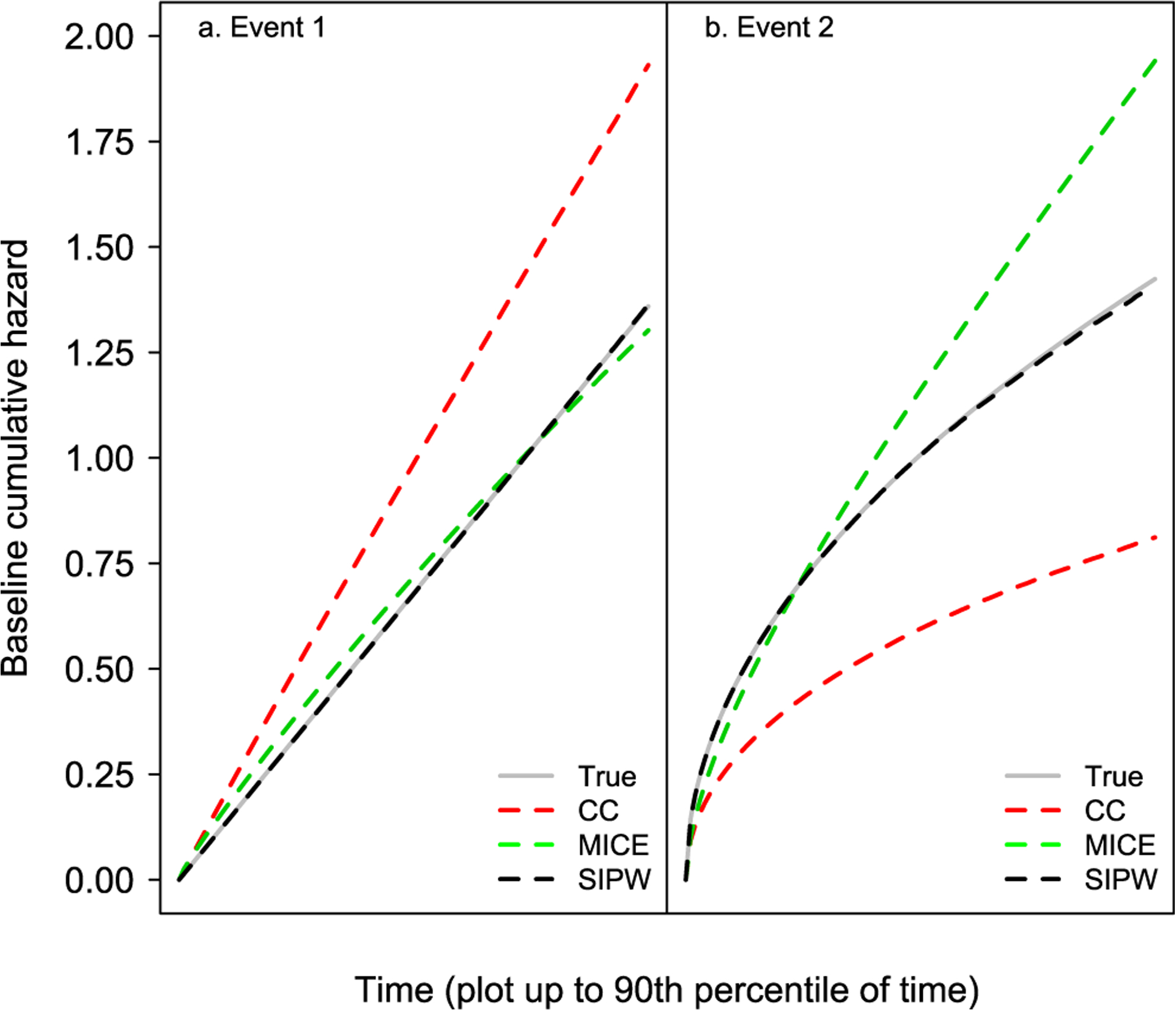
Simulation results corresponding to Scenario 3.

A similar pattern to the simulation results from Scenarios one and two is observed here. Specifically, the complete-case and the MICE analyses provide biased estimates, while the SIPW estimates are virtually unbiased. As expected, the biases of the complete-case and MICE analyses are more pronounced in Scenario 3 as a result of the higher missingness percent. Moreover, the empirical coverage probabilities were even lower for the complete-case and MICE analyses.

Analysis of return to care and death after the first gap in care

We illustrate the proposed methodology by analyzing data from AMPATH, a large HIV care and treatment program in western Kenya. The study sample consisted of 18,892 patients who initiated ART in one of the clinics in the AMPATH program and then became lost to clinic after ART initiation. Loss to clinic was defined here as no clinic visits for two months after the next scheduled visit (usually 90 days from their last clinic visit). This definition is clinically meaningful, because patients who miss a scheduled clinic visit for at least two months are expected to have run out of ART supplies for at least a month in our setting. It has been found that ART interruption is associated with a steep increase in HIV-RNA in the first few months (Touloumi et al. 2006), and that a treatment interruption can have a detrimental effect on the immune system of the patient (Mussini et al. 2009). Using a longer amount of time, one would miss many clinically important cases of a gap in care. Characteristics of these patients are shown in Tables 4, 5.

Table 4:

True gap in care and event status according to the successful patient tracing status.

	Successful patient tracing
	No	Yes
	n(%)	n(%)
True gap in care
No (=unreported death)	0 (−)	491 (19.3)
Yes	8,580 (52.5)	2,047 (80.7)
Unknown	7,774 (47.5)	0 (−)
Event
No event/unknown	7,774 (47.5)	1,387 (54.6)
Death	0 (−)	195 (7.7)
Return to care	8,580 (52.5)	956 (37.7)
	16,354	2,538

Table 5:

Descriptive characteristics of the study sample.

		Successful patient tracing	p-Value
	No	Yes
	(n=16,354)	(n=2,538)
	n(%)	n(%)
Gender
Female & non-pregnanta	9,946 (60.8)	1,279 (50.4)	<0.001
Female & pregnanta	1,019 (6.2)	328 (12.9)
Male	5,389 (33.0)	931 (36.7)
HIV status disclosed
No	6,111 (37.4)	861 (33.9)	0.001
Yes	10,243 (62.6)	1,677 (66.1)
Travel time to clinic
<30′	4,122 (25.2)	630 (24.8)	0.015
30–59′	5,075 (31.0)	861 (33.9)
1–2 h	4,047 (24.7)	612 (24.1)
2 + h	3,110 (19.0)	435 (17.1)
Level of care
Primary	5,004 (30.6)	810 (31.9)	<0.001
Secondary	8,714 (53.3)	1,253 (49.4)
Tertiary	2,636 (16.1)	475 (18.7)
	Median (IQR)	Median (IQR)	p-Value
Ageb, years	36.0 (30.2, 42.9)	36.5 (30.6, 43.6)	0.007
CD4b, cells/μL	155 (84, 235)	153 (81, 229)	0.352
Months on ART	10.5 (2.9, 24.4)	10.2 (2.9, 23.3)	0.394
Outreach worker ratioc (×100)	5.0 (4.0, 5.9)	5.0 (3.6, 5.9)	0.003

^aPrior to first loss to clinic

^bAt ART initiation.

^c# of outreach workers to total daily # of adult patients.

In total, AMPATH’s outreach program was applied to 4,118 (21.8%) lost patients. Of them, 2,538 (61.6%) were successfully traced and had their vital status actively ascertained. Out of these patients, 491 (19.3%) were found to be deceased and this indicates a substantial death under-reporting issue. Among the non-successfully traced lost patients, 8,580 (52.5%) returned to care and, therefore, these patients had a true gap in care. The potential predictors of interest included patient gender, pregnancy status at last clinic visit, age and CD4 count at ART initiation, HIV status disclosure, travel time to clinic, and the level of care of the clinic attended by each patient. To make the key MAR assumption more plausible, we also considered the ratio of the number of outreach workers to the average daily number of adult patients in the clinic as an auxiliary variable that could plausibly be related to the probability that a patient lost to program would be outreached (Table 5). In addition, this variable is expected to be associated with the outcome of death after a gap in care. This is because a clinic with more outreach workers (relatively to the daily number of patients) is expected to be better funded, better staffed, and to provide better care. These characteristics are in turn expected to be associated with a lower risk of death even in patients who become lost after having received care for some time. The overall estimated cumulative incidences of death and return to care after a gap in care, based on the SIPW method, are given in Figure 7.

Figure 7:

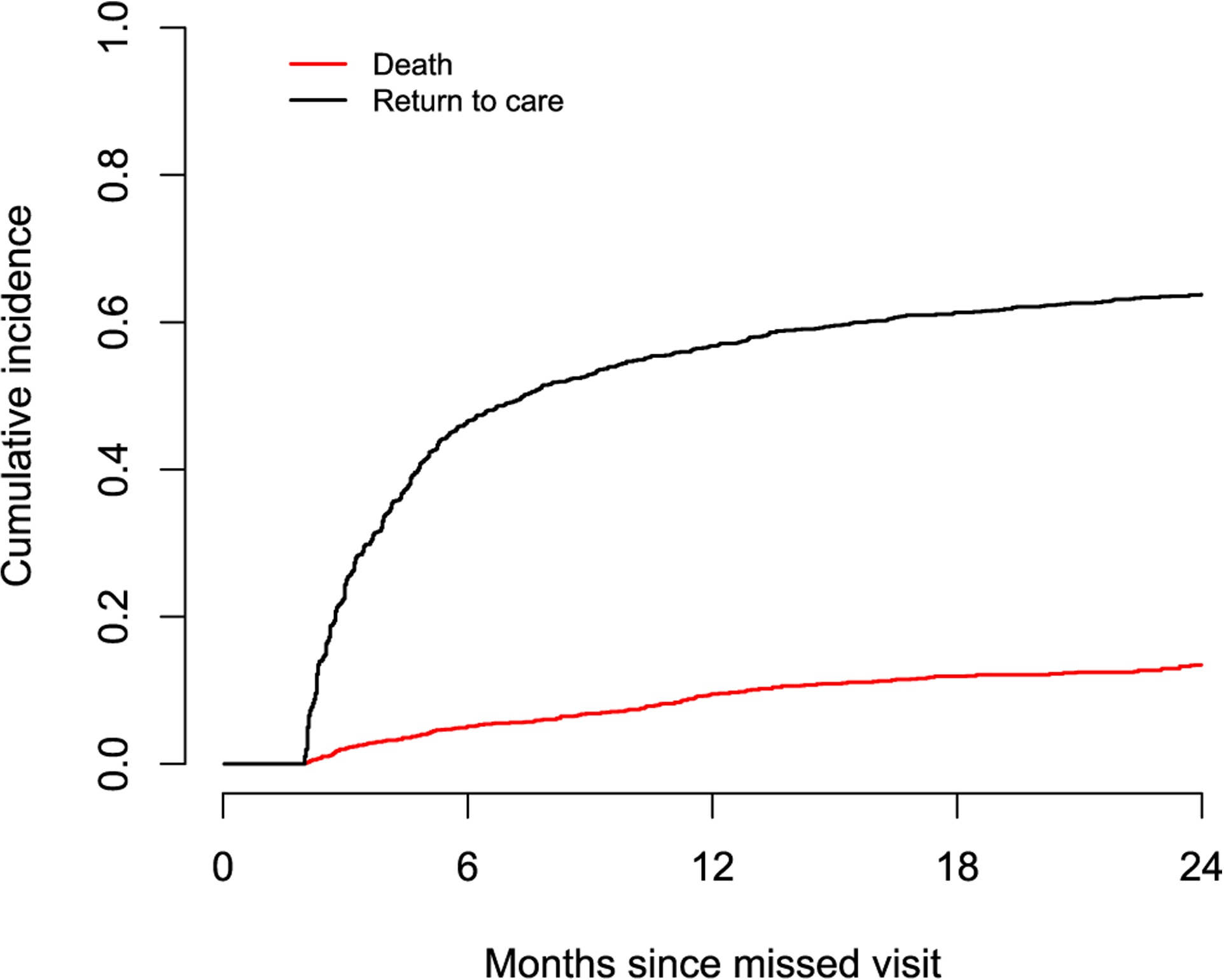
Cumulative incidence of death and return to care after the first gap in care.

In Figure 7, it appears that a large proportion of patients who have a gap in care return to care quickly after the gap in care and continue to re-engage over the next two years after the gap in care. The estimated cumulative incidence of return to care at 6, 12 and 24 months from the missed visit is 0.465, 0.568, and 0.638, respectively. The corresponding figures for the cumulative incidence of death are 0.051, 0.095, and 0.134. Effect estimates, based on the SIPW method, for factors potentially associated with the hazards of death and return to care after a gap in care are provided in Tables 6, 7 respectively. In these Tables, we also provide results from the naïve complete-case analysis and the MICE approach considered in Section 3.

Table 6:

Factors associated with death after a gap in care based on the naïve complete case analysis that ignores the non-outreached patients (CC), the multiple imputation by chained equations method with five imputations (MICE), and the proposed approach (SIPW).

	CC	MICE	SIPW
	CSHRa (p-Value)	CSHRa (p-Value)	CSHRa (p-Value)
Time on ART (per six months)	0.64 (<0.001)	0.80 (0.154)	0.62 (<0.001)
Gender
Female & non-pregnant	1.00 (−)	1.00 (−)	1.00 (−)
Female & pregnant	0.52 (0.057)	1.07 (0.883)	0.52 (0.073)
Male	0.90 (0.476)	1.07 (0.691)	0.99 (0.937)
Ageb (per 10 years)	1.05 (0.565)	1.00 (0.998)	1.03 (0.798)
CD4b (per 100 cell/μL)	0.72 (<0.001)	0.79 (0.093)	0.72 (<0.001)
HIV status disclosed	0.84 (0.250)	0.85 (0.368)	0.83 (0.252)
Travel time to clinic >30′	1.26 (0.221)	1.69 (0.037)	1.40 (0.098)
Level of care
Secondary/Tertiary	1.00 (−)	1.00 (−)	1.00 (−)
Primary	0.66 (0.022)	0.48 (0.098)	0.50 (<0.001)

^aCause-specific hazard ratio.

^bAt ART initiation.

Table 7:

Factors associated with return to care after a gap based on the naïve complete case analysis that ignores the non-outreached patients (CC), the multiple imputations by chained equations method with five imputations (MICE), and the proposed approach (SIPW).

	CC	MICE	SIPW
	CSHRa (p-Value)	CSHRa (p-Value)	CSHRa (p-Value)
Time on ART (per six months)	1.19 (<0.001)	1.24 (<0.001)	1.19 (<0.001)
Gender
Female & non-pregnant	1.00 (−)	1.00 (−)	1.00 (−)
Female & pregnant	1.14 (0.204)	1.41 (0.017)	1.14 (0.182)
Male	1.08 (0.274)	1.16 (0.011)	1.15 (0.080)
Ageb (per 10 years)	1.06 (0.140)	1.07 (0.012)	1.09 (0.060)
CD4b (per 100 cell/μL)	0.98 (0.422)	1.00 (0.633)	0.99 (0.535)
HIV status disclosed	1.01 (0.939)	1.03 (0.754)	1.01 (0.936)
Travel time to clinic >30′	0.81 (0.005)	0.91 (0.001)	0.81 (0.008)
Level of care
Secondary/Tertiary	1.00 (−)	1.00 (−)	1.00 (−)
Primary	1.37 (<0.001)	1.09 (0.263)	1.28 (0.003)

^aCause-specific hazard ratio.

^bAt ART initiation.

Factors associated with a decreased hazard of death after a gap in care based on the SIPW approach, include longer time on ART, pregnancy status (marginally significant result, p-Value=0.073 – pregnant women have generally less advanced disease), higher CD4 cell count, shorter travel time to clinic (marginally significant result, p-Value=0.098), and being treated at a primary clinic (Table 6). The naïve complete-case analysis of the successfully traced lost patients provides a less pronounced effect of travel time to clinic which is not statistically significant (p-Value=0.221), and a less pronounced effect of being in a primary care clinic. The MICE approach provides an effect of the opposite direction for pregnancy status (non-significant result, p-Value=0.883). Additionally, the MICE analysis provides a less pronounced effect of CD4 cell count (marginally significant result, p-Value=0.093), while it gives a more pronounced effect for travel time to clinic (significant result, p-value=0.037). Finally, the effect of a primary care clinic is only marginally significant based on the MICE analysis (p-Value=0.098). Factors associated with a higher rate of return to care after a gap in care based on the SIPW approach, include longer time on ART, male gender (marginally significant result, p-Value=0.080), older age (marginally significant result, p-Value=0.060), shorter duration of travel time to clinic, and being treated at a primary clinic (Table 7).

Based on the complete-case analysis, the effects of male gender and age appear attenuated and not statistically significant (p-Value: 0.274 and 0.140, respectively), while the effect of being in a primary care clinic appears more pronounced. Based on the MICE analysis, the effect of pregnancy is more pronounced and statistically significant (p-Value=0.017), the effect of male gender is statistically significant (p-Value=0.011), while the effects of travel time to clinic and of being in a primary care clinic are attenuated and the latter effect is not significant (p-Value=0.263). The discrepancy between the results from the naïve complete-case analysis and the proposed SIPW approach is attributed to the fact that the former approach does not take into account the auxiliary variable “number of outreach workers to average daily number of adult patients”, which needs to be accounted in order to make the MAR assumption more plausible in our setting. The discrepancy between the results from the MICE analysis and the proposed SIPW approach is attributed to the fact that the former approach imposes more model assumptions, some of which may be violated. The MICE approach requires all the three imputation models to be correctly specified and, also, that the distributional assumption on the event or censoring time X is correct. In contrast, the proposed SIPW approach only requires that the additivity assumption (i.e. no interactions) on the missingness probability model is satisfied.

We must one that, in this analysis, the computation time for the SIPW approach with 100 bootstrap replications for standard error estimation was only 60 s for each event type. No computational problems in the SIPW and MICE approaches were encountered in this analysis. The analysis of the remaining transitions in the model depicted in Figure 2, i.e. death while in care and gap in care after ART initiation, is presented in the Appendix.

Discussion

In this paper we propose a sieve inverse probability weighting (SIPW) estimator for semiparametric analysis of return to care and death after a gap in care. Analysis of these outcomes based on programmatic data is quite challenging as a result of death under-reporting. To recover part of the unreported mortality, we used information obtained from an intensive program of tracing patients who miss a clinic visit (double-sampling). These incomplete data on patient outcomes, combined with patient and clinic characteristics available prior to a gap in care plus auxiliary variables, were used to make more plausible the key missing at random (MAR) assumption. Our SIPW approach utilizes a generalized additive logit model for the probability of missingness, which is considerably more flexible compared to the traditional parametric logit models. Generalized additive models (Hastie and Tibshirani 1986) have been previously used for sensitivity analyses regarding the nonignorable missingness assumption, in the simpler case of univariate and non-censored incomplete outcome data (Scharfstein and Irizarry 2003). The estimation of the generalized additive model for the probability of missingness in our approach relies on B-spline sieve maximum likelihood estimation (Shen and Wong 1994; Zhang, Hua, and Huang 2010). Our simulation studies provide evidence for the validity of the proposed SIPW approach. They also indicate that a simple complete case-analysis can provide severely biased estimates in the presence of auxiliary variables which are associated with the probability of missingness. The bias from the complete-case analysis is proportional to the proportion of missingness. Moreover, our simulation experiments indicate that an MICE approach can provide biased estimates as a result of imposing more assumptions compared to the SIPW approach.

In this analysis, we considered the ratio of outreach workers to the average daily number of adult patients as an auxiliary variable. This variable is clearly associated with the probability of a successful patient outreach, that is the probability of non-missingness. It is also expected to be associated with the outcome process (even after conditioning on the covariates of interest), since a larger number of outreach workers is associated with more funding for the clinic, better staffing, and the provision of better care, which in turn are associated with better patient outcomes. Therefore, taking this variable into account via the SIPW method is crucial in order to make the MAR assumption more plausible in our setting. We must note that the SIPW approach is not useful for situations where the auxiliary variable is expected to be independent of the outcome given the covariates of interest. If one is willing to assume that the auxiliary variable is independent of the outcome given the covariates of interest, and if this variable is associated with missingness, a better approach to use is the instrumental variable framework (Bärnighausen et al. 2011; Tchetgen Tchetgen and Wirth 2017). This framework can deal with some missing not at random scenarios.

We must note here that, to estimate the time until return to care or death after a gap in care, we must only use data from patients who were traced. Including data from all patients who ultimately returned to care would render the MAR assumption invalid. This is because inclusion of data from patients returning to care who were not previously traced modifies the missingness indicator to $R_i^{\star }=\text{max}\left(R_i,{\Delta }_{i2}\right)$ (i.e., data are recovered from all those who returned plus those who were found by outreach). It is straightforward to understand why this new missingness indicator depends on the incomplete variables even after adjusting for covariates and auxiliary variables, thus violating the key MAR assumption, that is,

$$\text{Pr}\left(R_i^{\star }=1\mid G_i,X_i,{\Delta }_{i1},{\Delta }_{i2},W_i\right)\ne \text{Pr}\left(R_i^{\star }=1\mid W_i\right).$$

Our simulations (not shown) indicated that using outcome information from non-successfully traced patients could lead to bias in the effect estimates up to 115%. The probability of a successful outreach was higher for males or pregnant females, patients from clinics with more outreach workers, those with shorter travel time to clinic, older patients, and those with HIV status disclosed. Our MAR assumption allows the probability of a successful outreach to depend on all these factors. However, conditionally these factors and total time on ART, CD4 cell count at ART initiation, and level of care, the probability of successful outreach is assumed to be independent of the vital status, return to care status, and the time from the gap in care to death or return to care. A possible violation of our key MAR assumption is the scenario where outreach increases the likelihood of the traced patients returning to care. However, as shown in Table 4, the overall proportion of return to care among those who were traced was lower to that among those who were not traced. In addition, we do not have reasons to believe that, conditional on the variables included in the missingness probability model, the probability of a successful outreach is related to the vital status of the patient. Nevertheless, if concerns remain about a possible violation of the MAR assumption, one can perform a sensitivity analyses under a missing not at random selection model. This approach sheds light upon the potential robustness of the SIPW estimates against violations of the MAR assumption.

The results from our data analysis are consistent with ad hoc analyses of return to care performed to date (Geng, Odeny, and Lyamuya 2016; Rebeiro, Bakoyannis, and Musick 2017). Those analyses showed that a large percentage of patients with a gap in care re-engage in care shortly after the gap. This process of re-engagement in care has direct implication on estimates of retention in care, which would otherwise be underestimated if one simply used programmatic data without augmenting them with patient tracing or additional information on patients who are lost to program. On the other hand, the implications of undocumented transfers on the continuity of care of these patients are unknown. Clearly many patients re-engage quickly into care, but others appear to remain disengaged from care for extended periods of time (Geng, Odeny, and Lyamuya 2015).

An alternative approach to the B-spline sieve spaces used for the missingness probability model, is to use regression splines (such as B-splines) with a small number of internal knots (e.g. 3–5) that does not depend on sample size n. Even though this approach is less flexible compared to our original approach, it can be better suited for situations with many continuous covariates in the missingness model and/or a small sample size n and/or a small double-sample size. In such cases, estimating the parameters of the generalized additive model for the missingness probability based on B-spline sieve maximum likelihood may be problematic as some parameters may not be estimable. A practically relevant question is what is the smallest number of double-sampled observations under which the method is expected to have good performance. With small numbers of non-missing observations, it may be more appropriate to use parametric regression splines as mentioned above. In such cases, and assuming that the double-sampled observations are fewer than the non-double-sampled observations, one can use the rule of thumb of having at least 10 double-sampled observations per parameter to be estimated in the missingness model (Agresti 2002).

We must recognize that the IeDEA data are cluster-correlated as patients from the same clinic are expected to have correlated outcomes, and this was not addressed in the analyses presented in this article. To address this issue under the MAR assumption imposed in this paper, one needs to use GEE under a working independence assumption to estimate the probability of missingness, and then use the pseudo partial score function to estimate the parameters β_j. If the estimator for the missingness probability is consistent, then the arguments in Spiekerman and Lin (1998) imply that our estimator is consistent for the population-averaged parameters of the competing risks process under study. Standard error estimation can be easily performed using the nonparametric cluster bootstrap (Bakoyannis 2020; Field and Welsh 2007).

The proposed methodology provides a robust approach for valid inferences about return to care and death during a gap in care, in settings with death under-reporting. This methodology should be useful for a more complete accounting of the patient transition through the HIV care cascade. More realistic estimates of return to care and death will have profound effects on the validity of estimates on patient retention in care. Ultimately, these estimates will have significant consequences on program construction, resource allocation, policy and decision making at the highest levels.

Appendix: Analysis of the hazards of a first gap in care and death

In this Appendix, we provide the analysis of the hazards of death while in care and of a gap in care after ART initiation (i.e. the remaining hazards in the multi-state churn model depicted in Figure 2). Here, we focus on the first occuring event (death or gap in care) after ART initiation and, thus, the analysis can be based on methods for competing risks data (Bakoyannis and Touloumi 2012; Putter, Fiocco, and Geskus 2007). To account for the missing event types (i.e. death or gap in care) due to death under-reporting among the non-outreached lost patients, we use appropriate pseudolikelihood methods (Bakoyannis, Zhang, and Yiannoutsos 2019, 2020). In this analysis we include 38,490 patients who initiated ART in one of the clinics in the AMPATH program. These patients are a superset of the 18,892 patients who were identified as lost to clinic and analyzed in the main text of this manuscript. Characteristics of the 38,490 patients are shown in Table A1.

Of the 38,490 patients in our sample, 18,892 (49.1%) patients were identified as lost to clinic, 1,979 (5.1%) were reported as deceased without a prior gap in care, while the remaining 17,619 (45.8%) patients were alive and without a gap in care at the date of data request. In total, 2,538 (13.4%) lost patients were successfully traced by AMPATH outreach workers (Table A1). Of them, 491 (19.3%) were found to have died within two months from the next scheduled visit and this indicates a substantial death under-reporting issue. The potential predictors of interest included patient gender, pregnancy status at last clinic visit, age and CD4 count at ART initiation, HIV status disclosure, travel time to clinic, and the level of care of the clinic attended by each patient. To make the key MAR assumption more plausible, we also considered the ratio of the number of outreach workers to the average daily number of adult patients in the clinic as an auxiliary variable that could plausibly be related to the probability that a patient lost to program would be outreached (Table A1). The pseudolikelihood methods we use here require the specification of a (parametric) logistic model for the probability of an unreported death among the lost patients. For flexibility, we use cubic B-splines with three internal knots for the continuous covariates in this model (regression splines). Note that here, unlike the SIPW approach, the number of knots does not depend on the sample size n and thus the model involves only a finite-dimensional parameter (i.e. it is a parametric model). The overall estimated cumulative incidences of a first gap in care and death prior to the first gap in care are, based on the nonparametric maximum pseudolikelihood estimator by Bakoyannis et al. (2019), are given in Figure A1.

Table A1:

Descriptive characteristics of the study sample for the analysis of the first gap in care and death prior to the first gap.

	Passively ascertained outcome			p-Value
	In care	Death	LTCa
	(n=17,619)	(n=1,979)	(n=18,892)
	n(%)	n(%)	n(%)
Outreach
Not attempted	0 (−)	0 (−)	14,774 (78.2)	-
Not found	0 (−)	0 (−)	1,580 (8.4)
Found	0 (−)	0 (−)	2,538 (13.4)
True outcomeb
Death	0 (−)	0 (−)	491 (19.3)	-
Gap in care	0 (−)	0 (−)	2,047 (80.7)
Gender
Female & non-pregnantc	9,412 (58.9)	726 (43.1)	8,058 (51.8)	<0.001
Female & pregnantc	1,076 (6.7)	32 (1.9)	1,190 (7.6)
Male	5,488 (34.4)	926 (55.0)	6,320 (40.6)
HIV status disclosed
No	6,269 (35.6)	670 (33.9)	6,972 (36.9)	0.003
Yes	11,350 (64.4)	1,309 (66.1)	11,920 (63.1)
Travel time to clinic
<30′	4,570 (25.9)	480 (24.3)	4,752 (25.2)	<0.001
30–59′	6,153 (34.9)	679 (34.3)	5,936 (31.4)
1–2 h	4,346 (24.7)	482 (24.4)	4,659 (24.7)
2 + h	2,550 (14.5)	338 (17.1)	3,545 (18.8)
Level of care
Primary	5,777 (32.8)	649 (32.8)	5,814 (30.8)	<0.001
Secondary	9,561 (54.3)	1,176 (59.4)	9,967 (52.8)
Tertiary	2,281 (12.9)	154 (7.8)	3,111 (16.5)
	Median (IQR)	Median (IQR)	Median (IQR)	p-Value
Aged, years	37.9 (32.0, 45.4)	37.8 (31.7, 45.2)	36.0 (30.3, 43.1)	<0.001
CD4d, cells/μL	186 (113, 263)	106 (52, 179)	155 (83, 234)	<0.001
Outreach worker ratioe (×100)	5.0 (3.6, 5.9)	5.0 (4.0, 5.9)	5.0 (4.0, 5.9)	<0.001

^aLost to clinic.

^bAscertained through outreach.

^cAt or prior to ART initiation.

^dAt ART initiation.

^e# of outreach workers to total daily # of adult patients.

Figure A1:

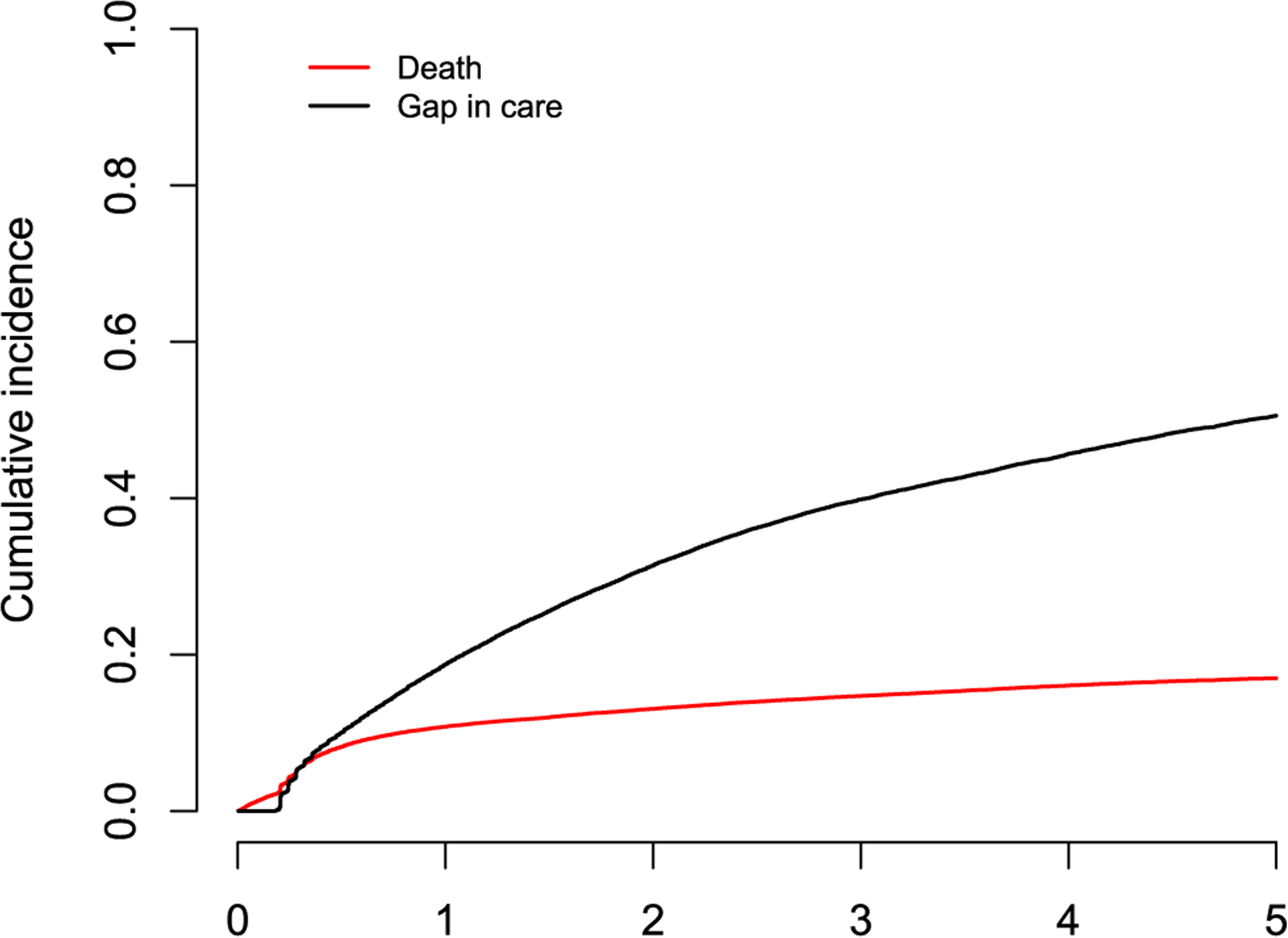
Cumulative incidence of death while in care and gap in care after ART initiation.

Table A2:

Factors associated with death while in care after ART initiation.

	CSHRa	95% CI	p-Value
Gender
Female & non-pregnant	1.000	-	-
Female & pregnant	0.529	(0.341, 0.820)	0.004
Male	1.306	(1.164, 1.465)	<0.001
Ageb, per 10 years	1.110	(1.035, 1.192)	0.004
CD4b, per 100 cell/μL	0.663	(0.608, 0.723)	<0.001
HIV status disclosed	1.072	(0.914, 1.257)	0.395
Travel time to clinic >30′	1.081	(0.945, 1.235)	0.256
Level of care
Secondary/Tertiary	1.000	-	-
Primary	0.804	(0.652, 0.992)	0.042

^aCause-specific hazard ratio

^bAt ART initiation

Table A3:

Factors associated with a first gap in care after ART initiation.

	CSHRa	95% CI	p-Value
Gender
Female & non-pregnant	1.000	-	-
Female & pregnant	1.169	(1.072, 1.274)	<0.001
Male	1.108	(1.042, 1.179)	0.001
Ageb, per 10 years	0.769	(0.742, 0.797)	<0.001
CD4b, per 100 cell/μL	0.981	(0.960, 1.002)	0.070
HIV status disclosed	0.927	(0.869, 0.990)	0.023
Travel time to clinic >30′	1.038	(0.987, 1.092)	0.148
Level of care
Secondary/Tertiary	1.000	-	-
Primary	1.067	(0.979, 1.163)	0.142

^aCause-specific hazard ratio

^bAt ART initiation

In Figure 7, it appears that a large proportion of patients who initiate ART have a subsequent gap in care. The estimated cumulative incidence of a gap in care at 1, 2, and 5 years since ART initiation is 0.187, 0.314, and 0.505, respectively. The corresponding figures for the cumulative incidence of death while in care are 0.108, 0.131, and 0.170. Effect estimates for factors potentially associated with the hazards of death while in care and gap in care are provided in Tables A2, A3 respectively.

Factors associated with a decreased hazard of death while in care, include pregnancy status (pregnant women have generally less advanced disease), female gender, younger age, higher CD4 cell count and being treated at a primary clinic (Table A2). Factors associated with a higher rate of a gap in care after ART initiation includes pregnancy, male gender, younger age, and non-disclosure of the HIV status (Table 7).