Non-Gaussian Analysis of Diffusion-Weighted MR Imaging in Head and Neck Squamous Cell Carcinoma: A Feasibility Study

Abstract

BACKGROUND AND PURPOSE

Water in biological structures often displays non-Gaussian diffusion behavior. The objective of this study was to test the feasibility of non-Gaussian fitting by using the kurtosis model of the signal intensity decay curves obtained from DWI by using an extended range of b-values in studies of phantoms and HNSCC.

MATERIALS AND METHODS

Seventeen patients with HNSCC underwent DWI by using 6 b-factors (0, 50–1500 s/mm²) at 1.5T. Monoexponential (yielding ADC_mono) and non-Gaussian kurtosis (yielding apparent diffusion coefficient D_app and apparent kurtosis coefficient K_app) fits were performed on a voxel-by-voxel basis in selected regions of interest (primary tumors, metastatic lymph nodes, and spinal cord). DWI studies were also performed on phantoms containing either water or homogenized asparagus. To determine whether the kurtosis model provided a significantly better fit than did the monoexponential model, an F test was performed. Spearman correlation coefficients were calculated to assess correlations between K_app and D_app.

RESULTS

The kurtosis model fit the experimental data points significantly better than did the monoexponential model (P < .05). D_app was approximately twice the value of ADC_mono (eg, in neck nodal metastases D_app was 1.54 and ADC_mono was 0.84). K_app showed a weak Spearman correlation with D_app in a homogenized asparagus phantom and for 44% of tumor lesions.

CONCLUSIONS

The use of kurtosis modeling to fit DWI data acquired by using an extended b-value range in HNSCC is feasible and yields a significantly better fit of the data than does monoexponential modeling. It also provides an additional parameter, K_app, potentially with added value.

The MR imaging technique known as DWI allows measurement of water diffusivity.¹ Because freedom of translational motion of water molecules is hindered by interactions with other molecules and cell membranes, DWI abnormalities can reflect changes of tissue organization at the cellular level.^2,3 These microstructural changes affect the motion of water molecules, and consequently alter the water diffusion properties and thus the MR imaging signal intensity. The signal intensity loss in DWI can be quantified by using the ADC, which is a measure of the average molecular motion that is affected by cellular organization and integrity. In the simplest models, the distribution of a water molecule diffusing from one location to another in a certain period of time is considered to have a Gaussian form with its width proportional to the ADC.² However, water in biological structures often displays non-Gaussian diffusion behavior.⁴ As a result, the MR signal intensity decay in tissue is not a simple monoexponential function of the b-value.^3,5

Several approaches have been used to model the nonlinear decay of DWI signal intensity when more than 2 b-values are acquired. These approaches include biexponential fitting, from which 2 components that hypothetically reflect 2 separate biophysical compartments can be derived,⁶ stretched-exponential fitting, which describes diffusion-related signal intensity decay as a continuous distribution of sources decaying at different rates,⁷ and diffusional kurtosis analysis, which takes into account non-Gaussian properties of water diffusion by measuring the kurtosis.⁸ Kurtosis represents the extent to which the diffusion pattern of the water molecules deviates from a perfect Gaussian curve. Unlike the biexponential model, the stretched-exponential and the kurtosis methods do not make assumptions regarding the number of biophysical compartments or even the existence of multiple compartments. ³ From the kurtosis analysis, 2 parameters are derived: the apparent diffusion coefficient (D_app) and the apparent kurtosis coefficient (K_app).

In the HN region, DWI has been used for characterizing and differentiating benign and malignant pathology in patients, ^9–19 evaluating treatment-induced tissue changes, especially after chemoradiation therapy,^20–22 and assessing persistent or recurrent cancer.^23,24 In previous DWI studies in HN cancer patients, a combination of 2 or 3 b-factors (eg, 0, 500, and 1000 s/mm²) was usually acquired, and the ADC values (ADC_mono) were calculated assuming that the signal intensity decay is a monoexponential function.^12,18,19,25 To our knowledge, no study has considered the non-Gaussian diffusion behavior of DWI data in HNSCC. The kurtosis model may lead to better fit of the experimental data.⁸ The diffusion parameters D_app and K_app provided by this model could offer potential value for longitudinal studies assessing early response in patients with HNSCC undergoing chemoradiation therapy.

The objective of this study was to test the feasibility of non-Gaussian fitting by using the kurtosis model of the signal intensity decay curves obtained from DWI by using an extended range of b-values in studies of phantoms and HNSCC.

Materials and Methods

Phantoms

Phantoms were prepared containing either Gd-DTPA-doped water or homogenized asparagus.⁸ Gd-DTPA was obtained from Magnevist (Bayer HealthCare Pharmaceuticals, Wayne, New Jersey).

Patients

Our institutional review board approved and issued a waiver of informed consent for our retrospective study, which was compliant with the Health Insurance Portability and Accountability Act. Between June 2008 and June 2009, 17 consecutive patients with HNSCC, referred for MR imaging by physicians at our institution, underwent a pretreatment clinical MR imaging examination that included DWI. Patient characteristics are given in Table 1.

Table 1.

Patient characteristics

Subject	Age (y)/Sex	Primary Cancer	ROIs
1	65/M	NPC	Primary, 2 nodes, and spinal cord
2	75/F	Tonsil	Primary, node, and spinal cord
3	84/M	BOT	Primary and spinal cord
4	55/M	BOT	Primary, 2 nodes, and spinal cord
5	70/M	Tonsil	Primary, node, and spinal cord
6	78/M	BOT	Primary and node
7	27/F	Tonsil	Primary, 2 nodes, and spinal cord
8	60/M	Tonsil	Primary and node
9	63/M	BOT	Primary, node, and spinal cord
10	66/M	BOT	3 nodes and spinal cord
11	51/M	BOT	Primary and node
12	60/M	BOT	Primary and 3 nodes
13	51/F	Tonsil	Primary, 2 nodes, and spinal cord
14	51/M	Tonsil	Primary, 2 nodes, and spinal cord
15	68/M	Tonsil	3 nodes and spinal cord
16	55/F	Tonsil	Primary and node
17	49/F	NPC	Primary, 2 nodes, and spinal cord

SCC pathology was confirmed by using needle biopsy at the primary HN tumor location at least 1 week before the MR imaging examination. Of the sites that contributed to the mean DWI parameter values for these 17 patients, primary tumors included 6 base of tongue, 7 tonsil, and 2 nasopharyngeal tumors, 28 were metastatic neck lymph nodes, and 12 were spinal cord (which served as a control region).

MR Imaging Data Acquisition

MR imaging data were acquired on a 1.5T Excite scanner (GE Health-care, Milwaukee, Wisconsin) by using either a 4-channel or 8-channel neurovascular phased array coil for signal intensity reception and a body coil for transmission. Accuracy was assessed on both the settings (1.5T by using a 4-channel neurovascular array coil, 1.5T by using an 8-channel neurovascular array coil) with phantoms at 25°C.

The patient study was done on either 4-channel (n = 10) or 8-channel (n = 7) coils and consisted of MR imaging covering the entire neck or oral cavity/tongue or nasopharynx. The standard MR acquisition parameters were as follows: rapid scout images, multiplanar (axial, coronal, and sagittal) T2-weighted, fat-suppressed, fast spin-echo images (TR, 5000 ms; TE, 102 ms; averages, 2; matrix, 256 × 256; section thickness, 5.0 mm; and gap, 2.5 mm for neck survey; for oral cavity/tongue or nasopharynx imaging, section thickness, 4.0 mm; gap, 1.0 mm), multiplanar T1-weighted images (TR, 675 ms; TE, 8 ms; averages, 2; section thickness, 5.0 mm; gap, 2.5 mm; matrix, 256 × 256). Standard T1- and T2-weighted imaging was followed by DWI. After DWI, Gd-DTPA contrast agent was injected and postcontrast multiplanar T1-weighted images were acquired.

For patients, diffusion-weighted images were obtained by using single-shot spin-echo echo-planar imaging with a pair of rectangular gradient pulses along 3 orthogonal axes. The imaging parameters were as follows: TR, 4000 ms; TE, 85–98 ms; averages, 4; section thickness, 5.0 mm; gap, 0 mm; FOV, 20–26 cm; matrix, 128 × 128; and 3 diffusion sensitizing directions. The b-values were 0, 50, 100, 500, 750, 1000, and 1500 s/mm². The duration of the DWI component of the examination was approximately 8 minutes. Four to 10 sections were acquired to cover the lesion.

DWI experiments were performed on phantoms by using the same type of sequence and b-values as for the HNSCC patients. There is a difference in loading of the coil between the studies of phantoms and patients. To obtain the best SNR characteristics in the phantom study, the experiments were performed with similar MR parameters as detailed above except for averages of 16 and section thickness of 15.0 mm.

Image Analysis

Image processing was performed by using customized software in Matlab (MathWorks, Natick, Massachusetts), based on SPM5 software routines (Wellcome Department of Cognitive Neurology, London, United Kingdom). The individual diffusion-weighted images for the 3 directions were automatically averaged on the scanner; hence, for subsequent analyses only the averaged diffusion-weighted images were included. For all of the 6 DWI images with a b-value > 0 s/mm², a corresponding image with b = 0 s/mm² was obtained. All 6 b = 0 images were aligned to correct for motion, by using an affine transformation in SPM5. Subsequently, all corresponding DWI images with a b-value > 0 s/mm² were transformed by using the same parameters obtained from the b= 0 images realignment. An averaged b = 0 image was obtained after realignment, with optimal SNR characteristics. Next, Gaussian smoothing was applied on all images with a full width at half maximum of 3 mm, which is approximately 3 times the in-plane voxel size.

For phantom data analysis, a ROI created by using the MRIcro software²⁶ (www.sph.sc.edu/comd/rorden/mricro.html) was positioned within the phantom of size approximately 64 mm³. Statistics (mean and SD) were derived from the values within the ROI. Combining data from both 4- and 8-channel coils was proved to be feasible, and no differences in ADC values were noted.

For each patient, masks were created by using MRIcro to select a ROI for each lesion (primary tumors and nodes). ROIs were manually drawn by an experienced neuroradiologist (with > 10 years of experience in reading MR imaging of the head and neck) on the averaged b = 0 image. All of the sections containing the tumor or nodal metastasis were outlined and analyzed. Fits were performed for all ROIs on a voxel-by-voxel basis with a Marquardt-Levenberg algorithm implemented in Matlab, as described previously by Lu et al.³ SNR for all ROIs for all diffusion-weighted images were calculated by dividing the maximum signal intensity within the ROI by the SD of the noise within an ROI of identical size outside the body.

The signal intensity versus b-factor from each voxel in the ROI, as extracted from DWI datasets acquired in the presence of diffusion-sensitizing gradients, was fitted with both monoexponential functions and non-monoexponential decay functions of the form

$$\text{ln}[S(b)]=\text{ln}[S(0)]-b\times {\mathrm{D}}_{\text{app}}+1/6b^2\times {{\mathrm{D}}_{\text{app}}}^2\times {\mathrm{K}}_{\text{app}},$$

where S is the signal intensity (arbitrary units), b is the b-value (s/mm²), D_app is the apparent diffusion coefficient (10⁻³ mm²/s), and K_app, a dimensionless parameter, is the apparent kurtosis coefficient. The fit parameters were not assigned initial values for the curve fitting. In addition to non-Gaussian fitting, monoexponential fitting was performed by using K_app=0 in the equation, yielding ADC_mono.

Heterogeneity of tumors was assessed by computing the SD of a normalized distribution of the voxels within each ROI.²⁷ Toward this end, the DWI-derived parameters ADC_mono, D_app, and K_app were first normalized for each individual ROI to a scale of [0, 100], with 0 as the minimum and 100 as the maximum value. Subsequently, the SD was calculated from these normalized distributions. This procedure yielded heterogeneity measures hADC_mono, hD_app, and hK_app.

Additionally, necrosis was assessed by the radiologist separately for the primary tumor and the neck nodal metastasis in each patient on both the pre-T2-weighted images and the post Gd-DTPA contrast T1-weighted images by means of visual inspection. Necrosis is hyper-intense on T2-weighted images and hypointense on postcontrast T1-weighted images. The MR imaging reading was scored on a scale of [0, 1], with 0 indicating no necrosis and 1 indicating necrosis (which included mild to severe necrosis).

Statistical Analysis

Statistical tests were performed in SPSS for Windows (release 15.0.1; SPSS, Chicago, Illinois).

To test the goodness of fit for the monoexponential and kurtosis models, the reduced χ² was calculated on a voxel-by-voxel basis, which is the sum of the differences between observed and expected outcome values, each squared and divided by the expectation, divided by the number of degrees of freedom in the model. To determine whether the kurtosis model provided a statistically improved fit over the monoexponential model, the differences between the results of the 2 approaches were tested by using an F test of the resulting sum of squares values, with P<.05 denoting statistical significance. In detail, the monoexponential fitting model has 5 degrees of freedom (7 data points minus 2 variables), and the kurtosis model has 4 degrees of freedom. In this situation, the ratio of the relative increase of sum of squares divided by the increase of degrees of freedom has to be >F (0.05, 1, 4) = 4.5.

To assess whether the kurtosis analysis also yields potential additional information to the standard ADC value, in terms of K_app, the Spearman rank-order correlation coefficient for K_app and D_app was calculated for both phantom and patient data. A high absolute Spearman correlation coefficient (|ρ|) between K_app and D_app would indicate that K_app does not have additional information, whereas a weak correlation coefficient might indicate that K_app is independent of D_app and therefore does reflect additional information.⁸

To explore the potentially increased sensitivity of D_app to reflect heterogeneity over ADC_mono, the differences in heterogeneity measures hADC_mono and hD_app were statistically tested by using a 2-sided Student t test. Additionally, to investigate whether the diffusion parameters, the potential additional information of the kurtosis analysis, and the heterogeneity values of ADC_mono, D_app, and K_app, are affected by necrosis, tumor lesions were divided into 2 categories: 0 = no necrosis, 1 = necrosis. Subsequently, a 2-sided Student t test was applied on these measures to assess statistical differences between necrotic and non-necrotic lesions.

Results

Phantom Experiments

Phantom experiments revealed perfect Gaussian behavior for the phantom containing Gd-DTPA-doped water (ADC_mono = 2.29±0.01 10⁻³mm²/s, D_app =2.31±0.02 10⁻³mm²/s, and K_app=0.02±0.02) and non-Gaussian behavior for the phantom containing homogenized asparagus (ADC_mono = 1.55 ± 0.07 10⁻³mm²/s,D_app=1.75±0.08 10⁻³mm²/s, and K_app= 0.28±0.05). The D_app values from the non-Gaussian kurtosis model were higher than the ADC_mono values from the monoexponential fit, as reported previously.³ The K_app in the homogenized asparagus phantom was substantially higher than the K_app in the water phantom, reflecting a significant departure from Gaussian diffusion.⁸

Comparison of Fitting Methods

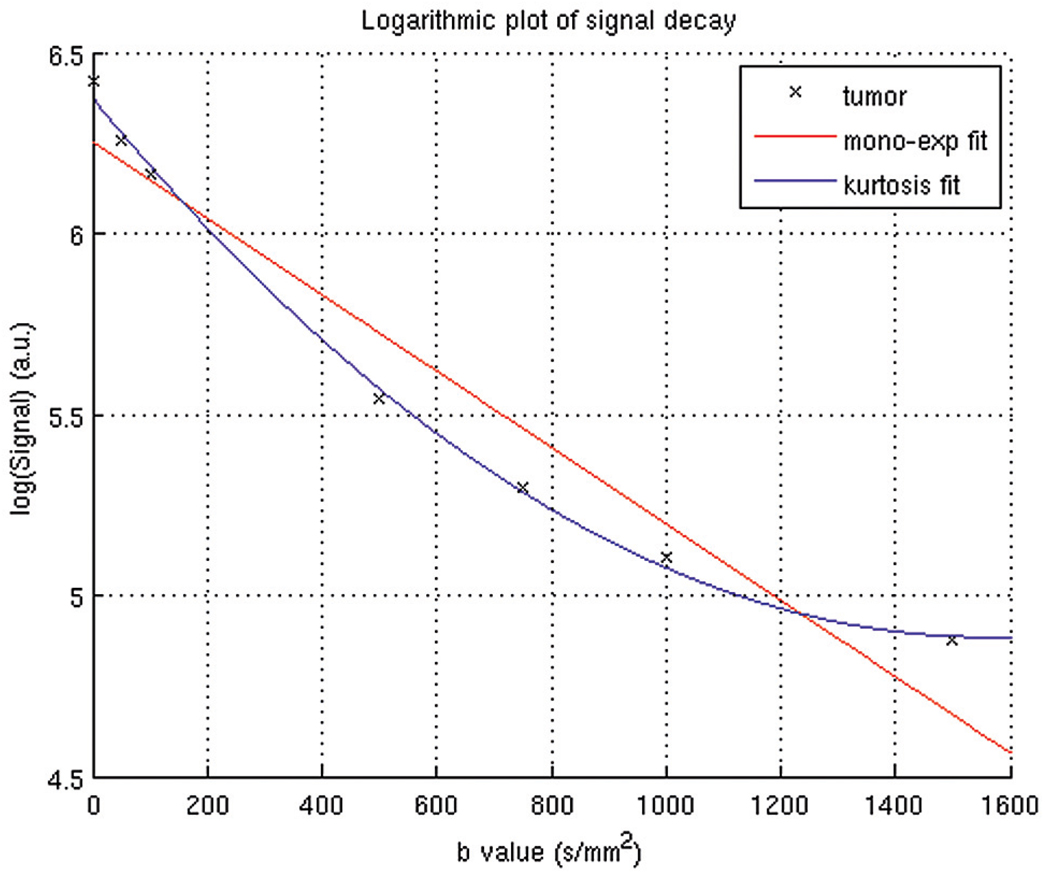
Figure 1 provides an example of the signal intensity decay curve of mean intensity of the right node of patient 12, as a function of the b-value. The plot is semilogarithmic, and the data points display a nonlinear decay. Also presented in this plot are the fitting curves from the monoexponential fitting procedure and the diffusional kurtosis analysis. It can be clearly seen that the non-Gaussian kurtosis analysis fits the data points substantially better than does the monoexponential fitting procedure. To assess whether these beneficial fit characteristics were also significant, an F test was performed on all ROIs. The F ratio obtained in this case (Fig 1) was 26.8, hence greater than F (0.05, 1, 4)= 4.5, indicating that the non-Gaussian kurtosis analysis was significantly (P < .05) better than the monoexponential fit. For all individual cases in the whole population, the non-Gaussian kurtosis analysis was always significantly better than the monoexponential fit, as calculated from the F test (P<.05). The median reduced χ² of all ROIs from the entire population was 0.008 (range, 0.001– 0.15) for the monoexponential fit and 0.002 (range, 0.0003– 0.15) for the kurtosis fit. The median SNR within the ROIs in the diffusion-weighted images acquired with the highest b-value (b = 0 1500 s/mm²) was 42 (range, 21–87).

Fig 1.

Logarithm of the MR signal intensity decay averaged over all voxels within the right node of patient 12 as a function of the b-value. The black crosshairs represent the experimental data, and the solid lines are the fitted curves (red is the monoexponential fit, blue is the non-Gaussian kurtosis fit).

Patients

In total, 17 patients were successfully scanned by using the extended b-value protocol. Table 2 shows the average estimated diffusion coefficients for various tissue structures, obtained by using monoexponential fitting and diffusional kurtosis analysis.

Table 2.

Average estimated diffusion coefficients derived from monoexponential fitting and diffusional kurtosis analysis in patients with squamous cell carcinoma head and neck cancer (n = 17)

Region (n)	ADCmono	Dapp	Kapp	ρ (Dapp and Kapp)
Node (28)	0.84 ± 0.24	1.54 ± 0.45	1.38 ± 0.37	−0.49 ± 0.35
BOT primary (6)	0.67 ± 0.22	1.32 ± 0.35	1.69 ± 0.54	−0.52 ± 0.42
Tonsil primary (7)	0.78 ± 0.20	1.46 ± 0.41	2.91 ± 3.92	−0.54 ± 0.27
NPC primary (2)	1.16 ± 0.19	2.21 ± 0.05	0.92 ± 0.17	−0.21 ± 0.34
Spine (12)	0.74 ± 0.08	1.44 ± 0.29	1.41 ± 0.15	−0.26 ± 0.42

Note:—n indicates number of regions (over all squamous cell carcinoma patients) contributing to the average; ADC_mono, apparent diffusion coefficient obtained from monoexponential fitting (10⁻³ mm²/s); D_app, apparent diffusion coefficient obtained from diffusional kurtosis analysis (10⁻³ mm²/s); K_app, apparent kurtosis coefficient obtained from diffusional kurtosis analysis (dimensionless); ρ(D_app and K_app), Spearman rank-order correlation coefficient for correlation between K_app and D_app. Averages are presented mean ± SD

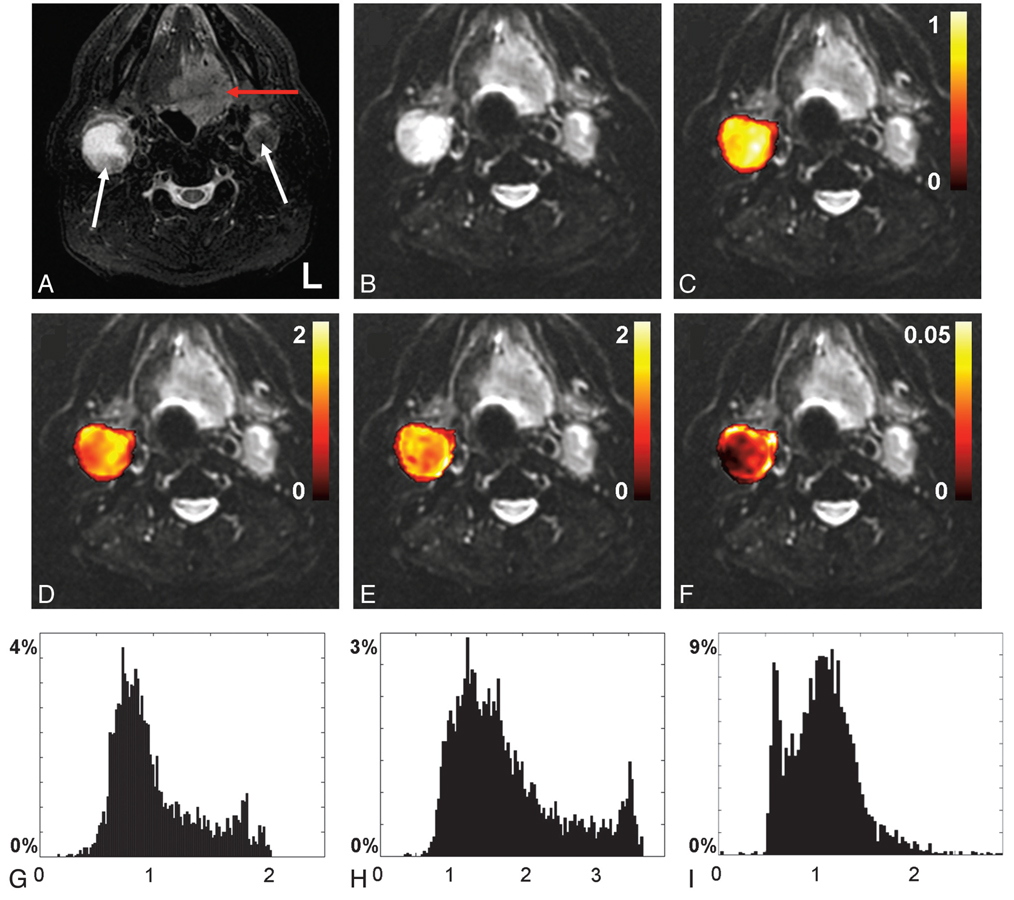
The ADC obtained from the diffusional kurtosis analysis (D_app) was about twice the value of the ADC obtained by monoexponential fitting (ADC_mono) (Table 2). Figure 2 shows the MR image series obtained from the oral cavity of patient 12. In Fig 2C–F, the calculated fitting parameters for the right node are visualized by using a mask overlay on the realigned mean b = 0 image. From the reduced χ² error estimate in Fig 2F, it can be observed that the fit deteriorates near the rim of the node. In Fig 2G–I, histogram distribution plots based on monoexponential and non-Gaussian fitting are shown. In Fig 2I, the histogram for K_app displays the presence of 2 distinct distribution peaks, at 0.5 and 1.1.

Fig 2.

Axial MR images from the oral cavity of a male patient diagnosed with base of tongue cancer (patient 12). A, T2 short tau inversion recovery image. B, Realigned mean b = 0 image. The red and white arrows in A indicate the primary tumor and metastatic nodes, respectively. C–F display voxel-by-voxel calculation outcomes for the right node presented as mask overlays on the realigned mean b = 0 image. G–I display the corresponding histogram distribution plots of the measures from C–E. C and G, Apparent diffusion coefficient obtained from monoexponential fitting (10⁻³ mm²/s). D and H, Apparent diffusion coefficient (10⁻³ mm²/s), (E and I) apparent kurtosis coefficient (dimensionless), and (F) reduced χ² error estimate, all obtained from the diffusional kurtosis analysis.

Potential Additional Information

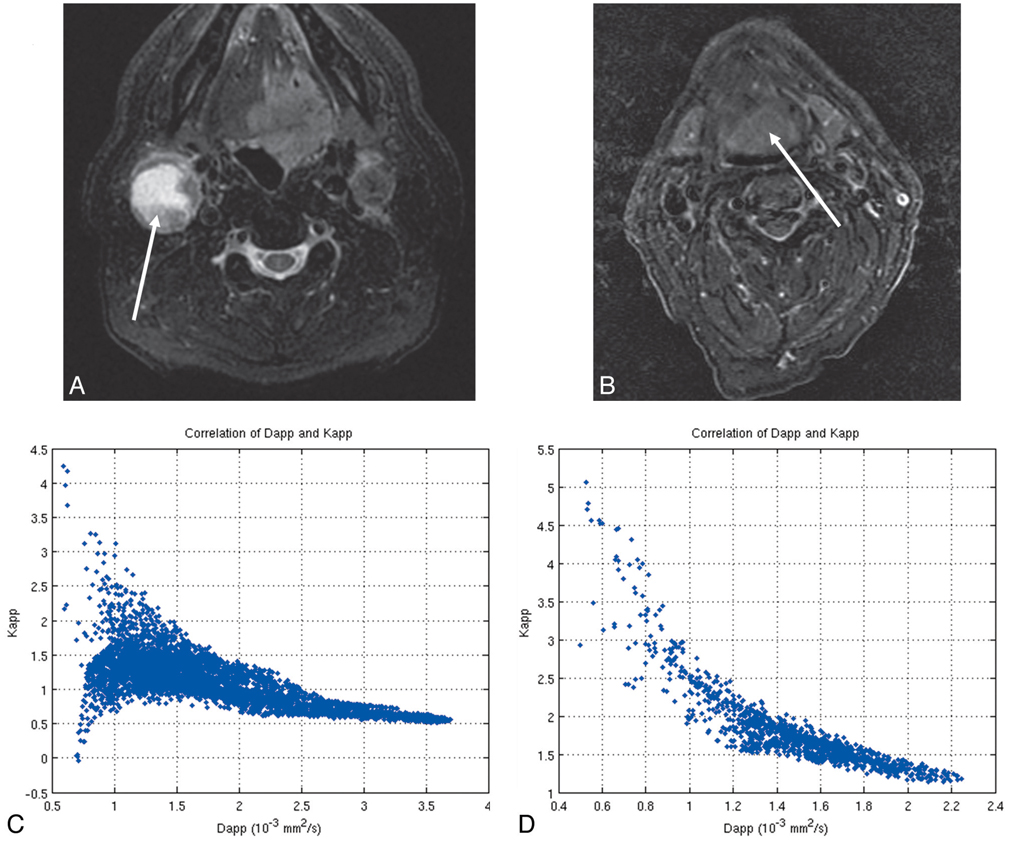
Aside from providing a better fit, the non-Gaussian kurtosis analysis may also yield new information (ie, the K_app [apparent kurtosis coefficient]) in addition to the standard ADC value. To assess the potential added value of this parameter, for all voxels of the tumor highlighted in Fig 3A (right node of patient 12), the D_app was plotted as a function of the K_app. The resulting scatterplot is given in Fig 3C. To investigate this relationship in a quantitative way, a Spearman rank-order correlation coefficient was calculated. The Spearman rank-order correlation coefficient for this case was −0.34, indicative of a weak correlation between the K_app and D_app. Fig 3D displays the D_app versus K_app plot of the primary tumor of patient 3 (Fig 3B). In this case, the Spearman rank-order correlation is −0.90. The range of absolute Spearman rho (|ρ|) for all tumor lesions (n = 43) of the population was 0.1 to 0.95, though for 44% of the lesions (n = 19) (|ρ|) < 0.5.

Fig 3.

T2 short tau inversion recovery images for (A) the right neck metastatic lymph node of patient 12 and (B) primary base of tongue tumor of patient 3 (ROIs are indicated with a white arrow). C and D display the corresponding scatterplots showing the correlation between the D_app (average apparent diffusion coefficient) and the K_app (apparent diffusional kurtosis) obtained from the diffusional kurtosis analysis. The Spearman rank-order correlation coefficient is −0.34 for C, indicating a weak correlation, and −0.90 for D, indicating a strong negative correlation.

The heterogeneity values for the DWI-derived parameters, averaged over all tumor lesions (n = 43), were hADC_mono = 18.2 ± 3.6, hD_app = 19.2 ± 3.5, and hK_app = 12.5 ± 4.6 (mean ± SD). The heterogeneity measure for the diffusion coefficient obtained by using the kurtosis analysis hD_app was statistically higher (P < .05) than the value hADC_mono obtained by using the monoexponential analysis.

We identified 25 tumor lesions with necrosis and 18 lesions with no necrosis; specifically, 23 metastatic neck nodes and 2 primary tumors were necrotic, whereas 5 nodes and 14 primary tumors were not necrotic. Due to the limited number of necrotic primary tumors (n = 2), no separate analysis was performed for the primary lesions. However, a separate analysis for the metastatic lymph nodes was performed, and it yielded significantly higher ADC_mono and D_app values and significantly lower K_app values for the necrotic nodes (P < .01). The differences in Spearman correlation coefficient between K_app and D_app and heterogeneity values hADC_mono, hD_app, and hK_app were not significant for the necrotic (n= 23) versus the non-necrotic (n = 5) neck nodal metastases (P < .1).

Discussion

In this study, we demonstrated the feasibility of using diffusional non-Gaussian (kurtosis) modeling to fit DWI data acquired by using an extended b-value range in studies of phantoms and HN tumors. Diffusion kurtosis represents the extent to which the diffusion pattern of the water molecules deviates from a perfect Gaussian curve.⁸ Because the deviation from Gaussian behavior is governed by the complexity of the tissue in which the water is diffusing, the diffusional kurtosis can be regarded as an index of tissue microstructural complexity.⁸ The degree of diffusional non-Gaussianity may be clinically relevant, as it is thought to arise from diffusion barriers, such as cell membranes and organelles, and water compartments.⁸

There is substantial evidence that the diffusion decay is of non-monoexponential origin; however, the exact nature is not well understood.⁶ Studies have been done on brain and prostate cancer by using non-monoexponential analysis with either biexponential or stretched exponential or kurtosis analysis. ^{5,6,8,28–30} In the present study we have used the approach of the diffusional kurtosis model, which does not provide information regarding intra- and extracellular compartments but allows an additional parameter, K_app, to be obtained that may potentially be more sensitive to pathologic changes.⁸ Other explanations for non-monoexponential diffusion behavior include macromolecule binding of water,³¹ restricted diffusion, ³² and a regime of fast exchange between multiple compartments. ³³ The elucidation of the exact nature of the non-monoexponential diffusion behavior and the theoretic validity of the kurtosis model were beyond the scope of the present study. A fair comparison of the kurtosis analysis with any other non-Gaussian analyses was beyond the scope of this study. A study by Minati et al compared 2 non-Gaussian models (biexponential and kurtosis) for the analysis of brain DWI in healthy volunteers and concluded that based on their experimental data, it was not possible to favor 1 of the 2 models.³⁴

As pointed out by Thoeny et al,³⁵ who assessed the influence of the choice of b-values on ADC values obtained from the parotid gland, it is essential to realize that the choice of b-values has a great impact on the magnitude of the ADC values, especially when calculated by using a monoexponential approach. DWI by using low b-values generally yields higher ADC values than does DWI by using high b-values. This difference can be attributed to the non-monoexponential behavior of the DWI signal intensity, which points toward the potential benefits of using non-monoexponential fitting (eg, biexponential or non-Gaussian fitting). If one chooses to perform a non-Gaussian fitting approach on DWI data obtained over an extended b-value range, it is important to consider the range of b-values. First, it is essential to include relatively low b-values (50 s/mm²), as some tissues display rapid signal intensity attenuation with low b-values, followed by a more gradual signal intensity reduction.¹ This initial rapid reduction is thought to be due to vascular capillary perfusion.¹ Second, it is advisable to include high b-values (>1000 s/mm²), as this is better for modeling the non-monoexponential nature of the decaying signal intensities. The anatomy of the head and neck region, with the intimate presence of air, bone, and acute changes in tissue bulk, promotes unwanted regional field distortions. ³⁶ Therefore, high b-values up to 3000 s/mm², typically used in brain³⁷ and prostate,³⁰ will not be achievable in head and neck due to the poorer SNR obtained with the current MR imaging acquisition technique. In the present study, the diffusion-weighted images acquired with b=1500 s/mm² are the images with the lowest SNR. These images still display excellent SNR characteristics (median, 42; range, 21–87). Additionally, the fits of the diffusion-weighted images in the present study display beneficial reduced χ² goodness-of-fit characteristics (reduced χ² <0.15). Therefore, we are confident about the quality of our data and in particular our choice of a maximum b-value of 1500 s/mm².

In the present study the average ADC_mono values for various structures in the 17 patients with HNSCC (Table 2) are in agreement with previously reported values in the literature. ^18,38,39 We obtained an average ADC_mono value of 0.84 ± 0.24 × 10⁻³ mm²/s for metastatic HNSCC neck lymph nodes (Table 2), which is in close agreement with values previously reported by Kim et al of 0.77 ± 0.11 × 10⁻³ mm²/s,³⁸ and values reported by Vandecaveye et al of 0.85 ± 0.27 × 10⁻³ mm²/s.³⁹ Furthermore, the obtained ADC_mono for the spinal cord of 0.74 ±0.08 × 10⁻³mm²/s is in the range of the values described by Wang et al of 1.02 ± 0.15 × 10⁻³ mm²/s.¹⁸

Note, however, that the average diffusion coefficients, the heterogeneity measures, and the necrosis assessment, as obtained in our study, should be interpreted with caution, due to the limited number of patients per structure (Table 2). However, our study is unique among DWI studies in HN cancers, as we performed a non-Gaussian analysis rather than the usual monoexponential analysis.

The ADC values estimated by using the monoexponential model were systematically lower than the D_app values obtained from the diffusional kurtosis model. This finding is in agreement with those of Lu et al, who observed the same phenomenon in brain tissue.³ Lu et al attributed this discrepancy to the nature of the diffusional kurtosis model, which is essentially a second-order polynomial fitting model. This model will always give better fitting results than a linear model.

Our phantom experiments yielded a non-0 K_app value for homogenized asparagus (which is known to have structure) and a 0 K_app value for water (which does not have structure) as consistent with literature.⁸ Previous studies have shown the advantage of K_app as a specific measure of tissue structure.^3,8 Although K_app was not necessarily independent of D_app for all tumors, 44% of the tumors displayed a low correlation coefficient, suggesting that K_app might provide additional information related to structure. Interestingly, hD_app was significantly higher than hADC_mono, which indicates that the kurtosis analysis– derived diffusion coefficient D_app is likely to be more sensitive to reflect heterogeneity than ADC_mono. It was observed in a subanalysis of the neck nodal metastases that necrosis does not affect the correlation between K_app and D_app, as well as the heterogeneity measures hADC_mono, hD_app, and hK_app. Our assessment of necrosis was limited, as we did not have pathology as a reference standard. However, we did observe significantly higher diffusion coefficients for necrotic metastatic lymph nodes than for non-necrotic nodes, which indicates that our necrosis assessment was accurate. As reflected in our small population study, necrosis may not have contributed significantly to the additional information retrieved by using the kurtosis analysis. Other processes such as hypoxia might play a role,⁴⁰ yet our current study design did not incorporate hypoxia measurements. Future studies with pathology might provide better insight. Although the exact nature of K_app has yet to be understood, both D_app and K_app may be more sensitive to pathologic changes in tumor physiology than diffusion coefficients obtained from monoexponential analysis.

In future studies, the parameters D_app and K_app provided by the kurtosis model could offer potential value for longitudinal studies assessing early response in HN cancer patients undergoing chemoradiation therapy.

Recently, there has been a shift to imaging at higher magnetic field strengths (3T or higher), as this provides a higher SNR, resulting in better spatial resolution.³⁶ However, imaging at higher magnetic field strengths is not without challenges, especially in the head and neck, where images can be degraded due to susceptibility artifacts.³⁶ Srinivasan et al have reported initial studies at 3T similar to the ones at 1.5T showing that mean ADC values were able to differentiate between benign and malignant pathology in the head and neck regions.^16,41

In addition to obtaining multiple diffusion-weighted images over a range of different b-values, one can also acquire multiple diffusion-weighted images over an increased number of noncollinear directions (diffusion tensor imaging).⁴² This technique yields, in addition to the ADC, the fractional anisotropy, which provides quantitative information about the orientational coherence of cellular structures. Diffusion tensor imaging has been proved to provide information about architectural structural changes induced by cancer⁴²; however, head and neck structures do not necessarily reflect a fiber composition. Therefore, the fractional anisotropy measure will most likely not be affected drastically by neoplastic head and neck tissue changes.

The study has few limitations. First, it is a cross-sectional feasibility study that analyzed data from only 17 patients to assess the benefits of the non-Gaussian kurtosis analysis of DW images. Second, although we were able to show that the kurtosis model yields a significantly better fit than does standard monoexponential fitting, we were not able to assess the pathologic relevance and sensitivity of the calculated diffusion coefficients. Third, although the MR imaging examinations were performed at least 1 week after biopsy, there is still a possibility that these biopsies might have influenced the DWI-derived parameters. However, visual inspection did not reveal any postbiopsy changes. Finally, the exact nature of the non-Gaussian behavior still needs to be elucidated.

Conclusions

The use of a diffusional non-Gaussian (kurtosis) model to analyze DWI data acquired by using an extended b-value range in HNSCC is feasible. The diffusional non-Gaussian model yields a significantly better fit of the experimental data than does monoexponential fitting. Furthermore, it provides an additional parameter, K_app, potentially with added value.

ABBREVIATIONS

ADC

apparent diffusion coefficient

BOT

base of tongue

DWI

diffusion-weighted imaging

Gd-DTPA

gadolinium-diethylene-triamine pentaacetic acid

HN

head and neck

HNSCC

head and neck squamous cell carcinoma

NPC

nasopharyngeal cancer

ROI

region of interest

SCC

squamous cell carcinoma

SNR

signal intensity-to-noise ratio