A Cooperative DNA Catalyst

Abstract

DNA catalysts are fundamental building blocks for diverse molecular information-processing circuits. Allosteric control of DNA catalysts has been developed to activate desired catalytic pathways at desired times. Here we introduce a new type of DNA catalyst that we call a cooperative catalyst: a pair of reversible reactions are employed to drive a catalytic cycle in which two signal species, which can be interpreted as an activator and an input, both exhibit catalytic behavior for output production. We demonstrate the role of a dissociation toehold in controlling the kinetics of the reaction pathway and the significance of a wobble base pair in promoting the robustness of the activator. We show near-complete output production with input and activator concentrations that are 0.1 times the gate concentration. The system involves just a double-stranded gate species and a single-stranded fuel species, as simple as the seesaw DNA catalyst, which has no allosteric control. The simplicity and modularity of the design make the cooperative DNA catalyst an exciting addition to strand-displacement motifs for general-purpose computation and dynamics.

Catalytic reactions play essential roles in chemical and biological systems, underlying a wide range of enzymatic activities involving RNA and proteins. In engineered molecular systems, DNA has also been shown to carry out non-covalent catalytic reactions,^1–6 opening up possibilities for embedding more sophisticated control within chemistry, materials, and medicine. For example, a DNA catalyst can be used for signal amplification in molecular diagnostics.^7,8 When composed together with other motifs, a DNA catalyst can enable a variety of functions, including signal restoration, which is critical for scaling up the complexity of DNA-based digital logic circuits,⁹ and weight multiplication, which is a basic component in DNA-based neural networks.¹⁰ Prior work has demonstrated that several properties of DNA catalysts can be well-controlled. By the mechanism of DNA strand displacement,¹¹ the reaction rate of a DNA catalyst can be controlled by the length of a toehold.⁶ A key property of a catalyst is that it serves as an input signal to trigger the production of an output signal without being consumed itself (Figure 1a): a small amount of input X can result in a much larger amount of output Y, facilitated by gate GY and fuel F. Moreover, allosteric control can be introduced by designing the gate to be initially inhibited and to react with the input only when a consumable activator signal A is present¹² (Figure 1b). It has been articulated that this type of activatable catalyst is central to the realization of adaptive memories and learning behaviors in DNA-based neural networks.^13,14

Figure 1.

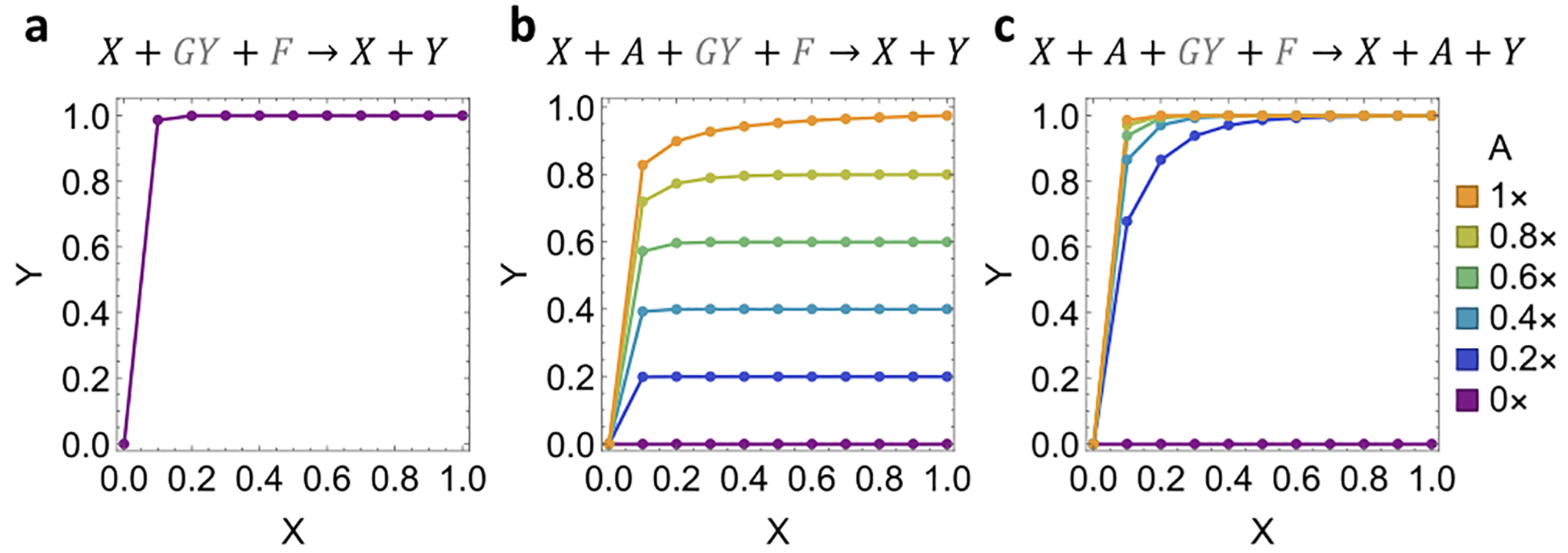
Simplified overall reaction and characteristic simulation of (a) a basic catalyst, (b) an allosteric catalyst, and (c) a cooperative catalyst. Signal and auxiliary species are colored in black and gray, respectively. Each plot shows the relative concentration of output Y at 1 h versus that of input X. The standard concentration (1×) is 100 nM. The initial concentrations of the gate GY and fuel F are 1× and 2×, respectively. The initial concentration of the activator A is shown in the legend.

In this work, we introduce a new type of catalyst that we call a cooperative catalyst: two signal species X and A cooperatively and catalytically produce output Y (Figure 1c). The additional signal can be viewed as an activator that provides allosteric control for X → X + Y without being consumed itself. This type of catalyst extends the functionality of DNA catalysts from unimolecular to bimolecular, satisfies the criteria for being used as a composable motif, and is sufficiently simple for building robust and scalable systems (Supplementary Note S2 and Figure S1).

Similar to the seesaw DNA catalyst,^9,15 a pair of reversible reactions are employed to entropically drive a catalytic cycle:

$$\text{X}+\text{A}+\text{GY}\rightleftarrows \text{XGA}+\text{Y}$$

$$\text{XGA}+\text{F}\rightleftarrows \text{X}+\text{A}+\text{GF}$$

Output Y is initially inhibited in a gate GY. Input X and activator A cooperatively react with the gate to release the output while becoming bound to the gate themselves. A fuel F then reacts with the input–activator-bound gate XGA, freeing up both the input and activator while generating a waste product GF. An excess amount of fuel continues to drive the reaction forward for output production.

Unlike the seesaw DNA catalyst, each reversible reaction here is a trimolecular reaction instead of a bimolecular reaction and is implemented with cooperative hybridization¹⁶ instead of toehold exchange⁶ (Figure 2a). The input and activator strands consist of a short toehold (T1 or T2) and a longer branch migration domain (S1 or S2). Each binds to an open toehold on one side of a double-stranded gate:output complex and competes with the output strand for binding to the gate strand in a branch migration process. When both strands reach the end of branch migration and become fully double-stranded, the output strand is attached to the gate by only a short toehold domain (T3), which can spontaneously dissociate. The input–activator-bound gate has a center toehold open, which now allows the fuel strand to bind. The fuel strand has two branch migration domains flanking a toehold, each initiating a competition with the input or activator for binding to the gate. Eventually both the input and activator strands are released, completing a catalytic cycle.

Figure 2.

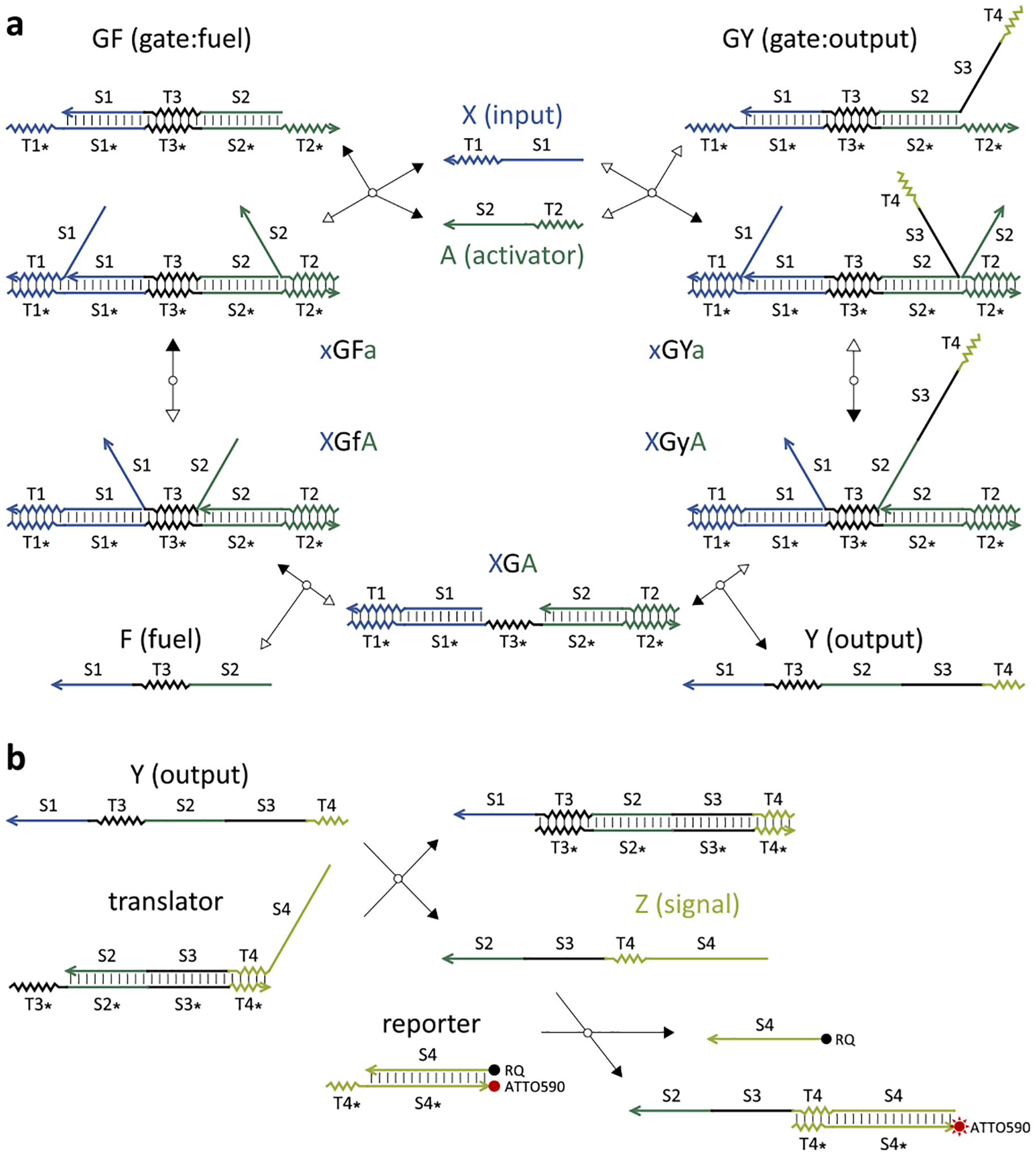
DNA strand-displacement implementation of a cooperative catalyst. (a) Catalytic reaction pathway. (b) Signal translation and reporting. Single strands are named with a single letter. Multistranded complexes are named with multiple letters indicating the strands of which they consist, where an uppercase letter indicates a strand that is bound by at least one branch migration domain and a lowercase letter indicates a strand that is bound by only a toehold. Forward and backward reactions are indicated by solid and open arrowheads, respectively. For simplicity, a clamp domain is not shown here but is illustrated in Figure S2.

In cooperative hybridization, each toehold binding step (with rate constant k_f), branch migration step (with rate constant k_b), and toehold dissociation step (with rate constant k_r) can occur independently rather than simultaneously as a pair. Thus, besides the representative states shown in Figure 2a, additional states are involved for understanding the behavior of the molecules, half of which are shown here (the other half are shown in Supplementary Note S3):

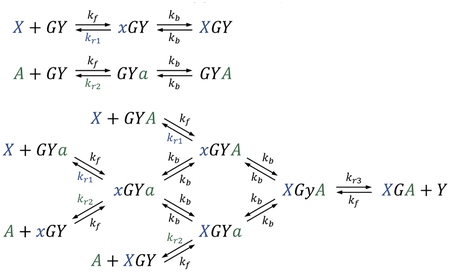
Clearly, when only input X or activator A is present, no output Y will be produced.

To differentiate the output strand from the fuel, a third branch migration domain (S3) is needed—this allows the output strand to participate in downstream reactions that require a toehold (T3) and two adjacent branch migration domains (S2 and S3). It is often desired that the input and output signals have the same format and independent sequences so that distinct DNA strand-displacement motifs can be composed together for more complex system behavior. To achieve that, a translator can be designed to react with the output strand Y and produce a signal strand Z that includes a toehold (T4) and a single branch migration domain (S4)—this reaction can be designed to be irreversible by including the toehold T4 in the output strand (Figure 2b). Importantly, the fuel strand can react only with the translator reversibly without producing any signal Z. After the signal has been translated, a previously developed reporter^14,17 can then be employed for fluorescence signal readout (Figure 2b).

With the above design, we set out to characterize the circuit behavior using fluorescence kinetics experiments (Supplementary Note S1) and to gain a quantitative understanding by comparing the data with simulation (Supplementary Note S3). We first demonstrated the cooperativity between the input and activator for output production. The output signal reached near-completion within 1 h when the input and activator strands were both present and remained low when either strand was absent (Figure 3).

Figure 3.

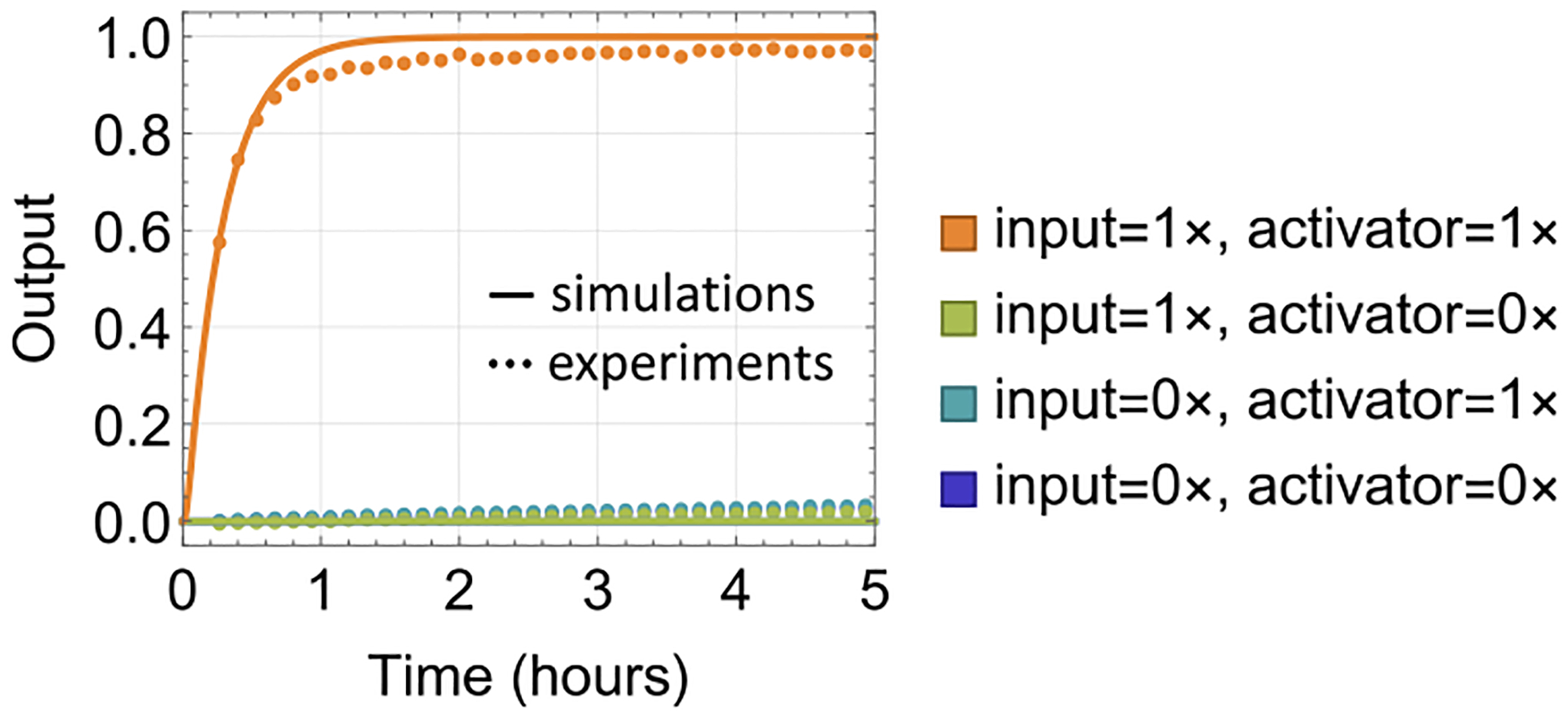
Cooperativity between the input and activator. The bottom three trajectories overlap. Here and in later figures, the standard concentration (1×) is 100 nM, and the initial concentrations of gate:output complex, fuel, translator, and reporter are 1×, 2×, 1.5×, and 1.5×, respectively.

Next, we investigated the catalytic property of the input when the activator is present. Previous studies of cooperative hybridization focused on irreversible reactions.^14,16 Here reversibility is central to the catalytic behavior, and thus, we must understand how the toehold responsible for reversibility (T3) controls the kinetics of the overall reaction pathway. Specifically, the rates of the two reactions depend on the length and sequence of T3 (Figure 4a): When the input and activator are both bound to the gate and fully branch-migrated, the dissociation rate of the output strand depends on T3. After the release of the output strand, when the fuel binds to the input–activator-bound gate, the probability that the fuel will successfully initiate a branch migration before dissociation also depends on T3. A shorter T3 would make the output dissociation rate higher but the success probability of fuel displacing the input and activator lower, and thus, it is undesired for this toehold to be either too long or too short. Moreover, it is known that the strand-displacement rate in toehold exchange reactions largely depends on the initiation toehold when its length is no shorter than the dissociation toehold.⁶ On the basis of these two considerations, we expected that a 7 nt T3 would result in fast kinetics of the overall system when both T1 and T2 contain seven nucleotides.

Figure 4.

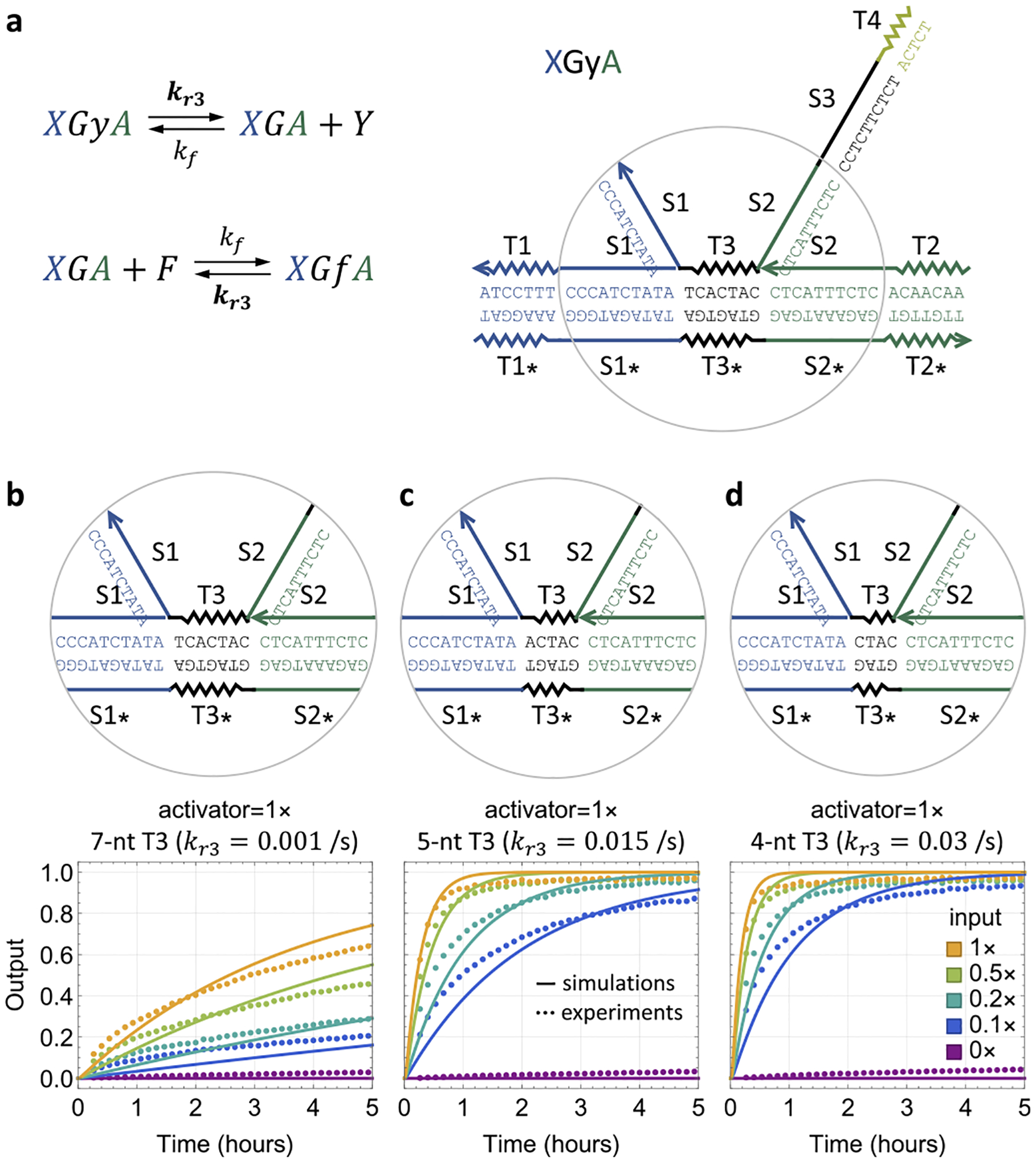
Catalytic property of the input. (a) Reaction rates (shown in bold) that depend on the sequence of toehold domain T3. (b–d) Simulation and fluorescence kinetics data with varying input concentration and with (b) 7 nt, (c) 5 nt, and (d) 4 nt T3 domains.

However, the experimental observation was surprising (Figure 4b): the kinetics was very slow, roughly the same as in simulations with the dissociation rate of T3 (k_r3) set to 0.001 s⁻¹. As toehold dissociation is commonly estimated as 10^(6−L) s⁻¹ for average sequences,¹⁸ where L is the length of the toehold, this value of k_r3 would correspond to a 9 nt toehold. A possible explanation here is the stacking energy between the ends of two DNA helices.¹⁹ While the role of coaxial base-stacking has been well-studied in understanding the kinetics of simpler strand-displacement reactions,¹⁸ the structure of the four-stranded molecule shown in Figure 4a is more complex: there are two stacking bonds between toehold T3 and the two branch migration domains S1 and S2, both of which contribute to the reversibility of cooperative hybridization. This situation is related to but distinct from an internal toehold within a three-stranded complex, where toeholds with four to seven nucleotides have been applied.^4,20

To explore whether faster kinetics could be achieved with a shorter T3, we reduced the toehold length to five or four nucleotides. An approximately 15–30-fold speedup was observed (Figure 4c,d), suggesting that the strand-displacement rate in reversible cooperative hybridization depends on both the initiation and dissociation toeholds, even when the initiation toeholds are longer. With a 4 nt T3, the catalytic property of the input was clearly demonstrated: with 0.1× input, the output reached near-completion within 5 h (Figure 4d).

We then showed that, like the input, a small amount of activator (e.g., 0.1×) was sufficient to catalyze output production (Figure 5b). Besides tuning the toehold lengths, we investigated whether a wobble²¹ (G·T base pair) in branch migration domains could be exploited to promote input or activator recycling without slowing down output production. Specifically, if there is a wobble in the S2 domain when the activator is bound to the gate, the process of activator release by the fuel would be biased forward (Figure 5a, first reaction, k_b > k_b′). If the same wobble also exists when the output is bound to the gate, branch migration involving the activator and output could also be biased to favor output release (Figure 5a, second reaction, k_b > k_b″) depending on the position of the wobble²² (Supplementary Note S5).

Figure 5.

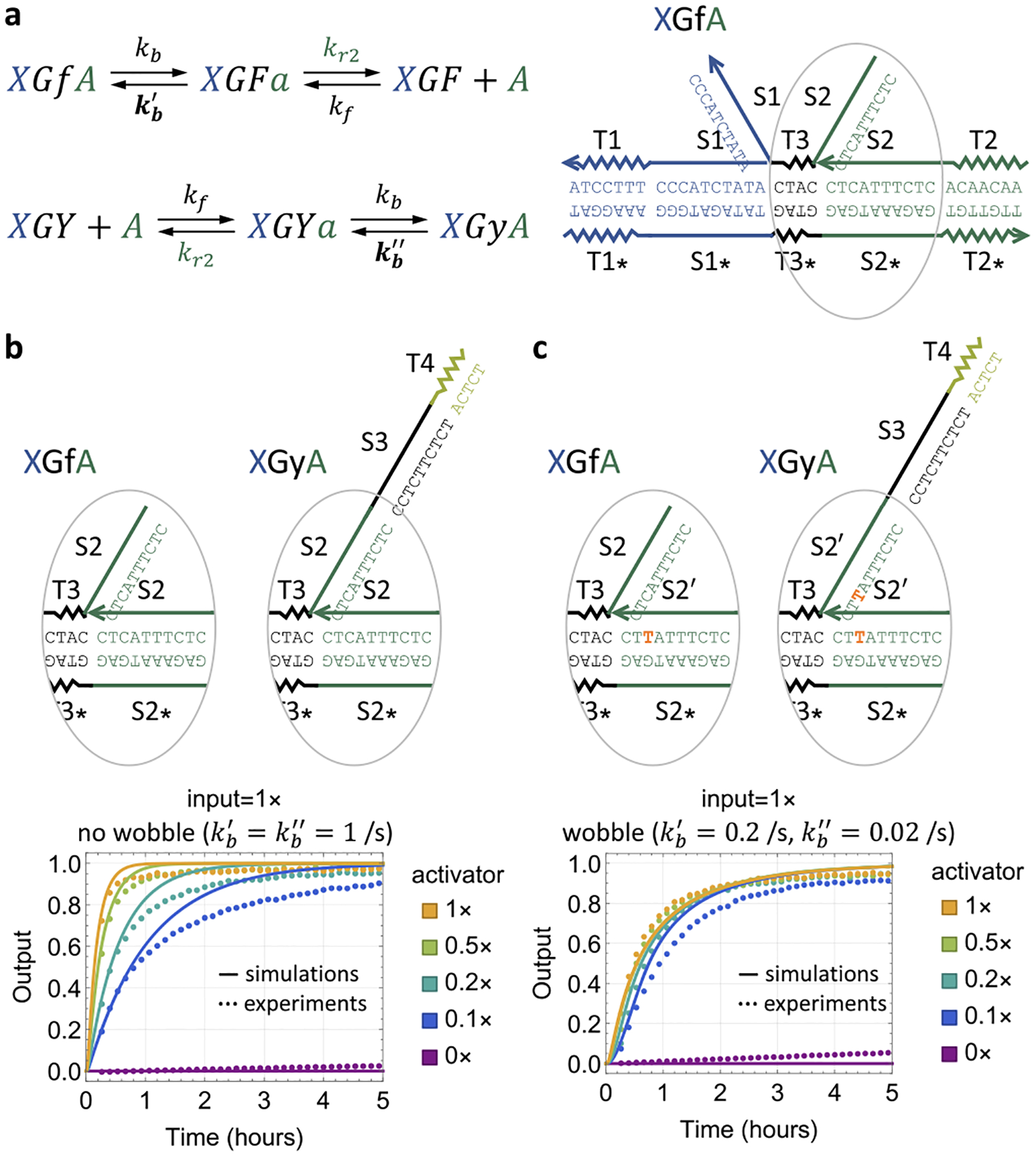
Catalytic property of the activator. (a) Reaction rates (shown in bold) that depend on the sequence of the branch migration domain S2. (b, c) Simulation and fluorescence kinetics data with varying activator concentration and (b) without or (c) with a wobble base pair in the S2 domain.

Experiments showed improvement in the catalytic property of the activator, indicated by the faster kinetics of the output production when the activator was 0.1× (Figure 5c). Interestingly, the improvement was particularly significant with unpurified gate:output and translator complexes (Figure S3), either with a wobble or with a mismatch²³ (non-Watson–Crick and nonwobble base pair). The impurity led to a behavior similar to the suppression of the activator by a threshold, where the output production appeared much slower compared to experiments with purified complexes. Introducing a wobble or mismatch in the S2 domain promoted the robustness of the activator, allowing it to catalyze output production even when its concentration was much lower than anticipated.

Comparing simulation with data, we estimated that the branch migration rate with a wobble is 0.02–0.2 s⁻¹ (Figure 5c and Figure S3), which is 5–50-fold lower than the branch migration rate with no wobble or mismatch.¹⁸ This is consistent with the previous studies on the kinetics of strand displacement with mismatches.^24–26

Finally, we demonstrated cooperative catalytic behavior with low concentrations of both the input and activator. The output production was near completion within 24 h even when the input and activator were both at 0.1× (Figure 6a). It is clear that the output concentration is not limited by either the input or activator concentration so long as they are both present (Figure 6b), illustrating a key property of a cooperative catalyst.

Figure 6.

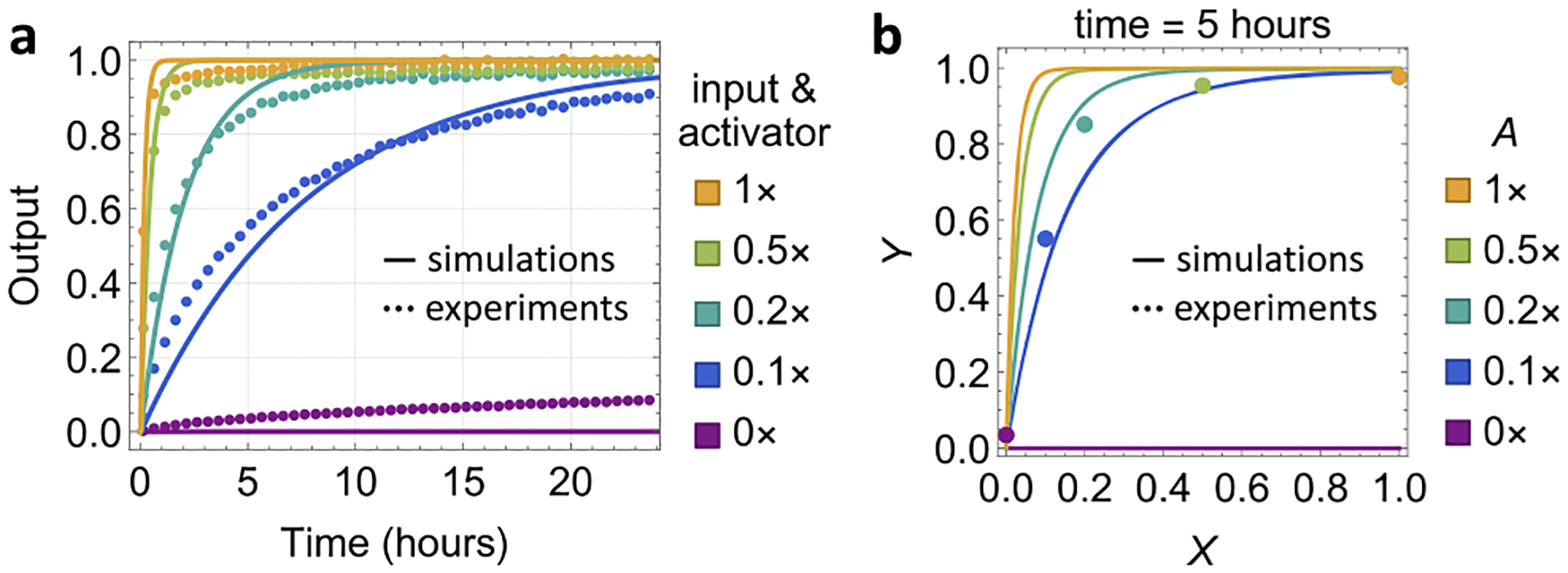
Demonstration of the cooperative catalyst. (a) Simulation and fluorescence kinetics data with varying input and activator concentrations. (b) Simulation and data of the output concentration at 5 h versus the input concentration. T3 is 4 nt. There is no wobble in the S2 domain.

The cooperative catalyst that we developed here will enable many advances in DNA circuits. For example, it could be used to build an AND gate with near-perfect signal restoration (Supplementary Note S6 and Figure S5) and a better threshold mechanism that combines the advantages of sequential²⁷ and competitive⁹ thresholding (Supplementary Note S7 and Figure S6). Like the seesaw gate used for a basic catalyst, the cooperative gate GY is also two-stranded—this structural simplicity is particularly important for maintaining the robustness of DNA circuits when synthesis errors are inevitable.¹⁷

In contrast to gate activation,¹² allosteric control of a DNA catalyst could also be accomplished by input activation.^28,29 However, these approaches require sequence dependence between the input and activator strands, and the inhibited input signal cannot participate in other reaction pathways. Both of these properties suggest limitations for composability with other DNA strand-displacement motifs. Importantly, our approach provides the same format of signal species without any sequence dependence between them, making it particularly suitable for further empowering DNA circuits with general-purpose computation and dynamics.^20,30,31