Technical Note: Temperature and Concentration Dependence of Water Diffusion in Polyvinylpyrrolidone Solutions

Abstract

Objective:

The goal of this work is to provide temperature and concentration calibration of water diffusivity in polyvinylpyrrolidone (PVP) solutions used in phantoms to assess system bias and linearity in apparent diffusion coefficient (ADC) measurements.

Method:

ADC measurements were performed for 40 kDa (K40) PVP of six concentrations (0, 10, 20, 30, 40, and 50% by weight) at three temperatures (19.5° C, 22.5° C and 26.4° C), with internal phantom temperature monitored by optical thermometer (±0.2° C). To achieve ADC measurement and fit accuracy of better than 0.5%, three orthogonal diffusion gradients were calibrated using known water diffusivity at 0° C and system gradient nonlinearity maps. Noise-floor fit bias was also controlled by limiting the maximum b-value used for ADC calculation of each sample. The ADC temperature dependence was modelled by Arrhenius functions of each PVP concentrations. The concentration dependence was modeled by quadratic function for ADC normalized by the theoretical water diffusion values. Calibration coefficients were obtained from linear regression model fits.

Results:

Measured phantom ADC values increased with temperature and decreasing PVP concentration, [PVP]. The derived Arrhenius model parameters for [PVP] between 0% and 50%, are reported and can be used for K40 ADC temperature calibration with absolute ADC error within ±0.016μm²/ms. Arrhenius model fit parameters normalized to water value scaled with [PVP] between 10% and 40%, and proportional change in activation energy increased faster than collision frequency. ADC normalization by water diffusivity, D_W, from the Speedy-Angell relation accounted for the bulk of temperature dependence (±0.035μm²/ms) and yielded quadratic calibration for ADC_PVP/D_W=(12.5±0.7)·10⁻⁵·[PVP]² - (23.2±0.3)·10⁻³·[PVP]+1, nearly independent of PVP molecular weight and temperature.

Conclusion:

The study provides ground-truth ADC values for K40 PVP solutions commonly used in diffusion phantoms for scanning at ambient room temperature. The described procedures and the reported calibration can be used for quality control and standardization of measured ADC values of PVP at different concentrations and temperatures.

Introduction:

Diffusion weighted imaging (DWI) offers non-invasive insight to tissue microstructure based on self-diffusion of water in biological tissues¹ as an imaging probe that reflects disease presence, progression or response to treatment^2–4. Apparent diffusion coefficient (ADC) is a quantitative biomarker derived from DWI^{5, 6} by fitting a mono-exponential model to signal decay as a function of b-value (diffusion weighting, determined by strength and timings of diffusion-encoding gradients). DW-MRI is a common technique and ADC maps are used for diagnostic and prognostic clinical applications^{2, 3, 6, 7}.

Widespread utilization of quantitative DWI in clinical studies at different sites and across multiple platforms requires quality control (QC) assessments for ADC accuracy and reproducibility^{6, 8}. Sources of technical variability must be characterized and controlled via QC relative to anticipated biologic/therapeutic diffusion changes⁶. Quantitative Imaging Biomarker Alliance (QIBA) metrology guidelines recommend that systematic bias characterization is performed using phantoms with known ADC values^{6, 9}. Since water mobility is dependent on temperature, knowledge, and control of temperature of diffusing media in phantoms are essential in the course of absolute measurements used for technical quality control (QC)^{10, 11}. While temperature dependence of ADC is typically not relevant in living tissue due to body temperature regulation, precise knowledge of temperature and water diffusion within polyvinylpyrrolidone (PVP) materials is a prerequisite for calibration of PVP-based DWI phantoms prior to their use in assessment of MRI scanner ADC bias and linearity.

DWI phantoms based on aqueous solutions of polyvinylpyrrolidone (PVP) provide mono-exponential DWI signal decay with increasing b-value^{12, 13} and have been used to validate quantitative DWI techniques. PVP solutions are preferred to pure water due to higher viscosity that dampen fluid convection, and their ADC values are tunable by changing PVP concentration to span the ADC range of human tissues. Given an adequate range and known diffusion properties, PVP-based phantoms may be used to assess MR system bias and linearity in ADC measurement^{6, 12} since such characterization requires comparison to true diffusivity values⁸.

Given that the water ADC in PVP phantoms depends on polymer molecular weight, solution concentration, and temperature, the issue of water diffusion calibration in PVP solutions has gained attention in recent studies^14–16. To mitigate temperature dependence of ADC measures, current multi-center QC programs have utilized temperature control of PVP materials using an ice-water bath¹⁴. Ice-water thermalization when performed properly provides accurate measurements, but requires relatively lengthy phantom preparation^{10, 14, 17, 18}. This has limited adoption in the clinical environment since phantom scanning at ambient temperature would offer a more practical advantage. Furthermore, the water diffusion coefficient for 0 to 50% PVP at room temperature spans the full tissue diffusivity range (~0.3 to 2.2μm²/ms) whereas at 0°C only half of the range is covered¹⁴. Assessment of MRI system bias and linearity for ADC beyond 2.2μm²/ms is not particularly relevant for human studies. However, ambient temperature diffusion QC protocols require precise knowledge of internal phantom temperature, or addition of an in-situ MR-visible thermometer¹¹, along with calibration of ADC values as a function of the given ambient temperature. Scan room temperature can vary across facilities, and a nominal 5° C temperature difference can translate to a large (>15%) phantom ADC variation.

The objective of this study was to investigate temperature and concentration dependence of ADC for PVP solutions contained in the QIBA/NIST phantom over the scanner room temperature range to provide ground truth ADC values and a calibration equation to facilitate standardization of quantitative DWI measurements for clinical trials across multiple MRI scanner systems.

Materials and Methods:

PVP DWI phantom and temperature control:

This study used a commercially-available (Caliber MR, Boulder, CO) QIBA/NIST diffusion phantom design containing an array of thirteen 20 ml vials with PVP-concentrations of 0%, 10%, 20%, 30%, 40% and 50% w/w of 40 kilo-Dalton (K40) polymer moiety in a spherical polyacrylic shell¹⁴.

Phantom DWI scans were performed at three room temperatures by setting the scan room thermostat to low, mid, and high settings. After the scan room equilibrated at a given setting, air temperature in the bore was noted and water at that temperature was used to fill the phantom shell. The phantom was then allowed to equilibrate in the bore for additional 3 hours. Internal phantom temperature was monitored using an MRI safe fiber optic temperature probe (OPSENS OPT-M model, Quebec, CA) with ±0.1° C accuracy. Temperature monitoring confirmed the thermal equilibrium during DWI data acquisitions at (19.5, 22.5, 26.4) ± 0.2° C.

DWI acquisition and gradient calibration:

Scans were performed on a clinical 3T scanner (Philips Ingenia sw v5.4, Best, Netherlands) with the phantom positioned at magnet isocenter in the head coil. DWI acquisition parameters were: single-shot spin-echo echo-planar imaging (EPI) with parallel imaging (SENSE) factor = 2; TR/TE = 4000ms/120ms; FOV = 200mm × 200mm and 1.5 × 1.5 × 5.0 mm³ acquired voxels; three 5mm slices with a 0mm gap centered on PVP tubes; 11 nominal b-values = 0, 250, … 2500 s/mm² along three orthogonal axes (i.e. X, Y and Z in magnet frame), and repeated as 10 dynamics where each loop through all b-values and directions required 4min 8sec. The TE was sufficiently short for the long-T2 PVP¹⁹ and constant TR over all b-values with dynamic averaging suppressed potential T1-bias. DWI for each direction, b-value and dynamic were stored as separate images to facilitate inspection for drift or artifact prior to averaging, and allow signal-to-noise-ratio (SNR) calculation²⁰ in subsequent processing.

To increase ADC measurement accuracy, a gradient calibration step (described in Supplement Materials) based on known ice-water diffusion coefficient²¹ was performed for each gradient channel used to encode diffusion. The measured b-value correction factors between 0.5% and 4% dependent on b-value and gradient-direction (Sup. Figure S1) were then applied to nominal b-values for ambient temperature ADC calculation. The trace-DWI were formed by geometric average of individual DWI directions, and direction-average b-value calculated after gradient calibration. The system gradient-nonlinearity (GNL) maps were constructed for direction-average b-values using vendor-provided GNL characteristics²². The predicted b-value bias was between −0.47% to 0.92% for phantom vials within 6cm of isocenter (Sup. Figure S2). The spatial GNL correction was then applied to calibrated gradient direction-average b-values (Sup. Fig. S2) to achieve <|0.5|% GNL bias for the ADC measurements.

PVP phantom ADC analysis:

A mono-exponential diffusion model was used to derive phantom ADC maps:

$${\text{S}}_{\text{b}}={\text{S}}_0·\text{exp}\left(-\text{ADC}·\text{b}\right)$$ (1)

To limit the ADC model fit bias due to the noise-floor to below 0.5%, the maximum b-value for the fit was determined by simulations (Sup. Figure S3). Briefly, DWI SNR was estimated by signal temporal mean and variance over the 10 dynamic DWI scans calculated on a pixel-by-pixel basis²⁰. This SNR was used to estimate noise-floor bias in ADC measurement via Monte-Carlo simulations as a function of b-value range and true diffusion between 0.25 to 2.5 μm²/ms (Sup. Fig. S3).

Room temperature PVP ADC calculation was then performed for trace-DWI over the range of b-values between 0 and b_max where b_max varied with PVP concentration: b_max = 1000, 1250, 1500, 2250, 2500, 2500 s/mm² for [PVP] = 0, 10, 20, 30, 40, 50%, respectively. After reconstructing ADC maps using calibrated b-values over sample-specific b-value ranges, 3D Slicer (v4.6.2) was used to extract mean values from VOIs manually placed on central 6 vials (Sup. Fig. S2). Only the central vial was used for [PVP] = 0%. The VOIs varied from 7 to 17 cm³ to exclude visible artifacts.

ADC(T) calibration:

The temperature dependence of VOI-mean water ADC in PVP was fit by Arrhenius model^{15, 21, 23}:

$$\text{ADC}=\text{A}·\text{exp}\left(-{\text{E}}_{\text{a}}/\text{RT}\right)$$ (2)

where A (mm²/s) is the diffusion coefficient in the limit of infinite temperature also termed “collision frequency” factor, E_a (kJ/mol) is the activation energy for translational diffusion of water molecules; R (kJK⁻¹ mol⁻¹) is the universal gas constant and T is the absolute temperature in Kelvin (K). Linear regression fitting of log-ADC(μm²/ms) versus inverse temperature, T (K), for individual PVP solutions was performed based on the equation:

$$\text{log}\left(\text{ADC}\right)=\text{C}1+\text{C}2·\left[\frac{1000}{\text{T}}\right]$$ (3)

The calibration coefficients, C1 and C2, and their corresponding standard error of the fit were tabulated for studied PVP solutions and temperatures between 19° C and 26° C. The resulting calibrations were compared to previously reported in the literature for K40^{15, 24, 25} and different polymer moieties K30, K90^{15, 16} in Supplemental Materials.

Arrhenius parameter [PVP] dependence analysis:

The Arrhenius model parameters were derived from calibration constants as:

$${\text{E}}_{\text{a}}=\text{C}2·\text{R};\text{A}=\text{exp}\left(\text{C}1\right),$$ (4)

and their confidence intervals obtained by error propagation from C1 and C2 fit errors. The concentration dependence of Arrhenius model parameters was modelled by linear relation between 0% and 40% [PVP] with intercepts fixed to water E_W and A_W values, respectively:

$$\text{A}={\text{A}}_{\text{W}}+{\text{K}}_{\text{A}}·\left[\text{PVP}\right];{\text{E}}_{\text{a}}={\text{E}}_{\text{W}}+{\text{K}}_{\text{E}}·\left[\text{PVP}\right]$$ (5)

Further characterization of concentration dependence relative to well-established water values (from Speedy-Angell (SA) relation^{21, 26}) was explored for normalized A_PVP/A_W and (Ea_PVP – Ea_W) Arrhenius parameters versus [PVP] < 40%. Linear models of these normalized Arrhenius parameters were constrained to intersect (A_[PVP]=0 / A_W) = 1 and (Ea_[PVP]=0 – Ea_W) = 0:

$$\frac{{\text{A}}_{\text{PVP}}}{{\text{A}}_{\text{W}}}={\text{K}}_{\text{AW}}·\left[\text{PVP}\right]+1;{\text{E}}_{\text{PVP}}-{\text{E}}_{\text{W}}={\text{K}}_{\text{EW}}·\left[\text{PVP}\right]$$ (6)

ADC([PVP]) calibration:

Finally, to isolate ADC dependence on PVP concentration from temperature dependence of water diffusion, ADC in PVP at all measured temperatures were normalized by pure water diffusivity via well-established Speedy-Angell^{21, 26}, D_W, at the corresponding temperatures and fit to a quadratic calibration function of %[PVP] with intercept constrained to 1:

$$\frac{{\text{ADC}}_{\text{PVP}}}{{\text{D}}_{\text{W}}}={\text{K}}_1·{\left[\text{PVP}\right]}^2+{\text{K}}_2·\left[\text{PVP}\right]+1.$$ (7)

The PVP concentration dependence model derived from this work was compared to NIST measurements¹⁹ and previously reported ADC values^{24, 25} for K40 water solutions studied across four scanner systems, as well as for K30 and K90 PVP moieties^{15, 16}. The overall calibration accuracy was estimated by the difference between calibrated and measured ADC.

All described analysis was performed in MATLAB R2019b (The Mathworks, Inc., Natick, MA), using “lscov” function for linear regression model fit and parameter error estimate.

Results:

Figure 1a shows the middle slice through the phantom representing the position and [PVP] of each vial with Figure 1b showing the corresponding ADC map for that slice. Measured ADC values decreased with increasing PVP concentration and decreasing temperature as summarized in Table 1. Plots of log(ADC) versus inverse temperature in Figure 1c illustrate Arrhenius model fit (Eqs.2,3) used to derive calibration coefficients, C1 and C2, by linear regression (Eq.3). Fit coefficients and their standard errors are reported in Table 2 for each studied PVP concentration. The fit parameter errors are increasing for higher [PVP]. The absolute fit ADC deviation from measured values was within ±0.016μm²/ms, and mean absolute calibration error over the full PVP water ADC range was 0.7%. These results can be used for ADC(T) calibration at known [PVP] concentrations according to Eq.3.

Figure 1:

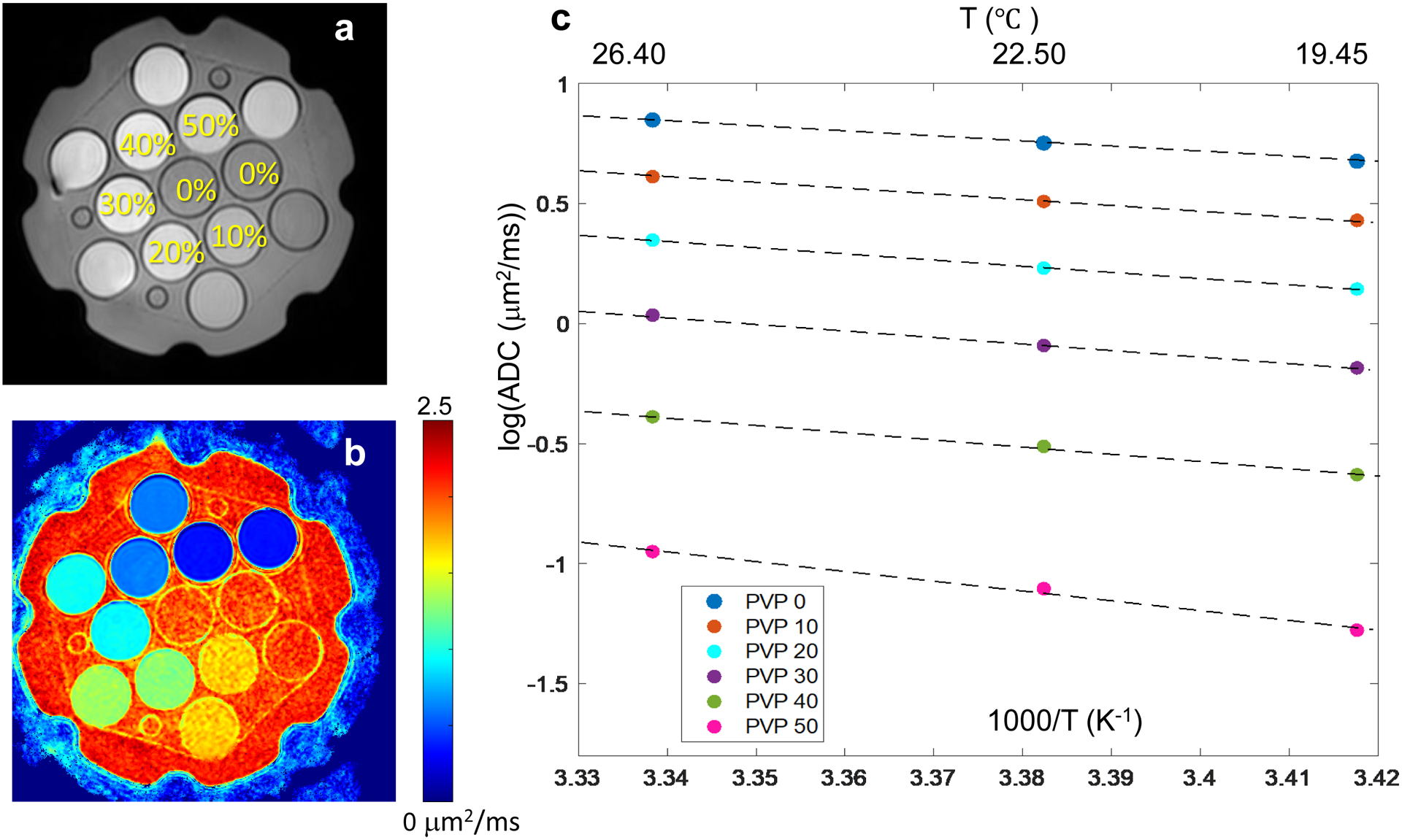
QIBA/NIST PVP diffusion phantom (a) MR image illustrating vials’ position and PVP %weight/weight concentration. (b) shows corresponding ADC map at 26.4° C, and (c) shows log of ADC values for each PVP concentration (data symbols color-coded in the legend) at three measured temperatures (top axis). Dashed lines display the linear fits to the log(ADC) data as a function of inverse temperature (bottom axis) with the corresponding measured ADC values and fit coefficients summarized in Tables 1 and 2, respectively.

Table 1:

Mean ADC values ± standard deviation in units of μm²/ms for water and five PVP concentrations (w/w) at three measured temperatures

[PVP]	19.5 °C	22.5 °C	26.4 °C
0%	1.975 ± 0.004	2.131 ± 0.003	2.346 ± 0.004
10%	1.545 ± 0.005	1.672 ± 0.006	1.853 ± 0.007
20%	1.162 ± 0.003	1.268 ± 0.003	1.426 ± 0.007
30%	0.832 ± 0.003	0.913 ± 0.004	1.036 ± 0.003
40%	0.529 ± 0.002	0.596 ± 0.002	0.673 ± 0.004
50%	0.276 ± 0.005	0.329 ± 0.003	0.383 ± 0.002

Table 2:

Linear regression fit coefficients ± standard error for log(ADC) dependence on inverse temperature data in Figure 1c based on Eq.3

[PVP]	C1	C2 (K)
0%	8.09 ± 0.03	−2.17 ± 0.01
10%	8.26 ± 0.10	−2.29 ± 0.03
20%	8.97 ± 0.19	−2.58 ± 0.06
30%	9.28 ± 0.23	−2.77 ± 0.07
40%	9.71 ± 0.56	−3.02 ± 0.17
50%	12.75 ± 1.39	−4.10 ± 0.40

Good alignment of current K40 calibration data to 3-year old multi-site data 0%, 20%, and 40% [PVP]²⁵, and other previous K40 PVP studies^{15, 24} at intermediate temperatures is shown in Sup. Figure S4a. This figure also illustrates that for intermediate PVP concentrations not directly calibrated in this work, the linear interpolation can be performed between two calibrated values. For instance, for Keenan, et al.²⁴, 20% PVP values (Sup. Fig. S4a, cyan asterisks) were derived by linear interpolation of reported ADC results for 18% and 25%²⁴. Higher deviation observed for 40% PVP from Keenan, et al.²⁴ (Sup. Fig. S4a, green asterisks) versus other studies could be due to low b_max = 900s/mm² used for the fit that likely limited contrast to noise ratio of derived ADC for this low mobility material.

Sup. Figure S4b further compares this K40 study to other available temperature calibrations for K30 and K90 PVP materials, where only lines derived from the fit coefficients are displayed on log(ADC) scale for greater clarity. The observed finite deviations of calibration lines indicate sensitivity to phantom molecular weight, temperature measurement errors and utilized b-values. For example, dynamic temperature scan in Wagner et.al.¹⁶ showed apparent temperature hysteresis for pure water (Sup. Fig. S4b, blue) and exhibits the largest deviation from Speedy-Angell calibration (Sup. Fig. S4b, red)²¹ compared to data from Mills²⁷ (Sup. Fig. S4b, cyan) and this study (Sup. Fig. S4b, black dots). The calibration differences are most pronounced for the high [PVP] 50% perhaps due to reduced contrast to noise at b_max=700s/mm² used in Wagner et.al.¹⁶ versus b_max=2500s/mm² used in this study. These results indicate that application of derived calibration constants for ADC(T) may be less accurate in the PVP solution of different molecular weights and at high concentrations.

The Arrhenius model parameters calculated from the corresponding C1 and C2 (Eq.4) for each PVP concentration are plotted in Figure 2. Fit parameter errors increased with increasing PVP concentration, potentially reflecting reduced contrast-to-noise ratio for the high [PVP] materials. With exclusion of 50% PVP outliers and fixing the intercepts to water parameter values, A and E_a approximately followed linear dependence on the PVP concentration between 10% and 40% as summarized in Table 3. While collision frequency factor A scaled with the PVP concentration (e.g., doubling for 20% versus 10% and 40% versus 20%), the activation energy E_a only increases moderately (from 19 to 25 kJ/mole) for these materials. However, deviation from the linear model in Eq.(5) were pronounced particularly for collision frequencies, suggesting limited accuracy of the corresponding linear model for the concentration dependence.

Figure 2:

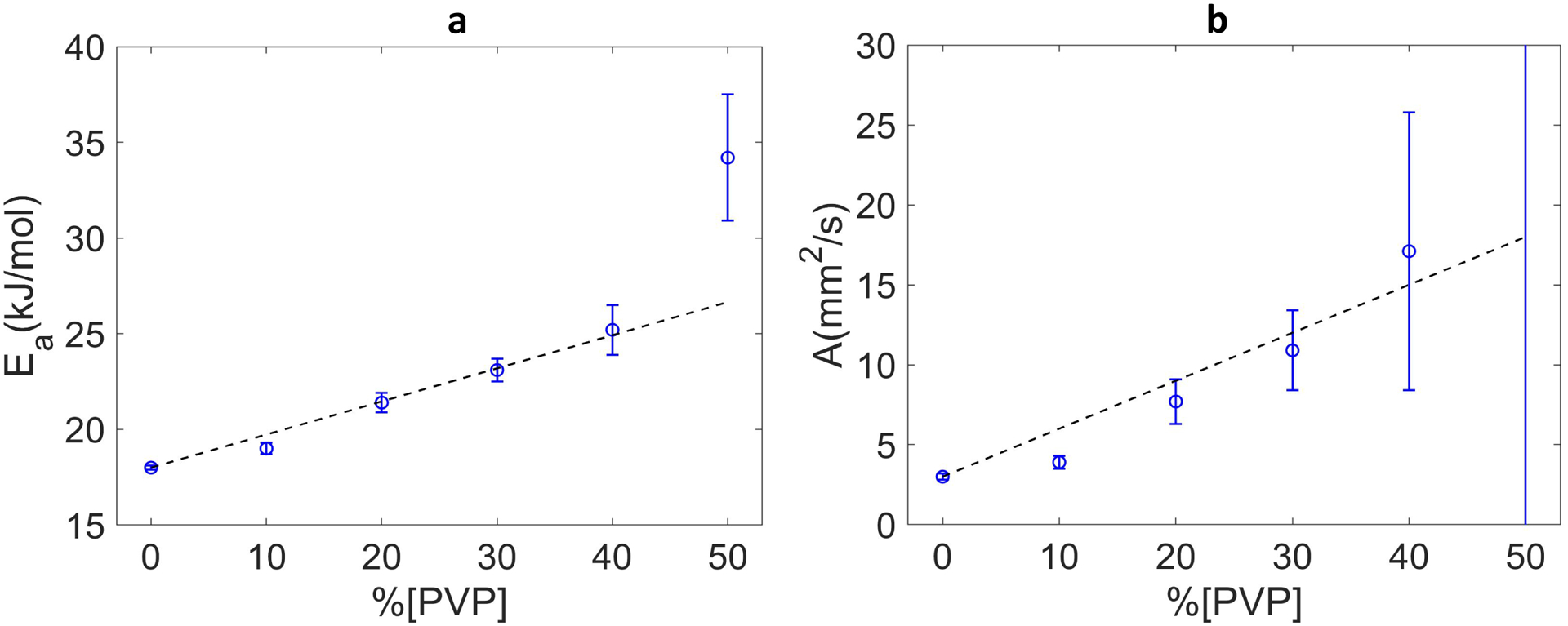
Arrhenius model fit parameter values and error bars are shown as a function of %PVP for activation energy, E_a, in (a) and for collision frequency factor, A, in (b). At 50% A was 350 ±470 mm²/s (outside of the plot). Dashed lines in both plots show the linear fits based on PVP 10–40% points with intercept fixed to appropriate water values 3mm²/s (for A) and 18kJ/mol (for E_a) and fit slopes of K_E = 0.173 ± 0.007(kJ/(mol%)) and K_A = 0.30 ± 0.03 (mm²/(s%)).

Table 3:

Derived Arrehenius model parameters ± standard error reported for each PVP concentration

[PVP]	Ea (kJ/mol)	A (mm2/s)
0%	17.99 ± 0.11	3.20 ± 0.15
10%	19.10 ± 0.26	3.94 ± 0.41
20%	21.41 ± 0.45	7.66 ± 1.40
30%	23.06 ± 0.56	10.88 ± 2.47
40%	25.24 ± 1.25	17.12 ± 8.72
50%	34.14 ± 3.33	350.40 ± 474.14

Figure 3a further explores concentration dependence of Arrhenius parameters normalized by the corresponding known values of pure water via Speedy-Angell. Higher apparent slope (Eq.6) of the concentration dependence for relative activation energy (K_EW=0.17±0.01 (kJ/mol%)) versus that of normalized collision frequency (K_AW=0.10±0.01 (1/%)) is consistent with observed reduction of ADC with increasing PVP concentration (Table 1) primarily due to increasing E_a with respect to that of pure water. This figure also highlights limited accuracy of the linear fit models of Eq.6, particularly for normalized collision frequencies, which could lead to the substantial calibration errors for ADC(T) calculation.

Figure 3:

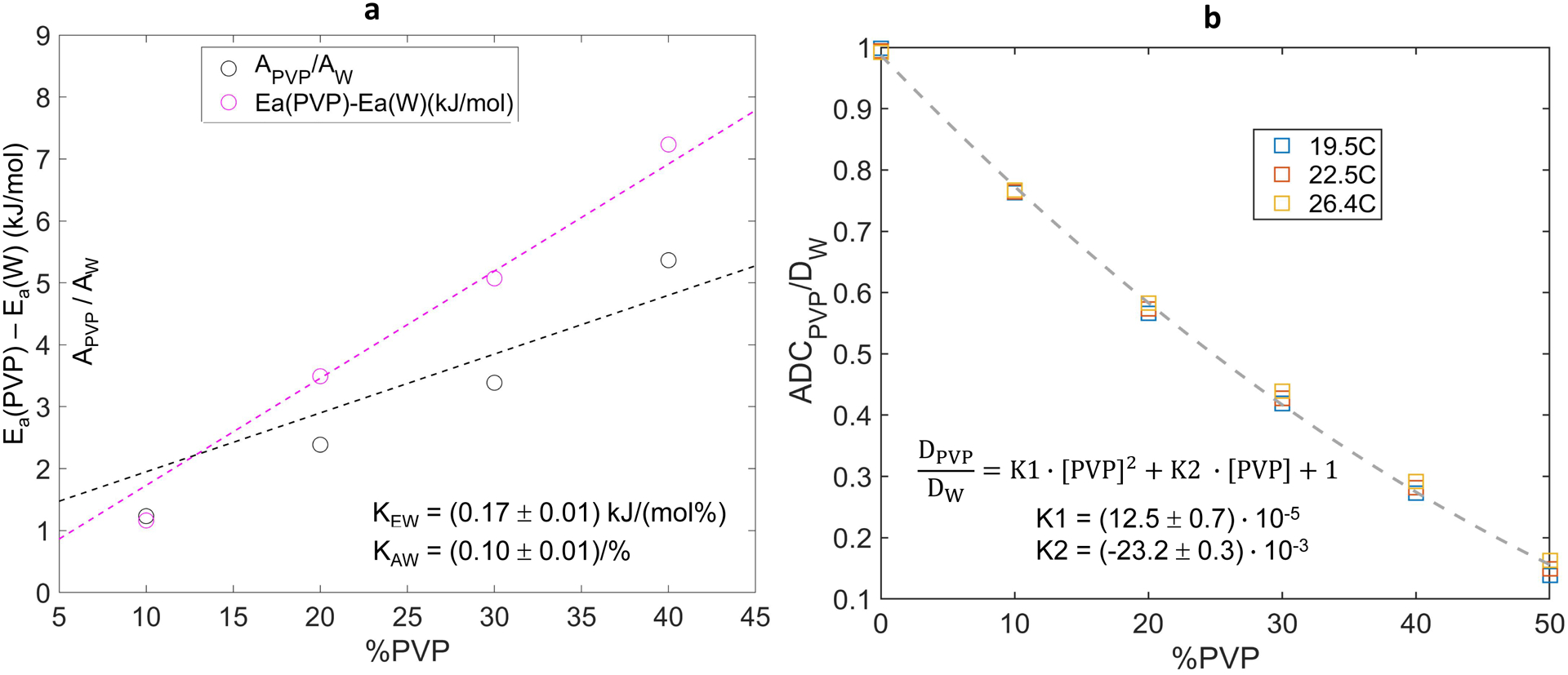
Concentration dependence of deviation from pure water (W) values of Arrhenius model fit diffusion parameters (collision frequency, A, and activation energy, E_a) is shown in (a) for 0% to 40% PVP. The vertical axis in (a) is common for difference in activation energies and ratio of collision frequencies relative to pure water. Measured ADC_PVP normalized to the theoretical diffusion value of pure water, D_W (calculated from Speedy-Angell relation) is shown in (b) for 0% to 50% PVP and three temperatures color-coded in the legend. Dashed curves show the linear (in a) and quadratic (in b) least squares fit for %PVP dependence over plotted ranges. The fit intercepts were constrained to 1 (for normalized A and ADC) and 0 (for E_a difference), and the fit slopes are listed on the figures.

As illustrated in Figure 3b, direct normalization of PVP water ADC by the corresponding theoretical pure water SA-values essentially accounts for the bulk of the observed ADC temperature dependence (in Fig. 1c). Moreover, these normalized data were reasonably well fit by a simple quadratic function of PVP concentration with only two free parameters (Eq.7: K1=(12.5±0.7)·10⁻⁵ and K2=(−23.2±0.3)·10⁻³), over the full studied concentration range, including [PVP]=50%. The maximum observed deviations from calibrated ADC values were ±0.035μm²/ms at 19°C (for 50% PVP) and 26°C (for 30% PVP). For this proposed quadratic calibration model, the mean absolute ADC error across the studied range of temperatures and PVP concentrations was 2.4%.

Sup. Figure S5 shows the summary of available PVP data from published sources and current “UM” study (color-coded in the legend) falling close to the proposed quadratic calibration curve using K1 and K2 values derived exclusively from UM data (Sup. Fig. S5, dashed). This preliminary analysis suggests possibility of universal calibration for PVP concentration nominally independent of temperature and PVP molecular weight. Comparable data dispersity for high precision measurements at multiple temperatures (Sup. Fig. S5a) versus multiple molecular weights and concentrations at a single temperature (Sup. Fig. S5b) indicates that experimental measurement errors are likely cause for the observed deviations from the provided calibration curve (Sup. Fig. S5, dashed).

Discussion:

The goal of this study was to provide accurate measurements of ADC values of different PVP concentrations over the range of scanner room temperatures to support quantitative use of PVP-based DWI phantoms. Phantom scanning at ambient temperature is generally more practical for the clinical scanner environment than thermal control via ice-water. Moreover, susceptibility artifacts adjacent to ice-cubes¹⁴ are avoided at room temperature. Assuming K40 phantom temperature is accurately measured within the range of 19–26° C, the estimated ADC values can be directly compared to the look-up table of ADC predicted using calibration constants from this study to assess system bias and linearity. Such calibration procedure would be limited to the tabulated PVP concentrations, or their linear interpolation. Its accuracy will also depend on the measurement accuracy of provided calibration coefficients and temperatures. Several factors that potentially improve calibration accuracy (mean error of 0.7%) of the current study compared to previous approaches^{15, 16, 24} reduced noise bias depending on maximum b-value used, direction-dependent gradient calibration and gradient nonlinearity correction.

A two-step alternative procedure is also demonstrated to estimate ADC within the room temperature range for arbitrary K40 PVP concentrations: (1) use well-established water diffusion value at the given temperature via the Speedy-Angell model^{21, 26}; and (2) scale this by the multiplicative factor, F, where F = 12.5×10⁻⁵ · [PVP]² – 23.2×10⁻³ · [PVP] + 1. Note, even though this multiplicative factor is independent of temperature, one still requires an accurate phantom temperature to properly estimate the pure water diffusivity value²¹. Therefore both methods would rely on an accurate temperature reading (<0.2°C). While temperature measurement is not the focus of this study, promising technology exists¹¹ that may provide a convenient in situ temperature readout.

Our results show that temperature dependence of pure water diffusion coefficient accounts for the bulk of ADC temperature dependence in PVP solutions. Finite residual dispersion ADC_PVP/D_W observed over the 19–26°C range could be partly due to experimental measurement error. When normalized by diffusion coefficient of pure water, ADC in PVP solutions followed an apparent quadratic dependence on PVP concentration, largely independent of temperature. Moreover, retrospective inspection of data from all available calibration studies^{15, 16, 24} including variable molecular weight PVP (K30, K40 and K90) indicated that the quadratic fit coefficients from this study apply remarkably well to all prior data, suggesting PVP ADC normalized to water is not a strong function of PVP molecular weight. This further suggests our proposed normalization procedure and K1 and K2 values derived from this study have general application for prediction of diffusion in PVP-based phantoms.

As discussed in Holz et.al.²¹, self-diffusion of water follows non-Arrhenius behavior in the 5 to 55 °C range; however over typical room temperatures, the Speedy-Angell (non-Arrhenius) fit shows good agreement to the Arrhenius model. This model also aligned well with the 20% and 40% 40K PVP results from previous multi-site study²⁵ and others^{15, 24} at intermediate temperatures. Based on the Arrhenius model, activation energy and temperature have greater effect on ADC relative to collision frequency factor. Increasing the temperature or decreasing the activation energy would increase the diffusion rate. In water-PVP solutions, collisions with solute particles, hydrogen bonding and lower solution temperature reduce molecular water displacement and measured diffusion. Increasing the PVP concentration resulted in steeper increase of activation energy difference from pure water compared to the collision frequency consistent with increased hydrogen bonding^{28, 29} between water and PVP being the driving factor for observed reduced diffusion in more concentrated solutions.

One limitation of the study is that only three temperatures were used similar to Pullens et.al.¹⁵ thus results cannot be confidently extrapolated outside of the measured range. Nevertheless, the observed good alignment with previous multi-scanner study at multiple temperatures²⁵ supports adequate fidelity of the performed calibration. Another limitation is that Arrhenius temperature calibration procedure does not account for concentration dependence and different molecular weight (e.g. K90 versus K30 in Wagner et.al.¹⁶). Furthermore, for specific [PVP] concentrations, temperature calibrations were evidently sensitive to changes in molecular weight over the K30 to K90 range. As illustrated, these limitations could be effectively circumvented for ADC normalization by SA water diffusion coefficient. More comprehensive studies of different molecular weight PVP solutions would be needed to establish accuracy of the proposed universal temperature and concentration calibration of water ADC.

In conclusion, to enable accurate ADC measurements and scanner DWI QC at ambient scan temperatures, precise and accurate calibration of water diffusion in PVP solutions at room temperatures is essential. As such, temperature and concentration dependence of ADC for 0–50% K40 PVP utilized in QIBA NIST DWI phantoms were studied within typical scan room temperature range and using regression model yielding a calibration equation for future use. Water diffusion in PVP solutions between 19°C and 26°C was well described by Arrhenius model. In addition, use of an alternative method to predict ADC as a function of [PVP] scaled to the theoretical diffusivity of water at the given room temperature is also presented and shown to be consistent with prior studied data, nominally independent of temperature and PVP molecular weight.