Benchmarking statistical methods for analyzing parent-child dyads in genetic association studies

Abstract

Genetic association studies of child health outcomes often employ family-based study designs. One of the most popular family-based designs is the case-parent trio design that considers the smallest possible nuclear family consisting of two parents and their affected child. This trio design is particularly advantageous for studying relatively rare disorders because it is less prone to type 1 error inflation due to population stratification compared to population-based study designs (e.g., case-control studies). However, obtaining genetic data from both parents is difficult, from a practical perspective, and many large studies predominantly measure genetic variants in mother-child dyads. While some statistical methods for analyzing parent-child dyad data (most commonly involving mother-child pairs) exist, it is not clear if they provide the same advantage as trio methods in protecting against population stratification, or if a specific dyad design (e.g., case-mother dyads vs. case-mother/control-mother dyads) is more advantageous. In this article, we review existing statistical methods for analyzing genome-wide marker data on dyads and perform extensive simulation experiments to benchmark their type I errors and statistical power under different scenarios. We extend our evaluation to existing methods for analyzing a combination of case-parent trios and dyads together. We apply these methods on genotyped and imputed data from multi-ethnic mother-child pairs only, case-parent trios only or combinations of both dyads and trios from the Gene, Environment Association Studies consortium (GENEVA), where each family was ascertained through a child affected by nonsyndromic cleft lip with or without cleft palate. Results from the GENEVA study corroborate the findings from our simulation experiments. Finally, we provide recommendations for using statistical genetic association methods for dyads.

Introduction

Studies of genetic associations of most human traits and diseases focus on population-based designs (e.g., case-control studies, cohort studies, or data from biobanks) especially for complex and heterogeneous disorders, where both genetic and environmental risk factors are likely involved. For rare disorders this often requires amassing cases sampled from multiple populations, which creates the possibility of type I error inflation due to confounding (as termed by epidemiologists) or population stratification (as referred to by geneticists). Family-based designs, on the other hand, play an important role in the investigation of genetic underpinnings of low frequency or rare disorders (e.g., birth defects) (Benyamin, Visscher and McRae, 2009). The case-parent trio design is one of the most popular family-based designs which consists of an affected child (i.e., the proband) and both parents. Statistical methods focused on transmission of variants within families, such as in case-parent trio design, protect against population stratification (Schwender et al., 2012). However, genetic information on both parents is often not available because it is more difficult to recruit biological fathers, which often leads to an abundance of information on mother-child dyads (Shi et al., 2008). As more multi-ethnic studies become possible, the value of family-based methods that are less prone to population stratification are key for studies of childhood diseases. It is essential to define the best suited analytical approach for each alternative family-based scenario, especially in the presence of a predominance of dyads in available samples.

Although statistical methodologies for population-based genome-wide association studies (GWAS) continue to evolve, less ongoing attention has been devoted to methods for family-based studies. While there exist methods for analyzing dyads, it is not clear if one method is consistently more advantageous over another for a given design, and if they have the same robustness against population stratification as full case-parent trios. Furthermore, methods for analyzing dyads were mostly developed 20 or more years ago when type I error performance and statistical power were evaluated at nominal significance levels instead of the more stringent genome-wide levels used now. Recently, Hecker, Laird and Lange (2019) compared type I error and power of methods for general pedigree designs under different founder genotype distribution schemes but only considered the case-parent trio design among nuclear family designs with no hybrid designs. Gjerdevik et al. (2020) compared the relative efficiency of different hybrid designs with the case-control and the case-parent trio designs using direct and indirect effects under log-linear models implemented in the HAPLIN program. However, Gjerdevik et al. (2020) focused on log-linear models only, power/sample size comparisons without any type I error calibration or compute time comparison, and were restricted to a homogenous racial/ethnic group.

In this paper, we benchmark multiple open-source statistical popular methods across both dyad and trio designs on multi-ethnic samples in terms of their compute times, type I error control, and statistical power for identifying common variant associations at stringent significance levels. We focus on identifying direct effects of common variants in offspring on their phenotype and not on indirect effects of parental genotypes. Using large-scale simulations, we compare and evaluate methods for three nuclear family designs (case-parent trios, case-mother dyads, and a combination of case-parent trios and case-mother dyads), plus two related hybrid designs (case-parent/control-parent trios, case-mother/control-mother dyads) under different parameter settings. Then, we apply these methods to genotyped and imputed data from multi-ethnic mother-child pairs only or trios only or combinations of both dyads and trios from the Gene, Environment Association Studies consortium (GENEVA).

Material and Methods

Model and notation

In the following, we consider a GWAS of individuals collected under different nuclear family study designs, particularly case-parent trios and case-parent dyads (typically mother-child pairs). All individuals are genotyped/imputed or sequenced genome-wide at p genetic variants (where p is of the order of millions), and their disease status of interest is measured. For simplicity, we only consider data on bi-allelic single nucleotide polymorphisms (SNPs). We are interested in testing for association between a SNP and the disease status. In the following subsections, we provide a brief overview of existing methods for analyzing different nuclear family and related hybrid designs.

Methods for case-parent trios

Consider a study of n case-parent trios, where n affected (case) offspring are ascertained from a population, and the affected offspring along with their parents are genotyped/imputed or sequenced. Whether information on parents’ disease status is needed depends on the statistical method used. This is the simplest family-based design and existing approaches for analyzing such data includes variations of the transmission disequilibrium test and mating-type-stratified regression approaches.

Transmission disequilibrium test (TDT):

The TDT was originally proposed to assess if one allele at a SNP is transmitted from heterozygous parents to their affected offspring more often than that expected under strict Mendelian transmission (Spielman, McGinnis and Ewens, 1993). This would indicate that the SNP being tested (or marker locus) is both linked and associated with a causal SNP (or disease-susceptibility locus, DSL) for the disease. Essentially, the TDT is a non-parametric test that does not require assumption about disease model or disease distribution in the population (Laird and Lange, 2006). Note, although the TDT does not require prior specification of any specific disease model, it implicitly assumes multiplicative effects of alleles (Fallin et al., 2002). It does not use parental phenotype information even when available. It is also referred to as the allelic TDT, and it boils down to McNemar’s test for a 2×2 contingency table that cannot accommodate covariates or provide estimates of relative risks (RRs). For a large enough sample size, the TDT statistic has a ${\chi }^2$ distribution with 1 degree of freedom (df) under the null hypothesis of no association or no linkage between the marker SNP and an unobserved DSL.

Although the TDT was originally proposed to test for linkage in the presence of association, it is now typically used as a test for association (Laird and Lange, 2006) where the goal is to detect a disease-associated SNP by considering alleles at several markers in a region sequentially rather than a single marker SNP in linkage disequilibrium (LD) with an unobserved DSL underlying the disease phenotype (Fallin et al., 2002). Presence of linkage but no association between the marker SNP and a DSL results in no association between the disease and the marker SNP (Laird and Lange, 2006). Presence of both linkage and association between the marker SNP and a DSL indicates presence of association between the disease and the marker SNP being tested. Henceforth, in general, any reference to the null hypothesis will refer to no association between the disease and the marker SNP. In particular, for the TDT-like methods, this null hypothesis will mean no association between the marker SNP and a DSL in the presence of linkage between them.

Genotypic TDT (gTDT):

The gTDT compares the case’s transmitted genotype at the SNP to the set of all possible genotypes the case could have inherited from the parental genotypes (Self et al., 1991, Schaid, 1999). Unlike the TDT, the gTDT considers individuals as units of analysis; can accommodate family-level covariates; assumes some pre-specified genetic inheritance model; and yields estimated RRs with their standard errors (Fallin et al., 2002). The gTDT uses a conditional logistic regression model and involves a numeric likelihood maximization that can be computationally burdensome at a genome-wide level. However, recently derived closed-form parameter estimates enable rapid genome-wide application of the gTDT when testing additive, dominant or recessive effects using Wald’s test (Schwender et al., 2012). The gTDT statistic has an asymptotic 1-df ${\chi }^2$ distribution under the null hypothesis. Like TDT, the gTDT too does not use parental phenotype information.

Generalized disequilibrium test (GDT):

This is a generalization of TDT-like family-based association method proposed to take advantage of larger pedigree information (Chen, Manichaikul and Rich, 2009). It assesses the genotypic differences between all discordant relative pairs; can model covariates and uses a score test, where the score is obtained from the quasi-likelihood function for a conditional logistic regression model. Unlike TDT or gTDT, the GDT uses parental phenotype information. Under the null hypothesis, the GDT statistic has an asymptotic $N\left(0,1\right)$ distribution that does not depend on the inheritance model for the DSL. For case-parent trios, a special case of the GDT called the GDT-PO is used where the score is a weighted sum of genotypic differences between phenotypically discordant parent-child pairs.

Mating-type-stratified conditional likelihood approach:

Similar to the genotype RR modeling of Schaid and Sommer (1993) and the retrospective likelihood-based approach of UNPHASED (Dudbridge, 2008), Fan et al. (2013) derived the conditional likelihood of parental mating type and offspring genotype at a SNP given the affected status of offspring under a specific inheritance model assuming Hardy-Weinberg equilibrium (HWE) and random mating in the parental generation. This approach does not use parental phenotype information, can handle missing parental data without imputation, and can be applied to data on trios, dyads and monads (henceforth, it is referred to as the TDM). The likelihood function is modeled using the two unknown genotypic relative risk (GRR) parameters and the minor allele frequency (MAF) at the marker SNP, obtained using the Newton-Raphson method. Additive, dominant, recessive or multiplicative effects may be assumed, and the resultant likelihood ratio test (LRT) statistic for the TDM has an approximate 1-df ${\chi }^2$ distribution under the null hypothesis. One need not assume any inheritance model (i.e., assume an unrestricted model) and the resultant TDM statistic has an approximate 2-df ${\chi }^2$ distribution under the null hypothesis.

Log-linear modeling approach:

The log-linear approach generalizes the TDT to include orthogonal tests of offspring vs. maternal genetic factors, and can accommodate different risk conferred by a single copy vs. two copies of a risk allele (Weinberg, Wilcox and Lie, 1998). This approach does not use parental phenotype information, provides RR estimates for offspring genotype and is generalizable to a wide range of causal scenarios. It lists all possible trio genotypes stratified by parental mating type and applies a Poisson regression to the expected counts of the different trio genotypes conditional on the affected status of the offspring. Inferences about association is carried out using asymptotically ${\chi }^2$-distributed LRT statistic. The ${\chi }^2$ df under the null is dictated by the number of GRR parameters, which in turn depends on the inheritance model and the causal scenario assumed. van den Oord, E J and Vermunt (2000) described how this log-linear approach can be implemented in LEM, a general computer program for analyzing categorical data. Later, a dedicated genetics software package, HAPLIN, was developed to implement such log-linear models not only for bi-allelic variants but also for multi-allelic variants and other generalizations (Gjessing and Lie, 2006, Gjerdevik et al., 2019). Using LEM or HAPLIN, one can test for offspring effects only using a 2-df test, maternal effects only in a separate 2-df test or both offspring and maternal effects in a 4-df test. P-values from the 2-df test of offspring effects are directly comparable to p-values from other TDT-like methods. While these 2-df and 4-df tests assume no particular inheritance model, one can also implement a 1-df test in HAPLIN assuming multiplicative effects of allele like the TDT.

Methods for case-mother dyads

In any study of nuclear families, genetic measurements are frequently missing for one parent. More often than not, fathers are missing: they can be harder to recruit, and paternity is inherently harder to be confident of than maternity (Shi et al., 2008). Consider a study of n case-mother dyads, where n affected (case) offspring are sampled from the population, and the affected offspring and their mothers are genotyped/imputed or sequenced. One might come up with a straightforward approach of applying the TDT (or any method for case-parent trio data) on such family pairs for whom the genotype of the father at the SNP of interest can be unambiguously inferred. However, this process of selectively including only unambiguous dyads and discarding ambiguous ones can lead to invalid inference due to biases that depend heavily on allele frequencies (Curtis and Sham, 1995).

TDT-like approaches:

The first appropriate methodological development for the analysis of nuclear family data with missing genetic information on one parent was the 1-TDT (Sun et al., 1999). It examines the difference between the GRRs of heterozygotes vs. homozygotes (two possible choices) by using all heterozygous parent-homozygous offspring and homozygous parent-heterozygous offspring pairs (Sun et al., 1998, Sun et al., 1999). Under the null hypothesis, these two GRRs are expected to be the same and the 1-TDT test statistic has an approximate $N\left(0,1\right)$ distribution. If the total number of afore-mentioned parent-child pairs is not large, an exact p-value can also be calculated under the binomial distribution. Like the TDT, the 1-TDT does not use parental phenotype information. The GDT-PO can also be directly applied to data with 1 missing parent. Unlike the 1-TDT, GDT-PO examines all heterozygous parent-homozygous offspring and homozygous parent-heterozygous offspring among available parents that are unaffected (recall, GDT only uses phenotypically discordant pairs). For a dataset where all offspring are affected and all their parents are unaffected, 1-TDT and GDT-PO become identical. The GDT-PO statistic has an asymptotic $N\left(0,1\right)$ distribution under the null hypothesis.

Mating-type-stratified likelihood approaches:

The TDM is another approach that may be applied to data on parent-child dyads alone and gives a 1-df or a 2-df ${\chi }^2$ test statistic under the null depending on whether a specific inheritance model is assumed or not. The log-linear approach, too, is flexible enough to handle missing genetic data on parents via the Expectation-Maximization (EM) algorithm (Weinberg, 1999), and can be implemented using programs such as LEM or HAPLIN.

Methods for case-mother dyads and case-parent trios combined

When conducting family studies, it is not always possible to collect only families of one structure. In practice, we may not have only case-parent trios or only case-mother dyads but combinations of both. Suppose we have $n_1$ complete case-parent trios and $n_2$ incomplete trios where, without loss of generality, the fathers are missing. Note, it does not matter here if the fathers or the mothers are missing since we are only assessing direct effects of inherited genotypes of offspring on their disease status.

TDT-like approaches:

Instead of ignoring one set of families depending on whether the sample size $n_1$ is larger than $n_2$ or not, Sun et al. (1999) proposed applying the TDT on all complete trios and the 1-TDT on all dyads and then combining the two statistics. The resultant combined statistic, denoted TDT_com, has an asymptotic $N\left(0,1\right)$ distribution. However, there is currently no software for TDT_com. One can instead implement the 1-TDT or the GDT-PO on all parent-child pairs without discarding any families.

Mating-type-stratified likelihood approaches:

As described before, the TDM and the log-linear models can also be used in this scenario.

Methods for case-parent/control-parent trios

Genetic association studies, whether family-based (e.g., case-parent trio design) or population-based (e.g., case-control design), have their own strengths and limitations; see Weinberg and Umbach (2005) for a comprehensive summary of their advantages and disadvantages. A hybrid design bringing the strengths of case-parent trio and case-control designs into a single analytic framework is the case-parent/control-parent trio design. Consider a study of n trios, where $n_1$ affected (case) and $n_2=n-n_1$ unrelated unaffected (control) offspring are sampled from the population, and all sampled offspring and their parents are genotyped/imputed or sequenced. Although control-parent trios are generally easier to recruit and, along with case-parent trios, can help guard against spurious signals due to segregation distortion, they are typically either not recruited or discarded from analysis even when available because the TDT or the gTDT is only applicable to trios with affected offspring (Deng and Chen, 2001).

TDT-like approaches:

A straightforward approach is to apply the TDT on case-parent trios alone (refer to this as TDT_D) and on control-parent trios separately (refer to this as TDT_C, which, in contrast to TDT_D, can be viewed as a test of transmission of the ‘non-risk’ allele at the DSL rather than the ‘risk’ allele), and then combine these two independent tests into a new test TDT_D+C (Deng and Chen, 2001). This TDT_D+C statistic has an asymptotic 2-df ${\chi }^2$ distribution under the null hypothesis. Deng and Chen (2001) additionally proposed TDT_DC, a contingency table association test of allele transmissions (from heterozygous parents) with disease status in unrelated offspring. This TDT_DC statistic has an approximate 1-df ${\chi }^2$ distribution under the null hypothesis and does not require equal numbers of case-parent and control-parent trios. Neither of these two TDT-like tests uses parental phenotype information.

Mating-type-stratified likelihood approaches:

A log-linear model can be used to combine the family-based case-parents-trio component and the population-based parent-parent component, thus not requiring genetic data on the control offspring (Weinberg and Umbach, 2005). The requirement of only the parental genotypes and the case genotypes provides a distinct advantage of log-linear models over TDT-like approaches for such hybrid designs. It assumes the disease is rare for the offspring of each parental genotype combination, mating symmetry, and Mendelian proportions in the population. It neither assumes Hardy-Weinberg equilibrium nor random mating. In the presence of population structure, one can generalize this log-linear model to include a disease-status by total-number-of-parental-alleles interaction term or 5 additional disease-status by mating-type interaction terms (note, 6 distinct unordered parental mating types are possible here). However, “[a] direct consequence of preferring the enlarged model is that the control portion of the data will not contribute to inference related to the risk parameters, and the population-based component, in effect, becomes statistically irrelevant” (Weinberg and Umbach, 2005).

Methods for case-mother/control-mother dyads

Consider a study of n dyads, where $n_1$ affected (case) offspring are ascertained, and $n_2=n-n_1$ unaffected (control) offspring are sampled. Genotype data are available on offspring and their mothers. There are fewer methods for this hybrid dyad design. No TDT-like methods have been proposed for this design but the log-linear approach using LEM or HAPLIN is applicable (Shi et al., 2008).

Simulation experiments

We first simulated $n=1,000$ trios using the LE program (Chen and Deng, 2001, Chen, Manichaikul and Rich, 2009) as follows, and for the relevant scenarios detailed below, we removed fathers from trios to obtain mother-child pairs (dyads). The LE program is a general program for simulating pedigrees with only 1 DSL (causal SNP) at a time and requires the following parameters as input: disease prevalence, disease allele frequency, genotypic penetrances, number of families, and structure of the pedigree. For simulating phenotypes, we set the parental phenotypes as 0 (control) always, and offspring as 1 (case) or 0 depending on whether we simulated a case- or a control-family. For genotypes, we simulated multiple independent replicates of only one bi-allelic causal SNP to ensure independence of SNPs needed to estimate type I error rate and statistical power. The main results are described for a fixed MAF at this causal SNP to ensure fair comparison of type I error and power across methods keeping all other parameters fixed (additional results for varying MAFs are included in the supplementary materials). We simulated only offspring GRR effects and assume different GRR values to generate both null and non-null SNPs. For our type I error and power analyses, we simulated 1 million null SNPs (GRR=1) and 10,000 non-null SNPs, respectively. In other words, we generated 1 million (or 10,000) independent and identically distributed replicates of 1,000 families for a single SNP. For non-null SNPs, we assume GRR=2 under four different inheritance models (additive, multiplicative, dominant, and recessive). Note, for GRR=1, the inheritance model does not influence the values of genetic penetrance, and hence data generated under different inheritance models are all identical. Our choices of other parameters, such as disease prevalence, MAF and sub-group specific sample sizes, are described later for specific scenarios.

We evaluated two classes of methods: TDT-like methods (TDT, gTDT, 1-TDT, GDT-PO, TDT_DC, TDT_D+C) and the mating-type-stratified likelihood approaches (HAPLIN). While the TDM and the log-linear modeling using LEM are also candidates for mating-type-stratified likelihood approaches, we excluded both. In many analyses, TDM faced issues with matrix inversion preventing successful model fit, leading to missing results for many SNPs. We also faced several roadblocks in implementing the current LEM executable genome-wide on a Unix cluster. Note, not all methods in each class are applicable for a given study design. We simulated two scenarios involving samples from either one or two homogenous ancestral populations mimicking situations without or with population stratification. In all our analyses, we specified an additive model for implementing gTDT, regardless of the genetic inheritance model we used to generate data. Implementation of TDT, 1-TDT, GDT-PO, TDT_DC and TDT_D+C do not require pre-specification of a genetic model since they implicitly assume multiplicative effects of alleles. For HAPLIN, the use of 2-df and 4-df tests implies no specific inheritance model is assumed. While we benchmarked type I error of methods for all simulation settings, only statistical power for the homogenous group was used for benchmarking since not all methods could maintain type I error in the presence of population stratification. We used QQ plots as well as type I error estimates with 95% confidence interval (CI) to evaluate type I error control at stringent levels, and compared power estimates calculated at the conventional genome-wide level $\left(5\times {10}^{-8}\right)$. The type I error and the power estimates at a fixed significance level (α) are calculated as the proportion of SNPs with p-values <α from the null and the non-null data respectively. An approximate asymptotic 95% CI for such an estimate $\left(\widehat{\alpha }\right)$ is calculated as $\left[\widehat{\alpha }-1.96\sqrt{\frac{\widehat{\alpha }\left(1-\widehat{\alpha }\right)}{N}}, \widehat{\alpha }+1.96\sqrt{\frac{\widehat{\alpha }\left(1-\widehat{\alpha }\right)}{N}}\right]$, where N is the total number of independent SNPs from which $\widehat{\alpha }$ is estimated.

Scenario 1: One homogenous genetic ancestry

All the parents were simulated from a single homogenous ancestral population with disease prevalence of 30%. While family-based designs are best suited for disorders with rare prevalence, we simulated data for a common disease prevalence to ease simulation time and computational resources needed for sampling millions of case families across several combinations of parameter values. A fixed MAF of 10% is assumed for the causal SNP. Under this scenario, both type I error and power are compared for all methods.

Scenario 1A: Case-mother dyads

The fathers from 1,000 case-parent trios are removed to obtain 1,000 case-mother dyads. Note, although we removed the fathers for this parent-child design, the mothers could have been removed instead and the inference on direct effects of offspring genotype from these methods would remain unchanged.

Scenario 1B: Case-mother dyads and case-parent trios combined

We removed fathers from the first 750 case-parent trios to obtain 750 case-mother dyads (75% of the dataset), leaving the remaining 250 case-parent trios (25% of the dataset).

Scenario 1C: Case-mother/control-mother dyads

We generated 500 case-parent trios and 500 control-parent trios independently. Removing the father from each trio resulted in 500 case-mother dyads and 500 control-mother dyads, which were analyzed together. For power calculations, besides this 50:50 case-control ratio among offspring, we also checked 70:30 and 30:70 ratios of case-control families.

Scenario 2: Two distinct genetic ancestry groups

This scenario considers existence of population substructure between families in the sample. We simulated the parents of 500 families from one homogenous ancestral population with disease prevalence of 30%, and the parents of the other 500 families from a separate ancestral population with a lower disease prevalence of 15%. The causal SNP was simulated to have an MAF of 10% and 3% respectively in the two populations. We analyzed a pooled sample for all methods. Additionally, for the mating-type-stratified likelihood approach, we applied HAPLIN to each ancestry group separately and then meta-analyzed using Fisher’s p-value combination method (Fisher, 1925, Ray, Pankow and Basu, 2016). Under this scenario, we compared type I error rates only.

Scenario 2A: Case-mother dyads

Fathers from all 1,000 case-parent trios (500 from each ancestral population) were removed to obtain 1,000 case-mother dyads.

Scenario 2B: Case-mother dyads and case-parent trios combined

From each ancestral group, we removed fathers of the first 75% of case-parent trios to obtain 750 case-mother dyads in total and combined this with the remaining 250 case-parent trios. This resulted in 375 case-parent trios and 125 case-mother dyads from each ancestral population.

Scenario 2C: Case-mother/control-mother dyads

We generated 500 case-parent trios and 500 control-parent trios independently. Among case-parent trios, 250 were simulated for each ancestral population. Similarly for the control-parent trios. Removing the father from each trio gave us 500 case-mother and 500 control-mother dyads in a genetically heterogeneous sample.

Application to GENEVA data on orofacial clefts

In GENEVA, case-parent trios were ascertained through cases with an isolated, nonsyndromic orofacial cleft (i.e., cleft lip; cleft palate; or cleft lip with palate). They were largely recruited through surgical treatment centers by multiple investigators from Europe (Norway and Denmark), the United States (Iowa, Maryland, Pennsylvania, and Utah) and Asia (People’s Republic of China, Taiwan, South Korea, Singapore, and the Philippines) over several years (Beaty et al., 2010). Type of cleft, sex, race, family history, and common environmental risk factors were collected through direct maternal interview. Genotyping on the Illumina Human610 Quadv1_B array with 589,945 SNPs was performed at the Center for Inherited Disease Research (https://cidr.jhmi.edu/). As part of two recent publications (Zhang et al., 2021, Ray et al., 2021), trio-aware phasing and re-imputation using the 1000 Genomes Phase 3 release 5 reference panel were performed. Among GENEVA participants who were re-imputed and used in these two articles, we restricted our analysis to the participants ascertained through nonsyndromic CL/P. We used ‘hard’ genotype calls: if the calls had uncertainty >0.1 (i.e., genotype likelihoods <0.9), they were treated as missing; the rest were regarded as observed genotype calls. All imputed SNPs were filtered to exclude any with $R^2<0.3$. All variants are on the forward strand.

We analyzed genotyped/imputed SNPs only and employed the following quality control measures using PLINK 1.9 (Chang et al., 2015): all SNPs with MAF<5% and any showing deviation from Hardy-Weinberg equilibrium (HWE) at $p<{10}^{-6}$ among parents were excluded; all genotyped SNPs with missingness >5% and Mendelian error rate >5% were also removed. Additionally, all trios with per-trio Mendelian error rate >5% were dropped. Our final GENEVA analytical dataset contained 5,204,784 autosomal SNPs, including both observed and imputed SNPs having MAF >5% among parents, for 1,487 multi-ethnic complete case-parent trios. Of these 1,487 complete trios, 891 trios were of Asian ancestry (including Malays from Singapore) and 575 were of European ancestry. The remaining 22 trios were from other racial/ethnic groups. Among 2,974 parents, 560 had missing phenotype information. There were 534 female and 953 male CL/P probands in total.

We analyzed three separate designs: case-parent trios only (considered here as the gold standard); case-mother dyads only; and trios and dyads combined. For the trios only dataset, we analyzed all 1,487 case-parent trios (a multi-ethnic sample). For the dyads only dataset, we removed the father from each trio and analyzed the resulting 1,487 case-mother pairs. For the combined dataset, we removed the father from 75% of all trios within each racial/ethnic group (consistent with the simulations for scenario 2B detailed above), yielding 1,116 multi-ethnic case-mother pairs and 371 multi-ethnic case-parent trios. We compared findings from the dyads only and the combined designs against the trios only design. Note, there are no control families in GENEVA, and hence no case-parent/control-parent or case-mother/control-mother design were considered. We analyzed the complete GENEVA dataset using TDT-like methods. We applied HAPLIN to the Asian and the European groups separately and then meta-analyzed results from the 2-df test for offspring genotype effects using Fisher’s p-value combination. We excluded the 4-df combined test of offspring or maternal effects in this comparison since we cannot rule out the influence of maternal genes on risk of clefts in offspring (Jugessur et al., 2010, Shi et al., 2012).

For each analysis, we defined independent loci by clumping all the genome-wide significant SNPs $\left(p<5\times {10}^{-8}\right)$ in a ±500 Kb span and with LD $r^2>0.2$ into a single genetic locus. We used the SNP2GENE function of FUMA (v1.3.6b; Watanabe et al., 2017) for clumping and mapping each locus to the gene nearest to the lead SNP. The index SNP for each locus was chosen as the most significant SNP. Since we performed multi-ethnic analysis, we separately used 1000G Phase 3 EUR and EAS as reference populations for LD calculation. For a given analysis, we found independent hits to be the same regardless of the ancestry of the reference group chosen for LD calculation. We defined the bounds of a locus as the minimum of lower bounds and the maximum of upper bounds across both ancestry groups. All genomic coordinates are given in NCBI Build 37/UCSC hg19.

Results

Simulation experiments: Type I error

Scenario 1A: One homogenous ancestry group, case-mother dyads

The QQ plots of all methods, except 1-TDT and GDT-PO, reside within the 95% CI for the expected distribution of p-values, indicating their correct type I error control (Figure 1). The 1-TDT and GDT-PO performed well at nominal error levels (${\lambda }_{1-TDT}=1$ and ${\lambda }_{GDT-PO}=1$) but showed some inflation at stringent error levels as indicated by the data points outside the 95% CI. The corresponding gold standards for all methods (i.e., methods applied to case-parent trios) maintained correct type I error, although the TDT-like methods were slightly conservative at stringent levels. The type I error estimates and their 95% CIs provide a granular view of type I error control of each method at specific significance levels (Table S1). For instance, the TDT-like methods were slightly conservative at all levels for case-parent trios while they were less conservative at nominal levels and more inflated at stringent levels for case-mother dyads. On the other hand, HAPLIN showed similar type I error control at all levels for case-mother dyads and case-parent trios. As expected, when all offspring are affected and all parents are unaffected, the 1-TDT and the GDT-PO results are identical for case-mother dyads. While these findings were based on SNPs with a fixed MAF, we also simulated data on null SNPs with varying MAFs and found qualitatively similar results (Table S2).

Figure 1:

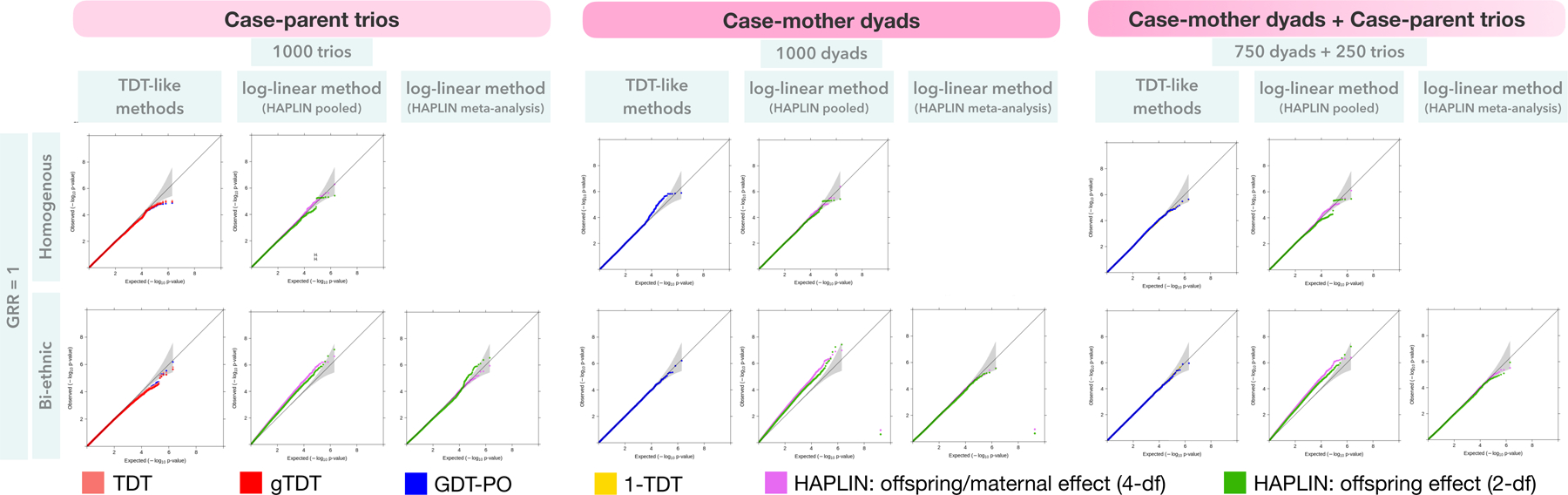
Type I error performance of the different combinations of methods and nuclear-family designs at stringent significance levels. Results are based on simulated data on either one or two homogenous racial/ethnic groups with 1 million null SNPs. For one homogenous sample, a common disease prevalence of 30% and MAF 10% was simulated. For bi-ethnic data, the second homogenous group had a disease prevalence of 15% and MAF 3%. All offspring were affected, and all parents were unaffected. Observed(−log₁₀p-values) are plotted on the y-axis and Expected(−log₁₀p-values) on the x-axis of these QQ plots. The gray shaded region in each QQ plot represents a conservative 95% confidence interval for the expected distribution of p-values.

Scenario 1B: One homogenous ancestry group, case-mother dyads and case-parent trios combined

All methods performed similar to the corresponding gold standard methods (Figure 1). Specifically, the TDT-like methods were slightly inflated at nominal levels and slightly conservative at more stringent levels (Table S1). HAPLIN showed better type I error control at more stringent levels compared to nominal levels. These results were robust to varying MAFs of the null SNPs (Table S2).

Scenario 1C: One homogenous ancestry group, case-mother/control-mother dyads

The QQ plots of HAPLIN, the only applicable method in this scenario, showed well-controlled type I error (Figure 2). For the corresponding case-parent/control-parent trio data, both HAPLIN and the TDT-like methods maintained correct type I error. Type I error estimates and corresponding 95% CIs, however, indicate the TDT-like methods were slightly conservative at all levels while HAPLIN was slightly inflated at nominal levels (Table S3). Results were robust to varying SNP allele frequencies (Table S4).

Figure 2:

Type I error performance of the different combinations of methods and hybrid family designs at stringent significance levels. Results are based on simulated data on 1,000 families from either one or two homogenous racial/ethnic groups with 1 million null SNPs. For one homogenous group, a common disease prevalence of 30% and MAF 10% was simulated. For bi-ethnic data, the second homogenous group had a disease prevalence of 15% and MAF 3% for the causal SNPs (note, null effect is assumed). Case-to-control ratio among offspring was 50:50, and all parents were unaffected. Observed(−log₁₀p-values) are plotted on the y-axis and Expected(−log₁₀p-values) on the x-axis of these QQ plots. The gray shaded region in each QQ plot represents a conservative 95% confidence interval for the expected distribution of p-values.

Scenario 2A: Two distinct ancestry groups, case-mother dyads

All TDT-like methods maintained appropriate type I error as indicated by their QQ plots lying within the 95% CI for the expected distribution of p-values (Figure 1 and Table S1). HAPLIN showed inflated type I error even at nominal significance levels (${\lambda }_{HAPLIN-2df}=1.34$ and ${\lambda }_{HAPLIN-4df}=1.60$). Inflation in HAPLIN was exacerbated in the presence of varying SNP allele frequencies (Table S2). These observations were reflected for the gold standards as well. When HAPLIN was applied to each ancestry group separately and then meta-analyzed, type I error was well-controlled at nominal (${\lambda }_{HAPLIN-2df}=1.02$ and ${\lambda }_{HAPLIN-4df}=1.00$) as well as stringent levels (Figure 1). However, for the corresponding gold standard, the QQ plots indicated type I error was well-controlled for the 4-df test but was inflated at stringent levels for the 2-df test.

Scenario 2B: Two distinct ancestry groups, case-mother dyads and case-parent trios combined

As before, all TDT-like methods exhibited well-controlled type I error rate while HAPLIN showed significant type I error inflation (Figure 1 and Table S1) particularly for varying SNP allele frequencies (Table S2). Meta-analysis of HAPLIN applied to ancestry-stratified data gave well-controlled type I error for both tests (Figure 1). We also simulated a skewed distribution of dyads and trios within each ancestral group; results indicated robustness of TDT-like methods to population substructure while HAPLIN showed even greater inflation if data are not stratified and meta-analyzed (Figure S1). It is worth noting that with real datasets one may not have clearly distinct groups to stratify and then meta-analyze.

Scenario 2C: Two distinct ancestry groups, case-mother/control-mother dyads

HAPLIN is the only method that could be evaluated here, and it showed considerable type I error inflation when applied to the pooled sample (Figure 2 and Table S3), particularly for varying SNP allele frequencies (Table S4). Meta-analysis of HAPLIN applied to ancestry-stratified data gave well-controlled type I error; no different from the corresponding gold standard (Figure 2). On the other hand, the TDT-like methods applicable only for the case-parent/control-parent design were slightly conservative. Note, we also simulated a skewed distribution of case and control offspring within each ancestral group, with all 500 case families coming from one group and all 500 control families from the other. Our results indicated robustness of TDT-like methods to extremely skewed distribution of case- and control families across ancestral groups while HAPLIN showed extreme type I error inflation (Figure S2).

Simulation experiments: Power

Scenario 1A: One homogenous ancestry group, case-mother dyads

All the TDT-like methods had similar statistical power to detect phenotype-genotype association (Figure 3a). HAPLIN was more powerful and, depending on the inheritance model, the 4-df test of offspring/maternal effects showed improved power over the 2-df test of offspring effects alone. The relative power of these methods was qualitatively similar across different MAFs and underlying inheritance model (Figure S3). For case-parent trios, the power estimates of these methods were not qualitatively very different at a given MAF and inheritance model; however, the relative behavior of these power curves showed slight variation with the inheritance model. All methods had reduced power for case-mother dyads compared to those for case-parent trios, as expected.

Figure 3:

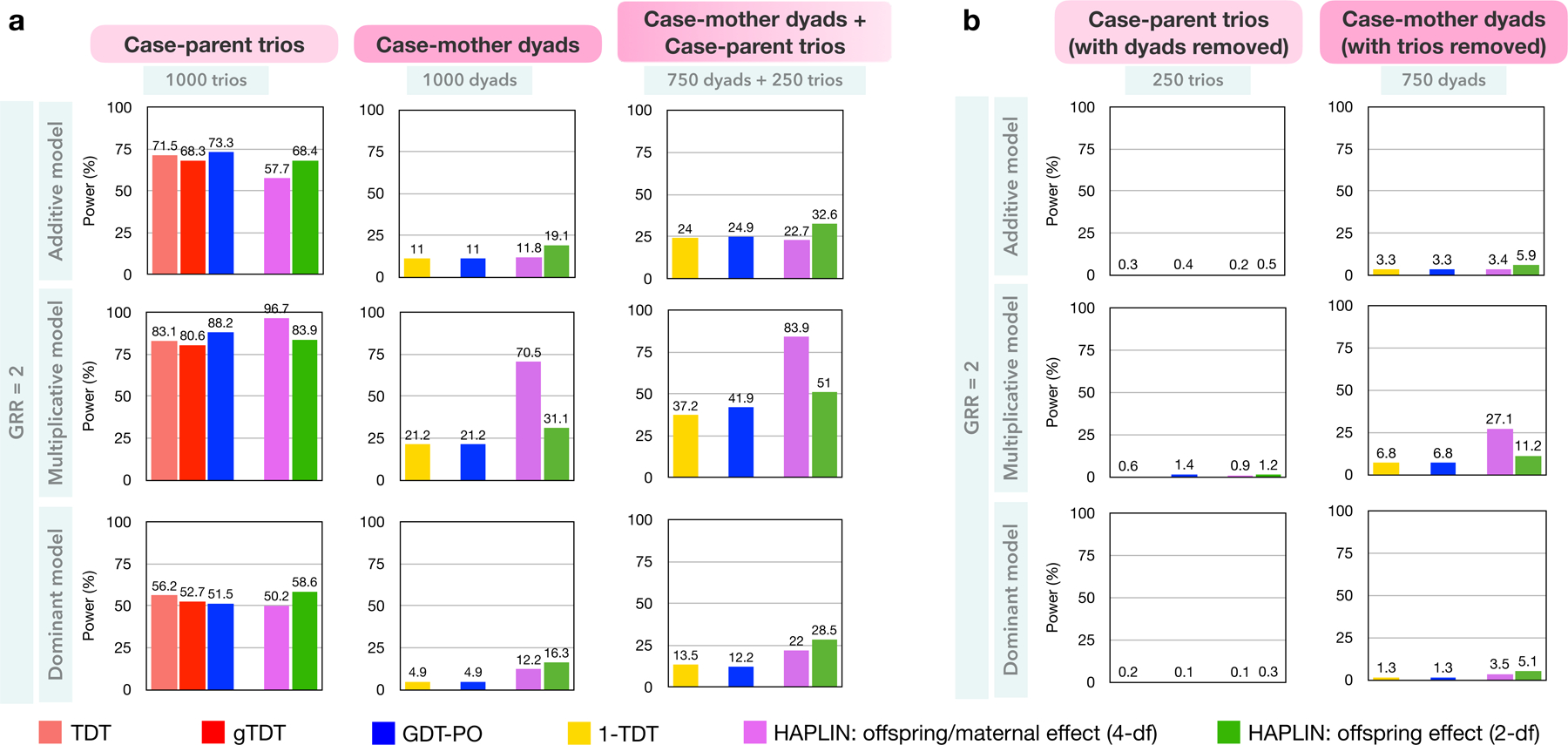
Statistical power for the different combinations of methods and nuclear-family designs at genome-wide significance level $\left(5\times {10}^{-8}\right)$. Results are based on simulated data on 1,000 families from one homogenous racial/ethnic group with 10,000 non-null SNPs at MAF 10% at the casual SNP, and a common disease prevalence of 30%. Results for data simulated using the recessive inheritance model are not shown due to nearly zero power of these methods at the chosen parameter values. All offspring were affected, and all parents were unaffected.

a. Comparison of designs with the same number of families of different compositions. b. Comparison of the combined analysis of 750 case-mother dyads and 250 case-parent trios against the scenarios when either all dyads or all trios are removed from analysis.

Scenario 1B: One homogenous ancestry group, case-mother dyads and case-parent trios combined

For a fixed number of families, all methods had improved power over analyzing case-mother dyads alone (Figures 3a and S3), again as expected. Further, discarding any type of family from a mixed family design like this resulted in substantial loss of statistical power (Figure 3b).

Scenario 1C: One homogenous ancestry group, case-mother/control-mother dyads

HAPLIN, the only applicable method, was nearly as powerful in the dyad design as in the full trio design (Figure 4). As the proportion of cases among offspring decreases, HAPLIN’s power also decreases. The 4-df test for offspring/maternal effect was unexpectedly more powerful than the 2-df test of offspring genotypic effect for a multiplicative inheritance model despite the larger df. Additionally, HAPLIN unexpectedly achieved better power for case-mother/control-mother dyads than case-parent/control-parent trios when the case-control ratio among offspring is low. These are, however, artifacts arising from this simulation experiment not satisfying the rare disease assumption (Figure S4). For the corresponding gold-standard design (i.e., case-parent/control-parent design), there are competing methods although they provided less power than HAPLIN. These findings were qualitatively similar across a range of MAFs (Figure S5). Between the two TDT-like methods, TDT_D+C was uniformly more powerful than TDT_DC across different MAFs regardless of the inheritance model and the case-control distribution among offspring, despite the higher df of TDT_D+C. In fact, the power difference between TDT_D+C and TDT_DC increased substantially with decreasing prevalence (Figure S4) and increasing MAF (Figure S5) across different inheritance models when the number of case families is at least as large as the number of control families. This relative behavior of TDT_D+C and TDT_DC power curves contradicts what Deng and Chen (2001) found likely because their conclusion was based on a high disease prevalence, equal numbers of case- and control-families only, dominant effects only, and an MAF of 50% (which, from an evolutionary genetics perspective, rarely happens for a disease allele) at a nominal significance level of 5%.

Figure 4:

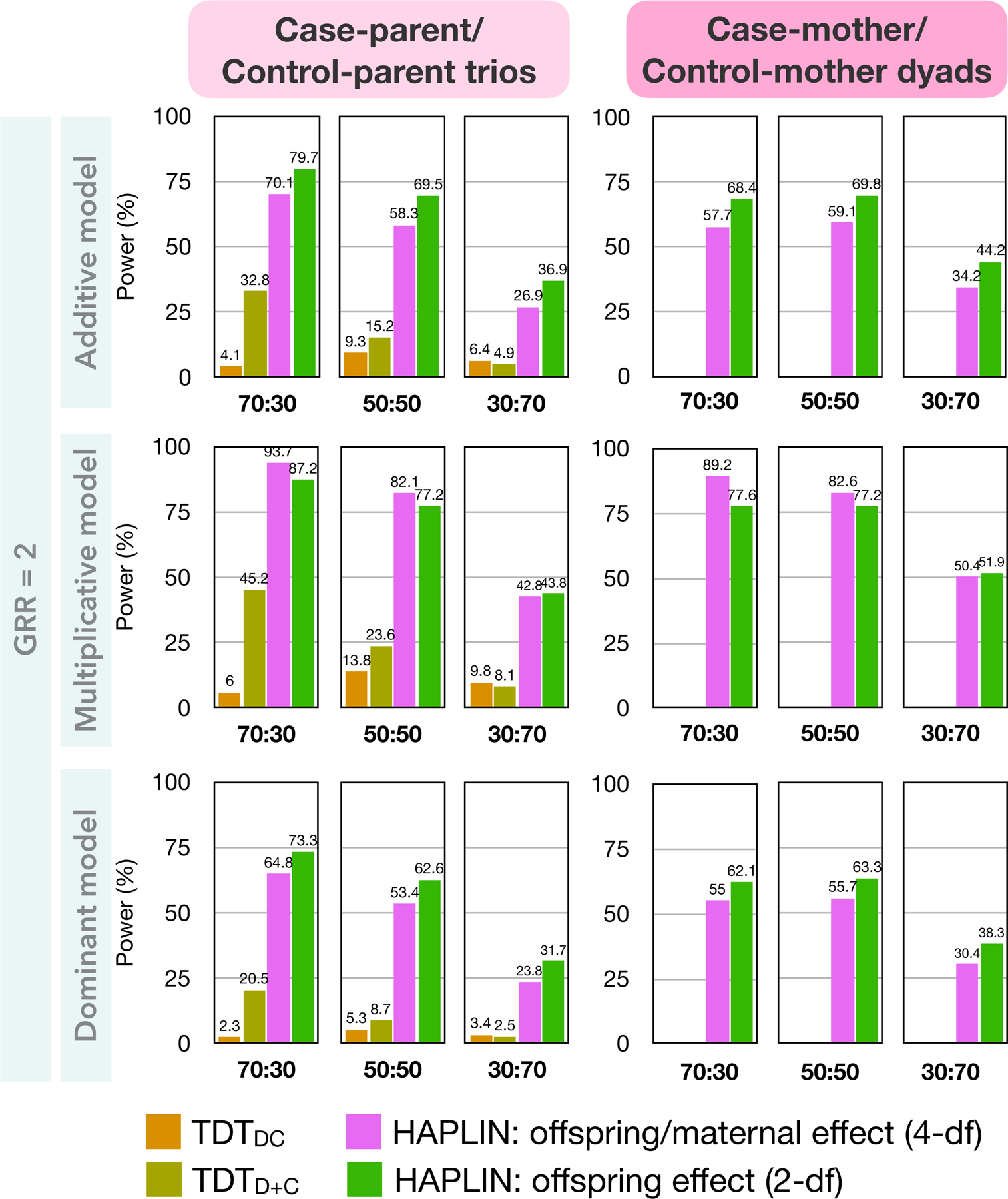
Statistical power for different combinations of methods and hybrid family designs at genome-wide significance level $\left(5\times {10}^{-8}\right)$. Results are based on simulated data on 1,000 families from one homogenous racial/ethnic group with 10,000 non-null SNPs at MAF 10% at the causal SNP, and a common disease prevalence of 30%. Results for data simulated using the recessive inheritance model are not shown due to nearly zero power of these methods at the chosen parameter values. Case-to-control ratio among offspring is either 70:30, 50:50 or 30:70. All parents are unaffected.

Application to GENEVA Data on Orofacial Clefts

Case-parent trios

To establish a gold standard, we first analyzed the complete case-parent trio data (pooled sample) using several TDT-like methods (TDT, gTDT and GDT-PO). As expected, TDT and gTDT gave nearly identical results with both replicating known signals for CL/P (Dixon et al., 2011, Beaty, Marazita and Leslie, 2016, Ray et al., 2021) at the conventional genome-wide threshold ($\text{p<}5\times {10}^{-8}$: 1p22.1 (ABCA4/ARHGAP29), 1q32.2 (IRF6), 8q24 (gene desert), 17p13.1 (NTN1), 18q12.1 (TTR, not a known cleft-associated region and could be spurious), and 20q12 (MAFB) (Figure 5). Further, 3p11.1 (EPHA3), 8q21.3 (DCAF4L2), and 10q25.3 (SHTN1) yielded suggestive significance ($\text{p<}{10}^{-6}$). The GDT-PO signals were somewhat attenuated compared to those from TDT/gTDT, and it failed to replicate the signals at/near genes TTR, DCAF4L2 and SHTN1. This may be due to the reduced sample sizes when only phenotypically discordant parent-child pairs contributed to the test statistic since some parents had more subtle ‘microforms’ or missing phenotype information.

Figure 5:

Manhattan plots for the different combinations of methods and nuclear family designs from the multi-ethnic GENEVA study on CL/P. The gTDT and the TDT are applicable to case-parent trio design $\left(n=1487\right)$ only. The 1-TDT (a generalization of TDT) is applicable to both case-mother dyad design $\left(n=1487\right)$ and the combined case-mother dyad case-parent trio design ($n_1=371$ trios, $n_2=1116$ dyads). The GDT-PO and HAPLIN methods are applicable to all three designs. Here, HAPLIN (2-df test of offspring genotypic effect) was applied on each racial/ethnic group separately and then meta-analyzed. The red and blue horizontal lines in each plot correspond to genome-wide $\left(5\times {10}^{-8}\right)$ and suggestive $\left({10}^{-6}\right)$ significance levels, respectively. The genome-wide significant loci for each method-design pair are annotated in dark gray and the suggestively significant loci in light gray.

We additionally analyzed the complete trios using HAPLIN. Unlike TDT-like methods, HAPLIN was not immune to type I error inflation due to population stratification (Figure S6). So, we analyzed Asian and European groups separately using HAPLIN and then meta-analyzed the results from the 2-df test for offspring effects (Figure 5). HAPLIN detected a new signal at 6p22.1 (TRIM26,$p=2.1\times {10}^{-8}$), which has no known relevance to CL/P and could be spurious. It failed to detect the EPHA3 signal.

Case-mother dyads

The 1-TDT and GDT-PO showed considerably reduced power to detect genetic associations compared to the case-parent trio analysis, as expected (Figure 5). At genome-wide significance, 1-TDT identified only the ABCA4/ARHGAP29, IRF6 and 8q24 signals compared to TDT/gTDT on complete trios. GDT-PO failed to identify any genome-wide significant signals. This lack of power for GDT-PO compared to 1-TDT is presumably in part due to smaller sample sizes and missing phenotype information in some mothers. HAPLIN, when meta-analyzed over Asian and European groups, detected only the IRF6 and 8q24 signals. It also detected an intergenic region at 4p14$\left(p=4.2\times {10}^{-8}\right)$, which may be spurious as it was not detected by the HAPLIN meta-analysis of complete trios and has not been previously reported in the cleft literature. It is possible our HAPLIN meta-analysis results were still inflated due to population stratification because each racial/ethnic group was not completely homogenous (participants were sampled from various countries). At the suggestive significance level, a few additional regions were detected, some of which may be spurious since they were not found in the corresponding analysis of the complete trios: 11p13 by 1-TDT; IRF6 and 3q29 by GDT-PO; 2p16.1, 6p22.1 and 17q22 by HAPLIN.

Case-mother dyads and case-parent trios combined

The 1-TDT and GDT-PO showed improved power over analyzing the same number of families consisting of case-mother dyads alone (Figure 5). At the genome-wide significance level, 1-TDT identified only the ABCA4/ARHGAP29, IRF6 and 8q24 signals while GDT-PO identified only the IRF6 signal when compared to TDT/gTDT signals for complete trios. HAPLIN, when meta-analyzed over Asian and European groups, detected only the IRF6 and 8q24 signals. Interestingly, HAPLIN did not detect the possibly spurious signal at 4p14 at the genome-wide threshold that it identified from case-mother dyads alone. At the suggestive significance level, 1-TDT detected the EPHA3, DCAF4L2, 11p13 (possibly spurious), NTN1 and MAFB signals; the GDT-PO detected the ABCA4/ARHGAP29, EPHA3, 6p21.31 (possibly spurious), 8q24, 11p13 (possibly spurious) and MAFB signals; and finally, HAPLIN detected the EPHA3, 4p14 (possibly spurious), 6p22.1 (possibly spurious), NTN1, 17q22 (possibly spurious) and the MAFB signals.

Comparison of Compute Times

We use genetic data on 8,015 SNPs in the region 8q24:128344410–132105518, which includes the known gene desert region strongly associated with risk to CL/P. Figure 6 shows the compute times on an Oracle Virtual Machine 6.1.24 (64bit) with Intel® Xeon® CPU E3–1270 v6 @3.80 GHz processor and 8GB of RAM. Across all three designs, the TDT-like methods had comparable compute times of <1 minute, which included loading and necessary formatting of data. HAPLIN applied on the pooled sample took at least 90 minutes to run for the case-parent trio design and took 2–3-fold more time for study designs with at most one missing parent. For multi-ethnic samples, application of HAPLIN on ancestry-stratified data and subsequent meta-analysis using Fisher’s method required nearly 1.5-fold increased time compared to HAPLIN applied on the pooled sample. For genome-wide scans, one can reduce compute time by using a built-in parallel implementation of HAPLIN if multiple cores are available.

Figure 6:

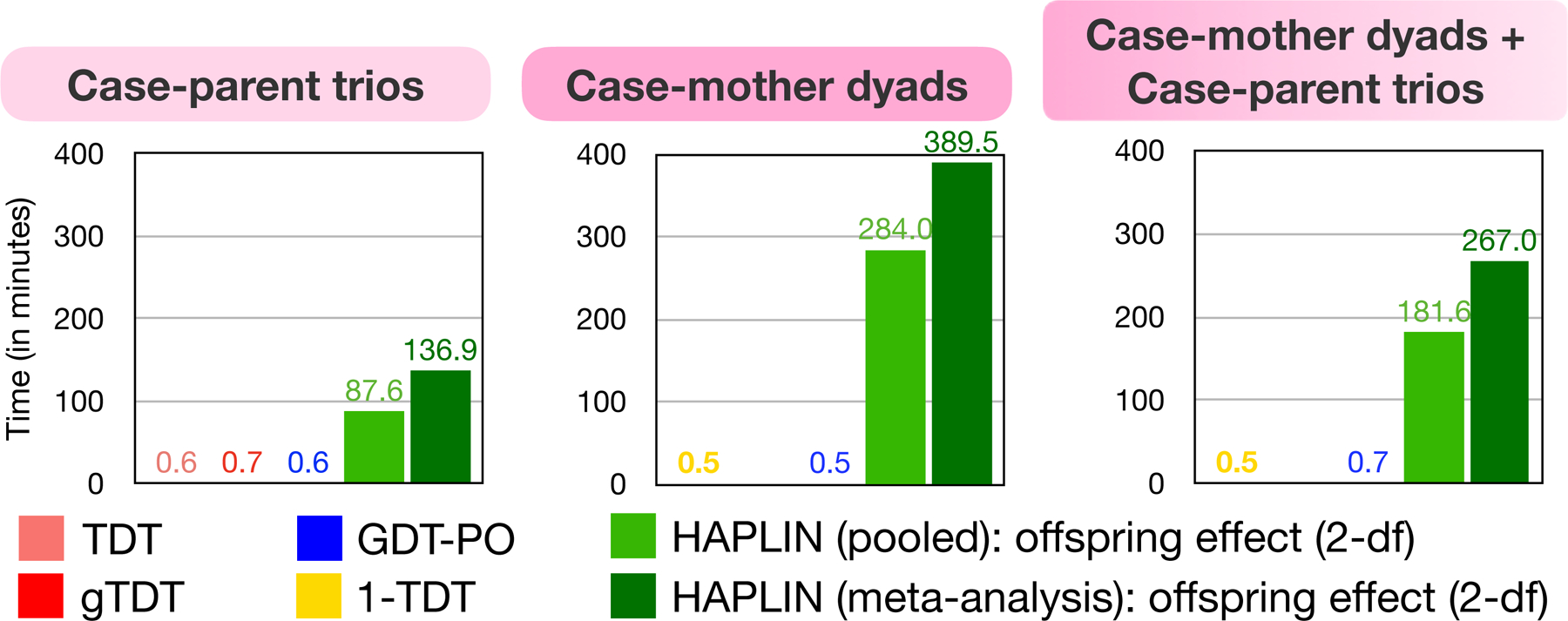
Compute times for the different combinations of methods and nuclear family designs from the multi-ethnic GENEVA study on CL/P. Results are based on a subset of the genetic data: 8,015 genotyped/imputed SNPs in the region chr8:128344410–132105518 that includes the known cleft locus 8q24.

Discussion

In this article, we reviewed and benchmarked existing open-source statistical methods for the genome-wide analysis of parent-child dyads against those available for case-parent trios. We considered case-mother dyads alone, a combination of case-mother dyads and case-parent trios, and combinations of case-mother/control-mother dyads. We compared these study designs against their corresponding gold standards: either case-parent trios alone or case-parent/control-parent trios. We used extensive simulation experiments, and array-based genetic data on trios ascertained through a child affected by CL/P from the GENEVA study with parental phenotypes when available. Although we used the methods for parent-child dyads exclusively on mother-child dyads, one could use them on father-child dyads, and theoretically on some combination of father-child and mother-child dyads assuming only direct effects of offspring genotypes are of interest and there is no mating asymmetry in the population.

This work was partly motivated by the Environmental influences on Child Health Outcomes (ECHO) study, a cohort collaboration that seeks to identify environmental and genetic exposures relevant to child development and disease. Genetic array data will be paired with a catalog of early childhood or maternal outcomes on more than 30,000 individuals in the United States comprising mother-child-father trios and mother-child pairs across these multi-ethnic ECHO cohorts. Given the expected genetic diversity of these cohorts, it is imperative to evaluate methods that can be applied individually to dyads or trios (or some combination) while taking maximal advantage of the family-based structure and information whenever possible. Similarly, it is essential to define the analytical approach best suited for each family-based design, especially since dyads are easier to recruit. Recommendations from this study will not only help identify the best strategies to use in diverse studies like the ECHO study, but also provide guidelines for other dyad design-based studies.

Recommendations

For case-parent trios, the TDT-like approaches (e.g., TDT, gTDT, GDT-PO) inherently circumvent the confounding due to population stratification by distinguishing between transmitted and non-transmitted parental alleles either in a contingency table framework or in a conditional regression framework. The non-transmitted parental alleles in a case-parent trio design– also referred to as the case-parental control design (Sun et al., 1998)– serve as matched genetic controls even when random mating and HWE assumptions are not met (Weinberg, Wilcox and Lie, 1998). Consequently, generalizations of these methods to accommodate a missing parent in the case-mother dyad design (e.g., 1-TDT, GDT-PO) or to accommodate control-parent families (e.g., TDT_D+C, TDT_DC) also protect against confounding due to population stratification.

For multi-ancestry data consisting of either case-mother dyads alone or a combination of case-mother dyads and case-parent trios, both 1-TDT and GDT-PO are useful. We recommend GDT-PO since it can model covariates in a regression framework. If there are many affected parents or parents with missing phenotypes, we recommend 1-TDT since, in this scenario, GDT-PO considers only phenotypically discordant relative pairs and hence less powerful than 1-TDT. If the dataset consists of one homogeneous genetic ancestry group, we recommend a log-linear approach (e.g., HAPLIN) as it is often more powerful than 1-TDT and GDT-PO. In particular, the 2-df test for offspring genotype effects alone under a log-linear model using LRT tends to be more powerful than the 1-df TDT under a dominant or a recessive genetic model since LRT uses information about the joint transmission from pairs of parents, rather than accounting for the parental transmissions of individual alleles (Weinberg, Wilcox and Lie, 1998, Weinberg, 1999). If the dataset is multi-ancestry but consists of identifiable genetic ancestry groups, we recommend using a log-linear approach on each homogeneous sub-group and then meta-analyzing the results. However, caution should be exercised in interpreting findings from these log-linear approaches on multi-ethnic data since it is often impossible to ensure each racial/ethnic group in any real dataset is truly homogenous. It is important to highlight that we did not include covariates to adjust for heterogeneity within each group or in the analysis of pooled sample.

For multi-ancestry data consisting of case-parent/control-parent trios, either TDT_DC or TDT_D+C may be used when there are many more control-families than case-families and the disease prevalence is not rare. Otherwise, we recommend using TDT_D+C since it showed improved power over TDT_DC in our experiments regardless of disease prevalence, disease allele frequency and inheritance model. Both these methods control type I error even when case- and control-parent trios come from different ancestral populations. Unfortunately, we do not have any recommendation if the data consist of multi-ancestry case-mother/control-mother dyads. A meta-analysis of results from a log-linear approach like HAPLIN can be used if the case-mother/control-mother dyads (or the case-parent/control-parent trios) come from one or more identifiable homogenous genetic ancestry groups. In this case, HAPLIN is usually considerably more powerful than TDT-like approaches; however, few populations are truly homogeneous and for rare diseases, it is often necessary to draw case-families from multiple racial/ethnic groups. We provide a summary of our recommendations in Table 1.

Table 1:

Recommended methods for testing direct effects of offspring genotypes on risk of a disease in different family study designs.

Type of nuclear family/ hybrid design	Applicable method(s)	Recommendation
		Type of analysis	Method	Software
Case-parent trios	TDT, gTDT, 1-TDT, GDT-PO, HAPLIN	1 genetic ancestry group	HAPLIN	https://cran.r-project.org/web/packages/Haplin/index.html
		Multiple genetic ancestry groups	gTDT	https://bioconductor.org/packages/release/bioc/html/trio.html
Case-mother dyads	1-TDT, GDT-PO, HAPLIN	1 genetic ancestry group	HAPLIN	https://cran.r-project.org/web/packages/Haplin/index.html
		Multiple genetic ancestry groups	GDT-PO, if there are covariates 1-TDT, if there are many parents affected or with missing disease status	https://www.chen.kingrelatedness.com/software/GDT/index.shtml
Case-mother dyads + Case-parent trios	1-TDT, GDT-PO, HAPLIN	1 genetic ancestry group	HAPLIN	https://cran.r-project.org/web/packages/Haplin/index.html
		Multiple genetic ancestry groups	GDT-PO, if there are covariates 1-TDT, if there are many parents affected or with missing disease status	https://www.chen.kingrelatedness.com/software/GDT/index.shtml
Case-parent/ control-parent trios	TDTDC, TDTD+C, HAPLIN	1 genetic ancestry group	HAPLIN	https://cran.r-project.org/web/packages/Haplin/index.html
		Multiple genetic ancestry groups	TDTD+C	https://github.com/RayDebashree/TDT-like-tests
Case-mother/ control-mother dyads	HAPLIN	1 genetic ancestry group	HAPLIN	https://cran.r-project.org/web/packages/Haplin/index.html
		Multiple genetic ancestry groups	<No recommendation>

Study limitations

We only considered methods from an extensive literature search with open-source implementation and an available manual. Other general classes of methods that could be used in one or more of our designs are family-based association test (FBAT), linear mixed models (LMM), and models based on generalized estimating equations (GEE). The FBAT approach generalizes the TDT non-parametrically to incorporate non-inbred pedigrees and can additionally handle missing parents (more generally missing founders), complex phenotypes, multi-allelic markers, and arbitrary genetic models (Laird and Lange, 2006, Hecker, Laird and Lange, 2019). It is exactly the TDT test when considering bi-allelic markers under an additive model from case-parent trios, and in the case of a missing parent 1-TDT is the non-parametric generalization of TDT. We did not use FBAT in our analyses since we did not consider any of the other generalizations implemented in FBAT. Variance component models, and more generally LMM, incorporate phenotypic information of parents unlike most TDT-like methods, and incorporate familial relationships through a covariance matrix reflecting kinship between pairs of individuals (Chen and Abecasis, 2007, Eu-Ahsunthornwattana et al., 2014). Chen et al. (2011) was one of the first to recommend the use of GEE over variance component strategy in family-based studies of dichotomous phenotypes. To our knowledge, both the LMM and the GEE approaches are more commonly used in GWAS of secondary phenotypes from extended pedigree data (Suktitipat et al., 2012, Ngwa et al., 2021). The focus of this work is on a dichotomous trait– the case-control status used to ascertain probands– and common markers. We have not considered methods for secondary phenotypes, particularly quantitative traits (Laird and Lange, 2008, Ewens, Li and Spielman, 2008), or methods tailored to rare variants, which are increasingly becoming available via high-throughput whole exome or whole genome sequencing techniques (Hecker et al., 2020).

We did not assess any indirect effects (e.g., maternal effect, parent-of-origin effect, imprinting) or any interaction effect (e.g., maternal-fetal genotype interactions, gene-environment interaction, epistasis) (Ainsworth et al., 2011). In this context, EMIM, a tool to estimate the afore-mentioned indirect and interaction effects using multinomial modeling of case-parent trios, case-mother dyads, and/or monads (Howey and Cordell, 2012) could be considered. We used the TDT-like methods exclusively as association tests (Laird and Lange, 2006), and did not explore their type I error rates separately for the other possible null hypothesis scenarios under the original “no linkage or no association” composite null hypothesis (Laird and Lange, 2008, Hecker, Laird and Lange, 2019). We also did not consider monads (Fan et al., 2013) or any other pedigree structure (Chen, Manichaikul and Rich, 2009, Hecker, Laird and Lange, 2019). We explored three different mother-child pair designs and their corresponding trio designs; other hybrid designs are certainly possible (Vermeulen et al., 2009, Gjerdevik et al., 2020) but are beyond the scope of this paper. We considered bi-allelic SNPs only (not considering multi-allelic or haplotype effects; Cordell, Barratt and Clayton, 2004, Gjessing and Lie, 2006). Our simulation framework is simple and do not reflect the usual complex genetic architecture underlying many disorders; however, we used a similar framework and parameter choices as used by many others (Deng and Chen, 2001, Chen, Manichaikul and Rich, 2009, Hecker, Laird and Lange, 2019). Our simulations did not involve any confounders since most TDT-like methods cannot accommodate covariate effects. We focused on either one or two homogenous genetic ancestry groups to consider effects of population substructure but did not consider the full range of admixture.

Nonetheless, it is important to bear in mind that we have undertaken the first attempt at benchmarking these popular methods at more stringent levels across both dyad and trio designs, across a multitude of modeling approaches and under different data types and structure. Here we provide some practical guidelines for an appropriate selection of methods to use in different potential scenarios present in consortium studies such as ECHO, or any other nuclear family-based study designs.

Data Availability Statement

The GENEVA data on clefts are publicly available on dbGaP (https://www.ncbi.nlm.nih.gov/gap/, study accession number phs000094.v1.p1).