Abstract
The human proteome contains a vast network of interacting kinases and substrates. Even though some kinases have proven to be immensely useful as therapeutic targets, a majority are still understudied. In this work, we present a novel knowledge graph representation learning approach to predict novel interaction partners for understudied kinases. Our approach uses a phosphoproteomic knowledge graph constructed by integrating data from iPTMnet, Protein Ontology, Gene Ontology and BioKG. The representations of kinases and substrates in this knowledge graph are learned by performing directed random walks on triples coupled with a modified SkipGram or CBOW model. These representations are then used as an input to a supervised classification model to predict novel interactions for understudied kinases. We also present a post-predictive analysis of the predicted interactions and an ablation study of the phosphoproteomic knowledge graph to gain an insight into the biology of the understudied kinases.
1. Introduction
Proteins are a fundamental building block of the complex molecular machinery employed by all living organisms. The collection of all the possible proteins that can be synthesized by an organism is known as the proteome1. Proteins interact with each other through distinct biochemical events to actuate the desired biological functions. Protein post-translational modification (PTM) is one such biochemical event that has played a major role in almost all the biological functions2.
Fundamentally, any given PTM event is made up of two members - an enzyme and a substrate. An enzyme is a protein responsible for facilitating the PTM event and the substrate is the protein undergoing the post-translational modification. Among all the types of PTM events, phosphorylation is the most common and well-studied and is implicated in a majority of cellular functions [3]. Phosphorylation is carried out by a class of enzymes known as kinases. Previously it was believed that the kinase-substrate interaction networks are fairly linear, and perturbation of a kinase would primarily affect its immediate substrate. But recent studies have shown that these interaction networks are highly interconnected and perturbation of a particular kinase or a substrate has the potential to affect large parts of the network [4].
With the advent of techniques such as mass spectrometry based high throughput proteomics, many new phosphorylation sites have been identified [5] but identifying kinases that phosphorylate these sites remains a challenging problem. Experimental studies on kinase-substrate interactions are time-consuming and expensive and most research has been focused on a small subset of the 550 protein kinases found in humans. Computational approaches that can accurately predict novel kinase-substrate interactions have the potential to increase our understanding of the human proteome. This increased understanding will in turn help accelerate identification of new therapeutic targets and the development of accompanying drugs to modulate these targets.
To this date, many tools have been developed to predict kinase-substrate interactions. Tools such as Scansite [6], NetPhospK [7], PPSP [8], GPS [9, 10] and PredPhosph [11] rely on the properties of protein sequences around the phosphorylation site also known as sequence motifs, to predict kinases most likely to be associated with the given phosphorylation site. But kinase-substrate interactions involve much more than sequence motifs and hence it is necessary to include contextual factors when making these predictions. Thus tools such as NetworKIN [12], PhosphoPICK [13], PhosphoPredict [14] and HeteSim [15] were developed that combine sequence and contextual information to make better predictions. But many of the above tools have significant limitations in terms of kinome coverage. This is partly due to the fact that these tools primarily rely on properties that can only be directly mapped to the kinases or substrates. Understudied kinases by their very nature have limited information and hence are not annotated with these properties making it difficult to use these tools.
Inspired by recent advancement in deep learning a new generation of tools are being developed to address these shortcomings. DeepKinZero [16] is a tool that takes inspiration from deep learning techniques in computer vision and employs a zero shot learning approach to transfer knowledge from well known kinases to understudied kinases. But similar to the first generation tools, it relies primarily on sequence information. LinkPhinder [17] takes a significantly different approach and formulates the task of predicting kinase-substrate interactions as a link-prediction task. It considers kinases, substrates and phosphorylation sites to be constituting a knowledge graph and uses knowledge graph completion algorithms to predict possible kinase-substrate interactions. A significant limitation of all the above tools is that they do not take advantage of the long range dependencies between kinases and substrates that are encoded in existing kinase-substrate interaction networks. In addition to this, they also fail to model the deeper biological connections that are only evident by looking at the vast body of biomedical knowledge being collected and organized in semantic databases such as Gene Ontology and Protein Ontology.
In recent years, there has been a significant increase in the amount of biological data. This has made it increasingly difficult to organize and derive knowledge from this data. Subsequently, semantic technologies that define a set of standards for organizing and linking data were adopted. Using such linked (semantic) data can provide us with knowledge that cannot be derived purely from protein sequences. They can help us craft algorithms that can truly capture the biological roles of kinases and substrates. In this work we present a novel approach of learning from semantic data. Since the goal of this work was to investigate if knowledge graph/semantic data can be useful in predicting kinase-substrate interactions we simplified the task by only predicting interactions at the kinase/substrate level instead of the kinase/phosphorylation site level. Nevertheless, we think that the kinase/substrate representations learned by our approach can be combined with tools working at sequence level such as DeepKinZero to obtain better predictions at finer resolutions.
2. Methods
2.1. Data
We construct the knowledge graph by including data from iPTMnet3, Protein Ontology (PRO)4, Gene Ontology (GO)5 and BioKG6. To begin with, we use human PTM data [Taxon code - 9606] from iPTMnet to construct a kinase-substrate interaction network. The iPTMnet data contains 26411 phosphorylation PTM events. Any given kinase-substrate pair can have multiple PTM events. We normalize these events to triples in the form of kinase → phosphorylates → substrate.
PRO defines protein classes and represents the hierarchical relationships among proteins, protein forms (proteoforms) and protein complexes within and across species7. The PRO data is arranged in the form of an acylic directed graph. Thus using PRO data we construct triples in the form of kinase/substrate → is_a → pro_entity and inverse triples in the form of pro_entity → has_a → kinase/substrate extending all the way to the root of the PRO tree to capture evolutionary relationships among the proteins encoded by the PRO ontology.
Gene Ontology organizes biological knowledge by specifying a controlled vocabulary to precisely describe the biological processes, molecular functions and subcellular localizations associated with gene products. Using GO we create triples in the form of kinase/substrate → annotated_with → go_term. Since GO terms themselves are arranged in the form of a directed acyclic graph (DAG), we create new triples in the form go_term_a → is_a → go_term_b extending uptil the root of the GO tree to capture the knowledge defined by the relational heirarchy of GO.
Similar to the above-mentioned data sources, there are many more data sources that can be integrated in our knowledge graph. Rather than performing this integration ourselves, we decided to take advantage of the BioKG database6. The authors of BioKG database provide a framework to automatically integrate data from numerous biomedical databases. Since BioKG framework is geared towards drug discovery analysis we integrated only a subset of the biomedical databases. Specifically we include data from UniPROT8, Reactome9, KEGG10 and STRINGS-DB11. This resulted in addition of new triples with following relations - protein-pathway associations, protein-disease associations, protein-genetic disorder associations, disease-genetic disorder associations, disease-pathway associations, protein-complex assocations and complex-pathway associations to our knowledge graph.
Once the above knowledge graph was built, we used it as a data source to train a machine learning model to predict interactions for understudied kinases.
2.2. Data preparation
As mentioned in the previous section, we start with a kinase-substrate interaction network constructed using PTM data and then enrich it with auxillary data to construct our knowledge graph. When training a machine learning model it is neccessary to ensure proper seperation of training, validation and testing data to prevent information leakage. Thus, even before we enrich the vanilla kinase-substrate network with auxillary data, we split the network into three subnetworks - training, validation and testing. The training network contains “kinase → phosphorylates → substrate” triples in addtion to the triples from auxillary data. Validation and testing networks contain only the kinase-substrate interaction triples in the form kinase → phosphorylates → substrate.
2.3. Knowledge graph learning approach
In recent years, many approaches to learn from knowledge graphs have been proposed. These approaches can be broadly grouped into four categories - 1) Tensor decomposition, 2) Geometric distance, 3) Deep learning and 4) Random Walk12. Tensor decomposition based approaches represent the entities and the relations as a giant 3D adjacency matrix (Tensor). This matrix is then decomposed into low dimensional vectors while still retaining the latent information about the graph structure and connectivity13,14. Geometric distance based approaches learn an embedding of the knowledge graph by representing the relation between the head and tail as a geometric transformation in the latent space15. Deep learning based approaches represent the entities and relations using a low dimensional embedding vector. Instead of deriving these embeddings using tensor decomposition or geometric factorization, these models use a neural network to optimize the embeddings to predict the probability of a triple in the knowledge graph being true or false16. Random walk based approaches take inspiration from advancements in natural language processing. They involve sampling a series of nodes (entities) from the knowledge graph. These series of nodes can be thought of as sentences in a language with every node representing a word in the sentence. These sentences are then used as an input corpus for a language model such as word2vec17 to learn a dense embedding for every node in the graph18.
A glaring short-coming of the random walk based approaches is that they do not take into account the triple structure of the knowledge graph. Specifically, existing methods such as DeepWalk18 and Node2Vec19 do not consider the directionality and the heterogeneity encoded by a triple when performing the random walk. They treat the relations in a knowledge graph as any other node in the graph. Hence, they cannot adequately capture the semantic meaning of the entities in the knowledge graph. To alay these shortcomings, alternative approaches that rely on metapaths have been proposed20. But contrary to the simpler approaches such as DeepWalk and Node2Vec, the performance of metapath based approaches is highly dependent on the choice of metapath. Additionally, choosing a metapath requires an in-depth knowledge of the schema of the knowledge graph under study, further diminishing their utility.
Hence, in this work, we propose a modified random walk based approach that takes inspiration from DeepWalk18, one of the simplest knowledge graph learning algorithms, to learn a representation of kinases and substrates in our phosphoproteomic knowledge graph. The fundamental assumption of any random walk based approach is that entities with similar meaning occur in similar contexts. But in a knowledge graph, the context is not only defined by the connectivity, but also by the type and the direction of the relationships. Hence, our approach makes a slightly different assumption. It assumes that the heterogeneous knowledge graph is a superimposition of three distinct graphs. The first graph contains only head entities, the second graph contains only relations and the third graph contains only tail entities. [Figure 1]. The heterogeneous knowledge graph can then be thought of as a function of the latent interactions between the entities from each of these three sub-graphs. To model this function, we modify the manner in which random walks are performed. Instead of sampling a series of nodes using traditional random walks, we sample a series of “triples” by performing a Triple Walk. This series of triples is then used as an input to a modified skip gram model to learn an embedding of all the entities and relations in the knowledge graph.
Fig. 1.
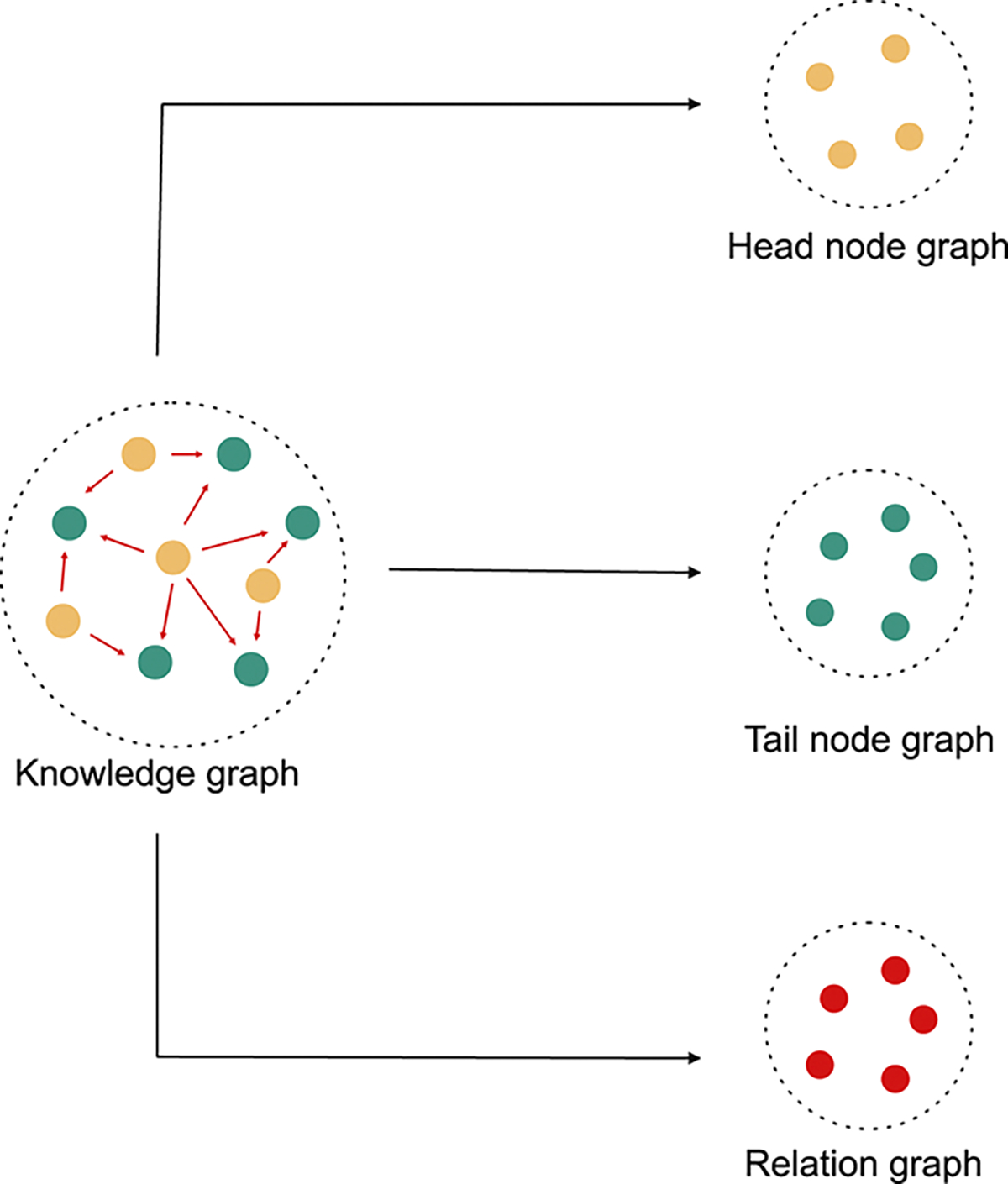
Knowledge graph represented as an overlapping graph of heads, relations and tails.
2.4. Deepwalk overview
Since our approach is inspired by DeepWalk approach, it is essential to understand all the steps that constitute the DeepWalk algorithm. On a very high level, the DeepWalk algorithm combines random walks on a graph with a language model such as Word2Vec17 to learn a vector representation of every node in the graph. Since the Word2Vec model plays a major role in the DeepWalk algorithm, it is essential to understand the steps involved in training a Word2vec model.
Word2Vec is a simple model used to learn dense vector embeddings of words21 in a given language. At its core it contains a single layered neural network that predicts if a particular word would occur in a given sentence. This task is similar to the task of filling the blanks in an incomplete sentence. For example, given an incomplete sentence - The quick brown fox _____ over the lazy dog, the word2vec model tries to predict a word that would occur in the blank space [Figure 2]. The word to be predicted is known as the target word and the words already present in the sentence are known as the context words. The target word can be either a positive_target or a negative_target. A positive_target is a word that is definitely known to “occur” in the given blank space. A negative_target is a word that is definitely known to “not occur” in the given blank space. The negative_target is created by randomly choosing a word from all the words constituting the vocabulary of the language. The length of the sentence is known as the window_size or the context_size of the model and the number of words in the entire corpus is known as the vocabulary of the language.
Fig. 2.
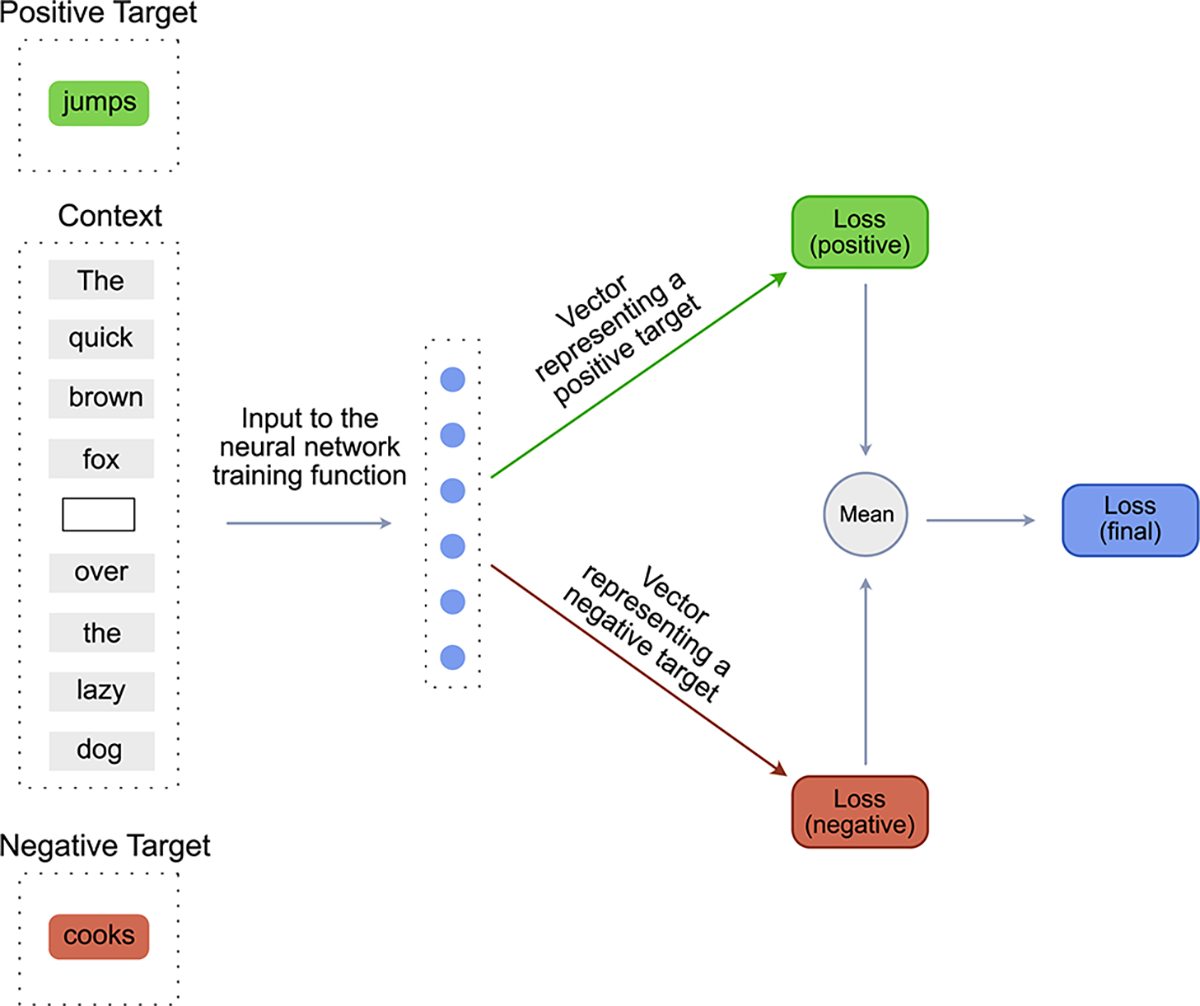
Word2vec model (CBOW) that predicts the target word given the context.
So to recapitulate, the inputs to a function training the Word2Vec model are the context, the positive_target and the negative_target [Figure 2]. This function then trains the model using the following three-step process.
The context words are used as an input to a single layered neural network to predict a vector representing the positive_target. The predicted vector is then compared with the vector of the ground truth positive word to calculate a positive_score. This score is then used to calculate a positive_loss.
The same context words, coupled with the same neural network are then used to predict a vector representing the negative_target. Then similar to step 1, the predicted vector is compared with the ground truth to calculate a negative_score. This score is then used to calculate a negative_loss.
The positive_loss and negative_loss are then combined using the mean function to calculate the final_loss. This final_loss is then used to backpropogate the errors and adjust the weights and biases of the neural network as well the embedding vectors of the context words.
The above process is repeated for every word in each sentence of the entire corpus. As the training progresses, the model learns which target words occur in which context. Once the model training is complete, the embeddings vectors of context words are retrieved to be used as a part of further downstream analysis.
Word2Vec model has two variants, CBOW (Continuous Bag of Words) and SkipGram. The model described above is the CBOW variant of the Word2Vec model. SkipGram variant is the exact inverse of the CBOW variant. In the SkipGram variant, instead of predicting a target_word, the model predicts a target_context. So the inputs to the training function of the SkipGram variant are the target_word, the positive_context and the negative_context [Figure 3]. The positive_context contains the words that are definitely known to “occur” around the target_word and negative_context contains the words that are definitely known to “not occur” around the target_word. The negative_context is created by randomly sampling words from the vocabulary of the language. The remaining steps in the training function are similar to the CBOW variant except for the inputs to the single layered neural network. Contrary to the CBOW variant, the input to the neural network is a target_word and the output is a tensor representing the context. This tensor is then compared with the tensor of the ground truth positive and negative contexts to obtain a positive and negative score. These scores are then used to calculate the respective losses, which are combined to get the final loss.
Fig. 3.
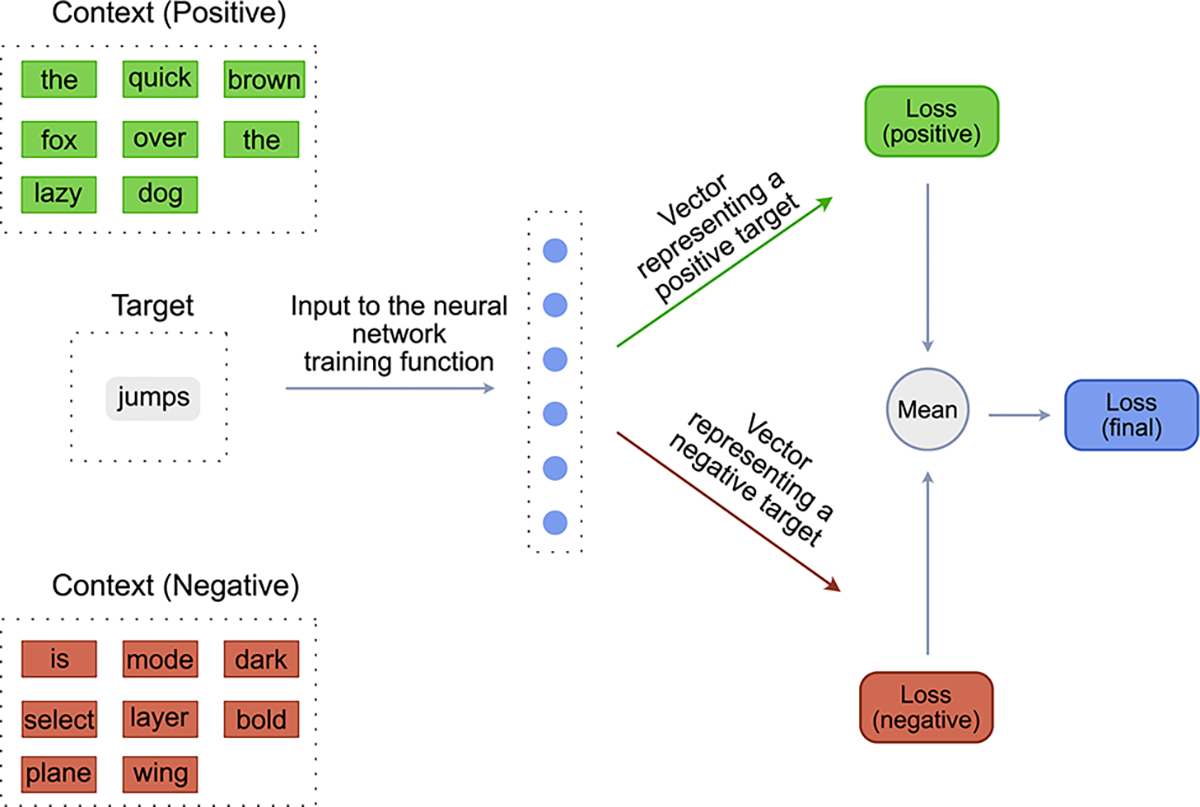
Word2vec model (SkipGram) that predicts the context given the target word.
The authors of the DeepWalk algorithm hypothesized that the language models work by sampling from a hidden unobservable language graph18. This means that every graph can be thought of as encoding the semantics of a hidden unobservable language. So, the first step of the DeepWalk algorithm is to perform short random walks on the graph to sample a series of nodes. The random walks performed in DeepWalk are a classical Markovian process22 i.e., the probability of selecting the next node in the walk is only dependent on the currently selected node. Now, these series of nodes can also be thought of as a series of words adding up to form a complete sentence. Thus performing N random walks on the graph can be thought of as sampling a set of N sentences from a graph. These sentences i.e., series of words are now used as an input to a language model such as the Word2Vec model to learn a dense vector representation of every node in the graph [Figure 4].
Fig. 4.
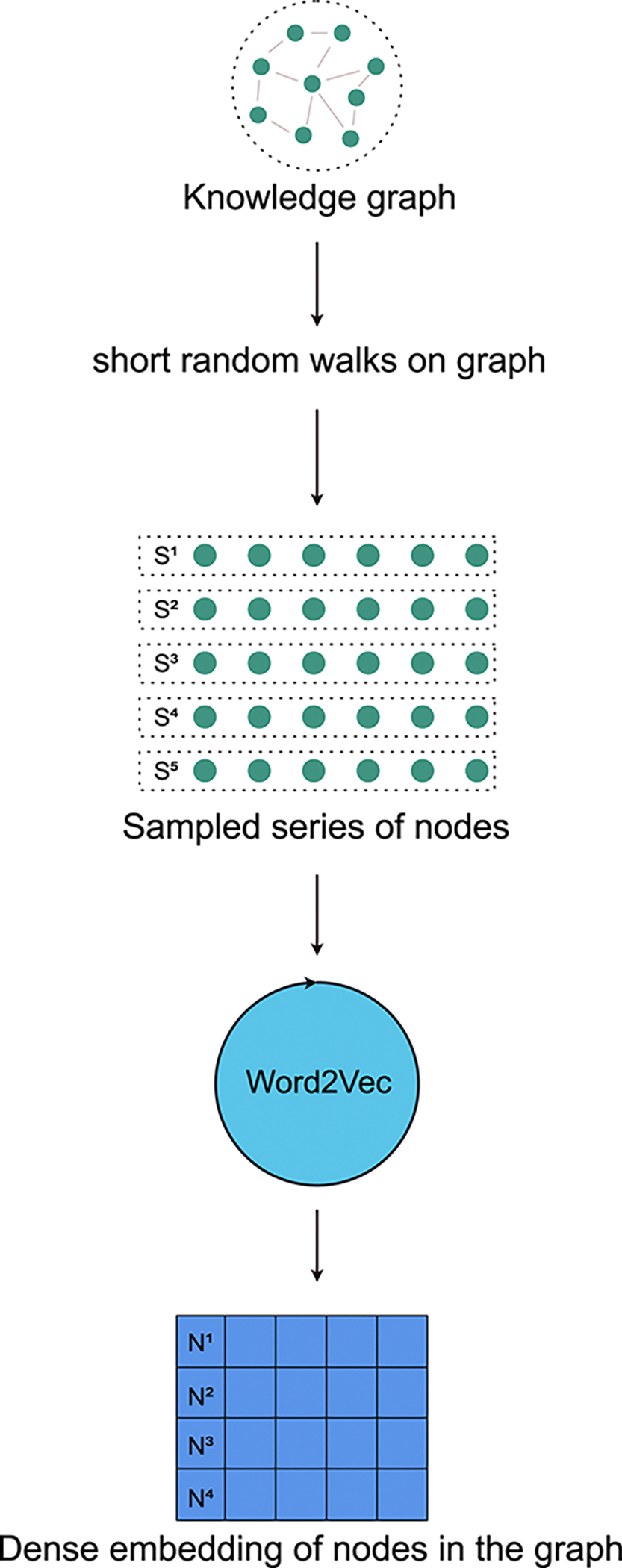
DeepWalk model
2.5. TripleWalk approach
As described earlier, a unit of information in a knowledge graph is encoded by a triple in the form of head → relation → tail. Thus, to learn an effective representation of a knowledge graph it is essential to consider this triple structure. The TripleWalk algorithm modifies the DeepWalk algorithm to effectively exploit this triple structure. It does so by modifying the process of performing the random walks and also the process of using these random walks to train the Word2Vec model.
In the DeepWalk approach of performing random walks, the directionality of the edges is not considered. At any point of time when the walker is on a head or a tail node, it has a choice of either selecting one of the tail nodes that come after a head node or one of the head nodes that come before the tail node. Since the walker does not take into account the directionality of the edges, it has an equal probability of choosing a head node or a tail node. If it samples a head node then it inadvertently ends up breaking the semantic organization of the underlying knowledge graph.
Contrary to the DeepWalk approach, the TripleWalk approach does not sample one node at a time, but samples one triple at a time. Thus, the probability of choosing the next triple in the walk is dependent only on the currently selected triple. Further, the TripleWalk approach also considers the directionality of the relation between triples. At any point of time, given a triple sequence T1 →T2 →T3 →T4 →T5, a triple walker at position T3 will only sample T4 and not T2. Thus, by sampling one triple at a time and by considering the directionality of the triple relations, the TripleWalk approach is able to preserve the semantic structure of the underlying graph when sampling a sequence to be used in the Word2Vec model.
Once these triple are sampled, the next step is to learn an embedding of entities that make up these triples. For this we lean on our assumption mentioned earlier, that considers a knowledge graph as a combination of three distinct graphs - head_graph, relation_graph and tail_graph that hold the heads, relations and tails respectively [1]. To model this assumption, the sampled triple sequence S = {(h1, r1, t1), (h2, r2, t2), (h3, r3, t3), (h4, r4, t4)} is split into three independent sequences holding heads (H = {(h1, h2, h3, h4)}), relations (R = {(r1, r2, r3, r4)}) and tails (T = {(t1, t2, t3, t4)}) respectively. These three independent sequences are then used to train a modified Word2vec model [5].
As described in section 2.4, the input to the function used to train Word2Vec model are the context, the positive_target and the negative_target. Thus, for every independent sequence, a context, a positive_target and a negative_target is created. This gives us a set of three contexts - head_context (Hc), relation_context (Rc) and tail_context (Tc), a set of three positive targets - head_pos_target (Hp), rel_pos_target (Rp) and tail_pos_target (Tp) and a set of three negative targets - head_neg_target (Hn), rel_neg_target (Rn) and tail_neg_target (Tn). All the above contexts and targets are then used as an input to a function used to train the Word2Vec model [Figure 6].
Fig. 6.
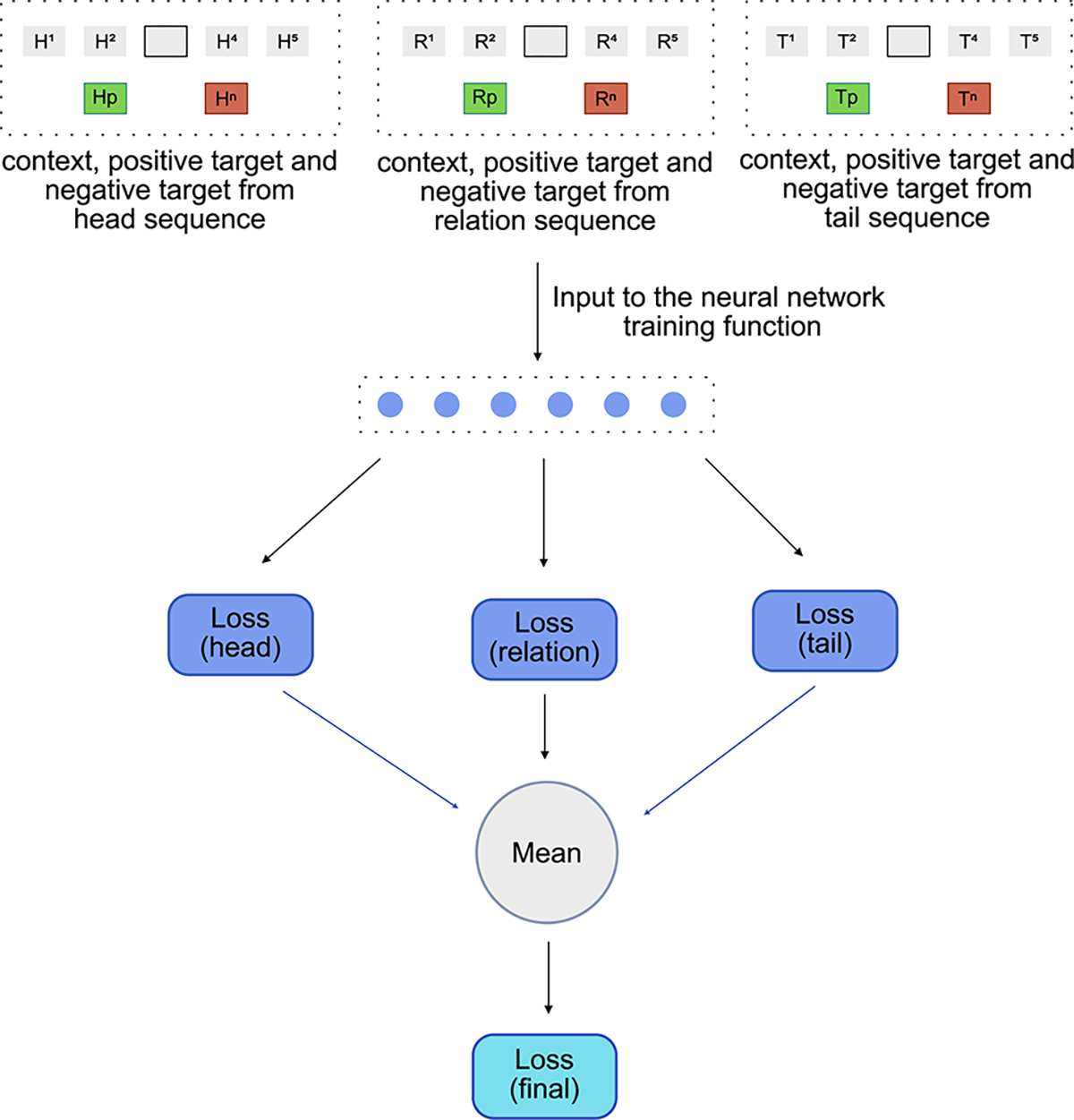
Modified Word2Vec model
The function used to train the Word2Vec model is similar to the one used in DeepWalk model. As described earlier, the DeepWalk training function optimizes the embedding vectors of the context nodes using a single layered neural network. Similar to the DeepWalk training function, the TripleWalk training function also contains a single layered neural network, but instead of optimizing a single context embedding, it jointly optimizes the three independent sets of context embeddings corresponding to the head, relation and tail contexts. To do so, it follows a four-step process
The head_context (Hc) along with the head_pos_target (Hp) and head_neg_target (Hn) are used to calculate a head_loss.
The relation_context (Rc) along with the rel_pos_target and rel_neg_target (Rn) are used to calculate a realtion_loss.
The tail_context (Tc) along with the tail_pos_target (Tp) and tail_neg_target (Tn)are used to calculate a tail_loss.
All these losses are then combined using the mean function to obtain a final_loss. This final_loss is then used to backpropogate the errors and adjust the weights and biases of the neural network as well the embedding vectors of all the three contexts.
The above process is repeated for every triple sequence sampled by the TripleWalk algorithm to minimize the final_loss. Once the training process is complete, the embedding vectors of the head context, relation context or the tail context are retrieved to perform further downstream analysis.
2.6. Supervised learning
The task of identifying new interactions in the kinase-substrate interaction network can be generalized to a binary classification task of predicting if a given interaction is true or false. For this, we use a classical supervised machine learning algorithm - Random Forest23. The input to the model is an embedding vector representing the target interaction and the output is a binary value representing the plausibility of the interaction being true or false. To construct an embedding vector denoting this interaction, we retrieved a list of all the kinase → phosphorylates → substrate triples from the knowledge graph. Then, in a given triple we retrieve the embedding vector for kinase entity from the head_context embeddings and for the substrate entity from the tail_context embeddings. Then according to the approach described by the authors of Node2Vec algorithm19, we combine these embeddings using the hadamard (⨀) operator to obtain the final interaction embedding vector .
2.7. Negative sampling
Since the supervised model is a binary classification model, we also need to have negative samples to represent the interactions that have a lower likelihood of being true. But adequate ground truth data about negative interactions is not available. There are existing databases such as negatome24 that provide a catalog of manually curated negative interactions, but we found that their coverage of negative interactions is not adequate. Hence, it is important to adopt a well-thought-out approach to generating negative samples to augement existing negative interaction data. Since knowledge graphs contain only positive samples, some approaches to generating negative samples have been proposed25. The most simple approach being corrupting a triple by randomly changing the head, relation or tail.
In this case, we were only interested in negative samples involving kinase-substrate interaction triples. Initially, we trained the supervised classification model using the naive negative sampling approach of corrupting the tails. The resulting model did not perform sufficiently (AU-ROC = 0.57). We hypothesized that the drop in performance was due to the fact that randomly corrupting the tails of triples did not yield samples that truly represented the underlying biology of a kinase-substrate interaction. Also, since the number of unknown kinase-substrate interactions is very high, there is an increased likelihood of true positive samples being labelled as negative samples. Hence, we decided to develop a better approach to generating negative samples. We assumed that if a kinase and a substrate were physically apart by being located in two distinct cellular components then the probability of them interacting is lower than if they were located in the same cellular component. To model this assumption, we generated negative samples using the following four-step process:
Create a filtered knowledge graph containing only kinase-substrate interaction triples and triples from the cellular component subtree of the GO ontology.
Generate an embedding of every kinase and substrate in terms of its subcellular location by performing graph representation learning on this knowledge graph.
Using this embedding, for every kinase sample N substrates that are as far away as possible in the embedding space by use cosine similarity to calculate the distance between a kinase and a substrate.
To balance out the possibility of the model being biased towards the subcellular location, combine the above sampled list with ground truth negative samples from negatome - a database containing manually curated negative samples24.
Finally, sample from the above list to create a definitive list of negative interactions.
After generating the negative samples using the above approach, we needed to verify if the generated negative samples contained substrates in cellular compartments that where distinct from kinases. Hence, we created a list of kinases that where located in the nucleus of the cell. Then we retrieved the negative interaction partners (substrates) for these kinases. We then visualized the embedding vectors of these kinases and substrates using a tSNE plot [Figure 7]. It can be observed that the nuclear kinases and the corresponding sampled negative substrates are fairly well seperated in the tSNE space.
Fig. 7.
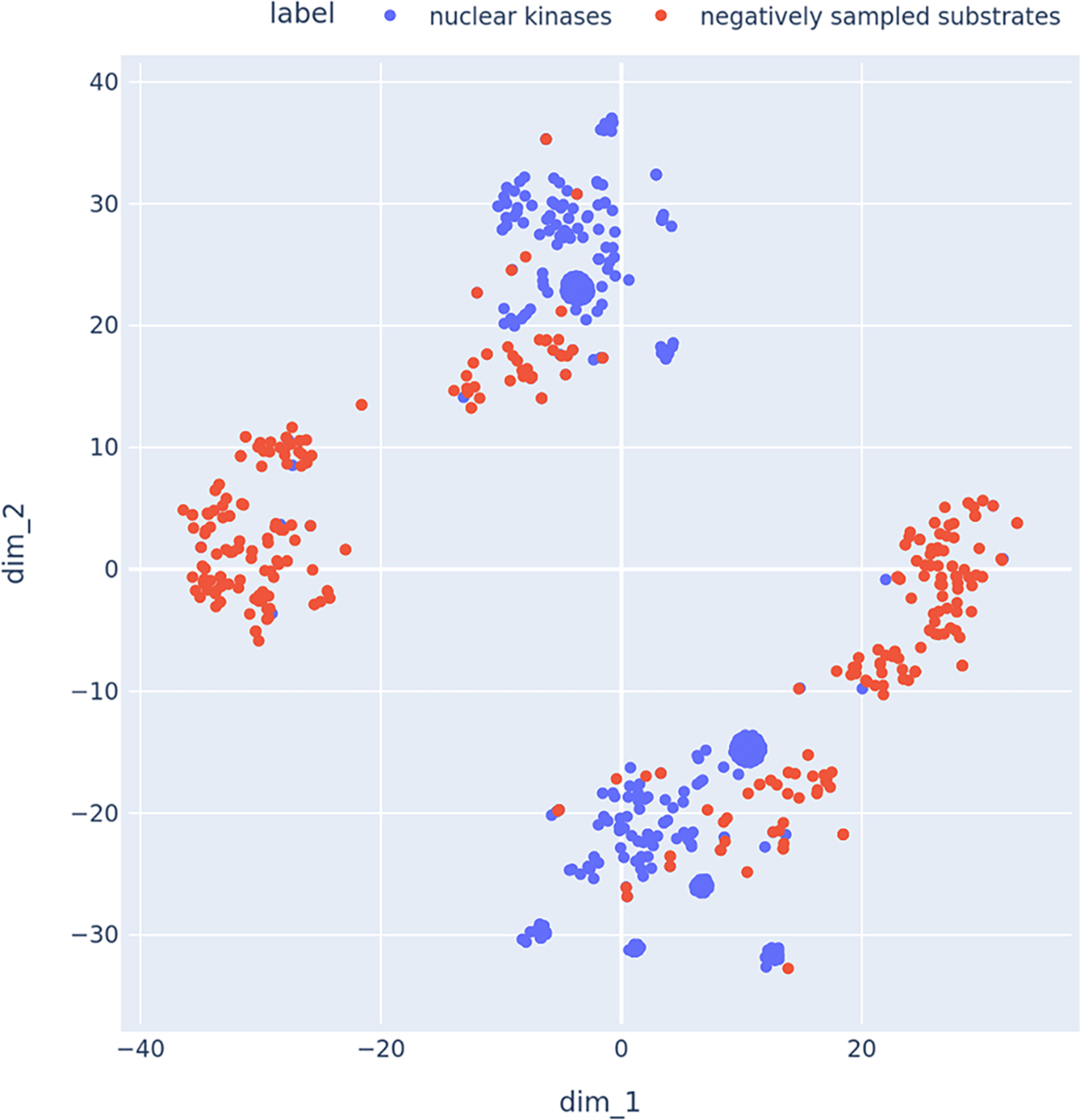
tSNE plot to visualize the embeddings of kinases and their analogous sampled substrates using the negative sampling technique described in section 2.7
2.8. Model training and evaluation
Our model training pipeline starts with a simple kinase-substrate interaction network containing only one type of triple : kinase → phosphorylates → substrate. We split this network into three subnetworks - training (60%), validation (20%) and testing (20%). We then augement the training network with auxillary triples to construct the full phosphoproteomic knowledge graph. This knowledge graph is then used to train the unsupervised component (Triple Walk model). The unsupervised component learns embeddings for every kinase and substrate in the phosphoproteomic knowledge graph. These entity embeddings are then passed to the supervised component (Random Forest model).
The input to the supervised component is a vector constructed by concatentating the embedding of a kinase and a substrate. This vector represents an interaction event between a kinase and a substrate. The output from the supervised component is a probability of the given kinase-substrate interaction being true. The validation network is used for hyperparameter tuning and the testing network is used to evaluate the final model performance [Figure 8]. We evaluate the model using Area Under Receiver Operating Characteristic Curve (AU-ROC), Precision and Recall [Table 3].
Fig. 8.
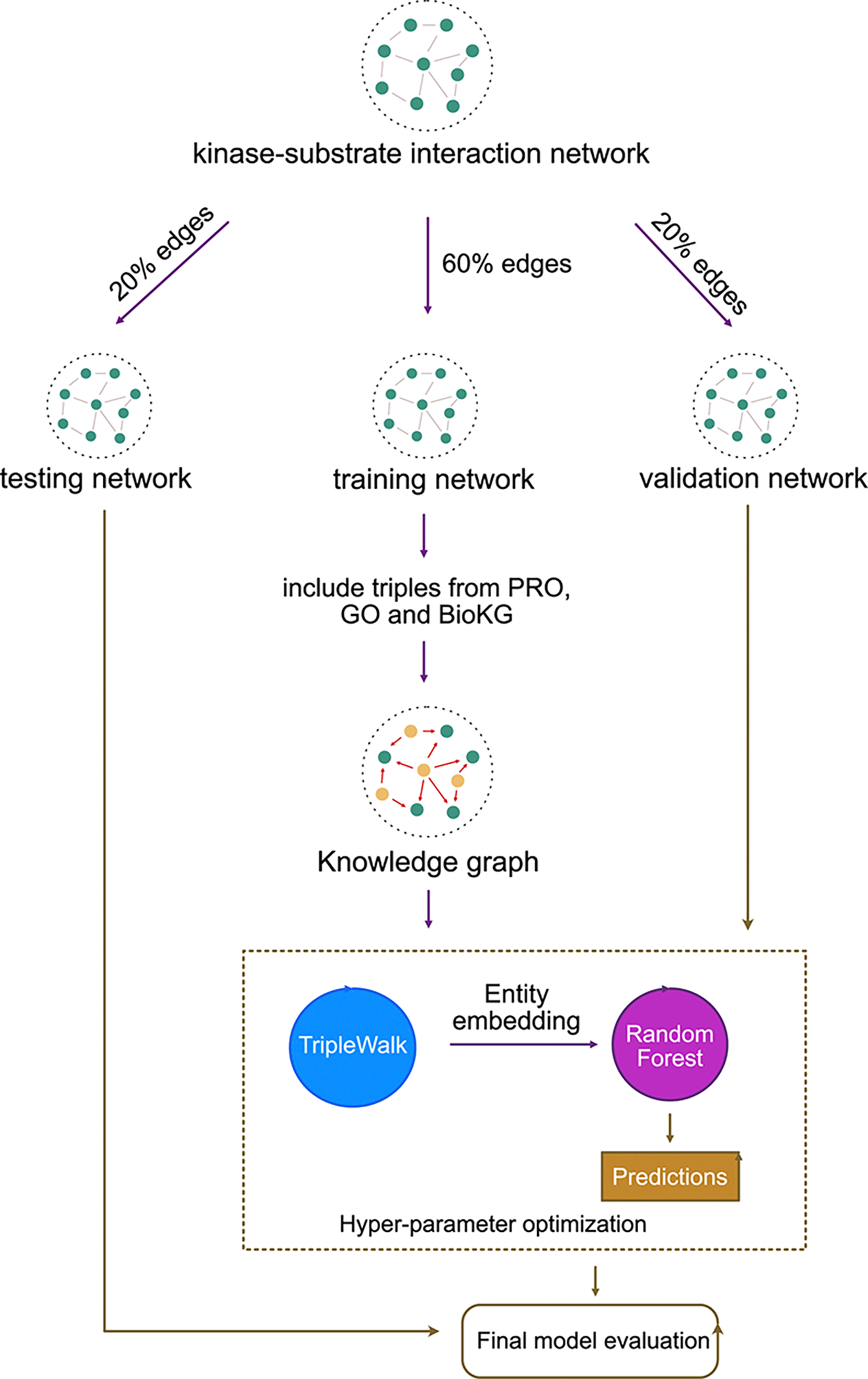
TripleWalk model training and hyperparameter optimization
Table 3.
Comparision of TripleWalk with existing kinase-substrate interaction prediction models.
| Model | AU-ROC | Precision | Recall |
|---|---|---|---|
| TripleWalk | 0.76 | 0.62 | 0.88 |
| LinkPhinder | 0.75 | 0.60 | 0.76 |
| NetPhospK | 0.52 | 0.61 | 0.17 |
| Scansite | 0.53 | 0.60 | 0.17 |
| NetworKIN | 0.55 | 0.59 | 0.36 |
2.9. Evaluation of unsupervised learning component
In addition to evaluating the final model, we also compare the unsupervised learning component (TripleWalk algorithm) with existing unsupervised knowledge graph learning methods. We compare our approach with two of the most commonly used random walk based approaches - DeepWalk18 and Node2vec19, one tensor decomposition based approach - DistMult26 and one distance based approach - TransE15. In addition to comparison with above methods, we also compare the SkipGram and the Continuous Bag of Words (CBOW) variants17 of all the random walk based methods. Finally, in addition to evaluating the interaction prediction performance, we also evaluate the embeddings on following tasks.
Kinase - Substrate classification : We formulate a binary classification task to classify kinases and substrates based on the learned embeddings. The classification task is a balanced classification task where we sample one substrate for each of the 408 human kinases. We then use the embeddings obtained by unsupervised learning to train a classifier to classify the entities as either a kinases or substrates.
Enzyme classification : All kinases can be generalized as enzymes. Enzymes are classified into six broad categories and numerous sub-categories based on the chemical reactions they catalyze. These enzyme categories are represented by an Enzyme Classification (EC) number. we use these EC numbers to create three sub-categories for kinases present in our kinase-substrate interaction network. We then use the embeddings of the kinases to formulate a one vs rest classification task to classify kinases into their respective categories.
3. Results
3.1. Model hyperparameters and performance
We optimize the parameters for the unsupervised component by using the Adaptive Asynchronous Halving Algorithm (ASHA)27 and for the supervised component using Random Grid Search algorithm. The best performing hyperparameters for the TripleWalk model are provided in table 1.
Table 1.
Best performing hyperparameters for the TripleWalk (SkipGram) model.
| Unsupervised (TripleWalk and SGNS) | |
| Parameter | Value |
| Batch Size | 128 |
| Learning Rate | 0.0004 |
| Embedding Dimension | 256 |
| Random walk length | 17 |
| Random walks per node | 6 |
| Early stopping delta (loss) | 0.1 |
| Early stopping patience (epochs) | 5 |
| Number of negative samples per positive sample | 2.0 |
| Supervised (Random Forest) | |
| Parameter | Value |
| Number of Estimators | 420 |
| Max depth | 176 |
| Split Criterion | Entropy |
| Max features | 128 |
| Min samples for split | 5 |
| Min samples at leaf | 4 |
The results from training all the models using the best hyperparameters are shown in table 2. To generate the results we split the kinase-substrate interaction network into K folds where K=10. This gave us 10 sets of training, validation and testing networks. Then for every fold we augemented the training network with auxillary triples and performed a complete training and evaluation run as shown in Figure 8. This gives us 10 scores where every score is slightly different from each other. The final score is the mean of all the 10 scores. The error measures indicate the standard deviation of the 10 scores. The data for training, validation and testing data for every fold is available in supplementary file 1 and the raw scores for evey fold are available in supplementary file 2. It can be observed that for our primary task of predicting a kinase-substrate interaction, the TripleWalk algorithm coupled with the SkipGram model outperforms all other types of algorithms. For the kinase classification task the TripleWalk algorithm coupled with CBOW model outperforms all other algorithms and for the enzyme classification task DeepWalk model coupled with the CBOW model gives the best results. It is worth noting that CBOW model has a much more consistent performance compared to the SkipGram model irrespective of the type of random walks. This might be due to the fact that in the CBOW model contrary to the SkipGram model, we predict the target word given the context words. This might have a regularising effect on the model, preventing it from learning the noise in the data and thus leading to a much more stable performance. It is also interesting to observe that Distmult, a tensor decomposition based approach shows competitive performance with random walk based methods, despite being a much simpler algorithm. The final predictions from our model are available in supplementary file 3.
Table 2.
Comparitive performance of unsupervised learning components on interaction prediction, kinase classification and enzyme classification
| Model | Interaction Prediction | Kinase classification | Enzyme classification | Model Type |
|---|---|---|---|---|
| TripleWalk (Skip Gram) | 0.79 (±0.01) | 0.67 (±0.03) | 0.59 (±0.02) | Directed Random Walk |
| TripleWalk (CBOW) | 0.71 (±0.03) | 0.84 (±0.02) | 0.68 (±0.03) | Directed Random Walk |
| DeepWalk (Skip Gram) | 0.60 (±0.01) | 0.57 (±0.01) | 0.61 (±0.02) | Undirected Random Walk |
| DeepWalk (CBOW) | 0.69 (±0.01) | 0.72 (±0.02) | 0.72 (±0.03) | Undirected Random Walk |
| Node2Vec (Skip Gram) | 0.62 (±0.01) | 0.60 (±0.04) | 0.62 (±0.03) | Biased Random Walk |
| Node2Vec (CBOW) | 0.71 (±0.01) | 0.70 (±0.03) | 0.67 (±0.03) | Biased Random Walk |
| Distmult | 0.63 (±0.01) | 0.78 (±0.02) | 0.67 (±0.04) | Tensor decomposition |
| TransE | 0.61 (±0.01) | 0.57 (±0.01) | 0.57 (±0.03) | Geometric distance |
After comparing our model with existing Random Walk based methods, we also compared our model with other kinase-substrate prediction models. Since many of the existing models do not publish their training, testing datasets and hyperparameters, it is difficult to perform a fair comparision among all the models. Hence for the purpose of this study, we used the predictions datasets published by authors of the LinkPhinder28 study. One thing to note is that compared to existing models, our model can only make predictions at the kinase-substrate level instead of the kinase-substrate-site level. The predictions from our model are in the form of a three column vector containing - [kinase, substrate, probability] and the predictions from existing models are in the form of a four column vector containing - [kinase, substrate, site, probability]. This means that for a given [kinase-substrate] pair our model will have only probability, but other models will have N probabilities corresponding to N sites. Hence, to make this comparision possible we reshaped the predictions data from other models to match our predictions data. To do so, we just selected the probability assigned to the top scoring site and used it as the probability of the given [kinase-substrate] pair interacting with each other.
The results from our comparision are shown in table 3 and the predictions used to generate the results are available in supplementary file 2. It can be observed that the knowledge graph based models such as TripleWalk and LinkPhinder show a significantly better performance compared to the sequence based models such as NetPhospK29 and Scansite30. Further, it can be observed that the TripleWalk model shows competitive performance compared to the LinkPhinder model despite not including sequence based features in the knowledge graph. This might be indicative of the fact that it would be beneficial to combine the knowledge graph construction approach proposed by LinkPhinder with the knowledge graph learning algorithm proposed by TripleWalk to further improve the performance.
3.2. Ablation Study
After building our models, we wanted to understand the factors that contribute to the improved predicitve performance. Model interpretability can be achieved by either building simpler models that are intrinsicly explainable or by post predictive analysis of the trained models. Since our framework consists of multiple models working together, the simplest approach to achieving interpretability in our system would be to quantify the change in predictive performance on changing the input data. For this we follow a two-part approach. In the first part we remove only a particular set of triples while keeping all other triples in knowledge graph. We then train the model using the hyperparameters shown in Table 1. In the second part, we keep triples related to only a particular subset of knowledge graph while removing all other triples.
Table 4 and Table 5 show the relative performance of models trained on specific subsets of the knowledge graph. It can be observed that on removing triples related to BIOKG while keeping triples related GO and PRO ontologies leads to a modest drop in performance. On the other hand training models with only the BIOKG triples without any ontology information leads to a pretty significant drop in performance. Further, training models with only GO or only PRO ontologies leads to a pretty significant increase in performance.
Table 4.
(Part A) Abalation study showing relative importance when a set of triples are removed from KG
| Data | Interaction Prediction |
|---|---|
| BIOKG complex (removed) | 0.75 (±0.01) |
| BIOKG pathways (removed) | 0.77 (±0.01) |
| BIOKG diseases (removed) | 0.78 (±0.01) |
| PRO (removed) | 0.79 (±0.01) |
| GO biological process (removed) | 0.79 (±0.03) |
| GO molecular function (removed) | 0.79 (±0.01) |
| COMPLETE KG | 0.79 (±0.01) |
Table 5.
(Part B) Abalation study showing relative importance when including only one set of triples in KG.
| Data | Interaction Prediction |
|---|---|
| BIOKG complex (only) | 0.60 (±0.02) |
| BIOKG Pathways (only) | 0.61 (±0.02) |
| BIOKG Diseases (only) | 0.63 (±0.02) |
| GO Biological Process (only) | 0.84 (±0.01) |
| GO Molecular Function (only) | 0.83 (±0.01) |
| PRO (only) | 0.82 (±0.01) |
| COMPLETE KG | 0.79 (±0.01) |
These results though interesting, are not entirely suprising. When we integrated the GO and PRO ontology information into our knowledge, we included the triples denoting relations all the way up to the root node of the ontology. This allowed our model to learn a much better representation of kinases and substrates in terms of their shared evolutionary, molecular and functional ancestory. BIOKG on the other hand includes triples that denote relationships only at the leaf node without following them up the ontology tree. Thus, even though it brings a lot of information, it is only useful in conjunction with a more complete picture provided by the ontologies.
3.3. Functional enrichment analysis
After validating our frameworks predictive performance, we studied the highest confidence predictions for kinases with the least amount of information. We retrieved the list of understudied kinases from Illuminating the Druggable Genome project (IDG)31. This gave us a list of 144 potenitally understudied kinases. We further filtered these kinases to only include the kinases that have at-most two recorded interactions in the iPTMnet database. This gave us a list of 68 kinases that are potentially understudied with respect to both IDG and iPTMnet. We then used the PredKinKG framework to predict novel interactions for these kinases. We filtered the predictions to only include high confidence predictions by setting the probability score cutoff at 0.95. Below we present the functional enrichment analysis of Q02779 (MAP3K10) using its 188 novel predicted substrates.
Since the target kinase is understudied and its biological functions is poorly understood, we hypothesized that studying the functions of the predicted substrates may provide us with clues about its biological roles. For this we perform a GO enrichment analysis using STRING DB11. Table 6 provides an overview of the top five GO terms (according to strength and FDR) enriched for every GO sub-ontology.
Table 6.
Enriched GO terms for Q02779 (MAP3K10) interaction partners
| Biological Process | |||
| GO:ID | DESCRIPTION | STRENGTH | FDR |
| GO:0090240 | Positive regulation of histone h4 acetylation | 1.65 | 0.005 |
| GO:0070601 | Centromeric sister chromatid cohesion | 1.65 | 0.005 |
| GO:0090400 | DNA ligation involved in DNA repair | 1.60 | 0.00091 |
| GO:0006978 | DNA damage response, signal transduction by p53 class mediator resulting in transcription of p21 class mediator | 1.45 | 0.0019 |
| GO:0042771 | Intrinsic apoptotic signaling pathway in response to dna damage by p53 class mediator | 1.24 | 0.0014 |
| Molecular Function | |||
| GO:ID | DESCRIPTION | STRENGTH | FDR |
| GO:0031490 | Chromatin dna binding | 1.03 | 0.0003 |
| GO:0070491 | Repressing transcription factor binding | 1.00 | 0.0014 |
| GO:0019901 | Protein kinase binding | 0.78 | 9.3E-15 |
| GO:0051721 | DNA-binding transcription factor binding | 0.78 | 6.02E-08 |
| GO:0061629 | RNA polymerase II-specific DNA-binding transcription factor binding | 0.75 | 4.32E-05 |
| Cellular Component | |||
| GO:ID | DESCRIPTION | STRENGTH | FDR |
| GO:0005719 | Lateral element | 1.48 | 0.0013 |
| GO:0005721 | Pericentric heterochromatin | 1.40 | 0.0003 |
| GO:0000778 | Condensed nuclear chromosome kinetochore | 1.37 | 0.0029 |
| GO:0000780 | Condensed nuclear chromosome, centromeric region | 1.24 | 0.0012 |
| GO:0051233 | Spindle midzone | 1.16 | 0.0025 |
GO enrichment analysis of the interaction network of Q02779 (MAP3K10) suggests that it might play an important role in the maintainence and upkeep of the cellular DNA and regulation of DNA transcription. We can observe that the GO term - GO:0090240 (Positive regulation of histone h4 acetylation) has the highest enrichment strength. Histone-H4 is a part of the nucleosome complex which is one of the fundamental structures related to DNA organization in eukaryotes. Acetylation of Histone-H4 is associated with a relaxation of the nuclear chromatin leading to an increased transcription factor binding32 and recruitement of protein complexes for repair of double-stranded breaks in the DNA33. In addition to histone acetylation, we can also observe that several GO terms related to DNA damage and repair are enriched: GO:0090400 (DNA ligation involved in DNA repair), GO:0006978 (DNA damage response, signal trans- duction by p53), GO:0042771 (Intrinsic apoptotic signaling pathway in response to dna damage by p53 class mediator). Analayzing the GO terms related to cellular component, it is evident that the interaction partners of Q02779 (MAP3K10) are mostly located in the nucleus near the chromosomes thus further cementing its role in DNA repair and transcription.
4. Discussion and Future work
In this work we have presented our framework for learning from a heterogenous knowledge graph to predict substrates for understudied kinases. We build a kinase-substrate knowledge graph by integrating data from ontologies such as GO and PRO and existing knowledge graph such as BIOKG. We then developed a novel knowledge-graph representation learning approach to learn better representations of kinases and substrates in this knowledge graph. Unlike many existing approaches, our framework can take advantage of semantic data from existing databases to exploit the knowledge of well studied kinases to make predictions for understudied kinases. We also perform an ablation study to quantify the relative importance of various components of our knowledge graph. We found that the heirarchical information from ontologies in combination with the factual information from existing knowledge graphs contributes significantly to learning a better representation of kinases and substrates.
A significant advantage of our methods over existing methods is the simplicity of the data representation and the simplicity of learning from this data representation. Existing machine learning systems require complex preprocessing and data transformation before the data is used for model training. These data transformations take a lot of manual effort and also have the potential to influence the model performance if done incorrectly. In our work, we present an alternative approach. We arrange the data in a very simple form containing only a list of triples. Each triple represent a discrete fact about the real world. We then propose a very simple random walk based algorithm to learn from this data. Since random walk based methods do not require the user to have any knowledge about the semantics or the structure of the underlying graph, our approach allows the user to scale their analysis without spending a lot of manual effort on studying the semantics of the underlying data. This property also means that our approach can be easily repurposed to target alternative domains. For example, the user could change the kinase-substrate knowledge graph to include only mouse data and thus repurpose the system to predict kinase-substrate interactions in mouse models. The user can also use our triple walk algorithm to learn a representation of knowledge graphs in a completely different domains such as social-networks, citation-networks or computer networks by using our publicly available python package34.
A significant shortcoming of our approach is that it can make predictions only at kinase/substrate level and not at the kinase/phosphorylation site level. Thus, as a next step of our study we plan to extend our model to make predictions at the phosphorylation site level by integrating with the approach proposed by Deznabi et al. in their DeepKinZero model. In addition to extending to model to site level, we also plan to integrate attention mechanism in our unsupervised knowledge graph learning component to get a better insight into the factors that contribute to learning a good representation of kinases and substrates.
Since the goal of this work was to develop a system to utilize semantic data (knowledge graphs) for the purpose of predicting kinase-substrate interactions, we did not perform an in depth comparision with existing kinase-substrate interaction prediction tools but only a superficial comparision as shown in Table 3. Alternatively, since we proposed a new knowledge graph learning algorithm that exploits the triple structure of the graph, we performed an in-depth comparision with existing knowledge graph learning algorithms [Table 2]. A direct comparison between our tool and the existing tools is not possible due to the differences in the data used for training the algorithms used in these tools. The data for positive samples is readily available from established databases, but data about negative samples is not readily available. Thus, every tool uses its own method to generate negative samples which complicates the comparision. A comprehensive evaluation will require a more focused approach that uses a standardized dataset with properly specified training, testing splits and negative samples. Since developing such a dataset is a non-trivial task, we plan to perform this comparision as its own independent study.
Supplementary Material
Fig. 5.
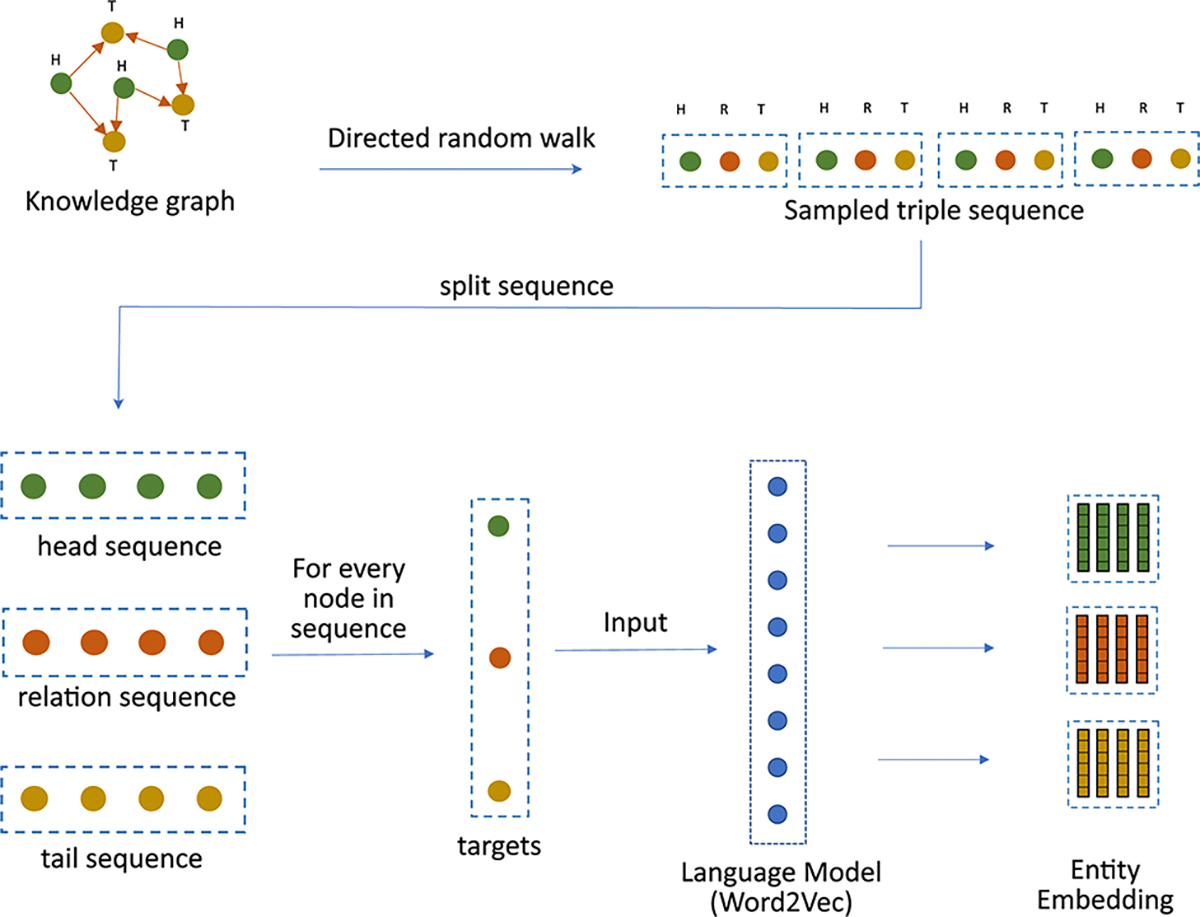
TripleWalk model
Acknowledgements
This work has been supported by the National Institutes of Health (Grant-R35GM141873) and Sigma Xi Grants in Aid of Research (Grant-G20201001105037737). We would also like to acknowledge the Data Science Institute and Center for Bioinformatics and Computational Biology at University of Delaware for providing computing resources through the Caviness and Biomix high performance computing clusters respectively.
Footnotes
Conflicts of interest
There are no conflicts to declare
Data availablility
The data and code used to perform the above analysis can be found at : https://github.com/udel-cbcb/ikg_v2_public.git. The code for the triple walk algorithm can be found at: https://github.com/udel-cbcb/triple_walk.git. The training, testing and validation data are available in supplementary file 1, the evaluation scores are available in supplementary file 2 and the predictions from the final model are available in supplementary file 3.
References
- 1.Paik Y-K, Jeong S-K, Omenn GS, Uhlen M, Hanash S, Cho SY, Lee H-J, Na K, Choi E-Y, Yan F, Zhang F, Zhang Y, Snyder M, Cheng Y, Chen R, Marko-Varga G, Deutsch EW, Kim H, Kwon J-Y, Aebersold R, Bairoch A, Taylor AD, Kim KY, Lee E-Y, Hochstrasser D, Legrain P and Hancock WS, Nature Biotechnology, 2012, 30, 221223. [DOI] [PubMed] [Google Scholar]
- 2.Uversky V, in Posttranslational Modification, Elsevier, 2013, p. 425430. [Google Scholar]
- 3.Huang H, Arighi CN, Ross KE, Ren J, Li G, Chen S-C, Wang Q, Cowart J, Vijay-Shanker K and Wu CH, Nucleic Acids Research, 2018, 46, D542D550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Natale DA, Arighi CN, Blake JA, Bona J, Chen C, Chen S-C, Christie KR, Cowart J, DEustachio P, Diehl AD, Drabkin HJ, Duncan WD, Huang H, Ren J, Ross K, Ruttenberg A, Shamovsky V, Smith B, Wang Q, Zhang J, El-Sayed A and Wu CH, Nucleic Acids Research, 2017, 45, D339D346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hill DP, Smith B, McAndrews-Hill MS and Blake JA, BMC Bioinformatics, 2008, 9, S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Walsh B, Mohamed SK and Nováek V, Proceedings of the 29th ACM International Conference on Information & Knowledge Management, 2020, p. 31733180. [Google Scholar]
- 7.Arighi CN, Drabkin H, Christie KR, Ross KE and Natale DA, Methods in Molecular Biology (Clifton, N.J.), 2017, 1558, 5778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.TheăUniProtăConsortium, Nucleic Acids Research, 2017, 45, D158D169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jassal B, Matthews L, Viteri G, Gong C, Lorente P, Fabregat A, Sidiropoulos K, Cook J, Gillespie M, Haw R, Loney F, May B, Milacic M, Rothfels K, Sevilla C, Shamovsky V, Shorser S, Varusai T, Weiser J, Wu G, Stein L, Hermjakob H and DEustachio P, Nucleic Acids Research, 2019, gkz1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kanehisa M, Nucleic Acids Research, 2000, 28, 2730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Szklarczyk D, Gable AL, Lyon D, Junge A, Wyder S, Huerta-Cepas J, Simonovic M, Doncheva NT, Morris JH, Bork P, Jensen LJ and Mering C, Nucleic Acids Research, 2019, 47, D607D613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alshahrani M, Thafar MA and Essack M, PeerJ Computer Science, 2021, 7, e341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ji Y, Wang Q, Li u. and Liu J, IEEE Access, 2019, 7, 162950162990. [Google Scholar]
- 14.Rabanser S, Shchur O and Günnemann S, arXiv:1711.10781 [cs, stat], 2017. [Google Scholar]
- 15.Bordes A, Usunier N, Garcia-Duran A, Weston J and Yakhnenko O, Advances in neural information processing system, 2013, 9. [Google Scholar]
- 16.Dettmers T, Minervini P, Stenetorp P and Riedel S, Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32, 20–30. [Google Scholar]
- 17.Mikolov T, Chen K, Corrado G and Dean J, arXiv:1301.3781 [cs], 2013. [Google Scholar]
- 18.Perozzi B, Al-Rfou R and Skiena S, Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, 2014, p. 701710. [Google Scholar]
- 19.Grover A and Leskovec J, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, p. 855864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dong Y, Chawla NV and Swami A, Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2017, p. 135144. [Google Scholar]
- 21.Almeida F and Xexéo G, arXiv:1901.09069 [cs, stat], 2019. [Google Scholar]
- 22.Bellman R, Indiana University Mathematics Journal, 1957, 6, 679684. [Google Scholar]
- 23.Breiman L, Machine Learning, 2001, 45, 532. [Google Scholar]
- 24.Blohm P, Frishman G, Smialowski P, Goebels F, Wachinger B, Ruepp A and Frishman D, Nucleic Acids Research, 2014, 42, D396D400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kotnis B and Nastase V, arXiv:1708.06816 [cs], 2018. [Google Scholar]
- 26.Yang B, Yih W.-t., He X, Gao J and Deng L, arXiv:1412.6575 [cs], 2015. [Google Scholar]
- 27.Li L, Jamieson K, Rostamizadeh A, Gonina E, Hardt M, Recht B and Talwalkar A, arXiv:1810.05934 [cs, stat], 2020. [Google Scholar]
- 28.Nováek V, McGauran G, Matallanas D, Vallejo Blanco A, Conca P, Muñoz E, Costabello L, Kanakaraj K, Nawaz Z, Walsh B, Mohamed SK, Vandenbussche P-Y, Ryan CJ, Kolch W and Fey D, PLoS Computational Biology, 2020, 16, e1007578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Blom N, Sicheritz-Pontén T, Gupta R, Gammeltoft S and Brunak S, PROTEOMICS, 2004, 4, 16331649. [DOI] [PubMed] [Google Scholar]
- 30.Obenauer JC, Cantley LC and Yaffe MB, Nucleic Acids Research, 2003, 31, 36353641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.2015, https://ncats.nih.gov/idg.
- 32.Vettese-Dadey M, Grant PA, Hebbes TR, Crane-Robinson C, Allis CD and Workman JL, The EMBO Journal, 1996, 15, 25082518. [PMC free article] [PubMed] [Google Scholar]
- 33.Dhar S, Gursoy-Yuzugullu O, Parasuram R and Price BD, Philosophical Transactions of the Royal Society B: Biological Sciences, 2017, 372, 20160284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gavali S, triple-walk: A pytorch extension library to perform triple walks on knowledge graphs, https://pypi.org/project/triple-walk/.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data and code used to perform the above analysis can be found at : https://github.com/udel-cbcb/ikg_v2_public.git. The code for the triple walk algorithm can be found at: https://github.com/udel-cbcb/triple_walk.git. The training, testing and validation data are available in supplementary file 1, the evaluation scores are available in supplementary file 2 and the predictions from the final model are available in supplementary file 3.


