Abstract
Time-frequency representations of electroencephalographic signals lend themselves to granular analysis of cognitive and psychological processes. Characterizing developmental trajectories of time-frequency measures can thus inform us about the development of the processes involved, as well as correlated traits and behaviors. We decomposed EEG activity in a large sample of individuals (N = 1692; 917 females) assessed at approximately three-year intervals from the age of 11 to their mid-20s. Participants completed an oddball task that elicits a robust P3 response. Principal component analysis served to identify the primary dimensions of time-frequency energy. Component loadings were virtually identical across assessment waves. A common and stable set of time-frequency dynamics thus characterized EEG activity throughout this age range. Trajectories of change in component scores suggest that aspects of brain development reflected in these components comprise two distinct phases, with marked decreases in component amplitude throughout much of adolescence followed by smaller yet significant rates of decreases into early adulthood. Although the structure of time-frequency activity was stable throughout adolescence and early adulthood, we observed subtle change in component loadings as well. Our findings suggest that striking developmental change in event-related potentials emerges through gradual change in the magnitude and timing of a stable set of dimensions of time-frequency activity, illustrating the usefulness of time-frequency representations of EEG signals and longitudinal designs for understanding brain development. In addition, we provide proof of concept that trajectories of time-frequency activity can serve as potential endophenotypes for childhood externalizing psychopathology and alcohol use in adolescence and early adulthood.
Keywords: time-frequency activity, adolescent development, endophenotypes, alcohol use, puberty, principal component analysis
2. Introduction
Understanding change in neural systems can help us characterize both the normative developmental trajectories of psychological processes and how variations in such trajectories contribute to the emergence of psychopathology or problematic behaviors. Time-frequency analysis of electroencephalographic signals (EEG) represents a useful tool in this endeavor. It is a signal processing method that decomposes EEG signals into fine-grained temporally- and spectrally-varying subcomponents, which in turn may better reflect cognitive processes than event-related potential (ERP) components (Donner and Siegel, 2011; Karakaş and Barry, 2017). The developmental trajectories of time-frequency features can illuminate the developmental course of important cognitive and psychological processes, as well as aspects of brain development more generally, such as whether change is primarily linear, such that change occurs at a constant rate over time, or nonlinear. If nonlinear, is it curvilinear, reflecting a largely continuous growth process, or does it comprise discrete phases? Characterizing the developmental trajectories of EEG activity associated with different cognitive, psychological and psychopathological processes can thus add important insights to this literature.
The P3 has attracted considerable interest in recent years as a means of studying age-related differences in neural correlates of cognitive processing (Riggins and Scott, 2020). This ERP component, typically elicited in the detection of rare target stimuli, is arguably the most studied measure in human cognitive electrophysiology and psychophysiological endophenotype research (Iacono et al., 2017; Polich, 2007). However, the P3 is not a unitary component (cf. Johnson, 1986); it is sometimes referred to as the late positive complex (e.g., Dien et al., 2004). The P3 appears to reflect an amalgamation of cognitive processes, including decision making, signal matching, stimulus-response mappings, attention and working memory (Barry et al., 2016; Polich, 2007; Verleger, 2020), making it difficult to draw firm conclusions regarding which specific processes might be reflected in age-related differences in P3 amplitude. Time-frequency analysis offers a potential solution to this conundrum. Research using time-frequency methods has shown that the P3 is a weighted mixture of at least two distinct processes – theta- and delta-band activity (Karakaş et al., 2000a, 2000b; Kolev et al., 1997) – that vary with respect to topographic distribution, EEG characteristics and associations with cognitive phenomena (Demiralp et al., 2001; Harper et al., 2017; Polich, 2007). Time-frequency analysis of EEG activity related to the P3 may therefore permit a fine-grained and informative approach to studying developmental change in the neural correlates of cognitive processes.
The majority of research into time-frequency activity in children and adolescents has used a cross-sectional design (see Malone et al., 2021 for a recent summary). In the aggregate, these studies indicate that aspects of cognitive control and other cognitive processes are reflected in specific time-frequency features, suggesting that characterizing developmental trajectories of those features can inform us about the development of the associated processes (Malone et al., 2021). Although not without limitations, longitudinal designs are indispensable for studying individual change, rather than age-related differences in mean level. Furthermore, longitudinal designs can assess whether developmental trajectories are modulated by individual characteristics, such as sex or genotype (Chorlian et al., 2017, 2015), or external influences, such as substance use and abuse. Despite these benefits, only one longitudinal study of time-frequency activity spanning more than a single year has been published, to our knowledge. Chorlian and colleagues (2015) examined theta activity eliciited by an oddball task during a time window chosen to coincide with the P3 response. They observed decreases in theta power elicited by a novelty oddball task throughout adolescence and early adulthood, with striking sex differences in the pattern of change.
Although informative, these results leave unexplored activity in frequency ranges other than theta. The oddball P3 is most prominent at more posterior sites, such as Pz, and delta activity is the most prominent influence on posterior P3 responses (e.g., see Figure 1 in Karakaş et al., 2000a). Reductions in parietal P3 amplitude constitute a particularly robust endophenotype for externalizing psychopathology, such as antisocial behavior and personality and substance abuse (Hicks et al., 2007; Iacono et al., 2002; Patrick et al., 2006). Understanding trajectories of change in endophenotypes is likely to enhance our understanding of the endophenotype itself (Iacono and Malone, 2011). Moreover, developmental trajectories may themselves constitute useful endophenotypes (Iacono et al., 2017). Trajectories can be estimated with greater precision than cross-sectional snapshots of an endophenotype, and they can inform us about timing of change in trajectory or trajectory shape, which may shed light on the nature of the endophenotype and the psychological, endocrinological or neural mechanisms it reflects. Characterizing the trajectories of time-frequency representations of the EEG activity associated with the parietal P3, particularly activity in the delta and slow theta range, offers the potential to add to our understanding of psychopathology and psychopathology risk.
We conducted the current investigation to address two broad aims. The first was to characterize developmental trajectories in time-frequency activity elicited in an oddball paradigm, the paradigm most often used to elicit the P3. The data for this investigation are well suited for this endeavor: repeated measures in a large, population-based sample of twins (N = 1692 individuals, 917 of them females), assessed as many as five times from 11 years of age to their mid-20s using identical stimulus delivery and recording procedures. We identified the relevant dimensions of time-frequency activity empirically, rather than selecting them a priori, sidestepping the subjectivity and sample-specificity inherent in specifying ROIs, which cannot be taken into account in statistical analyses. This permitted a comprehensive characterization of developmental trends. The extant research indicates that a decline in raw time-frequency power is a common feature of brain development in adolescence. Our approach permitted us to assess how common this is. That is, does this characterize all dimensions of time-frequency or is there variation in the pattern of change? Is there variation in the rate or timing of change in trajectories? Answers to these questions have important implications for our understanding of brain development.
Our second broad aim was to assess associations between trajectories of time-frequency activity and measures of externalizing behavior or psychopathology. Specifically, we assessed whether childhood externalizing psychopathology moderates trajectories of time-frequency activity and whether developmental trajectories themselves might predict externalizing behavior in the form of a measure of cumulative alcohol consumption between the ages of 11 and 24. This served as a preliminary test of the proposal we have made elsewhere that developmental trajectories might serve as useful endophenotypes (Iacono et al., 2017).
3. Method
3.1. Participants
The primary sample for this investigation consisted of the younger cohort of the Minnesota Twin Family Study (MTFS), an ongoing population-based longitudinal study of 1512 individual twins. Participants visited the laboratory at the age of 11 and at 3- to 4-year intervals thereafter to a target age of 24. A total of 1487 MTFS subjects had usable data for the laboratory task used here from at least one assessment. We included data from an additional 205 participants in the Enrichment Study (ES) of the MCTFR who completed an identical assessment at their intake, age-11 visit.1 Participants in both studies are same-sex twins who had been raised together. Approximately 60% of the participants in each cohort are monozygotic (MZ) twins. Table 1 provides the number of participants and their mean ages at each assessment wave. Participating families were representative of the state of Minnesota with respect to ethnic and racial background and socioeconomic status (Iacono et al., 1999; Keyes et al., 2009). See the Supplementary Material for demographic characteristics of the families. Not including ES participants, who only contributed data from the initial, age-11 assessment, 82% of participants provided data for three or more of the five total assessments and 94% completed at least two. All participants provided informed consent or assent, depending on their age at the time of each assessment, and these studies are conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).
Table 1:
Participant characteristics and task performance at each assessment wave
| Age | Correct | Reaction Time | P3 Amplitude | P3 Latency | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | N | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD |
| 11 | 1456 | 11.8 | 0.4 | 76.2 | 4.9 | 1189 | 221 | 35.9 | 10.4 | 567 | 91 |
| 14 | 1187 | 14.8 | 0.5 | 77.9 | 2.8 | 943 | 166 | 31.4 | 9.1 | 492 | 75 |
| 17 | 963 | 18.0 | 0.6 | 78.9 | 1.6 | 853 | 144 | 24.7 | 8.6 | 434 | 54 |
| 20 | 1083 | 21.4 | 0.8 | 78.9 | 1.6 | 832 | 152 | 22.9 | 8.2 | 417 | 53 |
| 24 | 1032 | 25.1 | 0.6 | 79.2 | 1.5 | 795 | 140 | 21.6 | 7.8 | 408 | 48 |
Note: N gives the number of participants with usable data at each wave. The column labeled Correct gives the mean number of correct responses to target stimuli (out of 80). Mean and SD are the mean and standard deviation of each measure. Reaction time and P3 latency are measured in ms, P3 amplitude in microvolts.
3.2. Experimental task
Participants completed the rotated heads oddball paradigm of Begleiter and colleagues (Begleiter et al., 1984). They sat in a darkened room in a comfortable chair with a high back to support the neck and a response button affixed to each arm of the chair, while viewing a sequence of 240 stimuli. One-third of the stimuli consisted of a bird’s eye view of a stylized head, including a nose and one ear. In half these target trials, the head was presented such that the ear appeared on the same side of the screen as the stylized head. In the other half, the head was rotated 180 degrees, putting the ear on the opposite side of the screen as it was on the head. The participant’s task was to press the left or right button to indicate whether the ear was on the left or right side of the head, respectively. The remaining 160 trials consisted of plain ovals, which participants were instructed to ignore. Stimuli were displayed for 100 ms. A trial consisted of a 500-ms prestimulus interval and a 1500-ms response window. The inter-trial interval followed a uniform random distribution between 1000 and 2000 ms. Participants were familiarized with the stimuli and procedure through 10 practice trials.
3.3. EEG recording
While participants completed this task, a Grass Neurodata 12 system was used to record EEG activity. For all participants, signals were collected from the midline parietal site (Pz) in addition to two adjacent lateral parietal sites via Ag/Ag-Cl scalp electrodes in an elastic electrode cap, with linked earlobes serving as a reference and an electrode on the shin as ground. Eyeblinks and other eye movements were recorded by means of two additional electrodes placed in a transverse arrangement above and immediately adjacent to one eye (over the outer canthus). High- and lowpass filter cutoff frequencies (half-amplitude) were 0.01 and 30 Hz, respectively, and amplifier roll-off was 6 dB per octave. Data were digitized at 256 Hz to 12 bits resolution and written to disk in 2-s epochs.
3.4. Cumulative alcohol use
Participants were asked about their substance use at each assessment, either in the context of a computerized substance use inventory (CSU; Han et al., 1999) or the Substance Abuse Module (SAM) of the Composite International Diagnostic Inventory (CIDI; Robins et al., 1990), a semi-structured interview administered to twins beginning at the age-17 assessment. Both instruments included very similar questions about four aspects of drinking: the amount typically consumed; the frequency of drinking; the maximum number of drinks consumed at one time; and the frequency of (CSU) or number of times becoming intoxicated (SAM). Responses were recoded to form 6- or 7-point ordinal scales, as described elsewhere (Malone et al., 2021; McGue et al., 2014). (See Table S1 in the Supplementary Material for details.) Because only 13 participants reported any use at the age-11 assessment (less than 1% of the sample), we excluded this assessment from our measure of cumulative use, which consisted of the mean score across the four assessment waves between age-14 and age-24 assessments. We required participants to have data from at least three occasions, resulting in a total of 1,233 participants, with 81% providing data for all four assessments. (The 210 ES subjects were ineligible by virtue of having EEG data only from one assessment, the initial age-11 assessment.)
Cronbach’s alpha among the four indicators of alcohol use, derived separately for each assessment wave using the psych package (Revelle, 2021), ranged from 0.81 to 0.94 (Mdn = 0.895). Figure S1 displays the distribution of scores on the combined drinking measure for each assessment wave. Twin intraclass correlations (ICCs), also computed using the psych package, characterizing the degree of similarity of twins at each assessment ranged from 0.52 to 0.68, indicating moderate to substantial twin similarity at each assessment wave. Our measure of alcohol use thus demonstrates a high degree of reliability.
3.5. Data analysis
3.5.1. Preprocessing
We screened the EEG signals via an in-house Matlab© (MATLAB, 2012) algorithm for amplitudes exceeding a threshold or transient artifacts as well as flat signals (constant voltage), supplemented by notes recorded at the time of each laboratory assessment to identify data that were unusable due to recording or technical issues.
3.5.2. Time-frequency transform
Time-frequency decomposition was conducted using functions in the Psychophysiology Toolbox Matlab toolbox (http://www.ccnlab.umd.edu/Psychophysiology_Toolbox/). EEG signals from individual trials were transformed into time- and frequency-specific estimates of total energy (both phase-locked and phase-independent) by means of the reduced interference distribution (RID) (Williams, 1996). As a member of Cohen’s class of transforms, the RID has several advantages over other methods of time-frequency representation, such as wavelets: it provides uniform resolution throughout the range of times and frequencies and preserves the marginals, meaning that its row and column means are identical to those of the raw signal. We downsampled signals to 64 Hz in both the time and frequency domains, resulting in a resolution of 15.625 ms and 0.5 Hz respectively, and averaged across all artifact-free target trials.
3.5.3. Exclusions
Participants with an accuracy rate less than 60% or with more than 10 false alarms (inappropriate button press to non-target stimuli) were excluded. In addition, we required at least 30 artifact-free trials. This resulted in a loss of 90 subject-assessments, 57 of them from the age-11 intake assessment, 3 from the age-24 assessment, and the rest distributed relatively equally among the remaining three assessments, producing the total sample size of 1692 given above (1487 from the MTFS and 205 from the ES.) The number of valid trials increased with assessment age, ranging from 74.4 at age 11 (SD = 9.1) to 79.1 at age 24 (SD = 3.7).
3.5.4. Principal component analysis
We conducted principal component analysis (PCA) on the time-frequency transforms of each subject’s EEG at Pz between 0 and 1250 ms after stimulus onset and between 0 and 7.5 Hz (Bernat et al., 2007; Bernat et al., 2005). As commonly used, PCA is a compressed sensing method to faithfully and parsimoniously represent a data matrix. It represents time-frequency energy in terms of two matrices: loadings and scores. The former consist of weights that effectively act as a linear filter: they accentuate the most salient aspects of the component, or the dimension of the EEG it represents, in time and frequency (Coles and Rugg, 1996). The latter reflect the degree to which those dimensions are manifest in a given time-frequency representation of the EEG, and can be thought of as the component’s ‘amplitude’ for a particular subject or subject-electrode.
After unfolding (or “matricizing”) the three-dimensional data array, Xitf, where i indicates participants, t time bins and f frequency bins into a Xitf matrix, we obtained principal components via the singular value decomposition, separately for each wave. We determined an appropriate number of components by means of cross-validation (see the Supplementary Material). Singular vectors were constrained to unit variance as is customary, which results in component loadings that are dimensionless, whereas component scores preserve the original units of energy (scaled power). To facilitate interpretation of the result, the component structure was varimax-rotated. To determine how similar solutions were across assessment waves, we computed Tucker congruence coefficients (Tucker, 1951). These allowed us to quantify the degree of similarity between all pairs of component loadings for a given assessment and the successive assessment. That is, we computed the congruence between varimax-rotated loadings at age 11 and age 14, between age 14 and age 17, and so on, thus assessing the degree to which the component structure was similar across assessment waves. Congruence coefficients equal the cosine of the angle between a pair of loadings. As such, values of 0 indicate that the angle between two sets of loadings is orthogonal, reflecting a complete lack of concordance between them, whereas values of 1 indicate that the angle between them is 0, reflecting perfect concordance.
3.5.4.1. Correlations among components and with P3
In a complementary assessment of the stability, or lack thereof, in component structure across ages, we computed Pearson correlation coefficients among component scores. Whereas component loadings are orthogonal and component scores uncorrelated, rotating components results in the loss of one or both forms of orthogonality (Jolliffe, 2002). This is no less true of varimax rotation, despite it being an orthogonal rotation. Normalizing components to unit length, as we did here, retains orthogonality of components but allows scores to correlate, thus permitting an assessment of associations among component scores. In addition, we computed correlations between each component and P3 amplitude in order to characterize patterns of covariance between the different components and P3, as well as change in such patterns with development. For this purpose, a computer algorithm identified the P3 as the (positive-going) peak with the greatest amplitude between 300 and 600–800 ms, the slower-developing responses of the youngest participants requiring extending the upper limit of the response window.
3.5.5. Statistical analyses
Trajectories of time-frequency activity. After establishing the equality of matched components across waves, we assessed the nature of change in time-frequency energy with development. Initial exploratory analyses, results of which are presented below, indicated that change in scores comprised two distinct phases, and that variance in scores decreased monotonically across assessment waves. This motivated us to fit piecewise regression models to the data. Based on exploratory analyses, we chose a linear function to characterize growth in each model piece. The change point, or inflection point (also known as the knot), is the age at which a transition occurs between phases of the growth trajectory.2
In the present situation, the change point age is unknown. Estimating this parameter from the data makes it a nonlinear problem: the regression coefficient capturing the magnitude of change subsequent to the knot depends on the value of the knot, which is itself unknown. To avoid the convergence problems nonlinear models are prone to, we adopted a two-step strategy, which converted the estimation problem into a linear one. In the first step, we used a grid search between age 11 and age 25 to identify the change point in trajectory of component scores that minimized model deviance (misfit). We subsequently used these estimates as known change points in linear mixed effects (LME) models of repeated measures of component scores. Scores were assumed to be determined by two linear functions of age, which yielded the rate of linear change before and after the change point, respectively (see the Supplementary Material).
In this parameterization, the intercept represents the estimated component score at the component trajectory’s inflection point. Models also included random intercepts at the individual and twin-pair level to account for within-subject and within-pair dependency. Missing data are inevitable in longitudinal studies, but LMEs accommodate missing data well: if the data are missing at random (MAR; Little and Rubin, 2002), such models yield unbiased estimates. In addition, LMEs permited us to use data from ES participants who were only assessed once with this particular protocol: they are nevertheless informative about mean level at age 11.
These were conducted using the R statistical computing environment (R Core Team, 2019). We used lme in the nlme package (Pinheiro et al., 2019) to fit growth models, because it allows for heteroskedastic model residuals, as well as flexibility in specifying a covariance structure for the within-subject residuals. We specified a continuous first-order autoregressive process (CAR1) for the residuals to account for autocorrelation in component scores over time. Unlike a standard AR1 process, CAR1 does not assume fixed and equal time intervals. Because sex differences in overall EEG power or ERP amplitudes are often observed, we included sex as a covariate of interest in our analyses to adjust trajectory estimates for any differences in overall component score level. For purposes of significance testing, we used Holm’s sequential multiple comparison procedure (Holm, 1979) to control the overall family-wise error rate across the 12 tests of growth parameters (two parameters related to age for each of six components), as well as the six tests of main effects of sex.
3.5.5.1. Sex as a potential moderator of trajectory shape
In light of the marked sex differences in trajectories observed by Chorlian and colleagues (2015), we examined sex differences in rates of change. For these and subsequent analyses, we computed Bayes factors (Kass and Raftery, 1995) as measures of the evidence favoring one model over a another (Wagenmakers, 2007) in addition to adjusted p-values associated with individual coefficient estimates. Approximations to Bayes factors can be obtained from the difference in Bayesian Information Criteria (BIC; Schwarz, 1978) values. Values of at least 3 are thought to indicate positive evidence in favor of the alternate model (Kass and Raftery, 1995). A value of 6, for example, corresponds to a posterior odds of 20:1 in favor of the model with the smaller value of BIC. That is, our focus is on model comparison rather than hypothesis-testing per se.
The results of Chorlian and colleauges (2015) constitute prior evidence of an important sex difference in trajectories of time-frequency power. We therefore also examined evidence for such sex differences in our data by means of the bias-corrected Akaike Information Criterion (AICc; Akaike, 1974; Hurvich and Tsai, 1989). Like differences between models in BIC, differences in AICc between models serve as measures of the weight of evidence in favor of a given model (Anderson, 2008). AICc and BIC differ in several important respects. However, one practical difference is that AIC tends to favor more complex models, which seemed appropriate in the context of determining whether there are sex differences in trajectory shape, given previous findings.
3.5.5.2. Growth curve parameters as predictors of drinking
Determining whether aspects of trajectories in time-frequency activity might predict cumulative alcohol use required a structural equation model (SEM), rather than our regression model. Piecewise SEM models treat intercept and the two slope parameters as latent variables. We used Mplus Version 8.7 for these analyses (Muthén and Muthén, 1998−−2017), which allow for definition variables, in combination with the MplusAutomation R package (Hallquist and Wiley, 2018). Definition variables permit the analyst to use individual-specific ages of measurement as loadings (cf. Sterba, 2014), rather than requiring loadings to be fixed across all participants. Trajectory change point estimates from our regression analyses were used to identify the two pieces of the piecewise growth model. Baseline models included sex effects on intercept and the slope of the first phase, as well as latent influences on intercept and the slope parameters (which are essentially random effects). The nested nature of the sample was accommodated via the COMPLEX option in Mplus, which uses a cluster-robust sandwich estimator to produce appropriate estimates of parameter standard errors. Our baseline models included estimating the mean level of cumulative alcohol use as well as its variance in order to provide an appropriate test of associations between growth curve latent variables (intercept and the two latent slopes) and cumulative use as an outcome measure. See the Supplementary Materials for additional details.
In a second step, we determined whether growth curve parameters predicted cumulative use. This consisted of estimating effects of the model intercept on cumulative alcohol use and then of both slope parameters as well. We used BIC and Bayes factors to assess the relative weight of evidence between the three models. The greater penalty imposed by BIC than AIC and its variants for each additional model parameter favors parsimonious models, which makes for a more stringent assessment of evidence that growth curve parameters were associated with alcohol use.
4. Results
4.1. Task performance and P3 across assessment ages
Table 1 provides the number of participants with valid data at each assessment wave as well as descriptive statistics regarding task performance. (Our total sample size exceeds the number of participants with valid data at any given assessment wave because a number of participants without usable data at the age-11 assessment had valid data at subsequent assessments. The main reasons for unavailable or unusable data were recording problems, highpass filter settings or electrode selections in the early days of the intake assessment that were incompatible with subsequent settings, lack of time to complete the task due to the length of the day and participant refusal.) Response accuracy, although already high at age 11, improved across waves, especially between age 11 and age 17. Variability in response accuracy showed a similar age-related trend. Mean reaction time decreased dramatically across assessment waves, this decrease being especially pronounced between the age-11 and age-14 assessments and somewhat less so between age-14 and age-17. The coefficient of variation was relatively equal across waves, indicating similar performance characteristics despite substantial age-related differences in mean reaction time (range, 0.17 to 0.19).
Table 1 also includes P3 amplitude and latency, along with their respective standard deviations, for each assessment age. A decrease with age is apparent for both: mean amplitude decreased by 60% and latency decreased by 72% between the age-11 and age-24 assessments. Although striking, the story these reductions tell about development is incomplete. In Figure 1 we have plotted the grand mean ERPs for each age. In addition to the marked decrease in overall amplitude and peak latency across assessments, which parallel reductions in P3 amplitude and latency, a change in ERP morphology is evident as well. Late activity following the P3 peak is particularly evident at the earliest waves, becoming less pronounced with development. Early peaks in the waveform, such as the P2 and N2 components, are little more than a momentary pause in the rise of the P3 at the youngest ages, but become more clearly resolved with development, and the P3 peak itself becomes increasingly localized in time. Figure S2 recapitulates this figure along with heatmaps (false color maps) of mean time-frequency power at each assessment wave. Power is concentrated at low frequencies. Low-frequency activity occurs initially throughout most of the response window, but, with development, becomes more localized in time and somewhat higher in frequency, echoing changes observed in the grand mean ERPs. These changes are notable, and we turn to the time-frequency dimensions underlying the ERP for aid in understanding them.
Figure 1:
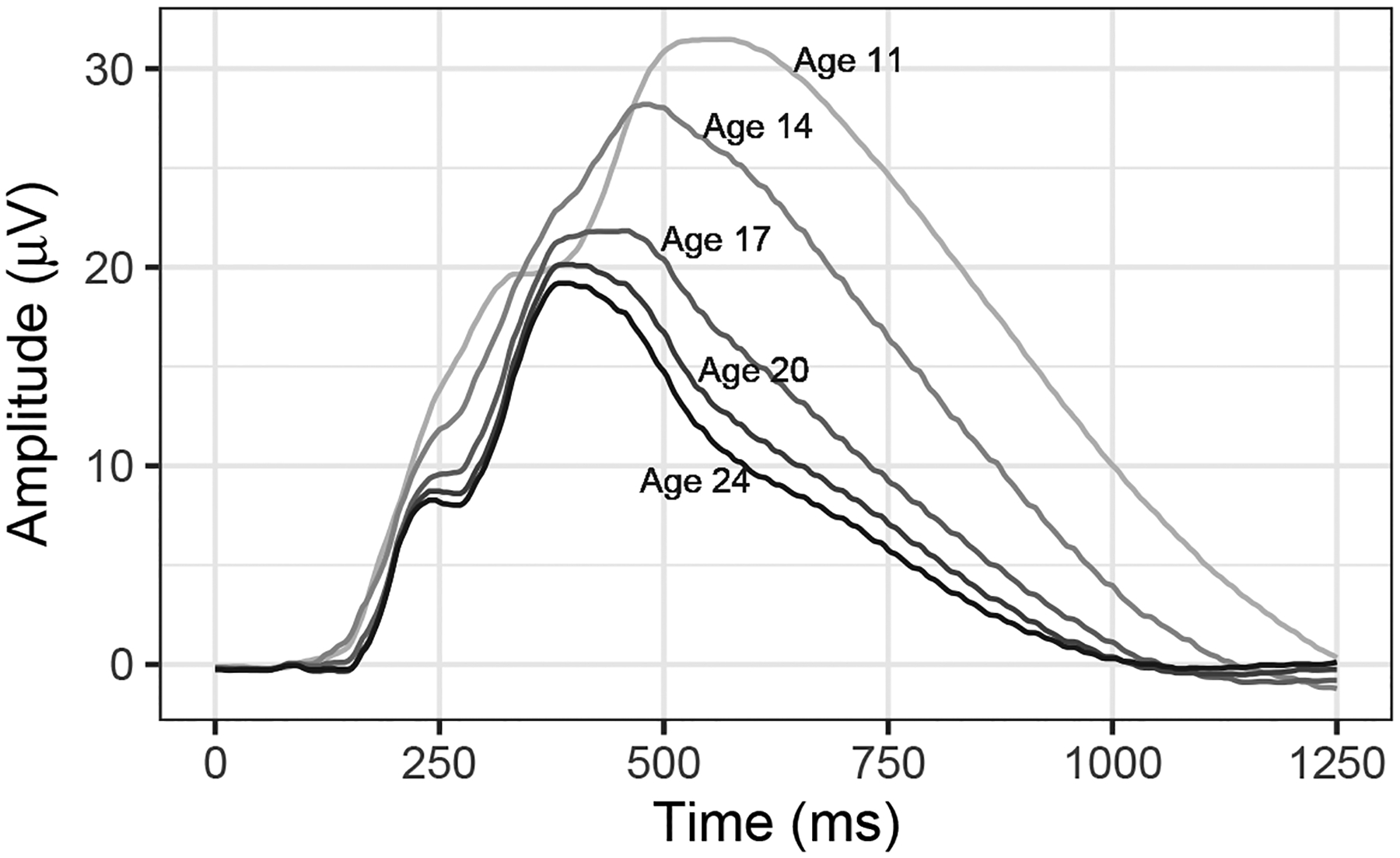
Grand-mean ERPs for each assessment wave.
4.2. Assessing time-frequency structure across age and assessment waves
Before proceeding with formal statistical assessment of parametric models of change in time-frequency activity and of factors that might influence trajectories of change, we conducted a series of exploratory analyses. These consisted of determining the degree of similarity in component loadings and the distribution of component scores across waves and fitting semi-parametric models to these scores as an agnostic approach to describing change in component scores with age, which we describe in some detail in the following three subsections.
4.2.1. Time-frequency structure: A bird’s eye view
Six principal components exceeded the cross-validation error threshold for the age-11 and age-24 waves, and five exceeded this threshold for the remaining waves. We therefore retained 6 components for further analysis, which accounted for 92.1 to 93.9% of the total variance in time-frequency energy. The resulting solutions were rotated so as to satisfy the Varimax criterion.
Before displaying these solutions, we first averaged component loadings – the weighted contribution of a given component to each time-frequency bin – and grand-mean ERPs across assessment ages in order to obtain summary representations of the data to orient the reader to what follows. The six components are ordered by their timing. Heatmaps (false color images) depicting the patterns of loadings are weighted by the mean score on each component, thus reflecting a component’s relative contribution to total time-frequency energy (cf. Dien et al., 2004). Red indicates the largest loadings, blue the smallest and green indicates intermediate values. The first component is a low-frequency component that largely spans the P2/N2 complex and the rise of the P3. Its maximum occurs at approximately the latency of the N2 component of the ERP, which is displayed at the top of Figure 2. The second and third components are the highest in frequency, extending into the slow theta range.3 Component 2’s maximum occurs at 375 ms, which approximately coincides with the inflection point near the height of the ERP, possibly corresponding to the P3a component. The third component spans the peak of the ERP, with a maximum at 515 ms. This appears likely to correspond to the P3b. The fourth component is the lowest in frequency and spans the peak of the ERP and a portion of the downward slope. The fifth component has its maximum at approximately 800 ms. This component may correspond to the late positive potential. The last component is a low-frequency component occurring at the very end of the response window likely reflecting variation among individuals with respect to the resolution of the late slow wave.
Figure 2:
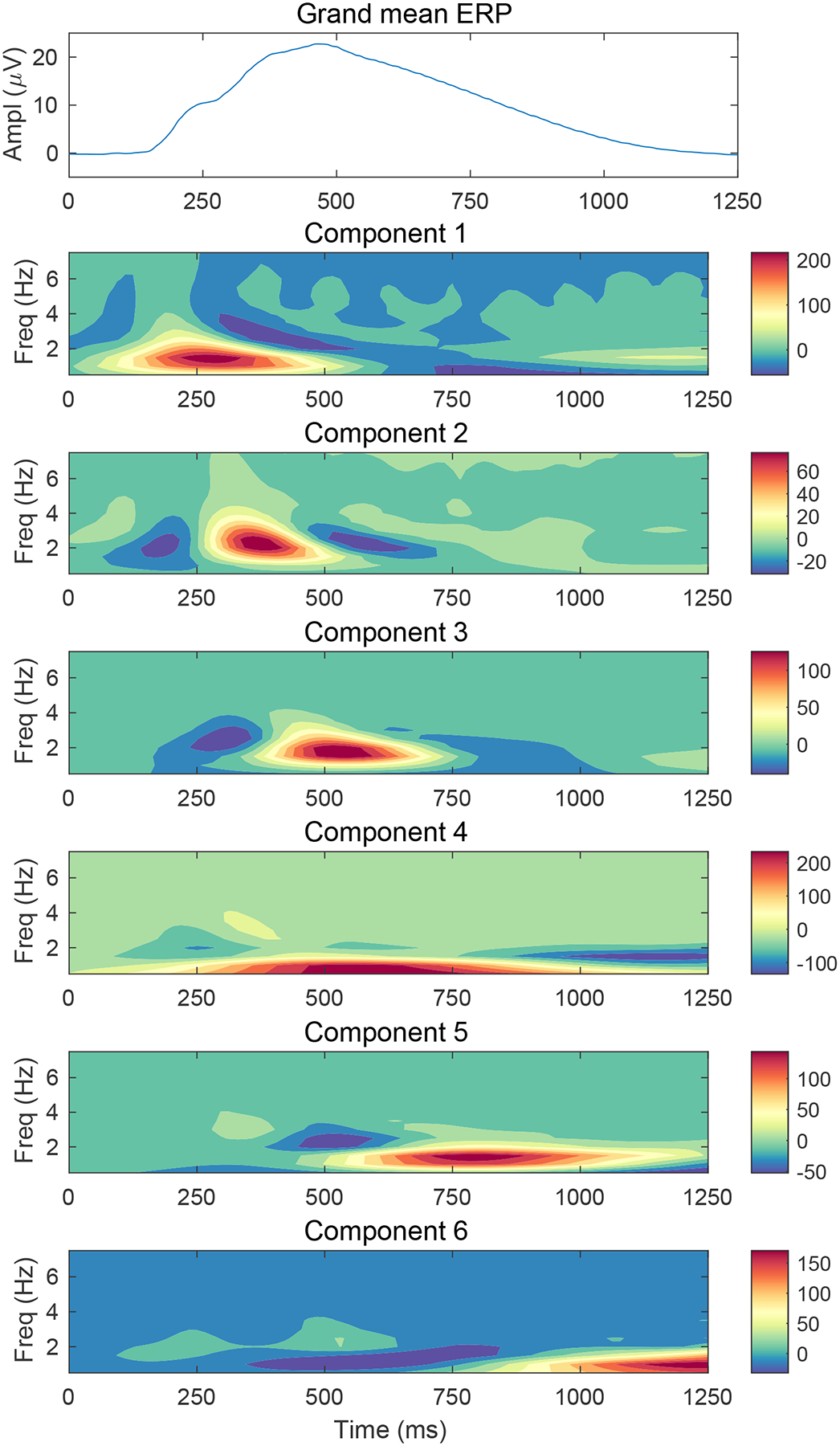
Average ERP and component loadings across assessment ages of 11 to 24. The average grand- mean ERP across assessment ages appears at the top. Heatmaps of loadings on each of the six components, averaged across assessment ages, appear below. Loadings have been weighted by each component’s mean score to facilitate comparison of their relative contribution to the total time-frequency energy. The grand mean ERP across all assessment ages appears in the top row.
4.2.2. How similar are the component loadings across assessment ages?
Whereas Figure 2 collapsed component loadings and grand mean ERPs across age, Figure 3 disaggregates these data, depicting heatmaps of the rotated loadings separately for each of the five assessment waves. Each column represents a different age. Loadings are unweighted here and therefore dimensionless. Components are ordered identically across columns based on their approximate timing as in Figure 2 to facilitate comparison across assessment ages, and the wave-specific grand mean ERP appears at the top of each column to permit evaluating the relationship between components and ERP. For instance, component 4, which spans much of the late positive complex, has a maximum value which lags the peak of the ERP by a relatively constant amount (115–175 ms) despite the fact that both occur increasingly early with age.
Figure 3:
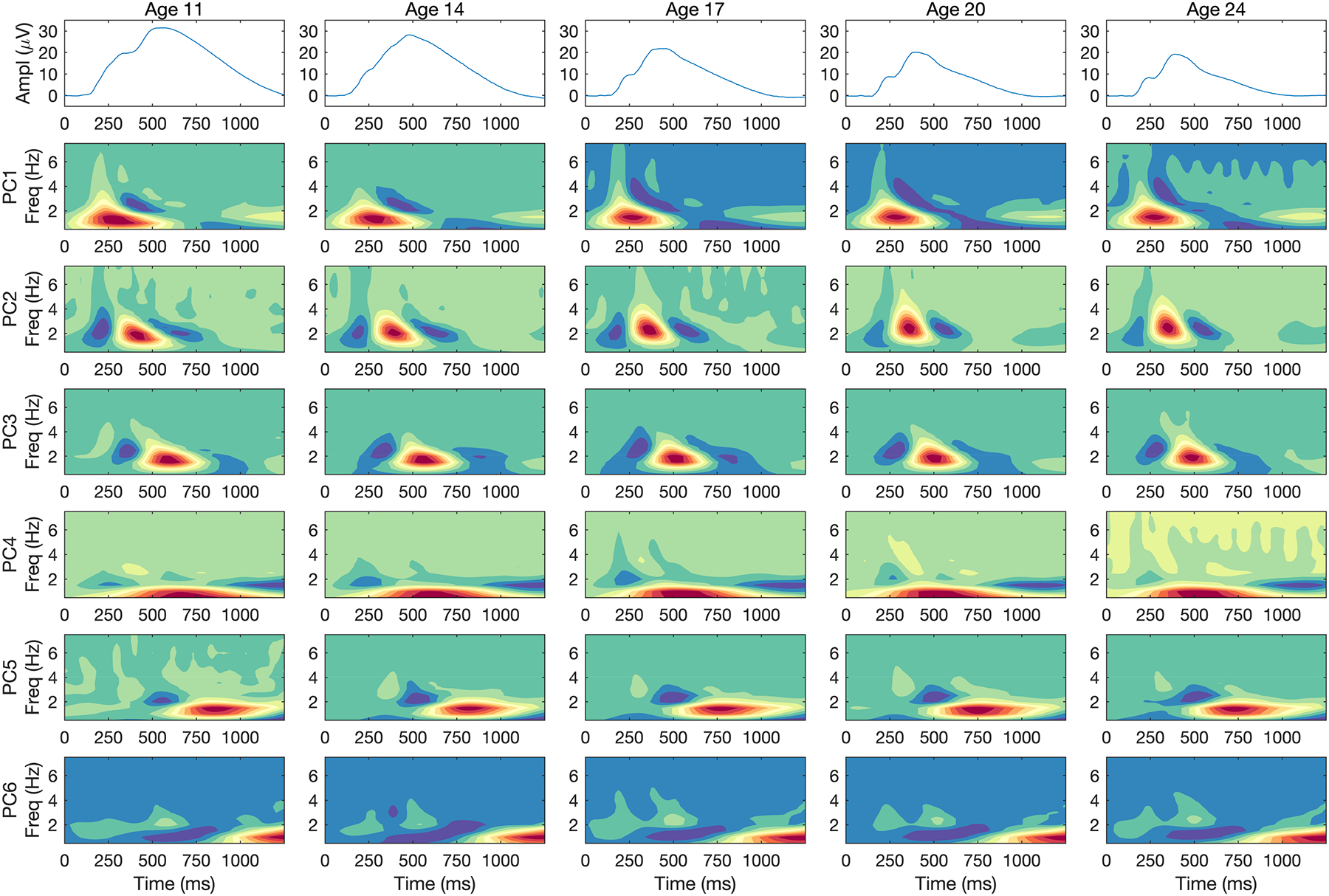
Component loadings by assessment wave. Heatmaps of the loadings of each of six components derived separately from average time-frequency energy values for each assessment wave. Solutions have been Varimax-rotated and ordered roughly by the timing of the locus of maximum loadings. The magnitude of each component’s loading on the different time-frequency bins is represented by means of color, with red indicating the largest values, blue the smallest, and green indicating intermediate values. The grand mean ERP for each assessment appears in the top row.
It is evident from the figure that the component loadings are similar across assessment ages. Tucker’s (1951) congruence coefficients provide a quantitative measure of similarity between a pair of component loading matrices. We computed congruence coefficients between loadings at successive assessment waves, with components matched by their timing as in Figure 3. Congruence coefficients equal the cosine of the angle between a pair of loadings. As such, values of 0 indicate that the angle between two sets of loadings is orthogonal, reflecting a complete lack of concordance between them, whereas values of 1 indicate that the angle between them is 0, reflecting perfect concordance. Complete results are provided in Figure S6. Coefficients were uniformly large for matched pairs of components (range, 0.91 to 1.00), with a median value of 0.98. As a rule of thumb, values of 0.95 or greater suggest that the two components can be considered equal (Lorenzo-Seva and Berge, 2006). These results indicate a high degree of congruence, with coefficients approaching unity with increasing age. By contrast, congruence coefficients between unmatched components were small and approached 0: the median coefficient ranged in absolute value from from 0.01 to 0.04. Thus, matched components were virtually identical and unmatched ones almost completely unrelated. This pattern of results constitutes strong evidence that the component structure is equivalent from one assessment age to the next.
If one scans each row in Figure 3, the striking similarity in component loadings from one wave to the next is evident. At the same time, however, subtle change is evident in several components. For instance, component 4’s maximum becomes progressively earlier in time with age, especially between the age-11 and age-17 assessments. Other components, such as components 1 and 2, increased somewhat in frequency and/or became more compact in time. Figure S6 in the Supplementary Material displays the component loadings organized by assessment age, which facilitates assessing the degree of component stability across age. The Supplementary Material also describes two ad hoc descriptive analyses of these small changes in component loadings, which lead to two conclusions: there are systematic shifts toward faster latencies, especially for components 3–5, and higher frequencies of components 1 and 2, and the stability in component loadings reflected so clearly in Tucker’s congruence coefficients is nevertheless compatible with noticeable, albeit subtle, change over the course of adolescent and early adult development.
4.2.3. Age-related trends in component scores
Having established the equality of matched components from one wave to the next, we examined the nature of change in scores across waves. Component scores reflect the degree to which a component is present in a participant’s time-frequency activity. As such, they serve as measures of a component’s “amplitude” (Coles and Rugg, 1996). We examined the distribution of component scores across assessment waves as well as the nature of mean trajectories in component scores. Panel a of Figure 4 depicts violin plots of the distribution of scores at each assessment wave, which indicate nonlinearity in the pattern of change in scores as well as a substantial reduction in variance across waves. We also fit a semiparametric smoothing spline model (Gu, 2013) to component scores as a function of chronological age, rather than wave, using the bigsplines package (Helwig, 2018), with the age basis consisting of segments joined by cubic splines and with sex as a nominal covariate to allow for sex differences in overall amplitude. In keeping with the exploratory nature of this analysis, we included a sex by age interaction term to allow trajectories to differ between male and female participants. Random effects corresponding to individual within twin pair accommodated the nested structure of the data. The number of knots for the spline function, which determines how much bend or “wiggliness” is allowed in modeling the association between age and component score, was chosen on the basis of generalized cross-validation. Panel b of Figure 4 depicts the model-implied trajectory along with 95% Bayesian confidence intervals for each component. Although subtle sex differences are evident, confidence intervals for the trajectories of males and females largely overlapped each other and trajectories were not qualitatively distinct. Trajectories are clearly nonlinear, and the particular nature of nonlinearity in these trajectories suggests that developmental change comprises two distinct phases, each with different rates of reductions in component scores.
Figure 4:
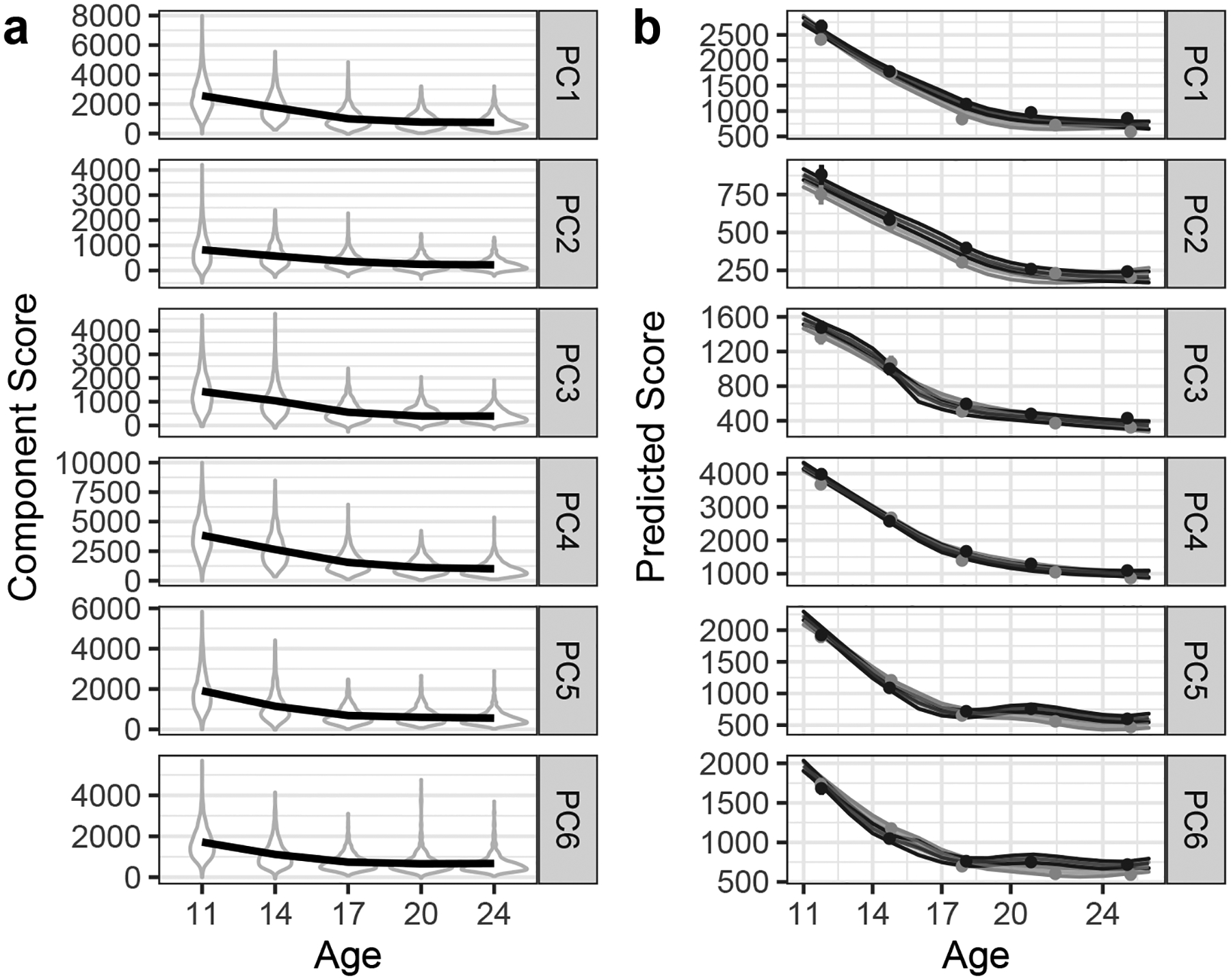
Trajectories and distributions of component scores. Age-related features of component scores are represented in two ways. Components are ordered as in Figure 2. Panel a: Distribution of scores at each assessment wave. Mean trajectories are modeled using a loess regression in ggplot2. Panel b: Trajectories of scores on matched components as predicted by smoothing spline models, with 95% confidence intervals around mean trajectories. Observed means are represented by filled circles, with 95% confidence intervals as vertical lines. Trajectories were allowed to vary by sex. Although there was substantial variation in actual age at each assessment, ages as a whole tended to cluster around the target ages, creating non-uniform age support for the smoothing splines, which likely produced the occasional bump or dip in the predicted trajectories.
4.3. Piecewise linear models of component-score trajectories
These results informed our statistical analyses, suggesting a piecewise linear model of change, with change points that varied by component. After obtaining estimates of the age at which the change point occurred for each component as described in the Method section, we fit linear piecewise regression models to component scores across assessment ages using lme, to allow for heteroskedastic residual variances and a CAR1 structure for their covariances. Two functions of age were estimated, one for each side of the change point (see Method). Consistent with the violin plots in Figure 4, estimates of residual variances decreased steadily across waves, with this decrease being greatest between the age-11 and age-17 assessments. Autoregressive coefficients ranged from 0.58 to 0.79, indicating substantial within-participant stability in component scores.
Parameter estimates for the fixed effects in these models appear in Table 2, along with the estimated inflection point age for each component. Inflection points occurred late in adolescence for all components, with some variability with respect to their specific timing. Attrition analyses described in the Supplementary Material suggested that the assumption that data were MAR is reasonable for these data, which makes parameter estimates unbiased. Regression coefficients are adjusted for main effects of sex and represent the expected change in component score (time-frequency energy) for a year increase in chronological age. As can be seen under the heading “Rate of Initial Change”, age was associated with initial reductions in time-frequency energy (component scores) up to the inflection point that were large relative to their standard errors, with p-values too small to include in the table (most exceeded machine precision and the largest equaled 1.5e-260). Table 2 also provides 95% confidence intervals for slope estimates. The absolute amount of change, as reflected in (partial) regression coefficients, was greatest for component 4. It was relatively small for components 2 and 3, the two low-theta components.
Table 2:
Parameter estimates from piecewise linear regression analyses and change-point age.
| Rate of Initial Change | Rate of Subsequent Change | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | Lower Bound | Upper Bound | t-value | Change Point | Estimate | Lower Bound | Upper Bound | t-value | |
| PC1 | −263.3 | −272.0 | −254.7 | −59.52 | 17.7 | −32.6 | −36.3 | −28.9 | −17.18 |
| PC2 | −69.5 | −73.1 | −65.8 | −37.26 | 19.5 | −5.1 | −7.4 | −2.7 | −4.16 |
| PC3 | −142.5 | −148.2 | −136.9 | −49.47 | 18.6 | −12.6 | −15.4 | −9.9 | −9.00 |
| PC4 | −422.2 | −436.8 | −407.6 | −56.64 | 17.2 | −71.0 | −77.0 | −64.9 | −22.97 |
| PC5 | −269.9 | −280.5 | −259.4 | −50.07 | 16.1 | −22.7 | −25.9 | −19.6 | −14.19 |
| PC6 | −209.8 | −219.7 | −199.8 | −41.45 | 16.4 | −11.9 | −16.2 | −7.5 | −5.37 |
Note: Parameter estimates represent the amount of change in component scores (time-frequency energy) for a year change in chronological age (independent of effects of sex), and these are provided separately for initial change and change after the inflection point (knot), along with lower and upper bounds of 95% confidence intervals. Both age effects are associated with 4027 df.
Under the heading “Rate of Subsequent Change” we present estimates of the rate of change after each inflection point, along with 95% confidence intervals around them. Comparing estimates of the two rates of change for a given component indicates that the magnitude of change was markedly greater (by approximately an order of magnitude) before the inflection point than after it. Although smaller in magnitude, the rates of absolute change after the inflection point were still significant by Holm’s sequential testing procedure: the largest adjusted p-value equaled 2.3×10−04 and the smallest was 8.9×10−109.
In order to assess the magnitude and significance of change in linear slope following the inflection point for each component, we subtracted the second slope estimate from the first, deriving standard errors for these estimates, and thus confidence intervals, by means of the delta method in the car package (Fox et al., 2020). These were large in magnitude and confidence intervals around them did not come close to 0, indicating a meaningful change in trajectory and supporting the validity of the piecewise model. For all components, paired coefficients were nearly equal in magnitude but opposite in sign, indicating a change in slope that largely – but not completely – offset the initial rate of change: the change in slope equaled between 83.2% and 94.3% of the absolute value of the raw change estimates for the first phase.
Thus, the rate of change between age 11 and each component’s inflection point was substantially greater than the rate of change after the inflection point, although the decline in component score was significant for all components, before and after the inflection point. Inflection points occurred relatively late in adolescence for all components, although there was variation of several years in the exact timing; inflection points for the two low-theta components (2 and 3) were close to age 20.
4.3.1. Model-predicted trajectories of change
These results provide clear evidence for the significance of estimates of rates of change, whether relative to the rate of initial change or in absolute terms. They do not by themselves indicate how adequate the piecewise linear model was to characterizing change in component scores. We therefore plotted the trajectories implied by model parameters in order to determine how well the piecewise linear model accounted for the observed data. These are depicted in Figure 5, along with 95% confidence intervals around them, obtained using the semi-parametric residual bootstrap method (Carpenter et al., 2003) as implemented in the lmeresampler package (Loy et al., 2021). Component means, and 95% confidence intervals around them, are plotted at the average assessment age for a given wave, which might deviate somewhat from the target age and was slightly different for male and female participants. The ordinate in each plot is individually scaled to permit seeing detail in the plotted data. Model-implied trajectories conformed very closely to observed mean scores at each assessment wave, indicating that a piecewise growth function characterizes change in time-frequency component scores well for each of the components. (In the Supplementary Material, we examine for comparison several models representing change as curvilinear, rather than piecewise linear. These models did not account for the observed data as well as the piecewise linear model.)
Figure 5:
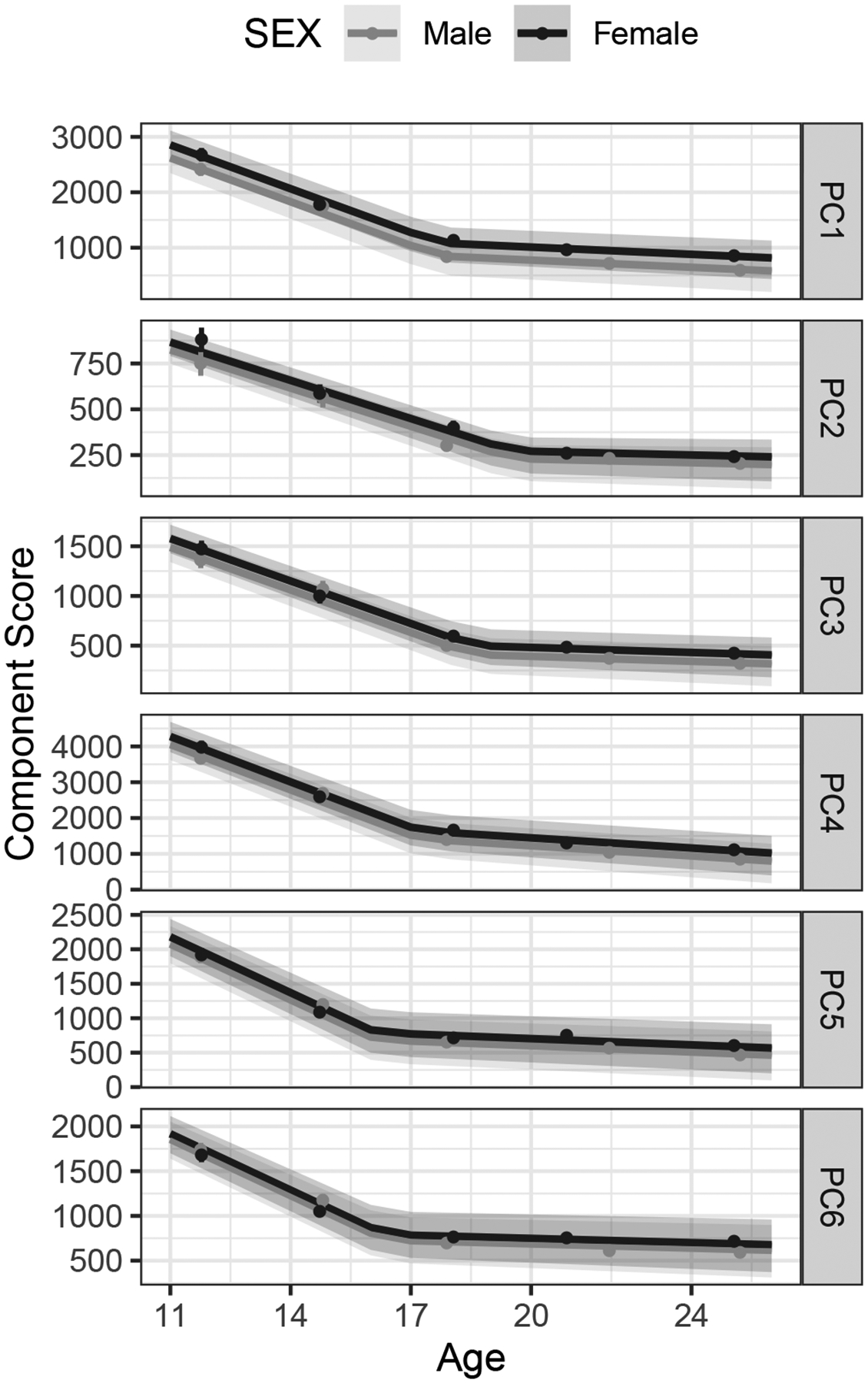
Model-implied trajectories of change in time-frequency components. The change point, or knot, was estimated separately for each component, and trajectories are plotted separately for males and females. Observed (measured) means are represented by filled circles, with 95% confidence intervals around them as vertical lines. The scale of the ordinate was allowed to vary across plots to emphasize detail in model- predicted trajectories.
4.4. Moderators of developmental change
4.4.1. Sex differences in level and slope
As expected, component scores were significantly greater overall for females than males in Wald tests with 858 df, with group differences in mean scores ranging from 42.1, for component 2, to 234.4, for component 1. Holm-adjusted p-values were all 0.006 or less, indicating that these amplitude differences were significant for all components.
By contrast, tests of the sex by age interaction terms yielded minimal evidence of sex differences in rates of change. Likelihood-ratio tests, on 2 df, were significant only for the latest two occurring components (5 and 6) p = 9.3×10−04 and 1.6 ×10−07, respectively. Bayes factors, based on the difference in values of BIC for models including the sex by age interaction terms relative to their corresponding main-effects models, strongly favored the sex-differences model for component 6, the late slow wave, with a value of 6517.8, which is consistent with the small adjusted p-value for this effect. They were less than 1 for the other five components, albeit barely so for component 5 (0.94), indicating stronger evidence in favor of the model including only a sex main effect. We conclude that a meaningful sex difference in overall rate of change is mainly evident for the late slow wave, although the rate of change in component–5 scores may also differ between sexes: the probability that the sex-difference model was correct given the data was only 0.49. In light of the findings of Chorlian and colleagues (2015), in the Supplementary Material we present AICc values for the different models. These suggested small sex differences in the linear rate of change before and after each trajectory’s inflection point.
4.4.2. Individual differences in pubertal status
Although results indicated minimal sex differences in rates of change, examining the mean scores for males and females suggested the possibility of a more nuanced situation than our statistical tests suggested. In particular, there is a small departure from a pattern of linear change in component scores between 11 and 17 in a manner that differs for males and females. The total amount of change during this span is almost identical for the two sexes, differing by no more than 0.2%, but for females the majority of change occurred early in adolescence, between 11 and 14, for all components (as much as 70%), whereas for males, the majority of change in components 1–4, as much as two-thirds, occurred between 14 and 17, and the relative amount of change during this interval was greater among males relative to females for all components. (See component 3 in Figure 5, for example. The direction of the male-female difference in mean scores for this component flipped between the age-11 and age-14 assessments and again between age 14 and age 17.) We speculated that this might be due to sex differences in the timing of puberty and rates of maturation. Although not commonly considered in relation to EEG measures, there is nevertheless evidence of effects of pubertal hormones on measures of brain organization and in shaping neural circuits (Bedny et al., 2018; Schulz et al., 2009), as well as sex differences in white matter microstructure (Ho et al., 2020). Testicular hormones during puberty appear particularly important for organizing synaptic plasticity in the hippocampus (Schulz et al., 2009), a possible source of the P3 (Halgren et al., 1980; see also Polich, 2007). Sex differences in the onset and course of pubertal development might result in subtly different trajectories of measures of brain function between male and female adolescents. The Pubertal Development Scale (PDS; Petersen et al., 1988), a self-report measure of bodily changes related to puberty, had been administered at the first two assessment waves as part of the comprehensive assessment of study participants. We therefore conducted follow-up analyses to determine whether variation in pubertal status might account for sex differences in component scores. We caution that these analyses are post-hoc and entirely exploratory.
A small number of participants were missing PDS ratings (n = 69), almost all from the intake assessment. Scores were fixed at the maximum score for the age-17 and subsequent assessments. We re-fit piecewise linear regression models with (mean-centered) PDS score as a time-varying covariate of interest in addition to the sex by age interaction terms. This resulted in significant improvements in model fit, with likelihood-ratio tests on 1 df ranging from 17.1 to 48.9 and adjusted p-values all less than or equal to 3.6×10−05. Bayes factors also provided strong indications that the posterior odds of the model including PDS score was correct. The smallest was 67.4 and all others were greater than 100. These values correspond to “very strong” and “decisive evidence,” respectively (Wetzels et al., 2011). Taken together, these results indicate a robust main effect of pubertal status on overall component score. More germane to our present purpose, we found that Wald tests of the two sex by age interaction terms for component 6 were not significant when adjusted for effects of PDS (Holm-adjusted p-values equal to 1). Thus, the apparent sex difference in rate of change on component 6 seems to be accounted for by sex differences in the timing of pubertal development. At the same time, adjusting for pubertal status did produce significant interaction between sex and the initial slope effect. This was only marginally significant, however, with an adjusted p-value of 0.049. This may represent a chance finding but might represent a sex difference not captured in our model; indeed, model-predicted trajectories in Figure 5 underestimate the difference in mean scores at the earliest ages for component 2. (See the Supplementary Material for a depiction of the trajectory predicted by a model including this one sex by age interaction.) Finally, estimates of initial level and initial slope were somewhat attenuated when adjusted for effects of pubertal status. The median reduction in coefficient magnitude equaled 17.2% and 34.4% for intercept and slope, respectively. All were still significant, but these somewhat unanticipated results indicate that pubertal status moderated trajectories of component score change.
4.5. Time-frequency components and their trajectories as developmental endophenotypes
4.5.1. Consistency of cross-sectional correlations among component scores
PCA yields orthogonal component loadings and uncorrelated component scores. Rotating components can make them more readily interpretable but results in the loss of one or both forms of orthogonality, even if the rotation itself is orthogonal (Jolliffe, 2002). The normalization used here retains orthogonality of components but allows scores to correlate, thus permitting an assessment of associations among component scores to determine how stable these might be across assessment ages. We computed Pearson correlation coefficients among components, as well as between each component and P3, to quantify the degree of stability (or change) in the pattern of associations among these measures. Figure 6 depicts the correlations graphically as a heatmap.
Figure 6:
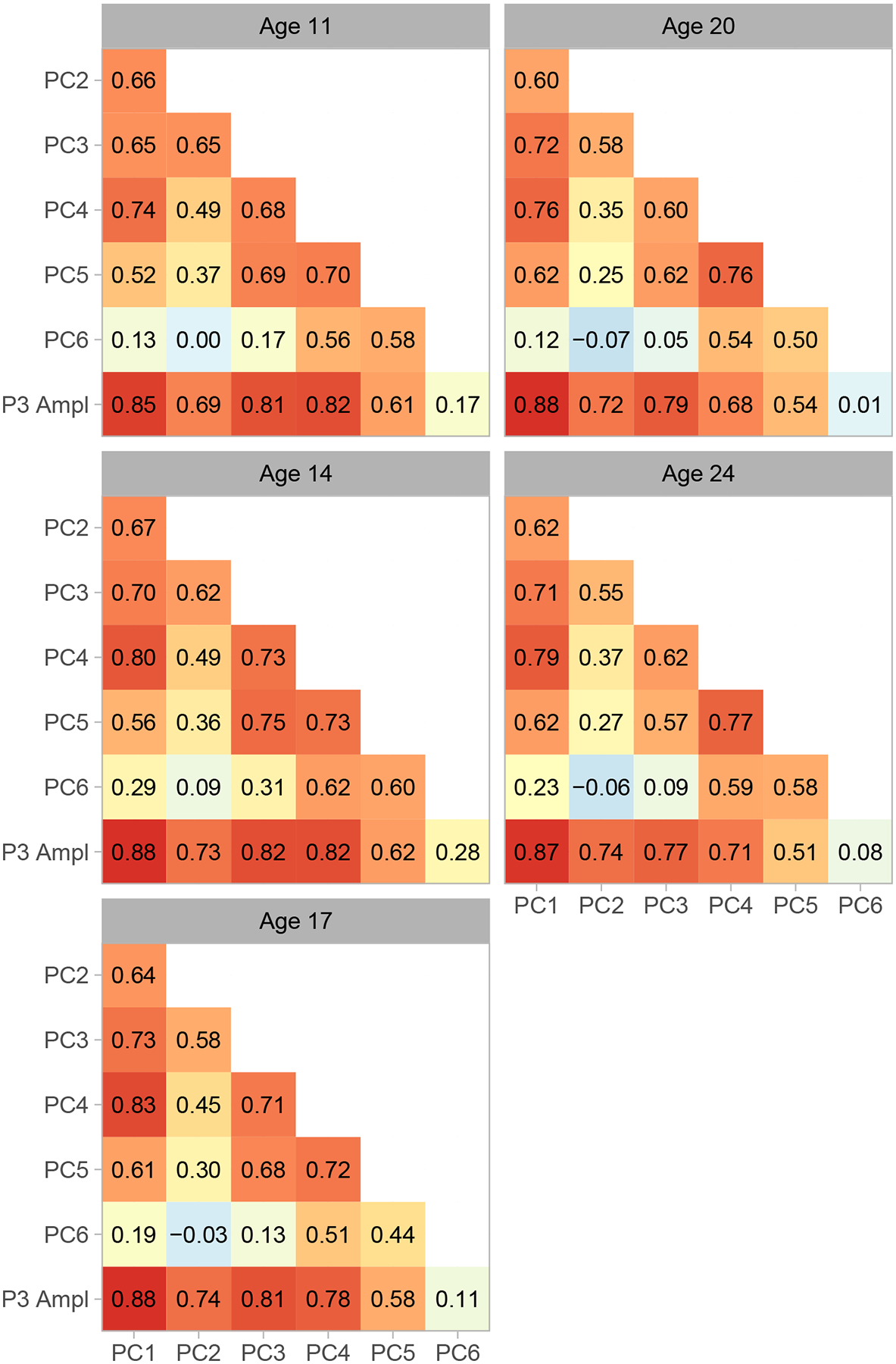
Correlations among components and P3. Matrices of Pearson correlation coefficients are depicted as heatmaps. Red indicates the most positive correlations, yellow the intermediate values, and light blue the smallest values (values near 0). Assessment waves are arrayed top to bottom and left to right.
The magnitude of the component 6–component 3 correlation was modest in adolescence and declined to near 0 by adulthood, and the correlation between component 6 and P3 amplitude showed a similar age-related trend. By contrast, correlations among the other components and between each component and P3 amplitude were stable across ages, especially for components 1–4. The component 1–P3 amplitude correlation in particular was large in magnitude and invariant across development. There was thus substantial stability in the way component scores related to one another as well as with P3 amplitude, echoing the stability of component loadings with development and standing in marked contrast to the pattern of change in ERP morphology. That the correlation between component 1 and P3 amplitude was uniformly large in magnitude across assessment ages is particularly striking.
4.5.2. Stability of component scores longitudinally
Figure 7 consists of a heat map of component-score correlations across assessment waves. Correlations between age-17 scores and scores from the early adulthood assessments were relatively uniformly large, indicating that they had become quite stable by this stage of development. In general, across-wave correlations tended to be moderate to large in magnitude, with the exception of component 6, the late slow-wave component.
Figure 7:
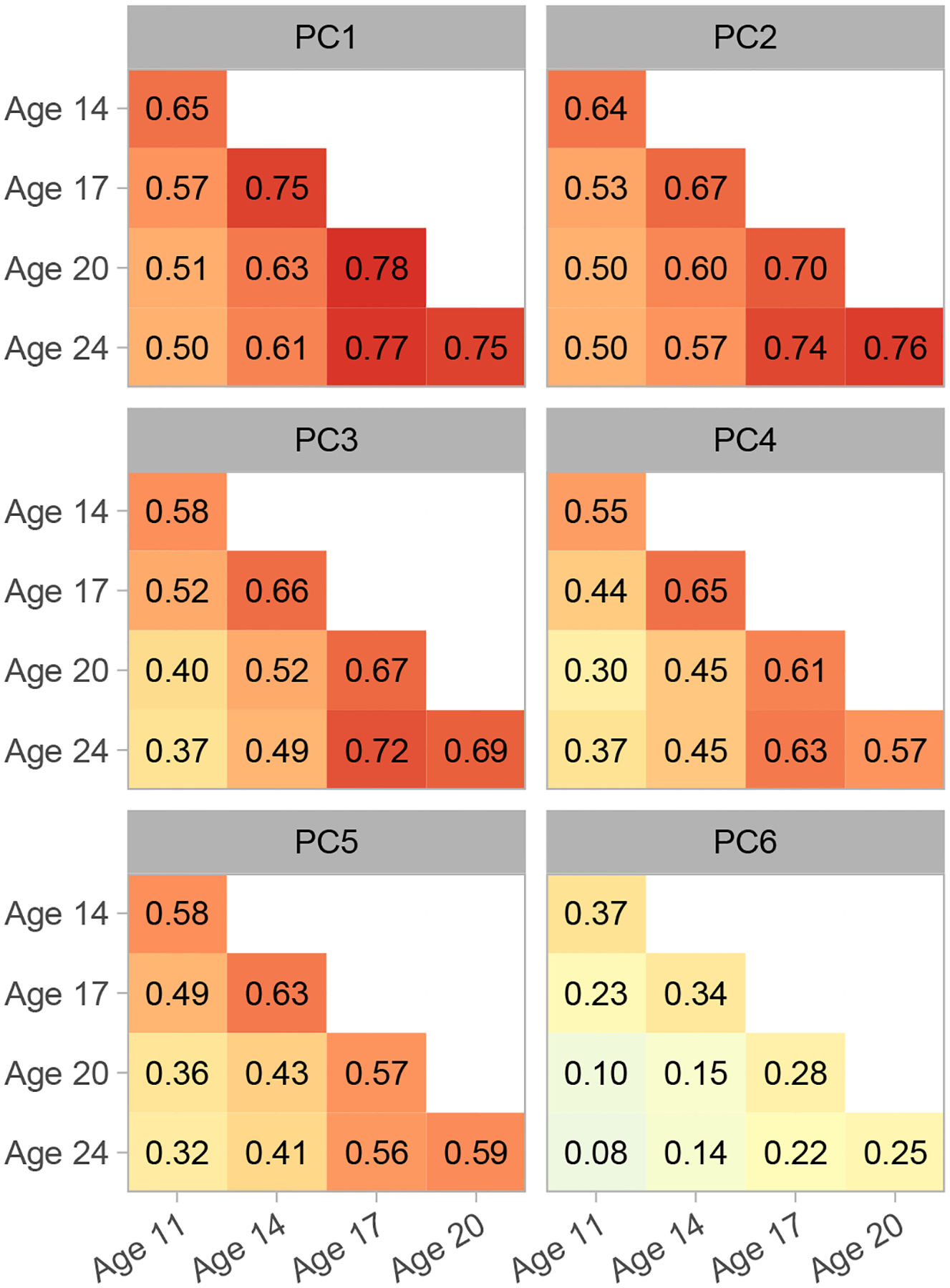
Stability of component scores across assessment waves. Matrices of Pearson correlation coefficients are depicted as heatmaps. Red indicates the most positive correlations, yellow the intermediate values, and light blue the smallest values (values near 0).
4.5.3. Trajectories of time-frequency component scores “predict” alcohol use
Log-likelihood values and model-fit statistics for SEM models assessing effects of growth curve parameters on cumulative alcohol use appear in Table 3. We assessed, and compare, three models: a baseline model consisting of the piecewise linear SEM model; a model adding the intercept in these models, reflecting overall level of component score magnitude at the inflection point, as a predictor of cumulative drinking; and a model including all three growth curve parameters (intercept and both slopes) as predictors of drinking.
Table 3:
Information-theoretic model fit statistics for growth models as predictors of cumulative alcohol use
| Log-likelihood | BIC | |||||
|---|---|---|---|---|---|---|
| Baseline | Intercept | Int/Slopes | Baseline | Intercept | Int/Slopes | |
| PC1 | −129808.6 | −129801.6 | −129762.2 | 259887.6 | 259880.7 | 259816.5 |
| PC2 | −126267.5 | −126255.4 | 252805.3 | 252788.3 | ||
| PC3 | −127815.3 | −127809.0 | −127753.8 | 255900.9 | 255895.6 | 255799.8 |
| PC4 | −132220.3 | −132219.8 | −132168.1 | 264710.8 | 264717.1 | 264628.4 |
| PC5 | −128900.1 | −128899.9 | −128865.7 | 258070.5 | 258077.4 | 258023.6 |
| PC6 | −129724.4 | −129723.4 | 259719.1 | 259724.4 | ||
Note: Model fit statistics for three different models predicting cumulative alcohol use. BIC is Schwarz’s Bayesian Information Criterion (Schwarz, 1978). The Baseline model includes growth curve parameters (plus the mean and variance for cumulative drinking). The Intercept model includes the piecewise linear model intercept as a predictor of cumulative drinking through age 24 (one additional parameter), whereas the Int/Slopes model includes both slopes as predictors of drinking as well (three additional parameters relative to the Baseline model). The model best supported by the evidence for each component is highlighted in gray.
The most likely model for component 2 was the Intercept model, indicating a significant association between the component 2 intercept and cumulative drinking. A pseudo-R2 statistic based on the difference in model likelihoods (Magee, 1990) equaled 0.016. (The likelihood-ratio based pseudo-R2 is a function in part of the sample N. The effective sample size in clustered samples is influenced by the different sources of dependency in the data and is therefore generally poorly defined in such samples. In addition, the effective sample size in the presence of missing data is unknown. We use the number of unique individual subjects here, which is consistent with Mplus’s estimates of BIC, which similarly depends on sample size. This may result in a slight overestimate of R2.) The Baseline model was most appropriate for component 6, the late slow wave component, indicating that parameters of the trajectory characterizing developmental change in this component were not associated with cumulative drinking.4
The model including all three growth curve parameters did not converge on a reproducible solution for components 2 and 6. For the remaining four components, however, the evidence favoring this model was unambiguous. The relative weight of evidence in favor of this model relative to the other models was 1, indicating that it almost certainly was the best model, and Bayes factors for this model relative to the intercept-only model were all so large as to be decisive. Pseudo-R2 values ranged from 0.045, for component 5, to 0.079 for component 5. Wald statistics for each individual growth curve parameter were less than .05 for 11 of the 12 parameters. Holm’s multiple comparison procedure yielded 9 adjusted p-values less than .05: the intercept and the second slope parameter for components 1, 3 and 4 and all three parameters of the component 5 trajectory in relation to cumulative drinking.
To aid in interpreting these findings, we re-expressed point estimates of the association between growth curve and drinking as a function of their respective standard deviations (Supplementary Material?). Expressing the results this way, a subject with a component-score intercept (level) one SD smaller than another subject would be expected to have a larger score on the cumulative drinking measure of between 0.70 and 1.75 units, depending on the component. A subject whose rate of change in the second phase of change in component score magnitude was one SD greater (more negative) than another would be expected to have a larger drinking score of between 0.45 and 1.75 units. To contextualize these results, a 1-SD difference between subjects in intercept or slope would be associated with the difference between drinking very infrequently (a few times a year) and drinking as much as once a week or more, on average, over the period from age 14 to age 24, or between having 1–3 drinks per occasion and at least twice that much over this same time period (see Table S1).
5. Discussion
We examined dimensions of time-frequency energy derived via PCA from task-related EEG activity in adolescents and young adults, who completed a rotated heads oddball paradigm used to elicit the P3 response as many as five times between the ages of 11 and 24. Principal component loadings were virtually identical from one assessment wave to the next, indicating that a common and stable set of time-frequency dynamics characterized EEG activity. Correlations between component scores and P3 amplitude were large in magnitude (for all but one component) and stable across assessment ages, indicating shared variance between the components and P3 that was largely unaffected by developmental changes in the latter. At the same time, subtle shifts in component timing, and, to a lesser extent, frequency, were evident as well. These changes were almost imperceptible from one assessment to the next but produced noticeable change in component loadings between 11 and 24 years of age. Component scores decreased with development in a nonlinear fashion. Piecewise linear models of change captured change in component scores well in that model-predicted trajectories conformed closely to the observed mean scores. Components differed with respect to overall magnitude, rate of decline and timing of the inflection point (change point). All these factors in concert produce the marked age-related change in the morphology and amplitude of the grand-mean ERP derived from the same EEG activity.
In a second set of exploratory analyses, we assessed performance of trajectories of component-score change as potential endophenotypes. Parameters describing aspects of the trajectories of change in component score – the intercept and two slope terms – were associated with a measure of cumulative alcohol use from middle adolescence into early adulthood. The intercept for component 2 predicted cumulative drinking, whereas the intercept and one or both slope parameters predicted cumulative drinking for four components. (We use the verb “predict” in the sense of statistical predictors of a dependent measure.) Although subjects’ heaviest drinking typically occurred toward the end of the period between 14 and 24, it is impossible to definitively determine the temporal sequence involving change in component score and drinking, which helps to establish causality. Nevertheless, these findings serve as proof of concept of the potential importance of developmental trajectories as endophenotypes and point to future research to move us closer to establishing cause and effect.
5.1. Normative developmental change and its correlates
5.1.1. Developmental trajectories of change in time-frequency component scores reflect two distinct phases
Despite variation among component scores in overall level and rates of change, developmental trajectories of change followed the same general pattern for all components and was well approximated by a piecewise linear regression model. That a piecewise model characterized change in components suggests that the brain development captured in these trajectories comprises two distinct phases. Estimates of the change point marking the transition between phases were relatively late in adolescence, although the exact timing varied by about 4 years (between 16 and 19 years of age), somewhat reminiscent of the Piagetian notion of horizontal décalage (Flavell, 1963). The first phase thus extended throughout most of adolescence, giving way to a second phase with a smaller rate of change in late adolescence and participants’ 20s. These findings are broadly consistent with findings of important structural brain development during adolescence which persist, albeit to a lesser degree, into early adulthood (e.g., Lenroot and Giedd, 2010; Bethlehem et al., 2022).
5.1.2. Sex and pubertal status effects on component scores
As expected, there were significant sex differences in overall level of component scores across age. By contrast with the findings of Chorlian and colleagues (2015), however, we found only weak evidence of sex differences in rates of change in component scores. Interaction effects were significant for the two latest-occurring components (5 and 6), but Bayes factors indicated that the evidence supported a significant difference only for component 6. The bias-corrected AIC yielded slightly stronger evidence for sex differences. Yet these amount to very slight sex differences in rates of linear change before and after trajectory inflection points, not qualitatively different trajectories. What is more, individual differences in pubertal development appeared to account for the apparent sex difference in component 6 score trajectory: adjusting component scores for scores on a self-reported scale of pubertal development resulted in nonsignificant sex by age interaction effects.
Main effects of pubertal status on component scores were significant, and including these scores attenuated estimates of rates of change in component score somewhat. Althought the magnitude of effects was small, these findings are consistent with evidence of important hormonal influences on brain structure and function in adolescence (Bedny et al., 2018; Ho et al., 2020; Schulz et al., 2009). However, we caution that analyses of pubertal status were all post-hoc and exploratory.
5.2. Individual differences in component-score trajectories: Growth curve parameters as predictors of alcohol use
Examining trajectories of change in an endophenotype can offer greater statistical power than estimating an endophenotype’s effect in a cross-sectional analysis. This advantage is shared by other approaches that aggregate over multiple time points. However, the latter loses information about change, such as whether an endophenotype alters the shape of a trajectory (e.g., rate of change), and timing. Trajectories of change may also predict important outcomes in their right: developmental trajectories may themselves constitute candidate endophenotypes. Indeed, our piecewise linear SEM models to “predict” cumulative alcohol use yielded several findings supported by the weight of evidence. Only component 6, the late slow wave, was unassociated with drinking. For the remaining five components, the intercept in growth models (component 2), the intercept and second slope (components 1, 3 and 4) or all three growth curve parameters (component 5) were associated with cumulative alcohol use. Smaller overall magnitudes of component scores and/or greater rates of the normative reduction in component scores with development are associated with increased levels of alcohol use across adolescence and early adulthood.
Our measures of drinking combine raw responses to improve their reliability. For instance, those typically having 1 to 3 drinks per occasion receive the same score, as do those typically having 7 to 10, which makes it difficult to quantify the magnitude of effects of growth curve parameters in the scale of the original variables. Nevertheless, rough estimates indicate that a 1-SD difference between individuals in overall level (intercept) or rate of change (slope) in component scores across adolescence and into adulthood is associated with the difference between having 1–3 drinks per occasion and more than twice that many across the period from adolescence into early adulthood. Individuals with smaller intercepts or more rapid rates of change in component scores were likely to consume more alcohol to a degree that appears meaningful.
These findings support our suggestion that developmental trajectories can serve as endophenotypes. It may be that smaller neural ensembles giving rise to the time-frequency activity captured in these components or less synchronized activity within these ensembles underlies the association between component magnitude or rates of change therein and cumulative alcohol use. Intercept–drinking associations are especially consistent with an explanation that a preexisting liability accounts for both reduced component score magnitude and increased drinking. Associations between rates of change in component score and drinking are also consistent with confounding by a preexisting liability. However, they are also consistent with the possibility that alcohol exposure adversely affects component score magnitude, such as via a neurotoxic or other effect. Examining the interplay between time-frequency energy and drinking or other forms of substance use in adolescence and into adulthood is thus likely to be informative about the causal processes at play.
Our results also have implications for conceptualizations of reductions in P3 amplitude as an endophenotype for externalizing psychopathology. Component 1 is a low-frequency component that spans the rise of the P3. Analogs of this component have been observed in two studies conducted on an independent sample of older male twins from the MCTFR (Gilmore et al., 2010; Yoon et al., 2015). Two findings are particularly germane: scores at age 17 on this component (component PC3 in Gilmore et al.) improved prediction of externalizing psychopathology groups over P3 amplitude in one study (Gilmore et al., 2010) and predicted the development of externalizing psychopathology by age 29 in the other (Yoon et al., 2015) These findings suggest that component 1 in particular might be a useful endophenotype for externalizing psychopathology, despite representing the rise of the P3 peak rather than the peak itself. Our results indicate that component 1 scores were uniformly and highly correlated with P3 amplitude (see Figure 6), suggesting that this early component is an important influence on P3 amplitude. EEG power producing the rise of P3 may reflect the sheer number of neurons recruited by the task, or the degree of consistency in recruitment of neural ensembles across trials. Accounts of P3AR as an endophenotype might therefore realize greater explanatory power from incorporating these findings and their implications. One would probably not suspect that this low-frequency activity is relevant to P3 amplitude and disinhibited behavior, let alone that it even exists, based purely on visual inspection of the observed signals: the peaks and troughs in the ERP are what are most salient to the eye. Yet these are due to different components, orthogonal to component 1. This interpretation of our findings attests to the usefulness of time-frequency representations of EEG signals and decomposing these representations by means of component models.
5.2.1. Normative developmental change and individual differences
Scores on all components decreased with development, which is consistent with findings that structural brain characteristics such as cortical gray matter volume and thickness decrease during adolescence and into early adulthood (e.g., Bethlehem et al., 2022), as well as with findings that gray matter volume is associated with EEG power (Smit et al., 2012). It may be that the brain becomes more efficient at processing information relevant to making the appropriate response in tasks such as the rotated heads task. Inhibitory influences may aid this process by suppressing irrelevant responses. Developmental changes in preparatory set may also be important, in that an appropriate set may facilitate efficient stimulus processing. Connectivity patterns may stabilize and thus support more efficient processing. An “exuberant proliferation” of synapses at the onset of adolescence and subsequent process of synapse elimination are thought to be important determinants of normative developmental change, which may be reflected in decreases in structural measures and – indirectly – EEG activity, such that connections supporting adaptive behavior are reinforced and appropriate responses are prioritized.
Some caution is warranted regarding this interpretation, however. Hill and colleagues have observed increases in auditory ERP amplitude in early adolescence in contrast to the general decrease in amplitude observed in visual ERP amplitude (Hill et al., 1999), indicating that the normative pattern of change in amplitude is modality-specific. It is nevertheless possible that a general explanation for age-related change is possible. The potential extent of neural ensembles recruited by a task may be only weakly related to gray matter volume. Nevertheless, gray matter volume decreases with age in prefrontal and parietal cortices, the latter likely particularly relevant to parietal EEG (Sowell et al., 2003). By contrast, the pattern of age-related change in the supramarginal gyrus, an area implicated in auditory target detection (Nourski, 2017), shows an inverted U-shape with respect to age-related gray matter volume (Sowell et al., 2003) very similar to the pattern of change in auditory P3 amplitude in Hill et al. Thus, the precise nature and timing of change may depend on modality, which in turn is likely influenced by the nature of age-related change in the brain regions involved.
Smaller scores were also associated with disinhibited behavior, in the form of higher levels of alcohol use. Does this suggest that those higher in the liability for externalizing psychopathology or disinhibited behavior are more mature than those lower in the externalizing liability? We think not. First, it is not logically necessary that influences on normative change are identical to influences on individual differences at a given moment in time. It might be that synapse elimination begins prematurely in those with an above-average liability for externalizing -– before some of the main developmentally relevant aspects of adolescence, which could compromise their capacity effectively to navigate developmental tasks. It might be that such individuals generally have fewer random synaptic connections to begin with, limiting the brain’s capacity to respond adaptively to experience. That is, if synapse overproduction at the very beginning of adolescence sets the stage for experience-expectant learning, it is reasonable to ask whether variation in the timing of overproduction and in the overall number of synapses produced might affect brain development and behavioral adaptation. Obviously, this is highly speculative, and direct evidence tying synapse overproduction and pruning to EEG activity is lacking. However, our results are consistent with this type of interpretation of individual differences in the context of normative developmental change.
5.3. Limitations
Our exclusive use of a single electrode limits our understanding of developmental trajectories in time-frequency activity in general. Raw baseline correction of time-frequency activity is common and allows a comparison with the approach of Chorlian et al. However, different baseline correction procedures might produce different age-related effects (cf. Liu et al., 2014). Had we been working with a higher-density electrode array, a multiway component model might have been more appropriate (Helwig and Snodgress, 2019; Malone et al., October 2018). In addition, because participating families were representative of the state of Minnesota during the birth years from which the sample was drawn, the overwhelming majority were white (96%). It seems unlikely that developmental trajectories would be markedly different in other ethnic or racial groups, but this is an empirical question we cannot address in the current sample.
5.4. Conclusions
A common set of dimensions of time-frequency activity characterized EEG activity in a large, representative, population-based sample of adolescents followed into early adulthood. These components are related to several important cognitive and neuromodulatory processes. Trajectories of change in component scores suggest that those aspects of brain development reflected in these components comprise two distinct phases, characterized by marked decreases in component amplitude throughout much of adolescence followed by smaller yet significant rates of decreases into early adulthood. Although the structure of time-frequency activity was stable throughout adolescence and early adulthood, we observed subtle change in component loadings as well. Our findings suggest that striking developmental change in ERPs emerges through gradual change in the magnitude and timing of a stable set of dimensions of time-frequency activity, illustrating the usefulness of time-frequency representations of EEG signals and longitudinal designs for understanding brain development. In addition, we demonstrate that aspects of normative trajectories of change in component scores reflecting EEG responses to stimuli in an oddball paradigm are sensitive to a complex form of potentially problematic behavior, consistent with our notion that such trajectories might serve as candidate endophenotypes for disinhibited behavior or psychiatric disorders (Iacono et al., 2017).
Supplementary Material
Acknowledgments:
Support for the research reported on here and preparation of this manuscript came from National Institutes of Health grants R37DA005147, R37AA009367, R01DA036216, T32DA037183 and R21AA02969.
Footnotes
Most ES participants were assessed by means of a similar, but not identical procedure that included high-density EEG recording at their age-11 assessment and follow-up visits. Only the intake assessment for the 205 participants included here used exactly the same software and recording system as the MTFS participants.
We use the term inflection point in its colloquial sense, as “a moment when significant change occurs or may occur” (from the Merriam-Webster online dictionary) and not in the mathematical sense of a point on a curve reflecting a change in trajectory from concave upward to downward, or vice versa.
Although some might object to our use of the term “slow theta” to refer to components with a peak frequency between 2.5 and 3 Hz, we note that there is a precedent for this in the literature (Goyal et al., 2020) and we argue that the time-frequency properties (loadings) of these two components differ from those of the other components that are lower in frequency. In addition, the precise frequency of synchronous behavior of neural ensembles likely depends on a host of factors, including task, participant age and spatial location. Insisting a priori that theta activity can only comprise activity between 4 and 7 Hz, say, risks reifying the construct, especially when different researchers use different frequency bounds.
Model comparison based on the bias-corrected AIC rather than BIC indicated that the Intercept model was almost as likely as the Baseline model for the late slow-wave component: probability of the Intercept model given the data was 0.479 relative to 0.521 for the Baseline model. However, the probability of the Intercept model by BIC was only 0.064. Therefore, although the Intercept model cannot be ruled out, the weight of evidence favors the Baseline model.
References
- Akaike H (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
- Anderson DR (2008). Model based inference in the life sciences: A primer on evidence (Vol. 31). Springer. [Google Scholar]
- Barry RJ, Steiner GZ, & De Blasio FM (2016). Reinstating the novelty P3. Scientific Reports, 6, 1–13. 10.1038/srep31200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedny M, Paus T, Doesburg SM, Giedd J, Hashemiyoon R, Kold B, Purdon PL, Rakic P, & Sisk CL (2018). Emergent brain dynamics: Prebirth to adolescence (Bensaich AA & Ribary U, Eds.; pp. 179–193). MIT Press. 10.7551/mitpress/11957.003.0013 [DOI] [Google Scholar]
- Begleiter H, Porjesz B, Bihari B, & Kissin B (1984). Event-related brain potentials in boys at risk for alcoholism. Science, 225, 1493–1496. 10.1126/science.6474187 [DOI] [PubMed] [Google Scholar]
- Bernat Edward M., Malone SM, Williams WJ, Patrick CJ, & Iacono WG (2007). Decomposing delta, theta, and alpha time-frequency ERP activity from a visual oddball task using PCA. International Journal of Psychophysiology, 64, 62–74. 10.1016/j.ijpsycho.2006.07.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernat Edward M., Williams WJ, & Gehring WJ (2005). Decomposing ERP time-frequency energy using PCA. Clinical Neurophysiology, 116, 1314–1334. https://doi.org/10.1.1.1054.7024 [DOI] [PubMed] [Google Scholar]
- Bethlehem RA, Seidlitz J, White SR, Vogel JW, Anderson KM, Adamson C, Adler S, Alexopoulos GS, Anagnostou E, Areces-Gonzalez A, et al. (2022). Brain charts for the human lifespan. Nature, 604(7906), 525–533. 10.1038/s41586-022-04554-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter JR, Goldstein H, & Rasbash J (2003). A novel bootstrap procedure for assessing the relationship between class size and achievement. Journal of the Royal Statistical Society: Series C (Applied Statistics), 52(4), 431–443. https://doi.org/0.1111/1467-9876.00415 [Google Scholar]
- Chorlian DB, Rangaswamy M, Manz N, Kamarajan C, Pandey AK, Edenberg H, Kuperman S, & Porjesz B (2015). Gender modulates the development of theta event related oscillations in adolescents and young adults. Behavioural Brain Research, 292, 342–352. 10.1016/j.bbr.2015.06.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chorlian DB, Rangaswamy M, Manz N, Meyers JL, Kang SJ, Kamarajan C, Pandey AK, Wang J-C, Wetherill L, Edenberg H, et al. (2017). Genetic correlates of the development of theta event related oscillations in adolescents and young adults. International Journal of Psychophysiology, 115, 24–39. 10.1016/j.ijpsycho.2016.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coles MGH, & Rugg MD (1996). Event-related brain potentials: An introduction. Oxford University Press. 10.1093/acprof:oso/9780198524168.003.0001 [DOI] [Google Scholar]
- Demiralp T, Ademoglu A, Comerchero M, & Polich J (2001). Wavelet analysis of P3a and P3b. Brain Topography, 13, 251–267. 10.1023/a:1011102628306 [DOI] [PubMed] [Google Scholar]
- Dien J, Spencer KM, & Donchin E (2004). Parsing the late positive complex: Mental chronometry and the ERP components that inhabit the neighborhood of the P300. Psychophysiology, 41, 665–678. 10.1111/j.1469-8986.2004.00193.x [DOI] [PubMed] [Google Scholar]
- Donner TH, & Siegel M (2011). A framework for local cortical oscillation patterns. Trends in Cognitive Sciences, 15, 191–199. 10.1016/j.tics.2011.03.007 [DOI] [PubMed] [Google Scholar]
- Flavell JH (1963). The developmental psychology of Jean Piaget. New York, NY: D. van Nostrand. [Google Scholar]
- Fox J, Weisberg S, & Price B (2020). car: Companion to applied regression. https://CRAN.R-project.org/package=car
- Gilmore CS, Malone SM, Bernat EM, & Iacono WG (2010). Relationship between the P3 event-related potential, its associated time-frequency components, and externalizing psychopathology. Psychophysiology, 47, 123–132. 10.1111/j.1469-8986.2009.00876.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goyal A, Miller J, Qasim SE, Watrous AJ, Zhang H, Stein JM, Inman CS, Gross RE, Willie JT, Lega B, et al. (2020). Functionally distinct high and low theta oscillations in the human hippocampus. Nature Communications, 11(1), 1–10. 10.1038/s41467-020-15670-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu C (2013). Smoothing spline ANOVA models. 2nd ed. In Springer Series in Statistics (2nd ed., Vol. 297). New York, NY: Springer. [Google Scholar]
- Halgren E, Squires N, Wilson C, Rohrbaugh J, Babb T, & Crandall P (1980). Endogenous potentials generated in the human hippocampal formation and amygdala by infrequent events. Science, 210, 803–805. 10.1126/science.7434000 [DOI] [PubMed] [Google Scholar]
- Hallquist MN, & Wiley JF (2018). MplusAutomation: An R package for facilitating large-scale latent variable analyses in Mplus. Structural Equation Modeling, 1–18. 10.1080/10705511.2017.1402334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han C, McGue MK, & Iacono WG (1999). Lifetime tobacco, alcohol and other substance use in adolescent minnesota twins: Univariate and multivariate behavioral genetic analyses. Addiction, 94(7), 981–993. 10.1046/j.1360-0443.1999.9479814.x [DOI] [PubMed] [Google Scholar]
- Harper J, Malone SM, & Iacono WG (2017). Theta-and delta-band EEG network dynamics during a novelty oddball task. Psychophysiology, 54(11), 1590–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helwig NE (2018). bigsplines: Smoothing splines for large samples. https://CRAN.R-project.org/package=bigsplines
- Helwig NE, & Snodgress MA (2019). Exploring individual and group differences in latent brain networks using cross-validated simultaneous component analysis. NeuroImage, 201, 116019. 10.1016/j.neuroimage.2019.116019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hicks BM, Bernat E, Malone SM, Iacono WG, Patrick CJ, Krueger RF, & McGue M (2007). Genes mediate the association between P3 amplitude and externalizing disorders. Psychophysiology, 44(1), 98–105. 10.1111/j.1469-8986.2006.00471.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill SY, Shen S, Locke J, Steinhauer SR, Konicky C, Lowers L, & Connolly J (1999). Developmental delay in P300 production in children at high risk for developing alcohol-related disorders. Biological Psychiatry, 46(7), 970–981. 10.1016/S0006-3223(99)00032-3 [DOI] [PubMed] [Google Scholar]
- Ho TC, Colich NL, Sisk LM, Oskirko K, Jo B, & Gotlib IH (2020). Sex differences in the effects of gonadal hormones on white matter microstructure development in adolescence. Developmental Cognitive Neuroscience, 42, 100773. http://www.sciencedirect.com/science/article/pii/S1878929320300219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 6, 65–70. [Google Scholar]
- Hurvich CM, & Tsai C-L (1989). Regression and time series model selection in small samples. Biometrika, 76(2), 297–307. [Google Scholar]
- Iacono William G., Carlson SR, Malone SM, & McGue M (2002). P3 event-related potential amplitude and the risk for disinhibitory disorders in adolescent boys. Archives of General Psychiatry, 59(8), 750–757. 10.1001/archpsyc.59.8.750 [DOI] [PubMed] [Google Scholar]
- Iacono William G., Carlson SR, Taylor J, Elkins IJ, & McGue M (1999). Behavioral disinhibition and the development of substance-use disorders: Findings from the Minnesota Twin Family Study. Development and Psychopathology, 11(4), 869–900. 10.1017/S0954579499002369 [DOI] [PubMed] [Google Scholar]
- Iacono William G., & Malone SM (2011). Developmental endophenotypes: Indexing genetic risk for substance abuse with the P300 brain event-related potential. Child Development Perspectives, 5, 239–247. 10.1111/j.1750-8606.2011.00205.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacono William G., Malone SM, & Vrieze SI (2017). Endophenotype best practices. International Journal of Psychophysiology, 111, 115–144. 10.1016/j.ijpsycho.2016.07.516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson R (1986). For distinguished early career contribution to psychophysiology: Award address, 1985. A triarchic model of P300 amplitude. Psychophysiology, 23, 367–384. 10.1111/j.1469-8986.1986.tb00649.x [DOI] [PubMed] [Google Scholar]
- Jolliffe IT (2002). Principal component analysis (2. ed.). Springer. [Google Scholar]
- Karakaş Sirel, & Barry RJ (2017). A brief historical perspective on the advent of brain oscillations in the biological and psychological disciplines. Neuroscience and Biobehavioral Reviews, 75, 335–347. 10.1016/j.neubiorev.2016.12.009 [DOI] [PubMed] [Google Scholar]
- Karakaş S, Erzengin OU, & Başar E (2000a). The genesis of human event-related responses explained through the theory of oscillatory neural assemblies. Neuroscience Letters, 285, 45–48. 10.1016/s0304-3940(00)01022-3 [DOI] [PubMed] [Google Scholar]
- Karakaş S, Erzengin OU, & Başar E (2000b). A new strategy involving multiple cognitive paradigms demonstrates that ERP components are determined by the superposition of oscillatory responses. Clinical Neurophysiology, 111, 1719–1732. 10.1016/s1388-2457(00)00418-1 [DOI] [PubMed] [Google Scholar]
- Kass RE, & Raftery AE (1995). Bayes factors. Journal of the American Statistical Association, 90(430), 773–795. 10.1080/01621459.1995.10476572 [DOI] [Google Scholar]
- Keyes MA, Malone SM, Elkins IJ, Legrand LN, McGue M, & Iacono WG (2009). The Enrichment Study of the Minnesota Twin Family Study: Increasing the yield of twin families at high risk for externalizing psychopathology. Twin Research and Human Genetics, 12, 489–501. 10.1375/twin.12.5.489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolev V, Demiralp T, Yordanova J, Ademoglu A, & Isoglu-Alkac U (1997). Time-frequency analysis reveals multiple functional components during oddball P300. Neuroreport, 8(8), 2061–2065. 10.1097/00001756-199705260-00050 [DOI] [PubMed] [Google Scholar]
- Lenroot RK, & Giedd JN (2010). Sex differences in the adolescent brain. Brain and Cognition, 72, 46–55. 10.1016/j.bandc.2009.10.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA, & Rubin DB (2002). Statistical analysis with missing data (Vol. 793). John Wiley & Sons. 10.1002/9781119013563 [DOI] [Google Scholar]
- Liu Z-X, Woltering S, & Lewis MD (2014). Developmental change in EEG theta activity in the medial prefrontal cortex during response control. Neuroimage, 85, 873–887. [DOI] [PubMed] [Google Scholar]
- Lorenzo-Seva U, & ten Berge JMF. (2006). Tucker’s congruence coefficient as a meaningful index of factor similarity. Methodology, 2, 57–64. 10.1027/1614-2241.2.2.57 [DOI] [Google Scholar]
- Loy A, Steele S, & Korobova J (2021). lmeresampler: Bootstrap methods for nested linear mixed-effects models. https://CRAN.R-project.org/package=lmeresampler
- Magee L (1990). R2 measures based on wald and likelihood ratio joint significance tests. The American Statistician, 44(3), 250–253. 10.1080/00031305.1990.10475731 [DOI] [Google Scholar]
- Malone SM, Wilson S, Bair JL, McGue M, & Iacono WG (2021). A co-twin–control analysis of adolescent and young adult drinking effects on learning and memory. Addiction, 116(7), 1689–1699. 10.1111/add.15334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone S, Helwig N, Harper J, & Iacono W (October 2018). Substance-abuse risk among adolescents is associated with increased impulsive errors and decreased theta power in a multiway analysis of Nogo EEG activity (Vol. 55, p. S123). Society for Research in Psychophysiological Research. [Google Scholar]
- MATLAB. (2012). Version 7.14.0.739 (R2012a). The MathWorks Inc. [Google Scholar]
- McGue M, Malone S, Keyes M, & Iacono WG (2014). Parent–offspring similarity for drinking: A longitudinal adoption study. Behavior Genetics, 44(6), 620–628. 10.1007/s10519-014-9672-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén LK, & Muthén BO (1998–2017). Mplus user’s guide (Eighth). Muthén & Muthén. https://www.statmodel.com/ [Google Scholar]
- Nourski KV (2017). Auditory processing in the human cortex: An intracranial electrophysiology perspective. Laryngoscope Investigative Otolaryngology, 2(4), 147–156. 10.1002/lio2.73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patrick CJ, Bernat EM, Malone SM, Iacono WG, Krueger RF, & McGue M (2006). P300 amplitude as an indicator of externalizing in adolescent males. Psychophysiology, 43(1), 84–92. 10.1111/j.1469-8986.2006.00376.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen AC, Crockett L, Richards M, & Boxer A (1988). A self-report measure of pubertal status: Reliability, validity, and initial norms. Journal of Youth and Adolescence, 17, 117–133. 10.1007/bf01537962 [DOI] [PubMed] [Google Scholar]
- Pinheiro J, Bates D, & R-core. (2019). nlme: Linear and nonlinear mixed effects models. https://CRAN.R-project.org/package=nlme
- Polich J (2007). Updating P300: An integrative theory of P3a and P3b. Clinical Neurophysiology, 118, 2128–2148. 10.1016/j.clinph.2007.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/ [Google Scholar]
- Revelle W (2021). psych: Procedures for psychological, psychometric, and personality research. Northwestern University. https://CRAN.R-project.org/package=psych
- Riggins T, & Scott LS (2020). P300 development from infancy to adolescence. Psychophysiology, 57, e13346. 10.1111/psyp.13346 [DOI] [PubMed] [Google Scholar]
- Robins L, Cottler L, & Babor T (1990). Composite international diagnostic interview-expanded substance abuse module (CIDI-SAM). St. Louis, MO: Authors. [Google Scholar]
- Schulz KM, Molenda-Figueira HA, & Sisk CL (2009). Back to the future: The organizational–activational hypothesis adapted to puberty and adolescence. Hormones and Behavior, 55, 597–604. 10.1016/j.yhbeh.2009.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461–464. https://www.jstor.org/stable/2958889 [Google Scholar]
- Smit DJ, Boomsma DI, Schnack HG, Pol HEH, & Geus EJ de. (2012). Individual differences in EEG spectral power reflect genetic variance in gray and white matter volumes. Twin Research and Human Genetics, 15(3), 384–392. 10.1017/thg.2012.6 [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, & Toga AW (2003). Mapping cortical change across the human life span. Nature Neuroscience, 6(3), 309–315. 10.1038/nn1008 [DOI] [PubMed] [Google Scholar]
- Sterba SK (2014). Fitting nonlinear latent growth curve models with individually varying time points. Structural Equation Modeling: A Multidisciplinary Journal, 21(4), 630–647. 10.1080/10705511.2014.919828 [DOI] [Google Scholar]
- Tucker LR (1951). A method for synthesis of factor analysis studies. Educational Testing Service; Princeton NJ. [Google Scholar]
- Verleger R (2020). Effects of relevance and response frequency on P3b amplitudes: Review of findings and comparison of hypotheses about the process reflected by P3b. Psychophysiology, 57, e13542. 10.1111/psyp.13542 [DOI] [PubMed] [Google Scholar]
- Wagenmakers E-J (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin & Review, 14(5), 779–804. 10.3758/BF03194105 [DOI] [PubMed] [Google Scholar]
- Wetzels R, Matzke D, Lee MD, Rouder JN, Iverson GJ, & Wagenmakers E-J (2011). Statistical evidence in experimental psychology: An empirical comparison using 855 t tests. Perspectives on Psychological Science, 6(3), 291–298. 10.1177/1745691611406923 [DOI] [PubMed] [Google Scholar]
- Williams WJ (1996). Reduced interference distributions: Biological applications and interpretations. Proceedings of the IEEE, 84, 1264–1280. 10.1109/5.535245 [DOI] [Google Scholar]
- Yoon HH, Malone SM, & Iacono WG (2015). Longitudinal stability and predictive utility of the visual P3 response in adults with externalizing psychopathology: Longitudinal P3 investigation of EXT. Psychophysiology, 52, 1632–1645. 10.1111/psyp.12548 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


