Spatio-Temporal Representation of the Pitch of Harmonic Complex Tones in the Auditory Nerve

Abstract

The pitch of harmonic complex tones plays an important role in speech and music perception and the analysis of auditory scenes, yet traditional rate-place and temporal models for pitch processing provide only an incomplete description of the psychophysical data. In order to test physiologically a model based on spatio-temporal pitch cues created by the cochlear traveling wave (Shamma, J Acoust Soc Am 78: 1622–1632), we recorded from single fibers in the auditory nerve of anesthetized cat in response to harmonic complex tones with missing fundamentals and equal-amplitude harmonics. We used the principle of scaling invariance in cochlear mechanics to infer the spatiotemporal response pattern to a given stimulus from a series of measurements made in a single fiber as a function of fundamental frequency F0. We found that spatio-temporal cues to resolved harmonics are available for F0s between 350 Hz and 1100 Hz and that these cues are more robust than traditional rate-place cues at high stimulus levels. The lower F0-limit is determined by the limited frequency selectivity of the cochlea, while the upper limit is caused by the degradation of phase-locking to the stimulus fine structure at high frequencies. The spatio-temporal representation is consistent with the upper F0-limit to the perception of the pitch of complex tones with a missing fundamental, and its effectiveness does not depend on the relative phase between resolved harmonics. The spatio-temporal representation is thus consistent with key trends in human psychophysics.

INTRODUCTION

Harmonic complex tones present in speech, animal vocalizations, and the sounds of musical instruments produce a strong pitch sensation at their fundamental frequency F0. Although the pitch of complex tones plays an important role in music, speech, and auditory scene analysis, the neural mechanisms for pitch perception are still poorly understood. Despite the report of pitch-selective neurons in the auditory cortex of a primate (Bendor and Wang, 2005), the computations underlying these cortical responses and the neural codes upon which these computations operate are unknown. Studies of the coding of harmonic complex tones in the auditory nerve (AN) and cochlear nucleus (CN) have primarily focused on temporal pitch cues available in interspike interval distributions (Javel, 1980; Evans, 1983; Palmer, 1990; Shofner, 1991; Rhode, 1995; Cariani and Delgutte, 1996a, b; Shofner, 1999; Wiegrebe and Winter, 2001; Winter et al., 2001; Cedolin and Delgutte, 2005; Sayles and Winter, 2008). These cues are closely related to the autocorrelation model of pitch, which accounts for a wide variety of pitch phenomena (Licklider, 1951; Meddis and Hewitt, 1991b, a; de Cheveigné, 2005). Fewer studies have focused on “place” or “spectral” cues based on the cochlear frequency map and the mechanical frequency analysis of individual harmonics in the cochlea (Sachs and Young, 1979; Cedolin and Delgutte, 2005). Such place cues provide an appropriate input to harmonic template models for pitch extraction (Goldstein, 1973; Wightman, 1973; Cohen et al., 1994). While either rate-place or interspike-interval information from AN fibers in cat supports precise pitch estimation over the F0 range of cat vocalizations (500–1000 Hz), neither representation is entirely consistent with human psychophysical data (Cedolin and Delgutte, 2005). The rate-place representation degrades with increasing sound level and also fails to predict the existence of an upper frequency limit for pitch (Schouten et al., 1962; Moore, 1973). The interval representation does not account for the greater salience of pitch based on resolved harmonics compared to pitch based on unresolved harmonics (Carlyon and Shackleton, 1994; Carlyon, 1998). Here, we investigate an alternative, spatio-temporal representation of pitch (Shamma, 1985) aimed at combining the advantages and overcoming the limitations of traditional representations.

Sinusoidal stimulation of the cochlea gives rise to a traveling wave that moves from base to apex, progressively slowing down as it approaches the cochlear location tuned to the stimulus frequency, where the phase of basilar membrane velocity changes rapidly (Robles and Ruggero, 2001). At frequencies within the range of phase-locking, this rapid phase transition is reflected in the timing of AN spike discharges (Anderson et al., 1970; Pfeiffer and Kim, 1975; van der Heijden and Joris, 2006; Palmer and Shackleton, 2009; Temchin and Ruggero, 2010). For harmonic complex tones, a rapid phase transition is expected to occur at the spatial locations tuned to each resolved harmonic (Figure 1). These spatio-temporal cues to resolved harmonics could be extracted by a neural mechanism sensitive to the relative timing of spikes from adjacent cochlear locations (Shamma, 1985; Carney, 1990a).

Figure 1.

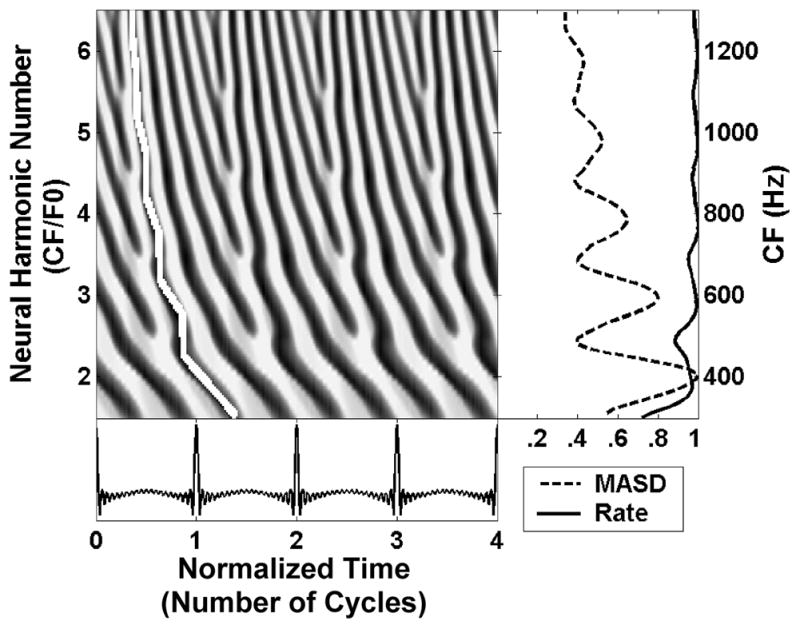
Spatio-temporal activity pattern of the Zhang et al. (2001) human peripheral auditory model in response to a harmonic complex tone with F0 of 200 Hz at 50 dB SPL. Left: The model response is displayed as a function of time (in dimensionless units t × F0) and cochlear place, which maps to CF, expressed as the dimensionless ratio CF/F0 (“neural harmonic number”). Fast variations in response latency with CF at integer neural harmonic numbers are highlighted by the white line. The right panels shows the spatial profiles of average rate (solid line) and mean absolute spatial derivative (MASD, dashed), derived from the spatio-temporal pattern on the left. The rate and MASD profiles are normalized by their respective maximum value.

We tested the spatio-temporal representation of pitch by recording the responses of AN fibers in anesthetized cats to harmonic complex tones with F0 varied in fine increments. We find that this representation is more robust to variations in stimulus level than the rate-place representation and also predicts an upper frequency limit to pitch consistent with psychophysical data.

MATERIALS AND METHODS

Spatio-temporal pitch cues in a peripheral auditory model

The spatio-temporal representation of pitch is based on phase transition cues to the frequencies of resolved harmonics created by the cochlear traveling wave. Figure 1 shows the spatio-temporal pattern of AN activity produced by a physiologically-realistic peripheral auditory model (Zhang et al., 2001) in response to a harmonic complex tone with missing fundamental at 200 Hz. The response pattern is shown as a function of both time (expressed in dimensionless units t×F0) and position along the cochlea, which maps to characteristic frequency (CF) The CF is expressed by the dimensionless ratio CF/F0 which we call “neural harmonic number”. In this example, a neural harmonic number of 3 corresponds to a CF of 600 Hz. As predicted, the latency of the traveling wave changes more rapidly with CF at cochlear locations tuned to low-order harmonics than for CFs in between two harmonics (white line in Figure 1). To extract these cues, we use a spatial derivative operation that simulates a hypothetical lateral inhibitory mechanism operating upon the spatio-temporal pattern of AN activity (Shamma, 1985). Specifically, we compute the point-by-point difference between adjacent rows in Fig. 1, then integrate the absolute value of the difference over time. The resulting “mean absolute spatial derivative” (MASD) shows local maxima at CFs corresponding to the frequencies of harmonics 2–6, while the average firing rate is largely saturated at this stimulus level (50 dB SPL per component). Thus, the model predicts that spatio-temporal pitch cues persist at stimulus levels where the rate-place representation is degraded.

The most direct way to study the spatio-temporal representation of pitch would be to measure the AN response to a given harmonic complex tone as a function of both time and CF. Since a fine, regular sampling of the tonotopic axis is hard to achieve with single unit recordings, we relied instead on the principle of scaling invariance in cochlear mechanics (Zweig, 1976) to infer the spatio-temporal response pattern from measurements made at a single cochlear location. In a cochlea with perfect scaling invariance, the response to a pure tone of frequency f at the cochlear location tuned to CF depends only on the ratio f/CF (Zweig, 1976). This means that the magnitude and phase of the cochlear response to a pure tone of frequency f_d at the location tuned to CF_d are equal to the magnitude and the phase of the response of the cochlear location CF_p to a f tone of frequency $f_p={CF}_p{f}_d/{CF}_d$. Thus, in order to obtain the spatial pattern of response to a tone of desired frequency f_d for the set of cochlear locations tuned to {CFd}, it suffices, in principle, to measure responses at one location tuned to CF_p to the set of probe frequencies $\{f_p\}={CF}_p{f}_d/\{{CF}_d\}$. The same reasoning applies to a harmonic complex tone in which all the components are multiples of a common fundamental. Thus, the spatio-temporal response pattern to a complex tone with a given F0 can, in principle, be inferred from the responses recoded in a single AN fiber to a series of complex tones with varying F0.

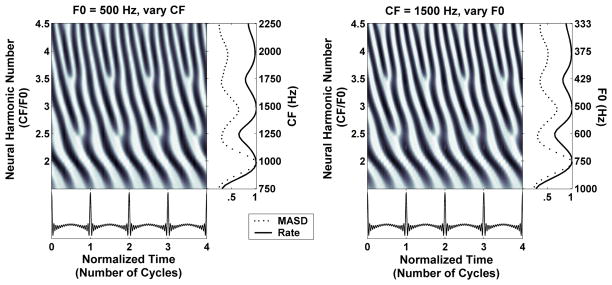
Figure 2 illustrates the scaling invariance principle using the Zhang et al. (2001) model of peripheral auditory processing for cat. The left panel shows the model spatio-temporal response pattern to a harmonic complex tone with fixed F0 (500 Hz) for CFs ranging from 750 to 2250 Hz. The right panel shows the model temporal response patterns at a single cochlear place (CF₀ = 1500 Hz) to a series of complex tones with F0s varying from 333 to 1000 Hz. The F0s and CFs were chosen so that the “neural harmonic number” CF/F0 ranges from 1.5 to 4.5 in both panels. In addition, the time axis is expressed in dimensionless units τ = t×F0 (number of stimulus cycles). The spatio-temporal response patterns for the two conditions are nearly indistinguishable: they both show fast latency changes around integer values of neural harmonic number (2, 3, 4), and relatively more constant latencies around non-integer harmonic numbers (2.5, 3.5). Average discharge rate and MASD, computed as in Figure 1, also exhibit nearly identical features in the two panels, with peaks at integer values of neural harmonic number and valleys in between. Thus, these model simulations support the use of scaling invariance to infer the response of a population of AN fibers to a given complex tone by measuring the response of a single AN fiber to a series of complex tones with varying F0.

Figure 2.

Illustration of the principle of cochlear scaling invariance using the Zhang et al. (2001) peripheral auditory model for cat. Left: Spatio-temporal response pattern of the model AN for CFs between 750 and 2250 Hz to a harmonic complex tone with an F0 of 500 Hz at 40 dB SPL. The response is displayed as a function of time (in normalized units t × F0) and cochlear place expressed as neural harmonic number (CF/F0). Right: Temporal response pattern of one model AN fiber (CF = 1500 Hz) to a series of harmonic complex tones with F0s varying from 333 to 1000 Hz. The response is shown in the same dimensionless coordinates as in the left. Rightmost panels show the spatial profiles of average discharge rate (solid lines) and mean absolute spatial derivative (dashed) derived from the response patterns at their immediate left. Rate and MASD profiles are normalized by their maximum.

Scaling invariance is a good approximation when applied to a local region of the cochlea, but does not hold over wide cochlear spans (Shera and Guinan, 2003; van der Heijden and Joris, 2006). Since, for each fiber, F0 was varied over a limited range in our experiments (about 1.6 octave), deviations from scaling invariance may not present a major problem, as Figure 2 suggests. This point is addressed further in the Discussion.

Neurophysiological procedure

Methods for recording from auditory-nerve fibers in anesthetized cats were as described by Cedolin and Delgutte (2005) and were approved by the Animal Care and Use Committees of both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology. Cats were anesthetized with Dial in urethane (75 mg/kg), with supplementary doses given as needed to maintain an areflexic state. The posterior fossa was opened and the cerebellum retracted to expose the auditory nerve. The tympanic bullae were opened to expose the round window. Throughout the experiment the cat was given injections of dexamethasone (0.26 mg/kg, I.M. every 4 hours) to prevent brain swelling, and Ringer’s solution (50 ml/day, I.V.) to prevent dehydration. General physiological state was assessed by monitoring heart rate, respiratory rate, exhaled CO2 concentration, and rectal temperature, which was maintained at 37°C by a thermostat-controlled heating pad.

The cat was placed on a vibration-isolated table in an electrically-shielded, soundproof chamber. A silver electrode positioned near the round window was used to measure the compound action potential of the AN in response to click stimuli, in order to assess the condition and stability of cochlear function.

Sound was delivered to the cat’s ear through a calibrated closed acoustic assembly driven by an electrodynamic speaker (Realistic 40–1377). Stimuli were generated by a 16-bit digital-to-analog converter (National Instruments NIDAC 6052E) using sampling rates of 20 or 50 kHz. Stimuli were digitally filtered to compensate for the transfer characteristics of the acoustic system.

Spikes were recorded with glass micropipettes filled with 2 M KCl. The electrode was inserted into the nerve and then mechanically advanced using a micropositioner (Kopf 650). The electrode signal was bandpass filtered (0.3–3 kHz), and fed to a custom spike detector. The times of spike peaks were recorded with 1-μs resolution and saved to disk for subsequent analysis.

A click at approximately 60 dB SPL was used as search stimulus. Upon isolation of a single unit, a frequency tuning curve was measured by an automatic tracking algorithm (Kiang and Moxon, 1974) using 50-ms tone bursts to determine the CF. The spontaneous firing rate (SR) of the fiber was measured over 20 s. The responses to complex-tone stimuli were then studied.

Stimuli

Stimuli were series of harmonic complex tones consisting of 19 equal-amplitude harmonics (numbers 2–20, i.e. excluding the fundamental). The fundamental frequency (F0) was stepped up and down such that the ratio of fiber’s CF to F0 (the “neural harmonic number”) typically varied from 1.5 to 4.5 in increments of ±1/8. This F0 variation causes harmonics 2 to 4 (which are important for determining the pitch of missing fundamental stimuli) to successively traverse the auditory filter centered at the CF. If these harmonics are resolved by the cochlea, there should be a regular modulation in both firing rate and response latency as F0 varies. Each complex tone series consisted of 25 ascending F0 steps and 25 descending steps, each lasting 200 ms, including a 20-ms transition during which the waveform for one F0 gradually decayed while overlapping with the gradual build up of the waveform for the subsequent F0. Responses were typically collected over 20 repetitions of the 10-sec stimulus with no interruption.

The sound pressure level of each harmonic was initially set at 10–15 dB above the fiber's threshold for a pure tone at CF. When possible, the stimulus level was then varied over a 20–30 dB range to investigate the robustness of the spatio-temporal representation. All stimulus levels in this paper refer to the sound pressure of one frequency component of the complex tone. Since the stimuli contain 19 equal-amplitude components, the overall sound pressure level is 12.8 dB higher.

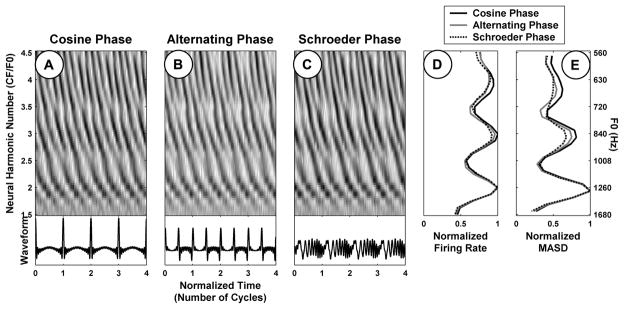
Psychophysical studies show that the pitch and pitch strength of harmonic complex tones containing resolved harmonics are largely independent of the phase relationships among harmonics (Houtsma and Smurzynski, 1990; Carlyon and Shackleton, 1994; Bernstein and Oxenham, 2005). In order to evaluate the robustness of the spatiotemporal representation to the phase pattern, three versions of each stimulus were generated with different phase relationships among the harmonics: cosine phase, alternating sine-cosine phase, and negative “Schroeder” phase (Schroeder, 1970). The three stimuli have the same power spectrum and autocorrelation function, but sharply differ in their temporal envelopes (Figure 9). The cosine-phase stimulus has a very “peaky” envelope periodic at F0. The envelope of the alternating-phase stimulus is also very peaky, but its periodicity is at 2×F0, even though the periodicity of the waveform remains at F0. Finally, a Schroeder phase relationship among the harmonics ensures the envelope is nearly flat.

Figure 9.

Effect of phase relationship among the harmonics on rate-place and spatio-temporal representations of pitch for one AN fiber (CF = 2530 Hz). A–C: Pseudo spatio-temporal response patterns to complex tone series with harmonics in cosine, alternating (sine-cosine), and Schroeder phase, respectively. The corresponding average rate and MASD profiles, normalized by their respective maxima, are plotted in D and E, respectively.

Data Analysis

The first step in the analysis was to select the spikes occurring during the 180-ms steady-state portion of each F0 step, excluding the 20-ms transition period between steps. The non-scaling conduction delay for each cochlear location (T_d parameter in Carney and Yin, 1988) was subtracted from the time of each spike. Period histograms were computed using 50 bins per cycle of F0 and displayed as a function of both time and F0, as in Figure 3. Period histograms obtained with the same F0 during the ascending and descending parts of the F0 sequence were added together. To apply scaling invariance, the time and F0 axes were expressed in dimensionless units τ = t×F0 (number of stimulus cycles) and n = CF/F0 (neural harmonic number), respectively (Fig. 3, left panels). Two metrics were computed from the resulting pseudo spatio-temporal response pattern: the average discharge rate, obtained by integrating each period histogram over time and converting to spikes/s, and the mean absolute spatial derivative (MASD), obtained by differentiating the pseudo spatio-temporal pattern with respect to neural harmonic number, then taking the absolute value and integrating over time.

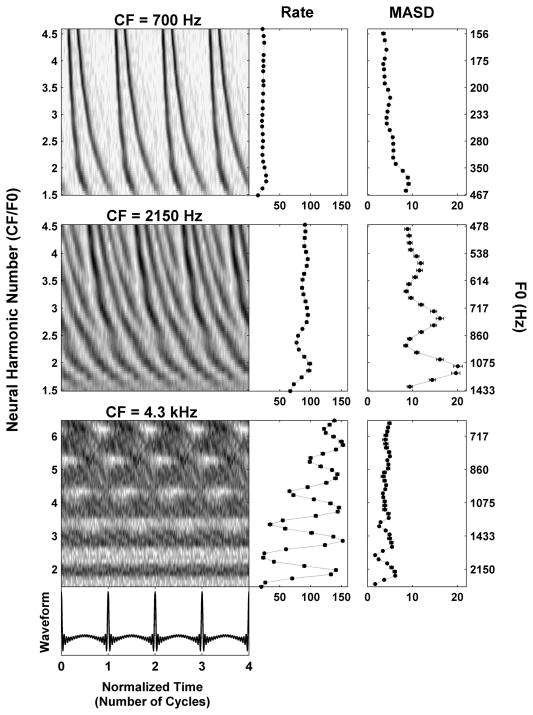
Figure 3.

Responses of three AN fibers with CFs of 700 Hz (top), 2150 Hz (middle) and 4300 Hz (bottom) to series of harmonic complex tones in cosine phase. Left panels: Pseudo spatio-temporal discharge pattern, displayed as a function of normalized time (horizontal axis) and neural harmonic number CF/F0 (vertical axis). Right panels: Firing rate and MASD derived from the corresponding pseudo spatio-temporal response patterns on the left.

Both the average rate and the MASD were plotted against neural harmonic number after smoothing by a three-point triangular filter with weights [¼, ½, ¼] (Fig. 3, right panels). Integer values of neural harmonic number occur when the fiber CF coincides with one of the harmonics of the stimulus, while the neural harmonic number is an odd integer multiple of 0.5 (2.5, 3.5, 4.5) when the CF falls halfway between two harmonics. Resolved harmonics are expected to result in peaks in either rate or MASD (or both) near integer values of the neural harmonic number.

We used “bootstrap” resampling (Efron and Tibshirani, 1993) of the spike trains recorded from each fiber in order to evaluate the statistical reliability of the estimates of average rate and MASD. Specifically, one hundred resampled data sets were generated by drawing with replacement from the set of spike trains, typically recorded over 20 stimulus repetitions. For each F0, spike trains in response to the ascending and descending part of the F0 sequence were drawn independently from each other. The average discharge rate and MASD were computed from each bootstrap data set, and the standard deviations of these measures were used to obtain error bars on the estimates.

To quantitatively describe the data from each fiber, a simple mathematical function was fit separately to profiles of average rate and MASD against neural harmonic number n:

$$f(n)=Acos(2\pi \varphi n)e^{\frac{-n}{n_0}}+{Be}^{\frac{-n}{n_0}}+C$$ (1)

This expression is the sum of an exponentially-decaying sinusoid in cosine phase, a constant term C and an exponential term. ϕ represents the normalized frequency of the oscillating component relative to the CF; the sinusoid peaks exactly at integer values of the neural harmonic number when ϕ=1. The function has 5 free parameters: the amplitude A and normalized frequency ϕ of the damped oscillation, the decay parameter n₀ of the exponentials (constrained to be the same for the baseline and oscillatory components), the amplitude B of the exponential term, and the constant term C. Equation (1) was fit to the data by the least squares method using the Levenberg-Marquardt algorithm as implemented by Matlab’s “lsqcurvefit” function. Figure 5A shows example fits to rate and MASD profiles for one AN fiber.

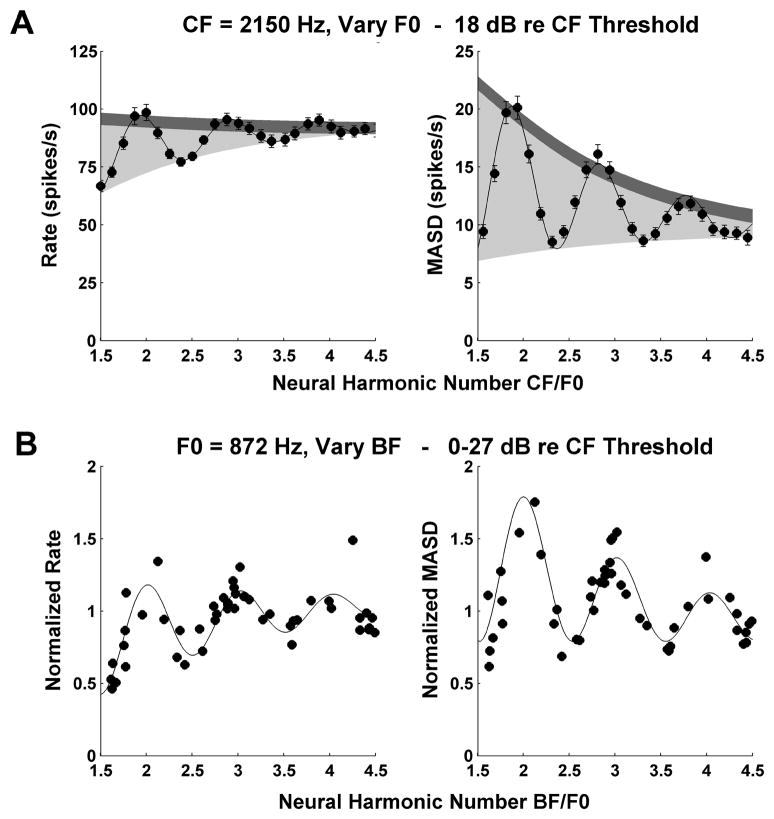
Figure 5.

A: Profiles of average rate (left) and MASD (right) against neural harmonic number for an AN fiber (CF = 2150 Hz, same fiber as in middle panel of Fig. 3) in response to a series of harmonic complex tones at 18 dB re. threshols. Filled circles show the data points, solid lines show best fitting curves based on Equation (1). Light shadings indicate the area between the top and bottom envelopes of the fitted curve. Dark shadings correspond to two typical standard deviations of the data points, estimated by bootstrap (see Methods). The ratio of these two quantities is used as an estimate of the strength of the pitch cues provided by each neural representation.

B: Interpolation method used for replotting rate and MASD as a function of best frequency (BF) across the AN fiber population for a specific stimulus F0 (872 Hz). Each symbol shows the normalized, interpolated rate (left) or MASD (right) at F0=872 Hz for one AN fiber. Solid lines show the best fitting curves based on Equation 1. The BF estimated from responses to harmonic complex tones is expressed in dimensionless units (BF/F0). Harmonics in cosine phase.

In order to assess the reliability of the rate-place and spatio-temporal cues to resolved harmonics, we compared the ability of the five-parameter model (Equation 1) to fit each rate-place or MASD profile with that of a three-parameter model lacking an oscillatory component (i.e. with A set to 0 in Equation 1). The pitch cues were only considered reliable if an F-test for the ratio of variances of the residuals indicated a significantly better fit (p<0.01) for the model with an oscillatory component.

In order to quantitatively characterize how well resolved harmonics are represented in rate and MASD profiles, we used the oscillatory fitted curves to compute metrics such as the “harmonic strength” (see page 13) and the best frequency for complex tones, the product ϕ×CF (Fig. 8). Specifically, we fit the model to 100 bootstrap resamplings of the rate and MASD data for each F0 series and computed the metrics for each bootstrap resampling. In Figures 6–8, we report the median values of these metrics across all bootstrap resamplings. These median values showed less variability across fibers compared to estimates based on the original data set.

Figure 8.

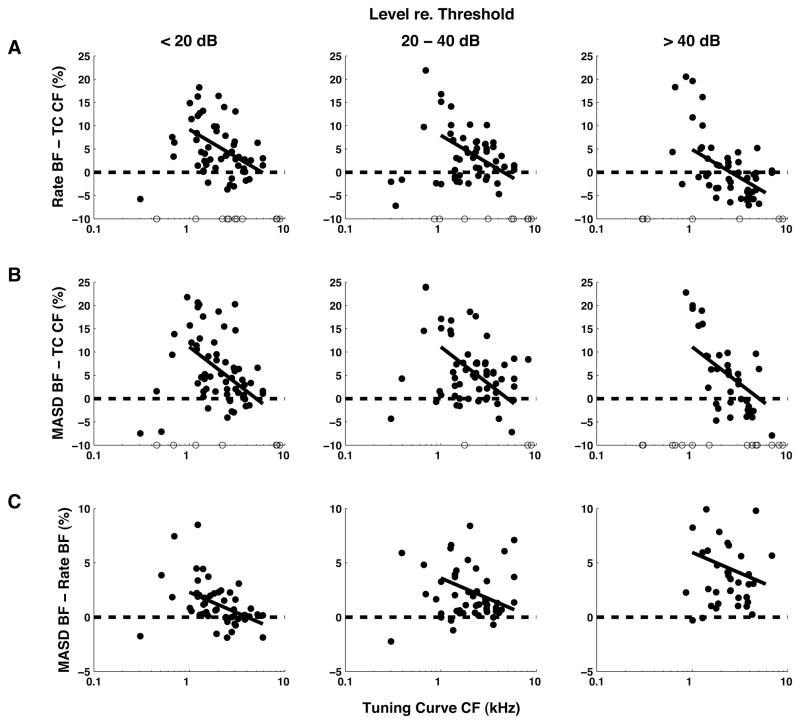
Relationships between BF estimated from rate and MASD profiles in response to harmonic complex tones, and CF estimates from pure-tone tuning curves. Filled circles show differences between estimates, expressed as a percentage of the tuning-curve CF. Results are grouped by stimulus level relative to each fiber’s threshold for a pure tone at CF. Open circles along the horizontal axis indicate measurements for which a BF could not be reliably estimated from rate or MASD profiles. Solid lines show the best fitting linear models (based on an analysis of covariance) across all levels for CFs above 1 kHz. Harmonics in cosine phase.

Figure 6.

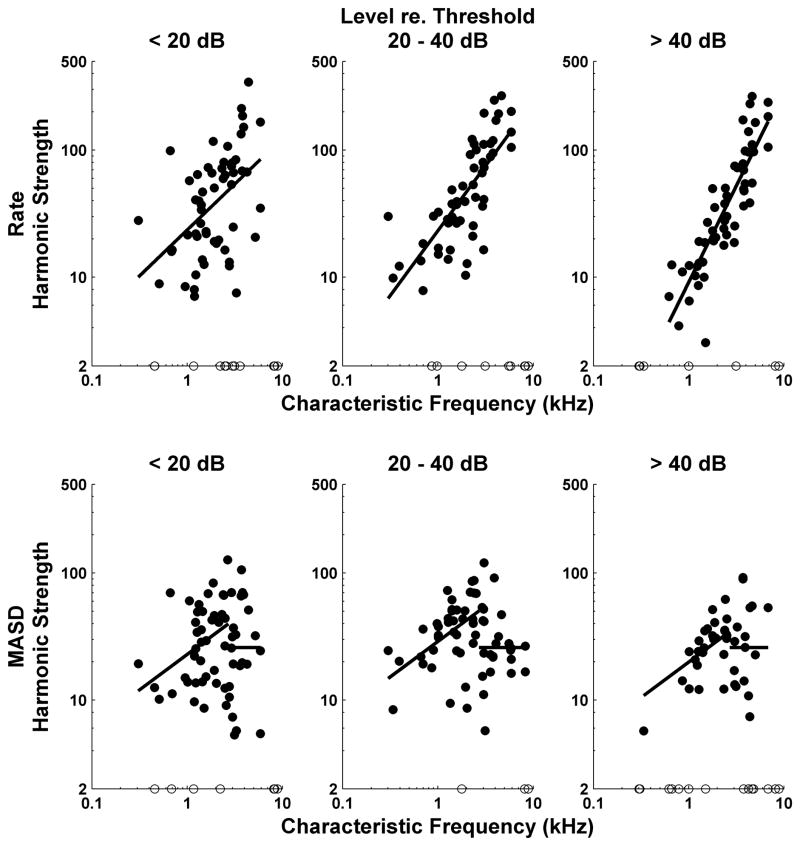
Strength of rate-place and spatio-temporal cues to resolved harmonics as a function of CF for the entire set of responses to complex tone series with harmonics in cosine phase. Filled circles show harmonic strengths computed from best-fitting curves to profiles of firing rate (top) and MASD (bottom) against neural harmonic number. Open circles along the horizontal axis show data points for which the best fitting curve had no reliable oscillatory component. Results are grouped by level relative to each fiber’s threshold for a pure tone at CF. Solid lines show best fitting lines across all level groups obtained from analyses of covariance. Separate analyses were performed for rate and MASD, and for CFs below and above 2700 Hz, respectively.

RESULTS

Our results are based on responses to 240 harmonic complex tones series recorded from 102 auditory-nerve fibers in 5 cats. Of these, 72 fibers (71%) had high SR (> 18 spikes/s, Liberman 1978), 4 had low SR (< 0.5 spike/s), and 26 (25%) had medium SR. The CFs of the fibers ranged from 300 Hz to 5900 Hz, with 55% between 1 and 3 kHz. We focused on fibers with CFs below 5–6 kHz because phase locking to the waveform fine time structure is critical for the spatio-temporal representation. Stimulus levels ranged from 5 to 85 dB SPL per component, with 80% of the data between 25 and 65 dB SPL.

Spatio-temporal pitch cues in single fiber responses

Figure 3 shows the responses to complex tone series with harmonics in cosine phase for three auditory-nerve fibers with CFs of 700 Hz (A), 2150 Hz (B) and 4300 Hz (C), respectively. The left panels show pseudo spatio-temporal patterns (based on period histograms) as a function of both normalized time (t×F0, horizontal axis) and neural harmonic number (CF/F0, vertical axis). The right panels show the average discharge rate and the mean absolute spatial derivative (MASD) obtained from the pseudo spatio-temporal response patterns on the left (see Methods) as a function of neural harmonic number. An additional vertical axis on the right shows the stimulus F0s corresponding to the neural harmonic numbers on the left axis.

For the low-CF fiber (Fig. 3, top), the response latency decreases monotonically with increasing neural harmonic number. This smooth variation is reflected in the absence of peaks at integer neural harmonic numbers in either rate or MASD. Thus, at this low CF, neither the rate-place nor the spatio-temporal representation provides evidence for resolved harmonics for F0s in the range tested (156–467 Hz). This is consistent with a previous report that rate-place cues to resolved harmonics are rarely observed for F0s below 400–500 Hz in cat due to the limited cochlear frequency resolution at low CFs (Cedolin and Delgutte, 2005).

The pseudo spatio-temporal response pattern of the fiber with CF at 2150 Hz (Fig. 3, middle) does show staircase-like variations in response latency with neural harmonic number that are qualitatively similar to those predicted by the peripheral auditory model in Figure 2. Specifically, the response latency varies rapidly with neural harmonic number near integer neural harmonic numbers, while it changes more slowly at neural harmonic numbers that are half way between integers. As a result, the MASD shows local maxima near neural harmonic numbers 2, 3 and 4, thus providing evidence for spatio-temporal pitch cues in the AN response. The mean firing rate also shows peaks at integer neural harmonic numbers, although they are less pronounced than those of the MASD at this moderate stimulus level (20 dB re. threshold).

The pseudo spatio-temporal response pattern of the 4.3 kHz fiber (Fig. 3, bottom) shows dark horizontal bands representing increased activity at integer values of the neural harmonic number. These bands are reflected in the rate-place profile, where harmonics 2-6 are resolved despite the relatively high stimulus level (30 dB re. threshold). This strong rate-place coding is consistent with the progressive sharpening of the bandwidths of cochlear filters relative to their center frequency with increasing CF (Kiang et al., 1965; Shera et al., 2002; Cedolin and Delgutte, 2005). In contrast, no obvious latency cues are apparent in the pseudo spatio-temporal response pattern, and the MASD only shows small peaks at neural harmonic numbers 2 and 3, which likely reflect increased Poisson-like noise when the firing rate is high rather than genuine spatio-temporal cues. This degradation in spatio-temporal cues at higher CFs is consistent with the steep decline in phase locking to the fine time structure above 3 kHz in the cat AN (Johnson, 1980).

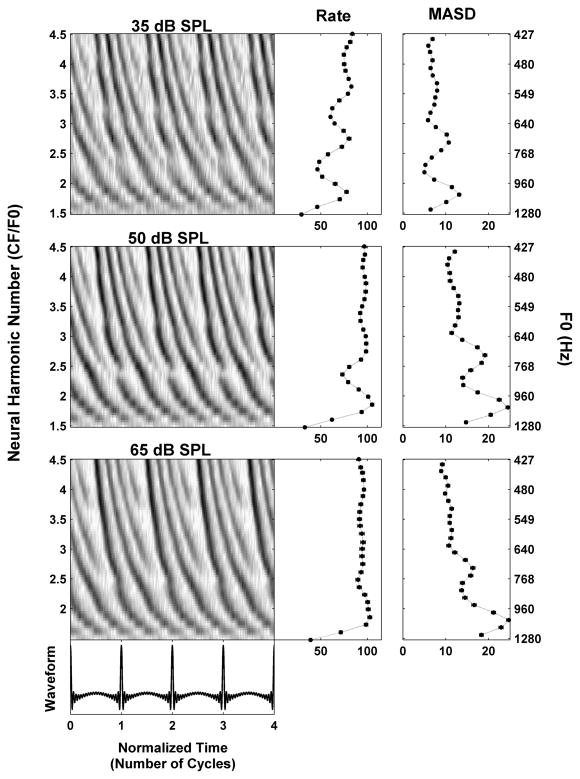
We have hypothesized that the spatio-temporal representation of pitch may be effective at higher stimulus levels where the rate-place representation breaks down due to saturation of the rate-level functions. Figure 4 shows the responses of an AN fiber (CF = 1920 Hz) to a series of harmonic complex tones at 10, 25 and 40 dB above the fiber’s threshold at CF (25 dB SPL). At the lower level (top), the second, third, and possibly fourth harmonic appear as distinct peaks in both rate and MASD profiles. As the level of each harmonic is increased to 25 dB above threshold (middle), the rate begins to saturate so that only the second harmonic is convincingly resolved. In contrast, strong latency cues to the second, third and possibly fourth harmonic are still present in the pseudo spatio-temporal response pattern, resulting in corresponding peaks in the MASD. At the highest level tested (40 dB re. threshold, bottom) the rate is almost completely saturated, while peaks at the second and third harmonic are still detectable in the MASD. This example supports our hypothesis that a spatio-temporal representation of pitch might still work at stimulus levels for which a strictly rate-based representation is severely degraded.

Figure 4.

Effect of stimulus level on the response of an AN fiber (CF = 1920 Hz) to a series of harmonic complex tones in cosine phase. Response is shown at 35 (top), 50 (middle) and 65 (bottom) dB SPL, respectively. The threshold for a pure tone at CF was 25 dB SPL. Same layout as in Figure 3.

Spatio-temporal representation of pitch by the AN fiber population

To quantitatively compare the strengths of the pitch cues provided by the rate-place and spatio-temporal representations, a mathematical function was fit independently to the profiles of average rate and MASD against neural harmonic number for each set of measured responses (see Methods). An example is shown in Figure 5A for the same fiber as in the middle panels of Figure 3 (CF = 2150 Hz). The fitted curves (solid lines) closely capture the oscillations in both rate and MASD profiles. The more pronounced these oscillations, the better individual harmonics are resolved. In Figure 5A, the oscillations for the MASD seem more prominent than those for the rate. We use the area between the top and bottom envelopes of the fitted curve (light shadings in Figure 5A) to characterize the strength of the oscillations in the rate and MASD profiles. Since the two metrics (rate and MASD) have different values (and units), the oscillation area was normalized by the median standard deviation of the data points (dark shadings in Fig. 6) in order to allow direct comparisons between the two representations. The standard deviations are obtained by bootstrap resampling of the spike trains across stimulus presentations (see Methods) and we use the median standard deviation across all F0s tested. The resulting metric, which we call harmonic strength, is analogous to the sensitivity index d’ in psychophysics (albeit with different units) in that it expresses the strength of the “signal” (the oscillation area) in units of standard deviation of the noise. The harmonic strengths for rate and MASD in Figure 5A are 19.6 and 41.0, respectively, consistent with the visual impression that harmonics are better represented in the MASD in this example.

Figure 6 shows harmonic strengths for both average rate (top) and MASD (bottom) plotted against CF for our entire set of responses to complex tones with harmonics in cosine phase. Separate plots are shown for low (<20 dB), moderate (20–40 dB) and high ( ≤ 40 dB) stimulus levels re. pure tone thresholds at CF. Solid lines show the linear models (based on analyses of covariance) that best fit the log transformed data across all level groups with the minimum number of free parameters. For the MASD, separate analyses of covariance were run for CFs below and above 2700 Hz, respectively.

The harmonic strength for rate increases significantly with CF (p < 0.001), consistent with the increase in relative sharpness of cochlear tuning (as expressed by the quality factor Q) (Kiang et al., 1965; Liberman, 1978). The harmonic strength for MASD also increases with CF (p < 0.001), but only up to 2700 Hz, suggesting that another factor–most likely the decrease in phase locking to the fine time structure – counteracts the improvement in cochlear frequency selectivity at higher CFs. Above 2700 Hz, the harmonic strength for MASD does nor depend statistically on either CF or level, as shown by the horizontal line.

Harmonic strengths for rate and MASD (below 2700 Hz) also differ in their level dependence. For rate, the analysis of covariance shows a significant effect of level group on harmonic strength (p <0.001) and a significant interaction (p = 0.009) between CF and level, indicating that the degradation in harmonic strength with increasing level is more pronounced for low CFs than for high CFs. The decrease in harmonic strength at high levels may be due to the broadening of cochlear filters, rate saturation, or both. In contrast, for MASD, the effect of level on harmonic strength for CFs below 2700 Hz barely reached statistical significance (p = 0.033). Post-hoc paired comparisons (with Bonferroni corrections) revealed no significant differences in MASD harmonic strengths between any pairs of levels. This result is consistent with our hypothesis that the spatio-temporal representation is more robust with level than the rate representation.

To directly compare the strengths of the rate-place and spatio-temporal representations of resolved harmonics for each fiber, we defined a normalized strength difference as the difference between the harmonic strength of the MASD and that of the rate, divided by their sum. This metric takes values between −1 and +1, with positive values indicating that the spatio-temporal representation is stronger than the rate-place representation. Figure 7 shows the normalized strength difference against CF for those measurements in which an oscillating curve could be reliably fit to both rate and MASD profiles. As in Figure 6, data are grouped by level relative to each fiber’s pure tone threshold at CF. We split the CF range into three groups (with cutoffs at 1350 and 2800 Hz) and ran a two-way analysis of variance on the normalized strength difference with level and CF groups as factors. There was a significant effect of CF (p < 0.001) and a significant interaction between CF and level (p = 0.034). We then ran post-hoc analyses (with Bonferroni corrections) to determine whether the mean strength difference in each condition is greater than zero (indicating the spatio-temporal code is better) or smaller than zero (indicating the rate code is better). For CFs below 1350 Hz, the mean strength difference was significantly greater than zero at intermediate and high levels, but not at low levels. For CFs between 1350 and 2800 Hz, the strength difference was only significantly greater than zero at high levels. For CFs above 2800 Hz, the mean strength difference was significantly smaller than zero at all levels. Thus, resolved harmonics are better represented in the MASD profile than in the rate-place profiles at higher stimulus levels, but only for CFs below 2800 Hz.

Figure 7.

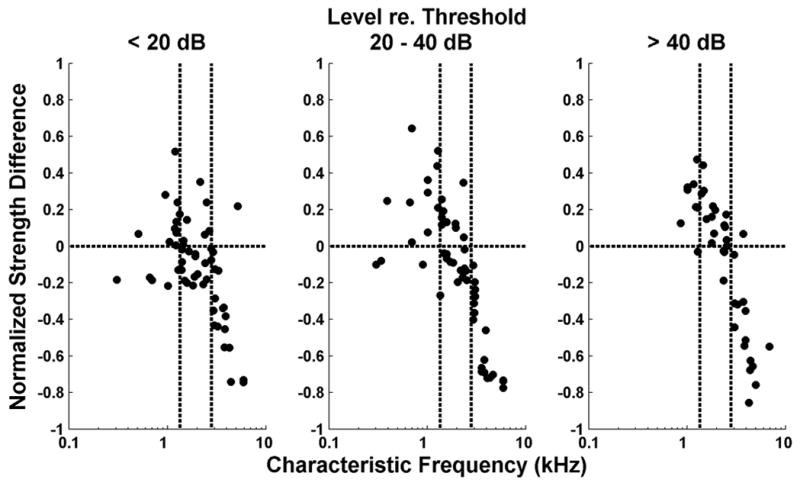
Comparison of the strengths of rate-based and spatio-temporal representations of pitch. Symbols show normalized strength differences as a function of CF for the AN fiber population. Positive values mean greater strength for the spatio-temporal representation. Results are grouped by level relative to each fiber’s threshold for a pure tone at CF as in Figure 6. Vertical dashed lines indicate the CF cutoffs used in the analysis of variance (see text). Harmonics in cosine phase.

Locations of rate and MASD peaks relative to the fiber CF

Both rate-place and spatio-temporal pitch codes are based on cues to the locations of resolved harmonics via local maxima in response profiles (rate or MASD) along the tonotopic axis. Pitch is putatively extracted by matching these cues to central harmonic templates. The exact locations of these local maxima along the tonotopic axis and their stability with respect to stimulus level are therefore important to the viability (or at least the simplicity) of pitch codes based on these cues. With pure tone stimuli, the best frequency (BF) of AN fibers (where the firing rate is maximal) is known to be dependent on stimulus level (Rose et al., 1971; Temchin and Ruggero, 2010), and such level dependence is likely to occur with harmonic complex tones as well. The situation is less clear for the MASD, which depends primarily on the phase pattern of the cochlear traveling wave. While AN fibers with CFs between 1 and 4 kHz often show an inflection point near the CF in their phase-frequency curves for pure-tone stimuli (Palmer and Shackleton, 2009; Temchin and Ruggero, 2010), this inflection seems to be level-dependent. In this section, we examine in detail the locations of local maxima in rate and MASD profiles and their level dependence.

A precise estimate of the peak locations in rate and MASD profiles can be obtained from the frequency of the oscillatory component of the fitted curve, i.e. the parameter ϕ in Equation 1. Specifically, the product of ϕ and the tuning-curve CF gives an estimate of the fiber’s best frequency (BF) based on responses to complex tones. When ϕ equals one, the BF matches the tuning-curve CF and the oscillations peak exactly at integer values of the neural harmonic number. In the example of Figure 5A, local maxima in rate and MASD profiles tend to occur slightly below integer values of the neural harmonic number. As a result, the BFs estimated by fitting both rate and MASD profiles (2210 and 2263 Hz, respectively) are slightly, but significantly higher than the CF estimated from the pure-tone tuning curve (2150 Hz).

Figure 8 shows the relationships between the BF estimates derived from rate and MASD profiles and the CF estimate from pure-tone tuning curves for our entire set of responses to complex tones with harmonics in cosine phase. Differences between estimates, expressed as a percentage of the tuning-curve CF, are plotted against the tuning-curve CF. Because a threshold tuning curve is only measured once for each fiber, the tuning curve CF provides a level-invariant reference for assessing the level dependence of the BF estimates based on rate and MASD. As in Figure 6, data in Figure 8 are grouped by level relative to each fiber’s pure tone threshold at CF. For a point to be included, the oscillatory component of the fitted curve (Equation 1) had to be statistically significant so that the BF could be reliably estimated. The CFs of excluded measurements are indicated by open circles along the horizontal axis in Figure 8. As in Fig. 6, solid lines show the best-fitting linear models across all level groups based on analyses of covariance for CFs above 1 kHz.

At low CFs, BFs estimated from both rate (Fig. 8A) and MASD (Fig. 8B) tend to be larger than the tuning-curve CF, with differences that can reach 20–25%. Despite considerable scatter in the data, these deviations exhibit a similar decreasing trend with increasing CF in all three level ranges. Overall, the majority of BF estimates based on rate or MASD are larger than the tuning curve CFs, except for the rate-based BF at high levels. Importantly, the analyses of covariance show a significant effect of level on BF for rate (p< 0.001), but not for MASD (p > 0.01), indicating that the BF based on MASD stable with level while the rate-based BF is not.

MASD-based BF estimates are generally larger than rate-based estimates at all levels (Fig. 8C). An analysis of covariance shows significant effects of both CF (p = 0.008) and level (p<0.001), but no interaction. The mean BF difference increases from 0.93% at low levels to 4.6% at high levels, but remains substantially smaller than the large deviations observed when comparing either BF to the tuning curve CF (Fig. 8A,B). These observations are consistent with measurements of basilar membrane velocity in the cochlear base for pure tone stimuli (Robles and Ruggero, 2001): At a given cochlear place, the frequency for which velocity amplitude is maximum is slightly lower than the frequency that maximizes the group delay (the derivative of the phase with respect to frequency). Moreover the frequency of maximal group delay appears to be more stable with level than that of maximum amplitude.

The finding that local maxima in the MASD profiles are relatively robust with level may appear to conflict with earlier data from AN fibers for either pure tones (Palmer and Shackleton, 2009; Temchin and Ruggero, 2010) or inharmonic complex tones (van der Heijden and Joris, 2006). These studies typically report either plots of phase against stimulus frequency on a linear scale for single fibers, or plots of phase against CF on a logarithmic scale for a sample of AN fibers. When inflection points (corresponding to a local maximum in the phase derivative) are present in these plots, their locations tend to be level dependent, in contrast to MASD maxima in the present study. The MASD is based on a derivative with respect to neural harmonic number CF/F0 in order to take advantage of cochlear scaling invariance. Phase plots from the earlier studies might show more level-invariant inflection points if they were replotted against neural harmonic number rather than linear frequency or log CF. A detailed comparison between these studies is difficult because of differences in stimuli and species (guinea pig for Palmer and Shackleton, chinchilla for Temchin and Ruggero, cat for van der Heijden and Joris and the present study), and because the MASD does not depend exclusively on phase but also on rate.

Both rate-place and spatio-temporal profiles are labeled line codes in that they require the position along the tonotopic axis to be “known” by higher centers where these profiles are putatively matched to harmonic templates. Traditionally, the label is assumed to be the CF obtained from a pure-tone tuning curve, but this threshold metric may not be appropriate for suprathreshold stimuli. The present results suggest that the BF based on spatio-temporal cues may be a suitable label because it is stable with level, and is obtained from responses to harmonic complex tones, which are more common in nature than pure tones.

Phase dependence

Psychophysical studies show that the pitch value and pitch strength of harmonic complex tones are generally not greatly affected by the phase relationships among the partials so long as the stimuli contain resolved harmonics (Houtsma and Smurzynski, 1990; Carlyon and Shackleton, 1994; Bernstein and Oxenham, 2005). To test whether the spatio-temporal representation is consistent with these perceptual observations, we measured responses to complex tones with harmonics in alternating sine-cosine phase and negative Schroeder phase as well as cosine phase. Figure 9 compares the responses to harmonic complexes differing in phase patterns for a fiber with a CF of 2520 Hz. In this example, F0 ranged from 560 Hz to 1680 Hz for all three stimuli. Based on previous results (Cedolin and Delgutte, 2005), we expect low-order harmonics to be well resolved in this F0 range, and this expectation is confirmed by the presence of peaks at neural harmonic numbers 2, 3 and 4 in the rate profiles for all three stimuli (Fig. 9D). The pseudo spatio-temporal response patterns are very similar for all three phase conditions (Fig. 9, A–C), as are the strong cues to resolved harmonics present in the MASD profiles (Fig. 9E).

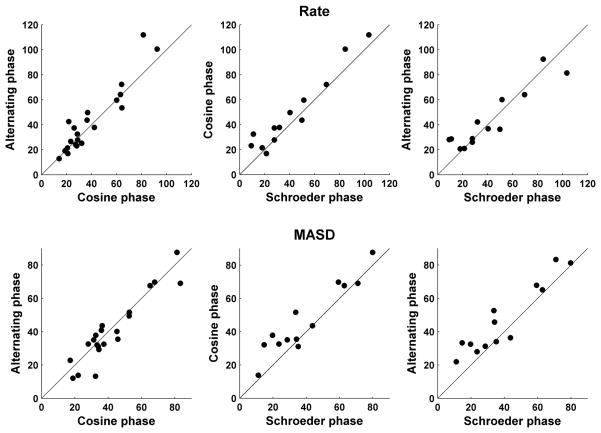
Figure 10 compares the harmonic strengths of the rate-place (top) and spatio-temporal (bottom) representations across a sample of AN fibers for every pair of phase patterns. The CFs of the fibers included in this sample range from 1 to 3 kHz. Harmonic strengths of the MASD for harmonics in cosine and alternating phase are very similar (A), and both are only slightly larger than the harmonic strengths for harmonics in Schroeder phase (B–C). Similarly, we found no statistically-significant difference between rate-based harmonic strengths for any of the three phase configurations (D–F), consistent with previous findings (Cedolin and Delgutte, 2005). These results suggest that the salience of pitch cues available in both the rate-place and spatio-temporal representations is to a large extent independent of the phase relationship among resolved harmonics, consistent with human psychophysical observations.

Figure 10.

Effect of phase relationships among the harmonics on the strength of the rate-place (top) and spatio-temporal (bottom) cues to resolved harmonics for a sample of AN fibers. Filled circles compare harmonic strengths derived from spatio-temporal patterns of response to complex tones with harmonics in cosine, alternating and Schroeder phase. CFs range from 1 kHz to 3 kHz. Solid lines indicate equality.

The phase invariance of the spatio-temporal representation may seem surprising given that this representation strongly depends on the phase pattern of the cochlear traveling wave along the tonotopic axis. However, if a harmonic is well resolved, its local phase pattern (near the place tuned to the harmonic frequency) will be similar to that of a single sinusoid regardless of the phase relationships between this harmonic and neighboring ones. The phase relationship between two neighboring resolved harmonics does affect the spatiotemporal response patterns at CFs that lie halfway between these two harmonics (compare Figures 9A and 9B for neural harmonic numbers near 2.5 and 3.5).

Pitch estimation from neural population responses

So far, we have relied on the assumption of cochlear scaling invariance to interpret profiles of rate and MASD as a function of CF/F0 for single fibers as being equivalent to spatial patterns along the tonotopic axis of the cochlea. We found that the spatio-temporal cues to resolved harmonics are most robust for CFs between 1 and 2.8 kHz. For comparison with psychophysical data, this CF range needs to be mapped into a range of stimulus F0. For this purpose, we used an interpolation procedure to replot our rate and MASD data as a function of BF for a given stimulus F0. Figure 5B illustrates this procedure for an F0 of 872 Hz. Because the F0 values tested for each fiber are chosen so that the ratio CF/F0 varies from 1.5 to 4.5 in steps of 1/8, few, if any, fibers provide data at this exact F0. However, fibers with CFs between 1300 Hz (1.5×872) and 3900 Hz (4.5×872) do provide data for F0s close to the desired 872 Hz. For each of these fibers, we used the fitted curves based on Equation (1) (as in Figure 5A) to interpolate the rate and MASD at the desired F0 (872 Hz). In addition, because average rates and MASD in response to the same stimulus can substantially differ among fibers with similar CFs, we normalized the firing rates (and MASD) of each fiber by their median value over all F0 tested.

Figure 5B shows the interpolated, normalized rates and MASD for an F0 of 872 Hz as a function of BF (expressed as neural harmonic number BF/F0) for all the fibers studied with harmonic complex tones in cosine phase at levels below 27 dB re. threshold. We use the BFs estimated from responses to complex-tones rather than the less reliable tuning curve CF, and we take the geometric mean of the BF estimates for rate and MASD when both are available. The interpolated data show considerably more scatter than typically seen in the single-fiber data (Fig. 3–4, Fig. 5A), reflecting the somewhat ad hoc normalization as well variability resulting from pooling data across a range of levels and across different animals. Despite this scatter, both rate and MASD tend to peak near integer values of the neural harmonic number. The same oscillating curve (Equation 1) was fit to the interpolated population data as for the single-fiber data. Since this function shows peaks at harmonically related BFs, we are effectively fitting a harmonic template to the profiles of rate and MASD along the tonotopic map in much the same way as in spectral models of pitch (Goldstein, 1973; Wightman, 1973; Cohen et al., 1994). For both rate and MASD, the period of the damped oscillation in the fitted curve (the parameter 1/ϕ in Equation 1) gives an estimate of the stimulus F0 from the neural population response. In this case, both F0 estimates (870 Hz for MASD and 855 Hz for rate) deviate by less than 2% from the actual F0 (872 Hz). However, since the independent variable for curve fitting is the BF derived from responses to harmonic complex tones, the F0 estimates are expected to be unbiased. More meaningful are the standard deviations of the F0 estimates (computed from the r.m.s. residuals and the Jacobian at the solution vector (Press et al., 1988)), which are a measure of their precision. In the example of Figure 5B, the standard deviations are about 1% of the actual F0.

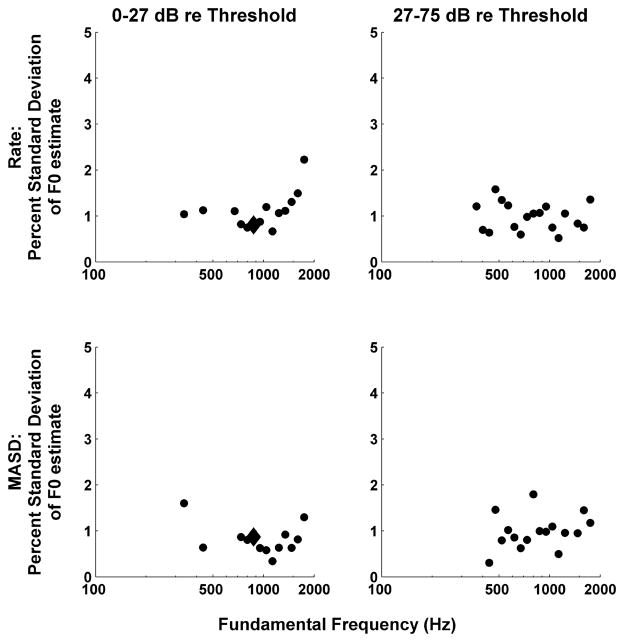
The analysis of Figure 5B was repeated for F0s ranging from 100 to 1600 Hz in 1/8-octave steps. Figure 11 shows the standard deviations of the F0 estimates based on rate and MASD profiles as a function of stimulus F0. Results are shown separately for two different level ranges, using a cutoff of 27 dB re. threshold that splits the data in two roughly equal halves. For both metrics and both level ranges, the standard deviations of the F0 estimates are mostly below 1.5% and show no strong dependence on F0. Data are only shown for F0s where an oscillatory curve could be reliably fit to the interpolated rate and MASD profiles (as assessed by an F test, see Methods). For some F0s, the sampling of BFs was sparse and/or oddly distributed, making F0 estimation unreliable. Such unpredictable sampling of the tonotopic axis is the very reason why we adopted an experimental design based on cochlear scaling invariance, which ensures a fine, uniform sampling of neural harmonic numbers for all fibers.

Figure 11.

Standard deviation of the F0 estimated from tonotopic profiles of interpolated rate (top) and MASD (bottom) as a function of stimulus F0 for two ranges of stimulus levels. Standard deviations are expressed as a percentage of the actual F0, and were computed by fitting Equation 1 to the rate and MASD profiles (as in Figure 5B) and using the Jacobian of the best-fitting parameter vector.

The lowest F0 for which a clear oscillatory component could be detected in either rate or MASD profiles was 336 Hz at lower levels, and 367 Hz at higher levels. It is harder to define an upper limit for F0 estimation based on MASD. At the higher levels, MASD-based F0 estimation tended to be less reliable than rate-based estimation for F0s above 1100 Hz, as expected from the degradation in phase locking. However, at the lower levels, F0 could be estimated from MASD profiles up to the highest value tested (1600 Hz). The MASD is likely to be overestimated at high frequencies due to intrinsic noise in neural firings. The spatial derivative operation amplifies high-frequency noise in temporal response patterns. This noise is not attenuated at the subsequent temporal integration stage because it is the absolute value of the spatial derivative that is integrated. If the noise is Poisson-like, as expected for AN fibers, then the higher the firing rate, the higher the noise. Thus, the oscillations in MASD profiles at high F0s may simply be noise modulations directly resulting from the observed oscillations in firing rate. Despite this difficulty, F0 estimation from MASD profiles was overall most effective for F0s between about 350 and 1100 Hz.

DISCUSSION

Spatio-temporal representation of pitch

We investigated the effectiveness of a spatio-temporal representation of the pitch of harmonic complex tones in the cat auditory nerve. We found that strong spatio-temporal cues to resolved harmonics are available in the responses of AN fibers whose CFs are high enough for harmonics to be sufficiently resolved (>1 kHz) but below the limit (~2.8 kHz) above which phase-locking is significantly degraded. For fibers with CF below 1 kHz, rate-place cues to resolved harmonics are also weak due to poor harmonic resolvability, consistent with earlier studies (Sachs and Young, 1979; Cedolin and Delgutte, 2005). At high CFs, on the other hand, the rate-place representation improves due to the progressive sharpening of cochlear tuning relative to the CF (Kiang et al., 1965; Shera et al., 2002; Cedolin and Delgutte, 2005), whereas the spatio-temporal representation degrades due to the decline in phase-locking (Johnson, 1980). In the CF range where it is effective, the spatio-temporal representation is more robust than the rate-place representation at high stimulus levels. Whereas the effectiveness of the rate-pace representation is limited by firing rate saturation (Sachs and Young, 1979), phase locking remains robust at levels where rate is saturated (Young and Sachs, 1979). Nevertheless, the spatio-temporal representation does degrade somewhat at high levels consistent with broader cochlear tuning and associated flattening in the frequency dependence of the phase response (Anderson et al., 1970; Palmer and Shackleton, 2009; Temchin and Ruggero, 2010).

Our primary results are based on the assumption of local scaling invariance in cochlear mechanics (Zweig, 1976), which holds only approximately (Shera and Guinan, 2003; van der Heijden and Joris, 2006). While scaling invariance implies cochlear filters with constant Q (the ratio of CF to bandwidth), Q is actually an increasing power function of CF in cat AN (Shera et al., 2002; Shera and Guinan, 2003; Cedolin and Delgutte, 2005). This power law (with an exponent of approximately 0.37) predicts that Q varies by no more than ±21% over the 1.6 octave range of CF/F0 spanned by our stimuli. Although not insignificant, these deviations are probably within the range of experimental error. Scaling invariance further prescribes that all temporal parameters of cochlear processing scale with CF, whereas some of these parameters such as the upper frequency limit of phase locking clearly do not (Johnson, 1980). Using model simulations, Larsen et al. (2008) found that assuming scaling invariance tends to overestimate phase locking to higher harmonics (relative to the mean neural harmonic number 3), and underestimate phase locking to lower harmonics. This effect can be discerned in the model results of Figure 2 where the decay of the MASD with increasing neural harmonic number is somewhat less pronounced in the right panel (where scaling invariance is assumed) than in the left panel (where it is not).

Our interpolation procedure for replotting rate and MASD as a function of BF for a given F0 (Fig. 5B) bears upon the issue of scaling invariance because, at least for rate, it eliminates the constant Q assumption. For the interpolated data, the spatio-temporal representation worked best for F0s between 350 Hz and 1100 Hz. Within that range, the stimulus F0 could be estimated with a standard deviation <2% based on data from only 30–50 AN fibers. These precision figures are only indicative, as they depend on experimental variables such as the number of fibers sampled and the distribution of CFs.

The F0 range over which the spatio-temporal representation of pitch is most effective in cat AN encompasses the 500–1000 Hz range of cat vocalizations (Brown et al., 1978; Shipley et al., 1991). What might be the corresponding range in humans? Evidence from both otoacoustic emissions and psychophysics suggests that cochlear frequency resolution may be up to three times finer in humans than in cats (Shera et al., 2002; Oxenham and Shera, 2003); but see Ruggero and Temchin (2005) for a contrary opinion. If so, the lower F0 limit for a viable spatio-temporal representation of pitch would be about 120 Hz in humans. The upper limit at about 1100 Hz would remain the same providing the frequency dependence of phase-locking is similar in cats and humans. This F0 range encompasses most of the range of spoken human voice (80–350 Hz), and the upper limit is roughly consistent with the ~1300 Hz upper limit of pitch perception for missing-fundamental stimuli containing many harmonics (Moore, 1973).

Neural codes for pitch

The spatio-temporal representation of pitch offers a number of advantages over traditional codes for the pitch of complex tones. It is more robust with stimulus level than the rate-place representation and, unlike the rate-place representation, predicts an upper frequency limit to the pitch of missing-fundamental stimuli roughly consistent with psychophysical data. While the autocorrelation (a.k.a. interspike interval) model of pitch has trouble predicting the stronger pitch produced by stimuli containing resolved harmonics compared to stimuli consisting entirely of unresolved harmonics (Carlyon and Shackleton, 1994; Carlyon, 1998; Bernstein and Oxenham, 2005; Cedolin and Delgutte, 2005), the spatio-temporal representation intrinsically requires resolved harmonics. The autocorrelation model also has trouble explaining the poor temporal pitch perception with cochlear implants (Shannon, 1983; Townshend et al., 1987) because phase locking of AN fibers is excellent with electric stimulation of the cochlea (Dynes and Delgutte, 1992; Shepherd and Javel, 1997). In contrast, the lack of a cochlear traveling wave with cochlear implants precludes the phase cues on which the spatio-temporal representation is based. Nevertheless, if pitch perception with resolved harmonics were based primarily on spatio-temporal cues, a second pitch mechanism would be required to account for the weak pitch produced by unresolved harmonics and stimulation through cochlear implants (de Cheveigné, 2005).

The pitch representation tested in this paper (Shamma, 1985) is called “spatio-temporal” because it makes use of both the spatial distribution of AN activity along the tonotopic axis and the precise phase locking of spikes to the fine time structure of the stimulus waveform. Other spatio-temporal models of auditory processing (Loeb et al., 1983; Shamma and Klein, 2000; Carney and Heinz, 2002) also critically depend on the relative timing of spikes from different cochlear locations and rely on the delays created by the cochlear traveling wave rather than postulating neural delay lines as in the autocorrelation model. Nevertheless these spatio-temporal models differ in important ways. All three models just cited differ from the present one in that they use cross-correlation (or equivalently coincidence detection) rather than lateral inhibition to compare the timing of spikes across cochlear locations. Both the Loeb et al. (1983) and the Shamma and Klein (2000) models involve cross-correlation over much wider extents of the tonotopic axis (CF separations of up to several octaves) than the local comparisons used in the present model. The wide tonotopic span of spatial correlations in the Shamma and Klein (2000) model is consistent with its purpose of explaining the formation of harmonic templates, and this model is compatible with the spatial derivative as a front end. While level-dependent changes in cochlear tuning play a critical role in the Carney et al. (2002) phase opponency model, the phase cues used by the present model directly follow from linear systems theory (Goldstein et al., 1971). Apparently, the cochlear nonlinearities are mild enough that the spatiotemporal phase cues are fairly robust over the level range tested.

In summary, while several models combining place and temporal information have been proposed for pitch and other perceptual phenomena, these models are clearly distinct, and each has to be evaluated on its own merit. The present study represents the first detailed physiological evaluation of a spatio-temporal pitch model.

Neural mechanisms for extracting spatio-temporal pitch cues

A key question is whether the spatio-temporal cues to resolved harmonics available in the patterns of AN activity are actually extracted in the central nervous system. A neural mechanism that extracts spatio-temporal cues must be sensitive to the relative timing of spikes from AN fibers innervating neighboring cochlear locations. Because phase locking to the waveform fine structure rapidly degrades in the ascending auditory pathway (Langner, 1992), an early brainstem processing site such as the cochlear nucleus or, perhaps, the medial superior olive (Loeb et al., 1983) is a logical place for such a mechanism.

The simplest possibility is a lateral inhibitory mechanism, as originally proposed by Shamma (1985) and implemented here via the MASD. There is evidence for lateral inhibition in the dorsal cochlear nucleus (DCN), where principals cells receive both excitatory input from AN fibers and a lower-CF inhibitory input from vertical cells (Voigt and Young, 1990). However, phase locking to the fine structure is generally poor in DCN cells (Lavine, 1971; Rhode and Smith, 1986), so these neurons seem ill suited for the fast temporal processing required to decode spatio-temporal cues. Nevertheless, neurons might perform the required computations in their dendrites even if they have poor phase locking due to subsequent lowpass filtering. On the other hand, while bushy cells in the ventral cochlear nucleus (VCN) show good phase locking, the BF of inhibition in these neurons appears to match the excitatory BF, i.e. the inhibition is not lateral (Caspary et al., 1994; Kopp-Scheinpflug et al., 2002). However, these experiments may not have been sufficiently sensitive to detect small BF differences, so that a role for lateral inhibition in processing spatiotemporal cues cannot be ruled out.

An alternative decoding mechanism for spatio-temporal cues is across-CF coincidence detection (Carney, 1994; Carney and Heinz, 2002) for which there is evidence in some phase-locking VCN units (Carney, 1990b; Joris et al., 1994; Wang and Delgutte, 2009). A potential difficulty is that fewer spike coincidences are expected at the cochlear locations tuned to resolved harmonics, i.e. rate and phase cues tend to oppose each other, whereas they act in synergy in a lateral inhibitory circuit. Thus a coincidence detection mechanism may work best at higher stimulus levels where the rate is saturated.

Conclusion

We tested a spatio-temporal representation of pitch based on phase cues to resolved harmonics that are created by the cochlear traveling wave and can, in principle, be extracted by a lateral-inhibition mechanism. This representation is effective over a range of F0s whose lower limit is determined by the frequency selectivity of the cochlea, while the upper limit is caused by the degradation in phase locking. In cats, the spatio-temporal representation is viable over the F0 range of cat vocalizations, and this correspondence may also approximately hold in humans due to the putatively sharper cochlear frequency tuning in that species. The spatio-temporal representation is consistent with key trends in pitch psychophysics, and is more robust than the rate-place representation at high stimulus levels.