Profiling hospitals by survival of patients with colorectal cancer

Abstract

Objective

To profile hospitals by survival rates of colorectal cancer patients in multiple periods after initial treatment.

Data Sources

California Cancer Registry data from 50,544 patients receiving primary surgery with curative intent for stage I-III colorectal cancer in 1994–1998, supplemented with hospital discharge abstracts.

Study design

We estimated a single Bayesian hierarchical model to quantify associations of survival to 30 days, 30 days to 1 year, and 1 to 5 years by hospital, adjusted for patient age, sex, race, stage, tumor site, and comorbidities. We compared two profiling methods for 30-day survival and four longer-term profiling methods by the fractions of hospitals with demonstrably superior survival profiles and of hospital pairs whose relative standings could be established confidently.

Principal findings

Interperiod correlation coefficients of the random effects are ρ̂₁₂ = 0.62 (95% credible interval 0.27,0.85), ρ̂₁₃ = 0.52 (0.20,0.76) and ρ̂₂₃ = 0.57 (0.19,0.82). The three-period model ranks 5.4% of pairwise comparisons by 30-day survival with at least 95% confidence, versus 3.3% of pairs using a single-period model, and 15%–20% by weighted multiperiod methods.

Conclusions

The quality of care for colorectal cancer provided by a hospital system is somewhat consistent across the immediate postoperative and long-term follow-up periods. Combining mortality profiles across longer periods may improve the statistical reliability of outcome comparisons.

INTRODUCTION

Survival after initial treatment is an important indicator of the quality of cancer care. Short-term (30-day) post-operative survival is commonly regarded as the most proximate measure of the skill of the surgeon and quality of the hospital in which surgery is performed (Schrag et al. 2000). Long-term survival is also important in assessing outcomes of care, since most deaths from colorectal cancer occur more than 30 days after surgery. Long-term survival may reflect the provision of appropriate adjuvant therapy (Andre et al. 2004; National Institutes of Health 1990), surveillance for cancer recurrence and new primary cancers (Desch et al. 2005; Renehan et al. 2002), and care of comorbid conditions. Currently, 5-year survival of patients with colorectal cancer in the United States exceeds 60% (American Cancer Society 2008), and more than 1.1 million people who have been diagnosed with colorectal cancer were alive in 2004 (National Cancer Institute 2007).

Provider profiling allows for assessment and comparisons of the outcomes of health care providers (Epstein 1995; McNeil, Pedersen, and Gatsonis 1992; Normand, Glickman, and Gatsonis 1997; Rosenthal et al. 1998). Results from profiling can influence policy-making, referrals, and patients’ selection of health care providers, and help with identifying and correcting quality problems, although evidence on its impact is mixed (Hannan et al. 2003; Marshall et al. 2000; Mukamel, and Mushlin 1998).

Profiling of surgical outcomes typically focuses on in-hospital or 30-day survival; little is known about the correlations between short- and long-term survival (Gatsonis et al. 1993; Normand et al. 1997). If some provider system characteristics influence both short- and long-term outcomes, we might expect positive correlations between short- and long-term performance measures. Models incorporating such correlations among survival rates in different periods may improve the statistical precision of profiling by combining information across periods. Furthermore, inter-period correlations of outcomes quantify the commonality of dimensions of quality pertaining to different phases of treatment. Therefore, such models are of both clinical and statistical interest.

We focus on the hospital as the unit of analysis because cancer care across the continuum from initial treatment to remission or death cannot generally be attributed to any single physician. Instead, care is typically delivered by a cluster of physicians and facilities affiliated with a single hospital, which might reasonably be held accountable for the quality of the entire process of care (Fisher et al. 2009) . Furthermore, hospitals are more likely than physicians to have sufficient numbers of patients to make profiling feasible with acceptable precision.

METHODS

Study Cohort and Data Source

This study used data from the California Cancer Registry (CCR) on California residents diagnosed with stage I–III colorectal cancer between 1994 and 1998 and receiving surgery with curative intent. Hospitals with fewer than 100 patients (89 of 289 hospitals with 10.7% of all patients) were excluded from the study because they had too few patients to contribute reliable information to the analysis.

The CCR data included patients’ age, gender, race/ethnicity, date of diagnosis, date of surgery, tumor site and stage, residence, and vital status. To ascertain patients’ vital status, registry staff matched records with the California Death Statistical Master File and National Death Index. Socioeconomic status was represented by the median household income of each patient’s census block of residence (rounded to the nearest $5000 to preserve confidentiality), based on linked 1990 Census data.

CCR data were linked to hospital discharge abstracts maintained by the California Office of Statewide Health Planning and Development. We identified patients’ discharge diagnosis codes shown on their hospital abstracts from 18 months before to 6 months after their diagnosis with colorectal cancer. To quantify the severity of comorbid illness we calculated the Deyo modification of the Charlson comorbidity index for use with administrative data (Charlson et al. 1987; Deyo, Cherkin, and Ciol 1992), excluding cancer diagnoses.

The institutional review boards of Harvard Medical School, the California Department of Health Services, and the Public Health Institute approved the study protocol. Because our study used existing data with encrypted identifiers, written informed consent was not required.

Study Variables

We adjusted for hospital casemix using the following patient characteristics as specified in Table 1, including clinical (tumor site and stage in 6 combinations, comorbidity), demographic (age, gender, race/ethnicity), and socioeconomic (median household income) variables. Hospital volume was defined by the number of patients undergoing cancer-related colorectal surgery in each hospital, as recorded in the CCR from 1994 through 1998, and categorized into the three volume strata, low (100–150 patients, 57 hospitals), medium (151–300 patients, 80 hospitals), and high (>300 patients, 63 hospitals). For each physician reported to be involved in treating at least 5 patients in our cohort, we tabulated the percentage of the physician’s patients seen in a single hospital. The outcome measures were survival in three time periods: the first 30 days after surgery, from 31 days to one year (among those surviving 30 days), and from one to five years (among those surviving one year).

Table 1.

Cohort characteristics, and coefficients of individual and hospital characteristics as predictors of mortality in three postsurgical periods

	Percent of cohort	Estimated coefficient (Standard Error) by period
		0–30 days	30 days– 1 year	1 year –5 years
Intercept		−4.044 (0.101)	−2.953 (0.057)	−1.071 (0.043)
Age 18–54	12.3	−1.565 (0.199)	−1.115 (0.084)	−0.811 (0.043)
Age 55–59	7.1	−0.924 (0.181)	−1.014 (0.100)	−0.817 (0.051)
Age 60–64	9.4	−1.041 (0.151)	−0.657 (0.076)	−0.638 (0.047)
Age 65–69	13.4	−0.771 (0.117)	−0.540 (0.066)	−0.512 (0.040)
Age 70–74	16.6	−0.515 (0.098)	−0.289 (0.054)	−0.308 (0.035)
Age 75–79	17.2	Ref	Ref	Ref
Age 80–84	13.2	0.322 (0.082)	0.308 (0.051)	0.372 (0.038)
Age 85+	10.8	0.923 (0.077)	0.845 (0.052)	0.927 (0.041)
Colon 1	17.5	−0.497 (0.087)	−0.475 (0.058)	−0.522 (0.036)
Colon 2	32.9	Ref	Ref	Ref
Colon 3	24.7	0.052 (0.065)	0.798 (0.039)	0.779 (0.030)
Rectal 1	7.9	−0.456 (0.129)	−0.440 (0.086)	−0.371 (0.048)
Rectal 2	8.4	−0.116 (0.106)	0.184 (0.067)	0.370 (0.042)
Rectal 3	8.7	−0.118 (0.114)	0.654 (0.061)	1.037 (0.040)
Income ≤ $27,500	22.3	0.259 (0.082)	0.163 (0.051)	0.154 (0.034)
Income $27,500–37,500	22.4	0.241 (0.081)	0.064 (0.052)	0.119 (0.033)
Income $37,500–52,500	27.3	0.157 (0.078)	0.071 (0.049)	0.088 (0.032)
Income ≥ $52,500	23.3	Ref	Ref	Ref
Income missing*	4.7	0.166 (0.138)	0.068 (0.085)	−0.072 (0.058)
Female	49.5	−0.196 (0.055)	−0.047 (0.033)	−0.229 (0.023)
Male	50.5	Ref	Ref	Ref
White	75.7	Ref	Ref	Ref
African American	6.0	0.018 (0.127)	0.001 (0.074)	0.217 (0.049)
Hispanic	9.6	−0.125 (0.102)	−0.087 (0.060)	0.009 (0.038)
Asian	8.3	−0.239 (0.128)	−0.359 (0.076)	−0.194 (0.045)
Other Race	0.4	0.315 (0.366)	−0.184 (0.276)	0.083 (0.163)
Charlson 0	64.1	Ref	Ref	Ref
Charlson 1	21.9	0.756 (0.070)	0.503 (0.040)	0.373 (0.027)
Charlson 2	7.8	1.358 (0.081)	0.979 (0.051)	0.810 (0.042)
Charlson ≥3	6.1	1.756 (0.077)	1.598 (0.050)	1.329 (0.048)
Volume 100–150	13.7	0.202 (0.089)	0.233 (0.052)	0.076 (0.041)
Volume 151–300	34.4	0.186 (0.072)	0.191 (0.040)	0.034 (0.033)
Volume > 300	51.9	Ref	Ref	Ref

Coefficients are from random effects logistic regression models

(Bold face represents p<0.05)

^*Income missing due to address that could not be geocoded to block group

Statistical Analysis

We fitted a logistic regression model for survival to the end of each period for patients who were alive at the beginning of that period, with hospital random effects for each period, correlated across periods. Covariates included patient demographic, socioeconomic and clinical characteristics and hospital volume categories, modeled with separate regression coefficients in each period. We used Bayesian methods to fit the model with MLwiN software (Browne 2009). Details of model specification and fitting are presented in the Statistical Appendix.

Model results included estimates of the variation of random effects for each period across hospitals as well as the correlation of the effects between each pair of periods, with 95% credible intervals (Bayesian equivalent of confidence intervals) for each estimate. For comparison we also fitted a similar model to only the period 1 data with a single random effect per hospital. We estimated a principal components analysis of the correlation matrix to quantify the common variation of random effects across the 3 periods.

We obtained draws from the distribution of the random effect for each hospital in each period. We combined these with the intercept and the coefficient corresponding to the hospital’s volume category to obtain a “hospital profile”, defined as the combination of hospital-specific coefficients that could be used to compare predicted probabilities of mortality for identical patients. We refer to calculation of profiles for 30-day survival from the 3-period model as the “reference method”.

As a summary of the precision of comparisons under various methods of profiling, we calculated posterior probabilities for each pair of hospitals indicating our degree of certainty that one hospital’s adjusted survival rate was superior to that of the other hospital. We calculated these comparisons using profiles from the base method, from the single-period model, and also using composite profiles that combined profiles across periods of the 3-period model with each of 4 weightings: (1) equal weights; (2) z-score weights, where each period’s score is divided by the random-effects standard deviation σ_t; (3) z-score weights, where each period’s score is divided by the empirical standard deviation of the estimated profiles in each period; (4) weighted so the average approximates the probability of survival across the 3 periods (Statistical Appendix).

We also calculated the posterior probability that each hospital was among the 25% of hospitals with the best survival profiles. Finally, we calculated correlations across hospitals of the profiles estimated using these 6 methods.

RESULTS

Characteristics of Study Cohort

The CCR data for the study period included 56,539 eligible patients at 289 hospitals. After exclusion of hospitals with fewer than 100 patients, our study cohort had 50,544 eligible patients (89.3% of all patients) at 200 hospitals. Of these, 49.5% were female, 75.7% white, 6.0% African American, 8.3% Asian, and 9.6% Hispanic, reflecting the racially diverse population of our site. The mean age of the cohort was 70.2 years (SD 12.6).

At the 200 hospitals included in the study, the patient-weighted median number of patients undergoing surgery was 307 cases with an inter-quartile range 200 to 423 cases. The unadjusted 30-day, 31 day to 1 year, and 1–5 years survival rates were 97.0%, 91.2% and 69.8%, respectively. Among physicians seeing at least 5 patients in our cohort, those for whom at least 80% of their patients received primary treatment in a single hospital included between 70% and 74% among attending physicians, medical oncologists, radiation oncologists, and surgeons.

Effects of Patient and Hospital Characteristics on Survival

Table 1 shows regression coefficients of patient and hospital characteristics in each time period. Increasing age, low income, and greater comorbidity were significant predictors of mortality in each period, while mortality was significantly lower in each period for Stage I colon or rectal cancer patients compared to Stage II colon patients. Other significant predictors of higher mortality in some but not all periods included treatment in a low- or medium-volume hospital, African American race, male sex, and (after 30 days) stage 3 colon cancer and stage 2 or 3 rectal cancer. Asian race predicted lower mortality after 30 days.

The estimated correlation coefficients ρ_st of the random effects across the three time periods were ρ₁₂ =0.62 (95% credible interval 0.27, 0.85), ρ₁₃=0.52 (CI=0.20, 0.76), and ρ₂₃=0.57 (CI=0.19, 0.82). These positive correlations indicate that hospitals that have better survival in one period tend to have better survival in other periods as well. Principal components analysis of the correlation matrix showed that 70% of the variance in the three correlated random effects is explained by a single principal component.

Estimated standard deviations (SD) of the hospital random effects (on the logit scale) in each period were σ₁=0.25 (CI= 0.17, 0.31), σ₂=0.09 (CI=0.02,0.13), and σ₃=0.14 (CI=0.10,0.16). These SD can be interpreted as measures of relative variation across hospitals of hazard of mortality, which thus is largest in the 30-day postoperative period. To illustrate, for a patient with average risk of 30-day mortality (3.0%) at a hospital with median mortality rate, the risks of mortality respectively at hospitals in the same volume category with moderately low (1 SD below median on the logit scale) and moderately high (1 SD above) mortality would be 2.4% and 3.8%. Corresponding moderately low and high risks of 30-day to 1 year mortality would be 8.1% and 9.5%, and for 1-to-5-year mortality would be 27.3% and 33.2%. The random effect standard deviation was larger than the effect of hospital volume in periods 1 and 3, and of comparable magnitude in period 2.

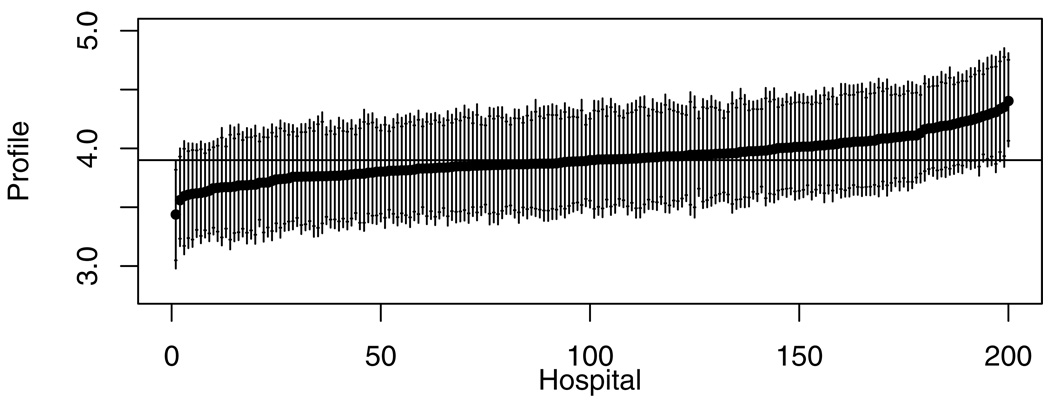
Hospital Profiles for 30-day Survival

Figure 1 illustrates hospital profiles for 30-day survival estimated under the reference method (using information from all 3 periods), represented by the linear prediction for a patient with average characteristics. Hospitals are displayed in the order of the posterior median case-mix-adjusted survival rate. The 90% and 95% credible intervals were wide compared to the variation in posterior medians, and only two hospitals were shown to be above or below the overall median with probability greater than 95%. The corresponding figure for intervals calculated under the single-period model was similar (data not shown).

Figure 1.

Profiling results for 30-day survival using the reference method, with hospitals ordered by estimated profile for survival (logit of probability of survival for patient with mean covariate values). The horizontal bar represents the median of the posterior distribution of provider profile. Each line segment represents the 95% posterior interval, with short horizontal line segments for the limits of the 90% posterior interval.

Pairwise Comparisons and High-ranking Hospitals Using Multiple Profiling Methods

We assessed the discriminating power of each of the six profiling methods described above by the number of pair-wise comparisons between hospital profiles that have a “significant” posterior comparison probability (>0.95) out of 19,900 possible pairwise comparisons (Table 2). The reference method yielded significant comparisons for 1076 (5.4%) of such pairs, while the single-period method did so for only 3.3% of pairs. The methods that weighted together profiles from the three periods distinguish many more pairs, ranging from 15.1% (Method 4) to 21.2% (Method 2). Similar relative results were obtained when the criterion was reduced to 90% certainty, with 31.1% of pairs being ranked at that level by Method 2.

Table 2.

Comparisons among 6 profiling methods: discriminating ability and correlations

Profiling method	Number (percent) of significant pairwise hospital comparisons*		Number of hospitals with P>80% of being in best 25%	Correlations with profiles from other methods
	At >95% probability level	At >90% probability level		Period 1, single-period model	Method 1 average profile	Method 2 average profile	Method 3 average profile	Method 4 average profile
Period 1 profile, 3-period model (“reference method”)	1076 (5.4%)	2613 (13.1%)	8	0.94	0.96	0.92	0.94	0.88
Period 1 profile, single-period model	676 (3.3%)	1840 (9.2%)	3	1	0.85	0.81	0.81	0.71
Method 1 average profile†	3130 (15.7%)	5146 (25.9%)	18		1	0.99	>0.99	0.97
Method 2 average profile†	4215 (21.2%)	6192 (31.1%)	24			1	0.99	0.97
Method 3 average profile†	3514 (17.7%)	5536 (27.8%)	20				1	0.98
Method 4 average profile†	2995 (15.1%)	4931 (24.8%)	17					1

^*Percentages are relative to 19,900 possible pairwise comparisons of 200 hospitals.

^†Average profiles weightings are (1) equal weights; (2) z-scored by random-effects standard deviation σ_t; (3) z-scored by empirical standard deviation of the estimated profiles in each period; (4) weighted to approximate profiling by the probability of survival through the 3 periods.

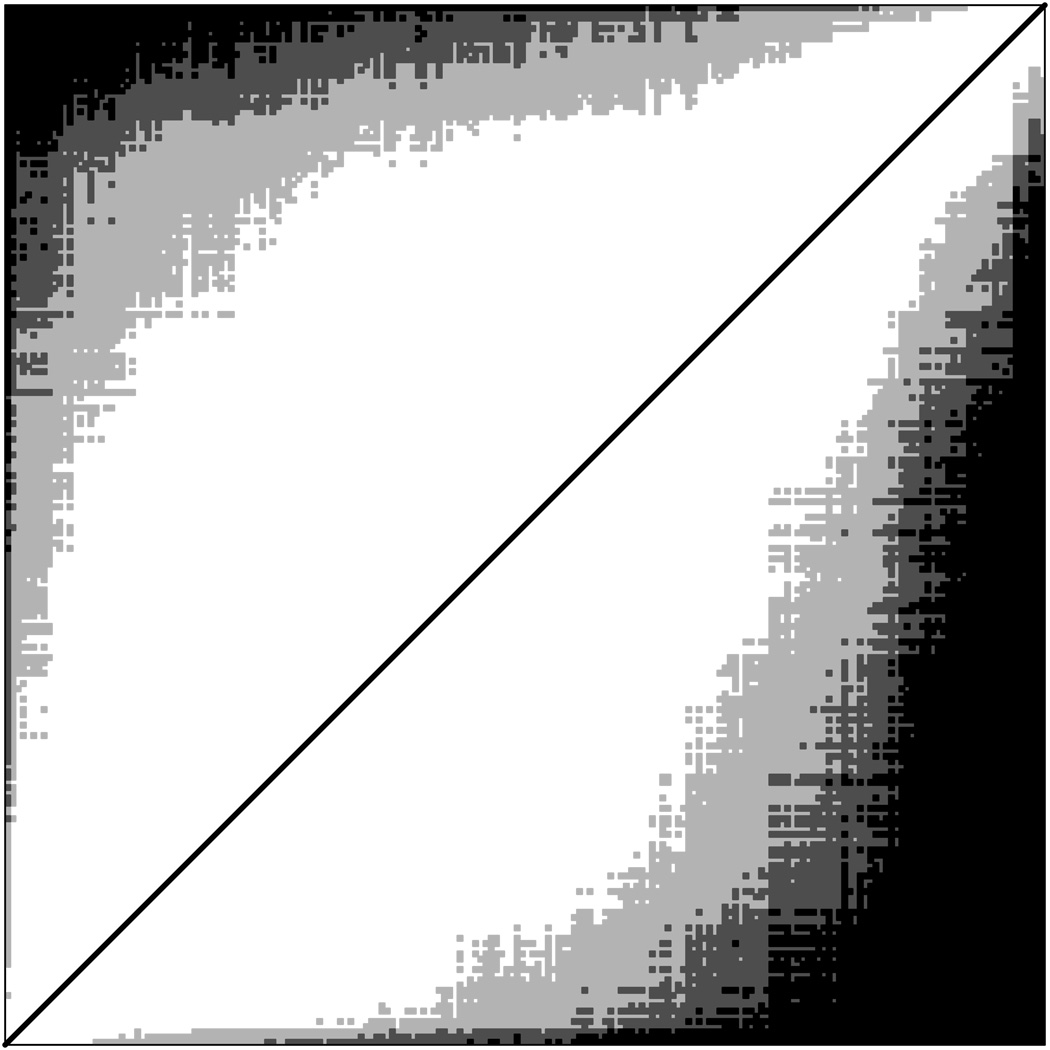
Figure 2 illustrates pairwise comparisons for the reference method (above diagonal) and weighted Method 2 (below diagonal), where black squares represent hospital pairs that can be ordered with probability>95% and dark and light gray squares respectively represent pairs with 90%<probability<95% and 80% <probability<90%. Hospitals whose profile scores differed more (further from the diagonal in the figure) were more likely to be confidently ordered. The greater density of the plot below the diagonal graphically illustrates the greater precision of comparisons using Method 2.

Figure 2.

Significant pairwise comparisons of hospital profiles. Triangle above diagonal is for reference method, below diagonal is for weighted method 2. In each triangle, hospitals are ordered by posterior median profile. Black squares indicate pairs for which ordering of profiles is >95% certain, dark gray squares indicate pairs for which ordering is between 90% and 95% certain, and light gray squares indicate pairs for which ordering is between 80% and 90% certain. The white area adjacent to diagonal represents pairs whose profiles are not sufficiently different to be ordered with probability >80%.

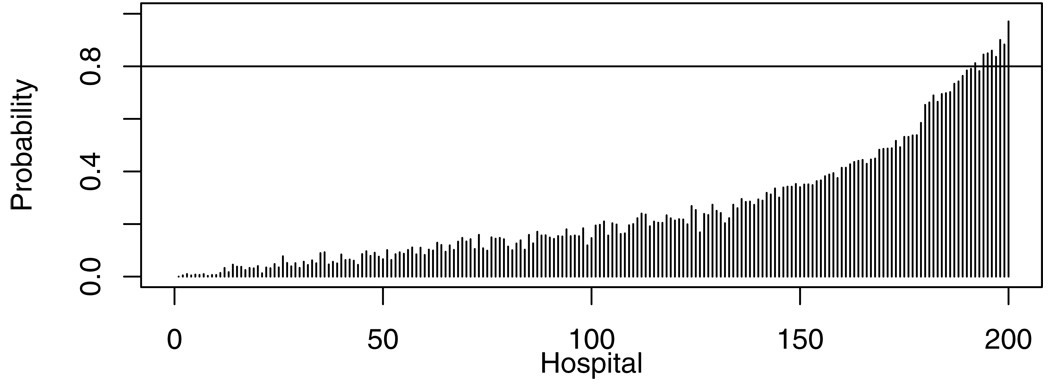
We compared methods on their ability to identify high-performing hospitals, defined as those with profiles in the top 25%, with at least 80% certainty (Table 2). While only 8 hospitals could be so identified by the reference method (Figure 3), 24 (or almost half of the 50 in the top 25%) could be so identified using Method 2.

Figure 3.

Posterior probabilities that each hospital’s profile is in the top 25% of all hospitals. The 8 hospitals crossing the horizontal line have probabilities >80% of being in the top 25%.

Consistency among Profiling Methods

Correlations among profiles from the 6 profiling methods were high (Table 2). The correlation of reference-method profiles with single-period profiles is 0.944 and with the weighted averages ranged from 0.880 to 0.962. Correlations between weighted average methods ranged from 0.967 to 0.996; among these methods, Method 4 yields the lowest correlations with the other methods.

DISCUSSION

One of the key challenges of healthcare provider profiling is that “gold-standard” outcome measures, such as mortality in specific episodes of illness, may have poor statistical reliability simply because the number of deaths or other adverse outcomes for any provider is too small. Strategies for addressing this challenge include combining information across outcome measures or conditions, using process measures or intermediate clinical outcomes such as complication rates, pooling information over a longer time period, or defining a larger unit of assessment (e.g., a hospital instead of an individual physician) (Clancy 2007; Jha 2006; Jha et al. 2007; Kerr et al. 2007; Krumholz et al. 2002). Each of these strategies involves a compromise in which greater statistical power is achieved at the cost of shifting the focus from what might otherwise be regarded as the target of “gold-standard” measurement, typically a direct estimate of a key clinical outcome (such as survival) during a recent time period for a single condition.

In this study, we combined two of these strategies (an extended 5-year sampling window and aggregation of data to the hospital level) with a third, extending the follow-up window for assessment of hospital-specific mortality risk. While 30-day postsurgical mortality is a common measure of the quality of surgery and postoperative care for colorectal cancer, only 7.9% of 5-year mortality for our cohort occurred during the first 30 days, limiting the amount of information available for comparisons among hospitals. Consequently only 3.2% of pairs of hospitals could be comparatively ranked with 95% certainty, using these data in combination with hospital volume. Because surgical volume accounts for only a modest part of the variation in mortality rates, it is essential to seek other information that could improve the precision of comparisons among hospitals.

Hence we investigated associations of 30-day mortality rates by hospital with mortality among survivors of this initial period for the same hospitals, divided into mortality from 31 days to 1 year postoperatively, and survival from 1 year to 5 years. During the second of these three periods, adjuvant therapies would typically be provided if clinically indicated, whereas cancer surveillance and survivorship care are the focus of the third period representing longer-term survival to 5 years. A multi-period model suggested strong correlations of survival rates among the three time periods after adjustment for patient case mix and hospital volume. Clinically, these associations suggest that there might be a common dimension of hospital quality affecting the entire 5-year period. This might be attributable in part to persistent effects of high-quality initial treatment and in part to a generalized dimension of quality manifested in better follow-up care by providers associated with higher-quality hospitals. Effects of hospital volume on mortality were similar across periods; other hospital characteristics not available for our analysis, such as process measures of follow-up care and surveillance, and structural measures of integration of primary and specialty care, might help to explain some of the residual common variation in quality (Bradley et al. 2006).

Statistically, these associations suggest that profiling could be made more precise by incorporating information from the later postoperative periods. This could be approached in two conceptually distinct ways. One approach would maintain 30-day mortality as the primary outcome measure and regard later mortality rates only as auxiliary information to improve estimation of this 30-day measure. This method, implemented as the “reference method” in our analysis, modestly improves on the model that uses only 30-day mortality data, almost doubling the number of hospital comparisons that can be made with 95% confidence.

Alternately, the strong positive correlations of hospital mortality rates across post-operative periods suggest that an index combining information across periods might be appropriate for hospital profiling. Such indices would no longer be interpreted purely as a measure of the quality of surgical care, but rather as a summary of the quality of care over a more extended period by providers serving patients with colorectal cancer of that hospital. Because information across all three periods is used more directly rather than only as a predictor of mortality rates in the first period, this alternative objective allows for more powerful comparisons among hospitals.

The four weighting methods for combining profiles across periods all generate more significant pairwise comparisons than the methods based on a single period profile. Different relative weightings of the periods lead to fairly similar results. A method that approximates profiling by total 5-year mortality produced results most dissimilar to those from 30-day mortality, since it was most affected by later (1-to-5-year postoperative) mortality, which constitutes the majority of total mortality in the first 5 years. The most statistically reliable profiles were produced by normalizing the profiles in each period to a common scale using Z scores before combining them (Method 2). Selection of a method for synthesizing survival across the 3 periods should consider both the statistical precision of the estimates (which favors Method 2) and the policy objective of giving substantial weight to direct measures of performance for primary treatment in the hospital, where relative variation is greatest (which favors the highly correlated Methods 1, 2, and 3).

Relative variation across hospitals in mortality is greatest in the immediate post-operative period. This not surprising since the hospital’s medical staff and facilities are likely to have the strongest effect on patient care during and immediately after inpatient treatment, while services involved in outpatient follow-up involve a more diffuse network of providers. Nonetheless we did find significant variation up to 5-years postoperatively, reflecting some combination of persistent effects of the quality of initial treatment and differences in the quality of follow-up care in the networks of physicians affiliated with different hospitals. None of the methods could reliably distinguish the better hospital in the majority of possible pairs, which is understandable because most hospitals fall into an intermediate range of similar quality. Nonetheless, hospitals that are fairly far apart in quality are likely to be distinguishable with 90% certainty. While this falls below the usual criterion of significance for generalizable scientific findings, we believe that an informed consumer or referring physician would reasonably consider this evidence when choosing a treatment facility (Davis, Hibbard, and Milstein March 2007). Similarly high or low performers can be identified as potential sites for studying best practices or problems, respectively, with adequate confidence for targeting quality improvement efforts.

Previous analyses of the same cohort showed variation across hospitals in other measures of treatment quality for colorectal cancer, such as rates of adjuvant chemotherapy for eligible patients and permanent colostomy rates after rectal cancer surgery (Hodgson et al. 2003a; Rogers et al. 2006b; Zhang, Ayanian, and Zaslavsky 2007; Zheng et al. 2006). Future studies might consider whether it would be appropriate to combine such measures with profiles of survival in a more comprehensive quality index. Other possible extensions involve combining information across conditions (other cancer sites), using similar statistical methods to determine which measures are most correlated and therefore might most appropriately be combined in profiling.

Our study had several limitations. First, we had only limited measures of patient characteristics, and our socioeconomic (SES) measures were limited to area-based income estimates. If patients with higher individual SES receive initial treatment at hospitals of higher quality and then have better resources and social support over the following years, correlations over time might be observed that are due to this unmeasured variation in patient casemix rather than hospital quality. Additional information that might be useful would include individual-level measures of income, education, and psychosocial support; more detailed clinical measures including severity of comorbidity, functional status, and body-mass index; and patient reports on interactions with the healthcare system. Such variables might help to explain the superior survival of Asian patients reported here and in previous studies (Edwards et al. 2005; Hodgson et al. 2003b; Rogers et al. 2006a).

Second, our models included only a single hospital structural measure (treatment volume) and no process measures. Additional measures of relevant hospital characteristics should improve the precision of profiling and help to identify the drivers of quality across periods. Third, we did not have reliable data on cause of death and therefore could not distinguish cancer-related and unrelated deaths. Fourth, we relied on hospital coding of comorbid conditions, which might not have been uniform, especially given the different incentives to hospitals in fee-for-service versus closed healthcare systems (Quan, Parsons, and Ghali 2002). Fifth, our data were limited to one state; future studies might investigate the consistency of these findings across more states with more recent data. We omitted the smallest 31% of hospitals, accounting for 10.7% of patients, from our analyses; these hospitals had too few patients to support reliable mortality profiling. Sixth, we could not determine whether the groupings of providers involved in treatment of our hospital-centered patient clusters correspond to physician networks that might be formed under an ACO payment model, although we did find that most physicians in any role tended to treat patients most of whom had received primary therapy at a single hospital. Seventh, for simplicity of presentation, volume was coded using indicator variables with somewhat arbitrary cutpoints; more flexible specifications might be explored in a profiling application. Finally, even with a dataset representing relatively large numbers of patients and hospitals, substantial statistical uncertainty remains in estimation of the random effects covariance parameters. While our analyses properly reflect this uncertainty, accumulation of more data over time and over more extensive areas would enable more precise estimation of these parameters and consequently sharpen inferences for model-based profiling. Such regional- or national-level modeling would also be necessary to apply these methods in smaller states where independent estimates of model parameters would be less precise.

In the future, quality measurement is likely to focus on assessing outcomes of care provided by “accountable care organizations” (ACOs) over entire episodes of illness, integrating quality in inpatient and outpatient settings, rather than on discrete processes or phases of care (Fisher et al. 2009). Such ACOs, many of which are likely to be hospital-centered, are authorized under the recently enacted Patient Protection and Accountable Care Act (Merlis 2010). Initiatives such as the Rapid Quality Reporting System of the American College of Surgeons are using this approach to evaluate the quality of cancer care (American College of Surgeons 2009). Methods such as those we have demonstrated to integrate outcomes over sequential time periods may contribute to developing and validating such quality measures.

STATISTICAL APPENDIX

Let Y_ijt be the indicator of survival for patient j of hospital i in period t. For a patient j that survived period t−1, Y_ijt = 1 if the patient survives during period t and Y_ijt = 0 otherwise, for t=1, 2, 3. Let X_ij denote patient demographic, socioeconomic and clinical characteristics and let Z_i denote hospital volume represented by dummy variables for volume categories. We allowed the relationship between survival and the patient and hospital characteristics to vary from period to period by including separate coefficients for each period. We model survival in period t (conditional on survival to the beginning of the period) by

$$P(Y_{\mathit{\text{ijt}}}=1|X_{\mathit{\text{ij}}},Z_i,{\theta }_t,Y_{\mathit{\text{ij}}(t-1)}=1)=F({\eta }_{\mathit{\text{ijt}}}),t=1,2,3$$ (1)

F (.) is the logit link function relating the linear part to the survival probability. The linear part of the model is

$${\eta }_{\mathit{\text{ijt}}}=x_{\mathit{\text{ij}}}^T{\alpha }_t+z_i^T{\beta }_t+{\gamma }_{\mathit{\text{it}}}$$ (2)

where α_t are coefficients of patient characteristics and β_t are coefficients of hospital characteristics, each in period t. The random effect γ_it is specific to hospital i in period t. We assume the random effects are normally distributed with within-provider covariance matrix Σ among random effects for the same hospital in different periods, where σ_t is the random-effects standard deviation for period t and ρ_st is the correlation coefficient between random effects for periods s and t.

After re-arranging the data matrix, this model can be treated as a mixed-effects model and fitted by Bayesian methods. We assumed flat priors for α _t and β_t and an inverse-Wishart prior for Σ with three degrees of freedom and with mean equal to the covariance matrix estimated by iterated generalized least squares.

The Bayesian model fitting procedure generates draws from the posterior distributions of all model parameters including coefficients α_t and β_t and hospital-specific effects γ_it . These draws can be used to calculate credible intervals (CI) for any functions of these parameters as well as posterior probabilities for comparative statements, allowing inferences such as comparing, ranking, and identifying outstanding or substandard providers. In profiling, we consider comparisons of predicted outcomes if patients with identical characteristics were hypothetically sent for treatment at each of the hospitals. In equation (2), the patient effects $x_{\mathit{\text{ij}}}^T{\alpha }_t$ are the same at every hospital and therefore hospital profiling involves comparisons across hospitals of $e_{\mathit{\text{ti}}}=z_i^T{\beta }_t+{\gamma }_{\mathit{\text{it}}}$, the sum of effects predictable from the hospital’s observed characteristics (volume) and the hospital-specific random effect. Inferences about these profiles are obtained by summarizing draws from the Bayesian model (posterior median and quantiles), and probabilities (that one hospital’s profile is better than another hospital’s profile, or that a hospital is among a top-ranked group) by calculating the fraction of draws for which the corresponding condition is true.

For comparison, we also estimated a model for 30-day survival alone, equivalent to the model given by (1)–(2) restricted to t=1. Because the two methods use different priors for variance components, the posterior distributions of the variance component σ₁ for 30-day survival are different in the two methods. To make the two methods more comparable, we used propensity score weighting to match these posterior distributions. We estimated a logistic model for the propensity score p(s) representing the probability that an estimated value s of σ₁ was from the method (A) sample (in the combined sample). For all comparisons, we then applied weight w_i=p(s_i)/(1− p(s_i)) to each Monte Carlo draw s_i made by method (B), while retaining unit weights for all draws from method (A). This technique makes the posterior distribution of the variance component similar in the two methods.

Comparisons of profiles for period 1 alone under the 3-period model to the methods combining 3-period profiles are straightforward since all are drawn under the same model. Multi-period method (4) approximates the mortality combined over the 3 periods by Taylor linearization of Σ_t S_t P_ti , where S_t is the fraction of patients alive at the beginning of period t and P_ti is the period-t mortality rate at hospital i. Expanding in the profiles e_ti and dropping constant terms yields a weighted combination ${\displaystyle {\sum }_t{S}_t\frac{{\mathit{\text{dP}}}_{\mathit{\text{ti}}}}{{\mathit{\text{de}}}_t}{e}_{\mathit{\text{ti}}}}\approx {\displaystyle {\sum }_t{S}_t{P}_t(1-P_t)e_{\mathit{\text{ti}}}}{S}_t{e}_{\mathit{\text{ti}}}$ where P_t is average period-t mortality.