Abstract
The brainstem auditory pathway is obligatory for all aural information. Brainstem auditory neurons must encode the level and timing of sounds, as well as their time-dependent spectral properties, the fine structure and envelope, which are essential for sound discrimination. This study focused on envelope coding in the two cochlear nuclei of the barn owl, nucleus angularis (NA) and nucleus magnocellularis (NM). NA and NM receive input from bifurcating auditory nerve fibers and initiate processing pathways specialized in encoding interaural time (ITD) and level (ILD) differences, respectively. We found that NA neurons, though unable to accurately encode stimulus phase, lock more strongly to the stimulus envelope than NM units. The spectrotemporal receptive fields (STRFs) of NA neurons exhibit a pre-excitatory suppressive field. Using multilinear regression analysis and computational modeling, we show that this feature of STRFs can account for enhanced across-trial response reliability, by locking spikes to the stimulus envelope. Our findings indicate a dichotomy in envelope coding between the time and intensity processing pathways as early as at the level of the cochlear nuclei. This allows the ILD processing pathway to encode envelope information with greater fidelity than the ITD processing pathway. Furthermore, we demonstrate that the properties of the neurons’ STRFs can be quantitatively related to spike timing reliability.
Keywords: Nucleus angularis, STRF, spectrotemporal tuning, cochlear nuclei, barn owl, response reliability
Introduction
The cochlea decomposes sound into its spectral components, creating a topographic organization of frequency tuning that is preserved throughout much of the brainstem. Auditory neurons extract relevant information from the cochlear output, such as timing, level and spectral fine structure, as well as the sound envelope. Sound localization studies in barn owls have defined two processing pathways that originate at the cochlear nuclei, nucleus magnocellularis (NM) and nucleus angularis (NA), which extract interaural time (ITD) and level (ILD) differences, respectively (Sullivan and Konishi, 1984; Takahashi et al., 1984) (Figure 1). This dichotomy of ITD and ILD brainstem processing is also present in mammals (Boudreau and Tsuchitani 1968; Goldberg and Brown, 1969; Guinan et al., 1972a,b; Yin and Chan, 1990; Tollin and Yin, 2002).
Figure 1.
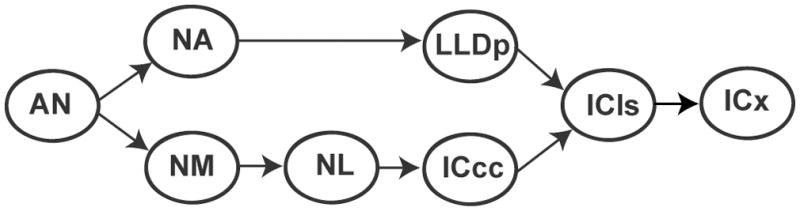
Schematic of the brainstem auditory system of the barn owl. Auditory nerve (AN) fibers bifurcate to project to both cochlear nuclei, nucleus angularis (NA) and nucleus magnocellularis (NM). NM is the first nucleus belonging exclusively to the ITD processing pathway and projects to nucleus laminaris (NL) where coincidence detection takes place. NL projects to the central core of the inferior colliculus (ICCc). NA projects to the pars posterior of the dorsal nucleus of the lateral lemniscus (LLDp); these nuclei comprise the ILD processing pathway. The ITD and ILD processing pathways converge on the lateral shell of the inferior colliculus (ICCls), which projects to the external nucleus of the inferior colliculus (ICx).
NA and NM receive inputs from the auditory nerve, whose fibers bifurcate (Carr and Boudreau, 1991). Neurons in NM and nucleus laminaris (NL) are able to phase lock to frequencies up to 9 kHz, indicating a spike timing resolution on the microsecond scale (Sullivan and Konishi, 1984; Gerstner et al.,1996; Köppl, 1997). Although neurons lose the ability to phase lock to high frequencies in the central nucleus of the inferior colliculus (ICCc), information on spectrotemporal attributes of the sound is preserved from NL to ICCc through envelope locking (Christianson and Peña 2007). In comparison to NM, neurons in NA do not display the same degree of temporal acuity. Instead, they have rate-level curves with a large dynamic range, making them more capable of encoding sound level changes with their firing rate (Sullivan and Konishi, 1984).
Along the same pathways, the auditory system encodes spectrotemporal features of sound, the fine structure and envelope. It has been suggested that encoding the spectrotemporal attributes underlies sound discrimination (Shannon et al., 1995; Wang et al., 1995; Chi et al., 1999; Nagarajan et al., 2002; Escabi et al., 2003; Suta et al., 2003; Woolley et al., 2005; Altmann et al., 2007; Atencio et al., 2007; Schneider and Woolley, 2010; Nelson & Takahashi, 2010). Here we address how spectrotemporal information is processed in the brainstem. We found that specific characteristics of spectrotemporal receptive fields (STRFs) of primary-like and onset type NA units enhance their response reliability to the stimulus envelope in comparison to NM units. This shows that not only do NA and NM specialize in encoding different sound localization cues, but they also differ in their selectivity to the sound’s envelope. This specialization endows the first stage of the ILD processing pathway with an enhanced ability to encode the stimulus envelope relative to the ITD pathway. Because the segregation into time and intensity pathways is present in the auditory system of both birds (Konishi, 2003) and mammals (Yin, 2002), these results are likely valid across species.
Methods
Surgery
Data were collected from 1 female and 2 male adult barn owls (Tyto alba) bred in captivity. The birds were anesthetized by intramuscular injection of ketamine hydrochloride (20 mg/kg; Ketaset) and xylazine (4 mg/kg; Anased) over the course of the experiment. The depth of anesthesia was monitored by toe pinch. They also received an intramuscular injection of prophylactic antibiotics (oxytetracycline; 20 mg/kg; Phoenix Pharmaceuticals) and a subcutaneous injection of lactated Ringers solution (10 ml) at the beginning for each experiment. Body temperature was maintained throughout the experiment with a heating pad (American Medical Systems, Cincinnati, OH). A metal headplate was implanted at the beginning of the first recording session by removing the top layer of the skull and affixing it with dental cement while the head was held in stereotaxic position with ear bars and a beak holder. A small steel post was also implanted to demarcate a reference point for stereotaxic coordinates. Subsequently, all recording sessions were performed while the head was held in place by the headplate. A well was created on the skull around the stereotaxic coordinates for NM and NA, using dental cement, and the skin was sutured around it. Subsequently, a craniotomy was performed at the coordinates for the recording site and a small incision was made in the dura mater for electrode insertion. At the end of a recording session, the craniotomy was sealed with Rolyan silicone elastomer (Sammons Preston, Bolingbrook, IL). After the experiment, analgesics (Ketoprofen, 10 mg/kg, Ketofen, Merial) were administered. Owls were returned to individual cages and monitored for recovery. Depending on the owl’s weight and recovery conditions, experiments were repeated every 7–10 days for a period of several weeks. These procedures comply with guidelines set forth by the National Institutes of Health and the Albert Einstein College of Medicine’s Institute of Animal Studies.
Acoustic stimulation
Dichotic stimulation was delivered in a double-walled sound-attenuating chamber (Industrial Acoustics). Custom software was used to generate stimuli and collect data. Earphones were constructed from a small speaker (Knowles 1914) and a microphone (Knowles 1319) in a custom-made case that fits the owl’s ear canal. The microphones were calibrated using a Bruel and Kjaer microphone, allowing us to translate voltage output into dB SPL. The calibrated microphones were used to calibrate the earphones at the beginning of each experiment while inside the owl’s ear canal. The calibration data contained the amplitudes and phase angles measured in frequency steps of 100 Hz. The stimulus generation software then used these calibration data to automatically correct irregularities in the amplitude and phase response of each earphone from 0.5 to 12 kHz (Arthur, 2004).
Acoustic stimuli consisted of pure tones and broadband noise bursts with a linear rise and fall time of 5 ms.
Electrophysiology
Brainstem structures were targeted by known stereotaxic coordinates. NM axons were recorded along the dorsoventral axis of nucleus laminaris (NL, Peña et al. 1996, Viete et al. 1997). NL location was determined by the stereotaxic coordinates and response properties (Peña et al. 1996). In NL, NM fibers are clearly differentiated from NL neurons by their response to sounds from only one ear. NM fibers were isolated and held by a loose patch method (Peña et al. 1996) in which the electrode serves as a suction electrode. Neural signals were sequentially amplified by a Multiclamp 700B and an AC amplifier (Tucker Davis, PC1).
NA was approached at a 5–10 degree angle in the coronal plane (Köppl and Carr, 2003). The recording site was determined by first locating NL and tilting the electrode laterally, until neural responses to only the ipsilateral side were found. NA units can be distinguished from other short latency, monaural-responding structures, namely NM and the auditory nerve, by their poor phase locking, which was measured online and confirmed post-hoc (see data analysis section). Nuclei downstream of NA, such as LLDp and the superior olive, are binaural and have longer latencies than NA, and can thus be easily distinguished. NA units were recorded using 5 mega-Ohm tungsten electrodes (A-M Systems, Carlsborg, WA) and amplified by a DP-301 Differential Amplifier (Warner Instruments, Hamden, CT).
A spike discriminator (SD1, Tucker-Davis Technologies, Gainesville, FL) converted neural impulses into TTL pulses for an event timer (ET1, Tucker-Davis Technologies), which recorded the timing of the pulses.
Data collection
To estimate the neurons’ frequency tuning, ten repetitions of 50 ms long tones were presented in steps of 500 Hz from 0.5 to 12 kHz with inter-stimulus interval (ISI) of 500 ms. To estimate the neurons’ phase-locking ability, 300 repetitions of 100 ms long tones were presented at the neurons’ best frequency at a suprathreshold intensity. The neurons’ rate-level responses were measured using ten repetitions of 50 ms broadband-noise bursts (1 to 12 kHz) presented in steps of 5 dB from 20 to 80 dB with an ISI of 500 ms.
Data used to determine the neurons’ STRF and their response reliability was collected as described by Christianson and Peña (2007). To measure STRFs we presented a string of de novo-synthesized broadband noise segments (unfrozen noise protocol) at two intensities, one within the dynamic range of the rate-level curve and one eliciting maximum response. To measure response reliability we used a ‘frozen noise’ protocol, in which a single broadband noise stimulus (1 to 12 kHz) was repeated. Two separate and unique noises with different intensities were randomly interleaved to minimize the effects of adaptation. In both cases noise segments were 500 ms long with a rise and fall time of 5 ms and an ISI of 300 ms. Stimuli were presented until approximately 4000 spikes had been collected at each stimulus intensity.
Data analysis
STRFs were extracted by reverse correlation (de Boer and de Jongh, 1978) from spike data collected during the unfrozen noise protocol, as described by Christianson and Peña (2007) and Keller and Takahashi (2000). In summary, a pre-event stimulus ensemble (PESE) is constructed from the 15 ms stimulus segments, sampled at 48 kHz, that precede each spike. Each element of the PESE is passed through a gammatone filter bank with 91 channels spaced linearly between 1 to 10 kHz. The stimulus envelope for each segment is extracted using the Hilbert transform, and averaged across the PESE. The resulting STRF consists of a 91 × 721 matrix of data points. The onset of the response to sound (first 100 ms) was excluded for the estimation of the STRF and the shuffled-autocorrelogram (SAC), considering only those spikes that occurred once the firing rate had reached a steady state by visual inspection of the PSTH. In most neurons, this steady state was reached well before 100 ms after the stimulus onset in both frozen and unfrozen noise protocols.
The neuron’s best frequency (STRFbf) was estimated from the excitatory peak value of the STRF. The spectral bandwidth and the temporal width of the STRFs (STRFbw and STRFtw, respectively) were measured at the half maximal response, passing through the excitatory peak. We also measured the magnitude of the suppressive field of the STRF (STRFsf). The amplitude of the STRFsf was defined as the most negative datapoint in the STRF matrix within 3 ms preceding the excitatory peak of the STRF. The 3-ms window was chosen empirically, by observing the delay and duration of the suppressive fields in the dataset. Because spike data were collected at different average binaural intensities for different neurons, we normalized the STRFsf by the average maximal power of the stimuli that were presented during the unfrozen noise protocol. We examined the relationship between the STRFsf and the mean amplitude of the suppressive field and the area of the suppressive field. For this analysis we considered all datapoints within the suppressive subfield smaller than half the STRFsf value. We found that the STRFsf was strongly correlated with the mean negative amplitude of the suppressive field (R=0.99, p<0.001), as well as with the area of the suppressive field (R=0.89, p<0.001). For its lower dimensionality and for being strongly correlated with the other two measurements, we thus used STRFsf for the rest of the analysis and modeling.
The STRF was used to predict the response of the neuron to a novel stimulus as previously described (Eggermont et al. 1983; Linden et al. 2003; Theunissen et al.2000; Christianson and Peña, 2007). This was achieved by convolving each frequency channel of the STRF with the corresponding frequency channel of a filtered stimulus and averaging across channels. The predicted and actual post-stimulus time histograms (PSTHs) of the neuron were compared by computing correlation coefficients.
The effective refractory period of NA and NM units was estimated from the inter-spike interval histograms (ISIHs) obtained from the unfrozen noise protocol, binned at 0.1 ms. The effective refractory period was measured as the shortest inter-spike interval which occurred at a spike count greater than 25% of the maximum spike count for any inter-spike interval.
We measured response reliability to the stimulus envelope by quantifying the reliability of the neural response to repeated presentations of the same stimulus with the SAC (Joris, 2003; Christianson and Peña, 2007). For this method, each spike train recorded during one presentation of the frozen noise stimulus is compared to all other spike trains recorded from other presentations of the same stimulus. For each possible combination, the forward time intervals for all spikes in the reference spike train relative to its partner are computed using a 50-microsecond bin width. A normalizing factor was used, N(N −1)r2ΔτD, where r is the mean firing rate, Δτ is the bin width of the correlogram, and D is stimulus duration. This produces a unity baseline, where a spike train with Poisson statistics will have a flat SAC of height 1. The main parameter considered here to quantify the ability of neurons to lock to the envelope is the height of the SAC’s peak at zero measured in number of normalized coincidences.
To verify our findings obtained with the SAC metric, we also quantified response reliability using the spike train distance metric Dspike[q] as described by Victor and Purpura (1996). The spike train distances were computed using a cost q of 20, where absolute spike times were given in milliseconds relative to the onset of the stimulus. This ensures that the spike train distance and SAC are calculated at the same temporal resolution, namely 50 microseconds.
To confirm units’ nucleus identity post-hoc, we took advantage of the observation that neurons which phase lock will exhibit damped oscillations in their SAC close to their best frequency (Louage et al., 2004; Joris et al., 2006). We quantified the frequency of oscillations in their SAC as the unique maximum, or best frequency, of the power spectral density (PSD) estimate.
Model
To study the relationship between the STRF of a neuron and its response reliability, we created artificial STRFs by combining two gamma-envelopes (one positive and one negative). This produced the excitatory and suppressive fields in the temporal dimension. We paired this with a Gaussian envelope in the spectral dimension (Figure 5A). We varied the magnitude of a suppressive field preceding the excitatory subfield while keeping the magnitude of the excitatory peak, the temporal and the peak latencies (both positive and negative) of the STRF constant. Each of these STRFs was convolved with a 500-ms long broadband noise (Figure 5B). The output of the convolution (Figure 5C) was subsequently normalized and passed through a linear input/output function estimated from the data (Figure 5D) by plotting observed PSTH spike-counts against PSTH spike-counts predicted by the STRF. The resulting PSTH-like filter output was decimated to a rate of 0.1 ms and used to generate a Poisson-like spike train (Chichilnisky, 2001; Schwartz, 2006; Figure 5E). After the spike trains were generated, we imposed absolute refractory periods of different durations (0.6 ms, 1 ms, 1.5 ms and 2ms) on them by removing all spikes that fell within that interval of a generated spike. The sampling rate of the PSTH was decreased from 48 kHz to 10 kHz to prevent saturation of the firing rate when spike trains were generated. Unlike real neurons, where threshold and refractory period act before spikes are generated, refractoriness in our model was imposed after spike generation. Thus, sampling rate decimation was necessary to prevent oversaturation of the firing rate at reasonable threshold values. Parameters of the model were set such that the firing rate produced at the average STRF negative-to-positive subfield magnitude ratio and estimated refractory period of NA was similar to the average firing rate observed in the data. We generated 1500 spike trains for each combination of refractory period and suppressive field magnitude. Results were averaged over five different noise stimuli. The spike trains produced by the model were analyzed with the SAC to quantify the effect of refractory period and suppressive field magnitude on reliability as described above. To verify our quantification using the SAC metric, we also quantified the output of the model using the spike train distance metric Dspike[q] using 450 spike trains for each suppressive field magnitude.
Figure 5.
Schematic description of the model. Model STRFs (A) were convolved with a noise stimulus (B). This PSTH-like filter output (C) was put through a linear input-output function estimated from the in vivo data (D). The resulting output was used to generate spike trains (E), which were analyzed using the SAC metric.
To control for the effects of bandwidth and temporal width of the STRF on response reliability, we created two additional models which varied each of these parameters while holding the other constant at a fixed suppressive subfield magnitude. The constant bandwidth was set at 600 Hz, while the constant temporal width was set at 1.37 ms (these values were estimated from the NA dataset). Spike trains were generated and quantified as described above.
Finally, we calculated SACs based on the output of our NA model and compared it to our results from electrophysiology. We convolved each NA unit’s STRF with the stimulus presented during the frozen noise protocol, which was used to record spike data for SAC calculation and was not used in computing the STRF. We normalized this convolution output and then used it to generate spike trains, as described above. The average firing rate of the spiketrains was closely matched to the mean observed firing rate of each neuron during the frozen noise protocol. These spike trains were then used to compute SACs. We compared the SAC peak heights predicted from the convolution of the STRF with the stimulus (predicted SAC peak height) to the SAC peak heights obtained from the spike-train data recorded in vivo (observed SAC peak height).
Results
Identification and characterization of NA and NM units
Datasets consist of 38 NA and 53 NM units. Neurons of both nuclei respond only to ipsilateral monaural stimuli. NM axons, which were recorded in dorso-ventral penetrations within NL, alternate between ipsilateral and contralateral monaural responses, clearly distinguishing them from NL neurons, which respond to binaural stimulation (Peña et al. 1996, Viete et al. 1997). NA can be distinguished from NM and NL units and auditory nerve fibers by their poor ability to lock to the phase of their best frequency (Köppl and Carr, 2003); phase locking in NA was quantified by measuring vector strength at the neurons’ estimated best frequency. The vector-strength values measured in this study are comparable to those reported by Sullivan and Konishi (1984) and Köppl and Carr (2003). Neurons that lock to the phase of their best frequency will also display periodic oscillations in their SAC (Figure 2D) whereas SACs of neurons that do not phase lock are smooth (Figure 2C, Louage et al., 2004; Joris et al., 2006; Christianson and Peña 2007). Taking advantage of this, we used the units’ SACs to further confirm their phase locking ability for both NA and NM by comparing the frequency of the periodicity of the SAC with the neurons’ best frequency. In NM, there was a strong correlation between the frequency of the SAC’s periodicity and the STRFbf (R= 0.99, p < 0.001). However, there was no correlation for NA units, confirming that they did not phase lock to their best frequency.
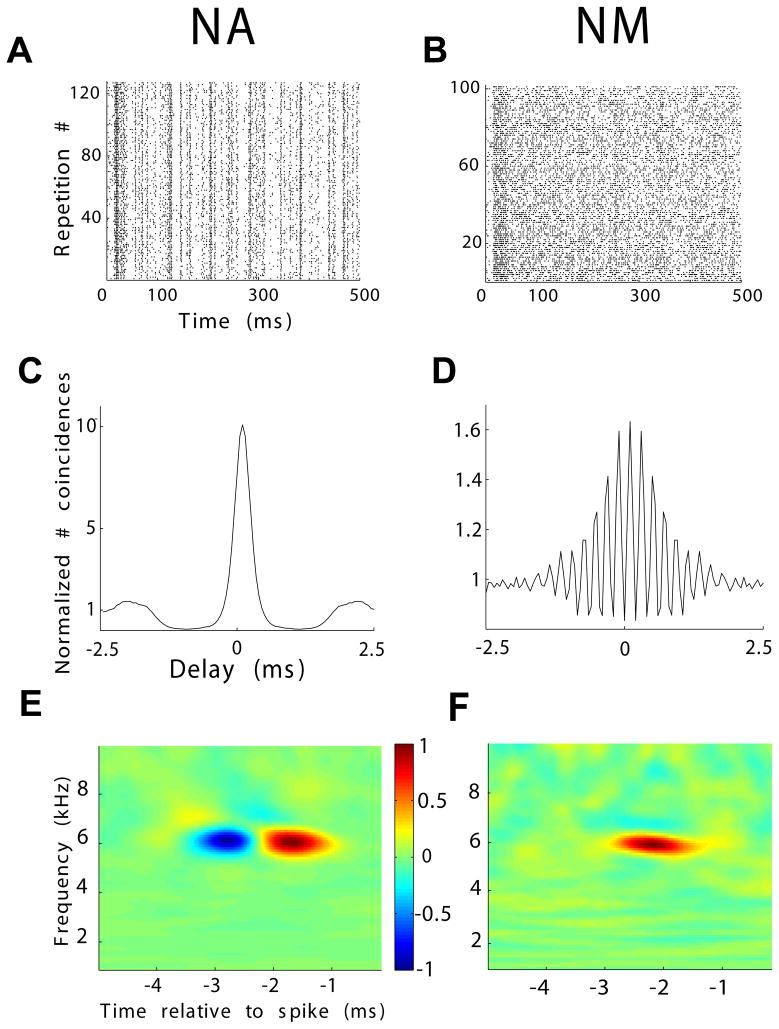
Figure 2.
NA and NM units exhibit gross differences in their response properties. Representative rasters are shown for the responses of NA (A) and NM (B) neurons to repeated presentations of the same stimulus (frozen noise). (C) SAC corresponding to the NA unit in (A) with a peak height of 10. (D) SAC corresponding to the NM unit in (B) with a peak height of 1.6. The high-frequency structure in D is a result of phase locking in NM. (E) A representative example of NA unit’s STRF. STRFbf = 6.1 kHz, STRFbw = 800 Hz, STRFtw = 0.9 ms. (F) A representative example of a NM unit’s STRF. STRFbf = 6 kHz, STRFbw = 500 Hz, STRFtw = 0.9 ms. Notice that the NA unit’s excitatory subfield is preceded by a suppressive field (blue), which is absent in NM.
Because the estimation of the STRF and the response reliability requires thousands of spikes, it was necessary to record exclusively from units that responded robustly throughout the 500 ms stimulus. Though this does not represent a problem in NM, our NA sample was biased towards mostly primary-like neurons and onset-type neurons with a sustained discharge. We defined onset-type neurons as those units whose ratio of peak firing rate (within the first 20 ms) to steady-state firing rate (during the last 400 ms) in response to unfrozen noise was equal to or larger than 10 (Rhode and Smith, 1986). In our dataset, two neurons met this criterion. Köppl and Carr (2003) classified 32% of NA neurons as primary-like and 6% as onset. Our dataset is therefore skewed towards the most common response type, which also spans the widest frequency range (Köppl and Carr, 2003).
To estimate the response latency, we measured the latency of the STRF excitatory peaks. NA and NM units had significantly different response latencies (NA: 1.9 ± 0.51 ms; NM: 2.25 ± 0.34 ms; medians significantly different by Kruskal-Wallis, p<0.005). Compared to response latencies previously reported for NM and NA (Sullivan and Konishi, 1984; Köppl and Carr, 2003, respectively), our values are about 0.5 ms shorter. However, both previous studies used PSTHs of responses to tone and/or noise stimuli with onset ramps to estimate first-spike latency. Our method of estimating response latency differs by taking into account the latency of spikes throughout the stimulus and by construction (see methods) avoids the confounding effect of stimulus onset ramp.
As reported by Sullivan and Konishi (1984), we also observed lower firing rates in NA than in NM, albeit those conclusions were based on spontaneous rates, whereas our observations are based on driven rates. We observed a mean response rate of 183 ± 110 spikes/s in our sample of primary-like NA units, measured during the first 50 ms of their response to unfrozen noise. This value is lower than that reported by Köppl and Carr (2003). Theirs, however, is saturation rate measured with tone stimulation, which makes the difference difficult to interpret. We did not measure saturation rate with tonal stimulation routinely. An estimate of effective refractory period was made by measuring the minimum inter-spike interval from ISIHs obtained with multiple repetitions of unfrozen noise. NA and NM units’ effective refractory periods were not significantly different (1 ± 0.38 ms and 0.8 ± 0.19 ms, respectively; p > 0.05, t-test).
Response reliability in NA vs. NM
We compared the stimulus-dependent spike-timing reliability in NA (n = 38) and NM (n = 40) upon repeated presentations of the same stimulus (frozen-noise protocol). Spike-timing reliability, as viewed here, is different from phase-locking reliability. Stimulus phase changes periodically and neurons can encode sound phase with high accuracy while firing at different times during the sound. Instead, by reliable spike timing, we refer to the likelihood of spikes to fire at a given time in different presentations of the same sound (Figure 2A and B). Under the assumption that auditory neurons respond to power increases within their preferred frequency band, high reliability indicates that the firing pattern could encode information about the spectral structure and envelope of a sound.
Spike trains were analyzed using SACs (Joris et al., 2006). The height of the SAC at zero time lag quantifies the likelihood that spikes will occur at the same time during a stimulus when it is presented repeatedly. We found that SAC peak heights were significantly larger in NA than in NM (Figure 3A; medians significantly different by Kruskal-Wallis test, p < 0.001). We found that SAC peak height was inversely correlated with STRFbf in both NA and NM (NA regression: −0.00072x + 6.8, R = 0.42, p<0.05; NM regression: −0.0002x + 2.7, R = 0.72, p<0.001, within 95% confidence bounds). To assess whether the difference in SAC peak height was due to a bias in the frequency range of neurons sampled in NA vs. NM, we compared the regression lines between best frequency and SAC peak height in both populations of cells. These regressions were significantly different (p < 0.001, t-test), indicating that for a given frequency NA units SAC peaks will be significantly larger than those observed in NM.
Figure 3.
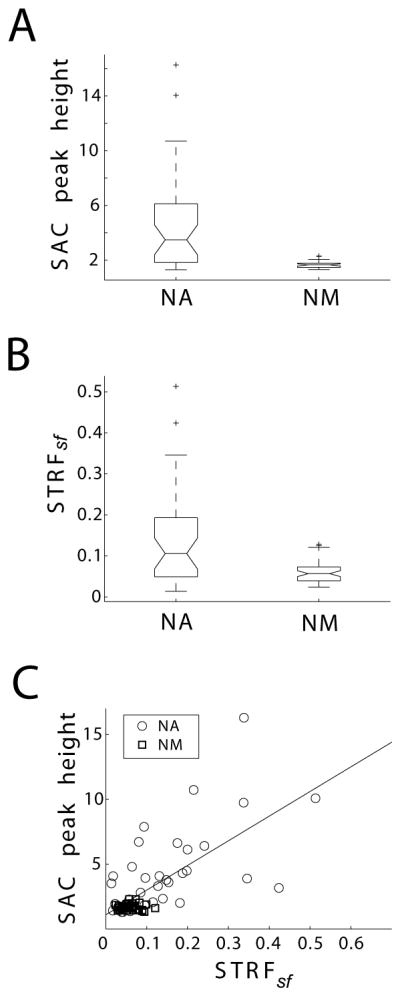
Quantification of response reliability (SAC peak height) and STRFsf across population data. (A) SAC peak heights (in units of normalized number of coincidences) are significantly larger in NA units (medians significantly different by Kruskal-Wallis test, p < 0.001), indicating that responses are more reliable in NA compared to NM; (B) STRFsf is significantly larger in NA units than in NM units (medians significantly different by Kruskal-Wallis, p<0.001). Boxes extend from lower quartile to upper quartile of the sample, with the center line marking the median. Outliers (+) are data points 1.5 times the interquartile range of the sample. (C) STRFsf and SAC peak height are correlated in NA (regression: 17x + 1.9, R=0.62, p < 0.001).
To verify the findings of the SAC metric using an additional measure of response reliability, we also computed the spike-train distance as described by Victor and Purpura (1996). Consistent with the SAC analysis, spike-train distances were significantly smaller in NA compared to NM (Supplemental Figure 1A; medians significantly different by Kruskal-Wallis test, p < 0.001). These results indicate that the firing pattern in NA is more invariant than in NM when the same stimulus is repeated.
Comparison of STRFs of neurons in NA vs. NM
To evaluate differences between NA and NM units’ STRFs (n = 36 and n = 53, respectively), we began by quantifying the STRFbf, STRFbw and STRFtw. We found a significant positive correlation between STRFbw and STRFbf in NM and NA (NM regression: 0.089x + 37, R = 0.69, p < 0.001; NA regression: 0.15x + 220, R = 0.36, p < 0.05). When plotted together, samples of the two populations of neurons overlap (not shown), but their regressions are significantly different (t-test, p<0.001). We also found an inverse correlation between STRFbf and STRFtw in both nuclei (NM regression: − 0.0002x + 2.2, R= −0.74, p < 0.001; NA regression: −0.00019x + 2.2, R= 0.72, p < 0.001). These regressions were not significantly different.
A conspicuous difference observed is that excitatory subfields of STRFs in NA were generally preceded by a suppressive field (Figure 2E; STRFsf), which was generally absent in NM units’ STRFs (Figure 2F). When quantifying the STRFsf, we found that its magnitude across NA units is in fact significantly larger than across NM units (Figure 3B; medians significantly different by Kruskal-Wallis, p<0.001). This STRF property is consistent with NA neurons being sensitive to the onset of power transients within the frequency band that they are tuned to (discussed below).
We used the neurons’ STRFs, computed with unfrozen noise, to predict the response to stimuli presented during the frozen-noise protocol and compared predicted and observed PSTHs. We found that the correlation coefficients between the predicted and observed PSTHs were significantly higher for NA units’ STRFs (median: 0.7) than for NM units’ STRFs (median: 0.62, Figure 4; medians significantly different by Kruskal-Wallis, p < 0.001). This indicates that linear filters, such as STRFs, are a better descriptor of NA neurons’ response behavior than they are for NM units.
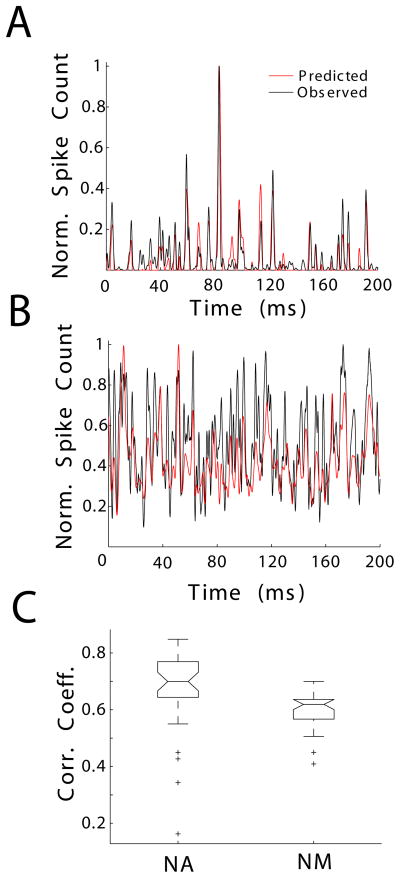
Figure 4.
STRFs more accurately predict the response of NA units than NM units. Example of observed (black) and predicted (red) PSTHs, given in units of normalized spike counts (Norm. Spike Count), from NA (A, correlation coefficient = 0.85) and NM (B, correlation coefficient = 0.7). (C) The correlation between the predicted and observed PSTHs (Corr. Coeff.) was compared across NA and NM. NA STRFs yielded better predictions of neural responses (medians significantly different by Kruskal-Wallis, p < 0.001). Boxes extend from lower quartile to upper quartile of the sample, with the center line marking the median. Outliers (+) are data points 1.5 times the interquartile range of the sample.
Relationship between STRF properties and response reliability
In NA, we found a significant correlation between STRFsf and SAC peak height (Figure 3C; regression: 17x + 1.9, R=0.62, p < 0.001), as well as between STRFbf and SAC peak height (regression: −0.00075x + 7.4, R = 0.32, p = 0.05). In NM we found that both STRFbw (regression: −0.0011x + 2.2, R=0.43, p<0.01) and STRFbf (regression: −0.0002x + 2.7, R = 0.72, p<0.001) were correlated with their SAC peak height. Because many of these parameters co-vary, we used multilinear regression analysis to determine which STRF features had the most power in modulating SAC peak height when considered together. For this analysis, STRFsf, STRFbw and STRFbf were normalized by their within-sample maxima. In NA, SAC peak was significantly influenced by STRFsf and STRFbf, where STRFsf was the dominant factor (Table 1). In NM, SAC peak was significantly affected only by STRFbf (Table 1). The lack of effect that STRFsf has on NM units’ SAC peak is likely due to STRFsf values spanning a very small range in NM. Also, it should be noted that STRFbf exerts a much more prominent effect on NA SAC peaks than on NM SAC peaks. This indicates that STRF features play a much greater role in modulating SAC peaks in NA than NM.
Table 1. Coefficients of multiple linear regression analysis.
Regression coefficients (Reg. Coeff.) and p-values for the multilinear regression analysis performed on STRFsf, STRFbw, STRFbf and SAC peak height data from NA and NM.
| Reg. coeff. (NA) | p (NA) | Reg. coeff. (NM) | p (NM) | |
|---|---|---|---|---|
| STRFsf | 10.16 | <0.001 | −0.09 | 0.57 |
| STRFbw | 2.57 | 0.28 | 0.17 | 0.57 |
| STRFbf | −7.95 | <0.001 | −1.4 | <0.001 |
Modeling the effects of STRF properties on response reliability
To assess the effect of varying specific STRF parameters on the response reliability of a neuron, we developed a simple model using artificial STRFs which were convolved with a stimulus, allowing us to generate artificial spike trains from the resulting output (Figure 5). We varied parameters of interest in the modeled STRFs to observe how they affected the reliability of the neural response, which was quantified using SACs.
Our primary interest was the effect of the magnitude of STRFsf on SACs. This suppressive field is consistent with sensitivity to the onset of power transients in the neuron’s preferred frequency band, making it more selective than a neuron without a suppressive field. To test whether greater spectrotemporal selectivity, as indicated by the presence of STRFsf, could account for greater response reliability, we ran the model varying STRFsf while holding STRFbw and STRFtw constant. Consistent with the observations in the NA units, we found that increasing the magnitude of the suppressive field created more patterned PSTHs and rasters (Figure 6A) and enhanced the reliability of spike trains, increasing the SAC peak height (Fig 6B). Although firing rates do change with varying STRFsf, the SAC is normalized with respect to the firing rate and this does not represent a confound (see Methods). Spike-train distances also decreased with larger STRFsf (Supplemental Figure 1B). Overall, these results indicate that STRFsf can account for enhanced response reliability observed in NA.
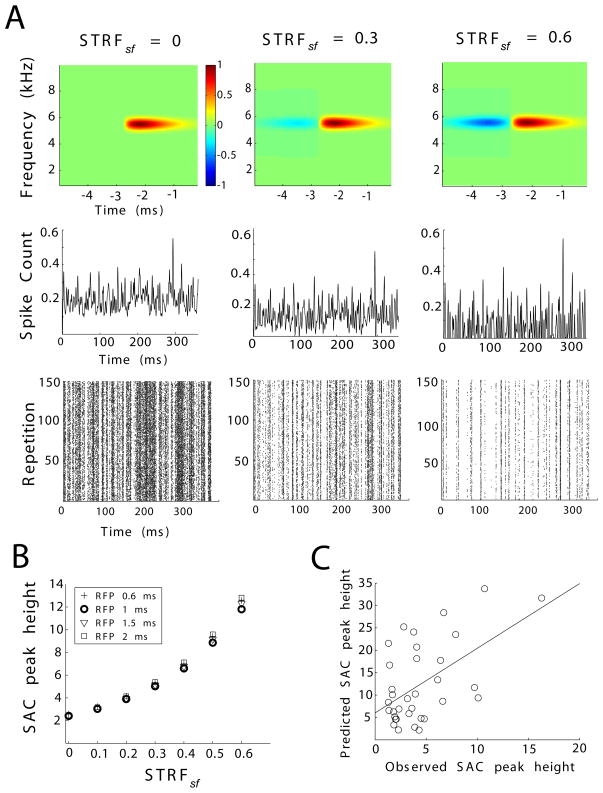
Figure 6.
Modeling the effects of STRF suppressive field on response reliability. (A) Representative STRFs (top), PSTHs (middle) and corresponding rasters (bottom) at suppressive field magnitudes (STRFsf) equal to, from left to right, 0, 0.3, and 0.6. PSTHs are shown as normalized predicted spike count. Quantification reveals that pre-excitatory suppressive fields enhance response reliability (SAC peak height, B, in units of normalized number of coincidences). Different refractory periods (RFP) were tested (indicated in B). Datapoints for RFP = 1 ms are enhanced for clarity. A refractory period of 1 ms most closely approximates the estimated refractory periods across NA and NM. (C) The SAC peak height predicted by the model is correlated with the in vivo observed SAC peak height (R = 0.54, p = 0.001).
Another difference between NM and NA units which could affect reliability is the larger STRFbw observed in NA. Our model showed that increasing STRFbw decreased the SAC peak height (Supplemental Figure 1C). This is consistent with our observation of an inverse correlation between SAC peak height and STRFbw in NM (see previous section). Furthermore, spike train distances increased with increasing STRFbw (Supplemental Figure 1D).
Our model simulated neurons with different refractory periods under the same STRF parameters. The refractory period did not grossly affect the relationship between SAC peak height and STRFsf (Figure 6B). The refractory periods estimated from ISIHs in our dataset were not significantly different between NA and NM. However, NA units’ larger STRFbw as compared to NM should, according to the model, decrease their response reliability. We observed that despite this difference, NA units’ response reliability is still significantly larger.
Finally, we tested how well our model could predict the relationship between STRFs and response reliability in the data. We used the model to generate spike trains from the STRF of each NA unit and computed SACs on these data. We found a correlation between the SAC-peak height obtained from our in vivo data and those predicted by our model (R = 0.54, p = 0.001, Figure 6C). The model, however, tended to overestimate the SAC peak height; this is to be expected, as our model did not incorporate any noise mechanism and all simulated spiking activity is purely stimulus driven. Despite the expected overestimation, this result indicates that our model captures the overall relationship between STRF shape and reliability.
Discussion
In this study we show that the degree of envelope locking of a neuron can be predicted by features of its STRF. We demonstrate a relationship between response reliability conferred by envelope locking and features of neurons’ spectrotemporal tuning. Primary-like and onset type neurons in NA, the first nucleus of the ILD processing pathway in barn owls, show more reliable responses to the stimulus envelope than NM units, the first nucleus of the ITD processing pathway. This locking to the stimulus envelope, which underlies the enhanced trial-to-trial response reliability in NA, is correlated with the amplitude of a pre-excitatory suppressive field in the STRFs.
Previous research has reported spatially independent, highly reproducible, neural responses to repeated stimuli in the lateral shell of the inferior colliculus (ICcl) of the barn owl (Keller and Takahashi, 2000). It has been demonstrated that neurons in ICcl are able to lock to the envelope of narrowband stimuli. On average, this envelope is virtually identical to a cross-section through the STRF at the neuron’s best frequency. Similar to our findings, the authors describe some neurons as having biphasic STRFs that display a trough followed by a peak. Our work demonstrates that these highly reproducible envelope-locked responses can already be observed in the cochlear nuclei, suggesting that the midbrain response is inherited from preceding processing stages. Keller and Takahashi (2000) proposed that information about the stimulus envelope may be passed to ICcl via the ILD processing pathway. Our work supports this hypothesis, provided that the quality of the envelope locking is preserved from NA to VLVp, the downstream nucleus that projects to ICcl. Our work further expands upon the work of Keller and Takahashi (2000) by demonstrating a relationship between the envelope features that the neurons are tuned to and the reliability of the neural response. The more selective a neuron is for envelope features, the more reliable its response will be.
Mammals, like barn owls, process ITDs and ILDs in parallel brainstem pathways. In owls both pathways cover approximately the same frequency range (Carr and Konishi 1990; Manley et al., 1988;, Köppl and Carr, 2003), while in mammals the overlap is more restricted (Yin & Chan, 1990; Tollin & Yin, 2005). There is evidence that both pathways converge over a broad range of frequencies in the inferior colliculus, where input from high frequency MSO neurons has been demonstrated (Loftus et al., 2010). Envelope locking has been observed in the mammalian ILD pathway, specifically in cells of the lateral superior olive and their afferents, the spherical bushy cells of the anteroventral cochlear nucleus and the medial nucleus of the trapezoid body (Joris & Yin, 1995; Joris, 1996; Joris and Yin, 1998). In the mammalian inferior colliculus, ITD tuning over a broad frequency range is dominated by envelope locking (Joris, 2003; Griffin et al., 2005). These studies show that envelope locking is observed in both the mammalian ITD and ILD pathways. However, the degree of envelope locking in the two pathways has not been compared in mammals. Given our data and the available evidence in mammals, it is possible that the ILD processing pathway in mammals would also encode envelope information with higher fidelity than the ITD processing pathway within the same frequency range.
STRFs and response reliability
NA units’ STRFs are characterized by a pre-excitatory suppressive field which is largely absent in NM units. The presence of suppressive fields in NA units’ STRFs indicates that the filter function of these neurons detects portions of stimuli where power in the preferred frequency band increases sharply, i.e. power transients or envelope fluctuations. These observations indicate that NA units are more selectively tuned to envelope features than NM units.
Studies across species and sensory systems have demonstrated that sensitivity to transients in input current (Mainen and Sejnowski, 1995; Suter and Jaeger, 2004; Rodriguez-Molina, 2007; Street and Manis, 2007) and stimuli (de Ruyter van Steveninck, 1997; Mechler et al., 1998; Rokem et al., 2006; Schmid et al., 2009) can generate precise, reliable neural activity. This is also supported by modeling studies (Kretzberg et al., 2001; Gutkin et al., 2003; Galán et al., 2008). We infer that NA units’ STRF properties are an expression of their tuning to transients, or envelope fluctuations, which leads to more reliable spike timing. It has also been suggested that inhibitory subfields may increase firing reliability and contribute to encoding natural stimuli in the auditory cortex (Narayan 2005; David et al., 2009), although such predictions have not always been confirmed by data (Schneider and Woolley 2010). Our work provides an example where those predictions are true.
Mechanisms of enhanced envelope locking
The α-dendrotoxin-sensitive low-threshold potassium channel (KLT) allows neurons to preferentially respond when a stimulus induces fast rates of depolarization (Ferragamo and Oertel, 2002; Slee et al., 2005; McGinley and Oertel, 2006; Gai et al., 2009). These properties of KLT make it a good candidate for explaining the cellular mechanism of pre-excitatory suppressive fields in NA’s STRFs. Interestingly, KLT has been shown to be present in both NA and NM (Reyes et al., 1994; Fukui and Ohmori, 2003, 2004). However, work by McGinley and Oertel (2006) demonstrated that populations of cells with different KLT conductance are sensitive to different rates of depolarization and have different integration windows. Difference in integration windows may underlie the observed differences in envelope locking capabilities between NA and NM.
Alternatively, fast changes in membrane potential have been shown to be associated with low spiking thresholds (Azouz and Gray, 2000). Peña and Konishi (2002) reported that spiking thresholds that occurred at the stimulus onset, when a large power transient is present, had lower thresholds than those of subsequent and spontaneous spikes. Similar mechanisms have also been described in the rat hippocampus (Henze and Buzsaki, 2001).
Escabi et al. (2005) observed an inverse relationship between STRF selectivity and firing rate. Using an integrate-and-fire model, they demonstrated that this observation could be accounted for by spiking thresholds. Street and Manis (2007) reported similar findings in the dorsal cochlear nucleus of the rat. Our model yields results consistent with their prediction. However, our in vivo data showed no correlation between neurons’ firing rates and STRFsf or spike reliability. This may be due to level of anesthesia or differences in spontaneous activity. Limitations of our model, which does not include a thresholding mechanism controlled by physiological parameters, prevent us from isolating the effects of threshold on response reliability. Although we cannot exclude thresholding as a mechanism to further enhance response reliability, the neurons’ selectivity for transients cannot be explained by a pure thresholding mechanism that does not take rates of depolarization into account.
Conclusion
In conclusion, we have found that primary-like and onset type NA units encode the envelope more reliably than NM units. A more selective spectrotemporal tuning characterizes responses in NA. These tuning properties are the result of greater sensitivity to a specific feature, power transients, within the frequency band that neurons prefer. Consistent with theory, the data show a correlation between the magnitude of the suppressive fields in NA STRFs and the reliability of the response to repeated presentations of the same stimulus. Our findings demonstrate that the adaptations that segregate auditory processing into timing and intensity pathways, manifested as temporal processing resolution, have an inverse effect on the ability to encode the stimulus envelope. If this inverse relationship arises directly from constraints of cellular computation, we expect that the general finding should be true in the auditory system of other species.
Supplementary Material
Acknowledgments
We are grateful to Bjorn Christianson and Brian Fischer for commenting on the manuscript and helping with the analysis. We would also like to specially thank Sharad Shanbhag for assistance with the experimental setup, and Adam Kohn, Odelia Schwartz and Sean Luo for feedback on data analysis.
Grant support: This work was supported by NIH grant CD007690
References
- Altmann CF, Doehrmann O, Kaiser J. Selectivity for animal vocalizations in the human auditory cortex. Cereb Cortex. 2007;17:2601–2608. doi: 10.1093/cercor/bhl167. [DOI] [PubMed] [Google Scholar]
- Arthur BJ. Sensitivity to spectral interaural intensity difference cues in space-specific neurons of the barn owl. J Comp Physiol A. 2004;190:91–104. doi: 10.1007/s00359-003-0476-1. [DOI] [PubMed] [Google Scholar]
- Atencio CA, Blake DT, Strata F, Cheung SW, Merzenich MM, Schreiner CE. Frequency-modulation encoding in the primary auditory cortex of the awake owl monkey. J Neurophysiol. 2007;98:2182–2195. doi: 10.1152/jn.00394.2007. [DOI] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci U S A. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boudreau JC, Tsuchitani C. Binaural interaction in the cat superior olive S segment. J Neurophysiol. 1968;31:442–454. doi: 10.1152/jn.1968.31.3.442. [DOI] [PubMed] [Google Scholar]
- Carr CE, Boudreau RE. Central projections of auditory nerve fibers in the barn owl. J Comp Neurol. 1991;314:306–318. doi: 10.1002/cne.903140208. [DOI] [PubMed] [Google Scholar]
- Carr C, Konishi M. A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chi T, Gao Y, Guyton MC, Ru P, Shamma S. Spectro-temporal modulation transfer functions and speech intelligibility. J Acoust Soc Am. 1999;106:2719–2732. doi: 10.1121/1.428100. [DOI] [PubMed] [Google Scholar]
- Chichilnisky EJ. A simple white noise analysis of neuronal light responses. Network. 2001;12:199–213. [PubMed] [Google Scholar]
- Christianson GB, Peña JL. Preservation of spectrotemporal tuning between the nucleus laminaris and the inferior colliculus of the barn owl. J Neurophysiol. 2007;97:3544–3553. doi: 10.1152/jn.01162.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David SV, Mesgarani N, Fritz JB, Shamma SA. Rapid synaptic depression explains nonlinear modulation of spectro-temporal tuning in primary auditory cortex by natural stimuli. J Neurosci. 2009;29:3374–86. doi: 10.1523/JNEUROSCI.5249-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Boer E, de Jongh HR. On cochlear encoding: potentialities and limitations of the reverse-correlation technique. J Acoust Soc Am. 1978;63:115–135. doi: 10.1121/1.381704. [DOI] [PubMed] [Google Scholar]
- de Ruyter van Steveninck RR, Lewen GD, Strong SP, Koberle R, Bialek W. Reproducibility and variability in neural spike trains. Science. 1997;275:1805–1808. doi: 10.1126/science.275.5307.1805. [DOI] [PubMed] [Google Scholar]
- Eggermont JJ, Aertsen AM, Johannesma PI. Prediction of the responses of auditory neurons in the midbrain of the grass frog based on the spectro-temporal receptive field. Hear Res. 1983;10:191–202. doi: 10.1016/0378-5955(83)90053-9. [DOI] [PubMed] [Google Scholar]
- Escabí MA, Miller LM, Read HL, Schreiner CE. Naturalistic auditory contrast improves spectrotemporal coding in the cat inferior colliculus. J Neurosci. 2003;23:11489–11504. doi: 10.1523/JNEUROSCI.23-37-11489.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escabí MA, Nassiri R, Miller LM, Schreiner CE, Read HL. The contribution of spike threshold to acoustic feature selectivity, spike information content, and information throughput. J Neurosci. 2005;25:9524–9534. doi: 10.1523/JNEUROSCI.1804-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferragamo MJ, Oertel D. Octopus cells of the mammalian ventral cochlear nucleus sense the rate of depolarization. J Neurophysiol. 2002;87:2262–2270. doi: 10.1152/jn.00587.2001. [DOI] [PubMed] [Google Scholar]
- Fukui I, Ohmori H. Developmental changes in membrane excitability and morphology of neurons in the nucleus angularis of the chicken. J Physiol. 2003;548:219–232. doi: 10.1113/jphysiol.2002.036285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukui I, Ohmori H. Tonotopic gradients of membrane and synaptic properties for neurons of the chicken nucleus magnocellularis. J Neurosci. 2004;24:7514–7523. doi: 10.1523/JNEUROSCI.0566-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galán RF, Ermentrout GB, Urban NN. Optimal time scale for spike-time reliability: theory, simulations, and experiments. J Neurophysiol. 2008;99:277–283. doi: 10.1152/jn.00563.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gai Y, Doiron B, Kotak V, Rinzel J. Noise-gated encoding of slow inputs by auditory brain stem neurons with a low-threshold K+ current. J Neurophysiol. 2009;102:3447–3460. doi: 10.1152/jn.00538.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kempter R, van Hemmen JL, Wagner H. A neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383:76–81. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Griffin SJ, Bernstein LR, Ingham NJ, McAlpine D. Neural sensitivity to interaural envelope delays in the inferior colliculus of the guinea pig. J Neurophysiol. 2005;93:3463–78. doi: 10.1152/jn.00794.2004. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Guinan SS, Norris BE. Single auditory units in the superior olivary complex. I: Responses to sounds and classifications based on physiological properties. Int J Neurosci. 1972a;4:101–120. [Google Scholar]
- Guinan JJ, Jr, Norris BE, Guinan SS. Single auditory units in the superior olivary complex. II: location of unit categories and tonotopic organization. Int J Neurosci. 1972b;4:147–166. [Google Scholar]
- Gutkin B, Ermentrout GB, Rudolph M. Spike generating dynamics and the conditions for spike-time precision in cortical neurons. J Comput Neurosci. 2003;15:91–103. doi: 10.1023/a:1024426903582. [DOI] [PubMed] [Google Scholar]
- Henze DA, Buzsáki G. Action potential threshold of hippocampal pyramidal cells in vivo is increased by recent spiking activity. Neuroscience. 2001;105:121–130. doi: 10.1016/s0306-4522(01)00167-1. [DOI] [PubMed] [Google Scholar]
- Joris PX. Envelope coding in the lateral superior olive. II. Characteristic delays and comparison with responses in the medial superior olive. J Neurophysiol. 1996;76:2137–2156. doi: 10.1152/jn.1996.76.4.2137. [DOI] [PubMed] [Google Scholar]
- Joris PX. Interaural time sensitivity dominated by cochlea-induced envelope patterns. J Neurosci. 2003;23:6345–6350. doi: 10.1523/JNEUROSCI.23-15-06345.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris PX, Louage DH, Cardoen L, van der Heijden M. Correlation index: a new metric to quantify temporal coding. Hear Res. 2006;216–217:19–30. doi: 10.1016/j.heares.2006.03.010. [DOI] [PubMed] [Google Scholar]
- Joris PX, Yin TC. Envelope coding in the lateral superior olive. I. Sensitivity to interaural time differences. J Neurophysiol. 1995;73:1043–1062. doi: 10.1152/jn.1995.73.3.1043. [DOI] [PubMed] [Google Scholar]
- Joris PX, Yin TC. Envelope coding in the lateral superior olive. III. Comparison with afferent pathways. J Neurophysiol. 1998;79:253–269. doi: 10.1152/jn.1998.79.1.253. [DOI] [PubMed] [Google Scholar]
- Keller CH, Takahashi TT. Representation of temporal features of complex sounds by the discharge patterns of neurons in the owl’s inferior colliculus. J Neurophysiol. 2000;84:2638–2650. doi: 10.1152/jn.2000.84.5.2638. [DOI] [PubMed] [Google Scholar]
- Konishi M. Coding of auditory space. Annu Rev Neurosci. 2003;26:31–55. doi: 10.1146/annurev.neuro.26.041002.131123. [DOI] [PubMed] [Google Scholar]
- Köppl C. Phase locking to high frequencies in the auditory nerve and cochlear nucleus magnocellularis of the barn owl, Tyto alba. J Neurosci. 1997;17:3312–3321. doi: 10.1523/JNEUROSCI.17-09-03312.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köppl C, Carr CE. Computational diversity in the cochlear nucleus angularis of the barn owl. J Neurophysiol. 2003;89:2313–2329. doi: 10.1152/jn.00635.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kretzberg J, Egelhaaf M, Warzecha AK. Membrane potential fluctuations determine the precision of spike timing and synchronous activity: a model study. J Comput Neurosci. 2001;10:79–97. doi: 10.1023/a:1008972111122. [DOI] [PubMed] [Google Scholar]
- Linden JF, Liu RC, Sahani M, Schreiner CE, Merzenich MM. Spectrotemporal structure of receptive fields in areas AI and AAF of mouse auditory cortex. J Neurophysiol. 2003;90:2660–2675. doi: 10.1152/jn.00751.2002. [DOI] [PubMed] [Google Scholar]
- Loftus WC, Bishop DC, Oliver DL. Differential Patterns of Inputs Create Functional Zones in Central Nucleus of Inferior Colliculus. J Neurosci. 2010;30:13396–13408. doi: 10.1523/JNEUROSCI.0338-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louage DH, van der Heijden M, Joris PX. Temporal properties of responses to broadband noise in the auditory nerve. J Neurophysiol. 2004;91:2051–2065. doi: 10.1152/jn.00816.2003. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Manley GA, Köppl C, Konishi M. A neural map of interaural intensity differences in the brain stem of the barn owl. J Neurosci. 1988;8:2665–2676. doi: 10.1523/JNEUROSCI.08-08-02665.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley MJ, Oertel D. Rate thresholds determine the precision of temporal integration in principal cells of the ventral cochlear nucleus. Hear Res. 2006;216–217:52–63. doi: 10.1016/j.heares.2006.02.006. [DOI] [PubMed] [Google Scholar]
- Mechler F, Victor JD, Purpura KP, Shapley R. Robust temporal coding of contrast by V1 neurons for transient but not for steady-state stimuli. J Neurosci. 1998;18:6583–6598. doi: 10.1523/JNEUROSCI.18-16-06583.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagarajan SS, Cheung SW, Bedenbaugh P, Beitel RE, Schreiner CE, Merzenich MM. Representation of spectral and temporal envelope of twitter vocalizations in common marmoset primary auditory cortex. J Neurophysiol. 2002;87:1723–1737. doi: 10.1152/jn.00632.2001. [DOI] [PubMed] [Google Scholar]
- Narayan R, Ergün A, Sen K. Delayed inhibition in cortical receptive fields and the discrimination of complex stimuli. J Neurophysiol. 2005;94:2970–2975. doi: 10.1152/jn.00144.2005. [DOI] [PubMed] [Google Scholar]
- Nelson BS, Takahashi TT. Spatial hearing in echoic environments: the role of envelope in owls. Neuron. 2010;67:643–655. doi: 10.1016/j.neuron.2010.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peña JL, Konishi M. From postsynaptic potentials to spikes in the genesis of auditory spatial receptive fields. J Neurosci. 2002;22:5652–5658. doi: 10.1523/JNEUROSCI.22-13-05652.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peña JL, Viete S, Albeck Y, Konishi M. Tolerance to sound intensity of binaural coincidence detection in the nucleus laminaris of the owl. J Neurosci. 1996;16(21):7046–7054. doi: 10.1523/JNEUROSCI.16-21-07046.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes AD, Rubel EW, Spain WJ. Membrane properties underlying the firing of neurons in the avian cochlear nucleus. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhode WS, Smith PH. Encoding timing and intensity in the ventral cochlear nucleus of the cat. J Neurophysiol. 1986;56:261–286. doi: 10.1152/jn.1986.56.2.261. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Molina VM, Aertsen A, Heck DH. Spike timing and reliability in cortical pyramidal neurons: effects of EPSC kinetics, input synchronization and background noise on spike timing. PLoS One. 2007;2:319. doi: 10.1371/journal.pone.0000319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokem A, Watzl S, Gollisch T, Stemmler M, Herz AV, Samengo I. Spike-timing precision underlies the coding efficiency of auditory receptor neurons. J Neurophysiol. 2006;95:2541–2552. doi: 10.1152/jn.00891.2005. [DOI] [PubMed] [Google Scholar]
- Schmid AM, Purpura KP, Ohiorhenuan IE, Mechler F, Victor JD. Subpopulations of neurons in visual area v2 perform differentiation and integration operations in space and time. Front Syst Neurosci. 2009;3:15. doi: 10.3389/neuro.06.015.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider DM, Woolley SM. Discrimination of communication vocalizations by single neurons and groups of neurons in the auditory midbrain. J Neurophysiol. 2010;103:3248–3265. doi: 10.1152/jn.01131.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, Simoncelli EP. Spike-triggered neural characterization. J Vis. 2006;6:484–507. doi: 10.1167/6.4.13. [DOI] [PubMed] [Google Scholar]
- Shannon RV, Zeng FG, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Slee SJ, Higgs MH, Fairhall AL, Spain WJ. Two-dimensional time coding in the auditory brainstem. J Neurosci. 2005;25:9978–9988. doi: 10.1523/JNEUROSCI.2666-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Street SE, Manis PB. Action potential timing precision in dorsal cochlear nucleus pyramidal cells. J Neurophysiol. 2007;97:4162–4172. doi: 10.1152/jn.00469.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan WE, Konishi M. Segregation of stimulus phase and intensity coding in the cochlear nucleus of the barn owl. J Neurosci. 1984;4:1787–1799. doi: 10.1523/JNEUROSCI.04-07-01787.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suta D, Kvasnák E, Popelár J, Syka J. Representation of species-specific vocalizations in the inferior colliculus of the guinea pig. J Neurophysiol. 2003;90:3794–3808. doi: 10.1152/jn.01175.2002. [DOI] [PubMed] [Google Scholar]
- Suter KJ, Jaeger D. Reliable control of spike rate and spike timing by rapid input transients in cerebellar stellate cells. Neuroscience. 2004;124:305–317. doi: 10.1016/j.neuroscience.2003.11.015. [DOI] [PubMed] [Google Scholar]
- Takahashi T, Moiseff A, Konishi M. Time and intensity cues are processed independently in the auditory system of the owl. J Neurosci. 1984;4:1781–1786. doi: 10.1523/JNEUROSCI.04-07-01781.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen FE, Sen K, Doupe AJ. Spectral-temporal receptive fields of nonlinear auditory neurons obtained using natural sounds. J Neurosci. 2000;20:2315–2331. doi: 10.1523/JNEUROSCI.20-06-02315.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tollin DJ, Yin TCT. The coding of spatial location by single units in the lateral superior olive of the cat. II. The determinants of spatial receptive fields in azimuth. J Neurosci. 2002;22:1468–1479. doi: 10.1523/JNEUROSCI.22-04-01468.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tollin DJ, Yin TC. Interaural phase and level difference sensitivity in low-frequency neurons in the lateral superior olive. J Neurosci. 2005;25:10648–10657. doi: 10.1523/JNEUROSCI.1609-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viete S, Peña JL, Konishi M. Effects of interaural intensity difference on the processing of interaural time difference in the owl’s nucleus laminaris. J Neurosci. 1997;17:1815–1824. doi: 10.1523/JNEUROSCI.17-05-01815.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
- Wang X, Merzenich MM, Beitel R, Schreiner CE. Representation of a species-specific vocalization in the primary auditory cortex of the common marmoset: temporal and spectral characteristics. J Neurophysiol. 1995;74:2685–2706. doi: 10.1152/jn.1995.74.6.2685. [DOI] [PubMed] [Google Scholar]
- Woolley SM, Fremouw TE, Hsu A, Theunissen FE. Tuning for spectro-temporal modulations as a mechanism for auditory discrimination of natural sounds. Nat Neurosci. 2005;8:1371–1379. doi: 10.1038/nn1536. [DOI] [PubMed] [Google Scholar]
- Yin TCT, Chan JCK. Interaural time sensitivity in medial superior olive of cat. J Neurophysiol. 1990;64:465–488. doi: 10.1152/jn.1990.64.2.465. [DOI] [PubMed] [Google Scholar]
- Yin TCT. Neural mechanisms of encoding binaural localization cues in the auditory brainstem. In: Oertel D, Popper AN, Fay PR, editors. Integrative Functions in the Mammalian Auditory Pathway. New York: Springer-Verlag; 2002. pp. 99–159. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.