Abstract
Cortical responses can vary greatly between repeated presentations of an identical stimulus. Here we report that both trial-to-trial variability and faithfulness of auditory cortical stimulus representations depend critically on brain state. A frozen amplitude-modulated white noise stimulus was repeatedly presented while recording neuronal populations and local field potentials (LFPs) in auditory cortex of urethane-anesthetized rats. An information-theoretic measure was used to predict neuronal spiking activity from either the stimulus envelope or simultaneously recorded LFP. Evoked LFPs and spiking more faithfully followed high-frequency temporal modulations when the cortex was in a “desynchronized” state. In the “synchronized” state, neural activity was poorly predictable from the stimulus envelope, but the spiking of individual neurons could still be predicted from the ongoing LFP. Our results suggest that although auditory cortical activity remains coordinated as a population in the synchronized state, the ability of continuous auditory stimuli to control this activity is greatly diminished.
Keywords: information theory, auditory system, brain state, desynchronized, synchronized
Introduction
The activity of the cerebral cortex depends on brain state. The most striking changes of brain state occur with the sleep cycle. Slow-wave sleep is characterized by a “synchronized” or “inactivated” state displaying low-frequency local field potential (LFP) fluctuations, corresponding to an alternation of “up states” of global activity and “down states” of network silence; in contrast, REM is characterized by a “desynchronized” or “activated” state in which large up-down alternations are suppressed (Steriade et al., 2001). Cortical state also varies within wakefulness, with desynchronized, higher frequency patterns seen during alert and attentive conditions while lower frequency oscillatory patterns are more typical of quiescence or drowsiness (Buzsaki et al., 1988; Wiest and Nicolelis, 2003; Gervasoni et al., 2004; Luczak et al., 2007; Poulet and Petersen, 2008; Luczak et al., 2009; Sakata and Harris, 2009). Attention and behavioral engagement can suppress low frequency LFP and EEG power (Bastiaansen et al., 2001; Fries et al., 2001; Chalk et al., 2010), suggesting that attention might affect cortical state by enhancing desynchronization.
Sensory responses have been observed to be state-dependent in multiple modalities (Livingstone and Hubel, 1981; Worgotter et al., 1998; Fanselow and Nicolelis, 1999; Gaese and Ostwald, 2001; Edeline, 2003; Castro-Alamancos, 2004a; Murakami et al., 2005; Otazu et al., 2009). Within the synchronized state, stimulus responses exhibit a complex nonlinear interaction between stimuli and ongoing activity such as stimulus-evoked “flips” between up and down states (Hasenstaub et al., 2007; Curto et al., 2009), as well as prominent adaptation at both thalamic and cortical levels (Castro-Alamancos, 2004b). It has been suggested that spontaneous excitability fluctuations may account for variability and ‘noise’ in sensory responses (Arieli et al., 1996; Azouz and Gray, 1999; Kisley and Gerstein, 1999; Petersen et al., 2003). In contrast, desynchronized brain states may better support the representation of temporally extended stimuli such as rapid stimulus trains (Castro-Alamancos, 2004a) and natural movies (Goard and Dan, 2009).
To investigate how brain state modulates cortical representations of continuous auditory stimuli, we recorded from neuronal populations in rat auditory cortex under urethane anesthesia, while presenting frozen amplitude-modulated white noise (AM Noise). Although anesthesia typically produces a synchronized pattern, under urethane the cortex can exhibit transient periods of desynchronization (Duque et al., 2000; Clement et al., 2008; Renart et al., 2010). This allowed us to compare responses across synchronized and desynchronized states. We find that in the desynchronized state the stimulus envelope is represented more faithfully in both LFPs and spiking activity, whereas in the synchronized state cortical activity is largely decoupled from the stimulus.
Materials and Methods
Experimental procedures
All experiments were carried out in accordance with protocols approved by the Rutgers University Animal Care and Use Committee. Six male Sprague-Dawley rats (250–450 g) were anesthetized with urethane (1.2–1.5 g/kg) plus supplementary doses of ketamine and xylazine (15 and 2 mg/kg), as required. In some experiments subcutaneous injections of dexamethasone (0.2–0.5 mg/kg) and atropine methyl-nitrate (0.1–0.2 mg/kg) were administered to lessen edema and secretions, respectively, and acepromazine (0.5–1 mg/kg) administered to regularize heart and breathing rhythms. Tracheotomy was performed to minimize noise from breathing. Animals were placed in a custom orbito-nasal restraint leaving the ears free. The temporal muscle was reflected and a 2×3 mm craniotomy drilled above left Te1 for dura removal before covering with 1% agar in ACSF. Sixteen or 32-channel silicon probes (NeuroNexus Technologies, Ann Arbor MI) were descended to putative layer V/VI (0.8–1.2 mm from surface), and auditory responses evaluated online to confirm electrode placement by response latency and tone responsiveness. Desynchronization of the EEG was induced by applying 30 s to 1 min of pressure to the tip of the tail (“tail pinch”), and also occurred spontaneously. Desynchronized epochs were identified as periods when the total spectral power below 6 Hz was significantly reduced for more than 5–10 s. Intermediate periods where the EEG was not clearly synchronized or desynchronized were not used in our analyses. Of the 6 experiments, only 4 yielded sufficient desynchronized epochs for statistical analysis.
All experiments were performed in a single-walled sound-proof chamber (IAC, Bronx NY). Acoustic stimuli consisted of a repeatedly presented 50 s frozen-noise stimulus, generated by pointwise multiplication of a Gaussian white noise carrier with an envelope made by exponentiating a band-pass filtered (1–100 Hz) second Gaussian white noise sequence. The resulting signal had a mean amplitude of 63 dB SPL (range ~30–100 dB SPL). Stimuli were delivered free field via a TDT RP2 processor, ED1 speaker driver and ES1 electrostatic speaker. An ACO-7012 microphone was placed by the ear and audio recorded to disk at 160 kHz, for sound level calibration and to control for extraneous noises during the experiment. Electrophysiological signals were amplified and recorded to disk at 20 kHz using custom software.
Data Analysis
Spike sorting was performed using previously described methods (Harris et al., 2000), and LFP extracted by lowpass filtering and downsampling the raw traces to 1.25kHz. LFP spectrograms were computed using the multitaper method (www.chronux.org), and coherence by Welch’s method (Mathworks, Natick MA). To measure spike count variability, the 50 sec stimulus was divided into successive 100 ms timebins. For each combination of neuron and timebin, a set of spike counts was accumulated over all stimulus repetitions where cortex was in the required state, and the Fano factor computed as variance divided by mean; if different numbers of stimulus repetitions occurred for different states, a random subset of those in the state with more was taken to equalize group sizes. Each cell’s mean Fano factor was computed for both states, by averaging over all timebins excluding any for which the Fano factor was undefined due to zero mean spike count.
To quantify how well individual neurons were entrained by the AM Noise stimuli, we used a “spike train prediction” method (Harris et al., 2003; Itskov et al., 2007). A function for predicting each neuron’s firing rate from the stimulus envelope was estimated from a “training set” of all but one stimulus repetitions, and its quality evaluated by comparing to the spike train observed on the remaining presentation (the “test set”). Prediction quality was assessed by the difference log-likelihoods of the test set spike train ts under the predicted firing probability f(t) relative to a constant probability given by the mean rate on the training set. The resulting likelihood ratio was divided by log2 and the number of test set spikes to yield an estimate of how many bits per spike a communicator of the test set spike train could save by knowing the stimulus envelope over knowing only the mean rate, and assuming spikes were generated by an inhomogeneous Poisson of rate f. Note that f was not chosen by directly maximizing Lf, but by one of two algorithms described below. The procedure was repeated with each stimulus repetition taking its turn as test set, and an average computed. Note that with this method, estimated information rates can be negative, if predictions perform worse than the mean firing rate.
Prediction functions were estimated by two methods. The first was a linear-nonlinear method, where the prediction function was fit by first finding the optimal linear filter for predicting the spiking activity, and then fitting a static nonlinear function that links this linear prediction to firing rates (Chichilnisky, 2001). Because the noise envelope was approximately white in the pass band of 1–100 Hz, the optimal linear filter could be obtained simply by computing the spike-triggered average (STA) of the envelope. The link function was constructed by binning the filter output into 100 bins, and computing the smoothed firing probability in each bin. For brevity we shall refer to this method as the “linear STA” method.
The second prediction method, termed the “2D STA” method, was simplified from the method of Sharpee et al. (Sharpee et al., 2006; Atencio et al., 2008). In this approach, firing probability was predicted as a nonlinear function of the stimulus envelope and its instantaneous derivative, at a fixed time-lag into the past. The stimulus envelope and its derivative were binned to form a 192 × 192 grid of possible signal and derivative values, and firing rates estimated in this 2D space using a smoothing method previously described for hippocampal place fields (Harris et al., 2001), in which a smoothed spike count map is pointwise divided by a smoothed occupancy map (13 pt Gaussian for both). For illustrative purposes, non-traversed portions of the grid are rendered in black in the 2D STAs in Figures 3 & 4. To predict the firing rate function on the test set, the rate map computed from the training set is used as a lookup table. The likelihood ratio was averaged over all cross-validation repeats, to yield a mean prediction quality as a function of the time lag parameter. The maximum of this curve was taken as prediction quality.
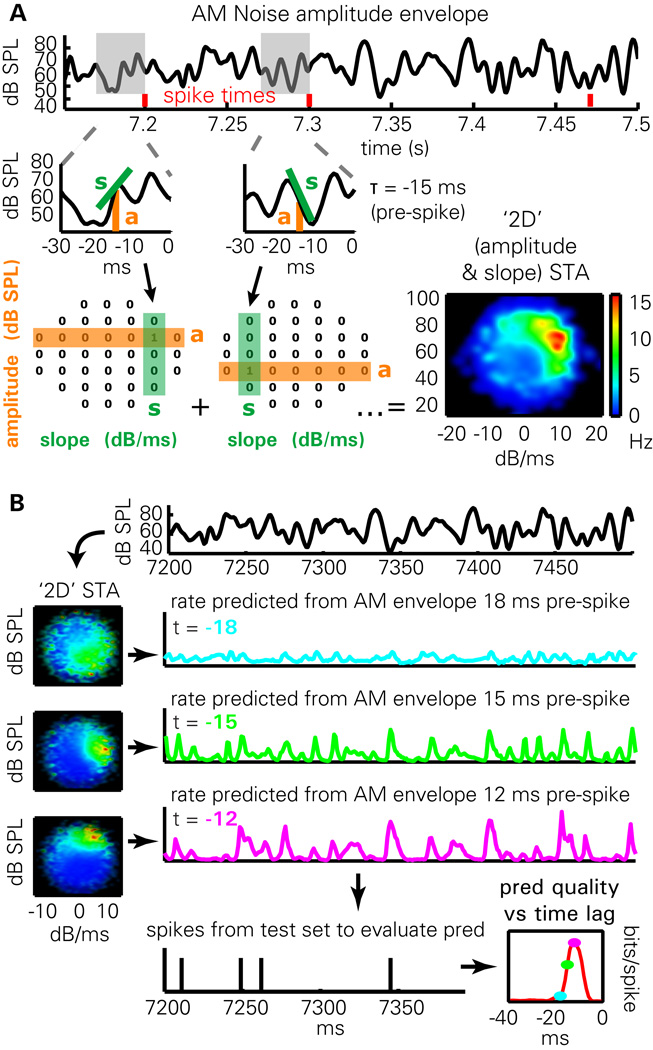
Figure 3. Methods for predicting spiking activity.
(A) Illustration of “2D STA” method. The amplitude and derivative of the envelope is computed at a fixed time lag before the occurrence of each spike (here 15 ms). The mean firing rate as a function of amplitude and derivative can then be computed by a smoothing method previously used to compute hippocampal place fields.
(B) Prediction from the 2D STA depends on time lag. Firing rate maps in amplitude/derivative space (2D STAs) are computed from a training set, for multiple time lags (cyan: 18 ms; green: 15 ms; magenta: 12 ms). To predict firing rate on the test set, the amplitude and derivative of the envelope, lagged appropriately, are used to index into the 2D STA. The quality of prediction is evaluated on the test set using the log-likelihood ratio of the observed spike train under the prediction, compared to the cell’s mean firing rate. The result (lower-right) is an estimate of prediction quality which varies as a function of time lag.
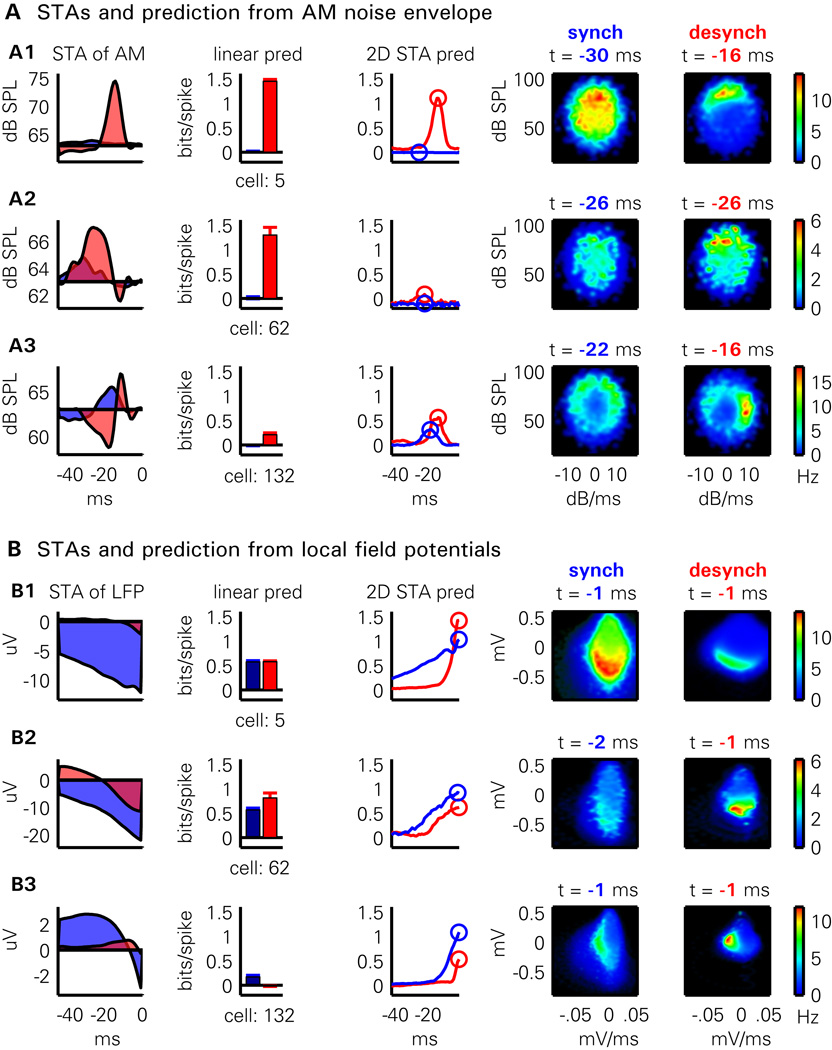
Figure 4. Example of the prediction methods for three illustrative neurons.
(A) Each row shows the prediction method applied to one neuron from the AM noise envelope. From left to right: the linear spike triggered average of the noise envelope in the desynchronized (red shading) and synchronized (blue shading) states; predictability for the cell assessed by the linear STA method for desynchronized (red bar) and synchronized (blue bar) states; predictability with the 2D STA method as a function of time offset in each state (red and blue curves); 2D STA plots for synchronized state for optimal time offset; 2D STA plots for desynchronized state for optimal time offset.
(B) Same plots as in (A), showing prediction of the same three cells from LFP. For further discussion of the plots, see text.
Results
To test the state-dependence of auditory cortical representation of continuous stimuli, we recorded neural populations using multisite silicon electrodes in auditory cortex of urethane-anesthetized rats. Acoustic stimuli consisted of a repeatedly presented 50 s frozen amplitude-modulated noise stimulus, whose amplitude envelope had power in the range 1–100 Hz.
An example of data collected with this method can be seen in Figure 1. LFPs during the synchronized state were dominated by a low-frequency (<10 Hz) pattern, whereas the desynchronized state LFPs exhibited greatly reduced low-frequency power (Figure 1A). The smaller narrowband oscillation at 3–4 Hz seen in the desynchronized state likely corresponds to volume-conducted hippocampal theta (which has a lower frequency than in awake rats, and occurs together with cortical desynchronization (Sirota et al., 2008)).
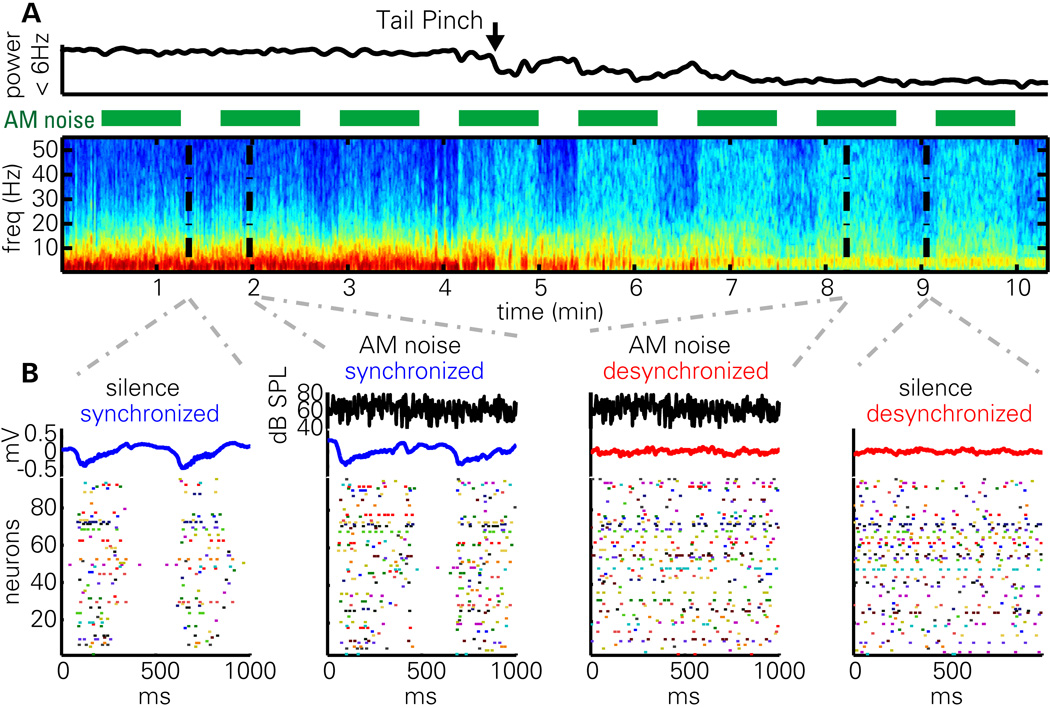
Figure 1. AM noise presentation in synchronized and desynchronized states.
(A) LFP power spectrogram and integrated power in 0–6 Hz band during a synchronized to desynchronized state transition following tail pinch. Green bars denote presentation of frozen AM noise stimuli. Note that low frequency power is generally reduced in the desynchronized state, with the exception of an ~4 Hz oscillation presumably reflecting volume-conducted hippocampal theta. Also note that stimulus presentation induces high frequency LFP power more prominently in the desynchronized state.
(B) 1 s epochs of activity during silence and stimulus presentation. Black traces denote noise envelope (for epochs during stimulus presentation); blue and red traces denote LFP; rasters show activity of a simultaneously recorded population of neurons. Note that the structure of population activity is highly dependent on brain state, but not strongly affected by sustained portions of the stimulus presentation.
Presentation of the stimulus did not change these low-frequency patterns, but it did cause an increase in higher frequency power, which was more prominent in the desynchronized state. Rasters of population activity (Figure 1B) show that the synchronized state consists of alternations between periods of generalized spiking activity (“up states”) accompanied by negative LFP deflections, and periods of very little spiking (“down states”), accompanied by positive LFP deflections; stimulus presentation did little to change this pattern. In the desynchronized state, such global oscillations were not seen, but instead cells fired more continuously during both AM Noise stimulation and silence.
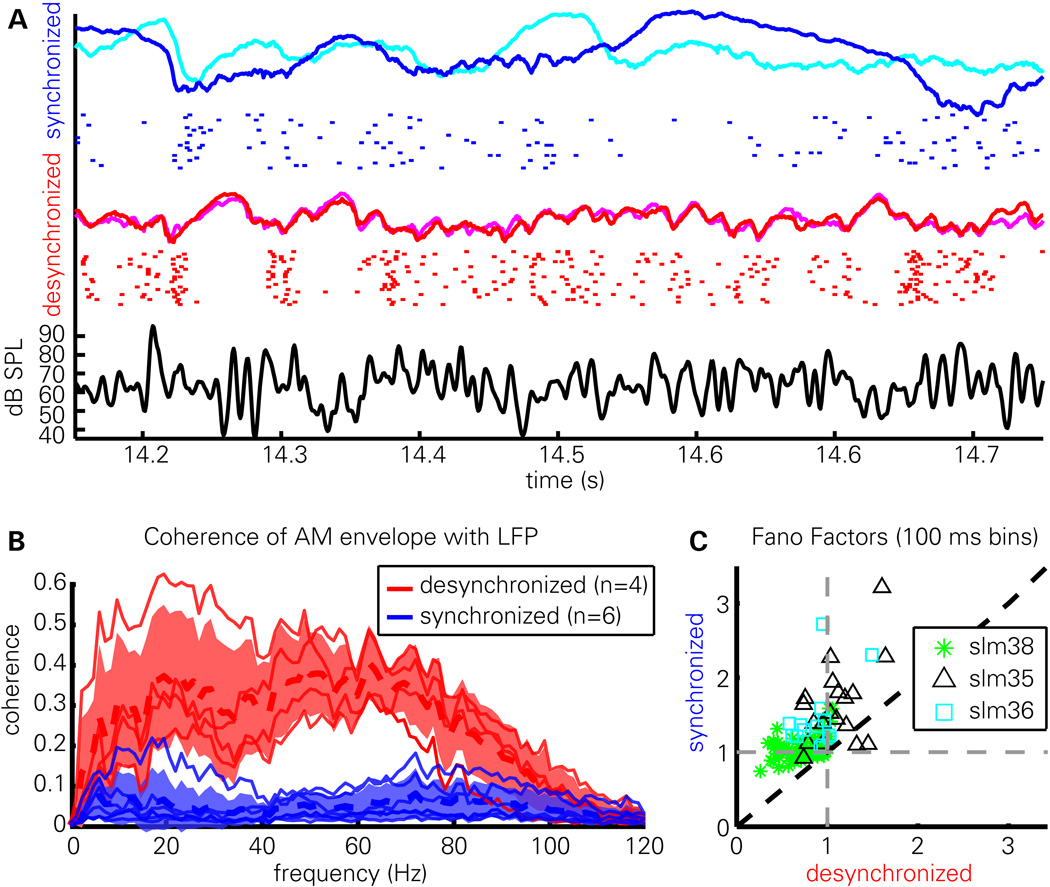
The use of a repeatedly-presented frozen-noise stimulus allowed us to examine the reliability with which the cortex responded to the stimulus. In Figure 2A are overlaid evoked LFPs from two presentations of the stimulus (synchronized: blue, cyan; desynchronized: red, magenta); below each pair of traces are a raster representation of a single neuron’s response to multiple stimulus repetitions. It can be seen that the response in the desynchronized state is highly reliable from trial to trial. In the synchronized state, cortical activity is modulated by the stimulus in a less reliable way. This reliability of LFP responses was quantified using the coherence of the evoked LFP with the stimulus envelope (Figure 2B). In all cases, the LFP showed greater coherence to the stimulus envelope in the desynchronized state. To quantify the reliability of spiking responses across multiple stimulus repetitions, we computed Fano factors for each cell in the two states (Figure 2C; see Methods). In the synchronized state, Fano factors were typically above 1 (p<.001, one-sample t-test; mean±SD:1.19±.36), indicating that spiking was more variable than expected from a (inhomogeneous) Poisson process, whereas in the desynchronized state Fano factors were typically below 1 (p<.001, one-sample t-test; mean±SD:.84±.25), indicating spiking was less variable than Poisson. A significant difference was also found between states (p<.001, paired t-test).
Figure 2. Reliability of cortical responses varies with brain state.
(A) Evoked LFPs (colored curves) from two presentations of the same AM noise snippet in desynchronized (red, magenta) and synchronized (blue, cyan) states, as well as raster representation of spikes from one cell in response to 22 repeated presentations in each state. Black curve (bottom) shows stimulus envelope. Note that both the LFP and spiking pattern is more reliable in the desynchronized state.
(B) Coherence (phase correlation) between the evoked LFPs and the AM noise envelope, measured in 6 animals (of which 4 showed sufficient desynchronized activity to enable accurate computation). Thin red and blue lines correspond to individual experiments; thick dashed lines represent the mean, shaded area indicates mean ± standard deviation across experiments.
(C) Fano factors quantifying the variability with which each cell responded to repeats of the stimulus in each state. The stimulus period was divided into successive 100 ms bins, a Fano factor computed for each, and averaged. Note that synchronized state Fano factors are typically greater (less) than 1 in the synchronized (desynchronized) state indicating supra- (sub-) Poisson variability.
We next set out to quantify the degree to which individual neurons were reliably entrained by the AM Noise stimuli. To do this, we used a “spike train prediction” method, in which the stimulus envelope was used to generate a predicted firing rate, which was then compared to the spike train actually observed. To avoid over-fitting we used cross-validation: parameters of the prediction function were estimated from one part of the data (the “training set”) and evaluated on another (the “test set”). Prediction was assessed by log-likelihood ratio compared to the prediction of constant mean firing rate, and normalized by the number of spikes, resulting in a measurement in bits/spike (see Methods).
Two methods were used to predict spike firing probability from the amplitude envelope. The first was based on convolution with a linear filter followed by a static nonlinearity (see Methods). To ensure results were not dependent on this specific prediction method, we also applied a second technique we termed the “2D STA,” simplified from the method of Sharpee et al. (Sharpee et al., 2006; Atencio et al., 2008). In this approach, firing probability was predicted as a nonlinear function of the amplitude and slope of the envelope at a fixed time lag in the past (Figure 3A). Figure 3B illustrates how both the shape of the 2D STA and quality of the prediction vary as a function of the time-lag. When quantifying predictions using this method, the value of time-lag giving optimal performance was used.
Three examples of this prediction can be seen in Figure 4A. In the desynchronized state, the first neuron (Figure 4A1) showed a preference for high amplitudes ~16 ms prior to spiking, visible as sharp peaks in the linear STA, and near the top of the 2D STA plot, with predictability of ~1.1–1.4 bits/spike for both methods. In the synchronized state, however, this predictability was completely abolished, with a flat linear STA and unstructured 2D STA plot. For the second neuron (Figure 4A2), the desynchronized linear STA showed a broad peak spanning -40 to -20 ms, yielding predictability of ~1.3 bits/spike. The 2D STA showed a diffuse peak in the upper half, with poorer predictability reflecting the inability of the amplitude and derivative at any single time point to accurately capture the lower-frequency amplitude modulations that drove this neuron. As with the first example, however, predictability according to both measures was abolished in the synchronized state. The third example cell (Figure 4A3) showed a complex receptive field structure in the desynchronized state, with a biphasic linear STA, and a sharp peak at the right side of the 2D STA plot indicating preference for the rising phase with a lag of ~16 ms. Unlike the other examples, this neuron did show some predictability in the synchronized state, but its 2D STA moved from a sharp peak to a more diffuse ring, indicating that loud sounds would make it fire, but with unreliable timing. Consistent with this picture, the linear STA in the synchronized state was broad but provided no information about spiking. These examples suggest that the two prediction methods give similar though not always identical results, but that with either method, predictions from stimulus envelope are worse in the synchronized state.
Cortical activity is not simply a deterministic function of sensory input, and cortical circuits can exhibit autonomous activity independent of external stimuli. Thus, even if a cell is poorly predicted from sensory stimuli, it is possible that its activity is strongly related to internally generated activity patterns. To determine whether this was the case, we applied the same methods to predict neural activity from the LFP signal (averaged over neighbouring recording shanks to avoid contamination by the neuron’s own waveform). The results of this analysis are seen in Figure 4B for the same three example cells as before. Prediction from LFPs was typically better with the nonlinear method. The optimal time-lag near 0 indicated that the instantaneous LFP amplitude and derivative was a good predictor of spiking. 2D STAs showed peaks to the left or below the origin, consistent with references to fire on the descending phase or trough of LFP oscillations. In contrast to prediction from stimulus, prediction from LFP was often better in the synchronized state, likely as a result of the strong modulation of population activity by up states and down states.
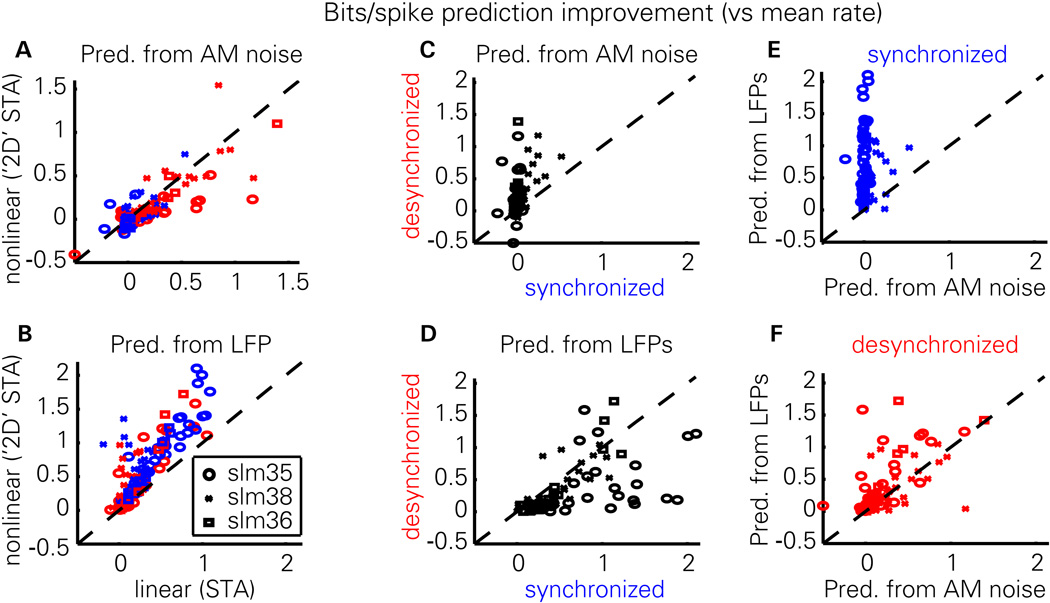
The intuition suggested by the above examples is confirmed by group-level analysis. The two STA methods produce highly correlated predictions (Figures 5A,B), with a slight advantage to the linear method when predicting from stimulus envelopes in the desynchronized state (Figure 5A; synchronized: p=0.051, desynchronized: p<0.001, paired t-test), and to the nonlinear method when predicting from LFPs in both states (Figure 5B; p<0.001, paired t-test). For further analyses, we therefore used the best method in each case (linear for AM noise envelope, 2D for LFP). Prediction from the AM noise envelope was better by a large margin in the desynchronized state (Figure 5C; p<0.001, paired t-test), while prediction from the LFP was generally better in the synchronized state (Figure 5D; p<0.001, paired t-test). Comparing prediction from LFP to prediction from the stimulus, we found that LFP prediction outperformed the poor AM Noise prediction by large margins in synchronized states (Figure 5E; p<0.001, paired t-test), and that in desynchronized states the LFP was also generally a better predictor of neural activity than the stimulus envelope (Figure 5F; p<0.005, paired t-test) when using the optimal method in each case.
Figure 5. Summary of predictability results.
(A) Predictability of each cell from noise envelope, for traditional linear STA and 2D STA methods. Red and blue symbols correspond to individual cells from desynchronized and synchronized states, respectively. Symbol shape indicates different recordings, for 3 experiments giving sufficient numbers of cells recorded in both states. For the 2D STA method, the time-lag giving optimal performance was used. (B) Predictability of each cell from LFP. Prediction from LFP is better with the nonlinear method, for both brain states. (C) Prediction from stimulus envelope is much better in the desynchronized than synchronized state. (D) LFPs typically predict spiking better in the synchronized than desynchronized state. (E) In the synchronized state, prediction is much better from the LFP than from the stimulus envelope. (F) Even in the desynchronized state, the best prediction is from the LFP.
Discussion
We analyzed the response of auditory cortical neurons to frozen-noise stimuli as a function of brain state under urethane anesthesia. In the synchronized state, the activity of individual neurons was strongly predictable from the LFP, but not from the stimulus. In the desynchronized state, however, neural activity could be well predicted from both the stimulus and the LFP.
The fact that neural activity in the synchronized state was strongly predictable from the LFP, an indicator of global neuronal activity, but only poorly predictable from the AM noise envelope, suggests that cortical activity had largely decoupled from the stimulus. Even in the desynchronized state, where spike times were predictable from the stimulus envelope, prediction from the LFP could be better still. If cortical activity were deterministically controlled by the stimulus, one would expect the LFP to predict any neuron’s activity as well as the stimulus envelope, but no better. The fact that spiking was better predicted by the LFP suggests that auditory cortex showed coordinated population activity beyond that imposed by the stimulus. Quantification of the predictability of spiking activity is subject to the caveat that the method of prediction chosen may not be optimal; however the use of two prediction methods (linear and 2D STA), whose results were highly correlated, helped mitigate this concern.
Cortical desynchronization can occur through both neuromodulatory input to the cortex, and increased tonic firing of thalamic relay neurons, which may in turn reflect neuromodulation in thalamus (Metherate et al., 1992; Steriade, 2004; Hirata and Castro-Alamancos, 2010). Desynchronization evoked by tail pinch or occurring spontaneously under urethane is accompanied by altered activity in multiple subcortical neuronal classes, including increased spiking of cholinergic neurons of the basal forebrain (BF) and pedunculopontine tegmental nuclei (PPT), which target the cortex and thalamus respectively (Duque et al., 2000; Manns et al., 2000; Boucetta and Jones, 2009). Desynchronization can be evoked under anesthesia by electrical stimulation of the BF, PPT, and other nuclei (Metherate et al., 1992; Dringenberg and Vanderwolf, 1997). Electrical stimulation of any one site, however, is likely to activate a larger subcortical network; for example, stimulation of the BF produces increased tonic firing in lateral geniculate nucleus (Goard and Dan, 2009), even though it does not directly project there (Kolmac and Mitrofanis, 1999). Thus, it seems probable that spontaneous, tail pinch-evoked, and BF/PPT stimulation-evoked desynchronization under urethane involve activation of complex but largely overlapping subcortical networks (Clement et al., 2008).
Although the AM noise stimulus was unable to reliably entrain cortical activity in the synchronized state, this is not because auditory sensory responses cannot occur in this state. Indeed robust responses to clicks, and to the onsets of tones and natural sounds occur in the synchronized state under urethane (Bartho et al., 2009; Curto et al., 2009; Luczak et al., 2009). Those repeatable responses that did occur in the synchronized state were typically seen after large transients (e.g. Figure 2A, at 14.2 s). Smaller amplitude modulations, by contrast, led to repeatable responses in the desynchronized but not synchronized state, suggesting that they had been “filtered out.” These results therefore complement data from other sensory modalities that suggest that the synchronized state leads to increased adaptation to prolonged or rapidly repeated stimuli. In barrel cortex, the response to a single stimulus is larger in synchronized/quiescent states than in desynchronized/information-processing states, but responses to rapidly repeated stimuli show more adaptation in synchronized states (Castro-Alamancos, 2004a). In auditory cortex, the response to the first click of a train is larger in passive than behaviorally engaged rats, but increased adaptation leads to a similar steady-state response at high repetition rates (Otazu et al., 2009); increased adaptation to 50 ms click pairs is also seen in the synchronized state under urethane (L. Hollender et al, Soc. Neurosci. Abs. #566.29, 2008). In visual cortex, the reliability of responses to natural movies is enhanced by BF stimulation, consistent with a “filtering out” of certain features of these prolonged stimuli in the synchronized state (Goard and Dan, 2009). This filtering, however, need not take place at the cortical level. Thalamic burst mode has been suggested to allow large “wake-up call” responses to stimulus transients, whereas tonic mode would provide a more linear representation of temporally extended stimuli (Sherman, 2001). In auditory as in other cortices, thalamic bursting is more common in synchronized states (Massaux et al., 2004).
Although for our analysis we divided data into the most synchronized and desynchronized states we recorded, a continuum of states, corresponding to a continuum of LFP and EEG power spectra, can be observed both under anesthesia (Clement et al., 2008; Curto et al., 2009) and during wakefulness (Gervasoni et al., 2004). We suggest that one consequence of cortical desynchronization is to put the cortex under progressively greater control of sensory stimuli, and to tone down the role of intrinsic dynamics in shaping population activity. In primates, attention causes decreased low-frequency LFP power in multiple areas (Fries et al., 2001; Chalk et al., 2010), broadly similar to the changes in low frequency power seen in our data. When an animal attends to a changing stimulus, one might imagine this allows cortical activity to more faithfully follow that stimulus, whereas an unattended stimulus would be less able to control neural spiking. Our data suggest such an effect could be achieved by placing the parts of the cortex that represent the attended stimulus in a more desynchronized state.
Acknowledgments
This work was supported by the National Institutes of Health (MH073245, DC009947), and the National Science Foundation (SBE-0542013 to the Temporal Dynamics of Learning Center, a National Science Foundation Science of Learning Center). We thank members of the Harris lab for productive discussions, Shuzo Sakata for assistance with pilot experiments and Artur Luczak for help with stimulus design.
Footnotes
Conflict of interest: none.
References
- Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- Atencio CA, Sharpee TO, Schreiner CE. Cooperative nonlinearities in auditory cortical neurons. Neuron. 2008;58:956–966. doi: 10.1016/j.neuron.2008.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19:2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartho P, Curto C, Luczak A, Marguet SL, Harris KD. Population coding of tone stimuli in auditory cortex: dynamic rate vector analysis. Eur J Neurosci. 2009;30:1767–1778. doi: 10.1111/j.1460-9568.2009.06954.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastiaansen MC, Bocker KB, Brunia CH, de Munck JC, Spekreijse H. Event-related desynchronization during anticipatory attention for an upcoming stimulus: a comparative EEG/MEG study. Clin Neurophysiol. 2001;112:393–403. doi: 10.1016/s1388-2457(00)00537-x. [DOI] [PubMed] [Google Scholar]
- Boucetta S, Jones BE. Activity profiles of cholinergic and intermingled GABAergic and putative glutamatergic neurons in the pontomesencephalic tegmentum of urethane-anesthetized rats. J Neurosci. 2009;29:4664–4674. doi: 10.1523/JNEUROSCI.5502-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, Bickford RG, Ponomareff G, Thal LJ, Mandel R, Gage FH. Nucleus basalis and thalamic control of neocortical activity in the freely moving rat. J Neurosci. 1988;8:4007–4026. doi: 10.1523/JNEUROSCI.08-11-04007.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castro-Alamancos MA. Absence of rapid sensory adaptation in neocortex during information processing states. Neuron. 2004a;41:455–464. doi: 10.1016/s0896-6273(03)00853-5. [DOI] [PubMed] [Google Scholar]
- Castro-Alamancos MA. Dynamics of sensory thalamocortical synaptic networks during information processing states. ProgNeurobiol. 2004b;74:213–247. doi: 10.1016/j.pneurobio.2004.09.002. [DOI] [PubMed] [Google Scholar]
- Chalk M, Herrero JL, Gieselmann MA, Delicato LS, Gotthardt S, Thiele A. Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron. 2010;66:114–125. doi: 10.1016/j.neuron.2010.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chichilnisky EJ. A simple white noise analysis of neuronal light responses. Network. 2001;12:199–213. [PubMed] [Google Scholar]
- Clement EA, Richard A, Thwaites M, Ailon J, Peters S, Dickson CT. Cyclic and sleep-like spontaneous alternations of brain state under urethane anaesthesia. PLoSONE. 2008;3:e2004. doi: 10.1371/journal.pone.0002004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curto C, Sakata S, Marguet S, Itskov V, Harris KD. A simple model of cortical dynamics explains variability and state dependence of sensory responses in urethane-anesthetized auditory cortex. J Neurosci. 2009;29:10600–10612. doi: 10.1523/JNEUROSCI.2053-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dringenberg HC, Vanderwolf CH. Neocortical activation: modulation by multiple pathways acting on central cholinergic and serotonergic systems. Exp Brain Res. 1997;116:160–174. doi: 10.1007/pl00005736. [DOI] [PubMed] [Google Scholar]
- Duque A, Balatoni B, Detari L, Zaborszky L. EEG correlation of the discharge properties of identified neurons in the basal forebrain. JNeurophysiol. 2000;84:1627–1635. doi: 10.1152/jn.2000.84.3.1627. [DOI] [PubMed] [Google Scholar]
- Edeline JM. The thalamo-cortical auditory receptive fields: regulation by the states of vigilance, learning and the neuromodulatory systems. Exp Brain Res. 2003;153:554–572. doi: 10.1007/s00221-003-1608-0. [DOI] [PubMed] [Google Scholar]
- Fanselow EE, Nicolelis MA. Behavioral modulation of tactile responses in the rat somatosensory system. J Neurosci. 1999;19:7603–7616. doi: 10.1523/JNEUROSCI.19-17-07603.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Gaese BH, Ostwald J. Anesthesia changes frequency tuning of neurons in the rat primary auditory cortex. JNeurophysiol. 2001;86:1062–1066. doi: 10.1152/jn.2001.86.2.1062. [DOI] [PubMed] [Google Scholar]
- Gervasoni D, Lin SC, Ribeiro S, Soares ES, Pantoja J, Nicolelis MA. Global forebrain dynamics predict rat behavioral states and their transitions. J Neurosci. 2004;24:11137–11147. doi: 10.1523/JNEUROSCI.3524-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goard M, Dan Y. Basal forebrain activation enhances cortical coding of natural scenes. Nat Neurosci. 2009;12:1444–1449. doi: 10.1038/nn.2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Henze DA, Csicsvari J, Hirase H, Buzsaki G. Accuracy of tetrode spike separation as determined by simultaneous intracellular and extracellular measurements. JNeurophysiol. 2000;84:401–414. doi: 10.1152/jn.2000.84.1.401. [DOI] [PubMed] [Google Scholar]
- Harris KD, Hirase H, Leinekugel X, Henze DA, Buzsaki G. Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. Neuron. 2001;32:141–149. doi: 10.1016/s0896-6273(01)00447-0. [DOI] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Hasenstaub A, Sachdev RN, McCormick DA. State changes rapidly modulate cortical neuronal responsiveness. JNeurosci. 2007;27:9607–9622. doi: 10.1523/JNEUROSCI.2184-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirata A, Castro-Alamancos MA. Neocortex network activation and deactivation states controlled by the thalamus. J Neurophysiol. 2010;103:1147–1157. doi: 10.1152/jn.00955.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itskov V, Curto C, Harris KD. Valuations for spike train prediction. Neural Compuation. 2007;20:644–667. doi: 10.1162/neco.2007.3179. [DOI] [PubMed] [Google Scholar]
- Kisley MA, Gerstein GL. Trial-to-trial variability and state-dependent modulation of auditory-evoked responses in cortex. J Neurosci. 1999;19:10451–10460. doi: 10.1523/JNEUROSCI.19-23-10451.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolmac C, Mitrofanis J. Organization of the basal forebrain projection to the thalamus in rats. Neurosci Lett. 1999;272:151–154. doi: 10.1016/s0304-3940(99)00614-x. [DOI] [PubMed] [Google Scholar]
- Livingstone MS, Hubel DH. Effects of sleep and arousal on the processing of visual information in the cat. Nature. 1981;291:554–561. doi: 10.1038/291554a0. [DOI] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62:413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Marguet SL, Buzsaki G, Harris KD. Sequential structure of neocortical spontaneous activity in vivo. ProcNatlAcadSciUSA. 2007;104:347–352. doi: 10.1073/pnas.0605643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manns ID, Alonso A, Jones BE. Discharge properties of juxtacellularly labeled and immunohistochemically identified cholinergic basal forebrain neurons recorded in association with the electroencephalogram in anesthetized rats. J Neurosci. 2000;20:1505–1518. doi: 10.1523/JNEUROSCI.20-04-01505.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massaux A, Dutrieux G, Cotillon-Williams N, Manunta Y, Edeline JM. Auditory thalamus bursts in anesthetized and non-anesthetized states: contribution to functional properties. J Neurophysiol. 2004;91:2117–2134. doi: 10.1152/jn.00970.2003. [DOI] [PubMed] [Google Scholar]
- Metherate R, Cox CL, Ashe JH. Cellular bases of neocortical activation: modulation of neural oscillations by the nucleus basalis and endogenous acetylcholine. JNeurosci. 1992;12:4701–4711. doi: 10.1523/JNEUROSCI.12-12-04701.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami M, Kashiwadani H, Kirino Y, Mori K. State-dependent sensory gating in olfactory cortex. Neuron. 2005;46:285–296. doi: 10.1016/j.neuron.2005.02.025. [DOI] [PubMed] [Google Scholar]
- Otazu GH, Tai LH, Yang Y, Zador AM. Engaging in an auditory task suppresses responses in auditory cortex. Nat Neurosci. 2009;12:646–654. doi: 10.1038/nn.2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen CC, Hahn TT, Mehta M, Grinvald A, Sakmann B. Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex. ProcNatlAcadSciUSA. 2003;100:13638–13643. doi: 10.1073/pnas.2235811100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulet JF, Petersen CC. Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature. 2008;454:881–885. doi: 10.1038/nature07150. [DOI] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata S, Harris KD. Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron. 2009;64:404–418. doi: 10.1016/j.neuron.2009.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpee TO, Sugihara H, Kurgansky AV, Rebrik SP, Stryker MP, Miller KD. Adaptive filtering enhances information transmission in visual cortex. Nature. 2006;439:936–942. doi: 10.1038/nature04519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman SM. Tonic and burst firing: dual modes of thalamocortical relay. Trends Neurosci. 2001;24:122–126. doi: 10.1016/s0166-2236(00)01714-8. [DOI] [PubMed] [Google Scholar]
- Sirota A, Montgomery S, Fujisawa S, Isomura Y, Zugaro M, Buzsaki G. Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm. Neuron. 2008;60:683–697. doi: 10.1016/j.neuron.2008.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M. Acetylcholine systems and rhythmic activities during the waking--sleep cycle. Prog Brain Res. 2004;145:179–196. doi: 10.1016/S0079-6123(03)45013-9. [DOI] [PubMed] [Google Scholar]
- Steriade M, Timofeev I, Grenier F. Natural waking and sleep states: a view from inside neocortical neurons. JNeurophysiol. 2001;85:1969–1985. doi: 10.1152/jn.2001.85.5.1969. [DOI] [PubMed] [Google Scholar]
- Wiest MC, Nicolelis MA. Behavioral detection of tactile stimuli during 7–12 Hz cortical oscillations in awake rats. NatNeurosci. 2003;6:913–914. doi: 10.1038/nn1107. [DOI] [PubMed] [Google Scholar]
- Worgotter F, Suder K, Zhao Y, Kerscher N, Eysel UT, Funke K. State-dependent receptive-field restructuring in the visual cortex. Nature. 1998;396:165–168. doi: 10.1038/24157. [DOI] [PubMed] [Google Scholar]