Abstract
The parieto-insular vestibular cortex (PIVC) is thought to contain an important representation of vestibular information. Here we describe responses of macaque PIVC neurons to three-dimensional (3D) vestibular and optic flow stimulation. We found robust vestibular responses to both translational and rotational stimuli in the retroinsular (Ri) and adjacent secondary somatosensory (S2) cortices. PIVC neurons did not respond to optic flow stimulation, and vestibular responses were similar in darkness and during visual fixation. Cells in the upper bank and tip of the lateral sulcus (Ri and S2) responded to sinusoidal vestibular stimuli with modulation at the first harmonic frequency, and were directionally tuned. Cells in the lower bank of the lateral sulcus (mostly Ri) often modulated at the second harmonic frequency, and showed either bimodal spatial tuning or no tuning at all. All directions of 3D motion were represented in PIVC, with direction preferences distributed roughly uniformly for translation, but showing a preference for roll rotation. Spatio-temporal profiles of responses to translation revealed that half of PIVC cells followed the linear velocity profile of the stimulus, one-quarter carried signals related to linear acceleration (in the form of two peaks of direction selectivity separated in time), and a few neurons followed the derivative of linear acceleration (jerk). In contrast, mainly velocity-coding cells were found in response to rotation. Thus, PIVC comprises a large functional region in macaque areas Ri and S2, with robust responses to 3D rotation and translation, but is unlikely to play a significant role in visual/vestibular integration for self-motion perception.
Introduction
Signals arising from the vestibular labyrinths are indispensable for many cognitive functions related to maintaining spatial orientation and interacting with the environment as we move through the world (Angelaki and Cullen, 2008). These functions include: the perception of self-motion (i.e., how we move in space, as reviewed by Guedry, 1974; MacNeilage et al., 2008), spatial constancy and memory (i.e., keeping our perceived world constant as we move our head and body, as reviewed in Klier and Angelaki, 2008), static visual orientation perception (i.e., the subjective visual vertical, see Bronstein, 1999; Vingerhoets et al., 2009) and locomotor navigation (Israel et al., 1993; Glasauer et al., 1994; Israel et al., 1997; Mittelstaedt and Jensen, 1999; Taube, 2007).
Many of these functions likely depend on cortical representations of vestibular signals. Unlike in other sensory systems, however, a ‘primary’ vestibular cortex, in which all cells respond exclusively to labyrinthine stimulation, has not been described. Rather, vestibular responses are found in many sensory and motor areas, typically in combination with visual, somatosensory, and/or motor-related signals. Some of these cortical areas may receive relatively direct vestibular input from ascending brainstem/cerebellar pathways, whereas others may be interconnected by cortico-cortical projections (Akbarian et al., 1992). Thus far, there is no clear evidence that cortical vestibular areas are hierarchically organized as in visual cortex (Felleman and Van Essen, 1991; Van Essen et al., 2001).
The area most often described as ‘vestibular cortex’ is the parieto-insular vestibular cortex (PIVC), which was first described by Pandya and Sanides (1973) on the basis of cytoarchitecture. They speculated that the macaque retroinsular cortex (Ri) may have a vestibular function (Pandya and Sanides, 1973). Nearly two decades later, it was shown that approximately half of neurons located in and around the lateral sulcus of both Java and squirrel monkeys responded to vestibular stimulation, with many cells showing convergent somatosensory and optokinetic responses (Akbarian et al., 1988; Grüsser et al., 1990a, b). No PIVC neurons responded to static tilt, leading to the conclusion that only canal-driven, and not otolith-driven, representations exist in PIVC (Akbarian et al., 1988). Since its first description by Grüsser and colleagues, no study has systematically quantified the vestibular response properties of PIVC neurons.
Here we identify PIVC for the first time in rhesus macaques and we quantify responses to an extensive set of stimuli, including 3D rotations, 3D translations, and 3D optic flow. Unlike the original conclusions of Grüsser and colleagues, we show that PIVC neurons are tuned to both rotation and translation, thus being driven by both semicircular canal and otolith signals. However, we found that PIVC responses are not selective to optic flow, a finding that places strong constraints on potential functions of this area in comparison with the extensive visual/vestibular convergence seen in extrastriate areas MSTd (Bremmer et al., 1999; Page and Duffy, 2003; Gu et al., 2006; Takahashi et al., 2007) and VIP (Schlack et al., 2002).
Materials and Methods
Subjects and Apparatus
Extracellular recordings were obtained from 4 hemispheres in 2 male rhesus monkeys (Macaca mulatta) weighing between 6–10kg. The surgical preparation, experimental apparatus, and methods of data acquisition have been described in detail previously (Gu et al., 2006; Fetsch et al., 2007; Takahashi et al., 2007). Briefly, each animal was chronically implanted with a circular molded, lightweight plastic ring for head restraint and a scleral coil for monitoring eye movements inside a magnetic field (CNC Engineering, Seatle, WA). Behavioral training was accomplished using standard operant conditioning procedures. All animal surgeries and experimental procedures were approved by the Institutional Animal Care and Use Committee at Washington University and were in accordance with NIH guidelines.
During experiments, the monkey was seated comfortably in a primate chair, which was secured to a six-degree-of-freedom motion platform (MOOG 6DOF2000E; East Aurora, NY). Three-dimensional movements along or around any arbitrary axis were delivered by this platform. In all experiments, the head was positioned such that the horizontal stereotaxic plane was earth-horizontal, with the axis of rotation always passing through the center of the head (i.e., the midline point along the interaural axis). Computer-generated visual stimuli were rear-projected (Christie Digital Mirage 2000; Cyrus, CA) onto a tangent screen placed ~30 cm in front of the monkey (subtending 90×90° of visual angle), and simulated self-motion through a three dimensional cloud of random dots (100 cm wide, 100 cm tall, and 40 cm deep). Visual stimuli were programmed using the OpenGL graphics library and generated using an OpenGL accelerator board (Quadro FX 3000G, PNY Technologies, Parsippany NJ, see Gu et al., 2006 for details). The projector, screen, and magnetic field coil frame were mounted on the platform and moved together with the animal.
Tungsten microelectrodes (Frederick Haer Company, Bowdoinham, ME; tip diameter 3 µm, impedance 1– 2 MΩ at 1 kHz) were inserted into the cortex through a transdural guide tube, using a hydraulic microdrive (Frederick Haer Co.). Behavioral control and data acquisition were accomplished using two separate software systems. For protocols involving sinusoidal motion stimuli, experiments were controlled by custom Spike2 scripts and data acquisition was coordinated by a CED Power 1401 system (Cambridge Electronic Design, Cambridge UK). For protocols involving transient motion stimuli, task control and data acquisition were accomplished by custom scripts written for use with the TEMPO system (Reflective Computing, Olympia, WA). Neural voltage signals were amplified, filtered (400 to 5000 Hz), discriminated (BAK Electronics, Mount Airy, MD) and displayed on an oscilloscope. The times of occurrence of action potentials and all behavioral events were recorded with 1 ms resolution. Raw neural signals were also digitized at a rate of 25 kHz using the CED Power 1401 for off-line spike sorting.
Anatomical localization
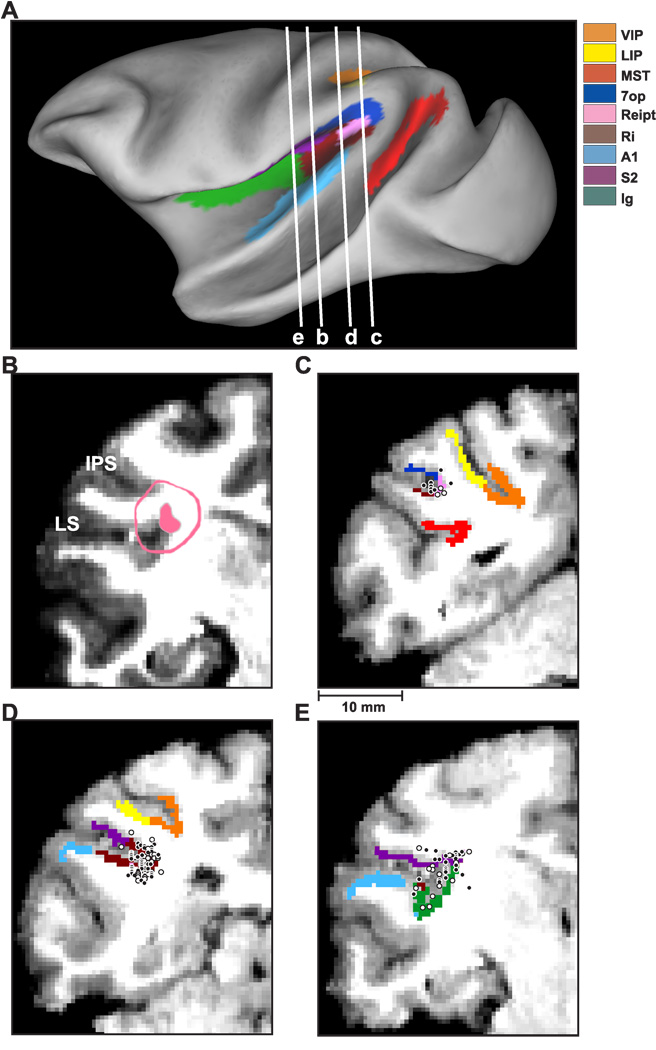
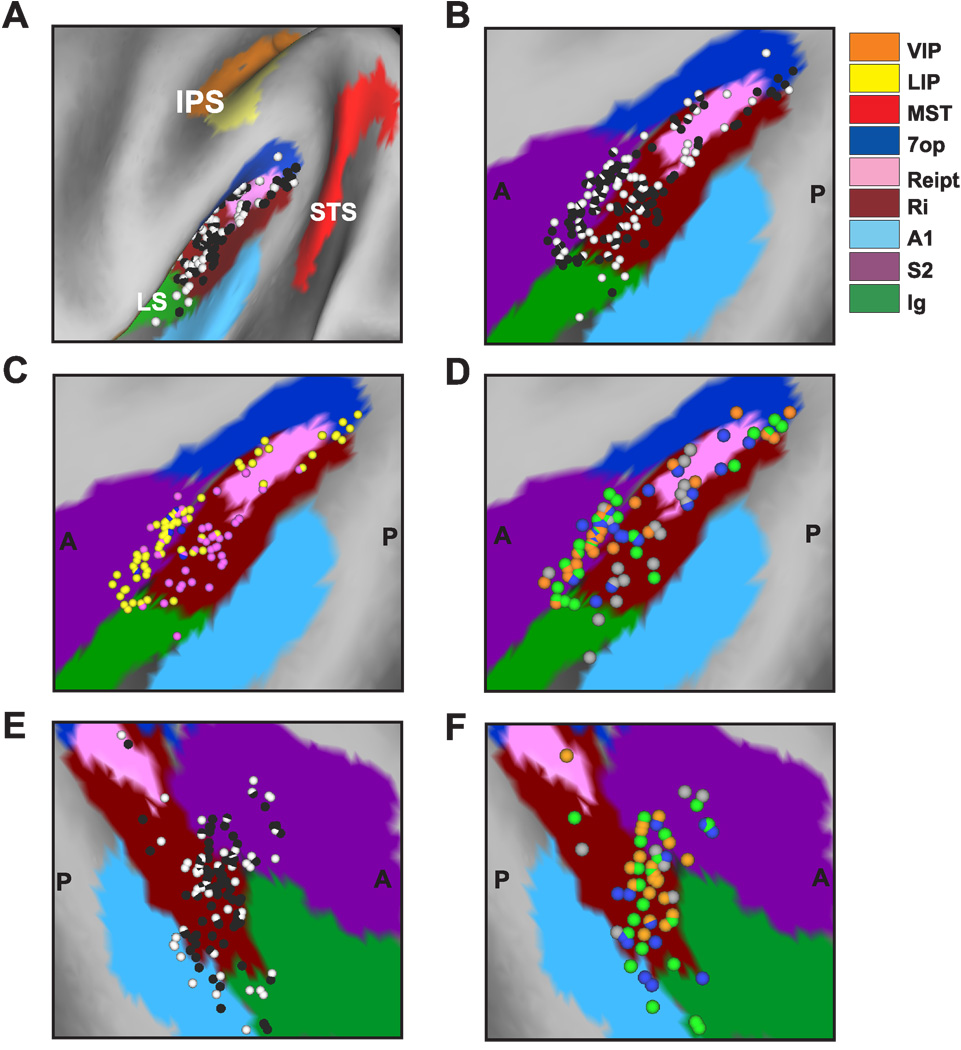
The relevant areas in the lateral sulcus were first identified using MRI scans. An initial (‘baseline’) scan was performed on each monkey prior to any surgeries using a high-resolution sagittal MPRAGE sequence (0.75 mm × 0.75 mm × 0.75 mm voxels). SUREFIT software (Van Essen et al., 2001) was used to segment gray matter from white matter. A second scan was performed after the head holder and recording grid had been surgically implanted. Small cannulae filled with a contrast agent (Gadoversetamide) were inserted into the recording grid during the second scan to register electrode penetrations with the MRI volume. The MRI data were converted to a flat map using CARET software (Van Essen et al., 2001) and the flat map was morphed to match a standard macaque atlas. The data were then refolded and transferred onto the original MRI volume (Fig. 1).
Figure 1.
Anatomical localization of recording sites in the left hemisphere of monkey U. (A) Inflated cortical surface illustrating the coronal sections drawn in B–E. (B) A coronal MRI image showing portions of the lateral sulcus (LS) and intraparietal sulcus (IPS). The filled pink region shows the dense core of signal produced by a manganese injection into the upper bank of the lateral sulcus, at a location where vestibular responses were identified physiologically. The outer pink contour shows the boundaries of the ‘halo’ of less intense signal surrounding the injection. Manganese-induced responses have been superimposed on the baseline MRI image for this animal (see Methods). (C)–(E) Coronal sections, spaced 4mm apart, are shown from posterior (C) to anterior (E); cells located within 2 mm of each section were projected onto that section. Filled symbols with white borders represent single units that showed clear responses during sinusoidal translation and/or rotation, whereas open symbols with black borders illustrate cells that showed no response.
To help localize our recording sites, we injected 0.1 mol/L manganese (Saleem et al., 2002) in Monkey U at a site where robust vestibular responses were encountered in the upper bank of the lateral sulcus. This was done using a microinjectrode (Chen et al., 2001; Chowdhury and DeAngelis, 2008), such that the area responding at the first harmonic of the stimulus (see Results) was first identified by recording neural activity through the microinjectrode. Mixed with the manganese was 10 mg/ml of the GABA agonist muscimol, such that we could verify the effectiveness of the injection prior to performing the MRI scan (technique developed by Snyder and colleagues, Liu et al., 2008). The manganese/muscimol cocktail was injected slowly (0.2 µl/min) using a minipump while neural activity was monitored. The effectiveness of the injection was verified on-line by the silencing of neuronal activity with ~20 minutes following injection of the manganese/muscimol cocktail. The MRI scan was performed within 2–3 hours after the injection, thus the diffusion of the manganese/muscimol cocktail remained rather restricted relative to the injection site. In addition, as there was not enough time for manganese to be transported trans-synaptically, the MRI image reflected the location of the injection site rather than its projection areas (Saleem et al., 2002).
To delineate the central core and halo regions around the manganese injection on the MRI scan, the post-injection MRI scan was first registered to the baseline MRI scan. This allowed us to better visualize the manganese injection relative to the gray and white matter boundaries. The central core region of the manganese signal was visible as a high-intensity zone that could be bounded effectively after image thresholding (filled pink region in Fig. 1B, coronal section taken as illustrated in Fig. 1A). This core region was surrounded by a more diffuse ‘halo’ of somewhat less intense signal. The boundaries of this halo region are illustrated by the pink contour in Fig. 1B. The location of the central core region is consistent with the intended injection site in the upper bank of the lateral sulcus, near the medial tip of gray matter.
With the MRI scans and functional boundaries as a guide, we carried out electrode penetrations to map an extensive region of cortex around the lateral sulcus that extended 15 mm along the anterior-posterior axis. Vestibular responses were recorded at depths between 11 mm (at the posterior extent) and 17 mm (at the anterior end) from the surface of the cortex. At the posterior end, the PIVC region was localized lateral to the border between VIP and LIP and above the superior temporal gyrus (Fig. 1C). The most posterior sections of PIVC were located at anterior-posterior coordinates similar to the vestibular-responsive neurons in area VIP (Chen et al. 2007) and anterior to most of the vestibular-responsive neurons in area MSTd (Gu et al., 2006). More anterior, the vestibular-responsive regions of the lateral sulcus were encountered beneath and lateral to area VIP (Fig. 1D). At the most anterior end, the upper bank of the lateral sulcus was the first (and only) gray matter encountered that modulated in response to sinusoidal vestibular stimuli (Fig. 1E). Note that both VIP and MSTd were identified electrophysiologically in these animals (as part of other published and/or ongoing studies) and the anatomical relationships between all three sites (VIP, PIVC and MSTd) were consistent with the MRI images. Thus, we are confident that neurons with vestibular responses that were assigned to PIVC were not mistakenly recorded in MSTd or VIP, and the lack of optic flow responses in PIVC neurons is consistent with the distinctions made on anatomical grounds.
Experimental protocol
While attempting to isolate single neurons, our search stimulus consisted of 0.5 Hz sinusoidal translations and rotations about the cardinal axes (lateral, fore-aft and up-down for translation; yaw, pitch and roll for rotation) in complete darkness. In initial experiments on the right hemisphere of monkey J, sinusoidal modulation was only evaluated on-line (146/566 of the total recorded cells). In later experiments, which comprised the majority of the data (420/566 cells), sinusoidal responses to translation (0.5Hz, ±10cm, ±0.1G) and rotation (0.5 Hz, ±7°) were saved for off-line analysis (see below).
If there was a clear, audible modulation to sinusoidal translation or rotation, we further examined the cell’s 3D spatio-temporal tuning by recording neural responses while the animal was translated along each of 26 directions sampled evenly around a sphere (as in previous studies, Gu et al., 2006; Takahashi et al., 2007). This included all combinations of movement vectors having 8 different azimuth angles (0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°) and 3 different elevation angles: 0° (the horizontal plane) and ±45° (for a subtotal of 8 × 3 = 24 directions). Two additional movement vectors, with elevation angles of −90° and 90°, corresponded to upward and downward directions, respectively. Each of these 26 movement trajectories had a total displacement of 13 cm, a duration of 2 s, and consisted of a Gaussian velocity profile with a peak velocity of 30 cm/s and a biphasic acceleration profile with a peak acceleration of ~0.1 G (0.98 m/s2).
Following this 3D translation protocol and as long as cell isolation was maintained, PIVC neurons were also tested with rotations about the same 26 vectors, which now represent the corresponding axes of rotation according to the right hand rule (Takahashi et al., 2007). For example, azimuth angles of 0° and 180° (elevation = 0°) correspond to pitch-up and pitch-down rotations, respectively. Azimuths of 90° and 270° (elevation = 0°) correspond to roll rotations (right-ear-down and left-ear-down, respectively). Finally, elevation angles of −90° or 90° correspond to leftward and rightward yaw rotation, respectively. Rotation amplitude was 9° and peak angular velocity was ~20°/s. Because the rotation protocol was always delivered last, a smaller number of neurons were tested with rotation stimuli. Note, however, that the 0.5 Hz sinusoidal protocol was delivered to all well-isolated cells during both rotation and translation; thus, the percentages of neurons with significant responses (Tables 1 and 2) provide a fair representation of the prevalence of rotation/translation selectivity in PIVC.
Table 1.
Statistics of response modulation during sinusoidal translation (0.5 Hz)
| Left-Right motion |
Fore-Aft motion |
Up-Down motion |
Max Direction |
||
|---|---|---|---|---|---|
| p_f1<=0.01 | All (n=420) | 110 (26%) | 100 (24%) | 104 (25%) | 185 (44%) |
| Upper bank (n=153) | 60 (39%) | 58 (38%) | 53 (35%) | 92 (60%) | |
| Tip (n=150) | 43 (29%) | 41 (27%) | 37 (25%) | 78 (52%) | |
| Lower bank (n=117) | 7 (6%) | 5 (4%) | 10 (8%) | 15 (13%) | |
|
p_f2<=0.01 & p_f1>0.01 |
All (n=420) | 45 (11%) | 42 (10%) | 35 (8%) | 67 (16%) |
| Upper bank (n=153) | 6 (4%) | 3 (2%) | 5 (3%) | 7 (5%) | |
| Tip (n=150) | 9 (6%) | 7 (5%) | 11 (7%) | 14 (9%) | |
| Lower bank (n=117) | 30 (26%) | 25 (21%) | 26 (22%) | 46 (39%) | |
|
p_f1>0.01 & p_f2 >0.01 |
All (n=420) | 265 (63%) | 278 (66%) | 281 (67%) | 168 (40%) |
| Upper bank (n=153) | 87 (57%) | 92 (60%) | 95 (62%) | 54 (35%) | |
| Tip (n=150) | 98 (65%) | 102 (68%) | 102 (68%) | 58 (39%) | |
| Lower bank (n=117) | 80 (68%) | 87 (74%) | 81 (69%) | 56 (48%) | |
Data shown represent number of cells and corresponding percentages relative to the total population (bold), upper bank, tip and lower bank for each row, respectively. Data recorded in monkey U (n=273: left hemisphere and 58: right hemisphere) and monkey J (n=23: left hemisphere and 66: right hemisphere).
Table 2.
Statistics of response modulation during sinusoidal rotation (0.5 Hz)
| Yaw rotation |
Roll rotation |
Pitch rotation |
Max Direction |
||
|---|---|---|---|---|---|
| p_f1<=0.01 | All (n=364) | 29 (8%) | 68 (19%) | 59 (16%) | 114 (31%) |
| Upper bank (n=136) | 17 (12%) | 40 (29%) | 33 (24%) | 64 (47%) | |
| Tip (n=126) | 7 (6%) | 23 (18%) | 20 (16%) | 37 (29%) | |
| Lower bank (n=102) | 5 (5%) | 5 (5%) | 6 (6%) | 13 (13%) | |
|
p_f2<=0.01 & p_f1>0.01 |
All (n=364) | 51 (14%) | 40 (11%) | 28 (8%) | 66 (18%) |
| Upper bank (n=136) | 7 (5%) | 9 (7%) | 4 (3%) | 9 (7%) | |
| Tip (n=126) | 17 (14%) | 9 (7%) | 6 (5%) | 19 (15%) | |
| Lower bank (n=102) | 27 (26%) | 22 (22%) | 18 (18%) | 38 (37%) | |
|
p_f1>0.01 & p_f2 >0.01 |
All (n=364) | 284 (78%) | 256 (70%) | 277 (76%) | 184 (51%) |
| Upper bank (n=136) | 112 (82%) | 87 (64%) | 99 (73%) | 63 (46%) | |
| Tip (n=126) | 102 (81%) | 94 (75%) | 100 (79%) | 70 (56%) | |
| Lower bank (n=102) | 70 (69%) | 75 (74%) | 78 (76%) | 51 (50%) | |
Data shown represent number of cells and corresponding percentages relative to the total population (bold), upper bank, tip and lower bank for each row, respectively. Data recorded in monkey U (n=247: left hemisphere and 51: right hemisphere) and monkey J (n=21: left hemisphere and 45: right hemisphere).
The translation and rotation protocols were delivered in separate blocks of trials and each included vestibular and visual stimulus conditions that were randomly interleaved, along with a null condition (platform stationary and no visual stimulus) to assess spontaneous activity. (1) In the "vestibular" condition, the monkey was translated or rotated in the absence of optic flow. The screen was blank, except for a fixation point that remained at a fixed head-centered location throughout the motion trajectory. Because the fixation point moved with the animal's head, there were no systematic eye movements other than small fixational saccades. (2) In the "visual" condition, the motion platform was stationary, while optic flow simulated movement through a three-dimensional cloud of stars. Note that all stimulus directions are referenced to body motion (real or simulated) when the data are plotted. To complete five repetitions of all 26 directions for each of the visual/vestibular conditions, plus five repetitions of the null condition, the monkey was required to successfully complete 26 × 2 × 5 + 5 = 265 trials for each of the translation and rotation protocols. Neurons were included in the sample if each stimulus in a block was successfully repeated at least three times. For 90% of neurons, we completed at least 5 repetitions of each stimulus.
For both the visual and vestibular conditions, the animal was required to fixate a central target (0.2° in diameter) for 200 ms before the onset of the motion stimulus (fixation windows spanned 2 × 2° of visual angle). The animals were rewarded at the end of each trial for maintaining fixation throughout the stimulus presentation. If fixation was broken at any time during the stimulus, the trial was aborted and the data were discarded. In addition to these ‘fixation’ protocols, most neurons were also tested using the same 26 motion trajectories in complete darkness (with the projector turned off). In these trials, there was no behavioral requirement to fixate, and rewards were delivered manually to keep the animal alert. Note that the order in which the ‘fixation’ and ‘darkness’ protocols were delivered varied among recorded cells, although the 3D translation protocol was always delivered before the rotation protocol. Thus, there were two possible sequences of these blocks of stimuli: 1) translation/fixation, rotation/fixation, translation/darkness, rotation/darkness, or 2) translation/darkness, rotation/darkness, translation/fixation, rotation/fixation. Because we found no significant differences in tuning properties or response magnitude between fixation and darkness conditions (Fig. 17), data have been combined in the presentation. Specifically, data for each cell are taken from the fixation condition, if available. If cell isolation was lost prior to delivery of the fixation protocol, then data were taken from the darkness condition. Note that each cell is represented only once in all population data figures.
Figure 17.
Comparison of responses under conditions of complete darkness versus visual fixation, plotted separately for translation (A, C, E) and rotation (B, D, F). All comparisons were made at the peak time of fixation responses. (A), (B) Scatter plots of peak-trough response amplitudes (Rmax−Rmin) during translation (n=41) and rotation (n=31), respectively. (C), (D) Scatter plots of DDI for the same cells as in A, B. (E), (F) Distribution of the difference in preferred direction under conditions of fixation and darkness, shown for translation (n=16) and rotation (n=4), respectively. Only neurons with unimodal spatial tuning at peak time for both fixation and darkness conditions are included in this comparison.
Data Analysis
Sinusoidal analysis
Quantitative data analyses were performed off-line using custom-written scripts in Matlab (The MathWorks, Natick MA). Responses from multiple cycles of sinusoidal stimulation were folded into a single cycle. Firing rates were then computed in 50ms bins (40 bins per cycle). A fast Fourier transform was applied to the binned data, giving the magnitude and phase of the first 20 harmonics of each response. To assess whether the response was significantly modulated at the fundamental component of the stimulus and/or its second harmonic, we computed two Fourier Ratios, which were defined as the fundamental frequency or second harmonic, respectively, over the maximum of the remaining harmonics (i.e., f1/max(f2,f3,f4,…,f20), and f2/max(f1,f3,f4,…,f20)). Statistical significance (p<0.01) of these ratios was assessed using a permutation test based on 1000 random reshufflings of the 40 response bins.
Response gains were computed from instantaneous firing rate (IFR) measurements. For each stimulus condition, IFRs from multiple cycles were “folded” into a single cycle by overlaying the neural responses, as follows. First, the time of occurrence of each spike was logged. IFR was then calculated as the reciprocal of the interspike interval, and assigned to the middle of the interval. For each stimulus cycle (e.g., the nth cycle), an integer multiple (n-1) of the stimulus period was subtracted from the times associated with all IFR values for that specific cycle. For example, for a frequency of 0.5 Hz, 2s would be substracted for cycle 2, 4s for cycle 3, etc. The result is to “fold” all instantaneous frequency values into a single stimulus cycle. This procedure provides no averaging, as all spike occurrences are represented in time.
The overlaid single cycle responses were fit with the sum of two sinusoids (first and second harmonics of the stimulus frequency) plus a constant DC term. Translation response gain was calculated as response amplitude (half of the peak-to-trough modulation) divided by the peak acceleration of the stimulus (as measured using a linear accelerometer) and was expressed in units of spikes/s per G (with G=9.81m/s2). Rotation response gain was calculated as response amplitude over peak angular velocity of the stimulus, in units of spikes/s per deg/s. Phase was expressed as the difference between peak response and peak stimulus acceleration (for translation) or velocity (for rotation). The ratio of the gains of the second harmonic and fundamental components (‘f2/f1 ratio’) was computed from the sum-of-sinusoids fit to indicate the dominant frequency modulation in the response. If the ratio was less than one, the response was considered dominated by the fundamental component. Note, however, that the significance of each harmonic modulation (f1 and f2) was evaluated separately using permutation tests on the two Fourier Ratios described above.
From these sinusoidal responses (lateral, up-down and fore-aft or yaw, pitch and roll), 3D direction preferences (azimuth, elevation) for translation and rotation were computed using a spatio-temporal convergence (STC) model (Angelaki, 1991, 1992). The spatiotemporal model is more general than the traditional cosine-tuning model; whereas the latter assumes zero response for directions perpendicular to the direction of maximal response, the spatiotemporal model allows for non-zero response along the perpendicular axis. In general, the STC model allows temporal dynamics and spatial properties to be intermingled, such that more than one temporal parameter (e.g., velocity and acceleration) can be simultaneously coded along different spatial directions. The spatiotemporal model was used here because it characterizes best the translation tuning of brainstem and cerebellar vestibular neurons (Bush et al., 1993; Angelaki and Dickman, 2000; Shaikh et al., 2005; Chen-Huang and Peterson, 2006).
By fitting this model, four parameters were computed for each cell: maximum response gain and phase, the preferred (maximum response) direction, and the response gain along the direction perpendicular to the preferred direction. The larger the magnitude of this perpendicular response relative to the preferred response, the larger the departure from traditional cosine tuning. We first computed the preferred direction in the horizontal plane by considering the response gain and phase along the lateral and fore-aft (for translation) or pitch and roll (for rotation) axes. The polar angle of this vector defined the azimuth angle of the 3D direction preference. Then we computed its elevation by fitting the STC model in the plane defined by the preferred azimuth vector and the vertical axis. This procedure, which was applied to the f1 gain and phase for all cells with significant first harmonic modulation along at least one motion direction, allows computation of the azimuth and elevation of the 3D direction preference in spherical coordinates, along with the corresponding gain and phase of the neuronal response along this preferred direction.
Temporal response analysis
To analyze neural responses to transient motion stimuli, we first constructed peristimulus time histograms (PSTHs) for each direction of translation and/or rotation. PSTHs were computed using 25 ms time bins and were smoothed with a 400 ms boxcar filter. The following procedure was used to identify and classify PSTHs with significant temporal modulation. First, we computed the distribution of spike counts (across stimulus repetitions) for each possible 400ms time window (in 25 ms steps) between 500–2000 ms after stimulus onset. We then identified the 400ms time windows containing the spike count distributions having the maximum and minimum average values. Each of these distributions was then compared to a baseline response distribution, obtained from the 400ms time window from −100 to 300 ms post-stimulus onset. Note that stimulus velocity has only reached 0.04% of its peak value (0.26% of peak acceleration) at 300ms, thus this interval effectively constitutes a baseline response. To avoid false positives, we required at least 4 overlapping time windows (spaced 25 ms apart and including the maximum or minimum time window defined above) to have spike count distributions that differed significantly from the baseline distribution (Wilcoxon signed ranks test, p<0.01). This statistical test identified a significant peak and/or trough in the PSTH for each stimulus condition and direction of movement (if they existed), and these criteria were found to agree well with classification of responses by eye.
Based on this procedure for identifying peaks and troughs, we divided temporal responses into two groups: monophasic and biphasic. For a monophasic response, there is only one significant peak or trough in the PSTH (but not both). For a biphasic response, both a significant peak and trough are identified. This classification was made independently for each motion direction with a significant peak and/or trough; otherwise the cell was considered unresponsive to stimulation in that direction. For a neuron to be considered to have significant temporal modulation in response to the set of transient stimuli, and to be considered further in quantitative analyses, it had to show a significant monophasic or biphasic response to at least two nearby directions (45° apart in azimuth or elevation). Neurons not meeting this criterion were considered unresponsive and were not considered further in subsequent analyses.
For neurons with significant temporal modulation as defined above, we investigated how direction tuning for translation and rotation depends on time and whether there are multiple times when a neuron shows distinct directional tuning. First, we calculated the maximum response across stimulus directions at each moment in time during the response. Specifically, for each 400ms time window (in steps of 25ms), we computed a direction tuning function and we extracted the peak response. This yields a peak response vector, R(t), which contains the maximal response across directions (irrespective of direction preference) for each time bin. This vector summarizes response strength as a function of time. Similarly, for each 400ms time window, we performed ANOVA to assess the statistical significance of directional selectivity at each time point. This yields a vector, p(t), that summarizes the significance of direction tuning as a function of time.
Next, we identified the local maxima of R(t) with the following criteria: 1) a local maximum is the largest value within a given neighbourhood (i.e., Rt>Rt+1 and Rt>Rt-1, where t represents time), and 2) the ANOVA values from p(t) must be significant (p<0.01) for 5 consecutive time bins centered on the putative local maximum. The set of local maxima so defined were thus ranked according to peak response value, thus generating a sequence f(n).
Starting from these local maxima, we identified time periods with distinct direction selectivity as follows. Beginning at the time point of the largest local maximum, f(1), we computed the correlation coefficient between the 3D direction tuning at this time bin and the 3D tuning of each other time bin. A contiguous temporal sequence of time bins that are significantly positively correlated with the tuning at f(1) defines a distinct temporal period of direction selectivity. If other local maxima, e.g. f(3), are included in the tuning peak centered on f(1), they are not considered further. This process is repeated for each of the putative local maxima, and the end result defines whether there are one, two, or more distinct time windows within which the neuron shows distinct directional selectivity. The times of local maxima at which distinct directional tunings are observed are referred to as ‘peak times’. Note that peak times and all temporal response profiles have been adjusted for the time delay (115 ms) intrinsic to the dynamics of the motion platform; that is, the delay between the motion command signal and the actual movement of the motion platform (see also Fetsch et al., 2007).
From this analysis of the time course of directional selectivity, we divided cells into 4 groups: 1) cells with 3 distinct temporal peaks of directional selectivity (“triple-peaked”), 2) cells with 2 temporal peaks of direction tuning (“double-peaked”), 3) cells with a single time period of directional selectivity (“single-peaked”), and 4) cells that were not significantly direction-selective in any time period (“not-tuned”). Each of these groups were characterized by 3, 2, 1 or 0 peak times, respectively. To visualize spatial tuning in 3D and to plot spherical data on Cartesian axes, mean firing rates at each peak time were transformed using the Lambert cylindrical equal-area projection (Snyder, 1987) and then plotted in a color contour plot as a function of azimuth and elevation to create a 3D tuning function. This produces a flattened representation in which the abscissa represents azimuth angle, and the ordinate corresponds to a sinusoidally transformed version of elevation angle. Note that the range of values represented by the color scale in each contour plot was chosen based on the minimum and maximum responses, rounded to the nearest 10 spikes/s.
The strength of directional tuning at each peak time was quantified using a direction discrimination index (DDI), given by (Takahashi et al., 2007):
| (1) |
where Rmax and Rmin are the maximum and minimum responses from the 3D tuning function, respectively. SSE is the sum squared error around the mean responses, N is the total number of observations (trials), and M is the number of stimulus directions (M=26). The DDI compares the difference in firing between the preferred and null directions against response variability, and quantifies a neuron’s reliability for distinguishing between preferred and null motion directions. Neurons with large response modulations relative to the noise level will have DDI values closer to 1, whereas neurons with weak response modulation will have DDI values closer to 0.
The preferred direction of a neuron for each stimulus condition was described by the azimuth and elevation of the vector sum of the individual responses (after subtracting spontaneous activity). In such a representation, the mean firing rate in each trial was considered to represent the magnitude of a 3D vector whose direction was defined by the azimuth and elevation angles of the particular stimulus (Gu et al., 2006). To plot the difference in 3D direction preferences (|Δ preferred direction|) between two stimulus conditions on Cartesian axes (Fig. 11B), the data were again sinusoidally transformed such that random combinations of directions on a sphere would result in a flat distribution of |Δ preferred direction|.
Figure 11.
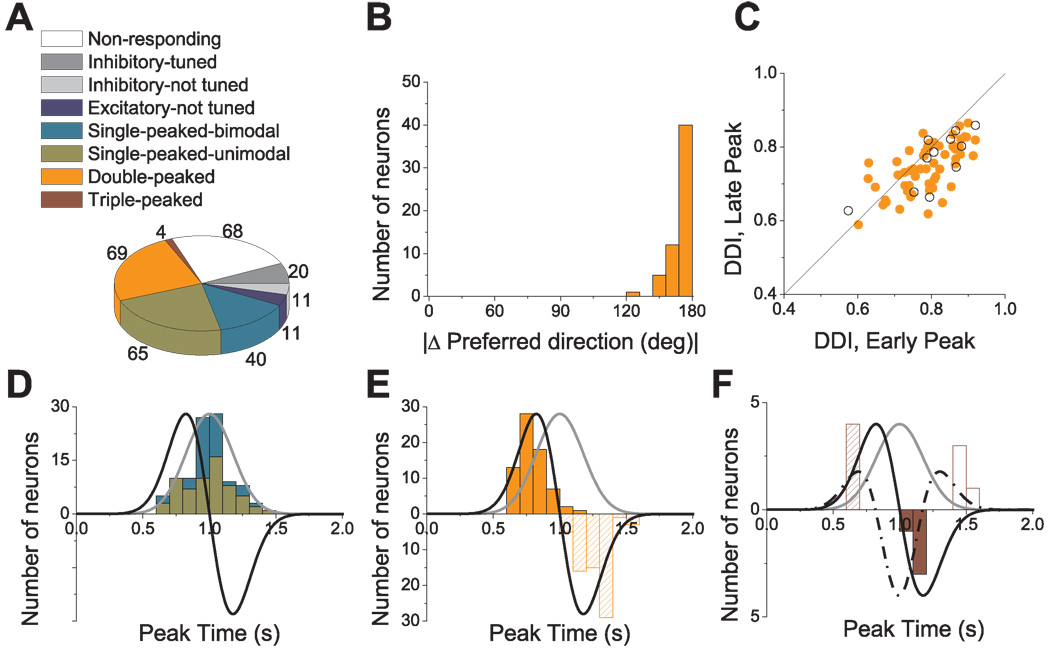
Population summary of the spatio-temporal tuning in response to transient 3D translation. (A) Categories of tuning among responsive cells (n=220). (B) Distribution of the 3D difference in preferred direction (|Δ Preferred direction|) between the two distinct spatial tuning peaks of double-peaked cells; data are shown for 58/69 double-peaked cells with direction tuning that was unimodal at both peak times. (C) Scatter plot of the direction discrimination index (DDI) characterizing the strength of directional tuning at the two peak times of double-peaked cells. Filled symbols represent cells with unimodal spatial tuning for both peak times (n=58). Open symbols represent cells with bimodal spatial tuning for at least one of the peak times (n=11). (D) Distribution of peak times for single-peaked cells. Green bars: cells with unimodal spatial tuning (n=65); Cyan bars: cells with bimodal spatial tuning (n=40). (E) Distribution of peak times for double-peaked cells (n=69). Solid and hatched bars indicate the first and second peak times, respectively. (F) Distribution of peak times for triple-peaked cells (n=4). Stimulus velocity (gray), acceleration (black) and jerk (dashed-dotted line) profiles are overlaid in D–F. Distributions of the second peak times for double-peaked and triple-peaked cells have reversed polarity (negative ordinate values) for illustrative purposes.
Note that the vector sum can reliably reflect the cell’s tuning preference only when the directional tuning profile is unimodal at the respective peak time. However, we found that this was not always the case for vestibular neurons in the lateral sulcus. Thus, we first classified the directional tuning at each peak time as ‘unimodal’ versus ‘bimodal’ (the later group also potentially includes ‘multimodal’ cells) as follows: First, we interpolated the 3D tuning data to 5° resolution in both azimuth and elevation, and then we adapted a multimodality test based on the kernel density estimate method (Silverman, 1981; Fisher and Marron, 2001; Anzai et al., 2007). This test generates two p values, with the first one (p_uni) for the test of unimodality and the second one (p_bi) for the test of bimodality. For example, if p_uni < 0.05 and p_bi > 0.05, unimodality is rejected and the distribution is classified as bimodal. If p_bi < 0.05 also, this could indicate the existence of more than two modes in the distribution (which here were lumped into the ‘bimodal’ category, as multimodal tuning was rarely observed). Accordingly, direction tuning was classified as either unimodal or bimodal for each peak time. Note, however, that distributions of 3D direction preferences (and |Δ preferred direction| between conditions) only contain data from peak times for which directional tuning is characterized as unimodal.
Results
We recorded from 566 well-isolated cells in both hemispheres of two macaques (monkey J: 235 neurons; monkey U: 331 neurons). We recorded from all cells encountered in the upper bank, lower bank or tip of the lateral sulcus within a large area extending 15 mm anterior to posterior. Although some recordings were made from both hemispheres in each animal, only the right hemisphere of monkey J (202 cells) and the left hemisphere of monkey U (273 cells) were systematically explored. Because of some differences in the placement of the recording grids, the most anterior extent of the lateral sulcus was only investigated in monkey J, whereas the most posterior extent of the area was only explored in monkey U.
As the electrode was lowered into the lateral sulcus, a search stimulus consisting of sinusoidal translation (left-right, fore-aft or up-down; 0.5 Hz, ±10 cm) or rotation (yaw, roll or pitch; 0.5 Hz, ±7°) was presented. More than half (68%) of well-isolated cells had audible response modulation to one of these stimuli in complete darkness. For those cells with audible modulation, we further tested their tuning properties in response to transient 3D displacements (see Methods). We begin by quantifying sinusoidal responses. Next, we analyze the spatio-temporal response characteristics to 3D transient motion. Finally, we describe neuronal responses to optic flow stimulation.
Sinusoidal Responses
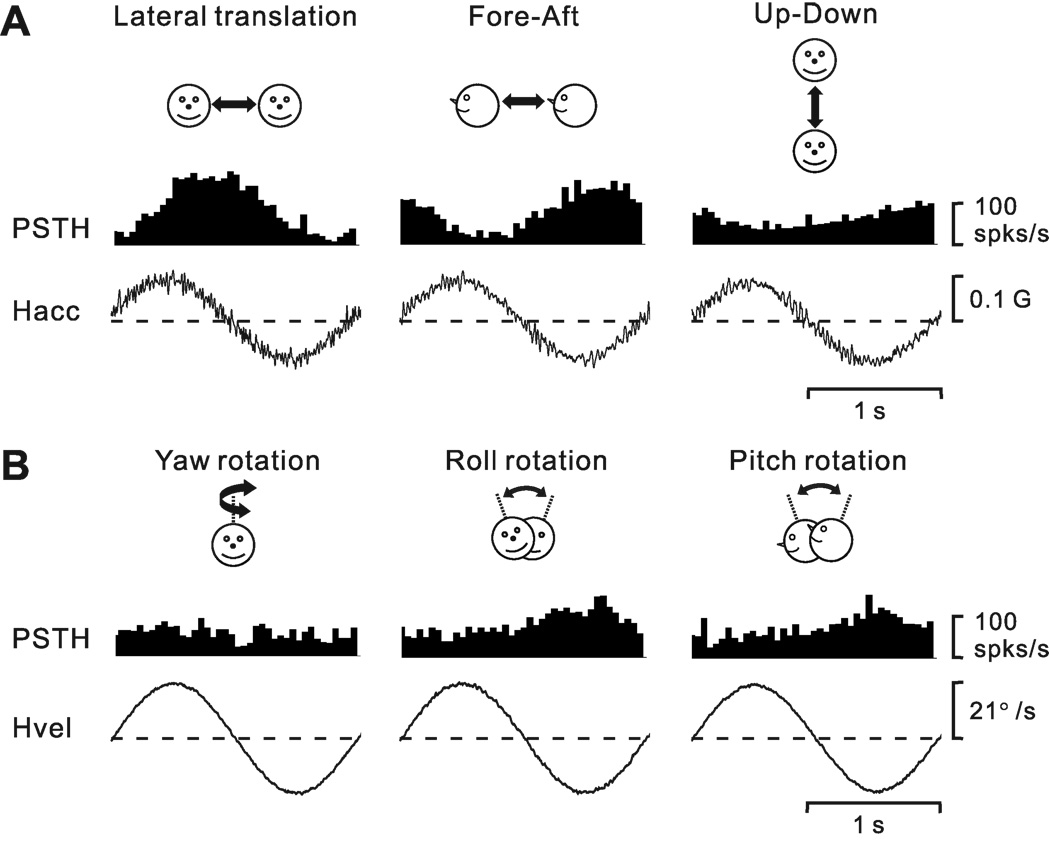
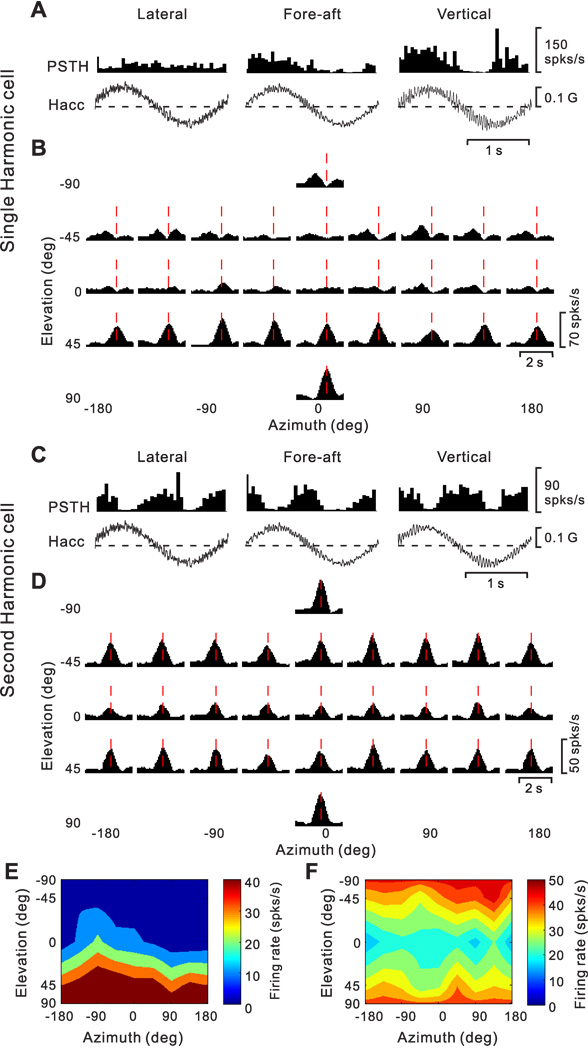
Sinusoidal responses from an example neuron during 0.5 Hz translation and rotation are illustrated in Fig. 2A and 2B, respectively. We determined whether each sinusoidal response was modulated significantly at the 1st (f1) or 2nd (f2) harmonic of the stimulus frequency, and then computed the gain ratio of these response harmonics (f2/f1, see Methods). The cell of Fig. 2 shows strong first harmonic modulation in response to lateral (708.1 spikes/s/G, p_f1<0.01) and fore-aft (546.8 spikes/s/G, p_f1<0.01) translation, with modest modulation in response to up-down translation (286.6 spikes/s/G, p_f1<0.01). In addition, the cell was also significantly modulated during roll (1.9 spikes/s/º/s, p_f1<0.01) and pitch (1.2 spikes/s/º/s, p_f1<0.01) rotation. In contrast, yaw rotation did not produce significant temporal response modulation (p_f1 >0.01).
Figure 2.
Peri-stimulus time histograms (PSTHs, averaged over multiple cycles) from an example neuron during 0.5 Hz sinusoidal translation (A) and rotation (B). Motion directions are indicated by the cartoon drawings. Stimulus traces shown represent linear acceleration (Hacc, A) or angular velocity (Hvel, B) of the head. The cell’s response modulated significantly during all three translation directions, lateral (708.1 spikes/s/G, p_f1<0.01, f2/f1=0.029), fore-aft (546.8 spikes/s/G, p_f1<0.01, f2/f1=0.114) and up-down (286.6 spikes/s/G, p_f1<0.01, f2/f1=0.159) motions. The cell also modulated significantly during roll (1.9 spikes/s/º/s, p_f1<0.01, f2/f1=0.236) and pitch (1.2 spikes/s/º/s, p_f1<0.01, f2/f1=0.409) rotations, but not during yaw rotation (p_f1>0.01 and p_f2>0.01).
Among 420 neurons for which sinusoidal translation responses were quantified off-line, 60% (252 cells) responded significantly along at least one axis of motion (left-right, fore-aft, or up-down). The majority (185/252, 73%) modulated significantly at the fundamental frequency of the stimulus (p_f1<0.01; Table 1). An additional 67 cells (26% of responding cells and 16% of the total population) modulated significantly only at the second harmonic frequency (p_f1>0.01 & p_f2<0.01; Table 1). Approximately equal percentages of neurons show significant response modulation during left-right, fore-aft and up-down translation (Table 1). Considering each axis of motion separately, ~25% of responses showed significant f1 modulation, ~10% had only significant f2 modulation, and ~65% of responses did not modulate significantly (Table 1).
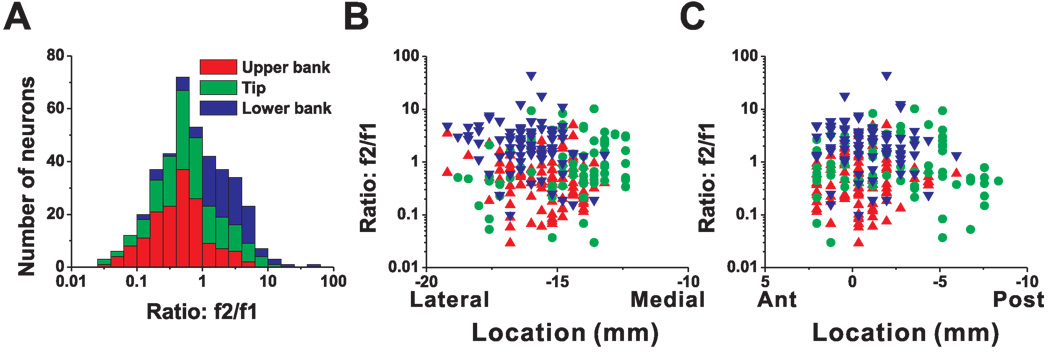
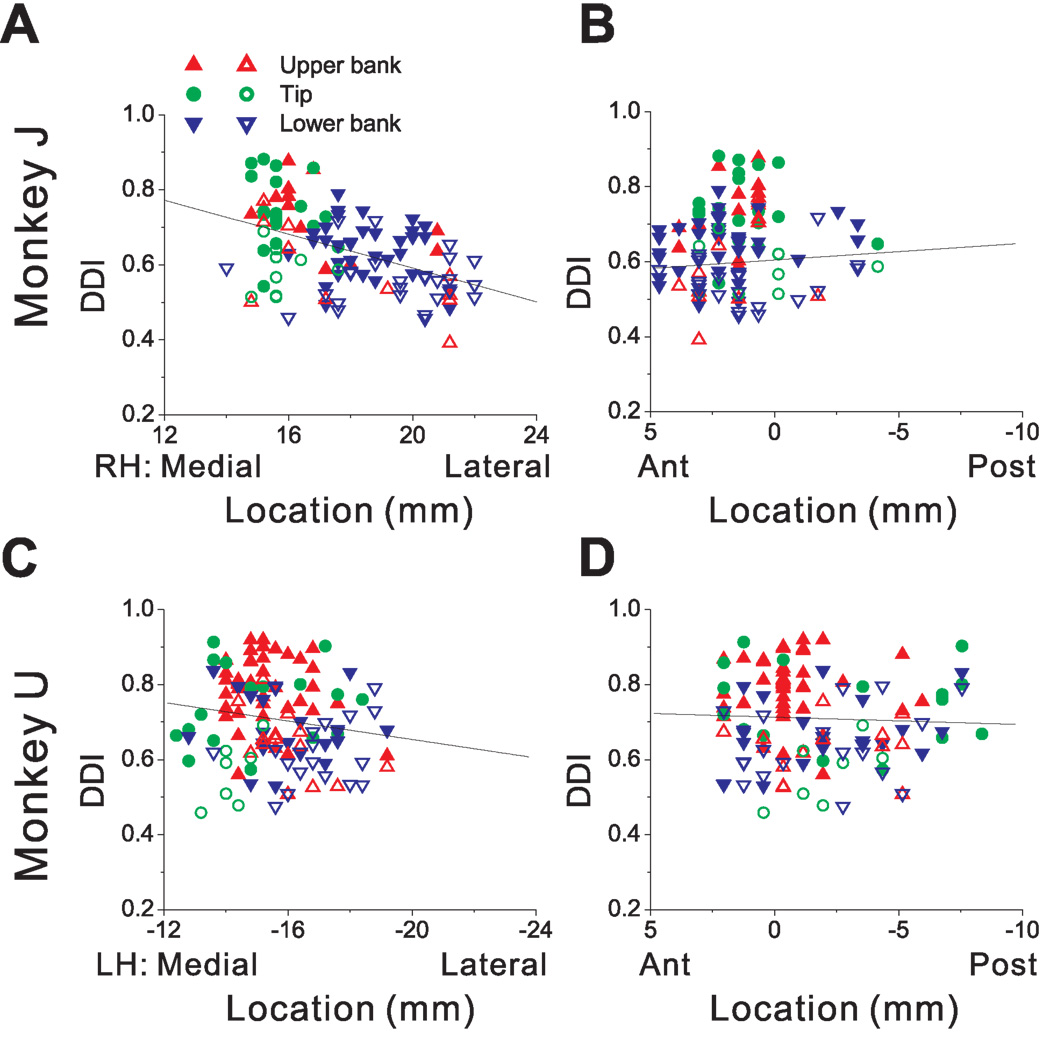
The distribution of neurons with significant response modulations at f1 and f2 (along the motion axis that elicited maximum response) depended on cell location within the lateral sulcus. As shown in Fig. 3 (see also Table 1), first-harmonic cells (p_f1<0.01) were most common in the upper bank and tip of the sulcus; second-harmonic cells (p_f1>0.01 & p_f2<0.01) were most common in the lower bank of the lateral sulcus. Fig. 3A shows the distribution of the f2/f1 ratio, color-coded separately for cells in the upper bank (red bars), tip (green bars) and lower bank (blue bars). Cells located in the upper bank of the lateral sulcus typically had small f2/f1 ratios (0.42 ± 0.21, geometric mean ± SE), whereas lower bank cells generally had a large f2/f1 ratios (1.99 ± 0.29); this difference was highly significant (p<0.001, Wilcoxon rank test). The cells located at the tip of the sulcus had f2/f1 ratios that were intermediate, with an average of 0.69 ± 0.28. There was no significant correlation between the f2/f1 ratio and the location of recording sites along the medial-lateral (r=−0.08, p=0.23, Fig. 3B) and anterior-posterior (r=0.01, p=0.83, Fig. 3C) dimensions.
Figure 3.
Relationship between the f2/f1 ratio (second/first harmonic of response modulation along the preferred direction of translation) and cell location within the lateral sulcus. (A) Distribution of f2/f1 ratio (n=420), plotted separately for cells recorded in the upper bank (red, n=153), tip (green, n=150), and lower bank (blue, n=117) of the lateral sulcus. (B), (C) Scatter plots of the f2/f1 ratio as a function of medial-lateral and anterior-posterior stereotaxic coordinates. Only cells from the left hemisphere of monkey U (n=273) are shown. Results were qualitatively consistent for monkey J, but not included here because sinusoidal responses were not saved for off-line analysis in many experiments (see Methods). Data are color-coded according to their location within the upper bank (red triangles), tip (green circles), and lower bank (blue triangles).
Results were largely similar for responses to sinusoidal rotation stimuli (Table 2), with a few notable differences. First, significant response modulations were less frequently seen for rotation than translation, and this was particularly true for first-harmonic (f1) cells (31% for rotation versus 44% for translation). Second, whereas responses to translation were equally common for each axis of motion, significant rotation responses (f1 or f2) were most common for the roll rotation axis (19%), and least common for the yaw axis (8%). In fact, the percentage of second-harmonic cells that responded to yaw rotation (14%; p_f1>0.01 & p_f2<0.01) was larger than the percentage of first-harmonic yaw-responsive cells (8%; p_f1<0.01) (see Table 2).
As for translation, single-harmonic responses to rotation were also more common in the upper than lower bank of the lateral sulcus. The mean f2/f1 ratios (geometric mean ± SE) were 0.64 ± 0.26 (n=136) for the upper bank, 0.83 ± 0.24 (n=126) for the tip of the sulcus, and 1.58 ± 0.31 (n=102) for the lower bank. The difference in f2/f1 ratio between the upper and lower banks was again highly significant (p<0.001, Wilcoxon rank test). There was a weak correlation between the f2/f1 ratio for rotation and cell location along the medial-lateral dimension (r=−0.13; p=0.05), such that the relative strength of second harmonic responses increases mildly as one moves laterally within the sulcus. No such correlation was found for the anterior-posterior dimension (p=0.62).
The percentage of cells responding to both rotation and translation was high. Among 364 cells tested with both sinusoidal translation and rotation, 255 had significant responses (p_f1<0.01 or p_f2<0.01) to either translation or rotation. Of these 255 cells, roughly half (137/255, 53%) were convergent, i.e., they showed significant response modulation (p_f1<0.01 or p_f2<0.01) during both rotation and translation. By comparison, 30% of cells (75/255) showed response modulation only during translation and 17% (43/255) modulated only during rotation. Thus, unlike a previous report involving measurements of responses to static tilt (Akbarian et al., 1988), we found strong evidence that many neurons in PIVC carry information about both translation and rotation of the subject.
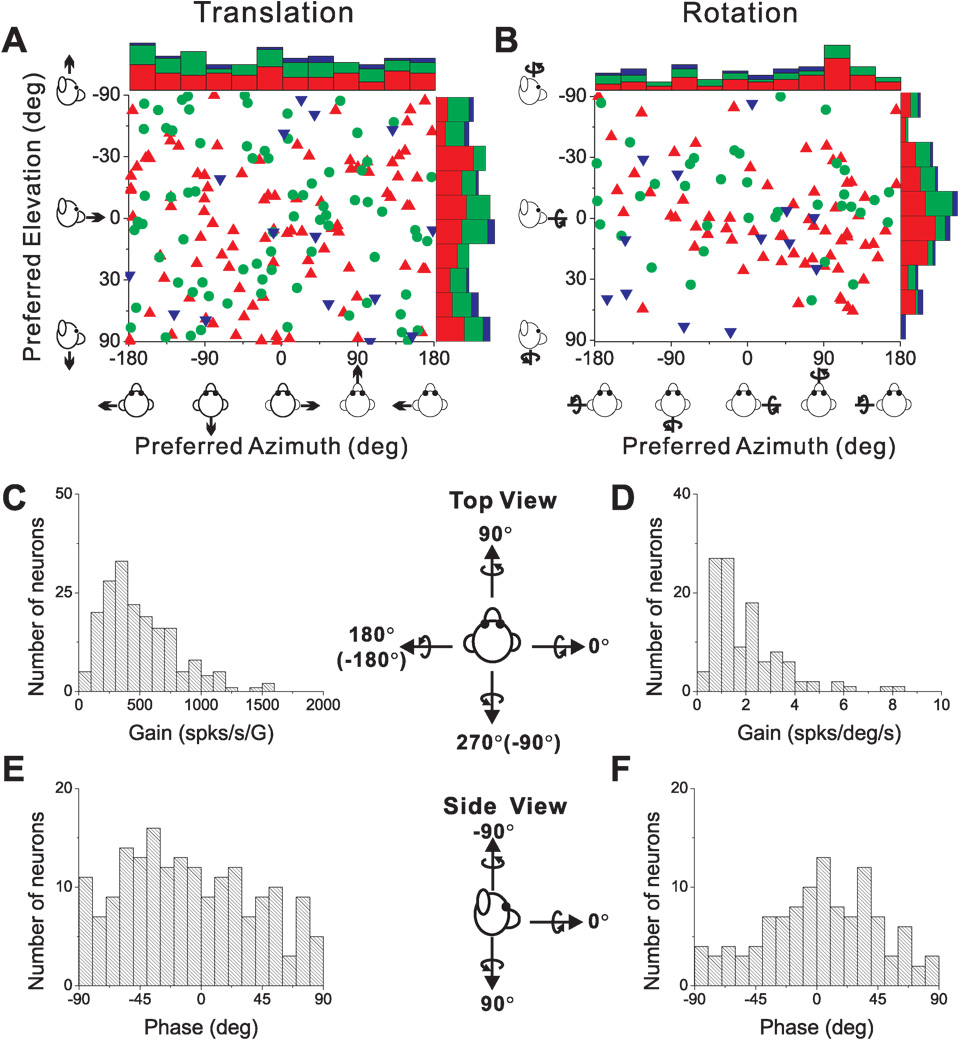
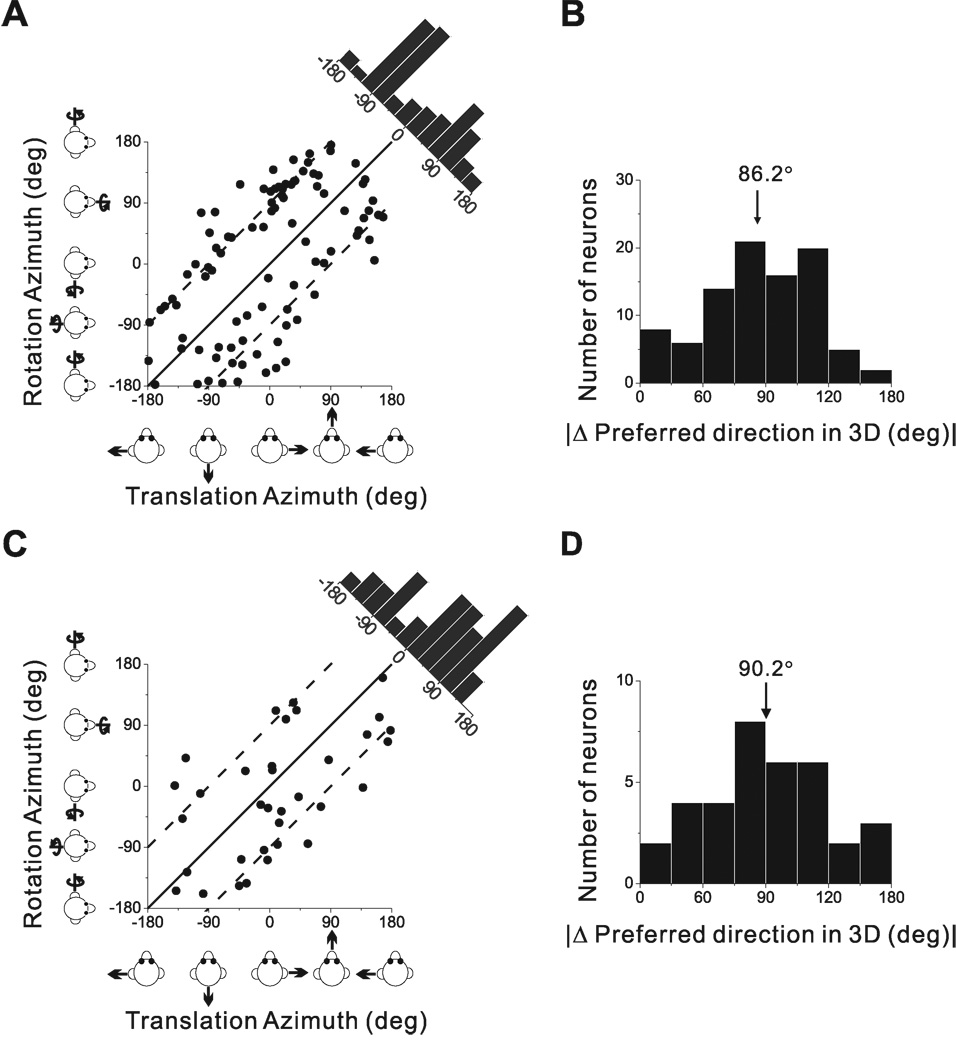
We used the f1 component of the response and a spatio-temporal convergence (STC) model (see Methods) to compute the preferred direction of translation or rotation in 3D for each neuron. The corresponding azimuth and elevation angles of the 3D direction preferences for translation and rotation are plotted for each cell in Fig. 4A and 4B, respectively. Each point in the scatter plots represents the preferred direction [azimuth, elevation] of a PIVC neuron, color-coded according to the location of the cell in the upper bank, tip or lower bank of the lateral sulcus (red, green and blue, respectively). The distributions of direction preferences do not show any clear dependence on cell location within the lateral sulcus. For translation (Fig. 4A), the marginal distributions of azimuth and elevation preferences (combining across cell locations) were not significantly different from uniform (p>0.05, uniformity test). The flat marginal distributions in Fig. 4A suggest that the distribution of direction preferences for translation is uniform on a sphere. For rotation (Fig. 4B), neither marginal distribution was uniform (p<0.05, uniformity test). Rather, both distributions were classified as unimodal (p_uni>0.05, modality test), with preferred directions tending to cluster around the roll axis (90° azimuth and 0° elevation). Because many cells in Fig. 4B preferred ~+90° azimuth and 73/114 were recorded from the left hemisphere, there was a predominance of neurons that preferred counter-clockwise (contralateral ear-down) roll. Note that only neurons with significant first harmonic responses were included in this analysis because of the requirements of the STC model.
Figure 4.
Summary of sinusoidal responses. (A), (B) Distributions of direction preferences for translation (n=185) and rotation (n=114), in spherical coordinates (scatter plots of elevation versus azimuth preferences). Uniform azimuth and elevation distributions reflect direction preferences that are uniformly distributed on a sphere. The data are plotted on Cartesian axes that represent the Lambert cylindrical equal-area projection of the spherical stimulus space. Histograms along the top and right sides of each scatter plot show the marginal distributions. Data are color-coded based on the location of cells in the upper bank (red), tip (green), and lower bank (blue) of the lateral sulcus. (C), (D) Distributions of neural response gain along the 3D preferred direction for translation and rotation, respectively. (E), (F) Distributions of neural response phase along the 3D preferred direction for translation and rotation, respectively. Only neurons with significant single harmonic responses (p_f1<0.01) along at least one motion direction are included.
For each first-harmonic cell, we computed the gain and phase of the response along the preferred motion axis in 3D. Distributions of gain and phase are shown in Fig. 4C,E for translation, and Fig. 4D,F for rotation. First-harmonic gains averaged 497.5 ± 22.1 (SE) spikes/s/G (range: 63–1585 spikes/s/G; Fig. 4C) for translation and 2.01 ± 0.14 (SE) spikes/s/°/s (range: 0.20–8.38 spikes/s/°/s; Fig. 4D) for rotation. Response phase relative to linear acceleration (expressed in the interval [−90, +90°]) was distributed roughly uniformly (p>0.05, uniformity test; Fig. 4E), with some neurons modulating in phase with linear velocity and some in phase with linear acceleration. A broad distribution of translation response phases is also a property of neurons in the brainstem (Angelaki and Dickman, 2000; Dickman and Angelaki, 2002; Chen-Huang and Peterson, 2006), cerebellum (Shaikh et al., 2005; Yakusheva et al., 2008) and thalamus (Meng et al., 2007; Meng and Angelaki, 2010) .
Response phase relative to angular velocity also varied among neurons, but had a unimodal distribution (p<0.05, uniformity test; p_uni>0.05, modality test; Fig. 4F), with a mean of 2.3 ± 4.0° (SE). Thus, the most common responses to rotation were in phase with angular velocity, as is commonly observed for neurons in the brainstem, cerebellum, and thalamus (Dickman and Angelaki, 2002; Shaikh et al., 2005; Meng et al., 2007; Marlinski and McCrea, 2008; Brooks and Cullen, 2009; Meng and Angelaki, 2010).
Responses to 3D transient translation: Temporal modulation
PIVC neurons with audible on-line response modulation during sinusoidal translation or rotation were next tested with a 3D transient translation protocol, consisting of 26 movement trajectories evenly spaced every 45° in 3D (Fig. 5A). Each 2s motion trajectory followed a smooth displacement, with a Gaussian velocity profile and the corresponding biphasic acceleration profile (Fig. 5B). For each movement direction, a peri-stimulus time histogram (PSTH) was computed with a bin size of 50ms. The response plotted for each bin was the average firing rate within a 400 ms sliding window centered on that bin (see Methods). We first describe the patterns of temporal modulation observed in responses of PIVC neurons to these transient translation stimuli.
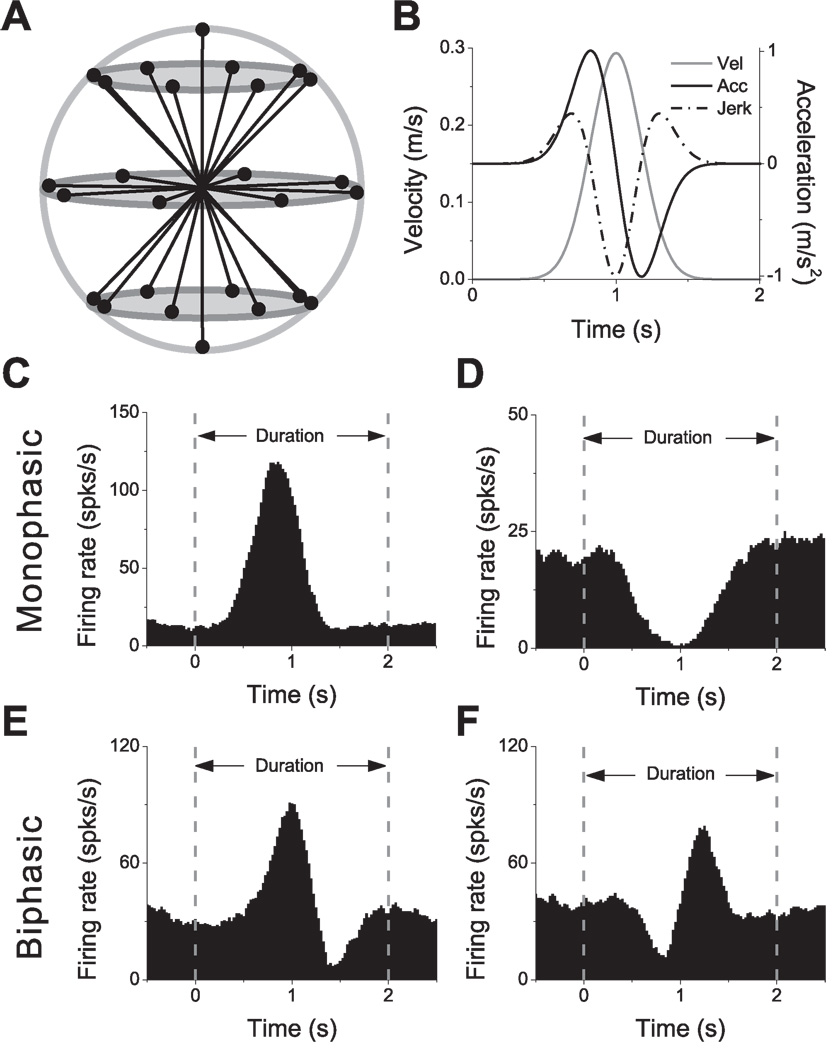
Figure 5.
Transient stimuli and examples of responses. (A) Schematic of the 26 movement trajectories evenly spaced in 3D, 45° apart in both azimuth and elevation. (B) The 2s translational motion stimulus: velocity (gray curve), acceleration (black curve) and jerk (dashed-dot curve). (C), (D) Example average PSTHs with monophasic-positive and monophasic-negative temporal response profiles, respectively. (E), (F) Example average PSTHs with biphasic responses. Dashed lines indicate the onset and offset of the stimulus.
The four most commonly-observed temporal response patterns are illustrated in Fig. 5C–F. The majority of responses were monophasic, having either a single peak (Fig. 5C) or a single trough (Fig. 5D) in the PSTH. Much less frequent were biphasic responses, having a distinct peak and trough within the PSTH (see Fig. 5E and 5F for peak-trough and trough-peak patterns, respectively). Among 288 cells tested with the transient translation protocol, 220 cells had significant monophasic or biphasic responses along a minimum of 2 nearby directions. The remaining 68 neurons were considered non-responsive by the criteria imposed for establishing significant temporal modulation (Methods), and were not considered further in the following analyses.
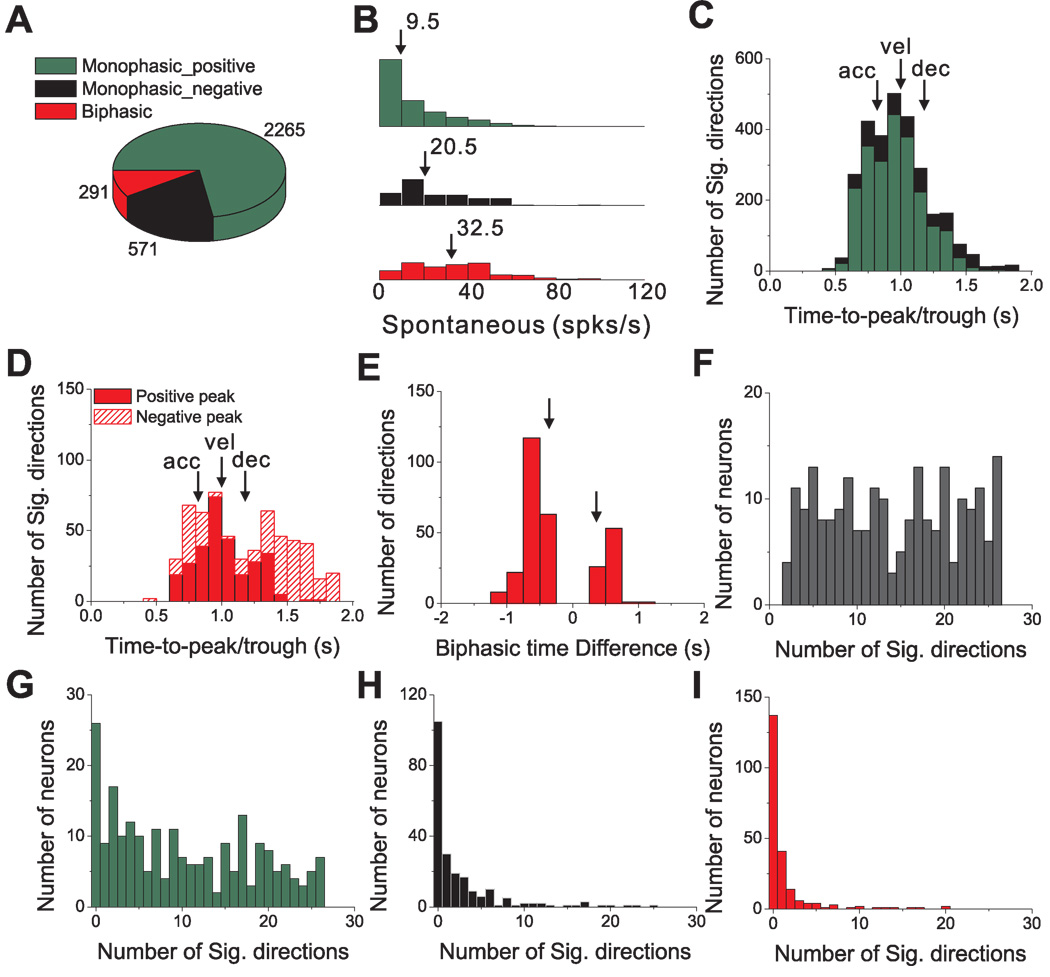
Considering all directions of translation with significant temporal modulation for these 220 cells, the prevalence of different temporal response patterns is summarized in Fig. 6. Nearly three quarters of all responsive directions (72.4%) were of the positive monophasic type, as compared to 18.3% that were negative monophasic, and 9.3% that were biphasic (Fig. 6A). Note that monophasic responses resemble the stimulus velocity profile and biphasic responses resemble the profile of linear acceleration (compare Fig. 5C–F with 5B). Such a correspondence may indeed be expected for cells with high spontaneous firing rates, such as those in the vestibular periphery (Goldberg and Fernandez, 1971), as this allows responses to be driven above and below the resting discharge. Spontaneous activity for PIVC responses, however, is generally much lower than in the vestibular periphery (Fig. 6B). Notably, biphasic and negative monophasic responses (i.e., those with significant decreases in firing rate below baseline) were characterized by higher spontaneous activity (median values of 32.5 spikes/s and 20.5 spikes/s, respectively) than positive monophasic responses (median of 9.5 spikes/s). All pairwise differences between these three groups were statistically significant (p<0.001, Wilcoxon signed-rank test).
Figure 6.
Summary of temporal response modulation during 3D transient translational motion. (A) Prevalence of monophasic positive (green), monophasic negative (black) and biphasic (red) temporal modulation profiles for all responsive motion directions (p<0.01) in 220 cells. (B) Histograms of spontaneous firing rates for monophasic positive, monophasic negative and biphasic responses; differences between groups were statistically significant (p<0.001, Wilcoxon signed-rank test). (C) Distribution of peak latency for monophasic responses. Vertical arrows mark the times of peak stimulus acceleration (‘acc’, at 0.82s), velocity (‘vel’ at 1s) and deceleration (‘dec’, at 1.18s). (D) Distributions of peak response latency for biphasic responses. Red filled bars represent peaks; red hatched bars represent troughs. (E) Distribution of the time difference between the peak and trough of biphasic responses. Vertical arrows mark the corresponding timing differences between peak stimulus acceleration and deceleration. (F) Distribution of the number of stimulus directions that elicit significant responses for each responding cell (n=220). (G)–(I) Distributions of the number of significant response directions, now separated for monophasic-positive (G), monophasic-negative (H) and biphasic (I) response profiles, respectively.
Thus, it is possible that responses of acceleration-sensitive neurons may appear to be positive monophasic because firing rate cannot be driven below an already low spontaneous activity level. Unlike in the vestibular periphery, many cortical neurons cannot faithfully represent a biphasic stimulus due to a response floor. In later sections, we show that spatio-temporal patterns of directional response, not temporal dynamics alone, may be more informative of the type of stimulus parameters encoded by these neurons. Thus, the representation of linear acceleration in PIVC may be more substantial than suggested by the 9% of biphasic responses in Fig. 6A (red).
Next, we examine the distributions of times at which firing rates reached their peak/trough response. The average time to peak/trough firing (relative to the start of the 2s-duration stimulus) was 0.95 s ± 0.01 (mean±SE) for positive monophasic responses and 1.08 s ± 0.01 for negative monophasic responses (Fig. 6C, green and black bars, respectively). These average values were significantly different from the time at which peak stimulus velocity occurred, 1.0 s (p<0.001, Wilcoxon signed rank tests). Indeed, the broad distributions in Fig. 6C suggest that the peak/trough of monophasic PSTHs could occur at the time of peak acceleration (0.82s, denoted by arrow labeled ‘acc’ in Fig. 6C), peak velocity (1s, ‘vel’) or peak deceleration (1.18s, ‘dec’). Thus, monophasic temporal profiles should not necessarily be considered as encoding only stimulus velocity.
The distributions of times of peaks (median=0.98 s) and troughs (median=1.43 s) for biphasic PSTHs were also broad (Fig. 6D, filled and hatched red bars, respectively), illustrating that the peak could occur either before or after the trough, and both peaks and troughs could be aligned to peak stimulus acceleration, velocity, or deceleration (arrows in Fig. 6D). The time difference between the peak and trough of each biphasic response had a much tighter distribution that was significantly bimodal (p_uni<0.01, uniformity test; p_bi=0.59, modality test), with the two modes corresponding to average time differences of −0.62 s ± 0.01 SE and 0.52 s ± 0.01 SE (Fig. 6E). For most (210/291) biphasic responses, the peak occurred before the trough (as in the example of Fig. 5E).
Most PIVC cells showed significant temporal response modulation along multiple motion directions. This is illustrated in Fig. 6F, which plots the distribution of the number of stimulus directions having significant response modulation for each of the 220 responsive cells. Some cells (24/220, 11%) had only a small number (<5) of responsive directions. Others (54/220, 25%) showed significant response modulation along most stimulus directions (>20). In Fig. 6G–I, the distribution of number of significant directions per cell is broken down by the type of temporal modulation. Most cells had many significant directions with positive monophasic responses (median = 9; Fig. 6G). In contrast, most cells had at most a few (and typically zero) significant negative monophasic (Fig. 6H) or biphasic (Fig. 6I) response profiles. The low proportions of negative-going responses per cell is likely due to the relatively low spontaneous rates of PIVC neurons (Fig. 6B). Overall, positive monophasic temporal responses to transient stimuli were predominant, with a range of peak response times relative to stimulus velocity and acceleration.
Responses to 3D transient translation: Dynamics of 3D direction tuning
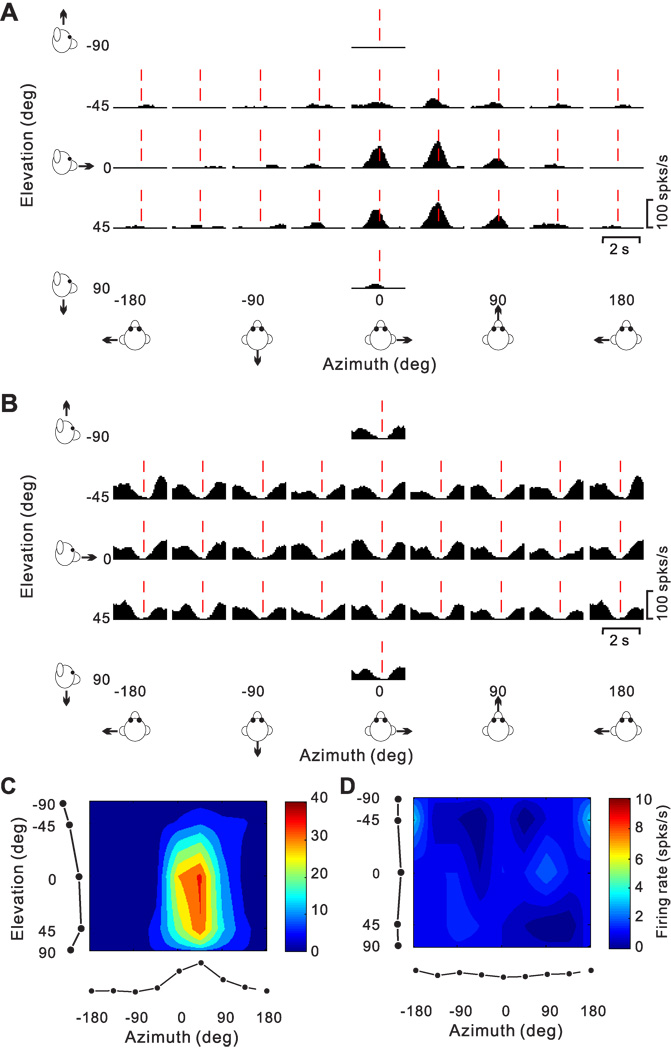
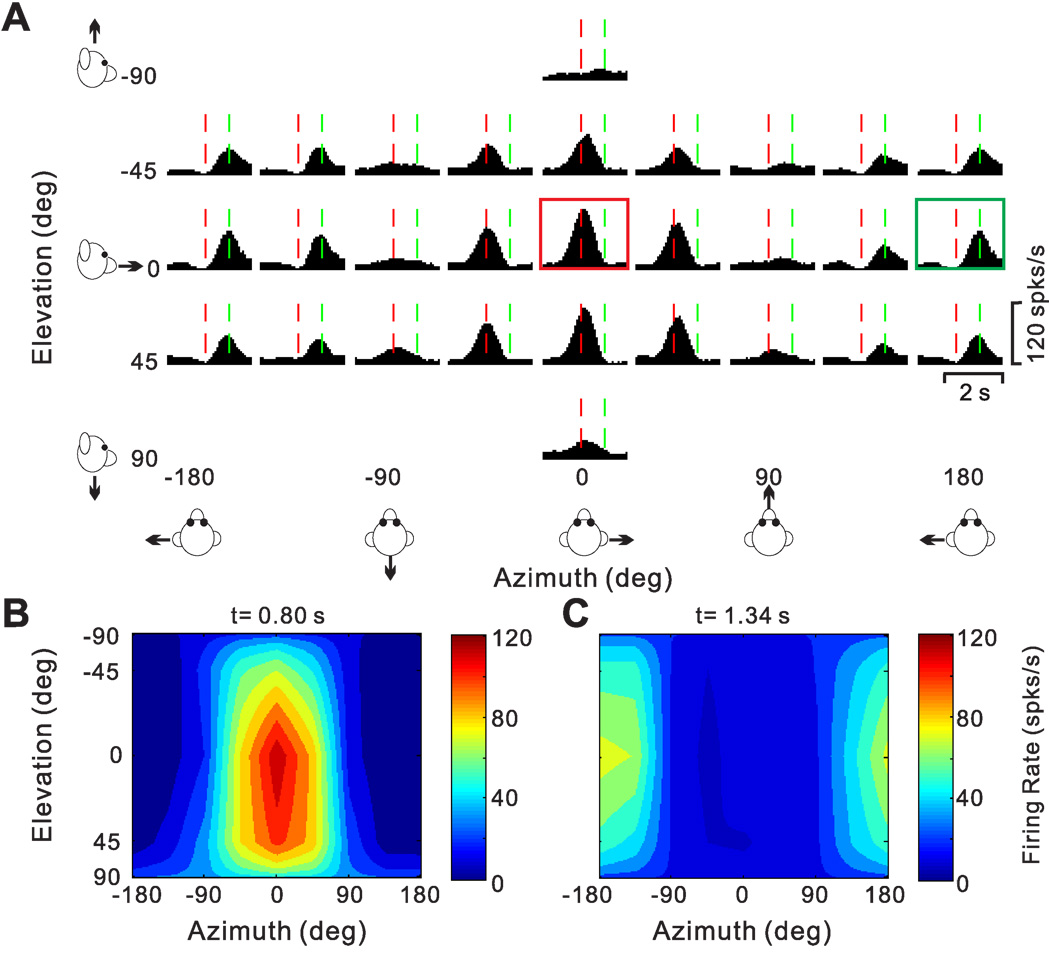
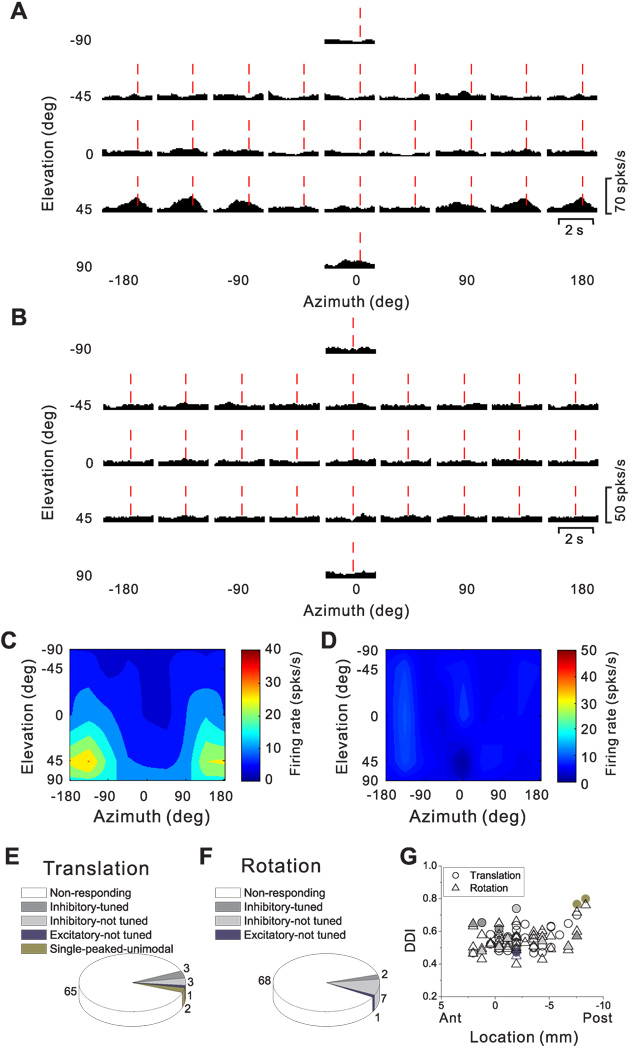
We now consider the pattern of temporal responses across all stimulus directions, to characterize how directional tuning changes with time during the response. We start with a few examples that illustrate the range of spatio-temporal response patterns observed across the population. Fig. 7A,B show the average PSTHs of two example cells for all 26 directions of translation, where each PSTH corresponds to a particular stimulus direction [azimuth, elevation] in spherical coordinates. The cell of Fig. 7A responds significantly to only 8 motion directions, 7 of which are monophasic-positive and 1 monophasic-negative. Red dashed lines show the peak response time for this neuron (see Methods), which is defined as the 25ms time bin at the center of the 400 ms time window that produces the largest departure in firing rate from the baseline response (peak time = 0.94 s for the cell of Fig. 7A).
Figure 7.
Responses of two PIVC neurons to 26 directions of transient translational motion. Azimuth and elevation are defined as in Fig. 4. (A) Average response PSTHs for a single-peaked neuron. Vertical dashed red lines indicate the peak time (0.94 s) when the maximum response across directions occurred. (B) Average response PSTHs for a neuron with inhibitory responses. Vertical dashed red lines indicate the peak time (1.2 s) when the minimum response across directions occurred. (C) Color contour map showing 3D directional tuning (Lambert cylindrical projection) at peak time for the cell in A (DDI=0.77). Tuning curves along the margins of the color map illustrate mean firing rates plotted versus elevation or azimuth (averaged across azimuth or elevation, respectively). (D) Color contour map showing spatial tuning at peak time of the inhibitory neuron in B; the cell was not significantly direction–selective at the peak time (shown) nor at any other time during the 2s duration of the motion stimulus.
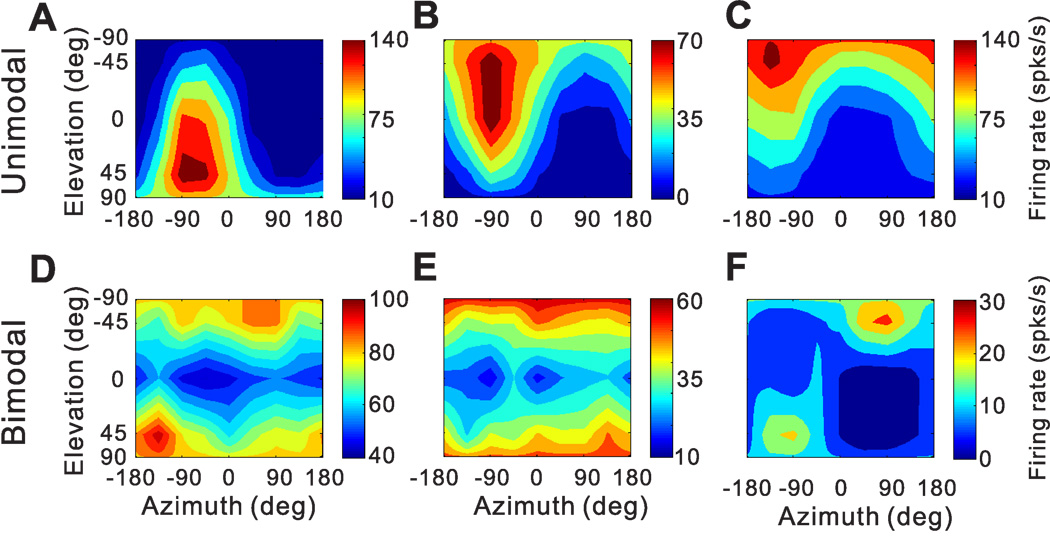
The 3D directional tuning of this neuron, computed at the peak time, is shown as a color contour map in Fig. 7C. In this map, mean firing rate (represented by color) is plotted as a function of azimuth and elevation. This cell was significantly tuned for direction of translation (ANOVA, p<0.001) and exhibited broad tuning with a preferred direction (computed from the vector sum) at 39° azimuth and 23° elevation, corresponding to a rightward and slightly downward motion trajectory. We refer to neurons with this type of spatiotemporal tuning as ‘single-peaked’ cells
Fig. 7B shows PSTHs for a PIVC cell with responses that were consistently suppressed for most (20/26, p<0.01) directions of translation. This cell did not show significant directional tuning (Fig. 7D), either at peak time (in this case, the time of minimum firing rate) or at any other time during the 2 s motion profile. We refer to this type of neuron as ‘inhibitory, not-tuned’.
Additional examples of cells with significant 3D directional tuning at peak time (ANOVA, p<0.01) are shown in Fig. 8. As illustrated by the examples in Fig. 8 A–C, many cells showed unimodal directional tuning; i.e., their direction tuning profile had a single peak, which could be quantified by the vector sum of responses. However, other cells with significant tuning had bimodal direction tuning profiles (Fig. 8D–F). Overall, we encountered 40/220 of these single-peaked cells with bimodal direction tuning. These cells respond maximally to two motion directions, typically 180° apart. As such, we did not attempt to quantify their directional preferences using the vector sum approach.
Figure 8.
3D translational direction tuning for six example neurons with (A–C) unimodal and (D–F) bimodal spatial tuning. Preferred directions (computed by vector sum) were [azimuth, elevation] = [−60.3°, 36.0°], [−82.4°, −43.4°] and [−138.2°, −63.2°] for the unimodal cells in A–C, respectively (DDI = 0.88, 0.86 and 0.88, respectively). The corresponding DDIs for the bimodal cells in D–F were 0.64, 0.65, and 0.79.
As described below, we frequently observed cells with two opposite directional preferences at different times. A potential concern is that spatially bimodal cells (Fig. 8D–F) might be an artifact of computing direction tuning using a 400ms time window. Thus, we also computed directional tuning using smaller time windows (100 and 200 ms), but found that most single-peaked-bimodal cells (34/40) retained bimodal direction tuning using the smaller time bins. Thus, we conclude that single-peaked bimodal cells are a genuine class of PIVC neurons having two direction preferences that occur simultaneously in time.
As alluded to above, many PIVC neurons showed different directional tuning at different times during the response. Fig. 9 illustrates an example of this type of spatiotemporal tuning. This neuron responded significantly to 22/26 motion directions, including 20 monophasic-positive responses and 2 biphasic responses. The peak time was 0.80 s (vertical red dashed lines), corresponding to the response maximum at [azimuth, elevation] = [0°, 0°] (Fig. 9A, red box). The 3D directional tuning of this cell at the peak time of 0.80 s is nicely unimodal (Fig. 9B). Closer inspection of the PSTHs in Fig. 9A shows, however, that some of the PSTHs have a clear response maximum later in time (e.g., green box in Fig. 9A, peak at 1.34 s). This pattern is mainly seen for motion directions around [azimuth, elevation] = [180°, 0°]. When the 3D direction tuning is computed from responses centered on the time bin at 1.34 s, a completely different tuning profile emerges (Fig. 9C). Whereas the early responses (0.80 s bin) have a direction preference (computed by vector sum) at an azimuth of −2.8° and an elevation of 14.4° (Fig. 9B), the direction preference of the late responses is shifted by approximately 180° to an azimuth of −175.7° and an elevation of −2.6° (Fig. 9C). The difference in 3D direction preference between the two time windows for this cell was 166.3°.
Figure 9.
Spatiotemporal responses for a double-peaked neuron. (A) Average PSTHs for each of 26 directions of translation. The PSTH in the red square illustrates the first response peak occurring at t = 0.80s (vertical red lines); the PSTH in the green square illustrates a second response peak occurring at t=1.34 s (vertical green lines). (B), (C) Color contour maps showing the 3D tuning at the two peak times indicated in A. The tuning for the first peak (red square in A) is shown in B, with a direction preference at azimuth −2.8° and elevation 14.4° (DDI=0.92). The tuning for the second peak (green square in A) is shown in C, with a direction preference at azimuth −175.7° and elevation −2.6° (DDI=0.86). The difference in direction preference between the two peaks is 166°.
Note that the two peaks of directional tuning in Fig. 9 occur earlier (0.80 s) and later (1.34 s) than the time at which stimulus velocity peaks (1 s), and closer to the times of peak and trough acceleration (0.82 and 1.18 s, respectively, Fig. 5B). Thus, although the response PSTHs of this neuron were mostly monophasic positive, rather than biphasic, this cell’s spatio-temporal response profile appears more consistent with coding of acceleration/deceleration than stimulus velocity. This conclusion is further reinforced by the ~180° spatial change in preferred direction between the two peaks, as acceleration-related responses would be expected to reverse sign on opposite sides of the peak velocity. We call cells such as the one in Fig 9 “double-peaked”, to distinguish them from the single-peaked cells in Fig. 7A and Fig. 8. Note that, unlike single-peaked bimodal cells, where the two opposite directional preferences occur simultaneously in time (i.e., within <25 ms of each other), the two directional peaks of double-peaked cells are distinct in time, and thus can be independently quantified.
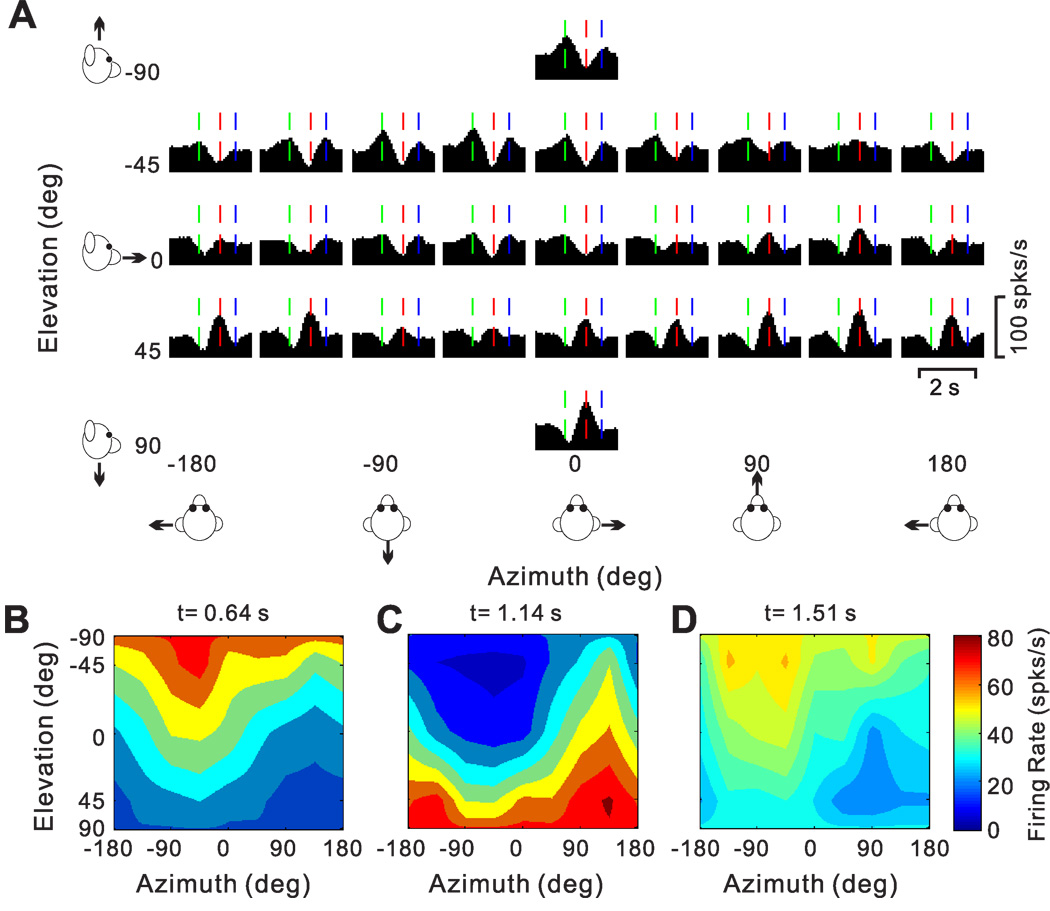
A handful of cells were characterized by 3 distinct temporal peaks of directional selectivity. The PSTHs of one such “triple-peaked” cell, which had 12 monophasic-negative and 10 biphasic response directions, are illustrated in Fig. 10A. Three times with distinct spatial tuning were identified, occurring at 0.64 s (vertical green lines), 1.14s (vertical red lines) and 1.51s (vertical blue lines). The corresponding 3D directional tuning profiles for each of these times are shown in Fig. 10B (direction preference at azimuth=−50.7° and elevation=−67.1°), Fig. 10C (preference at azimuth=124.6° and elevation= 60.1°) and Fig. 10D (preference at azimuth=−73.3° and elevation=−58.7°), respectively. Note that the directional tuning for the second peak has a preference that is ~180° away from the direction preferences of first and last peak times. The spatio-temporal profile of such triple-peaked cells may be consistent with coding the derivative of linear acceleration (jerk; see below).
Figure 10.
Responses of a triple-peaked neuron. (A) Average PSTHs for the 26 motion directions. Green, red and blue vertical lines mark three distinct peak times. (B), (C), (D) Color contour maps showing 3D tuning at the three peak times in A. Preferred directions were [azimuth, elevation]: [−50.7°, −67.1°] (B), [124.6°, 60.1°] (C) and [−73.3°, −58.7°] (D). The corresponding DDI values were 0.83, 0.77 and 0.75, respectively.
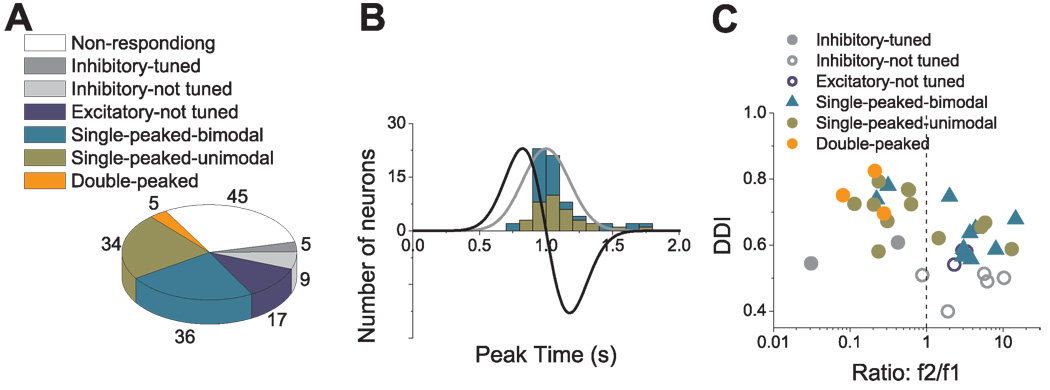
The frequency of occurrence of each cell type is summarized in Fig. 11A. There were a total of 31 inhibitory cells (31/220, 14.1%), 20 with directional tuning (ANOVA, p<0.01) and 11 cells that were not tuned at any time during motion (Fig. 11A, dark and light gray, respectively). The remaining 189 cells had excitatory responses along at least two nearby directions and have been subdivided as follows: 105 cells (48% of the 220 responsive neurons) were single-peaked, 69 cells (31.4%) were double-peaked, and 4 cells (1.8%) were triple-peaked (Fig. 11A). Finally, 11 of the excitatory cells were not significantly tuned (ANOVA, p>0.01) at any time during the motion profile (Fig. 11A, dark blue).
Cells with significant directional tuning (ANOVA, p<0.01) were further subdivided based on whether the spatial tuning was unimodal (e.g., Fig. 7A, Fig. 8A–C, Fig. 9 and Fig. 10) or bimodal (Fig. 8D–F) (see Methods). For single-peaked cells, more than half (65/105, 62%) were unimodal (Fig. 11A, green), whereas the remainder (40/105, 38%) were bimodal. Nearly all double-peaked cells (66/69) showed unimodal spatial tuning during at least one peak of directional tuning, and 84% (58/69) showed unimodal directional tuning for both peak times. With the exception of the first peak for one cell, all triple-peaked cells showed unimodal direction tuning. Because of the low incidence of bimodal directional tuning, double-peaked and triple-peaked cells were not further subdivided in the chart of Fig. 11A.
For double-peaked cells, we measured the change in preferred direction as the difference between the two distinct peaks of 3D spatial tuning. As for the example cell of Fig. 9, the two peaks of spatial tuning for all double-peaked cells were opposite in direction (Fig. 11B). On average, the change in direction was 159.5 ± 1.5° (SE), indicating that most cells show a complete direction reversal. These two peaks of directional tuning are generally not of equal strength, as illustrated by the fact that most data points fall below the diagonal in the scatter plot of the respective Direction Discrimination Indices (DDI; Fig. 11C). The DDI of the early peak was significantly greater (meaning stronger direction selectivity) than that of the later peak (Wilcoxon rank test, p<0.001), with DDI values averaging 0.79 ± 0.01 (SE) and 0.75 ± 0.01 (SE), respectively. Another measure of tuning strength, the magnitude of the vector sum, gave similar results, with average values of 299.8 ± 24 (SE) spikes/s/G for the early peak and 183.8 ± 14 (SE) spikes/s/G for the late peak (p<0.001, Wilcoxon rank test; data not shown).
Fig. 11D, E and F summarize the times of peak directional tuning for single-peaked, double-peaked and triple-peaked cells (see also Table 3). The peak time of single-peaked cells averaged 0.98 s ± 0.02 (SE) for unimodal cells (Fig. 11D, cyan, n=65) and 0.99 s ± 0.02 (SE) for bimodal cells (Fig. 11D, green, n=40); this difference was not significant (p=0.81, Wilcoxon rank test). Moreover, the average peak time for single-peaked cells does not differ significantly from the time of peak stimulus velocity (1s) (p>0.05, Wilcoxon rank test) and occurs significantly later than peak acceleration (0.82 s) (p<0.001, Wilcoxon rank test). The average duration of each period of directional tuning was 0.62 s ± 0.03 (SE) and 0.52 s ± 0.03 (SE) for unimodal and bimodal cells, respectively (Table 3).
Table 3.
Summary of peak time and spatial peak duration
| Translation | Peak Time | Peak Duration | |||
|---|---|---|---|---|---|
| Mean (s) ± SE | Range (s) | Mean (s) ± SE | Range (s) | ||
|
Single-peaked (n=105) |
Unimodal (n=65) | 0.98 ± 0.02 | 0.63 ~ 1.41 | 0.62 ± 0.03 | 0.18 ~ 1.45 |
| Bimodal (n=40) | 0.99 ± 0.02 | 0.66 ~ 1.31 | 0.52 ± 0.03 | 0.25 ~ 0.85 | |
|
Double- peaked (n=69) |
First peak | 0.79 ± 0.01 | 0.66 ~ 1.31 | 0.63 ± 0.01 | 0.35 ~ 0.92 |
| Second peak | 1.27 ± 0.01 | 1.06 ~ 1.58 | 0.56 ± 0.02 | 0.22 ~ 0.90 | |
|
Triple-peaked (n=4) |
First peak | 0.65 ± 0.02 | 0.61 ~ 0.69 | 0.50 ± 0.02 | 0.45 ~ 0.55 |
| Second peak | 1.12 ± 0.02 | 1.08 ~ 1.16 | 0.48 ± 0.04 | 0.38 ~ 0.55 | |
| Third peak | 1.50 ± 0.03 | 1.46 ~ 1.58 | 0.41 ± 0.06 | 0.32 ~ 0.60 | |
| Rotation | Peak Time | Peak Duration | |||
| Mean (s) ± SE | Range (s) | Mean (s) ± SE | Range (s) | ||
| Single-peaked, bimodal (n=36) | 1.08 ± 0.04 | 0.78 ~ 1.34 | 0.46 ± 0.04 | 0.18 ~ 0.72 | |
| Single-peaked, unimodal (n=34) | 1.09 ± 0.03 | 0.81 ~ 1.74 | 0.61 ± 0.04 | 0.28 ~ 1.32 | |
Fig. 11E shows the distribution of the two peak times for double-peaked cells. Average values of the early and late peak times were 0.79 s ± 0.01 (SE) (filled orange bars) and 1.27 s ± 0.01 (SE) (hatched orange bars), respectively. These values are close to, but significantly different from (p=0.009 and p<0.001, respectively; Willcoxon rank test), the times of peak acceleration and deceleration (0.82 s and 1.18 s, respectively; Fig. 11E, black curve). For double-peaked cells, the shift in direction preference was rapid: the time difference between the end of the first period of directional tuning and the beginning of the second period averaged 54.0 ms ± 5.3 SE (range: 25–300 ms).
For triple-peaked cells (Fig. 11F), the peak times were on average 0.65 s ± 0.03 (SE) (hatched red bars), 1.12 s ± 0.03 (SE) (filled red bars), and 1.50 s ± 0.03 (SE) (open red bars). By comparison, the three peaks of the derivative of linear acceleration (jerk) occurred at 0.69 s, 1s and 1.31 s (Fig. 11F, dash-dot line). The shifts between peaks of directional tuning were also rapid for triple-peaked cells, with the average times for the two direction reversals being 58.3 ms ( 8.3 (SE) and 41.7 ms ( 8.3 (SE), respectively. Thus, the pattern of reversals in direction preference and the timing of the multiple peaks of spatial tuning suggest that single-peaked responses are most closely related to velocity, whereas double-peaked cells carry information about acceleration/deceleration, and triple-peaked cells likely relate to the jerk of the movement. These results suggest a coding scheme that differs substantially from that seen in the vestibular periphery—acceleration and jerk may be represented in the temporal sequence of periods of directional selectivity rather than in the shape of the temporal response profile (PSTH) itself.
Relationship between sinusoidal and transient translation responses
The findings of second-harmonic cells during sinusoidal oscillations and cells with multiple periods of directional tuning during transient displacements raise the question of whether the two observations are related. More specifically, is it the double/triple-peaked cells, the bimodal singled-peaked cells or the spatially-untuned cells that exhibit second harmonic modulation? Fig. 12A,B,E and 12C,D,F show two typical example cells, comparing the sinusoidal and transient data. The example cell in Fig. 12A, B, E is dominated by first harmonic modulation during 0.5Hz sinusoidal translation (Fig. 12A) and was classified as double-peaked during transient translation (Fig. 12B). This cell’s 3D translation tuning (shown for the second peak time, as marked by vertical red dashed lines in Fig. 12B) is unimodal, with a preference for vertical translation (Fig. 12E). Note that the presence of multiple peaks of directional tuning does not result in second harmonic sinusoidal modulation, as long as the peaks are discrete in time (double-peaked cells). In contrast, the cell in Fig. 12C, D, F is dominated by second harmonic modulation and is characterized by a single temporal peak of directional tuning with a bimodal spatial tuning profile.
Figure 12.
Examples of cells with first harmonic (A, B, E) and second harmonic (C, D, F) responses, as tested during both sinusoidal and 3D transient translation protocols. (A) Average response PSTHs of a double-peaked cell during sinusoidal translation (0.5 Hz); the cell modulated during fore-aft (198.4 spikes/s/G, p_f1<0.01, p_f2>0.01, f2/f1=0.2, middle) and up-down (250 spikes/s/G, p_f1<0.01, p_f2>0.01, f2/f1=0.4, right), but not lateral motion (p_f1>0.01, p_f2>0.01, left). Hacc: Head acceleration. (B) Average response PSTHs during transient translation of the same double-peaked cell; red lines indicate the second peak time (1.2 s) when the maximum response across all directions occurred. (C) Average PSTHs of a second harmonic cell, responding to all directions of sinusoidal translation, lateral (p_f1>0.01, p_f2<0.01, f2/f1=4.9), fore-aft (p_f1>0.01, p_f2<0.01, f2/f1=4.6), and up-down (p_f1>0.01, p_f2<0.01, f2/f1=3.1). (D) Average response PSTHs for transient stimuli, showing significant temporal modulation along most (21/26) directions. Vertical red lines illustrate peak time (0.96 s). (E) Color contour map showing 3D tuning for the second peak time (DDI=0.84) for the cell shown in A, B. The cell’s tuning was unimodal (p_uni>0.05, modality test), with a preferred direction at azimuth −83.9° and elevation 76.9°.The spatial tuning for the first peak time (not shown) was also unimodal (DDI=0.78), with a preferred direction at azimuth 11.6° and elevation −53.8°. (F) Color contour map showing 3D spatial tuning at peak time for the 2nd harmonic cell shown in C, D; tuning was spatially bimodal (DDI=0.72).
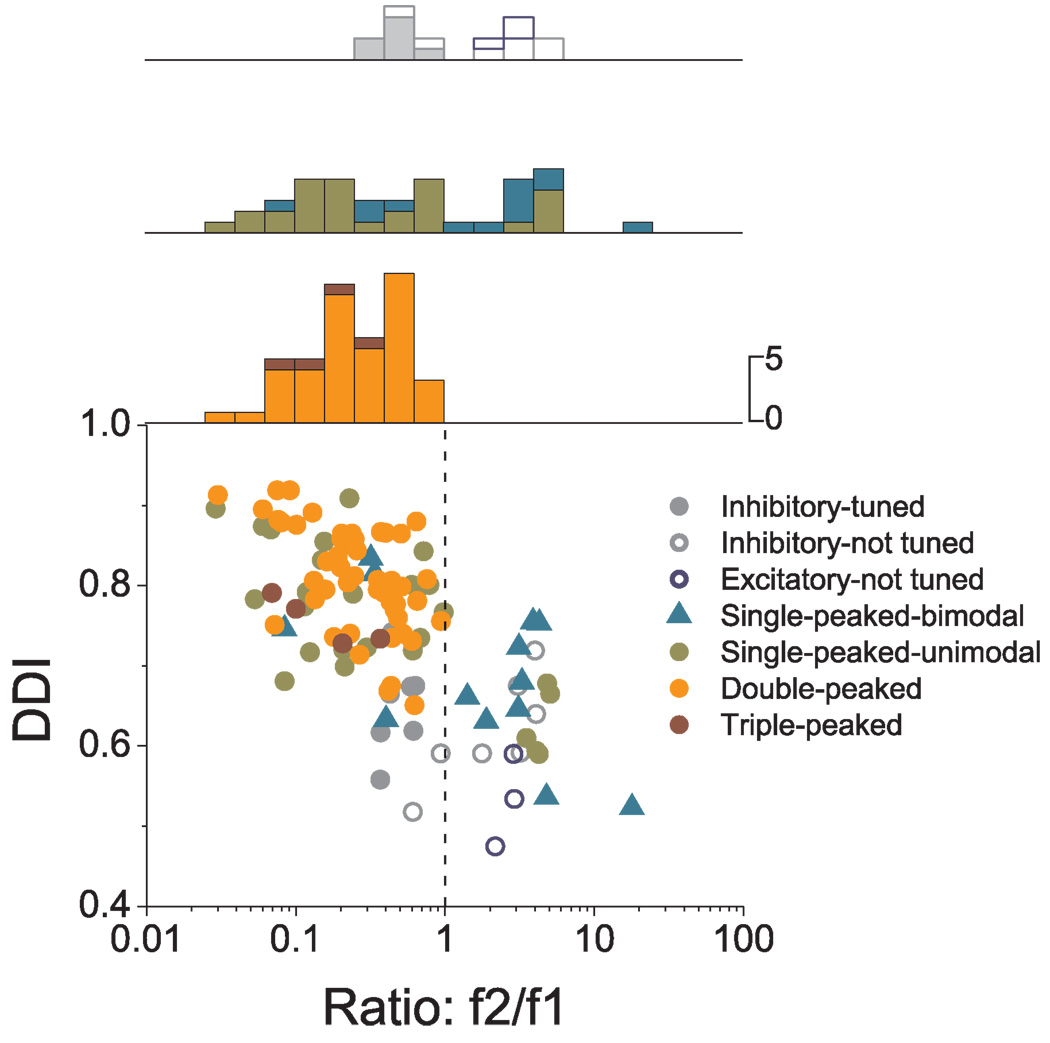
Fig. 13 summarizes these relationships for all cells with significant modulation under both conditions (see also Table 4). There is a robust negative correlation between tuning strength during transient motion (measured with DDI) and the second harmonic distortion (ratio f2/f1) (R= −0.68, p<0.001). In addition, there is a clear tendency for double-peaked, triple-peaked and single-peaked-unimodal cells to be characterized by f2/f1 ratios that are less than unity. In contrast, single-peaked-bimodal and untuned cells tend to be characterized by f2/f1>1 (Fig. 13; see also Table 4 for details).
Figure 13.
Comparison between sinusoidal responses (f2/f1 ratio) and 3D tuning (DDI). Each point in the scatter plot corresponds to one cell, and symbol shape/color reflects its classification as inhibitory (tuned or not tuned, filled or open gray circles, respectively), excitatory but not tuned (open blue circles), excitatory single-peaked (bimodal/unimodal, cyan triangles/green circles), double-peaked (orange circles), or triple-peaked (red circles). The top panels show the distribution of f2/f1 ratios for inhibitory (tuned and not tuned; gray bars) and excitatory not tuned cells (top histogram; blue bars), single-peaked cells (middle histogram; cyan and green bars), and double-peaked and triple-peaked cells (bottom histograms; orange and red bars, respectively).
Table 4.
Summary of sinusoidal responses (f2/f1 ratio) and 3D tuning (DDI) of different cell group
| Translation |
DDI (mean ± SE ) |
f2/f1 ratio (geometric mean ± SE) |
||
|---|---|---|---|---|
|
Inhibitory |
Not-Tuned (n=7) | 0.62 ± 0.02 | 2.07 ± 0.76 | |
| Tuned (n=7) | 0.65 ± 0.02 | 0.48 ± 0.47 | ||
|
Excitatory |
Not-Tuned (n=3) | 0.53 ± 0.03 | 2.63 ± 0.66 | |
|
Single- peaked |
Bimodal (n=28) | 0.69 ± 0.03 | 1.60 ± 1.14 | |
| Unimodal (n=13) | 0.76 ± 0.02 | 0.48 ± 0.47 | ||
| Double-peaked (n=49) | 0.81 ± 0.01 | 0.25 ± 0.30 | ||
| Triple-peaked (n=4) | 0.76 ± 0.02 | 0.15 ± 0.95 | ||
|
Rotation |
DDI (mean ± SE ) |
f2/f1 ratio (geometric mean ± SE) |
||
|
Inhibitory |
Not-Tuned (n=5) | 0.48 ± 0.02 | 3.59 ± 1.09 | |
| Tuned (n=2) | 0.58 ± 0.03 | 0.11 ± 0.47 | ||
|
Excitatory |
Not-Tuned (n=3) | 0.57 ± 0.01 | 2.81 ± 0.67 | |
|
Single- peaked |
Bimodal (n=10) | 0.65 ± 0.03 | 2.49 ± 1.09 | |
| Unimodal (n=12) | 0.69 ± 0.02 | 0.48 ± 0.47 | ||
| Double-peaked (n=3) | 0.76 ± 0.04 | 0.17 ± 0.98 | ||
Recall that the f2/f1 ratio depended on cell location within the lateral sulcus: upper bank cells had smaller ratios than lower bank cells, and there was a weak tendency for medially-located cells to have smaller f2/f1 ratios (Fig. 3). Here we also examine the relationship between tuning strength and cell location, and this comparison is done for both the right hemisphere of monkey J and the left hemisphere of monkey U, both of which were extensively explored (Fig. 14). In agreement with the sinusoidal results, cells in the upper bank had a larger average DDI value (0.73 ± 0.01 SE, n=104) than those in the lower bank (0.62 ± 0.01 SE, n=111), and this difference was significant (p<0.001, Wilcoxon rank test, data pooled across animals). In addition, there was a significant correlation between DDI and the medial-lateral coordinates (monkey J: r= −0.46, p<0.001, Fig. 14A; monkey U: r= 0.16, p=0.07, Fig. 14C); medial cells were more strongly tuned than lateral cells. No such relationship was seen along the anterior-posterior dimension (monkey J: r= −0.08, p=0.39, Fig. 14B; monkey U: r= 0.04, p= 0.62, Fig. 14D). Note that, because of differences in placement of the recording grid, the anterior/posterior extent of the recordings was different in animals J and U. The most anterior parts of the lateral sulcus (coordinates 2 to 5 mm) were only explored in animal J, whereas the most posterior parts of the lateral sulcus (coordinates −4 to −8 mm) were only explored in monkey U. Nevertheless, the majority of the data were collected more centrally in the lateral sulcus within an area that overlapped in the two monkeys.
Figure 14.
Relationship between tuning strength, as measured by DDI, and cell location within the lateral sulcus. Scatter plots of DDI (measured at the time when the maximum response across directions occurred) as a function of (A, C) medial-lateral and (B, D) anterior-posterior stereotaxic coordinates (shown in mm) for cells recorded in the right hemisphere (RH) of monkey J (top, n=113) and the left hemisphere (LH) of monkey U (bottom, n=122). To make the data more comparable between the two monkeys, the medial-lateral coordinates on the x-axis for monkey U (C) were reversed to run from positive to negative. Because of differences in placement of the recording grid, the anterior/posterior extent of the recordings was slightly different in animals J and U. Red symbols: upper bank; green symbols: tip; blue symbols: lower bank cells. Filled symbols indicate cells with significant spatial tuning during translation (ANOVA, p<0.01). Open symbols denote cells that were either not spatially tuned (ANOVA, p>0.01) or did not pass the criterion for significant temporal modulation.
Responses to 3D transient rotation
Whenever cell isolation was maintained after the 3D transient translation protocol was completed, neurons were further tested with 3D transient rotations (see Methods). Results are summarized in Fig. 15. Among 151 cells tested with the transient rotation protocol, 106 cells passed the criterion for significant temporal modulation (see Methods). As illustrated in Fig. 15A, most cells (70/106, 66.0%) were single-peaked (unimodal or bimodal, in roughly equal numbers), 5 (4.7%) were double-peaked, 14 (13.2%) were inhibited, and 17 (16.0%) were excitatory but not significantly tuned. The peak times for unimodal and bimodal single-peaked cells averaged 1.09 s ± 0.03 (SE) and 1.08 s ± 0.04 (SE), respectively (Fig. 15B), which were not significantly different from the time of peak stimulus velocity (p>= 0.02, Wilcoxon signed rank test). The distribution of peak times is not shown for double-peaked cells due to the small number of neurons; but see Table 3). Finally, similar to translation, unimodal single-peaked and double-peaked cells were generally characterized by single harmonic modulation, while the single-peaked-bimodal and untuned cells showed second harmonic modulation in response to sinusoids (Fig. 15C and Table 4).
Figure 15.
Population summary of the spatio-temporal responses to 3D rotation. (A) Classification of responsive cells (n=106). (B) Distribution of the peak times for single-peaked cells. Green bars: cells with unimodal spatial tuning (n=34); cyan bars: cells with bimodal spatial tuning (n=36). (C) Scatter plot of tuning strength (DDI at peak time) during transient rotation versus the f2/f1 ratio from sinusoidal rotation responses. Each point in the scatter plot corresponds to a cell, and symbol shape/color reflects its classification as inhibitory (tuned or not tuned, filled or open gray circles, respectively), excitatory but not tuned (open blue circles), excitatory single-peaked (bimodal/unimodal, cyan triangles/green circles), or double-peaked (orange circles).
Similar to translation tuning, cells recorded from the upper bank had higher DDI values for rotation (mean±SE: 0.64 ± 0.02, n=35) than cells recorded from the lower bank (0.60 ± 0.02, n=77) (p<0.001, Wilcoxon rank test). Cells recorded from the tip of the lateral sulcus (n=39) had a mean DDI value 0.60 ± 0.02 SE. For the right hemisphere of monkey J, there was a significant correlation between rotational DDI values and medial-lateral coordinates (r=−0.29, p=0.01), such that tuning strength was greater medially. This relationship was not significant for the left hemisphere of monkey U and there was no correlation for either animal along the anterior/posterior dimension (p>0.05).
Relationship between rotation and translation tuning
A subset of cells was tested with both the rotation and translation protocols, thus allowing a direct comparison between rotation and translation selectivity. For 92 cells with significant single harmonic modulation for both translation and rotation using 0.5 Hz sinusoidal motion, there was a clear tendency for translation and rotation direction preferences to differ by ~ 90°. This was true when considering either the azimuth component of the preferred direction (Fig. 16A) or the difference in the corresponding 3D preferred directions (Fig. 16B). Specifically, the distribution of azimuth difference between rotation and translation was bimodal (p<0.001, uniformity test; p_uni=0.006; p_bi=0.72, bimodality test) and clustered around ± 90° (Fig.16A, marginal distribution along the diagonal). For example, cells that prefer left-right translation (0° or ±180°, abscissa in Fig. 16A) also prefer roll rotation (±90°, ordinate in Fig. 16A). Similarly, cells that prefer forward/backward translation (±90°) tend to prefer pitch rotation (0° or ±180°). These relationships persist in 3D, where the absolute difference in 3D direction preference between rotation and translation (now expressed in the interval [0°, 180°]) was not uniformly distributed (p<0.001, uniformity test), but was rather unimodal (p_uni=0.91, modality test), with a mean of 86.2° ± 2.9 (SE) (Fig. 16B).
Figure 16.
Comparison of direction preferences between translation and rotation. (A), (C) Scatter plots comparing azimuth preferences for rotation and translation, shown for sinusoidal (n=92) and transient (n=35) responses, respectively. Solid and dashed lines illustrate 0° and ±90° differences between the preferred directions, respectively. Marginal distributions along the diagonal show the difference in preferred azimuth between translation and rotation. (B), (D) Histograms of the absolute differences in 3D direction preference between rotation and translation for sinusoidal and transient responses, respectively. For double-peaked or triple-peaked cells, preferred direction was calculated at the peak time that yielded the strongest spatial tuning. Data are shown only for cells with significant single harmonic modulation (A, B) or significant unimodal spatial tuning (C, D) for both translation and rotation.
Qualitatively similar results were observed using the 3D transient protocols. For 35 cells with significant temporal modulation and unimodal tuning under both the transient translation and rotation protocols, there was a tendency for translation and rotation preferences to differ by ~90° (Fig. 16C), although the distribution of differences in azimuth preferences was not significantly different from uniform (p=0.25, uniformity test). The difference in 3D direction preferences was, on average, 90.2° ± 5.4 (SE), and the distribution was unimodal and significantly non-uniform (p<0.001, uniformity test; p_uni=0.18, modality test). These results suggest that rotation and translation preferences in PIVC are spatially coordinated such that each cell preferring a given translation direction also responds maximally to rotations about an axis that is roughly perpendicular to the translation preference. This relationship is not typically seen for thalamus (Meng et al., 2007) and vestibular nuclei neurons in the macaque (Dickman and Angelaki, 2002; Bryan and Angelaki, 2009), but has been reported for vestibular nuclei neurons in the rat (Angelaki et al., 1993; Bush et al., 1993).
Comparison of responses during free viewing in darkness versus fixation
To examine whether eye movement conditions modulate the basic response properties of PIVC neurons, a subpopulation of cells (n=41 for translation, n=31 for rotation) were tested under both a visual fixation condition in which animals suppressed their vestibulo-ocular reflex (VOR) and a free viewing condition in complete darkness during which animals generated VOR-induced eye movements. Results are compared in Fig. 17. Peak-to-trough response modulation (Rmax-Rmin) in darkness was not significantly different from that during fixation (Fig 17A, p=0.81; Fig. 17B, p=0.40, Wilcoxon signed-rank test). However, tuning strength at peak time, as measured with DDI, was modestly but significantly lower in darkness than during fixation (p<0.001, Wilcoxon rank test) for both translation (Fig. 17C) and rotation (Fig. 17D). This occurs because response variability is larger in darkness than during fixation (p<0.001, Wilcoxon signed-rank test) and the DDI measure incorporates variability.
Finally, differences in direction preference between the fixation and darkness conditions were small for cells that were significantly tuned under both conditions (median direction difference: 12.2° for translation, Fig. 17E; and 17.8° for rotation, Fig. 17F). Thus, PIVC responses to vestibular stimuli have similar response modulation and directional preferences between fixation and darkness, although responses are more variable in darkness leading to greater DDI values in the fixation condition. These results suggest that rotation and translation responses mainly arise from vestibular (and/or somatosensory) cues rather than VOR suppression or pursuit-like signals. It should be noted, however, that the greater response variability during free viewing in darkness might result from eye movement signals in PIVC.
Responses to translational and rotational optic flow
For a subpopulation of PIVC neurons (n=74 for translation, n=79 for rotation), we also measured responses to optic flow using an experimental protocol in which the same set of directions of translation or rotation were simulated using optic flow (see Methods and Gu et al., 2006; Takahashi et al., 2007). Data from two example neurons are shown in Fig. 18. The cell in Fig. 18A,C is one of only two neurons that exhibited significant temporal modulation and direction tuning in response to transient translations simulated by optic flow, preferring downward and leftward movements (azimuth= −171.6°, elevation= 54.6°). The cell in Fig. 18B, D was more characteristic of the population in that it did not show any significant response to optic flow simulating translation, although it showed robust vestibular modulation (same cell as in Fig. 12A, B, E).
Figure 18.
PIVC neurons are generally unresponsive to optic flow. (A)–(D) Example PSTHs and direction tuning profiles for two cells, one that responded selectively to optic flow during the visual translation protocol (A, C; same cell as in Fig.12A, B, E) and another that did not show any response to optic flow (B, D; same cell as in Fig. 12C, D, F). Vertical red dashed lines indicate the respective peak times (1.3 s and 1.1 s, respectively). The cell in A,C had a preferred direction at azimuth −171.6° and elevation 54.6° (DDI=0.74). The cell in B, D was not spatially tuned. (E), (F) Categorization of PIVC neurons by responses to optic flow simulating translation (n=74) and rotation (n=78). (G) Scatter plot of visual DDI plotted as a function of the anterior-posterior coordinate of each electrode penetration (in mm). Data are shown for the left hemisphere of monkey U during translation (circles, n=38) and rotation (triangles, n=49). Color coding of data points is as described for panels E–F.
As summarized in Fig. 18E, F, the vast majority of PIVC cells were like the cell in Fig. 18B, D. Out of 96 cells tested with visual translation and/or rotation, only 13 cells (monkey J: n=2; monkey U: n=11) showed significant temporal response modulation for some direction of motion. Most of these neurons showed weak inhibitory or excitatory responses to all directions of motion. Only 2/74 cells tested during translation and 0/78 cells tested during rotation showed significant directional tuning for optic flow (e.g., Fig. 18A,C). Notably, the larger number of visually-modulated cells in monkey U might be explained by the fact that penetrations in this animal extended several mm more posterior than those in monkey J (Fig. 14B, D). Indeed, there was a significant correlation between visual DDI and the anterior-posterior coordinate of the electrode penetrations for both translation (r=−0.46, p=0.003) and rotation (r=−0.28, p=0.05) for monkey U (Fig. 18G). No significant correlation was seen for monkey J. As elaborated in the Discussion, the most posterior recording sites in monkey U may have extended into VPS (visual posterior sylvian area), which is located just posterior to PIVC and has been reported to have visual motion sensitivity. In contrast, optic flow selectivity is conspicuously absent from the anterior and middle portions of macaque PIVC (see Discussion).
Reconstruction of recording locations
Fig. 19 presents a summary of the recorded cells in the left hemisphere of monkey U (Fig. 19A–D; see also Fig. 1) and monkey J (Fig. 19E, F), as projected onto a flattened brain map. Each dot represents a cell, first identified according to the presence of audible response modulation during 3D translational or rotational sinusoidal motion (Fig. 19A, B, E; filled black symbols illustrate responsive cells). Areas within and around the lateral sulcus are color-coded according to the parcellation scheme of Lewis and Van Essen (2000a, b), with the exception of the pink area, which is taken from the Paxinos (2000) atlas. This region corresponds to what Pandya and Sanides (1973) and Grüsser (1990a, b) have described as ‘reipt’ and reit’, respectively (parietal and temporal retroinsular areas). Vestibular modulation during sinusoidal translation and/or rotation is found throughout area Ri (dark red) and the adjacent portions of the secondary somatosensory cortex (S2, purple). Only a handful of responsive cells were found in the granular insular cortex (Ig, green).
Figure 19.
Anatomical localization of recording sites within and around the lateral sulcus. (A) Lateral view of a 3D surface reconstruction of the left hemisphere of monkey U, with cell locations mapped onto the surface and with the three major sulci (IPS, LS, and STS) identified. Each dot corresponds to a cell, with black and white dots showing cells that were responsive and non-responsive to sinusoidal motion, respectively. (B)–(F) show flat maps of the brain areas around the lateral sulcus for the left hemisphere of monkey U (B–D) and the right hemisphere of monkey J (E, F). Different functional brain areas are color-coded as indicated in the legend. The color scheme for the data points representing individual cells is as follows. (A), (B), E): Black dots: responsive cells; white dots: non-responsive cells (sinusoidal testing). (C): Yellow dots: cells responding at the first harmonic to sinusoidal stimuli; pink dots: second-harmonic cells; blue dots: cells responding at both the first and second harmonics (sinusoidal testing). (D), (F): gray dots: inhibitory cells; green dots: single-peaked, unimodal cells; blue dots: single-peaked, bimodal cells and untuned excitatory cells; orange dots: double-peaked cells (transient translation testing).
Responsive neurons in monkey U have been further color-coded based on the type of sinusoidal modulation they exhibited (Fig. 19C): yellow dots illustrate cells that modulated at the first harmonic of the stimulus, pink dots show cells that modulated at the second harmonic and blue dots show cells with significant first and second harmonic modulation. Most first-harmonic cells were found at the border between Ri and S2 (upper bank of the lateral sulcus), whereas most second-harmonic cells were located in Ri (lower bank of lateral sulcus). Finally, Fig. 19D and F show cells recorded in the left hemisphere of monkey U and the right hemisphere of monkey J during the transient translation protocol. As expected, most single-peaked, unimodal (green) and double-peaked (orange) cells are encountered at the border between Ri and S2 (upper bank of the lateral sulcus), with inhibitory cells (gray) and both single-peaked, bimodal cells and untuned excitatory cells (blue) being more widely distributed within Ri.
Discussion
We have described robust vestibular responses to both translation and rotation in macaque PIVC. In contrast, the vast majority of PIVC neurons did not respond to optic flow stimulation, suggesting that PIVC does not play a major role in combining visual and vestibular cues for self-motion perception. Note, however, that combined visual-vestibular stimuli were not tested in this study, thus we cannot exclude the possibility that visual motion modulates vestibular responses in PIVC.
Anatomical Localization: where is macaque PIVC?
Using the parcellation scheme of Lewis and van Essen (LVE scheme: Lewis and Van Essen, 2000a, b), most PIVC neurons were recorded within area Ri and in the transition zones between S2, Ri and Ig (insular granular field) (Figs. 1, 19). There are notable differences in parcellation of these cortical areas between the LVE scheme and the Paxinos atlas (Paxinos, 2000). Specifically, the area denoted as ReI (also referred to as ‘reipt’) by Paxinos is smaller than area Ri in the LVE scheme (Fig. 19, pink vs. red areas). LVE area Ri includes all of Paxinos ReI but extends anteriorly into part, but not all of Paxinos area S2. In the Java monkey, Grüsser and colleagues used a nomenclature that is more consistent with the Paxinos map (see also Jones and Burton, 1976; Friedman et al., 1980; Akbarian et al., 1992): vestibular cells in two of their animals (RV and OL) were found mostly anterior to the fork where ReI ends and S2 begins in the Paxinos atlas. For their third animal (FP), vestibular cells appear to be more posterior, presumably in ReI (Grüsser et al., 1990b). The location of vestibular-responsive cells in our rhesus macaques is similar to that described by Grüsser et al. in the Java monkey: we find vestibular cells largely within LVE area Ri, whereas they occupy both areas S2 and ReI (mostly S2) of the Paxinos map.
Grüsser and colleagues concluded that ‘PIVC does not comprise a single anatomically-defined area; although it covers most of ReI, it also extends into the cervical (neck and shoulder) representation of secondary somatosensory area of the parietal operculum’ (Grüsser et al., 1990b). Notably, vestibular neurons in both our study and Grüsser’s studies are found largely within a single area, Ri, as defined in the LVE scheme. Thus, it is possible that functionally-defined PIVC is co-extensive with a single architectonically-defined area (Ri). Yet, within this region, there is some diversity of response properties. Cells located in the upper bank and tip of the lateral sulcus (near the border of Ri and S2) responded like typical vestibular neurons to sinusoidal stimuli, modulating at the first harmonic frequency of the stimulus and being spatially tuned to motion direction. Cells in the lower bank often modulated at the second harmonic frequency and either had bimodal directional tuning or none at all.
Otolith and canal inputs to PIVC
Our findings regarding rotation responses in PIVC are largely consistent with previous studies in Java monkeys (Akbarian et al., 1988; Grüsser et al., 1990b). Using mostly yaw rotation at different frequencies (0.1–1 Hz), they reported that roughly half of neurons recorded in the upper bank of the lateral sulcus modulated during yaw rotation, with modest response gains (mean of 0.11 spikes/s per °/s at 0.2 Hz, Grüsser et al., 1990b). We report that one-fifth of neurons modulate significantly during 0.5 Hz yaw rotation. We used a statistical criterion to define significant response modulation, whereas Grüsser and colleagues used a criterion of response gain > 0.04 spikes/s/°/s. In addition, we searched for responsive cells using a single frequency (0.5 Hz) and half the amplitude used by Grüsser and colleagues. Larger rotation amplitudes might have increased our percentage of significantly responsive neurons.
Whereas Grüsser and colleagues concluded that PIVC neurons do not exhibit otolith-driven responses to static tilt (Akbarian et al., 1988; Grüsser et al., 1990b), we show that PIVC neurons exhibit robust modulation during 3D translation. We did not test whether PIVC neurons in rhesus monkeys also lack static tilt sensitivity. If so, PIVC neurons would selectively signal dynamic motion rather than head orientation relative to the gravity. Future experiments using combined tilt/translation stimuli (e.g., Angelaki et al., 2004; Yakusheva et al., 2007) are necessary to determine whether PIVC neurons encode translation independent of head orientation.
We observed greater variety in response modulations to translation than rotation. Responses of single-peaked neurons were velocity-like, similar to rotation responses. However, responses of double-peaked neurons to translation had two directional preferences that were distinct in time and opposite in direction. This reversal in direction was fast (~50 ms) and the timing of the two spatial peaks roughly followed the biphasic time course of stimulus acceleration. We suggest that double-peaked cells encode acceleration/deceleration information. This coding scheme differs markedly from that seen in the vestibular periphery, where high spontaneous activity allows biphasic stimuli to be reliably represented in neural activity. Vestibular afferents respond to accelerations in one direction with an increase in discharge and to accelerations in the opposite direction with a decrease in discharge (Goldberg and Fernandez, 1971). In contrast, a population of cortical neurons with low spontaneous discharge may rely on the spatio-temporal pattern of activation to encode acceleration and deceleration components of the stimulus.
Absence of optic flow responses in PIVC
Grüsser and colleagues reported robust optokinetic responses in PIVC (Grüsser et al., 1990a). They used a traditional optokinetic stimulus by placing monkeys inside a rotating drum, thus eliciting a pattern of tracking eye movements known as ‘optokinetic nystagmus’ (OKN). Optokinetic responses in PIVC were typically aligned with the vestibular rotation preference of each cell and were either synergistic (firing rate increased during leftward yaw rotation and rightward OKN stimulation) or antagonistic (responses opposed each other during real-world rotation, Akbarian et al., 1988; Grüsser et al., 1990b). The latter responses in PIVC differ from those in the vestibular nuclei (Henn et al., 1974; Waespe and Henn, 1977a, b), thalamus (Buttner and Henn, 1976) and area 2v (Buttner and Buettner, 1978), where most interactions are synergistic.
We examined optic flow responses in PIVC using random-dot stimuli that were viewed by fixating monkeys trained to suppress reflexive eye movements. These stimuli evoke robust responses in cortical areas MSTd (Gu et al., 2006; Takahashi et al., 2007; Gu et al., 2008) and VIP (Schlack et al., 2002; Zhang et al., 2004; Chen et al., 2007). Our optic flow stimuli differ substantially from traditional OKN stimuli in their basic visual motion properties, and also in their efficacy in driving reflexive eye movements. OKN stimuli typically have low spatial frequencies (Schor and Narayan, 1981; de Graaf et al., 1990), and, unlike the optic flow used here, generate robust optokinetic nystagmus and after-nystagmus (Cohen et al., 1977). Using random-dot stimuli, we find that PIVC neurons do not exhibit sensitivity to optic flow, similar to neurons in the vestibular nuclei (Sheng Liu, Ayanna Bryan and Dora Angelaki, unpublished observations) and thalamus (Meng and Angelaki, 2010).
We encountered a few cells with modest optic flow responses in the most posterior electrode penetrations in monkey U (Fig. 18G). We suspect that these penetrations extended into an area known as the ‘parieto-temporal association area T3’ or ‘visual posterior sylvian area (VPS)’ (Jones and Burton, 1976; Guldin et al., 1992; Guldin and Grüsser, 1998; Dicke et al., 2008). Indeed, preliminary recordings in a different animal that extend more posterior to Ri encounter substantially more cells that are tuned to both vestibular and visual stimuli (Aihua Chen, unpublished observations). In squirrel monkeys, area VPS receives projections from insular and retroinsular cortex, parts of area 7, parieto-occipital and parieto-temporal visual areas, the pulvinar, and a portion of the upper bank of the temporal sulcus thought to be area MST (Akbarian et al., 1992; Guldin et al., 1992). Although we cannot firmly exclude the possibility that posterior portions of PIVC contain visually-responsive neurons, most (if not all) of PIVC does not.
Functions of PIVC
Grüsser and colleagues suggested that PIVC serves “to monitor the movement of the head in space” (Akbarian et al., 1988) and is “used for perception of head rotation” (Grüsser et al., 1990a). This conclusion was based on convergence of vestibular, visual (optokinetic), neck receptor, and somatosensory signals (Akbarian et al., 1988; Grüsser et al., 1990a). Indeed, Penfield (1957) reported vestibular sensations in patients by electrical stimulation of a region deep in the lateral sulcus around the superior temporal gyrus, bordering on auditory cortex.
Macaque PIVC neurons project directly to the vestibular nuclei (Akbarian et al., 1994), thus a functional role in gaze control has also been suggested (Akbarian et al., 1994). Yet, neither we nor Grüsser and colleagues noticed clear eye movement-related responses. Finally, Brandt and co-workers have reported that patients with lesions in the presumed human homologue of PIVC have significant impairments in perception of the visual vertical (Brandt et al., 1994; Brandt and Dieterich, 1999). Which, if any, of the above functions, is mediated by PIVC neurons remains to be determined, but our results argue against a major role of PIVC in visual-vestibular integration for self-motion perception.
Acknowledgements
We thank Amanda Turner, Krystal Henderson and Erin White for excellent monkey care and training. We also thank Tunde Adeyemo and the van Essen lab for assistance with the MRI localization. This work was supported by NIH R01-EY017866 (to DEA) and EY016178 (to GCD).
References
- Akbarian S, Grusser OJ, Guldin WO. Thalamic connections of the vestibular cortical fields in the squirrel monkey (Saimiri sciureus) J Comp Neurol. 1992;326:423–441. doi: 10.1002/cne.903260308. [DOI] [PubMed] [Google Scholar]
- Akbarian S, Grusser OJ, Guldin WO. Corticofugal connections between the cerebral cortex and brainstem vestibular nuclei in the macaque monkey. J Comp Neurol. 1994;339:421–437. doi: 10.1002/cne.903390309. [DOI] [PubMed] [Google Scholar]
- Akbarian S, Berndl K, Grusser OJ, Guldin W, Pause M, Schreiter U. Responses of single neurons in the parietoinsular vestibular cortex of primates. Ann N Y Acad Sci. 1988;545:187–202. doi: 10.1111/j.1749-6632.1988.tb19564.x. [DOI] [PubMed] [Google Scholar]
- Angelaki DE. Dynamic polarization vector of spatially tuned neurons. IEEE Trans Biomed Eng. 1991;38:1053–1060. doi: 10.1109/10.99068. [DOI] [PubMed] [Google Scholar]
- Angelaki DE. Spatio-temporal convergence (STC) in otolith neurons. Biol Cybern. 1992;67:83–96. doi: 10.1007/BF00201805. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Dickman JD. Spatiotemporal processing of linear acceleration: primary afferent and central vestibular neuron responses. J Neurophysiol. 2000;84:2113–2132. doi: 10.1152/jn.2000.84.4.2113. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Cullen KE. Vestibular system: the many facets of a multimodal sense. Annu Rev Neurosci. 2008;31:125–150. doi: 10.1146/annurev.neuro.31.060407.125555. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Bush GA, Perachio AA. Two-dimensional spatiotemporal coding of linear acceleration in vestibular nuclei neurons. J Neurosci. 1993;13:1403–1417. doi: 10.1523/JNEUROSCI.13-04-01403.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, Shaikh AG, Green AM, Dickman JD. Neurons compute internal models of the physical laws of motion. Nature. 2004;430:560–564. [Google Scholar]
- Anzai A, Peng X, Van Essen DC. Neurons in monkey visual area V2 encode combinations of orientations. Nat Neurosci. 2007;10:1313–1321. doi: 10.1038/nn1975. [DOI] [PubMed] [Google Scholar]
- Brandt T, Dieterich M. The vestibular cortex. Its locations, functions, and disorders. Ann N Y Acad Sci. 1999;871:293–312. doi: 10.1111/j.1749-6632.1999.tb09193.x. [DOI] [PubMed] [Google Scholar]
- Brandt T, Dieterich M, Danek A. Vestibular cortex lesions affect the perception of verticality. Ann Neurol. 1994;35:403–412. doi: 10.1002/ana.410350406. [DOI] [PubMed] [Google Scholar]
- Bremmer F, Kubischik M, Pekel M, Lappe M, Hoffmann KP. Linear vestibular self-motion signals in monkey medial superior temporal area. Ann N Y Acad Sci. 1999;871:272–281. doi: 10.1111/j.1749-6632.1999.tb09191.x. [DOI] [PubMed] [Google Scholar]
- Bronstein AM. The interaction of otolith and proprioceptive information in the perception of verticality. The effects of labyrinthine and CNS disease. Ann N Y Acad Sci. 1999;871:324–333. doi: 10.1111/j.1749-6632.1999.tb09195.x. [DOI] [PubMed] [Google Scholar]
- Brooks JX, Cullen KE. Multimodal integration in rostral fastigial nucleus provides an estimate of body movement. J Neurosci. 2009;29:10499–10511. doi: 10.1523/JNEUROSCI.1937-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryan AS, Angelaki DE. Optokinetic and vestibular responsiveness in the macaque rostral vestibular and fastigial nuclei. J Neurophysiol. 2009;101:714–720. doi: 10.1152/jn.90612.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush GA, Perachio AA, Angelaki DE. Encoding of head acceleration in vestibular neurons. I. Spatiotemporal response properties to linear acceleration. J Neurophysiol. 1993;69:2039–2055. doi: 10.1152/jn.1993.69.6.2039. [DOI] [PubMed] [Google Scholar]
- Buttner U, Henn V. Thalamic unit activity in the alert monkey during natural vestibular stimulation. Brain Res. 1976;103:127–132. doi: 10.1016/0006-8993(76)90692-2. [DOI] [PubMed] [Google Scholar]
- Buttner U, Buettner UW. Parietal cortex (2v) neuronal activity in the alert monkey during natural vestibular and optokinetic stimulation. Brain Res. 1978;153:392–397. doi: 10.1016/0006-8993(78)90421-3. [DOI] [PubMed] [Google Scholar]
- Chen-Huang C, Peterson BW. Three dimensional spatial-temporal convergence of otolith related signals in vestibular only neurons in squirrel monkeys. Exp Brain Res. 2006;168:410–426. doi: 10.1007/s00221-005-0098-7. [DOI] [PubMed] [Google Scholar]
- Chen A, Henry E, DeAngelis GC, Angelaki DE. Comparison of responses to three-dimensional rotation and translation in the ventral intraparietal (VIP) and medial superior temporal (MST) areas of rhesus monkey. Soc Neurosci Abstr. 2007;33:715–719. [Google Scholar]
- Chen LL, Goffart L, Sparks DL. A simple method for constructing microinjectrodes for reversible inactivation in behaving monkeys. J Neurosci Methods. 2001;107:81–85. doi: 10.1016/s0165-0270(01)00354-5. [DOI] [PubMed] [Google Scholar]
- Chowdhury SA, DeAngelis GC. Fine discrimination training alters the causal contribution of macaque area MT to depth perception. Neuron. 2008;60:367–377. doi: 10.1016/j.neuron.2008.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen B, Matsuo V, Raphan T. Quantitative analysis of the velocity characteristics of optokinetic nystagmus and optokinetic after-nystagmus. J Physiol. 1977;270:321–344. doi: 10.1113/jphysiol.1977.sp011955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Graaf B, Wertheim AH, Bles W, Kremers J. Angular velocity, not temporal frequency determines circular vection. Vision Res. 1990;30:637–646. doi: 10.1016/0042-6989(90)90074-u. [DOI] [PubMed] [Google Scholar]
- Dicke PW, Chakraborty S, Thier P. Neuronal correlates of perceptual stability during eye movements. Eur J Neurosci. 2008;27:991–1002. doi: 10.1111/j.1460-9568.2008.06054.x. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Angelaki DE. Vestibular convergence patterns in vestibular nuclei neurons of alert primates. J Neurophysiol. 2002;88:3518–3533. doi: 10.1152/jn.00518.2002. [DOI] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Wang S, Gu Y, Deangelis GC, Angelaki DE. Spatial reference frames of visual, vestibular, and multimodal heading signals in the dorsal subdivision of the medial superior temporal area. J Neurosci. 2007;27:700–712. doi: 10.1523/JNEUROSCI.3553-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher NI, Marron JS. Mode testing via the excess mass estimate. Biometrika. 2001;88:499–517. [Google Scholar]
- Friedman DP, Jones EG, Burton H. Representation pattern in the second somatic sensory area of the monkey cerebral cortex. J Comp Neurol. 1980;192:21–41. doi: 10.1002/cne.901920103. [DOI] [PubMed] [Google Scholar]
- Glasauer S, Amorim MA, Vitte E, Berthoz A. Goal-directed linear locomotion in normal and labyrinthine-defective subjects. Exp Brain Res. 1994;98:323–335. doi: 10.1007/BF00228420. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J Neurophysiol. 1971;34:635–660. doi: 10.1152/jn.1971.34.4.635. [DOI] [PubMed] [Google Scholar]
- Grüsser OJ, Pause M, Schreiter U. Vestibular neurones in the parieto-insular cortex of monkeys (Macaca fascicularis): visual and neck receptor responses. J Physiol. 1990a;430:559–583. doi: 10.1113/jphysiol.1990.sp018307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grüsser OJ, Pause M, Schreiter U. Localization and responses of neurones in the parieto-insular vestibular cortex of awake monkeys (Macaca fascicularis) J Physiol. 1990b;430:537–557. doi: 10.1113/jphysiol.1990.sp018306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Angelaki DE, Deangelis GC. Neural correlates of multisensory cue integration in macaque MSTd. Nat Neurosci. 2008;11:1201–1210. doi: 10.1038/nn.2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Watkins PV, Angelaki DE, DeAngelis GC. Visual and nonvisual contributions to three-dimensional heading selectivity in the medial superior temporal area. J Neurosci. 2006;26:73–85. doi: 10.1523/JNEUROSCI.2356-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guedry FE. Psychophysics of vestibular sensation. In: Kornhuber HH, editor. Handbook of sensory physiology. New York: Springer Verlag; 1974. pp. 1–154. [Google Scholar]
- Guldin WO, Grüsser OJ. Is there a vestibular cortex? Trends Neurosci. 1998;21:254–259. doi: 10.1016/s0166-2236(97)01211-3. [DOI] [PubMed] [Google Scholar]
- Guldin WO, Akbarian S, Grüsser OJ. Cortico-cortical connections and cytoarchitectonics of the primate vestibular cortex: a study in squirrel monkeys (Saimiri sciureus) J Comp Neurol. 1992;326:375–401. doi: 10.1002/cne.903260306. [DOI] [PubMed] [Google Scholar]
- Henn V, Young LR, Finley C. Vestibular nucleus units in alert monkeys are also influenced by moving visual fields. Brain Res. 1974;71:144–149. doi: 10.1016/0006-8993(74)90198-x. [DOI] [PubMed] [Google Scholar]
- Israel I, Fetter M, Koenig E. Vestibular perception of passive whole-body rotation about horizontal and vertical axes in humans: goal-directed vestibulo-ocular reflex and vestibular memory-contingent saccades. Exp Brain Res. 1993;96:335–346. doi: 10.1007/BF00227113. [DOI] [PubMed] [Google Scholar]
- Israel I, Grasso R, Georges-Francois P, Tsuzuku T, Berthoz A. Spatial memory and path integration studied by self-driven passive linear displacement. I. Basic properties. J Neurophysiol. 1997;77:3180–3192. doi: 10.1152/jn.1997.77.6.3180. [DOI] [PubMed] [Google Scholar]
- Jones EG, Burton H. Areal differences in the laminar distribution of thalamic afferents in cortical fields of the insular, parietal and temporal regions of primates. J Comp Neurol. 1976;168:197–247. doi: 10.1002/cne.901680203. [DOI] [PubMed] [Google Scholar]
- Klier EM, Angelaki DE. Spatial updating and the maintenance of visual constancy. Neuroscience. 2008;156:801–818. doi: 10.1016/j.neuroscience.2008.07.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis JW, Van Essen DC. Corticocortical connections of visual, sensorimotor, and multimodal processing areas in the parietal lobe of the macaque monkey. J Comp Neurol. 2000a;428:112–137. doi: 10.1002/1096-9861(20001204)428:1<112::aid-cne8>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- Lewis JW, Van Essen DC. Mapping of architectonic subdivisions in the macaque monkey, with emphasis on parieto-occipital cortex. J Comp Neurol. 2000b;428:79–111. doi: 10.1002/1096-9861(20001204)428:1<79::aid-cne7>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Liu Y, Yttri EA, Snyder LH. Soc Neurosci Abstr. Washington, DC: Society for Neuroscience; 2008. Reversible inactivation reveals that LIPv subserves general attention while LIPd subserves saccadic intention. [Google Scholar]
- MacNeilage PR, Ganesan N, Angelaki DE. Computational approaches to spatial orientation: from transfer functions to dynamic Bayesian inference. J Neurophysiol. 2008;100:2981–2996. doi: 10.1152/jn.90677.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marlinski V, McCrea RA. Activity of ventroposterior thalamus neurons during rotation and translation in the horizontal plane in the alert squirrel monkey. J Neurophysiol. 2008;99:2533–2545. doi: 10.1152/jn.00761.2007. [DOI] [PubMed] [Google Scholar]
- Meng H, Angelaki DE. Responses of ventral posterior thalamus neurons to three-dimensional vestibular and optic flow stimulation. J Neurophysiol. 2010 doi: 10.1152/jn.00729.2009. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng H, May PJ, Dickman JD, Angelaki DE. Vestibular signals in primate thalamus: properties and origins. J Neurosci. 2007;27:13590–13602. doi: 10.1523/JNEUROSCI.3931-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittelstaedt ML, Jensen W. Centrifugal force affects perception but not nystagmus in passive rotation. Ann N Y Acad Sci. 1999;871:435–438. doi: 10.1111/j.1749-6632.1999.tb09212.x. [DOI] [PubMed] [Google Scholar]
- Page WK, Duffy CJ. Heading representation in MST: sensory interactions and population encoding. J Neurophysiol. 2003;89:1994–2013. doi: 10.1152/jn.00493.2002. [DOI] [PubMed] [Google Scholar]
- Pandya DN, Sanides F. Architectonic parcellation of the temporal operculum in rhesus monkey and its projection pattern. Z Anat Entwicklungsgesch. 1973;139:127–161. doi: 10.1007/BF00523634. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Huang X-F, Toga AW. The rhesus monkey brain in stereotaxic coordinates. Orlando, Florida: Academic Press; 2000. [Google Scholar]
- Penfield W. Vestibular sensation and the cerebral cortex. Ann Otol Rhinol Laryngol. 1957;66:691–698. doi: 10.1177/000348945706600307. [DOI] [PubMed] [Google Scholar]
- Saleem KS, Pauls JM, Augath M, Trinath T, Prause BA, Hashikawa T, Logothetis NK. Magnetic resonance imaging of neuronal connections in the macaque monkey. Neuron. 2002;34:685–700. doi: 10.1016/s0896-6273(02)00718-3. [DOI] [PubMed] [Google Scholar]
- Schlack A, Hoffmann KP, Bremmer F. Interaction of linear vestibular and visual stimulation in the macaque ventral intraparietal area (VIP) Eur J Neurosci. 2002;16:1877–1886. doi: 10.1046/j.1460-9568.2002.02251.x. [DOI] [PubMed] [Google Scholar]
- Schor C, Narayan V. The influence of field size upon the spatial frequency response of optokinetic nystagmus. Vision Res. 1981;21:985–994. doi: 10.1016/0042-6989(81)90002-x. [DOI] [PubMed] [Google Scholar]
- Shaikh AG, Ghasia FF, Dickman JD, Angelaki DE. Properties of cerebellar fastigial neurons during translation, rotation, and eye movements. J Neurophysiol. 2005;93:853–863. doi: 10.1152/jn.00879.2004. [DOI] [PubMed] [Google Scholar]
- Silverman BW. Using kernerl density estimates to investigate multimodality. Journal of the Royal Statistical Society. 1981;43:97–99. [Google Scholar]
- Snyder JP. Map Projections: A Working Manual. U. S. Government Printing Office. 1987:182–190. [Google Scholar]
- Takahashi K, Gu Y, May PJ, Newlands SD, DeAngelis GC, Angelaki DE. Multimodal coding of three-dimensional rotation and translation in area MSTd: comparison of visual and vestibular selectivity. J Neurosci. 2007;27:9742–9756. doi: 10.1523/JNEUROSCI.0817-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taube JS. The head direction signal: origins and sensory-motor integration. Annu Rev Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001;8:443–459. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vingerhoets RA, De Vrijer M, Van Gisbergen JA, Medendorp WP. Fusion of visual and vestibular tilt cues in the perception of visual vertical. J Neurophysiol. 2009;101:1321–1333. doi: 10.1152/jn.90725.2008. [DOI] [PubMed] [Google Scholar]
- Waespe W, Henn V. Vestibular nuclei activity during optokinetic after-nystagmus (OKAN) in the alert monkey. Exp Brain Res. 1977a;30:323–330. doi: 10.1007/BF00237259. [DOI] [PubMed] [Google Scholar]
- Waespe W, Henn V. Neuronal activity in the vestibular nuclei of the alert monkey during vestibular and optokinetic stimulation. Exp Brain Res. 1977b;27:523–538. doi: 10.1007/BF00239041. [DOI] [PubMed] [Google Scholar]
- Yakusheva T, Blazquez PM, Angelaki DE. Frequency-selective coding of translation and tilt in macaque cerebellar nodulus and uvula. J Neurosci. 2008;28:9997–10009. doi: 10.1523/JNEUROSCI.2232-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yakusheva TA, Shaikh AG, Green AM, Blazquez PM, Dickman JD, Angelaki DE. Purkinje cells in posterior cerebellar vermis encode motion in an inertial reference frame. Neuron. 2007;54:973–985. doi: 10.1016/j.neuron.2007.06.003. [DOI] [PubMed] [Google Scholar]
- Zhang T, Heuer HW, Britten KH. Parietal area VIP neuronal responses to heading stimuli are encoded in head-centered coordinates. Neuron. 2004;42:993–1001. doi: 10.1016/j.neuron.2004.06.008. [DOI] [PubMed] [Google Scholar]