Spatial Anisotropy Analyses of Subcutaneous Tissue Layer: Potential Insights into its Biomechanical Characteristics

Summary

As the intermediate layer between the muscle and skin, the subcutaneous tissue frequently experiences shear and lateral stresses whenever the body is in motion. However, quantifying such stresses in vivo is difficult. The lack of such measures is partly responsible for our poor understanding of the biomechanical behaviors of subcutaneous tissue. In this study, we employ both ultrasound imaging and a novel spatial anisotropy measure - incorporating Moran’s I spatial autocorrelation calculations - to investigate the structuromechanical features of subcutaneous tissues within the extremities of sixteen healthy volunteers. This approach is based on the understanding that spatial anisotropy can be an effective surrogate for the summative, tensile forces experienced by biological tissue. We found that spatial anisotropy in the arm, thigh, and calf was attributed to the echogenic bands spanning the width of the ultrasound images. In both univariable and multivariable analyses, the calf was significantly associated with greater anisotropy compared to the thigh and arm. Spatial anisotropy was inversely related to subcutaneous thickness and was significantly increased with longitudinally oriented probe images compared to transversely orientated images. Maximum peaks in spatial anisotropy were frequently observed when the longitudinally oriented ultrasound probe was swept across the extremity suggesting that longitudinal channels with greater tension exist in the subcutaneous layer. These results suggest that subcutaneous biomechanical tension is mediated by collagenous/echogenic bands, greater in the calf compared to the thigh and arm, increased in thinner individuals, and maximal along longitudinal trajectories parallel to the underlying muscle. Spatial anisotropy analysis of ultrasound images has yielded meaningful patterns and may be an effective means to understand the biomechanical strain patterns within the subcutaneous tissue of the extremities.

Introduction

Subcutaneous tissue is the adipose rich layer under the skin associated with a number of well-described functional roles. It provides insulation to conserve internal body heat, acts as a cushion to protect deeper tissue and organs, serves as an energy and fluid reserve, and provides structural and circulatory support to the overlying dermis and epidermis. These myriad functions are embodied by the complex assembly of cells and tissues that constitute the subcutaneous layer: the pliable and energy rich adipocytes, the rich vascular and neural network that support and innervate the skin, the extensive connective tissue matrix that maintain structural integrity, the hair follicles and sweat ducts.

A relatively unrecognized aspect of subcutaneous tissue is its biomechanical properties. As the intermediate layer between the muscle and skin, the subcutaneous tissue frequently experiences shear and lateral stresses whenever the body is in motion (Hermanns-Lê et al., 2004). Even during simple movements such as respiration and hand motion, muscles and bones move laterally with respect to the skin(Guimberteau et al., 2005). As a consequence, the subcutaneous tissue must be sufficiently malleable to permit unconstrained movement while being rigorous enough to avoid complete untethering of the two layers. Moreover, it must provide adequate tensile resistance to preserve the structural integrity of the nerves and vessels that traverse it. These biomechanical characteristics are arguably integral for the proper functioning of subcutaneous tissue yet remain difficult to evaluate particularly within the in vivo setting (Gibson et al., 2006).

According to past studies, biological tissues are structurally dynamic and adaptive – responding and accommodating to mechanical forces. For instance, cells such as fibroblasts and vascular smooth muscles orient in the direction of principal strain (Bischofs and Schwarz, 2003, Kanda and Matsuda, 1994). Collagenous networks similarly align along the axis of tensile strain and form macroscopic asymmetries (Girton et al., 2002, Vader et al., 2009). This structural response to mechanical stimuli ensures that the tissue is equipped for future, comparable forces and exemplifies the notion that ‘structure’ follows ‘function’. For this reason, structural properties, such as spatial anisotropy, may be an effective surrogate for the summative, tensile forces experienced by biological tissue and thereby serve as a useful means to investigate the biomechanical behavior of subcutaneous tissue (Markenscoff and Yannas, 1979). Spatial anisotropy is a method to quantify the amount of preferential orientation or alignment present in a substance or image.

In this study, we employ both ultrasound imaging and a novel spatial anisotropy measure - incorporating Moran’s I spatial autocorrelation calculations - to investigate the structuromechanical features of subcutaneous tissues within the extremities of healthy volunteers. By obtaining multiple ultrasound images at three separate sites (arm, thigh, and calf), we investigate whether spatial anisotropies and thus indirectly tensile strains are associated with any meaningful anatomical patterns in vivo: do anisotropies increase with spatial scale?; are spatial anisotropies increased at specific extremity sites and are they related to subcutaneous layer thickness?; and are spatial anisotropies greater in the longitudinal or transverse directions (parallel or perpendicular to the long axis of the bone, respectively)? This study seeks to answer these questions and, in the process, obtain an improved understanding of the biomechanical strain patterns within the subcutaneous tissue of the extremities.

Methods

Subjects and Settings

Healthy participants were recruited via flyers placed throughout Boston campus areas near Beth Israel Deaconess Medical Center (BIDMC) and via postings in Craigslist (www.craigslist.org). Subjects were excluded if they were under 18 years old, pregnant, had a chronic skin condition (such as eczema, psoriasis), had a collagen disorder (scleroderma, mixed connective tissue disorder, Marfan's), or had a chronic medical condition requiring regular medication intake. To avoid circumstances where the complete subcutaneous layer was too thick for visualization by the ultrasound (4 cm depth window), a BMI less than 30 was also required. Sixteen healthy participants were recruited for this study. There were 11 females and 5 males with a demographic representation of 14 non-Hispanic Whites and 2 Asians. Participant’s age was 29 ± 7.2 (mean ± SD) years. Each subject was compensated for participation. The testing was performed in the BIDMC General Clinical Research Center and approved by the BIDMC Institutional Review Board.

Ultrasound Image

Three specific locations were evaluated – the lateral aspect of the arm, the inner aspect of the thigh, and posterior calf (Figure 1). These sites were chosen because they were previously evaluated in a study involving electrical impedance of subcutaneous tissue and represented three separate segments of the extremities that had subcutaneous layers sufficiently thick for image analyses.

Figure 1.

Body Sites Evaluated for this Study. Lateral aspect of the arm (upper left), medial aspect of the thigh (upper right), and posterior aspect of the calf (bottom).

The arm site was centered on the anterolateral aspect of the upper arm between the brachioradialis and triceps at approximately 8 cm above the lateral end of the cubital crease (Figure 2, left images). Participants laid supine on a hospital recliner in a relaxed state with the head elevated at 30 degrees. The arm was kept abducted at the shoulder approximately 30 degrees, the elbow flexed at 80 degrees, and the arm supinated such that the palm rested flat on the lower abdominal wall.

Figure 2.

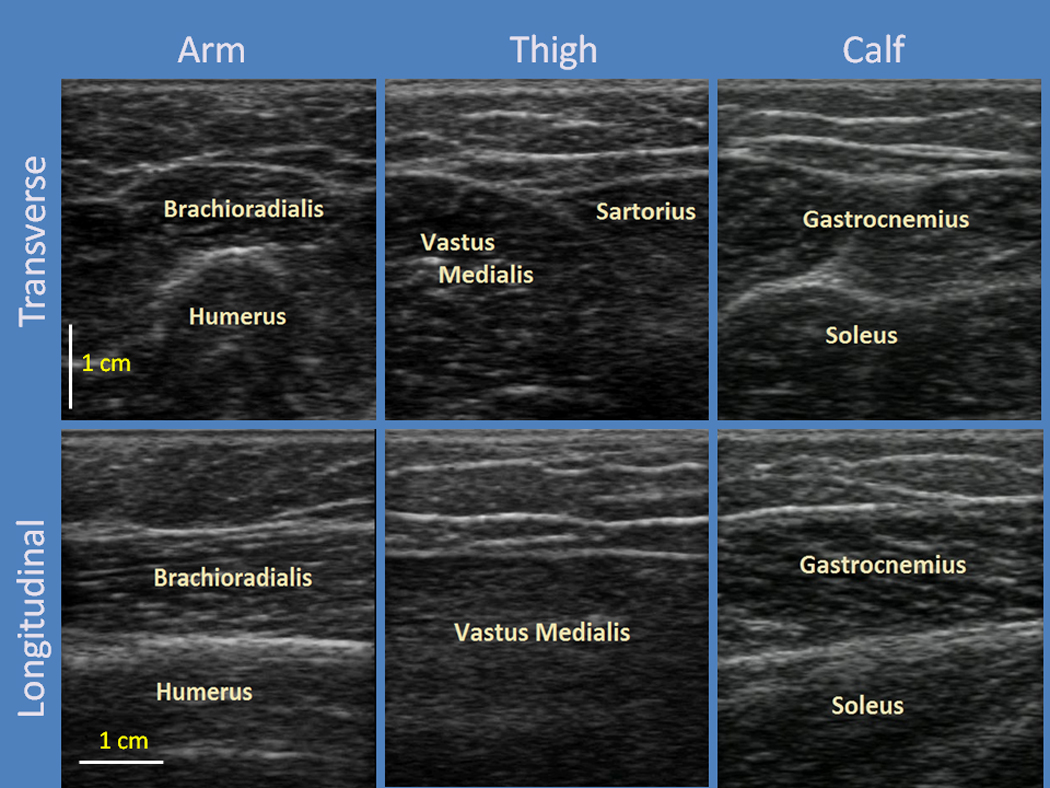
Ultrasound Images of the Three Body Locations. Arm (left column), Thigh (middle column), and Calf (right column). Images in the first row are transverse-oriented images while those in the second row are longitudinal-oriented.

The site for ultrasound imaging for the thigh was centered between the Vastus Medialis and Sartorius muscle approximately 10 cms above the medial end of the popliteal crease (Figure 2, middle images). During imaging of the thigh, participants laid supine on a hospital recliner in a relaxed state. The head was elevated at approximately 30 degrees with the arm rested to the side. To obtain optimal imaging of the inner thigh, the hips were gently flexed during 90 degree flexion of the knee and leg extroversion for maximal comfort.

The calf site was centered on the posterior aspect of the lower leg between the two heads of the gastrocnemius approximately 11 cms below the popliteal crease (Figure 2, right images). The participant laid prone with the legs extended and feet plantar-flexed on the hospital bed while the arm held a pillow at the level of the head. The order of testing for the three sites was randomized.

Ultrasound images were obtained at each testing site using a GE Logiq Book XP scanner (GE, Waukesha, Wisconsin) with a 38 mm linear array transducer (10 MHz, 8L-RS) and an imaging depth of 40 mm. The focal depth was kept at 12.5 mm. Ultrasound images were obtained by performing two video sweeps in a 6x6 cm square region (Figure 3). The first sweep involved a transducer moving distally while oriented in the transverse direction. This sweep acquired a 6.0 × 3.8 × 4.0 cm volume image. The second sweep had the transducer moving laterally while oriented in the longitudinal direction generating a 3.8 × 6.0 × 4.0 cm volume image acquisition (Figure 3). The ultrasound transducer was moved at a velocity of 1 cm/sec for a total of 6 seconds. The image acquisition rate was 50 Hz. A peripheral square grid was placed on the site to denote the exact distances traveled. The transducer probe was placed on the skin as light as possible to avoid tissue compression but robust enough to maintain adequate contact between the probe and skin for coherent images. The scans were obtained by three different examiners at separate times. Preliminary tests with two different examiners revealed that there was minute variability in sweep speeds, but generally no significant differences in spatial anisotropy measures.

Figure 3.

Illustration of the Ultrasound Sweeps. Sweeps were obtained in two ways: (1) Longitudinal-oriented probe moving posteriorly (left) and (2) Transverse-oriented probe moving distally (right).

Anisotropy Measurements

The video sweep file (.avi) was segmented into its separate individual ultrasound images in jpg format (approximately 300). The ultrasound-generated images are calibrated in equal dimensions across width and depth - approximately 103 pixels/cm. The bottom portion of each image was cropped to the level of 20 pixels deeper than the deepest point of the epimysium in the video sweep. The images were subsequently normalized by pixel intensity and processed using a Moran’s I spatial autocorrelation calculation (Moran, 1950). Moran’s I first calculates the correlation between each pixel and its neighbors and then averages across the whole image. The calculations are represented by the following formula:

$$I=\frac{{\displaystyle \sum _i}{\displaystyle \sum _j}{W}_{\mathit{\text{ij}}}}{N}\frac{{\displaystyle \sum _i}{\displaystyle \sum _j}{W}_{\mathit{\text{ij}}}(z_i-\overline{z})(z_j-\overline{z})}{{\displaystyle \sum _i}{(z_i-\overline{z})}^2}$$

where z_i represents the pixel intensity of a specific locus, z_j is the intensity of its neighboring pixel, and z̄ represents the average pixel intensity of the whole image. N is the total number of pixels within the image while W_ij is the weight matrix. The weight matrix specifies which neighboring pixels are to be used in the correlational analyses and thus confers the analysis with significant flexibility in determining the effects of directionality and spatial separation on spatial autocorrelation (Luna et al., 2005). For example, the horizontal spatial autocorrelation between neighbors distanced 5 pixels apart and within a 30 degree angular window is represented by the following weight matrix:

$$\left[\begin{array}{ccccccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$

In nearly all ultrasound images and across all spatial scales, the greatest spatial autocorrelation was found along the horizontal (lateral) axis while the smallest was along the vertical axis. To derive spatial anisotropy, this study focused on the horizontal and vertical axes at spatial scales (distance separation) of 1 to 10 pixels. Moreover, we limited our anisotropic analyses to these cardinal axes because we were primarily interested in the lateral stress of the subcutaneous tissue. The horizontal and vertical spatial autocorrelations were used to derive spatial anisotropy using the following formula:

$$\mathit{\text{Anisotropy}}=\frac{e^{I_{\mathit{\text{HORIZ}}}}-e^{I_{\mathit{\text{Vert}}}}}{e^{I_{\mathit{\text{HORIZ}}}}+e^{I_{\mathit{\text{Vert}}}}}$$

Maximal horizontal anisotropy had a value of +1, and maximal vertical anisotropy had a value of −1. A value of zero indicated the absence of any anisotropy. The global anisotropy was obtained by calculating the anisotropy for each pixel then averaging across the image. These calculations were performed at separation distances of 1 to 10 pixels (approximately equivalent to 0.1 to 1.0 mm) to investigate the effect of spatial scale on anisotropy. The validity of the global anisotropy method was confirmed in a set of images of varying anisotropies - including pictures with varying numbers of horizontal and vertical lines, with sine waves of varying wavelengths and amplitudes, and with ultrasound images with qualitatively different amounts of anisotropy (high vs. medium vs. low). The separation distance of up to 1.0 mm did well in distinguishing these features, and larger separation distances (particularly > 2.0 mm) in fact led to more incongruent results due to prevalence of images with thin subcutaneous layer (<5.0 mm) and to inconsistencies in the vertical autocorrelations. Larger spatial scales led the vertical autocorrelation matrix to correlate structures that were not structurally related, i.e. a collagenous band and vessel. The 1 mm cutoff was ultimately determined to be the optimal level at which the lateral and vertical contributions to the anisotropy were appropriately balanced given the amount of subcutaneous tissue thicknesses. The type of image format (raw vs. jpg) had little impact on the overall anisotropy results. Anisotropy remained robust within levels of 0.04 for differing depths as large as 50 pixels.

Global anisotropy was calculated for all images contained within both the transverse and longitudinal video sweeps. Images with imaging artifacts (e.g. shadows from air bubbles within the gels) or blood vessels with diameters greater than 0.5 cm width (thus potentially contributing to greater global anisotropy) were excluded from analyses. These measurements were automated with Matlab 2009b (Mathworks, Natick, MA). The base program for Moran’s I spatial autocorrelation was obtained from Matlab Central (Hebeler, 2008) and substantially modified for this study.

Statistical analysis

Spatial anisotropy was determined at each body site and for spatial scales 0.2, 0.4, 0.6, 0.8, and 1.0 mm by (1) taking the average of the spatial anisotropy across each video sweep (“mean spatial anisotropy”) and (2) identifying the greatest spatial anisotropy within each sweep (“maximum spatial anisotropy”). To determine whether spatial anisotropy was significantly different between longitudinal and transverse orientations at each body site and within-subject, we performed a Wilcoxon signed-rank test for both mean and maximum spatial anisotropy measures.

To identify factors associated with spatial anisotropy, a mixed effects model was used to account for across-subject and within-subject factors. The mean and maximum spatial anisotropy at the spatial scale of 10 was designated as dependent variables while location, subcutaneous thickness, and probe orientation were entered as independent variables. Subcutaneous thickness was obtained by averaging the distances between the lower border of the dermis and the upper border of the epimysium images in five images equally distributed across the video sweep. The mixed effects model was considered ideal for the clustered, hierarchical data – i.e. within each individual, there are three evaluated body sites (arm, thigh, and calf) and within each body site there are two orientations (transverse vs. longitudinal). SAS version 9.2 software (SAS Institute Inc., Cary, NC) was used for statistical calculations.

Results

Figure 4 shows a topographic representation of anisotropy in a sample subcutaneous layer. With increasing spatial scales, greater spatial anisotropy is seen where the echogenic bands are visualized in the ultrasound image. This heightened anisotropy was particularly evident for those bands spanning the whole width of the ultrasound image. Global anisotropy of the subcutaneous layer generally increased in value with greater spatial scale – maximizing at either 0.8 or 1.0 mm depending on the body site or probe orientation. Global anisotropy values for several sample images are shown in Figure 5.

Figure 4.

Topographic Representation of Spatial Anisotropy in a Sample Subcutaneous Layer. Spatial anisotropy was calculated for spatial scales 1 to 10 (~ 0.1 – ~1.0 mm). Only even scales are depicted here.

Figure 5.

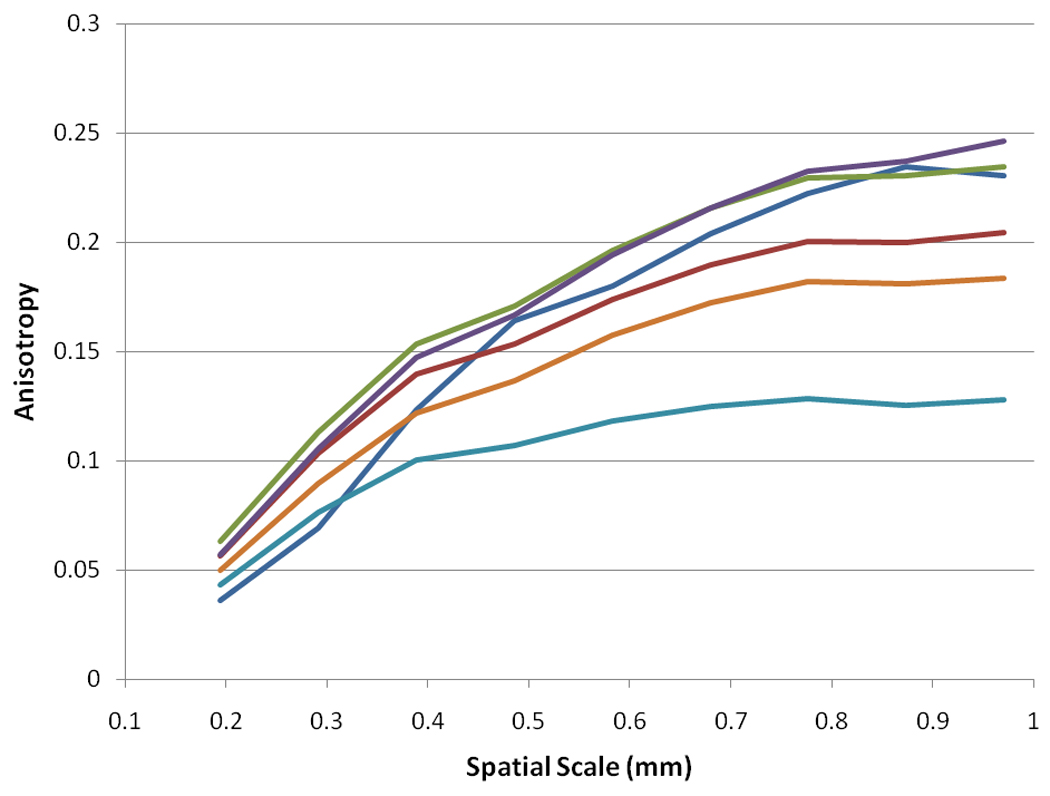
Spatial Anisotropy vs. Spatial Scale in Representative Samples.

As shown in Table 1A and 1B, the mean spatial anisotropy (the average anisotropy across the video sweep) ranged from 0.05 to 0.24, while the maximum spatial anisotropy (the maximum anisotropy within the sweep) ranged from 0.06 to 0.28. No image was associated with a negative global anisotropy – i.e., a vertical or shallow-to-deep oriented anisotropy. In general, greater spatial scales were associated with greater mean and maximum anisotropy; the calf region was associated with greater anisotropies compared to the thigh and arm; and the longitudinally oriented images were associated with greater anisotropies compared to transverse images. This latter observation was confirmed by the Wilcoxon Ranked Sum test which showed statistically significant differences between the longitudinal and transverse images particularly at larger spatial scales. These differences between the two probe orientations were accentuated further when the maximal anisotropy values were considered.

Table 1.

Table 1A: Mean Spatial Anisotropy – Role of Location, Orientation, and Spatial scale
LOCATION		MEAN SPATIAL ANISOTROPY
		0.2 mm		0. 4 mm		0.6 mm		0.8 mm		1.0 mm
Arm	Transverse	0.053 ± 0.007		0.128 ± 0.018		0.158 ± 0.024		0.179 ± 0.028		0.180 ± 0.028
	Longitudinal	0.056 ± 0.008		0.133 ± 0.022		0.165 ± 0.030		0.188 ± 0.036		0.192 ± 0.037
	p-value		0.05		0.03		0.02		0.02		0.02
Thigh	Transverse	0.051 ± 0.007		0.123 ± 0.018		0.153 ± 0.024		0.176 ± 0.028		0.179 ± 0.028
	Longitudinal	0.054 ± 0.009		0.129 ± 0.023		0.160 ± 0.031		0.183 ± 0.037		0.186 ± 0.038
	p-value		.004		.005		0.02		0.03		0.04
Calf	Transverse	0.062 ± 0.008		0.153 ± 0.017		0.194 ± 0.019		0.223 ± 0.020		0.226 ± 0.020
	Longitudinal	0.063 ± 0.008		0.156 ± 0.019		0.198 ± 0.022		0.231 ± 0.024		0.236 ± 0.023
	p-value		0.25		0.16		0.08		0.04		0.003

Table 1B: Maximal Spatial Anisotropy – Role of Location, Orientation, and Spatial scale
		MAXIMAL SPATIAL ANISOTROPY
		0.2 mm		0.4 mm		0.6 mm		0.8 mm		1.0 mm
Arm	Transverse	0.063 ± 0.008		0.149 ± 0.020		0.184 ± 0.028		0.208 ± 0.032		0.212 ± 0.032
	Longitudinal	0.068 ± 0.010		0.164 ± 0.028		0.204 ± 0.038		0.235 ± 0.047		0.240 ± 0.046
	p-value		0.004		0.005		0.006		0.006		0.008
Thigh	Transverse	0.060 ± 0.010		0.142 ± 0.025		0.177 ± 0.034		0.204 ± 0.041		0.208 ± 0.043
	Longitudinal	0.065 ± 0.010		0.156 ± 0.025		0.194 ± 0.034		0.223 ± 0.042		0.228 ± 0.045
	p-value		0.009		0.002		0.003		0.001		<0.001
Calf	Transverse	0.072 ± 0.010		0.176 ± 0.022		0.221 ± 0.025		0.256 ± 0.026		0.260 ± 0.023
	Longitudinal	0.075 ± 0.010		0.185 ± 0.021		0.236 ± 0.025		0.276 ± 0.029		0.284 ± 0.029
	p-value		0.03		0.02		0.003		<0.001		<0.001

Multivariable statistical analyses for anisotropy at spatial scale of 1.0 mm showed that subcutaneous thickness, body site, and probe orientation were all significantly associated with spatial anisotropy. Greater subcutaneous thickness is associated with reduced mean and maximum spatial anisotropy. After accounting for subcutaneous thickness and probe orientation, the calf was associated with greater anisotropy whereas the arm was associated with lower anisotropy by both measures. Longitudinal probe orientation is associated with greater anisotropy, particularly for maximum spatial anisotropy.

Figure 6 demonstrates sample variances of anisotropy across longitudinally and transversely-oriented sweeps by body site. In general, the longitudinally-oriented, posteriorly-moving sweeps generated greater variance in spatial anisotropy than the transversely-oriented, distally-moving sweeps. This variability was particularly evident at larger spatial scales and was not limited to a single body site. In many cases, a single peak could be seen in the longitudinally-oriented sweeps and frequently correlated with the subcutaneous tissue overlying intermuscular spaces. The peaks were defined as areas where both the 1.0 mm spatial anisotropy and the linear slope estimates for the four largest anisotropy measures (i.e. slope for the anisotropy vs. spatial scale plot – which projects the anisotropy at even greater scales) were at least one standard deviation above the mean values for the full sweep. Out of 16 samples, 9 arm, 7 thigh, and 13 calf regional sweeps had anisotropy peaks located within 2.5 mm of the intermuscular region. The intermuscular region was defined as the location where the intermuscular space and subcutaneous tissue conjoined. Figure 7A–C illustrates the correlation between images with maximal anisotropy and intermuscular fascia. Based on a binomial distribution analysis, the probability of having these or any greater amounts of correlations with intermuscular fascia (~5.0 mm thickness) within 2.5 mm of the peak region (~5.0 mm in thickness) in a 60 mm sweep region is 0.05, 0.25, and <0.001 at the arm, thigh, and calf respectively.

Figure 6.

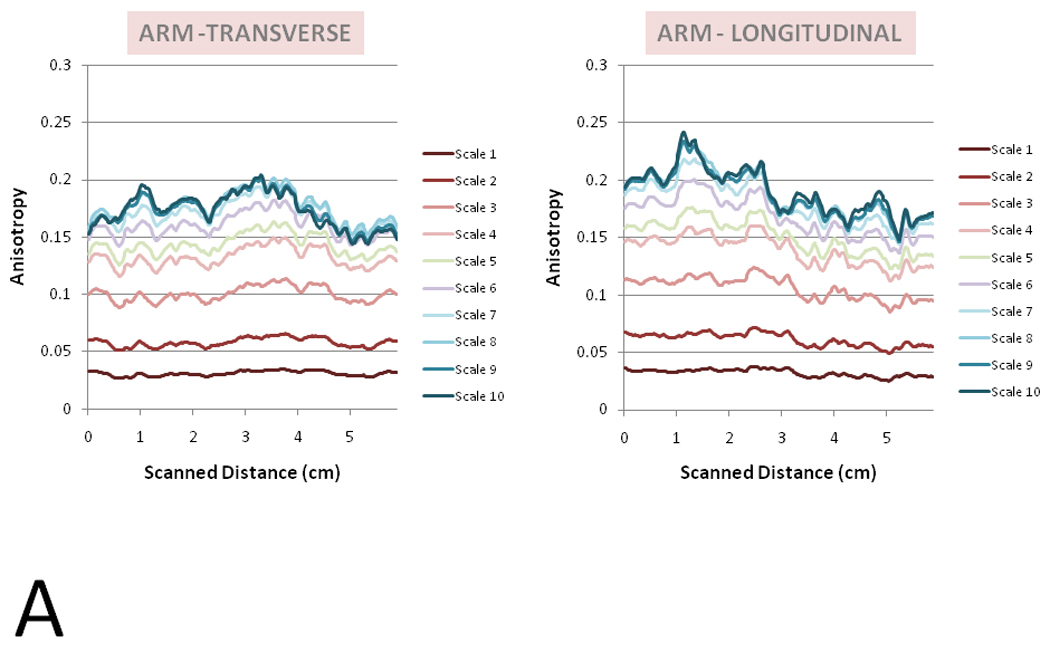
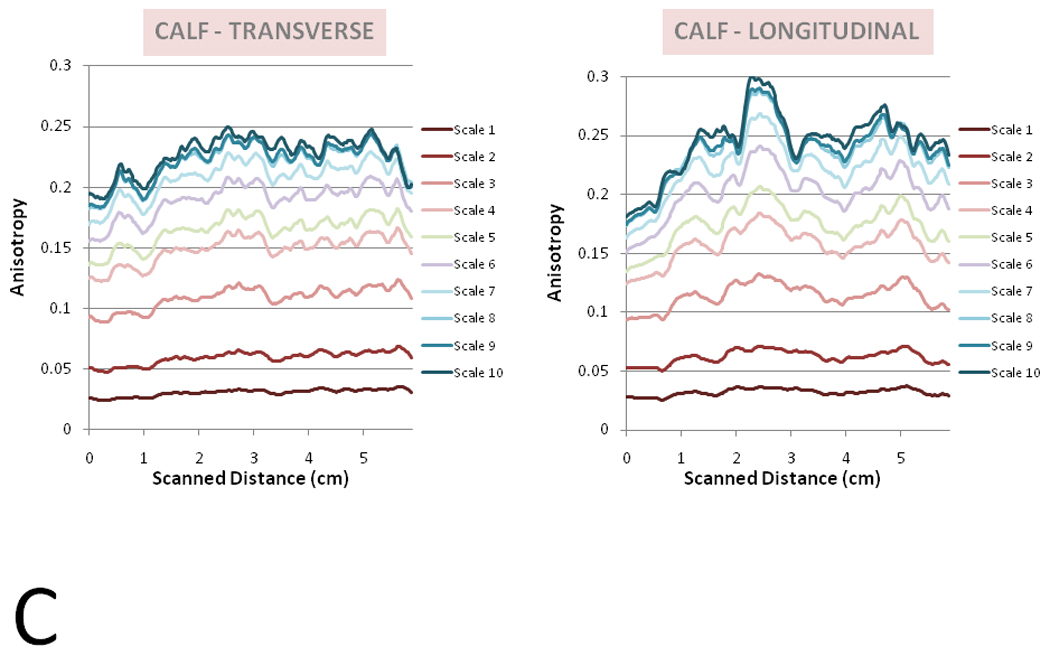
A–C: Spatial Anisotropy in Ultrasound Sweeps. Spatial Anisotropy across a 6 cm sweep is graphed here for spatial scales 1 to 10 for transverse (left) and longitudinal (right) orientations. A representative sample from the arm (Figure 6A), thigh (6B), and calf (6C).

Figure 7.

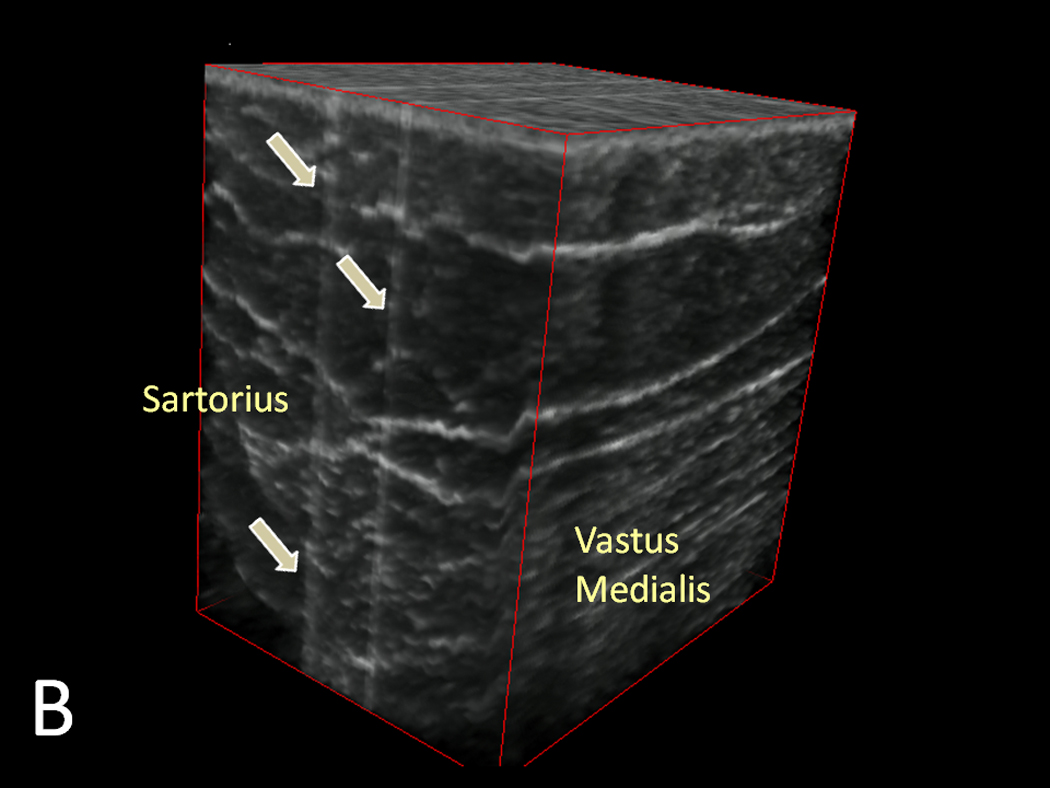
A–C: Three-dimensional Reconstructed Ultrasound Images of the arm (7A), thigh (7B), and calf (7C). Slices with maximal anisotropy is made opaque and delineated by the grey arrows. Performed through ImageJ software (version 1.44k, National Institutes of Health, Bethesda, MD, USA)

Discussion

The structuromechanical properties of the subcutaneous layer are poorly understood and have not been extensively studied. This may partly be due to the general lack of appreciation for subcutaneous tissue’s mechanical behavior during physical activity and for its role in protecting its traversing structures (e.g. nerve and blood vessels) from shear and tensile forces. The lack of understanding may also be due to the overall unavailability of techniques that can effectively extract mechanical information about the subcutaneous layer, particularly within the in vivo setting.

Few animal studies, however, have provided some relevant insights into subcutaneous tissue. Based on ex-vivo rat subcutaneous tissue samples under uniaxial tension, the instantaneous elastic response of subcutaneous tissue was found to be highly linear up to 50% strain (Iatridis et al., 2003). This is unlike other specialized connective tissues, such as cartilage or tendons, where the elastic response is decidedly non-linear (e.g. ever intensifying tension with increasing strain) due to the increasing recruitment of fibers as tensile forces rise. The linear elastic response of subcutaneous tissue suggests that nearly most of the structural components within the tissue are already recruited - sensing the tensile forces within the tissue– even at low strain levels and thus theoretically exhausted of any extra reserve to resist additional strain. In addition, the elastic modulus of subcutaneous tissue was approximately 2.75 kPa, several orders of magnitude lower than many other solid tissues in the body - indicating that as biological tissues go, subcutaneous tissue is not especially stiff (Iatridis et al., 2003). Moreover, the relatively short viscoelastic relaxation time seen in the study revealed that subcutaneous tissue quickly accommodated to each additional strain by reducing its resistive tension.

Based on these findings, one would understandably conclude that subcutaneous tissue is simply ill-equipped to resist any tensile/shear forces and thus mechanically incapable of protecting the internal nerves/vessels during physical activity or trauma. However, the rat subcutaneous tissue used in the study is notably different from the human subcutaneous layers analyzed in this study in one important respect: the subcutaneous muscle of the rat ventral/lateral wall was removed prior to the biomechanical tests. Although subcutaneous muscles do not typically exist in humans (except for areas in the head, neck, and hand – e.g. platysma), in our samples, the echogenic bands within the subcutaneous layer may act to resist tensile forces much in the way that the subcutaneous muscle and its adjacent connective tissue would have probably done in the rat subcutaneous sample. Indeed, the echogenic bands were the structures highly correlated with increased spatial anisotropy across multiple scales whereas areas of high adipose (and low band) content showed no consistent change in anisotropy. Furthermore, the spatial anisotropy at band locations frequently increased with greater spatial scales suggesting that the echogenic bands operate at a macroscopic level - likely beyond the 1 mm range evaluated in this study - to resist tensile force along the span of an extremity.

The functional significance of these echogenic bands is presently unclear. Histologically, these bands are composed of collagenous fibers surrounded by mucinous proteoglycans and glycosaminoglycans. Considering collagen’s role in tensile resistance and the evident association between echogenic bands and spatial anisotropy, these bands likely provide the tensile protection to the internal structures that is inadequately provided by the adipose tissue alone (Knight et al., 1990). The mucinous, gel-like properties of the neighboring glycosaminoglycan may also facilitate sliding between collagen fibers and thereby provide the shear plane needed for the skin to slide over muscle during movement. Interestingly, the subcutaneous collagen of rodents has been observed to assume this shearing role with elastin serving the important role of maintaining elasticity (Kawamata et al., 2003).

If indeed spatial anisotropy is correlated with the direction and intensity of mechanical stress as we posit, this study provides some revealing insights into the mechanical behaviors of the extremity and its subcutaneous tissue. The statistically significant increase in longitudinal anisotropy as compared to transverse anisotropy indicates that the subcutaneous layer is not isolated from the mechanical stress induced by muscle activity. At all three investigated sites, the subcutaneous tissue overlied muscles that effectively ran parallel to the longitudinal axis of the extremity and thus plausibly experienced greater tensile force in the longitudinal direction during muscle contraction. Based on the ultrasound images of the subcutaneous layer, the echogenic bands form sheets spanning the length and circumference of the extremities. The consistent identification of greater spatial anisotropy in one direction was not naturally anticipated and speaks to both the nature in which these collagenous bands are organized (much like a tablecloth crimped when two points are tugged) and the sensitivity of our anisotropic measure.

In both our univariable and multivariable analyses, the subcutaneous layers of the calf was significantly associated with greater anisotropy compared to those at the thigh and arm, whereas the subcutaneous tissue of the thigh had greater anisotropy compared to the arm’s after accounting for subcutaneous thickness and probe orientation. Based on these results, gastrocnemius muscles may generate greater subcutaneous stresses compared to the Sartorius and Vastus Medialis, while these latter muscles may generate greater biomechanical stresses compared to the brachioradialis and biceps brachii. Although these anisotropy measures do not directly assess actual, immediate muscular stress, they may conceivably represent the composite forces generated by the muscle over the span of the day or of even greater periods of time. Considering the importance of leg muscles in ambulation (a daily activity), the study’s results are logical and consistent with this hypothesis. Nevertheless, studies that directly measure muscle stress are needed to confirm our supposition.

The inverse relationship between spatial anisotropy and subcutaneous thickness also indicates that mechanical stress is distributed across the subcutaneous tissue. Thicker subcutaneous tissues are more likely to disperse the mechanical forces and thus are associated with reduced spatial anisotropy. Thinner subcutaneous tissues, on the hand, are subjected to similar forces but over a smaller area. As a consequence, thinner subcutaneous layers are generally associated with greater echogenic band densities and thus spatial anisotropy. These results may carry implications for plastic surgeons interested in optimizing the amount of collagenous bands in the subcutaneous tissue to reduce development of “cellulite” (Gasperoni and Salgarello, 1995) or for massage therapists seeking to understand how manual interventions can affect subcutaneous tissue composition in various individuals. Indeed, deep mechanical massage has been shown to increase the amount of subcutaneous collagen bands in a porcine model (Adcock et al., 2001). This corroborates the assertion that collagenous bands are derivatives of mechanical stress but must also be understood within the context that subcutaneous thickness may significantly modify the distribution of mechanical stresses and therefore greatly moderate the response in band production and formation.

Based on our data, the ultrasound sweeps with longitudinal-oriented images were associated with greater variance in spatial anisotropy compared to the corresponding sweeps with transverse-oriented images. Not only did maximal anisotropy measures generate greater statistical differences between the two directions when compared to the statistical calculations using mean anisotropy, but the longitudinally-oriented sweeps generally revealed a visible peak in the spatial anisotropy vs. sweep distance map. The concept of longitudinal channels with greater mechanical stresses is not new and has been previously proposed by manual therapists. Variations on terms referring to this concept include “Anatomy Trains” (Myers, 2009) or “Myofascial Sequences” (Stecco, 2004) and are based on the notion that connective tissue structures serve as an “ectoskeleton” helping to mediate force transmissions across muscles and joints (Huijing, 1999a, Huijing, 1999b, Huijing, 2009, Benjamin, 2009). The fact these these peaks were significantly correlated with intermuscular spaces at the arm and calf intimate that these fascial planes help integrate mechanical stresses between muscles and transmit forces into more superficial layers such as the subcutaneous tissue. The lack of statistical significance at the thigh may be attributed to the somewhat oblique path of the Sartorius muscle and our determination of spatial anisotropy solely along the longitudinal axis of the extremity. This is in contrast with the calf where the intermuscular fascia between the gastrocnemius muscles aligned well with the longitudinal axis of the leg. Conceivably, calculating spatial anisotropy parallel to the Sartorius muscle would generate a more distinct correlation with the intermuscular plane.

This study relied on images directly acquired from the ultrasound device to calculate spatial anisotropy in the subcutaneous layer. As a result, only the spatial anisotropies in the transverse or longitudinal direction were calculated. For future studies, computational manipulation of video sweeps may be performed to reconfigure the images and generate anisotropies along different axes. This study had additional limitations. Ultrasonography inherently produces anisotropic images because it relies on impedance of acoustic waves traveling from skin to deeper layers. Vertical structures (spanning from superficial to deep) poorly reflect acoustic waves traveling in a vertical trajectory and thus are not well characterized on ultrasound images. Spatial anisotropy will nearly uniformly yield lateral anisotropies in ultrasonography and thus must be interpreted with this limitation in mind. Moreover, the lateral resolution of our ultrasound was approximately 0.5 to 1.0 mm – within the spatial range where the autocorrelations were performed. Although this spatial range was preliminarily tested and determined to have construct validity, our analyses clearly depends on the effectiveness of image processing program in interpolating data (adding pixels in the lateral direction). Furthermore, although no significant differences between two examiners were identified in this study, intra- and inter-examiner differences in ultrasound imaging acquisition must be considered since variations in ultrasound probe pressure can theoretically affect spatial anisotropy measures. In addition, this study is limited by the small sample size, limited number of body sites, and its focus on the relaxed state. Future studies should consider not only increasing the number of subjects and body sites but also diversifying the number of physical positions and states assessed (e.g. tensed muscle during flexion) to better grasp the generalizability of our findings. Finally, as stated previously, spatial anisotropy is merely a marker of structural tension and not a direct measure of biomechanical force.

Despite these limitations, the spatial anisotropy technique used in this study has a number of advantages: it is capable of determining the spatial anisotropy in any desired direction and spatial scale given the flexibility of the Weight matrix in the Moran’s I spatial autocorrelation; it is apparently sensitive enough to detect relative differences between images with different probe orientations and from different body sites; it is easily applied to a widely available, non-invasive imaging technique (ultrasonography); and it may reflect the composite, summative tensile behavior of the tissue considering that structures do not likely conform to transient and infrequent forces. As an imaging analytical technique, spatial anisotropy has yielded some meaningful patterns and may be a useful and efficient way for evaluating the biomechanical properties of subcutaneous layer and possibly other tissues.

Conclusion

The application of spatial anisotropy measures to in vivo ultrasound images has revealed various morphological patterns within the subcutaneous tissue layer of the extremities. These patterns may provide important insights into the biomechanical properties of the subcutaneous layer. Although, at present, the mechanical functions of subcutaneous tissue remains largely unknown, this study suggests that subcutaneous tissue is not structured in a random manner and that newer techniques such as spatial anisotropy will be important in elaborating its biomechanical role.

Table 2.

Factors Associated with Mean and Maximal Spatial Anisotropy

	Mean Anisotropy		Maximal Anisotropy
	Odds Ratio	p-value	Odds Ratio	p-value
Location
Thigh (Ref)	-	<0.0001	-	<0.0001
Arm	0.94		0.94
Calf	1.03		1.02
Subcutaneous Thickness (cm)	0.90	<0.0001	0.88	<0.0001
Orientation
Transverse (Ref)	-	0.03	-	0.0002
Longitudinal	1.02		1.06