Competition for visual selection in the oculomotor system

Abstract

During behavior, the oculomotor system is tasked with selecting objects from an ever-changing visual field and guiding eye movements to these locations. The attentional priority given to visual targets during selection can be strongly influenced by external stimulus properties or internal goals based on previous experience. Although these exogenous and endogenous drivers of selection are known to operate across partially overlapping time scales, the form of their interaction over time remains poorly understood. Using a novel choice task that simultaneously manipulates stimulus- and goal-driven attention, we demonstrate that exogenous and endogenous attentional biases change linearly as a function of time after stimulus onset and have an additive influence on the visual selection process in rhesus macaques (Macaca mulatta). We present a family of computational models that quantify this interaction over time and detail the history-dependence of both processes. The computational models reveal the existence of a critical 140-180 ms attentional “switching” time, when stimulus and goal-driven processes simultaneously favor competing visual targets. These results suggest that the brain uses a linear sum of attentional biases to guide visual selection.

Introduction

Visual selection is the process by which the brain’s attentional mechanisms target one location in the visual field for the purpose of perceptual enhancement or saccade planning (Awh et al., 2006). In the primate oculomotor system, two distinct attentional processes are known to drive visual selection: sensory-driven exogenous (“bottom-up”) attention and goal-driven endogenous (“top-down”) attention (Desimone and Duncan, 1995; Egeth and Yantis, 1997; Kastner and Ungerleider, 2000; Awh et al., 2006; Knudsen, 2007). Exogenous attention is automatic and can reliably be “captured” by a flashed object (Yantis and Jonides, 1984; Nakayama and Mackeben, 1989; Yantis and Jonides, 1996; Egeth and Yantis, 1997) or pop-out stimulus (Joseph and Optican, 1996), even if these cues are uninformative or task-irrelevant (Liu et al., 2005; Giordano et al., 2009). Endogenous attention is a voluntary process that supports the monitoring of peripheral targets or locations, has been shown to improve discriminability and speed of information accrual at monitored locations, and varies flexibly with task demands such as cue validity (Giordano et al., 2009).

Recent work has shown that sensory- and goal-driven attention are subserved by distinct brain mechanisms (Kastner and Ungerleider, 2000; Corbetta and Shulman, 2002; Giordano et al., 2009; Ross et al., 2010). These mechanisms are likely to interact, based on the observation that exogenous attention to a distractor location interferes with endogenous attention to a target located elsewhere in the visual field (Theeuwes and Burger, 1998). However, the nature of this interaction remains unknown, because endogenous and exogenous manipulations of competition have been studied in isolation only (Beck and Kastner, 2009). How is competition resolved when stimulus- and goal-driven factors simultaneously drive the selection of different targets in the visual field?

To address this problem, we developed a simple two-target, free reaction time decision task, in which we simultaneously manipulate sensory- and goal-driven attentional processes by varying the relative luminance and relative reward values of the targets. Through parametric variation of luminance contrast and expected reward, and by using reaction time as a proxy for internal selection dynamics, we investigate how attentional biases derived from these stimulus properties evolve in time after target onset. In particular, when luminance and reward favor different targets, we find that the selected target location is strongly influenced by reaction time: fast reaction times lead to a stronger sensory-driven attentional bias, while slow reaction times lead to a stronger goal-driven attentional bias. We present a family of computational models to quantify the interaction between luminance and reward biases in time, as well as their dependence on prior experience. Our best-fitting model demonstrates that bottom-up and top-down biases combine linearly at all times to drive visual selection, and although reward bias is shaped by previous experience, luminance bias is not.

Methods

Experimental Preparation

Two adult male rhesus macaques (Macaca mulatta) participated in the study (Monkey A and Monkey S, 9.5 kg and 8.4 kg, respectively at the start of the experiments). Both animals had been used previously in other experiments studying eye movements but were naive to the choice task used in this study. Identical training protocols were used for both animals (see below). Prior to behavioral training, each animal was instrumented with a head restraint prosthesis to allow fixation of head position and tracking of eye position. All surgical and animal care procedures were approved by the New York University Animal Care and Use Committee and were performed in accordance with the National Institute of Health guidelines for care and use of laboratory animals.

Each monkey was behaviorally trained for several weeks in an unlit sound-attenuated room (ETS Lindgren). Eye position was constantly monitored with an infrared optical eye tracking system sampling at 120 Hz (ISCAN). Eye positions were digitized at 1 kHz. Visual stimuli were presented on an LCD screen (Dell Inc) placed 34 cm from the subjects’ eyes. The visual stimuli were controlled via custom LabVIEW (National Instruments) software executed on a real-time embedded system (NI PXI-8184, National Instruments).

Luminance-Reward Selection (LRS) Task

Each monkey performed the two-alternative choice task shown in Figure 1b. Two identically sized rectangular stimuli with a 3-to-1 aspect ratio served as the targets in this task, with each target associated with a different value of liquid reward. The long axis of each target subtended 2° of visual arc. Target 1 (T1) was oriented so that the long axis was vertical, and Target 2 (T2) was oriented so that the long axis was horizontal (Fig 1b). The monkeys were motivated to find the target associated with the highest value of liquid reward. The mean value of the liquid reward associated with each target was kept constant for blocks of 40 - 70 trials, after which a new mean for each target was assigned. We randomized the number of trials in each block to discourage an influence by the number of trials completed in a block. The mean of the reward values tested varied between 0.04 mL/trial and 0.21 mL/trial across blocks. Changes in reward magnitude between block transitions were unsignaled, and a Gaussian-distributed variability (standard deviation = 0.015 mL) was added to the value associated with both targets on every trial. Adding variability to reward magnitude across trials ensured that we could perform regression analyses and increased the subjects’ uncertainty about the times of reward block transitions.

Figure 1. Conceptual Motivation and Behavioral Task.

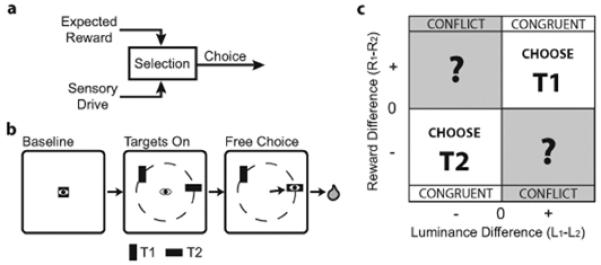
(a) Schematic of the oculomotor selection process. Target selection may be driven by sensory drive and/or expected reward, after which the selected target is used to guide choice behavior. (b) Luminance-Reward Selection (LRS) task. Following baseline fixation, two iso-eccentric targets appear at random locations and the subject is immediately free to choose either target. Target reward magnitudes and differences are fixed in blocks of 40-70 trials and reward block transitions are unsignaled. Target luminance magnitudes and differences are randomly chosen on each trial (see Methods). (c) Expected target choice behavior, plotted as a function of luminance contrast and reward difference between the two targets. When both properties favor selection of the same target (Congruent condition), we expect a strong choice bias toward that target. When luminance contrast and reward difference each favor a different target (Conflict condition), however, it is unclear which target will be selected.

The luminance of T1 was randomly chosen on each trial from a log-uniform distribution of values ranging from 0.01 to 12.15 candelas/m². The minimum of this distribution was set above the psychophysical threshold for stimulus detection during a single-target delayed saccade task for both monkeys. After the luminance parameter for T1 was chosen, the luminance of T2 was assigned such that the mean luminance across both targets was 6 candelas/m². Although the luminance of one target was informative about the luminance of the other target, the randomized target locations guaranteed that subjects could not determine the location of a dim target from the location of a bright target. On each trial, target luminance values were chosen independently from the rewards associated with T1 and T2.

Each monkey performed saccadic eye movements for liquid rewards. The monkeys started each trial by placing both hands on proximity sensors, after which a red square was centrally presented. The monkeys were required to fixate within 2° of the center of the red square for a 500 - 800 ms baseline period. After the baseline, the central red square was extinguished and two red targets (T1 and T2) were presented at random locations in the visual periphery at a 10° eccentricity from the central fixation. We randomized the spatial locations of each target on each trial to reduce the influence of previous experience on the allocation of spatial attention at the start of each trial. The separation between target pairs was constrained to be at least 90° on each trial. Target onset cued the subjects to perform a free-choice saccade to one of the two targets. After the saccade was completed, fixation was maintained for 300 ms at the chosen target, following which the appropriate reward was delivered less than 500 ms after the eye movement was completed. Each trial lasted 890 to 1400 ms, and only one choice could be made per trial. Trials were separated by a 1000-1500 ms inter-trial interval (ITI) beginning at the end of the time of reinforcer delivery. No visual stimuli were presented during the ITI. The range of trial durations derives from the variability in the amount of time taken by the monkeys to select and execute their eye movements. Relative to the duration of the trial, this time was short (mean +/− sd reaction time 168+/−31 ms for Monkey A, 192+/−30 ms for Monkey S). Reaction times shorter than 100 ms, mediated by express saccades (Sommer, 1997), were rare in data from each animal: 1060 trials in Monkey A and 480 trials in Monkey S, or 3% and 1% of all trials, respectively. These data were included in all model fits shown here, and our results were unaffected by their exclusion.

A trial was aborted if the monkey failed to align its gaze within 2° of the center of the fixation or choice targets. When an abort was detected, all visual stimuli were extinguished immediately, no reinforcers were delivered, and the trial was restarted after a 1200 - 1800 ms intertrial interval. Both monkeys rarely aborted trials (4% for Monkey A, 5% for Monkey S). Aborted trials were excluded from further analyses. The data analyzed were 37,816 completed trials for Monkey A (30,938 after excluding the first 10 trials from each block) and 54,026 completed trials for Monkey S (43,774 after excluding the first 10 trials from each block). Data reported here were collected after at least 3 weeks of training on the choice task.

Computational Models of Choice Behavior

We developed computational models of choice behavior to describe steady-state choice behavior and dynamic choice behavior.

Steady-state choice behavior: A generalized linear model (GLM) was fit to steady-state choice behavior to explain choices in terms of choice biases derived from luminance contrast and reward difference after the current reward distribution was learned:

$${\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)={\text{B}}_{\text{L}}-{\text{B}}_{\text{R}}+\text{constant}$$ (1)

where p_T1 and p_T2 are the probability of choosing T1 or T2, respectively, B_L is the luminance-driven choice bias and B_R is the reward-driven choice bias. The exact form of the model is:

$${\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)=\text{L}(\alpha +{\gamma }_{\text{L}}T)-\text{R}(\beta +{\gamma }_{\text{R}}T)+\text{constant}$$ (2)

where L encodes the luminance contrast (log₁₀(L _T1/L _T2)) on the current trial, R encodes the mean reward difference for the current block, and T encodes reaction time on the current trial. In all fits of this model, L and R range from [−1,1], and T ranges from [0,1]. This required us to map luminance contrast (L) from the domain (−2,2) candelas/m² onto (−1,1) for both monkeys. Reward difference (R) was mapped from (−0.2,0.2) mL onto (−1,1) for Monkey A, and from (−0.07,0.07) mL onto (−1,1) for Monkey S. This 3-fold decrease in range was used to correct for Monkey S’s comparatively higher sensitivity to reward differences.

To allow for the possibility that reward information does not become available until a fixed delay after target onset, the reward bias, B_R, was treated as a piecewise linear function that has value β*R at reaction times between 0 and T_min ms, and follows the time-dependent form R(β – γ_RT) when T> T_min. To enforce this piecewise linearity, reaction time (T) was mapped from (128,300) ms onto (0,1) for Monkey A, and from (81,300) ms onto (0,1) for Monkey S. Reaction times less than T_min = 128 or 81 ms, respectively, were linearly mapped onto negative values of T in the B_L expression, but clamped to 0 in the B_R expression. These T_min values were chosen from the range 0-300 ms to minimize the deviance of model fits based on Eqn (2) (see below). In practice, these optimal fits resulted in β ≈ 0 for both monkeys. Therefore, we omitted β from both steady-state fits with only minimal increase of deviance (see Table 1). In all models, the fit quality was similar whether B_R was piecewise linear or not, because most of the reaction times in our data are greater than 128 ms.

Table 1.

Steady State Model – Monkey A

Sample Total = 30,938 trials

Model Parameters	# Parameters	AIC	δAIC
Bias Only	1	42,887	3,356
α	2	41,376	1,845
β	2	41,855	2,324
α, β	3	40,298	767
α, β, δT	4	40,296	765
α, β, δLR	4	40,296	765
α, β, γR	4	39,896	365
α, β, γL	4	39,834	303
α, γL, γR	4	39,531	0
α, β, γL, γR	5	39,528	−3
α, β, γL, γR, δLR	6	39,526	−5

Steady State Model – Monkey S Sample Total = 43,774 trials
Model Parameters	# Parameters	AIC	δAIC
Bias Only	1	60,682	7,139
α	2	60,574	7,031
β	2	54,235	692
α, β	3	54,104	561
α, β, δT	4	54,102	559
α, β, δLR	4	54,102	559
α, β, γR	4	53,723	180
α, β, γL	4	53,898	355
α, γL, γR	4	53,543	0
α, β, γL, γR	5	53,541	−2
α, β, γL, γR, δLR	6	53,539	−4

The α and β coefficients in Eqn (2) measure the initial choice bias derived from luminance contrast and reward difference, respectively, when T = 0. The γ_L and γ_R coefficients specify the rate of change of these choice biases over time. Model parameters were fit through a logistic regression of luminance contrast and reward difference on individual trials, excluding the first 10 trials after each block transition. Therefore, this model studies competitive interactions between contrast and reward at steady state, i.e. after the animal has learned the current reward distribution. The independent variable specified a binary encoding of choice behavior on individual trials, with 1 indicating choice of T1 and 0 indicating choice of T2. All parameters of Eqn (2) were fit using the glmfit command in Matlab (Mathworks) using a logit link function. Although the constant term was unconstrained in the GLM, all constants were zero in the fits and therefore are not reported here. Model predictions for a given set of regressor values were obtained using the glmval command in Matlab. This function returns an estimate of p_T1, the probability of choosing Target 1.

We performed model selection to determine the relationship between all regressors and choice behavior. We fit multiple models using subsets of the coefficients specified by Eqn (2) and tested the reduction in deviance between each pair of models using a likelihood-ratio statistic called Akaike’s Information Criterion (AIC; Akaike, 1974). The AIC estimates the information lost by approximating the true process underlying the data by a particular model (Burnham and Anderson, 1998). For each candidate model, the AIC is computed as

$$\text{AIC}=\text{Deviance}+2\text{k}$$ (3)

where the deviance is the maximized log-likelihood of the model fit and k is the number of parameters. This measure balances the quality of each fit against the increase in model complexity due to the addition of more model parameters (Lau and Glimcher, 2005). The differences in AIC values across models represent the degree of evidence in favor of the best-fitting model, and give a sense of the contribution of each model component when two models differ by inclusion of one parameter. The larger the difference in AIC, the less plausible a model is compared to the best model; values greater than 10 on this scale provide strong support for the model with the smallest AIC value (Burnham and Anderson, 1998). We checked goodness-of-fit by using the best model to predict mean choice behavior (excluding 10 trials following transitions between reward blocks) as a function of reaction time (see Fig 6). We chose not to use cross-validation or bootstrapping methods to further test goodness-of-fit because the AIC already provides a conservative estimate of fit quality and the mean predicted choice behavior was consistent with experimental data using a model with only four parameters.

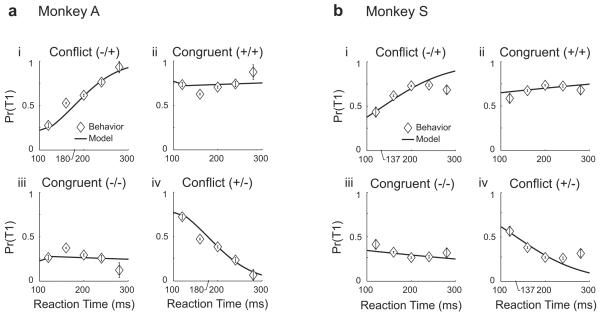
Figure 6. Time evolution of predicted and observed choice probabilities during congruent and conflict scenarios.

(a) Monkey A. (i) In the first conflict scenario, luminance favors T2 and reward favors T1. The bias favors selection of T2 at 100 ms and T1 at 300 ms, with the transition point occurring at 180 ms. (ii) In the first congruent scenario, both luminance and reward favor T1. The bias favors selection of T1 throughout the range of observed reaction times. (iii) The opposite congruent scenario from (ii), favoring T2. (iv) The opposite conflict scenario from (i), favoring T1 and then T2. (b) Same as a for Monkey S. In (i) the transition point occurs at 137 ms.

We also extended the steady-state computational model to test other forms of the dependence between choice behavior, reaction time, luminance and reward. Specifically, we tested an extension of the steady-state model that adds a (δ _TT + δ_LRL*R) term to Eqn (2). The δ _T and δ_LR coefficients describe the influence of reaction time alone and the multiplicative interaction between luminance contrast and expected reward on choice behavior, respectively. AIC values for these model extensions are presented to test whether these terms significantly improve model performance (see Tables 1 and 2).

Table 2.

Dynamic Choice Model – Monkey A (10 trial lag)

Sample Total = 36,500 trials

Model Parameters	# Parameters	AIC	δAIC
Bias Only	1	50,576	3,719
α i	12	48,985	2,128
β i	11	49,416	2,559
αi, βi	22	47,787	930
αi, βi, δiT	33	47,765	908
αi, βi, δiLR	32	47,196	339
αi, βi, γiR	32	47,349	492
αi, βi, γiL	33	47,767	910
αi, γiL, γiR	33	46,857	0
αi, βi, γiL, γiR	43 (lost significance)	46,823	−34
αi, βi, γiL, γiR, δiLR	53 (lost significance)	46,803	−54

Dynamic Choice Model – Monkey S (10 trial lag) Sample Total = 53,424 trials
Model Parameters	# Parameters	AIC	δAIC
Bias	1	74,037	15,038
α i	12	73,854	14,855
β i	11	59,684	685
αi, βi	22	59,430	431
αi, βi, δiT	33	59,408	409
αi, βi, δiLR	32	59,410	411
αi, βi, γiR	32	58,960	−39
αi, βi, γiL	33	59,197	198
αi, γiL, γiR	33	58,999	0
αi, βi, γiL, γiR	43 (lost significance)	58,749	−250
αi, βi, γiL, γiR, δiLR	53 (lost significance)	58,729	−270

Dynamic choice behavior model: To investigate the dependence of choice behavior on previous experience, we extended the steady-state choice behavior model in Eqn (2) to incorporate the influence of luminance contrast and experienced reward values during previous trials:

$${\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)=\sum _{i=0}^{-t}({\alpha }_i{\text{L}}_i+{{\gamma }_i}^{\text{L}}{\text{T}}_0\text{L})-\sum _{i=-1}^{-t}({{\text{R}}_i}^{\text{T}1}-{{\text{R}}_i}^{\text{T}2})({\beta }_i+{{\gamma }_i}^{\text{R}}{\text{T}}_0)+\text{constant}$$ (4)

where the subscript i indexes the value of a coefficient or regressor on trial i with respect to the current trial. R_i^T1 and R_i^T2 represent experienced reward on trial i if the subject chose T1 or T2, respectively. The reward regressor associated with the unchosen target was set to zero on each trial. Therefore, unlike the steady-state choice behavior model, the dynamic choice behavior model makes no assumptions about steady-state behavior and can be used to model changes in choice biases both within and across trials.

The reaction time regressor, T₀, represents reaction time on the current trial (i = 0) only, and uses the same piecewise-linear encoding for each animal described previously. This resulted in β _i ≈ 0 for both animals. We generated variants of equation (4) using subsets of parameters from the full model, and tested the reduction in deviance between each pair of models using the AIC statistic (Table 2). All model fits presented here reflect p<0.05 confidence (Student’s t-test) for all parameter values. Here, we present a 10-trial lag in the dynamic choice model to discover the influence of non-zero regressor coefficients on previous trials while still achieving the desired level of confidence for all fits. We tested models with a lag parameter greater than 10 trials and found that higher-order lag coefficients either were not statistically significant (Student’s t-test) or, when significant, the coefficients at lags greater than 10 trials were all approximately equal to zero. These results indicate that including more than 10 trials in the past is not relevant for understanding choice behavior under the circumstances studied here.

The dynamic choice behavior model is more informative than the steady-state choice behavior model about the drivers of choice behavior on each trial as a function of trial lag. However, this advantage occurs at the expense of significantly increased model complexity. The large number of coefficients necessary to model changing choice biases means we cannot test nonlinear interactions between luminance contrast and reward with the limited numbers of trials available. By contrast, we can use the steady-state choice behavior model to study both linear and nonlinear models of selection. For this reason, both steady-state and dynamic choice behavior models are useful for understanding the processes that drive selection.

Results

A simple conceptual model of selection is that “top-down” expected reward and “bottom-up” sensory input channels drive visual selection, which then drives choice behavior (Fig 1a; Awh, Armstrong, & Moore, 2006; Knudsen, 2007; Theeuwes, 2010). To understand how these drivers interact, we parametrically varied the strength of each driver by training two monkeys to perform a Luminance-Reward Selection (LRS) task (Fig 1b, see Methods) and treating choice behavior as a proxy for visual selection in our analysis. We reasoned that each monkey would show a strong choice bias for one target when reward and luminance differences both favored the selection of the same target (Congruent scenarios; Fig 1c). However, it was unclear which target would be selected when reward and luminance drove selection of different targets (Conflict scenarios).

Figure 2 summarizes behavioral data from two monkeys that performed the LRS task (37,816 trials Monkey A; 54,026 trials Monkey S). Saccade reaction times for both animals were typically within 100-300 ms (Fig 2a(i), 2b(i); express saccades not shown). Since perceptual deficits caused by exogenously captured attention become weaker over time (Bisley and Goldberg, 2003; Giordano et al., 2009), we analyzed the relationship between luminance contrast (calculated using log₁₀(L _T1/L _T2)), where L_k represents the luminance of target k, and target choice probability as a function of reaction time.

Figure 2. Reaction Time Governs The Influence of Luminance Contrast and Reward Difference on Choice Behavior.

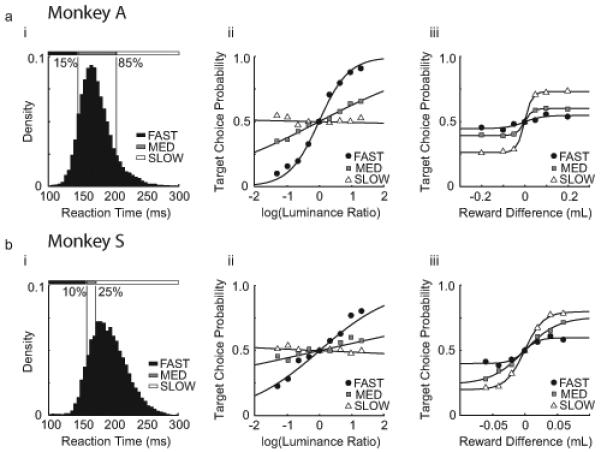
(a) (i) Histogram of free choice reaction times for Monkey A. Data are partitioned into “Fast,” “Medium” and “Slow” categories to illustrate the variability of choice behavior over time. (ii) Summary of target choice probability vs log₁₀(L _T1/L _T2) for the two targets, grouped according to the three reaction time categories described in a(i). (iii) Summary of target choice probability vs reward difference for the two targets, grouped according to the three reaction time categories described in a(i). (b) Same as a for Monkey S. Reaction time category boundaries were chosen so that marginal choice curves were qualitatively similar.

We partitioned each monkey’s reaction time histogram into three categories (Fast, Medium and Slow; Fig 2a(i)) using boundaries chosen to illustrate the variability of choice behavior over time. These boundaries were different across animals, due to idiosyncratic differences in reaction time distributions and time-dependent selection biases. Then we calculated the marginal probability of choosing a target as a function of luminance contrast for all trials with zero reward difference, and grouped these data according to the three reaction time categories. Fig 2a(ii) shows that luminance contrast strongly influences choice probability when reaction time is fast (<140 ms), but these variables become weakly related when reaction time is slow (>200 ms). We observed the opposite relationship when the same analysis was applied to trials with variable reward and zero luminance contrast (Fig 2a(iii)). In these data, reward is weakly related to choice probability when reaction time is fast, but these variables become strongly related when reaction time is slow. These results are qualitatively consistent across reaction time categories for both monkeys (Fig 2b(ii-iii)). However, when compared over absolute time, these data suggest that the reward sensitivity of Monkey S is larger and increases more rapidly after target onset than that of Monkey A.

The marginal choice probability profiles shown in Figure 2 suggest that exogenous and endogenous attention evolve over different time scales, with sensory-driven attention dominating early after target onset, and reward-driven attention dominating later in the trial. Given that these processes are supported by distinct mechanisms in the brain (Kastner and Ungerleider, 2000; Corbetta and Shulman, 2002; Giordano et al., 2009), their influence over choice behavior could be additive when reward difference and luminance contrast are varied simultaneously. To test this hypothesis, we developed the steady-state choice behavior model (Eqns 1,2, and see Methods).

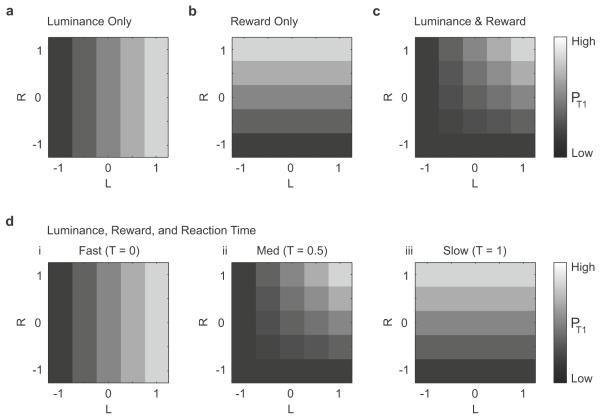
Figure 3 presents the steady-state model for four special cases. When α = 1 and all other parameters are set to zero, the model specifies that target choice probability is a function of luminance contrast alone (Fig 3a). Similarly, when β = −1 and all other parameters are zero, target choice probability is a function of reward difference alone (Fig 3b). When α = 1 and β = −1, target choice probability depends jointly on luminance contrast and reward difference (Fig 3c). Finally, Figure 3d shows a model parameterization that qualitatively reproduces the reaction time dependence of L and R implied by the marginal choice curves in Figure 2. This parameterization is described in equation (5) below:

$${\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)=\text{L}(1-\text{T})+\text{TR}$$ (5)

For fast reaction times (T = 0), Eqn (5) specifies that target choice probability is a function of luminance contrast only. For intermediate reaction times (T=0.5), target choice probability depends jointly on luminance contrast and reward difference. For slow reaction times (T=1), target choice probability is a function of reward difference only.

Figure 3. Predicted choice behavior using different parameterizations of the linear model described in Eqn (2).

(a) Luminance contrast dependence when α = 1 and all other parameters = 0. (b) Reward difference dependence when β = −1 and all other parameters = 0. (c) Joint dependence on luminance contrast and reward difference when α = 1, β = −1 and all other parameters = 0. (d) Target choice transitions from (i) pure luminance contrast dependence at fast reaction time, to (ii) joint luminance-reward dependence at intermediate reaction time, to (iii) pure reward difference dependence at slow reaction time when α = 1, β = 0, γ_L = −1 and γ_R = −1. In each panel, the probability of choosing Target 1, p_T1, is shown in grayscale.

The model parameterization shown in Eqn (5) also makes specific predictions concerning the time evolution of the bias terms, B_L and B_R, during congruent and conflict scenarios (Fig 4). During congruent scenarios, when both L and R favor the same target, the net choice bias (B_L - B_R) favors a single target for all reaction times. During conflict scenarios, when L and R favor different targets, the net choice bias transitions from favoring T1 to T2, or vice versa, at a critical “switching” point, T_switch.

Figure 4. Time evolution of GLM bias predictions for congruent and conflict scenarios.

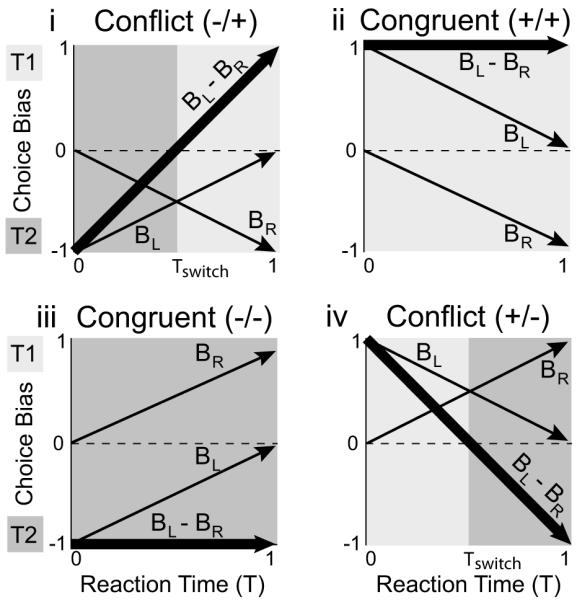
(i) In the first conflict scenario, luminance contrast favors T2 and reward difference favors T1. The sum over bias terms transitions from −1 to +1 with increasing reaction time, illustrating a change in the selected target from T2 to T1 over time. (ii) In the first congruent scenario, both luminance contrast and reward difference favor T1. The sum over bias terms is maintained at +1 for all reaction times. Therefore, the model predicts T1 as the selected target regardless of reaction time. (iii) The opposite congruent scenario from (ii), favoring T2. (iv) The opposite conflict scenario from (i), favoring T1 and then T2. Each panel assumes the parameterization described in Figure 3d.

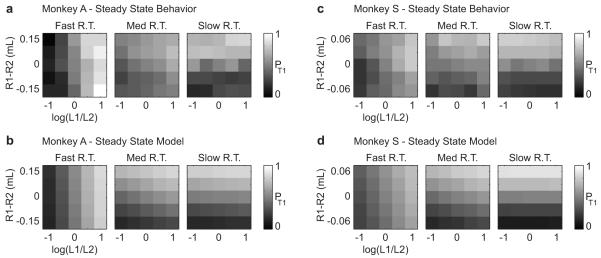
Figure 5a summarizes T1 choice probability, p_T1, for Monkey A’s behavior during trials when luminance contrast and reward difference were varied simultaneously. Behavioral data are grouped according to the reaction time categories shown in Figure 2a(i). In these data, luminance contrast is the primary driver of choice probability when reaction time is fast, luminance contrast and reward difference jointly drive choice probability when reaction time is intermediate, and reward difference is the primary driver of choice probability when reaction time is slow. These behavioral results are consistent across animals (Fig 5c) when grouped by reaction time category.

Figure 5. GLM fits reproduce the behaviorally observed time-dependent transition from luminance to reward dependence of target choice.

(a) Summary of T1 choice probability, p_T1, as a function of log luminance ratio (x-axis), reward difference (y-axis) and reaction time for Monkey A behavioral data. In each panel, data are pooled over the corresponding reaction time interval from Figure 2 a(i). (b) Statistical fit of the data from (a) using the GLM described in Eqn (6). (c) Choice plots for Monkey S, obtained by grouping behavioral data using the reaction time intervals from Figure 2 b(i). (d) Statistical fit of the data from b using the GLM described in Eqn (7).

In separate analyses, we fit the steady-state choice behavior model to behavioral data from each animal on a single trial basis, excluding the first 10 trials from each reward block (see Methods). Table 1 presents the Akaike Information Criterion (AIC) values for variants of Eqn (2) that include subsets of parameters from the full model. Of all linear models tested, the lowest AIC value occurs for models of the form described in Eqn (2). A nonlinear extension to Eqn (2) that incorporates an additional δ_LRLR term did not significantly improve the model fit (Table 1).

The optimal parameterization of Eqn (2) for each animal is described in Eqns (6-7) below:

$$\text{Monkey}\text{A}{\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)=\text{L}(1.9-3.0\text{T})-\text{R}(-3.3\text{T})$$ (6)

$$\text{Monkey}\text{S}{\log }_{10}\left(\frac{p_{T1}}{p_{T2}}\right)=\text{L}(1.5-2.4\text{T})-\text{R}(-3.5\text{T})$$ (7)

Figures 5b,d show the T1 choice probabilities predicted by these models for both monkeys. As suggested by their low AIC values (Table 1), the models shown in Eqns (6-7) provide a good quantitative fit to the behavioral data. These fits do not change substantially when express saccades are included (as shown) or excluded (not shown) from the training data.

A prediction of the steady-state choice behavior model is that target choice bias switches from one target to the other over time during conflict scenarios. We tested this prediction by summarizing T1 choice probability for all congruent and conflict scenarios in our behavioral data and plotting this as a function of reaction time (Fig 6). We then overlaid the T1 choice probability values that are predicted by Eqns (6-7). The model predictions provide a strong quantitative fit to the behavioral data, consistent with the low AIC values shown in Table 1. Notably, during conflict scenarios, the choice probability transitions between targets at times near T_switch = 180 ms for Monkey A and T_switch = 137 ms for Monkey S, which are predicted by the steady-state choice models.

To relax the assumption of reward-driven behavior at steady-state and therefore study the influence of prior experience on choice bias, we extended the model from Eqn (2) to include data from the previous 10 trials (see Methods, Eqn (4)). In this dynamic choice behavior model, T₀ encodes reaction time on the current trial, L_i encodes luminance contrast on the current trial, and (R_i^T1-R_i^T2) encodes the experienced reward on preceding trial i (see Methods). All variables are scaled for consistency with the GLM fits shown in Eqns (6-7). The coefficients α_i, β_i, γ_i^L and γ_i^R specify the weighting of the associated parameter values on indexed trial i. Table 2 shows the AIC values for variants of Eqn (4) that include subsets of parameters from the full model, similar to the analysis shown in Table 1. We were unable to fit a nonlinear interaction parameter, δ_i^LR L_i (R_i^T1-R_i^T2), while maintaining p<0.05 for all parameters in the model, likely due to sampling limitations. Of all models tested, the lowest AIC value occurs for linear models of the form described in Eqn (4).

Figure 7 presents the parameter fits for the dynamic choice behavior model. For Monkey A, α_i = 2.85 on the current trial, but drops to approximately zero for previous trials (Fig 7a). γ_i^L exhibits similar behavior. By contrast, γ_i^R decays monotonically from 1.99 on the previous trial to 0.36 at a 10 trial lag. These results are qualitatively similar for Monkey S (Fig 7b). This confirms that, in the context of the LRS task, the luminance contrast kernel is dominated by the current trial only, whereas the reward difference kernel takes a weighted sum of rewards experienced at a trial lag of at least 10 trials.

Figure 7. Luminance and reward bias kernels for history-dependent GLM.

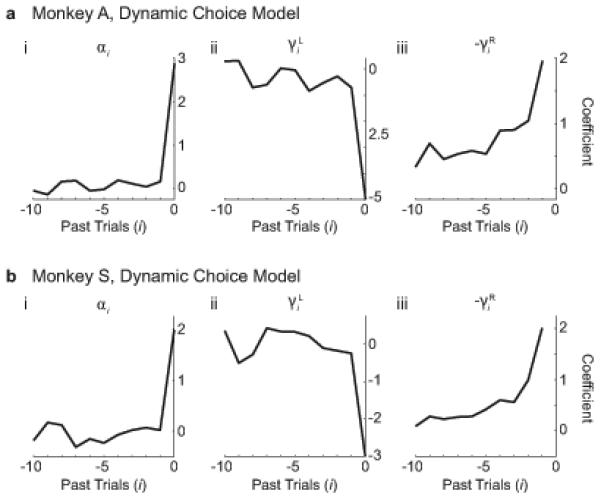
(a) Monkey A. (i) Luminance coefficients (α_i). (ii) Coefficients for reaction time and luminance interaction terms (γ_i^L). (iii) Coefficients for the reaction time and reward interaction terms (γ_i^R). (b) Same as a for Monkey S.

Discussion

In this study, we use a novel Luminance-Reward Selection (LRS) task to demonstrate that choice biases derived from top-down and bottom-up processes combine linearly in time to drive selection. We quantify the dependence of these biases on reaction time and prior experience using computational models of steady-state and dynamic choice behavior. Based on this quantification, the models in Eqns (6-7) predict - and the behavioral data in Figure 6 confirm - that competing sensory and reward-driven processes drive a “switch” in target selection bias at T_switch ≈ 140-180 ms. Our findings in monkeys agree with and build substantially on the human attentional literature, which has shown that visual selection is completely stimulus-driven at time scales <150 ms, while volitional control based on expectancy drives selection at later times (Theeuwes, 2010).

Two features of the LRS paradigm were critical to the recovery of our findings: simultaneous manipulation of top-down and bottom-up attention, and spatial randomization of target locations. Most previous studies of the competitive interaction between top-down and bottom-up processes manipulate attention using separate target and distractor stimuli. Typically, a pre-cue illuminates first, followed by a distractor at some delay, followed by a cue to perform a movement (Reynolds et al., 1999; Bisley and Goldberg, 2003; Giordano et al., 2009; Liu et al., 2009). In such paradigms, spatial attention is allocated to the pre-cue before attention is captured by the distractor, and reward-driven endogenous attention is allocated when the cue appears after the distractor. Therefore, multiple forms of attention are deployed over partially overlapping time intervals. In such cases, the time course of their evolution and interaction is difficult to map without presenting competing stimuli simultaneously and allowing the subject to react immediately, as we do here.

Presenting the two targets at random spatial locations on each trial allowed us to control for the influence of spatial attention on choice behavior. Previous work has shown that spatial biases induced by cueing have a suppressive influence on exogenous attention (Liu et al., 2009) and can improve acuity in the attended area at the expense of unattended areas (Montagna et al., 2009). These data suggest that pre-existing spatial attention may bias competition between stimulus- and goal-driven attention. We reasoned that repeated presentation of two targets to a predictable set of locations might lead to similar biases. In principle, randomization should lead to the deployment of reward-driven attention only and provide an unbiased measurement of its competitive interaction with sensory drive.

Reaction Time Dependence of Selection Biases

The time scales underlying top-down and bottom-up selection processes have been a major focus of experimental work over the last 20 years. Human behavioral studies using the Additional Singleton Task (Kim & Cave, 1999; Theeuwes, 1992; Theeuwes et al, 2000), in which a distractor singleton is presented at a variable delay before a target singleton, have established that the interference effect of a distractor is present at SOAs of up to 150ms before the target singleton. These results in humans are consistent with our observation in monkeys that time-varying stimulus- and reward-driven selection biases can have a balanced influence on behavior at “switching” times that range from 140-180 ms. It is interesting that Monkey S appears to pursue a reward-maximizing strategy by waiting until well after this transition (mean reaction time = 192+/−31 vs T_switch = 137 ms), while Monkey A exhibits greater exogenously-driven behavior (mean reaction time = 168+/−30 vs T_switch = 180 ms).

Although the physiology of top-down and bottom-up competition remains poorly understood, there is experimental support at the single neuron level for “switching” between bottom-up and top-down selection biases at the time scales discussed here. Recordings from isolated V4 neurons in behaving monkeys show that firing rate modulations occur after 175 ms when the animal is looking for a color singleton among an array of targets (Ogawa and Komatsu, 2004), while these modulations do not occur when the monkeys search for a shape singleton. Other studies have demonstrated the dominant influence of salient stimuli on neural activity at times <150 ms in IT (Chelazzi et al., 1998; Chelazzi et al., 2001), PPC (Constantinidis and Steinmetz, 2005) and LIP (Buschman and Miller, 2007). These time scales are consistent with the time-varying stimulus- and reward-driven choice biases described here, and the neural activity may therefore reflect attentional “switching” during competition.

Evidence for Additive Drivers of Selection

An extensive literature has investigated the nature of competitive interactions between top-down and bottom-up attention. The biased competition theory of selective attention (Desimone and Duncan, 1995; Desimone, 1998) has been especially influential. One of its three basic principles of control suggests that competition can be biased by reward-driven and stimulus-driven factors. In this framework, competition between systems is integrated, and the target that is selected in the up-stream processors will be biased-for by down-stream processors. Importantly, biased competition implies a joint - and potentially nonlinear - dependence of choice behavior on sensory and goal-directed processes. Here we show that the effects of these processes on choice behavior are additive over the 100-300 ms reaction time scale studied. One interpretation of these findings is that competition between systems may not be integrated over this time scale. Instead, the dissociable influence of luminance and reward biases on selection implies that top-down and bottom-up processes are functionally independent during the LRS task.

The brain is known to combine information about decision variables using a weighted sum in the auditory (Green, 1958) and visual systems (Young et al., 1993; Landy et al., 1995; Kinchla et al., 1995), and there is recent evidence for this in parietal association cortex (Ipata et al., 2009). Our steady-state model fits demonstrate that a relatively simple linear model is sufficient to reveal the time evolution of choice biases and their influence on behavior at reaction times from 100-300 ms. Future work can investigate the deviation of observed choice behavior from model predictions at reaction times longer than 250 ms during congruent scenarios for Monkey A, and during conflict scenarios for Monkey S.

The behavioral data shown here are consistent with a race between two signals that favor separate targets. The race paradigm has been used previously to model the dynamics of behavior (Logan, G. D., & Cowan, 1984; Boucher et al., 2007). These models connect with our analysis, in which the luminance and reward signals shown in Eqn (1) could serve as inputs to the race signals for each target. Future analysis of our data using a race model may provide greater insight into the reaction time distributions shown in Figure 1.

Changing Selection Bias as Changing Utility

One interpretation of the time dependent selection biases shown here is that the utility of targets changes as a function of reaction time. For the monkeys to make a choice on each trial, they must integrate information regarding the luminance and reward magnitudes of the targets by first converting these values into a “common currency” from which they can be compared (Sugrue et al., 2005; Kable and Glimcher, 2009). Only then can the monkeys form a subjective value for each target and make a choice. Interestingly, the manner in which luminance and reward are converted to this common currency changes over time in the LRS task. Early in a trial, the subjective value of choosing the bright target is highly driven by exogenous attention. As time progresses, however, endogenous attention increases the weighting placed on the high reward magnitude target.

Implications for Priority Map Formation

On a physiological level, our findings are consistent with the formation of two spatial priority maps in the brain that drive the selection process in an additive manner. In lateral intraparietal cortex (area LIP), there is evidence for priority map formation based on visual salience (Gottlieb et al., 1998; Bisley and Goldberg, 2003) and expected reward (Platt and Glimcher, 1999; Bendiksby and Platt, 2006; Rorie et al., 2010). Since LIP receives direct input from dorsal visual areas, it is possible that this area encodes spatial priority based on exogenously-captured attention, in addition to expected reward. This interpretation could reasonably be extended to frontal areas such as the frontal eye fields (FEF), which share strong reciprocal connections with LIP.