Multisensory calibration is independent of cue reliability

Abstract

Multisensory calibration is fundamental for proficient interaction within a changing environment. Initial studies suggested a visual-dominant mechanism. More recently, a cue-reliability based model, similar to optimal cue-integration, has been proposed. However, a more general, reliability-independent model of fixed-ratio adaptation (of which visual-dominance is a sub-case) has never been tested.

Here, we studied behavior of both humans and monkeys performing a heading-discrimination task. Subjects were presented with either visual (optic-flow), vestibular (motion-platform) or combined (visual/vestibular) stimuli, and required to report whether self-motion was to the right/left of straight ahead. A systematic heading-discrepancy was introduced between the visual and vestibular cues, without external feedback. Cue-calibration was measured by the resulting sensory adaptation.

Both visual and vestibular cues significantly adapted in the direction required to reduce cue-conflict. However, unlike multisensory cue-integration, cue-calibration was not reliability-based. Rather, a model of fixed-ratio adaptation best described the data, whereby vestibular adaptation was greater than visual adaptation, irrespective of relative cue-reliability. The average ratio of vestibular to visual adaptation was 1.75 and 2.30 for the human and monkey data, respectively. Furthermore, only through modeling fixed-ratio adaptation (using the ratio extracted from the data), were we were able to account for reliability-based cue-integration during the adaptation process.

The finding that cue-calibration does not depend on cue-reliability is consistent with the notion that it follows an underlying estimate of cue-accuracy. Cue-accuracy is generally independent of cue-reliability and its estimate may change with a much slower time-constant. Thus, greater vestibular vs. visual (fixed-ratio) adaptation suggests lower vestibular vs. visual cue-accuracy.

INTRODUCTION

Integration of input from multiple sensory sources is required for coherent perception and adept interaction with the environment. However, inherent noise and the probabilistic nature of our senses make this task particularly challenging (Knill and Pouget, 2004). Hence the brain requires a proficient strategy for multisensory integration. Optimal integration schemes predict that multiple sensory cues should be weighted in accordance with their relative reliabilities, such that reliable cues are more influential than less reliable cues (Yuille and Bülthoff, 1996; Jacobs, 1999; Landy and Kojima, 2001). Indeed, a number of paradigms have demonstrated reliability-based cue-combination when integrating multisensory input (Ernst and Banks, 2002; van Beers et al., 2002; Alais and Burr, 2004).

Reliability-based cue-combination is considered optimal in that it maximizes precision (synonymous here with reliability; defined by the inverse variance). Nonetheless, it may not account for accuracy, agreement between perception and the environment. If, e.g., a sensory cue is biased, reliability-based cue-combination may result in a biased perception (Watt et al., 2005). Although there are circumstances in which reliability-based cue-combination may still be beneficial even with biased cues (Scarfe and Hibbard, 2011), cue-calibration would enhance the accuracy of multisensory perception. However, without external feedback it may not be possible to assess a sensory system’s accuracy. In this case, the best the brain can do, is detect the relative bias between different sensory systems. Given a systematic discrepancy, sensory cues may undergo mutual calibration in order to achieve “internal consistency” (not to be confused with “external accuracy”, Burge et al., 2010).

Several groups have suggested a reliability-based model for multisensory calibration, whereby the extent of adaptation is determined by each cue’s relative reliability (Ghahramani et al., 1997; Witten and Knudsen, 2005; Burge et al., 2010). Reliability-based adaptation seems a logical extension of reliability-based cue-combination, particularly since the traditional view of visual-dominant adaptation (Rock and Victor, 1964) has been challenged by accounts of visual recalibration (Lewald, 2002; Atkins et al., 2003). However, the most reliable cue might not always be the most accurate (Ernst and Di Luca, 2011). Furthermore, there is still evidence for visual-dominant effects (Knudsen, 2002; Spence, 2009). In fact, visual-dominant adaptation is only a sub-case of a generalized fixed-ratio adaptation model, whereby cues adapt towards one another at a fixed ratio regardless of cue-reliability (possibly according to the underlying estimates of cue-accuracy). Yet, a model of fixed-ratio adaptation has never been quantitatively compared to reliability-based adaptation. Hence the manner, principles and extent to which multiple sensory systems adapt to one-another remains fundamentally missing.

Perception of self-motion and heading-direction relies particularly on visual and vestibular input (Guedry, 1974; Warren and Hannon, 1988; Ohmi, 1996). We have previously shown in a heading discrimination task that visual-vestibular integration largely follows reliability-based cue-combination, for both humans and monkeys (Gu et al., 2008; Fetsch et al., 2009). In this study, we probe the nature of visual-vestibular calibration by introducing a systematic discrepancy between visual and vestibular cues, in the same heading discrimination task, and assessing the resulting perceptual adaptation of the individual cues.

MATERIALS AND METHODS

Separate experiments were performed on humans and monkeys. Details of the apparatus, stimuli and basic task design, previously published for both humans (Fetsch et al., 2009; MacNeilage et al., 2010; Gu et al., 2010) and monkeys (Gu et al., 2007; Gu et al., 2008; Fetsch et al., 2009; Gu et al., 2010), are briefly summarized below together with the methods specific for this study. For further details please see the previous publications.

Human experiment

Nine human subjects (four male) participated in this study. All signed informed consent, and the study was approved by the Washington University Human Research Protection Office. Subjects were seated comfortably in a cockpit-style chair and restrained safely with a five-point racing harness. Each subject wore a custom made thermoplastic mask which was attached to the back of the chair for head stabilization. The chair, a 3-chip DLP projector (Galaxy 6; Barco, Kortrijk, Belgium) and a large projection screen were all mounted on a motion platform (6DOF2000E; Moog, East Aurora, NY) to provide synchronized visual and vestibular input. The projection screen (149 × 127 cm) was located ~70 cm in front of the eyes, subtending a visual angle of ~94° × 84°. Subjects were enclosed in a black aluminum superstructure, such that only the display screen was visible in a darkened room, and wore active three-dimensional glasses (CrystalEyes 3; RealD, Beverly Hills, CA) in order to provide stereoscopic depth cues. The field of view through the glasses was ~70° × 90°.

The subjects’ task was to discriminate heading direction (two-alternative forced-choice, right or left of straight ahead), after presentation of a single-interval stimulus. Subjects were instructed to focus on a central fixation point throughout the duration of the trial. Trials were initiated and choice selection was reported via button press on a handheld unit. Subjects received trial timing related feedback through headphones. However, no feedback about correct or incorrect choices was provided.

The stimulus presented was either vestibular-only, visual-only or simultaneously combined vestibular and visual cues. The vestibular-only stimulus was inertial-motion of the platform in darkness (no optic flow cues). The visual-only stimulus was optic-flow motion simulation, without inertial-motion of the platform. The combined vestibular and visual stimulus comprised inertial motion in conjunction with synchronized optic flow. Although additional cues, such as proprioception and somatosensation, could also be present during inertial motion, we refer to this condition as ‘vestibular’ because primate performance depends strongly on intact vestibular labyrinths (Gu et al., 2007). The stimulus velocity followed a 4-sigma Gaussian profile with duration 1s and total displacement 13cm. Peak velocity was 0.35 m/s and peak acceleration was 1.4 m/s².

The optic flow simulated self-motion of the subject through a random-dot cloud. Visual cue reliability was varied by manipulating the motion coherence of the optic flow pattern, i.e., percentage of dots moving coherently. Three levels of coherence were used: high (100% coherence), medium (50% coherence) and low. The latter was subject-specific, determined such that the subject’s visual threshold was larger than his/her vestibular threshold. Vestibular reliability was fixed throughout the trials. For each session, the actual reliability ratio of the visual/vestibular cues, extracted from single cue psychophysical data, was used for analysis (see section data analysis below). Subjects were given several practice sessions prior to data collection in order to familiarize themselves with the experiment, and in order to extract subject-specific coherence levels for low visual reliability.

Seven heading directions were tested: straight ahead and three to each side. Heading angles were varied in small steps, spaced roughly logarithmically around straight ahead, and presented using the method of constant stimuli. The eccentricities of the heading angles were changed in accordance with the level of visual coherence, such that low visual coherence trials had larger heading direction angles. This was necessary in order to span the psychometric region of interest adequately, since lower coherences yield a wider psychometric curve.

Each experimental session consisted of three consecutive blocks, as follows:

1. A pre-adaptation block comprised cues from only a single (visual-only/vestibular-only) modality, interleaved. The resulting psychometric curves were used to deduce the baseline bias and individual reliability of each modality for the subjects. This block comprised [10 repetitions] × [2 stimuli (visual-only/vestibular-only)] × [7 heading angles] = 140 trials.

2. An adaptation block. In this block, only combined visual-vestibular cues were presented. Across the trials, a discrepancy between the visual and vestibular cues was introduced incrementally: Δ = ±2°, 4°, 6°, 8°, 10°; and then held at ±10° for the remainder of the block. The discrepancy was introduced incrementally in order to prevent awareness of the subject. By convention, the sign of Δ indicated the orientation of discrepancy: positive Δ represented an offset of the vestibular cue to the right and visual cue to the left; negative Δ indicated the reverse. Only one discrepancy orientation, positive or negative, was used per session. Eight repetitions were run for each Δ increment, and an additional seven repetitions were run for maximum Δ (±10°), resulting in [(8 × 5 + 7) repetitions] × [7 heading angles] = 329 trials.

3. A post-adaptation block. During this block, adaptation of the individual (visual/vestibular) cues was measured by single-cue trials, similar to the pre-adaptation block. The single-cue trials were interleaved with combined-cue trials (with Δ = ±10°, as in the end of the adaptation block) in order to maintain the adaptation whilst it was measured. This block comprised [10 repetitions] × [3 stimuli (visual-only/vestibular-only/combined)] × [7 heading angles] = 210 trials.

In total, there were 679 trials in a session, which typically lasted ~60 min. Subjects participated in 12 such sessions: [2 session repeats] × [3 coherences (high/med/low)] × [2 deltas (positive or negative)]. For one subject, low coherence data were not collected; for another, medium coherence data were not collected. Hence these two subjects participated in eight sessions. Sessions were sorted by low, medium and high reliability ratio using the actual cue thresholds (see data analysis section below). In order to test whether there was any influence of measuring both cues in the same session, three subjects participated in eight additional sessions during which cues were tested individually: [2 cues (visual/vestibular)] × [2 coherences (high/low)] × [2 deltas (positive or negative)]. The single-cue protocol was identical to the standard protocol, but all single-cue trials of the other (non-tested) cue were removed. Single-cue trials of the cue being tested and combined-cue trials remained unchanged. There were no observable differences between the results of single-cue sessions and standard sessions. The data presented here are from the standard sessions only. In total N=100 experimental sessions were analyzed from the nine human subjects in this study.

Monkey experiment

Four male rhesus monkeys (Macaca mulatta) participated in the study. All procedures were approved by the Animal Studies Committee at Washington University. Monkeys were head fixed and seated in a primate chair that was anchored to a motion platform, identical to the platform used in the human experiment. Also mounted on the platform were a stereoscopic projector (Mirage 2000; Christie Digital Systems, Cypress, CA), a rear-projection screen and a magnetic field coil (CNC Engineering, Enfield, CT) for measuring eye movements (Judge et al., 1980). The projection screen (60 × 60 cm) was located ~30 cm in front of the eyes, subtending a visual angle of ~90° × 90°. Monkeys wore custom stereo glasses made from Wratten filters (red #29 and green #61, Kodak), which enabled rendering of the visual stimulus in three dimensions as red-green anaglyphs.

As in the human experiment, the monkeys’ task was to discriminate heading direction (two-alternative forced-choice, right or left of straight ahead), after presentation of a single-interval stimulus. The monkeys were required to fixate on a central target during the stimulus, and then report their choice by making a saccade to one of two choice targets (right/left) illuminated at the end of the trial. Like in the human experiment, the stimulus presented was either vestibular-only, visual-only or simultaneously combined vestibular and visual stimuli. The stimulus velocity followed a 4-sigma Gaussian profile with the same parameters as the human experiment: duration 1s; total displacement 13cm; peak velocity 0.35 m/s; peak acceleration 1.4 m/s². Ten heading directions were tested: five to each side. Heading angles were varied in small, logarithmically spaced, steps around straight ahead, and presented using the method of constant stimuli.

The optic flow simulated self-motion of the monkey through a random-dot cloud. Visual cue reliability was varied by manipulating the motion coherence of the optic flow pattern, i.e., percentage of dots moving coherently. Two levels of coherence were used: high (100% coherence) and low. Low coherence was monkey specific – determined such that the monkey’s visual threshold was larger than his vestibular threshold. Vestibular reliability was fixed throughout the trials. For each session, the actual reliability ratio of the visual/vestibular cues extracted from the data was used for analysis (see section data analysis below).

The monkey experimental session was similar to that of the humans, also comprising pre- adaptation, adaptation and post-adaptation blocks. However, at the end of a trial, monkeys were either rewarded or not rewarded with a portion of water/juice. Reward strategy was manipulated in order not to interfere with the adaptation, as described here below:

1. The pre-adaptation block comprised visual-only/vestibular-only/combined cues, interleaved. For some sessions the combined stimulus was excluded. The monkey was rewarded for correct choices 95% of the time and not rewarded for incorrect choices. The 95% correct reward rate was used in order to accustom the monkey to not getting rewarded all of the time, as was the case in the post-adaptation block described below. This block was used to deduce the baseline bias and individual reliability (psychometric curve) of each modality for the monkeys. It comprised [10 repetitions] × [3 stimuli (visual-only/vestibular-only/combined)] × [10 heading angles] = 300 trials. When the combined stimulus was excluded, the block comprised 200 trials.

2. In the adaptation block, only combined visual-vestibular cues were presented. A discrepancy of Δ = ±10° was introduced between the visual and vestibular cues for the entire duration of the block. Like the human experiments, the sign of Δ indicated the orientation of discrepancy: positive Δ represented an offset of the vestibular cue to the right and visual cue to the left; negative Δ indicated the reverse. Only one discrepancy orientation was used per session. During this block, the monkey did not make direction choices. Rather, he was rewarded only for keeping his eyes fixated on the central target for the duration of the trial. Choice targets were not presented at the end of the trial. That way, the reward did not generate any bias for visual/vestibular cues, and perceptual adaptation reflects the mutual influence of the modalities on one-another. This block typically comprised [50 repetitions] × [10 heading angles] = 500 trials.

3. During the post-adaptation block, the adaptation of the individual (visual/vestibular) modalities was measured by single-cue trials, interleaved with the combined-cue trials (with Δ = ±10° as in the adaptation block). The combined-cue trials were run in the same way as in the adaptation block - rewarded by eye-fixation alone with no heading direction choice. They were included in order to retain adaptation. The probability of reward for single-cue trials worked slightly differently to the pre-adaptation block, in order not to perturb the adaptation: When the single-cue trial was at a heading angle, such that if it were a combined-cue trial the other modality would be to the same direction (right/left), the monkey was rewarded as in the pre-adaptation block (95% probability reward for correct choices; no reward for incorrect). If however, the other modality would have been to the opposite side, a reward was given probabilistically (70%, no matter what the choice). This value was chosen since it roughly represents the correct choice rate in a normal heading discrimination task. This block typically comprised [20 repetitions] × [3 stimuli (visual-only/vestibular-only/combined)] × [10 heading angles] = 600 trials. At least 10 repetitions were required in this block for the session to be included in the study.

A typical session comprised ~1400 trials (~2.5 hours in total) and was run at either high/low coherence, with either positive/negative delta. Sessions were sorted by low, medium and high visual to vestibular reliability ratio (RR) using the actual cue thresholds (see data analysis section below). For each monkey there were at least four repetitions for each discrepancy orientation (positive and negative Δ) at both high and low RR. Medium-RR data were of a similar quantity. Monkey C was missing three out of the eight high-RR sessions since 100% visual coherence did not reliably result in high-RR, and coherence cannot be increased greater than 100%. In total N=108 experimental sessions were analyzed from the four monkeys in this study. One medium-RR data-point had a large vestibular shift (>10°) hence it was excluded from Figures 4 and 5. However it was in line with the results and was included in all data analyses and regressions.

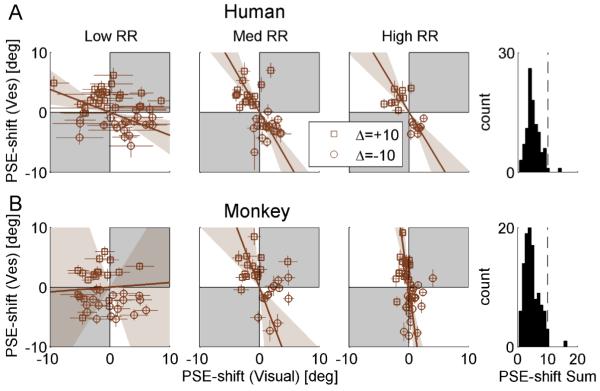
Figure 4. Adaptation ratio.

Population data are presented for both humans (A) and monkeys (B). Data in the first, second and third column are sorted by low, medium and high reliability ratio (RR, ratio of visual to vestibular reliability), respectively. Each data-point represents the adaptation observed in one experimental session, plotted as the shift in vestibular point of subjective equality (PSE) vs. the shift in visual PSE. PSE-shift was calculated as the difference between the pre-adaptation and post-adaptation PSEs. Error bars on the data-points represent ± 1 SD of the PSE-shift (calculated by bootstrapping the psychometric curve data 2000 times). Squares and circles represent sessions with positive Δ (vestibular to the right of visual) and negative Δ (vice-versa) discrepancies, respectively. The brown solid lines represent type-II regressions of the data-points, weighting each data-point by its inverse (mean visual and vestibular) standard deviation. The regression lines were constrained to pass through the origin. The brown shaded regions represent the 95% confidence bands of the regression lines (from 1000 bootstrapped datasets). Gray shading indicates regions where vestibular and visual cues shift in the same direction (unexpected by ‘internal consistency’ theory). Histograms (far right column) indicate that the sum of the absolute visual and vestibular shifts (across all RRs) were primarily < 10° (vertical dashed line). N=45, 38, 17 (100 total) for human low, medium and high RR, respectively. N=36, 28, 44 (108 total) for monkey low, med and high RR, respectively.

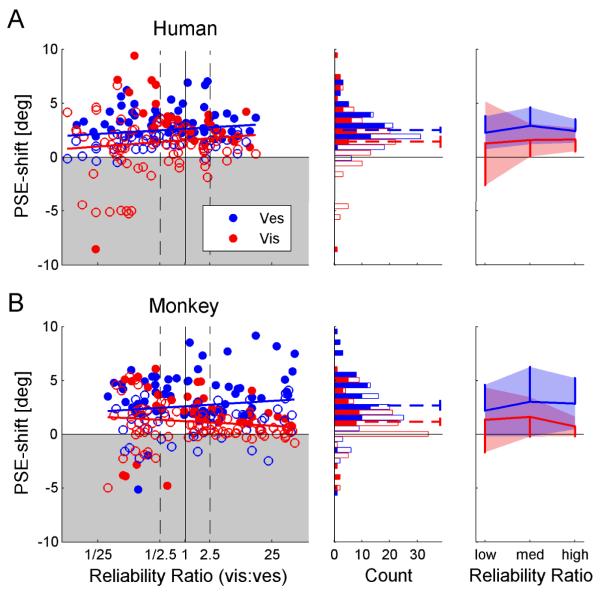
Figure 5. Correct direction PSE-shift.

Human (A) and monkey (B) data were normalized by the direction of cue discrepancy, such that positive values represent a PSE-shift in the expected direction, and negative values represent a PSE-shift in the unexpected direction (gray shaded region). In the left column, the shift in the point of subjective equality (PSE) for vestibular (blue) and visual (red) cues is plotted as a function of reliability ratio (RR, ratio of visual to vestibular reliability). Filled data points represent significant shifts. The blue and red regression lines represent the linear fit of the visual and vestibular PSE-shifts, respectively. Black dashed vertical lines mark the RRs used to sort the data by low, medium and high RR. Blue and red histograms (middle column) display the vestibular and visual PSE-shift distributions, respectively. Filled bars in the histograms represent significant PSE-shifts. Dashed lines represent the mean PSE-shifts, presented with 95% confidence intervals. Mean PSE-shifts, grouped by low, medium and high RR, are presented in the rightmost column. Shaded regions represent ±1 standard deviation, and vertical lines represent one standard deviation. N=100 for the human data and N=108 for the monkey data.

Monkeys were able to perform ‘fixation-only’ trials (as presented in the second and third block) interchangeably with the standard ‘heading-discrimination’ trials (as presented in the first and third block) without any difficulty and they did not need to be cued in advance which type of trial they were doing. This is because they were required to fixate during the stimulus regardless of the type of trial. After the stimulus, either the monkey was rewarded for fixating up until this point (‘fixation-only’ trials) or the central fixation point would disappear and choice targets would appear on the screen (‘heading-discrimination’ trials) cueing the monkey that he has to make a selection.

Data analysis

Data analysis was performed with custom software using Matlab R2006a (The MathWorks, Natick, MA) and the psignifit toolbox for Matlab (version 2.5.6; Wichmann and Hill, 2001a; 2001b). Psychometric plots were defined as the proportion of rightward choices as a function of heading angle, and calculated by fitting the data with a cumulative Gaussian distribution function. For each experimental session, separate psychometric functions were constructed for visual and vestibular cues pre- and post-adaptation. The psychophysical threshold and point of subjective equality (PSE) were the standard deviation (SD, σ) and mean (μ), respectively, deduced from the fitted distribution function. The PSE represents the heading angle of equal right/left choice proportion, i.e., perceived straight ahead, also known as the bias. Visual/vestibular adaptation was measured as the difference between the pre- and post-adaptation PSEs.

For <2% of the post-adaptation distribution functions there was only one data-point that was not zero or one (there were no distribution functions with only zeros and ones). This resulted from a large PSE shift to a region where the curve was sparsely sampled. For these sessions, it was difficult to determine the SD of the cumulative Gaussian. Hence, the pre-adaptation SD was used as a Bayesian ‘prior’ for fitting the post-adaptation psychometric plot. The ‘prior’ was a raised cosine function which touched 0 at the 95% confidence limits of the pre-adaptation SD.

The reliability ratio (RR) was defined as the ratio of the visual to vestibular reliabilities and calculated for each session individually. Cue reliability was computed by taking the inverse of the threshold squared, using the geometric mean of the pre- and post-adaptation thresholds extracted from the fitted psychometric curves. Both for human and monkey experiments, the data were divided into three RRs: low-RR (RR ≤ 2.5⁻¹), med-RR (2.5⁻¹< RR < 2.5) and high-RR (RR ≥ 2.5). Since behavioral performance could change over time due to a ‘practice’ effect, we did not assume that RRs were equal across sessions of the same subject with the same coherence. We therefore calculated the RR for each session individually.

When calculating a linear regression between two dependent variables, each containing uncertainty/noise in their measurements, a type-II regression was used (the perpendicular distances between the data-points and the regression line were minimized).

RESULTS

Behavioural data of the nine human subjects who participated in the human experiment and four monkeys from the monkey experiment were analyzed and are presented in this study. Before presenting the data, we first introduce a brief theoretical background upon which data analysis was based, followed by simulation of the experimental outcome according the theoretical predictions.

Theoretical framework for multisensory adaptation in the absence of external feedback

When presented with an environmental stimulus S, individual sensors (e.g., A and B) will estimate S based on their individual estimator functions: ${\widehat{S}}_A=f_A\left(S\right)$ and ${\widehat{S}}_B=f_B\left(S\right)$, where ${\widehat{S}}_A$ and ${\widehat{S}}_B$ represent their respective estimates. The ‘internal consistency’ hypothesis predicts that if the expectancies of the estimates, $E\left({\widehat{S}}_A\right)$ and $E\left({\widehat{S}}_B\right)$, are not equal, then (in the absence of external feedback) estimator functions will adapt towards one-another to achieve equality and internal consistency. Cue adaptation direction will be dependent on the cues’ discrepancy, Δ:

$$\Delta ={\widehat{S}}_B-{\widehat{S}}_A$$ (Eq. 1)

such that f_A will adapt proportional to +Δ and f_B will adapt proportional to −Δ. However, the rate and extent of adaptation may be different for the cues. How the two estimator functions adapt towards one-another can follow either one of the following principles:

1. Bayesian prediction of multisensory adaptation

The model of reliability-based adaptation (RBA) predicts that the extent to which each estimator function adapts is dependent on the cues’ reliabilities. This was described by Ghahramani et. al. (1997) as the weighted delta rule:

$$\begin{array}{cc}\hfill \delta f_A\left(S\right)& =\eta \cdot w_B\cdot \Delta \hfill \\ \hfill \delta f_B\left(S\right)& =\eta \cdot w_B\cdot (-\Delta )\hfill \end{array}$$ (Eq. 2)

where δf _A and δf_B are the additive changes to the cue estimators, η is the adaptation rate (small positive constant), w_A and w_B are the weights calculated by the cues’ relative reliabilities:

$$\begin{array}{cc}\hfill w_A& =\frac{r_A}{r_A+r_B}\hfill \\ \hfill w_B& =\frac{r_B}{r_A+r_B}\hfill \end{array}$$ (Eq. 3)

and cue reliability (r_A and r_B) is defined as the inverse variance:

$$\begin{array}{cc}\hfill r_A& =1∕{\sigma }_A^2\hfill \\ \hfill r_B& =1∕{\sigma }_B^2\hfill \end{array}$$ (Eq. 4)

Note that w_A + w_B = 1 and that the weights for multisensory adaptation are complementary to those used for multisensory integration. Namely, for cue-integration w_A is used to weight cue-A’s estimate and w_B is used to weight cue-B’s estimate. But, for cue-adaptation the extent of cue-A’s adaptation is determined by w_B and the extent of cue-B’s adaptation is determined by w_A. This is because the more reliable a cue, the higher it will be weighted during integration, and the less it will undergo calibration (and vice versa).

2. Fixed-ratio prediction of multisensory adaptation

Fixed-ratio adaptation (FRA) predicts that cues adapt at a fixed ratio irrespective of relative reliability. Thereby, estimator functions will adapt according to:

$$\begin{array}{cc}\hfill \delta f_A\left(S\right)& =\eta \cdot \Delta \hfill \\ \hfill \delta f_B\left(S\right)& =C\cdot \eta \cdot (-\Delta )\hfill \end{array}$$ (Eq. 5)

where C is a constant. A sub-case of FRA is visual-dominant adaptation (VDA), where the ratio of non-visual cue adaptation to visual adaptation tends to infinity (only the non-visual cue adapts).

Visual-vestibular adaptation - simulation

In order to explain the expected outcome of visual-vestibular adaptation, we simulated performance for the task used in this study according to the theoretical framework presented above. Two models of adaptation were simulated: RBA and VDA. The simulation paradigm was a replica of the human experimental protocol, which was similar to the monkey protocol except for a few slight differences as detailed in the Methods section. Psychophysical discrimination of heading direction was simulated in a two-alternative forced-choice task (right or left of straight ahead). Like the actual experiments, the stimulus comprised either vestibular-only (inertial-motion), visual-only (optic-flow) or simultaneously combined vestibular and visual cues. Simulated psychometric curves depict the ratio of rightward choices as a function of stimulus heading direction (Figure 1, middle three columns). The point of subjective equality (PSE) was extracted from the fitted Gaussian cumulative distribution function, and represents a cue’s estimate for straight-ahead.

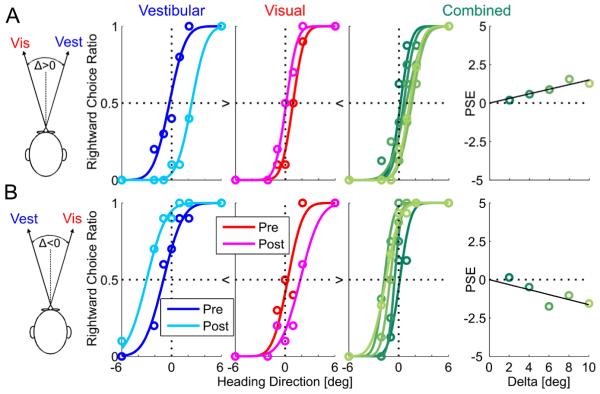
Figure 1. Simulation of multisensory adaptation.

Idealized behavioral responses in a heading discrimination task based on vestibular, visual or both (combined) cues, according to: reliability based adaptation (RBA; A) and visual dominant adaptation (VDA; B). Psychometric plots (middle three columns) represent the simulated ratio of rightward choices, as a function of heading direction. Data (circles) were fitted with cumulative Gaussian functions (solid lines). Baseline performance is presented for vestibular and visual cues by the blue and red curves, respectively. After introducing a heading discrepancy (Δ=10°), vestibular and visual cues adapted to cancel out the discrepancy (cyan and magenta post-adaptation curves, respectively). For RBA, cues shifted according to the visual vs. vestibular reliability ratio (RR), i.e.: for RR=5 (top row) the vestibular cue shifted 5 times more than the visual cue; for RR=1 (second row) cues shifted equally, and for RR=1/5 (third row) the visual cue shifted 5 times more than the vestibular cue. For VDA, the visual cue did not shift (pre- and post-adaptation curves are superimposed); only the vestibular cue shifted. This happens irrespective of RR (RR=1 was used for the example presented here). Dark to light shades of green show the combined-cue responses during adaptation, while gradually increasing Δ = 2°,4°,6°,8°,10°. The combined-cue’s axis (zero) is defined by the heading midway between the cues (schematics on the left). In the rightmost column, the combined-cue point of subjective equality (PSE) is plotted as a function of delta. Solid black lines represent regressions through the origin. For RBA, regression slopes followed the RR: positive for higher visual weighting (top row), negative for higher vestibular weighting (third row) and zero for equal weighting (second row). For VDA the regression demonstrated maximal visual weighting (slope = ½; bottom row).

All baseline (pre-adaptation) simulations were generated with PSE=0, i.e., no heading direction bias. Precision of individual psychometric curves was controlled by setting the variance of the underlying Gaussian functions (Eq. 4). To induce a cue conflict, a discrepancy between the visual and vestibular headings was introduced incrementally: Δ = 2°,4°,6°,8°,10°. Cue adaptation was simulated according to RBA and VDA, and measured by the resulting shift in the visual/vestibular PSEs. For these simulations, multisensory adaptation achieved ‘internal consistency’, namely: visual/vestibular PSEs shifted a combined 10° to cancel out the introduced Δ. We did not simulate the actual time-course of adaptation, but rather the endpoint (from pre- to post-adaptation) according to the ratio of vestibular to visual adaptation predicted by the models. The simulated shifts are presented in Figure 1: vestibular pre- and post-adaptation psychometric curves are presented in blue and cyan respectively; and visual pre- and post-adaptation psychometric curves are presented in red and magenta, respectively.

For RBA (Fig. 1A), both visual and vestibular cues shifted towards one-another. The extent to which each cue shifted was dependant on reliability ratio (RR, ratio of visual to vestibular reliability). Visual and vestibular reliabilities were calculated according to Equation 4, using the variances extracted from the fitted Cumulative Gaussian functions. Three different RRs were simulated: when RR=5 the vestibular cue shifted 5 times more vs. visual (top row), when RR=1 both cues shifted equally (second row) and when RR=1/5 the visual cue shifted 5 times more vs. vestibular (third row). For VDA (Fig. 1B), only the vestibular curve shifted, whilst the visual curve did not shift. This happens irrespective of RR.

The combined-cue responses during the adaptation block can provide insight into the type of adaptation. However, analysis of these data first requires definition of the reference frame because there is no absolute heading direction for the combined-cue when individual cues are discrepant. In this study, the combined-cue axis (zero) was artificially defined by the heading midway between the visual and vestibular cues. Hence, during the simulated adaptation block, the visual and vestibular heading angles were +Δ/2 and −Δ/2, respectively. As Δ increased, both cues headings’ became more eccentric but remained symmetric around the combined-cue zero. For each value of Δ, the combined psychometric curve was calculated (second column from the right, Fig. 1). The combined-cue PSE was then extracted and plotted as a function of Δ (rightmost column, Fig. 1). Positive or negative combined-cue-PSE values therefore indicate higher visual or vestibular weighting, respectively. Zero PSE indicates equal weighting.

The combined plots presented here should therefore not be mistaken to represent a psychometric shift. In fact, according to both model simulations (RBA and VDA) the combined-cue response doesn’t shift, in world coordinates, during adaptation. Rather, the observed changes in combined PSE are due to increasing Δ and the concurrent increase in heading eccentricity of the individual cues. Why do both RBA and VDA not predict a shift in the combined-cue? If cue-combination and cue-adaptation follow the same model, then the combined-cue will not shift. This is because during cue-adaptation, cues converge on the initial cue-combination. For example, i) visual dominant cue-combination always aligns the combined response with the visual cue; during VDA, only the vestibular cue adapts until it is aligned with the visual cue. Hence the combined cue will not change during VDA. ii) During RBA, visual and vestibular cues shift according to the weights of Equation 3 - the same weights used for reliability-based cue-combination (RBCC). Hence the combined cue response will remain unchanged during RBA. If, however, different models were used for cue-combination and cue-adaptation, the combined response would shift during adaptation. This issue is further discussed in the last section of Results.

Therefore, in this simulation, the slope of combined PSE vs. Δ (rightmost column, Fig. 1) is simply an indication of cue weighting: a positive vs. negative slope indicates higher visual vs. vestibular weighting, respectively. A zero slope indicates equal weighting. For RBA: when RR=5 the combined response was weighted more by the visual cue (positive slope; top row), when RR=1/5 it was weighted more by the vestibular cue (negative slope; third row) and when RR=1 there was equal weighting (zero slope; second row). For VDA: the combined response always aligns with the visual cue (at +Δ/2). Hence the combined-PSE vs. Δ always demonstrates the maximum slope, ½ (bottom row).

Visual-vestibular adaptation - examples

In the simulation presented in Figure 1, a cue conflict of Δ = +10° was used (vestibular cue offset to the right; visual to the left). The predictions for Δ = −10° (vestibular cue offset to the left; visual to the right) are the same, but with shifts in the reverse direction. In the actual experiments, both orientations of Δ were used. Hence when analyzing the data, the predicted cue-shifts for positive vs. negative Δ are equal, but opposite in sign/direction.

Figure 2 shows representative psychophysical data from one human subject. Two experimental sessions are presented, for both possible orientations of cue conflict (Δ = ±10°). Motion dot coherence was 100% and RR>1 for both examples (cue reliabilities were calculated using Eq. 4 and the fitted Gaussian functions). Cue shifts are presented here with 95% confidence intervals for the PSE, calculated by bootstrapping the psychometric curve: For Δ = +10° (Fig. 2A) the vestibular PSE shifted from −0.3° [−0.9, 0.4] to 2.4° [1.6, 3.2] and the visual PSE shifted from 0.9° [0.4, 1.5] to 0.1° [−0.4, 0.6]. For Δ = −10° (Fig. 2B) the vestibular PSE shifted from −1.0° [−1.8, −0.2] to −3.0° [−4.4, −1.9] and the visual PSE shifted from 0.3° [−0.3, 1.0] to 1.8° [1.0, 2.8].

Figure 2. Example of human multisensory adaptation.

Two example sessions of visual-vestibular adaptation, from one human subject, are presented. For both sessions, visual coherence=100% (RR >1). Plotting conventions are the same as Figure 1. However, opposite visual-vestibular heading discrepancies (Δ) were used for the two examples: In (A) Δ was positive. Hence results can be compared directly to the simulation results of Figure 1 (which also used positive Δ). In (B) Δ was negative. Hence, shifts are expected in the reverse direction. R²≥0.9 for all psychometric fits.

For both examples, visual and vestibular psychometric curves shifted in the direction required to reduce cue conflict (similar to the RBA simulation, Figure 1A). However, unlike the simulations, ‘internal consistency’ was not achieved: vestibular + visual cues shifted only a combined 2.7° + 0.8° = 3.5° for the example in Figure 2A, and 2.0° +1.5° = 3.5° for the example in Figure 2B; less than the introduced discrepancy of 10°. The (absolute) ratio of vestibular to visual PSE adaptation was 2.7°/0.8° = 3.4 for the example in Figure 2A and 2.0°/1.5° = 1.3 for the example in Figure 2B; compared to the RR predictions of 1.9 and 1.1, respectively. The positive (Fig. 2A) and negative (Fig. 2B) slope of the combined-PSE vs. Δ indicate higher weighting of the visual cue, as expected for RR>1.

Similarly, Figure 3 shows representative psychophysical data of two experimental sessions from one monkey (Δ = ±10°). Motion dot coherence was 100% and RR>1 for both examples (cue reliabilities were calculated using Eq. 4 and the fitted Gaussian functions). Cue shifts are presented here with 95% confidence intervals for the PSE, calculated by bootstrapping the psychometric curve: For Δ = +10° (Fig. 3A) the vestibular PSE shifted from 0.5° [−1.4, 2.3] to 4.0° [2.7, 5.7] and the visual PSE shifted from −0.3° [−0.9, 0.7] to −0.5° [−1.1, 0.0]. For Δ = −10° (Fig. 3B) the vestibular PSE shifted from 0.6° [−0.9, 2.2] to −6.6° [−8.7, −4.9] and the visual PSE shifted from 0.8° [−0.3, 1.7] to 2.3° [1.8, 3.0].

Figure 3. Example of monkey multisensory adaptation.

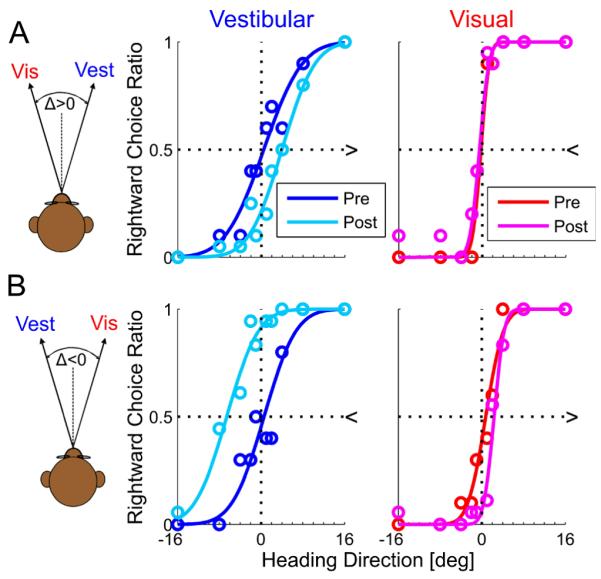
Two sessions from one monkey of visual-vestibular adaptation are presented. For both sessions, visual coherence=100% (RR>1). Plotting conventions are the same as Figures 1 and 2. Opposite visual-vestibular heading discrepancies (Δ) were used for the two examples: In (A) Δ was positive. Hence results can be compared directly to the simulation results of Figure 1 (which also used positive Δ). In (B) Δ was negative. Hence, shifts are expected in the reverse direction. Unlike Figures 1 and 2, there are no combined-cue data during the ‘adaptation’ trials from the monkey experiment. R²≥0.9 for all psychometric fits.

Similar to the human examples, visual and vestibular psychometric curves shifted in the direction required to reduce cue conflict, but did not achieve ‘internal consistency’: the combined vestibular + visual shift was 3.5° + 0.3° = 3.8° for the example in Fig. 3A and 7.2° + 1.6° = 8.6° for the example in Figure 3B. The (absolute) ratio of vestibular to visual adaptation was 3.5°/0.3° = 11.7 for the example in Figure 3A and 7.2°/1.6° = 4.5 for the example in Figure 3B; compared to the RR predictions of 15.9 and 5.7, respectively. There were no behavioral responses during the adaptation block of the monkey experiments due to experimental constraints (the monkeys were rewarded for fixation only during the adaptation block and therefore did not make heading selections, see methods).

Cue adaptation ratio changes with cue reliability

To quantify the results across experimental sessions, we first used an analysis based on cue adaptation ratio, as previously done by Burge et. al. (2010). Because visual and vestibular cues are expected to adapt towards one-another, their psychometric shifts should always be opposite in direction. Hence the ratio of vestibular to visual shift should always be negative. Also, shift directions should reverse for positive vs. negative Δ. Therefore a single data-point, plotted as the vestibular vs. visual psychometric curve shift is expected to lie in quadrant-II of the Cartesian plane (top-left: positive vestibular shift, negative visual shift) for positive Δ; and in quadrant-IV (bottom-right: negative vestibular shift, positive visual shift) for negative Δ. Hence, a regression line of pooled vestibular vs. visual shifts is expected to have negative slope, with two possible extremes: a vertical line would indicate only vestibular (and no visual) shift; a horizontal line would indicate only visual (and no vestibular) shift.

RBA predicts that the magnitude of the visual to vestibular shift ratio should be dependent on RR. Specifically, for high-RR the vestibular shift is expected to be larger in magnitude than the visual shift, i.e., near-vertical regression line. For low-RR, the visual shift is expected to be larger in magnitude than the vestibular shift, i.e., near-horizontal regression line. Finally for medium RR, comparable magnitudes are expected, i.e., regression line with slope around −1. In contrast, FRA predicts that the slope will be fixed according to a constant adaptation ratio, such that the same slope would be seen for low, medium and high RR. A special case of FRA is VDA which predicts a vertical regression line - only vestibular adaptation, irrespective of RR.

In order to test which model best depicts cue adaptation, the data were sorted by low, medium and high RR and the vestibular vs. visual shifts plotted (Fig. 4). The results clearly contradicted the VDA model, since visual shifts were observed. In fact, for both the human (Fig. 4A) and the monkey (Fig. 4B) data, there seemed to be an influence of RR on cue adaptation, suggestive of RBA and not FRA. As predicted by RBA, high-RR data approach a vertical line (third column of Fig. 4; especially for the monkey data) vs. low-RR data, which approach a horizontal line (first column of Fig. 4). Such conclusions would be similar to those of Burge at. al. (2010), who concluded that visual/haptic cue adaptation follows the RBA model. However, these results need to be treated with caution due to the large changes in variability observed for different RRs. Specifically, variability of visual PSE-shifts increased with decreasing RR - as discerned by the distribution of data along the x-axis (Fig. 4; these changes in variability are quantified below and in Fig. 5, rightmost column). In fact, data variability itself can strongly influence the orientation of the regression lines (we elaborate on this point in the Discussion). Hence these plots are not adequate to conclude that cue-adaptation follows RBA.

If cue adaptation were to achieve ‘internal consistency’, then the absolute sum of cue shifts would equal 10°. When summing the absolute visual and vestibular PSE shifts (histograms in Fig. 4), it is very apparent that cue adaptation does not reach ‘internal consistency’. In fact, for almost all of the data, the sum of PSE shifts was <10°. This is not surprizing given the limited length of our experiments. Visual inspection of the cue-shift plots from Burge at. al. (2010) indicate the same to be true for visual-haptic adaptation.

Complete adaptation (internal consistency) is actually not a requirement to test the models. This is because, according to the theoretical framework presented above, the ratio of cue adaptation would be the same after partial adaptation as for complete adaptation. However, due to the large variability in cue shifts (as described above) the adaptation ratio may not adequately represent individual sessions. Furthermore, cues sometimes shifted in the ‘unexpected’ direction (marked by the gray regions in Fig. 4; especially the visual cue at low-RR). Therefore, in order to gain further insight into the effects of cue reliability on adaptation, we next analyzed adaptation magnitude separately for visual and vestibular cues.

Cue adaptation magnitude does not correlate with relative cue reliability

The magnitude of individual-cue PSE shifts were plotted as a function of RR (Fig. 5, leftmost column). Blue and red circles represent vestibular and visual shifts, respectively; filled circles indicate significant shifts. For both the human (Fig. 5A) and the monkey (Fig. 5B) data, linear regressions were calculated separately for the visual and vestibular cues. Dependence of cue adaptation magnitude on RR was assessed by testing whether the p-value of Pearson’s correlation coefficient was less than 0.05. Strikingly, there were no significant correlations between vestibular or visual PSE-shifts vs. RR: In the human data, R=0.16 (p=0.11) and R=0.11 (p=0.29) for the vestibular and visual correlations, respectively. This is in contrast to the RBA prediction of a positive correlation for vestibular PSE shifts and a negative correlation for visual PSE shifts. In the monkey data, a small tendency for opposite dependence was seen, but the slopes were not significantly different from zero. R=0.12 (p=0.23) and R=−0.13 (p=0.19) for the monkey vestibular and visual correlations, respectively.

The vestibular cue adapts more than the visual cue, irrespective of reliability ratio

The distributions of vestibular and visual PSE shifts (for all RRs pooled) are presented by blue and red histograms in Figure 5 (middle column), respectively. The filled sections in the bars represent significant shifts. Cue shift distributions were analyzed statistically under the null hypothesis of no shift, and p-values were calculated using t-tests and the Bonferroni correction for multiple comparisons. The mean vestibular and visual shifts (blue and red dotted lines superimposed on the histograms) were significantly positive, i.e., in the ‘expected’ direction, for both the human (Fig. 5A) and the monkey (Fig. 5B) data (p<0.0001 for all four comparisons). Furthermore, the average vestibular shift was significantly greater than the average visual shift, both in the human (p<0.01) and the monkey (p<0.0001) data. The ratio of vestibular to visual PSE-shift was around 2:1 (1.75 for humans and 2.30 for monkeys).

When grouping the data by low, medium and high RR (rightmost column) the mean vestibular PSE shift (blue) was always greater than the mean visual shift (red), even for low RR. This too is demonstrated for both the human and monkey data, and is contrary to the RBA prediction. Furthermore, comparing the mean PSE shift for low-RR vs. high-RR (separately for visual and vestibular cues), revealed no significant differences for either the human or monkey data (p>0.2 for all four comparisons, using a t-test). However, we did find that the standard deviation for visual PSE-shifts (red vertical lines) was significantly greater at low-RR than high-RR, for both the human and monkey data (p<0.0001, using a chi-square test and the Bonferroni correction for multiple comparisons). In contrast the standard deviations for vestibular PSE-shifts (blue vertical lines) remained unchanged, for both the human and monkey data (p>0.1). Hence, the only factor dependant on RR was visual PSE-shift variability.

The finding that the vestibular cue shifts more, and the visual cue less than expected by RBA, is also demonstrated when analyzing proportional cue shifts. For this analysis, proportional PSE shifts were calculated as follows:

$$\begin{array}{cc}\hfill \text{Proportional}\text{Visual}\text{PSE}\text{Shift}& =\frac{\text{Visual}\text{PSE}\text{Shift}}{\mid \text{Visual}\text{PSE}\text{Shift}\mid +\mid \text{Vestibular}\text{PSE}\text{Shift}\mid }\hfill \\ \hfill \text{Proportional}\text{Vestibular}\text{PSE}\text{Shift}& =\frac{\text{Vestibular}\text{PSE}\text{Shift}}{\mid \text{Visual}\text{PSE}\text{Shift}\mid +\mid \text{Vestibular}\text{PSE}\text{Shift}\mid }\hfill \end{array}$$ (Eq. 6)

It should be noted that when cues shift in the unexpected direction, calculating the proportional PSE shift may be an ill-posed problem.

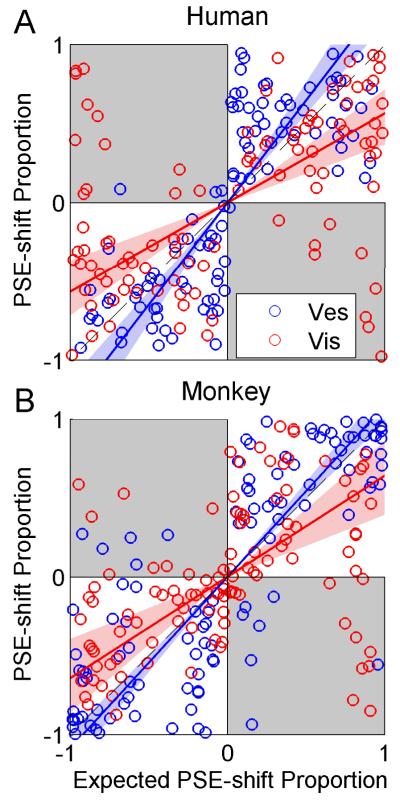
Expected proportional PSE shifts were predicted by the relative cue reliabilities according to RBA. In Figure 6, the proportional shift data are plotted vs. the expected proportional shifts. Blue and red lines represent regressions for the vestibular and visual data, respectively, and shaded regions represent 95% confidence bands of the regressions based on 1000 bootstrapped datasets. The diagonal (dashed) lines represent the expected regression if proportional shifts were to follow prediction. Significance was judged by whether or not the 95% confidence band included the diagonal. In the human data (Fig. 6A) the relative vestibular shift was significantly greater than expected, and the relative visual shift was significantly less than expected. In the monkey data (Fig. 6B) the relative vestibular shift was greater (albeit not significantly) than expected, and the relative visual shift was significantly less than expected.

Figure 6. Actual vs. expected proportional PSE-shift.

Actual vs. expected proportional PSE-shifts are plotted for the human (A) and monkey (B) data. Blue and red lines represent type-II regressions of the vestibular and visual data (blue and red circles), respectively. The regression lines were constrained to pass through the origin. Blue and red shaded regions represent 95% confidence bands of the regressions. If PSE shifts were to follow the RBA predictions, the regression for both cues would lie on the line y=x (dashed black line). Gray shading represents regions where adaptation was in the unexpected direction.

A model of fixed ratio adaptation better accounts for visual and vestibular PSE shifts

Our findings that cue adaptation magnitude does not correlate with relative cue reliability and that the vestibular cue adapts more than the visual cue, irrespective of reliability ratio (Fig. 5), strongly implicate a FRA model. Furthermore, by dividing the average vestibular shift by the average visual shift, we found that the ratio representative of the FRA model was roughly 2:1. However, cue adaptation-ratio analysis on a session-by-session basis, as described by Burge at. al. (2010) and in our comparable Figure 4, seemed to suggest that there might also be a reliability based component. Hence, we performed additional analysis in order to see whether RBA or FRA would best describe the individual session adaptation ratios.

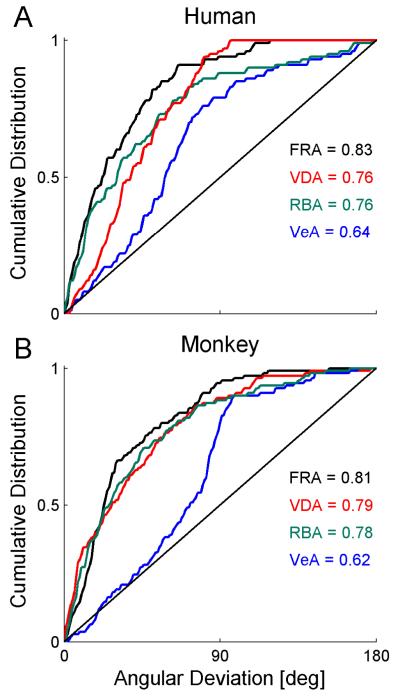
Each session’s adaptation-ratio can be described by the angle it subtends on the Cartesian plane (as seen in Fig. 4). To compare the various models, we calculated the difference between each data-point’s angle and the models’ predicted angles. A 0° difference would indicate perfect alignment between the data and model prediction; a 180° difference would indicate that the data behaved diametrically opposite to the model’s prediction. We compared four models: Fixed ratio adaptation (FRA), visual dominant adaptation (VDA), reliability-based adaptation (RBA) and vestibular dominant adaptation (VeA). VeA, which predicts only visual and no vestibular adaptation, is not a viable model. It was introduced here only for the sake of comparison because it is the complementary form of VDA and hence also a sub-case of FRA, at the other extreme to VDA. For FRA, the actual vestibular-visual adaptation ratio extracted from the mean PSE shifts (Fig. 5) was used: 1.75 and 2.30 for humans and monkeys, respectively.

The cumulative distribution of the angular deviation of the data from each model is presented in Figure 7. Model fits were quantified by taking the mean of the cumulative distribution. These are annotated on the plots. Essentially, the mean of the cumulative distribution is equivalent to the normalized area under the curve. For a perfect model, all angular deviations would be 0. Hence the cumulative distribution, and mean thereof, would be 1. A random model would produce, on average, a diagonal cumulative distribution (solid black lines in Figure 7) with a mean value of 0.5. The cumulative distribution means were used to compare the models statistically using t-tests. In order to minimize the number of comparisons, VeA was not compared statistically since it was apriori not considered a viable model. Two model comparisons were made: RBA vs. FRA and RBA vs. VDA.

Figure 7. Adaptation data was best represented by a fixed ratio model.

When plotted on the Cartesian plane, vestibular vs. visual PSE adaptation can be described by a vector. The angle of that vector represents the ratio of vestibular to visual adaptation. Here we compared the adaptation-angles extracted from the data, to those predicted from four different models: Fixed ratio adaptation (FRA), visual dominant adaptation (VDA), reliability-based adaptation (RBA) and vestibular dominant adaptation (VeA). The cumulative distribution of the difference between the actual and predicted angles, was plotted for both the human (A) and monkey (B) data. The black diagonal line represents the average cumulative distribution for random angles. The mean of the cumulative distribution is presented on the plots for each model.

The results indicate that even for session-by-session shift-ratio analysis (which suggested an element of RBA in Fig. 4), FRA best describes the data for both humans (Fig. 7A) and monkeys (Fig. 7B). FRA was significantly better than RBA for the human (p=0.012, after the Bonferroni correction for multiple comparisons), but not monkey, data (p>0.2). VDA and RBA were statistically indistinguishable for both the human and monkey data (p>0.8 for both). As expected, VeA provided the worst model fit.

Fixed ratio adaptation accounts for reliability based cue combination

We have previously shown, with the same heading discrimination task used in this study, that visual and vestibular cues follow reliability based cue combination (RBCC; Gu et al., 2008; Fetsch et al., 2009). Knowing that RBCC is employed, we can study the behaviour of the combined visual and vestibular cues, during and after adaptation, in light of RBCC. This could provide additional insight into the type of adaptation that the cues underwent. According to RBCC, the combined heading perception is a weighted sum of the individual cues. Hence, the combined-cue heading perception will depend on how the individual cues themselves have adapted. The predictions for combined-cue heading perception are very different for RBA vs. FRA. Combined-cue heading behaviour can therefore indicate whether the underlying adaptation followed RBA or FRA.

In order to explain the different predictions of RBA and FRA for the combined cue estimate, we return to a concept that we introduced in Results section Visual-vestibular adaptation - simulation. If cue-combination and cue-adaptation follow the same model, then the combined-cue response should not shift during adaptation. This can be understood intuitively as follows: when individual cues are disparate, without external feedback they will adapt to converge on their combined-cue estimate. E.g., for visual dominance, the initial combined-cue estimate is the visual cue, which is itself the endpoint of convergence according to VDA; for a reliability based model, the initial combined-cue estimate is the weighted average, which is itself the endpoint of convergence according to RBA. Hence, the combined-cue estimate should remain unchanged throughout the process of adaptation. If however cue-adaptation uses a different model to cue-combination, then combined-cue perception should change during adaptation.

For this analysis, we used the combined-cue behaviour during adaptation, available in the human (but not monkey) data. The combined-cue heading bias in relation to the visual and vestibular cues was extracted from the data by finding the slope of the combined-cue-PSE vs. Δ. As explained above and presented in Figures 1 and 2, the slope of the combined-cue-PSE vs. Δ ranges from −½ to ½. A slope of ½ would indicate complete visual dominance, and a slope of −½ would indicate completed vestibular dominance. A slope of zero would indicate equal weighting of visual and vestibular cues. RBCC could therefore be quantified by the slope of the combined-cue-PSE vs. Δ.

In Figure 8A we demonstrate, through simulation, the predicted responses of the RBA and FRA models to an introduced heading discrepancy (Δ) between the cues. Like the simulation for Figure 1, the visual cue was presented at −Δ/2 and the vestibular cue at +Δ/2. Pre-adaptation, combined-cue PSE slopes that would result from visual or vestibular cue dominance are represented by the red and blue solid lines, respectively, and the RBCC is represented by the dark green line (Fig. 8A; same for FRA and RBA). Pre-adaptation curves can be understood as follows: visual dominance would result in a combined-cue-PSE vs. Δ slope of ½ (red line) and vestibular dominance would result in a slope of −½; for RR>>1, RBCC asymptotes to visual dominance, whereas for RR~0 it asymptotes to vestibular dominance.

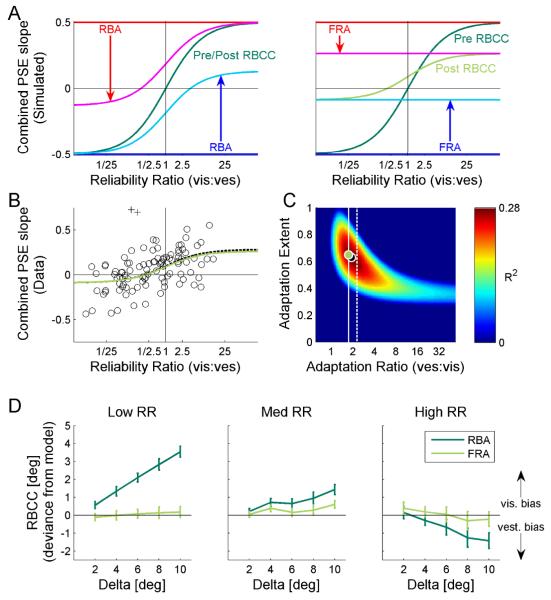
Figure 8. Fixed ratio adaptation accounts for reliability based cue combination.

(A) We present a simulation of the expected reliability based cue combination (RBCC) adaptation. RBCC was quantified by the slope of the combined-cue-PSE vs. delta (as presented in Fig. 1 and 2). Two models of adaptation were simulated: reliability based adaptation (RBA, left plot); and fixed ratio adaptation (FRA, right plot). For FRA, a vestibular to visual adaptation ratio of 1.75 was used (as extracted from the actual cue shifts). For both simulations, partial (65%) adaptation is presented, i.e., the cues did not reach ‘internal consistency’. Prior to adaptation, combined-cue-PSE slopes that would result from visual or vestibular cue dominance are represented by the red and blue horizontal lines, respectively, and post-adaptation by magenta and cyan curves, respectively. RBCC is represented by the dark green and light green curves, pre- and post-adaptation, respectively. For RBA, RBCC remained unchanged (pre- and post-adaptation curves are superimposed). For FRA, the RBCC curve amplitude changed and its y-cut became non-zero. (B) The actual data of combined-cue-PSE vs. Δ slopes is presented (circles). Two outliers are marked by ‘+’ symbols. The optimal FRA model fit is represented by the black dashed curve, and the model fit with adaptation ratio constrained at 1.75 is presented by the light green curve. (C) The R²-values of the FRA model fit for all possible parameters of adaptation-ratio and - extent are presented. The light green and (partially hidden) black dots represent the R²-values for the ratio-constrained and optimal fits, respectively. The white vertical lines represent the adaptation-ratio extracted from the human (solid) and monkey (dashed) data. (D) The average difference between the actual combined PSEs and the models’ predictions are presented. Dark and light green lines show the deviances for RBA and FRA, respectively. Error bars represent the standard error of the mean.

As we demonstrated above, ‘internal consistency’ was not achieved in our data. Hence we did not constrain the models to complete adaptation; rather the extent of adaptation was a parameter which ranged from 0 (pre-adaptation) to 1 (internal consistency). In this simulation, an adaptation-extent of 0.65 was used. The vestibular to visual adaptation ratio used for the FRA simulation was 1.75, since this was the actual ratio extracted from the data (Fig. 5A). Post-adaptation, cyan and magenta lines represent the combined-PSE slope that would result from visual and vestibular dominance, respectively. Similar to pre-adaptation, post-adaptation RBCC asymptotes to these curves. For RBA (Fig. 8A, left) the cues adapted according to the same weights as RBCC. Hence the RBCC remained unchanged even after adaptation (superimposed on the dark green curve). In contrast, according to FRA the cues adapted at a fixed ratio irrespective of RR (Fig. 8A, right). Since adaptation followed different weights to cue-combination, the RBCC response changed during adaptation (light green curve).

For FRA, two major changes are evident in the RBCC curve: i) the entire curve shifted vertically, as seen by the y-intercept, and ii) the curve narrowed, as seen by the reduced y-amplitude. The former resulted directly from the ratio of vestibular to visual adaptation, and the latter resulted directly from the extent of adaptation. Hence, according to FRA, the combined-cue response can be predicted based on two model parameters: i) the ratio of vestibular to visual adaptation, and ii) the extent of adaptation. These predictions are very different to RBA, which predicts no change to cue-combination during adaptation.

The actual RBCC data are presented in figure 8B (circles). Data were fit by the following function:

$$f\left(BR\right)=A\cdot \frac{RR-1}{RR+1}+B$$ (Eq. 7)

where RR is the visual to vestibular reliability ratio, and A and B are parameters used for optimization. A and B have a one-to-one relationship with the extent and ratio of adaptation as follows:

$$\begin{array}{cc}\hfill A& =\frac{1-extent}{2}\hfill \\ \hfill B& =\frac{extent\cdot (ratio-1)}{2\cdot (ratio+1)}\hfill \end{array}$$ (Eq. 8)

Hence, each combination of the two parameters (adaptation-ratio and adaptation-extent) represents a specific RBCC curve. The goodness of fit (R²) was calculated for each curve according to the standard formula:

$$R^2=1-\frac{residualsumofsquares}{totalsumofsquares}$$ (Eq. 9)

Since the curves were defined externally in order to span the parametric range (and not fitted to the data) some curves provided a worse fit than the data mean. For these curves, Equation 9 would result in a negative value. Hence R² was truncated at 0.

Figure 8C presents the R² values for all possible combinations of adaptation-ratio and adaptation-extent. The optimal fit is represented by a dashed line in Figure 8B and a black dot in Figure 8C. According to the FRA model, we should be able to predict the RBCC fit based on the adaptation-ratio and adaptation-extent. Whilst the adaptation-extent may be unknown (these data are taken during the course of adaptation), the adaptation-ratio should follow the same ratio extracted from the cue shifts, presented above (Fig. 5). The actual adaptation-ratio extracted from the data is represented by the solid white line in Figure 8C (the dashed white line represents the ratio from the monkey data). Fitting the function according to the actual adaptation-ratio (with only one free parameter, adaptation-extent) resulted in a RBCC fit almost identical to the optimal fit. This is presented by the light green curve in Figure 8B and the light green dot in Figure 8C. In contrast, the RBA prediction was worse than the data mean. This can be seen by the dark blue region at the bottom of Fig. 8C, since the RBA curve (which does not change during adaptation) is essentially identical to a FRA curve with adaptation-extent=0 (as seen in Fig. 8A). The very finding that the combined response undergoes adaptation indicates that cue combination and cue adaptation cannot be using the same model/weights. The finding that FRA can account for RBCC provides further support for the FRA model.

Finally, the deviance of the actual combined-cue-PSE values (as a function of Δ) from the FRA and RBA predictions is presented in Figure 8D. The actual combined-cue PSE values were closer to the initial (pre-adaptation) visual cue for low-RR, and initial vestibular cue for high-RR, than predicted by RBA (dark green lines). These data indicate that the visual and vestibular cues did not shift according to RBA. In contrast, FRA adaptation predictions, using the parameters from Figure 8, were indistinguishable from the actual combined-cue-PSE values, for all RR (light green curves).

DISCUSSION

In this study, we probed the nature of multisensory cue-calibration in the absence of external feedback. We found that given a heading-direction discrepancy between visual and vestibular cues, both cues underwent mutual adaptation towards one-another. Quantitatively, the extent of individual cue adaptation followed a fixed ratio, irrespective of relative cue reliability. Specifically, the ratio of vestibular to visual adaptation was roughly 2:1 for both humans and monkeys. This finding is particularly striking, since during cue-integration, visual and vestibular cues are weighted according to their relative reliabilities (Gu et al., 2008; Fetsch et al., 2009; Butler et al., 2010). Our results therefore indicate that multisensory cue-integration and cue-calibration follow different mechanisms/principles: cue-integration is reliability-based; whereas cue-calibration follows a fixed ratio.

Reliability based cue-integration has been demonstrated in a number of multisensory paradigms (van Beers et al., 1999; Jacobs, 1999; Landy and Kojima, 2001; Ernst and Banks, 2002; van Beers et al., 2002; Gepshtein and Banks, 2003; Knill and Saunders, 2003; Alais and Burr, 2004; Jurgens and Becker, 2006; Gu et al., 2008; Fetsch et al., 2009; Butler et al., 2010). However, quantitative testing of the nature of multisensory cue-calibration is lagging. Burge et. al. (2010) recently pioneered a paradigm to quantitatively test the reliability based model for visual-haptic calibration. They reported that visual-haptic cues follow a model of reliability-based adaptation. In our study, we emulated their paradigm, but with visual-vestibular calibration. When using similar methods of analysis, also our data suggested an influence of relative reliability on cue adaptation. However, additional analysis revealed that visual-vestibular calibration is much better accounted for by a model of fixed-ratio adaptation than reliability-based adaptation.

In order to explain why analyzing the data according to the previous methods (Fig. 4) could suggest reliability-based adaptation even if adaptation was not reliability based, we present a simulation in Figure 9: Each subplot displays a simulated probability density function corresponding to the subplots of Figure 4. The probability density functions were plotted by colour-scale: red representing high probabilities and blue, low probabilities. All probability density functions were generated as the combination of two bivariate Gaussians: ‘two’ – one for positive and one for negative Δ; and ‘bivariate’ - for visual and vestibular shifts. The Gaussian means for visual and vestibular shifts were the same across all plots: (−1°, 1°) for positive Δ, and (1°, −1°) for negative Δ. Since the means were of equal magnitude and the same for all RRs, the simulated probability density functions did not represent reliability-based adaptation.

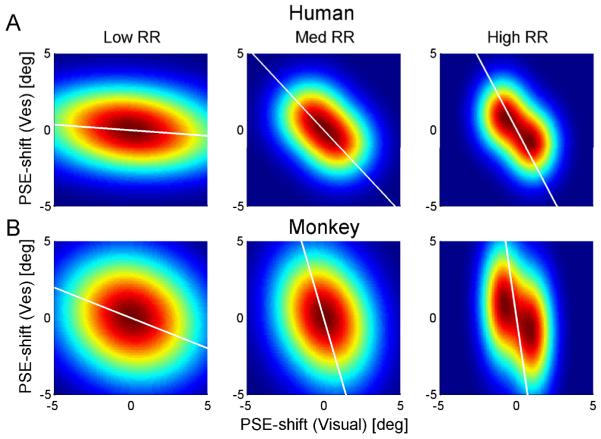
Figure 9. Simulated effects of visual PSE-shift variability.

Each subplot presents a simulated probability density function (PDF) corresponding to the subplots in Figure 4. Left, middle and right columns represent low, medium and high reliability ratios (RRs), respectively. All PDFs were generated from two bivariate Gaussians: one with mean (1°,-1°) and the other with mean (−1°,1°). Gaussian variances were set according to the actual PSE-shift variances extracted from the human and monkey data (A and B, respectively). Vestibular PSE-shift variance was set according to the overall variance, and did not change for different RRs: 2.4° for the human data and 7.0° for the monkey data. Visual PSE-shift variance was set individually for low medium and high-RR: 15.0°, 2.3° and 1.2°, respectively, for the human data; and 9.0°, 3.4° and 0.8°, respectively, for the monkey data. A type-II regression line of 2000 data-points, generated from each PDF, is displayed in white. The regression lines were constrained to pass through the origin.

The Gaussian variances were taken from the actual data (the same variances were used for positive and negative Δ Gaussians). As we previously described (Fig. 6, right column), vestibular PSE-shift variability was unchanged across RRs, whereas visual PSE-shift variability was strongly dependant on RR. (In itself, this result is not surprising since RR was controlled in the experiment by manipulating visual motion coherence only.) Therefore for the Gaussians we used the overall vestibular PSE-shift variance for all RRs, and specific visual PSE-shift variances for low, medium and high-RR. Hence the only difference between the RRs (columns in Fig. 9) was the variability of visual PSE-shifts.

A type-II regression line of 2000 data-points, generated from each probability density function in Figure 9, is displayed in white. The regression lines are strikingly similar to those of the actual data (Fig. 4). They too approach the horizontal for low-RR and vertical for high-RR. However, their differences in orientation exist exclusively due to visual PSE-shift variance, since there were no other differences between the simulations. Hence, changes in variability alone can cause changes in the orientation of the regression lines, similar to those seen in the data. Therefore regression line orientation may not accurately represent the ratio of cue adaptation. Visual inspection of the data in Burge at. al. (2010) seems to indicate that there too, visual PSE-shift variability could change with RR. Hence, additional analysis may be required to verify the model of adaptation.

The analyses in our paper strongly argue that visual-vestibular calibration follows fixed-ratio and not reliability-based adaptation. Particularly, we found that neither visual nor vestibular adaption correlated with RR. Rather, cue-shifts remained constant regardless of whether the visual or the vestibular cue was more reliable, indicating that cue-calibration does not follow the same mechanism as cue-integration. The fact that our findings were consistent for both humans and monkeys consolidates these results. Even the vestibular to visual shift ratio (approximately 2:1) was similar for humans and monkeys. Finally, only through modeling fixed-ratio adaptation (using the ratio extracted from the data), were we were able to account for reliability-based cue-integration during the adaptation process.

Ernst and Di Luca (2011) suggest that using relative cue-reliability for multisensory calibration may be a sub-optimal strategy, because a cue’s variance does not necessarily determine the probability of it being biased. This brings us back to the difference between reliability and accuracy: Reliability is the inverse variance of the probability distribution that describes the contribution of a sensory signal to the perceptual estimation. In contrast, accuracy is the probability that the sensory signal truly represents the real-world physical property. Accuracy and reliability are therefore different properties. Hence relative cue-reliability may not be a good indication as to which cue most likely requires calibration.

If the goal of multisensory cue-integration is optimal perception (in the sense of improving precision) a reliability-based model makes sense. In contrast, assuming that the goal of cue-calibration is improvement of cue accuracy, an accuracy-based mechanism would seem more appropriate. The brain’s estimate of cue-accuracy probably has a much longer time-constant than that of cue-reliability. Accordingly, it is possible that our finding of fixed-ratio adaptation is only relatively fixed, but a change in cue-accuracy could change the rate of adaptation. Our finding of higher vestibular vs. visual adaptation suggests that the visual cue is more accurate than the vestibular cue in heading discrimination. In this study we manipulated cue-reliability; however we did not manipulate cue-accuracy. In order to test the hypothesis that cue-calibration follows relative accuracy, cue-accuracy would need to be manipulated.

The proposal that cue-accuracy is more important than cue-reliability for multisensory calibration is in line with Gori et. al. (2008; 2010) who found that during development children do not integrate visual and haptic cues optimally. But rather, touch dominates discrimination of size, and vision dominates discrimination of orientation - even in conditions in which the dominant sense is far less precise than the other. They propose that the sensory dominance may reflect cross-modal calibration, where the more accurate sense calibrates the other (Burr and Gori, 2011).

Visual dominance has been a prevalent theory (Rock and Victor, 1964; Brainard and Knudsen, 1993). Hence it has been used as a standard by which to compare reliability-based models (van Beers et al., 2002; Burge et al., 2010). However, visual-dominant adaptation does not represent the general reliability-independent alternative. In fact, it is only a specific sub-case of fixed-ratio adaptation (where the ratio of non-visual to visual adaptation tends to infinity). In this study we present fixed-ratio adaptation as a novel, yet simple, model and recommend using it as a reliability-independent standard by which to compare reliability-based models. Our finding that visual-vestibular calibration actually follows the fixed-ratio adaptation model clearly highlights its relevance.

In conclusion, our results indicate that visual-vestibular cue-calibration does not follow the same mechanism as cue-integration. Cue-integration is reliability based; whereas cue-calibration follows a fixed ratio. It is possible that fixed-ratio adaptation may be only relatively fixed, and that the ratio of adaptation may change with cue-accuracy. In order to test this, multisensory cue-adaptation needs to be tested as a function of relative cue-accuracy.