Abstract
Postmortem and functional imaging studies of patients with psychiatric disorders, including schizophrenia, are consistent with a dysfunction of interneurons leading to compromised inhibitory control of network activity. Parvalbumin (PV)-expressing, fast-spiking interneurons interacting with pyramidal neurons generate cortical gamma oscillations (30 – 80 Hz) that synchronize cortical activity during cognitive processing. In postmortem studies of schizophrenia patients, these interneurons show reduced PV and glutamic acid decarboxylase 67 (GAD67), an enzyme that synthesizes GABA, but the consequences of this downregulation are unclear. We developed a biophysically realistic and detailed computational model of a cortical circuit including asynchronous release from GABAergic interneurons to investigate how reductions in PV and GABA affect gamma oscillations induced by sensory stimuli. Networks with reduced GABA were disinhibited and had altered gamma oscillations in response to stimulation; PV-deficient GABA synapses had increased asynchronous release of GABA, which decreased the level of excitation and reduced gamma-band activity. Combined reductions of PV and GABA resulted in a diminished gamma-band oscillatory activity in response to stimuli, similar to that observed in schizophrenia patients. Our results suggest a mechanism by which reduced GAD67 and PV in fast-spiking interneurons may contribute to cortical dysfunction in schizophrenia and related psychiatric disorders.
Introduction
Patients with schizophrenia exhibit reduced gamma oscillatory activity in response to sensory stimuli and cognitive events (Gallinat et al., 2004; Light et al., 2006; Ferrarelli et al., 2008; Roach and Mathalon, 2008; Spencer et al., 2008). Gamma-band (30–80 Hz) oscillations accompany many forms of sensory information processing, including working memory, and are modulated by attention (Singer, 1999; Jensen et al., 2007). Experimental studies (Atallah and Scanziani, 2009; Cardin et al., 2009; Sohal et al., 2009; Whittington et al., 2011) and computational models (Wang and Buzsáki, 1996; Traub et al., 1997; Börgers et al., 2005; Tiesinga and Sejnowski, 2009) have implicated inhibitory (IN) interneurons, and in particular the parvalbumin (PV)-expressing fast-spiking (FS) interneurons, in generating gamma-band activity by synchronizing spiking in pyramidal (PY) neurons.
One of the most consistent findings in schizophrenia postmortem studies is a reduction in the expression of parvalbumin in cortical inhibitory neurons (Lewis et al., 2005; Torrey et al., 2005), a reduction also observed in several animal models of schizophrenia (for review, see Powell et al., 2011). The reduction in this calcium-binding protein was implicated in the altered stimulus-evoked gamma oscillatory activity observed in schizophrenia patients and in animal models of the disease (Lewis et al., 2011; Phillips et al., 2011).
In developmental animal models, PV levels can become undetectable (as determined by immunoreactivity) in a fraction of interneurons after application of NMDA receptor antagonists during early postnatal life (Wang et al., 2008; Powell et al., 2011); alternatively, in response to chronic administration of NMDAR antagonists, PV immunoreactivity as well as that of glutamic acid decarboxylase 67 (GAD67) (the main GABA-producing enzyme in cortex) appear to be uniformly reduced in mature PV+ interneurons in vitro and in vivo (for review, see Powell et al., 2011). These reductions correlated with reduced inhibitory drive of pyramidal neurons in the adult prefrontal cortex (Homayoun and Moghaddam, 2007; Zhang et al., 2008). However, the biophysical link between reduced parvalbumin/GAD67 expression and alterations in gamma oscillatory activity remains elusive.
It is possible that reduced PV levels contribute to the alteration of inhibitory control of network activity (Caillard et al., 2000). To test this hypothesis, we simulated a computational cortical circuit model to study the possible causal relationship between reduced parvalbumin and impaired gamma oscillations, which depend on and are thought to be generated by dynamic interaction between pyramidal and interneuron subpopulations (Tiesinga and Sejnowski, 2009). Consistent with recent experimental results (Manseau et al., 2010), reducing PV at GABAergic synapses in the model reduced gamma-band activity and increased asynchronous release of GABA, resulting in reduced responses to strong sensory-like stimuli and weakened transient storage of stimulus-related excitation. When both PV and GABA were reduced, the gamma-band oscillatory activity in response to stimuli was reduced, similar to what is observed in schizophrenia patients. In summary, our results suggest a possible causal link between reduced PV in inhibitory interneurons and the physiological changes observed in schizophrenia. In addition, these results suggest that activity-dependent changes in GABA release may be critical in shaping the properties of network gamma oscillatory activity.
Materials and Methods
Pyramidal neurons
We modeled pyramidal neurons by a two-variable, one-compartment Morris–Lecar (1981) model modified to model cortical neurons (Prescott et al., 2006). The pyramidal neurons in the model had sodium (GNa), potassium (GK), leak (GL), and adaptation (GA) conductances governed by the following equations
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where Vm is the membrane potential, w is the recovery variable, and z is the adaptation variable. The values of parameters were as follows:
The synaptic current (ISYN) and external current (IEXT) are described below.
Interneurons
Dynamics of the fast-spiking inhibitory interneurons were modeled by the Wang–Buzsáki (1996) model, in which the membrane potential is governed by the following equation:
| (7) |
The sodium current was given by , with m∞ = αm/(αm + βm), αm(V) = −0.1(V + 35)/(exp(− 0.1 (V + 35)) −1), and βm(V) = 4exp(− (V + 60)/18).
The inactivation variable of sodium current was given by dh/dt = φ(αh(1 − h) − βhh), with αh(V) = 0.07exp(− (V + 58)/20) and βh(V) = 1/(exp(−0.1(V + 28))+ 1).
The potassium current was given by IK = gKn4 (V − EK), with the activation variable dn/dt = φ(αn(1 − n) − βnn), with αn(V) = −0.01 (V + 34)/(exp(−0.1(V + 34))− 1) and βn(V) = 0.125exp (− (V + 44)/80).
The leak current was given by IL = gL(V − EL). The values of parameters were as follows: gNa = 35 ms/cm2, gK = 9 ms/cm2, gL = 0.1 ms/cm2, ENa = mV, EK = −90 mV, EL = −65 mV, Cm = 1 mF/cm2, φ = 5.
Network configuration and synaptic connectivity
The network model contained 900 neurons of which 720 were PY neurons and 180 were IN neurons. The model neurons were organized in a 30 × 30 square lattice, with each fifth neuron an inhibitory neuron. Each neuron could form synaptic connections with probability (pC) with any of its peers found within a predefined square footprint with sides of length LF. Connection probabilities and footprint sizes for different neurons were as follows: . Synapses between interneurons could be established with probability [consistent with the connection probability of ~0.78, as reported by Galarreta and Hestrin (2002)]. Data on the exact values of connection probabilities and synaptic footprints of different cell types are not fully available at the moment; thus, in some simulations we verified that the dynamics of our model network are robust with respect to a specific choice of connectivity parameters. Network oscillations in gamma range could be obtained for a range of connectivity/footprint choices, provided that peak synaptic conductances were rescaled to maintain the balance between net excitatory to net inhibitory drives to each model neuron. Neurons on the boundary of the lattice received less recurrent connectivity and thus were compensated by receiving an additional excitatory input (at a fixed Poisson rate) that was not part of a network to avoid boundary effects.
AMPA and NMDA synapses
Both PY and IN model neurons received AMPA and NMDA currents, modeled as described below. The dynamics of AMPA synaptic conductance was modeled as an instantaneous rise followed by the exponential decay, as follows:
| (8) |
NMDA conductance activation was modeled according to the standard formalism (Jahr and Stevens, 1990):
| (9) |
| (10) |
NMDA conductance was incorporated both in PY neurons and in interneurons, with differences as described below.
Recent experimental evidence (Wang and Gao, 2010) indicates that FS PV-positive interneurons in prefrontal cortex receive NMDA inputs from excitatory pyramidal neurons; however, the peak NMDA conductance is smaller, and the time scale of NMDA conductance decay is faster compared with the NMDA receptor kinetics in pyramidal neurons (Wang and Gao, 2010). We incorporated these experimental data in our computational model of cortical network by setting the relaxation time of slow NMDA conductance component ( ) on interneurons to be faster than that of slow NMDA conductance component at PY–PY synapses ( ), and by keeping the peak NMDA conductance at FS–PY synapses smaller than that at PY–PY synapses
| (11) |
The resulting synaptic current (from a single presynaptic neuron) due to the activation of AMPA and NMDA conductances was as follows:
| (12) |
where EAMPA = 0 mV. Other parameters were as follows:
GABAA synapses
The goal of this study was to understand how the abundant asynchronous release of GABA from synaptic terminals of PV-deficient fast-spiking interneurons affects cortical processing. Because asynchronous release is likely to rely on the amount of readily releasable GABA vesicles, we incorporated short-term synaptic plasticity in our model of GABAergic transmission. Fast-spiking PV-positive interneurons can fire at frequencies >20 Hz, and because the coupling between calcium channels and calcium sensors at their synapses is in the nanometer range (Bucurenciu et al., 2008) synaptic short-term depression (rather than synaptic short-term facilitation) is likely to dominate. This assumption is further strengthened by findings that P/Q-type synaptic calcium channels (associated with reliable transmitter release and short-term depression) mediate GABA release from synaptic terminals of cortical fast-spiking interneurons (Zaitsev et al., 2007). Thus, depression but not facilitation of neurotransmitter release was incorporated in our model.
The phenomenological model of GABA synaptic transmission included both stimulus-locked and asynchronous release (Volman et al., 2007, 2010). Following Tsodyks et al. (2000), we assumed that, at any moment of time, synaptic “resource” (representing transmitter vesicles) can be in one of three states: actively released (Y), temporarily not available (Z), ready to be released (X). Equations that describe the trafficking of resource between these three states are
| (13) |
| (14) |
| (15) |
The above equations incorporate two modes of GABA release. Phasic release is time locked to synaptic action potential (which invades the synapse at time tSPIKE) and is parameterized by the “resource usage parameter” U. Asynchronous release of GABA is given by the time-dependent variable ξ(t), which at any time T can take values of either 0 or ξ̃ (corresponding to the absence or presence of asynchronous event at time T ). We further assumed that the rate η(c) of asynchronous release (probability to observe asynchronous event in time window [t, t + Δt]) depends on the level of presynaptic residual calcium, C, and is given by:
| (16) |
where η̃ is the maximal possible rate of asynchronous release that would occur in the complete absence of parvalbumin (see next paragraph), and Ka isthecalcium affinity of asynchronous release machinery (Volman et al., 2007, 2010).
The dynamics of residual calcium in synaptic boutons of FS PV-positive interneurons is critically shaped by the presence of calcium buffers, most notably parvalbumin. Parvalbumin binds calcium ions at a relatively slow rate; thus, a quasi-steady-state approximation (valid for fast buffering) cannot be used here; instead, the buffer kinetics was described with differential equations. Further, the slow binding rate of parvalbumin implies that its impact might be more dominant during the late, slower, phase of calcium extrusion (when calcium is in submicromolar regime), which is the situation for residual calcium that drives asynchronous release. The following equations describe the dynamics of residual calcium in presynaptic boutons of fast-spiking interneurons:
| (17) |
| (18) |
where β is the maximal rate with which residual calcium is cleared from synaptic terminal by active pumps, KP is the affinity of a pump for calcium, γ controls the amount of per-spike increase in residual synaptic calcium, C0 is the extracellular calcium concentration, and a constant term IP ensures that, in the absence of spikes, synaptic residual calcium is ~50 nM. In addition to the action of calcium extrusion pump, calcium ions are buffered by parvalbumin (total concentration of parvalbumin is parameterized by bt) with forward rate k+ (bound calcium unbinds with backward rate k−) (Lee et al., 2000).
The resulting synaptic current (from a single presynaptic neuron) due to the activation of GABAA receptors was as follows:
| (19) |
| (20) |
where we set τGABA = 8 ms; EGABA = −75 mV. Other parameters were as follows: , ξ̃ = 0.01, Ka = 0.2 μM, β = 5 μM/s, KP = 0.4 μM, γ = 80 μM/s, C0 = 2 mM, IP = 0.1102 μM/s, k− = 0.95 s−1, k+ = (k−/0.051) μM−1 · s−1, τD = 2 ms, τR = 0.2 s, U = 0.3, η̃ = 0.03, and bt = 100 μM. In some simulations, we varied the values of some parameters (e.g., τR, U, η̃, bt) to test their role in shaping the properties of inhibitory synaptic transmission and subsequent effect on collective activity in our model networks.
Equations of the model were numerically integrated using fourth-order Runge–Kutta methods with a time step of Δt = 0.05 ms.
Parvalbumin deficit scenarios
We considered two different scenarios to address the importance of parvalbumin deficit in a subpopulation of fast-spiking interneurons. In the first scenario, which we term the “neuron deficit” scenario, the concentration of parvalbumin was reduced to zero in a fraction, F[PV] = 0, of randomly selected model interneurons. Thus, for example, F[PV] = 0 = 0.4 corresponds to the case when PV concentration is set to zero in 40% of model interneurons (but remains at its baseline value of 100 μM in other interneurons). Such nonuniform reduction of parvalbumin content has been observed in the perinatal ketamine animal model of schizophrenia in early development (Powell et al., 2011). In the second scenario, which we call the “concentration deficit” scenario, the concentration of parvalbumin was reduced to the same amount in all model interneurons. This scenario is likely to reflect the response of adult neural circuitry to chronic application of ketamine (Kinney et al., 2006; Behrens et al., 2007). In reality, one might have a mix of two scenarios; the effect of heterogeneity in PV distribution on the collective electrical activity will be reported elsewhere.
Network stimulation and generation of activity
In addition to intranetwork synapses from other PY and IN neurons, each model neuron received stimuli from outside the circuit that was required to generate electrical activity in the network. This stimulation was modeled as Poisson spike trains that activated AMPA, NMDA, and GABAA conductances on model neurons (NMDA/AMPA conductance ratio and kinetics of all conductances were the same, as described in AMPA and NMDA synapses, above). To reduce the computational complexity associated with the detailed modeling of thousands of synaptic inputs that impinge on the biological neuron, each model neuron in our network received all “out of the network” excitatory stimulation through one canonic excitatory conductance, and all out of the network inhibitory stimulation through one canonic inhibitory conductance. Thus, the stimulation frequency of this conductance in our model should be looked at as corresponding to the sum over spiking frequencies of many of the biological neurons that contribute to the canonic conductance activation. By the same token, an increase in the canonic stimulation frequency represents a proportional increase in firing frequencies of many biological neurons that contribute to it (e.g., a twofold increase in the excitatory stimulation frequency would mean that PY neurons outside of the network had their firing rates increased by a factor of 2). Peak canonic conductances were as follows: . The conductances from neurons outside the network onto IN model neurons were stimulated at 500 Hz (this stimulation frequency was kept constant in all simulations reported in this article), and the conductances to PY model neurons were stimulated at the rate vSTIM, for which we assumed a value of 250 Hz in the baseline scenario. We varied vSTIM as needed to simulate a range of inputs levels. In particular, to investigate the response to strong stimulus, we modeled a strong stimulus as a transient (40 ms) and large (up to fivefold) but physiologically relevant increase in the rate of pyramidal neurons stimulation. The basal stimulation frequency in these conditions was 150 Hz.
Methods of analysis
Time-frequency spectrograms were computed on local field potential (LFP) traces (defined as network-averaged membrane potential) using wavelet transforms (complex Morlet wavelet), with an LFP sampling rate of 20 kHz. For steady-state dynamics (constant vSTIM), plots of spectral power versus frequency were obtained by averaging the time-frequency spectrogram over time. For brief stimulus presentations (see Figs. 5, 6), plots of spectral power versus frequency were obtained by time averaging over the stimulus duration (40 ms, in stimulus) or for 200 ms after stimulus cessation (after stimulus). In all plots, the spectral power of LFP is reported in units of square millivolts.
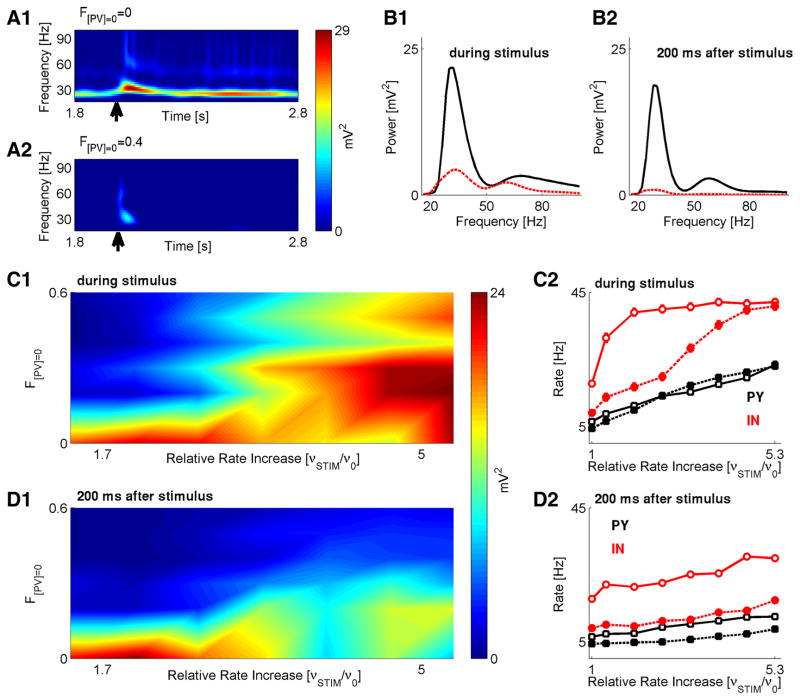
Figure 5.
Parvalbumin deficit causes reduced response to stimuli. A1, A2, Spectrograms (time frequency) of network LFP, for baseline scenario (A1) and scenario with PV deficiency (F[PV] = 0 = 0.4, A2). In both cases, stimulus was presented at T = 2 s (arrow) and lasted for 40 ms. Stimulus rate was 400 Hz. B1, Spectral response averaged over time duration of stimulus presentation for baseline (black) versus the PV-deficient (red) models. B2, Spectral response averaged over time duration of 200 ms after stimulus cessation for baseline (black) versus PV-deficient (red) models. Stimulus rate was 400 Hz. C1, Magnitude of spectral power peak (time average over stimulus duration) versus F[PV] = 0 and relative (to the baseline stimulation of v0 = 150 Hz) increase in stimulation rate. C2, Firing rates of PY (black) and IN (red) model neurons during the 40 ms stimulus, in baseline (solid line) versus the F[PV] = 0 = 0.4 model (dashed line). D1, Magnitude of spectral power peak (time average over 200 ms after stimulus) versus F[PV] = 0 and relative (to the baseline stimulation of v0 = 150 Hz) increase in stimulation rate. D2, Firing rates of PY (black) and IN (red) model neurons in the time window of 200 ms after the stimulus, in baseline (solid line) versus the F[PV] = 0 = 0.4 model (dashed line).
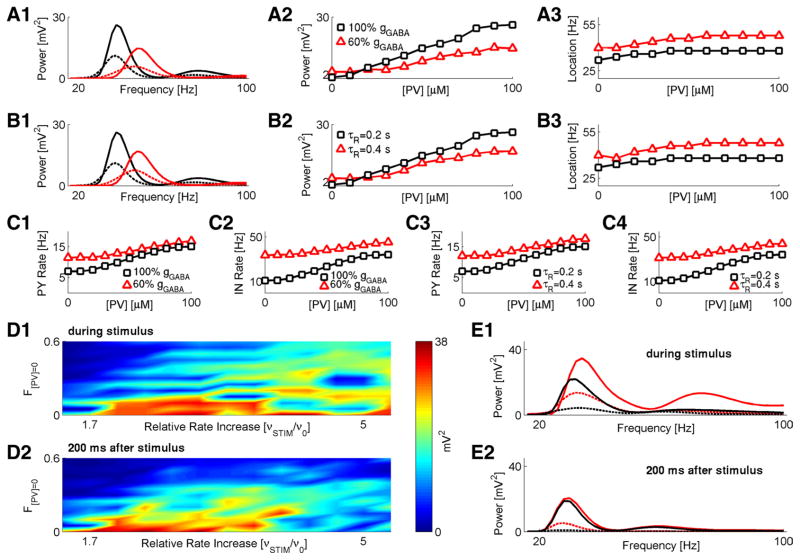
Figure 6.
Reduced GAD67 exacerbates the effect of parvalbumin deficit on network activity. A1, Spectral power plots for the scenario in which PV deficit is accompanied by reduced GABA conductance: gGABA at 100% of its baseline value and [PV] = 100 μM (solid black); gGABA at 100% of its baseline value and [PV] = 40 μM (dashed black); gGABA at 60% of its baseline value and [PV] = 100 μM (solid red); gGABA at 60% of its baseline value and [PV] = 40 μM (dashed red). A2, A3, Quantification of spectral peak power (A2) and frequency (A3) changes versus different PV concentrations and alterations in GABA conductance. Black squares, gGABA at 100% of its baseline value. Red triangles, gGABA at 60% of its baseline value. Network stimulation frequency was vSTIM = 250 Hz. B1, Spectral power plots for the scenario in which PV deficit is accompanied by slower time τR of GABA synapse recovery from depression: τR = 0.2 s and [PV] = 100 μM (solid black); τR = 0.2 s and [PV] = 40 μM (dashed black); τR = 0.4 s and [PV] = 100 μM (solid red); τR = 0.4 s and [PV] = 40 μM (dashed red). B2, B3, Quantification of spectral peak power (B2) and frequency (B3) changes versus different PV concentrations and altered time of GABA synapse recovery from depression. Black squares, τR = 0.2 s. Red triangles, τR = 0.4 s. Network stimulation frequency was vSTIM = 250 Hz. C1–C4, Firing rates of PY (C1, C3) and IN (C2, C4 ) model neurons for different scenarios shown in A and B. D1, Magnitude of spectral power peak (time average over stimulus duration) versus F[PV] = 0 and relative (to the baseline stimulation of v0 = 150 Hz) increase in stimulation rate. D2, Magnitude of spectral power peak (time average over 200 ms after stimulus) versus F[PV] = 0 and relative increase in stimulation rate. Color scale is the same for D1–D2. E1, Spectral power over the time duration of stimulus presentation (40 ms) for different scenarios: gGABA at 100% of its baseline value and F[PV] = 0 = 0 (solid black); gGABA at 100% of its baseline value and F[PV] = 0 = 0.4 (dashed black); gGABA at 60% of its baseline value and F[PV] = 0 (solid red); gGABA at 60% of its baseline value and F[PV] = 0 = 0.4 (dashed red). E2, Spectral power over 200 ms following stimulus cessation; keys are the same as in E1. In both E1 and E2, stimulus rate was vSTIM = 400 Hz.
Results
Gamma oscillations in cortical network model
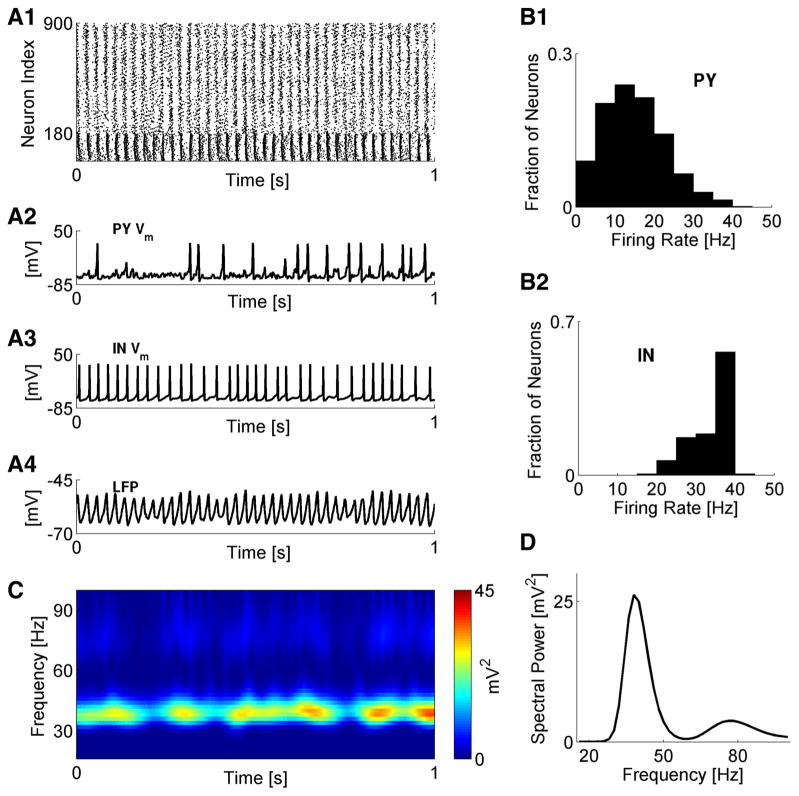
Figure 1 shows typical dynamics in the baseline cortical network model. Both PY and IN neurons were engaged in collective oscillatory activity, which, however, was not fully synchronized (Fig. 1A). The model pyramidal neurons fired action potentials at an average rate of 15 ± 8 Hz (Fig. 1B1) and irregularly participated in cycles of collective activity (Fig. 1A2). Interneurons fired action potentials at much higher rates (33 ± 5 Hz) (Fig. 1B2) and exhibited more regular recruitment into collective oscillation cycles (Fig. 1A3). The ongoing oscillatory activity was reflected in the local field potential (Fig. 1A4). Spectral analysis (see Materials and Methods) also disclosed a dominant frequency peaking at ~40 Hz (Fig. 1C,D) corresponding to gamma-band oscillations.
Figure 1.
Properties of gamma oscillations in cortical network model. A1, Raster plot of network dynamics (IN neurons are 1–180). A2, A3, Membrane potentials of sample PY and IN neurons. A4, Local field potential (computed as average over membrane potentials of all neurons). B1, B2, Distributions of firing rates for PY (B1) and IN (B2) neurons. C, Spectrogram (time-frequency) of network LFP. D, Time-averaged distribution of spectral power from C. For all plots, network stimulation frequency was vSTIM = 250 Hz.
Oscillations emerge as a result of reciprocal interaction between PY and IN subpopulations
Consistent with recordings from cortical circuits (Whittington et al., 2011), gamma oscillations in the model network emerged as a result of reciprocal interaction between subpopulations of pyramidal neurons and interneurons. Key properties (location of and power at the dominant frequency) were controlled by varying the strength of coupling between PY and IN subpopulations. This may be particularly relevant to schizophrenia, in light of the findings that inhibitory synaptic coupling from PV+ basket interneurons to PY neurons is compromised in this disorder (Glausier and Lewis, 2011). Thus, we explored how different aspects of GABA coupling in our model network may affect the power and the frequency of gamma oscillatory activity.
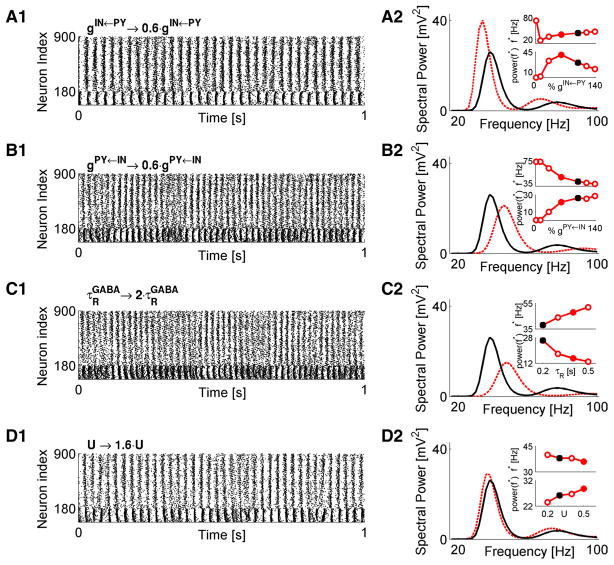
To start with, we explored the role of PY coupling to IN neurons. This was motivated by results showing that, in a neonatal animal model of schizophrenia, the excitatory drive to IN neurons is reduced compared with the control of saline-treated animals (Pinto-Duarte et al., 2010). In Figure 2A1, the dynamics of a model network was altered by decreasing the coupling from PY to IN subpopulations. As the PY-to-IN coupling was decreased, the peak gamma power increased up to a certain point (Fig. 2A2), but decreased for still weaker coupling strengths (Fig. 2A2, bottom inset). The frequency of peak power exhibited for a most part a monotonic dependence on the strength of PY-to-IN coupling, approaching the beta range for lower gIN←PY (Fig. 2A2, top inset). In the limit gIN←PY → 0, pyramidal drive to IN neurons became insignificant, thus effectively disinhibiting the PY subpopulation (Fig. 2A2, left-most point in both insets). In this regime, the power peak moved to ~80 Hz (reflecting the disinhibited network) and was greatly reduced.
Figure 2.
Gamma oscillations are modulated by synaptic coupling between PY and IN populations. A1, Raster plot of network dynamics for scenario in which PY-to-IN synaptic coupling was reduced to 60% of its value in the baseline model (Fig. 1 A). A2, Time-averaged distribution of spectral power of this model (red) and the baseline model (black). Insets show the dependence of location (top) and magnitude (bottom) of power peak on the relative strength of PY-to-IN coupling. Closed black and red circles are for the corresponding scenarios shown in the main plot. B1, B2, Raster plot (B1) and spectral characterization (B2) of network dynamics for scenario in which IN-to-PY coupling was varied. Interpretation of data follows that shown in A. C1, C2, Raster plot (C1) and spectral characterization (C2) of network dynamics for scenario in which GABA recovery time was varied. Interpretation of data follows that shown in A. D1, D2, Raster plot (D1) and spectral characterization (D2) of network dynamics for scenario in which strength of per spike synaptic response was varied. Interpretation of data follows that shown in A. For A–D, the network stimulation frequency was vSTIM = 250 Hz.
We next tested the effect of varying the strength of IN-to-PY coupling. This manipulation was motivated by results showing decreased inhibitory drive onto pyramidal neurons after chronic exposure to the NMDAR antagonist ketamine (Zhang et al., 2008) and the recent finding that GABAA receptor α1 subunit mRNA expression (a receptor subunit that is associated with the inhibitory synapses established by PV+ basket interneurons) is selectively reduced on PY neurons in schizophrenia (Glausier and Lewis, 2011). Note, however, that, because our model does not incorporate detailed receptor subunit composition, the manipulation on GABA conductance could also be taken to represent a change in available GABA due to the altered expression of GABA-synthesizing enzyme GAD67. Weaker IN-to-PY coupling decreased the peak power magnitude and moved the peak frequency to higher frequencies (Fig. 2B1,B2). In the limit gPY←IN → 0, the pyramidal subnetwork became disinhibited, the power peak moved to ~75 Hz, and its magnitude was dramatically reduced, again reflecting a loss of dominant frequency.
Short-term depression at GABA synapses can dynamically decrease synaptic efficacy in an activity-dependent manner. Depression could affect the amount of available GABA in a way that depends on the stimulation frequency of a synapse. At the same time, experimental evidence suggests that GABA availability is compromised in schizophrenia because of the reduced levels of GABA-synthesizing enzyme GAD67 (for review, see Benes and Berretta, 2001; Akbarian and Huang, 2006). Thus, another possible way to mimic the change in GAD67 levels in our model (in addition to the one described in Fig. 2B) would be to alter the parameters of synaptic depression at GABA synapses. In this view, for example, increasing the recovery time of GABA synapse from short-term depression would decrease GABA availability and would thus correspond to the reduced level of GAD67. The same effect is expected to occur by lowering the value of U (which models the strength of phasic GABA release)—this would decrease the capacity of GABA synapse for phasic release. To test how GABA synaptic depression could affect the dynamics in our model, we varied the recovery time and the usage parameters. Longer recovery times from depression reduced the magnitude of power peak and moved the peak frequency to a higher gamma regime (Fig. 2C1,C2). Because more prolonged depression reduces synaptic activity, these results are consistent with the ones shown in Figure 2, B1 and B2. On the other hand, varying the parameter U (which controls the fractional amount of “synaptic resource” used by a synapse per each spike) had only weak effect on the spectral properties of collective activity (Fig. 2D1,D2).
Gamma activity is suppressed by asynchronous release of GABA from PV-deficient terminals
The results in Figure 2 suggest that short-term plasticity of GABA release from interneuron synapses could critically mold the properties of collective oscillations in cortical networks. GABA synaptic terminals in our model network incorporated both phasic (stimulus-locked) and asynchronous releases of GABA. Earlier studies have shown that asynchronous release of both glutamate and GABA could dramatically influence the processing of synaptic information by neurons. The asynchronous release of glutamate prolongs the temporal window for spike generation (Iremonger and Bains, 2007) and may serve as a mechanism of gain modulation in early development (Volman et al., 2010). On the other hand, asynchronous release of GABA generates long-lasting inhibition (Hefft and Jonas, 2005) and thus may affect the excitability of its postsynaptic neuron. We therefore set out to explore the influence of the asynchronous release of GABA on collective neuronal activity in our model network.
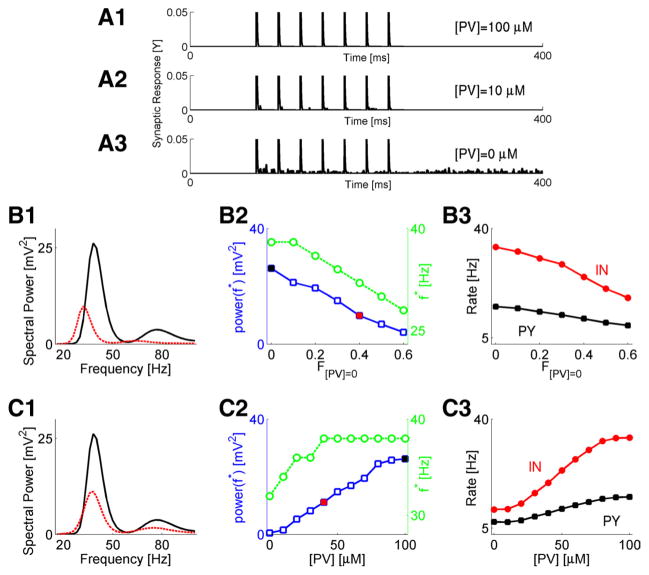
In a representative model synaptic terminal, the asynchronous GABA release was virtually nonexistent in the baseline conditions due to the effective buffering of residual synaptic calcium by parvalbumin (100 μM parvalbumin in each interneuron) (Fig. 3A1), became stronger for a lower concentration of parvalbumin (10 μM parvalbumin in each interneuron) (Fig. 3A2), and was much more pronounced when the PV concentration was zero (Fig. 3A3).
Figure 3.
Deficit in parvalbumin impairs gamma-band activity through asynchronous GABA release. A, Examples of synaptic response (Y) for different concentrations of parvalbumin at model synapses: the baseline model with [PV] = 100 μM (A1); [PV] = 10 μM (A2); [PV] = 0 μM (A3). Synapses were stimulated by seven spikes at 40 Hz. To facilitate presentation of asynchronous release, the phasic part of synaptic response was truncated. B, Characterization of activity in the neuron deficit model. B1, Spectral power plots of baseline model (F[PV] = 0 = 0, black) versus the F[PV] = 0 = 0.4 model (red). B2, Magnitude (blue circles) and location (green circles) of spectral power peak versus the fraction of IN neurons with zero PV. Black and red points correspond to those shown in left plot. B3, Rates of PY (black) and IN (red) neurons firing versus the F[PV] = 0. C, Characterization of activity in concentration deficit model. C1, Spectral power plots of baseline model ([PV] = 100 μM, black) versus the [PV] = 40 μM model (red). C2, Magnitude and location of spectral power peak versus the PV concentration. C3, Rates of PY (black) and IN (red) neurons firing versus the PV concentration.
For a preset fraction of randomly selected model IN neurons, the level of PV was set to zero at all synapses (Materials and Methods); this model is referred to as a neuron deficit model. The greater the number of neurons with a PV deficit, the higher the reduction of the peak power, and the more the frequency of peak power shifted toward the beta range (Fig. 3B1,B2). This change in collective dynamics was paralleled by changes in neuronal firing rates: the firing rates of both PY and IN neurons were reduced for a higher deficit of PV neurons (Fig. 3B3).
In another model, we reduced the concentration of PV in all IN neurons by the same amount, as observed after continuous exposure to ketamine in primary neurons, or repetitive exposures in adult animals (Kinney et al., 2006; Behrens et al., 2007); this model is referred to as a concentration deficit model. Lowering the PV concentration (higher deficit) also significantly reduced the magnitude of the power peak and shifted the frequency of peak power toward the beta range (Fig. 3C1,C2). As in the neuron deficit model, this change in collective dynamics was paralleled by changes in neuronal firing rates, which reduced the firing rates of both PY and IN neurons at lower PV concentrations (Fig. 3C3).
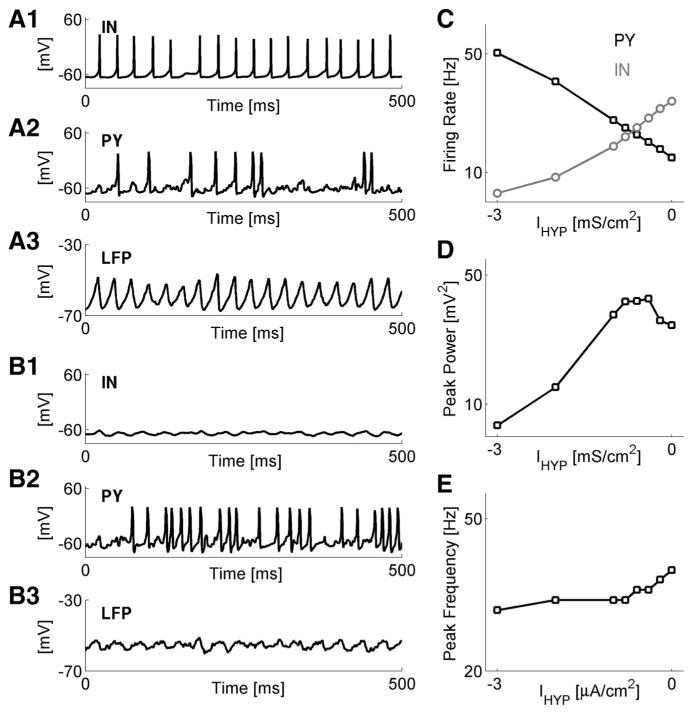
Because in the model interneurons made synaptic contacts on both pyramidal neurons and other interneurons, the asynchronous release of GABA stemming from the PV deficit at GABA synapses could affect network oscillations either via inhibition of interneurons or via inhibition of pyramidal neurons. To determine the importance of mutual inhibition between interneurons, we simulated intact networks without a parvalbumin deficit, F[PV] = 0 = 0), in which constant hyperpolarizing current IHYP was injected into all of the interneurons. Asynchronous release of GABA in these intact networks was virtually nonexistent; this allowed us to focus on the role of interneuronal firing rate in network oscillations. For a sufficiently large hyperpolarizing current, the firing rate of interneurons diminished to very low values, while the firing rates of the pyramidal neurons significantly increased, indicative of disinhibition (Fig. 4A, baseline model; Fig. 4B, IHYP = −3 μA/cm2; and Fig. 4C). The spectral power peak was also reduced to low values for strongly hyperpolarizing current (Fig. 4D), while the location of the dominant frequency showed weak but consistent dependence on IHYP (Fig. 4 E). Although the reduction in peak power was qualitatively similar to the reduction in PV-deficient networks, the disinhibition of pyramidal neurons activity observed during interneuron hyperpolarization (Fig. 4C) contrasted with the decreased PY firing rates obtained for PV-deficient networks (Fig. 3B3,C3). In the PV deficit scenario, the desynchronized GABA release hyperpolarized both interneurons and pyramidal neurons, thus reducing the power of gamma oscillations by hyperpolarization of the former, while preventing the disinhibition of the latter.
Figure 4.
PV deficiency at GABA synapses prevents the disinhibition of network dynamics. A, Representative membrane potentials and LFPs obtained for scenarios of intact networks (F[PV] = 0 = 0), in which all model interneurons were subject to hyperpolarizing DC current IHYP. A1–A3, Membrane potential of sample interneuron (A1), membrane potential of sample pyramidal neuron (A2), and local field potential (A3) for the case IHYP = 0 μA/cm2. B, The same as in A, but for IHYP = 3 μA/cm 2. C, Network-averaged firing rates of model PY (black squares) and IN (gray circles) neurons versus the magnitude of IHYP. Data points are averages ± SEM. D, Magnitude of spectral power peak versus the magnitude of IHYP. E, Location of spectral power peak versus the magnitude of IHYP.
Thus, parvalbumin deficit at GABA synapses (introduced either as a deficit in IN neurons that express parvalbumin or as a uniform reduction in PV concentration in all interneurons) impairs collective gamma oscillations through reduced synchronization of GABA release. Such resynchronization of GABA release hyperpolarizes both the interneurons and the pyramidal neurons (and thus reduces their firing rate) and prevents the disinhibition of pyramidal population.
Asynchronous release of GABA from PV-deficient terminals suppresses responses to stimuli
Above, we showed how the properties of network gamma oscillatory activity are shaped by the constant stimulation frequency. One of the most reliable deficits in studies in schizophrenia patients is a reduction in the spectral power of event-related (sensory or cognitive event-evoked) gamma activity (for review, see Sun et al., 2011). During such sensory or cognitive events, the firing rates of afferent neurons can increase several fold for a short time. Asynchronous release of neurotransmitter increases following intense synaptic stimulation (Goad and Stevens, 1994; Manseau et al., 2010). The synapses from interneurons with a deficit in parvalbumin may exhibit increased stimulus-induced resynchronization of GABA release if interneurons respond to sensory stimulation by increasing their firing rates (as a result of the increased activity of pyramidal cells population), which could also lead to reduced spectral power in gamma band and the reduced response to sensory stimuli.
We investigated the response of our model network to transient stimuli of varying strength. To reduce the possibility of abundant asynchronous release during intense baseline activity, and to make the network more compliant with the notion of baseline spontaneous state, the basal stimulation frequency was set to vSTIM = 150 Hz in the simulations below, resulting in basal firing rates of ~5 Hz for PY neurons, which is in accordance with experimental results (Stride et al., 1974) (Fig. 5C2). To model a “strong” stimulus that would result in event-related gamma activity, the stimulation frequency of PY model neurons was instantaneously increased (by up to approximately fivefold, in the range from 200 to 800 Hz) for 40 ms, after which vSTIM was reset to its baseline value. The stimulation frequency of inhibitory interneurons was kept at 500 Hz at all times. Keeping in mind that each canonic stimulation synapse in our model (through which the stimulation is delivered to a neuron) really represents a “lumped” effect of many biological neurons that project their synapses to the given model neuron, a fivefold increase in stimulation frequency would correspond to a physiologically plausible approximately fivefold increase in firing rates of biological neurons. Note also that in response to a strong stimulus model PY neurons also increased their firing rates up to approximately fivefold, in linear relation to the increase in their stimulation frequency (Fig. 5C2).
The spectral response of a network to brief stimulus (Fig. 5A2) was weaker for a network with reduced PV in interneurons (compared with the baseline model) (Fig. 5A1) during both the presentation of a stimulus and the window of 200 ms after stimulus cessation (Fig. 5B1,B2). The effect of reducing PV on the magnitude of spectral power peak was consistent over a wide range of stimuli intensities and levels of PV (Fig. 5C1,D1). The peak in the spectral power during the stimulus presentation was lower for higher PV deficiencies and weaker stimuli (Fig. 5C1). For 200 ms after stimulus cessation, the spectral power peak was significantly lower for higher PV deficiencies and weaker stimuli (Fig. 5D1), indicating a reduced ability to transiently store stimulus-related information. Consistent with previous results, this was primarily correlated with changes in firing rates of IN neurons, while the firing rates of PY neurons did not change substantially (Fig. 5C2,D2).
Reduced GABA synaptic transmission exacerbates the reduction of gamma oscillation power by parvalbumin deficit
Postmortem studies of schizophrenia brains show reduction in PV and in the levels of the GABA-synthesizing enzyme GAD67 (for review, see Benes and Berretta, 2001; Akbarian and Huang, 2006). Reduced levels of GAD67 imply a deficit of GABA synaptic transmitter, which would alter the properties of inhibitory control of network activity. Because of the role played by PV+ basket interneurons in the generation of gamma oscillatory activity, such alteration in GABA transmission is expected to affect the propensity of a network to generate collective activity in the gamma range; however, the effect of GAD67 alterations in reduced PV conditions is not clear. Thus, we used our computational model to probe the combined effect of reduced PV and GAD67 on network collective activity.
We first investigated how uniform (applied equally to all interneurons in our model network) alterations in properties of GABA synaptic transmission and PV concentration would affect the characteristics of steady-state network dynamics. Experimentally observed reduction in GAD1/GAD67 transcripts and immunoreactivity in schizophrenia may imply deficits in GABA synaptic transmission in the disease (for review, see Akbarian and Huang, 2006). In our model, a reduction in GABA synaptic transmission could be implemented as a reduction in GABA synaptic conductance (both gPY←IN and gIN←IN). As Figure 6, A1 and A2, shows, a reduction of gPY←IN and gIN←IN to 60% of their values in the baseline model caused a significant reduction in peak spectral power over a wide range of PV concentration values. For lower GABA conductance, the frequency at the peak power showed a shift toward higher gamma range (Fig. 6A3), thus suggesting that the effect of reduced GABA is to reduce the power of gamma activity by network disinhibition, consistent with the data shown in Figure 2. This was further confirmed by the observation that the firing rates of both PY and IN neurons were higher in the “low GABA” scenario, compared with the firing rates in the baseline network (Fig. 6C1,C2, black squares for the baseline model and red triangles for the low GABA model).
Our leading assumption was that the reduced GAD67 levels correspond to lower GABA conductance. An alternative scenario is the one in which a reduced expression of GABA-synthesizing enzyme would lead to longer GABA turnover, thus effectively increasing the recovery time from short-term synaptic depression. Figure 6, B1 and B2, shows that the effect of slower GABA recovery was qualitatively similar to that of lower GABA conductance—the peak spectral power was reduced for slower τR (recovery time from short-term synaptic depression) across a wide range of PV concentration values (Fig. 6B2), and the location of spectral power peak had shifted toward higher gamma frequencies, suggesting network disinhibition (Fig. 6B3). This is confirmed by higher firing rates of PY and IN neurons under conditions of slower GABA recovery (Fig. 6C3,C4, black squares for baseline model and red triangles for the “slow GABA recovery” model).
Next, we investigated the effect of altered GABA synaptic transmission on the network response to strong and brief stimulation when PV is reduced. As before, we considered the neuron deficit scenario, in which PV concentration was set to zero in a fraction F[PV] = 0 of model interneurons and the synapses they make. We further assumed that GABA synaptic conductance is reduced only at those synapses that are made by model interneurons with zero PV concentration (i.e., GABA synaptic conductance is reduced in a fraction F[PV] = 0 of interneurons and is colocalized with reduced parvalbumin). To further facilitate the comparison with the effects of PV deficit alone (Fig. 5), we used the same stimulation scenario as for the conditions shown in Figure 5. Specifically, the baseline stimulation frequency was vSTIM = 150 Hz. For a strong stimulus, the stimulation frequency was instantaneously increased (in the range from 200 to 800 Hz) for 40 ms, after which vSTIM was reset to its baseline value.
As shown in Figure 6, D and E, a reduced GABA synaptic conductance on PV-deficient networks significantly affected the response to brief stimuli. Spectral power peak during stimulus presentation was weaker for more severe PV deficiency (higher values of F[PV] = 0 in Fig. 6 D1), in qualitative agreement with the effect of PV as shown in Figure 5C1. During the 200 ms window after stimulus cessation, the magnitude of the spectral power peak was significantly lower for higher PV deficiencies and weaker stimuli (Fig. 6D2), again qualitatively consistent with the effect of PV alone as shown in Figure 5C2. A quantitative comparison between the two scenarios (manipulation on PV in the model with baseline GABA conductance vs the model with reduced GABA conductance) further confirmed the downregulating effect of PV deficit on the power of gamma oscillatory activity (Fig. 6E1,E2). Interestingly, the spectral response to a stimulus in a network with intact PV (F[PV] = 0 = 0) was stronger for a network with lower GABA conductance (Fig. 6E1,E2, solid black line for gGABA at 100% vs solid red line for gGABA at 60%), reflecting the fact that for lower GABA conductance the network is more disinhibited and thus easier to excite.
Discussion
In our model, reduced parvalbumin in synapses of fast-spiking interneurons affected network oscillations, and asynchronous release of GABA correlated with reduction of oscillatory power. One possibility is that the alteration in oscillatory activity occurred through increased asynchronous release of GABA (Manseau et al., 2010). However, a direct causal link between asynchronous release and impaired gamma activity remains to be established. Asynchronous release of GABA increased the probability of synaptic release for hundreds of milliseconds following synaptic stimulation; thus, the inhibition was effectively extended in time. Börgers et al. (2005) previously used computational models to show that temporally distributed inhibition (resulting from temporally asynchronous activity of interneurons) reduced the amplitude of the background gamma activity, impaired the response of the network to stimuli, and increased the distractability of the response, consistent with our observations of a reduced response to stimuli in networks with reduced PV in the interneurons. This mechanism does not necessarily require the activity of interneurons to be asynchronous, but rather depends on asynchronous synaptic transmission. Asynchronous spiking of interneurons may indeed act in concert with the synaptic mechanism studied here. The relative role of interneuron synchronization and asynchronous release of GABA in setting the network rhythm remains to be investigated.
The asynchronous release of neurotransmitter is present even at glutamatergic central synapses, which could also affect the dynamics of the network (Lau and Bi, 2005; Jones et al., 2007; Chang and Mennerick, 2010; Manseau et al., 2010). The propensity of a synapse to exhibit asynchronous release likely depends on spatial organization of the active zone and on the presence of calcium buffers with different kinetics/mobility (Nadkarni et al., 2010). In the present study, we used a phenomenological approach to model the relation between synaptic calcium and asynchronous neurotransmitter release. Effects of active zone geometry, calcium diffusion, and buffer mobility were neglected. We anticipate that including these detailed features in the model (which comes at the expense of dramatically increased computational complexity) will not qualitatively change conclusions regarding the role of asynchronous release in mediating the effects of parvalbumin deficit on gamma range activity. How the complexity of synaptic microphysiology might affect the collective activity remains to be tested with more detailed models.
The spectral properties of collective oscillations in our model were strongly dependent on the strength and dynamics of the interactions between PY and IN subpopulations. More importantly, these results predict that the availability and release of synaptic GABA directly affect collective oscillations. In particular, the lack of PV at synaptic terminals of fast-spiking interneurons decreased gamma-band synchronization by increased asynchronous release of GABA.
Several studies have reported that stimulus-evoked collective oscillatory activity (assessed in a time window up to ~300 ms after stimulus presentation) was altered in schizophrenia patients (Ferrarelli et al., 2008; Hirano et al., 2008; Roach and Mathalon, 2008; Spencer et al., 2008; Uhlhaas and Singer, 2010). Some studies showed that early evoked gamma-band response (50–150 ms after stimulus cessation) was reduced in schizophrenia (Hirano et al., 2008; Roach and Mathalon, 2008; Spencer et al., 2008). In another study, gamma power was reduced only in a window 220–350 ms after a stimulus (Gallinat et al., 2004). These differences could be explained in our model by the differing ability of the stimuli used in these studies to “switch on” asynchronous GABA release. In another study, the spectral power of evoked gamma-band oscillations was reduced in EEG recordings from frontal cortices of human schizophrenia patients (Ferrarelli et al., 2008). Furthermore, a recent study found that PV expression correlates with reduction of evoked gamma oscillations in an animal model of the disease (Phillips et al., 2011). These results, together with our modeling studies suggest that a deficit in parvalbumin expression in PV interneurons may partly explain the pathophysiology of schizophrenia.
Reduced inhibitory drive in schizophrenia has been attributed to reduced expression of GAD67, the enzyme responsible for most of the GABA synthesis in the brain (Akbarian and Huang, 2006). A decreased inhibitory drive would intuitively lead to increased firing rates of both pyramidal neurons and interneurons. In our model, a reduction in the strength of the GABA “signal” to pyramidal neurons (implemented either as a reduction in peak synaptic conductance or as a more prolonged recovery from synaptic depression) (Fig. 2B) decreased the peak spectral power and shifted it toward higher frequencies. This network disinhibition was not dependent on PV concentration (Fig. 6). However, lowering the PV concentration decreased neuronal firing rates (Fig. 6C). Thus, PV reduction may be a mechanism used by interneurons to maintain network homeostasis and to compensate for the increased firing rate incurred by a compromised GAD67 functionality. Interestingly, data from cultured neurons show that reduction in GAD67 is followed by the reduction in the PV content (Kinney et al., 2006). Preliminary results of our model incorporating the dynamic homeostatic-like changes in both GABA conductance and PV concentration at synaptic terminals of PV+ interneurons support this possibility (data not shown).
Acute disinhibition of pyramidal neurons had been previously suggested as the underlying mechanism of the propsychotic effects of NMDAR antagonists such as phencyclidine and ketamine (Olney et al., 1999; Homayoun and Moghaddam, 2007). These antagonists induce psychotic symptoms in humans and trigger an outbreak in schizophrenia patients (Javitt and Zukin, 1991; Krystal et al., 1994). The heightened sensitivity of PV+ interneurons to NMDA antagonists (Homayoun and Moghaddam, 2007) may be attributed to differences in NMDA receptor kinetics and expression in PY versus PV+ neurons (Wang and Gao, 2010), and some modeling studies (Spencer, 2009) support this. Our simulations further support disinhibition of the network following decreased GABA conductances.
It is important to note, however, that these acute effects of NMDAR antagonists do not produce the long-term alterations in parvalbumin and GAD67 expression modeled in our study (Behrens et al., 2007). Nonetheless, the reduction in GAD67 and PV immunoreactivity in PV+ interneurons observed following prolonged application of NMDA antagonists suggests a critical role for NMDA transmission in the maintenance of proper GABAergic synaptic transmission (Kinney et al., 2006; Behrens et al., 2007; Zhang et al., 2008). Indeed, several studies performed in mice with postnatal downregulation of NMDARs in PV interneurons have shown an increased sensitivity of the cortical network to the acute effects of NMDAR antagonist exposures (Belforte et al., 2010; Carlen et al., 2011). Furthermore, acute pharmacological blockade of NMDARs with several NMDAR antagonists in a neurodevelopmental animal model produced deficits in PV interneurons and decreased the evoked gamma power (Phillips et al., 2011). These results strongly suggest that NMDA hypofunction and GABA dysfunction are part of the pathophysiological chain of events leading to the onset of schizophrenia.
Genetic disruption of NMDAR function in PV interneurons in the NMDAR ablation model produced an increased excitability of pyramidal neurons with increased spontaneous activity in the 30–80 Hz range (Belforte et al., 2010; Korotkova et al., 2010; Carlen et al., 2011). Pilot studies performed with our model show that the relative spectral power of spontaneous activity in high beta and lower gamma range was increased when the NMDA conductance was set to zero on interneurons (the “spontaneous state” was achieved by reducing the external stimulation to both PY and IN neurons to produce firing rates of ~1–3 Hz in these neurons). The model further suggested that the NMDAR blockade-induced increase in the relative spectral power was weaker for a network with deficit in PV concentration, consistent with the recent experimental findings suggesting the same trend in animal models (Phillips et al., 2011). More detailed modeling studies, incorporating small differences in NMDA subunit composition between PY and PV+ neurons, will further delineate the interaction of NMDA hypofunction and dysfunctional GABA transmission in schizophrenia.
Although PV reduction can account for some of the changes reported in schizophrenia and related neuropsychiatric disorders, several other alterations in neural circuitry are well documented in schizophrenia. As discussed above, the changes in GAD67 expression, as well as the reduced excitatory drive supporting the hypothesis of NMDA hypofunction should be incorporated in the model to obtain a full picture of the alterations observed in schizophrenia. Nonetheless, a deficit in PV may be an important step leading to other pathological dynamics associated with schizophrenia. How these different processes interact to reproduce the full etiology and pathology of schizophrenia remains to be investigated in joint experimental and modeling studies.
Acknowledgments
This study was supported by NIH Grants NS059740 and MH091407, and the Howard Hughes Medical Institute. Numerical simulations were performed using computational resources of the National Science Foundation (NSF)-sponsored Center for Theoretical Biological Physics at University of California San Diego under NSF Grant NSF PHY-0822283.
Footnotes
Author contributions: V.V., M.MB., and T.J.S. designed research; V.V. performed research; V.V., M.MB., and T.J.S. analyzed data; V.V., M.M.B., and T.J.S. wrote the paper.
References
- Akbarian S, Huang HS. Molecular and cellular mechanisms of altered GAD1/GAD67 expression in schizophrenia and related disorders. Brain Res Rev. 2006;52:293–304. doi: 10.1016/j.brainresrev.2006.04.001. [DOI] [PubMed] [Google Scholar]
- Atallah BV, Scanziani M. Instantaneous modulation of gamma oscillation frequency by balancing excitation with inhibition. Neuron. 2009;62:566–577. doi: 10.1016/j.neuron.2009.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens MM, Ali SS, Dao DN, Lucero J, Shekhtman G, Quick KL, Dugan LL. Ketamine-induced loss of phenotype of fast-spiking interneurons is mediated by NADPH-oxidase. Science. 2007;318:1645–1647. doi: 10.1126/science.1148045. [DOI] [PubMed] [Google Scholar]
- Belforte JE, Zsiros V, Sklar ER, Jiang Z, Yu G, Li Y, Quinlan EM, Nakazawa K. Postnatal NMDA receptor ablation in corticolimbic interneurons confers schizophrenia-like phenotypes. Nat Neurosci. 2010;13:76–83. doi: 10.1038/nn.2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benes FM, Berretta S. GABAergic interneurons: implications for understanding schizophrenia and bipolar disorder. Neuropsychopharmacology. 2001;25:1–27. doi: 10.1016/S0893-133X(01)00225-1. [DOI] [PubMed] [Google Scholar]
- Börgers C, Epstein S, Kopell NJ. Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc Natl Acad Sci U S A. 2005;102:7002–7007. doi: 10.1073/pnas.0502366102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucurenciu I, Kulik A, Schwaller B, Frotscher M, Jonas P. Nanodomain coupling between Ca2+ channels and Ca2+ sensors promotes fast and efficient transmitter release at a cortical GABAergic synapse. Neuron. 2008;57:536–545. doi: 10.1016/j.neuron.2007.12.026. [DOI] [PubMed] [Google Scholar]
- Caillard O, Moreno H, Schwaller B, Llano I, Celio MR, Marty A. Role of the calcium-binding protein parvalbumin in short-term synaptic plasticity. Proc Natl Acad Sci U S A. 2000;97:13372–13377. doi: 10.1073/pnas.230362997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardin JA, Carlén M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai LH, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlen M, Meletis K, Siegle JH, Cardin JA, Futai K, Vierling-Claassen D, Ruhlmann C, Jones SR, Deisseroth K, Sheng M, Moore CI, Tsai LH. A critical role for NMDA receptors in parvalbumin interneurons for gamma rhythm induction and behavior. Mol Psychiatry. 2011 doi: 10.1038/mp.2011.31. Advance online publication. Retrieved November 4, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CY, Mennerick S. Dynamic modulation of phasic and asynchronous glutamate release in hippocampal synapses. J Neurophysiol. 2010;103:392–401. doi: 10.1152/jn.00683.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrarelli F, Massimini M, Peterson MJ, Riedner BA, Lazar M, Murphy MJ, Huber R, Rosanova M, Alexander AL, Kalin N, Tononi G. Reduced evoked gamma oscillations in the frontal cortex of schizophrenia patients: a TMS/EEG study. Am J Psychiatry. 2008;165:996–1005. doi: 10.1176/appi.ajp.2008.07111733. [DOI] [PubMed] [Google Scholar]
- Galarreta M, Hestrin S. Electrical and chemical synapses among parvalbumin fast-spiking GABAergic interneurons in adult mouse neocortex. Proc Natl Acad Sci U S A. 2002;99:12438–12443. doi: 10.1073/pnas.192159599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallinat J, Winterer G, Herrmann CS, Senkowski D. Reduced oscillatory gamma-band responses in unmedicated schizophrenic patients indicate impaired frontal network processing. Clin Neurophysiol. 2004;115:1863–1874. doi: 10.1016/j.clinph.2004.03.013. [DOI] [PubMed] [Google Scholar]
- Glausier JR, Lewis DA. Selective pyramidal cell reduction of GABAA receptor α1 subunit messenger RNA expression in schizophrenia. Neuropsychopharmacology. 2011;36:2103–2110. doi: 10.1038/npp.2011.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goad Y, Stevens CF. Two components of transmitter release at a central synapse. Proc Natl Acad Sci U S A. 1994;91:12942–12946. doi: 10.1073/pnas.91.26.12942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hefft S, Jonas P. Asynchronous GABA release generates long-lasting inhibition at a hippocampal interneuron-principal neuron synapse. Nat Neurosci. 2005;8:1319–1328. doi: 10.1038/nn1542. [DOI] [PubMed] [Google Scholar]
- Hirano S, Hirano Y, Maekawa T, Obayashi C, Oribe N, Kuroki T, Kanba S, Onitsuka T. Abnormal neural oscillatory activity to speech sounds in schizophrenia: a magnetoencephalography study. J Neurosci. 2008;28:4897–4903. doi: 10.1523/JNEUROSCI.5031-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homayoun H, Moghaddam B. NMDA receptor hypofunction produces opposite effects on prefrontal cortex interneurons and pyramidal neurons. J Neurosci. 2007;27:11496–11500. doi: 10.1523/JNEUROSCI.2213-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iremonger KJ, Bains JS. Integration of asynchronously released quanta prolongs the postsynaptic spike window. J Neurosci. 2007;27:6684–6691. doi: 10.1523/JNEUROSCI.0934-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahr CE, Stevens CF. A quantitative description of NMDA receptor-channel kinetic behavior. J Neurosci. 1990;10:1830–1837. doi: 10.1523/JNEUROSCI.10-06-01830.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Javitt DC, Zukin SR. Recent advances in the phencyclidine model of schizophrenia. Am J Psychiatry. 1991;148:1301–1308. doi: 10.1176/ajp.148.10.1301. [DOI] [PubMed] [Google Scholar]
- Jensen O, Kaiser J, Lachaux JP. Human gamma-frequency oscillations associated with attention and memory. Trends Neurosci. 2007;30:317–324. doi: 10.1016/j.tins.2007.05.001. [DOI] [PubMed] [Google Scholar]
- Jones J, Stubblefield EA, Benke TA, Staley KJ. Resynchronization of glutamate release prolongs synchronous CA3 network activity. J Neurophysiol. 2007;97:3812–3818. doi: 10.1152/jn.01310.2006. [DOI] [PubMed] [Google Scholar]
- Kinney JW, Davis CN, Tabarean I, Conti B, Bartfai T, Behrens MM. A specific role for NR2A-containing NMDA receptors in the maintenance of parvalbumin and GAD67 immunoreactivity in cultured interneurons. J Neurosci. 2006;26:1604–1615. doi: 10.1523/JNEUROSCI.4722-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korotkova T, Fuchs EC, Ponomarenko A, von Engelhardt J, Monyer H. NMDA receptor ablation on parvalbumin-positive interneurons impairs hippocampal synchrony, spatial representations, and working memory. Neuron. 2010;68:557–569. doi: 10.1016/j.neuron.2010.09.017. [DOI] [PubMed] [Google Scholar]
- Krystal JH, Karper LP, Seibyl JP, Freeman GK, Delaney R, Bremner JD, Heninger GR, Bowers MB, Jr, Charney DS. Subanesthetic effects of the noncompetitive NMDA antagonist, ketamine, in humans. Psychotomimetic, perceptual, cognitive, and neuroendocrine responses. Arch Gen Psychiatry. 1994;51:199–214. doi: 10.1001/archpsyc.1994.03950030035004. [DOI] [PubMed] [Google Scholar]
- Lau PM, Bi GQ. Synaptic mechanisms of persistent reverberatory activity in neuronal networks. Proc Natl Acad Sci U S A. 2005;102:10333–10338. doi: 10.1073/pnas.0500717102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Schwaller B, Neher E. Kinetics of Ca2+ binding to parvalbumin in bovine chromaffin cells: implications for [Ca2+] transients of neuronal dendrites. J Physiol. 2000;525:419–432. doi: 10.1111/j.1469-7793.2000.t01-2-00419.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis DA, Hashimoto T, Volk DW. Cortical inhibitory neurons and schizophrenia. Nat Rev Neurosci. 2005;6:312–324. doi: 10.1038/nrn1648. [DOI] [PubMed] [Google Scholar]
- Lewis DA, Fish KN, Arion D, Gonzalez-Burgos G. Perisomatic inhibition and cortical circuit dysfunction in schizophrenia. Curr Opin Neurobiol. 2011 doi: 10.1016/j.conb.2011.05.013. Advance online publication. Retrieved November 4, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Light GA, Hsu JL, Hsieh MH, Meyer-Gomes K, Sprock J, Swerdlow NR, Braff DL. Gamma band oscillations reveal neural network cortical coherence dysfunction in schizophrenia patients. Biol Psychiatry. 2006;60:1231–1240. doi: 10.1016/j.biopsych.2006.03.055. [DOI] [PubMed] [Google Scholar]
- Manseau F, Marinelli S, Mendez P, Schwaller B, Prince DA, Huguenard JR, Bacci A. Resynchronization of neocortical networks by asynchronous release of GABA at autaptic and synaptic contacts from fast-spiking interneurons. PLoS Biol. 2010;8:e1000492. doi: 10.1371/journal.pbio.1000492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadkarni S, Bartol TM, Sejnowski TJ, Levine H. Modelling vesicular release at hippocampal synapses. PLoS Comp Biol. 2010;6:e1000983. doi: 10.1371/journal.pcbi.1000983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olney JW, Newcomer JW, Farber NB. NMDA receptor hypofunction model of schizophrenia. J Psychiatr Res. 1999;33:523–533. doi: 10.1016/s0022-3956(99)00029-1. [DOI] [PubMed] [Google Scholar]
- Phillips KG, Cotel MC, McCarthy AP, Edgar DM, Tricklebank M, O’Neill MJ, Jones MW, Wafford KA. Differential effects of NMDA antagonists on high frequency and gamma EEG oscillations in a neurodevelopmental model of schizophrenia. Neuropharmacology. 2011 doi: 10.1016/j.neuropharm.2011.04.006. Advance online publication. Retrieved November 4, 2011. [DOI] [PubMed] [Google Scholar]
- Pinto-Duarte A, Bonjean M, Behrens MM, Sejnowski TJ. Neonatal exposure to NMDA receptor antagonists halts the maturation of parvalbumin-positive fast-spiking interneurons, leading to altered network activity in adulthood. Soc Neurosci Abstr. 2010;36:363.21. [Google Scholar]
- Powell SB, Sejnowski TJ, Behrens MM. Behavioral and neurochemical consequences of cortical oxidative stresson parvalbumin-interneuron maturation in rodent models of schizophrenia. Neuropharmacology. 2011 doi: 10.1016/j.neuropharm.2011.01.049. Advance online publication. Retrieved November 4, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, Ratté S, De Koninck Y, Sejnowski TJ. Nonlinear interaction between shunting and adaptation controls a switch between integration and coincidence detection in pyramidal neurons. J Neurosci. 2006;26:9084–9097. doi: 10.1523/JNEUROSCI.1388-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach BJ, Mathalon DH. Event-related EEG time-frequency analysis: an overview of measures and an analysis of early gamma band phase locking in schizophrenia. Schizophr Bull. 2008;34:907–926. doi: 10.1093/schbul/sbn093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer W. Neuronal synchrony: a versatile code for the definition of relations? Neuron. 1999;24:49–65. 111–125. doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
- Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer KM. The functional consequences of cortical circuit abnormalities on gamma oscillations in schizophrenia: insights from computational modeling. Front Hum Neurosci. 2009;3:33. doi: 10.3389/neuro.09.033.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer KM, Niznikiewicz MA, Shenton ME, McCarley RW. Sensory-evoked gamma oscillations in chronic schizophrenia. Biol Psychiatry. 2008;63:744–747. doi: 10.1016/j.biopsych.2007.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stride M, Deschênes M, Oakson G. Inhibitory processes and interneuronal apparatus in motor cortex during sleep and waking. I. Background firing and responsiveness of pyramidal tract neurons and interneurons. J Neurophysiol. 1974;37:1065–1092. doi: 10.1152/jn.1974.37.5.1065. [DOI] [PubMed] [Google Scholar]
- Sun Y, Farzan F, Barr MS, Kirihara K, Fitzgerald PB, Light GA, Daskalakis ZJ. Gamma oscillations in schizophrenia: mechanisms and clinical significance. Brain Res. 2011;1413:98–114. doi: 10.1016/j.brainres.2011.06.065. [DOI] [PubMed] [Google Scholar]
- Tiesinga P, Sejnowski TJ. Cortical enlightenment: are gamma oscillations driven by ING or PING? Neuron. 2009;63:727–732. doi: 10.1016/j.neuron.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrey EF, Barci BM, Webster MJ, Bartko JJ, Meador-Woodruff JH, Knable MB. Neurochemical markers for schizophrenia, bipolar disorder, and major depression in postmortem brains. Biol Psychiatry. 2005;57:252–260. doi: 10.1016/j.biopsych.2004.10.019. [DOI] [PubMed] [Google Scholar]
- Traub RD, Jefferys JG, Whittington MA. Simulation of gamma rhythms in networks of interneurons and pyramidal cells. J Comput Neurosci. 1997;4:141–150. doi: 10.1023/a:1008839312043. [DOI] [PubMed] [Google Scholar]
- Tsodyks M, Uziel A, Markram H. Synchrony generation in recurrent networks with frequency-dependent synapses. J Neurosci. 2000;20(RC50):1–5. doi: 10.1523/JNEUROSCI.20-01-j0003.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlhaas PJ, Singer W. Abnormal neural oscillations and synchrony in schizophrenia. Nat Rev Neurosci. 2010;11:100–113. doi: 10.1038/nrn2774. [DOI] [PubMed] [Google Scholar]
- Volman V, Gerkin RC, Lau PM, Ben-Jacob E, Bi GQ. Calcium and synaptic dynamics underlie reverberatory activity in cultured neuronal networks. Phys Biol. 2007;4:91–103. doi: 10.1088/1478-3975/4/2/003. [DOI] [PubMed] [Google Scholar]
- Volman V, Levine H, Sejnowski TJ. Shunting inhibition controls the gain modulation mediated by asynchronous neurotransmitter release in early development. PLoS Comp Biol. 2010;6:e1000973. doi: 10.1371/journal.pcbi.1000973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang CZ, Yang SF, Xia Y, Johnson KM. Postnatal phencyclidine administration selectively reduces adult cortical parvalbumin-containing interneurons. Neuropsychopharmacology. 2008;33:2442–2455. doi: 10.1038/sj.npp.1301647. [DOI] [PubMed] [Google Scholar]
- Wang HX, Gao WJ. Development of calcium-permeable AMPA receptors and their correlation with NMDA receptors in fast-spiking interneurons of rat prefrontal cortex. J Physiol. 2010;588:2823–2838. doi: 10.1113/jphysiol.2010.187591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittington MA, Cunningham MO, LeBeau FE, Racca C, Traub RD. Multiple origins of the cortical gamma rhythm. Dev Neurobiol. 2011;71:92–106. doi: 10.1002/dneu.20814. [DOI] [PubMed] [Google Scholar]
- Zaitsev AV, Povysheva NV, Lewis DA, Krimer LS. P/Q-type, but not N-type, calcium channels mediate GABA release from fast-spiking interneurons to pyramidal cells in rat prefrontal cortex. J Neurophysiol. 2007;97:3567–3573. doi: 10.1152/jn.01293.2006. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Behrens MM, Lisman JE. Prolonged exposure to NMDAR antagonist suppresses inhibitory synaptic transmission in prefrontal cortex. J Neurophysiol. 2008;100:959–965. doi: 10.1152/jn.00079.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]