Abstract
Cryopreservation of engineered tissue (ET) has achieved limited success due to limited understanding of freezing-induced biophysical phenomena in ETs, especially fluid-matrix interaction within ETs. To further our understanding of the freezing-induced fluid-matrix interaction, we have developed a biphasic model formulation that simulates the transient heat transfer and volumetric expansion during freezing, its resulting fluid movement in the ET, elastic deformation of the solid matrix and the corresponding pressure redistribution within. Treated as a biphasic material, the ET consists of a porous solid matrix fully saturated with interstitial fluid. Temperature-dependent material properties were employed and phase change was included by incorporating the latent heat of phase change into an effective specific heat term. Model-predicted temperature distribution, the location of the moving freezing front, and the ET deformation rates through the time course compare reasonably well with experiments reported previously. Results from our theoretical model show that behind the marching freezing front, the ET undergoes expansion due to phase change of its fluid contents. It compresses the region preceding the freezing front leading to its fluid expulsion and reduced regional fluid volume fractions. The expelled fluid is forced forward and upward into the region further ahead of the compression zone causing a secondary expansion zone; which then compresses the region further downstream with much reduced intensity. Overall, it forms an alternating expansion-compression pattern which moves with the marching freezing front. The present biphasic model helps us to gain insights into some facets of the freezing process and cryopreservation treatment that could not be gleaned experimentally. Its resulting understanding will ultimately be useful to design and improve cryopreservation protocols for ETs.
Keywords: biphasic, poro-elastic, engineered tissue, cryopreservation, model simulation
Introduction
With advances in tissue engineering technology shepherding development more rapidly toward functional products, it has become increasingly important to cultivate long term storage options for these constructs in order to realize manufacturing, storage, and distribution strategies necessary to achieve clinical product integration [1, 2]. Cryopreservation holds promise in this regard. However, current cryopreservation technology has achieved only limited success as a result of the damage incurred during freeze and thaw cycles [3–6].
Tissue damage during freeze and thaw cycles can be attributed to some combination of direct cell injury via intracellular ice formation, apoptosis, water redistribution and damage to the extracellular support structures [3–6]. Generation of localized regions of expansion and compression resulting from temporally and spatially evolving transitions of the local water content between the fluid and solid phases can lead to changes in both the intra- and extracellular environments that could affect tissue survival and function post-thaw. Maintaining the integrity, structure, and functionality of this extracellular environment, including the ECM, local vasculature, and local fluid content, is critical toward maintaining cell function and survival. It is important to quantify the evolving mechanical response of engineered tissue (ET) during freezing and to determine its effects on this local environment post-thaw as the cell-environment interaction plays a crucial role in determining key components of cell phenotype including cellular viability, morphology, growth, and various cellular functions [7–9]. Development of a validated model could augment experimental evidence yielding critical insight into phenomena like fluid transport that are difficult to obtain experimentally to help characterize the mechanical response of the ET during freezing and lend a valuable tool to aid in the optimization of tissue-dependent freeze-thaw protocols.
Development of a theoretical model for the process takes place in the ET during cryo-treatment is complicated by the heterogeneous, viscoelastic, and composite nature of tissue as well as the mathematical complexity of tracking temperature and phase changes in the model. Contemporary modeling strategies driven by questions surrounding cryosurgery have focused on incorporating phase change effects into a Pennes bioheat equation and quantifying the thermal history obtained to compare with post-surgery tissue injury [10–14]. Some investigators have developed models coupling the bioheat equation and associated phase change effects with stress analysis, treating tissue either as a linear elastic or elastic-perfectly plastic solid [11–17]. Although insightful, these approaches didn’t take the complex interaction between fluid and solid ECM into consideration. As the mechanics of soft tissues are intimately tied to the fact that they contain significant volumes of mobile interstitial fluid that can be redistributed in response to solid matrix deformation and altered pressure fields, a model incorporating this aspect is clearly needed.
Previous researchers have adopted either biphasic or poroelasticity theory to describe soft tissue mechanics [18,19]. Biphasic theory was developed from mixture theory (see review in Cowin and Doty) [20] assuming the tissue is composed of intimately mixed fluid and solid phases where the changes in proportions of each phase are dependent on deformation histories. It was first applied to study soft tissues mechanics by Mow et. al. [18]. Poroelasticity theory was originated by Biot for analysis of soil consolidation [21] and later applied by Simon [19] to the study of soft tissue mechanics with the idea that tissue is a fluid-saturated sponge-like matrix. Both models are equivalent under the assumption of incompressibility [19].
Biphasic theory provides a continuum framework that has been utilized to characterize the mechanics of various soft tissues including cartilage, arterial wall, vertebral disk, brain tissues, and interstitium [18, 19, 22–29]. Biphasic models have been applied to characterize macromolecular transport in tissue matrix for enhanced drug delivery [22], to describe swelling effects brought on by changes in local ion concentrations [22,30,31], to explore the balance between fluid infusion and lymphatic drainage under normal and edematous conditions [27], to study the response of cartilage and the behavior of temporal-mandibular joint disc [32], to characterize macromolecular transport from an injection site into the gray matter of the central nervous system [28], and to characterize the behavior of tissue such as articular cartilage in confined compression [29]. Formulations for previous works are applicable for studying process and events at constant temperature.
To further our understanding of the effects of a freeze-thaw process on soft tissues, in this work, we have developed an ET model by adopting a modified biphasic formulation that includes the effects of temperature and phase changes. Various temperature-dependent physical properties were directly incorporated. We employed the model to simulate the directional freezing of thin strip of ET and to examine the resulting elastic deformation of the ET along with the corresponding pressure redistribution and fluid movement.
Methods
Overview
We first present the biphasic formulation for the thermo-elastic deformation of an ET undergoing a freezing process with temperature and phase changes. We then apply this formulation to simulate the physical events of the freezing of a thin strip of ET, including the spatial and temporal variation in temperature distribution, the propagation of freezing front, the associated non-uniform tissue expansion, the corresponding pressure redistribution across the marching freezing front, and the resulting fluid movement. Model predictions are validated using experimental data reported in Teo et al. [33]
Formulation
We assume the ET can be modeled as a locally homogeneous, biphasic mixture consisting of chemically inert, immiscible solid and fluid phases. The solid matrix represents the interconnecting, polymer ECM skeleton and is assumed to behave linear-elastically undergoing small deformation. It is immersed in the surrounding fluid phase, which is considered inviscid, interacting with the solid skeleton through a diffusive drag coefficient incorporated as a hydraulic conductivity. In addition, inertial terms are deemed negligible. The formulation for the thermo-elastic deformation of the biphasic ET including both temperature and phase change is given as the follows:
Conservation of mass
Denoting φf, φs as the respective volume fraction for the fluid and solid polymer phases, v as the velocity vector of the fluid phase, and u as the displacement vector of the solid phase, the conservation of mass for the mixture can be written as
| (1) |
Conservation of linear momentum
Consider σf and σs as the stress tensors for the fluid and solid phases and d as the diffusive drag coefficient at the interface between two phases, the momentum equations can be written as the following for the fluid and solid phases respectively:
| (2) |
| (3) |
Constitutive equations
The constitutive equations for fluid and solid phases are
| (4) |
| (5) |
where p denotes the hydrostatic pressure, ε signifies the elastic strain tensor, αT symbolizes the thermal coefficient of linear expansion, T indicates the instantaneous temperature, Tref refers to the reference temperature, e stands for the volumetric expansion associated with phase change from water to ice, and F(T) designates the mass fraction of frozen tissue at a prescribed temperature in the mushy zone where the fluid progressively becomes ice. λ and μ denote Lame’s constants and can be related to the Young’s modulus E and Poisson’s ration v as [34]: and .
Note that on the right hand side of Eq. (5), within the bracket, the first term accounts for the strain contribution to the solid polymer matrix arising from thermal expansion of the neighboring fluid due to temperature change; while the second term accounts for that from volume expansion due to phase change within mushy zone as the fluid solidifies. A full description of the additional thermal strain components due to temperature and phase change are described in He and Bischof [11]. Note that the first term in the bracket is an approximation as the thermal expansion coefficient, technically, should be integrated over the range of temperature change to account for the temperature dependence of the material properties. The approximation was made to aid in numerical implementation noting that the contribution from the second term is dominant and much larger. The elastic strain ε is related to displacement gradients through
| (6) |
Darcy’s law
The relative movement between the fluid and solid matrix phases can be described by Darcy’s law written as
| (7) |
where Khyd conveys the hydraulic conductivity of the ET, which is related to diffusive drag coefficient d through
| (8) |
Transient temperature change in the biphasic ET mixture
To describe the spatiotemporal temperature history, the Pennes bioheat equation was adopted with a modified effective specific heat term [34] to account for the latent heat effects associated with phase change. Neglecting the effects of blood perfusion and metabolic heat generation, the governing equation for the cryo-treatment of the ET can be written as
| (9) |
where KT is thermal conductivity of the tissue, ρ is the density. The effective specific heat is the sum of cp and cL where cp is the standard specific heat associated with temperature change at a constant pressure, cL represents the additional energy transfer per unit mass associated with latent heat due to phase change over the “mushy” range of temperature. Note that cL was obtained by dividing the assumed latent heat of fusion for the fluid in the ET (~ L = 300 J/g [11,35]) over the temperature range through which the water content in ET progressively becomes ice. Consequently, the quantity obtained by integration of the area under the cL vs. T curve is equivalent to the latent heat of fusion, i.e.
| (10) |
where Tlower and Tupper mark the upper and lower limits of the mushy zone over which phase change occurs.
Solution algorithm
To tie all equations together, we first combine Eqs. (4) and (5) leading to the expression for the total stress σ as
| (11) |
where σe is the elastic stress accounting for the stress associated with the elastic deformation of the polymeric solid matrix, written as
| (12) |
Summing Eqs. (2) and (3) then substituting Eq. (11) yields the stress equilibrium equation as follows
| (13) |
Equation (13) states that any elastic deformation of the matrix is driven by both local pressure gradients and tissue expansion associated with temperature changes as well as that due to the phase change of the interstitial fluid to ice upon freezing.
The equation governing the pressure diffusion was obtained by substituting Eq. (7) into (1), i.e. the substitution of the generalized Darcy’s law into the continuity equation, leading to
| (14) |
Equations (9), (13), (14) together describe the complex spatiotemporal changes in temperature T, deformation of the matrix u, and interstitial pressure p. The temperature variations and phase changes, caused by the heat loss, induce regional volume and pressure changes leading to localized deformation and the development of mechanical stresses in the solid matrix. The resulting time rate of change in the dilatation of the matrix is related to the diffusion of the interstitial pressure through hydraulic conductivity in the mixture. The resulting pressure gradients drive the movement of interstitial fluid leading to a new equilibrium state.
Model validation
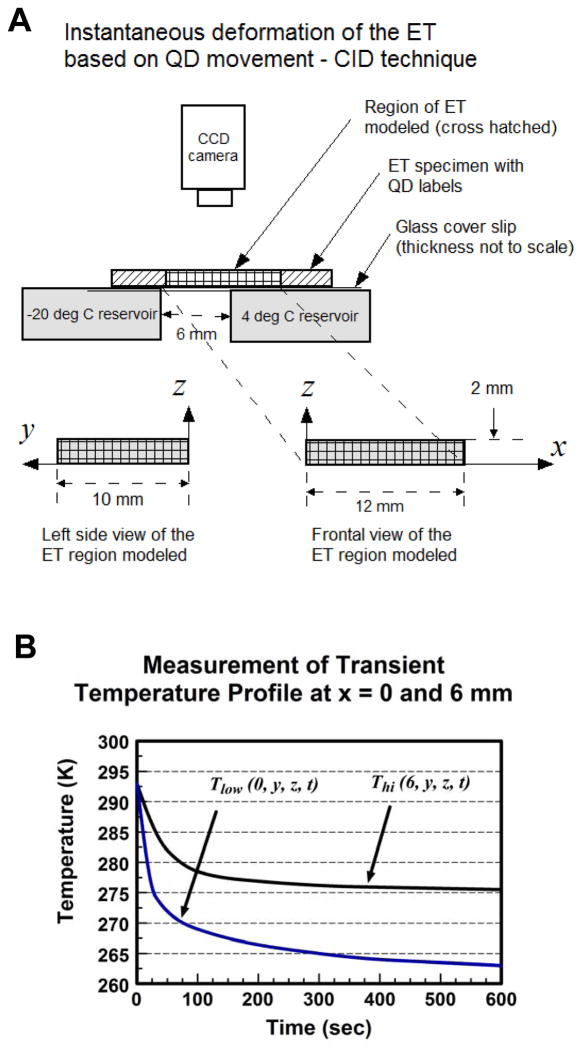
To demonstrate the validity of the formulation, we modeled the directional freezing of a thin ET strip as described in Teo et. al. [33] and compared model predictions with their experimental measurements. A brief description of the referenced is given wherein they measured the instantaneous deformation of a thin ET strip under directional freezing using a quantum dot-mediated cell image deformetry (CID) technique. The ET strip (approximate dimensions 48 × 20 × 2 mm) was constructed by seeding labeled quantum dots in a fibroblast-seeded type-1 collagen matrix and incubating for 24 hours. Initially at room temperature 20°C, directional freezing of the specimen was carried out by placing the specimen over a thin cover slip placed between two temperature reservoirs maintained at −20°C and 4°C with a 6 mm space between them (Fig. 1A). Through the freezing process, the specimen was imaged from a stationary camera above every 10 seconds and the time-varying sequence of local deformation rates of the ET was derived from the relative movement of quantum dots following CID technique [36]. The instantaneous location of the moving freezing front was monitored throughout the experiment.
Fig. 1.
A) A diagram illustrating the experimental setup used by Teo et al [33] to measure the ET’s response to directional freeze by employing the CID technique. B) Experimentally measured temperature profiles recorded on either side of the ET across the gap [37].
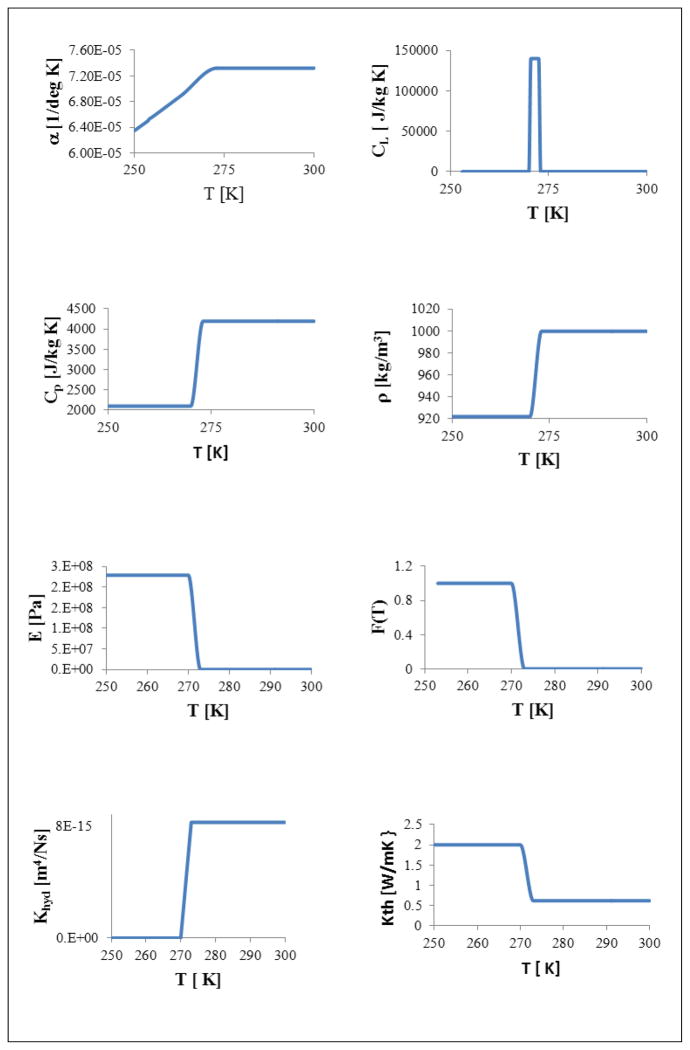
To validate our model formulation, a 3D model for the ET specimen, comprising dimensions of 10 × 12 × 2 mm (width × length × height), initially at 20°C, was subjected to the sudden application of −20°C temperature at one end where x = 0 at time t = 0. The ET was modeled as a biphasic mixture with fluid and solid matrix phases in a fully saturated state at a given initial porosity of ϕf(x, y, z, t = 0) = 0.914 [33]. Temperature-dependent properties for fluid and solid matrix phases were employed and the release of latent heat through the icing phase change was included. Temperature-dependent material properties used, including αT (thermal expansion coefficient), cP (Specific heat at constant pressure), cL (Effective specific heat accounting for latent heat), ρ (density), E (Young’s modulus), F(T)(Mass fraction of frozen tissue in mushy state), Khyd (Hydraulic conductivity) and KT (thermal conductivity) are summarized in Table 1 and illustrated in Fig. 2. Using the above formulation, the transient thermal-mechanical interaction was simulated for 500 sec.
Table 1.
Physical properties and parameters used in the current model
| Notation | Values | Sources | |
|---|---|---|---|
|
| |||
| αT | Thermal expansion coefficient [1/K] | 1.5 e-5 (7.323 + 0.04344 T + 6.105 e-5 T2) if T ≤ 263 K | [11] |
| Vary linearly if 263 K < T < 272.53 K | |||
| 7.323 e-5 if T ≥ 272.53 K | |||
|
| |||
| cL | Energy transfer/unit mass associated with latent heat [J/kg K] | 0 if T ≤ 270 K | [11]
|
| 140,000 if 270.5 K ≤ T ≤; 272.5 K | |||
| 0 if T ≥ 273 K | |||
| * Integration over mushy zone sums to L (latent heat change during freeze/thaw) | |||
|
| |||
| cp | Specific heat [J/kg K] | 2,099.5 if T ≤ 270 K | [11] Adjusted mushy zone. |
| Vary linearly if 270 K < T < 273 K | |||
| 4,194.7 if T ≥ 273 K | |||
|
| |||
| E | Young’s modulus [Pa] | 2.29 e8 if T ≤ 270 K | [11]
|
| Vary linearly if 270 K < T < 273 K | |||
| 2.29 e5 if T ≥ 273 K | |||
|
| |||
| F | Mass fraction of frozen portion of tissue | 1 if T ≤ 270 K | [11] Adjusted mushy zone. |
| Vary linearly if 270 K < T < 273 K | |||
| 0 if T ≥ 273 K | |||
|
| |||
| Khyd | Hydraulic conductivity [m4/Ns] | ~ 0 if T ≤ 270 K | [29] Adjusted to zero fluid flow in frozen region. |
| Vary linearly if 270 K < T < 273 K | |||
| 7.5 e-15 if T ≥ 273 K | |||
|
| |||
| KT | Thermal conductivity [W/m°C] | 2 if T ≤ 270 K | [11] Adjusted mushy zone. |
| Vary linearly if 270 K < T < 273 K | |||
| 0.62 if T ≥ 273 K | |||
|
| |||
| ρ | Density [kg/m3] | 921 if T ≤ 270 K | [11] Adjusted mushy zone. |
| Vary linearly if 270 K < T < 273 K | |||
| 999 if T ≥ 273 K | |||
|
| |||
| φf(t=0) | Initial porosity | 0.914 | [38] |
|
| |||
| Tref | Reference temperature [K] | 273 K | Temp at which phase change starts |
Fig. 2.
Temperature dependent material properties: αT (thermal expansion coefficient), cP (Specific heat at constant pressure), cL (Effective specific heat accounting for latent heat), ρ (density), E (Young’s modulus), F(T)(Mass fraction of frozen tissue in mushy state), Khyd (Hydraulic conductivity) and KT (thermal conductivity).
For the model dimension, a length of 12 mm was chosen to incorporate the 6 mm gap between temperature reservoirs described in the experiment as well as to provide additional mechanical anchoring consistent with the experiment at the far end of the model. Taking advantage of the symmetry with respect to zx-plane, the model considered only half of the actual geometry.
Boundary, initial conditions, and internal constraints (BC, IC)
Time-dependent temperature profiles Tlow (t) and Thi (t) recorded experimentally at x = 0 and 6 mm respectively [37] are summarized in Fig. 1B and they were employed as BC (x = 0) and internal constraints (x = 6) in the model, written as:
| (15) |
| (16) |
Another Dirichlet type BC needed for Eq. (9) was applied to the bottom surface of the ET supported by the 4°C reservoir, written as:
| (17) |
An insulated temperature BC was applied to the bottom surface of the ET above the gap but supported by the cover slip (0 ≤ x ≤ 6 and z = 0) and to the plane of symmetry (y = 0) as
| (18) |
where n represents the unit surface normal. A small amount of natural convective heat exchange is allowed on the top (z = 2) and the side (y = 10) surfaces of the ET written as
| (19) |
where hconv is the natural convective heat transfer coefficient in air and Troom = 20°C is the ambient room temperature.
Structurally, the bottom surface of the model (z = 0) is fully constrained written as:
| (20) |
At the low temperature end of the model where x = 0, the surface was free to expand in the y and z directions, but constrained in the x direction as shown:
| (21) |
A symmetry condition was employed at the plane y = 0 written as:
| (22) |
The remaining surfaces including the side wall (y = 10), the top (z = 2), and the back (x = 12) surfaces of the model were left unconstrained.
Fluid was prohibited from moving back into regions already in frozen state. Further, fluid was prohibited from moving across the surface where x = 0, or from exiting the domain through the bottom where the glass slide provided containment at z = 0 and from the plane of symmetry where y = 0, summarized as:
| (23) |
Zero pressures were applied at all other surfaces as indicated:
| (24) |
Numerical implementation
The model was meshed incorporating 1,440 quadratic elements throughout the domain and transient numerical analysis was performed using COMSOL 4.1 (COMSOL, Inc.) for 500 sec. The solution was judged to have been independent of the mesh size as doubling and tripling of the mesh density vertically then horizontally within the gap region led to no significant changes in the results. An implicit time stepping method was employed using a variable time-step controlled by a backward differentiation formula algorithm with the maximum step constrained to 0.1 sec. The tolerances for each iteration k were set to 1e-8 m for displacements, 0.01 Pa for pressure, and 0.01 °C for temperature, where convergence was satisfied when the error estimate, for all groups j, was smaller than the corresponding tolerance as follows:
| (25) |
Notes
We carried out model simulation for half of the geometry to take advantage of the symmetry with respect to plane y = 0. To facilitate the comparison with experimental measurement, we mirrored modeling results in post-processing to allow visualization of the entire ET.
Results
Propagation of the freezing front
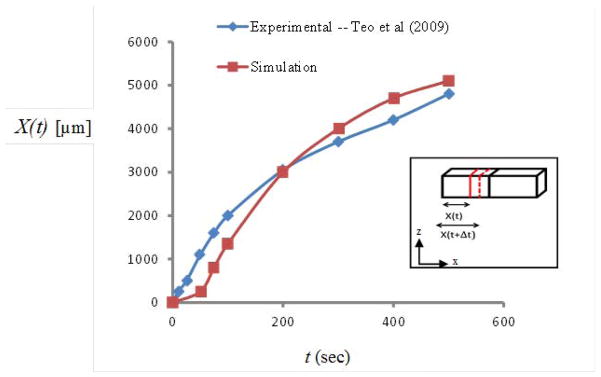
As time progresses a temperature gradient is established across the tissue gap with colder temperatures originating near the low temperature reservoir then marching toward the higher temperature end. As the temperatures drop below 0°C within portions of the ET, the localized tissue enters a mushy state as its fluid content is progressively converted into ice. As temperatures plummet, the mass fraction of ice to water continues to increase until all of the fluid content is effectively frozen. The freezing front X(t) can be defined as the location of the leading edge (farthest from cold reservoir) of this expanding region of icing at any time t. Model-predicted X(t) along the top surface show reasonably good agreement with that recorded from the CID experiments [33] (Fig. 3). The slopes of the X(t) curve reflect the speed of the propagating freezing front. Steeper initial slopes indicate that the front marches more quickly initially as heat extraction is more efficient closer to the low temperature reservoir where early axial temperature gradients are relatively steep. As time evolves and the front progresses across the gap moving farther from the low temperature reservoir, the axial temperature gradient decreases and the freezing front marches with reduced speed as heat extraction becomes less efficient.
Fig. 3.
Model-predicted (in red) and experimentally determined (in blue) [33] locations of the freezing front at different time steps.
Transient expansion and compression rates associated with the freezing front propagation
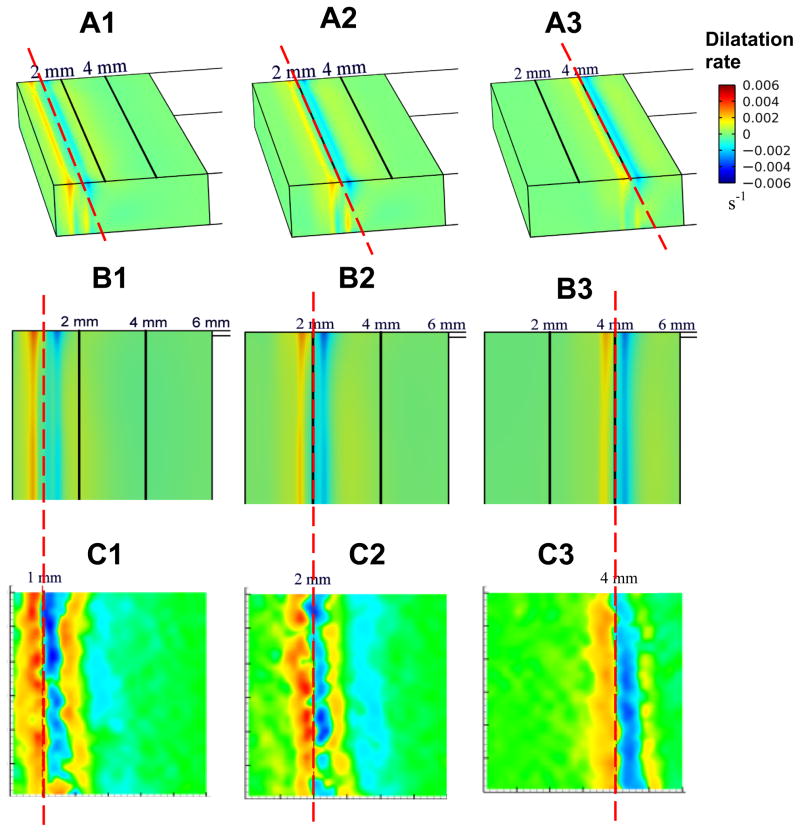
The spatiotemporal changes in temperature distribution along with the associated fluid phase change within the mushy zone result in localized expansion or compression in the ET. We first present model-predicted dilatational rates in 3D contour plots for three time steps (t = 85, 140, 310 sec) corresponding to freezing front locations of X(t) = 1, 2, 4 mm, respectively, as shown in Figs. 4A1–A3. These plots revealed an alternating pattern of expansion (in yellow, red) and compression (in blue), with the freezing front (referenced dash line in red) being centered between the initial expansive and compressive zones. Ahead of this initial compressive zone, the ET continues to experience alternating local bands of expansion and compression with decreasing intensities. The downstream intensity of this cyclic response diminishes as the front traverses the gap over time. This alternating pattern of expansion-compression extends throughout the thickness of the ET, but the bands appear more constricted and shifted slightly left near the bottom where any axial ET movement is resisted by the constraints from the bottom surface of the ET.
Fig. 4.
A1) Contours showing model predicted 3D dilatation rate in the ET when the freezing front is at location x = 1 mm, A2) x = 2 mm, and A3) x = 4 mm. B1) 2D Contour of dilatation rate at the upper surface of the ET when the freezing front is at location x = 1 mm, and B2) x = 2 mm, and B3) x = 4 mm. C1) Contours showing measurement of 2D dilatation rate derived using CID [33] when the freezing front is at location x = 1 mm, C2) x = 2 mm, and C3) at location x = 4 mm. Reference line over A1, A2 and A3 and that across B1–C1, B2–C2 and B3–C3 pairs are to highlight the instantaneous location of the freezing front between modeling predication and measurement.
For direct comparison with measurement data available, we included the corresponding 2D contour plots showing dilatation rates at the upper surface of the ET (Figs. 4B1–B3) and compared them with experimental measurements of Teo et al [33] (Figs. 4C1–C3) using the same scales. As in the prior 3D plots, the 2D plots indicate an alternating pattern of expansion and compression beginning with a regional expansion within the mushy zone where phase change occurs. The freezing front is centered between the foremost zones of expansion and compression. Although the responses appear to be more intense in the experiment, our model predictions show reasonably good qualitative agreement with the experimental observations in terms of the alternating pattern and the band locations at each time step.
Comparison of x-deformation rates on the top surface at various front locations
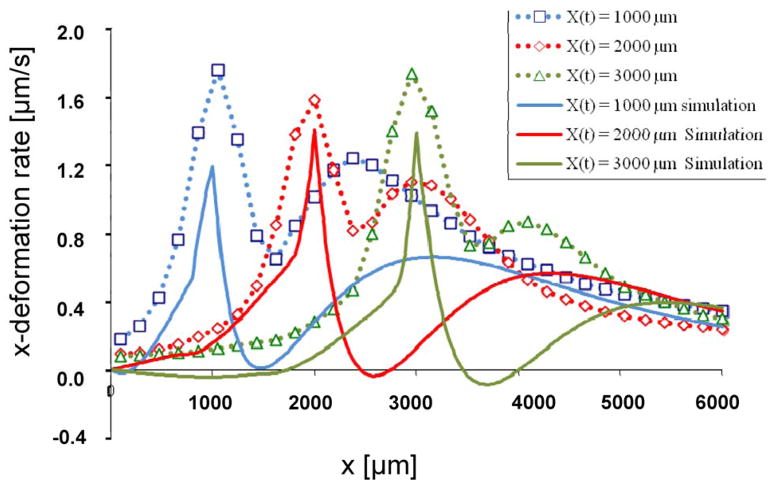
We calculated x-deformation rates at the upper surface of the ET when t = 85, 140, and 215 sec., corresponding to the front locations of x = 1, 2, and 3 mm, respectively. A comparison with measurements using CID technique [36] shows our model was able to capture the essential characteristic response of the ET (Fig 5). They exhibit alternating damped responses with decreasing amplitudes and wider wavelengths. Results show that the x-deformation rates increase throughout the mushy zone culminating in a maximum x-deformation rate corresponding to the location of the front at the leading edge of the freezing tissue. Ahead of the front, in the first compressive zone, the deformation rates decrease. Further ahead of this region, there is a second rise in the deformation rate, corresponding to a second region of expansion, preceded by a second fall in deformation rates consistent with the regions of compression. Thus, the regions of increasing x-deformation rate in the model correspond to regions of expansion, while regions undergoing decreases in the x-deformation rate correspond with regions of compression. The overall magnitude of the deformation rate is mitigated in the simulation, and regions exhibiting alternating expansion and compression ahead of the front experience weaker gradients and prolonged changes in the deformation rate when compared with experimental observations. These differences are likely due to the uncertainty in properties used, including Khyd and E (see Discussion).
Fig. 5.
Deformation rates calculated from simulation (solid line) and derived using CID (dotted line) [33] taken from the top surface of the TE when the freezing front is located at 1,000 (blue), 2,000 (red), and 3,000 (green) μm, or 1, 2, 3 mm, respectively. The corresponding time steps are 85, 140 and 215 seconds.
Fluid movement associated with tissue deformation
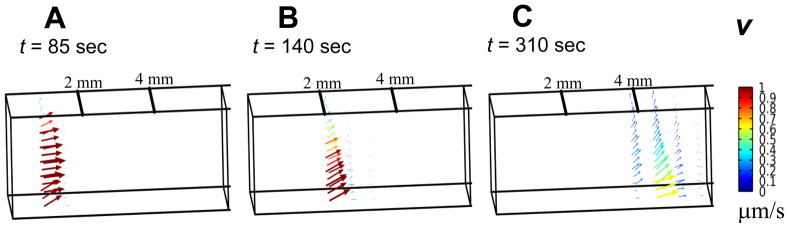
The mechanical response of the ET is governed by a combination of the solid matrix elastic properties and the interstitial fluid conductive properties. Results presented in both Figs. 6 and 7 indicate that there is a compressive zone directly preceding the freezing front. Fluid velocity fields corresponding to front locations of x = 1, 2, and 4 mm are illustrated as 3D vector plots in Fig. 6A–C. These results indicate that there is fluid expulsion out of the early region of compression preceding the freezing front. They suggest that as the freezing front marches in x-direction, the fluid content in the ET is forced axially in x-direction as well as upward into the immediate regions ahead of the compression zone. Consequently, there is a redistribution of fluid both axially and upward as the freezing front propagates.
Fig. 6.
Fluid velocity vector plots when the freezing front is at location A) x = 1 mm, B) x = 2 mm, and C) x = 4 mm, respectively
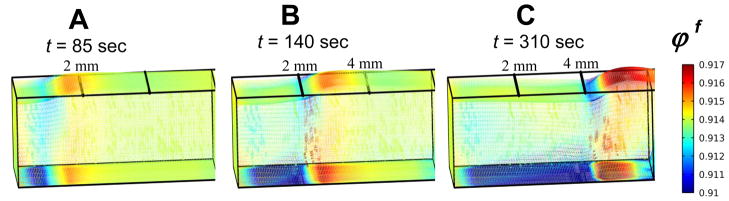
Fig. 7.
Model-predicted instantaneous fluid volume fractions in the Et when the freezing front location is at A) x = 1 mm, B) x = 2 mm, and C) x = 4 mm, respectively. Note that the initial volume fraction is ϕ f (x, y, z, t = 0) = 0.914
For small deformation, the fluid volume fraction φ f is a function of the instantaneous dilatation and the initial porosity φ f(t=0) as follows:
| (26) |
Instantaneous fluid volume fraction contours corresponding to the same freezing front locations of x = 1, 2, and 4 mm corroborate the fact that fluid is expelled from the compression zone immediately preceding the front (Fig. 7A–C). Results indicate that the fluid volume fraction decreases in this compressed zone and increases in the region preceding it, suggesting that the fluid is being redistributed and forced forward axially as the front proceeds. Furthermore, fluid volume fraction remains slightly diminished in regions behind the freezing front, including both region in mushy state and that frozen state. Our results indicate that the redistribution of fluid may play a key role in the soft tissue response to cryo-treatment, particularly, in eliciting the alternating pattern of expansion and compression observed experimentally.
Strain and stress profiles in the ET
As the mushy and frozen regions continue to expand, sequentially enveloping larger portions of the ET axially, transient strain and stress profiles evolve within it along with the progressing freezing front. The volumetric strain is the dilatational strain imparted on the tissue matrix calculated as the trace of the elastic strain tensor, written as:
| (27) |
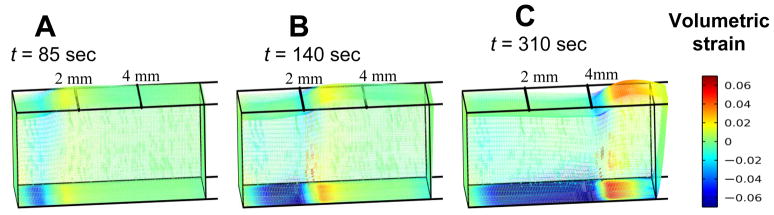
Instantaneous snapshots of the evolving volumetric strain profiles developed in the ET at times corresponding to front locations of X(t) = 1, 2, and 4 mm, respectively, are shown in Figs. 8A–C. These results indicate that as the front journeys distally, there are characteristic regions which move with the freezing front. The growing mushy and frozen regions behind the freezing front are clearly subjected to compressive volumetric strain as the tissue in this region undergoes thinning after the front has passed. Although we have indicated previously that the mushy region undergoes expansion, it occurs primarily in the axial direction due to the quasi-1D nature of the front propagation in the axial direction. This axially-dominated expansion along with the displacement constraints at the end surface, where x = 0, and at the bottom surface of the ET collectively lead to the reduction of the ET’s vertical dimension and hence its strain at the z-direction, particularly in the deep layers of the ET. Note that the compressive strains diminish near the upper surface of the ET because the upper surface is left traction free. Another region exhibiting stronger compressive volumetric strain is the region preceding the freezing front due to the vigorous expansion of the ET in the x-direction at region behind the propagating freezing front. In summary, the regions undergoing large compressive strains include 1) the deep regions of the mushy and frozen zones due to vertical thinning and boundary constraints, and 2) the region immediately preceding the marching freezing front as it is compressed axially by the rapid expansion of the ET behind the freezing front. Results also reveal expansive strains developing at region just forward of the compressed region.
Fig. 8.
Volumetric strains in the ET when the freezing front is at location A) x = 1 mm, B) x = 2 mm, and C) x = 4 mm, respectively.
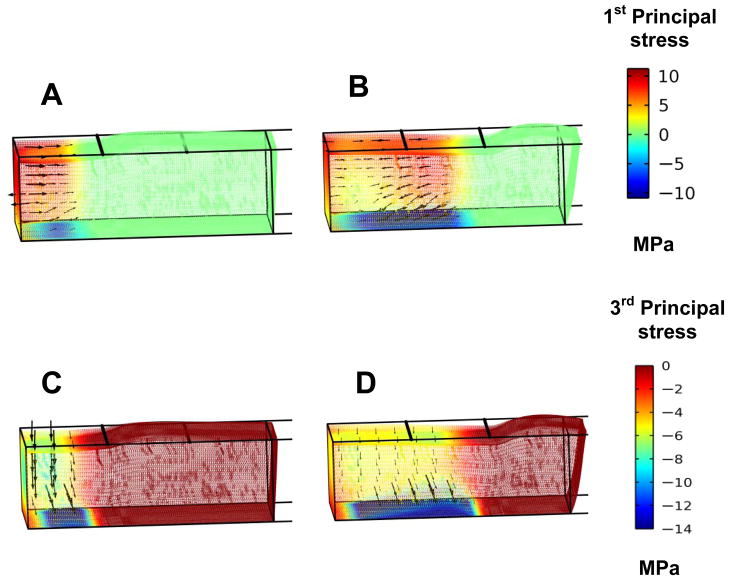
Combined principal stress contour and vector plots help to clarify that the mushy zone undergoes axial expansion as a results of phase change resulting in vertical compression and the subsequent thinning of the regional ET. Plots of the first principal stresses show they are expansive within most of the mushy zone, while they become compressive and directed back toward the cold reservoir only within the deepest layers affected by the boundary constraints (Fig. 9A, B). The superimposed vectors align primarily in axial direction due to the quasi-1D nature of the expansion within the region driven by phase change and its consequential expansion as the front moves in the same direction. Plots of the third principal stresses show this same region is under a vertical compressive stress consistent with the thinning of the regional ET (Figs. 9C, D).
Fig. 9.
The first principal stress in the ET when the freezing front is at location A) x = 2 mm, and B) x = 4 mm. The third principal stress when the freezing front is at location C) x = 2 mm, and D) x = 4 mm.
Front propagation results in alternating regions of expansion and compression
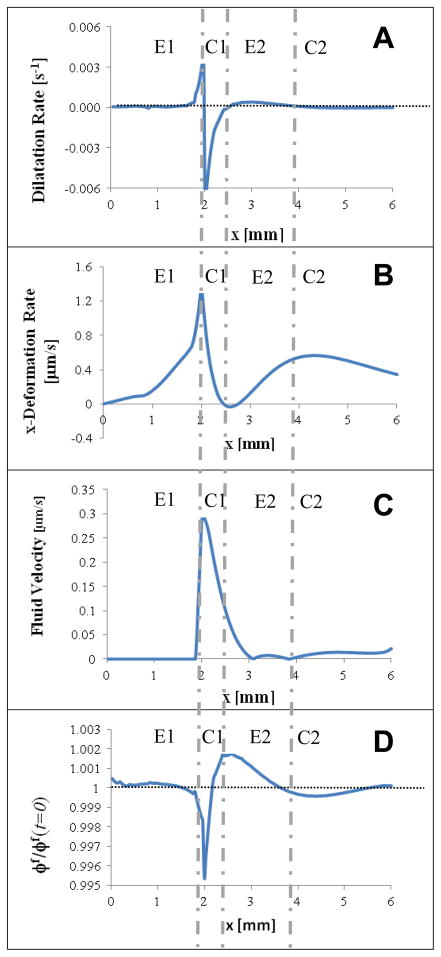
Both simulation and experimental results indicate that the directional freezing process in a thin strip of ET results in a tissue response characterized by alternating regions of expansion and compression. To further explain it, we summarized distributions of model-predicted results, including dilation rates, x-deformation rate, fluid velocity magnitude, and volume fraction in Figs. 10A–D, when the traveling freezing front is at x = 2 mm (corresponds to t = 140 sec). They were taken along a line running axially on the upper surface of the ET. Vertical broken lines across four subplots were added to highlight the successive regions labeled as E1 (Primary Expansion), C1 (Primary Compression), E2 (Secondary Expansion), and C2, (Secondary Compression). These responses show regions of expansion (E1 and E2) are characterized by positive dilatation rates and increasing x-deformation rate. Meanwhile, the region of primary compression (C1) is characterized by negative dilatation rates and decreasing x-deformation rates. We anticipated the responses at C2 to be similar; the corresponding magnitudes are however relatively small. The region of initial compression, C1, indicates increasing fluid velocity in the region followed by decreasing magnitudes in early part of region E2 due to fluid expulsion and movement from C1 to E2 (Fig. 10C). This fluid expulsion results in decreased fluid volume fraction in the first half of the compressed region C1. The increased fluid volume fraction in the second half of C1 through region E2 is caused by the rapid influx and fluid movement from the compression in region C1 (Fig. 10D). Together, the fluid velocity and fluid volume fraction indicate fluid is expelled from the compressed region and channeled axially into the preceding region. These alternating pattern observed also illustrates how the elastic response of the solid matrix and the dissipative response of fluid conductance are coupled together in each region as time proceeds.
Fig. 10.
2D profiles taken from the upper surface of the ET when the freezing front is at location x = 2 mm (t = 140 sec): A) dilatational rate, B) x-deformation rate, C) fluid velocity, and D) normalized fluid volume fraction with ϕ f(t = 0) = 0.914 as the normalization factor. To aid in visualizing the alternating response, vertical broken lines were added to highlight the four successive regions labeled as E1 (primary expansion), C1 (primary compression), E2 (secondary expansion), and C2 (secondary compression).
Discussion
Biphasic model of tissue response including effects of temperature and phase changes
Biphasic model has been widely applied to study soft tissue mechanics for processes at constant temperature. The current model augmented the biphasic formulation with additional terms to account for the effects of temperature change and phase transition of the fluid. They are coupled to a heat equation to track temperature histories driven by the applied thermal loads. Our model results illustrate the importance of accounting for the biphasic tissue response and suggest that fluid redistribution plays major role in the resulting alternating expansion-compression response observed experimentally.
ET mechanical responses
Both model predictions and experimental observations indicate that the front propagation generates a transient, alternating pattern of expansion and compression that originates with an initial expansion in the mushy zone and oscillates with diminishing intensities ahead of the front. These results suggest that as the front progresses across the gap, horizontal expansion is initiated within the mushy zone driven by the conversion of the local fluid portion of the ET into ice. This horizontal expansion along with the constraints at the end surface where x= 0 and the bottom surface (glass-slide interface) resulted in a vertical thinning of the ET within the mushy zone and already-frozen regions (Figs. 5, 7, 8, 9 and 10).
Beyond the freezing front, the fluid content has not undergone phase change, leaving these regions unexpanded. Instead, the axial expansion from the mushy zone leads to its intrusion into the preceding zone where it encounters resistance arising from the compression of the local tissue (Figs. 4, 5, and 8). Thus, axial expansion driven by fluid phase change results directly in a region of primary axial expansion preceded immediately by a region of primary compression driven directly by the encroachment of this expanding region.
Beyond the zones of primary expansion and compression, fluid movement becomes integral in sustaining the alternating expansion-compression response observed experimentally. Our results highlight the importance of fluid redistribution in perpetuating the oscillatory response of the ET. Fluid velocity and volume fraction data (Figs. 6 and 7) suggest that fluid is squeezed axially out of the zone of primary compression and channeled into neighboring regions ahead as the front progresses. This fluid efflux out of the compressed region inundates the region ahead resulting in a region of secondary volumetrically-uniform expansion corresponding to a vertical thickening of the ET in this region. If this region of expansion is strong enough, it’s encroachment on the tissue ahead will results in a secondary region of compression. The model confirms the importance of incorporating fluid conductance along with solid matrix stiffness properties in achieving appropriate alternating mechanical responses.
Our modeling results, along with previous observation of Han et. al. [38], indicate that fluid movement during a freezing process could result in permanent changes to the fluid content in the local tissue environment. Interstitial fluid movements affect the microenvironment experienced by resident cells which could lead to changes in the intracellular activities and affect the trans-membrane water and ion transports, thereby possibly affecting cellular phenotypic expression and the overall tissue functions. This fluid redistribution in the tissue could be exacerbated by thawing and surface evaporation, even as the tissues appear viable through freezing and are thus worth examining. Our modeling results highlight the importance of understanding how changes in the local water content and redistribution in the ECM could affects cellular phenotype, behavior and tissue quality and functions.
Limitations
Temperature-dependent material properties
Using material properties taken from literature (Table 1) this current model yields results with reasonably good agreement with experimental measurement. Limitations in the material properties, however, lead to under-prediction in deformation rates. Specifically, there are uncertainties on the temperature-dependencies of the material properties used. Since many of them are not readily available, they were derived from that of water with the assumption that most soft tissues contain high water volume fractions. Properties such as the elastic stiffness of the solid matrix and the hydraulic conductivity of the ET carry greater uncertainty as they are highly tissue-dependent. The major differences between our modeling results and experimental observation can be attributed to the uncertainties in these two temperature-dependent material properties. Measurements of temperature-dependent material properties of the ET are currently underway in our lab.
Ionic Effects
Previous investigators have shown that changes in ionic concentrations could lead to tissue swelling because of the effect of cations in reducing repulsive forces between negatively charged groups in the polymer matrix [30, 31]. During the freezing process, the fluid movement could be complicated by changes in both fluid partial pressure and ion concentration gradients induced by water movement. Furthermore, tissue architecture could be altered post-thaw by destruction of mechanisms that maintain the appropriate ion balance in the tissue. In this work, we have assumed the fluid movement driven by temperature and phase changes are much larger than that due to ionic concentration gradients and osmotic potentials.
Tissue thinning
While both the computational and experimental data [33] do predict thinning of the ET in the frozen region, it is difficult to make quantitative comparison between them. The experimental observation was taken from the specimen after freeze and thaw which included significant effects from water evaporation from the surface during both of the processes. Our current model does not have the effect of evaporation or thawing included.
Vitrification
Because of the difficulties associated with extracellular ice formation during cryo-preservation, cryo-protective agents (CPA) are often utilized to minimize damage by vitrifying tissues into a glass-like state [2,17,39,40]. While providing promising results for the preservation of morphology and mechanical properties, vitrification generates a unique set of challenges including the limiting toxicity of high CPA concentrations as well as achieving uniform CPA distributions in tissues or organs [2, 40]. As the vitrifying agents will force changes in the behavior of the freezing tissues, this subject is beyond the scope of our current model.
Continuum approximation
Although the current model provides insight into the macro-scale responses of the tissue, the cell-ECM exchanges at microscopic scale are neglected. Tissues contain cells which, in turn, envelope cytosols with water content. On the micro-scale level, there are fluid exchanges across the plasma membrane between the cell and extracellular compartments driven by osmotic partial pressure gradients. Changes in the extracellular environment could affect water transport directly and ion concentrations as described previously.
Boundary conditions
Idealization of boundary conditions could also contribute to difference between model prediction and experiment. Near the cold reservoir, we constrained the end surface (x = 0) from having any displacement in x-direction. At the bottom surface (z = 0), the ET is fully constrained. It is likely that these boundary conditions are over-constrained. Our assumption is that the ET will not move once the tissue preceding this region becomes frozen. In actuality, the tissue in the preceding region may not be completely frozen during early time steps. A small amount of horizontal movement of the ET and some slippage between its bottom surface and the glass slide could develop. Collectively, they could cause a small over-prediction in the strains and stresses, particularly near the low temperature reservoir early in the simulation and at the bottom surface of the ET throughout the transient. We did not include the cover slip in the model, since we used temperature measurements from ref. [37] as the boundary loading (at x = 0) and as the internal constraints (at x=6) as shown in eq. 15, 16. Thus, effects of any possible heat exchange across the cover slip are included in the temperature measurement data we used.
One may question the mismatch in thermal-mechanical properties at the interface between frozen ET adhering to glass cover-slip could induce regional strain and stress concentrations in the ET. In actuality, at any given time during the freezing process, the mechanical interaction at the ET/cover-slip interface is likely to vary spatially from the unfrozen zone, to the transitional mushy zone, to the already-frozen zone for their respective different physical properties, leading to regional variations in mechanical interaction from slippage to complete tethering. To address the above question, let’s first consider the part of the ET already in frozen state. The volume expansion associated with tissue water phase change was reported to be 0.087 [16], suggesting a liner expansion coefficient of 0.029. Through the freezing process, the glass cover-slip will shorten by ~ 3 × 10−6/°C (its linear expansion coefficient). A comparison suggests the former is dominant and the latter has negligible effect. Next, let’s consider the part of the ET still in unfrozen state. The linear expansion coefficients for the ET are ~ 7×10−5/°C. Comparing it with that from glass cover-slip (~ 3×10−6/°C), the latter amounts to ~ 4.3%. Thus, the linear contraction of the glass cover-slip is relatively small compared with that of the unfrozen ET above it. The above estimates in ratios should provide upper bounds for the extreme scenarios. In our current model, we elected to consider the bottom surface to be fully constrained (Eq. 20). Our results of volume strains distributions in the ET revealed the elevated volume strains near the bottom surface caused by the boundary constraints (Fig. 8).
Modeling structural (tissue matrix) damages
One may ask if any tissue structural damages through freeze thaw process could be predicted by the extension of this current modeling approach. It is a challenge that can be addressed by adopting a constitutive equation for the solid matrix that includes damage description and damage thresholds to be validated by extensive experiment data.
Continuing efforts
In addition to the measurement of temperature-dependent mechanical properties, other aspects that require attention include 1) the role of deformation-dependent hydraulic conductivity, 2) the effects of nonlinear mechanical properties of the solid matrix (e.g. hyperelastic or other nonlinear models), 3) the possible effect of finite deformation and nonlinear kinematics, and 4) the extension of the modeling approach for failure prediction. These are among the future goals in our evolving modeling efforts to capture the underlying physics, their implications in biology, with minimal engineering assumptions while addressing the questions we are studying.
Conclusions
To further our understanding of the effects of freeze-thaw process on soft tissues, we have developed a model based on linear biphasic continuum formulation that includes spatial and temporal changes in temperature as well as the effect of phase changes. Simulation results revealed, as the heat being taken away, the propagation of the freezing front accompanying the continuing evolving and expanding mushy zone, the instantaneous temperature distribution, tissue deformation, and fluid redistribution. Model predictions were validated using experimental data. Results show that the mechanical response of ET to directional freezing is prompted primarily by its axial expansion, driven by phase change in the mushy zone. Its compression at the region immediately preceding the freezing front leads to fluid expulsion and fluid redistribution and its subsequent alternating patterns of localized expansion and compression. Our model highlights the importance of using biphasic formulation to understand the tissue response to freezing treatment.
Supplementary Material
Acknowledgments
This work was supported in part by NIH/NIBIB through grant RO1-EB008388 to BH. JW and CJC wish to thank Ka Yaw Teo for supplying experimental data used in our model validation.
Nomenclature
- αT
hermal expansion coefficient
- λ
Lame constant
- μ
Shear modulus
- ρ
Density
- σ
Total stress tensor
- σe
Elastic stress tensor
- ϕf
Volume fraction of the fluid phase
- ϕs
Volume fraction of the solid phase
- cp
Specific heat at constant pressure
- cL
Effective specific heat accounting for latent heat
- d
Diffusive drag coefficient
- e
Dilatational strain due to water phase change
- ε
Elastic strain of the matrix
- εvol
Volumetric strain of the matrix
- E
Young’s modulus
- F(T)
Mass fraction of frozen tissue in mushy state [11]
- Khyd
Hydraulic conductivity
- KT
Thermal conductivity
- L
Latent heat of fusion for the fluid
- p
Hydrostatic pressure
- T
Temperature
- Tref
Reference temperature (0°C = 273 K)
- Troom
Room temperature (20°C = 293 K)
- u
Displacement of solid tissue matrix
- v
Fluid velocity
- X(t)
Instantaneous location of the freezing front at time t
References
- 1.Karlsson JOM, Toner M. Long-term storage of tissues by cryopreservation: Critical issues. Biomaterials. 1996;17(3):243–256. doi: 10.1016/0142-9612(96)85562-1. [DOI] [PubMed] [Google Scholar]
- 2.Pancrazio JJ, Wang F, Kelley CA. Enabling tools for tissue engineering. Biosensors & Bioelectronics. 2007;22(12):2803–2811. doi: 10.1016/j.bios.2006.12.023. [DOI] [PubMed] [Google Scholar]
- 3.Mazur P. Cryobiology: the freezing of biological systems. Science. 1970;168(934):939–49. doi: 10.1126/science.168.3934.939. [DOI] [PubMed] [Google Scholar]
- 4.Mazur P. Freezing of living cells: mechanisms and implications. Am J Physiol. 1984;247(3 Pt 1):C125–42. doi: 10.1152/ajpcell.1984.247.3.C125. [DOI] [PubMed] [Google Scholar]
- 5.Mazur P. Stopping biological time. The freezing of living cells. Ann N Y Acad Sci. 1988;541:514–31. doi: 10.1111/j.1749-6632.1988.tb22288.x. [DOI] [PubMed] [Google Scholar]
- 6.Zhmakin AI. Fundamentals of Cryobiology: Physical Phenomena and Mathematical Models. Springer; 2009. [Google Scholar]
- 7.Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310(5751):1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 8.Pedersen JA, Swartz MA. Mechanobiology in the third dimension. Annals of Biomedical Engineering. 2005;33(11):1469–1490. doi: 10.1007/s10439-005-8159-4. [DOI] [PubMed] [Google Scholar]
- 9.Kumar S, Ulrich TA, Pardo EMD. The Mechanical Rigidity of the Extracellular Matrix Regulates the Structure, Motility, and Proliferation of Glioma Cells. Cancer Research. 2009;69(10):4167–4174. doi: 10.1158/0008-5472.CAN-08-4859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He X, Bischof JC. Quantification of temperature and injury response in thermal therapy and cryosurgery. Crit Rev Biomed Eng. 2003;31(5–6):355–422. doi: 10.1615/critrevbiomedeng.v31.i56.10. [DOI] [PubMed] [Google Scholar]
- 11.He X, Bischof JC. Analysis of thermal stress in cryosurgery of kidneys. J Biomech Eng. 2005;127(4):656–61. doi: 10.1115/1.1934021. [DOI] [PubMed] [Google Scholar]
- 12.Rabin Y, Steif PS. Analysis of Thermal Stresses around a Cryosurgical Probe. Cryobiology. 1996;33(2):276–90. doi: 10.1006/cryo.1996.0028. [DOI] [PubMed] [Google Scholar]
- 13.Rabin Y, Steif PS. Thermal stress modeling in cryosurgery. International Journal of Solids and Structures. 2000;37(17):2363–2375. [Google Scholar]
- 14.Zhang J, Sandison GA, Murthy JY, Xu LX. Numerical simulation for heat transfer in prostate cancer cryosurgery. J Biomech Eng. 2005;127(2):279–94. doi: 10.1115/1.1865193. [DOI] [PubMed] [Google Scholar]
- 15.Hoffmann NE, Bischof JC. Cryosurgery of normal and tumor tissue in the dorsal skin flap chamber: Part II--injury response. J Biomech Eng. 2001;123(4):310–6. doi: 10.1115/1.1385839. [DOI] [PubMed] [Google Scholar]
- 16.Shi X, Datta AK, Mukherjee Y. Thermal stresses from large volumetric expansion during freezing of biomaterials. J Biomech Eng. 1998;120(6):720–6. doi: 10.1115/1.2834885. [DOI] [PubMed] [Google Scholar]
- 17.Rabin Y, Steif PS. Thermal stresses in a freezing sphere and its application to cryobiology. Journal of Applied Mechanics-Transactions of the Asme. 1998;65(2):328–333. [Google Scholar]
- 18.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: Theory and experiments. J Biomech Eng. 1980;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 19.Simon BR. Multiphase Poroelastic Finite Element Models for Soft Tissue Structures. Applied Mechanics Reviews. 1992;45(6):191–218. [Google Scholar]
- 20.Cowin S, Doty SB. Tissue Mechanics. Springer; New York, NY: 2007. [Google Scholar]
- 21.Biot MA. General theory of three-dimensional consolidation. J Appl Phys. 1941;12:155–164. [Google Scholar]
- 22.Netti PA, Baxter LT, Boucher Y, Skalak R, Jain RK. Macro- and microscopic fluid transport in living tissues: Application to solid tumors. Aiche Journal. 1997;43(3):818–834. [Google Scholar]
- 23.Lanir Y. Biorheology and Fluid Flux in Swelling Tissues. 1. Bicomponent Theory for Small Deformations, Including Concentration Effects. Biorheology. 1987;24(2):173–187. doi: 10.3233/bir-1987-24210. [DOI] [PubMed] [Google Scholar]
- 24.Lanir Y. Biorheology and Fluid Flux in Swelling Tissues. 2. Analysis of Unconfined Compressive Response of Transversely Isotropic Cartilage Disk. Biorheology. 1987;24(2):189–205. doi: 10.3233/bir-1987-24211. [DOI] [PubMed] [Google Scholar]
- 25.Gu WY, Lai WM, Mow VC. A mixture theory for charged-hydrated soft tissues containing multi-electrolytes: Passive transport and swelling behaviors. Journal of Biomechanical Engineering-Transactions of the Asme. 1998;120(2):169–180. doi: 10.1115/1.2798299. [DOI] [PubMed] [Google Scholar]
- 26.Oomens CWJ, Vancampen DH, Grootenboer HJ. A Mixture Approach to the Mechanics of Skin. Journal of Biomechanics. 1987;20(9):877–885. doi: 10.1016/0021-9290(87)90147-3. [DOI] [PubMed] [Google Scholar]
- 27.Swartz MA, Kaipainen A, Netti PA, Brekken C, Boucher Y, Grodzinsky AJ, Jain RK. Mechanics of interstitial-lymphatic fluid transport: theoretical foundation and experimental validation. J Biomech. 1999;32(12):1297–307. doi: 10.1016/s0021-9290(99)00125-6. [DOI] [PubMed] [Google Scholar]
- 28.Chen X, Sarntinoranont M. Biphasic finite element model of solute transport for direct infusion into nervous tissue. Ann Biomed Eng. 2007;35(12):2145–58. doi: 10.1007/s10439-007-9371-1. [DOI] [PubMed] [Google Scholar]
- 29.Lu YL, Wang W. Interaction between the interstitial fluid and the extracellular matrix in confined indentation. Journal of Biomechanical Engineering-Transactions of the ASME. 2008;130(4):041011:1–10. doi: 10.1115/1.2939310. [DOI] [PubMed] [Google Scholar]
- 30.Lai WM, Hou JS, Mow VC. A Triphasic Theory for the Swelling and Deformation Behaviors of Articular-Cartilage. Journal of Biomechanical Engineering-Transactions of the ASME. 1991;113(3):245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- 31.Myers ER, Lai WM, Mow VC. A continuum theory and an experiment for the ion-induced swelling behavior of articular cartilage. J Biomech Eng. 1984;106(2):151–8. doi: 10.1115/1.3138473. [DOI] [PubMed] [Google Scholar]
- 32.Spilker RL, Nickel JC, Iwasaki LR. A biphasic finite element model of in vitro plowing tests of the temporo mandibular joint disc. Ann Biomed Eng. 2009;37(6):1152–64. doi: 10.1007/s10439-009-9685-2. [DOI] [PubMed] [Google Scholar]
- 33.Teo KY, Dutton JC, Han B. Spatiotemporal Measurement of Freezing-Induced Deformation of Engineered Tissues. Journal of Biomechanical Engineering-Transactions of the Asme. 2010;132(3):031003-1–031003-8. doi: 10.1115/1.4000875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fung YC. Foundations of Solid Mechancis. Prentice Hall; 1965. [Google Scholar]
- 35.Espinoza Vallejos PA, Dustin C. Carbon Foam filled with phase change materials for passive temperature management. Proceedings of the COMSOL Multi-physics Users Conference; Boston. 2005. [Google Scholar]
- 36.Raffel M. A practical guide. Springer; New York: 2007. Particle image velocimetry. [Google Scholar]
- 37.Teo KY, DeHoyos TO, Dutton JC, Grinnell F, Han B. Effects of freezing-induced cell-fluid-matrix interactions on the cells and extracellular matrix of engineered tissues. Biomaterials. 2011;32(23):5380–5390. doi: 10.1016/j.biomaterials.2011.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Han B, Miller JD, Jung JK. Freeezing induced fluid-matrix interaction in poroelastic material. AMSE J of Biomech Eng. 2009;131:021002-1–021002-8. doi: 10.1115/1.3005170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Taylor MJ, Song YC, Brockbank KGM. Vitrification in Tissue Preservation: New Developments. In: Benson E, Fuller B, Lane N, editors. Life in the Frozen State. London: CRC Press LLC, Boca Raton; 2004. pp. 603–641. [Google Scholar]
- 40.Rabin Y, Steif PS. Letter to the editor: analysis of thermo-mechanical stress in cryopreservation. Cryo Letters. 2005;26(6):409–11. author reply 412. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.