Abstract
We studied the effects of increased sodium conductance on firing rate and gain in two populations of conductance-based, single-compartment model neurons. The first population consisted of 1000 model neurons with differing values of seven voltage-dependent conductances. In many of these models, increasing the sodium conductance three-fold unexpectedly reduced the firing rate and divisively scaled the gain at high input current. In the second population, consisting of 1000 simplified model neurons, we found that enhanced sodium conductance changed the frequency-current (FI) curve in two computationally distinct ways, depending on the firing rate. In these models, increased sodium conductance produced a subtractive shift in the FI curve at low firing rates because the additional sodium conductance allowed the neuron to respond more strongly to equivalent input current. In contrast, at high input current, the increase in sodium conductance resulted in a divisive change in the gain because the increased conductance produced a proportionally larger activation of the delayed rectifier potassium conductance. The control and sodium-enhanced FI curves intersect at a point that delimits two regions in which the same biophysical manipulation produces two fundamentally different changes to the model neuron's computational properties. This suggests a potentially difficult problem for homeostatic regulation of intrinsic excitability.
Keywords: stomatogastric ganglion, biophysical model, multiplicative gain control, frequency-current relationship, homeostasis
Introduction
The electrical excitability of spiking neurons is often characterized by measuring the action potential frequency in response to injected current to generate a frequency-current (FI) curve. The slope of the FI curve is referred to as the gain of the neuron. Changes to the FI curve (Holt and Koch, 1997; Chance et al., 2002; Prescott and De Koninck, 2003) can be additive (a change in rheobase, the minimum current required to elicit spiking) or multiplicative (a change in FI curve slope). Multiplicative changes to the FI curve are of interest because they are thought necessary to implement complex behaviors such as coordinate transformations for reaching motions (Salinas and Thier, 2000) and detection of looming objects in the visual field (Gabbiani et al., 2002). Changes to the neuronal input-output relationship (gain control) are thought to be fundamental mechanisms by which neurons maintain appropriate response levels to the changing features of their synaptic inputs (Destexhe et al., 2003; Silver, 2010) and can alter the computational properties of neurons (Lundstrom et al., 2009; Silver, 2010).
The number and kind of voltage-dependent conductances in each neuron determines its excitability and the way it responds to external drive. Therefore, it is of interest to understand how the FI curves and gains of spiking neurons depend on the Na+ conductance. The initial purpose of this study was to determine the effects of raised Na+ conductance on neuronal gain. Because intrinsic conductance densities can be quite variable across neurons of the same cell type (Golowasch et al., 1999; Swensen and Bean, 2005; Schulz et al., 2006, 2007; Goaillard et al., 2009), we generated a set of models in which each individual model was constructed with random maximal conductances. This approach, to assess the robustness of a given phenomenon by probing parameter space in a randomized fashion, has been employed before (Goldman et al., 2001; Prinz et al., 2004; Günay et al., 2008; Taylor et al., 2009; Marder, 2011; Marder and Taylor, 2011) and provides information about whether a model behavior is unique relative to the space of many similarly constructed models.
Our initial expectation was that increasing the Na+ conductance would enhance excitability across a wide range of inputs. Instead, this study shows that, while excitability is enhanced at low current injection levels, the opposite often occurs with high current injection that results in high firing rates. Thus, increases in Na+ conductance in response to decreased activity (Desai et al., 1999) would be homeostatic for conditions of low external drive, but might produce paradoxical anti-homeostatic changes at higher levels of external drive. These results suggest revisions of our thinking about what the targets of homeostatic regulation should be to ensure a neuron can stably regulate its gain.
Materials and Methods
Simulations
Simulations were run on a multi-core personal computer using MATLAB (The MathWorks). The model used in the computational experiments was derived from a model that has been previously described in detail (Turrigiano et al., 1995; Liu et al., 1998). This version of the model removed all of the calcium-dependent homeostatic mechanisms leaving only static biophysical conductances. Our results are produced by running the model with a full set of conductances and a reduced version of the model in which many of the conductances were removed. The full-conductance model has seven active conductances as well as a leak conductance. These active channels are Na+ (fast sodium), Kd (delayed rectifier potassium), KCa (calcium-gated potassium), (transient calcium), (slow calcium), A (potassium), and H (hyperpolarization-activated mixed cation). The reduced model has Na, Kd, A and leak channels.
All currents besides calcium are calculated as
where i represents the individual channel type, p is the power to which the activation variable is raised, ḡi the maximal channel conductance, the activation state variable, and hi the inactivation state variable. Vm is membrane potential and Ei is reversal potential for that channel type. The potassium reversal potential is -80 mV, the sodium reversal potential is 50 mV, and the mixed cation reversal potential for IH is -20 mV. The leak reversal potential is -50 mV.
Channel activation (m) and inactivation (h) are calculated as:
All values for m∞, h∞, τm, τh, p and the calcium dynamics are as described previously (Turrigiano et al., 1995; Liu et al., 1998) and reproduced here. The correctness of our implementation of the model was verified by comparing model output to published results.
| Channel | m∞ | h∞ | τm | τh |
|---|---|---|---|---|
| Na | ||||
| CaT | ||||
| CaS | ||||
| A | ||||
| Kca | ||||
| Kd | ||||
| H |
Reversal potential for the calcium channels is calculated by the Nernst equation based on the current intracellular calcium concentration
Where R = 8.314472 (J/K/mol), T = 273.15 + 23.5 °K, z = +2, F = 9.649 × 104 (C/mol). Calcium concentrations were calculated as in (Liu et al., 1998):
To build a database of 1,000 full-conductance models and 1,000 reduced models, we began with two large sets of candidate models and then selected those that fired tonically at a rate of 3 to 7 Hz, with a coefficient of variation less than 0.05 when injected with a current of 0.2 nA/nF. The coefficient of variation was calculated from the last 2 seconds of simulation data from each model neuron. The candidate models were generated by randomly selecting active conductances from a uniform distribution ranging from 0.5 to 238 μS/nF for Na+, Kd, KCa and A and from 0.1 to 4.5 μS/nF for , and H conductances. Leak was set to 0.01 μS/nF in all cases. Expression of conductances in units of μS/nF (and similarly for currents as nA/nF) is used to normalize for cell membrane area. The full-conductance and reduced conductance candidate models were generated with statistically independent conductance values.
We simulated both sets of models at a range of current injection steps. The injected current, Iinj, ranged from -2 nA/nF to 10 nA/nF with finer steps in the lower Iinj values. Each model was run for 3 seconds of simulation time with a time step of 0.01 ms. We then re-ran each model with the maximal sodium conductance tripled from its original value. For all models we recorded firing rate. For a subset of models we also recorded the voltage and channel state (activation and inactivation) history.
Analysis
All analysis was done with custom scripts written in MATLAB. Firing rate was calculated as the inverse of the mean inter-spike interval. The first second of data was discarded for each run to allow the simulation to equilibrate and frequency was only computed from the steady-state firing rate. Rheobase was computed as the lowest value of injected current that yielded a non-zero firing rate. Voltage threshold was computed at 10 nA/nF current injection as the point on the action potential rising phase where the derivative of the voltage trajectory reached 100 V/s. Voltage threshold was only computed in models that fired action potentials at 10 nA/nF current injection (n = 984). Gains were computed in two separate ways. When computed over the entire FI curve at one time we fit an exponential function times a line using the following equation:
To measure the gain we took the derivative of that function to yield:
In these equations r∞ is the asymptotic value of the exponential, r0 is the initial value of the exponential and τr is the time constant of the exponential. At higher values of x the curve is dominated by the line and the variable m defines the slope and b defines the y-intercept. In nearly all cases these functions fit FI curves extremely well with r2 values > 0.95. When fitting only the high and low current injection regions of the FI curve, we fit line segments because fitting a line to a restricted section of the FI curve resulted in fits with lower errors. One-tailed t-tests were used when sample means were compared to zero and a paired t-test was used when comparing paired samples. Histograms were fit with normal distributions for comparison regardless of whether those distributions were Gaussian. Figures were generated in MATLAB and finished in Inkscape (inkscape.org).
Results
Firing rate change in a biophysically complex model
We constructed a population of 1000 model neurons, each with 7 separate active conductances, selected to have tonic firing at 0.2 nA/nF current injection, similar to those used in Liu et al. (1998), and based on voltage clamp data reported by Turrigiano et al. (1995) (see Methods). In this population the maximal conductances were randomly assigned. For each model generated in this fashion, we determined whether it would generate tonic spiking when a current of 0.2 nA/nF was injected. Only models that showed stable tonic firing (coefficient of variation of its spike train < 0.05) were included in this population.
We initially subjected model neurons to a range of biophysical changes that have been observed experimentally in response to long-term sodium blockade (Desai et al., 1999). This included reducing the delayed rectifier potassium current (IKd), increasing the sodium current or both. We noticed unexpected activity decreases for large increases in the sodium conductance at high current injection levels and thus chose to study this manipulation in detail. While our choice to triple the sodium conductance parameter was arbitrary, using a large change yields a consistent effect that is easier to study than more subtle manipulations in a highly variable population. Smaller changes similar to those observed experimentally (Desai et al., 1999) yielded a proportional effect size suggesting that our results are not dependent on a large manipulation (data not shown).
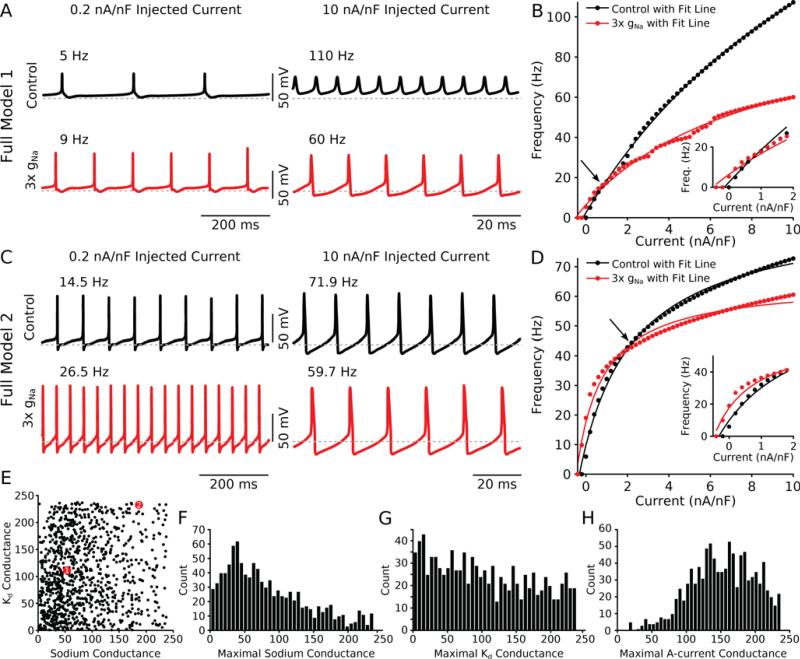
To assess model excitability over a range of input currents we measured the FI curve for all models in the population. In one example full conductance model neuron (Fig. 1A), the firing rate increased with low current injection (0.2 nA/nF) when sodium conductance was increased by a factor of three (Figure 1A, left traces, black: control, red: 3× gNa). For high current injection into the same model neuron (10 nA/nF), the opposite occurred (Fig. 1A, right traces) and increasing the Na+ conductance led to decreased firing rates. The FI curves for this neuron (Fig. 1B) intersect near the middle of the dynamic range (arrow). A second example full conductance neuron (Fig. 1C) from the population has different firing behavior because it has different maximal conductances but retains the same qualitative changes to its excitability (Fig. 1D) in response to Na+ conductance increases and thus also has FI curves that intersect (arrow).
Figure 1. Full models show divisive gain change at high firing rates.
(A) Voltage traces from a single model neuron at low injected current (0.2 nA/nF, left column) and high injected current (10 nA/nF, right column) demonstrate that tripling the sodium conductance increases the firing rate at low current injection levels (5 Hz to 9 Hz) but decreases the firing rate at higher current injection levels (110 Hz to 60 Hz). Red traces have tripled sodium conductance. (B) FI curve for this example model shows enhanced excitability at low rates (inset) and divisive gain change at higher rates. Lines indicate fits to the data points (control: r2 = 0.99, 3× gNa: r2 = 0.99). Arrow indicates crossover point. (C,D) Same as (A,B) for another example model (control: r2 = 0.99, 3× gNa: r2 = 0.98). (E) Distribution of the sodium and Kd conductances for the entire 1000 model database. Each black dot represents one model. Models drawn as larger red circles represent the models shown in (A,B, model 1) and (C,D, model 2). (F) Distribution of all the sodium conductances across the population. The selection criterion for this population favors lower values of maximal sodium conductance. (G) Distribution of all the maximal delayed rectifier potassium (Kd) conductances across the population. (H) Distribution of all the maximal A-current conductances across the population.
As expected, in this database of biophysically complex models with randomly generated conductances (Figs. 1 E-H show the range of parameters present in the population), we observed a wide variety of spiking behaviors and FI curves (Liu et al., 1998; Goldman et al., 2001). For many models in the database (~300 out of 1000 models), high input currents lead to a reduction in the gain, a multiplicative scaling operation thought to underlie important neuronal computations (Salinas and Thier, 2000; Gabbiani et al., 2002; Silver, 2010). At low firing rates, increased Na+ conductance usually (~970 out of 1000 models) led to a decrease in the rheobase of the neuron. Qualitatively, this meant that the firing rate of the models with high Na+ conductance was increased at smaller input current, but decreased at larger input current relative to control which lead to the FI curves intersecting (Fig. 1B,D, arrows). The change in rheobase could be explained easily since enhanced Na+ conductance leads to a hypolarized voltage threshold allowing a smaller amount of input current to drive spiking in the model. The decreased gain at higher input current, however, required a more detailed analysis of the interaction between the sodium and delayed rectifier potassium conductances which we address later.
Reduced model database shows subtractive shift at low rates and divisive change at high rates
Next, we sought to understand if the above results could be reproduced in a more simplified biophysical model. Reduced models are more amenable to detailed biophysical analysis and allow for the precise identification of mechanisms that underlie specific behaviors. The reduced model we generated contained only Na+ and delayed rectifier potassium (IKd) conductances along with an A-type potassium (IA) and leak conductance (see Methods). While the INa and IKd are responsible for the spike generating mechanism, IA promotes type 1 FI curve dynamics, such that the model neuron can fire at arbitrarily low rates (Connor and Stevens, 1971; Connor et al., 1977; Dayan and Abbott, 2001). We selected this model because it is a generic representation of the core features of many types of spiking neurons. Thus, these results should apply broadly to neurons with a spiking mechanism similar to the one in this model. All further results presented in this study were generated with the reduced model.
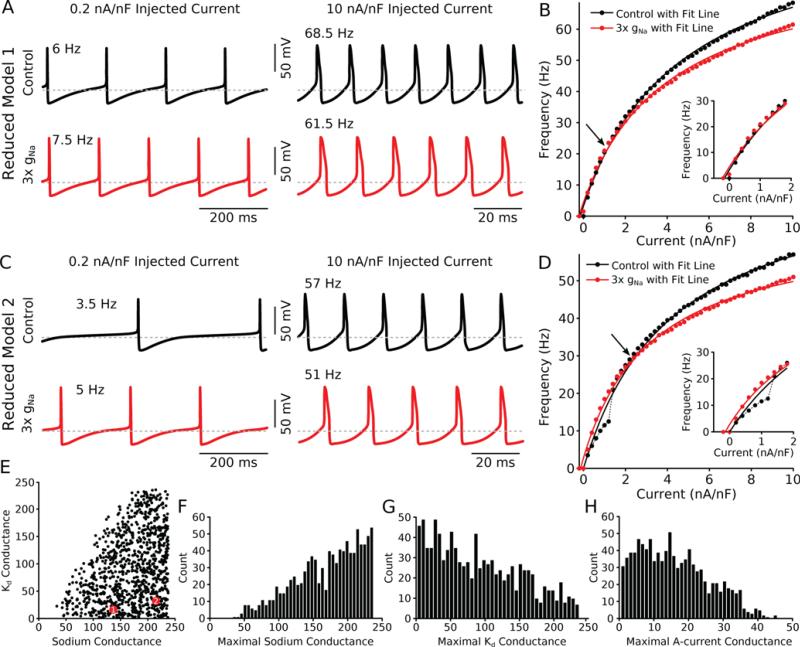
We next generated a population of 1000 reduced models each with random conductances and selected to have tonic firing at 0.2 nA/nF current injection. In an example reduced neuron (Fig. 2A) we observed the same firing rate changes reported for the full-conductance models and the same qualitative features in the FI curves (Fig. 2B). An additional example model neuron also had similar firing (Fig. 2C) and FI curve properties (Fig. 2D). We measured the FI curves of all the models in the population (Figs. 2E-H, range of parameters present in the population) and repeated this process after increasing the maximal Na+ conductance by a factor of three. As in the full conductance models, this population showed an increase in the excitability of the neuron at low firing rates when Na+ conductance was tripled. As the input current increased, additional Na+ conductance decreased the firing rate for equivalent input current (Figs. 2B,D, red FI curves). As before, this meant that the two FI curves intersected one another (Figs. 2B,D, arrows).
Figure 2. Reduced models show divisive gain change at high firing rates.
(A) Voltage traces from a single reduced model neuron at low injected current (0.2 nA/nF, left column) and high injected current (10 nA/nF, right column) demonstrate that tripling the sodium conductance increases the firing rate at low current injection levels (6 Hz to 7.5 Hz) but decreases the firing rate at higher current injection levels (68.5 Hz to 61.5 Hz). Red traces have tripled sodium conductance. (B) FI curve for this example model shows enhanced excitability at low rates (inset) and divisive gain change at higher rates. Lines indicate fits to the data points (control: r2 = 0.99, 3× gNa: r2 = 0.99). Arrow indicates crossover point. (C,D) Same as (A,B) for an additional example model (control: r2 = 0.98, 3× gNa: r2 = 0.99). Black dotted line in D (main panel and inset) connects individual control data points and highlights that there are models that experience rapid changes in frequency over the input current range. (E) Distribution of the sodium and Kd conductances for the entire, 1000 model database. Each black dot represents one model. Models drawn as larger red circles represent the models shown in (A,B, model 1) and (C,D, model 2). (F) Distribution of all the sodium conductances across the population. The selection criterion for this population favors higher values of maximal sodium conductance. (G) Distribution of all the maximal Kd conductances across the population. The selection criterion for this population favors lower values of maximal Kd conductance. (H) Distribution of all the maximal A-current conductances across the population.
These observations indicated that the fundamental mechanisms that were responsible for generating a subtractive shift in rheobase and a divisive change in gain at high firing rates under conditions of high Na+ conductance were present in this reduced model. Furthermore, in comparison to the full model, the divisive gain change in the reduced model was highly robust and present in the majority of the models generated in this manner (984 out of 1000 models) even though the conductances of individual models were highly variable (Figs. 2E-H).
Finally, to ensure that our results were not dependent on very large changes to the sodium conductance, we reran our simulations with conductance changes more similar to those observed experimentally. After activity deprivation, cultured neurons have been reported to undergo a 1.3× increase in their sodium conductance (Desai et al., 1999). When increasing the sodium conductance by this amount we observed approximately a 25% decrease in the gain compared with the full effect (data not shown) suggesting that the reported effect size is proportional to the sodium conductance change and that our results were not dependent on a large manipulation size.
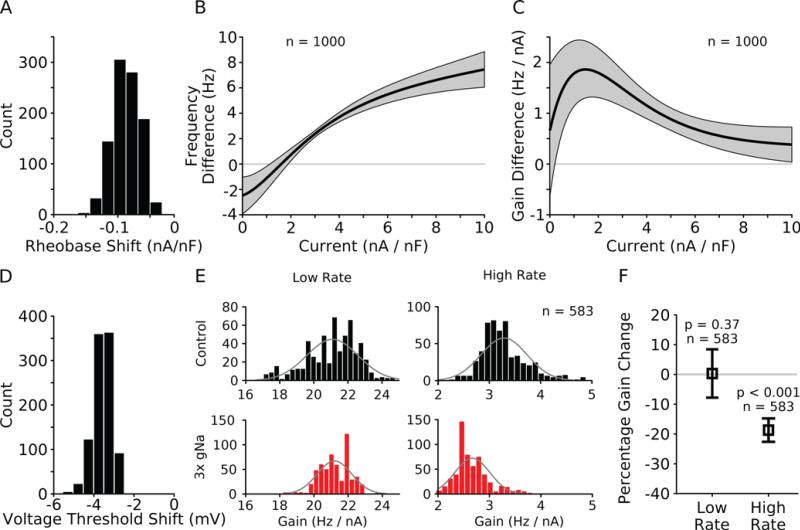
To quantify these observations across the population, we first determined whether increasing the Na+ conductance by a factor of three in the population of reduced models changed the rheobase. When Na+ conductance was increased, rheobase was decreased in all models in the population (Fig. 3A, rheobase shift from control to 3× gNa averaged about -0.1 nA/nF). To measure the change in excitability generated over the entire input current range we fit an exponential function multiplied by a line to the FI curves from the population (see Methods). In general, this function fit the FI curves extremely well (r2 > 0.95 in most models). For each model we fit both the control and 3× Na+ conductance FI curves and then subtracted the two fit lines from one another (control minus enhanced Na+ conductance). When these differenced fit lines were averaged over the entire population, a picture of the changes in the excitability emerged (Fig. 3B, black line: mean, gray region: ± one standard deviation, n = 1000). As expected, at low current injection levels the mean difference was negative indicating that the firing rate was higher with enhanced sodium conductance than in the control condition. Conversely, at higher current injection levels the value of the difference curve was positive indicating that the control FI curve had higher firing rates in this range. Finally, the current injection level that yielded a zero frequency difference value corresponds to the crossover point of the FI curves and fell near 1.5 nA/nF current injection.
Figure 3. Enhanced sodium conductance causes a subtractive shift at low rates and a divisive gain change at high rates.
(A) The rheobase (current threshold) decreases in all models when sodium conductance is increased. Histogram plots values by which rheobase shifts when going from control to 3× gNa. All shifts are negative indicating that the shift occurs in all 1000 models. (B) Subtraction of FI curve fits (control – 3× gNa) show that the difference is reliably negative at low rates and positive at high rates suggesting a subtractive shift at low rates, a crossover point and a divisive gain change at high rates. Gray area represents one standard deviation (n = 1000). (C) Subtraction of the derivatives of the FI curve fits shows the input current at which the models experience the largest gain difference. Gray area represents one standard deviation (n = 1000) to 3× control value. (D) Voltage threshold is hyperpolarized in all models that spike at high current injection (n = 984) when Na+ conductance is increased. (E) Histograms of gain distributions of low and high firing rates for each model under control and 3× gNa conditions. At low firing rates, the distributions have similar means while at high rates, gain is reduced (black: control, red: 3× gNa, n = 583). Model population was sub-selected to ignore FI curves with jumps in frequency that correspond to missed spikes. Gray lines are Gaussian distributions with the same means and variances as the data in the histograms. (F) Gain changes significantly at high rates but not at low rates. Gain changes are plotted as percentages to normalize between low and high firing rates (low rate: 0.3 ± 8.1 %, p = 0.37, n = 583; high rate: -18.7 ± 3.9 %, p < 0.001, n = 583, one sample t-test).
Fitting the FI curves also allowed computing the gain by taking the derivative (the slope) of the fit line equation (see Methods). To measure where the gains of the FI curves were most different, we subtracted the derivatives of the control and 3× gNa FI curves from one another (Fig. 3C, black line is the mean, gray region ± one standard deviation, n = 1000, control minus enhanced sodium conductance). The maximum gain difference was near 1.5 nA/nF current injection, very close to the crossing over point (Fig. 3B, zero crossing). We also computed the change in voltage threshold in the population by measuring when the rate of rise of an action potential exceeded 100 V/s. In all models that spiked at high current injection, we observed a decrease in the voltage threshold indicating that spikes could be initiated from a lower starting voltage when Na+ conductance was tripled (Fig. 3D, voltage threshold shifted about -4 mV from control to 3× gNa, n = 984).
The mean gain difference at low current injection was approximately one standard deviation above zero (Fig. 3C, gray region) which seemed large given the similarity of many FI curves in this range (Fig. 2B). The large difference could be explained by observing that several control FI curves had low gain at low input current but large and abrupt changes in gain as input current was increased (see Fig. 2D dotted line for an example, effect occurs in 417 models out of 1000). Inspection of voltage traces determined that this phenomenon was because these models had failed spikes at low current injection levels during which the neuron would depolarize to near threshold, nearly spike, and then return to rest. As input current increased, these peri-threshold depolarizations turned into action potentials, rapidly increasing the firing rate.
We subselected those models from the population that displayed tonic spiking at all low current injection levels (not just at the initial level of 0.2 nA/nF). In those 583 models we fit line segments to both the control and 3× Na+ conductance FI curves at both low and high current injection and compared the slopes (Fig. 3E). For this analysis, we fit line segments because the low and high regions of the FI curves were not well fit by the curves used previously. The slopes of the line segments at low rates were very similar (Fig. 3E, left column, control: 21.9 ± 1.5 Hz/nA, 3× Na+: 21.2 ± 1.0 Hz/nA, n = 583), whereas a noticeable difference was present in the slopes at higher rates (Figure 3E, right column, control: 3.3 ± 0.5 Hz/nA, 3× Na+: 2.7 ± 0.3 Hz/nA, n = 583). We measured the percent change in each model at low and high rates and found that there was no significant change at low rates (Fig. 3F, low rate: 0.3 ± 8.1 %, p = 0.37, n = 583, t-test) whereas the slope was significantly changed at high firing rates (Fig. 3F, high rate: 18.7 ± 3.9 %, p < 0.001, n = 583, t-test). Taken together, these results show that the population of models that fired tonically through the entire low frequency range had a subtractive shift in their FI curves with no slope change at low rates and a divisive change in gain at high firing rates all in response to a single conductance change.
Mechanism of gain change at higher firing rates
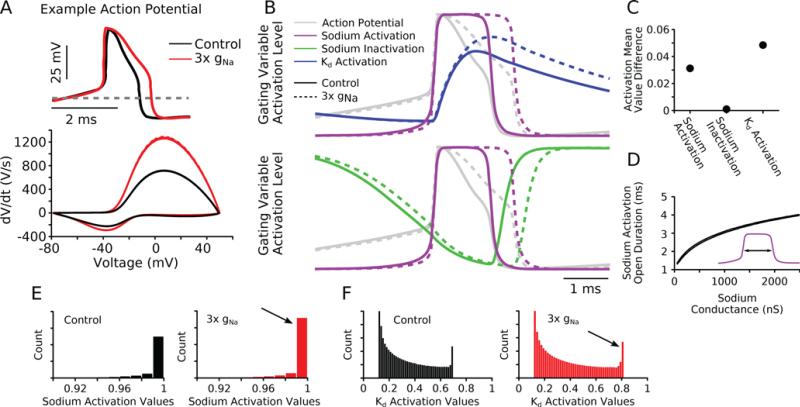
To understand how the targeted change to the Na+ conductance was producing a divisive change in gain at higher firing rates in the reduced model neurons, we investigated the activation level of the individual spiking conductances during an action potential with 10 nA/nF current injection. We first compared a spike from a representative model neuron (model #1 shown in Figure 2) before and after changes to the Na+ conductance (Fig. 4A, top panel). There was no change in mean voltage with increased Na+ conductance computed over a single interspike interval (data not shown). However, we did notice that individual spikes became wider with increased Na+ conductance. Additionally, increasing the Na+ conductance hyperpolarized the voltage threshold for spike initiation, as we previously noted (Fig. 3D).
Figure 4. Sodium conductance changes lead to a proportionally greater activation of Kd conductance which lowers the firing rate overall.
(A) Top: An example action potential from a single model being injected with 10 nA/nF of current from the population (model 1 from Figure 2) was overlaid from both control and 3× gNa conditions. Enhanced sodium conductance widens the action potential. Bottom: A phase plot of the same action potential shows that the voltage initially rises faster and then repolarizes more slowly followed by a final phase of more rapid repolarization when compared with control. (B) Gating variables during the action potential shown in (A). The normalized action potential is plotted in gray for comparison. Solid lines represent control; dotted lines represent 3× gNa. Top: High sodium activation is prolonged (purple dotted line). This leads to enhanced activation of the Kd conductance (blue dotted line). Bottom: No major changes to the amplitude of the sodium inactivation are observed (green). (C) The difference of gating variable values (3× gNa minus control) shows that while the wider spikes lead to greater mean gNa activation, the Kd activation variable is enhanced proportionally more. There is no change in the mean level of activation for the sodium inactivation. Values are adjusted for firing rate. (D) The time spent by the sodium activation in the open state is prolonged continuously when the sodium maximal conductance is increased up to ten fold (2500 nS). Two (nearly identical) lines are plotted corresponding to the two models shown in Figure 2. Inset: Schematic of the quantity being measured, the time when the sodium activation variable value is greater than 0.96 during an action potential. (E) Histogram of sodium channel activation variable values over a train of action potentials (black: control, red: 3× gNa). Arrow highlights that with 3× gNa the gate is more likely to be open (a taller bar indicates more time spent in the open state). Axis is zoomed in to highlight high values of activation. (F) Histogram of Kd activation variable values during a train of action potentials (black: control, red: 3× gNa). Arrow highlights that with 3× gNa the Kd activation has consistently higher values indicating increased open probability.
To more quantitatively analyze the change in spike width we plotted the change in voltage relative to the voltage (Fig. 4A, bottom panel). In both cases, the most depolarized voltage value achieved remained approximately unchanged (near the sodium reversal potential). With enhanced Na+ conductance, single action potentials depolarize more rapidly (a higher rate of rise). Conversely, the repolarization of the spike on the downstroke phase was initially slower than control, but the final phase of repolarization was more rapid than control leading to an overall lengthening of the spike.
To understand how increased sodium conductance and wider spikes were leading to a reduction in firing rate (equivalent to an increase in the interspike interval) at high current injection, we plotted the sodium channel activation variable (m in the classic Hodgkin and Huxley formalism (Hodgkin and Huxley, 1952)), the sodium channel inactivation variable (h) and the Kd channel activation variable (n) during a single action potential (Fig. 4B). We compared traces from control (Fig. 4B, solid lines) with those generated after the Na+ conductance had been increased three-fold (Fig. 4B, dashed lines). We lined up the traces based on the rising phase of the Na+ channel activation variable (Fig. 4B, purple lines) and superimposed the corresponding action potential with voltage normalized to be between 0 and 1 (Fig, 4B, gray traces, same spike as in Fig. 4A). Because the increased sodium conductance prolongs the depolarization of the neuron, keeping the sodium channels open longer (Fig. 4B, purple, top and bottom panels), more time must elapse before sufficient sodium channels are inactivated to reduce the inward current to a point where the Kd current can effectively oppose it. This change by itself was sufficient to explain the wider spikes but not the increased interspike interval.
The change in the interspike interval can be explained by comparing the action potential voltage trajectory with the Kd channel activation (Fig. 4B, blue, top panel). The Kd channel has slow activation kinetics when compared with the sodium channel. Because of the prolonged depolarization of the neuron during an action potential when Na+ conductance was tripled, the Kd channels had more time to activate, reaching a higher maximum activation level during a spike (Fig. 4B, blue, top panel). The slow decay of the Kd activation variable is ultimately responsible for increasing the interspike interval (lowering the firing rate). Contrary to Kd, the Na+ inactivation (Fig. 4B, green, bottom panel) had little change in its amplitude or kinetics and simply shifted its trajectory to match the wider action potential.
We quantified the change in open probability normalized for firing rate of these three gates between control and enhanced Na+ conductance and found that for any changes in the Na+ activation there was a disproportionate increase in the Kd open probability (Fig. 4C). In contrast, there was no change in the open probability of the Na+ inactivation gate between the two conditions tested. Thus the lower firing rate observed with enhanced Na+ maximal conductance is due to a prolonged depolarization of the voltage that leads to a greater activation of IKd ultimately slowing the overall firing rate.
Because greater spike width due to larger Na+ conductance seemed to be critical for firing rate changes via enhanced Kd channel activation, we ran two example models (the models pictured in Figure 2) over a much larger maximal sodium conductance parameter range (Fig. 4D, figures shows two nearly superimposed curves). The model population had sodium conductances ranging between 0.5 – 250 nS/nF under control. We further extended this range to cover a 10 fold increase ranging from 5 – 2500 nS/nF and measured the length of time the Na+ activation gate stayed open during an action potential (Fig. 4D, inset schematic: double arrow indicates measured quantity). As expected, this duration continued to increase with continually increased maximal Na+ conductance providing evidence that the explanation for how more Na+ conductance can lead to lower firing rates is accurate in this model.
Finally, we plotted histograms of the values of each activation variable over a train of action potentials to visualize more clearly how the Na+ conductance change influenced the open probabilities of each gate. These histograms count the frequency of each value of the activation variables and thus indirectly measure how long the gate spends in the open state. The Na+ activation rapidly switched between the entirely open or closed configuration. When the Na+ conductance was increased, the activation variable spent more time in the open state (Fig. 4E, arrow) which can be seen as an increase in the height of the bar at values near 1.0. The values of the Kd activation were greater overall with increased Na+ conductance than those observed under control (Fig. 4F, arrow) indicating that the Kd conductance was activated more strongly. Taken together, these results show that increasing the Na+ conductance enhances the proportion of a spike phase that the Na+ channel activation spends in the fully open state (Fig. 4E, arrow). That enhanced activation leads to a larger activation of the Kd conductance (Fig. 4F, arrow) that ultimately leads to a reduction of the firing rate by delaying the subsequent spikes.
Crossover point variance suggests a more complex homeostatic regulator
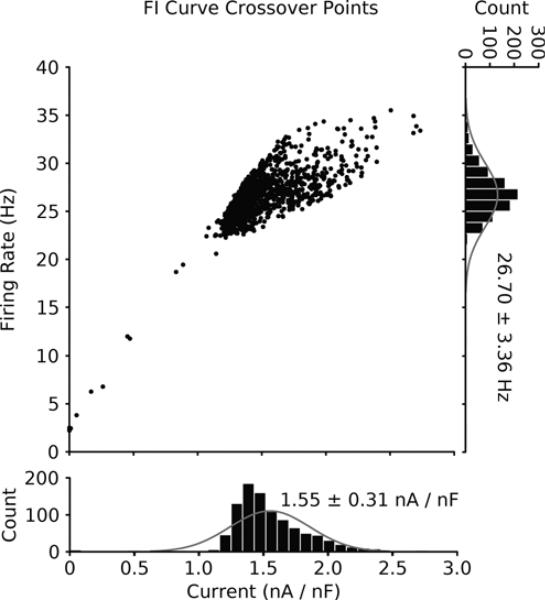
As mentioned above, a consequence of the observed rate-dependent FI curve modulation is that the control and enhanced Na+ FI curves intersect. The intersection point represents the input current and frequency value at which the subtractive shift in the FI curve transitions into a divisive change in the gain. We measured how the crossover point changes between each model in the database of 1000 reduced model neurons. For each set of FI curves (control and three-fold increased Na+ conductance) we used the fit lines computed previously and calculated where these two curves intersected. We found variance in the distribution of the crossover points both in terms of the current values and the frequency values at which they occurred (Fig. 5A). This indicated that there was no fixed current or frequency value that delimits the regions in which enhancing the Na+ conductance either produces a subtractive shift in the FI curve or a divisive gain change. We binned both the current and frequency values of the transition and found that the current values had a large peak around 1.4 nA with a tail at higher current values and that the frequency values were roughly normally distributed (Fig. 5A, histograms, gray lines are normal distributions with mean and variance equal to the data in the histograms). Overall, these findings indicate that, in general, a homeostatic regulator of excitability cannot be implemented based on fixed readouts because these values will vary in real neurons.
Figure 5. FI curve crossover point occurs at diverse values of both frequency and current.
The crossover points for all the reduced models are plotted in input current vs. frequency space (n = ~1000, few models had no intersection or extreme values for their crossover points and are omitted for clarity). The crossover point represents the value of current and frequency that separates the two effects enhanced sodium has on the control FI curve. The scatter plot highlights that the crossover points from each model occur at many different values of frequency and current. Histograms of the current values (bottom: 1.55 ± 0.31 nA/nF) and frequency values (right: 26.7 ± 3.36 Hz) are plotted along with representative normal distributions (gray lines) that have equivalent means and variances.
Discussion
Nervous systems show remarkable resilience in their ability to remain functional when perturbed by neuromodulators (Marder and Bucher, 2007) and by temperature changes (Rosbash, 2009; Tang et al., 2010, 2012). Responses to such global changes and more targeted genetic or pharmacological manipulations are often modest, suggesting that compensatory or degenerate mechanisms are a core feature of nervous systems. Neurons in functioning circuits are faced with the task of continuously modulating their excitability in response to changing inputs and altered environmental conditions. In this study, we asked how targeted increases in the number of sodium channels would influence the excitability of a model neuron. At higher firing rates increased Na+ conductance led to a surprising reduction of the firing rate and the outcome of a Na+ conductance increase depended on the firing rate of the neuron. We conclude that this phenomenon poses a difficult problem for neurons attempting to maintain their excitability by changing conductance densities and suggests they must not only match a target level of mean activity but also match a target input-output relationship.
Sodium conductance changes as a mechanism for gain control
The experimental and theoretical study of gain control has elucidated in detail how the properties of synaptic input trains alter neuronal gain (Destexhe et al., 2003) and how some biophysical properties influence the shape of the input-output relationship (Desai et al., 1999; Lundstrom et al., 2008, 2009; O'Leary et al., 2010). Neurons in vivo are subject to high rates of synaptic input that introduce membrane voltage fluctuations and membrane conductance changes (Pare et al., 1998; Destexhe and Pare, 1999; Harvey et al., 2009). These two properties of in vivo neurons have been shown to have a significant influence on the FI curve (Holt and Koch, 1997; Chance et al., 2002; Mitchell and Silver, 2003; Prescott and De Koninck, 2003; Prescott et al., 2006). Alternate mechanisms for gain control such as synapses with short-term depression have also been proposed as mechanisms for multiplicative gain control (Abbott et al., 1997; Rothman et al., 2009). Comparatively little attention, however, has been focused on cell-autonomous methods of gain control such as the regulation of intrinsic conductances (Moyer Jr. et al., 1996; Cantrell and Catterall, 2001; Zhang and Linden, 2003; Schulz, 2006).
We present a population of model neurons in which the gain is divisively scaled at higher firing rates while there is a subtractive shift in the FI curve at low rates, both in response to an increase in the Na+ conductance. This mechanism is significant because it represents an intrinsic form of gain control in which the neuron can itself influence its input-output relationship by changing its intrinsic properties rather than integrating synaptic inputs over which it has no direct control.
The idea that the entire input-output property of a neuron is the key quantity that must be homeostatically regulated has been proposed previously (Stemmler and Koch, 1999; Triesch, 2007; Lundstrom et al., 2008, 2009). These previous studies have related basic biophysical properties such as conductance ratios (Lundstrom et al., 2008), timescales of biophysical variables (Lundstrom et al., 2009), maximization of information transfer (Stemmler and Koch, 1999) and the statistical distribution of inputs (Triesch, 2007; Wark et al., 2007) to the FI curve. The work presented in this study work has implications for defining the properties of a homeostatic mechanism that could regulate the entire input-output property of neurons, not just the mean firing rate. Additionally, our study reinforces the idea that neurons in functioning networks cannot always rely on single conductance changes to have a single effect on excitability.
The dynamics of sodium channel activation and inactivation are complex (Carter and Bean, 2011) as are the effects of sodium conductance changes on excitability. Upregulation of the sodium conductance can lead to increases in excitability (Hodgkin, 1975; Cantrell and Catterall, 2001) but also decreases (Günay et al., 2008). Somatic excitability is enhanced by dendritic sodium channel block in pyramidal neurons of the weakly electric fish (Fernandez et al., 2005), chronic TTX treatment leads to decreased EPSC frequency at hippocampal CA3 recurrent synapses (Kim and Tsien, 2008), blocking activity in layer 5 cortical interneurons with TTX enhances pyramidal cell dendritic responses (Murayama et al., 2009) and repeated light stimulation enhances the response of visual neurons by increasing sodium currents in Xenopus tadpoles (Aizenman et al., 2003). Our study adds to the literature describing unexpected excitability changes following altered sodium conductance.
Correlations between maximal conductance measurements
Previous work has shown that ion channel mRNA levels may co-vary (Schulz et al., 2006, 2007) and that conductances are not regulated in isolation (Desai et al., 1999; O'Leary et al., 2010). Instead, individual conductances may be tightly correlated with other conductances, sometimes with those that have opposite functions suggesting that neurons use multiple mechanisms to reach a homeostatic set point. The models generated for this study had conductance values consistent with the generation of tonic firing. When we plotted the gain of each model versus its baseline sodium conductance, we found no linear relationship between these quantities (data not shown) suggesting that gain is not inherently higher with more Na+ conductance for models in the population. The gain changes observed in this study occurred only after the baseline models were perturbed, effectively altering the balance between the conductances.
We additionally considered models with multiple conductance changes similar to those seen in experimental work in activity-deprived neurons in which Na+ and Kd conductances change in concert (Desai et al., 1999). In those experiments, sodium conductance increased by a factor of 1.3× and Kd conductance decreased by 0.6× after chronic tetrodotoxin blockade. Both sodium and Kd conductances changes of that magnitude independently decreased the gain at high firing rates. When combined in the model, they produced approximately 50% of the full effect we report for a 3× sodium conductance increase (data not shown). It is possible that if a dramatic change to the Na+ conductance occurred in a real nervous system due to a genetic alteration, for example, other conductances might compensate (Alkon, 1984; Mee et al., 2004; Swensen and Bean, 2005; Laezza et al., 2007; Lorenzetto et al., 2009). Even though such a process is not explicitly possible in our model, the voltage dependent, and thus inexorably linked, conductances compensated for one another regardless of this. As we have shown, the enhancement of the Na+ conductance results in an enhancement of the Kd conductance that was strong enough to lower the firing rate overall. Thus, the opposing nature of the Na+ and Kd conductances, and their joint dependence on the voltage, causes them to provide a rudimentary mechanism for homeostatic control in response to a single perturbation even though we did not explicitly endow the model with a mechanism to achieve this.
The reduced models presented in our study did not simulate calcium entry during action potentials. The increases in sodium conductance resulted in wider action potentials which would likely lead to increased calcium entry in real neurons. Calcium is well-known to trigger a variety of intracellular processes which could influence the input-output relationship of real neurons or trigger additional homeostatic feedback mechanisms in ways not addressed by these simulation results.
Reliable neuromodulation in a simple model
An interesting question that arises from observing variability in nervous systems is that it can seem unclear how neuromodulators can have reliable effects on their targets if those targets are highly heterogeneous (Marder and Thirumalai, 2002). In practice, external stimuli such as therapeutic drugs affect the majority of a population in a similar manner even though it is self-evident that individuals in that population must have brain circuits constructed with different numbers of neurons, different synaptic weights and different histories of neuromodulation and activation. Previous work has investigated this phenomenon experimentally (Grashow et al., 2009). Theoretical work has shown how a model neuron with a diverse parameter space can be robust to change but still respond reliably to neuromodulation (Goldman et al., 2001) and investigated the structure of the parameter space of heterogeneous models with similar behavior (Achard and De Schutter, 2006). Our study fits into this conceptual framework by demonstrating a highly consistent FI curve change in a population of heterogeneous models in response to the same conductance density change.
Implications for homeostatic control mechanisms
Commonly, work describing neuronal homeostasis has made the implicit assumption that the mean firing rate of a neuron is the quantity that should be controlled (Turrigiano et al., 1995, 1998). However, it is well appreciated that neurons can have a large range of firing rates and a key property of neuronal computation is that neurons can meaningfully respond to a wide variety of input levels. This requires a homeostatic feedback process that not only ensures that mean firing rate remains at a reasonable level but instead ensures that the entire input-output relationship is kept in a computationally meaningful range. Our study demonstrates that changing intrinsic conductances can sometimes lead to anti-homeostatic effects on the input-output relationship.
Footnotes
Author Contributions: TK and EM designed the study, JC performed the simulations, TK and JC did the analysis, TK and EM wrote the paper. All authors contributed editorial revisions.
The authors state no conflicting interests.
References
- Abbott LF, Varela JA, Sen K, Nelson SB. Synaptic Depression and Cortical Gain Control. Science. 1997;275:221–224. doi: 10.1126/science.275.5297.221. [DOI] [PubMed] [Google Scholar]
- Achard P, De Schutter E. Complex Parameter Landscape for a Complex Neuron Model. PLoS Comput Biol. 2006;2:e94. doi: 10.1371/journal.pcbi.0020094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aizenman CD, Akerman CJ, Jensen KR, Cline HT. Visually Driven Regulation of Intrinsic Neuronal Excitability Improves Stimulus Detection In Vivo. Neuron. 2003;39:831–842. doi: 10.1016/s0896-6273(03)00527-0. [DOI] [PubMed] [Google Scholar]
- Alkon DL. Calcium-Mediated Reduction of Ionic Currents: A Biophysical Memory Trace. Science. 1984;226:1037–1045. doi: 10.1126/science.6093258. [DOI] [PubMed] [Google Scholar]
- Cantrell AR, Catterall WA. Neuromodulation of Na+ channels: An unexpected form of cellular platicity. Nature Reviews Neuroscience. 2001;2:397–407. doi: 10.1038/35077553. [DOI] [PubMed] [Google Scholar]
- Carter BC, Bean BP. Incomplete Inactivation and Rapid Recovery of Voltage-Dependent Sodium Channels During High-Frequency Firing in Cerebellar Purkinje Neurons. J Neurophysiol. 2011;105:860–871. doi: 10.1152/jn.01056.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chance FS, Abbott L, Reyes AD. Gain Modulation from Background Synaptic Input. Neuron. 2002;35:773–782. doi: 10.1016/s0896-6273(02)00820-6. [DOI] [PubMed] [Google Scholar]
- Connor JA, Stevens CF. Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. The Journal of Physiology. 1971;213:31–53. doi: 10.1113/jphysiol.1971.sp009366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor JA, Walter D, McKown R. Neural repetitive firing: modifications of the Hodgkin-Huxley axon suggested by experimental results from crustacean axons. Biophys J. 1977;18:81–102. doi: 10.1016/S0006-3495(77)85598-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. 1st ed. The MIT Press; 2001. [Google Scholar]
- Desai NS, Rutherford LC, Turrigiano GG. Plasticity in the intrinsic excitability of cortical pyramidal neurons. Nat Neurosci. 1999;2:515–520. doi: 10.1038/9165. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Pare D. Impact of Network Activity on the Integrative Properties of Neocortical Pyramidal Neurons In Vivo. J Neurophysiol. 1999;81:1531–1547. doi: 10.1152/jn.1999.81.4.1531. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Pare D. The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Fernandez FR, Mehaffey WH, Turner RW. Dendritic Na+ Current Inactivation Can Increase Cell Excitability By Delaying a Somatic Depolarizing Afterpotential. J Neurophysiol. 2005;94:3836–3848. doi: 10.1152/jn.00653.2005. [DOI] [PubMed] [Google Scholar]
- Gabbiani F, Krapp HG, Koch C, Laurent G. Multiplicative computation in a visual neuron sensitive to looming. Nature. 2002;420:320–324. doi: 10.1038/nature01190. [DOI] [PubMed] [Google Scholar]
- Goaillard J-M, Taylor AL, Schulz DJ, Marder E. Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci. 2009;12:1424–1430. doi: 10.1038/nn.2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS, Golowasch J, Marder E, Abbott LF. Global Structure, Robustness, and Modulation of Neuronal Models. The Journal of Neuroscience. 2001;21:5229–5238. doi: 10.1523/JNEUROSCI.21-14-05229.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-Dependent Regulation of Potassium Currents in an Identified Neuron of the Stomatogastric Ganglion of the Crab Cancer Borealis. J Neurosci. 1999;19:RC33–RC33. doi: 10.1523/JNEUROSCI.19-20-j0004.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grashow R, Brookings T, Marder E. Reliable neuromodulation from circuits with variable underlying structure. Proceedings of the National Academy of Sciences. 2009;106:11742–11746. doi: 10.1073/pnas.0905614106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günay C, Edgerton JR, Jaeger D. Channel Density Distributions Explain Spiking Variability in the Globus Pallidus: A Combined Physiology and Computer Simulation Database Approach. J Neurosci. 2008;28:7476–7491. doi: 10.1523/JNEUROSCI.4198-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, Tank DW. Intracellular dynamics of hippocampal place cells during virtual navigation. Nature. 2009;461:941–946. doi: 10.1038/nature08499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A. The Optimum Density of Sodium Channels in an Unmyelinated Nerve. Philosophical Transactions of the Royal Society of London Series B, Biological Sciences. 1975;270:297–300. doi: 10.1098/rstb.1975.0010. [DOI] [PubMed] [Google Scholar]
- Hodgkin A, Huxley A. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt GR, Koch C. Shunting inhibition does not have a divisive effect on firing rates. Neural Comput. 1997;9:1001–1013. doi: 10.1162/neco.1997.9.5.1001. [DOI] [PubMed] [Google Scholar]
- Kim J, Tsien RW. Synapse-Specific Adaptations to Inactivity in Hippocampal Circuits Achieve Homeostatic Gain Control while Dampening Network Reverberation. Neuron. 2008;58:925–937. doi: 10.1016/j.neuron.2008.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laezza F, Gerber BR, Lou J-Y, Kozel MA, Hartman H, Craig AM, Ornitz DM, Nerbonne JM. The FGF14(F145S) mutation disrupts the interaction of FGF14 with voltage-gated Na+ channels and impairs neuronal excitability. J Neurosci. 2007;27:12033–12044. doi: 10.1523/JNEUROSCI.2282-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Golowasch J, Marder E, Abbott LF. A Model Neuron with Activity-Dependent Conductances Regulated by Multiple Calcium Sensors. The Journal of Neuroscience. 1998;18:2309–2320. doi: 10.1523/JNEUROSCI.18-07-02309.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzetto E, Caselli L, Feng G, Yuan W, Nerbonne JM, Sanes JR, Buffelli M. Genetic Perturbation of Postsynaptic Activity Regulates Synapse Elimination in Developing Cerebellum. PNAS. 2009;106:16475–16480. doi: 10.1073/pnas.0907298106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundstrom BN, Famulare M, Sorensen LB, Spain WJ, Fairhall AL. Sensitivity of firing rate to input fluctuations depends on time scale separation between fast and slow variables in single neurons. J Comput Neurosci. 2009;27:277–290. doi: 10.1007/s10827-009-0142-x. [DOI] [PubMed] [Google Scholar]
- Lundstrom BN, Hong S, Higgs MH, Fairhall AL. Two computational regimes of a single-compartment neuron separated by a planar boundary in conductance space. Neural Comput. 2008;20:1239–1260. doi: 10.1162/neco.2007.05-07-536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Colloquium Paper: Variability, compensation, and modulation in neurons and circuits. Proceedings of the National Academy of Sciences. 2011;108:15542–15548. doi: 10.1073/pnas.1010674108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding Circuit Dynamics Using the Stomatogastric Nervous System of Lobsters and Crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nature Neuroscience. 2011;14:133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Thirumalai V. Cellular, synaptic and network effects of neuromodulation. Neural Netw. 2002;15:479–493. doi: 10.1016/s0893-6080(02)00043-6. [DOI] [PubMed] [Google Scholar]
- Mee CJ, Pym ECG, Moffat KG, Baines RA. Regulation of Neuronal Excitability Through Pumilio-Dependent Control of a Sodium Channel Gene. J Neurosci. 2004;24:8695–8703. doi: 10.1523/JNEUROSCI.2282-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell SJ, Silver RA. Shunting Inhibition Modulates Neuronal Gain during Synaptic Excitation. Neuron. 2003;38:433–445. doi: 10.1016/s0896-6273(03)00200-9. [DOI] [PubMed] [Google Scholar]
- Moyer JR, Jr., Thompson LT, Disterhoft JF. Trace Eyeblink Conditioning Increases CA1 Excitability in a Transient and Learning-Specific Manner. J Neurosci. 1996;16:5536–5546. doi: 10.1523/JNEUROSCI.16-17-05536.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murayama M, P|[eacute]|rez-Garci E, Nevian T, Bock T, Senn W, Larkum ME. Dendritic encoding of sensory stimuli controlled by deep cortical interneurons. Nature. 2009;457:1137–1141. doi: 10.1038/nature07663. [DOI] [PubMed] [Google Scholar]
- O'Leary T, van Rossum MCW, Wyllie DJA. Homeostasis of intrinsic excitability in hippocampal neurones: dynamics and mechanism of the response to chronic depolarization. The Journal of Physiology. 2010;588:157–170. doi: 10.1113/jphysiol.2009.181024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pare D, Shink E, Gaudreau H, Destexhe A, Lang EJ. Impact of Spontaneous Synaptic Activity on the Resting Properties of Cat Neocortical Pyramidal Neurons In Vivo. J Neurophysiol. 1998;79:1450–1460. doi: 10.1152/jn.1998.79.3.1450. [DOI] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y. Gain control of firing rate by shunting inhibition: Roles of synaptic noise and dendritic saturation. Proceedings of the National Academy of Sciences. 2003;100:2076–2081. doi: 10.1073/pnas.0337591100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, Ratte S, De Koninck Y, Sejnowski TJ. Nonlinear Interaction between Shunting and Adaptation Controls a Switch between Integration and Coincidence Detection in Pyramidal Neurons. J Neurosci. 2006;26:9084–9097. doi: 10.1523/JNEUROSCI.1388-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Rosbash M. The Implications of Multiple Circadian Clock Origins. PLoS Biol. 2009;7:e1000062. doi: 10.1371/journal.pbio.1000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman JS, Cathala L, Steuber V, Silver RA. Synaptic depression enables neuronal gain control. Nature. 2009;457:1015–1018. doi: 10.1038/nature07604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Thier P. Gain Modulation: A Major Computational Principle of the Central Nervous System. Neuron. 2000;27:15–21. doi: 10.1016/s0896-6273(00)00004-0. [DOI] [PubMed] [Google Scholar]
- Schulz DJ. Plasticity and Stability in Neuronal Output Via Changes in Intrinsic Excitability: It's What's Inside That Counts. J Exp Biol. 2006;209:4821–4827. doi: 10.1242/jeb.02567. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard J-M, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard J-M, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proceedings of the National Academy of Sciences. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver RA. Neuronal arithmetic. Nat Rev Neurosci. 2010;11:474–489. doi: 10.1038/nrn2864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stemmler M, Koch C. How voltage-dependent conductances can adapt to maximize the information encoded by neuronal firing rate. Nature Neuroscience. 1999;2:521–527. doi: 10.1038/9173. [DOI] [PubMed] [Google Scholar]
- Swensen AM, Bean BP. Robustness of Burst Firing in Dissociated Purkinje Neurons with Acute or Long-Term Reductions in Sodium Conductance. The Journal of Neuroscience. 2005;25:3509–3520. doi: 10.1523/JNEUROSCI.3929-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang LS, Goeritz ML, Caplan JS, Taylor AL, Fisek M, Marder E. Precise Temperature Compensation of Phase in a Rhythmic Motor Pattern. PLoS Biol. 2010;8:e1000469. doi: 10.1371/journal.pbio.1000469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang LS, Taylor AL, Rinberg AR, Marder EE. Rhythmic Circuit to Short and Long-Term Temperature Changes. J Neurosci. 2012 doi: 10.1523/JNEUROSCI.1443-12.2012. (submitted) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor AL, Goaillard J-M, Marder E. How Multiple Conductances Determine Electrophysiological Properties in a Multicompartment Model. The Journal of Neuroscience. 2009;29:5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triesch J. Synergies Between Intrinsic and Synaptic Plasticity Mechanisms. Neural Computation. 2007;19:885–909. doi: 10.1162/neco.2007.19.4.885. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, LeMasson G, Marder E. Selective regulation of current densities underlies spontaneous changes in the activity of cultured neurons. The Journal of Neuroscience. 1995;15:3640–3652. doi: 10.1523/JNEUROSCI.15-05-03640.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- Wark B, Lundstrom BN, Fairhall A. Sensory adaptation. Current Opinion in Neurobiology. 2007;17:423–429. doi: 10.1016/j.conb.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Linden DJ. The other side of the engram: experience-driven changes in neuronal intrinsic excitability. Nature Reviews Neuroscience. 2003;4:885–900. doi: 10.1038/nrn1248. [DOI] [PubMed] [Google Scholar]