Dynamic Estimation of Task-Relevant Variance in Movement Under Risk

Abstract

Humans take into account their own movement variability as well as potential consequences of different movement outcomes in planning movement trajectories. When variability increases, planned movements are altered so as to optimize expected consequences of the movement. Past research has focused on the steady-state responses to changing conditions of movement under risk. Here, we study the dynamics of such strategy adjustment in a visuomotor decision task in which subjects reach toward a display with regions that lead to rewards and penalties, under conditions of changing uncertainty. In typical reinforcement-learning tasks, subjects should base subsequent strategy by computing an estimate of the mean outcome (e.g., reward) in recent trials. In contrast, in our task strategy should be based on a dynamic estimate of recent outcome uncertainty (i.e., squared error). We find that subjects respond to increased movement uncertainty by aiming movements more conservatively with respect to penalty regions, and that the estimate of uncertainty they use is well characterized by a weighted average of recent squared errors, with higher weights given to more recent trials.

Introduction

Humans take uncertainty into account when planning and executing movements, including movements around obstacles (Sabes and Jordan, 1997; Sabes et al., 1998) or toward targets whose location is uncertain (Körding and Wolpert, 2004; Tassinari et al., 2006). Humans also take visuomotor uncertainty into account when planning a fast reaching movement under risk (Trommershäuser et al., 2003b, a; Trommershäuser et al., 2006; Maloney et al., 2007). In these experiments, humans reach under a time constraint at a visual display consisting of a target region and neighboring penalty region. On each trial, hits on the target that meet the time constraint yield financial rewards and hits on the penalty yield losses. Human performance in these tasks nearly optimizes expected gain. Humans change movement strategy in response to changing uncertainty when movement uncertainty is changed artificially in a virtual environment (Trommershäuser et al., 2005), using a visuo-motor reflex (Hudson et al., 2010), or is naturally larger in one direction than another (Gepshtein et al., 2007). In choosing when to move, humans also choose a near-optimal tradeoff of motor and visual uncertainty (Battaglia and Schrater, 2007).

However, the foregoing work addresses steady-state behavior and leaves open many questions about what sort of dynamic adjustment or learning drives these changes. This contrasts work on gain optimization in more abstract decision tasks, such as “bandit” tasks (Bayer and Glimcher, 2005; Sugrue et al., 2005; Daw et al., 2006; Behrens et al., 2007). There, participants’ choices and associated neural signals are well characterized by a process that dynamically tracks an estimate of the mean gain expected for an option, as embodied by reinforcement learning models using delta rules or reward gradients (Sutton and Barto, 1998). The role of uncertainty in learning tasks has also been a question of sustained interest. Although there are reported neural correlates of uncertainty (e.g., by Behrens et al., 2007; Li et al., 2011) and even of “risk prediction errors” suggesting a mechanism for how these are learned (Preuschoff et al., 2008), it has been relatively difficult to verify these hypothesized learning dynamics behaviorally. This is because, in these tasks, uncertainty about the mean payoff tends to contribute only indirectly to behavior, such as by controlling the stepsizes for updates (Courville et al., 2006; Behrens et al., 2007; Li et al., 2011) or the degree of exploration (Daw et al., 2006; Frank et al., 2009).

In this study, we use reinforcement-learning methods to study dynamic strategic adjustment in a visuomotor decision task in which subjects must cope with movement consequences whose uncertainty changes over time. In our task, the gain-optimizing strategy is determined by the uncertainty (i.e., variance) in the movement endpoint, not its mean, offering an opportunity to examine how humans learn second-order statistics from feedback when these statistics have relatively direct behavioral consequences. Indeed, straightforward application of a mean-estimating reinforcement rule to our task predicts a qualitatively different pattern of results, and thus offers a crucial comparison point for ensuring we are isolating behavioral adjustments related to changing uncertainty.

Methods

Stimuli and procedure

Subjects performed a rapid reaching movement and attempted to hit a target region displayed on a touchscreen while, on a subset of trials, avoiding a partially overlapping penalty region (Fig. 1). Subjects began each trial with their right index finger pressing the CTRL key of a keyboard firmly attached to a table. A fixation cross was displayed for 1 s, followed by the target display. Subjects could begin the reach at any time after stimulus display, but were constrained to complete the movement within 400 ms.

Figure 1.

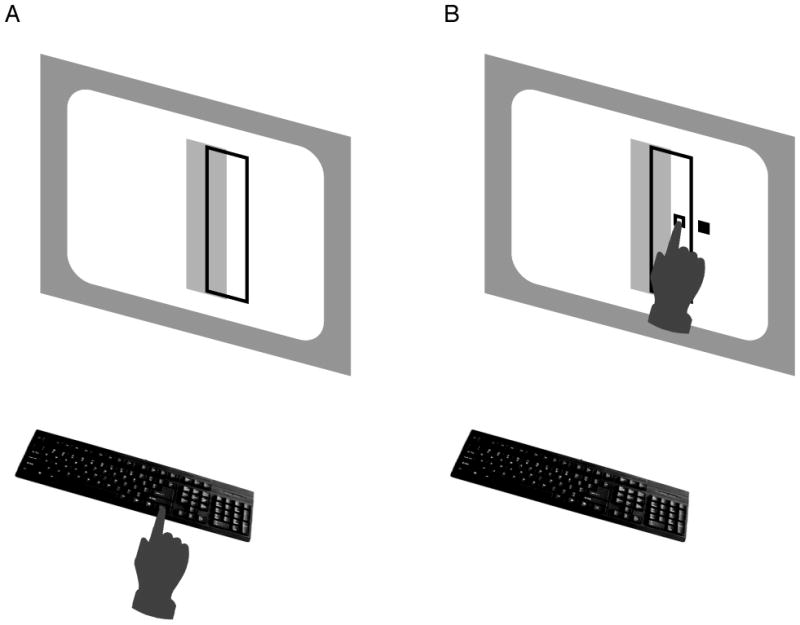
Stimuli and task. A, The initial stimulus display consisted of a green outlined target region and an overlapping red penalty region (here shown as outlined black and solid gray, respectively). Participants performed a speeded reach with the right hand, attempting to hit the target while avoiding the penalty region. B, After the movement was complete, a small white square indicated the reach endpoint. A small blue square was also displayed, randomly displaced horizontally away from the reach endpoint (here shown as open and filled squares, respectively). The participant received 1 point (4¢) for each endpoint within the target region and lost 5 points for hitting the penalty region. Slow movements (> 400 ms) led to a 10-point penalty.

The target was a green outlined rectangle, 182×64 mm, located 37 mm left or right of the center of the display, viewed from a distance of 40 cm. On target-only trials, only the green rectangle was displayed. On penalty trials, an overlapping solid red penalty rectangle of the same size was displayed, displaced left or right of the target rectangle by half its width (Fig. 1A). The display background was black.

Task-relevant variability was manipulated by adding a horizontal perturbation to the movement endpoint. When the finger reached the screen within the time constraint, two small squares were displayed: a white square at the actual endpoint of the movement (with horizontal position x_hit), and a blue square (with horizontal position x_fb) shifted horizontally from that position by a random amount: x_fb = x_hit + Δ (Fig. 1B). Although this is perhaps a somewhat unnatural task, our focus here is on how subjects contend with changing variability, as we already know that subjects can change strategy with changing uncertainty. You might think of the perturbed movement endpoints as analogous to typing or playing a game on a cellphone touchscreen for which the feedback you receive often appears inconsistent with the location you thought you touched.

The movement perturbation Δ was normally distributed with zero mean and a standard deviation (SD), σ_pert, that could change from trial to trial. σ_pert followed a “sample-and-hold” trajectory. The initial value of σ_pert was chosen randomly and uniformly from a range of 3.7 to 18.4 mm. σ_pert remained constant for an epoch that lasted for 75 to 150 trials; the epoch length was chosen randomly and uniformly over that range. At the end of the epoch a new value of σ_pert and epoch length were chosen similarly, and so on until the end of the block of trials.

Subjects participated in one training and two experimental sessions. The training session consisted of 300 target-only trials. Experimental sessions consisted of 420 trials, including 140 target-only trials and 280 penalty trials, with equal numbers of trials with the target on the left or right, and for penalty trials, equal numbers of trials with the penalty region to the left or right of the target. Both training and experimental sessions began with an additional 12 warmup target-only trials; the data from the warmup trials were not analyzed.

Reward feedback was based on the position x_fb of the shifted, blue square. If the square fell within the target region, the subject earned one point (4¢). If it fell within the penalty region, they lost 5 points. In the overlap region, both the reward and penalty were awarded. Movements that failed to meet the time constraint resulted in a 10-point penalty. If subjects began the movement before the stimulus was displayed, the trial was re-run. Subjects were given feedback at the end of every trial with the results of that trial, and were told their cumulative score at the end of each session. Note that since the rewards are fixed, most of our qualitative conclusions (though not, quantitatively, the ideal-observer analysis for maximizing expected gain) are robust to nonlinearity in the utility of the outcomes, e.g. risk sensitivity or loss aversion.

Apparatus

The experiment was controlled by a PC and stimuli were presented on an ELO Touchsystems (Menlo Park, CA) ET1726C 17-in CRT display with touchscreen, with claimed positional measurement accuracy SD of 2 mm. Stimulus timing and display were controlled using the Psychophysics Toolbox package (Brainard, 1997; Pelli, 1997).

Subjects

Seven subjects (4 female, 3 male) ran in the experiment including one author (MSL). All had normal or corrected-to-normal vision. All but one (JMF) were right-handed and all used the right hand to perform the reaches. Subjects signed a consent form approved by the NYU University Committee on Activities Involving Human Subjects. They were paid a base fee plus a bonus based on performance in the task. Bonuses ranged from $2.80 to $14.44 for a single practice or experimental session.

Ideal-performance model

We treat ideal performance as the choice of an aimpoint that results in maximum expected gain. Such a strategy must take into account the stimulus display (the locations of payoff and penalty regions), the reward and penalty values, as well as the total task-relevant uncertainty. For our task, both the target and penalty regions are large vertical rectangles, so tall as to be impossible to miss in the vertical direction. Thus, this is effectively a one-dimensional task, and we only model the choice of horizontal aimpoint x_aim. On any given trial, movement uncertainty has two components: the subject’s own motor uncertainty σ _motor and the experimenter-imposed outcome uncertainty σ_pert, resulting in overall uncertainty ${\sigma }_{\text{overall}}=\sqrt{{\sigma }_{\text{pert}}^2+{\sigma }_{\text{motor}}^2}$. In reaching tasks such as these, we find endpoint distributions to be well approximated by a Gaussian distribution (Trommershäuser et al., 2005) and so, for the purposes of modeling ideal behavior in this task, we assume that when a participant aims at location x, endpoints will be distributed as a Gaussian with variance ${\sigma }_{\text{overall}}^2$.

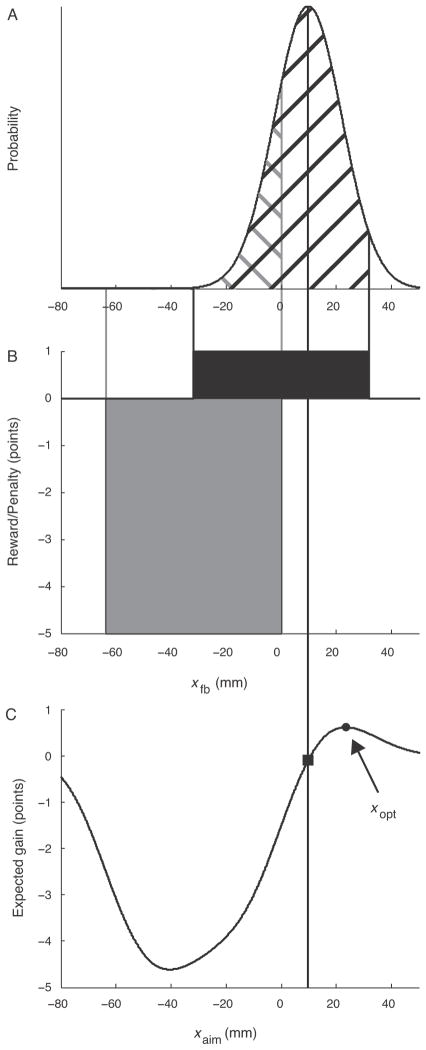
If the participant had precise knowledge of σ_overall, then they could select an ideal strategy for the task, i.e., choose an aimpoint that maximized expected gain, providing the best tradeoff between maximizing hits on the target while minimizing occasional hits on the penalty region. Figure 2 illustrates the computation of the optimal aimpoint x_opt for this “omniscient” observer who somehow has knowledge of the value of σ_overall for the current trial. Figure 2A shows the distribution of movement feedback locations x_fb resulting from a particular value of x_aim (indicated by the vertical black line through all three panels). The experimenter-imposed gain function is shown in Figure 2B, with the corresponding probabilities of hitting the target or penalty indicated by the black and gray cross-hatching in Figure 2A, respectively. The expected gain for this aimpoint is indicated by the black square in Figure 2C, and is computed as the sum of the target and penalty values weighted by the respective probabilities:

$$EG(x_{\text{aim}})=1\times P(\text{hit}-\text{target}\mid x_{\text{aim}},{\sigma }_{\text{overall}})-5\times P(\text{hit}-\text{penalty}\mid x_{\text{aim}},{\sigma }_{\text{overall}}).$$ (1)

Figure 2.

Expected gain and optimal strategy. A, Illustration of the distribution of perturbed reach endpoints x_fb for reaches with aimpoint x_aim (indicated by the black vertical line). B, Experimenter-imposed rewards (black) and penalties (gray). The probability of hitting the target or penalty is indicated by the black and gray cross-hatching in A. C, Expected gain as a function of aimpoint. The black square indicates the expected gain for the example in A. The black circle corresponds to the optimal aimpoint x_opt resulting in maximum expected gain.

Figure 2C shows expected gain as a function of aimpoint. The aimpoint corresponding to the peak of the curve (the black circle) is the optimal strategy x_opt.

Figure 3 shows the optimal strategy x_opt as a function of overall noise variance. As one might expect, increased noise leads an optimal omniscient participant to aim further away from the penalty region. In this figure, the vertical lines bound the region of ${\sigma }_{\text{overall}}^2$ values that occurred in our study (across participants and epochs).

Figure 3.

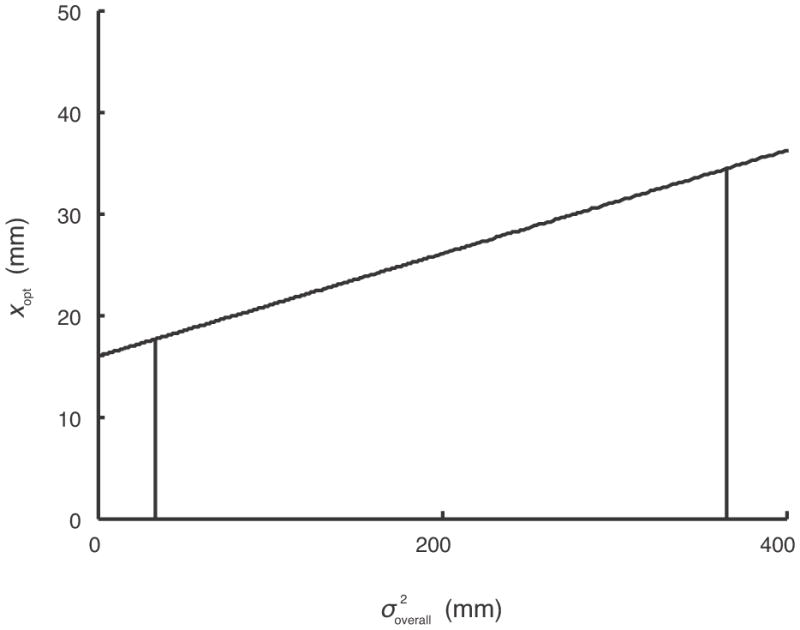
Optimal aimpoint x_opt as a function of overall variance. The vertical lines indicate the range of experienced overall variance in our experiments across participants and epochs. Optimal aimpoint is approximately a linear function of variance.

Analyses of dynamic learning

We are interested in determining how strategy on a given trial is determined based on the outcomes of previous trials. The model of ideal performance described above suggests that subjects should track the variance of recent perturbations, and then (by analogy with the informed ideal observer) choose an aimpoint, on each trial, that is linear in their current variance estimate.

Accordingly, in our task, large perturbations should drive (variance-estimating, gain optimizing) participants to adopt large variance estimates, and thus aim far from the penalty area; small perturbations should have the opposite effect. Such a strategy can be equivalently described in terms of trial-to-trial relative behavioral adjustments. To wit, an unexpectedly large perturbation (relative to the previous variance estimate) should drive a participant to increase their variance estimate, and thus subsequently aim further away from the penalty area, relative to previous aimpoints.

Importantly, a large perturbation should have this effect regardless of whether that perturbation drove the reinforced location x_fb toward or away from the penalty. Even if the current aimpoint is outside the target, and yet a large perturbation led to an “undeserved” reward, the variance-tracking optimal strategy would treat the large perturbation as evidence for large uncertainty, possibly moving the aimpoint even further outside the target on the next trial, even though the previous aimpoint was rewarded. A strategy based on tracking the mean perturbation, analogous to a reinforcement learner, will instead adjust aimpoints to compensate for the average perturbation, aiming closer to the center of the target (and thus closer to the penalty) after trials with large perturbations that move the reinforced location x_fb further away from the penalty. (Because the position of the penalty is randomly to the left or right of the target, we conduct all our analyses using coordinates for x in which positive values indicate the direction away from the penalty region, rather than left or right.) Note that this will be the qualitative direction of update even in a variance-sensitive version of the mean-tracking approach in which the variance estimate controls the stepsize for the update (Dayan and Long, 1998; Dayan et al., 2000; Courville et al., 2006; Preuschoff and Bossaerts, 2007).

To contrast these two approaches — tracking the variance vs. tracking the mean perturbation — and to verify that aimpoints were related to variance rather than mean tracking, we will compare strategies that compute aimpoints based on the average of recently experienced squared perturbation (an estimator for the variance) to those that track the average of the perturbations themselves (the mean). We consider models that compute the aimpoint x_aim as a linear function of the statistics of recently experienced perturbations. As an approximation to the ideal model, this tractable approach is justified in that within the range of values of ${\sigma }_{\text{overall}}^2$ that confronted participants, the optimal aimpoint was approximately a linear function of ${\sigma }_{\text{overall}}^2$ (Fig. 3), and hence of ${\sigma }_{\text{pert}}^2$ as well.

Regression analyses

We will begin by examining a particularly simple model in which the current aimpoint is based solely on the most recently experienced perturbation. For such a prediction to be made, the current trial must be a penalty trial (participants should aim at the center of the target on target-only trials). Thus, we will regress the current reach endpoint on penalty trials against either the previously experienced perturbation or squared perturbation. Participants only experience the perturbation on trials in which the finger arrived at the display screen prior to the timeout; for trials in which the reach was too slow, the perturbed location was not displayed. In subsequent analyses, we will examine models that base the strategy on more than one previously experienced perturbation (on more than one previous trial). To compare these models on an equal basis, all models are fit only to penalty trials in which there were at least 15 previously experienced perturbations in the same session (excluding warmup trials).

We will also determine whether current strategy is based on a longer history than merely the most recently experienced perturbation. To do so, we will conduct “lagged regressions” where, instead of using only the most recently experienced squared perturbation as a regressor, we will include the 8 most recently experienced squared perturbations as regressors.

In our analyses, the dependent variable is each trial’s movement endpoint and the explanatory variables are previously experienced perturbations that might contribute to a subject’s variance estimate. This is motivated by the form of the ideal strategy conditional on knowing the variance. However, because the movement endpoints arise in sequence, they could be sequentially correlated with one another in a way not fully accounted for by the perturbations (Lau and Glimcher, 2005). Such autocorrelation could arise, for instance, as a result of other sorts of higher-level strategic adjustment. This is problematic because in ordinary least-squares regression analysis, one underlying assumption is that the dependent variables are independent of one another, conditional on the explanatory variables. To ensure correct statistical estimation in the presence of potential autocorrelation, we use a technique analogous to that used by Lau and Glimcher (2005), who pointed out the problem in the context of a similar analysis of a reinforcement learning task. To predict the movement endpoint for trial n, in addition to the regressors relevant to the analysis (e.g., the previous trial’s squared perturbation), we also include as nuisance regressors the movement endpoints from previous penalty trials, thereby allowing the model to account explicitly for any residual autocorrelation.

To determine the number of previous trials to include, we first ran the lagged regression described above with, as added regressors, from 0 to 8 previous penalty trials’ endpoints. We compared the results of these regressions using both the AIC and BIC (summed over subjects) and found that both criteria attained a minimum with the addition of 3 previous penalty trials. Thus, to ensure correct statistical estimation in the presence of possible autocorrelation, in all regression results and model fits reported in this paper (e.g., Figs. 6–9), we include the 3 previous penalty trials’ movement endpoints as additional regressors. In addition, in any analysis in which we report the variance accounted for by a regression or model, we base our results on the remaining variance. By remaining variance we mean the variance accounted for by the model over and above the variance accounted for by the 3 previous-trial regressors.

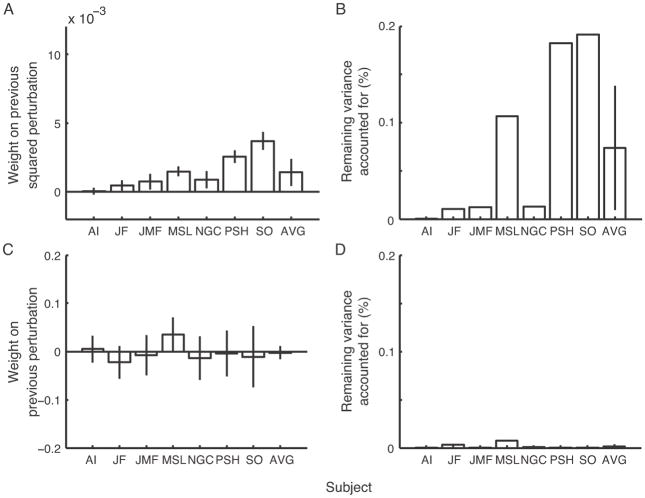
Figure 6.

Response to the previously experienced perturbation. A linear regression was computed to predict each trial’s reach endpoint as a function of the most recently experienced squared perturbation (A and B) or raw perturbation (C and D). Plotted are the regression weights (A and C, with 95% confidence intervals) and remaining variance (see Regression analyses for the definition of remaining variance) accounted for (B and D), as well as across-subjects averages and ±2 SE.

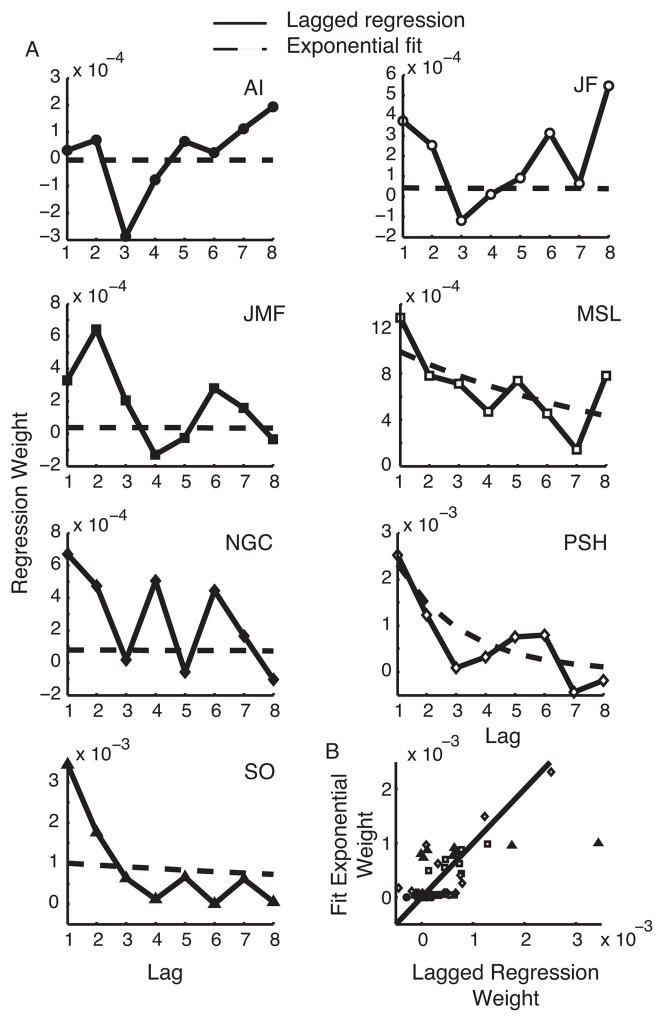
Figure 9.

Exponential model versus lagged regression. A, Lagged regressions (solid lines, from Fig. 7) and exponential weights (from fits of Model 2, “Exponential variance only”) for each participant. Note the ordinate scale varies across subjects. B, Scatterplot of lagged regression vs. exponential model weights.

Model fits

We will also consider parametric models that, like the lagged regression, base the current trial’s strategy on a weighted sum of recently experienced perturbation. These models, like the results of the lagged regression shown below, give the greatest weight to the most recent trials, by using weights that decay exponentially with the lag. We will compare several different models of this form to ask about the relative importance of variance- and mean-estimation in subjects’ choices. We begin by describing the most complex model we fit to the data; the other models are nested simplifications of this model.

The models assume that the aimpoint in each penalty trial is a linear combination of previously experienced perturbations and/or squared perturbations. Participants experience a perturbation (i.e., see a display indicating the actual and perturbed endpoints as in Fig. 1B) on any trial (penalty or target-only) in which the reach arrived at the display screen within the experimenter-imposed time constraint. We index these “useable” trials (not a warmup trial, no timeout) by i= 1,2,···,N, where N is the total number of useable trials in that experimental session. The regression is computed to model data only for those useable trials j meeting two additional constraints: j is a penalty trial and j> 15 (so there are enough previous trials on which to base the prediction). For such a trial j, the model for the reach endpoint is

$$x_{\text{hit},j}=B+w_s\sum _{i=1}^{j-1}{e}^{-(j-i-1)/{\tau }_s}{\mathrm{\Delta }}_i^2+w_p\sum _{i=1}^{j-1}{e}^{-(j-i-1)/{\tau }_p}{\mathrm{\Delta }}_i+{\epsilon }_j.$$ (2)

Here, Δ_i is the value of the perturbation in useable trial i, where positive values indicate a perturbation in the direction away from the penalty region (i.e., rightward when the penalty was to the left of the target, and leftward otherwise). w_s and τ_s are the weight and exponential time constant for squared perturbations, and w_p and τ_p are the weight and time constant for perturbations. B is a bias term; think of it as the mean aimpoint in the absence of any information about the current perturbation. Finally, reach aimpoints are perturbed by motor noise ε_j that has zero mean, is normally distributed, independent over trials, and has standard deviation σ_motor. Thus, there are five parameters modeling the aimpoint (B, w_s, τ_s, w_p and τ_p ) and one noise parameter σ_motor. The estimated noise parameter is simply the standard deviation of the residuals. The models were fit to the data of both experimental sessions by maximum likelihood, separately for each subject.

Early trials in the session have fewer previous perturbations to contribute to the model’s prediction of the current trial’s value of x_hit. We also fit models in which the weight on ${\mathrm{\Delta }}_i^2$ were normalized by ${\displaystyle \sum _{i=1}^{j-1}}{e}^{-(j-i-1)/{\tau }_s}$ (and similarly for the weights on Δ_i ). These models behaved similarly to the unnormalized versions summarized here.

We will compare seven different models:

1. “Exponential mean and variance” described by Eq. 2,

2. “Exponential variance only” that omits the terms based on previously experienced perturbations (i.e., forcing w_p = 0),

3. “Exponential mean only” that omits the terms based on previously experienced squared perturbations (i.e., forcing w_s = 0),

4. “1-back variance and mean” that only considers one previously experienced trial (i.e., forcing τ_s and τ_p to be vanishingly small),

5. “1-back variance only” that considers one previously experienced squared perturbation (i.e., small τ_s and w_p = 0 ),

6. “1-back mean only” that considers one previously experienced perturbation (i.e., small τ_p and w_s = 0), and

7. “Aimpoint bias alone” (i.e., w_s = w_p = 0).

Each of these models was fit to the data for each subject separately by maximum likelihood. Models 5 and 6 are formally identical to the linear regressions described in the previous subsection, and Model 4 is an analogous bivariate linear regression. Many pairs of models are nested in the sense that one model is a constrained version of the other, and thus may be compared using the nested hypothesis test (Mood et al., 1973, pp. 440–442).

Results

Raw endpoint data

Results for two individual subjects are shown in Figure 4. For each subject, panel A shows the trajectory of imposed outcome uncertainty (σ_pert ) over the two experimental sessions. We estimated each subject’s motor uncertainty, σ_motor, as the standard deviation of the horizontal location of movement endpoints relative to the center of the target, pooled across all trials in the training session and all no-penalty trials in the two experimental sessions (excluding any trials in which the participant failed to arrive at the target in time). Overall uncertainty was estimated as the combination of these two independent sources of uncertainty, as noted before (see Ideal-performance model).

Figure 4.

Data for two subjects. A, Perturbation magnitude σ_pert across experimental sessions 1 (solid line) and 2 (dashed line). B, Data points: Reach endpoints plotted relative to the center of target, with positive values corresponding to endpoints located away from the penalty region relative to target center. Data are plotted only for penalty trials in which the reach was completed within the time constraint. Lines: Aimpoints based on the optimal omniscient strategy, i.e., assuming knowledge of both σ_motor as well as the current trial’s value of σ_pert.

Comparison to the optimal “omniscient” strategy

Figure 4B shows the optimal aimpoints for each penalty trial in the experimental sessions (the solid and dashed lines) as well as the actual endpoints for all penalty trials in which the reach arrived at the screen prior to the timeout. An aimpoint or endpoint value of zero corresponds to the center of the target, and positive values correspond to landing points shifted away from the penalty, allowing us to sensibly plot data together for trials in which the penalty region was to the left or right of the target. The plotted optimal aimpoints are based on each trial’s value of σ_overall (see Fig. 3), which, in turn, depends on the value of σ_pert, which was not available to the participants. Hence, we refer to this as the optimal “omniscient” strategy. Nonetheless, there is some indication in Figure 4B, especially for PSH, that the participant’s strategy was affected by changing uncertainty; endpoints land further from the penalty region during periods of greater outcome uncertainty.

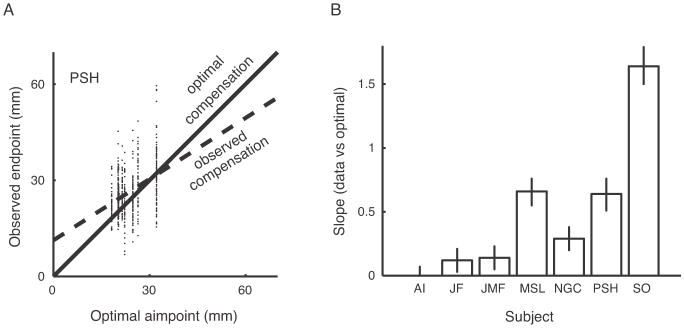
We determined the degree to which participants compensated for changing uncertainty by comparing reach endpoints to those predicted by the optimal omniscient strategy. Figure 5A plots reach endpoints for one subject as a function of optimal omniscient endpoints. A linear regression (dashed line) indicates that there was substantial compensation for changing uncertainty by this subject. The amount of compensation in response to the applied perturbation varied across subjects (Fig. 5B), and was significant for six of the seven participants. Most subjects compensated less than called for by the optimal omniscient strategy, but one subject (SO) overcompensated.

Figure 5.

Compensation for uncertainty. A, Scatterplot of reach endpoints as a function of the optimal aimpoint using the omniscient strategy. The solid identity line corresponds to the optimal omniscient strategy. The dashed regression line indicates the degree to which this participant responded to changes in outcome uncertainty. B, Regression slopes for all seven participants. Error bars are 95% confidence intervals. Six of seven participants had a significant degree of compensation for changing uncertainty. Most participants undercompensated, but one, SO, overcompensated.

Response to recently experienced perturbations

In the preceding analysis, participants’ strategies of aimpoint selection were compared to the omniscient strategy, which assumes the participant has access to the current trial’s value of σ_pert. Of course, although aimpoints were sensitive to this parameter, its value was not told to the participants, and furthermore was changed over trials. Thus this sensitivity must have arisen by participants adjusting their strategy in light of experience, e.g. by dynamically estimating outcome uncertainties to formulate their aimpoints on each trial.

Our remaining analyses seek to characterize these dynamic adjustments by studying the dependence of aimpoints on recent experience. Rather than specifying a full Bayesian ideal updater (Behrens et al., 2007), we seek to determine what statistics of recent observations influence the aim strategy, and in so doing, to probe a key difference in the present task from many reinforcement learning tasks that have been studied with similar analyses (Corrado et al., 2005; Lau and Glimcher, 2005). Gain optimization in reward learning tasks is typically driven by estimating mean payoffs (e.g., with delta-rule or gradient-climbing algorithms; Sutton and Barto, 1998; Dayan and Abbott, 2005), so as to choose the option with highest rewards. However, in the present task, the key statistic determining the optimal strategy is the variance of the perturbations, not their mean.

Figure 6 illustrates the results of regressing the current reach endpoint on penalty trials against either the previously experienced squared perturbation (panels A and B) or the previously experienced perturbation (panels C and D). The influence of the previously experienced squared perturbation on the current trial’s reach endpoint is significant averaged across observers (t(6) = 2.86, 1-tailed p = 0.014), and is significant individually for 6 out of 7 participants (Fig. 6A), although the degree of influence (Fig. 6A) and remaining variance accounted for by this regression (Fig. 6B) differ substantially across participants. The regression coefficients are all positive, indicating that larger squared perturbations lead participants to aim further away from the penalty, as expected. The remaining variance accounted for is quite small, because the 3 previous-penalty-trial regressors in the analysis (see Regression analyses) soak up most of the variance that would otherwise have been attributed to the squared-perturbation regressor. In contrast, the previously experienced perturbation (not squared) does not have a significant influence on the current reach endpoint averaged across observers (t(6) = −0.36, 1-tailed p = 0.63). This influence is not significant for any individual observer and the signs of the regression coefficients are inconsistent across subjects (Fig. 6C).

In typical reinforcement-learning paradigms, behavior on a given trial is correlated with recently experienced reinforcement. We examined the additional impact of reinforcement on strategy in our task by repeating the analysis of Fig. 6, adding in additional regressors based on reinforcement from the previous penalty trial. We computed regressions based on whether the previous penalty incurred a reward, a penalty, or both, and an additional regression based on the overall score from the previous penalty trial. The additional variance accounted for by inclusion of these regressors was quite small and the weights on these regressors were significant only for three subjects in the regression that included target-hits. We conclude that changes in aimpoint are primarily a response to recently experienced squared perturbations, rather than merely to reinforcement signals.

Next, to study how participants combined perturbations from multiple trials into an estimate, while making minimal parametric assumptions about the form of this combination, we conducted a similar regression where, instead of using only the most recently experienced squared perturbation as a regressor, we included the 8 most recently experienced squared perturbations as regressors. This is equivalent to assuming subjects aim proportional to a variance estimate, which is itself constructed from a weighted average of previous perturbations. The weights on each recent perturbation vary substantially across subjects (Fig. 7). The average influence of perturbations differs significantly from zero for 4 of the 8 lags (p < .05), and approaches significance for one other lag. The overall trend is noisy, but appears to weight more recent perturbations more heavily than those further in the past.

Figure 7.

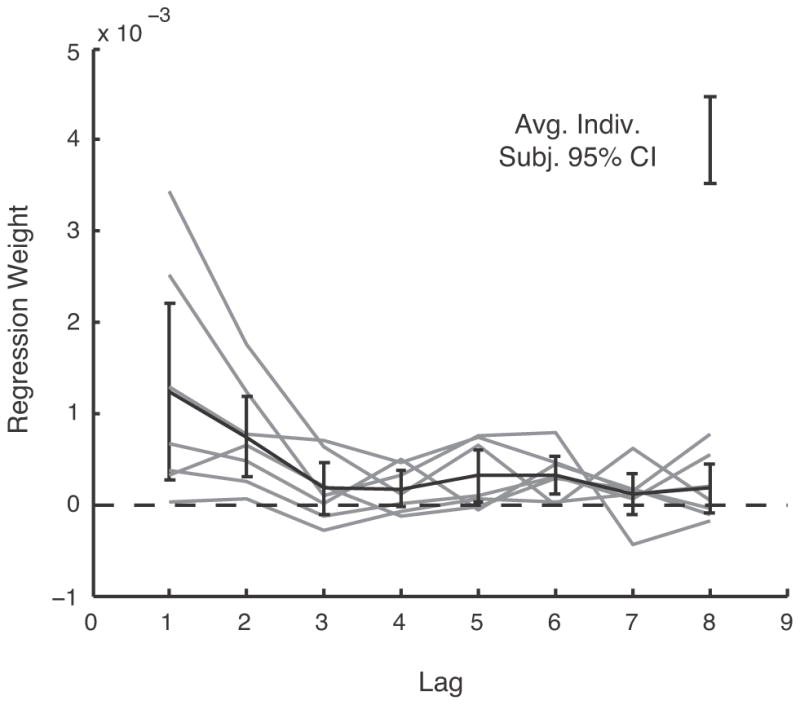
Lagged regression. Results of a regression predicting each trial’s reach endpoint as a linear combination of the previous 8 trials’ squared perturbations. Gray: individual subjects. Black: Group average and ±2 SE error bars. The isolated error bar at the upper right represents the average, over subjects and lags, of the 95% CI from the individual linear regressions.

This decay appears, at least on the average (which is an estimator for the population-level effect; Holmes and Friston, 1998), roughly exponential in shape. Such an exponential form to the lagged dependence is predicted if subjects track their variance estimate by an error-driven running average (here, of squared perturbations; e.g., Preuschoff et al., 2008).

Parametric models

The results of the lagged regression indicate that participants base their choice of reach aimpoints on several recently experienced perturbations, with greater weight placed on more recent trials. However, characterizing the lagged dependence given so few structural assumptions about its form requires a large number of free parameters and introduces concerns of overfitting. Therefore, in order to directly capture the effects of squared and non-squared perturbations together in a single model, and to characterize this dependence over arbitrary timelags, we next adopted the parameterization suggested by the previous analysis. That is, we considered models that weight recently experienced perturbations using weights that decay exponentially with lag.

First, we tested whether this approach was justified by comparing the fit to data of the unconstrained model from Figure 7, to the corresponding model assuming exponentially decaying weights (Model 2). Although the latter has many fewer free parameters, it fit the data nearly as well. In particular, penalizing the fit for the free parameters using either the AIC or BIC criterion (because the two models are not nested; Schwarz, 1978), the exponential model fit better for every participant, by an average AIC difference of 88 and BIC difference of 114.

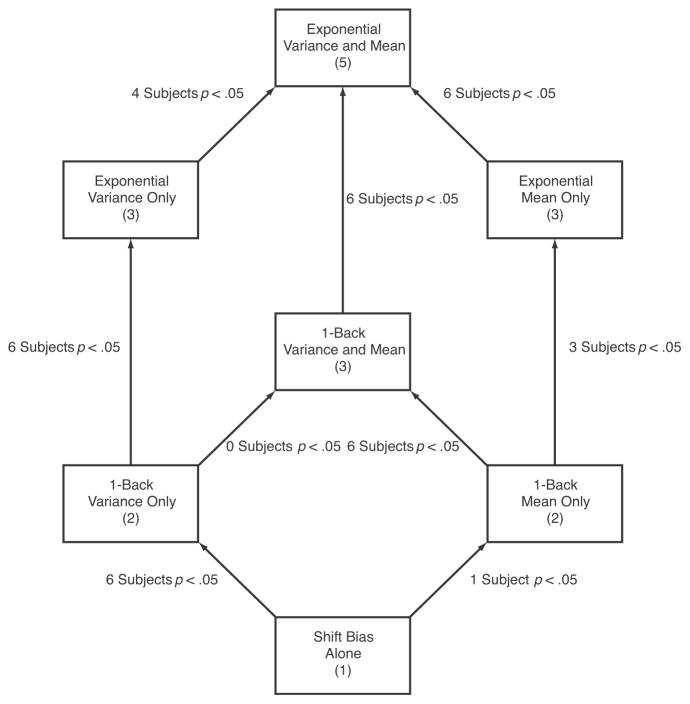
Figure 8 presents the results of the model comparisons. Each rectangle corresponds to one of the 7 models, and gives the number of model parameters (excluding the noise parameter σ_motor required by every model). Arrows indicate nesting between models, with more complex models placed higher in the figure. Next to each arrow is an indication of the number of subjects of the 7 for whom the hypothesis test rejected the null hypothesis (p< .05, with no corrections for multiple tests) indicating that the extra parameters in the more complex model were justified.

Figure 8.

Model comparison. Rectangles indicate each of the 7 models fit to the data and the number of model parameters for each (excluding the noise parameter). Arrows indicate model nesting, with the more complex model placed higher in the figure. Labels on the arrows indicate the results of nested hypothesis tests done individually for each participant.

We can summarize the model comparison tests as follows. First, in every case in which the more complex model of the pair adds squared perturbations as a predictor (3 model comparisons), the model comparison supports the addition of parameters for 6 out of 7 subjects. Second, for any 1-back model that includes predictions based on squared perturbations, model comparisons justify the addition of an exponential weighting of past trials for 6 out of 7 subjects (there are 2 such model comparisons). Finally, the evidence is somewhat weaker for the usefulness of including nonsquared perturbations for prediction. Model comparisons that add in these regressors are significant for one or no subjects for the 1-back models (there are 2 such model comparisons). But, adding in an exponential weighting of nonsquared regressors is significant for 3 or 4 out of 7 subjects (there are 2 such model comparisons). Thus, combining all of these observations, the evidence for Model 2 (Exponential variance only) is strongly supported by the data, indicating that participants base their aimpoints on an estimate of perturbation variance based on an exponentially weighted average of previously experienced squared perturbations. But, there is some evidence for a response to an exponentially weighted average of past perturbations. We should note, however, that Model 1 (Exponential mean and variance), which also includes perturbations for prediction, explains very little additional variance as compared to Model 2 for most subjects; in the median across subjects, the variance accounted for by Model 1 is only a factor of 1.173 larger than that accounted for by Model 2.

How does Model 2, which uses only squared perturbations, compare to Model 3 (Exponential mean only), which uses only raw perturbations as regressors? Although the relative fits of these two models to the data cannot be tested using classical methods, since they are not nested, the two models do contain the same number of free parameters so their raw goodness of fit (e.g., in terms of variance accounted for) can be fairly compared. Excluding subject AI, for whom neither model explains an appreciable fraction of the remaining variance, for five of the subjects, Model 2 fares much better. For all 6 subjects other than AI, the fit of Model 2 is preferred in terms of log likelihood (equivalent to an AIC or BIC calculation, since the numbers of parameters are identical). For four subjects, the ratio of remaining variance accounted for (Model 3 relative to Model 2) ranges from .03–.08. However, for two subjects (JF and NGC), Model 3 explains nearly as much remaining variance as Model 2 (ratios of .69 and .67, respectively). Thus, for these two subjects especially, a series of perturbations away from the penalty resulted in responses closer to the penalty in subsequent trials (and vice versa) in addition to the predicted response to large (squared perturbations) driving responses away from the penalty.

The models involving responses to the mean perturbation use a coordinate system for both the perturbations and responses in which positive values are for perturbations or movement endpoints shifted away from the penalty. In the motor-adaptation literature, one typical scenario is to study adaptation to a particular fixed perturbation of all movements (say, 3 cm rightward), regardless of movement direction or endpoint. We have also performed model comparisons on our data of this sort, looking for leftward changes of endpoint in response to recent rightward perturbations in the models involving response to mean perturbation. Model comparisons that add in an exponential weighting of nonsquared perturbations have far less support, showing significant results for only 2 out of 7 subjects (compared to 3 or 4 subjects as noted above) and for this coding of perturbation, the ratio of variance accounted for by Model 1 compared to Model 2 is only 1.039. Thus, we have no evidence for response to the mean perturbation coded relative to world (rather than target-penalty) coordinates.

Figure 9 compares the lagged regression results from Figure 7 with the corresponding parametric model that exponentially weights previously experienced squared perturbations (Model 2). Figure 9A shows the weights on the 8 previously experienced squared perturbations from the lagged regression (solid lines) and the weights based on the exponential fits of Model 2 (dashed lines) separately for each subject. The correspondence is reasonable for the subjects with the largest weights (note that the ordinate scales vary across subjects). For the others, the correspondence seems weaker. The reason for this can be seen more clearly in a scatterplot of the weights fit by both techniques (Fig. 9B). For several subjects, the weights from the lagged regression vary considerably compared to those huddled just above zero from the exponential fit of Model 2. The reason is that the best-fit time constants (τ_s ) were often large (ranging from 1.1 to 112 trials), whereas the lagged regression was constrained to explain the data using only the 8 most recently experienced perturbations.

In summary, we have demonstrated that humans change the movement plan for a reach in response to experimenter-imposed changes in task-related variance in movement under risk. In this task with explicit perturbation of reinforced movement outcome, participants’ strategies appear to be suboptimal, and vary substantially over participants. Nevertheless, almost all participants responded to changes in the variance of the perturbation, shifting their aimpoint further away from the penalty region when perturbation variance was increased. However, participants varied substantially in both the magnitude of response to changes in movement outcome variability as well as the time constant of the exponential average of past squared perturbations that controlled that change in aimpoint. Some subjects also varied strategy in response to the mean perturbation, but this effect was, for most subjects, far smaller.

Discussion

This experiment aimed at exploring how humans dynamically estimate and respond to variability in the outcome of movement under risk. Participants performed rapid reaches at a target while attempting to avoid a neighboring penalty region. The experimenter-imposed variability was much larger than motor variability, was repeatedly changed, and was visible to participants because the actual and perturbed reach endpoints were displayed simultaneously. Most participants responded to increased movement outcome uncertainty by aiming further away from the penalty region. We characterized the trial-by-trial dynamics of this adjustment, and distinguished it from other potentially confounding adjustments related to trial-by-trial tracking of and compensation for the mean perturbation.

Descriptively, our data appear to be well characterized by a model in which subjects track variance by an exponentially-weighted average over past squared perturbations. This is a mechanistically plausible model with obvious analogies to well studied neural mechanisms (e.g., Montague et al., 1996). Unlike ideal-observer Bayesian estimators, which for nontrivial change processes can typically be solved only numerically (e.g., Behrens et al., 2007), such a weighting is easy to compute online. In particular, as has been pointed out in studies of the dopaminergic system (Bayer and Glimcher, 2005), an exponential weighting results from maintaining only a running average over observations (in this case, squared perturbations), and at each trial adjusting this by a delta rule to reduce the difference between the obtained squared perturbation and the current estimate: in effect, the prediction error for the (squared) prediction error. In reinforcement learning models, the same rule for mean-tracking (i.e., the prediction error rule for learning mean, non-squared payoffs) is the basis for the familiar Rescorla-Wagner (1972) and temporal-difference learning (e.g., Montague et al., 1996; Sutton and Barto, 1998) models.

Accordingly, in studies of discrete decision tasks for reward, a result analogous to Figure 7 for the lagged (not squared) rewards has repeatedly been reported, and has there been interpreted as evidence for such a learning rule (Bayer and Glimcher, 2005; Corrado et al., 2005; Lau and Glimcher, 2005). The suggestion that variances might also be estimated by a similar running-average rule of the squared errors has roots as far back as the model of Pearce and Hall (1980), at least when re-interpreted in statistical terms (Sutton, 1992; Dayan and Long, 1998; Dayan et al., 2000; Courville et al., 2006; Preuschoff and Bossaerts, 2007), and neural correlates for variance estimates, errors in them, or other related quantities have also been reported (Preuschoff et al., 2006; Behrens et al., 2007; Preuschoff et al., 2008; Roesch et al., 2010; Li et al., 2011). In particular, Preuschoff et al. (2008) report correlates in human insula for a sequential “risk prediction error” generalizing the one suggested here. The present results go some way toward filling in the previously somewhat thin behavioral support for this type of hypothesized variance-tracking mechanism. Because in reinforcement learning tasks, the uncertainty affects behavior only indirectly, the timecourse of variance estimation has not, to our knowledge, previously been directly estimated or visualized as a function of lagged observations across trials in the way reported here. Of course, to verify this suggestive relationship, it remains to examine behavior like in the present task together with neural measurements or manipulations. One important difference, which may be relevant to the underlying neural mechanisms, is that the neural work discussed above concerns variance in reward amounts, rather than movement endpoints, as in the current experiment. In the reward setting, it has even been suggested (Roesch et al., 2012) that the prediction error for reward carried by dopamine drives the variance tracking as well (e.g., it is somehow squared in a downstream plasticity rule); such a mechanism is unlikely to apply to variances in quantities other than reward.

A related point is that whereas the delta rule for mean tracking has a well understood relationship with an ideal-observer model (in particular, it arises asymptotically in the Kalman filter), it remains to be understood the extent to which similar weighted averaging rules approximate the variance estimates that would arise for Bayesian variance estimation, and if so, for what change process. However, one hallmark of exact Bayesian change tracking across many change processes (DeWeese and Zador, 1998), but which does not hold in our approximate model, is that it is much easier to detect an increase as compared to a decrease in variability. This is because of the likelihood function relating variance to samples: A single outlier can be strong evidence for an increase in variance, whereas in equivalent circumstances a near-mean observation (or even a sequence of them) is not symmetrically strong evidence that variance has decreased. Thus, since in the current experiment, movement outcome variability can suddenly increase or decrease within a session, if participants are engaging in Bayesian variance tracking, one might expect a shorter time constant for adaptation of reach strategy to increases in variance than to decreases. We have looked for and failed to find this in the present data, although the variance trajectories we used were not designed for this analysis.

In previous work, we have often demonstrated optimal behavior in reaching tasks similar to this one, indicating that humans can take into account their own movement uncertainty in planning reaches under risk (Trommershäuser et al., 2003a, b), even when that uncertainty is altered surreptitiously by the experimenter (Trommershäuser et al., 2005; Hudson et al., 2010). And, an estimate of perceptual and motor uncertainty is used in a manner reasonably consistent with predictions of a Kalman filter in adapting to average error in motor tasks (Baddeley et al., 2003; Burge et al., 2008).

In the current experiment, although we have not computed an ideal-performance model for our experimental conditions, the inter-subject variability makes it clear that performance is not near-optimal for all participants. Our results indicate that optimal performance is mostly achieved in reaching-under-risk experiments in which the conditions are reasonably natural (Trommershäuser et al., 2003a, b; Trommershäuser et al., 2005; Hudson et al., 2010). When the task is slow and deliberative (Landy et al., 2007) or the feedback conditions involve an obviously artificial perturbation as they do here, performance becomes suboptimal and large inter-subject differences arise. We also note that optimally tracking a changing quantity, and then dynamically responding optimally with respect to these estimates trial-by-trial, is a qualitatively different and arguably more difficult criterion than making optimal decisions in the steady state. Nevertheless, what is clear from our analysis is that humans can and do use a dynamic estimate of current uncertainty, based on recently experienced errors, to plan reaches under risk.