Digital morphometry of rat cerebellar climbing fibers reveals distinct branch and bouton types

Abstract

Cerebellar climbing fibers provide powerful excitatory input to Purkinje cells, which represent the sole output of the cerebellar cortex. Recent discoveries suggest that climbing fibers have information-rich signaling properties important for cerebellar function, beyond eliciting the well-known all-or-none Purkinje cell complex spike. Climbing fiber morphology has not been quantitatively analyzed at the same level of detail as their biophysical properties. Because morphology can greatly influence function, including the capacity for information processing, it is important to understand climbing fiber branching structure in detail, as well as its variability across and within arbors. We have digitally reconstructed 68 rat climbing fibers labeled using biotinylated dextran amine (BDA) injected into the inferior olive and comprehensively quantified their morphology. Climbing fiber structure was considerably diverse even within the same anatomical regions. Distinctly identifiable primary, tendril, and distal branches could be operationally differentiated by the relative size of the subtrees at their initial bifurcations. Additionally, primary branches were more directed toward the cortical surface and had fewer and less pronounced synaptic boutons, suggesting they prioritize efficient and reliable signal propagation. Tendril and distal branches were spatially segregated and bouton dense, indicating specialization in signal transmission. Furthermore, climbing fibers systematically targeted molecular layer interneuron cell bodies, especially at terminal boutons, potentially instantiating feed-forward inhibition on Purkinje cells. This study offers the most detailed and comprehensive characterization of climbing fiber morphology to date. The reconstruction files and metadata are publicly distributed at NeuroMorpho.Org.

Introduction

Climbing fibers (CFs), the axon terminals of inferior olivary neurons, arborize in the molecular layer of the cerebellar cortex, where they each wrap around a single Purkinje cell (PC). CFs exert powerful excitation onto PCs, the sole output of the cerebellar cortex. Moreover, they can evoke plasticity in parallel fiber synapses (Ito et al., 1982), the only other excitatory input to PCs. CFs can therefore influence all signals downstream from the cerebellar cortex.

The role of CFs in cerebellar function is intensely debated. Recent experiments revealed that CF signal variation carries information, beyond all-or-none signaling, that conveys timing and provides a sophisticated mechanism for plasticity (Maruta et al., 2007; Mathy et al., 2009). CF morphology provides rich empirical evidence to be analyzed across populations as well as branch-by-branch within the individual tree. Size and branching complexity distinguish neuron types and often reflect functional adaptations. Axonal branch topology and bouton distributions define synaptic connectivity and affect spike propagation (Manor et al., 1991; Raastad and Shepherd, 2003; Sasaki et al., 2012).

Previous quantification of CF morphology has been limited, as either CFs were not digitally reconstructed (Sugihara et al., 1999; Nishiyama et al., 2007; Cesa et al., 2011) or primarily served as comparative controls to experimental manipulation (Rossi et al., 1993; Bravin et al., 1999). CFs within the lobule sulcus extend less toward the cortical surface than CFs in the bank or gyrus (Nishiyama and Linden, 2004), but no other morphologically distinct CF subtypes are known. In contrast, there are regional differences in compartmentalization (Sugihara et al., 2001) and molecular expression (Hawkes and Leclerc, 1987; Sawada et al., 2008). CFs also consist of recognizably different branch types, including thick primary and beaded-thread-like tendril branches (Cajal, 1909–1911; Sugihara et al., 1999). These branches may be functionally distinct, but their morphologies have yet to be quantitatively differentiated.

Molecular layer interneurons play an important role in cerebellar circuit dynamics. CFs can evoke long-term depression in interneurons, influencing PC inhibition (Mittmann and Häusser, 2007). Additionally, interneurons can modify CF-induced calcium dynamics in PCs (Callaway et al., 1995), providing a potential mechanism for dendritic compartmentalization of the CF signal. CFs are also believed to contact interneuron somata (Scheibel and Scheibel, 1954; Palay and Chan-Palay, 1974; Sugihara et al., 1999), but this aspect has not yet been quantified.

Here we have digitally reconstructed 68 rat CFs labeled with biotinylated dextran amine to fully characterize their morphology at the tree, branch, and bouton levels. We demonstrate substantial diversity that cannot be attributed to differences across anatomical regions or to distinct CF subclasses. Moreover, we introduce a simple morphometric definition that quantitatively distinguishes different branch types including primary and tendril, revealing their distinct spatial patterns. Furthermore, we report significant differences in the density, structure, and distribution of terminal and en passant boutons across CFs and branch types. Finally, we show that CFs overlap with interneuron somata beyond chance expectation, suggesting targeted circuit formation. Altogether, these results provide a comprehensive structural foundation to understand CF function.

Materials and Methods

Histological Procedures

Surgical and labeling procedures were described previously (Sugihara et al., 1999; 2000). The experimental protocols were approved by the Institutional Animal Care and Use Committee of Tokyo Medical and Dental University. A 5 month old Long-Evans male rat weighing 320 g was anesthetized with an intraperitoneal injection of ketamine (42 mg) and xylazine (2.5 mg) and placed in a stereotaxic apparatus with the head 45° nose-down. The foramen magnum was opened, and the inferior olive was approached with glass injection pipette from the dorsal surface of the caudal medulla. Biotinylated dextran amine (BDA: catalog #D-1956; 10,000 MW; Molecular Probes, Eugene, OR) was dissolved in saline at a concentration of 10%. A glass micropipette (tip diameter, 4 µm) filled with this solution was inserted into the right inferior olive, and pressure injections (0.05 µl) were made in three points. The climbing fibers (CFs) described in this study were labeled by an injection centered in the medial area of the caudal part of the medial accessory olive (subnucleus c: Sugihara and Shinoda, 2004).

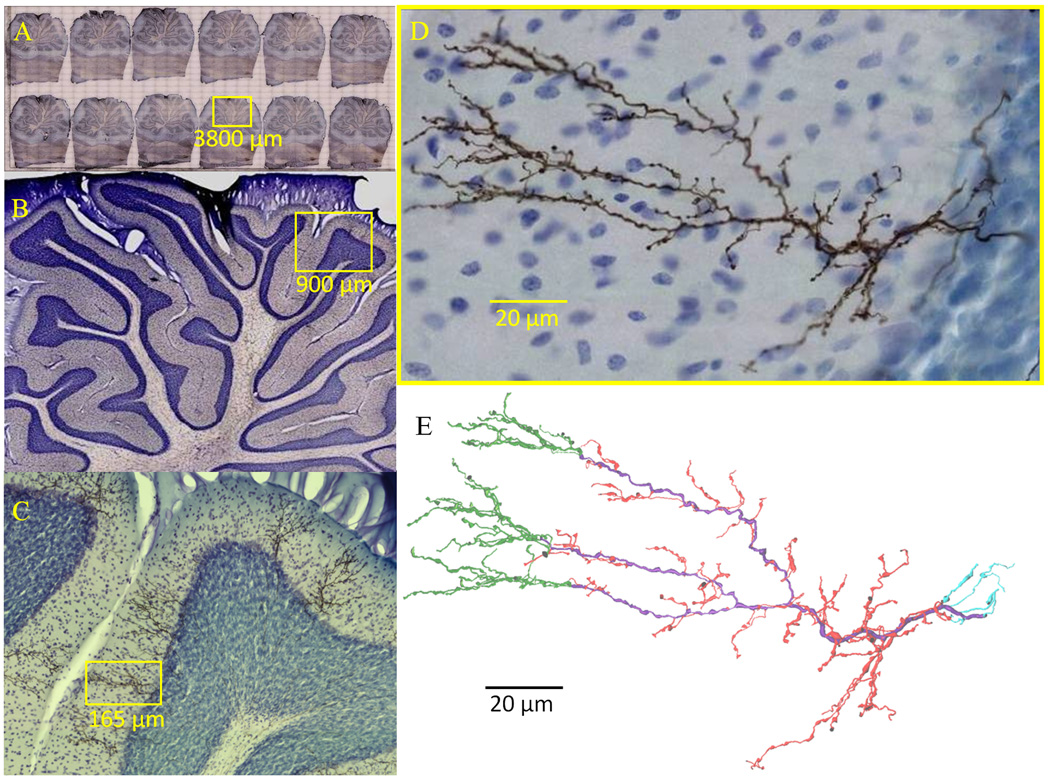
After a survival period of 8 days, the animal was deeply anesthetized with ketamine (150 mg/kg) and xylazine (12 mg/kg), and perfused through the ascending aorta. Chilled perfusate (400 ml, 4°C) containing 0.8% NaCl, 0.8% sucrose, and 0.4% glucose in 0.05 M phosphate buffer, pH 7.4, was followed by cold fixative (200 ml, 4°C) containing 5% paraformaldehyde, 1% picric acid, 0.23% NaOH, and 4% sucrose in 0.05 M sodium phosphate buffer (pH 7.4, ~4°C, ~200 ml) delivered over 30 min. The cerebellum and medulla oblongata were dissected and kept in the same fixative overnight at 4°C, then in 30% sucrose plus phosphate buffer saline (PBS: 0.01 M, pH 7.4), for 2 days. The brain was embedded in 10% gelatin containing 20% sucrose plus PBS at 31°C. The gelatin block was hardened in the fixative to which 30% sucrose was added for two days (4°C). Parasagittal sections of 50 µm thickness were then cut with a freezing microtome. Serial sections were collected in multicellular containers with PBS, incubated with biotinylated HRP-avidin complex (50 µl in 10 ml PBS plus 0.15 % Triton-X 100: Elite ABC kit KT-6100, Vector Laboratories, Burlingame, CA) for 48 hours. The sections were then rinsed in Tris buffer (50 mM, pH 7.4) and incubated with cobalt acetate (0.5 %) dissolved in Tris buffer for 10 min. Sections were rinsed with Tris buffer for 1 h and then with PBS for 15 min. BDA was then visualized by incubating the sections for 60 minutes in a solution containing diaminobenzidine (0.5 mg/ml), glucose oxidase (Itoh et al., 1979; 0.01 mg/ml; G-6125, Sigma-Aldrich, Saint Louis, MO), ammonium chloride (4 mg/ml), and beta-D(+)-glucose (1 mg/ml) in PBS followed by PBS washes. After counterstaining with thionine, which non-selectively stains chromatin in cell bodies, the sections were mounted on chrome alum-gelatinized slides, dried overnight, and coverslipped with Permount. Each of the 12 sections contains 6 to 9 completely labeled CFs all within lobules 6 and 7. Figure 1A–D show representative histological material. The sampled volume encompasses ~15% of the vermis or 6% of the total cerebellar cortex.

Figure 1.

Climbing fiber (CF) histology. (A–D) Rat cerebellar climbing fibers anterogradely labeled with biotinylated dextran amine. Yellow boxes indicate regions magnified in subsequent panel. Somata are counterstained with thionine (blue). E. CF digital reconstruction and branch types: primary (purple), tendril (red), retrograde (cyan), and distal (green). Radius thickened 1.5× for clearer visualization.

Image Acquisition and Digital Reconstruction

The approximately planar span and sagittal orientation of adult CFs increases the probability of finding complete trees entirely confined within an individual slice. Only and all CFs with clear and complete labeling within a single tissue section were selected for reconstruction. Every selected CF was visually checked for structural truncation, including searching adjacent slices to verify that no branches were lost due to sectioning. Each CF was captured as a stack of images under Köhler illumination using an Olympus AX70 microscope equipped with a motorized stage and Optronics Microfire mounted digital camera. Images were acquired every 0.33 µm in depth with a 100× (NA = 1.3) oil-immersion objective and an additional 200% electronic zoom factor. Image stacks were blindly deconvolved with AutoDeblur (AutoQuant Imaging, Watervliet, NY) and CFs were digitally traced with Neurolucida (MBF Bioscience, Williston, VT). Variations of this method were also tested to seek an optimal procedure. A small numbers of CFs were reconstructed with Neuromantic (Myatt et al., 2012; http://www.reading.ac.uk/neuromantic) or with Neuron_Morpho (Brown et al., 2005) or else traced directly from the slide through the camera live feed rather than from the image stack. Similar to previous findings (Brown et al., 2005; Anderson et al., 2010), each of these alternatives produced equivalent reconstructions, so all CFs were pooled together in a collective sample (N=68).

After reconstruction, CFs were semi-automatically checked for tracing errors such as 0 µm diameter points (Halavi et al., 2008; http://neuromorpho.org/neuroMorpho/StdSwc1.21.jsp). Verified errors were then fixed prior to morphological analysis. A sample of CF reconstructions (N=35) were visually inspected for accuracy by carefully comparing and overlaying the digital morphology with the live microscope images. Resultant modifications were negligible and did not alter results, suggesting high precision levels. Digital reconstructions consisted of ASCII files representing each tracing point (~2500 per CF) with an identity number, a “type” tag (axon, en passant bouton, etc., see below), the X, Y, and Z position, local radius, and the identity of the preceding tracing point (“parent”) in the path to the CF origin (Ascoli et al., 2001). Every point can be viewed as the end of a cylinder or truncated cone, called a “compartment” (see also diademchallenge.org/faq.html). Each compartment has a unique parent (except the origin, which has none), and can have 0, 1, or 2 daughters, respectively corresponding to a terminal tip, continuation of the branch, or bifurcation. A series of compartments between two bifurcations or between a bifurcation and a termination is called a “branch” (internal or terminal, respectively). Fig. 1E shows a representative complete reconstruction, and Fig. 2 displays all reconstructed CFs.

Figure 2.

Collage of all 68 CF digital reconstructions. Radius thickened 1.5× for clearer visualization.

In order to correct for tissue shrinkage, each of the twelve slices (nominally sectioned at 50 µm) was sampled in at least three locations for actual mounted thickness, yielding a measure of 14±1 µm across the entire sample. All reconstruction z values were increased by the same constant factor of 3.5 (≈50/14), since variability was similar within and between sections.

Bouton and Interneuron Analysis

Boutons were identified based on large and abrupt diameter increase as well as increased intensity and range-of-focus relative to adjacent regions along the branch (Shepherd et al., 2002). Both a conservative and a liberal choice of thresholds for diameter and intensity change were tried. The former method resulted in counting 77±9.0% of the boutons labeled in the latter. However, all relative differences detected by our analyses were preserved, and all conclusions reached in this study remain consistent across the two methods. The liberal criterion resulted in a total bouton count similar to past studies (Rossi et al., 1993; Sugihara et al., 1999), and is presented in the Results.

We define interbouton distance (IBD) as the axonal length from a bouton to the previous bouton toward the CF origin along the branch path, similar to previous measures of dendritic spine distances (Konur et al., 2003). Distances between boutons that crossed branch types (e.g. primary and tendril, see below) were not included in the results presented here. However, we verified that including these distances in the analysis did not alter any of the conclusions. Two interbouton distances were measured: between bouton centers (IBD_center) and from one bouton end to the next bouton beginning (IBD_edge). To test whether boutons were regularly spaced, two surrogate data sets were generated by randomly shuffling the bouton positions along the tree. In the first surrogate data set, boutons were randomized as points (i.e., without regard to bouton length), and IBD_center was measured. In the second, randomization was performed taking into account bouton lengths so as to avoid their spatial overlap, and both IBD_center and IBD_edge were used as interbouton distances.

Boutons overlapping with somata of molecular layer interneurons in the image plane within reciprocal focal depth of 1 µm were counted as potential contacts. The 1 µm threshold accounts for light diffraction as well as extrasynaptic glutamate transmission (Szapiro and Barbour, 2007; Okubo and Iino, 2011). To provide a control for potential contacts with interneuron cell bodies, boutons were virtually detached from the CF tree and their positions randomly shuffled in the molecular layer within the 3D bounding box of the given CF, without allowing multiple boutons to spatially overlap. Retrograde boutons, those located within the Purkinje cell layer (Scheibel and Scheibel, 1954; Palay and Chan-Palay 1974; Sugihara et al., 1999), were accordingly omitted from this particular analysis.

Synaptic contact of CF boutons to NG2-expressing cells has been reported (Lin et al., 2005). In the present study, we cannot distinguish CF boutons that make synaptic contact to NG2-expressing cells because these glial components were not specifically labeled in our preparation. Therefore, some of the cells that we counted as molecular layer interneurons may actually consist of NG2-expressing cells. However, the fraction of counted cell bodies corresponding to glial cells is likely very small, because NG2-expressing cells are much less numerous than molecular layer interneurons (Fig. S1 of Lin et al., 2005), and CF boutons make contact onto glial processes, not cell bodies (Lin et al., 2005).

Comparison of CFs to Other Neuron Types

Several digital reconstructions of neuronal morphology were downloaded from NeuroMorpho.Org (version 5.3) for comparative analyses. All data sets from rodent brain were considered potentially relevant if they consisted of five or more cells with substantial axon tracing. A total of 218 axons over 11 data sets met these criteria: 51 rat temporal sulcus neurons (Helmstaeder et al., 2009); 7 rat prefrontal cortex neurogliaform cells (Povysheva et al., 2007); 54 basket, 30 Martinotti, 15 bitufted, 6 bipolar, and 5 double bouquet cells, all from rat somatosensory cortex (Wang et al., 2002); 6 rat somatosensory spiny stellate cells (Staiger et al., 2004); 13 rat hippocampal dentate gyrus interneurons (Mott et al., 1997); 13 rat hippocampal CA3b interneurons (Ascoli et al., 2009); and 18 mouse visual cortical cells (Dumitriu et al., 2007). For CF comparison, the average of each morphometric was first computed within every data set, and the mean and standard deviation of these averages across data sets (N=11) were used for a one-sample t test against the CF average of the same morphometric.

The dendritic trees of ten Purkinje cell from four studies were also downloaded from NeuroMorpho.Org (Rapp et al., 1994; Roth and Häusser, 2001; Vetter et al., 2001; Martone et al., 2003). In these reconstructions, dendrites were considered CF targets if their diameter was 1.7 times larger than the mean, consistent with anatomical measurements distinguishing smooth from spiny Purkinje dendrites (Larramendi and Victor, 1967). With this criterion, the height extent of ‘smooth’ (CF-targeted) dendrites in the 10 Purkinje cells was 84±11% of the total dendritic tree, similar to the experimentally reported value of 86% (Ichikawa et al., 2002).

Statistical Analysis and Glossary of Morphometrics

Morphometric analysis was performed using the freeware program L-Measure (Scorcioni et al., 2008; http://krasnow1.gmu.edu/cn3), the commercial Neurolucida Explorer (MBF Bioscience, Williston, VT), and Microsoft Excel 2007. Excel Solver (2007) was used for linear discriminant analysis of bifurcation types, performing 1000 iterations for parameter optimization. For analysis consistency, the origin of each CF was always considered as the first bifurcation. Unless stated otherwise, values are reported as mean ± standard deviation and 2-tailed t test was performed for significance (1- or 2-sample, paired or unpaired, depending on analysis). The conventional power (p<0.05) was employed after correcting for multiple comparisons as appropriate, namely with Bonferroni’s method for sets of independent parameters (Bonferroni, 1936) and by false discovery rate for partially interdependent measures (Benjamini and Hochberg, 1995). Kolmogorov-Smirnov test was used to test whether data could be rejected as being normally distributed. All linear correlation values (R) were measured using Pearson’s correlation coefficient. To test if CF subtypes could be identified by combinations of morphological properties, we used principal component and cluster analyses, following previously established protocols for neuron morphological classification (Tsiola et al., 2003; McGarry et al., 2010). Silhouette width (Rousseeuw, 1987) was used to quantify degree of clustering. Significant clustering was based on comparison to randomly shuffled principal components (N=5 repeated trials, 2-tailed Wilcoxon signed-rank test).

A proportion of reconstructed CFs was randomly sampled to measure the number of bouton/interneuron soma overlaps and interneuron density across the molecular layer, as well as the proportion of retrograde boutons overlapping with Purkinje somata. Running mean and standard deviation were logged as sample size increased. The sample size was deemed sufficient when three consecutive means and standard deviations were within 5% of each other.

The morphological measures are defined as the following:

• Branch Order: Number of bifurcations between a given branch and the CF origin.

• Branch Path Length: Sum of all compartment lengths that make up a branch, where a branch is defined as the region between two bifurcations or a bifurcation and a termination. The sum of all branch path lengths for a CF equals its tree length.

• Branch Path Tortuosity: Difference between Euclidean and path distance (see below) from the beginning to the end of a branch, normalized by path distance (1 – Euclidean Distance / Path Distance).

• Branching Angle: Angle between a bifurcation and the end points of its daughter branches.

• Caulescence: Prominence of the main path, i.e. the path across bifurcations from the CF origin to a termination that always leads to the greatest length at each bifurcation (Brown et al., 2008). Caulescence is measured by ∑ |l − r| / ∑ (l + r), where l and r are the total lengths of daughter subtrees from their mutual bifurcation to their terminations, and the sum is taken over all bifurcations of the main path.

• Daughter Diameter Ratio: Ratio of the diameter of the larger to the smaller daughter branch originating from the same bifurcation. Diameter is measured at the first compartment of each branch.

• Daughter / Parent Diameter Ratio: Ratio of the diameter of the larger daughter to its parent branch. Diameter is measured at the first compartment of the daughter and the last compartment of the parent branch.

• Fractal dimension: Space-filling ability of the tree, also known as Hausdorff dimension, measured with the box-counting method (Samsonovich and Ascoli, 2003). The returned value is between 1 and 3, where 1 means the structure does not fill space more than a straight line, and 3 means it fills space as well as a three-dimensional solid.

• Height, Width, and Depth: Euclidean dimensions containing 95% of the CF tree along its three principal components ordered from largest to smallest, respectively.

• Interneuron Density: Number of interneuron somata per µm³ scaled by a convenience factor of 1000.

• Path Distance: Distance along the path from the CF origin. This metric is termed ‘distance’ to differentiate it from size-based metrics such as tree length and branch path length.

• Polar Direction: Weighted average of the arbor orientation. The sine of each of 18 twenty-degree bins is multiplied by the proportion of CF length it contains, then averaged across bins.

• Polar Magnitude: Weighted average of the orientation absolute extent. The cosine of each of the 18 bins is multiplied by the proportion of CF length it contains, then averaged across bins.

• Roundness: Ratio between the surface area of the soma and the spherical area corresponding to its maximum diameter. The returned value is between 0 and 1, where 1 corresponds to perfectly circular cross sections.

• Terminal Degree: Number of terminal tips in a subtree.

• Tree Length, Surface Area, and Volume: The summed lengths, surface areas, and volumes over all compartments for the entire tree.

• Vertex Ratio: Ratio between the numbers of bifurcations with two versus one immediately terminating daughter branches. Values above 1 or below 0.5 are characteristic of symmetric or asymmetric trees, respectively. Intermediate values are indicative of random trees and can shed light on the growth process (Berry and Flinn, 1984).

• Wiring Density: Ratio between tree length and total invaded volume (the product of Height, Width, and Depth), scaled by a convenience factor of 1000.

Availability of Additional Histological Material

This work opens the possibility for many future animal model or developmental comparisons, both by providing necessary baseline data (which are also useful to generate quantitative hypotheses) and by elucidating the morphologically relevant features (thus aiding future research designs). We already have available preparations of similarly labeled CFs in two animal models at the moment: 3-aminopyridine-treated rats (denervation-reinnervation model), whose CFs show significant growth and sprouting (Aoki and Sugihara, 2012), and X-ray-irradiated rats (Sugihara et al., 2000). While digitally reconstructing these morphologies is beyond the scope of the present report, we are eager to send the histological slides to anyone willing to analyze them upon request.

Results

Climbing fiber morphometry reveals high wiring density, branching asymmetry, and diversity

The height, width and depth of climbing fibers (CFs) were small given the number of branches and length (Table 1). This was captured by their considerable wiring density, on average 26 times higher than for other axon types (see Materials and Methods), suggesting that each individual CF is tightly packed within its target field. In contrast, fractal dimension, which might be expected to increase with wiring density as more space is filled, was similar to other axon types despite their lower wiring density. Thus, CFs are not spatially spread out, but instead cluster heterogeneously within the volume they invade.

Table 1.

Climbing fiber tree (top) and branch (bottom) morphological properties.

Tree Level Metrics (N=68)	Mean±SD (Range)	CV
Height (µm)	155±35 (90–242)	0.23
Width (µm)	79±26 (56–164)	0.33
Depth (µm)	12±7.3 (4.5–50)	0.60
Number of Branches	328±138 (117–675)	0.42
Tree Length (µm)	2318±680 (1104–4149)	0.29
Tree Surface Area (µm2)	3737±1430 (1154–9263)	0.38
Tree Volume (µm3)	703±456 (124–2597)	0.65
Wiring Density (µm−2)	25±21 (3.1–103)	0.82
Fractal Dimension	1.23±0.06 (1.09–1.43)	0.048
Max Branch Order	37±11 (15–65)	0.31
Vertex Ratio	0.48±0.12 (0.29–1.04)	0.26
Caulescence	0.86±0.05 (0.59–0.94)	0.063
Branch Level Metrics (N >10000)	Mean±SD (Range 2.5– 97.5%)	CV
Branch Path Length (µm)	7.1±7.6 (0.51–28)	1.1
Branch Path Tortuosity	0.19±0.17 (0–0.59)	0.88
Branching Angle (°)	87±42 (13–165)	0.48
Daughter Diameter Ratio	1.9±1.1 (1.0–4.8)	0.57
Daughter / Parent Diameter Ratio	0.70±0.42 (0.21–1.7)	0.60

The vertex ratio revealed low branching symmetry resulting from a large proportion of CF bifurcations with a terminating branch stemming off a continuing tree rather than bifurcations splitting into two terminating branches or into two continuing subtrees. Indeed the CF average vertex ratio (Table 1) was significantly lower than for other axon types (0.65±0.11, p<0.001). Additionally, caulescence, measuring the prominence of the main path within the arbor (Brown et al., 2008), was significantly larger for CFs (Table 1) than for other axon types (0.61±0.10, p<10⁻⁴). Low vertex ratio and high caulescence provide quantitative measures that extend previous qualitative descriptions of CF as “primary” stalks giving rise to collateral “tendril” offshoots (Palay and Chan Palay, 1974; Sugihara et al., 1999).

The cerebellum is regarded as structurally modular, with a repeating microcircuit (Eccles et al., 1967; Ito, 1984) that performs common computational operations across regions (Raymond et al, 1996; Wolpert et al., 1998). Given the relationship between morphology and connectivity, and the one-to-one mapping between CFs and Purkinje cells, one might assume CF morphology to be stereotypical as well, simplistically reducing the CF role as a single large distributed synapse on the Purkinje cell (Llinás and Nicholson, 1976). On the contrary, the statistical variability of numerous metrics (Table 1) demonstrates considerable morphological diversity. Even measures with relatively smaller coefficients of variation (CVs) showed wide value ranges. To appreciate the potential biological implication of this observation, CFs can again be compared to other axon types (see Materials and Methods). Although other axons project to numerous cells and presumably have complex functional states in relation to their larger networks, their morphological variability was comparable or smaller than that of CFs in almost all morphological properties reported in Table 1 (not shown). CF variability was also similar to that of ten Purkinje cell dendrites, even if these were pooled from different rats, mice, and guinea pigs, while CFs were all from a single subject. The only morphometric with clearly smaller variability in CFs was caulescence, suggesting that CFs systematically exhibit a prominent main path.

Climbing fiber arbors have preferential orientation and bimodal distribution

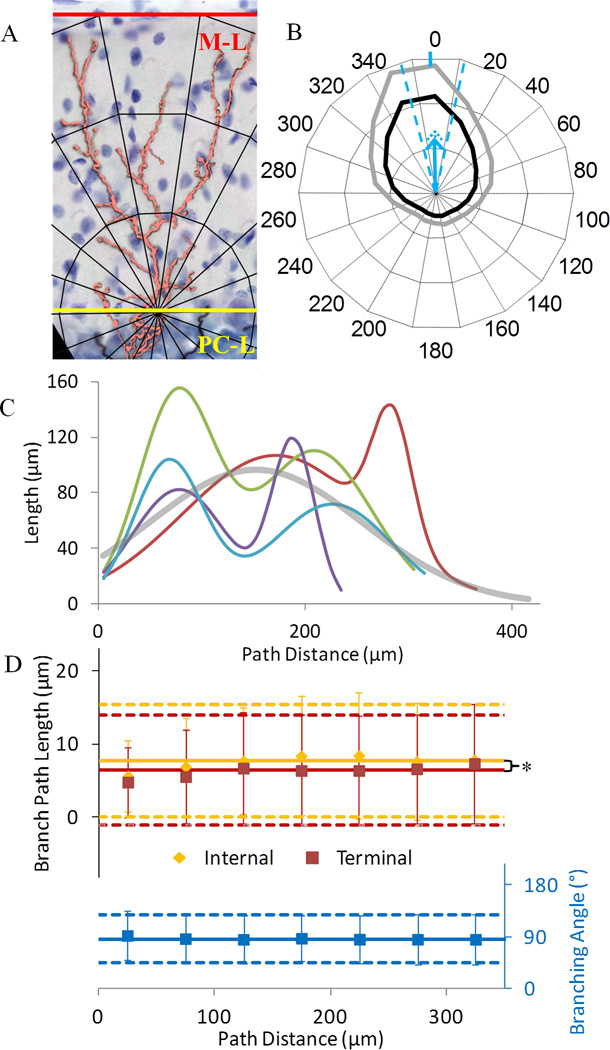
Morphometric distributions across tree location and distance relate to synaptic and growth patterns. The polar histogram of tree length indicates preferential CF growth toward the cortical surface (Fig. 3A,B). Polar direction (−2±14°) was not significantly different from perpendicular to the Purkinje cell layer, and was quite invariant given a maximum potential spread of 360°. Correspondingly, the polar magnitude (blue arrow in Fig. 3B) was significantly positive (0.37±0.09, p<10⁻⁴, one-sample t-test, N=68). For context, the minimum and maximum values of this measure are −1 (the whole tree exactly aligned away from the cortical surface) and 1 (all towards the cortical surface), with 0 being non-polar or symmetrically polar. Therefore, CFs are significantly polar. This contrasts with their absolute orientation, which was nearly isotropic due to pronounced cortical foliation (not shown).

Figure 3.

Morphometric distributions across distance. A. Representative CF orientation toward the cortical surface, through the molecular layer (M-L, red) and perpendicular to the Purkinje cell layer (PC-L, yellow). B. Polar histogram of the fraction of CF length in each angular bin. The inner circle represents uniform spatial distribution. The second and third concentric circles demark fractional lengths twice and three times the bin average, respectively. Black and gray lines are mean and mean plus standard deviation of fractional length across CFs. For example, length in the 0° bin is on average more than twice as large as in the 60° bin. The vertical blue tick on the outer circle near the 0° label and the blue dashed lines represent respectively mean and standard deviations of polar direction across CFs. The polar magnitude mean and standard deviation (blue and dotted arrows, respectively) are 0.37±0.09, where equal directionality across all bins would yield a value of 0 (at the circle center), and all length being within the 0° bin would yield a value of 1 (outermost concentric circle). C. Variable but consistently bimodal length distribution across path distance for four representative CFs (different colors). The average across all CFs (thick gray) is unimodal. D. Constant branch path length (N=22,254) and bifurcation angle (N=11,127) across path distance. Internal branches are significantly longer than terminal branches at path distances between 75 and 275 µm. Error bars are standard deviations. The number of branches ranges by bin from 207 to 2197. Solid and dashed lines represent grand mean and standard deviation, respectively.

Even though CFs were spatially directed, their length distribution across path distance towards the cortical surface was considerably heterogeneous and generally bimodal (Fig. 3C). To quantify the bimodal distribution, the length of each CF as a function of path distance was fitted by least square error with the sum of two Gaussians. The average coefficient of determination R² for the bimodal best fits was 0.77±0.09, indicating that a mix of two Gaussians on average explained nearly 80% of the dependence of CF length on path distance. The average path distances for the two modes were 109±40 and 257±43 µm (N = 68), respectively. This suggests location variability within each mode, but the large separation between modes confirmed CF bimodality overall. The first mode (closer to the origin) was wider (standard deviations of first and second modes respectively 62±26 and 43±20 µm, N=68) and contributed 54±24% of the Gaussian mix, where 50% would be equal mode proportions and 0% or 100% would indicate unimodality. This bimodal length distribution may relate to functionally and morphologically distinct subtrees within the same CF (see also ‘Morphological analysis of bifurcation and branch types’ and Fig. 5F below). Interestingly, the length distribution for all CFs averaged together (gray line in Fig. 3C) concealed individual CF bimodality, and the best fit for this overall distribution was unimodal.

Figure 5.

Operational definition and analysis of branch types. A. Representative examples of the three bifurcation types in primary stalks: splitting into two primary daughters (PPP), into one primary and one non-primary (PPN), and into two non-primary daughters (PNN). B. Optimal linear separators for bifurcation types (sample sizes: PPN, 763; PPP, 88; PNN, 155). Functions defining separators were as follows, where DVR is the daughter volume ratio, VP is the volumetric proportion, the ∩ symbol indicates AND Boolean logic, and y is the classification for bifurcation i: y_i= [(PPP = (VP_i > 0.31) ∩ (VP_i > −2.01 × DVR_i + 1.33); PNN = (VP_i < 0.31) ∩ (VP_i < −2.01 × DVR_i + 1.33); PPN = (DVR_i < 0.51) ∩ (−0.65 × DVR_i − 0.02 < VP_i < −2.01 × DVR_i + 1.3)]. C. Log-log frequency distributions of terminal degree (number of terminations) of non-primary subtrees stemming from PPN (red) and PNN (green) bifurcations. Arrows point to means ± standard deviations. D. All branch types differ in polarity relative to the vector from the CF origin to the primary tree center of mass (Y axis), whereas values of 1, 0, and −1 would respectively indicate directions parallel, orthogonal, and anti-parallel to the primary vector. The width of each wedge indicates standard deviation. R: retrograde; P: primary; T: tendril; D: distal. E. Relative branch type contributions to CF size. Error bars are standard deviations (N=68). F. Tendril and retrograde branches combined and distal branches largely underlie CF bimodality (cf. Fig. 3C). The branch type length distributions across path distance are compared to the two modes extracted from the whole trees (gray lines).

Branch path length did not change systematically across path distance (Fig. 3D top), with large and fairly constant variability. These characteristics applied similarly for individual CFs (not shown) and when all branches were pooled together across trees. Internal branches were generally longer than terminal branches across path distance. The large coefficient of variation (CV) for scalar branch path length (1.0 and 1.2 for internal and terminal, respectively, Table 1) suggests that branches are emitted irregularly. The distribution of branching angles (Fig. 3D bottom), and thus CF polarity, was also constant across distance, both in individual CFs (not shown) and at the population level. CF distributions of several other metrics (Table 1) were also analyzed as a function of path distance, both absolute and normalized by the maximum distance for each CF. As for branch path length and branching angle, the variability of these other metrics at different distances was equal to or greater than when pooling all branches together from the entire tree. Therefore, CF variability is not explained by systematic morphological differences across distance.

Climbing fiber morphology is largely independent of regional location

To check if CF morphology varied by anatomical location, we measured a comprehensive battery of (25) morphometrics from several pair-wise regional groups, namely right-left, medial-lateral, lobules 6–7, rostral-caudal within lobules, and sulcus-bank/gyrus (Fig. 4A). No significant differences were found for any comparison (four examples shown in Fig. 4B), except for CFs located in the sulcus, which had lower polar magnitude than those located in the bank or gyrus. This result quantitatively extends previous observations that CFs in the sulcus distributed their extent further away from the cortical surface compared to CFs along the bank or gyrus (Nishiyama and Linden, 2004). No other morphometrics differed between these two groups, including polar direction, which indicated direction of growth similarly perpendicular to the Purkinje cell layer (0±5° and −3±14° for sulcus and bank/gyrus, respectively). However, the small sample size for CFs in the sulcus warrants cautious interpretation. For all regions and morphometrics, CVs were generally as high as or higher than those provided in Table 1.

Figure 4.

Morphological comparison across anatomical subregions. A. Gray cerebellar surface renderings (modified from http://www.nesys.uio.no/Database/5-Precerebellar_atlas) with depictions of analyzed regions and corresponding CF grouping symbols. Left and right groups are divided at the vermal midline. Medial and lateral groups respectively include CFs less than or greater than 150 µm away from the vermal midline from either direction. B. Pair-wise comparisons of regional groups. No significant differences are found between regional groups except for lower polar magnitude of sulcus CFs than for bank/gyrus CFs. Error bars are standard deviations; gray shading signifies population standard deviation around the mean.

To test for distinct morphological subtypes other than by regional location, we analyzed the frequency distribution of all individual morphometrics. None appeared bi- or multi-modal (not shown), nor were they significantly different from Gaussian (Kolmogorov-Smirnov, 2-tailed). Principal component and cluster analyses were performed next to seek multivariate morphometric subgroups (Dumitriu et al., 2007). Clusters of the first six principal components (accounting for >95% of overall variance) were compared to five samples obtained by randomly shuffling principal component values across CFs. The actual data did not appear any more clustered than the shuffled controls, and their average silhouette width was not significantly different (0.13 vs. 0.13±0.02 respectively for actual vs. randomized data, N=5, p>0.9). Finally, no individual principal component could be rejected from being normally distributed across CFs (Kolmogorov-Smirnov, 2-tailed). Altogether these results suggest that this CF population, beyond one regional difference for a single morphological property, does not consist of morphologically-distinct subtypes. Instead, morphological diversity appears as an inherent CF property within and across regional groupings.

Morphological analysis of bifurcation and branch types

Two morphologically distinct branch types are readily recognized in CFs: “primary” (P) thick, relatively smooth, stalks; and “non-primary” (N) beaded threads with large, dense boutons separated by thin axonal segments (Palay and Chan-Palay, 1974; Sugihara et al. 1999). The CF origin crossing the Purkinje-molecular layer boundary is always a primary branch. Moreover, non-primary branches never give rise to primary daughters. Based on these descriptive observations, we devised an operational procedure to systematically identify and quantitatively define distinct CF branch types. Starting from the origin, we first differentiated primary bifurcations based on their daughters (see examples in Fig. 5A): bifurcations splitting into two P daughters (PPP); bifurcations splitting into one P and one N daughter (PPN); and bifurcations splitting into two N daughters (PNN). When either daughter type was ambiguous, we tagged bifurcations as ‘uncertain’ (252 out of 2651 total bifurcations, ~10%).

The ‘certain’ bifurcations displayed dramatic differences in two specific morphometrics, namely the volume proportion, or total volumetric fraction of the two stemming subtrees relative to the entire CF; and the daughter subtree volume ratio, which measures the volumetric imbalance between the two subtrees. Specifically, the volume proportion was much higher for PPP than PNN bifurcations (0.68±0.22 vs. 0.14±0.07, p<10⁻⁴), while the daughter volume ratio was much lower for PPN (0.06±0.09) than for either of the other two bifurcation types (PPP: 0.63±0.22, p<10⁻⁴; PNN: 0.50±0.24, p<10⁻⁴). Thus, the two subtrees of PPP bifurcations have similar tree volumes, and together constitute a substantial proportion of the total CF volume. The primary subtree of PPN bifurcations was substantially larger than the other, and their joint volume varies over a large range. The two subtrees of PNN bifurcations also had similar tree volumes, but their sum only amounted to a small proportion of the CF tree. Linear discriminant analysis demonstrated that these two characteristics almost perfectly separate the three bifurcation types, with less than 2% of incorrect assignments (Fig. 5B). Given the effectiveness of volumetric proportion and daughter volumetric ratio to operationally distinguish CF bifurcation (and thus branch) types, the ‘uncertain’ cases were assigned accordingly. All other morphometrics unrelated to those that differ by definition were similar for all tree bifurcation types, including branching angle (Fig. 3D).

Morphological comparisons of distinct branch types may reveal potential functional differences. First we compared the size of non-primary subtrees arising from distinct bifurcations. Non-primary subtrees stemming from PPN bifurcations had significantly fewer terminal tips (Fig. 5C) than those from PNN bifurcations (3.0±5.2 vs. 14±11, p<10⁻⁴), suggesting that they might constitute different types of subtrees. We therefore distinguished the subtrees that originate from PNN bifurcations, calling their branches ‘distal’ in light of the location along the CF tree. We call most non-primary subtrees of PPN bifurcations ‘tendril’, consistent with their previously described thinner, bouton dense branches (Scheibel and Scheibel, 1954; Palay and Chan-Palay, 1974; Sugihara et al., 1999). The low number of branches per tendril subtree suggests that the nets around P branches are typically composed of numerous small arbors. The remaining subtrees of PPN bifurcations extend branches back into the Purkinje cell layer, therefore potentially synapsing with Purkinje somata, and are referred to as ‘retrograde’. The same morphometrics separating PPN from PPP and PNN bifurcations also discriminated between PPN bifurcations giving rise to retrograde and tendril subtrees. Specifically, retrograde-stemming bifurcations (plotted as unfilled maroon squares in the upper left corner of Fig. 5B) had higher volume proportion (0.97±0.07 vs. 0.39±0.28, p<10⁻⁴) and lower daughter volume ratio (0.02±0.03 vs. 0.06±0.09, p<10⁻⁴) than tendril-stemming bifurcations.

Distinct branch types all dramatically differed in polarity, i.e. their direction of growth relative to the line from the CF origin to the center of mass of the primary tree (Fig. 5D). Primary branches were (expectedly) most aligned with the main axis of growth, while distal branches displayed a more moderate tendency to grow parallel to this direction. Tendril branches were nearly perpendicular, and retrograde fibers had a negative (anti-parallel) polarity. Pair-wise polarity differences between all branch types were highly significant (p<10⁻⁴). Tendril and distal branches were otherwise morphologically similar, especially compared to primary branches, e.g. in diameter (tendril, 0.42±0.28; distal, 0.41±0.25; primary, 0.71±0.39 µm) and branch path length (tendril, 6.5±7.2; distal, 7.1±7.8; primary, 8.7±8.2 µm). Retrograde branches were also similar to other non-primary branches except for having the longest branch path lengths (10.5±11.0 µm), which might relate to the demands of their synaptic target.

Tendril and distal branches made up the largest proportion of length, yet primary branches had similar volumetric extent due to their larger diameters (Fig. 5E). Tendril branches concentrated at a more proximal path distance from the origin than distal branches (Fig. 5F), largely explaining the bimodal distribution of CF length (cf. Fig. 3C). The mean tendril and distal path distances were not significantly different from the first and second CF modes, respectively (113±39 vs. 104±32 µm and 240±54 vs. 231±52 µm, respectively). The coefficients of variation for the respective distribution pairs were also not statistically different (0.65±0.55 and 0.53±0.19 for tendril and first mode; 0.21±0.16 and 0.23±0.20 for distal and second mode, respectively). Distal branches contributed a smaller proportion of total tree length mode than the second mode (35±10% vs. 46±24%, p<0.01) due to a moderately overlapping contribution of the tendril distribution to the second mode (Fig. 5F). Length proportions were not significantly different for tendril and the first mode (50±10% vs. 54±24%, respectively).

Climbing fiber bouton characterization

Boutons are the synaptic transmission sites. Therefore, characterizing their distributions and morphology is critical for understanding CF function. CFs had 268±65 boutons (N=68), similar to earlier reports (Rossi et al., 1993; Sugihara et al., 1999; see however Bravin et al., 1999). Bouton Euclidean length (2.34±1.15) and width (0.94±0.34) were also fully consistent with previous electron microscopy measures (Cesa et al., 2011). Tendril, retrograde, and distal bouton morphometrics were essentially equivalent and are jointly referred to as 'non-primary'. Primary branches had a lower volumetric proportion of boutons (p<10⁻⁴) despite their significantly larger bouton surface area (Table 2), due to their significantly smaller diameter ratio between boutons and adjacent interbouton segments (p<10⁻⁴). This suggests that primary branches have distinctive bouton properties compared to non-primary branches, possibly reflecting functional constraints (see Discussion).

Table 2.

Climbing fiber bouton morphological properties for entire tree (top) and individual boutons (bottom).

Tree Level N	Primary 68	Non- Primary 68
Number of Boutons	30±11	238±65
Terminal / En Passant Ratio	0	0.46±0.12
Bouton Volume Proportion (%)	57±9.3	68±7.3
Proportion of Terminations with Terminal Boutons (%)	n/a	48±12
Bouton Level N (EP) N (Term)	Primary 2040 0	Non- Primary 11154 5033
Bouton / Interbouton Diameter Ratio	1.5±0.56	2.0±0.72
En Passant Surface Area (µm2)	14±9.3	6.8±4.9
Terminal Surface Area (µm2)	n/a	5.5±4.1
En Passant Length (µm)	3.2±1.6	2.4 ±1.2
Terminal Length (µm)	n/a	1.9±1.0
En Passant Diameter (µm)	0.94±0.36	0.64 ±0.24
Terminal Diameter (µm)	n/a	0.68±0.28
En Passant Length / Diameter Ratio	4.4±2.0	4.7±2.2
Terminal Length / Diameter Ratio	n/a	3.8±2.4

Number and density of tendril and distal boutons were similar to each other and both significantly higher than other types (Fig. 6A). They are therefore the major signal transmitting branch types for their separate spatial domains. Retrograde boutons constituted 3.0% of the total count, a lower proportion than previously reported (Sugihara et al., 1999). However, this discrepancy only amounts to 1.8% of the total number of boutons per CF, suggesting general consistency with earlier data. Primary branches were significantly less bouton dense than non-primary branches (Fig. 6B). Moreover, longer CFs had lower non-primary, but not primary, bouton density (Fig. 6B). The proportions of terminations ending in boutons also decreased with the number of tree branches (R=−0.66, p<10⁻⁴, not illustrated). Bouton morphology differed between primary and non-primary branches and between terminal and en passant (EP). Primary branch boutons (EP only) were longer and wider, while non-primary en passant boutons were longer than but similarly wide to non-primary terminal boutons (Table 2). The proportionality of terminal bouton length to diameter was shallower (Fig. 6C) and weaker (R=0.14, N=5033) than for primary (R=0.39, N=2040) and non-primary en passant boutons (R=0.44, N=11,154). Terminal boutons were overall more spherical than en passant boutons (Fig. 6D). Moreover, for all branch types, wider boutons had wider neighboring boutons (R=0.43±0.12, p<10⁻⁴).

Figure 6.

CF boutons differ by branch type and terminal vs. en passant position. A. Bouton proportions (wedge sizes) and counts per CF (mean ± standard deviation) by branch type. B. Relationship between linear bouton density (number of boutons per 100 µm) and tree length across CFs. Unlike in primary branches, non-primary bouton density decreases with increased tree length. C. Scatter plot of bouton path length vs. diameter for all boutons (N=18,227) colored by type. En passant bouton path length strongly correlates with diameter (purple and orange lines). For terminal boutons the correlation is also positive (solid black line) but less than unitary (black dashed line, with Y intercept raised for visual comparison). Colored ovals are standard deviations for the three bouton types centered at the respective means. Primary boutons (purple) are larger than non-primary (orange and black) in both diameter and path length. D. Gallery of representative boutons. En passant boutons are distinctly elongated along the path compared to the more spherical terminal boutons.

Interbouton distance (IBD) was measured in all branch types to explore how regularly spaced boutons are along the CF tree. The coefficient of variation of distances between bouton centers (IBD_center) was significantly smaller compared to randomized boutons (CV=0.75±0.11 vs. 0.93±0.12, N=68 CFs, p<10⁻⁴), indicating regularity in bouton positions. Randomization that avoided bouton overlaps produced the same variability (CV=0.93±0.14, p>0.9). Thus, the constraint bouton length imposes on their minimum proximity cannot explain the observed regular spacing. Distances measured between bouton edges (IBD_edge) had larger CV (1.12±0.14) due to the added variability of bouton length, but still significantly smaller than random (CV=1.21±0.14, p<0.01). Therefore, although IBDs vary within CFs, boutons are spaced more regularly than random. Moreover, longer boutons had greater following IBDs (R=0.14±0.10 vs. 0.00±0.09 for randomized boutons, p<10⁻⁴), which partially underlies CF bouton position regularity. Interestingly, the correlation between bouton length and the preceding IBD was not significant, suggesting some functional specificity.

Climbing fibers target molecular layer interneurons beyond chance

CFs excite molecular layer interneurons, providing feed-forward inhibition to Purkinje cells. However, the connectivity of this circuit has yet to be quantified. Cell bodies were counterstained with thionine (Fig. 1) to analyze the number of CF boutons that overlap with interneuron somata (‘potential contacts’). Each CF made 44±15 potential contacts (18±6.0% of total boutons), with different contribution by branch and bouton type (Fig. 7A). The proportion of boutons that overlapped with interneuron somata was similar for primary (20±10%), tendril (19±9.0%), and distal en passant boutons (16±7.9%), as well as tendril and distal terminal boutons (16±8.4% and 17%±10%, respectively). To test whether CF and interneuron somata make targeted potential contacts, the number of overlaps were compared to chance overlaps upon random bouton shuffling (Fig. 7B). CF boutons had significantly more juxtapositions with interneuron cell bodies than randomly expected (p<0.001), particularly for terminal boutons (p<10⁻⁴), though en passant boutons were also significant (Fig. 7C). Broken down by branch type, all boutons except distal en passant overlapped with interneurons beyond chance (Fig. 7D). This suggests that CF potential contacts with interneuron somata, especially on terminal boutons, are likely functional. Although most CF-interneuron overlaps occur with dendrites (Nishiyama et al, 2007), somatic overlaps involved nearly one in five CF boutons, potentially providing a substantial contribution to olivo-cerebellar feed-forward inhibition.

Figure 7.

CF boutons systematically overlap with molecular layer interneuron somata. A. Number of overlaps of terminal (hatched) and en passant boutons onto interneuron somata per CF by branch type. B. Representative CF superimposed with both its actual boutons and an equal number of boutons randomly shuffled within the CF bounding box (large rectangular dotted border). Actual boutons that do and do not contact interneurons are colored maroon and gold, respectively. Shuffled boutons that do and do not contact interneurons are colored dark and light green, respectively. Example regions (smaller solid and dashed squares) are enlarged upper right above the figure to appreciate detail. CF and bouton radii are thickened 1.5× for clearer visualization. C. Interneuron overlap ratio between actual and shuffled boutons. Potential contacts between CF boutons and interneuron somata occur significantly more than by chance (horizontal dashed unity line). D. Further distinction by branch type. Only distal en passant boutons do not overlap with interneurons significantly beyond chance. Error bars are 95% confidence intervals.

Interneurons are commonly divided into basket cells in the inner third and stellate cells in the outer third of the molecular layer (Palay and Chan-Palay, 1974), though a morphometric classification analysis (Sultan and Bower, 1998) strongly suggests that these cells comprise a single type with continuous morphological differentiation across depth. To examine if CFs have a greater tendency to overlap with basket- or stellate-like somata, the proportion of CF-somata potential contacts were measured in the inner, middle, and outer third of the molecular layer. The resulting values (45±10%, 37±14%, and 18±12%, respectively; N=12 CFs, see ‘Methods’ for sample size determination) indicate that CFs overall tend to juxtapose with basket-like interneurons more than with stellate-like interneurons. These findings were branch-type specific. Basket-like proportion was especially high for primary and tendril branches, both having ~2/3 of their bouton-somata overlaps in the inner third layer. In contrast, the potential contacts of distal boutons with interneuron somata increased in proportion towards the cortical surface (10±21%, 39±35%, and 51±38% for inner, middle, and outer thirds, respectively). This result was not due to a change in interneuron density across the molecular layer, which was relatively constant (interneuron density = 0.50±0.11, 0.53±0.09, 0.44±0.09, see ‘Methods’).

Purkinje cell somata were also stained, and could be unambiguously identified as the underlying target ("paired Purkinje cell") of 48 of the 68 CFs. We reconstructed these somata to compare their geometry (surface area, perimeter length, and roundness) with the overlying CF morphology. None of these measures significantly correlated with any CF morphometric, either for the entire CF tree or for just the retrograde branches or boutons (not shown). The proportions of retrograde boutons that did and did not overlap with the paired Purkinje cell soma were also measured. The former was nearly three times as common as the latter (74±37% vs. 26±37%; N=10 CFs, see ‘Methods’ for sample size determination). None of the boutons that did not overlap with the paired soma overlapped with other labeled Purkinje cell soma; however, the possibility exists that some Purkinje somata were too faintly labeled to observe.

Discussion

Climbing fibers (CFs) have intrigued scientists ever since Cajal’s times. Unlike typical axons, CFs primarily synapse on single Purkinje cells immediately upon entering the principal neuron layer. This 1-1 relationship is accompanied by stereotypical physiology across cerebellar regions, including the signature ‘complex spike’, low frequency rhythmic firing, and uniform conduction time from the inferior olive (Sugihara et al., 1993). The present study investigated whether cerebellar stereotypy extends to CF morphology. CF size and shape are considerably diverse both at the tree and branch levels, as well as in the morphometric distribution across distance. Morphological variability of CFs was similar to that of axon types contacting many target cells. Lack of regional differences and morphological clusters suggests that such diversity is an irreducible population characteristic rather than reflecting distinct subclasses.

We found comparable variability in Purkinje dendritic trees, especially isolating the proximal dendrites where CFs synapse based on branch diameter (see ‘Materials and Methods’). CFs and Purkinje cells may exert a reciprocal morphological influence (Rossi and Strata, 1995; Sotelo and Dusart, 2009). Our finding that Purkinje cell body size and shape do not correlate with CF morphology suggests that only dendrites might systematically affect CF structure and vice versa. The effect of CFs on Purkinje cells is central to all functional models of the cerebellum (Houk et al., 1996). Since the variability found in CFs likely relates to the underlying Purkinje dendritic tree, the CF influence on Purkinje cell signaling and timing will be best addressed by reconstructing and biophysically modeling paired CF and Purkinje cells. The present detailed quantification of CF morphology provides a structural foundation to understand their computational role.

CFs are composed of primary and tendril branches. We introduced a simple and accurate definition to operationally identify these branch types as well as distal and retrograde fibers based on quantitative and intuitive morphological measurements. This method reproducibly and automatically labels all branches, allowing their first comprehensive analysis. Primary branches were thicker than non-primary branches and had larger, less densely distributed boutons. Primary boutons were also more similar in diameter to adjacent interbouton regions. A consequence of these properties would be lower axial resistance, suggesting that primary branches highly prioritize propagation speed and reliability. Since these branches give rise to the remaining CF tree, propagation failures would have drastic consequences. Primary branches presumably provide the basic CF framework, faithfully tracking the Purkinje cell principal dendritic trunk. Primary branches are thus like communication highways, ensuring that signals reach distal territories fast and efficiently. Still, over half of the primary branch volume was taken up by boutons which, although less than for other branch types, suggests that primary branches provide considerable signal transmission as well.

Primary branches give rise to the more targeted tendril and distal branches, together supplying the vast majority of CF synapses. Tendril branches often follow similar routes as their primary parents, possibly targeting nearby branches on Purkinje dendrites akin to local roadways. Tendril branches summed up to three times the length and four times the bouton count of primary branches, clearly outnumbering their signaling capacity. Distal branches differed in location along the CF and orientation from both tendril and primary branches, suggesting functionally distinct contacts onto separate dendritic domains of Purkinje cells. In contrast to primary branches, the large diameter ratio between boutons and axonal shaft in tendril and distal branches may optimize effective synaptic transmission and plasticity, while possibly providing a mechanism for signal filtering. Retrograde branches accounted for a minor fraction of boutons. However, their location in the Purkinje cell layer implies distinct synaptic targeting which may enhance, or differentiate altogether, their computational role.

The axonal placement of CF boutons directly maps onto synapses with Purkinje cell dendrites, therefore bearing straight functional relevance. On average CFs had a bouton every 8.7 µm, which is sparse compared to six other axon types measured by Shepherd et al. (2002), with spacing that ranged from 2.6 to 9.9 µm. Even within the cerebellum, parallel fibers had a bouton every 5.2 µm, nearly twice the density of CFs, with small and similar sample-to-sample variability (CV≈0.2). Boutons were distributed semi-regularly along the CF, also similarly to the aforementioned axons (Shepherd et al., 2002). In contrast, axonal boutons on neocortical pyramidal neurons were spaced randomly (Hellwig et al., 1994). Axonal bouton spacing regularity, therefore, is common but not universal. Moreover, longer CF boutons were spaced farther apart. A quantitatively similar correlation was found between spine head diameters and inter-spine distance (Konur et al., 2003), suggesting a shared pre- and post-synaptic homeostatic phenomenon. Optimization of CF interbouton distances to balance depolarization across the underlying dendrites would constitute an important determinant of signal summation in Purkinje cells.

In another example of morphological homeostasis, smaller CFs tended to be bouton-denser, partially compensating for their lower synaptic number. This is again analogous to the tendency of hippocampus principal neurons with smaller-than-average dendrites to have larger-than-average trees (Samsonovich and Ascoli, 2006). The net result is lesser morphological variation (in CF total bouton number or hippocampal cell total dendritic span), which may increase biophysical stability. The underlying developmental or maintenance mechanism must be specific since it affects some CF branches (distal and tendril) but not others (primary). Morphological homeostasis is non-trivial as the opposite relationship is characteristically typical of biological systems (taller trees have longer branches etc.). Within CFs, for example, longer boutons had larger diameters.

Length and diameter were more independent in terminal than in en passant boutons, possibly due to their post-synaptic locations. While en passant boutons typically synapse along Purkinje dendritic shafts, terminal boutons may be more frequent at terminal endings or different cell types. Indeed, while all bouton types except distal en passant overlapped with molecular layer interneurons beyond chance, terminal bouton-interneuron potential contacts were statistically most significant. Interneurons contact a large number of other Purkinje cells, completing a classic feed-forward inhibitory microcircuit. Although we could only visualize bouton overlaps with somata, most CF-interneuron overlaps occur with dendrites. Nishiyama et al. (2007) sampled CF branches to count 9.26 interneuron dendrite appositions per 100 µm of CF. Extrapolation to the total size of CFs studied here would provide a figure of 215 potential contacts with interneuron dendrites. Together with our count of somatic overlaps, CFs may average up to 259 bouton-interneuron overlaps. This value must be considered an upper bound since it nearly equals the total number of CF boutons. CF-interneuron overlaps might transmit functional information even without actual contacts, via glutamate spillover presumably from CF-to-Purkinje cell synapses (Szapiro and Barbour, 2007). Most CF boutons could thus excite both Purkinje cell and interneurons. Our data suggest that CFs are at least as well-suited to excite interneurons as Purkinje cells. Definitively associating functional contacts to bouton-interneuron overlaps will require measurement of molecular or biophysical influences. Ultrastructural analysis may reveal synaptic contacts or their absence. Given the possibility of volume transmission, however, even electron microscopy cannot (dis)prove functional axo-somatic relationships. The statistical results at the population level of our light-microscopy reconstructions strongly suggest feed-forward circuit organization.

Do CF boutons target interneuron somata or vice versa? CFs and interneurons develop in the same period (Altman, 1972; Zhang and Goldman, 1996; Sugihara, 2005, 2006), impeding causal inference. Interneurons also receive synapses from parallel fibers and other interneurons, while CF boutons exciting interneuron somata synapse with Purkinje cell dendrites. The observed CF-interneuron spatial targeting might result from better survival rates for interneurons or CFs with functional contacts. CF population size is drastically reduced into maturity (Sugihara, 2005; Hashimoto et al., 2009). Purkinje soma inhibition by molecular interneurons may also be necessary to establish one-to-one Purkinje-CF pairing (Nakayama et al., 2012). Fully explaining the observed spatial targeting will require controlling and measuring the relation among CF and interneuron chemical cues, their proximity, and survival rate.

Through deposition in the public NeuroMorpho.Org database (Ascoli et al., 2007), these 68 CF reconstructions can be further re-analyzed beyond the present characterization, compared or combined with future CF reconstructions, and loaded into neuron simulation environments (Hines and Carnevale, 2001) to test the influence of morphology on biophysical properties. To the best of our knowledge, these are also the first available CF digital tracings with identified branch types and fully reconstructed boutons. As such, they might serve as essential building blocks for anatomically realistic cerebellar network models. The necessity to include plausible circuit connectivity into simulations of the cerebellar cortex has been recognized for at least 35 years (Pellionisz et al., 1977). Only much more recently, however, have the required computational power and infrastructures become available (Gleeson et al., 2007). The large set of digital CF morphologies described in this study provides both a useful source of data and powerful constraints for large-scale modeling efforts.

This collection might also constitute the first detailed reconstructions of the complete axonal terminal field reported for any neuronal class in the mammalian brain. Their comprehensive morphological analysis could thus reveal insights into basic function that may also apply through other regions of the central nervous system.