Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Apr 30.
Published in final edited form as: J Neurosci. 2012 Oct 31;32(44):15489–15494. doi: 10.1523/JNEUROSCI.1865-12.2012

Adaptation of spike timing precision controls the sensitivity to interaural time difference in the avian auditory brainstem

Matthew H Higgs 1,2, Marina S Kuznetsova 2,3, William J Spain 1,2,4
PMCID: PMC3518488  NIHMSID: NIHMS418861  PMID: 23115186

Abstract

While adaptation is widely thought to facilitate neural coding, the form of adaptation should depend on how the signals are encoded. Monaural neurons early in the interaural time difference (ITD) pathway encode the phase of sound input using spike timing rather than firing rate. Such neurons in chicken nucleus magnocellularis (NM) adapt to ongoing stimuli by increasing firing rate and decreasing spike timing precision. We measured NM neuron responses while adapting them to simulated physiological input, and used these responses to construct inputs to binaural coincidence detector neurons in nucleus laminaris (NL). Adaptation of spike timing in NM reduced ITD sensitivity in NL, demonstrating the dominant role of timing in the short-term plasticity as well as the immediate response of this sound localization circuit.

Adaptation is ubiquitous in neural systems and serves a variety of functional roles. For example, in sensory systems, adaptation can attenuate the response to persistent inputs while preserving the response to input changes (Fairhall et al., 2001; Wen et al., 2009). A common form of adaptation is the accommodation of action potential firing rate (Adrian and Zotterman, 1926) caused by changes in neuronal membrane properties (Lancaster and Adams, 1986; Schwindt et al., 1988; Abolafia et al., 2011); another prominent mechanism is synaptic depression (Chung et al., 2002; Cook et al., 2003). In the neural pathway responsible for sound localization, a different type of adaptation may be required, because early stages of the pathway represent information about the relative phase of sound arriving at the two ears using precise spike timing rather than firing rate. In the present studies, we investigated the properties and function of such adaptation in the avian auditory brainstem in vitro.

The main components of the ITD detection circuit in the avian brainstem are the monaural neurons of nucleus magnocellularis (the avian cochlear nucleus, NM), which generate spike output phase-locked to the sound, and the binaural coincidence detector neurons of nucleus laminaris (NL), which receive excitatory inputs from ipsilateral and contralateral NM and are sensitive to the interaural phase difference (IPD) between sound arriving at the two ears (see Figure 1) (Parks and Rubel, 1978; Carr and Konishi, 1990; Warchol and Dallos, 1990). The firing rate of NL neurons is highest when NM inputs from both sides arrive in phase (0° IPD) and lowest at 180° (Reyes et al., 1996). NL neurons maintain robust IPD sensitivity despite changes in sound intensity, in part because of mechanisms that limit the effect of changes in NM firing rate (Cook et al., 2003; Peña et al., 1996).

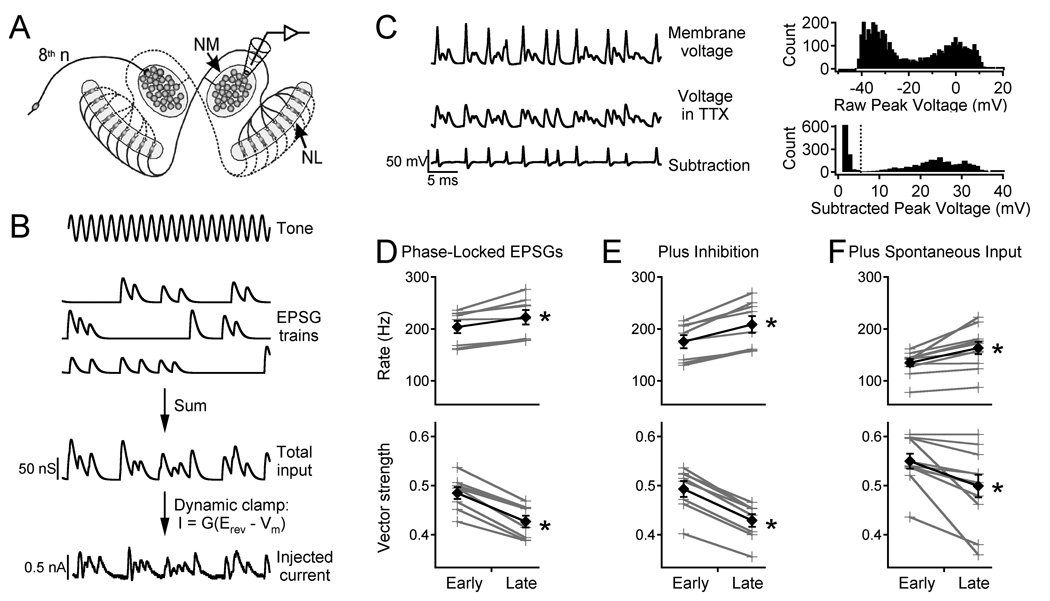
Figure 1. NM adaptation to simulated tonal stimuli.

Figure 1

Open in a new tab

A. Circuitry of the first-order (NM) and second-order (NL) neurons in the chick auditory system and the in vitro recording location. B. Simulated 1000 Hz tone, EPSG trains for 8th nerve fibers, the total applied conductance, and the current injected into the NM neuron in dynamic clamp. C. Traces show response in control ACSF (top), in 0.5 µM TTX (middle), and the difference (bottom). Top histogram shows raw peak voltages. Bottom histogram shows subtracted peak voltages, illustrating the separation between noise and spikes. Dotted line indicates spike detection level. D. Top: firing rate for early and late responses (grey crosses, individual cells; black diamonds, average). Bottom: vector strength. E. Same as D with addition of inhibitory conductance to the same neurons. F. Same as D in different neurons tested with simulated spontaneous input before the simulated sound-evoked input.

Recently, we discovered a novel type of adaptation in NM neurons, which develops over several seconds, is caused by slow inactivation of the low-threshold potassium current (IKlt) mediated by Kv1 channels, and is characterized by an increase in firing rate and a decrease in spike timing precision (Kuznetsova et al., 2008). The present study tests the hypothesis that its downstream effect is a reduction of IPD sensitivity in the coincidence detector neurons in NL.

MATERIALS & METHODS

All animal procedures complied with the National Research Council Guidelines for the Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee of the Seattle Veterans Affairs Health Care System.

Brain slice preparation

Chick brainstem slices were prepared as described previously (Slee et al., 2005). Chicks (embryonic stage E21 or post-hatch stage P1, male or female) were decapitated, and the brainstem was dissected under ice-cold artificial cerebrospinal fluid (ACSF) composed of (in mM) 130 NaCl, 3 KCl, 2 CaCl2, 1.25 NaH2PO4, 26 NaHCO3, 2 MgCl2, and 10 dextrose, kept at pH 7.3–7.4 by bubbling with carbogen (5% CO2, 95% O2). Coronal sections (200 µm) were cut using a vibratome and stored in ACSF at 35°C for 30 minutes and at room temperature thereafter. Experiments were done at 33–35°C in ACSF with 100 µM picrotoxin to block GABAA receptors and 20 µM DNQX or 10 µM CNQX to block AMPA/kainite receptors.

Electrophysiology

Whole-cell recordings were obtained using standard techniques (Reyes et al., 1994; Slee et al., 2005). Patch pipettes (2–4 Mµ) were pulled from borosilicate glass and coated with Sylgard. The pipette solution contained (in mM) 105 K-gluconate, 2.5 MgCl2, 31.15 KCl, 0.05 CaCl2, 10 HEPES, 2 Na2ATP, 0.5 Na-GTP, 0.1 EGTA, and 0.5–1% biocytin (pH adjusted to 7.2–7.3 with KOH; 280 mOsm). Data were corrected for the liquid junction potential (6 mV). Recordings were performed using an Axoclamp 2B amplifier in bridge mode. For dynamic clamp, the reversal potential (Erev) of the synaptic current was set by an analog circuit, which converted the conductance command (G) into current (I) based on the membrane potential (Vm) according to I = G(Erev − Vm). Membrane potential was low-pass filtered at 30 kHz (8-pole Bessel filter) and sampled at 100 kHz using an Instrutech ITC-16 data acquisition board and a Macintosh computer. Stimuli and data acquisition were controlled by custom macros in Igor Pro.

Inputs to NM neurons

Stimulus waveforms simulated the excitatory synaptic conductances (EPSGs) from multiple presynaptic neurons during an acoustic input (Reyes et al., 1996; Kuznetsova et al., 2008). Each waveform was described by six parameters: (1) sound frequency (F = 1000 Hz), (2) number of presynaptic cells (N = 3), (3) average firing rate of each presynaptic cell (AFR = 250 Hz), where the firing probability on each sound cycle is AFR / F, (4) jitter (0.14 ms), the SD of a Gaussian random variable that determines each spike time (Warchol and Dallos, 1990; Fukui et al., 2006), (5) peak amplitude of each unitary EPSG (Amax = 25–60 nS; adjusted to produce output firing rates of ~200 Hz), and (6) EPSG time constant (τ = 0.25 ms). Each EPSG was generated as an alpha function, G(t) = A(t / τ) exp(1 − t / τ). Synaptic depression was simulated as described by Cook et al (2003):

A=D[1−exp(−Δtτf)+A0(1−S)exp(−Δtτf)]+(1−D)[1−exp(−Δtτs)+A0(1−S)exp(−Δtτs)]

where A is the peak amplitude of the synaptic event, A0 is the amplitude of the previous event, Δt is the interval from the previous event, S is the fractional depression, D is the fast recovery fraction, τf is the fast recovery time-constant, and τs is the slow recovery time-constant. Parameter values were chosen to match published data (Brenowicz and Trussell, 2001) (S = 0.45, D = 0.6, τf = 20 ms, τs = 350 ms). Each stimulus was 10 s long, with identical segments from 0–1 s and 9–10 s that were unique to each trial. To investigate the effect of inhibition, a constant 10 nS conductance with Erev = −37 mV (Howard et al., 2007) was added on every other trial. The complete stimulus included 10 trials separated by 10 s recovery intervals.

To simulate spontaneous activity, we generated stimuli mimicking spontaneous firing of three 8th nerve fibers in silence (Saunders et al., 2002), using a Poisson process with a mean firing rate of 24.6 Hz for each fiber. Each stimulus consisted of 10 seconds of spontaneous activity followed by a 10 second “tonal” input with AFR = 200 Hz.

NL experiment 1: using recorded NM spike trains to construct the input

Spike trains were converted into simulated EPSC trains (Figure 2A) using previously reported parameters (Kuba et al., 2005; Slee et al., 2010) and the synaptic depression model described above. Each unitary EPSC was a double exponential function with a rise time constant of 0.14 ms and a decay time constant of 0.25 ms (similar to recorded EPSCs in the middle-frequency region of NL). For simplicity, this experiment was designed to eliminate slow adaptation in NL. Thus, rather than presenting long stimuli to NL, the EPSC trains were randomly sampled to extract 100 ms “unadapted” inputs (200–700 ms after stimulus onset, excluding the initial fast adaptation) and “adapted” inputs (9200–9700 ms). Each monaural input to NL was the sum of 40 unitary inputs (generated from the spike trains of 4 NM neurons assigned to that side). The two monaural inputs were added with IPDs from 0° to 180° and injected into neurons in the caudal two thirds of NL (tuned to sound frequencies of approximately 500 to 2000 Hz (Rubel and Parks, 1975)). The “binaural” input for each IPD was generated from the same “monaural” segments to control for spike train variability, and “adapted” and “unadapted” trains were generated from NM responses to identical input waveforms. The complete stimulus included 80 repeats at each of seven IPDs, separated by 200 ms recovery intervals.

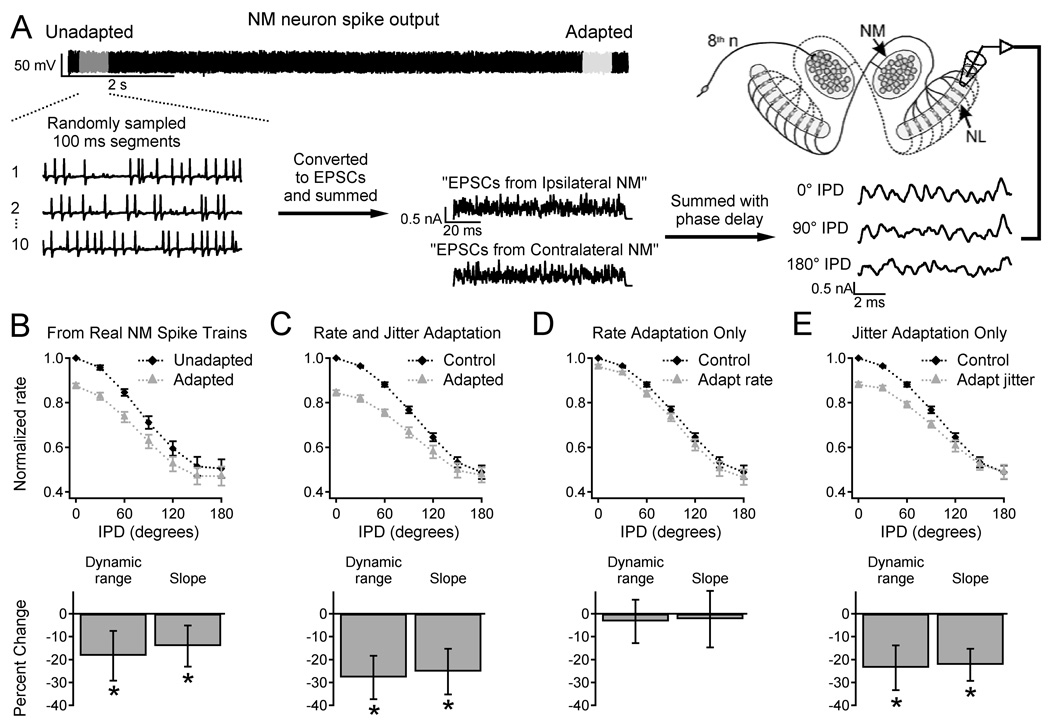
Figure 2. NM adaptation reduces IPD sensitivity in NL.

Figure 2

Open in a new tab

A. Generation of inputs to NL. Unadapted or adapted NM output was sampled and converted to EPSCs. “Monaural” inputs representing the output of 40 NM cells (generated using 10 spike trains from each of 4 NM neurons) were summed with different IPDs and injected into NL neurons. B. Results with inputs generated from real NM spike trains (as shown in A). Top: firing rate vs. IPD for unadapted (black diamonds) and adapted input (grey triangles). Data were normalized to the firing rate with unadapted input at 0° IPD. Bottom: percent change in dynamic range and slope of the firing rate-IPD relationships. C. Results with simulated input spike trains with adaptation of firing rate and jitter. D. Results with simulated rate adaptation only. E. Results with simulated jitter adaptation only.

NL experiment 2: varying NM firing rate and jitter separately

Simulated NM spike trains (100 ms) were generated by the method used for NM stimulation and converted into EPSC trains as described above. The NM firing rates were 202 Hz (“unadapted”) or 222 Hz (“adapted”) and the spike time jitter was 194 µs ("unadapted") or 214 µs ("adapted"), based on the results of our experiments in NM described above. Four conditions ("unadapted control", "adapted rate and jitter", "adapted rate only", and "adapted jitter only") were each presented 20 times in random order.

NL experiment 3: adaptation in NM and NL

Simulated binaural inputs of 10 s duration were injected into NL neurons. The four conditions described above were presented, simulating the adaptation as an exponential change with a time constant of 2 s (rate constant = 0.5 s−1), based on experimentally determined rate constants of 0.42 ± 0.15 s−1 for firing rate and 0.55 ± 0.20 s−1 for jitter. To reproduce our "early" (200–700 ms) and "late" (9200–9700 ms) data (assuming that adaptation begins at stimulus onset), the initial and adapted rates were 199 and 222 Hz, and the initial and adapted levels of jitter were 184 and 214 µs, respectively. The simulated IPD was varied in a saw-tooth pattern from 0° to 180° to 0° in 500 ms cycles, starting 200 ms after stimulus onset. Each condition was presented three times to each cell.

TTX subtraction for action potential detection

To detect the small action potentials characteristic of the auditory nuclei (Reyes et al., 1994; Kuba et al., 2006) and to increase the accuracy of spike time measurements, the slice was superfused with tetrodotoxin (TTX, 0.5 µM) to block sodium channels and the stimulus was repeated. The response in TTX was subtracted from the control recording (Figure 1C), and the spike times were measured from the remaining action potential train, at the peak of each spike. To verify that the peaks were action potentials, we determined the distribution of peak amplitudes for each cell. Data were accepted only if there was a clear separation between smaller noise and larger spikes.

Data analysis

Adaptation in NM was measured by the mean firing rate, spike time jitter, and vector strength in 500 ms windows; most data reported are for the "early response" (200–700 ms) and the "late response" (9200–9700 ms). Jitter was defined as the standard deviation of a Gaussian fit to the periodic PSTH. Vector strength, a measure of phase-locking to periodic stimuli, was calculated as described by Goldberg and Brown (1969), where n is the number of spikes and θi is the phase of each spike:

Vs=1n(∑i=1ncos θi)2+(∑i=1nsin θi)2

For NL neurons, the firing rate-IPD curves were characterized by the dynamic range (D) (rate at 0° – rate at 180°), and the slope (S) between 60° and 120°. For experiments where the IPD was varied continuously, firing rates were obtained in 50 ms windows and averaged across the repeats of each condition. The rate modulation for each IPD cycle was measured by least-squares fitting of a cosine function: r = ravg + a cos(IPD). The rates at 0° and 180° IPD were taken from the cosine fit, plotted versus time, and fitted with single-exponential functions. For statistical comparisons, the dynamic range was measured from the exponential fits at 0.45 s (for the first IPD cycle) and 9.45 s (for the last cycle).

Statistics

Data are reported as mean ± standard error of the mean. Comparisons were performed using paired, two-tailed t-tests. For single comparisons, differences were considered significant when p < 0.05. Multiple comparisons were performed by ANOVA and post-hoc t-tests with Bonferroni's criterion for significance: p < 0.05 / number of comparisons.

RESULTS

Adaptation in NM

Our previous studies showed that NM neurons exhibit slow adaptation of firing rate and spike timing precision (Kuznetsova et al., 2008). The present experiments investigated whether this adaptation would occur under a wider range of physiological conditions (including inhibition and spontaneous 8th nerve activity) and generated high-quality spike time data for constructing inputs to NL neurons. NM neurons were stimulated using inputs with natural statistics (Figure 1A, B; see Materials & Methods) delivered by dynamic clamp (Kuznetsova et al., 2008). Each stimulus was 10 s long, with identical segments from 0–1 s and 9–10 s, and a simulated inhibitory conductance was added on every other trial. Because the action potentials in NM and NL neurons are unusually small (Reyes et al., 1994), the stimuli were delivered in control solution and again in tetrodotoxin (TTX) to block sodium channels, and the responses were subtracted to isolate the action potentials (Figure 1C). Adaptation was measured by comparing the early response (200–700 ms) and the late response (9200–9700 ms) (Figure 1D). The firing rate increased by an average of 9.2 ± 1.8% during this stimulus (top panel, N = 8, p = 0.003), while the vector strength decreased by 11.9 ± 1.1% (bottom, p = 0.00002); the corresponding spike jitter increased by 12.7 ± 2.0% (p = 0.0003). The significance of the vector strength data was confirmed by Rayleigh's test. With a 500 ms measurement window, a typical firing rate of ~200 Hz, and 5 trials per condition (with or without inhibition; see below), approximately 500 spikes were available for each measurement, giving p < 0.01 for vector strength > 0.1.

Adaptation was also observed when the excitatory input was combined with a constant inhibitory conductance (Figure 1E); in this case firing rate increased by 18.6 ± 2.6% and vector strength decreased by 13.1 ± 0.6% (p = 0.0006 and 1 × 10−6 respectively).

Because 8th nerve inputs to NM are spontaneously active in silence (Saunders et al., 2002), in some experiments we applied simulated spontaneous synaptic input with a random temporal pattern (see Materials & Methods) before the phase-locked stimulus. The simulated sound-evoked input still caused adaptation of firing rate and vector strength (Figure 1F, N = 11, p = 0.002 and 0.007 respectively).

Effects on IPD sensitivity in NL

Adapted NM neurons with reduced spike timing precision will produce less synchronous input to downstream coincidence detector neurons in NL. We predicted that this would lower the NL firing rates at favorable IPDs, reducing IPD sensitivity. To test this prediction, we sampled real NM spike trains from "unadapted" and "adapted" periods to construct simulated binaural input with varied IPDs, which was injected into NL cells (Figure 2A; see Materials & Methods). In all NL neurons, the firing rate was highest for 0° IPD and lowest for 180°. Consistent with our prediction, NM adaptation reduced the dynamic range (D) of the NL response by 18.1 ± 2.8% (N = 7, p = 0.002), primarily because of a lower firing rate at 0° IPD, and reduced the slope (S) of the firing rate-IPD curve by 14.1 ± 5.7% (N = 7, p = 0.04) (Figure 2B).

Our next experiments investigated the individual effects of spike time precision and firing rate. Inputs to NL were generated from artificial spike trains that simulated NM output before and after adaptation, and were otherwise identical to the inputs described above. Simulated adaptation of firing rate and spike jitter reduced D by 28.2 ± 2.5% (N = 7, p = 0.0005) and lowered S by 24.4 ± 9.4% (p = 0.02) (Figure 2C). Inputs with increased firing rate alone had no significant effect on D or S (Figure 2D). However, increased jitter alone reduced D by 23.9 ± 1.5% (p = 0.0001) and lowered S by 24.8 ± 3.5% (p = 0.0004) (Figure 2E).

Combined adaptation in NM and NL

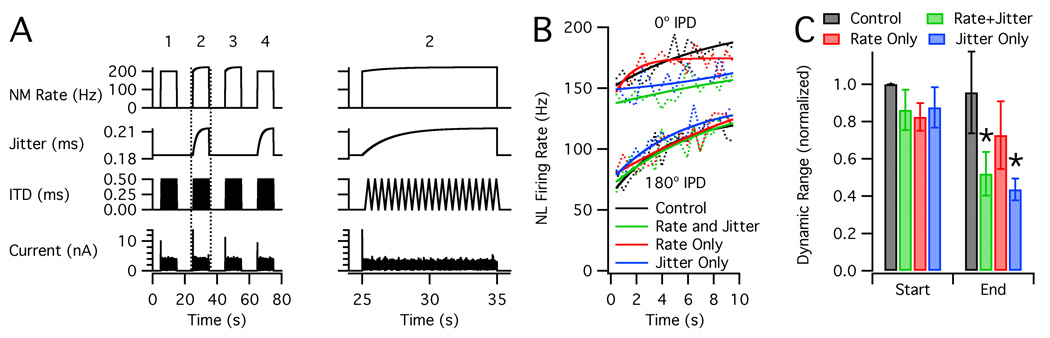
Although our studies focused primarily on the downstream effects of adaptation in NM, it is reasonable to expect that NL neurons will also adapt, affecting their responses to NM input. To investigate this, we stimulated NL cells with 10 s trains of simulated NM input with a saw-tooth variation of IPD (Figure 3A; see Materials & Methods). Trials were performed with no input adaptation (control), adaptation of input rate and jitter, adaptation of rate only, and adaptation of jitter only. All of the data showed a slow increase of NL firing rate during each stimulus, which was observed at all IPDs (Figure 3B). In the conditions with adaptation of input jitter, the increase of NL firing rate at 0° IPD was less, and thus, D decreased over time (Figure 3C). The final values of D for the rate + jitter and jitter-only conditions were significantly lower than the control values (n = 8, p = 0.015 and 0.016, respectively), whereas the rate-only condition was not significantly different from the control. These data confirm that adaptation of input jitter will reduce IPD sensitivity in NL. In contrast, the adaptation in NL increased firing rate but did not significantly affect IPD sensitivity with constant input jitter.

Figure 3. Combined adaptation in NM and NL.

Figure 3

Open in a new tab

A. Stimulus with four conditions: (1) control without input adaptation, (2) adaptation of input rate and jitter, (3) rate only, and (4) jitter only. Plots show (from top to bottom) average firing rate of each input cell, jitter, ITD, and injected current. Condition 2 (inside dotted lines) is expanded at right. The current scale was adjusted for each cell to produce physiological firing rates. B. Mean NL firing rates (dotted lines, n = 8) and exponential fits (solid lines) at 0° IPD (top) and 180° (bottom). C. Dynamic range, normalized by the "start" value for the control condition. The "start" values represent the first IPD cycle, and the "end" values represent the last cycle. Asterisks indicate significant differences from control.

DISCUSSION

Our previous studies showed that NM neurons adapt to sustained input with an increase in firing rate and a decrease in spike timing precision, both mediated by slow inactivation of Kv1 channels (Kuznetsova et al., 2008). Other reports have also shown changes in spike time precision caused by adaptation (Higley and Contreras, 2006) or neuromodulation (Billimoria et al., 2006). Our present results show a functional consequence for downstream neurons; the reduction of spike time precision in NM lowers the IPD sensitivity of coincidence detector cells in NL. These neurons adapt similarly; the adaptation in NL does not directly reduce IPD sensitivity, but the influence of NM adaptation is preserved when sustained input is transmitted through both stages of the pathway. The dominant effect of NM spike timing (versus rate) is consistent with other studies showing that the downstream effects of NM firing rate are limited by synaptic depression (Cook et al., 2003) (which was included in our algorithm used to generate input to NL). In vivo, the influence of NM firing rate may be reduced further by inhibition (Peña et al., 1996).

Our in vitro data suggest that small changes in spike timing precision in the cochlear nucleus could regulate the sensitivity of sound localization in vivo. This view is supported by studies in a variety of species, which demonstrate that exceedingly small shifts in ITD can change perceived sound location (Klumpp and Eady, 1956; Wakeford and Robinson, 1974; Moiseff and Konishi, 1981). Under our experimental conditions, an ~10% decrease in spike timing precision in NM was magnified to an ~18% reduction in dynamic range in NL. The real effect of Kv1 inactivation might be greater, because we measured spike output at the NM somas rather than the synaptic terminals in NL. Because Kv1 channels are the dominant K+ channel along myelinated axons (Mert, 2006), Kv1 inactivation may cause additional jitter as action potentials travel to the terminals.

Although our studies were performed in a chicken brainstem preparation, we predict that similar adaptation may occur in mammals. While some mechanisms of ITD processing may differ between birds (for review see Konishi, 2003) and mammals (McAlpine, 2005), ITD processing in all species relies on precise spike timing. In order to transmit timing information, avian and mammalian auditory brainstem display similar anatomical and physiological specializations. The membrane properties of mammalian cochlear spherical bushy cells (SBCs) resemble those of NM neurons, and are dominated by IKlt (Schwarz and Puil, 1997). Because IKlt has similar properties in the avian and mammalian cochlear nuclei (Reyes et al., 1994; Rothman and Manis, 2003), SBCs will likely adapt much like NM neurons. We predict that slow adaptation caused by IKlt inactivation in the cochlear nucleus will cause a slow degradation of ITD discrimination that is independent of sound location but specific to the sound frequency. Results of recent human psychophysical experiments (Brown et al., 2012) are consistent with this prediction.

Acknowledgements

This material is based upon work supported in part by the U.S. Department of Veterans Affairs, Office of Research and Development, Biomedical Laboratory Research Program. Funding was provided by a Veterans Affairs Merit Review to W.J.S., a Veterans Affairs Epilepsy Center of Excellence, and NIDCD Grant No. 5F31DC009176 (M.S.K.). We thank Jason Haensly for help performing the experiments with simulated spontaneous input to NM. We thank Sean Slee, Adrienne Fairhall, Marc Binder, David Perkel, and Ed Rubel for helpful discussions, Fred Rieke for comments on a previous version of the manuscript, and Sue Usher for excellent technical assistance.

Footnotes

Conflict of interest: none

REFERENCES

  1. Abolafia JM, Vergara R, Arnold MM, Reig R, Sanchez-Vives MV. Cortical auditory adaptation in the awake rat and the role of potassium currents. Cereb Cortex. 2011;21:977–990. doi: 10.1093/cercor/bhq163. [DOI] [PubMed] [Google Scholar]
  2. Adrian ED, Zotterman Y. The impulses produced by sensory nerve-endings: Part II. The response of a Single End-Organ. J Physiol. 1926;61:151–171. doi: 10.1113/jphysiol.1926.sp002281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Billimoria CP, DiCaprio RA, Birmingham JT, Abbott LF, Marder E. Neuromodulation of spike-timing precision in sensory neurons. J Neurosci. 2006;26:5910–5919. doi: 10.1523/JNEUROSCI.4659-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brenowitz S, Trussell LO. Maturation of synaptic transmission at end-bulb synapses of the cochlear nucleus. J Neurosci. 2001;21:9487–9498. doi: 10.1523/JNEUROSCI.21-23-09487.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brown AD, Kuznetsova MS, Spain WJ, Stecker GC. Frequency-specific, location-nonspecific adaptation of interaural time difference sensitivity. Hear Res. 2012 Jun 23;2012 doi: 10.1016/j.heares.2012.06.002. [Epub ahead of print] PubMed PMID: 22732693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Carr CE, Konishi M. A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chung S, Li X, Nelson SB. Short-term depression at thalamocortical synapses contributes to rapid adaptation of cortical sensory responses in vivo. Neuron. 2002;34:437–446. doi: 10.1016/s0896-6273(02)00659-1. [DOI] [PubMed] [Google Scholar]
  8. Cook DL, Schwindt PC, Grande LA, Spain WJ. Synaptic depression in the localization of sound. Nature. 2003;421:66–70. doi: 10.1038/nature01248. [DOI] [PubMed] [Google Scholar]
  9. Fairhall AL, Lewen GD, Bialek W, de Ruyter van Steveninck RR. Efficiency and ambiguity in an adaptive neural code. Nature. 2001;412:787–792. doi: 10.1038/35090500. [DOI] [PubMed] [Google Scholar]
  10. Fukui I, Sato T, Ohmori H. Improvement of phase information at low sound frequency in nucleus magnocellularis of the chicken. J Neurophysiol. 2006;96:633–641. doi: 10.1152/jn.00916.2005. [DOI] [PubMed] [Google Scholar]
  11. Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
  12. Higley MJ, Contreras D. Balanced excitation and inhibition determine spike timing during frequency adaptation. J Neurosci. 2006;26:448–457. doi: 10.1523/JNEUROSCI.3506-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Howard MA, Burger RM, Rubel EW. A developmental switch to GABAergic inhibition dependent on increases in Kv1-type K+ currents. J Neurosci. 2007;27:2112–2123. doi: 10.1523/JNEUROSCI.5266-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Klumpp RG, Eady HR. Some measurements of the interaural time difference thresholds. J Acoust Soc Am. 1956;28:859–864. [Google Scholar]
  15. Konishi M. Coding of auditory space. Annu Rev Neurosci. 2003;26:31–55. doi: 10.1146/annurev.neuro.26.041002.131123. [DOI] [PubMed] [Google Scholar]
  16. Kuba H, Ishii TM, Ohmori H. Axonal site of spike initiation enhances auditory coincidence detection. Nature. 2006;444:1069–1072. doi: 10.1038/nature05347. [DOI] [PubMed] [Google Scholar]
  17. Kuba H, Yamada R, Fukui I, Ohmori H. Tonotopic specialization of auditory coincidence detection in nucleus laminaris of the chick. J Neurosci. 2005;25:1924–1934. doi: 10.1523/JNEUROSCI.4428-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kuznetsova MS, Higgs MH, Spain WJ. Adaptation of firing rate and spike-timing precision in the avian cochlear nucleus. J Neurosci. 2008;28:11906–11915. doi: 10.1523/JNEUROSCI.3827-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lancaster B, Adams PR. Calcium-dependent current generating the hyperpolarization of hippocampal neurons. J Neurophysiol. 1986;55:1268–1282. doi: 10.1152/jn.1986.55.6.1268. [DOI] [PubMed] [Google Scholar]
  20. McAlpine D. Creating a sense of auditory space. J Physiol. 2005;566:21–28. doi: 10.1113/jphysiol.2005.083113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mert T. Kv1 channels in signal conduction of myelinated nerve fibers. Rev Neurosci. 2006;17:369–374. doi: 10.1515/revneuro.2006.17.3.369. [DOI] [PubMed] [Google Scholar]
  22. Moiseff A, Konishi M. Neuronal and behavioral sensitivity to binaural time differences in the owl. J Neurosci. 1981;1:40–48. doi: 10.1523/JNEUROSCI.01-01-00040.1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Parks TN, Rubel EW. Organization and development of the brain stem auditory nuclei of the chicken: primary afferent projections. J Comp Neurol. 1978;180:439–448. doi: 10.1002/cne.901800303. [DOI] [PubMed] [Google Scholar]
  24. Peña JL, Viete S, Albeck Y, Konishi M. Tolerance to sound intensity of binaural coincidence detection in the nucleus laminaris of the owl. J Neurosci. 1996;16:7046–7054. doi: 10.1523/JNEUROSCI.16-21-07046.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Powers RK, Sawczuk A, Musick JR, Binder MD. Multiple mechanisms of spike-frequency adaptation in motoneurones. J Physiol Paris. 1999;93:101–114. doi: 10.1016/s0928-4257(99)80141-7. [DOI] [PubMed] [Google Scholar]
  26. Reyes AD, Rubel EW, Spain WJ. Membrane properties underlying the firing of neurons in the avian cochlear nucleus. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Reyes AD, Rubel EW, Spain WJ. In vitro analysis of optimal stimuli for phase-locking and time-delayed modulation of firing in avian nucleus laminaris neurons. J Neurosci. 1996;16:993–1007. doi: 10.1523/JNEUROSCI.16-03-00993.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Rothman JS, Manis PB. Kinetic analyses of three distinct potassium conductances in ventral cochlear nucleus neurons. J Neurophysiol. 2003;89:3083–3096. doi: 10.1152/jn.00126.2002. [DOI] [PubMed] [Google Scholar]
  29. Rubel EW, Parks TN. Organization and development of brain stem auditory nuclei of the chicken: tonotopic organization of n. magnocellularis and n. laminaris. J Comp Neurol. 1975;164:411–433. doi: 10.1002/cne.901640403. [DOI] [PubMed] [Google Scholar]
  30. Saunders JC, Ventetuolo CE, Plontke SK, Weiss BA. Coding of sound intensity in the chick cochlear nerve. J Neurophysiol. 2002;88:2887–2898. doi: 10.1152/jn.00381.2002. [DOI] [PubMed] [Google Scholar]
  31. Schwarz DW, Puil E. Firing properties of spherical bushy cells in the anteroventral cochlear nucleus of the gerbil. Hear Res. 1997;114:127–138. doi: 10.1016/s0378-5955(97)00162-7. [DOI] [PubMed] [Google Scholar]
  32. Schwindt PC, Spain WJ, Foehring RC, Chubb MC, Crill WE. Slow conductances in neurons from cat sensorimotor cortex and their role in slow excitability changes. J Neurophysiol. 1988;59:450–467. doi: 10.1152/jn.1988.59.2.450. [DOI] [PubMed] [Google Scholar]
  33. Slee SJ, Higgs MH, Fairhall AL, Spain WJ. Two-dimensional time coding in the auditory brainstem. J Neurosci. 2005;25:9978–9988. doi: 10.1523/JNEUROSCI.2666-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Slee SJ, Higgs MH, Fairhall AL, Spain WJ. Tonotopic Tuning in a Sound Localization Circuit. J Neurophysiol. 2010;103:2857–2875. doi: 10.1152/jn.00678.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wakeford OS, Robinson DE. Lateralization of tonal stimuli by the cat. J Acoust Soc Am. 1974;55:649–652. doi: 10.1121/1.1914577. [DOI] [PubMed] [Google Scholar]
  36. Warchol ME, Dallos P. Neural coding in the chick cochlear nucleus. J Comp Physiol [A] 1990;166:721–734. doi: 10.1007/BF00240021. [DOI] [PubMed] [Google Scholar]
  37. Wen B, Wang GI, Dean I, Delgutte B. Dynamic range adaptation to sound level statistics in the auditory nerve. J Neurosci. 2009;29:13797–13808. doi: 10.1523/JNEUROSCI.5610-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES