Efficiency of Extracting Stereo-driven Object Motions

Abstract

Most living things and many nonliving things deform as they move requiring observers to separate object motions from object deformations. When the object is partially occluded, the task becomes more difficult because it is not possible to use 2-D contour correlations (Cohen, Jain, & Zaidi, 2010). That leaves dynamic depth matching across the un-occluded views as the main possibility. We examined the role of stereo cues in extracting motion of partially occluded and deforming 3-D objects, simulated by disk-shaped random-dot stereograms set at randomly assigned depths, and placed uniformly around a circle. The stereo-disparities of the disks were temporally oscillated to simulate clockwise or counterclockwise rotation of the global shape. To dynamically deform the global shape, random disparity perturbation was added to each disk’s depth on each stimulus frame. At low perturbation, observers reported rotation directions consistent with the global shape, even against local motion cues, but performance deteriorated at high perturbation. Using 3-D global shape correlations, we formulated an optimal Bayesian discriminator for rotation direction. Based on rotation discrimination thresholds, human observers were 75% as efficient as the optimal model, demonstrating that global shapes derived from stereo cues facilitate inferences of object motions. To complement reports of stereo and motion integration in extra-striate cortex, our results suggest the possibilities that disparity selectivity and feature tracking are linked, or that global motion selective neurons can be driven purely from disparity cues.

Introduction

The world is populated with objects that deform as they move. Observers thus have to parse object motions from shape changes. When viewing a tiger moving behind bushes an observer can only see disparate motion through openings between bushes. The observer has to extract the tiger’s movement using these disparate motion signals, while disregarding the shape deformations caused by these movements (some of which cause local motions in the opposite direction). A number of processes have been identified in the computational and psychophysical literature that could help in these tasks. If a moving contour is visible, inferences can be made about shape (Cipolla & Giblin, 2000) and motion (Caplovitz & Tse, 2007a, 2007b; Rokers, Yuille, & Liu, 2006). If the object is partially occluded so that the contour is sparsely sampled, shape properties can help to infer motion direction for rigid (Lorenceau & Alais, 2001; Shiffrar & Pavel, 1991) and non-rigid (Cohen et al., 2010) objects, and motion can reveal shapes through pattern integration (Nishida, 2004). If the contour is completely occluded, visible patterns of velocities can be used to perceive 3-D shape for rigid (Koenderink & van Doorn, 1975, 1991) and non-rigid (Akhter, Sheikh, Khan, & Kanade, 2008; Bregler, Hertzmann, & Biermann, 2000; Jain & Zaidi, 2011) objects. In addition, stereo disparities can support perception of 3-D shape (Tsai & Victor, 2003) and tracking the direction of moving features (Ito, 1997; Lu & Sperling, 1995, 2001). In this study, we go beyond these results to investigate whether dynamic stereo-cues can help to infer object motion, and whether that relies on inferring 3-D shape.

Figure 1 shows sample frames from the stimuli used in the experiments (to be viewed using red-green anaglyphs). A set of disks spaced uniformly around a circle is varied in depth on each frame to create a sampled 3-D shape. The underlying shape was rotated from frame to frame resulting in depth variations of the disks and thus simulating a transverse wave, i.e. with wave motion orthogonal to element motion. There are thus three types of motion present within the stimulus, 1) z motion: the apparent local motion in depth at each disk location caused by local disparity changes, 2) Local-xy motion: the local clockwise/counterclockwise apparent motion between neighboring disk locations and 3) Global-xy rotation: the global clockwise/counterclockwise rotation of the underlying shape discretely sampled at equal intervals by the disks. However, when fixating at the center of Movies 1, 2, 4 and 5 through red-green anaglyphs, the dominant percept is that of a shape rotating clockwise. What are the cues that enable domination of global-xy motion? Viewed monocularly, each image in the movie is homogeneous with no shape cues and no correlations between successive frames, eliminating any luminance-based or contrast-based motion-energy cues. Therefore, dynamic disparity shifts are the sole cue used to infer the global motion.

Figure 1.

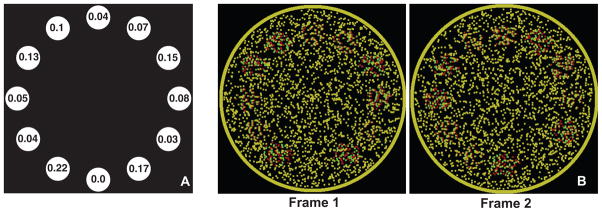
A) Schematic of a sample frame of the movies used in Experiment 1. Each disk is a random-dot stereogram with the indicated stereo-disparity in arc min. B) Screen shots of two frames of a movie as red-green stereograms.

Previous studies have shown than humans can extract motion of stereo-defined rigid shapes and researchers have argued for both a dedicated stereo-motion sensor (Patterson, 1999) as well as more general salient-feature based motion mechanisms (Lu & Sperling, 2002). It has also been shown that perceived apparent motion direction in 3D space is affected by stereo-defined depth, albeit to a much lesser degree than spatial location in the image plane (Green & Odom, 1986; Prins & Juola, 2001). Previous studies that examined interactions of local motion with stereo-motion used luminance defined local motions and showed that luminance defined local motions interfere with and even override the perceived direction of stereo-motion (Chang, 1990; Ito, 1997). Our study is different in both design and intent. First, our stimuli were devoid of any luminance or texture-based motion information and second, the purpose of the study was to examine how local stereo-motions are integrated into a coherent percept of a nonrigid object in motion. Further, we used variants of these stimuli to measure human efficiency in using stereo cues for global motion, as compared to an optimal statistical model.

There is evidence for some separation of form and motion processing in the ventral and the dorsal cortical streams respectively (Ungerleider, Mishkin, Ingle, & Goodale, 1982), but the phenomena discussed above require neural interactions between form and motion mechanisms, which are being identified gradually (Kourtzi, Krekelberg, & van Wezel, 2008; Van Essen & Gallant, 1994). As for stereo cues, some neurons in area MT (DeAngelis, Cumming, & Newsome, 1998) and MST (Roy, Komatsu, & Wurtz, 1992) are jointly tuned to disparity and motion direction, and dorsal area V3B/KO is a possible site for integration of stereo and motion signals (Ban, Preston, Meeson, & Welchman, 2012), but the neural substrates of combining local stereo contributions into global object motions have not been investigated. The methods and results of this study could provide a framework for such investigations.

General Methods

Apparatus

Stereo movies were displayed on a Planar SD2620W Stereo/3D display consisting of two LCD monitors placed orthogonal to each other, with a beam-splitter to combine the images (Figure 2). In LCDs, the liquid crystal material modulates plane-polarized light. The two LCD’s in the Planar set-up are manufactured so that the plane of polarization from one monitor is perpendicular to the polarization plane in the light path of the other monitor. When stereo pair images from the two monitors are viewed through crossed-polarizing glasses, the observer sees only one monitor with each eye, resulting in a single, fused stereoscopic image. The resolution for each eye was 1920×1200 pixels with a refresh rate of 60 Hz. A chin-rest stabilized head position at a distance of 1.0 m. The experiments were conducted in a dark room.

Figure 2.

Stereo-display system using two monitors and a beam splitter (Planar Inc., SD2620W)

Stimuli

The stimuli consisted of 12 random-dot stereogram disks (Julesz, 1971) placed uniformly around a circle 2.6 deg of visual angle (dva). Thus, the radii joining the center of the disks to the center of the circle divided the circle into 12 equal angles called the inter-spoke angle. Each disk was 0.95 dva in size consisting of 50 dots and was refreshed independently on every stimulus frame. The disks were embedded in noise dots at zero disparity to eliminate any monocular cues to motion direction. We varied the depths of the disks to create 3-D shapes by assigning crossed stereo-disparities drawn independently from a Gaussian distribution with a mean of either 3.4 or 6.8 arc min (shape amplitude). During a trial, the shape was rotated around the depth axis resulting in depth oscillations of the disks that either maintained their location in the image plane (Experiment 1) or moved in the opposite direction to the shape rotation (Experiment 2). The 3-D shape was randomly deformed on each frame by adding disparity perturbation independently to each disk (perturbation amplitude), chosen from a Gaussian distribution with mean of 0, 0.9, 1.7, 3.4, 6.8, or 13.6 arc min. There were 12 images per movie presented at a rate of either 2.5 or 5 Hz (chosen randomly) resulting in a rotation speed of 75 or 150 deg/s and stimulus duration of 4.8 or 2.4s. A circular frame 3.8 dva in radius was presented around the stimulus at the screen depth to aid binocular fusion. A fixation cross (0.11 × 0.11 dva) was presented for 0.5 s at the beginning of each trial followed by stimulus presentation. The first image was presented for 1s to aid fusion. Observers reported the perceived direction of global-xy rotation by pressing a key. Both experiments consisted of 40 repetitions for each condition, spread over 20 blocks of 48 trials. Stimuli were generated using the Psychtoolbox (Brainard, 1997; Kleiner, Brainard, & Pelli, 2007; Pelli, 1997) for MATLAB (The Mathworks^™, USA).

Experiment 1: Disparity defined motion

In this experiment, the shape was rotated by the inter-spoke angle on each image frame. Thus, the disks did not move in the image plane, but appeared to oscillate back and forth in depth in a manner consistent with clockwise or counterclockwise rotation of a deforming shape (Figure 3 and Movies 1–3). To rule out the possibility of observers using any monocular cues to perform the task, we conducted a control experiment where stimuli were presented to either right or left eye randomly.

Figure 3.

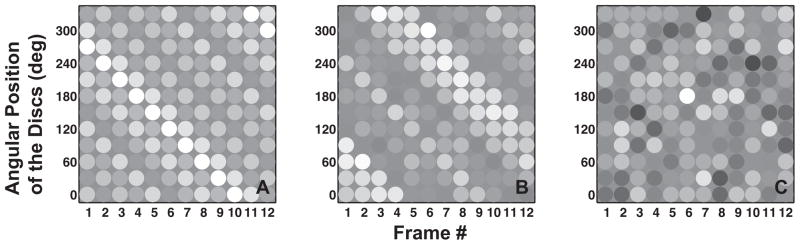
Panels A, B and C show the space-time diagrams for sample stimuli used in Experiment 1 under no noise, small noise and large noise conditions, respectively. Disparities are depicted using gray-scale with zero disparity depicted by medium gray. The downward oriented lines in Panels A and B show a clear clockwise rotation while a lack of such oriented lines in Panel C correspond to an absence of coherent shape rotation.

Experiment 2: Global versus Local motion

To oppose stereo-defined shapes versus local motions as the driving factor in the observers’ responses, the shape was rotated by 80% of the inter-spoke angle, thus creating shortest/slowest local-xy motion (Weiss, Simoncelli, & Adelson, 2002) in the direction opposite to the global-xy shape motion (Figure 4 and Movies 4–6). To ascertain the role of this local-xy motion we conducted a control experiment where we set the shape and perturbation amplitudes to zero and each disk was assigned a uniform cross-disparity value of 6.8 arc min. Observers’ task was the same, 2-AFC direction discrimination.

Figure 4.

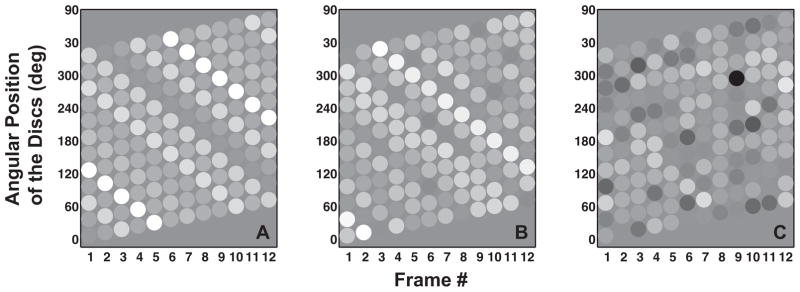
Panels A, B and C show the space-time diagrams for sample stimuli used in Experiment 2 under no noise, small noise and large noise conditions, respectively. Disparities are depicted using gray-scale with zero disparity depicted by medium gray. The downward oriented lines formed by discs with similar brightness (disparity) in Panels A and B show a clockwise rotation of the shape even when the local motion of each disk is in the counter-clockwise direction as shown by the upward tilt of each row. A lack of such downward oriented lines in Panel C correspond to an absence of coherent shape rotation, even though local apparent motion signals are still present.

Observers

Nine uninformed observers (8 females, 1 male) and one of the authors (AJ) completed all the conditions in the two experiments. Observers provided written consent prior to their participation and were compensated for their time. All experiments were conducted in compliance with the protocol approved by the IRB at SUNY College of Optometry and the Declaration of Helsinki.

Results

Experiment 1: Disparity defined motion

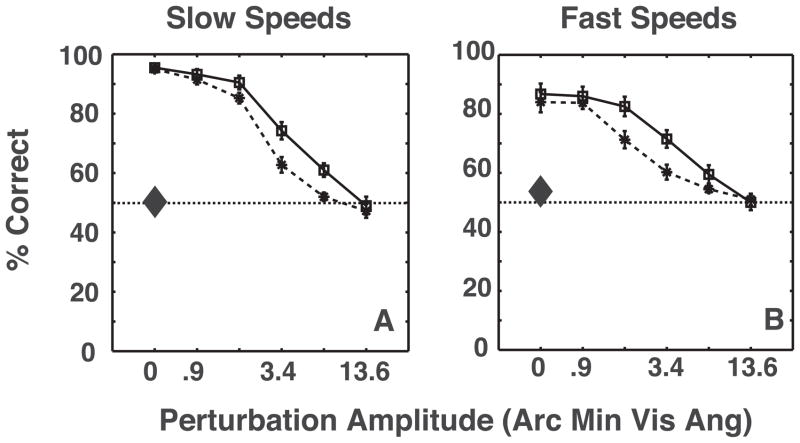
Figures 5A and 5B show mean performance for 10 observers as a function of perturbation amplitude for the two shape amplitudes and the two presentation rates. In the absence of perturbation, observers were able to discern the direction of global-xy rotation reliably, despite the fact that the only motion for each disk was z-motion orthogonal to rotation direction. Performance decreased monotonically with increasing perturbation amplitude, but improved with increased shape amplitude. This suggests that observers relied, at least partly, on some form of shape matching or rotation-template to achieve this task. Observers performed better at slower presentation rates, which is in agreement with previous findings for third-order motion stimuli (Lu & Sperling, 1995), and consistent with the fact that stereo-motion perception declines at higher temporal frequencies. Alternately, the possibility of a decline in stereo-shape extraction at faster presentation rates (Foley & Tyler, 1976) cannot be ruled out as a cause, although Tseng et al. (2006) showed that observers are sometimes unable to discriminate motion direction of stereo-defined gratings, even when they clearly perceive the grating. Performance declined for both grating and motion detection at higher temporal frequencies. The interaction between shape amplitude and perturbation amplitude and perturbation amplitude and presentation rate is likely due to a ceiling effect at lower values of perturbation amplitude. Finally, the chance level performance on the monocular control task, shows that the task required extraction of stereo-based depth information.

Figure 5.

Average of 10 observers’ performances as a function of perturbation amplitude at slow and fast presentation rates in Experiment 1. Solid lines and dashed lines correspond to large and small shape amplitudes, respectively. The large diamonds show chance performance on the monocular control task. The error-bars depict the standard error of the mean. A three-way repeated measures ANOVA revealed significant effects of perturbation amplitude (F(5,45) = 214.33, p ⋘ 0.0001), shape amplitude (F(1,9) = 24.11, p = 0.0008 and presentation rate (F(1,9) = 17.41, p = 0.0024). There was also a significant interaction between shape amplitude and perturbation amplitude (F(5,45) = 6.04, p = 0.0002) and perturbation amplitude and presentation rate (F(5,45) = 7.48, p ⋘ 0.0001). Observers performed at chance for the control tasks, both at slow speeds (t(9) = 0.22, p = 0.83 and t(9) = 2.28, p = 0.05).

Experiment 2: Global versus Local motion

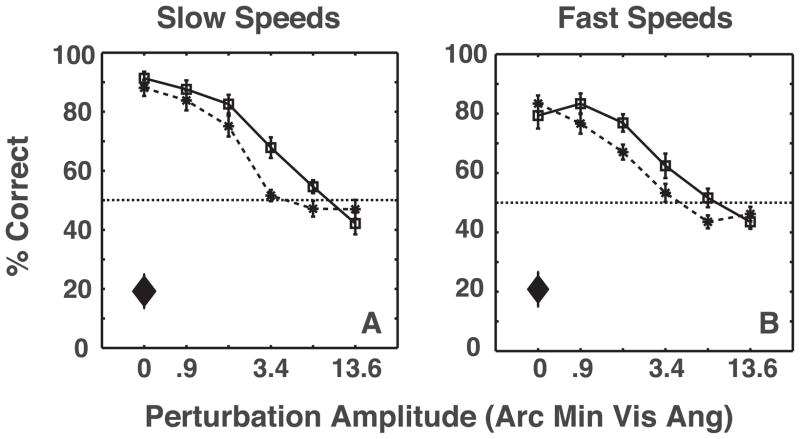
There are two plausible strategies that observers could have used to discern rotation direction in Experiment 1. They could have extracted a 3-D shape on each frame and compared shapes across frames to determine the rotation direction, or they could have determined the local-xy motion direction for each disk and performed a pooling operation to determine object rotation. In Experiment 2, the shape was rotated by 80% of the inter-spoke angle between presentations, which resulted in the shortest/slowest local-xy motion (Weiss et al., 2002) being in the direction opposite to the global-xy shape rotation. This allowed us to compare the role of global shape cues and local motion signals in inferring object motion. Figure 6A and 6B show that despite the presence of distracting local-xy motions that were opposite to global-xy rotation, results of Experiment 2 were similar to Experiment 1: observers’ performance declined monotonically with perturbation amplitude, but improved with shape amplitude and presentation rate. The main difference was that at large values of perturbation amplitude, when global shape changed drastically from frame to frame, observers based rotation reports on the direction of local motion, as shown by points lying reliably below 50%. These results show that observers weigh local motion signals more for large dynamic shape deformations, and global shape cues more when the shape-correlations are higher due to smaller deformations, suggesting that the cues are weighted proportional to relative reliability.

Figure 6.

Average of 10 observers’ performances as a function of perturbation amplitude at slow and fast presentation rates in Experiment 2. Solid lines and dashed lines correspond to large and small shape amplitudes, respectively. The diamonds show the effects of local motion when the global shape had zero amplitude. The error-bars depict the standard error of the mean. A three-way repeated measures ANOVA revealed significant effects of perturbation amplitude (F(5,45) = 78, p ⋘ 0.0001), shape amplitude (F(1,9) = 26.93, p = 0.0006 and presentation rate (F(1,9) = 18.76, p = 0.0019). There was also a significant interaction between shape amplitude and perturbation amplitude (F(5,45) = 6.86, p = 0.0001). Observers performed significantly below chance on the control task for both slow (t(9) = 5.41, p = 0.0006) and fast (t(9) = 5.03, p = 0.001) presentation rates.

Finally, on the control condition with binocular viewing, observers perceived shape rotation in the direction of the strongest local-xy motion for both slow and fast presentation rates. Our experiment design is validated by the fact that observers’ percept favored local-xy motion direction in absence of stereo-defined shape (control condition) but favored global-xy rotation direction in presence of stereo-defined shape (main experiment). It should be pointed out that while the global shape cues were no longer reliable at large values of perturbation amplitude, the local-xy motion was also affected to some extent, and thus observers do not perceive global rotation in the direction of local-xy motion on 100 % of the trials (Figure 6A and 6B).

Models

Efficiency of stereo-driven object motion perception

To estimate observers’ efficiency, we compared their performance on the 3-D global-xy rotation direction discrimination task to that of an optimal Bayesian decoder. The decoder was implemented by calculating the plausibility ratio (MacKay, 2003) for clockwise and counter-clockwise rotations i.e. the ratio of the posterior probabilities for clockwise rotation, P(cw |T_i), and counter-clockwise rotation, P(cc | T_i), for each transition, T_i, between frames (Equation 1) :

$$\frac{P(cw\mid T_i)}{P(cc\mid T_i)}=\frac{{\displaystyle \sum _{\forall {\theta }_{cw}}}{P}_i(cw)·P^G(T_i\mid {\theta }_{cw})}{{\displaystyle \sum _{\forall {\theta }_{cc}}}{P}_i(cc)·P^G(T_i\mid {\theta }_{cc})}$$ (1)

In this and subsequent equations the superscripts ‘G’ and ‘L’ correspond to global-xy and local-xy motion, respectively. The prior probabilities, P_i (cw) and P_i (cc), were set to 0.5 to correspond with the experiment design. For any transition between two frames, P^G(T_i | θ_k) the likelihood distribution of getting the two shapes on the transition T_i, given each rotation angle θ_k, was computed based on the deviation from a perfect shape matching $d_{{\theta }_k}^i$, defined as the sum of squared differences between the global shapes on two successive frames rotated by θ_k (Equation 2):

$$P_G(T_i^G\mid {\theta }_k)=\frac{e^{-d_{{\theta }_k}^i}}{{\displaystyle \sum _{\forall \theta }}{e}^{-d_{\theta }^i}},{\theta }_k\in (-\pi :\pi /6:5\pi /6)$$ (2)

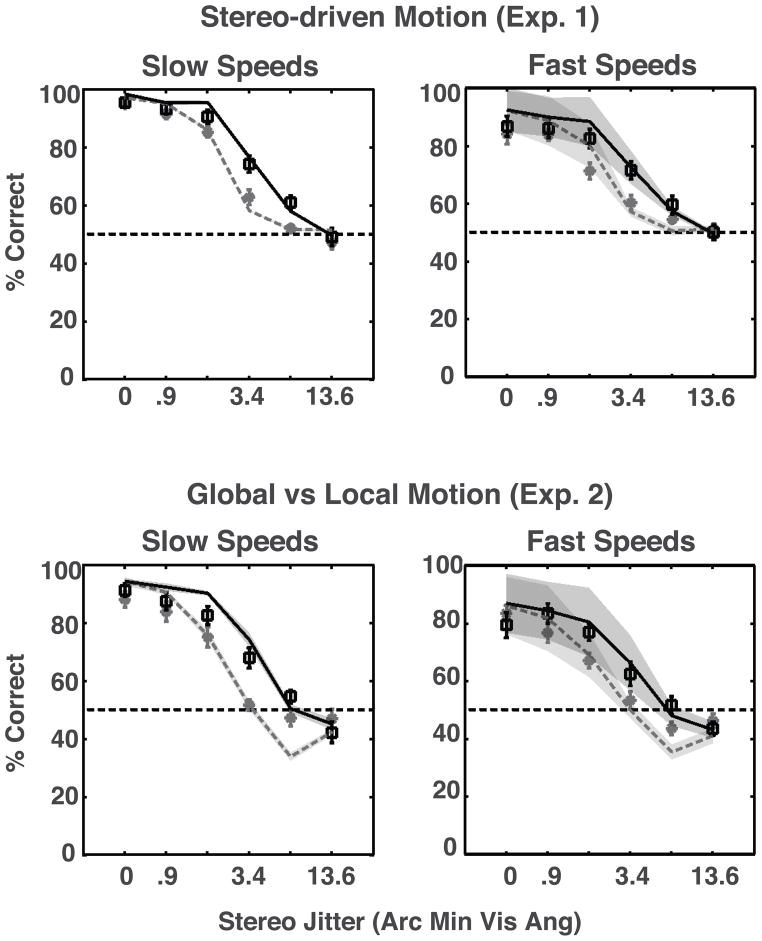
We assumed that judgments on each transition are independent of other transitions; therefore, the plausibility ratio for each trial was taken as the product of the ratios calculated for all transitions during that trial. The outcome of the trial was taken as clockwise if the trial ratio was larger than 1.0 and as counter-clockwise otherwise. Finally, the total numbers of correct direction decisions were tallied to get an accuracy proportion over all trails belonging to each condition. Figures 7A and 7B show the model’s performance as a function of perturbation amplitude on the stimuli used in Experiments 1 and 2.

Figure 7.

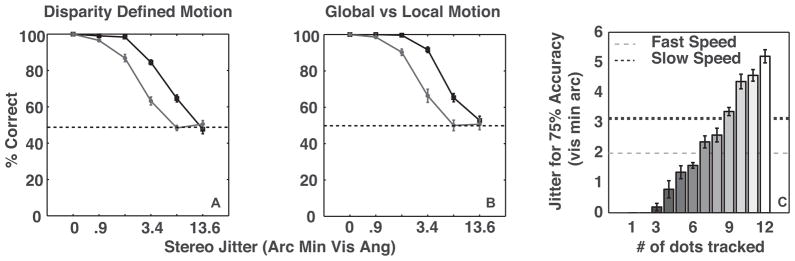
(A) Performance of the optimal model as a function of perturbation amplitude on the stimuli used in Experiment 1 and (B) Experiment 2. The solid and dashed lines correspond to the performance at large and small shape amplitudes, respectively. (C) Bars depict perturbation amplitude at 75% accuracy for the optimal model using subsets of dots (equivalently percent of available information), and lines show average perturbation amplitude at 75% accuracy for 10 observers at low (dotted) and high (dashed) presentation rates. The error-bars depict the standard error of the mean.

In order to compare the observers’ mean performance to the model’s, we used the magnitude of perturbation amplitude at 75% accuracy as performance efficiency. Higher efficiency implies that the process can tolerate more shape deformation before the performance drops to 75%. In order to vary the efficiency of the model, we varied the number of disks tracked, which can be considered to be the fraction of total available information used. Figure 7C, shows that the efficiency of the model increases monotonically with the number of disks tracked i.e. as it utilizes a larger fraction of the available information. The two horizontal lines show mean observer efficiency for the two presentation rates at the greater shape amplitude. For the lower presentation rate, observers were 75% as efficient as the Bayesian optimal decoder showing that the underlying neural processes are extremely efficient. Observers are thus either optimally tracking 9 disks or suboptimally tracking a greater number of disks in order to achieve a similar efficiency. Studies examining multiple-object tracking typically have found that only four objects can be tracked simultaneously (Intriligator & Cavanagh, 2001; Pylyshyn & Storm, 1988), while some other studies have shown the number of objects that can be tracked is dependent on the motion speed and can be as high as eight for very slow moving targets (Alvarez & Franconeri, 2007). Thus, while nine appears to be a large number for the moderate speeds used in the current experiment, it must be pointed out that multiple object tracking studies typically entail random and independent motion for each of the elements, which is not the case in the current study. Therefore, we believe that the limitations on the number of elements that can be tracked found in multiple object tracking studies does not have a strong bearing on the current finding. Further, it has been shown that for slow speeds objects are tracked as a group (Alvarez & Franconeri, 2007).

Combination of global shape and local motion cues

There are two main differences between the empirical and simulated graphs, and the differences are diagnostic. First, unlike the model’s performance, observers’ performance was less than perfect even for the no deformation condition (Figure 5). Measurement noise or internal noise in the system may be the cause. Second, when local-xy motion was opposite to global-xy rotation in Experiment 2, observers’ performance was reliably below chance for large deformations. This suggests that observers also use local-xy motion information to discern global-xy rotation direction as the global shape cue becomes less reliable.

In order to account for the observed data, we added three parameters to the Bayesian model. First, we added a multiplicative noise term to account for the less than perfect performance for the zero deformation condition. This noise term reflects both sensory measurement noise and internal neural noise. Second, we modified the likelihood function to include both a local-xy motion term and a global shape term. The local likelihood function was calculated for each disk for clockwise and counterclockwise motion in a similar fashion as the global shape-correlation based likelihood function (Equation 3).

$$P_L(T_i^L\mid {\theta }_k)=\frac{e^{-d_{{\theta }_k}^i}}{{\displaystyle \sum _{\forall \theta }}{e}^{-d_{\theta }^i}},{\theta }_k\in (-\pi /6,\pi /6)$$ (3)

The composite likelihood function was computed by combining the global likelihood function weighted by the correlation coefficient σ_θ and a scaling parameter Φ, which reflected the relative emphasis on local-xy motion and global shape cues for each individual observer (Equation 4). N is the total number of disks.

$$P_L(T_i^L+T_i^G\mid cw)=\sum _{\forall {\theta }_{cw}}{\rho }_{{\theta }_{cw}}·P(T_i^G\mid {\theta }_{cw})+\frac{\mathrm{\Phi }}{N}·\prod _{n=1}^{N}P(T_i^L\mid {\theta }_{cw})$$ (4)

Third, we added a depth scaling parameter to the model to simulate both a compressive interaction between neighboring disparity targets (Westheimer, 1986; Westheimer & Levi, 1987) and relative weights assigned to changes in depth vs changes in position in the fronto-parallel plane for calculating apparent motion for each stereogram. In summary, the model was fit to the data with three parameters, measurement/internal noise, depth scaling and relative weights for local-xy motion signals and global shape cues. Previous studies have shown that disparity thresholds decrease with increase in exposure duration (Foley & Tyler, 1976; Ogle & Weil, 1958; Shortess & Krauskopf, 1961). Thus, in order to model the effect of presentation rates we fitted the noise parameter while keeping the other two parameters fixed.

The model fit well to most observers’ data (14 out of 20 fits passed a chi-squared goodness-of-fit test at p>0.05). We then calculated the average and the 95% confidence interval of the fits. Figure 8 compares the model’s fit to the average of the 10 observers’ data. The model captures the trends in the average data extremely well, accounting for below chance performance for large deformations in Experiment 2, and better performance at the larger shape amplitude and slower presentation rate.

Figure 8.

Squares and stars show mean observer performance for large and small shape amplitude, respectively. Curves depict means of the fitted curves. The shaded areas represent 95% confidence intervals for the curves. The error bars depict standard error of the mean.

We can estimate internal noise in our model from the direction discrimination versus perturbation amplitude curves in a manner similar to the estimation using threshold vs noise curves (Nagaraja, 1964; Pelli & Farell, 1999). The knee of the curve occurs when external noise is equal to internal noise. Figure 5 shows that the absolute value of the external noise where the knee occurs varies with the shape amplitude suggesting a multiplicative nature for the internal noise. The noise estimates yielded by the model (0.29 and 0.49, for small and large shape amplitudes, respectively) correspond well to the values at the knees. The parameter for the relative weights of local motion and global shape varied considerably between observers with values ranging from 0.18, where the observer relied primarily on global shape based cues, to 1.25, where the observer relied more on local-xy motion signals (a value of 1 implies equal weights). Since, there was a constant reference frame present throughout the trial duration observers could have extracted relative depth for each disk fairly accurately after allowing for some lateral compressive interactions (Westheimer, 1986; Westheimer & Levi, 1987). Therefore, the depth scaling parameter primarily refers to the weights given to changes in depth versus changes in x-y position. The mean value for the parameter was 0.045, implying that observers primarily relied on lateral separation for computing local-xy motion rather than on separation in depth, which is in agreement with the previous findings on perception of apparent motion in 3D space (Erkelens & Collewijn, 1985; Green & Odom, 1986; Prins & Juola, 2001).

General Discussion

The early history of studying the connections between stereo and motion had a number of distinguished contributors, but many of the attempts used stimuli in which it was difficult to discern stereo-driven motion (Wade, 2012). The invention of dynamic random-dot stereograms (Julesz, 1971) made it possible to study the phenomena systematically (Chang, 1990; Erkelens & Collewijn, 1985; Patterson, 1999). By using sinusoidal depth corrugations without texture or luminance cues, (Lu & Sperling, 2002; Patterson, 1999) showed that humans can extract translation directions of motions defined solely by dynamic changes in disparity. Our conditions are different from the depth corrugations because the disparity islands are separated by space and perturbed with disparity noise. Ito (1997, 1999) used a random dot display divided into squares, either 1/16 or 1/2 of the squares were differentiated as a figure by disparity cues. In an apparent motion paradigm, observers perceived lateral motion over motion-in-depth in both cases, but only in the 1/16 case was there evidence of using global shape. Unlike in the 1/16 case, the disparity defined shape in our stimuli does not shift laterally to a new location, instead only the disparity in each disk is changed so that there are two possible xy-motion outcomes on each trial. These stimuli enable us to go beyond previous work to study how local stereo-motion signals are combined with stereo-defined shape cues to infer global motion of a deforming object.

Once disparity is extracted, it is possible to build direction selective models that use this information (Patterson, 1999), similar to models of extracting motion energy from luminance contrast through temporal delays and correlations (Adelson & Bergen, 1985; van Santen & Sperling, 1984; Watson & Ahumada, 1985). However, there is evidence that a general feature-tracking mechanism computes motion from a saliency map contributed to by many properties such as disparity, shape, etc. (Lu & Sperling, 2002). While these mechanisms provide explanations for various phenomena associated with stereomotion per se, they do not explain how local stereomotions signals may be integrated into coherent object motion for a general case of deforming objects. Ito (1999) proposed two parallel processes for computing stereomotion, first, a process that extracts shapes and edges from disparity and matches them across frames, second, a more local process that matches disparity values to its nearest region with similar disparity value. While, the local motion signals and global shape based components of our model were not designed to correspond to these processes, they do share some properties. Thus, in some ways, our model compares the relative contribution of the two processes and the fitted parameters show that most observers (9 out of 10) predominantly relied on global shape based cues to extract global motion.

We showed that observers are 75% as efficient as an optimal Bayesian decoder when discerning rotation direction of a dynamically deforming object defined purely by stereo cues. This high efficiency contrasts with the low efficiencies for perceiving point-light biological motion (J. M. Gold, Tadin, Cook, & Blake, 2008) and band-pass filtered faces (J. Gold, Bennett, & Sekuler, 1999), which are 0.4–2.5 % and 0.5–1.5%, respectively. Even simple motion direction tasks for dynamic random-dot stimuli, yield efficiencies of only 35% (Watamaniuk, 1993). Further, studies examining stereoscopic depth perception using random-dot stereograms have found human efficiency ranging from 20 % to about 1 % depending on stimulus dot density (Cormack, Landers, & Ramakrishnan, 1997; Harris & Parker, 1992; Wallace & Mamassian, 2004). However, human observers are extremely good at matching shapes under rotational transformations, especially for small angles of rotation that were used in the current study (Graf, 2006; Lawson & Jolicoeur, 1998; Marr, 1995). While the neural mechanisms involved in extracting motion of deforming objects are not clear, our modeling approach suggests a plausible mechanism that takes advantage of high efficiency of the visual system to compare shapes across rotational transformations.

The efficiency for 3-D shapes is lower than for 2-D deforming objects made of orthogonal local motions Cohen et al. (2010). For 2-D objects, observers were 90 % as efficient as an optimal Bayesian decoder and even out-performed the decoder when the shapes were symmetric. This difference can partly be attributed to the higher sensitivity to 2-D displacements than to 3-D disparity defined position changes (Erkelens & Collewijn, 1985; Prins & Juola, 2001). Moreover, the shapes deformed randomly in our stimuli, whereas in most natural cases the deformations are fairly systematic and smooth, which could allow the visual system to take advantage of continuity and improve performance.

The stimuli used in current experiments consisted of uniformly sampled disparity defined 3D shapes. While, this design allowed us to isolate, examine and quantify the role of disparity cues in extracting global motion of deforming objects it represents an over-simplified version of real world objects. Indeed, most occluded objects are not sampled uniformly nor do the visible patches occur at the same eccentricity through out the visual field. In such cases, it is possible that information from the fovea region is weighted more than information in periphery due to a decline in stereo-acuity with eccentricity (Cumming & DeAngelis, 2001; Parker, 2007; Wardle, Bex, Cass, & Alais, 2012). Further, 2D shapes formed by visible patches can be used to extract motion as well and Cohen et al. (2010) have shown that humans are not only extremely efficient at using 2D shapes but can also use abstract properties such as symmetry to extract object motion.

It is well known that local motion direction is affected by global context and various mechanisms have been suggested ranging from simple combination rules (Movshon, Adelson, Gizzi, & Newsome, 1985; Weiss et al., 2002) for translation motion to regularization principles for more complex motions (Hildreth, 1984; Ullman, 1979). The dynamic and random distortions used in our stimuli enabled us to explore the role of global form in integrating local motion signals. Our results cannot be explained by theories that consider only local motion interactions (Hildreth, 1984; Ullman, 1979), since performance drops drastically when sections of the stimuli are occluded, even though local motion interactions remain intact for the visible sections. Instead, our findings that observers can extract global motions of deforming 3D objects when strongest local motions are in the orthogonal (z motion) or even opposite direction (local-xy motion) to the global shape rotation add to the literature on interactions between the ‘form’ and ‘motion’ streams of neural processing (Nishida, 2011). Electrophysiology and fMRI have shown that Glass (1969) patterns activate motion areas, MT/MST, in a manner similar to motion cues (Krekelberg, Dannenberg, Hoffmann, Bremmer, & Ross, 2003), and point-light simulations of biological motion activate both dorsal and ventral streams (Grossman et al., 2000; Peuskens, Vanrie, Verfaillie, & Orban, 2005). Studies examining interactions between form and motion streams have provided evidence for both late (Rao, Rainer, & Miller, 1997) and early interactions (Lorenceau & Alais, 2001). Our results provide further evidence for late interactions given that motion was invisible when viewed monocularly, i.e. observers had to extract the disparity-defined shape in order to see it rotate.

It is worth considering possible neural substrates for our perceptual results. fMRI measurements have shown that visual area V3A is sensitive to stereoscopic stimuli (Backus, Fleet, Parker, & Heeger, 2001) and to feature-tracking (Caplovitz & Tse, 2007b). It remains to be seen whether some neurons contribute to both, or whether the combination is in V3B/KO (Ban et al., 2012). Moreover neurons in MT and MST respond to disparity and motion (Roy et al., 1992). Global motion is probably processed in MSTd (Duffy & Wurtz, 1991) and not MT (Hedges et al., 2011), but it remains to be tested whether these neurons could be driven by stereo-driven motion.