Retinotopic Patterns of Correlated Fluctuations in Visual Cortex Reflect the Dynamics of Spontaneous Perceptual Suppression

Abstract

While viewing certain stimuli, perception changes spontaneously in the face of constant input. For example, during “motion induced blindness” (MIB), a small salient target spontaneously disappears and reappears when surrounded by a moving mask. Models of such bistable perceptual phenomena posit spontaneous fluctuations in neuronal activity throughout multiple stages of the visual cortical hierarchy. We used fMRI in humans to link correlated activity fluctuations across human visual cortical areas V1 through V4 to the dynamics (rate and duration) of MIB target disappearance. We computed the correlations between the time series of fMRI activity in multiple retinotopic sub-regions corresponding to MIB target and mask. Linear decomposition of the matrix of temporal correlations revealed spatial patterns of activity fluctuations, irrespective of whether or not these were time-locked to behavioral reports of target disappearance. The spatial pattern that dominated the activity fluctuations during MIB was spatially non-specific, shared by all sub-regions, but did not reflect the dynamics of perception. By contrast, the fluctuations associated with the rate of MIB disappearance were retinotopically-specific for the target sub-region in V4, and the fluctuations associated with the duration of MIB disappearance states were target-specific in V1. Target-specific fluctuations in V1 have not previously been identified by averaging activity time-locked to behavioral reports of MIB disappearance. Our results suggest that different levels of the visual cortical hierarchy shape the dynamics of perception via distinct mechanisms, which are evident in distinct spatial patterns of spontaneous cortical activity fluctuations.

Introduction

Perception sometimes changes spontaneously between distinct interpretations of the same sensory input (Blake and Logothetis, 2002; Deco and Romo, 2008). For example, during “motion-induced blindness” (MIB), a salient visual target spontaneously disappears and reappears when surrounded by a moving mask (Figure 1A) (Bonneh et al., 2001; Donner et al., 2008; Bonneh and Donner, 2011). Models of such “bistable” perceptual phenomena posit that the dynamics of perception are caused by intrinsic (independent of stimulus changes) fluctuations in neuronal activity across multiple stages of the visual cortical hierarchy (Blake and Logothetis, 2002; Wilson, 2003; Freeman, 2005; Kim et al., 2006; Moreno-Bote et al., 2007; Noest et al., 2007; Gigante et al., 2009). These fluctuations, in turn, are produced by the interplay of adaption within specialized populations of neurons, interactions between these populations, and “noise”. According to these models, MIB occurs because of fluctuations in the activity of retinotopically-organized neuronal populations processing the target across visual cortical areas.

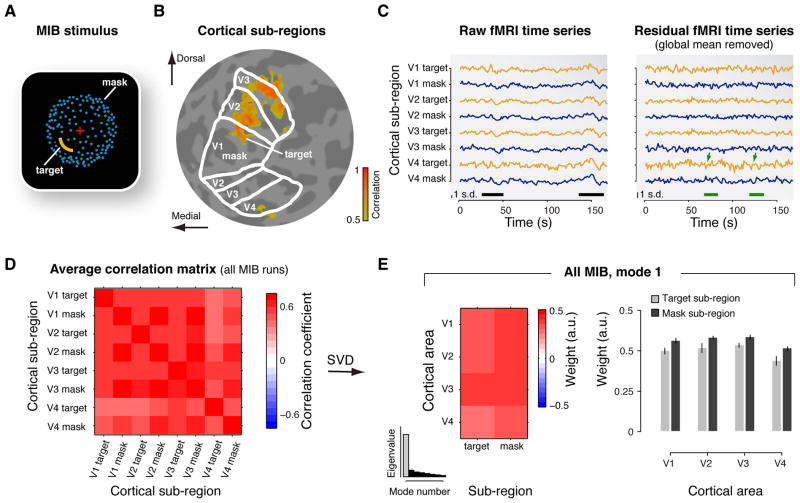
Figure 1. Correlation structure of cortical activity during MIB.

(A) Snapshot of the dynamic MIB stimulus. A salient yellow target was surrounded by a moving dot pattern (blue), which appeared as a rotating sphere. The target was presented in different visual field quadrants for different subjects. While viewing this stimulus, subjects repeatedly experienced and reported the spontaneous disappearance and reappearance of the target. (B) Cortical sub-regions. Separate localizer protocols delineated the sub-regions corresponding retinopically to the MIB target and the surrounding mask, within each of V1-V4 (highlighted for V1). The figure shows an example map of cortical responses to flickering probe stimulus presented at the spatial location of the MIB target. Colors represent correlation between measured activity and stimulus alternations (threshold: r > 0.5). The map is superimposed on a flattened representation of the subject’s occipital lobe. The borders of areas V1, V2, V3, and V4 are indicated as white outlines. The probe in the lower-left visual-field quadrant evoked responses in the dorsal sub-regions of right hemisphere visual areas V1-V3, and in the corresponding sub-region of area V4. (C) Example fMRI time series during one run of MIB. Left panel: “Raw” fMRI time series of the eight cortical sub-regions (yellow traces: target sub-regions; blue traces: mask sub-regions). The black bars at the bottom mark epochs of strong global fluctuations shared by all sub-regions. Right panel: Residual time series after removing the global mean across all sub-regions. The green bars and arrows mark epochs of anti-correlated fluctuations in the target and mask sub-regions of V4 (compare traces for target and mask subregions). Note the smaller scale than in the left panel. (D) Correlation matrix showing pair-wise correlation coefficients, for each pair of ROIs, averaged across all MIB runs and the six subjects. (E) Spatial mode, averaged across subjects. Left: Map of the spatial mode weights. The spatial modes are vectors, whose elements are re-organized as matrices (4 cortical areas × 2 subregions) for illustration. Right: Bar graph of the spatial mode weights. (Error bars: SEM, N=6) Inset: histogram of the eigenvalues. Gray bar, eigenvalue corresponding to the first spatial mode.

It has long been known that neuronal activity in visual cortex fluctuates continuously in the face of constant sensory input (Heggelund and Albus, 1978; Arieli et al., 1996; Fiser et al., 2004; Fox and Raichle, 2007; Faisal et al., 2008; Ringach, 2009). These fluctuations are correlated across visual cortical areas at a “global” spatial scale (Leopold et al., 2003; Nir et al., 2006; Yeo et al., 2011). However, optical imaging in monkeys (Tsodyks et al., 1999; Kenet et al., 2003) and fMRI in humans (Heinzle et al., 2011) revealed also spatially-specific fluctuations that reflect the retinotopically-organized intrinsic anatomical connectivity of cortical networks.

The goal of the present study was to determine which spatial patterns of cortical fluctuations, the global or the retinotopically-specific ones, are linked to the dynamics of bistable perception. To identify these patterns, we applied an alternative analysis approach to fMRI data recorded during MIB. Most previous studies of perceptual bistability used subjects’ behavioral reports of their perceptual changes to quantify the underlying fluctuations of activity in visual cortex (Leopold and Logothetis, 1996; Polonsky et al., 2000; Blake and Logothetis, 2002; Tong et al., 2006; Donner et al., 2008; Sterzer et al., 2009). However, there is not necessarily an instantaneous, and one-to-one, mapping between neuronal activity in visual cortex and perceptual reports (Lamme, 2003). During bistable perception, some activity fluctuations may directly culminate in a reported perceptual transition, whereas others might lay the foundation for these transitions, or affect the stability of perceptual states, without being closely coupled to the reports (Lumer and Rees, 1999; Lee et al., 2007). By exploiting the intrinsic temporal correlations between fMRI time series, our analysis quantified ongoing cortical fluctuations, irrespective of whether or not they were time-locked to behavioral reports of target disappearance. The analysis revealed spatial patterns of correlated fluctuations across multiple retinotopic sub-regions, corresponding to target and mask, in visual cortical areas V1 through V4. The spatial patterns whose fluctuations reflected the rate and duration of MIB both exhibited retinotopic specificity for the target sub-region, but in distinct cortical areas.

Materials and Methods

The current study is based on a re-analysis of fMRI data from a previously published study of MIB (Donner et al., 2008). In the following, we focus on the procedures unique to the present re-analysis of those data.

Subjects and scanning sessions

Data were acquired from six healthy subjects with normal or corrected-to-normal vision (one female, age range: 25 – 35 years). The experiments were conducted with the written consent of each subject and in accordance with the safety guidelines for fMRI research, as approved by the University Committee on Activities Involving Human Subjects at New York University.

Each subject participated in multiple scanning sessions prior to the main experiments: one to obtain a high-resolution anatomical volume for cortical surface extraction, one to define retinotopically-organized visual cortical areas, and one to identify the sub-regions of these areas corresponding to the target and mask locations (see below for details).

Experimental protocols

Subjects participated in several sessions of the main experiments involving three experimental conditions: MIB, fixation, and periodic stimulation. All six subjects participated in the MIB experiments (between 19 and 27 runs). Three of the subjects also participated in the fixation (between 10 and 15 runs) and periodic stimulation experiments (between two and four runs). Subjects were supine and viewed the screen through an angled mirror. The scanner room was dark.

During MIB, subjects fixated a central cross and reported the disappearance and reappearance of a static yellow contour (the “target”) surrounded by a moving blue random dot pattern (the “mask”) (Figure 1A). Target and mask were separated by a black “protection zone”. The target was presented in one of the four visual field quadrants, which was selected individually for each subject to maximize the percentage of viewing time that the target was invisible. The size of the target was then adjusted to be as large as possible while maintaining a minimum MIB strength (20% of viewing time invisible). Each run lasted 180 s. Subjects reported their perception of the target by depressing a button with the middle (visible) or index finger (invisible) of the right hand. Thus, subjects continuously depressed a button with the same hand throughout each run.

During fixation runs, subjects fixated a central cross, which was presented on an otherwise black screen. Each run lasted 180 s.

During periodic stimulation, subjects fixated a central cross and viewed a block-alternation (15 cycles of 16.8 s, i.e., 0.0595 Hz) between two complementary diagonal arrangements of probe stimuli. Each of these probes was centered in one visual field quadrant, and each had the same spatial configuration and eccentricity as the MIB target, but flickered at 8 Hz. Each run lasted 252 s.

Perceptual dynamics

The perceptual dynamics of MIB target disappearance were quantified, separately for each run, by means of two different measures: rate and duration. MIB rate was computed as the number of target disappearances per minute. MIB duration was computed as the median duration of all target disappearances across a run. The median, rather than the mean, was used as a measure of central tendency because the distributions of perceptual state durations were skewed (Figure 1 in (Donner et al., 2008)). Both parameters (rate, duration) were used for a different median split of MIB runs: high- versus low-rate and long- versus short-duration. Each median split was done separately for each subject.

MRI data acquisition

Data were acquired with a 3 T Allegra MRI scanner (Siemens Medical Systems, Erlangen, Germany) equipped with a transmit head coil (NM-011) and a four-channel phased-array receive surface coil (NMSC-021; both Nova Medical, Wakefield, MA) positioned at the back of the head. We measured blood oxygenation level dependent (BOLD) changes in MRI signal intensity using an echoplanar pulse sequence with the following parameters: repetition time, TR = 1.2 s; echo time, TE = 30 ms; flip angle, 72°; 64 × 64 matrix; voxel size, 3 × 3 × 3 mm; 22 slices oriented roughly perpendicular to the calcarine sulcus, covering the occipital lobe and part of the temporal and parietal lobes. In retinotopic mapping sessions we used the same imaging parameters with the following exceptions: TR = 1.5 s; flip angle, 75°; 27 slices. At the beginning of each session, we acquired an anatomical T1-weighted MPRAGE volume in the same slices as the functional volumes, but with twice the inplane resolution (voxel size, 1.5 × 1.5 × 3 mm).

fMRI preprocessing

Data from the beginning of each functional run were discarded (10 volumes from each run of MIB and fixation; 14 volumes from each run of the retinotopic mapping and periodic stimulus alternation experiments) to minimize the effect of transient magnetic saturation, and to allow the hemodynamic response to reach steady state baseline. We compensated for head movements within and across runs with standard procedures (Jenkinson et al., 2002). Within each region of interest (ROI; see Regions of Interest below) and each run, the time series of each voxel was converted from arbitrary intensity units to percent modulation (to compensate for distance from the coil and partial volume effects). We then averaged the time series across voxels in each ROI, high-pass filtered the average ROI time series (cutoff: 0.01 Hz), and finally converted the average ROI time series into units of standard deviation (i.e., z-scores).

The anatomical volume from each session was aligned to a high-resolution anatomical volume (acquired in a different scanning session) by an automated robust image registration algorithm (Nestares and Heeger, 2000). The resulting alignment parameters were used to resample the functional data from the localizer runs of each scanning session to the image space of the high-resolution anatomy. Cortical surfaces were extracted from the high-resolution anatomy to visualize and define the ROIs on computationally-flattened representations of the occipital cortex. The alignment parameters were also used to transform the ROIs from the coordinates of the high-resolution anatomical volume to the image space of each session. This enabled us to extract the mean time series from each ROI for each run in each scanning sessions.

Regions of interest (ROIs)

Retinotopic maps in human visual cortex were measured using standard procedures (Wandell et al., 2007) to identify visual field maps corresponding to V1, V2, V3, and V4 in each individual subject following the conventions of Wandell et al. (Wandell et al., 2007).

In a separate session, subjects completed eight to ten runs of the periodic stimulation experiment described above. We used these data to identify the sub-regions V1-V4 that corresponded to the target in MIB experiments (Figure 1B), as well as these sub-regions’ retinotopic complements for the other three visual field quadrants. To minimize any possible co-registration errors, we repeated between two and five of these target localizer runs within each session of the MIB experiments and further restricted the sub-regions (for details, see (Donner et al., 2008)).

We also performed three to five repeats of the periodic stimulation experiment in the fixation experiment sessions. These data constituted the periodic stimulation condition used for validating our analysis approach (Figure 5), but they were not used for restricting the ROIs.

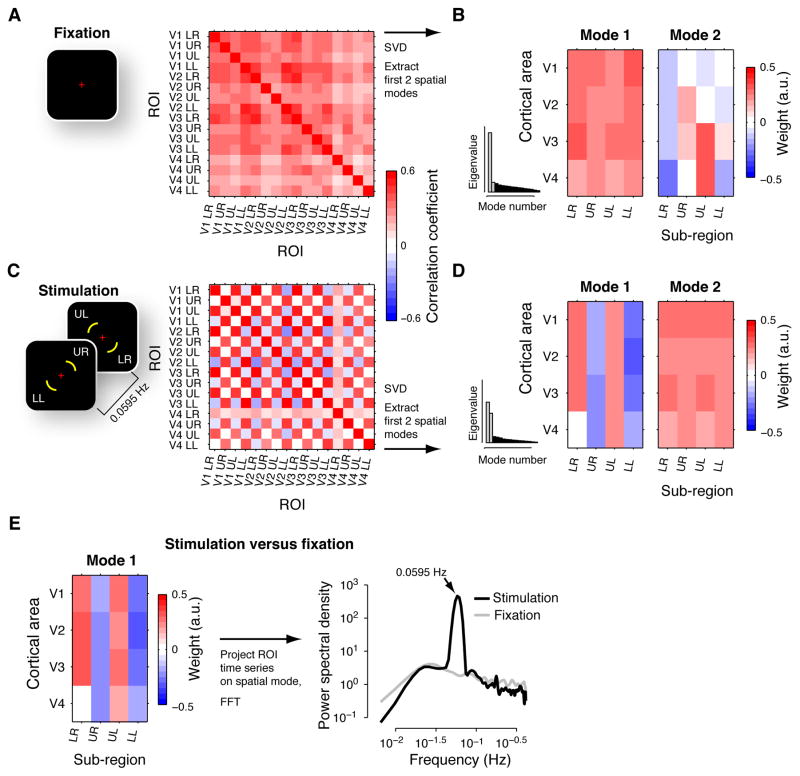
Figure 5. Spatial modes of activity during fixation and periodic stimulation.

(A) Correlation matrix for fixation. Left: Stimulus during fixation condition. Right: correlation matrix, averaged across subjects. Within each of V1-V4, four ROIs were defined as the subregions that corresponded retinotopically to a portion of each of the four visual field quadrants (see stimulus snapshot in panel C): “LR”, lower right quadrant of the visual field; “UR”, upper right; “UL”, upper-left; “LL”, lower-left. (B) Maps for the first two spatial modes during fixation, averaged across subjects, are shown along with histograms of the average eigenvalues (corresponding eigenvalues highlighted in gray). The spatial modes were re-organized as matrices (4 cortical areas × 4 sub-regions) for illustration. (C) Correlation matrix for periodic visual stimulation. Left: Snapshots of stimuli during periodic stimulation. Visual field locations in white are indicated for illustration only. Right: Correlation matrix, averaged across subjects. Same format as panel A. (D) First two spatial modes during periodic stimulation. Same format as panel B. (E) Difference between stimulation and fixation. Left panel: Map of the first spatial mode, averaged across subjects. Right panel: Power spectra of the spatial mode’s time series during fixation and stimulation. Note the prominent peak at the stimulation frequency (absent for fixation).

To identify cortical sub-regions responsive to the moving mask, subjects completed two to four runs in which the mask pattern alternated periodically (15 cycles of 16.8 s) between moving and static dots. This allowed us to define the sub-regions corresponding to the mask in each of V1-V4. The target sub-region was excluded from the mask sub-region in each visual area (for details, see (Donner et al., 2008)).

For the MIB experiment, two sub-regions per cortical area (target and mask sub-regions) were analyzed, yielding eight ROIs in total. For the periodic stimulation and fixation experiments, four sub-regions per cortical area (corresponding to the four visual field quadrants) were analyzed, yielding 16 ROIs in total.

Spatial modes of activity fluctuations

A multivariate linear decomposition, principal component analysis (PCA), identified spatial patterns (“spatial modes”) across visual area ROIs, for which the activity co-varied over time. We implemented PCA by means of singular value decomposition (SVD, (Mitra and Pesaran, 1999; Friston and Büchel, 2004)). Our analysis approach was motivated by the notion that cortical fMRI responses reflect an approximately linear mixture of multiple components (Cardoso et al., 2012), with possibly distinct underlying electrophysiological signals (Maier et al., 2008; Cardoso et al., 2012). We chose PCA rather than other linear decompositions (such as independent component analysis (Cole et al., 2010)) because it generalized for comparing between different experimental conditions described below. For the analysis of the MIB data, we focused on the first spatial mode, for two reasons: (i) during MIB, the first spatial mode accounted for by far the greatest proportion of the variance in the data than the remaining modes (the eigenvalue for the first mode was more than six times larger than the eigenvalue for the second mode; Figure 1E); and (ii) this simplified the interpretation because the orthogonality of the spatial modes (see below) can obscure the interpretation of the higher modes.

For each run i, the ROI time series were combined into a single matrix M_i, with one row for each successive time point (TR) and one column for each ROI. For the main analyses, M_i was 140 TRs x 8 ROIs (target and mask sub-regions for each of V1-V4, see Regions of Interest above). We computed the covariance between the time series from each pair of ROIs (i.e., the columns of M_i) according to:

$$C_i={M_i}^T{M}_i,$$ (1)

where C_i was an 8 × 8 covariance matrix for run i. Because the variance of each z-scored ROI time series was 1, the covariance matrices were identical to the correlation matrices. The matrices C_i were then averaged across runs, separately for each subject. The resulting mean covariance matrices were used for two separate stages of analysis (two variants of PCA).

Spatial modes of the activity fluctuations within one condition

In the first stage of the analysis, we applied SVD to the covariance matrices from individual experimental conditions (e.g., all MIB runs), to decompose these matrices into multiple orthogonal spatial modes:

$$C=V\lambda V^T,$$ (2)

where C was an 8 × 8 covariance matrix (averaged across runs), with one element per ROI-pair, λ was an 8 × 8 matrix containing the eigenvalues of C on its diagonal (sorted in decreasing order), and V was an 8 × 8 matrix with the orthonormal eigenvectors of C in its columns. Superscript T denotes matrix transposition. Each of the eigenvectors (i.e., each column of V) defined a spatial mode (i.e., a pattern of correlated activity fluctuations across the 8 ROIs). The first column of V was the first spatial mode and corresponded to the largest eigenvalue. The analysis was repeated separately for each individual subject.

Please note that the same V (i.e. the same set of spatial modes) could have also been obtained by applying SVD to the matrix of the time series data, M_i, rather than their covariance matrix. We describe it in terms of the decomposition of the covariance matrices, because this generalizes for comparing between different experimental conditions (see below).

We calculated the time series corresponding to a given spatial mode p, separately for each run i:

$$t_i=M_{i}p,$$ (3)

where vector t_i was a time series (140 TRs), M_i was a data matrix (140 TRs x 8 ROIs), and p was a spatial mode (i.e., one of the columns of V). The fluctuation amplitude corresponding to a given spatial mode was quantified, separately for each run, as follows:

$$s_i={t_i}^T{t}_i=p^T{C}_{i}p,$$ (4)

where s_i was the square of the scalar L² -norm of vector t_i. To convert the fluctuation amplitude into units of percent variance accounted for, we normalized s_i by the total variance in C_i (i.e., the sum of its eigenvalues).

Spatial modes of the ratios of the activity fluctuations in two conditions

The second stage of the analysis identified spatial modes that accounted for most variance during one condition relative to another condition. We formalized this as a solution to the “generalized eigenvalue problem” (Friston and Büchel, 2004)), finding a vector (spatial mode) p₁ that satisfied the following equation and maximized λ₁:

$$C_1{p}_1={\lambda }_1{C}_2{p}_1$$ (5)

where C₁ and C₂ were the mean 8 × 8 covariance matrices (as defined above) for two conditions (e.g., high-rate and low-rate MIB). In other words, the spatial mode p₁ maximized the ratio of the variances it accounted for in C₁ and C₂. We identified p₁ by decomposing the matrix C₂⁻¹C₁:

$${C_2}^{-1}{C}_1=V\lambda V^T,$$ (6)

where λ was an 8 × 8 matrix containing the eigenvalues of C₂⁻¹C₁ on its diagonal, and V was an 8 × 8 matrix with the eigenvectors of C₂⁻¹C₁ in its columns. If C₁ and C₂ were identical, then C₂⁻¹C₁ = I (their product equaled the identity matrix) and λ = I. If C₁ was a copy of C₂ scaled up by factor k, then C₂⁻¹C₁ = λ = kI. In all realistic scenarios, the eigenvalues on the diagonal of λ differed, indicating that the spatial modes in the columns of V accounted for different proportions of the variance in C₁ relative to C₂. The first column of V corresponding to the largest eigenvalue λ₁ was the first spatial mode p₁ (see eq. 5). We performed two comparisons (Figure 3): high-versus low-rate MIB (based on target disappearance rate); and long- versus short-duration MIB (based on median target disappearance duration).

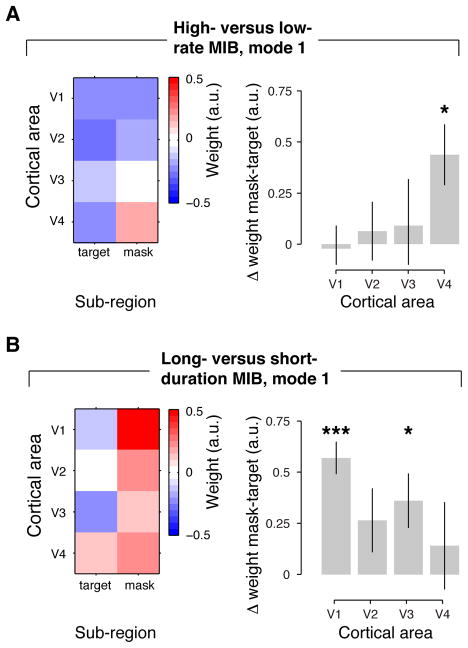
Figure 3. Spatial modes corresponding to differences in the dynamics of MIB.

(A) Difference between high- and low-rate MIB runs (median split based on disappearance rate). Left panel: Map of first spatial mode (same format as in Figure 1E). Right panel: Retinotopic specificity for individual cortical areas. Retinotopic specificity was computed as the mean difference in spatial mode weights for mask and target sub-regions. (B) Long- versus short-duration MIB (median split based on median duration of target disappearance). Same format as A. (Error bars, SEM across N = 6 subjects; *, p < 0.05; **, p < 0.01; ***, p < 0.001, two-sided t-tests).

Averaging and visualizing spatial modes

For visualizing the spatial modes (Figures 1, 3, and 5), we averaged them across subjects and re-organized them into matrices with dimensions “cortical area” x “sub-region”. The overall sign of the spatial modes (i.e., eigenvectors) is arbitrary. Thus, individual spatial modes might have opposite signs and cancel each other out during averaging. We implemented the following procedure to check for such sign flips. Each individual spatial mode was projected onto a “reference” vector, which was the average of the “raw” (i.e., unaligned) individual spatial modes. If there had been a flip in the sign of any of the individual spatial modes, its projection would have been negative. In that case, the sign of the spatial mode was flipped back, multiplying its elements by −1. After aligning the individual spatial modes in that way (if necessary), the spatial modes were again averaged together. While this procedure enabled alignment of the spatial modes in case of sign flips, it was not needed for the main results of this article, since there were (by chance) no sign flips for any of the individual spatial modes featured here.

Characterizing temporal fluctuations of spatial modes

To test for differences in the strength of the fluctuations of the spatial modes between conditions (Figures 2 and 4), we first quantified the fluctuation strength in terms of percent variance explained, within each individual run (see above). We then compared the fluctuation strengths between conditions by means of a two-sided permutation test (Efron and Tibshirani, 1998), separately for each individual subject. In another analysis (Figure 5E), we calculated the time series t_i corresponding to each spatial mode (eq. 3), and characterized their temporal structure by means of spectral analysis (Welch’s averaged periodogram method). For each of a number of successive time windows (overlap: 95%), the fast Fourier transform was computed with 256 points (spectral resolution of 0.0033 Hz). We calculated the power spectra from 0.0065 Hz to 0.4167 Hz (Nyquist frequency at 1.2 s TR). The resulting power spectra were averaged across runs and subjects.

Figure 2. Percent variance accounted for by first spatial mode during MIB.

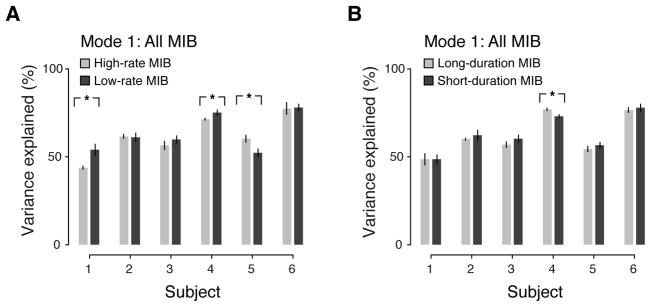
The first spatial mode extracted from all MIB runs (i.e., global component, Figure 1E) was used to determine percent variance accounted for in different subsets of MIB runs. (A) Percent variance accounted for in high- versus low-rate MIB runs. (B) Percent variance accounted for in long- versus short-duration MIB runs. (Error bars, SEM across runs; *, p < 0.05; **, p < 0.01; ***, p < 0.001, two-sided permutation tests).

Figure 4. Percent variance accounted for by spatial modes associated with the dynamics of MIB.

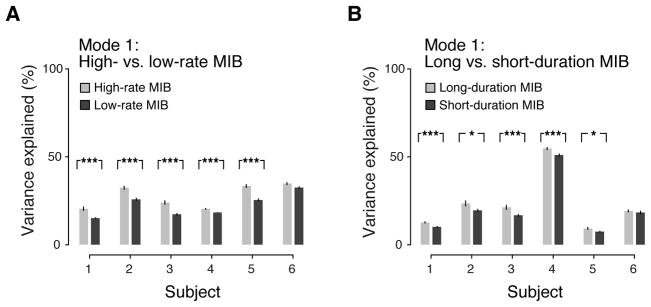
The first spatial modes from the second analysis stage (Figure 3) were used to determine percent variance accounted for in different subsets of MIB runs. (A) Percent variance accounted for by first spatial mode for high- versus low-rate MIB (Figure 3A). (B) Percent variance accounted for by first spatial mode for long- versus short-duration MIB (Figure 3B). (Error bars, SEM; *, p < 0.05; **, p < 0.01; ***, p < 0.001, two-sided permutation tests).

Testing the overall retinotopic specificity of spatial modes (retinotopic specificity index)

A scalar “retinotopic specificity index” quantified the spatial modes’ overall retinotopic structure, across the four cortical visual areas. This index was computed based on the group average spatial modes shown in Figures 1, 3, and 5. The spatial mode weights were extracted from each retinotopic sub-region. We then averaged the spatial mode weights across all pairs of retinotopically corresponding sub-regions, and, separately, across all pairs of retinotopically non-corresponding sub-regions. Both averaging procedures comprised three subsequent steps: (i) averaging the spatial mode weights across the two sub-regions within each pair; (ii) discarding the sign; (iii) averaging across pairs. Discarding the sign in step (ii) accounted for the different signs of different sub-region pairs (e.g., target and mask sub-regions). We then computed the difference between the averages for the pairs of corresponding sub-regions and for the pairs of non-corresponding sub-regions. Finally, this difference was normalized by the maximum absolute spatial mode weight of all sub-regions to express the retinotopic specificity index in units of percentage. We used a permutation procedure (Efron and Tibshirani, 1998) to assess the statistical significance of the index. Repeating the above procedure 1000 times after randomly permuting the labels of the sub-regions yielded a null distribution of indices, against which we compared the observed index to obtain a p-value.

Testing the target specificity in individual cortical areas

To assess the target-specificity separately for each visual area (V1 through V4), we computed the difference between the spatial mode weights of mask and target sub-regions within each area (Figure 3). The mask-target differences were computed based on the spatial modes of individual subjects and tested against zero by means of two-sided t-tests across the six subjects. T-tests were chosen for two reasons: (i) the quantification of retinotopic specificity should take into account both the sign and the magnitude of the difference between mask and target subregions; (ii) linear combinations of spatial mode weights are likely to be normally distributed. Indeed, chi-square tests did not reject the hypothesis that the empirically observed differences came from a normal distribution.

Results

In a previous report, we quantified the mean response modulations, time-locked to behavioral reports of target disappearance and targe re-appearance, within individual visual cortical areas (Donner et al., 2008). Here, we instead used a multivariate linear decomposition technique to identify spatial patterns (henceforth termed “spatial modes”) across visual cortical areas V1-V4, for which the activity co-varied during MIB, irrespective of the timing of subjects’ behavioral reports (see Materials and Methods). We first defined two retinotopic sub-regions, corresponding to MIB target and mask, within each cortical area (Figure 1A, B). We then correlated the fMRI time series corresponding to each pair of sub-regions (Figure 1C, left panel), separately for each 3 min run of MIB (between 19 and 27 runs, depending on the subject), and averaged the resulting matrix of correlations across runs (Figure 1D). In our analyses, the correlation matrices were identical to covariance matrices because the fMRI time series were z-scored. The correlation matrices were then decomposed in two stages. In the first stage, we decomposed the average correlation matrices from all MIB runs, to identify the spatial modes that accounted for most of the variance (fluctuation) in the multivariate fMRI time series. Each spatial mode corresponded to a pattern of correlated activity fluctuations that were distributed across the cortical sub-regions. The spatial modes were vectors with one number per sub-region. We call each of these numbers a “spatial mode weight” because it quantified the sub-region’s contribution to the spatial pattern of activity fluctuations. In the second analysis stage, we decomposed the correlation matrix from half of the MIB runs (e.g., high-rate of MIB), multiplied with the inverse of the correlation matrix from the other half of the MIB runs (e.g., low-rate MIB). This identified spatial modes that accounted for most variance in the first condition relative to the second condition. If, for example, a spatial mode occurred in both conditions and fluctuated equally strongly in both, it was discarded by this analysis. If, by contrast, a spatial mode fluctuated more strongly in the first condition, it was revealed by the analysis. While the first analysis stage characterized the general spatial structure of correlated fluctuations in cortical activity (Fox and Raichle, 2007; Ringach, 2009; Cole et al., 2010), we found that the second stage was critical for linking these fluctuations to the dynamics of perception.

The Results are organized as follows. First, we characterize the overall correlation structure and the first spatial mode during MIB. Second, we present the spatial modes that specifically reflected the dynamics (rate and duration) of MIB target disappearance. Third, we validate our analysis approach by showing that it yielded the expected spatial modes in two conditions, for both of which we expected to find retinotopic specificity, based on previous studies using similar protocols (Ringach, 2009; Heinzle et al., 2011): fixation of an otherwise blank screen, and periodic alternations between two complementary spatial stimulus configurations.

Non-specific first spatial mode during MIB

Activity during MIB was dominated by a strong, “global” (retinotopically non-specific) component, which was, however, not linked to the dynamics of MIB. The time series of the eight cortical subregions exhibited several epochs of high-amplitude fluctuations in activity, which were shared by all cortical sub-regions (Figure 1 C, left panel, marked by the black bars). Similarly strong and global fluctuations were found in all runs and subjects. Consequently, the average correlation matrix was largely homogenous, with similar correlation coefficients across all pairs of subregions (Figure 1D).

Global fluctuations of high amplitude are commonly observed in fMRI measurements during “rest” (Cole et al., 2010) (see also Spatial Modes of Activity during Fixation and Periodic Visual Stimulation below). Some portion of these fluctuations may be caused by non-neuronal physiological factors (e.g., respiration) (Birn et al., 2006; Bianciardi et al., 2009b). However, electrophysiological measurements of cortical population activity have shown fluctuations (of similar strength and global spatial structure) that accounted for the fMRI signal fluctuations (Leopold et al., 2003; Scholvinck et al., 2010). We, therefore, infer that the global signal fluctuations observed here also reflected, at least in part, neuronal activity.

The first spatial mode provided by the first stage of our linear decomposition analysis reflected the global component of the ongoing activity fluctuations evident in Figure 1C (left panel). The spatial mode weights of all sub-regions had the same sign (red in Figure 1E), which accounted for by far the largest proportion of variance in the multivariate time series (Figure 1E, compare first bin in inset histogram with the other bins). Note that the sign of a cortical sub-region in the spatial mode (i.e., blue or red) is irrelevant; what matters, is whether different sub-regions have identical or different signs. While there was a trend for retinotopic specificity (i.e., different weights for target and mask sub-regions), this was not statistically significant. We tested the retinotopic specificity of the spatial mode in two complementary approaches (see Materials and Methods). First, we quantified the overall specificity (irrespective of cortical area) in the group average spatial modes in terms of a scalar retinotopic specificity index. This index would have been larger than 0% if the spatial mode weights were more similar for retinotopically corresponding than for non-corresponding sub-regions. The index was not significantly different than expected by chance (p = 0.99, permutation test, N = 8 sub-regions). Second, we tested the difference between the spatial mode weights of mask and target sub-regions, separately for each cortical area (V1 through V4). These were not significant in any of V1 through V4, albeit approaching significance for V4.

In each subject, the time series of the first spatial mode (Materials and Methods, eq. 3) was strongly correlated with the mean time series across all sub-regions in each individual subject (p < 10⁻³, permutation test based on randomly shuffling individual runs). Thus, the first spatial mode of activity during MIB indeed closely reflected the global component of fluctuations evident in the raw fMRI time series.

The global component (i.e., the first spatial mode) accounted for a substantial fraction of the total variance in cortical activity (between 50% and about 80% depending on the subject), but it was not consistently linked to the perceptual dynamics of MIB (Figure 2). We used two complementary parameters to summarize the dynamics of MIB: the rate of target disappearance events and duration of target invisible states (Table 1). In two subjects, the first spatial mode fluctuated more for low-rate than for high-rate MIB runs, whereas it showed the opposite effect in another subject, and no difference in the remaining three (Figure 2A). Combined across subjects, there was no evidence for any difference in fluctuation strength between high-rate and low-rate MIB runs (p = 0.71, two-sided permutation test). Likewise, the first spatial mode showed no difference in five of the subjects (Figure 2B), and there was also no evidence for a difference in fluctuation strength between long-duration than for short-duration MIB runs after combining across subjects (p = 0.63, two-sided permutation test).

Table 1.

Statistics of MIB dynamics.

Subject	1	2	3	4	5	6
Disappearance rate (# reports min−1)	3.7 (2.3, 6.0)	9.3 (4.3, 12.0)	12.3 (7.7, 15.3)	9.7 (6.8, 10.7)	14.0 (7.3, 14.9)	21.7 (12.7, 22.3)
Median disappearance duration (s)	1.6 (0.9, 2.1)	1.7 (1.0, 4.0)	1.3 (0.6, 1.6)	1.7 (1.1, 3.2)	0.8 (0.6, 1.3)	0.6 (0.5, 0.8)
Percentage of trials in same group for median splits based on MIB rate and duration	64.3	63.2	71.4	25.9	41.7	39.1

Numbers are medians (2.5, 97.5 percentiles) across runs.

Specific spatial modes reflecting differences in the dynamics of MIB target disappearance

In contrast to the global component, two retinotopically-specific spatial modes exhibited fluctuations that were reliably associated with the rate or the duration of MIB target disappearance (Figures 3 and 4). These two spatial modes were revealed by the second stage of our analysis. Although both contained some specificity for the target sub-region, their detailed spatial structures were distinctly different from one another (Figure 3). In the first spatial mode for high- versus low-rate MIB (Figure 3A), the target-specificity within areas was statistically significant only in V4 (t₅ = 2.94, p < 0.05), but neither in V1 (t₅ = −0.20, p = 0.85), nor in V2 (t₅ = 0.44, p = 0.68) or V3 (t₅ = 0.40, p = 0.71). By contrast, the first spatial mode for long- versus short-duration MIB (Figure 3B) exhibited significant target-specificity in V1 (t₅ = 7.19, p < 0.01), but not in V4 (t₅ = 0.66, p = 0.54). Some degree of target-specificity was also evident in V2 and V3 (V2: t₅ = 1.70, p = 0.14; V3: t₅ = 2.71, p < 0.05; pooled across V1-V3: t₅ = 5.41, p < 0.01).

We note that the opposite signs for target and mask sub-regions evident in the spatial modes are consistent with competitive neuronal interactions within cortical areas (Carandini and Heeger, 2012). Competitive interactions between non-overlapping stimuli are well established for area V4 (Reynolds et al., 1999), and they may play a key role in the spontaneous perceptual alternations in phenomena like MIB (Blake and Logothetis, 2002). However, when discarding the global component, the opposite signs are, in principle, also consistent with no correlation between the target- and mask-specific sub-regions (Murphy et al., 2009; Cole et al., 2010).

These retinotopically-specific spatial modes accounted for a smaller fraction of the variance than the global component, but they were reliably linked to perception (Figure 4). The variance explained ranged from ~15% to ~35%, and from ~5% to ~55%, across subjects for the high-versus low rate and the long- versus short-duration, respectively. Since several inevitable noise sources other than neuronal variability (e.g., scanner noise, residual head motion, vascular noise, respiration) contribute to the total variance of the fMRI signal, these numbers represent a lower bound for the true percentage of neuronal variability explained by these spatial modes. Importantly, the high- vs. low rate spatial mode consistently accounted for a larger fraction of the variance during runs with high disappearance rate than runs with low disappearance rate (Figure 4A). Conversely, the long- vs. short-duration spatial mode consistently accounted for a larger fraction of the variance during runs with long disappearance duration than runs with short disappearance duration (Figure 4B).

It is notable that target-specificity was evident in the first spatial modes distinguishing between high- and low-rate MIB (Figure 3A) and long- and short-duration MIB (Figure 3B), despite the fact that the overall correlation structure was dominated by the global component (Figure 1D). The correlation matrices for the separate median splits were also dominated by the global component (data not shown). Since the global component did not fluctuate more strongly during high- than low-rate MIB, nor during long- than short-duration MIB (Figure 2), it was discarded by the second stage of our analysis. Indeed, removing a proxy of the global component (the mean across all eight time series) from the raw fMRI time series by linear regression (see (Donner et al., 2008)) typically revealed epochs of salient anti-correlated fluctuations between the target and mask sub-region in the residual time series (see area V4 in the right panel of Figure 1C, marked with green bars and arrows). This highlights the importance of the second stage of our analysis for revealing spatial models associated with the dynamics of MIB.

The retinotopic specificity of V1 modulations during MIB has not yet been discovered based on conventional report-triggered averaging procedures (Donner et al., 2008; Hsieh and Tse, 2009; Scholvinck and Rees, 2009a). Using report-triggered averaging, we previously identified a spatial pattern of cortical modulations during MIB (Donner et al., 2008), which closely resembled the high- versus low-rate spatial mode identified by the present analysis. During target disappearance reports, the fMRI responses decreased specifically in the target sub-region of V4, followed (a few seconds later) by a retinotopically non-specific decrease in activity across all of V1 and V2 (Donner et al., 2008). The similarity between the results from both analysis approaches may have reflected the fact that the “high-rate” runs contained many report-related transients, which consequently contributed strongly to the correlation structure. To test this idea, we repeated the present analysis on the residual fMRI time series after removing (by linear regression) the event-related modulations time-locked to reports (see (Donner et al., 2008)) for the calculation of event-related modulations), and found no evidence for retinotopic specificity (particularly not in V4) in the high- versus low-rate mode. The long- versus short-duration mode was, however, nearly unchanged and retained highly significant specificity in V1 (t₅ = 4.99, p < 0.01) after removing the report-related modulations. We conclude, therefore, that the high-versus low-rate mode, but not the long- versus short-duration mode, largely reflected fluctuations coupled to behavioral report.

There was no strong and systematic relationship between the rate and duration of target disappearance. The correlation between both parameters across the runs was not statistically significant in four of the six subjects, and the individual correlation coefficients ranged from negative to positive (mean: 0.14). If the two median splits had been orthogonal, the percentage of trials in the same (upper or lower) bin would have been 50%. By contrast, if the median splits had been perfectly correlated (anti-correlated), that percentage would have been 100% (0%). In line with the correlation coefficients, the actual percentages of overlap lay in between these two extremes, but generally closer to the “orthogonal scenario” (Table 1). When averaged across subjects, the percentage of trials in the same bin was 50.93%. Note that the rate of disappearance events and the duration of target-invisible states may become decoupled through a third parameter, the duration of target-visible states. A longer invisible duration on some runs does not necessarily lead to a lower disappearance rate: if the visible duration shortens correspondingly, the rate remains constant. Conversely, a higher disappearance rate on some runs does not necessarily lead to a shorter invisible duration: if the visible duration shortens correspondingly, the invisible duration remains constant. In sum, the two parameters used here, the rate and duration of MIB target disappearance, quantified two largely separate processes governing the perceptual dynamics.

Spatial modes of activity during fixation and periodic visual stimulation

Fluctuations of cortical activity during fixation were also (like MIB) dominated by a strong global component, and contained retinotopically-specific structure (Figure 5). We analyzed four subregions within each cortical area, one per visual field quadrant. In these analyses, we focused on the first and the second spatial mode, for two reasons: (i) during fixation, the homogenous structure of mode 1 (no systematic differences in spatial modes weights between cortical subregions) for fixation, combined with the large number of sub-regions (16), imposed no specific constraints on the structure of mode 2 (Figure 5B); (ii) during periodic stimulation, mode 2 had an eigenvalue almost as large as mode 1 (Figure 5D).

Just as observed during MIB (Figure 1D), the correlation matrix during fixation was largely homogenous (Figure 5A). Accordingly, all sub-regions had the same sign in the first spatial mode (red in panel B, top left), which accounted for the largest proportion of variance in the multivariate time series (Figure 5B, first bin in inset histogram). The retinotopic specificity index for this spatial mode was not significant (p = 0.99, permutation test; N = 8 sub-regions).

But the fluctuations also exhibited retinotopically-specific structure, which was evident in the second spatial mode that accounted for the second largest proportion of variance (Figure 5B). Corresponding sub-regions in different visual cortical areas tended to have the same sign in the spatial modes. This was most pronounced for the sub-regions corresponding to the lower right visual field quadrant (blue throughout the first column denoted “LR” in the map of the second spatial mode). The other three sub-regions were less homogenous, but showed a similar trend. Consequently, this spatial mode had a retinotopic specificity index that was significantly larger than expected by chance (index: 15.93%, p < 0.05, permutation test, N = 16 sub-regions). This is consistent with the conclusion from a number of previous optical imaging and fMRI studies, that the spatial structure of spontaneous activity fluctuations during rest is shaped by the intrinsic (e.g., retinotopically-specific) anatomical connectivity of the visual cortex (Ringach, 2009).

The spatial and temporal structure of cortical activity fluctuations also reflected activity evoked by periodic visual stimulation (Figure 5C, D). Two diagonally arranged visual field quadrants were stimulated in phase with one another (in anti-phase with the other two quadrants) at a fixed temporal frequency (0.0595 Hz). Thus, within V1-V3, the dorsal part of the left hemisphere was stimulated in phase with the ventral part of the right hemisphere and the ventral part of the left hemisphere was stimulated in phase with the dorsal part of the right hemisphere. This spatial pattern of fMRI responses was revealed by our analysis; correlations were positive for the sub-regions that were stimulated simultaneously, and negative for the sub-regions receiving anti-phase stimulation (Figure 5C). This structure of positive and negative correlations was evident in the first spatial mode (Figure 5D), for which the retinotopic specificity index was significant (index: 48.02%, p < 10⁻³, permutation test, N = 16 sub-regions).

The spatial mode that fluctuated most strongly during periodic stimulation relative to fixation (second stage of the analysis) also revealed the spatiotemporal structure of the stimulus-evoked responses. Again, the structure of positive and negative correlations evoked by the periodic stimulation was evident in the first spatial mode (Figure 5E), for which the retinotopic specificity index was again significant (index: 47.16%, p < 0.001, permutation test; N = 16 sub-regions). Further, the time series of the spatial mode identified by this analysis exhibited a prominent peak at the stimulation frequency during stimulation, but not during fixation (Figure 5E). Taken together, the results from the fixation and periodic stimulation experiments validate our approach for characterizing the correlated fluctuations in cortical activity.

Discussion

It has long been known that neuronal activity in visual cortex continuously fluctuates, even in the face of constant sensory input (Heggelund and Albus, 1978; Arieli et al., 1996; Fiser et al., 2004; Fox and Raichle, 2007; Faisal et al., 2008). While the spatial structure of fluctuations of population activity is predominantly global across the visual cortex (Leopold et al., 2003; Nir et al., 2006; Yeo et al., 2011), previous fMRI studies revealed also retinotopically-specific components (Haynes et al., 2005; Lauritzen et al., 2009; Freeman et al., 2011; Heinzle et al., 2011). But how are these fluctuations related to the spontaneous dynamics of perception? We addressed this question by linking spatial modes of fluctuations of activity in visual cortex to the statistics of the spontaneous perceptual suppression dynamics in MIB (rate and duration of disappearance states), irrespective of the timing of subjects’ behavioral reports of the perceptual changes. The rationale behind this approach was that some (perhaps many) of the activity fluctuations contributing to the perceptual dynamics may not be correlated in time with the behavioral reports (Lumer and Rees, 1999; Lee et al., 2007).

Our findings can be summarized as follows. Fluctuations of activity during constant (or absent) visual input (MIB and fixation) were dominated by a global component, which was homogenous across all of V1-V4 (Figure 1 and Figure 5 A, B). This global component exhibited fluctuations of large amplitude (accounting for at least 50% of the variance in the fMRI measurements), which were, however, not systematically related to the perceptual dynamics of MIB (Figure 2). By contrast, the spatial modes that were reliably linked to perception were retinotopically-specific for the target and exhibited fluctuations of smaller amplitude (Figures 3 and 4). The spatial mode corresponding to high versus low rate of target disappearance was target-specific in V4, but not V1 (Figure 3A), whereas the spatial mode corresponding to long versus short duration of target disappearance was target-specific in V1, but not V4 (Figure 3B). These target-specific V1 fluctuations were decoupled in time from disappearance reports, which may explain why they had been overlooked by previous studies of MIB focusing on cortical fluctuations time-locked to perceptual reports (Donner et al., 2008; Hsieh and Tse, 2009; Scholvinck and Rees, 2009a).

By linking V1 activity to the stability of perceptual suppression, our results shed new light on the role of V1 in bistable perception (Leopold and Logothetis, 1996; Wilke et al., 2006; Lee et al., 2007; Donner et al., 2008; Maier et al., 2008; Libedinsky et al., 2009). Our results suggest that different levels of the visual cortical hierarchy shape the dynamics of MIB via different mechanisms. One implication of this is that realistic computational models of MIB need to contain at least two processing levels. The same conclusion had previously been reached for models of binocular rivalry, based on other empirical results (Blake and Logothetis, 2002; Wilson, 2003; Freeman, 2005), suggesting that this may be a general principle underlying all bistable perceptual phenomena (Gigante et al., 2009).

It is unlikely that the target-specific V1 fluctuations were caused by the subjects’ motor responses, or ongoing changes in arousal. First, spatially-selective modulations in visual cortex are inconsistent with such nonspecific effects. Second, and more importantly, if due to motor responses, the target-specific V1 fluctuations should have been correlated in time with behavioral reports (and should have reflected the rate of these reports), contrary to what was observed here and in our previous study using report-triggered averaging (Donner et al., 2008).

It is also unlikely that the target-specific V1 fluctuations reflected changes in top-down, selective attention. Top-down attention modulates spatially-specific correlations between visual cortical areas (Haynes et al., 2005; Lauritzen et al., 2009) and the dynamics of MIB (Scholvinck and Rees, 2009b). Attention may even be necessary for instigating normal bistable perceptual dynamics (Zhang et al., 2011). But it seems unlikely to find a strong attentional modulation in V1 but none in V4 (Kastner and Ungerleider, 2000). Therefore, the structure of the spatial mode associated with the disappearance duration is inconsistent with top-down attention.

What, then, underlies the target-specific V1 fluctuations, and their link to duration of perceptual suppression? One possible scenario is that the V1 fluctuations were caused by fixational eye movements and, consequently, affected the duration of perceptual suppression states by changing the cortical adaption state. The target representation in V1 is gradually weakened by adaptation, which is inherited by the target representation in V4. Transients in V1 cause a rapid recovery from adaptation, strengthening the V4 target representation and shortening perceptual suppression states. V1 transients may be generated by microsaccades (Martinez-Conde et al., 2004; Hsieh and Tse, 2009; Bonneh et al., 2010), which shift the target representation to a neighboring, non-adapted location in the retinotopic map (Martinez-Conde et al., 2004). Fewer microsaccades lead to fewer target-specific V1 transients, longer adaptation of the target representation and longer perceptual suppression. Microsaccades elicit retinotopically-specific transients in V1 by driving neurons processing the static target more strongly than neurons processing the mask (Bair and O’Keefe, 1998; Martinez-Conde et al., 2000). Because of the sluggish hemodynamics, fewer target-specific V1 transients during runs with long disappearance states produce target-specific fMRI fluctuations with larger amplitudes. Because the target-specific V1 fluctuations were neither correlated with the target-specific V4 fluctuations, nor with behavioral reports, they must have affected perceptual state durations without immediately culminating in a change in the V4 target representation and report, for example by accumulating slowly in V4 (Gigante et al., 2009). While speculative, future studies using high-resolution monitoring of microsaccades during fMRI, and adopting our analysis approach, could test (specific aspects of) this scenario.

The scenario described in the preceding paragraph identified fixational eye movements and adaption as factors that may drive fluctuations of the target representation in V1 and contribute to the duration of perceptual suppression states. But stimulus-independent activity fluctuations may have occurred in V1 for many reasons other than fixational eye movements. They may have emerged locally within early visual cortex, or they may have been mediated by cortico-cortical (Moore and Armstrong, 2003; Haynes et al., 2005; Ekstrom et al., 2008; Siegel et al., 2008; Gregoriou et al., 2009; Lauritzen et al., 2009) or thalamo-cortical (Wilke et al., 2009; Saalmann et al., 2012) long-range interactions.

Our results have broader implications for the use of spontaneous fMRI signal fluctuations to identify so-called “resting-state” networks in the human brain (Biswal et al., 1995; Fox and Raichle, 2007; Vincent et al., 2007; Honey et al., 2009; Cole et al., 2010; Sadaghiani et al., 2010). The fluctuations assessed by the majority of these studies occur at coarse spatial scales spanning multiple cortical areas. Such large-scale fluctuations reflect, at least to some extent, cortico-cortical connections (Honey et al., 2009) and they have been linked to behavioral state (Bianciardi et al., 2009a) and perceptual performance (Fox and Raichle, 2007; Sadaghiani et al., 2010). Our present results put the focus on the fluctuations of specific cortical sub-populations within individual cortical areas. Although smaller in amplitude, these fluctuations reliably index the dynamics of perception.