A Computational Framework for Understanding Decision Making through Integration of Basic Learning Rules

Abstract

Nonassociative and associative learning rules simultaneously modify neural circuits. However, it remains unclear how these forms of plasticity interact to produce conditioned responses. Here we integrate nonassociative and associative conditioning within a uniform model of olfactory learning in the honeybee. Honeybees show a fairly abrupt increase in response after a number of conditioning trials. The occurrence of this abrupt change takes many more trials after exposure to nonassociative trials than just using associative conditioning. We found that the interaction of unsupervised and supervised learning rules is critical for explaining latent inhibition phenomenon. Associative conditioning combined with the mutual inhibition between the output neurons produces an abrupt increase in performance despite smooth changes of the synaptic weights. The results show that an integrated set of learning rules implemented using fan-out connectivities together with neural inhibition can explain the broad range of experimental data on learning behaviors.

Introduction

Synaptic plasticity underlying different kinds of behavioral plasticity has been identified in many brain structures in both vertebrates (Malenka and Bear, 2004) and invertebrates (Burrell and Li, 2008; Szyszka et al., 2008). At its most basic, synaptic plasticity involves experience-dependent changes in the strength of synaptic connectivity between neurons (Hebb, 1949). Two major classes of learning include nonassociative (Lubow, 1973; Van Slyke Peeke and Petrinovich, 1984) and associative learning (Rescorla, 1988), which are referred to in the machine learning literature as “unsupervised” (Hebbian) and “supervised” (Bishop, 2006). However, despite their occurrence in the same neuropils (Malenka and Bear, 2004), and even potentially operating at the same synapses (Cassenaer and Laurent, 2007, 2012), these two forms of learning are commonly considered to operate independently and to be governed by different learning rules. How these two classes of learning could interact within the same neuronal circuitry, and in such a way that they can account for the trajectory of acquisition of conditioned responding in behavioral experiments, remains largely unexplored.

We feel that this interaction is essential for explaining the trajectory of learning behavior over a series of experiences. In particular, animals frequently show an abrupt transition from little or no response to a stable, high level of responding over the course of only a few acquisition trials (Rock and Steinfeld, 1963; Gallistel et al., 2004). Abrupt transitions contrast with the assumption in most models of conditioning of an incremental and quasi-smooth increase in associative strength (Rescorla and Wagner, 1972; Pearce and Hall, 1980).

Olfactory processing in the honeybee is an excellent model for studying sensory processing and plasticity in this context. Both unsupervised (Chandra et al., 2010; Locatelli et al., 2013) and supervised (Faber et al., 1999; Müller, 2002; Fernandez et al., 2009) forms of plasticity have been identified in the honeybee olfactory system in the brain. These different types of learning have distinct parallels in olfactory processing in the mammalian brain (Brennan and Keverne, 1997; Wilson and Linster, 2008; Linster et al., 2009). While being commonly described as different types of learning governed by different learning rules, these two forms of learning may infact represent subclasses of a generic learning paradigm. For example, lack of explicit reward (unsupervised learning) may be treated as a form of negative reinforced learning when an expected positive reward is not delivered. This is because, as we argue below, both unsupervised learning and negative reinforced learning increase the strength of connections to a neural center that prevents a response (in our example below). Only unsupervised learning increases this strength weakly relative to negative reinforcement. Both forms of learning can therefore be described by similar learning rules, which may operate on different timescales. In honeybees, for example, learning about the lack of an association of an odor with nectar or pollen is an important form of learning, and the presence of unrewarding flowers has an important influence on choice behavior in freely flying honeybees (Drezner-Levy and Shafir, 2007).

In this study we propose a set of generic learning rules that together account for a variety of experimental data on reinforced and unreinforced odor learning. These rules have been implemented in a model of the honeybee olfactory system. Combination of these learning rules with mutual inhibition between the output neurons was necessary to account for an abrupt shift in responsiveness as training progresses using smooth increments in underlying synaptic weights, as required by a threshold-like decision process (Gallistel et al., 2004). We show, using data from an artificial odor sensor array based on metal oxide sensors (Vergara et al., 2012), that the model may not only reveal hypotheses about neural function but also have applicability to engineered solutions to odor detection (Muezzinoglu et al., 2008, 2009a).

Materials and Methods

Proboscis extension response conditioning

Methodologies for the data presented in Figures 1 and 2 have been reported in detail by (Fernandez et al., 2009; Chandra et al., 2010). Proboscis extension response (PER) conditioning of individual honeybee workers (all female) has been widely used as a procedure to assay learning and memory (Bitterman et al., 1983; Smith et al., 2006). The advantage of the PER procedure is that it allows for precise control over a variety of parameters, e.g., interstimulus interval, intertrial interval, training and testing intervals, and contingency between conditioning stimuli, that are critical for associative conditioning (Bitterman et al., 1983; Rescorla, 1988). Briefly, honeybees are collected from the colony, brought into the lab, and then restrained in small plastic or metal harnesses. The harnesses allow bees to freely move their mouthparts (proboscis) and antennae. An odor “conditioned stimulus” is controlled by an automated delivery system that can be programmed to deliver a constant stimulus for 4 s. A conditioning trial consists of pairing an odor (conditioned stimulus) with a small droplet (0.4 μl) of 0.5–1.5 m sucrose/water solution as the unconditioned stimulus. The sucrose is first touched to the honeybee's antennae, which contain sucrose-sensitive taste receptors. This elicits proboscis extension, upon which the sucrose is applied to the proboscis and completely consumed. Many studies have evaluated the pairing conditions necessary for producing robust associative conditioning (Bitterman et al., 1983). Under optimal conditions, one to a few pairings of odor with sucrose is usually sufficient to attain PER to odor, which is the conditioned response. Many studies using appropriate control procedures have now shown that the odor response reflects associative pavlovian conditioning (Bitterman et al., 1983).

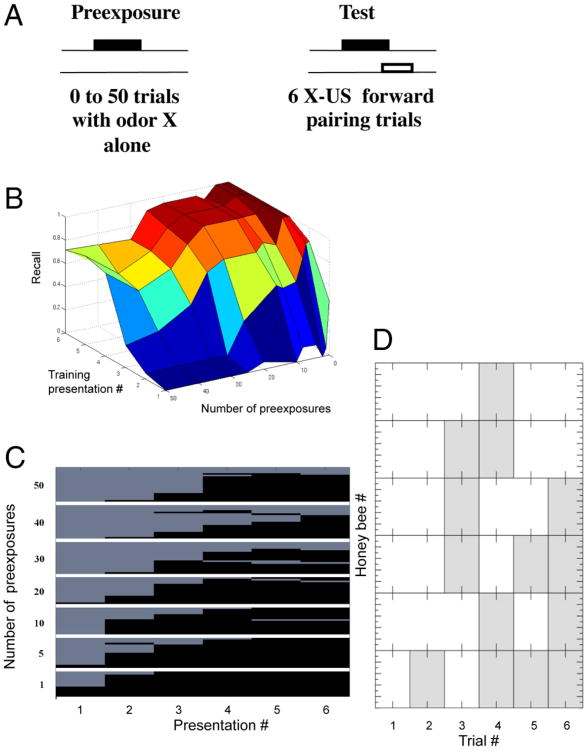
Figure 1.

Latent inhibition. A, Odor conditioning protocol for the LI experiments. The odor was first presented from 0 to 50 times (preconditioning) in different groups of honeybees before applying odor conditioning during the test phase. The protocol for the test phase produces robust and long-lasting associative conditioning (Menzel, 1990). The number of responses across six trials of the test phase, as a function of the number of preconditioning trials, is the measure of LI. B, 3D plot of the recall value versus the number of pre-exposures and the number of training presentations. Performance in honeybees that received 20–30 or more pre-exposures is poorer relative to groups that received fewer pre-exposures. C, Proboscis extension (black) versus no extension (light gray) after different numbers of pre-exposures to the odorant (top to bottom 50, 40, 30, 20, 10, 5, to 1 pre-exposures). Each of the rows represents one honeybee, and each figure shows mean levels of responding over a group of 15–20 honeybees. D, An example of behavior in a subset of honeybees at the transition from not responding to responding.

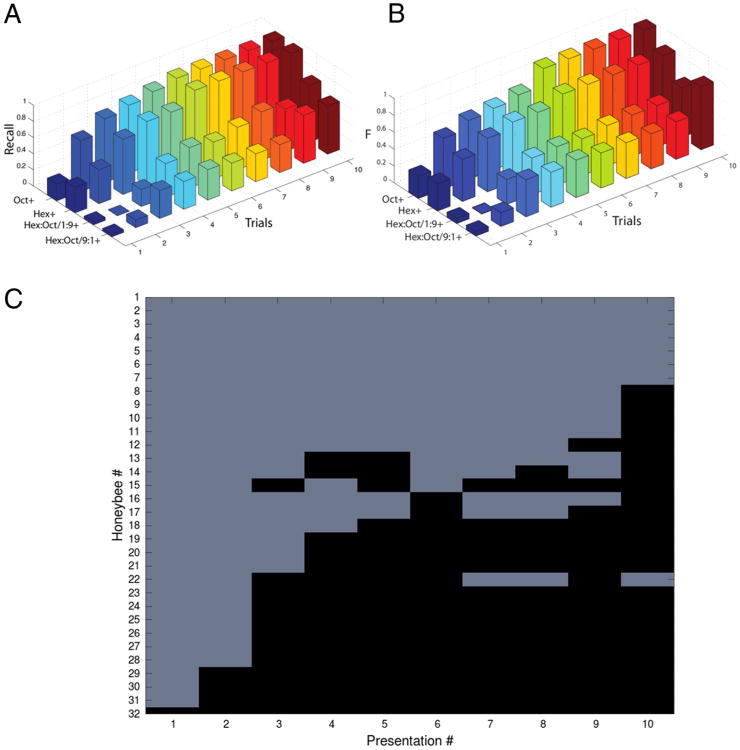
Figure 2.

Discrimination conditioning. A, Recall in a discrimination task between hexanol and octanone, and a mixture of 9:1 + hexanol – octanone versus 1:9−.B, The harmonic mean of precision and recall (F-value; Table 1). After 2–3 training presentations there is a sharp transition in the performance in odor discrimination. The learning timescale, measuring in numbers of trials, is fairly fast compared with the number of pre-exposures required for LI. C, Responses of 32 honeybees subjected to training. There are three main types of behavior: (1) honeybees that are insensitive to training in that they never begin to respond to the rewarded odor; (2) honeybees that fluctuate between extension or retraction (e.g., #13 and 14); and (3) honeybees that learn very quickly the extension protocol.

Latent inhibition

Latent inhibition (LI) is an important way that animals in general learn to not process information about stimuli that are irrelevant (Lubow, 1973). We have recently worked out the conditions needed to produce LI in honeybees (Chandra et al., 2010). Honeybees are first “pre-exposed” to an odor without association with sucrose reinforcement. After a set number of pre-exposure trials the odor is associated with reinforcement in a way that produces robust associative conditioning. As a result of pre-exposure animals typically learn about the odor slowly relative to “novel” odors, which are conditioned identically either within animals on alternate trials (presented using the pseudorandom sequence above) or in different animals.

Discrimination conditioning

Animals are exposed to two types of conditioning trials (A and X) presented in a pseudorandomized sequence (repetitions of AXXAXAAX until a desired number of A-type and X-type trials is reached) (Smith et al., 1991; Fernandez et al., 2009). During one type of trial an odor is associated with sucrose reinforcement. During the other type of trial a different odor is presented without reinforcement. The two types of trials are alternated as the A-type across animals, so that half the animals start with a reinforced trial and the other half with an unreinforced trial. Honeybees typically learn to respond with PER to the reinforced odor and not to the unreinforced odor. The degree of difficulty can be increased by lowering the concentration of odors or by using binary odor mixtures that differ in the ratios of the two components (e.g., 8:2 vs 2:8).

Structural organization of the honeybee olfactory system

Olfactory processing in the honeybee brain (Mobbs, 1982; Rybak and Menzel, 1993) is an excellent model for studying sensory processing and plasticity in the context of decisions. Information distributed across ∼50,000 olfactory sensory cell axons projects from the periphery to the antennal lobe (AL) of the brain, where axons from cells that express the same receptors converge onto the same area, called a “glomerulus.” There are ∼160 glomeruli in the AL. Dendrites from five projection neurons (PNs) innervate each glomerulus and send output via two tracts to the mushroom bodies (MB) or the lateral protocerebrum (Kirschner et al., 2006; Rössler and Zube, 2011). In addition, several different types of excitatory and inhibitory local interneurons interconnect glomeruli to transform the sensory input into a spatiotemporal output across the ∼800 PN axons (Abel et al., 2001). These axons project onto ∼170,000 intrinsic Kenyon cells (KCs) on the MB. Individual KCs require quasi-simultaneous inputs from several PN axons to reach firing threshold, and then they shut down quickly via recurrent, inhibitory feedback (Mazor and Laurent, 2005). The projection of fewer axons onto far more numerous dendrites of KCs, combined with intrinsic properties and fast shutdown of the KCs, helps to transform the spatiotemporal input into a distributed, spatial code for an odor identity (Huerta et al., 2004), and it may increase the speed of odor classification (Strube-Bloss et al., 2012). Finally, the 170,000 KC axons project to the α-lobes of the MB (Strausfeld, 2002) where they synapse onto dendrites of ∼400 extrinsic neurons (ENs; Rybak and Menzel, 1993), which provide output to other – possibly premotor - centers that control, among other things, conditioned reflexes such as proboscis extension (described below). The AL, MB, and ENs (Mauelshagen, 1993; Menzel and Manz, 2005; Okada et al., 2007) have also been established as sites for biogenic amine-driven modulation related to both nonassociative and associative plasticity (Szyszka et al., 2008; Fernandez et al., 2009; Locatelli et al., 2013). The latter type of plasticity has been related specifically to a small group of modulatory neurons, one of which (VUMmx1; Hammer, 1997) projects to both the AL and MB.

Model

The model of the MB is described by (García-Sanchez and Huerta, 2003; Huerta et al., 2004; Huerta and Nowotny, 2009) that uses a simple McCulloch–Pitts approximation (McCulloch and Pitts, 1990) of the KCs and the ENs of the MB. Given an odor-dependent activity in the PNs of the AL by x, the activity in the KCs is given by $y_i=\Theta ({\sum }_{j=1}^{N_{\mathit{\text{AL}}}}{c}_{\mathit{\text{ij}}}{x}_j-b)$, where Θ(.) is a nonlinear step function that integrates the synaptic input from the AL given by the activity level x_j; N_AL denotes the number of PN neurons in the AL; c_ij is the connectivity matrix from the AL to the KCs; and b is the activation threshold. All these parameters can be set up such that there is preservation of information from the AL to the MB as described by (García-Sanchez and Huerta, 2003). The next processing layer is a population of ENs that readout the activity levels of the KCs. As described in the text, the activity of ENs is given by $z_i=\Theta \left({\sum }_{j=1}^{N_{\mathit{\text{KC}}}}{w}_{\mathit{\text{ij}}}{y}_j-\frac{1}{N_{\mathit{\text{Extrinsic}}}}{\sum }_{j=1}^{N_{\mathit{\text{extrinsic}}}}{\sum }_{i=1}^{N_{\mathit{\text{KC}}}}{w}_{\mathit{\text{ji}}}{y}_i\right)$, in this case N_KC is the number of KC neurons, and the second term in the equation reflects the inhibition that arrives from the other ENs. This mechanism self-regulates to provide 50% level of activation on the extrinsic cells to be able to have two separate populations of ENs responding for the action of extension or retraction. Note that this model does not reflect the learning mechanisms yet. It only provides the activity regulation through the processing layers. Moreover, since it is known that the default behavior of the honeybee is proboscis retraction we use an initial probability of connection between the PN and the KC neurons of 10% that leads to better overall performance in the classification tasks in the simulation. The initial random connections of KCs to the retraction group of ENs are set to 25% in contrast to the extensor group that is set to a very low value such that the default behavior of the model in response to odor stimulation is retraction, as it should be experimentally.

Proboscis extension and retraction is essential for feeding, and honeybees are fully capable of proboscis extension and retraction when they first emerge as adults. Also, at this stage one of their first tasks for the colony is to feed developing larvae (Ament et al., 2010), which involves the need for extension and retraction. Therefore it is likely that the essential extension and retraction networks are intact at emergence. There is also considerable evidence that many brain structures, including the MB intrinsic (Kenyon) cells, continue to change in the adult both as a function of age and experience (Withers et al., 1995; Maleszka et al., 2009). So it is possible that the extension and retraction networks are influenced by both of these factors in the adult.

The initial set of connections in the model was generated by a Bernoulli process such that with probability p a connections will be set to 1 and with probability (1 – p) will be 0. The learning rules that we apply later allow increasing the connections by one unit with some given probability or reduce it by one unit. The connections cannot be negative in this model.

Precision and recall as measures of performance

When determining how well a system has learned to discriminate between stimuli one may just measure how often the system gives the wrong answer. In other words it would measure the error. This measure of how well the system does might not be useful for situations in which we need to characterize the performance of a system that by default provides a negative answer (proboscis retraction). The honeybee natural reaction to novel odors is proboscis retraction. This implies that most of the responses of the honeybee will be negative with only a few positive (proboscis extension). If one measures error as defined above as a function of the wrong answers, then the honeybee is always correct even without learning because most of the time its response is negative. This, however, would not adequately or accurately characterize learning performance. This is the problem the field of information retrieval has encountered for a long time. The concepts of “precision” and “recall” avoid this ambiguity. They are very useful in a large spectrum of applications in information retrieval and machine learning (Hripcsak and Rothschild, 2005; Olson and Delen, 2008).

Precision refers to the fraction of positive (extension) responses that are correct. For example, when animals are trained to two stimuli with one reinforced the other not (A + /X −), they should respond to A but not to X. Precision is calculated as shown in Table 1, where tp is the number of “true positive” responses to A and fp is the number of “false positive” responses to X. Precision therefore ranges from a low of 0 (i.e., tp = 0) to a maximum value of 1 (fp = 0).

Table 1. Description of precision, recall, and F measures applied to the latent inhibition and discriminating conditioning task.

	PER
	Extended	Not extended
Reinforcedodor(A+)	True positive (tp)	False positive (fn)
	P↑	P○
	R↑	R↓
	F↑	F↓■
Unreinforced odor (X−)	False positive (tp)	True negative (tn)
	P↓	P○
	R○	R○ ■
	F↓	F○

Precision (P) = tp/(tp + fp); ↑ increase; ○ no change; Recall (R) = tp/(tp + fn); ↓ decrease; F = 2 × (P × R)/(P + R). Level of inhibition of PER is relatively low or relatively high ■.

Recall measures more directly how often an appropriate response occurs to the rewarded alternative. Using the A +/X− example, recall is calculated from the total number of tp and fn responses to A (Table 1). Recall also ranges from a low of 0 (tp = 0) to a high of 1 (fn = 0) when an animal always responds to A.

Precision and recall measure different things. A high precision value approaching 1 means that when an animal responds the response is correct. Few or no fp responses to X − occur. Clearly, an animal that always responds to A but not to X has a high precision. However, an animal may also have missed responding to A on several trials, which would lead to a high fn. In the extreme, a single response to A over many A trials and no response to X would also lead to high precision. So high precision could also reflect low recall because precision is insensitive to fn. Recall also has a shortcoming. An animal may have responded appropriately to A every time it occurred, but it may also have responded to X− (fp > 0). Thus high recall could also mean low precision. Because of these limitations, a more useful measure is F, which is the harmonic mean of precision and recall (Table 1). F can separate conditions under which both precision and recall are high from when one or both are low. The harmonic measure can be generalized to give different weights to precision and recall depending on the problem and the application. However, that requires one to know the exposure of the honeybees in real environments to the odorants of interest. This requires a study of honeybee behavior in natural environments.

Sensor array data

The ethanol and ethylene data were obtained using an artificial sensor array of 16 metal oxide sensors in a controlled experimental manifold using a fully computerized environment with minimal human intervention with a constant total flow (Vergara et al., 2012). The full original dataset is available at the University of California, Irvine (UCI) Machine Learning Repository (Vergara et al., 2012). The odorants were delivered to the sensors at different concentrations ranging from 10 particles per million (ppm) to 600 ppm. The model presented here learns to discriminate between the ethanol and ethylene at any of the available concentrations. Features from the sensors are used as representative input to the MBs as described by (Muezzinoglu et al., 2009a; Vergara et al., 2012).

Results

We first will analyze behavioral experiments to understand the dynamics of unsupervised and supervised olfactory learning in honeybees. To understand unsupervised learning we will revisit experiments on LI (Chandra et al., 2010). To understand supervised learning we will analyze data in a discrimination task at different levels of complexity (Fernandez et al., 2009). These two experiments are the basis for the computational framework of this study.

Activation and repression underlie a behavioral response

It is clear that the PER (see Materials and Methods) requires activation of a neural network that controls a motor program involved in extension of the proboscis. Therefore, it is reasonable to assume in our model that such a network exists and is modified by convergent, simultaneously active inputs from olfactory and taste pathways. Modification of these networks via specific learning rules allows odor, which normally does not elicit PER, to come to elicit PER.

A second assumption in our model is less intuitively obvious. Specifically, it regards what happens when PER fails to occur. We assume the existence of neural activity that inhibits PER in the case of true and false negative responses (lack of PER to an unrewarded and to a rewarded odor, respectively; Table 1). It also fails to inhibit PER in the case of a false positive (PER to an unrewarded odor). This assumption is supported in principle by two reports. First, presentation of any odor during an ongoing PER elicited by sucrose feeding can abruptly terminate PER (Dacher and Smith, 2008). Second, association of sucrose stimulation of the antennae, which unconditionally elicits PER in motivated “hungry” honeybees, with electroshock in the context of a specific odor leads to withholding of the PER to both that odor and to sucrose presented in the context of that odor (Smith et al., 1991). Both procedures imply an active repression-like process underlying either retraction of the proboscis after it is extended (Dacher and Smith, 2008) or context-based withholding of PER when it normally should occur (Smith et al., 1991). Finally, we assume that plasticity can modify this inhibitory reflex under conditions when the response is incorrect. A false positive response (PER to an unrewarded odor) should strengthen this inhibition, whereas a false negative (lack of PER to a rewarded odor) should weaken it.

We model these two networks as separate “extension” and “retraction” centers. It may well be that these exist as distinct neural networks in the honeybee brain. However, they do not need to be distinct. They may be partially or completely overlapping. The differences between extension and retraction in these cases may involve differential activation of different components of the network.

PER-based supervised and unsupervised learning in the honeybee

To measure animal performance we will use three commonly used measures in the information retrieval and pattern recognition literature (Olson and Delen, 2008; Table 1): precision, recall and F. Precision characterizes the fraction of positive (PER) responses that are correct, while recall measures more directly how often an appropriate response occurs to the rewarded odor. F is the harmonic mean of precision and recall (see Materials and Methods). The use of precision, recall, and F for behavioral analyses has several advantages over the more traditional measures, such as response probability. First, these measures are widely used to compare performance of computer-based machine learning algorithms. Results from biological studies and machine learning algorithms would therefore be more comparable and help link experimental and engineering problems. Second, these measures are independent of the method for scoring behavioral data from many different animals and different behavioral protocols. Therefore, these measures provide a standardized way for comparing data across different conditioning tasks and between biological and machine learning experiments, particularly in regard to difficulty of the task.

We have chosen two different types of learning, LI and discrimination conditioning, which have been often studied using PER conditioning in the honeybee because they are representative of the unsupervised and supervised aspects of learning in the insect brain. When honeybees are presented with an odor several times without reinforcement, they subsequently require several more trials to learn this odor in excitatory PER conditioning than they require to learn other odors they have not experienced (Chandra et al., 2010). This process, LI, provides further evidence that plasticity modifies some components of the circuitry between sensory inputs and motor centers to alter inhibition/repression of the PER. The protocol that has been used to generate LI in honeybees involves unreinforced pre-exposure to a target odor (X−) for a number of trials. Pre-exposure treatment is followed by a series of test trials that involve excitatory conditioning of the same odor (X+). LI is evident when honeybees that received pre-exposure learn slowly relative to how well they would learn about X had it not been pre-exposed.

Chandra et al. (2010) exposed groups of honeybees to different numbers of pre-exposure trials (Fig. 1A). Groups differed from a low of zero pre-exposures (control group) to a group that received 50 pre-exposures. In most cases, LI required 15–20 unreinforced presentations before it had an effect on excitatory conditioning. Therefore, it is a slower process than excitatory conditioning, which usually requires one to a few trials to reach a robust response criterion (Menzel, 1990). Furthermore, the strength of LI increased rapidly with an increase in the number of unreinforced trials above 20 and reached a maximum at ∼30 trials.

In the LI protocol it is only possible to calculate recall for the test trials, because there is only a reinforced odor and we cannot calculate the false positives, which is necessary to estimate precision. Therefore, there can only be true positive and false negative responses. By definition, a PER to a reinforced odor is a true positive response. Conversely, the lack of a PER to a reinforced odor is a false negative. For example, over six reinforced trials with an odor, a honeybee might fail to respond on the first four trials and then respond with PER on the last two (i.e., 000011 where 0 indicates no response and 1 a PER). The first four trials would count as false negatives (fn = 4) and the last two as true positives (tp = 2); by convention we count the first trial because we analyze the evolution of recall over trials. For this example, recall is 2/(2 + 4) = 0.33.

Behavioral data from (Chandra et al., 2010), now recast in terms of recall, are shown in Figure 1B and C. These data show mean recall across six reinforced trials with ∼20 honeybees in each group. In groups that received fewer than 20 pre-exposures, mean recall rises rapidly in the first two or three trials toward a maximum of close to 1.0 (perfect recall) by the fourth trial. There is no indication in these groups that pre-exposure affected the rate of excitatory conditioning, because the rate of increase in recall is equivalent to the group that received zero pre-exposures. With 20 or more pre-exposures the slope of recall declines, and with 30 or more pre-exposures this decline is evident even in the later conditioning trials. This delay in the increase as a function of pre-exposure is LI. Moreover, there is a rapid onset of LI between 20 and 30 trials. This rapid, almost nonlinear, increase as honeybees reach a threshold for responding will be an important outcome of the model below.

The acquisition curves shown in Figure 1B reflect at each trial the average response across a group of 10–20 honeybees. The increase in response across trials arises from the increase in the percentage of bees in the group that begin responding at each trial. Many honeybees begin responding at a particular trial and then show consistent responses on subsequent trials (Fig. 1C). However, other bees showed an inconsistent pattern at the time of transition, which involved switching back and forth one or more times from not responding to responding (Fig. 1D). This pattern is typical in a subset of honeybees selected for PER conditioning (Smith et al., 1991). The consistency in switching in most honeybees and the brief back-and-forth response patterns in a few will be important for discussion of the modeling results below.

Discrimination conditioning has been widely used to assay how well honeybees can perceptually distinguish two or more stimuli (Smith et al., 2006), one associated with reward (A+) and the other not (X−) (Fig. 2A,B). In this case, all three values (precision, recall, and F) can be calculated because of the use of a reinforced and an unreinforced stimulus on separate trials. We have recast behavioral data from (Fernandez et al., 2009), who conditioned honeybees in PER to discriminate two pure odors (hexanol and 2-octanone) or binary mixtures of those two odors that differed in ratios (9:1+ vs 1:9– or vice versa). In these experiments, both recall and F increased rapidly starting just after the first trial for easy tasks, such as discrimination of the pure odors. But F remained relatively lower for the more difficult discrimination task involving discrimination of the mixtures. In that case F remained low for the first few trials then increased rapidly to an asymptotic value, where it remained for the remainder of the trials. It is therefore clear that discrimination of the mixtures is more difficult than discrimination of the more perceptually distinct pure odorants.

As with LI training, honeybees differed in the trial at which they began to show a conditioned response (Fig. 2C). Furthermore, some honeybees began responding and then responded consistently thereafter. For a few honeybees reliable extension of proboscis was preceded by several trials when the animal switched between extension and retraction (Fig. 2C, bees #13–17 and #22). This transitional switching behavior occurs much more often during discrimination conditioning than for LI conditioning (Smith et al., 1991; Fernandez et al., 2009).

Discussion of these datasets, and recasting them in terms of precision, recall, and F, has served three purposes. First, we could easily compare performance on two different learning paradigms (LI and discrimination conditioning), which would not be as clearly possible with analysis of acquisition curves per se. For LI there is only one curve (X+), whereas for discrimination conditioning there are two (A+ and X−). Second, using a common measure we can compare the task difficulty within a learning task (mixtures vs pure components in discrimination conditioning) or between tasks. In the latter case LI takes many more trials to learn than discrimination conditioning. So the timescale for learning differs between the two tasks. Third, learning in both cases is nonlinear. LI and discrimination conditioning require different numbers of trials to learn, but learning is rapid once a threshold number of trials is reached. Finally, some bees begin responding and consistently respond thereafter, whereas other bees switch back and forth between responding and not responding before making a decisive switch.

Model of decision making in honeybee

To explain the behavioral responses of the honeybee for protocols designed to explore unsupervised (LI) and supervised (discrimination conditioning) learning, we used a simple model of the insect brain involving the AL and MB (Huerta et al., 2004). The AL is the first synaptic contact for olfactory sensory cells in the insect brain (Hildebrand and Shepherd, 1997). The neural networks in the AL set up spatiotemporal response patterns that are distinct for each odor (Stopfer and Laurent, 2000; Bazhenov et al., 2001; Fernandez et al., 2009). The spatiotemporal patterned input from the AL is converted to a distributed spatial pattern in the far more numerous cells of the MB (Perez-Orive et al., 2002,2004; Szyszka et al., 2005), and the MB is an important locus of memory consolidation in insects (Heisenberg, 2003). The construction of this model is essential for our results, so we present first the general idea behind the model design. Later we will show how this model can explain the behavioral data.

The input to the model of the MB is the spatiotemporal pattern of activity among PNs from the AL, x, which is transferred to the MBs, y, by means of a connection matrix, c (Fig. 3). Each KC in the MB integrates the synaptic input as, $y_i=\Theta ({\sum }_{j=1}^{N_{\mathit{\text{AL}}}}{c}_{\mathit{\text{ij}}}{x}_j-b)$, where N_AL is the number of PNs in the AL, b is set to determine the average level of activity of the KCs as shown by (Huerta and Nowotny, 2009), and the gain function of the neuron for this particular model is Θ(u), which is 0 if u ≤0, and 1 if u > 0. The connectivity matrix was drawn from a Bernoulli process such that the probability from a PN to a KC is set to a 10% (García-Sanchez and Huerta, 2003). Note that despite these models are simplifications of a realistic model neurons, one can show that the computational results obtained by these simplified models can be reproduced by realistic spiking neurons (Nowotny et al., 2005). Moreover, as we will show below, they are sufficient to explain the behavioral experiments of LI and discrimination conditioning outlined above.

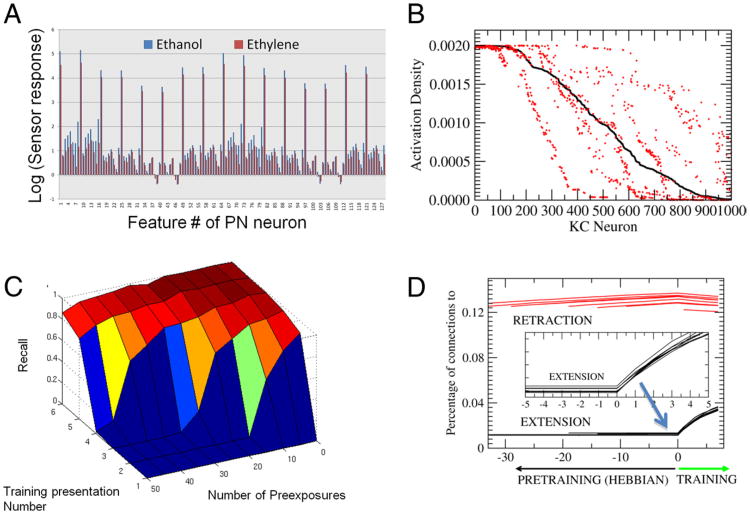
Figure 3.

Model of the MB. The PNs send afferents into the calyx of the MB, where they make connections to KCs. KCs project to ENs with plastic connections w_ij. Initially, the weights of these connections are strongest to the “retraction” group. The MB outputs can be divided into two groups of output neurons that compete with each other via inhibitory connections. The extension group activates the proboscis and the retraction group either retracts it if it is extended or holds it in the retracted state.

We assume two functional populations of ENs (z) that receive input from the KCs and project output to premotor centers. One group represents proboscis extension, z^E = {z₁,…, z_NExtrinsic/2} and another one retraction, z^R = {z_{NExtrinsic/2+1}, …, z_NExtrinsic}, where N_Extrinsic is the total number of ENs. These two populations of neurons mutually inhibit each other; the neurons of the same functional population inhibit each other as well. The ENs that receive more synaptic input will fire, while the other ENs will be silent (Huerta and Nowotny, 2009; Huerta et al., 2004, 2012). If active ENs mostly belong to z^E(z^R) the response would trigger proboscis extension (retraction). The EN responses are mediated by the synaptic integration of all the inputs from the KCs as $z_i=\Theta ({\sum }_{j=1}^{N_{\mathit{\text{KC}}}}{w}_{\mathit{\text{ij}}}{y}_j-\mathit{\text{inh}}),\text{with}\mathit{\text{inh}}=\frac{1}{N_{\mathit{\text{Extrinsic}}}}\sum _{j=1}^{N_{\mathit{\text{extrinsic}}}}{\sum }_{j=1}^{N_{\mathit{\text{KC}}}}{w}_{\mathit{\text{ji}}}{y}_j$ being the inhibition that is identical for all the output neurons, and N_KC is the total number of KCs (see Materials and Methods). The inhibitory connections are not modified by plasticity.

Connections from the KCs to the ENs are plastic. The connections are w_ij, which will be modified according to unsupervised (Hebbian) learning rules as well as by supervised rules that indicate what set of connections will be paired with reward, +1, or punishment, −1. The rules that are most effective in learning a discrimination task require that the positive reward signal (sucrose) depolarizes and evokes response in the extensor neurons, while negative reward (no sucrose when they expected it) depolarizes the retractor neurons. With this approach the same basic rules (but operating at different timescales) can be applied to describe unsupervised and supervised learning. The rules consistent with (Houk, 1995; Dehaene and Changeux, 2000; Huerta and Nowotny, 2009) can be formalized as follows.

Rule 1

Unsupervised Hebbian learning operates all the times and produces small changes of the weights as defined by parameter μ ≪ 1:

$$w_{\mathit{\text{ij}}}(t+1)=\{\begin{array}{ll}{w}_{\mathit{\text{ij}}}(t)+1\hfill & \text{if}{y}_j>0\text{and}{z}_i>0\text{with probability}\mu p_{+}\hfill \\ w_{\mathit{\text{ij}}}(t)-1\hfill & \text{if}{y}_j>0\text{and}{z}_i=0\text{with probability}\mu p_{-}\hfill \\ w_{\mathit{\text{ij}}}(t)\hfill & \text{otherwise}\hfill \end{array}$$

Rule 2

Positive reward. Reinforce the connections to the extension (E) group and depress the connections to the retraction (R) group.

$$w_{\mathit{\text{ij}}}(t+1)=\{\begin{array}{ll}{w}_{\mathit{\text{ij}}}(t)+1\hfill & \text{if}{y}_j>0\text{and}i∊E\text{with probability}{p}_{+}\hfill \\ w_{\mathit{\text{ij}}}(t)-1\hfill & \text{if}{y}_j>0\text{and}i∊R\text{with probability}{p}_{-}\hfill \\ w_{\mathit{\text{ij}}}(t)\hfill & \text{otherwise}\hfill \end{array}$$

Rule 3

Lack of an expected reward (punishment) because there was no sucrose when proboscis is extended. Depress input to the E group and enhance input to the R group:

$$w_{\mathit{\text{ij}}}(t+1)=\{\begin{array}{ll}{w}_{\mathit{\text{ij}}}(t)-1\hfill & \text{if}{y}_j>0\text{and}i∊E\text{with probability}{p}_{-}\hfill \\ w_{\mathit{\text{ij}}}(t)+1\hfill & \text{if}{y}_j>0\text{and}i∊R\text{with probability}{p}_{+}\hfill \\ w_{\mathit{\text{ij}}}(t)\hfill & \text{otherwise}\hfill \end{array}$$

In a general sense Rule 2 implies that a positive reward leads to activation of the extension group of neurons and suppression of the retraction group. Rule 3 implies that a negative reward leads to activation of the retraction group of neurons and suppression of the extension group.

The rules can be compacted to resemble the model proposed by (Houk, 1995; Dehaene and Changeux, 2000) in one single mathematical form as follows:

$$w_{\mathit{\text{ij}}}(t+1)=w_{\mathit{\text{ij}}}(t)+\{\begin{array}{cc}{y}_j\text{sgn}\left(z_i^e-\frac{1}{2}\right)R(e)& \text{with probability}P\left(e,\text{sgn}\left(z_i^e-\frac{1}{2}\right)\right)\\ 0& \text{rest}\end{array}$$ (1)

where sgn() takes on either +1 or −1 and index e can take values of R+ for positive reward, R− for negative reward, and NR for no reward. With this notation $z_i^{R+}=\left\{1,\dots ,1,0,\dots ,0\right\}$, $z_i^{R-}=\left\{0,\dots ,0,1,\dots ,1\right\}$, and $z_i^{NR}$ corresponds to any combination of 0 and 1 induced by the stimulus x_j. Thus, the change in the reward signal, R(R−) = 1, reflects the model of (Dehaene and Changeux, 2000), the evaluation of $z_i^e$ implies the existence of synaptic tags, and the transition rates $P(e,\text{sgn}(z_i^e-\frac{1}{2}\left)\right)$ capture the timescales of the unsupervised and supervised learning. In general the unsupervised learning is a slower process denoted by the parameter μ ≪ 1. It has been shown by (Nowotny and Huerta, 2012; Huerta, 2013) that Equation (1) is nearly equivalent to one of the most successful algorithms in pattern recognition called support vector machines.

Selection of a particular rule (e.g., Rule 2 vs Rule 3) can be achieved based on coincidence of activities of presynaptic and postsynaptic neurons (near simultaneous activation is required for facilitation and the lack of postsynaptic activity leads to depression) assuming that reward signal leads to selective activation of the extension group through specific synaptic pathway (e.g., AMOA1 receptors sensitive to octopamine; Sinakevitch et al., 2011).

Latent inhibition

We first determined whether the model of plasticity embodied in the equations (1) is a qualitative valid description of LI. To obtain realistic odor stimulation patterns, we used output from an array of 16 artificial sensors stimulated by ethanol and ethylene at concentrations from 10 to 1000 ppm (Vergara et al., 2010, 2012) collected over a period of 36 months (data public). This array includes several different features, such as the relative change in the conductance of the sensor during odor stimulation and several dynamical characteristics of the sensor responses (Muezzinoglu et al., 2009b). We consider each of these features to represent an input neuron for the model. Figure 4A shows average firing rates of all sensor-based input neurons for two different odors: ethylene and ethanol. Sensor responses to the two odors were statistically very similar. However, despite the similarity each sensor pattern activated a different array of KCs with some degree of overlap (Fig. 4B). The odor was presented many times (trials) triggering plasticity (as described above) at the KC output synapses. We will use one of these two odors to simulate the LI experiment and then below we will use both odors to model the discrimination experiment.

Figure 4.

LI using artificial sensor array data. A, Features obtained by the artificial sensor array made of metal-oxide sensors measuring ethanol and ethylene at various levels of concentrations ranging from 10 to 800 ppm. Each of the features are extracted from the time series recorded from the sensors reflecting the relative change and rates of change of the conductance levels in the sensors as described by Vergara et al. (2012). These data are available in at the UCI Machine Learning Repository (Vergara et al., 2012). B, Percentage of KCs that are activated for ethanol (black) and ethylene (red) for the completed at a set recorded in the sensor array. KC activity was ranked highest (left) to lowest (right) for responses to ethanol. Approximately 100 model KCs responded equally strongly to both ethanol and ethylene (left side of the x-axis). The remaining KC responses differentiated one odor from the other. In some cases the KC response to ethanol was higher than to ethylene (red dots below the black line), whereas in other cases the response to ethanol was lower than to ethylene (red dots above black). C, Recall measure solving the LI task in the model using the Hebbian rules described in the text. Note the qualitative similarities with Figure 1C; more pre-exposure reduces conditioning performance. D, Evolution of the percentage of connections to the extensor group and the retraction group for pre-exposures ranging from 0 to 50. The lines for the decreasing numbers of pre-exposures start farther to the right. All cells start at the same low connectivity. During pre-exposure the number of connections into the extensor group (black) becomes reduced because of the Hebbian rule. The connections to the retraction group (red), on the other hand, start spreading due to the repetitive coactivation of the retraction group neurons and the KCs. Once the conditioning protocol starts, the connections into the extension group are quickly reinforced, and connections to the retraction group are reduced. However, the starting points were a function of the number of pre-exposures. More pre-exposure produced fewer connections in the extension group and more connections in the retraction group. So the relative delay in conditioning with higher pre-exposures resulted from having to overcome the change in connections to both groups of ENs. In these simulations we used N_KC = 5000, μ = 0.1, b is dynamically set to reach activity levels of 5% in the KCs as indicated by (Huerta and Nowotny, 2009), the positive and negative learning rates p+ = 0.1 (but they can be varied) and p− = 0.05; see more details by Huerta and Nowotny, 2009). Note that there is abroad range of parameter values that lead to very similar qualitative results.

In the first set of experiments we first presented N trials of ethanol with no reward. Then we presented the same odor with a simulated reward signal. N was varied between 0 and 50. Figure 4C shows recall versus training presentation number (followed by reward) for different numbers of pre-exposures N. When the number of pre-exposures was low, training stimuli led to immediate increases in the extension response (Fig. 4C) and of the synaptic weights to the ENs that drive proboscis extension (Fig. 4D). In contrast, when number of pre-exposures was high, the model first showed no activity in the ENs. As training progressed, a trial was reached when there was an abrupt increase in the probability of the ENs becoming active. This result is similar to the experimental observation shown in Figure 1, and it proposes an explanation for what is happening when an animal is first trained to a particular odor with no reward. Unsupervised learning requires co-occurrence of presynaptic and postsynaptic activity. In our model, the group of neurons that is responsible for retraction is always active before learning. So when any stimulus is present the neurons that are active in the calyx will get their synapses potentiated on the retraction group. Therefore, according to Rule 1, unreinforced pre-exposure leads to slow progressive enhancement of the inputs to the group of neurons responsible for proboscis retraction (Fig. 4D), and this synaptic drive must first be overcome when the same odor becomes paired with reward. While input to the group of neurons responsible for proboscis extension is getting progressively stronger over first few trials, it does not change the model response until it exceeds a critical point when it becomes stronger (for a given odor) than the input to the groups of neurons responsible for retraction. This competition between the extension and retraction group is the source of the strong nonlinearity in proboscis extension as conditioning progresses.

Discrimination conditioning

Ethanol and ethylene trigger very similar responses in the artificial sensor array as can be seen in Figure 4A, and they therefore present a difficult discrimination problem. We thus used these two odorants for the odor discrimination task in the model. In these simulations a specific input (ethanol in the dataset) is paired with sucrose and ethylene was followed by punishment (see above, Model of decision making in honeybee, Rule 3). The probability of synaptic changes p+ and p− was set to 0.1, although there is a range of values that leads to the same effect (we explored 0.05–0.2 with the same result). To determine the generalization ability of the learning process, one dataset (one trial of sensor array response to an odor) was used for training and another different and nonoverlapping dataset was used for testing. The test set allowed us to track how the model was performing throughout the training session. The model should change the connections only if the odor belonged to the training set. In machine learning it is very important to test the performance of the model with a set that has not been presented during training. It is the best way to determine how well the model really learned general data, because it is possible that the model over learns and badly fails on the unseen data.

In Figure 5A we present the performance results (evolution of F-measure) in the test set, first, using ethanol as the positively reinforced odor and, second, ethylene as the negative one. It shows that at presentation number 3–5, suddenly the system starts to associate reliably ethanol (or ethylene) with the reinforcement. If one tracks in parallel the evolution of the percentage of the connections to the extension group (Fig. 5B), it can be seen that a smooth change in the number of connections can trigger the nonlinear jump in learning after 3–5 trials such that the two groups of competing neurons receive sufficient input to quickly tilt the decision toward extension. In fact, if one looks at the changes of the relative ratio of connections into the extensor and retractor group there is no sharp boundary in the ratio of connections at the point of the behavioral transition (Fig. 5C). That is, there is no indication from the ratio of connections that the output from the model has switched from retraction to extension.

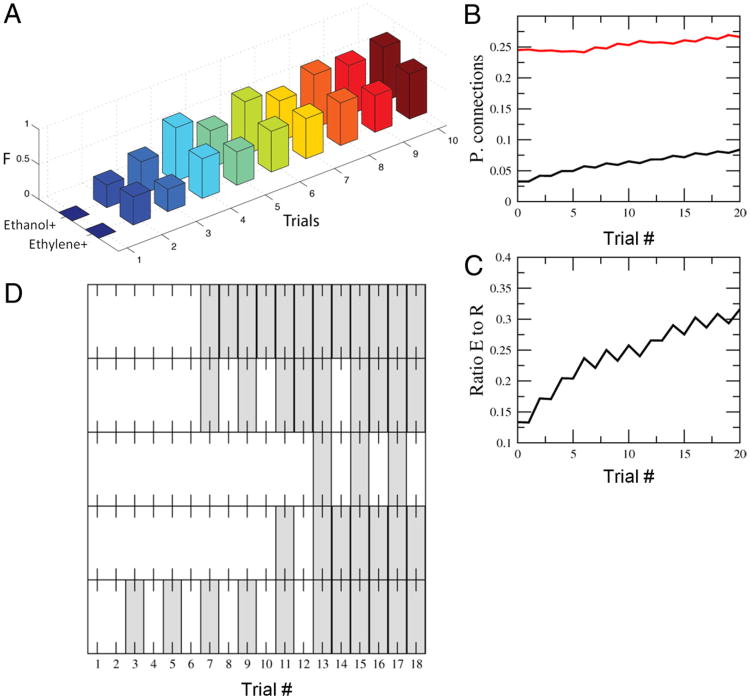
Figure 5.

Discrimination conditioning using artificial sensor array data. A, F-measure evolution of the model discriminating ethanol +/ethylene− and ethylene+/ethanol − from the database collected using the artificial sensor arrays. Note the similarities with Figure 2A. B, The evolution of the probability of forming connections into the extension (black) and retraction groups (red). C, The ratio between the number of connections to the extensor group divided by the connections to the retraction group. The number of connections into the extensor group increases but it does not need to reach a 50% level to be able to accurately solve the discrimination task. D, Illustration of the behavior in different iterations of the model. Some iterations showed a very consistent transition (top) where as others showed some degree of inconsistency. This is similar to the behavior data in Figure 1D. We used the same parameter values as in Figure 4.

We also found that transition from reliable retraction to reliable extension was characterized by the set of trials when the model response changed back and forth between extension and retraction. This dynamics was most obvious in individual runs (Fig. 5D) and corresponded to similar observation in behavior experiments (Fig. 2). In the model this occurs in a subset of runs because of the input variability across trials. Near the transition point some inputs led to extension while others, activating slightly larger fraction of retraction neurons, still led to retraction.

Impact of each learning rule on discrimination conditioning

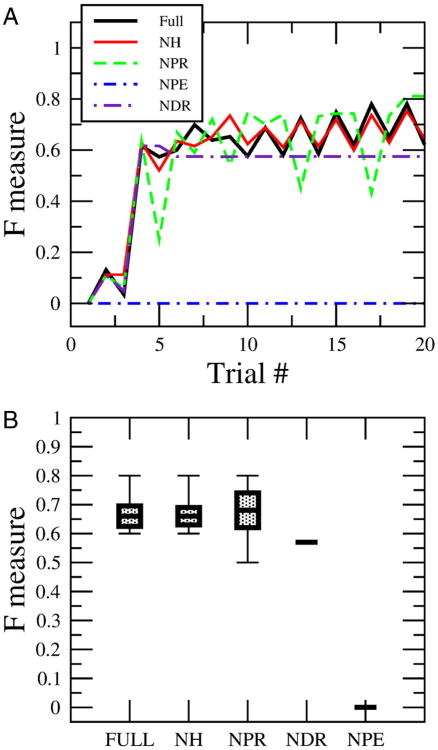
We then tested the specific impact on discrimination conditioning by removing different components of learning from Rules 1–3 (Fig. 6). We analyzed learning performance over 20 trials. The model in effect describes two stages of acquisition. First, the full model reaches an abrupt transition in responding after a few (3–5) trials (Fig. 6A). Second, after this transition the performance continues to increase slowly as the pattern of synaptic connections is further refined. Extension of the trials beyond 20 would lead to a gradual increase to F-values near 1.0.

Figure 6.

Dissection of the impact that different learning rules have on performance in solving the discrimination task. A, Evolution of the performance in the discrimination task between ethanol and ethylene as a function of the number of presentations during single runs of the model. The black line (full) shows the performance using the full set of rules. The red line (NH) shows the performance by eliminating the pure Hebbian rule, which is Rule 1. The green line (NPR) shows the performance by eliminating the condition that activates connections into the retraction group in the Rule 3. The blue line (NPE) eliminates the positive reinforcement to the extensor group in Rule 2, which blocks learning completely. And finally the violet curve shows the performance by eliminating the condition that removes the connections into the retraction group (NDR) in Rule 3. B, The same as A, but taking the steady state reached after 20 presentations of learning. We also have the error calculated by running the simulations 10 times. We used the same parameter values as in Figure 4.

Without Rule 1 that provides unsupervised Hebbian learning (no Hebbian; NH), there was no change in the performance in the system for the discrimination task because the timescale of the synaptic changes due to the unsupervised learning is at least 10–20 times slower than reinforcement learning. Hebbian learning plays an important role by preconditioning the circuit without reward (e.g., LI experiment) but is far less important during an odor discrimination task.

Alteration of the other rules produced more significant changes in performance. Without the potentiation of retraction embodied in Rule 3 (no potentiation retraction; NPR), which increases the connections to the retraction group during negative reinforcement, the performance remained at similar median levels as the full rule. However, the ranges of performance after 20 trials as shown in Figure 6B are twice the full rule, which means the learning became less stable. Removal of Rule 2 in a situation when an animal does not extend its proboscis to a reinforced odor (no depression retraction; NDR) makes the learning less efficient, and the performance reaches an absolute asymptote within 20 trials that is lower than the full rule. At this point there was no further improvement in performance in the absence of this component of Rule 2. Finally, the component of Rule 2 that reinforces connections to the extension group makes learning possible. Without it (no potentiation of extension; NPE) learning is impossible.

Finally, Equation 1, consistent with Houk (1995) and Dehaene and Changeux (2000), embodies a unified formalism capable of embodying all the semisupervised and fully supervised tasks described in this paper. This analysis shows that there is a delicate balance in the way the learning rules can operate together. If we eliminate or tamper some of the rules the ability to learn degrades and sometimes may disappear completely.

Discussion

Supervised and unsupervised forms of learning coexist in neuronal circuits, which imply that they interact in some way. Both forms of learning exist in parallel in several forms (Rescorla, 1988) in behavioral conditioning experiments. In the conditioning examples we have shown above, presentation of odor alone (unsupervised; Rule 1) reduces the salience of that odor for subsequent conditioning experiments. The same experience, odor presentation, is present during reinforced (supervised) learning, which produces a very different behavioral result (Rule 2). Furthermore, after an odor has been associated with a specific reinforcement, presentation of odor with a reduced reinforcement, or no reinforcement at all, can produce strong conditioned inhibition (Rule 3; Rescorla, 1969; Stopfer et al., 1997). In this study using a combination of behavioral experiments from honeybees and computational modeling we developed a set of plasticity rules that can account for a variety of experimental data with learning protocols involving both unsupervised and supervised learning.

How can these two forms of plasticity be integrated to account for the behavioral changes and the temporal dynamics of the change in responses? Let us first revisit the current models of reinforced learning. One of the most important requirements is the existenceof “synaptic eligibility traces” (Houk, 1995) or “synaptic tags” (Frey and Morris, 1997), which are necessary to implement learning. Typically the conditioned stimulus is presented and followed by a reward (sucrose in the honeybee). Synaptic tags or traces, at least at the presynaptic level, have to remain elevated, even without electrical activity in the cell, such that it can remember what output neuron to pair (unpair) when the reward (punishment) arrives. The basic model (Houk, 1995) is that when the stimulus is present and it elicits the correct behavior, the delayed reward leads to release of neuromodulator such as dopamine (mammals; Heisenberg, 2003; Schultz, 2010) or octopamine (insects; Hammer, 1993; Farooqui et al., 2003; Heisenberg, 2003) and the synaptic connections that have elevated synaptic tags change their synaptic efficacy (Cassenaer and Laurent, 2012). This basic model has been revised and has been analyzed in several forms (Izhikevich, 2007). But the timescales observed at the behavioral level to coordinate unsupervised and supervised learning still have to be unified in a consistent framework.

To characterize interaction between supervised and unsupervised learning rules, we used two classical experimental protocols. The first experiment, LI, involves pre-exposure of an odor without reinforcement. To measure learning during pre-exposure, this treatment is followed by trials with the same odor accompanied by reward. More unrewarded pre-exposures led to a requirement for more reinforced trials to reach a learning criterion. The first part of this protocol (odor followed by no reward) represents unsupervised learning but should be also equivalent to supervised learning with odor followed by mild punishment. In the second experiment, discrimination conditioning, the task was to discriminate between two similar odors, when one odor was followed by reinforcement and another one was not.. The two behavioral experiments differ typically in how long it takes for honeybees to begin to respond correctly; more trials are required for LI. Also, in both scenarios the increase at the behavioral switching point was rapid. This rapid switch from no response to response over a short subset of acquisition trials is a general phenomenon in many conditioning experiments with a wide array of animals (Gallistel et al., 2004).

As a framework to implement plasticity rules that could account for these experimental data, we developed a simplified model of neural circuits in the MBs of the honeybee brain that process olfactory sensory information and relate it to reinforcement through identified modulatory pathways (Sinakevitch and Strausfeld, 2006; Schröter et al., 2007; Sinakevitch et al., 2010). KCs are the intrinsic cells in the MBs (Strausfeld et al., 2009). KC dendrites receive input from the axons of PNs from the AL, which is the first-order neural network that processes input from olfactory receptor cells. The model assumes that axons from KCs project to extrinsic premotor neurons that are organized into two competing (through lateral inhibition) populations responsible for proboscis extension and retraction. Activity in one of the two groups of ENs represents a decision to withhold or extend the proboscis.

Plasticity of synaptic connections was implemented as a set of rules. (1) In the absence of reward, synaptic weights slowly decay when presynaptic activity is followed by no response in the postsynaptic cell (extension group) and slowly increase when presynaptic activity leads to postsynaptic activation (retraction group). (2) A positive reward is equivalent to activation of the extension group of neurons and suppression of the retraction group. (3) A negative reward is equivalent to activation of the retraction group of neurons and suppression of the extension group. For both Rules 2 and 3, the suppression of one or the other groups of output neurons embodies Rule 1 but at a faster timescale. With this approach we can use the same basic learning rule for supervised and unsupervised protocols simply by assuming the difference in the timescale across which the two forms of learning operate.

The mechanism underlying decision making in our model is relatively simple. Initially the majority of the connections from the KCs of the MB are pointing into the retraction group of neurons. As the training procedure starts to operate, specific connections corresponding to the trained odor from the KCs to the output neurons get increased, while the corresponding connections pointing to retraction are eliminated. The connections from odors that have not been paired with sucrose are not strong enough to activate the extension group, although there is always some small probability of having false positives because of overlap of patterns activated by similar odors. Once a critical mass of connections into the extension group is achieved, lateral inhibition provides the mechanism to shut down the retraction neurons. The inhibitory mechanism combined with the smooth modification of the balance of the synaptic weights provides the nonlinearity of the switch in behavior from retraction to extension. Because the only requirement for this to occur is competition between output groups of neurons, we suggest that this may be a general phenomenon.

In addition, since there is a competition between the retraction and extension group, sometimes, the dynamics of the decision function fluctuates between both possible outcomes when using odorant at concentration levels that are sitting near the boundary of the decision function. Indeed, it is harder to discriminate between odors at lower concentrations than at higher ones. Since we are presenting odors at random concentrations some the examples presented earlier on are more difficult to separate from each other. From the statistical point of view, the more examples or odorants presented to the system the better is the estimation of the decision function. The standard deviation associated with the estimation of the synaptic weights of the optimal decision function is going to be better with a larger number of presentations. This fluctuation behavior during learning observed in the model also matches experimental observations.

We found that this model was capable of consolidating specific observations from two major classes of behavioral experiments. (1) In the case of LI, odor trials with no reward led to slow enhancement of connections to the retraction group. Therefore, when the stimulation protocol was changed to include a reward, it took more trials to “unlearn” this effect and to enhance connections to the extension group sufficiently to achieve the correct response. (2) Discrimination conditioning involved alternating presentation of rewarded and unrewarded odors. For similar odors (that overlap significantly in respect to the active projections from KCs to ENs), enhancement of connections to the extension group during reinforced odor presentation was followed by weakening of nearly the same set of connections during unreinforced odor presentation. Therefore, only a small subset of connections to the extension group representing the difference between these two odors remained enhanced. As a result it took many trials for the extension group to win and to suppress activity in the retraction group. In contrast, for very different odors, the enhancement of connections to the extension group during rewarded odor trials occurred much faster, and it required fewer trials before the extension group could win the competition with the retraction group.

To conclude, our study combined, for the first time, supervised and unsupervised forms of learning in one simple set of learning rules. We assumed that unsupervised learning is a continuous process occurring on the background of any learning, and it is characterized by a slower timescale than supervised learning. According to our model, the lack of reward for proboscis extension is classified as a punishment (negative reward) and, therefore, the same set of rules was applied by at different timescales. A combination of these rules let us explain a range of behavioral experiments. This model will help to refine engineered solutions to odor detection and discrimination, and it may also generalize to other problems in pattern recognition. It also allows us to make hypotheses about the nature of interactions among sensory and premotor centers in the brain, which are testable in the honeybee brain using imaging (Szyszka et al., 2005; Fernandez et al., 2009) and electrophysiological recordings (Strube-Bloss et al., 2011). In fact, recordings from ENs of the honeybee MB during differential conditioning, which we have modeled here, have shown complex switching similar to what our model would predict. Many ENs increase responses to the reinforced odor, whereas responses to the unreinforced odor show both decreases and increases in different units (Strube-Bloss et al., 2011). It remains to be determined how this switching behavior might relate to premotor processing in our model.