SnB version 2.3: triplet sieve phasing for centrosymmetric structures

Abstract

A new version of the direct-methods program SnB has been developed. This version incorporates the triplet sieve method for phasing centrosymmetric structures in a way that is transparent to users. The triplet sieve procedure may decrease significantly the time required to achieve a solution for such structures.

1. Introduction

SnB is a computer program (Miller et al., 1994; Weeks & Miller, 1999; Weeks et al., 2002) that implements the direct-methods phasing algorithm known as Shake-and-Bake (DeTitta et al., 1994; Weeks et al., 1994). Shake-and-Bake is an example of a ‘multi-solution’ or ‘multi-trial’ procedure (Germain & Woolfson, 1968). First, multiple trial structures are created by a random-number generator that is used to assign initial atomic coordinates. Then, these trial structures are subjected to a dual-space refinement procedure that automatically and repetitively alternates reciprocal-space phase refinement, either by using the tangent formula (Karle & Hauptman, 1956) or by reducing the value of the minimal function (Debaerdemaeker & Woolfson, 1983), with complementary peak picking in real-space to impose physical constraints. Potential solutions are identified on the basis of figures of merit such as the minimal function (Rmin) itself or a crystallographic R factor (Rcryst) calculated at the end of SnB refinement.

The time required to achieve a solution depends on (1) the computational time of an individual SnB refinement cycle and (2) the success rate or percentage of trial structures that refine to solutions. Success rate can be increased by providing a better-than-random set of starting atoms or phases. For example, the phasing program SHELXD (Schneider & Sheldrick, 2002), which is also based on the Shake-and-Bake algorithm, uses Patterson minimum functions (Buerger, 1959; Nordman, 1966) to derive sets of starting atoms that are, in some way, consistent with the Patterson function. Alternatively, the triplet sieve method (Smith et al., 2007) uses an integer minimal principle to provide a subset of perfect, or nearly perfect, initial phases that can be expanded using standard Shake-and-Bake refinement.

Direct methods rely on the fact that the structure invariants or triplet phases,

$${\phi }_{HK}={\phi }_H+{\phi }_K+{\phi }_{-H-K},$$ (1)

are approximately equal to 0 if the corresponding values of A_HK = 2N^−1/2|E_HE_KE_−H−K| are large. (N is the number of non-H atoms in the unit cell, and the |E|s are normalized structure factors.) In the centrosymmetric case, φ_HK equals 0 or 180 degrees only, and, given a subset of φ_HK which are all equal to 0, it is possible to solve the system of homogeneous equations (eqn. 1) with the triplet sieve technique and to obtain the desired subset of perfectly correct phases. However, two complications exist. First, the number of phases (NSP) appearing in the triplets involved in the sieving process must be limited to a small number with the very largest |E| values in order to avoid inclusion of φ_HK with values of 180 in the set used for sieving. If such triplets are included, it cannot be guaranteed that the correct set of phases can be found. Consequently, NSP is significantly smaller than the total number of reflections that need to be phased in an SnB job. In some cases, it will be necessary to iteratively reduce NSP in order to find a solution, but there is also a minimum value of NSP below which solutions will never be found. To avoid inclusion of triplets with values of 180 degrees, use of the sieving technique should also be limited to structures with fewer than ∼100 atoms in the asymmetric unit. The second complication to the sieving process is that, depending on the number of phases required to fix the origin in the particular space group as well as the nature of the triplet interactions among the NSP phases, the homogeneous system of equations will have a variable number of degrees of freedom leading to the generation of a variable number of sieve phase sets or trial structures.

2. Materials and Methods

The sieving process can be incorporated into the Shake-and-Bake procedure, as illustrated in Figure 1, with the addition of three new operational parameters. These parameters are the number of sieve phases (NSP), the reduction in number of phases (SPR) considered in each successive sieving step, and the minimum number of phases to be used for sieving (NSPmin). A subroutine implementing the procedure described by Smith et al. (2007) was added to the SnB program, and the additional steps introduced by triplet sieving are indicated by a gray background in the flow chart. If the structure is centrosymmetric and the number of atoms in the asymmetric unit is less than 100, the variable ‘UseSieve’ is set to TRUE, and the phases of the trial structures are generated by the new subroutine. If the degrees of freedom (DF) are too large, the number of phases used for sieving is reduced, and the trial phase sets are regenerated. If satisfactory trial structures can not be generated, the variable ‘UseSieve’ is set to FALSE, and the program reverts to standard SnB operation using trial structures with randomly positioned atoms.

Fig. 1.

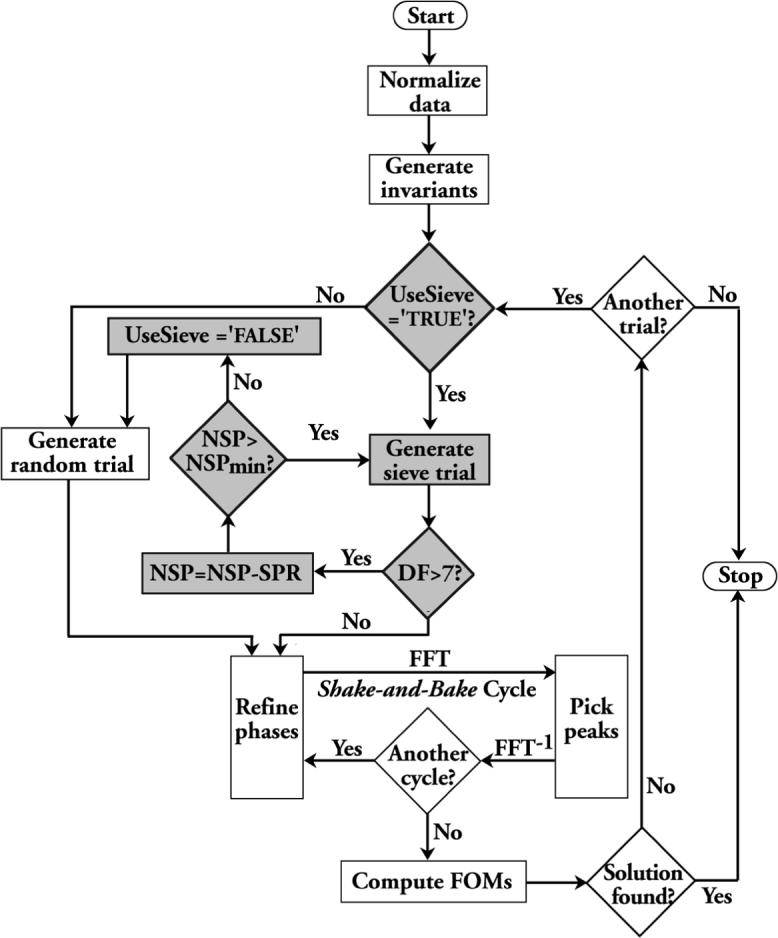
A flow chart illustrating the SnB algorithm after incorporation of the triplet sieving method.

The modified SnB program was applied to the 15 centrosymmetric test data sets listed in Table 1. First, using the deposited CIF file, basic crystallographic information including space group, cell parameters, and chemical formula was input to SnB. Then, using the DREAR package (Blessing & Smith, 1999) in SnB, E-values were generated from the observed intensity data. As a final initialization step, reflection and invariant files were generated containing 10N reflections and 100N triplets, respectively. Next, the sieving procedure was carried out, and the three sieve parameters were varied in order to find a combination of values that would optimize the effciency of the Shake-and-Bake procedure for these structures. In all cases, a small number (0.1N) of conventional SnB refinement cycles was added to expand the set of phased reflections and to improve the quality of the phases. Finally, the best values of the sieve parameters were chosen, and a final SnB job was run for each data set in order to measure the time required to obtain a solution. Solutions were identified on the basis of mean phase errors when compared to correct phase sets computed using the known atomic coordinates.

Table 1.

Test structures and crystallographic information. `Ratio' is the time required to achieve a solution without sieving divided by the time required with sieving.

ID	Chemical Formula	Atoms (ASU)	Space Group	Ratio	Reference
1	C12H10O3	15	P21/n	5.4	Howie et al. (2001)
2	C30H32N2O6	19*	P21/c	14.4	Sun et al. (2002)
3	C34H42B2N2O4	21*	P21/n	25.6	Kliegel et al. (2002a)
4	C42H56N2O2	23*	P21/n	12.4	Lynch (2002)
5	C44H38O4	24*	$P\stackrel{‒}{1}$	20.8	Vande Velde et al. (2002)
6	C44H52N4 · C2H5OH	26*	C2/c	98.5	Camiolo et al. (2001)
7	C36H62	36	P21/c	0.47	Bragg et al. (2002)
8	C30H22O6S	37	P21/c	4.1	Krishnakumar et al. (2002)
9	C34H26N2O	37	P21/c	81.8	Zhuang et al. (2002)
10	C24H12N6 · 4CHCl3	46	P21/n	16.0	Alfonso & Stoeckli-Evans (2001)
11	C33H49B6N3O11 · 0.5C4H10O	57.5	$P\stackrel{‒}{1}$	7.9	Kliegel et al. (2002b)
12	C41H78O11Si8	60	$P\stackrel{‒}{1}$	70.0	Arnold & Blake (2001)
13	C50H66O6 · C3H7NO	61	P21/c	6.4	Bryan & Levitskaia (2002)
14	3C40H32O2 · 4C6H6	75*	$P\stackrel{‒}{1}$	44.5	Ohba et al. (2002)
15	C60H102N6O18	84	$P\stackrel{‒}{1}$	5.6	Pletnev et al. (1980)

^*: Structures which crystallize with a crystallographic center of symmetry in the middle of the molecule. In such cases, the number of atoms in the asymmetric unit is half of the molecule.

3. Results

As a result of the test jobs, the parameter values (all a function of the size of the structure) given in Table 2 were chosen as default values. The results of the final jobs showing a comparison of the time required to yield SnB solutions with and without the sieve procedure is presented in Table 1. This comparison shows that the computing time required for 14 of the 15 test structures is reduced by a factor of 4.1 to 98.5 when sieving is included. The average reduction factor is 29.5.

Table 2.

Parameters for the combined SnB/sieve procedure.

Parameter	SnB alone	SnB with sieving
Total reflections (phases)	10N	10N
Triplets	100N	100N
Peaks to select	N	N
SnB cycles	0.5N	0.1N
No. sieve phases (NSP)	NA	1.5N-4N†
Sieve phase reduction (SPR)	NA	0.15N
Min. sieve phases (NSPmin)	NA	0.5N

^†: The initial set of sieve reflections is chosen utilizing a binary search for the first instance of non-origin degrees of freedom as described in section 5 of Smith et al. (2007).

The modified version of the SnB program with the sieve procedure included with the default parameter values determined in this study is now available as version 2.3 from the SnB website, http://www.hwi.buffalo.edu/SnB/. Unlike earlier versions of SnB, version 2.3 also contains a tool for automatic solution detection that permits calculations to be terminated as soon as a solution is found. Thus, full advantage can be taken of the new sieving feature.