Development of a Sampling-Based Global Sensitivity Analysis Workflow for Multiscale Computational Cancer Models

Abstract

There are two challenges that researchers face when performing global sensitivity analysis (GSA) on multiscale in silico cancer models. The first is increased computational intensity, since a multiscale cancer model generally takes longer to run than does a scale-specific model. The second problem is the lack of a best GSA method that fits all types of models, which implies that multiple methods and their sequence need to be taken into account. In this article, we therefore propose a sampling-based GSA workflow consisting of three phases – pre-analysis, analysis, and post-analysis – by integrating Monte Carlo and resampling methods with the repeated use of analysis of variance (ANOVA); we then exemplify this workflow using a two-dimensional multiscale lung cancer model. By accounting for all parameter rankings produced by multiple GSA methods, a summarized ranking is created at the end of the workflow based on the weighted mean of the rankings for each input parameter. For the cancer model investigated here, this analysis reveals that ERK, a downstream molecule of the EGFR signaling pathway, has the most important impact on regulating both the tumor volume and expansion rate in the algorithm used.

1. INTRODUCTION

Recently, computational cancer models across different biological scales, i.e., multiscale cancer models, have garnered much attention for its potential to help move the field of integrative cancer systems biology towards clinical implementation [1-3]. Because model parameters defining biological properties at different scales are generally not produced by a single laboratory, studying the dynamic system behaviors governed by a fixed set of parameters is inappropriate. This implies that the influence of the perturbations of these parameters on the overall system behavior needs to be further investigated [4]. Sensitivity analysis has been widely accepted as a useful tool for this purpose, especially when it is not possible or practical to conduct numerous wet-lab experiments [5]. There are two types of sensitivity analysis methods: local sensitivity analysis (LSA) and global sensitivity analysis (GSA). Because LSA (one-at-a-time parameter variation method) only allows one parameter to change each time, for analyzing complex biosystems, such as cancer, GSA is believed to be more appropriate for accessing a parameter’s sensitivity because it allows multiple parameters to change simultaneously.

Thus far, a number of GSA techniques have been developed, especially in the engineering field, and include response surface methodology, Monte Carlo analysis (sampling-based approach), and variance decomposition procedures (variance-based approach). GSA methods have also been applied to systems biology models [4, 6-8], but most of them focus on the analysis of signaling pathways. To assess the context-dependent relationship between different biological scales of interest, we have previously provided an applicable GSA strategy based on the integration of Monte Carlo and resampling methods as well as the repeated use of analysis of variance (ANOVA) [9]. Read et al., also developed a GSA method based on statistical techniques to link simulation results back into the original biology domain in order to determine the confidence of the simulation-derived predictions [10]. However, there is no single ultimate solution that best fits all types of systems biology applications, i.e., each method has its advantages and disadvantages [11]. A particular method may be favored over another depending on the specific model being studied and the objectives of the analysis. Hence, in identifying inputs critical for certain outputs, it is better to consider multiple methods together

In this article, we present a sampling-based GSA workflow that accounts for multiple GSA methods together. We chose sampling-based GSA methods because they are relatively easy to implement and to demonstrate the applicability of the workflow; the focus here is not on whether or not variance-based methods are always more superior over sampling-based ones. Specifically, in addition to the ANOVA-based method, two other sampling-based GSA methods, i.e., partial rank correlation analysis (PRCA) and Sobie’s multivariate linear regression analysis (MLRA; capable of prioritizing parameters for non-linear computational models) [12], are also an integral part of the workflow. After an initial parameter ranking is produced with a specific GSA method, parameters are grouped by ANOVA using statistical comparison procedures. In the end, we generate a summarized parameter sensitivity ranking sorted by the strength of influence that each input parameter exerts on model output. We exemplify the feasibility of the workflow using a 2D multiscale agent-based model previously developed for simulating non-small cell lung cancer (NSCLC) [13]. The identified critical model parameters (on the molecular level) may have the potential to serve as therapeutic targets in treating NSCLC.

2. METHODS

2.1 Multiscale Non-Small Cell Lung Cancer Model

The 2D agent-based NSCLC model [13] encompasses both molecular and microscopic (i.e., multi-cellular) scales, and we only briefly introduce its key development methods here. An epidermal growth factor (EGF)-induced, EGF receptor (EGFR)-mediated signaling pathway is implemented at the molecular scale, and includes seven main components (see Fig. 1a for an illustration of the simplified pathway). At the microscopic scale, a lattice-based 2D biochemical microenvironment is constructed and populated with diffusive chemical cues including EGF, glucose, and oxygen (see Fig. 1b for model setup). Each cell (or agent) in the model carries a self-maintained signaling pathway, and as a simulation run progresses, these cells constantly sense changes in environmental factors, interact with other cells, and adjust their behavior according to a set of predefined biological rules. A molecularly-driven cellular phenotypic decision algorithm (Fig. 1a) is established to determine cell phenotypic transitions upon molecular changes: PLCγ-dependent migration and ERK-dependent proliferation (see [13] for detail). This algorithm is derived from and supported by experimental studies [14, 15]. In the model, each lattice grid can be occupied by one cell or remain empty at a time; if a cell decides to migrate or proliferate, it will search for a neighborhood location to move to or for its offspring to occupy. The model is able to quantify the relationship between extracellular stimuli, intracellular signaling dynamics, and multi-cellular tumor growth and expansion. Thus, it can be used to investigate the cross-scale effects of simultaneous molecular parameter variations on tumor ‘outcome’ at the microscopic scale.

Figure 1.

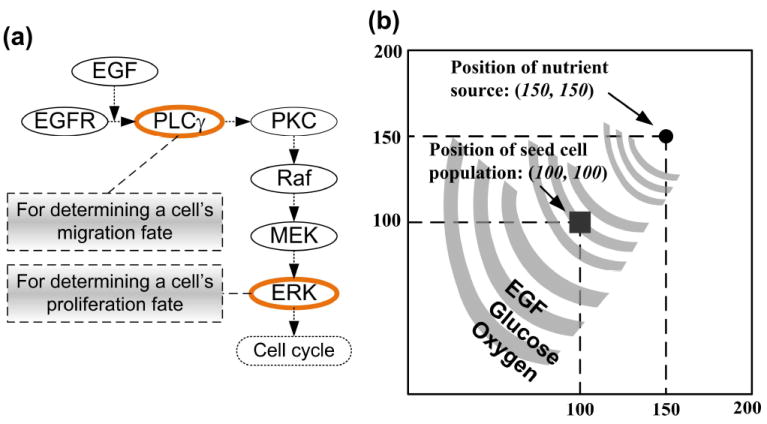
Introduction of the 2D agent-based model. (a) Schematic representation of the signaling pathway. In short, EGFR is activated by binding to extracellular EGF, inducing receptor dimerization and autophosphorylation. The bound receptor forms a docking site for the signaling molecule PLCγ, which then activates the Raf signal through PKC. This process initiates the ERK signaling cascade, which is involved in cellular proliferation, differentiation, and survival. The rates of change of PLCγ and ERK are employed to determine cell migration and proliferation chances for the next step. (b) A virtual 2D microenvironment with a discrete lattice containing 200 × 200 grid points. A single, distant blood vessel representing a “nutrient source” is located at (150,150). The nutrient source is the most attractive location for the chemotactically-acting tumor cells (i.e., cells tend to move towards the nutrient source). When the first cell reaches the nutrient source, a simulation run is terminated. The diameter of each cell and the unit interval of the 2D microenvironment are all 10μm.

2.2 Global Sensitivity Analysis Workflow

We propose a GSA workflow consisting of three phases (Fig. 2): pre-analysis (for preparing the basic input sampling data set), analysis (for performing sensitivity analysis with three GSA methods and for quantifying the distribution of the sensitivity index), and post-analysis (for producing the final summarized parameter ranking). We will explain each phase using the 2D NSCLC multiscale model (described in section 2.1) as a practical example. Note that, to investigate the effects of how molecular changes in individual cancer cells percolate throughout and across the scales of a cancer system, the model output (i.e., biological response of the tumor) no longer consists of the behaviors of output signals or signal activation patterns (as it is in most current signaling pathway studies [16]); instead, the output is the tumor’s growth and expansion rate, two phenotypic behaviors at the microscopic level driven by the implemented molecular network. Similar to previous studies [17-19], we will use the number of elapsed time steps as a measure for “tumor expansion rate,” and the final number of live cells for “tumor volume.”

Figure 2.

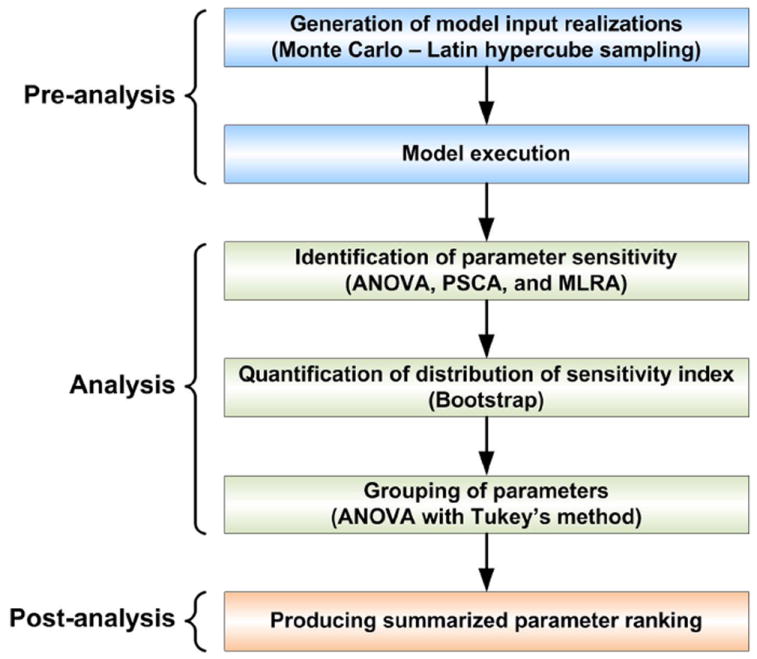
Workflow of the global cross-scale sensitivity analysis, which is composed of three phases: pre-analysis, analysis, and post-analysis.

2.2.1 Pre-Analysis

Continuous input parameters are first partitioned into mutually exclusive ranges of values, and each individual range is termed a parameter level. In our case, we only consider the initial concentrations of pathway components as input parameters to demonstrate the applicability of the GSA workflow. When the number of parameters or parameter levels is large, exploring the entire parameter space is computationally impractical. For example, suppose we have K parameters and for each parameter we have N levels, for a total of N^K combinations. The number of simulations grows exponentially as K or N increases. The other fact rendering exploring the entire space impractical is that this/any 2D multiscale cancer model takes a relatively long time to finish, because each cell has to undergo a series of pathway analysis throughout the course of the simulation. Hence, we use a random sampling of input parameters to render the large number of variation combinations computationally manageable. Specifically, as implemented in [9], we use the Latin hypercube sampling (LHS) method to generate 2000 random sets of parameter values, and thus 2000 sets of simulation results will be generated correspondingly. For simplicity, we call each set of parameter values along with the corresponding two tumor output values an observation. Thus, at the end of the pre-analysis phase, we have 2000 observations, and we refer to the 2000 observations as the original sample.

2.2.2 Analysis

The sensitivity indices for the three sampling-based GSA methods are as follows: the F value for ANOVA calculated by the F-test [9], the magnitude of the partial correlation coefficient for PRCA, and the magnitude of the regression coefficient for MLRA. For all analyses, the bigger the value of the sensitivity index is, the larger the influence that the (molecular) parameter has in determining the (microscopic) system output. We note here that, based on the original sample obtained at the pre-analysis phase, each of the three GSA methods can already yield their own parameter rankings. However, there is still the possibility that the sample data is biased (regardless of how sophisticated the LHS method is), which would make the resultant ranking incorrect. Thus, we further quantify the sampling distribution of the sensitivity index for each GSA. As implemented in [9], to understand such distributions (of F value, partial correlation coefficient, and regression coefficient, respectively), we use bootstrap resampling [20], which repeatedly samples the original sample with replacement and forms a new sample that is the same size as the original sample. The most attractive feature of this approach is that we do not have to run the multiscale cancer model again, thereby saving a great deal of time. In practice, we again generate 1000 bootstrap samples (including the original sample) and then apply each GSA to each bootstrap sample to calculate the sensitivity index values. As a result, with respect to each model output (tumor volume or expansion rate), for each GSA, there will be 1000 sensitivity index values (each corresponding to a bootstrap sample) generated for each input parameter. We then draw probability distributions of sensitivity indices from these results.

Next, to discriminate between two closely ranked input parameters, we use ANOVA with Tukey’s method (also known as Tukey’s studentized range test) [21]. Tukey’s method is a single-step multiple pairwise comparison procedure which, in conjunction with ANOVA, can determine which parameter means across the groups are significantly different from the others. In brief, suppose we have N treatment groups: ANOVA examines the difference across the N group means as a whole, and Tukey’s method looks for statistically significant differences between each pairs of the groups. In our case, each input parameter is regarded as a treatment group, containing 1000 sensitivity index data. We note that other statistical methods for performing multiple comparison tests, such as Duncan’s test, Scheffe’s procedure, and the Waller-Duncan k-ratio t test can be used as a substitute for Tukey’s method; however, detailed discussion of this topic is beyond the scope of this article, and interested readers should refer to [22]. If the difference between the means of two originally closely ranked input parameters is statistically significant (unless otherwise noted, all statistical comparisons are conducted at the 5% confidence interval), they will be assigned to different groups; if not, they will remain in the same group. Parameters from the same group are assumed to have similar effects on the model output, and thus will be reassigned the same rank. In practice, for all three GSA methods, a rank of 1 is assigned to the input with the highest sensitivity index in a parameter ranking, and the largest value of rank is assigned to the input of least importance (i.e., lowest sensitivity index).

2.2.3 Post-Analysis

Since there is no one-stop GSA method for all types of systems applications, we propose an approach to synthetically take into account the parameter rankings produced by all of the GSA methods. This approach calculates the weighted mean of the rankings for each input parameter, according to the following equation:

$$S_i=\sum _{j=1}^N{k}_j{r}_{i,j}\left(i=1,2,\dots ,M\right)\mathrm{and}\sum _{j=1}^N{k}_j=1,$$ (1)

where i refers to the ith of M parameters, j refers to the jth of N GSA methods; r_i,j represents a specific rank for the ith parameter with respect to the jth GSA method; k_j represents the weight for the jth GSA method; S_i is the final score for the ith parameter. The smaller the S_i, the more important is the given parameter. The weights are normalized to sum up to 1. Figure 3 illustrates the process of producing the summarized (or integrated) parameter ranking. In practice, GSA methods can be set with different weights (i.e., the coefficient k), depending on the researchers’ experience or prior knowledge. For example, for a specific model, methods that have been proven to be more suitable than others may have higher weights, while others have lower weights. However, for simplicity and because we have no a priori knowledge regarding which GSA method is more powerful than others for this particular multiscale cancer model, we set k_j = 1/N (j = 1,2,…,N), meaning that all GSA methods are equally important.

Figure 3.

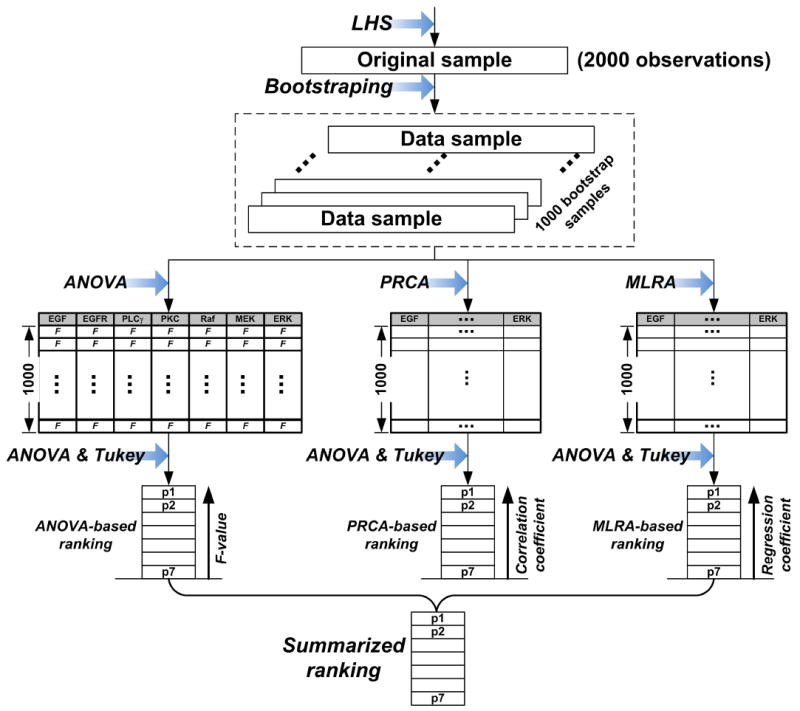
Process for producing the final summarized parameter ranking. All three GSA methods (ANOVA, PRCA, and MLRA) generate their own individual parameter rankings based on the same 1000 bootstrap samples. Note that all GSA methods use ANOVA and Tukey’s method to perform parameter grouping. The summarized ranking is obtained using Eq. (1).

3. RESULTS

The agent-based model was implemented in C/C++. In each simulation, a total of 49 seed cells arranged in a 7 × 7 square were initially positioned in the 2D lattice. The first 2000 sets of parameter combinations (i.e., the original sample) were created with Matlab 2008 (Mathworks, Inc.). All statistical analysis programs for running ANOVA, Tukey’s method, and bootstrap resampling were developed with SAS/STAT 9.3 (SAS Institute). Each GSA method took approximately three minutes to obtain the ranking results on a Dell workstation (Pentium-4 1.7 GHZ, 2.0 GB RAM). Input parameters are the initial concentrations of the seven EGFR pathway components (Fig. 1a). Table 1 summarizes the input parameter variation ranges and corresponding levels.

TABLE 1.

Parameter variation ranges and corresponding levels of input parameters. Variation ranges were set large enough to cover the entire possible parameter space. The variation range for each parameter was partitioned into levels by means of evenly spaced intervals. Standard values are taken from the literature [31, 32].

Input	Standard value (nM)	Variation range	Number of levels
EGF	2.65	0~10.0-fold	10
EGFR	80	0~2.0-fold	10
PLCγ	10	0~2.0-fold	10
PKC	10	0~2.0-fold	10
Raf	100	0~3.0-fold	12
MEK	120	0~4.0-fold	10
ERK	100	0~10.0-fold	20

3.1 Individual Parameter Rankings

For all three GSA methods (ANOVA, PRCA, and MLRA), conducted using the 1000 bootstrap samples, the individual ranking results are shown in Fig. 4. All GSA ranking results find ERK to have the most significant impact on both, tumor volume and expansion rate, a result which further emphasizes the potential therapeutic value of ERK in suppressing overall tumor growth. In tumor volume evaluation, MEK remains among the top three parameters in all rankings, but it is far less important than ERK in influencing the tumor volume outcome because there is a big difference in each corresponding sensitivity index value between MEK and ERK. In tumor expansion rate evaluation, other than ERK, both PLCγ and EGFR are determined to be critical by all of the GSA methods. As expected, for each model output, the different GSA methods each produce different ranking results.

Figure 4.

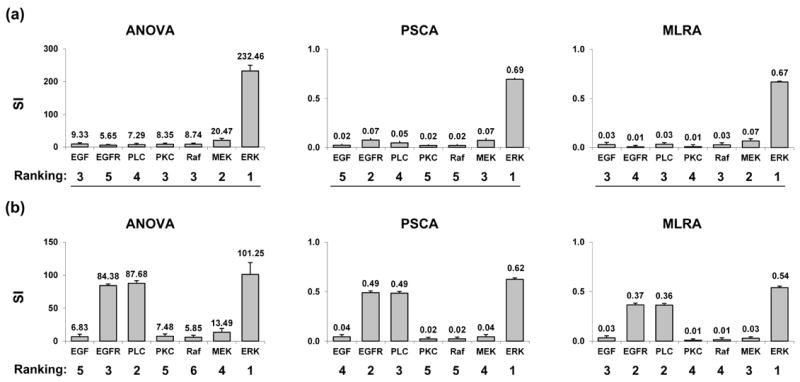
Individual parameter ranking results from 1000 bootstrap simulations for ANOVA, PRCA, and MLRA, with respect to (a) the final number of live cells – tumor volume and (b) the number of simulation steps – tumor expansion rate. SI stands for sensitivity index. Columns, mean; bars, SD.

3.2 Summarized Ranking

For the three equally-weighted GSA methods, the value of each weight, k_j (j=1,2,3) for Eq. (1) is 1/3. The summarized parameter rankings with respect to tumor volume and expansion rate are shown in Fig. 5. From this figure, one can easily identify whether a component is critical, as well as what the component’s position relative to other molecules in the pathway is. In tumor volume evaluation (Fig. 5a), ERK is the most critical parameter, followed by MEK. This result is most similar to the ranking obtained by using ANOVA and MLRA (Fig. 4a). That ERK is the most important parameter affecting tumor volume is not surprising, since ERK decides a cell’s proliferation fate in our phenotypic decision algorithm of the 2D NSCLC multiscale model [13]. However, in tumor expansion rate evaluation (Fig. 5b), ERK remains the most critical parameter, followed by PLCγ and EGFR. This is somewhat surprising, since we assumed that PLCγ would have the most significant impact on tumor expansion because it is the determinant of cell migration fate [13]. The identified important parameters by the final summarized ranking with respect to tumor expansion rate are in agreement with all of the three individual parameter rankings (Fig 4b).

Figure 5.

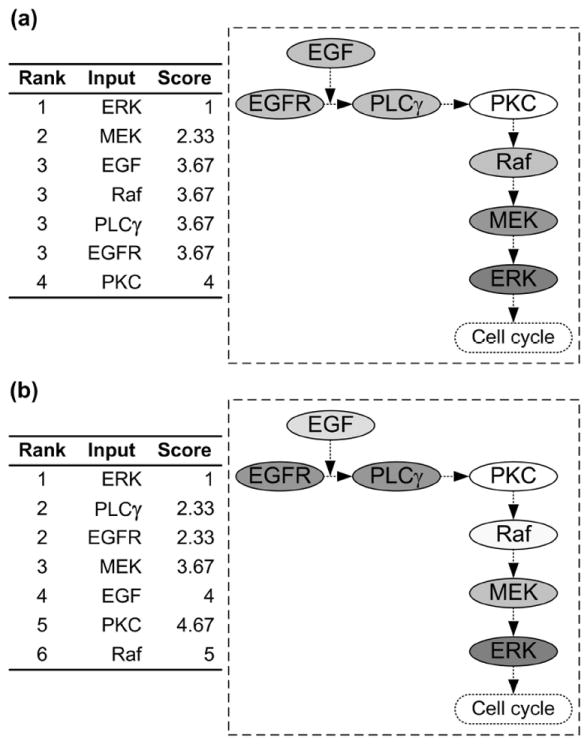
Final summarized parameter ranking according to Eq. (1) with respect to (a) tumor volume and (b) tumor expansion rate. The ranking results (table) are shown on the left of each panel, while the right (pathway figure) identifies the potential of each component for serving as a therapeutic target. A molecule with a higher ranking is associated with a deeper background color.

4. DISCUSSION AND FUTURE WORK

Each sensitivity analysis method (whether GSA or LSA type) has its own key assumptions, limitations, and demands regarding the time and effort needed for application and interpretation [11]. With that in mind, we have presented a sampling-based GSA workflow into which a number of helper techniques, such as LHS sampling, Bootstrap resampling, and ANOVA with Tukey’s method for parameter grouping are introduced, and have applied the workflow to a previously developed multiscale NSCLC model [13]. Overall, the workflow provides solutions to (1) how to render the large number of parameter variation combinations computationally manageable, (2) how to effectively quantify the sampling distribution of the sensitivity index for each GSA to address the computational intensity issue, and finally (3) how to discriminate between two closely ranked input parameters. Parameter ranking results indicate that, for the model used here, ERK is the most critical parameter at the molecular scale chiefly regulating the two tumor growth indices, i.e., tumor volume and expansion rate, on the multi-cellular level. Cautiously extrapolated, this finding therefore supports therapeutic efforts that seek to target ERK to control tumor expansion in NSCLC. Furthermore, by extending the model to incorporate drug-cell interactions [23-27], the GSA can also be used to help develop optimal drug treatment strategies for individual patients.

The workflow introduced here is flexible in that some methods can be substituted with others at the investigators’ choice. For example, at the pre-analysis phase, in order to introduce the uncertainty of the parameters into the model, we use LHS to randomly select parameter values from their respective probability distributions. In fact, there are many other approaches to process random sampling (see [28]), and this research topic has been extensively studied in the statistics and engineering fields. We choose to use a uniform probability distribution, i.e., equal probability of selection, for all of the input parameters because the distributions of the parameters are unknown to us. If any of the parameter distributions is known a priori, this knowledge (or literature data) should be applied to the model to improve the accuracy of the parameter sampling. However, the probability distributions of parameter values for real biological systems are usually unknown, and it is thus reasonable to use a uniform distribution as the default [29]. Also, as mentioned earlier, we can employ techniques other than Tukey’s method along with ANOVA to quantify the distribution of the sensitivity index, and other types of GSA methods [11, 30] can be integrated into the workflow as well.

As noted before, it is expected that different GSA methods produce different parameter rankings with respect to either tumor growth index (i.e., tumor volume or expansion rate). This prediction is precisely what we find in our analysis, and it highlights the importance of the adjusted, summarized parameter ranking method, using Eq. (1), which integrates the individual parameter rankings. This way, a model parameter (pathway component) is identified to be critical only when all or most of the GSAs agree. In both tumor volume and expansion rate evaluation, PKC is assigned the lowest ranking by most of the GSAs, and thus is deemed to be a less important parameter. However, this conflicts with our previous LSA study’s results [17], where the model is observed to be sensitive to variations in PKC. Since the LSA method only varies a single parameter at a time while keeping all others fixed, we believe it only accesses the baseline of the effect of perturbations in each individual parameter. By incorporating multiple methods, the proposed GSA analysis procedure inherently indicates to the researcher how strong the produced ranking is—in particular, how certain the evaluation of a molecule’s importance is. A consistently high ranking indicates that a molecule is likely a good therapeutic target, since the multiple confirming analyses add to the robustness of the results. While it may be difficult to choose the “best” or “surest” method of analysis per se, this “across-GSA methods analysis” should increase confidence in the result, which is essential once treatment strategy choices are deduced from it.

We focus on computing the ranking of the parameters, not on understanding what level of difference would make a parameter more critical than others. In practice, this is the researcher’s responsibility to determine this level, which also depends on the model being investigated. Although the ANOVA with Tukey’s method can divide the parameters into different groups from a statistical point of view, the result should be used only as a reference to the assessment of difference between groups.

As described, our multiscale model spans two biological scales: molecular signaling and multicellular scales; a molecularly-driven cell phenotype decision algorithm was established to link the two scales. In this study, we focused our parameter analysis on a subset of model parameters, i.e., on concentrations of pathway components, simply to demonstrate the applicability of the GSA workflow. However, other scale-specific parameters (e.g., association and dissociation kinetic rates on the molecular scale, oxygen and glucose concentration profiles on the multicellular scales, etc.) and the threshold parameters (specifically, for ERK and PLCγ) for linking molecular changes to cellular phenotypic determination can be varied simultaneously together with the pathway parameters to obtain a more complete ranking of pathway ‘signatures.’ While this will incur overload computational cost, it is particularly important for a multiscale model to be useful in rationally designing multi-target or multi-component therapies. This topic has not been fully addressed yet by the multiscale modeling community.

In summary, we have presented a GSA workflow accounting for multiple GSA methods together to identify critical parameters at the molecular level that have significant impact on tumor volume and expansion rate on the microscopic level. Applying the workflow to a previously developed multiscale lung cancer model, ERK is found to be the most important molecule in regulating both tumor evaluation indices, thus indicating its potential to serve as a therapeutic target in NSCLC. In the future, kinetic rate constants will also be considered as molecular parameters, and their cross-scale effects will be examined together with the signaling pathway component concentrations. Currently, we only use the GSA workflow to perform sensitivity analysis when a simulation task is finished, but it is reasonable to hypothesize that parameter rankings are changing over the course of the simulation. Hence, we plan to perform GSA at regularly spaced time intervals, producing a map of time-dependent dynamic parameter rankings, which may provide additional and useful information to moleculartargeted cancer research.

Abbreviations

ANOVA

Analysis of Variance

EGF

epidermal growth factor

EGFR

EGF receptor

ERK

extracellular signal-regulated kinase

GSA

global sensitivity analysis

LSA

local sensitivity analysis

MAPK

mitogen activated protein kinase

MEK

mitogen activated protein kinase kinase

MLRA

multivariate linear regression analysis

PLCγ

phospholipase Cγ

PKC

protein kinase C

PRCA

partial rank correlation analysis