Abstract
The processing speed of the brain depends on the ability of neurons to rapidly relay input changes. Prior theoretical and experimental studies of the time scale of population firing rate responses arrived at controversial conclusions, some advocating an ultra-fast response scale while others arguing for an inherent disadvantage of mean encoded signals for rapid detection of the stimulus onset. Here we assessed the time scale of population firing rate responses of neocortical neurons in experiments performed in the time domain and the frequency domain in vitro and in vivo. We show that populations of neocortical neurons can alter their firing rate within 1 millisecond in response to somatically delivered weak current signals presented on a fluctuating background. Signals with amplitudes of miniature postsynaptic currents can be robustly and rapidly detected in the population firing. We further show that population firing rate of neocortical neurons in vitro and in vivo can reliably encode weak signals varying at frequencies up to ~200–300 Hz, or ~50 times faster than the firing rate of individual neurons. These results provide coherent evidence for the ultra-fast, millisecond time-scale of cortical population responses. Notably, fast responses to weak stimuli are limited to the mean encoding. Rapid detection of current variance changes requires extraordinarily large signal amplitudes. Our study presents conclusive evidence showing that cortical neurons are capable of rapidly relaying subtle mean current signals. This provides a vital mechanism for the propagation of rate-coded information within and across brain areas.
INTRODUCTION
Within 150–200ms humans can process complex natural images and relate them to the visual world (Thorpe et al., 1996). In a color-discrimination task, monkeys can make perceptual decisions even within 30ms (Stanford et al., 2010). To perform cognitive tasks requiring interactions between multiple brain regions in such short time intervals, neuronal ensembles must be able to rapidly detect and transmit input changes. Sensory stimuli can reach the cortex quickly, e.g. within 5–10ms in the somatosensory system (Swadlow, Hicks, 1996). However, the mechanisms governing the speed of intracortical communication are poorly understood and largely debated (London et al., 2010; Koendgen et al., 2008; Silberberg et al., 2004). Recently, London and coworkers found that cortical neurons are extremely sensitive to changes of their input: injection of a subtle 25pA current into a single cortical neuron can change population firing rate in a local cortical circuit (London et al., 2010). Yet, the cellular basis of this remarkable sensitivity and the response time scale is unknown. Theoretically it is understood that an input signal can be communicated to a neuronal population via two channels. First, a current can be added to the input of all neurons in a population, thus leading to the change of the mean input current. This strategy is plausible for neuronal communication, since a change of the mean current in postsynaptic neurons is the primary effect of synaptic transmission. Second, the variance of input current fluctuations can be changed, such that the signal modulates the variance of the input fluctuations in all neurons, similar to the amplitude modulation strategy widely used in radio communication. Indeed, in the neocortex the changes in the activity of excitatory and inhibitory populations of neurons can accurately track each other (Okun, Lampl, 2008), such that excitation and inhibition remain balanced. In this case, a perturbation to the network would result only in a change of input variance to each neuron while changing little the mean input current. Thus, changing the variance of the input may represent an additional way of communication between neuronal populations (Lindner, Schimansky-Geier, 2001; Silberberg et al., 2004). Which of the two signal encoding strategies may underlie the rapid communication between populations of cortical neurons? Theoretical analysis suggests that changes of the input mean can mediate fast population responses of the leaky integrate and fire model neurons and other models with rapid action potential initiation (Fourcaud-Trocme et al., 2003). At the same time, an early study suggested that the variance encoding strategy permits extremely fast population rate encoding of strong alternations of the variance of the input to neocortical neurons (Silberberg et al., 2004). Here, we show that (1) populations of visual cortex neurons respond immediately to subtle 20pA change of mean input current in the soma, (2) populations of cortical neurons in vivo can encode fast varying signals up to 200–300Hz in their firing; (3) populations consisting of a few thousand neurons can reliably detect small changes of mean input current within the first few milliseconds after stimulus onset.
MATERIALS AND METHODS
All experimental procedures used in this study were in accordance with the guidelines published in the European Communities Council Directive (86/609/EEC, 1986) and conformed to US National Institutes of Health regulations. Experimental protocols were approved by the respective local animal welfare committees (Bezirksregierung Arnsberg, Germany, and Institutional Animal Care and Use Committee of University of Connecticut, USA).
In vitro intracellular recordings were made in slices of rat visual cortex. The details of slice preparation and recording were similar to those previously used (Volgushev et al., 2000). The Wistar rats (P21–P28, Harlan, USA) were anaesthetized with isoflurane (Baxter, USA), decapitated, and the brain was rapidly removed. One hemisphere was mounted onto an agar block and 350μm thick sagittal slices containing the visual cortex were cut with a vibrotome (Leica, Germany) in ice cooled oxygenated solution. After cutting, the slices were placed into an incubator where they recovered for at least one hour at room temperature before transferring them in to the recording chamber. The solution used during the preparation of the slices had the same ionic composition as the perfusion/extracellular solution. It contained (in mM) 125 NaCl, 2.5 KCl, 2 CaCl2, 1 MgCl2, 1.25 NaH2PO4, 25 NaHCO3, 25 D-glucose and was bubbled with 95% O2 and 5% CO2. Recordings were made with the slices in submerged conditions at 28–32°C. Temperature in the recording chamber was monitored with a thermocouple positioned close to the slice, 2–3mm from the recording site. Whole-cell recordings using patch electrodes were made from layer 2/3 pyramidal neurons, selected under visual control using Nomarski optics and infrared videomicroscopy. The patch electrodes were filled with K-gluconate based solution (in mM: 130 K-Gluconate, 20 KCl, 4 Mg-ATP, 0.3 Na2-GTP, 10 Na-Phosphocreatine, 10 HEPES) and had a resistance of 4–6MΩ. All recordings were performed using the bridge mode of Axoclamp-2A amplifier (Axon Instruments, USA). After amplification and low-pass filtering at 10 kHz, data were digitized at 20kHz and fed into a computer (Pentium4; Digidata 1440A interface and pCLAMP software, Molecular Devices). The membrane potential responses to injected current recorded were processed offline in Matlab (The Mathworks, Natick, MA). For each cell and each frequency, spikes were detected in membrane potential traces as positive zero crossings, and their times extracted as {tj}, j = 1-N. Current injections lasted 46s, and were separated by a recovery period of 60 – 100s. In some experiments synaptic transmission was blocked by adding 25μM APV, 5μM DNQX and 80μM PTX to the extracellular solution. All chemicals were obtained from Sigma, USA, unless stated otherwise.
In vivo intracellular recordings were made in adult cats (3.0–4.5kg). Surgery and animal maintenance were similar to those used in our previous studies (Volgushev et al., 2002). Anaesthesia was induced with a mixture of ketamine hydrochloride (Ketanest, Parke-Davis GmbH, Germany, 0.3mL/kg, i.m.) and Rompun (Bayer, Germany, 0.08mL/kg, i.m.). Surgery was started after stable anaesthesia with complete analgesia was achieved. Sometimes this required additional doses of the anaesthetic. After tracheal and arterial cannulations, the animal was placed in a stereotaxic frame, the skull was exposed and a craniotomy (about 5mm diameter) was done over area 17 of the visual cortex centered at P4/L3 (Horsley-Clark). A brass-cylinder (diameter 20mm) was cemented over the opening. The holder for hydraulically driven micromanipulator (Narishige Instruments, Japan) was mounted onto the skull with screws and dental cement. All wound edges and pressure points were treated with a local anaesthetic (Xylocaine, Astra GmbH, Germany) every 5–8 hours. Muscle relaxation with alcuronium chloride (Alloferin, ICN Pharmaceuticals, Germany) and artificial respiration were started either at this point, or earlier during the surgery, to avoid respiratory depression due to additional doses of the anaesthetic. Thereafter adequate anaesthesia was maintained throughout the experiment by a gas mixture of N2O: O2 (70:30) and 0.2–0.4% halothane (Eurim-Pharm, Germany). Artificial respiration was performed with a cat/rabbit ventilator (Model 6025, Ugo Basile, Biological Research Apparatus, Comaria-Varese Italy). The volume (20–40cm3) and the rate of stroke (7–15 per minute) were adjusted to maintain end-tidal CO2 between 3.5 and 4.0%. End-tidal CO2, body temperature, heart rate, blood pressure and EEG were continuously monitored. Body temperature was maintained around 37–38°C. Fluid replacement was achieved by the intraarterial administration of 6mL of Ringer solution containing 1.25% glucose, per hour. Paralysis was maintained by i.a. infusion of alcuronium chloride (0.15mg/kg/h) in Ringer's solution. The experiments lasted usually 2–4 days. At the end of the experiment, animals were sacrificed with an overdose of anaesthetics. In vivo intracellular recordings from visual cortical neurons were made with sharp electrodes filled with 2M potassium acetate. Electrode resistance was 80–120MΩ. Recordings were made using the bridge mode of Axoclamp-2B amplifier (Axon Instruments, USA). After amplification and low-pass filtering at 10kHz, the data were digitized at 20kHz and stored on a computer (Pentium4; Digidata 1322A, Axon Instruments, USA). Current injections lasted 30s, and were separated by a recovery period of 60 – 100s. For each cell and each frequency, spikes were detected in membrane potential traces as with the same methods as in the in vitro recordings.
Assessing the frequency response function of neuronal populations
To assess the frequency response of neuronal populations we have somatically injected currents which were composed of a sinusoid signal of frequency f immersed in different realizations of a noise for in vitro experiments, or without added noise in vivo. A constant DC current was added to maintain a target firing rate of ~5Hz. Currents were injected in 30–46s episodes, with 60–100s intervals between the injections. For each recording condition, in vitro with correlation time constant of injected noise τI=5ms or τI=50ms or in vivo, currents were injected in n=4…10 different neurons. The vector strength r characterizes phase-locking of neurons' firing to the periodic stimulus. r was computed using all recordings for a frequency f in each recorded cell individually and subsequently averaged across cells. In each cell, responses to several frequencies were recorded. The number and length of recordings were as follows. In vitro recordings with τI=5ms were obtained in 9 cells, were each cell contributed totally ~9000 spikes to frequencies f (f= 3 Hz, 5 Hz, 50 Hz, 110 Hz, 230 Hz, 370 Hz, 515 Hz). In vitro recordings with τI=50ms were obtained in 10 cells, were each cell contributed ~9000 spikes to frequencies f (f=3 Hz, 5 Hz, 50 Hz, 110 Hz, 230 Hz, 370 Hz, 515 Hz). In vivo recordings were obtained in 4 cells, were each cell contributed ~1000 spikes to individual frequencies f (f=3 Hz, 13 Hz, 50 Hz, 110 Hz, 200 Hz, 300 Hz, 400 Hz, 500 Hz, 600 Hz). Parameters of injected currents were adjusted to obtain similar amplitudes of membrane potential fluctuations and similar firing rates (ν) in all in vivo and in vitro experiments: in vitro τI=5ms, membrane potentials fluctuations −56±6.2 mV, ν=4.5±1.2 Hz; in vitro τI=50ms, membrane potentials fluctuations −48.1±7.4 mV, ν=5.2±0.9 Hz; in vivo membrane potentials fluctuations −49.1±7.1 mV, ν=5.6±2.2 Hz.
To determine the statistical significance of phase locking of recorded spikes to periodic input current stimulation, we used a randomization test. This test was carried out for spikes recorded for each input frequency f and each cell separately. The value of the experimentally obtained vector strength r was compared to values obtained for data sets of the same size but randomized phase. 10,000 independent realizations of random sets {x'j} where each x'j ∈ N(0,1), j=1…N (number of spikes recorded in a cell in response to the input frequency f) were used to generate 10000 realizations of phase randomized sets of spike times t'j = (mod(tj·f,1) + x'j)/f. This procedure keeps the number of spikes equal to that obtained experimentally but eliminates any original phase preference. For each of the randomized sets of spike times, the corresponding vector strength was calculated r's = abs(ΣjN exp(i2πft'j))/N. For the r's -distribution we calculated the 95th-percentile, which is the value below which 95% of the randomly drawn r's can be found. The probability to obtain by chance a value above the 95th percentile is 5%. The 95th percentile of the r's distribution was taken as the single cell significance level for the modulation frequency f. The maximal 95-percentile values obtained among cells recorded with the same modulation paradigm are shown in the respective figure as significance levels.
Step onset detection
To quantify the speed of step onset detection we assume a theoretical decoder that reports a step change of input current if the population firing rate falls outside the 95% confidence boundary of pre-step distribution. We calculate the probability of step detection as a function of the number of neurons that receive the common current step (equivalent to the number of realizations N) and time delay T after the step. To obtain the probability of step detection by N neurons within a time interval Tms after the step onset, we composed 1000 trial sets; each consisting of N randomly selected sweeps. In each trial set, we determined whether the spike count in the interval T after step onset fell outside the 95% percentile of the corresponding pre-step distribution. The number of trial sets, which fulfill this condition, provides an estimate of the probability for a population of N neurons to detect the step change within a time T after step onset. The probability to detect a step change within the time t is equivalent to the cumulative probability to encounter a spike count larger than the 95% percentile (or smaller than the 5% percentile if the firing rate is decreased) of the spike count distribution before the step onset. For an increase of firing rate this can be computed as 1–CDF(P(N, ν2t), Percentile(P(N, ν1t), 0.95)), where CDF is the cumulative distribution function. For the decrease of firing rate we compute detection probability as CDF(P(N, ν2), Percentile(P(N,ν1t),0.05)–1). Here, P(N, ν1t) is the spike count probability distribution, where p is the probability to fire a spike given the average population rate ν1 and N the number of neurons is the initial probability distribution of spike counts and P(N, ν2t) is the distribution of spike counts after the step change.
RESULTS
Layer 2/3 pyramidal neurons which mediate computation within and communication between different cortical areas (Gilbert and Wiesel, 1979) are particularly relevant for sensory processing. To directly test how populations of L2/3 cortical neurons respond to subtle input changes, we examined their firing rate dynamics in response to small amplitude current steps immersed in a fluctuating background. Currents I(t) for in vitro injection into the soma through a patch electrode were digitally synthesized offline using the equation:
| (1) |
Here and in all following experiments, I0 is a constant current set to maintain a target firing rate of 5Hz. η(t) is an Ornstein-Uhlenbeck process with zero mean, unit variance and correlation time τI=5ms, and σ is the standard deviation of the resulting background current noise. This noise component ση(t) mimics the effective somatic current produced by a large number of balanced excitatory and inhibitory synaptic inputs in vivo (Destexhe et al., 2003). Im·Step(t) describes the signal, in this case positive and negative steps of amplitude Im and duration of 300ms as in (Silberberg et al., 2004) which were interleaved with no stimulus (noise only) periods of 300ms. One stimulation cycle lasted for 1.2s, with time cause defined by Step(t) in Eq.1, where mod(t, 1.2s) denotes t modulo the period length of 1.2s (see Figure 1C). To guarantee weak stimulation, the amplitude was set to Im=20pA, which corresponds to amplitudes of unitary postsynaptic currents resulting from the activation of a single excitatory or inhibitory presynaptic fiber (Hestrin, 1993; Stern et al., 1992). When applied without noise, steps of this small amplitude led to an approximated first spike latency >100ms, even for holding potentials close to the spike threshold (Figure 1 A,B; −55mV). A 20pA up or down step in the current mean evoked a mean membrane potential change of ~1–2mV and left membrane potential fluctuation variance unaffected. To test whether populations of neocortical neurons can detect these small changes at their inputs, we injected currents with different realizations of the noise component in 15 L2/3 pyramidal cells (Figure 1 E). Cell firing during individual responses to current injection did not show an obvious relation to the mean current step (Figure 1D bottom trace). The population firing rate, however, clearly changed with the onset and offset of step stimuli, as revealed by the peristimulus time histogram of the spike times constructed over all repetitions pooled from all 15 cells. It would be plausible to expect that the low-pass filtering of input currents by the membrane RC-circuit should carry over to the firing rate dynamics. Surprisingly however, in response to the current steps presented on an in vivo-like background, the population firing rate already changed within the first 1–2 milliseconds after stimulus onset, substantially faster than the neuron's mean membrane potential (Figure 1E). Rapid change of the population firing rate at the onset and offset of current steps is clearly seen at zoom-in of the initial portions of step responses (Figure 1F). The population rate rapidly conveyed both positive and negative changes of the mean current and could increase by 185% or decrease by 75% within a millisecond (Figure 1F). How important is the presence of a substantial, in vivo like background activity for the ultrafast changes of population firing rate in response to subtle changes of the mean input current? To clarify the role of the noise component in fast population responses we conducted control experiments with no noise component added (η(t) = 0, Figure 2A,B). In this case, only low intrinsic noise of in vitro preparation, e.g. due to spontaneous transmitter release and channel noise was present (Jacobson et al., 2005; Steinmetz et al., 2000). Results presented in Figures 1 and 2 clearly demonstrate that populations of layer 2/3 neocortical neurons can respond to step-like changes of the mean input very rapidly, on millisecond time scale. This is the first demonstration of fast detection of weak mean encoded stimuli in the time domain. Notably, previous studies of the speed of cortical population encoding performed in the time domain and in the frequency domain reported controversial results. The only study conducted so far in the time domain in layer 5 pyramids failed to detect and quantify the fast onset in response to mean current changes and concluded that encoding of mean changes is intrinsically slow and only variance-encoded signals can be detected fast (Silberberg el al. 2004). On the contrary, frequency domain studies reported that layer 5 pyramidal neurons can encode remarkably fast stimuli up to 200-300 Hz (Koendgen et al. 2008, Higgs, Spain 2008), suggesting that mean signals can be detected at a limiting time scale of ~1/(2 π 200Hz)<1ms. To resolve this contradiction, it is necessary to study encoding of mean and variance-coded signals under the same experimental conditions and in neurons of the same type. Therefore, we next studied responses of layer 2/3 pyramidal neurons to variance-coded signals in time domain, and to mean-coded signals in the frequency domain.
Figure 1.
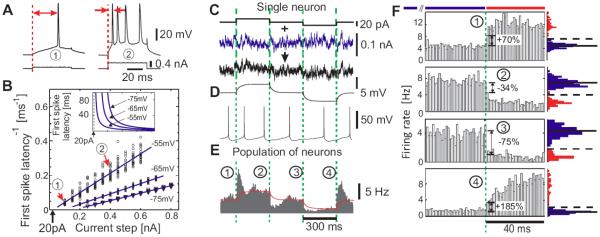
Encoding of current steps by single neurons and populations in vitro. (A) Responses of a L2/3 neuron to 0.1nA and 0.4nA steps. Red arrows: first spike latency. (B) Inverse first spike latency vs. step amplitude (N=20 for each step) and linear fits (blue lines). Red arrows: responses in (A). Inset: first spike latency vs. step amplitude as derived from linear fits of the inverse first spike latency (same current scale). (C) Current steps (top) and current steps immersed in fluctuating current (τI = 5ms) (bottom). To ensure weak stimulation, we chose current steps of 20pA which in (A) correspond to an approximated latency >100ms. (D) Membrane potential response to subthreshold current steps as in (C, top) (average, N=20) and to current in (C, bottom). (E) Population firing in response to steps immersed in different realizations of fluctuating current, bin size 1ms. Peristimulus time histogram is constructed over all repetitions pooled from all 15 cells (~175min; ~52000 spikes) by aligning the evoked spike trains with the onset of current steps. Red line: membrane potential from (D, top). (F) Zoom-in on responses in (E). Blue and red histograms denote distributions of spike counts in 1ms-bins 120ms before (blue) and 40ms after each step (red). In the distributions before the step solid horizontal lines denote the mean and dashed lines 3 s.d.. Dashed green lines in C–F indicate the onset of steps.
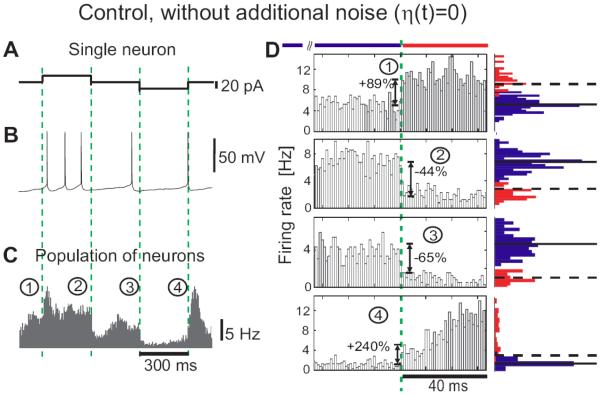
Figure 2.
Encoding of current steps by single neurons and populations in vitro under minimal noise conditions. (A) Current steps, (B) an example of membrane potential response to current in (A). (C) Population response to current steps with intrinsic noise only (η (t)=0) pooled from all 11 cells (~81 min; ~ 24380 spikes); bin size 1ms. (D) Zoom-in of responses from C. Red and blue histograms show distributions of spike counts in bins 120ms before (blue) and 40ms after each step (red), as indicated by the red and blue horizontal bars. In the distributions before the step horizontal lines show the mean rate (solid) and 3 standard deviations (dashed). Dashed green lines in A–D indicate the step onset, same notation as in Figure 1.
Low susceptibility to variance coded signals
Since the fluctuations in the activity of excitatory and inhibitory populations accurately track each other in cortical networks (Okun and Lampl, 2008; Renart et al., 2010), a perturbation to the network can result predominantly in a change of input current variance, with little or no change in its mean. Theoretical studies showed that changing the input current variance may represent a viable way of communication between neuronal populations (Lindner and Schimansky-Geier, 2001; Naundorf et al., 2005b; Silberberg et al., 2004; Fourcaud-Trocme and Brunel, 2005). To test this conjecture and to directly compare the two encoding strategies in L2/3 pyramidal neurons, we studied the firing rate dynamics in vitro in response to step-like changes in the variance of the fluctuating input current:
| (2) |
As in the experiments described above, the constant current component I0 was used to achieve a target firing rate of 5Hz and η(t) was the Ornstein Uhlenbeck process with τI = 5ms. εv is the magnitude of the standard deviation increase, εv=0.5 or εv=2 in our experiments. mod(t, 2s) denotes t modulo the period length of 2s, so that every second the standard deviation of the fluctuating input was switched between σ and σ(1+ εv). To facilitate a comparison between the variance vs. the mean encoding strategies, a protocol with the same time course was repeated for steps of mean current synthesized as
| (3) |
with Im=20pA. A 20pA mean current step evoked a mean membrane potential change of ~1-2mV and left membrane potential fluctuation variance unaffected. The εv=2 step increased the standard deviation of the membrane potential fluctuations by ~1-2 mV but left the mean voltage unaffected. Confirming the results described above, small amplitude 20pA-steps of the mean current induced pronounced changes of the population firing rate of layer 2/3 neurons, with clear instantaneous firing rate changes at the onset of positive and negative steps (Figure 3C). In contrast, a step-like increase of the standard deviation of the input current with comparable magnitude (εv=0.5) failed to elicit a measurable firing rate response (Figure 3A). When we increased the magnitude of the variance step to εv=2, which corresponds to a 3-fold σ-increase (Figure 3B), the increased input current fluctuations elicited a substantial firing rate response. These results are consistent with the large variance changes which were necessary to elicit a firing rate response in neocortical neurons studied in time domain (Silberberg et al. 2004) and in frequency domain (Boucsein et al., 2009), as well as with cortical neurons' firing rate dependence on current variance (Rauch et al., 2003). In responses to large variance changes the population firing rate exhibited virtually instantaneous components arising within 1–2ms after the stimulus onset (Figure 3B). The instantaneous components of the response to 3σ steps were comparable in magnitude and speed to the instantaneous components in responses to small amplitude steps of the mean current (Figure 3B,C). The tonic firing rate during the 3σ step changed significantly less than during response to subtle 20pA mean current steps. These results reveal a substantial difference in firing rate responses of layer 2/3 pyramidal neurons to signals encoded via these two strategies. Minor changes of the mean input current induce a virtually instantaneous change of firing rate at the step onset, followed by a robust change of the stationary firing rate. Thus, both the onset and duration of small changes in the mean input current are reflected in the population firing with high temporal precision. In contrast, large changes in the input variance appear to be necessary to affect the population firing rate, whereby the response is predominantly transient with a weak stationary component. These results confirm the observation of Silberberg et al. (2004) that large variance changes are necessary to elicit a population firing rate response (e.g. Fig. 1B, 4B in Silberberg et al. 2004). However, our results (Figure 3) also show that to achieve a same size tonic rate component, much larger changes of the variance than of the mean are needed. This would bias the comparison in favor of variance changes, and might have been a reason why in their land-mark study Silberberg et al. (2004) concluded that only variance changes can evoke fast population response, but overlooked the game-changing feature of fast onset dynamics in response to mean current changes.
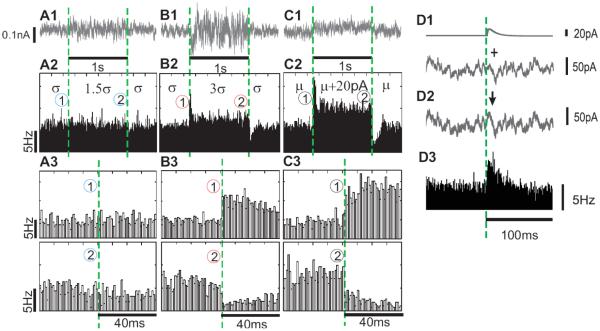
Figure 3.
Population response to changes in variance (A,B) or mean (C) of the input current (A–C) Examples of fluctuating currents (τI = 5ms) with step-like changes in the standard deviation σ by 50% (A1, σ→1.5σ→σ), by 200% (B1,σ→3σ→σ) or step-like changes of the mean current μ (C1, μ→μ+20pA→μ). Population firing rate changes in response to injection of currents as in A1–C1, 2530 realizations (A2), 5214 realizations (B2) and 2706 realizations (C2). (A3–C3) Zoom-in of responses to the onset and offset of step-changes in A2–C2. (D) EPSC-like current pulse immersed in fluctuating background (D1–D2) is reliably detected by a population of neurons (D3, 7600 realizations). In all subfigures, dashed green lines indicate the onset of steps or EPSCs, bin size 1ms.
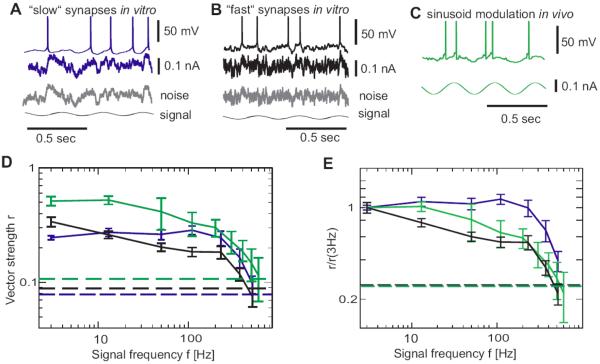
Figure 4.
Frequency encoding in neocortical neurons (A,B) Responses of L2/3 neurons in vitro to fluctuating current with periodically modulated mean and long correlation time τI = 50ms, (A, “slow synapses”, blue) or short correlation time τI = 5ms (B, “fast synapses”, black). Bottom gray traces show the corresponding fluctuating component and the signal. In A–C injected current is shown below each trace. (C) Response of a cat visual cortical neuron in vivo to sinusoidal current injection (green). (D) Frequency dependence of vector strength r for modulation paradigms in A–C (same color code), dashed horizontal lines indicate the corresponding single cell 95% significance level. For each frequency f, the vector strength r was first computed using all recordings from each recorded cell and subsequently averaged across cells. (E) Data from (D) displayed as normalized vector strength r/r(3Hz).
Detection of PSCs by populations of neurons
To further corroborate fast transmission of subtle mean current signals in cortical neuronal populations we studied the firing rate dynamics of L2/3 pyramidal neurons in response to EPSC-like currents immersed in a fluctuating background. EPSC-like currents with rise time 1ms and decay time 10ms were synthesized as f(t)=εe(exp(−t/10ms)−exp(−t/1ms)), with εe chosen such that the peak amplitude of each current pulse was 20pA (Figure 3 D1), and added to a fluctuating background current ση(t) every 300ms (ti=300ms·i with i=1–152; I0 and ση(t) as in Eqs. 1–3). Injected currents I(t) were synthesized as
| (4) |
The firing rate of a population of cortical neurons changes quickly and robustly in response to the fast, small amplitude EPSC (Figure 3D). So far, ability to trigger an immediate spiking response in populations of postsynaptic cells has been demonstrated only for the exceptionally strong cortical synapses with the postsynaptic current amplitudes of ~200 pA or above (Galarreta and Hestrin 2001). Yet, the overwhelming majority of cortical synapses are much weaker, with postsynaptic current amplitudes of ~20pA or smaller (Stern et al. 1991) and PSP amplitudes well below 1 mV (Matsumura et al. 1996, Tables 2,3 therein). Our results show that activity at such weak synapses can be rapidly detected by postsynaptic population of a few thousand neurons on the background of substantial, in vivo-like fluctuations. Thus, a population of neurons receiving fast, small amplitude EPSC from just one common presynaptic cell, can reliably detect a single presynaptic spike and propagate this information to downstream cells. This indicates that the population firing rate response to a single additional spike or a minor current injection, as observed in local cortical circuits (London et al., 2010), can be mediated via the mean-current signaling channel alone.
In vivo and in vitro response to periodic stimuli
To directly compare the time scale of population responses to step stimuli in the time and in the frequency domain, we measured the frequency response function of layer 2/3 pyramidal neurons. To facilitate a comparison with recent in vitro work in other types of cortical cells (Koendgen et al., 2008; Boucsein et al., 2009) we obtained the frequency response function by measuring the response to each input frequency individually. The resulting frequency response function allows us to identify the bandwidth of reliably encoded frequencies which is closely connected to the time scale of the rising phase in the population response (Brunel et al 2001, Fourcaud-Trocme et al 2003). Currents I(t) for somatic injection into neurons, were composed of a sinusoid signal of frequency f immersed in a noise. A constant current I0 was added to maintain target firing rate of 5 Hz.
| (5) |
The noise mimicking in vivo synaptic bombardment was generated as an Ornstein-Uhlenbeck process η(t) with a correlation time τI=5ms or τI=50ms, standard deviation σ and signal to noise ratio εm/(εm+ σ) =0.26 (Figure 4A,B). The ability of neurons to encode signals of frequency f was quantified using the vector strength (Goldberg and Brown, 1969; Zheng and Escabi, 2008; Joris et al., 2010) r = abs(Σj=1Nexp(i2πftj))/N, where tj are the spike times and N the number of spikes. Here, each spike is represented by a vector of unit length and a phase between 0 and 2π defined by the spike time modulo the stimulus period. If all spikes are emitted at the same phase of the oscillation cycle then r is maximal (r=1), indicating a perfect encoding of the input frequency. If spikes occur at random phases, the vector strength is close to zero (r~0), indicating that the signal frequency is not encoded in the firing rate. We have assessed the frequency response function of layer 2/3 pyramidal neurons by calculating vector strength in responses to different frequencies (3–515Hz see Materials and Methods section for more details). Frequency response functions in Figure 4D,E show that that layer 2/3 pyramidal neurons in vitro can reliably encode weak periodic signals up to cut-off frequencies fc~200–300Hz in their population firing rate. Furthermore, input signals varying at frequencies of hundreds of Hz were encoded for both short (τI=5ms) or long (τI=50ms) correlation time constants (Figure 4D,E blue and black curves). Can cortical neurons in vivo also encode such high frequency signals in their population firing? To assess this question, we made intracellular recordings from regular spiking neurons in area 17 of cat visual cortex in vivo, and studied their firing rate dynamics in response to injection of sinusoidally modulated currents of amplitude εm =50pA and different frequency f: I(t)=I0+εm sin(2πft). No noise was added to the injected current because membrane potential fluctuations were produced by synaptic bombardment due to the background inactivity in vivo (Figure 4C). Frequency response function of visual cortex neurons in vivo showed high cut-off frequency of 200-300 Hz (Figure 4D, green curve), closely corresponding to the in vitro measurements. In vivo background current contains AMPA and NMDA receptor mediated components which strongly differ in the resulting current correlation times τNMDA ≥ 50ms and τAMPA ≤ 5ms (Zito and Scheuss, 2007; Hestrin, 1993; Stern et al., 1992). For in vitro experiments, we therefore have used synthetic noise with a short (τI=5ms) or long (τI=50ms) correlation time constants to match the in vivo noise constituents. To assess the effect of noise spectral composition on frequency response function, we normalized the vector strengths obtained in the three experiments to the response at the lowest frequency r(f)/r(3Hz). The in vivo transfer function of neurons was enclosed by the transfer functions measured in vitro with τI=50ms and τI=5ms noise. This finding is consistent with the mixture of AMPA and NMDA receptor-mediated components present in the fluctuations of somatic net current in cortical neurons (Zito and Scheuss, 2007). These results demonstrate that cortical neurons in vitro and in vivo can encode input signals over a broad bandwidth, with cut-off frequency fc of ~200–300 Hz. This implies a response time scale of ~1/(2 π 200Hz)<1ms, which corresponds to the fast time scale measured in our experiments with step-stimuli (Figures 1–3).
How many neurons are needed to rapidly detect a subtle step-like change of the mean input?
To address this question, we assume a theoretical decoder that reports a step change of input current if the population firing rate falls outside the 95% confidence boundary of pre-step distribution (see Figure 5A,B and Materials and Methods section for details). Using the data from the step experiments (Figure 1) we calculated for this decoder the probability of step detection as a function of the number of neurons that receive the common current step (equivalent to the number of realizations N) and time delay T after the step onset. Figures 5C,D illustrate that a small current step can be detected in the firing of 7400 neurons with 88% probability within the first ms after the step onset, and with > 99% probability within 2ms after the onset. The functional dependence of detection probability on the time elapsed after the step onset (Figure 5C) or on the number of neurons N in the population (Figure 5D) can be well approximated by a tanh-function, as can be expected from a decoder operating on two binomial distributions with different stationary rates. In the firing of 3700 neurons, the input current step is detected with a probability of 73% within 1 ms, and with >95% within 2ms after the onset. Even in the firing of ~2000 neurons the step is reliably detected (>95%) within no more than 3ms. These results show that populations of 2000 or more cortical neurons can operate on an ultra-fast time scale of 1–2ms, conveying even minor input changes on a time scale significantly faster than the membrane time constant of the neurons.
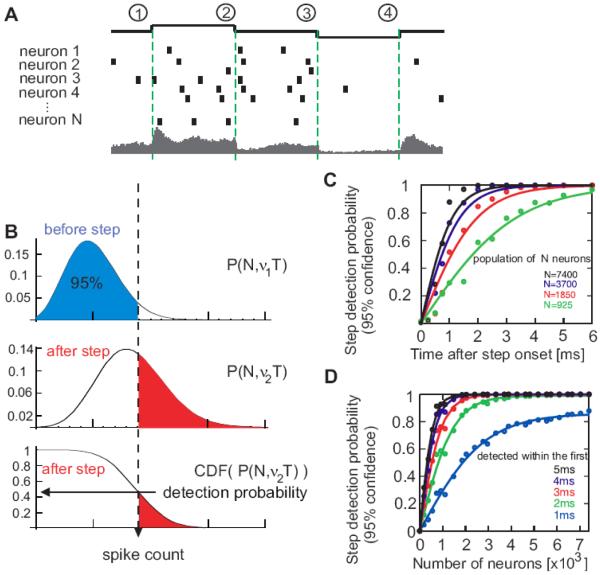
Figure 5.
Detection of population firing rate changes induced by changes of the mean input current (A) Illustration of step encoding in the population firing rate of N neurons. Top to bottom: timing of current steps; spike responses of neurons 1-N, with vertical bars representing individual spikes and the resulting peristimulus time histogram of the population firing rate (bottom, data from Figure 1E). (B) Illustration of a theoretical decoder. Binomial distributions P(N, ν1T) of spike counts before the step, P(N, ν2T) after the step and its cumulative distribution CDF(P(N, ν2T)). Form the latter the probability that after-step spike count is outside the 95% boundary of the pre-step distribution is determined (hor izontal arrow). This corresponds to the probability of step detection with 95% confidence. (C,D) Probability of step detection vs. time after step onset (C) and number of neurons (C) as calculated from data in Figure 1C–F and averaged across conditions (1)–(4). Circles denote the data points and solid lines denote fits of the form f(T)=tanh(bT) or f(N)=a tanh(bN), respectively. Note that a popula tion of 7400 neurons (equiv. to the number of realizations) can detect 88% of steps within the first 1ms.
DISCUSSION
In this study we demonstrate that populations of neurons in rat neocortex (1) can change their firing rate in response to small step-like changes of the mean input current very fast, within 1–2 ms, and (2) can encode in their firing periodic signals up to frequencies of 200–300 Hz, in vivo and in vitro. Results obtained in both time domain and frequency domain imply ultra-fast, sub-millisecond time scale of population responses. We further show, that (3) populations consisting of a few thousand neurons can reliably detect small changes of mean input within 1–2 ms.
Ultra-fast time scale of population response in theory and experiments
Our results provide direct evidence that incoming signals, represented as changes of the mean input current, could be detected within 2ms in the population firing of ~2000 neurons and within 1ms in a population of ~7000 neurons. Although it is plausible to assume that low-pass filtering by the membrane could carry over to the firing rate dynamics, we show that neuronal ensembles are capable of operating on a time scale significantly shorter than the membrane time constant. The fast encoding is not limited to strong synapses (Galarreta, Hestrin 2001), but already a signal with an amplitude of typical cortical unitary postsynaptic current of 20pA (Hestrin, 1993; Stern et al., 1992) can change population firing rate on a millisecond time scale. Previously, such fast encoding has been considered possible only for the variance-coded signals (Silberberg et al., 2004) defining the prevailing dogma of the field that variance encoding is superior to mean encoding in transmitting fast signals. This dogma was largely based on the observation that the firing rate response to a small mean current change develops slower than the response to a large change of the input variance (Silberberg et al 2004) and partly supported by high cut-off frequency in responses to periodic variance modulation (Boucsein et al., 2009). Despite the fact that the time scale of the initial mean-induced firing rate transient has neither been quantified nor sufficiently resolved experimentally, the ultra-fast transmission of rate encoded signals was deemed impossible. Here we refute this notion, showing that subtle changes of the mean input can be detected by populations of cortical neurons on a millisecond scale. Thus, mean-encoding channel can operate with subtle signals on an ultra-fast time scale. We corroborate this conclusion by demonstrating that the population firing rate of neocortical neurons in vivo and in vitro can reliably encode frequencies up to ~200–300Hz, which is about 50 times higher than the firing rate of individual neurons. These results resolve the contradiction between two recent studies that arrived at several-fold different estimates of cut-off frequency in responses of layer 5 pyramidal neurons to periodic mean modulated signals (Koendgen et al., 2008; Boucsein et al., 2009). Our results further extend these findings showing that (1) weak high frequency modulation in the mean input can be reliably relayed by populations of layer 2/3 pyramids, which mediate communication between cortical regions. (2) This input sensitivity is not restricted to in vitro conditions but rather neocortical neurons in vivo under natural synaptic bombardment can reliably encode high frequency inputs in their population firing rate. (3) The in vivo frequency response is close to that in vitro obtained for noise with correlation time constants of 5ms and 50ms. Since in our experiments in the time domain (latency of responses to steps) and in the frequency domain (frequency response function) were performed under very similar conditions, i.e. on neurons of the same type, using injection of the current stimuli of similar amplitudes, with the same range of membrane potential fluctuations and the firing rates, we can directly compare the response time scale measured in these two paradigms. The response time of a simple low-pass filter is related to the cutoff frequency fc as 1/(2πfc). The cut-off frequency fc ≈ 200–300Hz assessed in our experiments (Figure 4) and in a recent study on layer 5 pyramidal neurons (Koendgen et al., 2008), corresponds to a response time scale below one millisecond. This estimate is in agreement with the response time scale found in current step experiments (Figures 1–3). Thus, coherent evidence from in vitro and in vivo measurements in the time and frequency domains supports the conclusion that cortical neuron populations can indeed communicate on an ultra-fast millisecond time scale using mean-coded signals.
Prior theoretical work showed that a population of the most simple model neurons, leaky integrate and fire (LIF) neurons (Tuckwell, 1988), can faithfully represent input signals of arbitrary frequency in changes of the firing rate (Brunel et al., 2001; Lindner and Schimansky-Geier, 2001; Naundorf et al., 2005a), and alter its firing rate instantaneously in response to a small step-like change of the mean or variance of the input current (Brunel et al., 2001). In contrast to the LIF model neurons which are equipped with an instantaneous spike generation mechanism, the response time scale successively decreases in populations of conductance based models if the time scales involved in spike generation are increased to capture the activation kinetics of sodium channels (Fourcaud-Trocme et al., 2003). In all variations of conductance-based Hodgkin-Huxley type models and their approximations studied so far, the response to fast varying inputs of frequencies f higher than the firing rate of individual neurons is attenuated proportional to 1/f, thus limiting the reliably encoded frequency range (Fourcaud-Trocme et al., 2003; Naundorf et al., 2005a; Fourcaud-Trocme and Brunel, 2005). For an average firing rate of 1–5Hz which is typical for cortical neurons, only input frequencies up to ~10–20Hz could be reliably encoded by conductance based models (Fourcaud-Trocme et al., 2003; Naundorf et al., 2005a). The attenuation of responses to signals beyond fc of ~10–20Hz leads to a slow response time scale (~8–16ms) which is close to the membrane time constant (Fourcaud-Trocme et al., 2003). Results reported here demonstrate that populations of cortical neurons in vitro and in vivo firing at approximately 5Hz can reliably encode low amplitude input signals varying at frequencies up to 200–300Hz, and detect subtle changes of mean current on the corresponding ultra-fast millisecond time scale. We propose to call this phenomenon the “Brunel effect” because such ultra fast responses were first predicted by Nicolas Brunel and co-workers and shown to be specific to integrate and fire type neuron models, or more generally models with rapid spike dynamics (Brunel et al., 2001; Fourcaud-Trocme et al., 2003; Naundorf et al., 2005a). We also confirmed the rapid population dynamics in response to changes of input variance predicted by such models. However, we observe these rapid firing rate changes only for large changes of input variance. We find that a 3-fold increase of the standard deviation evoked a fast population rate transient, while a 50% increase of the standard deviation did not lead to a measurable change of the population firing rate. According to shot noise theory, the input current variance (σ2) in a balanced cortical network is proportional to the average firing rate (van Kampen 2007). This implies that a moderate 50% increase of the standard deviation necessitates a collective firing rate increase of 125%, and a 3-fold increase of standard deviation requires a dramatic 9-fold increase of the average firing rate in a network associated with corresponding increase of the metabolic energy demands.
Changing the mean or the variance: two viable strategies for cortical communication?
Comparison of the population firing rate responses to changes of the input mean or its variance revealed a substantial difference in the response dynamics. Even small changes of the mean input current induced an instantaneous change of population firing rate at the step onset and a robust change of the stationary firing rate. In contrast, only large changes in the input variance could affect the population firing rate, whereby the response was predominantly transient with little stationary component. This difference in response dynamics indicates the intriguing possibility of different computational strategies implemented in the neuronal communication channels that are using mean coded and variance coded signals. Population firing can be rapidly altered either by even a minor change of the input mean, or by an extraordinarily large change of the input variance. Functionally, these two encoding schemes could serve different purposes: the ultrafast detection of small mean current changes could underlie fast cortical processing of rate-coded signals, while a variance encoding scheme could function as a filter which relays quickly only strong network perturbations.
Acknowledgements
We are grateful to M. Chistiakova, J. Chrobak, A. Frolov, I. Fleidervich, M. Gutnick, H. Read and H. Swadlow for fruitful discussions. This work is supported by Bundesministerium fuer Bildung und Forschung grants 01GQ0430, 01GQ07112 (FW, MV), German-Israeli Foundation grant 906-17.1/2006 (FW, MV), University of Connecticut startup funds (MV), Federal Program of Russian Department of Education and Russian Foundation for Basic Research (AM), Goettingen Graduate School for Neurosciences and Molecular Biosciences (TT) and by the Max Planck Society (TT,FW).
Footnotes
Conflict of Interest: None
REFERENCES
- Boucsein C, Tetzlaff T, Meier R, Aertsen A, Naundorf B. Dynamical response properties of neocortical neuron ensembles: Multiplicative versus additive noise. J Neurosci. 2009;29:1006–1010. doi: 10.1523/JNEUROSCI.3424-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N, Chance F, Fourcaud N, Abbott LF. Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys Rev Lett. 2001;86:2186–2189. doi: 10.1103/PhysRevLett.86.2186. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Contreras D. Neuronal Computations with Stochastic Network States. Science. 2006;314:85–90. doi: 10.1126/science.1127241. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Pare D. The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NM, Tolias AS. Decorrelated neuronal firing in cortical micro circuits. Science. 2010;327(584):584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Fourcaud-Trocme N, Brunel N. Dynamics of the instantaneous firing rate in response to changes in input statistics. J Comput Neurosci. 2005;18:311–321. doi: 10.1007/s10827-005-0337-8. [DOI] [PubMed] [Google Scholar]
- Fourcaud-Trocme N, Hansel D, van Vreeswijk CA, Brunel N. How spike generation mechanisms determine the neuronal response to fluctuating inputs. J Neurosci. 2003;23:11628–11640. doi: 10.1523/JNEUROSCI.23-37-11628.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galarreta M, Hestrin S. Spike Transmission and Synchrony Detection in Networks of GA-BAergic Interneurons. Science. 2001;292:2295–2299. doi: 10.1126/science.1061395. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Wiesel TN. Morphology and intracortical projections of functionally characterised neurones in the cat visual cortex. Nature. 1979;280:120–125. doi: 10.1038/280120a0. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;22:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Hestrin S. Different glutamate receptor channels mediate fast excitatory synaptic currents in inhibitory and excitatory cortical neurons. Neuron. 1993;11:1083–1091. doi: 10.1016/0896-6273(93)90221-c. [DOI] [PubMed] [Google Scholar]
- Higgs MH, Spain WJ. Conditional bursting enhances resonant firing in neocortical layer 2–3 pyramidal neurons. J Neurosci. 2009;(29):1285–1299. doi: 10.1523/JNEUROSCI.3728-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson GA, Diba K, Yaron-Jakoubovitch A, Oz Y, Koch C, Segev I, Yarom Y. Subthreshold voltage noise of rat neocortical pyramidal neurons. J Physiol. 2005;564(1):145–160. doi: 10.1113/jphysiol.2004.080903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev. 2010;84:541–577. doi: 10.1152/physrev.00029.2003. [DOI] [PubMed] [Google Scholar]
- Koendgen H, Geisler C, Fusi S, Wang X-J, Luescher HR, Giugliano M. The dynamical response properties of neocortical neurons to temporally modulated noisy inputs in vitro. Cereb Cortex. 2008;18:2086–2097. doi: 10.1093/cercor/bhm235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindner B, Schimansky-Geier L. Transmission of noise coded versus additive signals through a neuronal ensemble. Phys Rev Lett. 2001;86:2934–2937. doi: 10.1103/PhysRevLett.86.2934. [DOI] [PubMed] [Google Scholar]
- London M, Roth A, Beeren L, Haeusser M, Latham PE. Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature. 2010;466:123–7. doi: 10.1038/nature09086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumura M, Chen D, Sawaguchi T, Kubota K, Fetz EE. Synaptic interactions between primate precentral cortex neurons revealed by spike-triggered averaging of intracellular membrane potentials in vivo. J Neurosci. 1996;16(23):7757–67. doi: 10.1523/JNEUROSCI.16-23-07757.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naundorf B, Geisel T, Wolf F. Action potential onset dynamics and the response speed of neuronal populations. J Comput Neurosci. 2005a;18:297–309. doi: 10.1007/s10827-005-0329-8. [DOI] [PubMed] [Google Scholar]
- Naundorf B, Geisel T, Wolf F. Dynamical response properties of a canonical model for type-I membranes. Neurocomputing. 2005b;65:421–428. [Google Scholar]
- Okun M, Lampl I. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nat Neurosci. 2008;11:535–537. doi: 10.1038/nn.2105. [DOI] [PubMed] [Google Scholar]
- Rauch A, La Camera G, Luscher H-R, Senn W, Fusi S. Neocortical pyramidal cells respond as integrate-and-fire neurons to in vivo-like input currents. J Neurophysiol. 2003;90:1598–612. doi: 10.1152/jn.00293.2003. [DOI] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris K. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silberberg G, Bethge M, Markram H, Pawelzik K, Tsodyks M. Dynamics of population rate codes in ensembles of neocortical neurons. J Neurophysiol. 2004;91:704–709. doi: 10.1152/jn.00415.2003. [DOI] [PubMed] [Google Scholar]
- Stanford TR, Shankar S, Massoglia DP, Costello MG, Salinas E. Perceptual decision making in less than 30 milliseconds. Nat Neurosci. 2010;13:379–385. doi: 10.1038/nn.2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz PN, Manwani A, Koch C, London M, Segev I. Subthreshold Voltage Noise Due to Channel Fluctuations in Active Neuronal Membranes. J Comp Neurosci. 2000;(9):133–148. doi: 10.1023/a:1008967807741. [DOI] [PubMed] [Google Scholar]
- Stern P, Edwards FA, Sakmann B. Fast and slow components of unitary EPSCs on stellate cells elicited by focal stimulation in slices of rat visual cortex. Physiology. 1992;449:247–278. doi: 10.1113/jphysiol.1992.sp019085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swadlow H, Hicks P. Somatosensory cortical efferent neurons of the awake rabbit :Latencies to activation via supra- and subthreshold receptive fields. J Neurophysiol. 1996;75:1753–1759. doi: 10.1152/jn.1996.75.4.1753. [DOI] [PubMed] [Google Scholar]
- Thorpe S, Fize D, Marlot C. Speed of processing in the human visual system. Nature. 1996;381:520–522. doi: 10.1038/381520a0. [DOI] [PubMed] [Google Scholar]
- Tuckwell H. Introduction to Theoretical Neurobiology. Cambridge University Press; 1988. [Google Scholar]
- van Kampen NG. Stochastic Processes in Physics and Chemistry. 3rd ed. North Holland: 2007. [Google Scholar]
- Volgushev M, Vidyasagar TR, Chistiakova M, Yousef T, Eysel U. Membrane properties and spike generation in rat visual cortical cells during reversible cooling. J Physiol. 2000;522:5976. doi: 10.1111/j.1469-7793.2000.0059m.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volgushev M, Pernberg J, Eysel U. A novel mechanism of response selectivity of cortical neurons. J Physiol. 2002;540:307–320. doi: 10.1113/jphysiol.2001.012974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Escabi M. Distinct roles for onset and sustained activity in the neuronal code for temporal periodicity and acoustic envelope shape. Neuroscience. 2008;28:14230–14244. doi: 10.1523/JNEUROSCI.2882-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zito K, Scheuss V. NMDA Receptor Function and Physiological Modulation. In: Squire L, editor. The New Encyclopedia of Neuroscience. Academic Press; Oxford, UK: 2007. pp. 276–283. [Google Scholar]