Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field

Abstract

The development and validation of new peptide dihedral parameters are reported for the OPLS-AA force field. High accuracy quantum chemical methods were used to scan φ, ψ, χ₁, and χ₂ potential energy surfaces for blocked dipeptides. New Fourier coefficients for the dihedral angle terms of the OPLS-AA force field were fit to these surfaces, utilizing a Boltzmann-weighted error function and systematically examining the effects of weighting temperature. To prevent overfitting to the available data, a minimal number of new residue-specific and peptide-specific torsion terms were developed. Extensive experimental solution-phase and quantum chemical gas-phase benchmarks were used to assess the quality of the new parameters, named OPLS-AA/M, demonstrating significant improvement over previous OPLS-AA force fields. A Boltzmann weighting temperature of 2000 K was determined to be optimal for fitting the new Fourier coefficients for dihedral angle parameters. Conclusions are drawn from the results for best practices for developing new torsion parameters for protein force fields.

INTRODUCTION

Molecular dynamics and Monte Carlo simulations of proteins have diverse applications in many areas of biophysics, biochemistry, structural biology, and pharmacology. This includes simulated annealing for the refinement of crystallographic and NMR structures,^1,2 free energy perturbation calculations in drug design,^3,4 study of reactions,^5,6 and modeling the folding pathways of fast-folding peptides.^7,8 In these classical molecular mechanics (MM) calculations, it is imperative that high quality force fields are utilized if accurate predictions are to be obtained. Since its introduction over 15 years ago, the OPLS-AA force field for proteins,⁹ and its modification, OPLS-AA/L,¹⁰ have been widely employed in the simulation of biological systems. Studies of the performance of various force fields have generally found that OPLS-AA and OPLS-AA/L perform well,^11,12 particularly for quantities that are dependent upon nonbonded parameters. However, some studies have noted weaknesses in the ability of the force fields to reproduce properties that are heavily dependent upon torsional energetics.^13,14

The OPLS-AA force field has followed a consistent philosophy throughout the course of its development. Non-bonded parameters are optimized to reproduce experimental liquid phase properties, and torsional parameters are fit to available experimental or quantum chemical data. Due to limitations in the available computational power at the time, many of the original peptide dihedral torsion parameters were fit to ab initio quantum mechanics (QM) scans performed at the Hartree–Fock level of theory with small basis sets. This was improved upon in the OPLS-AA/L force field, where local MP2 with a larger basis set was used to evaluate single-point energies at optimized HF geometries. The resultant changes enhanced the performance of the force field for reproducing QM conformer energies for blocked alanine dipeptides and tetrapeptides. While at the time these computations were advanced, current resources permit higher level investigations and possible further improvements.

In recent years, there have been significant advances in quantum chemical methods and computational power. Several recent studies have systematically evaluated the performance of various QM methods and basis sets for the conformational energies of short peptides.^15,16 Of particular note was the recent study by Kang and Park,¹⁶ which demonstrated that numerous affordable levels of theory are capable of producing relative conformer energies for the blocked alanine and proline dipeptides with excellent agreement to the “gold standard” CCSD(T) extrapolated to the complete basis set limit. It is from this study that the quantum methods employed in the present parametrization were selected.

There has been some debate as to the best methods for fitting protein force field torsion parameters. It has been argued that as the intention is to use protein force fields in condensed phase simulations, the effects of solvent need to be incorporated, either implicitly in ab initio data used for parametrization¹⁷ or by directly fitting to reproduce experimental properties in solution.^18,19 It remains to be demonstrated whether the dihedral parameters obtained in this fashion are different from and superior to those obtained by fitting to gas phase ab initio scans. When fitting to ab initio scans, various weighting schemes have been suggested^20,21 in an attempt to prioritize reproduction of the most important parts of the energy surface. The most common method is the inclusion of a Boltzmann factor in the weighting, which improves the accuracy for the low energy minima regions at the cost of the high energy barriers. The caveat to this approach is that minima for short peptides do not reflect completely minima in full proteins, and thus too low of a weighting temperature may be inappropriate.

In this work, φ–ψ energy surfaces for blocked glycine and alanine dipeptides were evaluated along with χ₁ and χ₂ scans for the remaining amino acids with modern high-level quantum chemical methods. New dihedral parameters for use with the OPLS-AA force field were determined to improve the agreement with these surfaces. These parameters were used to evaluate blocked alanine dipeptide and tetrapeptide relative conformational energies, and comparisons were made to both data in the literature and our own calculations. Molecular dynamics simulations were run for several test systems with the new force field parameters, and the results were compared with available experimental data.

METHODS

Ab Initio Scans

Amino acids (X) blocked with acetyl and N-methyl groups (Ace-X-NMe) were prepared in Gaussview.²² All gas-phase relaxed scans of the blocked dipeptides were performed with the ωB97X-D²³ functional using the 6-311+ +G(d,p) basis set in Gaussian 09.²² Scans were performed in 15° increments from −180° to 180° in forward and reverse directions with the lowest energy path taken to remove any hysteresis due to frustration (trapped methyl rotations, etc.). Single-point energy evaluations with the double hybrid functional B2PLYP-D3BJ^24,25 and the Dunning basis set aug-cc-pVTZ²⁶ were made at each of the minimized geometries. In the case of the alanine and glycine dipeptides, full two-dimensional scans of φ and ψ were performed. As fully scanning φ is not possible with proline, two scans of ψ were executed with the proline ring held fixed in the optimized “down” conformation of Kang and Park.¹⁶ with the peptide bond either cis or trans.

For χ₁ and χ₂, 6–12 scans were performed for each amino acid with different backbone and side chain conformations. Scans were made with φ and ψ fixed at values corresponding to both alpha helical (−60°,−45°) and β sheet (−135°,135°) conformations. All heavy atom χ angles not being scanned were fixed to values from a survey of protein crystal structures,²⁷ with enough scans being run to capture a majority of the well populated conformations. Due to the good agreement between the ωB97X-D and B2PLYP-D3BJ scans for χ₁, all scans for χ₂ were performed at the ωB97X-D level, with B2PLYP-D3BJ single-point calculations only being performed if it was determined that peptide-specific χ₂ parameters were necessary for that χ₂ angle. Complete energies and optimized geometries from the scans can be found in the Supporting Information.

OPLS-AA Dihedral Parameter Fitting

The torsional potential energy in the OPLS-AA force field takes the form in eq 1 where ϕ is the dihedral angle and V₁, V₂, V₃, and V₄ are the

$$\begin{array}{l}{E}_{\text{torsion}}={\displaystyle \sum _i\frac{V_1^i}{2}\lceil 1+\cos ({\phi }_i)\rceil }+\frac{V_2^i}{2}\lceil 1-\cos (2{\phi }_i)\rceil \\ +\frac{V_3^i}{2}\lceil 1+\cos (3{\phi }_i)\rceil +\frac{V_4^i}{2}\lceil 1-\cos (4{\phi }_i)\rceil \end{array}$$ (1)

Fourier coefficients to be optimized. The total energy also includes the bond-stretching, angle-bending, and nonbonded (Coulomb plus Lennard-Jones) terms.⁹ There are six dihedral angles for the peptide backbone that are given parameters in the OPLS-AA force field: φ (C–N–Cα–C), ψ (N–Cα–C–N), φ′ (C–N–Cα–Cβ), ψ′ (Cβ–Cα–C–N), φ″ (C–N–Cα–Hα), and ψ″ (Hα–Cα–C–N). The values of the parameters for these angles in the OPLS-AA and OPLS-AA/L force fields are found in Table S1. Starting from the original OPLS-AA parameters, the values of V₁, V₂, and V₃ for φ, φ′, ψ, and ψ′ were optimized using the alanine and glycine QM data weighted by 0.928 and 0.072 respectively, corresponding to the relative abundance of glycine to all other amino acids in the human proteome. V₄, having minima/maxima every 90°, is reserved for dihedrals expected to have matching behavior, like biaryl torsions.²⁸ Accordingly, V₄ was set here to zero throughout to avoid overfitting. In the case of proline, the φ and φ′ optimized for glycine and alanine were adopted and unique proline ψ and ψ′ were fit to the proline QM scans.

The parameter optimization was performed with a steepest decent algorithm to minimize a Boltzmann-weighted error function evaluated between relative energies based on the lowest-energy structure from the B2PLYP-D3BJ/aug-cc-pVTZ//ωB97X-D/6-311++G(d,p) scans and analogous molecular mechanics scans. The MM scans were carried out with BOSS²⁹ using the program’s dihedral driver function in the gas phase to scan the dihedral angle in 15° increments, while allowing all other degrees of freedom to optimize, as in the QM scans. The Boltzmann-weighted error function in eq 2 was used

$$\text{Error}=\sqrt{\frac{{\displaystyle {\sum }_n{(E_{\mathrm{MM}}-E_{\mathrm{QM}})}^2{\mathbf{e}}^{-E_{\mathrm{QM}}/k_{\mathrm{B}}T}}}{n}}$$ (2)

where k_B is the Boltzmann constant and T is atemperature for preferentially weighting the low-energy regions of the potential energy surface. Backbone parameters were optimized for T values of 500, 1000, 2000 K, and without the Boltzmann weighting, corresponding to T = ∞. The error for each set of parameters was evaluated as both an unweighted root-mean-square deviation (RMSD) and employing each of the weighting temperatures, as provided in Table S1. Error values using the OPLS-AA and OPLS-AA/L parameters were also evaluated in this fashion (Table S1).

The torsional parametrization for peptide side chains in OPLS-AA focuses on two χ₁ terms, χ₁ (N–Cα–Cβ–Xγ) and χ₁′ (C–Cα–Cβ–Xγ) for each Xγ, and, in most cases, one χ₂ term, χ₂ (Cα–Cβ–Xγ–Yδ). The remaining contributors such as for H–Cα–Cβ–Xγ use standard parameters taken from small molecules such as ethane or propane. The fitting procedure for the χ dihedrals was mostly identical to that used for φ and ψ, but minimizing the average per scan Boltzmann weighted error for multiple one-dimensional scans rather than a full surface. χ₁ parameters were optimized for all individual residues at 2000 K, and then parameters were optimized simultaneously for groups of residues to determine the smallest number of unique χ₁ and χ₁′ values necessary to provide a good reproduction of the QM surfaces. An improvement of 20% in the error weighted at 2000 K over a clustered parameter was used as an initial cutoff for a unique parameter to be tested in aqueous phase simulations. In cases where rotamer distributions in dipeptide simulations did not match experiment, despite where the parameter fell given the initial cutoff, parameters were split or combined as necessary to produce good agreement with experiment. For the few residues where this approach was still unsuccessful, the population differences in experiment and simulation were converted into energies using a Boltzmann factor and the χ₁ parameters were adjusted to correct the relative energies of the minima in the MM scans.

For χ₂, most residues were again optimized individually at 2000 K and comparisons were made to MM scans performed with the parameter for the appropriate side chain analogue, e.g., alkane parameters were used for the χ₂ of leucine. Peptide-specific χ₂ parameters were added in those cases where the improvement over the nonpeptide parameter was significant (>20% improvement for the error evaluated at 2000 K). For glutamine and glutamate, the χ₂ parameters were empirically adjusted with the same procedure used for the χ₁ parameters.

Alanine and Proline Dipeptide and Alanine Tetrapeptide Gas-Phase Conformer Energies

As previous studies have examined the lowest energy conformers of the alanine and proline dipeptides at the CCSD level,^15,16 the data available in the literature is sufficient for comparison to the molecular mechanics results. Twenty-seven conformers of the blocked alanine tetrapeptide (Ace-Ala-Ala-Ala-NMe) have been previously identified by DiStasio et al.³⁰ and relative energies were calculated at the RI-MP2(CBS)//HF/6-31G** level of theory. While RI-MP2(CBS) should perform well for the energies, the geometry optimization at the Hartree–Fock level is not ideal. Without the inclusion of the electron correlation energy, the geometry may be misrepresented. Accordingly, we optimized the 27 conformers of the blocked tetrapeptide at the ωB97X-D/6-311++G(d,p) and M06-2X³¹/6-31+G(d) levels of theory with the Gaussian09 program.²² Single-point calculations were performed on the respective optimized geometries with aug-cc-pVTZ and jun-cc-pVQZ³² basis sets to explore the effect of increasing basis set size on the calculated relative energies. Conformers 21, 23, 24, and 27 were found to have poor agreement in geometry between the two density functionals, with RMSD values for the φ and ψ values greater than 15° and were thus omitted from the comparisons with the force field results.

The C7eq, C5, C7ax, and α′ conformers of the blocked alanine dipeptide, the tCd, tCu, cAd, cAu, tAu, cFd, and cFu conformers of the blocked proline dipeptide,¹⁶ and the 23 tetrapeptide conformers with concurrent geometry were minimized with the BOSS program using a Broyden– Fletcher–Goldfarb–Shanno (BFGS)^33–36 method with an energy tolerance of 0.0001 kcal/mol for the OPLS-AA, OPLS-AA/L, and the newly derived parameters. None of the force fields found the β₂ and α_L alanine dipeptide conformers to be true minima, so their energies were evaluated by fixing φ and ψ at the optimized values from the ωB97X-D/6-311++G(d,p) calculation of Kang and Park¹⁶ and allowing the rest of the molecule to optimize. Two of the tetrapeptide conformers were not found to be minima for the newly optimized force fields and were omitted from further comparisons. The remaining 21 conformers were prepared in AmberTools14³⁷ with the ff99,³⁸ ff99SB,³⁹ and ff99SB-NMR¹⁹ force fields and were minimized with the NAMD software package.⁴⁰

Molecular Dynamics Simulations

All MD simulations were performed with NAMD⁴⁰ employing CHARMM-formatted parameter files⁴¹ for all force fields tested, which are provided in the Supporting Information. For all simulations, a temperature of 300 K and pressure of 1 atm were maintained with a Nose–Hoover Langevin piston barostat with a piston period of 100 fs and a piston dampening time scale of 50 fs and a Langevin thermostat with a damping coefficient of 1 ps⁻¹. Nonbonded cutoffs were employed at 11 Å with a smoothing function starting at 9 Å, with particle mesh Ewald used to treat long-range electrostatics. The systems were solvated in cubic water boxes with edge lengths ranging from 25 to 58 Å. Sodium and chloride ions were added to neutralize the charges in the system and provide approximately a 150 mM concentration of salt. A 2 fs time step was employed with the use of SHAKE and SETTLE.

Triplicate 205 ns simulations were run for an unblocked alanine pentapeptide (Ala₅) with and glycine tripeptide (Gly₃) with protonated C-termini with the first 5 ns discarded as equilibration. The remaining amino acids, with the exception of proline, were simulated for 205 ns as blocked dipeptides, again in triplicate with the first 5 ns discarded as equilibration. Values and error bars throughout the paper represent the mean and standard deviation of the calculated quantities from the triplicate runs. Ala₅ and Gly₃ simulations were run with each of the four weighting temperatures examined in this work, as well as the previous OPLS-AA and OPLS-AA/L force field. Dipeptide simulations were performed with OPLS-AA, OPLS-AA/L, and the new parameters optimized at 2000 K. As each system was studied for 600 ns with at least three different force fields, over 50 μs of validating simulations have been executed. In analyzing the molecular dynamics simulations for the short alanine and glycine peptides, the definitions of secondary structure, the three sets of Karplus parameters for calculating J couplings, and the experimental error values used to calculate χ² from Best et al.⁴² were employed. For the dipeptide simulations, only the first set of Karplus parameters, that of Hu and Bax,⁴³ was employed. χ₁ rotamer populations were determined by dividing the range of χ₁ values into three equal sized bins, corresponding to the p (+60°), t (180°) and m (−60°) conformers. Definitions of p, t, and m for valine, isoleucine, and threonine were adopted from the work of Dunbrak and co-workers²⁷ and are depicted in Figure 1.

Figure 1.

Diagram of the definition of rotamers m/t/p employed in this work.

The proteins ubiquitin and GB3 were started from the PDB structures 1UBQ⁴⁴ and 1P7E⁴⁵ and gradually heated to 300 K over 400 ps before 205 ns simulations were run. Both the heating period and the first 5 ns were discarded as equilibration, and simulations were performed in triplicate for each protein. All other simulation parameters were identical to those used for the dipeptides. For calculation of backbone J couplings of the full protein, both the 1997 empirical Karplus parameters⁴³ used for the dipeptides and another empirical model developed from work with GB3⁴⁶ are employed. Side chain J couplings were calculated for couplings to methyl side chains with the set of Karplus parameters developed by Vögeli et al.,⁴⁶ while all other couplings employed Karplus parameters from Perez et al.⁴⁸

RESULTS

Fitting Backbone Parameters to the QM Potential Energy Surfaces

After new parameters were determined for alanine and glycine, two-dimensional contour plots were produced for the φ–ψ potential energy surface for the QM, OPLS-AA, OPLS-AA/L, and the new 2000 K parameters (Figure S1). The new optimized backbone parameters (Table S1) display a significant improvement for glycine compared to the OPLS-AA and OPLS-AA/L force fields. For the glycine surface, OPLS-AA has an unweighted RMSD of 1.603 kcal/mol, compared to an unweighted RMSD of 0.956 kcal/mol for the parameters optimized at 2000 K and 1.091 kcal/mol for the parameters optimized at 500 K. Each new parameter set performs better compared to OPLS-AA for errors evaluated at every weighting temperature. This suggests general improvement of the fit to the QM surface, rather than improvement of regions of the potential energy surface at higher or lower relative energies at the expense of the other. The fits with the new parameters to the alanine surface also show significant improvement compared to OPLS-AA and OPLS-AA/L. For the 2000 K optimized alanine parameters, the unweighted RMSD is 0.927 kcal/mol, compared to 1.261 kcal/mol for OPLS-AA and 1.381 kcal/mol for OPLS-AA/L. The gains are again general across most weighting temperatures. Attempts to optimize new parameters for glycine or alanine separately yield minimal improvement (10% or lower), and so sharing parameters is appropriate.

The OPLS-AA/L force field performs poorly for glycine, with an unweighted RMSD compared to the QM scan of 3.005 kcal/mol. Comparison of the two-dimensional φ–ψ surfaces for OPLS-AA/L and B2PLYP-D3BJ/aug-cc-pVTZ (Figure S1) reveals qualitative differences. As OPLS-AA/L was originally derived solely for alanine and the other amino acids containing a β carbon, use of the same backbone parameters for glycine when it was ignored in the fitting was a poor choice.

Evaluating Alanine and Proline Dipeptide and Alanine Tetrapeptide Conformer Energies

Provided in Table S5 are the relative energies for the C7eq, C5, C7ax, and α′ conformers with OPLS-AA, OPLS-AA/L, and the new parameters. For comparison, values from the literature calculated at the CCSD/CBS//ωB97X-D/6-311++G(d,p)¹⁷ and DF-LCCSD(T0)/DF-MP2/aug-cc-pVTZ¹⁶ levels of theory are included. OPLS-AA, OPLS-AA/L and the new parameters optimized at 500, 1000 and 2000 K perform quite well for the true minimum energy conformations, each having an RMSD of 0.30 kcal/mol or lower. This is comparable to the error between the two high-level ab initio methods of 0.18 kcal/mol. If the two conformations that are not true minima are included in the calculation of the RMSD, the errors for the 500, 1000, and 2000 K optimized parameters increase modestly to 0.61, 0.49, and 0.45 kcal/mol, respectively. In contrast, the corresponding RMSDs for OPLS-AA and OPLS-AA/L increase significantly, to 1.60 and 0.97 kcal/mol, suggesting that these force fields are less successful in reproducing the relative energies of all areas of the potential surface.

These same parameters, as well as AMBER ff99, ff99sb, and ff99sb-NMR were used to evaluate the conformers of the alanine tetrapeptide, with the results in Table 1. The RIMP2(CBS)//HF/6-31G** energies, results with the AMOEBA force field²⁰ from the literature, and the results from our ωB97X-D/jun-cc-pVQZ//ωB97X-D/6-311++G(d,p) and M06-2X/jun-cc-pVQZ//M06-2X/6-31+G(d) calculations can also be found in Table 1. The performance for these density functionals with smaller basis sets and a comparison of the φ and ψ values for the optimized geometries for the three levels of theory can be found in Tables S6, S7, and S8. The RMSD between the calculated energies for the three different quantum methods (Table 1) range from 0.60 to 0.93 kcal/mol, which serves as a useful measure for a limit of potential accuracy of the force fields. Several of the optimized geometries are depicted in Figure 2.

Table 1.

Relative Conformer Energies (kcal/mol) for the Blocked Alanine Tetrapeptide Calculated with Various ab Initio and DFT Methods and Molecular Mechanics Force Fields

conformer number	RI-MP2a	ωB97X-Db	M06-2Xc	OPLS-AA	OPLS-AA/L	500 K	1000 K	2000 K	unweighted	ff99d	ff99sbe	ff99sb-NMRf	Amoebag
1	4.13	4.72	4.95	4.21	3.63	5.51	5.14	4.50	3.61	4.85	4.42	6.77	3.07
2	4.19	4.71	4.96	3.77	3.60	4.88	4.64	4.22	3.68	5.09	4.79	6.81	3.62
3	0.57	0.57	1.96	0.00	0.04	0.00	0.09	0.13	0.32	2.86	1.60	2.50	0.00
4	5.73	6.14	6.62	4.86	4.30	6.01	5.69	5.09	4.25	7.25	5.39	7.32	4.07
5	5.26	5.79	6.26	5.93	3.56	6.05	5.49	4.96	4.24	4.35	5.03	7.23	3.96
7	6.67	6.95	7.25	5.39	6.12	5.42	5.47	5.45	5.48			4.67	7.64
8	4.64	5.62	5.31	7.97	5.20	5.94	5.62	5.37	5.39	7.46	5.36	6.90	5.45
9	7.92	7.79	9.22	7.21	7.45	6.45	6.60	6.58	6.67	7.64	5.89	7.12	10.01
10	7.79	8.80	8.54	10.88	7.67	8.11	7.23	6.86	5.69	5.44	4.14	8.50	6.34
11	0.00	0.46	0.56	0.36	0.32	0.10	0.17	0.31	0.48	0.03	0.40	0.30	0.75
12	0.29	0.00	0.00		0.00	0.19	0.00	0.00	0.00	0.00	0.00	0.00	0.75
13	3.66	4.02	4.34	2.67	2.69	3.51	3.34	3.15	3.02	3.87	4.07	5.80	3.56
14	4.68	4.78	5.36		3.26	6.38	5.68	5.30	4.84	3.02	4.92	6.52	4.66
15	2.19	2.84	2.33	4.01	1.80	3.00	2.47	2.09	2.11	4.49	2.57	4.63	2.28
17	3.42	3.15	3.98		0.15	4.41	4.43	4.35	4.28	6.32	3.92	5.10	2.32
18	1.91	2.42	2.70	0.72	0.87	1.30	1.18	1.22	1.52	1.57	2.49	3.95	2.19
19	3.82	3.97	4.73	2.34	2.55	2.47	2.48	2.52	2.76	3.59	3.41	4.79	4.25
20	1.76	2.46	3.06		0.40	3.10	2.47	2.33	2.31	−0.40	2.31	3.55	3.18
22	5.82	6.84	7.31			5.72	5.76	5.80	5.82	5.04	5.25	5.77	6.87
25	2.50	3.43	3.76	4.26	0.41	3.21	2.54	2.41	2.44		2.01	1.60	2.87
26	0.67	1.89	2.10		−1.00	2.77	1.87	1.67	1.59	−2.87	0.65	1.48	1.6
RMS RI-MP2		0.60	0.93	1.54	1.42	1.03	0.77	0.71	0.97	1.74	1.05	1.70	0.99
RMS ωB97X-D	0.60		0.60	1.30	1.78	0.88	0.86	0.94	1.38	1.98	1.32	1.47	1.12
RMS M06-2X	0.93	0.60		1.72	2.04	1.18	1.20	1.29	1.75	2.08	1.52	1.40	1.25

^aReference ³⁰.

^bωB97X-D/jun-cc-pVQZ//ωB97X-D/6-311++G(d,p).

^cM06-2X/jun-cc-pVQZ//M06-2X/6-31+G(d).

^dReference ³⁸.

^eReference ³⁹.

^fReference ¹⁹.

^gReference ²⁰.

Figure 2.

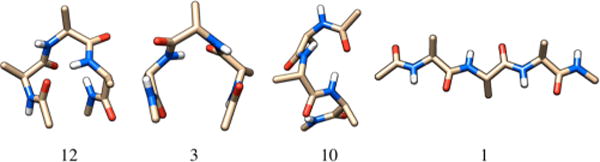
Four of the conformers of the blocked alanine tetrapeptide optimized at the ωB97X-D/6-311++G(d,p) level of theory. Here, 12 and 3 are global minima depending upon the level of theory, 10 is the highest energy conformer with the ωB97X-D functional, and 1 is the extended conformation.

The OPLS-AA and OPLS-AA/L force fields have been compared previously for their performances for the first 10 conformations in this set to results from LMP2/cc-pVTZ(-f)//HF/6-31G*calculations.¹⁰ For this limited subset and level of theory, the reported the RMSD values in the energies from OPLS-AA and OPLS-AA/L were 1.47 and 0.56 kcal/mol, respectively, suggesting superior performance of the OPLS-AA/L force field. However, by extending the analysis to all 27 conformations and using the RIMP2(CBS) results, the RMSD for OPLS-AA/L increases to 1.42 kcal/mol, while the OPLS-AA RMSD rises to 1.54 kcal/mol. OPLS-AA does fail to locate a larger number of minimum conformations than the OPLS-AA/L calculations, which should also be taken into account.

The new parameter sets that used a Boltzmann weighting factor all outperform the previous two iterations of OPLS-AA, regardless of which quantum method is used for comparison, with the parameters optimized at 1000 K performing the best on average. For the parameters derived by fitting directly to the potential energy surface without using a Boltzmann weighting factor, the performance was decidedly poorer, roughly comparable to that of OPLS-AA. Compared to the RIMP2-(CBS) data, the RMSD for the 1000 K parameters was 0.77 kcal/mol, roughly half that of the OPLS-AA and OPLS-AA/L results. This is also comparable to the RMS error between RIMP2(CBS) and the other two quantum methods, which suggests the accuracy of the parameters may be at the limit of the quality of the quantum data available for fitting.

Comparisons were also drawn with the AMBER 99 family of force fields, which represent a direct lineage of torsion parameters, with AMBER ff99sb improving over AMBER ff99 by fitting to better quantum chemical data, and AMBER ff99sb-nmr improving over AMBER ff99sb by including an empirical correction to improve agreement between simulated and experimental NMR measurements. Notably, there is consistent improvement in the number of conformers correctly reproduced and generally for their energies, even for the experimentally derived parameters. Much of the error in the early AMBER force fields can be attributed to conformers 7 and 10, which have poorly reproduced geometries with ff99 and ff99SB, particularly conformer 7, which optimizes to be almost redundant to conformer 12. Both of these conformers are better represented with ff99sb-NMR, with conformer 7 now a unique minimum. While the RMSD in energies increases from ff99sb to ff99sb-nmr for two of the three quantum data sets, no attempt was made to penalize ff99sb or ff99 for failing to reproduce conformers. If one includes the calculated energy for the (incorrect) conformer 7 to the RMSD for ff99sb, ff99sb-nmr then out performs ff99sb for all three quantum methods. Given the improved performance of ff99sb-nmr in molecular dynamics simulations, this suggests it is more important to accurately capture a larger range of the alanine φ–ψ potential energy surface rather than more accurately reproducing the relative energies of a small subset of regions. The new OPLS-AA parameters that used a Boltzmann weighting factor outperformed all AMBER versions in terms of relative energies and geometries. It is possible, however, that the two minima that were missed by the OPLS-AA force field may be reproduced by the AMBER parameters. The RMSD for the conformer energies with the new OPLS-AA parameters were quite similar to the latest parametrization of Amoeba, a next-generation force field including higher multipole moments and polarizability. However, Amoeba was reported to reproduce all of the tetrapeptide minimum energy conformations, which, as previously noted, may be an important feature.

The force field results for the conformers of the blocked proline dipeptide compared to the high level ab initio results from the literature are provided in Table S9, and the values of the parameters are in Table S10. Included are the new proline-specific ψ and ψ′ fit against the QM scans and the new optimized leucine parameters for χ₁ and χ₁′. Both OPLS-AA and OPLS-AA/L perform rather poorly for the proline conformer energies compared to the CCSD(T) results, with RMSD values for the relative energies exceeding 1.5 kcal/mol. The new parameters perform significantly better, with an RMSD compared to the QM results of only 0.26 kcal/mol.

Molecular Dynamics Simulations of Ala₅ and Gly₃

The χ² for the simulated J couplings compared to NMR experiments⁴⁹ and secondary structure percentages for the alanine pentapeptide and the glycine tripeptide from simulations run with OPLS-AA, OPLS-AA/L, and the parameters developed here are found in Table 2. For the alanine pentapeptide, two values are provided for the second Karplus parameter model, the first includes all 27 measurements, and the second value in parentheses omits the ³J(H_N,Cβ) couplings, which have been noted to be difficult to accurately reproduce with the Karplus relation.⁵⁰ Similarly, for the glycine tripeptide two values are provided, with the second value omitting 3J(C′,C′) and ²J(N,C_α) couplings. With the Karplus parameters used difficulties in producing the experimental value for the first ²J(N,C_α) coupling for the glycine tripeptide have been noted by others.¹⁸ This demonstrates a need for a full set of glycine-specific Karplus parameters. The improvement for both alanine and glycine with the new force field parameters that employed a Boltzmann weighting factor compared to both previous OPLS-AA versions is significant, with some χ² being reduced by over a factor of 2. For the alanine pentapeptide, the higher percentage of the polyproline II conformation and the lower percentage of “alpha” conformations with our new parameters is more in line with experimental results for short alanine peptides from spectroscopic sources.⁵¹ For the alanine pentapeptide, the χ² is approaching that of the more computationally demanding AMOEBA at 0.99,²⁰ although in this solution-phase test AMOEBA outperforms our simpler model. While the parameters optimized at 1000 K performed the best (by a very small margin) for the gas phase quantum chemical tetrapeptide energies, the 2000 K parameters performed better in the solution-phase tests (although again by a slim margin). The new parameters that did not utilize a Boltzmann weighting factor performed the worst of all, demonstrating that some method of preferentially weighting the minimum energy data is needed for optimal generation of force field parameters. On the basis of these results, the backbone parameters developed with a weighting temperature of 2000 K were employed for our new force field, named OPLS-AA/M. The decision was also made to employ the same weighting temperature in developing parameters for the side chain dihedrals.

Table 2.

Results of Aqueous Phase Simulations for the Alanine Pentapeptide and Glycine Tripeptide with OPLS-AA, OPLS-AA/L, and New Parameters Employing Different Boltzmann Weighting Temperatures

	χ2 model 1	χ2 model 2	χ2 model 3	% alpha	% beta	% PPII
Ala5
OPLS-AA	2.31 ± 0.03	2.60 ± 0.05 (1.87 ± 0.01)	2.73 ± 0.03	14.3 ± 1.0	48.0 ± 0.3	36.9 ± 0.6
OPLS-AA/L	2.35 ± 0.04	4.96 ± 0.19 (2.51 ± 0.05)	3.36 ± 0.09	29.6 ± 1.3	31.5 ± 0.6	38.0 ± 0.8
500 K	1.51 ± 0.01	2.49 ± 0.02 (1.12 ± 0.01)	1.88 ± 0.01	15.0 ± 0.8	35.5 ± 0.3	46.0 ± 0.4
1000 K	1.22 ± 0.03	2.67 ± 0.02 (0.86 ± 0.02)	1.66 ± 0.02	14.6 ± 0.5	32.1 ± 0.3	50.4 ± 0.7
2000 K (OPLS-AA/M)	1.16 ± 0.02	2.61 ± 0.02 (0.80 ± 0.02)	1.61 ± 0.01	11.7 ± 0.8	33.1 ± 0.5	53.5 ± 0.2
unweighted	3.56 ± 0.16	3.83 ± 0.07 (3.52 ± 0.20)	3.99 ± 0.18
Gly3
OPLS-AA	6.29 ± 0.04 (4.31 ± 0.03)	8.97 ± 0.02 (6.81 ± 0.02)	7.71 ± 0.03 (5.44 ± 0.03)
OPLS-AA/L	6.40 ± 0.05 (4.79 ± 0.07)	8.45 ± 0.07 (7.21 ± 0.10)	7.11 ± 0.06 (5.84 ± 0.09)
500 K	3.87 ± 0.07 (2.01 ± 0.06)	5.11 ± 0.09 (3.38 ± 0.09)	4.20 ± 0.08 (2.33 ± 0.07)
1000 K	3.31 ± 0.04 (1.50 ± 0.03)	4.32 ± 0.06 (2.69 ± 0.05)	3.52 ± 0.05 (1.75 ± 0.04)
2000 K (OPLS-AA/M)	3.11 ± 0.07 (1.37 ± 0.08)	4.02 ± 0.08 (2.48 ± 0.08)	3.28 ± 0.08 (1.58 ± 0.07)
unweighted	3.71 ± 0.03 (1.41 ± 0.01)	4.40 ± 0.02 (2.36 ± 0.01)	3.77 ± 0.02 (1.56 ± 0.01)

Fitting Side-Chain Parameters

In many molecular mechanics programs, dihedral parameters are designated by a sequence of atom type numbers, which specify unique Coulomb and van der Waals parameters for the four atoms in the angle. This constrains two pairs of amino acids to share χ₁ parameters: valine and isoleucine, and glutamine and lysine. While in principle an additional atom type could be added with the same Coulomb and van der Waals parameters, the need to do so would suggest the torsion parameter is compensating for other effects. To avoid this problem, the original OPLS-AA force field for proteins took a sparse approach to χ₁ parameters, assigning unique parameters only to χ₁ angles incorporating different elements (serine and cysteine), with all amino acids having a γ-carbon sharing the same χ₁ parameters. As shown below, this approach is perhaps too sparse, as it breaks down in certain cases, most notably for asparagine and aspartate, where the γ-carbon is very polar. The OPLS-AA/L force field, on the other hand, included new χ₁ parameters for most amino acids, even the pairs with overlapping types, requiring extra effort in implementation. The present work strikes a balance, systematically determining the fewest number of separate χ₁ parameters that would provide significant improvement over the OPLS-AA force field, without requiring new atom types or other practices that can promote overfitting. In cases where the distribution of rotamers still disagrees significantly with experiment even after improving the fit to the QM scans, alterations were made to the parameters as necessary to improve agreement with NMR and crystallographic data.

Cysteine and serine, having a γ sulfur and oxygen atom, were given unique χ₁ parameters, which can be found in Table S2. The results of MD simulations with the new cysteine and serine parameter were compared to rotamer distributions from NMR studies of denatured proteins⁵² and “coil libraries” drawn from regions of crystal structures that lack well-defined secondary structure motifs.⁵³ These two measures are thought to probe the intrinsic conformational properties of disordered proteins and, thus, provide useful benchmarks for our dipeptide simulations. However, neither measure directly probes the χ₁ conformational preferences of dipeptides, and so parameters were only adjusted when rotamer distributions in solution differed significantly from experiment in the MD simulations (generally >20% mean unsigned error (MUE) for the three conformers, p, m, and t). Both serine and cysteine displayed enough deviance from the experimental data to merit adjustment of the parameters (Table S4). The modifications needed were small, reflecting changes in relative conformer energies on the order of 0.10–1.00 kcal/mol. These empirically adjusted parameters only produced small increases in the error of the MM scans (Table S2), still performing better than OPLS-AA and OPLS-AA/L.

To test the short hydrocarbons side chains, a single set of χ₁ parameters for valine and isoleucine were optimized, followed by a set of parameters for leucine alone, and a final set for valine, isoleucine, and leucine all together. The improvement in fit compared to the QM scans gained by separating leucine into its own parameter was less than 20% for the Boltzmann-weighted error at 2000 K. The small magnitude of the improvement suggests leucine, isoleucine, and valine, each possessing hydrocarbon side chains, may be able to share the same set of χ₁ parameters. In the experimental works, the χ₁ angle of leucine predominately (~70%) occupies the m conformation, followed by roughly 28% t and a negligible population of p. The joint valine/isoleucine/leucine parameter produced the opposite populations for m and t (Table S4) in the leucine simulations, while the parameter optimized for leucine alone produced excellent agreement with experiment. The rotamer populations for valine and isoleucine displayed only small variations between the valine/isoleucine/leucine and valine/isoleucine parameters. Thus, separate parameters were implemented in the new OPLS-AA force field for the β-branched residues and leucine.

Molecular mechanics scans for threonine, bearing both a γ oxygen and carbon, were performed with the new serine and valine/isoleucine/leucine χ₁ parameters (Table S2). Compared to OPLS-AA (Table S2), the improvement in the error between the QM and MM scans is significant, demonstrating the transferability of the parameters. Simulations of the threonine dipeptide displayed similar biases in χ₁ populations as serine, tending to favor the rotamer with oxygen in the m conformation over the p conformation. This was improved by use of the same empirically adjusted oxygen χ₁ parameter as was developed for serine and the β-branched hydrocarbon parameter (Table S4).

Asparagine and aspartate were found to require significantly different χ₁ parameters from all other amino acids (Table S2), with a large negative V₁ for χ₁. This is unsurprising, given that the γ-carbon is part of a highly polar moiety. Sufficient further improvement resulted when asparagine and aspartate were fit separately, meriting the testing of individual parameters. In this case, χ₁ distributions were improved significantly for asparagine with its individual parameters; however, for aspartate the percentage of m was too large. This could be a reflection of overfitting to errors in the electrostatic model for the charged side chain when asparate is allowed its own parameters. Utilizing the joint asparagine/aspartate parameter for asparate succeeds in reducing the population of conformer m but overcompensates, causing t to become the predominate conformation. Thus, the final parameters asparate were chosen to split the difference of populations between the joint and separate parameters (Table S4).

Methionine benefits greatly when given a unique χ₁ parameter from leucine, receiving an approximately 2-fold reduction in error, perhaps due to the more polarizable nature of sulfur. Glutamate and arginine also displayed significant reduction in error with unique parameters over adoption of the leucine parameters. Agreement between simulation and experiment for methionine and arginine was then found to be good, requiring no further adjustment of their parameters. The glutamate parameters, however, overestimated the population of t compared to m and perhaps most alarmingly produced almost no population of p. Reducing the magnitude of V₁ for glutamate produced rotamer populations in good agreement with experiment (Table S4).

Glutamine and lysine, which are obliged to share a parameter, present an interesting philosophical challenge. Although the combination of atom types in their χ₁ is unique, all of the side chain carbons have nonpolar hydrocarbon atom types. The improvement by providing a unique parameter was greater than 20%, and thus, a new parameter was implemented for testing. While the population of t was slightly overestimated with these parameters compared to the available experimental data, the overall agreement was still very good (Table S4).

For the aromatic residues, phenylalanine and tyrosine produced quantum mechanical and molecular mechanical χ₁ scans almost identical to each other, and thus optimized to nearly the same parameters. For simplicity, the phenylalanine parameters were used for both amino acids. Parameters for neutral histidine were optimized for the data scanned with the proton at the ε and δ nitrogens simultaneously. Protonated histidine and tryptophan were both found to require unique parameters. In the case of tryptophan, empirical reweighting was found to be necessary, but only by a slim margin.

In the original OPLS-AA force field, only peptide-specific χ₁ dihedral parameters were assigned. Any χ angles further along the side chain were assigned the same parameters as the equivalent side-chain analogues. Here scans were performed in a similar fashion to χ₁, and new χ₂ parameters were fit independently for most amino acid (Table 3S). Only asparagine, aspartate, methionine, and the various protonation states of histidine displayed enough of an improvement to merit unique χ₂ parameters. As leucine was not found to require a peptide-specific χ₂, lysine and arginine, which bear similar hydrocarbon χ₂ dihedrals, were omitted from this analysis. Glutamine and glutamic acid, which according to crystal structure distributions should have a large population of t χ₂ angles were empirically adjusted to increase the population of this rotamer. An approach to the χ₂ parameters as rigorous as what was employed for χ₁ is beyond the scope of this work, in part due to the lack of NMR data for comparison to our simulated rotamer distributions. It should however be noted that agreement with the crystal structure χ₂ rotamer distributions was generally good for most residues.

Molecular Dynamics Simulations of Blocked Dipeptides

The mean unsigned error in simulated ³J(H_N,H_α) compared to NMR experiments⁵⁴ for the OPLS-AA, OPLS-AA/L, and OPLS-AA/M parameters for each of the dipeptides is plotted in Figure 3. The calculated J couplings improved significantly over the previous two force fields, with the RMSD lowering from 0.97 Hz with OPLS-AA and 0.79 Hz with OPLS-AA/L to 0.35 Hz with OPLS-AA/M. This compares favorably to a recent modification of the OPLS-AA force field that introduced residue-specific backbone parameters,⁵⁵ which had an RMSD for 19 blocked dipeptides of 0.42 Hz. The improvement demonstrates that our new backbone parameters derived for alanine and glycine are transferable to all other amino acids.

Figure 3.

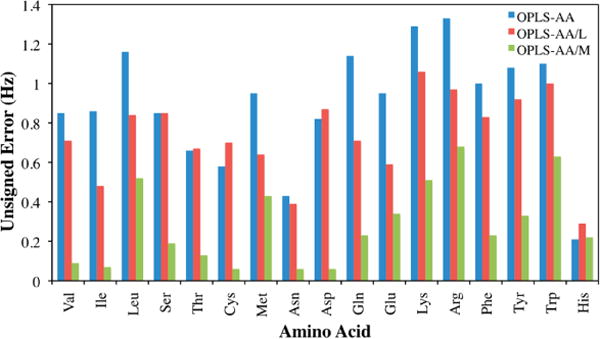
Comparison of the unsigned error in Hertz for the dipeptide ³J(H_N,H_α) couplings for each amino acid with the OPLS-AA, OPLS-AA/L, and OPLS-AA/M force fields.

The average χ₁ rotamer populations from the dipeptide simulations were plotted against both the average NMR rotamer distribution for denatured ubiquitin and protein G (Figure 4) and a protein coil library (Figure S2). It should be noted that in our dipeptide simulations where a single residue is present, the individual OPLS-AA/L parameters were used, despite the fact that there would be problems implementing them in CHARMM and MCPRO formatted parameter files for a full protein due to overlapping atom types, as previously discussed. Our new parameters, which can be easily implemented, provide a large improvement in the χ₁ distributions over OPLS-AA/L and OPLS-AA, notably for valine, cysteine, threonine, methionine, asparagine, aspartate, and lysine. Most importantly, the new parameters lack any rotamers with populations in the extremes of 100% and 0%. Populations at these values suggest serious potential problems with the transferability of a parameter to different environments. The mean unsigned error over all rotamer populations compared to the NMR data improved from 25.5% with OPLS-AA and 20.5% with OPLS-AA/L to 15.1% before empirically reweighting parameters and 9.9% after, with a similar trend observed compared to the coil library data (MUEs of 23.1% for OPLS-AA, 21.11% for OPLS-AA/L, 14.4% before and 10.0% after the empirical adjustments).

Figure 4.

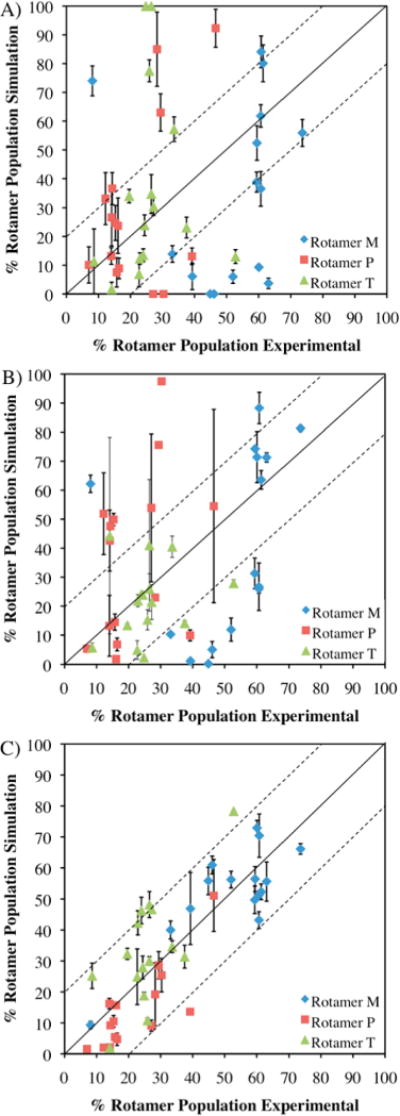
Percentage populations of each rotamer from MD simulations of blocked dipeptides versus the average populations for each amino acid from NMR experiments on denatured ubiquitin and protein G. Results are given for OPLS-AA (A), OPLS-AA/L (B), and OPLS-AA/M (C). Dashed lines delineate the region of populations that fall within ±20% of the experimental result. Error bars for simulations represent the standard deviation in the populations from triplicate 200 ns simulations.

Molecular Dynamics Simulations of Proteins

The RMSD in Hertz for the calculated ³J couplings from the simulations of ubiquitin and GB3 compared to experiment are provided in Table 3. Experimental values were compiled from a range of sources^{21,43,46–48} and can be found in the Supporting Information. Three sets of χ₁ couplings are provided for ubiquitin: ³J(H_α,H_β) couplings, ³J(C′,C_ϒ) couplings, and a set of ³J(N,C_ϒ) and ³J(C′,C_ϒ) couplings for the side chain methyls of valine, isoleucine, and threonine. To avoid redundancy, couplings reporting on these isoleucine, valine, and threonine residues were omitted from the calculation of the RMSD values for the other χ₁ sets. For GB3, only ³J(H_α,H_β) couplings and a set of ³J(N,C_ϒ) and ³J(C′,C_ϒ) couplings for methyl groups on beta branched amino acids were analyzed. All couplings calculated in this work can be found in an SI Excel file. An RMSD over all measurements for each protein was also calculated for all available χ₁ couplings and backbone couplings calculated with the 2007 Karplus parameters. Plots of the RMSD values for the coordinates of the backbone atoms compared to the starting structures over time for the first run with each force field are plotted in SI Figure 3.

Table 3.

Results of Aqueous Phase Simulations for Ubiquitin and GB3 with OPLS-AA, OPLS-AA/L, and OPLS-AA/M

	backbone couplings 1997 RMSDa,b	backbone couplings 2007 RMSDa,c	3J(Hα, Hβ) RMSDa	3J(C′,Cϒ) RMSDa	methyl Cϒ couplings RMSDa	RMSD overalla,d
Ubiquitin
OPLS-AA	0.84 ± 0.02	1.02 ± 0.04	3.26 ± 0.08	1.43 ± 0.01	0.91 ± 0.05	1.84 ± 0.03
OPLS-AA/L	0.71 ± 0.03	0.89 ± 0.03	3.10 ± 0.05	1.14 ± 0.03	0.64 ± 0.02	1.70 ± 0.01
OPLS-AA/M	0.59 ± 0.02	0.74 ± 0.04	1.88 ± 0.12	0.85 ± 0.04	0.43 ± 0.07	1.12 ± 0.06
GB3
OPLS-AA	0.90 ± 0.02	0.91 ± 0.02	3.71 ± 0.09		0.68 ± 0.04	1.46 ± 0.01
OPLS-AA/L	1.11 ± 0.10	1.04 ± 0.11	3.38 ± 0.08		0.90 ± 0.04	1.46 ± 0.06
OPLS-AA/M	0.87 ± 0.03	0.81 ± 0.02	1.52 ± 0.13		0.80 ± 0.06	0.91 ± 0.04

^aRMSD values in Hertz.

^bCalculated with the Karplus parameters from ref 43.

^cCalculated with the Karplus parameters from ref 46.

^dUsing the backbone couplings calculated with the Karplus parameters from ref 46.

Improvement was observed for the OPLS-AA/M force field compared to OPLS-AA and OPLS-AA/L for both backbone and side chain couplings. For ubiquitin, the RMSD for all couplings dropped from 1.84 Hz with OPLS-AA and 1.70 Hz with OPLS-AA/L to 1.12 Hz with OPLS-AA/M. RMSD values for the J couplings were recently reported for ubiquitin and GB3 as 1.41 and 1.44 Hz for AMOEBA and as 1.43 and 0.89 Hz for the ff99sb-ildn force field.²⁰ The data for other force fields in the literature is difficult to compare directly as simulation conditions, number of couplings, Karplus parameters, and other factors examined can differ. However, as OPLS-AA/M gave overall RMSD values of 1.12 and 0.91 Hz, the new force field should perform well in direct tests against other current force fields.

CONCLUSION

New peptide dihedral parameters were developed for the OPLS-AA force field by fitting to state-of-the-art QM torsional energy scans for blocked dipeptides. These new parameters significantly out-perform the previous two iterations of the OPLS-AA force fields in their ability to reproduce both gasphase conformer energies for longer peptides and aqueous phase experimental properties in molecular dynamics simulations. It was necessary to empirically modify the χ₁ torsion parameters to improve agreement with experimental rotamer distributions for only five amino acids: serine, cysteine, aspartate, glutamate, and tryptophan. These residues bear either a heteroatom, negative charge close to the backbone, or a sizable conjugated ring system and thus may represent a particular challenge for a point-charge force field without explicit polarization. Alternatively, as the empirically adjusted parameters still generally had small errors compared to the QM scans, it is possible that for these residues the number of different scans with different backbone and χ values was insufficient. Regardless, the transferability of dihedral parameters developed against high-level gas phase quantum chemical data to condensed phase simulation of peptides was demonstrated.

In fitting new parameters to ab initio QM surfaces, it was found to be absolutely necessary to employ some method of preferentially fitting to the lower energy regions of the surface. This is particularly true for the two-dimensional φ–ψ surface, where the relative energies in some barrier regions exceed 20 kcal/mol. The common Boltzmann weighting scheme was found to perform very well, but the results were best when a high weighting temperature (T = 2000 K) was employed. It must be kept in mind that for the blocked alanine dipeptide, for example, values of φ and ψ that correspond to conformations that are ubiquitous in folded proteins can have relative energies exceeding 4 kcal/mol, so a generous weighting temperature is necessary to ensure all relevant parts of the potential energy surface are included.

It was also demonstrated that comparison of a force field’s performance for reproducing the minimum-energy conformations and their relative energies for the blocked alanine tetrapeptide in gas phase can provide a computationally inexpensive first look at the accuracy of new peptide backbone dihedral parameters. While not absolutely correlated to the reproduction of experimental J couplings for the alanine pentapeptide, the test was able to discriminate between good and poor performers, especially when comparing force fields with the same nonbonded parameters. It was also demonstrated that an empirically driven modification of the popular ff99 series of AMBER force fields still produced some improvement in the number of gas-phase QM conformers reproduced for the alanine tetrapeptide. Together with our work on the OPLS-AA force field, this suggests deriving dihedral torsion parameters from QM data and empirically need not be considered divergent approaches, at least to within the accuracy of the currently available experimental data.