Abstract
Ion channel opening and closing is fundamental to cellular signaling and homeostasis. Gates that control K+ channel activity were found both at an intracellular pore constriction and within the selectivity filter near the extracellular side but the specific location of the gate that opens Ca2+-activated K+ channels has remained elusive. Using the Methanobacterium thermoautotrophicum homolog (MthK) and a stopped-flow fluorometric assay for fast channel activation, we show that intracellular quaternary ammonium blockers bind to closed MthK channels. Since the blockers are known to bind inside a central channel cavity, past the intracellular entryway, the gate must be within the selectivity filter. Furthermore, the blockers access the closed channel slower than the open channel, suggesting that the intracellular entryway narrows upon pore closure, without preventing access of either the blockers or the smaller K+. Thus, Ca2+-dependent gating in MthK occurs at the selectivity filter with coupled movement of the intracellular helices.
Introduction
Calcium ions regulate diverse cellular processes including synaptic transmission, muscle contraction, exocytosis, gene transcription, and cell motility1. These complex processes are controlled by Ca2+ channels, as well as proteins that respond to increases in cytosolic Ca2+, including Ca2+-dependent ion channels2. The ubiquitously expressed large conductance voltage and Ca2+-activated K+ (BK) channel, for example, binds Ca2+ to a cytosolic domain called a gating ring, resulting in large increases in K+ conductance that hyperpolarizes the cell membrane and decreases electrical excitability3. By coupling membrane excitability to intracellular Ca2+ concentrations, BK channels serve as key elements in the regulation of Ca2+-dependent cellular processes. To understand the molecular events underlying normal or pathophysiological Ca2+ signaling, it is necessary to clarify how Ca2+ binding opens BK channels.
The BK channel (Slo1) is a member of the eukaryotic Slo family of K+ channels4 that evolved from prokaryotic K+ channels, such as the MthK channel from Methanobacterium thermoautotrophicum, which is similarly activated by cytosolic Ca2+ (Fig. 1a)5–8. The ability to express and purify large quantities of MthK for functional and structural analyses has advanced MthK as a model for Ca2+-dependent gating in BK channels. X-ray crystallography studies show that the cytosolic Ca2+-binding gating rings for the BK and MthK channels are structurally related9–11 (Fig. 1a) and undergo similar Ca2+-dependent conformational changes as shown by crystal structures of these domains in the presence and absence of calcium12. In contrast to the BK channel, however, structural models are available for the isolated MthK pore domain13 and full-length MthK channel5, both in a putative open conformation, facilitating the interpretation of structure-function relationships in channel gating (Fig. 1a). (There is no structure of the MthK channel pore in a putative closed conformation.) In this context, it is important that MthK channels lack the voltage-sensor domains that confer voltage dependence on BK channels, thereby isolating the mechanism for Ca2+-dependent gating and simplifying experimental determination of the gating mechanism in MthK compared to BK. Understanding how the MthK pore opens and closes in response to Ca2+ thus provides a solid context for interpretation of gating studies of eukaryotic Slo channels, including BK.
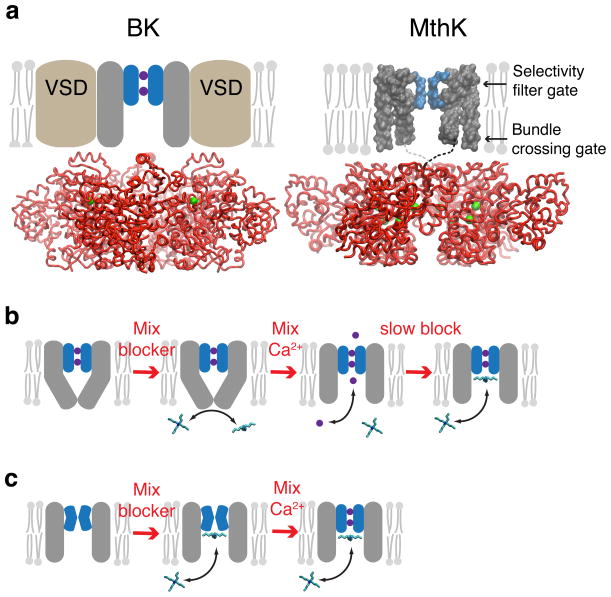
Figure 1. Blockers as probes for Ca2+-dependent gate location in K+ channels.
(a) Comparison of BK (left) and MthK (right) channel architectures. The gating rings (red ribbons) with bound Ca2+ (green spheres) are structurally conserved between BK (pdb 3U6N) and MthK (pdb ILNQ). The unknown transmembrane structure for BK is illustrated with voltage sensor domains (VSDs, brown) and pore domain (grey) with selectivity filter (blue). MthK lacks VSDs and the full-length protein structure is available, except for linkers between pore and gating ring (dashed lines). Locations of two putative gates are indicated by arrows. Only two subunits for the transmembrane domains are illustrated for clarity. (b) The gated access model: the pore-domain has a bundle-crossing gate that prevents QA blocker binding to the aqueous vestibule. Rapid activation by Ca2+ results in immediate channel activity (purple circles and arrow) followed by blocker binding just below the selectivity filter. (c) The selectivity filter gate model: blocker has access to the binding site in both closed and open channels and steady-state block is reached before MthK is activated by Ca2+.
Two gate locations that control ion permeation have been proposed in K+ channels — a structural constriction at the intracellular side of the pore, called a ‘bundle crossing’, and a structurally undefined closing of the selectivity filter14. A large aqueous vestibule that lies between these two possible gate locations forms a binding site for quaternary ammonium (QA) channel blockers, which have provided a tool for probing the gating mechanism15,16. In the case of voltage-gated channels, numerous functional studies have shown that activation gating involves the opening of an intracellular gate14,17,18. Alternatively, several types of ligand-gated channels, including BK channels19–22, have been proposed to employ a different activation gating mechanism that involves changes at the selectivity filter23–28. However, the studies in support of selectivity filter gating in BK channels are not definitive due to the complexity of BK channel gating (voltage- and Ca2+-dependent gating) combined with the use of voltage dependent blockers, leading to uncertainty in identification of the gate location.
Subsequent structural studies of several prokaryotic channels, employing various channel mutations, have provided molecular models of open and closed channel states29–35, strengthening the notion that many channels employ an intracellular bundle crossing gate. Although only the open state structure of the MthK pore is available, it was proposed that the closed channel has an intracellular bundle-crossing gate similar to KcsA, based on the sequence homology between MthK and KcsA in the pore region36. In a previous study37, we showed that membrane voltage controls a selectivity filter gate and not a bundle-crossing gate in MthK, but it was not determined whether this gate is also controlled by Ca2+.
Here we investigate the mechanism of Ca2+-dependent gating using purified MthK channels reconstituted into lipid bilayers of defined composition. We show that Ca2+-dependent gating occurs at the selectivity filter, and not at the bundle crossing, by detecting closed-channel block by large QA molecules that bind immediately below the selectivity filter. By utilizing a stopped-flow-based flux assay38,39, Ca2+ and blocker are very quickly applied to MthK liposomes with the time-resolution essential for discriminating between gate locations. Tetrapentylammonium (TPeA) binds ~100-fold slower to the closed state than to the open state, indicating a significant conformational change during closing that reduces but does not eliminate blocker access. These results suggest that hydrated potassium ions, which are smaller, also have rapid access to the aqueous vestibule beneath the selectivity filter. We propose that Ca2+ binding to the gating ring may induce an expansion at the intracellular channel entryway that leads to opening of the primary conduction gate at the selectivity filter. Such a mechanism may be conserved in the Slo K+ channel family, including the BK channel.
Results
To probe whether activation of MthK channels by Ca2+ occurs by opening a bundle-crossing or a selectivity filter gate (Fig. 1a), we examined the state-dependence of channel block by quaternary ammonium (QA) ions that bind between the two candidate gate locations, immediately below the selectivity filter16,37,44,45. If MthK has a bundle-crossing gate closure (Fig. 1b), QA blockers do not have access to the binding site within the pore when the channels are closed. Alternatively, if MthK channels have a selectivity filter gate, QA blockers may access the binding site when the channels are closed, in a size-dependent manner (Fig. 1c). Thus, if QA blockers bind within closed MthK channels, gating must occur above the binding site, implicating the selectivity filter as the Ca2+-dependent gate.
To investigate whether closed channels can be blocked, we incubated closed MthK channels (in the absence of Ca2+) with blocker, then rapidly activated the channels with Ca2+ and measured the channel activity. If the gate is at a bundle crossing, blockers do not have access to the channel in the closed state and rapid opening with Ca2+ will result in maximal channel activity followed by slower blocker binding within the pore and a subsequent decrease in activity (Fig. 1b). This sequence of events was observed in studies of voltage-dependent K+ (Kv) channels, demonstrating gated blocker access in those channels15,46. If the Ca2+-dependent MthK gate is at the selectivity filter, blockers may access their binding site in the closed channel and rapid opening with Ca2+ will only show the activity of the fraction of unblocked channels (Fig. 1c).
To distinguish between these two models, several conditions have to be met. First, to measure MthK block by QA molecules in the closed state we need to assess the channel activity immediately following activation by Ca2+; both Ca2+ application and the activity measurement must be done with high time resolution. Second, the rate of channel activation by Ca2+ must be faster than the rate of QA blocker binding. Third, MthK channels must be closed in the absence of Ca2+.
We satisfied the first condition by using a stopped-flow instrument with millisecond time resolution to rapidly mix MthK-reconstituted liposomes with Ca2+ and Tl+ (Fig. 2a and Supplementary Fig. 1). Tl+ enters the liposomes through open MthK channels and quenches an internal fluorescent dye (ANTS, Fig. 2b). Thus, the initial rate of fluorescence quenching is a measure of the channel activity, obtained only 2 ms following the application of Ca2+ (the instrument dead time) by fitting the fluorescence decline to a stretched exponential function (Methods, Eq. 1) and calculating the Tl+ flux rate at 2 ms from this fit (Methods, Eq. 2).
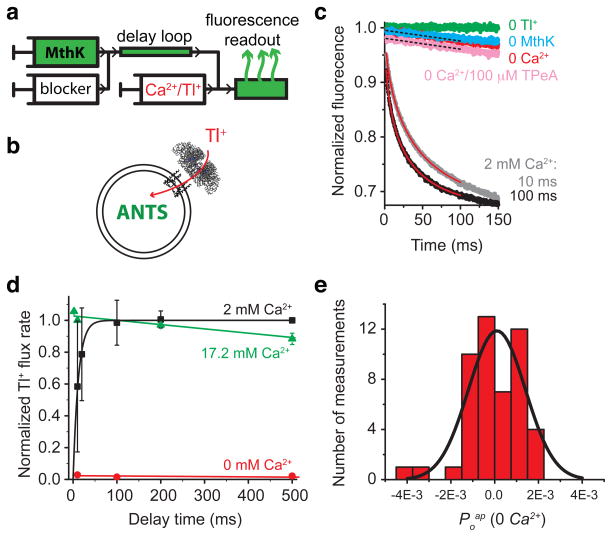
Figure 2. MthK is closed in 0 Ca2+ and is activated quickly with Ca2+.
(a) Schematic representation of the sequential-mixing stopped-flow device. The mixing sequence for a closed-state block assay is shown from left to right (see also Supplementary Fig. 1). MthK-reconstituted liposomes are mixed with blocker and incubated in a delay loop for a defined time interval followed by mixing with activating Ca2+ and fluorescence-quenching Tl+ into an optical cell for fluorescence readout. (b) Open MthK channels allow Tl+ entry (red arrow) into the liposomes, quenching the fluorescence of the encapsulated ANTS dye. (c) Fluorescence quench curves for MthK liposomes after 10 or 100 ms (grey and black, respectively) incubation with 2 mM Ca2+. Flux rates were from fits to stretched exponentials (red lines). Control fluorescence is in the absence of Tl+ (green). A small leak of Tl+ into liposomes is observed in experiments without Ca2+ (red), similar to the leak in MthK-free liposomes (cyan). The non-specific Tl+ leak in MthK-liposomes was also measured in the presence of 100 μM TPeA (pink). A linear fit was used to analyze the slow Tl+ leak signals (black dotted lines). (d) Relative Tl+ flux rates as a function of Ca2+ incubation time for 0 (red), 2 (black), and 17.2 mM (green) Ca2+. Symbols are the mean ± s.d. from three (or two for 0 mM Ca2+) independent measurements. (e) Histogram of 49 independent estimates of apparent open probability in the absence of Ca2+ (Poap(0 Ca2+), calculated using Eqs. 4–8 in Methods). The average value was −0.00004 ± 0.0002 (mean ± s.e.m.). The histogram was fit with a Gaussian distribution (black line) with mean at Poap(0 Ca2+) = 0.0001 ± 0.0003 (0.01 ± 0.03%) and standard deviation σ = 0.0013 ± 0.0003.
Ca2+ rapidly activates MthK
The second condition necessary to measure closed-state channel block is that MthK activation has to be fast. We measured the rate of MthK activation by incubating MthK liposomes with several Ca2+ concentrations in the delay loop and then mix with Tl+ (Supplementary Fig. 1a). As expected, longer incubations with Ca2+ resulted in faster fluorescence quenching (increased channel activity) (Fig. 2c). At 2 mM Ca2+ the time course of MthK activation was fit with a single exponential function with a time constant of 12.1 ± 0.4 ms (Fig. 2d, black squares; Eq. 3). To achieve an even faster activation rate, we increased the [Ca2+] to 17.2 mM where full activity was reached during the mixing dead time, indicating that the activation time constant is in the μs regime, faster than we can measure with our time resolution (Fig. 2d, green). Thus, by using 17.2 mM Ca2+ we could ‘instantaneously’ activate MthK channels and meet our second experimental criterion. We also observed that after a few seconds MthK channel activity declined (Supplementary Fig. 2), similar to what was previously reported using electrophysiological recordings with MthK from E. coli spheroplasts47, but not observed in steady-state single-channel recordings in lipid bilayers6–8. This process did not interfere with our blocker studies, which were performed within a few hundred ms of channel activation (see below).
Open probability of MthK in the absence of Ca2+
To satisfy the third requirement for measuring closed-state channel block, we estimated the open probability of MthK channels under our experimental conditions in the absence of Ca2+. A non-zero open probability (Po) in the absence of Ca2+ would result in blocker binding to the fraction of channels that are open, which would diminish our ability to discriminate between the gated-access and state-independent access models. Channel openings in zero Ca2+ are undetected in most single channel recordings in lipid bilayers 6,8 and we expected a similar result using our flux assay.
In the absence of Ca2+, very slow fluorescence decays are observed for MthK liposomes, similar to those recorded in protein-free controls, suggesting that the channel activity in the absence of Ca2+ is extremely low, as expected from previous results using single channel recording (Fig. 2c). Thus, most of this Tl+ influx in zero Ca2+ is due to non-specific Tl+ leak across the liposomal membrane38. To quantify such low channel activity, we determined the flux contribution, if any, arising from rare MthK openings, by subtracting the non-specific leak obtained in the presence of saturating concentrations of channel blocker, which is a measure of the true membrane “leak” because any flux through the channels is now blocked. Since the result is a difference between two very small numbers, we performed a statistical analysis of 49 experimental estimates of this very small influx rate (Fig. 2e). This analysis showed that the residual ion permeability through MthK channels in the absence of Ca2+ is statistically indistinguishable from zero (Fig. 2e, Supplementary Note).
TPeA blocks closed MthK channels with slow kinetics
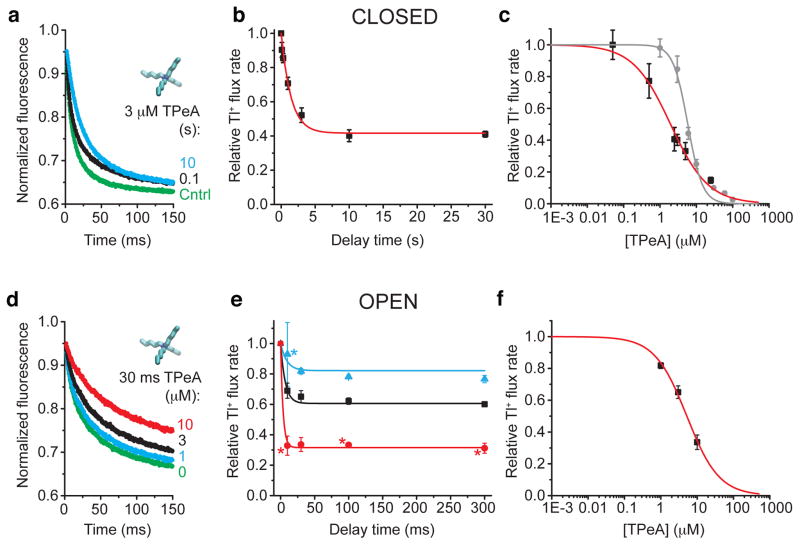
With all of the necessary experimental conditions met, we addressed our central question; do QA blockers bind to closed channels? Blocker binding to closed MthK would indicate that the channels lack a bundle-crossing gate and must close at the selectivity filter. For this, we incubated MthK channels with TPeA in the absence of Ca2+ followed by very rapid channel activation to detect whether the blocker had bound to the closed channels (Fig. 2a). The fluorescence decay was slower for longer blocker incubation periods, suggesting that TPeA was indeed able to bind to and block closed MthK channels (Fig. 3a). Short incubations with TPeA (~100 ms) resulted in little inhibition, whereas incubations for greater than 1 s led to substantial inhibition of channel activity (Fig. 3b). A single-exponential fit to these results yields an equilibration time constant of ~2 seconds (Fig. 3b, red line; Eq. 10) from which we extracted blocker kinetics (konclosed = 0.14 ± 0.02 μM−1 s−1) and affinity (KDclosed = 2.1 ± 0.2 μM) of TPeA to closed MthK (Fig. 3b, Eq. 11, see also Table).
Figure 3. TPeA blocks closed and open MthK.
(a) Fluorescence quench traces after closed state incubation with 3 μM TPeA for 0.1 (black), 10 s (cyan), and no blocker control (green) (average of 4–7 repeats). (b) Relative Tl+ flux rates versus incubation time from data as in a. Red line is a fit with eq. 10 and 11 (τeq = 1.6 ± 0.2 s, KDclosed = 2.1 ± 0.2 μM, konclosed = 0.14 ± 0.02 μM−1 s−1). (c) Dose-response curve for closed state TPeA equilibrium block after 10 s blocker incubation. Red line is a Hill equation fit (eq. 12, KDclosed = 2.0 ± 0.2, nH = 0.84 ± 0.08). Dose response curve for open state block after the 2 ms mixing time (grey circles). The grey line has no theoretical meaning. (d) Fluorescence quench traces after 30 ms incubation with 17.2 mM Ca2+ to measure open state block by 0 (green), 1 (cyan), 3 (black) or 10 μM (red) TPeA (average of 4–7 repeats). (e) Relative Tl+ flux rates versus incubation time with open MthK for three [TPeA], colored as in d. The results were simultaneously fit to Eq. 11 (lines; KDclosed = 4.6 ± 0.2 μM, konclosed = 20 ± 3 μM−1 s−1). (f) Dose-response curve for TPeA binding to open MthK after 30 ms incubation with blocker (results from e) was fit by the Hill equation (red line; KDopen = 5.2 ± 0.3 μM, nH = 0.98 ± 0.07). Mean ± s.d. from at least three independent samples, except for experiments marked (*) in e, where n=2.
Table 1.
Apparent blocker dissociation constants and kinetics
| Blocker | MthK state | KDap (μM) | konap (μM−1 s−1) | *koffap (s−1) |
|---|---|---|---|---|
| TPeA | Open | 4.6 ± 0.2 | 20 ± 3 | 92 ± 14 |
| Closed | 2.1 ± 0.2 | 0.14 ± 0.02 | 0.29 ± 0.05 | |
| bbTBA | Open | 2.1 ± 0.2 | 17 ± 2 | 35 ± 6 |
| Closed | 0.7 ± 0.2 | 0.018 ± 0.002 | 0.012 ± 0.004 | |
| BrbTBA | Closed | 2.6 ± 0.4 | 0.028 ± 0.005 | 0.07 ± 0.02 |
koffap = konap KDap
To further characterize closed MthK block, we measured the TPeA dose-response curve by equilibrating the closed channel for 10 s with various blocker concentrations and recording channel activity (Fig. 3c, red). A fit using the Hill equation (Eq. 12) provided another estimate of the apparent closed-state dissociation constant, KDclosed = 2.0 ± 0.2 μM, similar to what we found above (Fig. 3b), and a Hill coefficient of 0.84 ± 0.08 (Fig. 3c, blue dotted line), which is lower than 1, the predicted Hill coefficient for a bimolecular reaction model for blocker binding to MthK (Eq. 12). It is possible that the TPeA dose response is shallower than expected because our measurement of closed-state block requires opening the channel. If the blocker affinity changes after the channel opens, then at higher blocker concentrations, where the blocker equilibration rate is faster, the blockers may partially equilibrate to open channels within our instrument dead time, thus contaminating our closed channel block measurements. To determine whether this is the case, we measured the blocker binding to the open state.
TPeA blocks open MthK channels with fast kinetics
To investigate TPeA block of open MthK channels we used a sequential-mixing protocol in which MthK liposomes were first incubated with Ca2+ and blocker prior to assaying channel activity (Supplementary Fig. 1b). As expected, the fluorescence decay was slower as the blocker concentration was increased (Fig. 3d). Additionally, steady state block was reached in ~30 ms (Fig. 3e), which was faster than expected given our previous determinations using single-channel block in lipid bilayer recordings37. We estimated the open-state apparent blocker dissociation constant and kinetics by globally fitting Eq. 11 to the equilibration time course for three different blocker concentrations (Fig. 3e, lines). The fitted values for the apparent open-state dissociation and on-rate constants were KDopen = 4.6 ± 0.2 μM, higher than for closed MthK, and konopen = 20 ± 3 μM−1 s−1, much faster than for closed MthK (for direct comparison, see Table), confirming that TPeA blocks MthK in a state-dependent manner and that open-state blocker kinetics is fast. We also plotted the TPeA dose-response curve for the results using 30 ms incubation with TPeA, which resulted in another estimate (using Eq. 12) of KDopen = 5.2 ± 0.3 μM with a unitary Hill coefficient, as expected for a bimolecular interaction between blocker and open MthK (Fig. 3f).
The fast TPeA open-state kinetics and the state-dependence of TPeA block suggest that our closed-state block measurements may indeed reflect an additional component of re-equilibration towards open-state block during the mixing dead time. To evaluate the degree of “contamination”, we designed an experiment to measure directly the amount of blocker binding to the MthK open state that occurs during this time. To do this, we simultaneously mixed MthK liposomes with TPeA, high Ca2+ and Tl+ (Supplementary Fig. 1d) and immediately measured the activity so that only the amount of open-state TPeA block occurring during the mixing dead time was measured (Fig 3c, grey). TPeA concentrations below ~6 μM did not result in significant decreases in the measured Tl+ flux rate (Fig. 3c, grey symbols) and the apparent closed-state inhibition measured at these concentrations (Fig. 3c, red symbols) reflects mostly the degree of closed-state block. Consequently, our closed state blocker equilibration measurements using 3 μM TPeA (Fig. 3b) should accurately reflect the affinity and kinetics for closed-state block. The apparent closed state inhibition by TPeA concentrations at ~6 μM and higher reflect a mixture of closed- and open-state block, with rapid blocker re-equilibration after channel opening (overlap of grey and red symbols in Fig. 3c).
A model for state-dependent MthK block by TPeA
We refined our estimates of the thermodynamic and kinetic parameters for closed-state block by analyzing the TPeA dose-response curve in Fig. 3c using a state-dependent model that explicitly accounted for blocker re-equilibration during stopped-flow mixing. As expected, because at 3 μM TPeA there was little blocker re-equilibration to the open state (Fig. 3b), using this model led to minor adjustments of the TPeA closed-state block parameters (Supplementary Note). Specifically, the estimates of KDclosed, konclosed and koffclosed were lowered by small amounts: ~40% (from 2.1 to 1.3 μM), ~20% (from 0.14 to 0.11 μM−1 s−1), and ~50% (from 0.29 to 0.14 s−1), respectively (compare Table to Supplementary Table). The model also fits well the sub-unitary slope of the TPeA dose-response curve (Supplementary Fig. 3) by incorporating the blocker re-equilibration, which was significant at concentrations higher than ~6 μM (Fig. 3c, red and grey symbols).
These results provide a model for both closed- and open-state MthK channel block with a modest state-dependence in blocker affinity and a large state-dependence in blocker kinetics (Table). This suggests that TPeA encounters a steric obstacle or energy barrier before reaching its binding site in the closed channel. To explore this possibility, we investigated the kinetics of closed-state binding for two other QA blockers, bromobenzyltributylammonium (Br-bTBA) and N-(4-[benzoyl]benzyl)-N,N,N-tributylammonium (bbTBA). These blockers have benzyl-containing groups that are less flexible than alkyl chains and may increase the blocker hydrodynamic radius. bbTBA in particular is larger than TPeA and is thus predicted to encounter greater hindrance to binding inside the closed channel.
Larger QA molecules block closed MthK with slower kinetics
Br-bTBA and bbTBA are QA blockers with either a single brominated benzyl group or two benzyl groups, respectively, attached to the central nitrogen (Fig. 4a, structure insets, Fig. 5b). Using our flux assay, we found that 3 μM Br-bTBA blocked ~50% when applied to closed MthK channels, similar to TPeA, while only 1 μM bbTBA was sufficient to block the same amount, indicating higher affinity for the closed MthK. Unlike TPeA, however, Br-bTBA equilibration required tens of seconds, while the larger bbTBA requires ~6 times as long, as illustrated by the closed-state blocking time courses (Fig. 4a, black squares and red circles). The apparent on-rates estimated from these results show that Br-bTBA and bbTBA bind ~5-fold and ~8-fold slower than TPeA (Table), consistent with the larger, more rigid aromatic ring structures that may increase the hydrodynamic radii relative to TPeA (Fig. 5b).
Figure 4. Br-bTBA and bbTBA block closed MthK more slowly than TPeA.
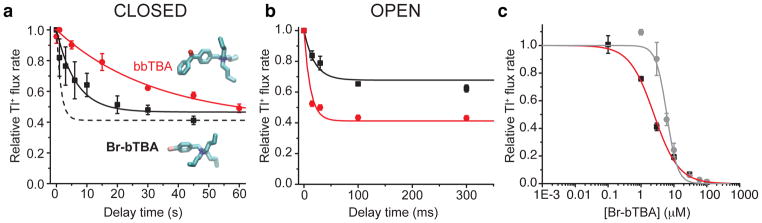
(a) Relative Tl+ flux rates as a function of Br-bTBA and bbTBA (structures inset) incubation with closed MthK channels. Blocker equilibrations were fit to exponential functions, τBr-bTBA = 9 ± 3 seconds, τbbTBA = 32 ± 7 seconds (Eq. 10, black and red solid lines, respectively). The fitted blocker time course for TPeA (from Fig. 3b) is shown for comparison (black dashed line). (b) Relative Tl+ flux rates versus incubation time with open MthK for 1 (black squares) and 3 μM (red circles) bbTBA. The results were simultaneously fit to Eq. 11 (lines; KDopen = 2.1 ± 0.2 μM, konopen = 17 ± 2 μM−1 s−1). (c) Closed state Br-bTBA dose response curve for 45 s blocker incubations prior to activation of MthK by 17.2 mM Ca2+ (black squares). The results were fit to the Hill equation (red line; KDclosed = 2.5 ± 0.2, nH = 1.16 ± 0.09). Dose response for open state Br-bTBA block measured during the instrument dead time (grey circles). Grey line has no theoretical meaning. Symbols are the mean ± s.d. from at least three (only two for bbTBA data in b) independent measurements.
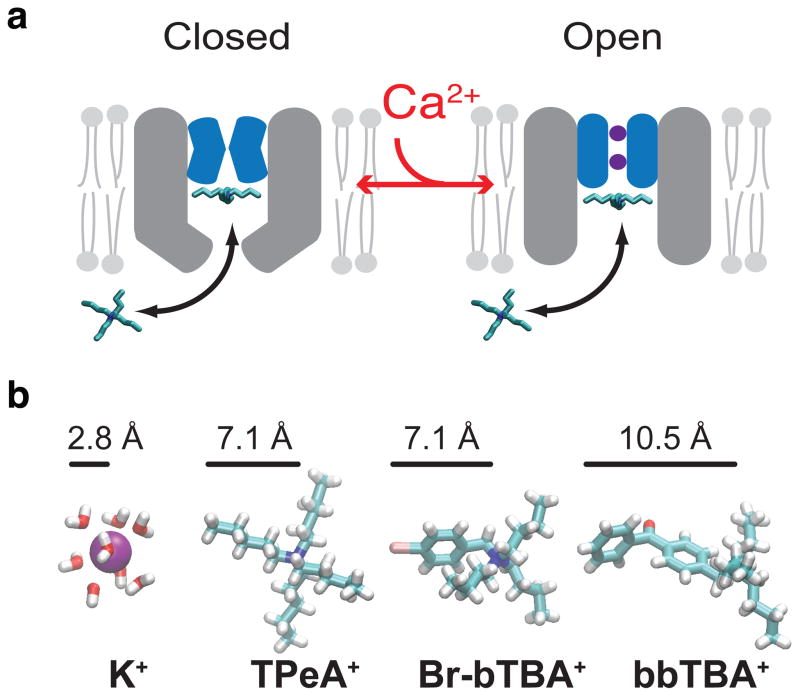
Figure 5. Closure at the MthK selectivity filter is accompanied by a conformational change near the intracellular entryway.
(a) Model for QA block of the closed and open MthK channel. The selectivity filter is non-conductive in the absence of Ca2+ and the intracellular entryway (grey) is narrowed but still allows blocker/K+ entry into vestibule (left). Channel activation opens the selectivity filter gate (purple K+ inside blue filter) and increases blocker access rate into the pore (right). (b) The radius of a hydrated K+ is smaller than the extended structures in TPeA+, Br-bTBA+ and bbTBA+, suggesting that K+ can access the closed MthK intracellular entryway despite the constriction.
Because bbTBA block of closed channels was much slower than TPeA block, we measured the kinetics of open channel block by equilibrating 1 and 3 μM bbTBA with Ca2+-activated MthK channels (Fig. 4b). The results indicate that bbTBA binds to open MthK as quickly (konopen = 17 ± 2 μM−1 s−1) as TPeA (Table). We also evaluated whether the closed-state block parameters for Br-bTBA are ‘contaminated’ by open-state block re-equilibration, as observed for TPeA (Fig. 3c). We tested whether Br-bTBA equilibrates rapidly with the open state by applying the blocker simultaneously with Ca2+ and Tl+ to measure the amount of block occurring during the 2 ms mixing time (Fig. 4c, grey circles). At 3 μM Br-bTBA, the open-state block during the mixing time was very low, indicating that our measurement for the closed-state block at this concentration (Fig. 4c, black squares) is very little affected, similar to what we found for TPeA (compare Fig. 4c and Fig. 3c).
We also measured the Br-bTBA open-state block parameters using single-channel bilayer recordings and found that the affinity and on-rate are almost identical to those of TPeA and bbTBA37, indicating that the three blockers have similar fast access to the MthK open state (Supplementary Fig. 4), whereas they have much slower and different access rates to the closed state (Fig. 4a). This suggests that the entryway to the MthK aqueous vestibule narrows upon channel closure.
Discussion
The gating mechanisms in eukaryotic Ca2+- and voltage-gated BK channels have been explored using blockers19,21,48–53 and thiol-modifying probes20,22 to assess conformational changes within the pore. Taken together, most of these studies are suggestive of a gating mechanism ‘deeper’ inside the pore than for Kv channels54, though a molecular gating model has yet to be firmly established55. In particular, the complexity of the BK channel, namely the confounding interplay of voltage-dependent gating, Ca2+-dependent gating, and voltage-dependent block has hindered a definitive demonstration that BK gating occurs at the selectivity filter. Here, we elucidated the mechanism of Ca2+-dependent gating in MthK, a prokaryotic BK channel homologue with a conserved Ca2+-dependent gating ring but devoid of voltage-sensing domains5, thus allowing unhampered study of the Ca2+-dependent gate. Using a flux assay with high time-resolution38,39, we were able to characterize the closed-state block of MthK by QA blockers (Fig. 1), and find that Ca2+ induces changes at the intracellular channel entryway, which controls K+ conductance via a gate at the selectivity filter.
We found that TPeA blocks MthK with state-dependent kinetics, suggesting a conformational change near the bottom of the pore in the closed state. One possible change that could lead to slower block of the closed state is a reduction in the size of the intracellular entryway (Fig. 5a). We examined this possibility further using Br-bTBA and bbTBA, two QA molecules with benzene-containing groups that are more rigid and in the case of bbTBA longer than the pentyl groups in TPeA (Fig. 5b). Br-bTBA and bbTBA bind ~5-fold and ~8-fold slower to the closed state than TPeA, respectively (comparing kon values in Table), consistent with the hypothesis that there is a steric barrier slowing the entry of the QA blockers into the channel vestibule in the closed state (Fig. 5a). The slower access rate suggests that the radius of the entryway to the closed state is comparable to the radii of the blockers56,57. The radii of the extended blocker structures (Fig. 5b) are between 7 and 11 Å but the effective hydrodynamic radii may be different. For example, the flexibility of alkyl chains may reduce the effective size of TPeA (to about ~4.5 Å)58. Thus, we can safely assume that the entrance to the closed pore is likely larger than 5 Å in radius, about twice the hydrated radius of K+ (~2.8 Å, Fig. 5b). We conclude that K+ should be able to readily enter the closed channel vestibule, indicating the absence of an intracellular bundle crossing gate for permeant ions.
Thus, the channel closure in zero Ca2+ that occurs at the selectivity filter is coupled to a conformational change such as a partial bundle crossing-like movement that fails to constrict the entryway enough to prevent ion and blocker access into the pore. We previously observed a similar effect for voltage-dependent closure of MthK37. These conformational changes may serve as an allosteric pathway, connecting the binding of Ca2+ at the intracellular gating ring to the selectivity filter gate at the extracellular side of the pore. Coupling between movements at the bundle crossing and the selectivity filter has also been shown to occur in other channels such as KcsA59,60 and KV channels61 during activation-coupled inactivation. However, in these channels the expansion of the intracellular entryway is coupled to a closing of the selectivity filter rather than an opening as proposed here for MthK and recently for K2P channels62.
Recent experimental and computational studies have explored how the size of the intracellular entryway may influence the conductance of K+ channels. In BK channels, two glutamate residues at the entryway were systematically mutated to vary the effective electrical resistance for K+ entry63. Using tryptophan substitutions at these sites, Geng et al. estimated that the radius of the entryway was reduced from ~9 Å for the wild-type to ~5 Å in the mutant. The narrow opening in the mutant BK (smaller than the size of TPeA) would be expected to slow the kinetics of block by large blockers, such as TPeA, with relatively little effect on K+ movement. Indeed, the outward K+ current in the mutant BK channel was reduced by only ~30%63. Furthermore, molecular dynamics simulations of a Shaker K+ channel64 and an open structure of KirBac3.131 suggest that K+ enters the pore cavity with essentially no energy barrier when the opening is comparable to the size of a hydrated K+, consistent with blocker studies of inward rectifier channels where QA block is significantly slowed for blockers larger than tetrapropylammonium (~4 Å radius)57. Hydrated K+ ions likely have rapid access into the closed MthK channel vestibule and are prevented from passing through the selectivity filter.
The state-dependence of TPeA block in MthK shows that the blocker on-rate for closed channels is ~140-fold slower than for open channels (Table). This fold change is similar to the state-dependent rates (~200-fold slower) for chemical modification by MTS reagents of a residue (A313C) deep inside the BK channel pore20. It appears that both MthK and BK channels allow probe accessibility deep into the non-conducting channel. Though the rate of modification by MTS reagents and binding of QA blockers reflect different reactions, the similarity in state-dependent rates suggests that similar conformational changes may occur at the intracellular entryway of these homologous channels. Supporting this conclusion, mutation of a residue deep inside the pore of MthK (A88D) results in a constitutive open state65, similar to what was observed using mutagenesis66,67 or MTS modification20 of nearby residues in the BK channel. MTS modification rates and gating perturbation by mutagenesis, however, may reflect state-dependent changes of a specific side chain, whereas blocker state-dependence reports on the overall access into the cavity and is likely less sensitive to the local environment of individual side chains.
Our experiments using the liposome-based flux assay uncovered properties of MthK block that contrasted with our previous results from single channel recording in planar lipid bilayers. First, the measured open-state affinity for both TPeA and bbTBA near 0 mV suggests the blockers bind to MthK in liposomes with a six-fold lower affinity than to MthK in planar bilayers. Second, the kinetics of block/unblock were even more sensitive to the experimental context; the TPeA kinetics were ~50-fold faster for MthK in liposomes as compared to bilayers37. Since the functional properties of ion channels, such as KcsA38 and BK68, can be regulated by lipid bilayer thickness, it is possible that the greater thickness of decane-containing planar lipid bilayers69 may alter the intracellular entrance to the open MthK channel, thereby inducing tighter blocker binding with slower on- and off-rates. Alternatively, the differences in lipid composition or the presence of Tl+, a modulator of BK channel gating70, may influence MthK gating or QA block. Despite the increased kinetics in liposomes, bbTBA for example still accesses open MthK ~5-fold slower than BK although faster than QA molecules were reported to access other K+ channels56,57. This suggests that MthK has a cavity similar in size to BK channels, albeit somewhat smaller19,22,50. Regardless of these differences, however, the mechanism of Ca2+ activation was not disrupted by changes in the lipid bilayer; MthK channels are completely closed in the absence of Ca2+ and activate with millimolar Ca2+ concentrations in both liposomes and bilayers.
In conclusion, the selectivity filter is the Ca2+-dependent gate for K+ permeation in MthK. This gating mechanism is markedly different from the gating mechanisms of KcsA and voltage-dependent channels, in which expansion of the intracellular entryway leads to inactivation, a closure of the selectivity filter. In MthK, however, Ca2+ binding elicits conformational changes of the gating ring and expansion of the intracellular pore entryway, which are coupled with opening of a selectivity filter gate. This mechanism has likely been conserved from prokaryotes to the eukaryotic Slo family of K+ channels, including BK.
Methods
MthK purification and reconstitution
MthK channels were expressed and purified as previously described37. Unless indicated otherwise, all reagents were obtained from Sigma-Aldrich and procedures were performed at 25 °C. N-(4-[benzoyl]benzyl)-N,N,N-tributylammonium (bbTBA) was from Spectra Group Limited Inc. and 4-bromobenzyltributylammonium bromide (Br-bTBA) was custom-made (The Chemistry Research Solution LLC). Molecular models of QA blockers were created using the program eLBOW40. Protein was purified in 100 mM KCl, 20 mM Tris (pH 7.6), with 5 mM N-decyl-β-D-maltopyranoside (DM, Anatrace), stored for one night at 4 °C, and run through a Superdex 200 gel filtration column (GE Healthcare) immediately before reconstitution into liposomes (large unilamellar vesicles). Protein reconstitution was similar to methods recently published38. 15 mg of 1,2-dioleoyl-sn-glycero-3-phosphocholine and 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-1-glycerol] (3:1 DOPC:POPG, Avanti Polar Lipids) were dried in a round-bottom flask under nitrogen gas and further dried overnight in a vacuum desiccator. Liposomes were prepared in 100 mM KNO3, 10 mM HEPES (pH 7.0), 25 mM 8-aminonaphthalene-1,3,6-trisulfonic acid, disodium salt (ANTS, Life Technologies) (reconstitution buffer). Lipids were solubilized in 1.5 mL reconstitution buffer by the addition of 35 mg CHAPS (Anatrace) and sonicated to clarity using a bath sonicator (Avanti Polar Lipids). Purified MthK protein was added to the solubilized lipids at a concentration of 30 μg/mg lipid and incubated for 30 minutes. Liposomes were formed by detergent removal using 1 g of SM-2 Biobeads (BioRad) added with an additional 1.5 mL of reconstitution buffer and rotated in a glass tube for 2 hours. The resulting liposome suspension was sonicated for 20 s in a bath sonicator (Branson) and extruded through a 100 nm pore polycarbonate filter (Avanti Mini-Extruder). Extravesicular ANTS was removed using PD-10 desalting columns (GE Healthcare) using 140 mM KNO3, 10 mM HEPES (pH 7.0) (flux buffer). For the contents-mixing assay (Supplementary Fig. 2), MthK liposomes were made as above, except that the internal solution contained either 25 mM ANTS or a membrane impermeant fluorescence quencher, 90 mM p-Xylene-Bis-Pyridinium bromide (DPX, Life Technologies). The ANTS-containing liposomes were mixed with DPX-containing liposomes for 10 ms before mixing with pH 11.7 buffer (to give a final pH of 8.5) containing either 0 Ca2+ (control, black symbols) or 17.2 mM Ca2+ (red symbols), and the ANTS fluorescence was recorded for 10 s. If liposome fusion had occurred, the ANTS- and DPX-containing solutions would mix, resulting in fluorescence quenching. As a control, the ANTS-loaded liposomes were mixed with 90 mM DPX in the presence of 1% Triton X-100, which permeabilizes the liposomes to measure the maximum quenching response.
Stopped-flow Tl+ flux assay
Tl+ quenches the fluorophore ANTS fluorescence and serves as a K+ mimic being able to permeate K+-conducting channels. Taking advantage of MthK permeability to Tl+, channel activity was monitored by the time-course of ANTS quenching (Fig. 2b). MthK activity was assayed by estimating the initial Tl+ flux rate following rapid mixing of ANTS-loaded liposomes with a Tl+-containing buffer using a SX-20 stopped-flow spectrofluorometer (Applied Photophysics Leatherhead, UK) following38,41 (see Supplementary Fig. 1 for diagrams of the mixing protocols described below). Because of the unavoidable heterogeneity in liposome sizes, the fluorescence quench time course cannot be described by a single exponential, and the results between 2 (instrumental dead time) and 100 ms were fit to stretched exponential functions (Eq. 1) and the rates of this fitted stretched exponential function at 2 ms, defined as the Tl+ flux rate in our measurements, were calculated from fit parameters (Eq. 2, derived in ref. 42)42 using MATLAB (MathWorks).
| (1) |
| (2) |
where Ffinal and Finitial are the final and initial fluorescence values, respectively. The empirical parameters τo and β are the time constant and the exponential-stretch parameter, respectively, and reflect the dispersity of liposome sizes as well as changes in channel activity occurring during the measurement.
In order to record the channel activation and block time-courses, two sequential solution mixings were performed, separated by a programmed delay (≥ 10 ms) that occurs in the delay loop (Fig. 2a, Supplementary Fig. 1). The solutions used were: Premix solution, 140 mM KNO3, 10 mM HEPES (pH 11.7); Control solution, 140 mM KNO3, 10 mM HEPES (pH 8.5); and Quench solution, 50 mM TlNO3, 94 mM KNO3, 10 mM HEPES (pH 8.5). Initially, MthK liposomes (in flux buffer, above) were mixed 1:1 with Premix solution to set the mixture pH to 8.5 in the delay loop. The sample was then mixed 1:1 with either Control solution or Quench solution in the optical cell for recording ANTS fluorescence. Channel was activated by the addition of 2x [Ca2+] to the Premix solution and 1x [Ca2+] to the Control and Quench solutions (to account for the dilution that occurs in each mixing reaction). Closed-state channel block was studied by the addition of 2x [blocker] to the Premix solution in the absence of Ca2+, 1x [blocker] and 34.4 mM Ca2+ to the Control or Quench solution. To measure activation or block on a time-scale faster than 10 ms, we introduced 2x [Ca2+] with or without 2x [blocker] in the Quench solution (with dead time of 2ms) instead of through the delay loop. We observed a small systematic dilution error during the first mixing, and nulled the discrepancy between additions of blocker during mix 1 versus mix 2 by the addition of 5% higher [blocker] in the zero-delay protocol. Because MthK requires Ca2+ to open, only channels reconstituted with the cytoplasmic gating ring facing the extra-liposomal solution contribute to the MthK activity measurements. Individual sample-experiment combinations were repeated 3–7 times, and Tl+ flux rate determinations were highly reproducible and averaged. Except where noted, at least three independent proteoliposome preparations were studied and the reported results denote mean ± standard deviation.
Data analysis and modeling
Average Tl+ flux rates were further analyzed using Origin 6.0 (OriginLab). All rates were internally normalized to the maximum activity from experimental controls. The apparent MthK activation rate at 2 mM Ca2+ was estimated by fitting the time course of the Tl+ flux rates to a single exponential:
| (3) |
where t is delay time between solution mixing, k(t) is the Tl+ flux rate at time t, and τa is the apparent time constant for channel activation.
To estimate MthK activity in nominally 0 Ca2+ (no Ca2+ buffers were used), we compared the Tl+ influx rates observed with liposomes in the absence of Ca2+ to the Tl+ influx rate observed in 17.2 mM Ca2+. Tl+ flux rates are very slow in 0 Ca2+, and we could not employ a stretched exponential fit in this case (Eq. 1). Instead, we fit the data between 2 and 100 ms to a linear function (Eq. 4), which determined the geometric slope of the fluorescence data, m, at 0 ms, defined as the activity measurement for these very slow quench traces. In order to normalize the low activity, slope m, to the maximal activity in 17.2 mM Ca2+, we obtained an estimation of the maximal geometric slope at 0 ms by fitting the high Ca2+ fluorescence quench curves to the modified stretched exponential function (Eq. 5, derived in ref. 42)42. We used here Eq. 5 and not Eq. 1 (which was used to analyze channel activity for all other experiments) because the stretched exponential function described in Eq. 1 does not have a finite slope at 0 ms (Eq. 4 is a Taylor approximation of Eq. 5 for the initial Tl+ flux). The slope of Eq. 5 at 0 ms (Eq. 6) was calculated from best-fit parameters to estimate the control MthK activity rate, mcontrol.
| (4) |
| (5) |
| (6) |
To distinguish between slow Tl+ entry due to non-specific movement of TlNO3 across liposome membranes and specific movement of Tl+ through MthK channels in the absence of Ca2+, we recorded in immediate succession the slow fluorescence decay in the absence and presence of saturating channel blocker (100 μM TPeA), yielding two activity estimates mtotal and mlipid, respectively. Ion movement through the mostly closed MthK channels, mchannel, then was obtained by subtracting the Tl+ flux across the liposomal membranes from the total Tl+ flux (Eq. 7) and the estimated apparent MthK open probability in the absence of Ca2+, Poap(0 Ca2+), was estimated by normalizing to the control activity in high Ca2+ (Eq. 8).
| (7) |
| (8) |
These measurements were performed 49 times (employing two independent liposome preparations) and the estimates of Poap(0 Ca2+) were plotted in a histogram and fitted to a Gaussian distribution (Eq. 9).
| (9) |
where A is the amplitude, xc is the center of the distribution, and σ is the standard deviation.
Blocker equilibration time courses were fit with a single exponential decay:
| (10) |
where kfinal is the final Tl+ flux rate (after blocker equilibration) and τeq is the apparent blocker equilibration time constant.
In order to extract the blocker (B) affinity and kinetics, blocker equilibration to either open or closed channels (MthK), is modeled as a bimolecular reaction:
Because the blocker concentration is much larger than the channel concentration, the fraction of channels without blocker bound decays exponentially, with an equilibration time constant (Eq. 10) determined by the blocker kinetics. The steady-state activity is determined by the blocker dissociation constant (Eq. 11):
| (11) |
where KDclosed and konclosed are the closed-state blocker dissociation and on-rate constants, respectively, and [B] is the blocker concentration. Equilibration to the open state follows the same expression, using the parameters KDopen and konopen, the open-state blocker dissociation and on-rate constant, respectively.
Blocker dose-response curves were fit with the Hill equation:
| (12) |
where KDap is the apparent blocker dissociation constant, [B] the blocker concentration, and nH the Hill coefficient.
Gramicidin Tl+ flux assay
Gramicidin (gA) was reconstituted into large unilamellar vesicles using 3:1 DOPC:POPG and DC22:1PC lipids using published protocols41 for the experiments shown in Supplementary Fig. 2b to rule out QA blockers as lipid bilayer modifiers41 and also Ca2+-induced liposome fusion as a control for Ca2+-induced desensitization of MthK (Supplementary Note). Fluorescence quench rates were measured as described above after exposure to Ca2+ or blockers for various time intervals. Small decreases in flux in the presence of Ca2+ are likely due to Ca2+ block of gA channels43.
Single channel analysis using planar lipid bilayers
Single MthK channels were recorded using Axopatch 200A (Molecular Devices) in planar lipid-decane bilayers consisting of 3:1 POPE:POPG lipids (Avanti Polar Lipids), as previously described37. For the experiments in Supplementary Fig. 4, channels were recorded in symmetric 200 mM K+ (190 mM KCl, 10 mM KOH), 10 mM HEPES (pH 8.5/HCl) and activated by trans 5 mM Ca2+ with and without 0.5 μM Br-bTBA (also in trans) at − 100 mV, − 25 mV, and +25 mV. Analysis was done using QuB (www.qub.buffalo.edu) to fit closed and open dwell time distributions with an open-channel block scheme (see Supplementary Fig. 4), as described37. Transitions between open (O) and open-blocked (OB) states were used to estimate the open state dissociation constant Kdopen and the voltage dependence, Kdopen(V), was fit with a K+-coupling model, Eq. 13 (see Posson et al.37):
| (13) |
where KDlow is the maximal blocker affinity, KDV is an affinity amplitude for the exponential term and z is the valence for blocker-K+ coupling.
Supplementary Material
Acknowledgments
We thank C. Boiteux for providing a coordinate file for a hydrated K+ and D. Kim and A. Accardi for critically reading the manuscript. This work was supported by a NRSA postdoctoral fellowship from the National Institutes of Health (F32GM087865) to D.J.P., National Institutes of Health grants R01GM021342 to O.S.A and R01GM088352 to C.M.N., and an Irma T. Hirschl Career Scientist Award to C.M.N.
Footnotes
Author Contributions
All authors designed the research; D.J.P. and R.R. acquired and analyzed the experimental data; All authors wrote the paper.
Competing financial interests
The authors declare no competing financial interests.
References
- 1.Berridge MJ, Lipp P, Bootman MD. The versatility and universality of calcium signalling. Nature reviews. Molecular cell biology. 2000;1:11–21. doi: 10.1038/35036035. [DOI] [PubMed] [Google Scholar]
- 2.Clapham DE. Calcium signaling. Cell. 2007;131:1047–1058. doi: 10.1016/j.cell.2007.11.028. [DOI] [PubMed] [Google Scholar]
- 3.Yang H, Zhang G, Cui J. BK channels: multiple sensors, one activation gate. Frontiers in physiology. 2015;6:29. doi: 10.3389/fphys.2015.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Salkoff L, Butler A, Ferreira G, Santi C, Wei A. High-conductance potassium channels of the SLO family. Nature reviews. Neuroscience. 2006;7:921–931. doi: 10.1038/nrn1992. [DOI] [PubMed] [Google Scholar]
- 5.Jiang Y, et al. Crystal structure and mechanism of a calcium-gated potassium channel. Nature. 2002;417:515–522. doi: 10.1038/417515a. [DOI] [PubMed] [Google Scholar]
- 6.Zadek B, Nimigean CM. Calcium-dependent gating of MthK, a prokaryotic potassium channel. The Journal of general physiology. 2006;127:673–685. doi: 10.1085/jgp.200609534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li Y, Berke I, Chen L, Jiang Y. Gating and inward rectifying properties of the MthK K+ channel with and without the gating ring. The Journal of general physiology. 2007;129:109–120. doi: 10.1085/jgp.200609655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pau VP, Abarca-Heidemann K, Rothberg BS. Allosteric mechanism of Ca2+ activation and H+-inhibited gating of the MthK K+ channel. The Journal of general physiology. 2010;135:509–526. doi: 10.1085/jgp.200910387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ye S, Li Y, Chen L, Jiang Y. Crystal structures of a ligand-free MthK gating ring: insights into the ligand gating mechanism of K+ channels. Cell. 2006;126:1161–1173. doi: 10.1016/j.cell.2006.08.029. [DOI] [PubMed] [Google Scholar]
- 10.Yuan P, Leonetti MD, Pico AR, Hsiung Y, MacKinnon R. Structure of the human BK channel Ca2+-activation apparatus at 3.0 A resolution. Science. 2010;329:182–186. doi: 10.1126/science.1190414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wu Y, Yang Y, Ye S, Jiang Y. Structure of the gating ring from the human large-conductance Ca(2+)-gated K(+) channel. Nature. 2010;466:393–397. doi: 10.1038/nature09252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yuan P, Leonetti MD, Hsiung Y, MacKinnon R. Open structure of the Ca2+ gating ring in the high-conductance Ca2+-activated K+ channel. Nature. 2012;481:94–97. doi: 10.1038/nature10670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ye S, Li Y, Jiang Y. Novel insights into K+ selectivity from high-resolution structures of an open K+ channel pore. Nature structural & molecular biology. 2010;17:1019–1023. doi: 10.1038/nsmb.1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yellen G. The moving parts of voltage-gated ion channels. Quarterly reviews of biophysics. 1998;31:239–295. doi: 10.1017/s0033583598003448. [DOI] [PubMed] [Google Scholar]
- 15.Armstrong CM. Interaction of tetraethylammonium ion derivatives with the potassium channels of giant axons. The Journal of general physiology. 1971;58:413–437. doi: 10.1085/jgp.58.4.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhou M, Morais-Cabral JH, Mann S, MacKinnon R. Potassium channel receptor site for the inactivation gate and quaternary amine inhibitors. Nature. 2001;411:657–661. doi: 10.1038/35079500. [DOI] [PubMed] [Google Scholar]
- 17.Xie C, Zhen XG, Yang J. Localization of the activation gate of a voltage-gated Ca2+ channel. The Journal of general physiology. 2005;126:205–212. doi: 10.1085/jgp.200509293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Oelstrom K, Goldschen-Ohm MP, Holmgren M, Chanda B. Evolutionarily conserved intracellular gate of voltage-dependent sodium channels. Nature communications. 2014;5:3420. doi: 10.1038/ncomms4420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wilkens CM, Aldrich RW. State-independent block of BK channels by an intracellular quaternary ammonium. The Journal of general physiology. 2006;128:347–364. doi: 10.1085/jgp.200609579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhou Y, Xia XM, Lingle CJ. Cysteine scanning and modification reveal major differences between BK channels and Kv channels in the inner pore region. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:12161–12166. doi: 10.1073/pnas.1104150108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thompson J, Begenisich T. Selectivity filter gating in large-conductance Ca(2+)-activated K+ channels. The Journal of general physiology. 2012;139:235–244. doi: 10.1085/jgp.201110748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhou Y, Xia XM, Lingle CJ. Cadmium-cysteine coordination in the BK inner pore region and its structural and functional implications. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:5237–5242. doi: 10.1073/pnas.1500953112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Flynn GE, Zagotta WN. Conformational changes in S6 coupled to the opening of cyclic nucleotide-gated channels. Neuron. 2001;30:689–698. doi: 10.1016/s0896-6273(01)00324-5. [DOI] [PubMed] [Google Scholar]
- 24.Bruening-Wright A, Schumacher MA, Adelman JP, Maylie J. Localization of the activation gate for small conductance Ca2+-activated K+ channels. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2002;22:6499–6506. doi: 10.1523/JNEUROSCI.22-15-06499.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Proks P, Antcliff JF, Ashcroft FM. The ligand-sensitive gate of a potassium channel lies close to the selectivity filter. EMBO reports. 2003;4:70–75. doi: 10.1038/sj.embor.embor708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Contreras JE, Holmgren M. Access of quaternary ammonium blockers to the internal pore of cyclic nucleotide-gated channels: implications for the location of the gate. The Journal of general physiology. 2006;127:481–494. doi: 10.1085/jgp.200509440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rapedius M, et al. State-independent intracellular access of quaternary ammonium blockers to the pore of TREK-1. Channels (Austin) 2012;6:473–478. doi: 10.4161/chan.22153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Garg P, Gardner A, Garg V, Sanguinetti MC. Structural basis of ion permeation gating in Slo2.1 K+ channels. The Journal of general physiology. 2013;142:523–542. doi: 10.1085/jgp.201311064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution. Nature. 2001;414:43–48. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 30.Cuello LG, Jogini V, Cortes DM, Perozo E. Structural mechanism of C-type inactivation in K(+) channels. Nature. 2010;466:203–208. doi: 10.1038/nature09153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bavro VN, et al. Structure of a KirBac potassium channel with an open bundle crossing indicates a mechanism of channel gating. Nature structural & molecular biology. 2012;19:158–163. doi: 10.1038/nsmb.2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Clarke OB, et al. Domain reorientation and rotation of an intracellular assembly regulate conduction in Kir potassium channels. Cell. 2010;141:1018–1029. doi: 10.1016/j.cell.2010.05.003. [DOI] [PubMed] [Google Scholar]
- 33.Alam A, Jiang Y. High-resolution structure of the open NaK channel. Nature structural & molecular biology. 2009;16:30–34. doi: 10.1038/nsmb.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McCusker EC, et al. Structure of a bacterial voltage-gated sodium channel pore reveals mechanisms of opening and closing. Nature communications. 2012;3:1102. doi: 10.1038/ncomms2077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Payandeh J, Scheuer T, Zheng N, Catterall WA. The crystal structure of a voltage-gated sodium channel. Nature. 2011;475:353–358. doi: 10.1038/nature10238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jiang Y, et al. The open pore conformation of potassium channels. Nature. 2002;417:523–526. doi: 10.1038/417523a. [DOI] [PubMed] [Google Scholar]
- 37.Posson DJ, McCoy JG, Nimigean CM. The voltage-dependent gate in MthK potassium channels is located at the selectivity filter. Nature structural & molecular biology. 2013;20:159–166. doi: 10.1038/nsmb.2473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rusinova R, Kim DM, Nimigean CM, Andersen OS. Regulation of ion channel function by the host lipid bilayer examined by a stopped-flow spectrofluorometric assay. Biophysical journal. 2014;106:1070–1078. doi: 10.1016/j.bpj.2014.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.McCoy JG, et al. A KcsA/MloK1 chimeric ion channel has lipid-dependent ligand-binding energetics. The Journal of biological chemistry. 2014;289:9535–9546. doi: 10.1074/jbc.M113.543389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Moriarty NW, Grosse-Kunstleve RW, Adams PD. electronic Ligand Builder and Optimization Workbench (eLBOW): a tool for ligand coordinate and restraint generation. Acta crystallographica. Section D, Biological crystallography. 2009;65:1074–1080. doi: 10.1107/S0907444909029436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ingolfsson HI, Andersen OS. Screening for small molecules’ bilayer-modifying potential using a gramicidin-based fluorescence assay. Assay and drug development technologies. 2010;8:427–436. doi: 10.1089/adt.2009.0250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Berberan-Santos MN, Bodunov EN, Valeur B. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential) Chem Phys. 2005;315:171–182. [Google Scholar]
- 43.Bamberg E, Apell HJ, Alpes H. Structure of the gramicidin A channel: discrimination between the piL, D and the beta helix by electrical measurements with lipid bilayer membranes. Proceedings of the National Academy of Sciences of the United States of America. 1977;74:2402–2406. doi: 10.1073/pnas.74.6.2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Choi KL, Mossman C, Aube J, Yellen G. The internal quaternary ammonium receptor site of Shaker potassium channels. Neuron. 1993;10:533–541. doi: 10.1016/0896-6273(93)90340-w. [DOI] [PubMed] [Google Scholar]
- 45.Piechotta PL, et al. The pore structure and gating mechanism of K2P channels. The EMBO journal. 2011;30:3607–3619. doi: 10.1038/emboj.2011.268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Holmgren M, Smith PL, Yellen G. Trapping of organic blockers by closing of voltage-dependent K+ channels: evidence for a trap door mechanism of activation gating. The Journal of general physiology. 1997;109:527–535. doi: 10.1085/jgp.109.5.527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kuo MM, Maslennikov I, Molden B, Choe S. The desensitization gating of the MthK K+ channel is governed by its cytoplasmic amino terminus. PLoS biology. 2008;6:e223. doi: 10.1371/journal.pbio.0060223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vergara C, Latorre R. Kinetics of Ca2+-activated K+ channels from rabbit muscle incorporated into planar bilayers. Evidence for a Ca2+ and Ba2+ blockade. The Journal of general physiology. 1983;82:543–568. doi: 10.1085/jgp.82.4.543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Miller C, Latorre R, Reisin I. Coupling of voltage-dependent gating and Ba++ block in the high-conductance, Ca++-activated K+ channel. The Journal of general physiology. 1987;90:427–449. doi: 10.1085/jgp.90.3.427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li W, Aldrich RW. Unique inner pore properties of BK channels revealed by quaternary ammonium block. The Journal of general physiology. 2004;124:43–57. doi: 10.1085/jgp.200409067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li W, Aldrich RW. State-dependent block of BK channels by synthesized shaker ball peptides. The Journal of general physiology. 2006;128:423–441. doi: 10.1085/jgp.200609521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tang QY, Zeng XH, Lingle CJ. Closed-channel block of BK potassium channels by bbTBA requires partial activation. The Journal of general physiology. 2009;134:409–436. doi: 10.1085/jgp.200910251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhou Y, Lingle CJ. Paxilline inhibits BK channels by an almost exclusively closed-channel block mechanism. The Journal of general physiology. 2014;144:415–440. doi: 10.1085/jgp.201411259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Liu Y, Holmgren M, Jurman ME, Yellen G. Gated access to the pore of a voltage-dependent K+ channel. Neuron. 1997;19:175–184. doi: 10.1016/s0896-6273(00)80357-8. [DOI] [PubMed] [Google Scholar]
- 55.Cox DH, Hoshi T. Where’s the gate? Gating in the deep pore of the BK(Ca) channel. The Journal of general physiology. 2011;138:133–136. doi: 10.1085/jgp.201110681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.French RJ, Shoukimas JJ. Blockage of squid axon potassium conductance by internal tetra-N-alkylammonium ions of various sizes. Biophysical journal. 1981;34:271–291. doi: 10.1016/S0006-3495(81)84849-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Guo D, Lu Z. Kinetics of inward-rectifier K+ channel block by quaternary alkylammonium ions. dimension and properties of the inner pore. The Journal of general physiology. 2001;117:395–406. doi: 10.1085/jgp.117.5.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mason SA, et al. The contribution of hydrophobic residues in the pore-forming region of the ryanodine receptor channel to block by large tetraalkylammonium cations and Shaker B inactivation peptides. The Journal of general physiology. 2012;140:325–339. doi: 10.1085/jgp.201210851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Cuello LG, et al. Structural basis for the coupling between activation and inactivation gates in K(+) channels. Nature. 2010;466:272–275. doi: 10.1038/nature09136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wylie BJ, Bhate MP, McDermott AE. Transmembrane allosteric coupling of the gates in a potassium channel. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:185–190. doi: 10.1073/pnas.1319577110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Panyi G, Deutsch C. Cross talk between activation and slow inactivation gates of Shaker potassium channels. The Journal of general physiology. 2006;128:547–559. doi: 10.1085/jgp.200609644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dong YY, et al. K2P channel gating mechanisms revealed by structures of TREK-2 and a complex with Prozac. Science. 2015;347:1256–1259. doi: 10.1126/science.1261512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Geng Y, Niu X, Magleby KL. Low resistance, large dimension entrance to the inner cavity of BK channels determined by changing side-chain volume. The Journal of general physiology. 2011;137:533–548. doi: 10.1085/jgp.201110616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Fowler PW, Sansom MS. The pore of voltage-gated potassium ion channels is strained when closed. Nature communications. 2013;4:1872. doi: 10.1038/ncomms2858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Shi N, Zeng W, Ye S, Li Y, Jiang Y. Crucial points within the pore as determinants of K(+) channel conductance and gating. Journal of molecular biology. 2011;411:27–35. doi: 10.1016/j.jmb.2011.04.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chen X, Aldrich RW. Charge substitution for a deep-pore residue reveals structural dynamics during BK channel gating. The Journal of general physiology. 2011;138:137–154. doi: 10.1085/jgp.201110632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Chen X, Yan J, Aldrich RW. BK channel opening involves side-chain reorientation of multiple deep-pore residues. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:E79–88. doi: 10.1073/pnas.1321697111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Yuan C, O’Connell RJ, Jacob RF, Mason RP, Treistman SN. Regulation of the gating of BKCa channel by lipid bilayer thickness. The Journal of biological chemistry. 2007;282:7276–7286. doi: 10.1074/jbc.M607593200. [DOI] [PubMed] [Google Scholar]
- 69.Fettiplace R, Andrews DM, Haydon DA. The thickness, composition and structure of some lipid bilayers and natural membranes. The Journal of membrane biology. 1971;5:277–296. doi: 10.1007/BF01870555. [DOI] [PubMed] [Google Scholar]
- 70.Piskorowski RA, Aldrich RW. Relationship between pore occupancy and gating in BK potassium channels. The Journal of general physiology. 2006;127:557–576. doi: 10.1085/jgp.200509482. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.