Abstract
One of the major findings from multi-modal neuroimaging studies in the past decade is that the human brain is anatomically and functionally organized into large-scale networks. In resting state fMRI (rs-fMRI), spatial patterns emerge when temporal correlations between various brain regions are tallied, evidencing networks of ongoing intercortical cooperation. However, the dynamic structure governing the brain’s spontaneous activity is far less understood due to the short and noisy nature of the rs-fMRI signal. Here we develop a wavelet-based regularity analysis based on noise estimation capabilities of the wavelet transform to measure recurrent temporal pattern stability within the rs-fMRI signal across multiple temporal scales. The method consists of performing a stationary wavelet transform (SWT) to preserve signal structure, followed by construction of “lagged” subsequences to adjust for correlated features, and finally the calculation of sample entropy across wavelet scales based on an “objective” estimate of noise level at each scale. We found that the brain’s default mode network (DMN) areas manifest a higher level of irregularity in rs-fMRI time series than rest of the brain. In 25 aged subjects with mild cognitive impairment and 25 matched healthy controls, wavelet based regularity analysis showed improved sensitivity in detecting changes in the regularity of rs-fMRI signals between the two groups within the DMN and executive control networks, compared to standard multiscale entropy analysis. Wavelet based regularity analysis based on noise estimation capabilities of the wavelet transform is a promising technique to characterize the dynamic structure of rs-fMRI as well as other biological signals.
Keywords: Entropy, Networks, Multiscale, Complexity, Dynamics
Introduction
Spontaneous neuronal activity patterns occur over a multitude of spatial and temporal scales and intricately relate to how the brain encodes and stores information (Logothetis et al. 1995; Ainsworth et al. 2012). Recurring spatial patterns observed using functional MRI (fMRI) suggested the existence of intercortical networks spanning the brain (Biswal et al. 1995; Lowe et al. 1998). This evidenced the brain dynamically employing multiple regions of the brain, even structurally distant ones, in parallel during both task and rest conditions (Raichle et al. 2001; Beckmann et al. 2005; Damoiseaux et al. 2006). In particular, the functional connectivity of the brain at rest has drawn considerable interest from the observance that many cortical regions involved in higher level processing (e.g. learning, decision making, and memory) are integrated into several resting-state networks (RSN) (Greicius et al. 2004; Seeley et al. 2007). However, the spatial pattern announcing a network’s presence is typically constructed from time-averaged correlations in the fMRI signal; this paints a static picture of the brain that reveals little about the temporal structure and the ensuing dynamics. In this paper, we investigate the repetitive nature of the RSN spatial patterns by evaluating the regularity of the resting-state fMRI (rs-fMRI) signal, i.e. the similarity of repeating temporal patterns to previous realizations.
The observed rs-fMRI time series signal represents intrinsic blood oxygen level dependent (BOLD) activity that is directly correlated with neuronal activation (Logothetis et al. 2001). Evidence of spontaneous BOLD fluctuations suggests stochastic processes govern neuronal activity. The spectrum of such a process can be estimated from the time-series and describes its second central moment. The rs-fMRI spectrum exhibits a power-law shape at low frequencies f−β for f ≤ 0.2 Hz) (He et al. 2010). Power-law behaviors are ubiquitous natural phenomena that typically indicating an underlying complexity. Famously, they arise from scale-free organization and are the hallmark of ‘emergent’ systems described by self-organized criticality (Bak et al. 1987). In the brain, they lay a general dynamic foundation describing how neurons can rapidly reorganize to communicate over both small and large distances with equal ease (Chialvo, 2010). However, a given spectral shape describes a variety of stochastic processes, and does not determine the temporal dynamics.
A powerful approach to describing temporal dynamics involves characterizing the entropy, a measure of the average uncertainty associated with predicting future values or sequence of values. In particular, scale-free measures based on predicting future values, given some prior knowledge, accurately describe the nonlinear behavior of chaotic systems (Grassberger and Procaccia, 1983; Eckmann and Ruelle, 1985). However, these scale-free measures rely on long, (largely) noise free signals that are not typically obtained in measurements of biological systems (e.g. rs-fMRI). Efforts to understand the complexity of brief physiological signals in the presence of noise led to practical measures based on pattern recurrence within a single scale. In a seminal study, Pincus introduced approximate entropy (ApEn) as a regularity measure of closely repeating signal patterns (Pincus, 1991). In words, ApEn and its variants (e.g. sample entropy (Richman and Moorman, 2000)) measure the (negative logarithmic) likelihood of m+1-length patterns closely repeating (i.e. separated by less than a threshold r), provided they were close for the first m points. Higher values implicate increasingly unpredictable intrinsic behavior, in the absence of noise. However, noise is also characterized by unpredictability.
Subsequently, multiscale entropy (MSE) analysis was developed to differentiate complex processes from random fluctuations by exploiting dissimilarities between the signal and noise across multiple time scales (Costa et al. 2002). In MSE analysis, the entropy of a signal is calculated across multiple, coarse-grained temporal scales obtained with a series moving average filters. Systems with a f−1 power spectrum exhibit constant entropy over various time scales, whereas random noise shows a marked decrease in entropy at longer time scales (as random fluctuations are smoothed out). Recently, using MSE analysis, we showed gray matter rs-fMRI signal fluctuations to be highly irregular with a close resemblance to a f−1-like signal (Smith et al. 2014); highlighting the multiscale approach to rs-fMRI signal analysis over single scale measures with greater noise sensitivity (Liu et al. 2012; Wang et al. 2014). However, MSE analysis dramatically reduces signal length at each scale, reducing statistical power, and inextricably ties the resulting entropy to changes in SNR across scales (Nikulin and Brismar, 2004).
In this report, we aim to characterize the repetitive nature of rs-fMRI temporal structure across multiple scales with a maximal distinction from the effects of noise. To this end, we describe a wavelet-based approach that provides significant improvement to the characterization of rs-fMRI signal regularity in the following ways. First, in addition to any nonlinear structure, the presence of intrinsic nonstationary processes, i.e. how variable the moments of the signal distribution are over time, within the rs-fMRI signal (Chang and Glover, 2010) will also contribute to the measured regularity. This nonstationary structure is preserved with high fidelity across multiple scales using the stationary wavelet transform (SWT). Second, the voxel noise level is estimated using wavelet-based de-noising schemes (Donoho and Johnstone, 1994; Donoho, 1995; Chang et al. 2000) and used to tune sensitivity to the irregularity of the intrinsic signal.
Theory
A step-by-step outline of the wavelet-based regularity algorithm is given in Table I, and a visual depiction is shown in figure 1. A brief description is given here. First, we perform a voxelwise SWT decomposition of the rs-fMRI signal in to J sequences, where the maximum scale depends on the signal length, and the sampling rate. Second, we estimate the voxel noise level from its D1 scale using a data driven approach. Third, at each of the remaining voxel sequences D2-DJ, we construct a set of time-delayed subsequences. Lastly, for each sequence D2-DJ, we measure the average regularity with which m+1-length subsequences recur within the estimated voxel noise level.
Table I.
Wavelet-based Regularity analysis algorithm.
| Algorithm steps | |
|---|---|
For each voxel time series:
| |
For each sequence Dj for j = 2, …, J:
|
Figure 1.
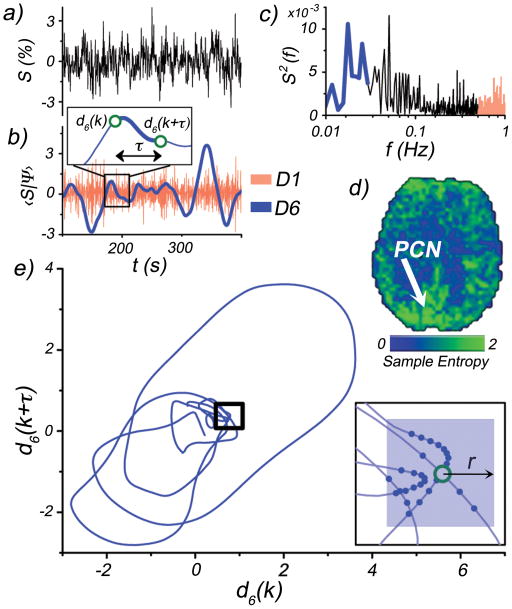
A depiction of the wavelet-based regularity analysis. a) A representative rs-fMRI signal selected from voxel located within the precuneus (PCN) of a representative subject (MNI coordinates: −10, −52, 26), b) Stationary wavelet transform of rs-fMRI signal. Only two scales shown for illustrative purposes: D1 (red) and D6 (blue). The intensities of the D1 scale fluctuations are used to estimate the noise level. Inset depicts an example of an m=2 subsequence construction. The k-th subsequence (d(k), d(k+τ)) is formed from time points separated by a time delay τ (first minimum in the auto-mutual information function). This is performed for each scale Dj. c) Power spectrum of rs-fMRI signal. High (red) and low (blue) frequency bands show where D1 and D6 wavelet scales exhibit sensitivity, respectively. d) Sample Entropy map of the D6 scale. Arrow indicates PCN location of rs-fMRI signal. e) Phase space plot of subsequences (m = 2) taken from D6 scale time course. Inset: outlined region magnified, with solid blue points indicating recurrent patterns within r, of the k-th subsequence (open green circle).
Wavelet Decomposition
We seek to investigate the dynamic structure of the intrinsic BOLD signal through decomposition of the observed rs-fMRI signal into multiple sequences describing distinct temporal scales. Spontaneous BOLD activity can be modeled from a stochastic process where the measured BOLD time series represents the output from an ordered sequence of discrete random variables {X(ti), i =1, …, N}. Recent work shows BOLD activity to be locally nonstationary (Chang and Glover, 2010), meaning the realization of a single random variable, i.e. the measured value at a particular point in time, is determined according to a time-dependent marginal probability mass function, p(x, t) = Pr{X(ti) = x}. This intrinsically nonstationary structure contains important information about the dynamics of the BOLD signal. Wavelet-based analyses are built upon a local frequency representation that makes them ideally suited for nonstationary systems. Local decomposition presents a major advantage over conventional methods such as Fourier analyses that spread local information across the entire signal. A second advantage of wavelet decomposition arises from its noise estimation capabilities. The observed rs-fMRI signal is contaminated by additive Gaussian noise:
| (1) |
where ε(i) are independent and identically distributed (iid) with N(0, σε). Wavelet thresholding procedures estimate a threshold based on σε that can be used for local noise adaptation.
The SWT is a common tool in pattern analysis due to its preservation of signal length and temporal structures (Nason and Silverman, 1995). Its primary advantage over the discrete wavelet transform (DWT) lies in its shift invariance, meaning temporal translations of the signal yield the same set of coefficients. Specifically, the DWT critically subsamples the total number of wavelet coefficients at each scale, capturing only the minimal amount of information to reconstruct the original signal. However, small translations of the original signal can lead to large changes in the wavelet coefficients and obscure local features that are not precisely aligned with the DWT subsampling lattice (Strickland, 1997; Olivo-Marin, 2002; Starck et al., 2007; Hasan and Anbarjafari, 2011). The SWT is performed by convolving y with a set of orthogonal low pass (scaling) and high pass (wavelet) functions: ϕj(k) and ψj(k), respectively. These functio ns are formed through dilations and translations of a ‘father’, ϕ, and ‘mother’, ψ, wavelet (Mallat, 1989):
| (2a) |
| (2b) |
where the level, j, and translation, k, indices parameterize the frequency subband and temporal window, respectively. The resulting coefficients, aj(k) and dj(k), represent temporally local energy densities of a given subband:
| (3a) |
| (3b) |
where ωn = (2 * TR)−1 is the highest sampled frequency. The subbands form a dyadic set with the lowest scale D1 arising from the highest half of the full frequency range. Overall, a J-level decomposition yields J band-pass sequences {D1, …, DJ} and a single low-pass sequence AJ:
| (4a) |
| (4b) |
where J is the coarsest selected level, with a temporal resolution ~2J, containing two subbands, DJ and AJ. The band-pass scales Dj are ideal for analysis of the non-stationary rs-fMRI signal due to their local time-frequency characteristic. The AJ sequence is a low-pass filtered version of the original signal that is excluded. This is a complementary approach to the typical procedure in rs-fMRI analysis where the Fourier transform is used to band-pass the signal within a specified range.
Experimental and theoretical work strongly indicates the rs-fMRI signal is described by a f−β distribution (Bullmore et al. 2003; He et al. 2010). A subsampled (by 2j) set of f−β wavelet coefficients is normally distributed and strongly stationary within each scale (Wornell, 1993). As in equation 1, the band-pass coefficients can be expressed as a sum:
| (5) |
where the noise coefficients, εj(k), are also iid and normally distributed, N(0, σε). The set of coefficients, {Xj}, represent the filtered BOLD signal within the Dj scale with:
| (6) |
where is the total variance of the subsampled Dj sequence.
Subsequence Construction
The presence of serial correlated behavior within a signal naturally inflates subsequence recurrence (i.e. neighboring subsequences remain close), and decreases entropy. Intrinsic correlations in rs-fMRI are induced by, e.g. cardiac and respiratory fluctuations (Friston et al. 2000; Smith et al. 2001), and are preserved by the SWT. We use a time delay approach employed in scale-free measures of chaotic systems (Grassberger and Procaccia, 1983; Eckmann and Ruelle, 1985) to construct strongly decorrelated m-length subsequences. The q-th subsequence is written as:
| (7) |
where τ is the delay. In this report we use the auto-mutual information function (Fraser, 1986) to estimate the total correlation (not just linear) present between coefficients within each sequence Dj separately. The degree of correlation is minimized using a time delay τ equal to the function’s first minimum. The resulting number of patterns is then Nm = N − (m − 1)τ, where N is the signal length and τ is scale dependent.
Regularity
We are interested in the regularity of the intrinsic signal Xj within each scale Dj. We measure regularity using the sample entropy (HS):
| (8) |
where Cm(r) is the correlation sum (Eckmann and Ruelle, 1985). The correlation sum measures the recurrence probability of m-length subsequences within a tolerance distance r:
| (9) |
where is the distance between and , two m-length subsequences, and Θ is the Heaviside function. Typically r is set as a percentage of the signal standard deviation, r = r0σDj, where r0 is adjusted such that r is greater than most of the noise. However, this conventional approach results in high HS values for both noisy signals, and intrinsically irregular signals.
In this report, we seek to estimate the noise level directly from the voxel time series and obtain an approximate measure of . From equations 5 and 7 the relationship between and the difference between observed signal subsequences, , is:
| (10) |
Here is the difference between Dj subsequences of noise whose components are distributed such that:
| (11) |
In signals with a majority of the power concentrated at low frequencies the noise level, σε, can be approximated from the median absolute deviation of high frequency scale (D1) coefficients (Donoho and Johnstone, 1994):
| (12) |
Note that σε is calculated using a subsampled (by 2) D1 sequence to reduce any residual correlation between d1 coefficients. Most of the power in rs-fMRI signals is focused below 0.1 Hz. This corresponds to a maximum sampling time TRmax = 2.5 s, such that the D1 scale corresponds to the frequency range 0.1 – 0.2 Hz. While longer sampling times will result in an overestimation of the noise level (the D1 scale will dip below 0.1 Hz), the median absolute deviation is a robust measure that mitigates signal bias, compared to the standard deviation. From equation 6, the distribution of the components for can be similarly estimated by:
| (13) |
We approximate using a soft wavelet thresholding (Antonini et al. 1992) of the observed subsequence differences, :
| (14) |
where (a)+ represents the maximum between the argument a and zero, and t is a noise level threshold to be estimated. The effect of equation 16 is to reduce each coordinate of towards zero by t. Several thresholds have been developed and employed in signal denoising schemes (Donoho and Johnstone, 1994; Donoho, 1995). The data driven BayesShrink approach is suited for signals with information situated across several scales (Chang et al. 2000). BayesShrink defines a scale-dependent threshold that minimizes the Bayes risk of the estimate, :
| (15) |
In this report we calculate the distance between subsequences using the maximum norm, ||a||∞ = max(|a(1)|, …, |a(m)|), which returns the absolute value of the component with the largest magnitude. The estimated distance between the intrinsic subsequences is then given by:
| (16) |
The overall result of equations 14–16 is to find the components of two subsequences with the largest absolute distance between them, and reduce that distance by a factor t that depends on both the noise and signal levels. This threshold optimally (Bayes risk) retains information pertaining to the intrinsic signal, while suppressing the random effects of noise. Further, t will quickly converge zero as SNR increases above σxj/σε = 1. Substituting equation 16 into equation 9 we obtain an upper estimate of Cm:
| (17) |
The (a)+ condition is dropped since the Heaviside function equals one for arguments greater than zero. This allows the t to be folded into the definition of threshold distance, r, which is defined to be (and ) are inserted into equation 8 to obtain an estimate to HS:
| (18) |
In general we find equation 18 represents a lower bound to the true regularity, H̃S ≤ HS, where equality is approached as the noise level decreases. H̃S yields high values for intrinsically irregular signals, and low values for regular and or noisy signals.
r0 determination
In wavelet-based regularity analysis we introduce a minimum threshold size, t, for each voxel time series. t represents the smallest resolution at which repeating patterns of the intrinsic signal can be reliably confirmed. This minimum threshold enables the adjustment of the total threshold, rt = r0σX + t, to produce the maximum HS attributable to the intrinsic signal (minimal noise contribution). This adjustment entails minimizing and fine-tuning the scaling factor r0 of the intrinsic signal variance, σX. However, in this report, we seek to maximize the distribution of HS obtained across a set of signals with the constraint that the same r0 be used for all time series (all voxels across all brains). We employ a simple scheme to find the smallest r0 that maximizes the range of observed HS values:
For each signal, determine the smallest r0 that results in the largest HS (taken across all scales):r0v = min{r0 ≥ 0: HS = max{HS ∈ ℝ}}
Select the largest r0v across the set of all signals: r0b = max{r0v}
In words, these two steps involve varying r0 separately for each voxel until the local HS reaches a maximum (while still remaining defined). The maximum r0 obtained from the set of all voxels (across all brains) is then selected. This ensures each voxel (across all brains) is normalized with the same scaling factor and that all voxels have a defined (non-infinite) HS. In this manuscript, we computed HS for the range of scaling factors r0 = 0 – 0.5, in 0.05 increments. We observed r0 = 0.1 to be the lowest scaling factor such that all voxel HS values, taken across both groups, remained defined.
Methods
The wavelet-based regularity analysis was applied to three data sets: 1) A simulated data set to quantify the dependence on serially correlated fluctuations, and SNR. 2) A multiband rs-fMRI data set to investigate the intrinsic irregularity across an extended number of time scales. 3) A cognitive data set to investigate the sensitivity of the proposed method on a clinical population. Results are compared to conventional MSE analysis.
Simulated Data
To quantify the effects of temporal correlation, noise and signal length on H̃S and provide a comparison with MSE analysis, we simulated time series with power spectrums of the form f−1 corresponding to pink noise. Time series were generated by convolving a 1/fα impulse response function with a white noise time series. Convolution is implemented in the frequency domain by multiplying the corresponding discrete transfer function with a white noise spectrum. Taking the discrete Fourier transform of the product results in a discrete time series whose power spectrum coefficients approximate a continuous 1/fα noise process (Mandelbrot and Van Ness, 1968; Papoulis, 1984). The specific steps for generating a 1/fα noise time series have been previously described (Kasdin, 1995) and are listed in Appendix A. The method of modeling 1/fα noise time series has two primary advantages over conventional methods such as autoregressive moving average (ARMA) based models: 1) it is scale invariant, and 2) it has no limitation to a particular band size. The dependence on the signal signal-to-noise ratio was investigated by adding iid Gaussian white noise to the generated f−1 time series. The SNR of the resulting signal, y, is evaluated as:
| (19) |
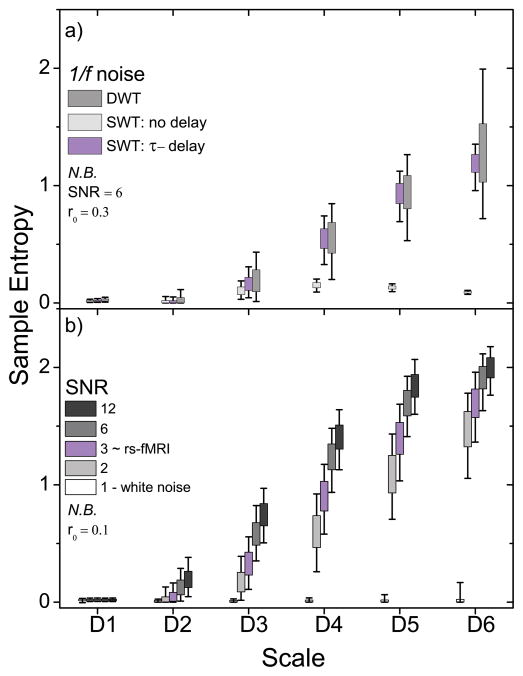
To illustrate the effect of serial correlated behavior on the measured regularity, we compare the τ-delay approach described in this report to two additional approaches for constructing subsequences (Fig. 2a), a multilevel SWT decomposition with no time delay and a DWT decomposition approach with no time delay. The latter approach is carried out in an identical fashion to the second approach, with the exception that a DWT is used to decompose the simulated time series.
Figure 2.
Wavelet-based regularity analysis of simulated f-1 data (N=1024) depicting the effects of serial correlations and changes in SNR. a) Comparison of subsequence construction using a delay time (τ) adjusted for serial correlated behavior, no delay time (τ = 1), and a discrete wavelet transform (DWT) method that forms maximally whitened subsequences (see text). b) Entropy values for signals with SNR = 1 (white noise), 2, 3, 6, and 12 are shown. Subsequences were formed with τ adjusted for serial correlated behavior.
Experimental Data
Two sets of rs-fMRI scans were performed. 1) Resting state MRI was performed with a 3T Siemens TIM Trio system. A long rs-fMRI scan was performed on 5 healthy young volunteers (age 21 ± 2 years), using multiband gradient-echo EPI with a fourfold acceleration factor. Imaging parameters were: FOV = 256 mm, TR=500 ms, 1032 time points, TE = 30 ms. 2) Analysis of 50 data sets, 25 cognitively normal (clinical dementia rating scale (CDR) = 0, 70 ± 4 years) and 25 mild cognitively impaired (CDR = 0.5, 74 ± 5 years) individuals, from Healthy Aging and Senile Dementia (HASD) program project have also been carried out. For the HASD data, resting state fMRI data were collected on a 3T Siemens TIM Trio system. Each subject had 2 rs-fMRI scans using standard gradient echo EPI (FOV = 256 mm, matrix = 64×64, 36×4 mm slices, TR|TE = 2200|27ms, FA = 80, 164 acquisitions for 6 minutes each scan), along with a high-resolution (1×1×1 mm3) 3D T1-weighted MPRAGE scan. Subjects were instructed to keep their eyes open and focus on a fixation cross during the scan.
Preprocessing
The rs-fMRI data were pre-processed as follows: compensation for rigid body correction for head movement using the MCFLIRT (Jenkinson et al. 2002) algorithm in the FSL software (default parameters, with final sinc interpolation), linear detrend and reduction of spurious variance by regression of nuisance waveforms derived from head motion correction (including derivatives of motion) and ROI extracted time series in white matter and cerebrospinal fluid (CSF). White matter and CSF time series were obtained similar to (Chang and Glover, 2009) by reverse-normalizing (see Normalizaion and Group Analysis section below) 6 mm spheres at MNI coordinates (26, −12, 35) and (19, −33, 18), respectively, to the native space of each subject.
Wavelet-based Regularity Analysis parameters
The stationary wavelet transform was performed voxel-wise on fMRI data sets using the WaveLab850 toolbox (Buckheit et al. 2005). The Daubechies wavelet (fourth order smoothness, db4) was used in this study for its balanced temporal and frequency specificity. HS is calculated voxel-wise and scale-wise using the parameters m(+1) = 1(2), r0 = 0.1. The adjustable parameter r0 is chosen to maximize the total range of entropy values measured across all voxels. The m-length subsequences are formed from time delayed points where the delay time is determined by the first minimum in the auto-mutual information function (Fraser and Swinney, 1986; Roulston, 1999) using the CRP toolbox (Marwan et al. 2007). The median absolute deviation of the highest temporal frequency scale is more robust to outliers than the standard deviation and is used to estimate the noise level in all data sets.
Multiscale Entropy Analysis parameters
MSE analysis (Costa et al. 2002; Costa et al. 2005) is a widely technique employed to understand signal regularity across multiple time scales. MSE analysis has been used to understand gait dynamics in humans (Costa et al. 2003), EEG signal irregularity in schizophrenia and autism (Takahashi et al. 2010; Catarino et al. 2011), and age dependent changes in heart rate irregularity (Costa and Healy 2003; Costa et al. 2008). To mitigate the effects of noise, MSE analysis implements a coarse graining procedure that behaves as a low-pass moving average filter (see Supporting Information (SI)). MSE analysis takes advantage of the tendency for uncorrelated noise to converge to its mean through successive averaging. The coarse graining procedure averages s-consecutive time points to create a new time series . Note the length of the new time series is reduced by a factor s. Each new time point is given by the sum:
| (20) |
Sample entropy is then calculated for each new time series gs. MSE analysis of the CDR 0 and CDR 0.5 groups were performed by coarse graining voxel time series across three scales: s = 2, 3, and 4. The corresponding signal lengths for each scale were Ns = 80, 53, and 40. Sample entropy parameters were varied with the greatest group differences occurring for m(+1) = 1(2), r0= 0.3.
Group Analysis
The transformation from each subjects brain to the MNI space was carried out using FSL’s FLIRT (Jenkinson and Smith, 2001; Jenkinson et al. 2002) and FNIRT (Anderson et al. 2010) algorithms in the following steps: 1) The mean functional volume for each subject was co-registered to their structural volume using an affine registration with 6 DOF. 2) The structural volume was transformed to the MNI 2 mm structural template using an affine registration with 12 DOF followed by a nonlinear registration using FNIRT (default parameters). Univariate group statistics were investigated scalewise with one sample and two sample t-tests. A single voxel and single scale threshold of p=0.005 was selected. Single scale cluster size statistics were obtained within a whole brain mask using AlphaSim (Forman, 1995; Ward, 2000) implemented in the REST toolbox (Song et al., 2011). Additional AlphaSim parameters used were a cluster connection radius of 3mm (i.e. approximately the distance between the center of two 2 mm voxels sharing an edge) and a Gaussian filter width of 4 mm. A single scale cluster threshold of P=0.0125 was then selected corresponding to a minimum cluster size of 60 voxels. This size corresponds to ~1/1500th of the total gray matter volume (Luders et al., 2002). This provides good cortical resolution while still being able to detect diffuse activation. A scalewise corrected P-value of P=0.05 was obtained (Bonferroni) for multiple comparisons across four scales. Differences in the multivariate statistical distributions defined across scales were also obtained using Hotelling’s T2-test. This test is based on comparing the distance between mean entropy vectors (i.e. the set of HS values taken across all scales for a single voxel) normalized by a pooled covariance matrix of all subjects in a group. The direction of effect was established using simultaneous confidence intervals as well univariate t-tests at each scale. The single voxel threshold was also chosen to be p=0.005. The cluster threshold was chosen P=0.05 rather than P=0.0125 as the correction for multiple comparisons across scales is naturally incorporated in Hotelling’s T2-test. A minimum cluster size of 44 voxels was determined, however, we use 60 voxels instead to remain consistent with the univariate values.
Group independent component analysis (ICA) was performed with 40 components using the GIFT package (Calhoun and Adali, 2013). Single subject maps were obtained by back-reconstruction and converted to z-maps. The group RSN were then computed with a one sample t-test (p < 0.0001, familywise error corrected) performed across all subjects. Nine resting state networks were visually identified (see Fig. S3 in SI).
Results
Simulated Data
Constructing subsequences from neighboring points results in entropy values heavily weighted by the degree of serial correlation present. The result is inflated subsequence recurrence that can be seen in figure 2a (no delay) where the sample entropy comes to a modest rise with increasing scale before dropping dramatically. Ideally this weighting is removed by whitening the subsequences, i.e. removing any correlation between points. We significantly reduce the correlation between points by introducing a delay between subsequence points. We compare the SWT τ-delay approach to an approach using a DWT to decompose the rs-fMRI signal. The DWT naturally whitens serial correlations by subsampling the number of time points, producing 2−jN coefficients for the j-th scale (Wornell, 1993). However, uniform subsampling has two major limitations that conspire to drastically vary the observed signal irregularity (Fig. 3a): a) recurring patterns must be translated such that their features are similarly sampled by the DWT at each recurrence, and b) subsampling progressively reduces the sample size (number of subsequence comparisons) with increasing scale, by a factor of ~(j+1)2. Stemming from the central limit theorem, reducing sample size increases the associated uncertainty in the estimation of the underlying population mean. These two drawbacks are particularly problematic when characterizing the regularity of signals stemming from nonlinear processes where patterns recur at non-uniform rates. On the other hand, the SWT τ-delay approach dramatically increases the number of subsequence comparisons (compared to the DWT method), reducing the entropy variation. Further, the mean entropy values across scales are comparable with the DWT method indicating the subsequences are effectively whitened. The results presented below are obtained using the τ-delay approach. The dependence on SNR is shown in figure 2b. As with any measure of a noisy signal, wavelet-based regularity exhibits a dependency on SNR. Increasing SNR will increase entropy as the estimated noise threshold becomes smaller relative to signal fluctuations. However, the effect of SNR is significantly reduced at the level of that typically found in rs-fMRI. There is only a 15% increase in entropy when increasing SNR from 3 to 12 (a 300% increase) at the highest wavelet scale. Increasing SNR does not guarantee an increase in entropy, i.e. a noisy sine wave will always have low entropy, even as the SNR is tuned up.
Figure 3.
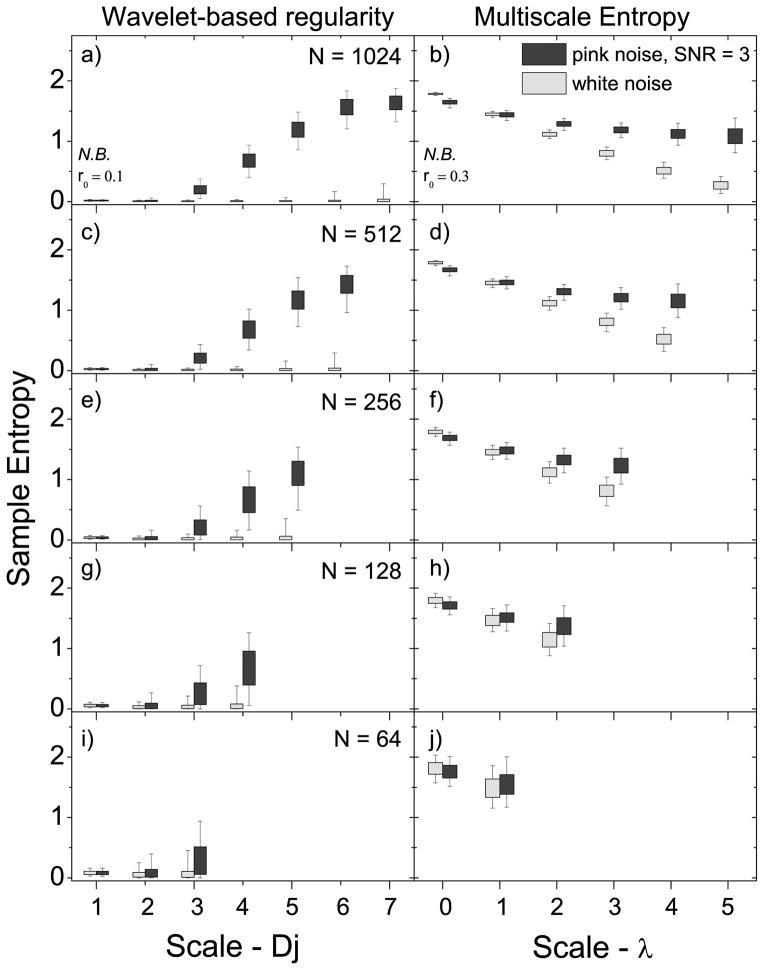
The effect of signal length (N) on the ability to distinguish f−1 noise (with SNR = 3) from white noise for the wavelet-based regularity analysis (left side) presented in this paper and MSE analysis (right side). a–b) N = 1024, c–d) N = 512, e–f) N = 256, g–h) N = 128, and i–j) N = 64. The last three rows represent signal lengths typically studied in rs-fMRI. The scale λ = 0 corresponds to the original signal. Box plots show the 5-25-75-95 percentiles.
Figure 3 compares the entropy ranges of simulated pink noise signals with SNR = 3 to simulated white noise signals using the wavelet-based method presented here and MSE analysis, for signals of several lengths: N = 64, 128, 256, 512, and 1024. At all signal lengths, a significant increase of the pink noise over white noise entropy is observed over a majority of scales using the wavelet based approach. For lengths N ≲ 128, increases are limited to the highest scales. MSE analysis, on the other hand, only shows significant increases above λ ~ 2, and only in signals with N ≲ 128.
Multiband rs-fMRI Data
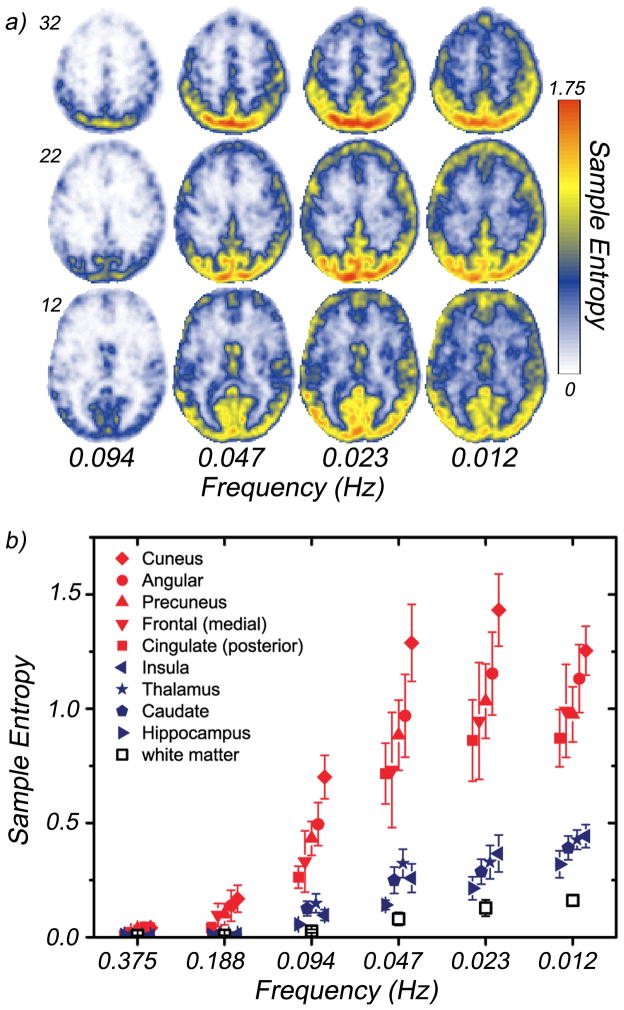
We obtained 4-D fMRI data with long time series (1024 sampled volumes) and a sampling rate of 2 Hz (TR = 0.5 s) from five healthy young volunteers. Figure 4a shows average entropy maps for four of the seven wavelet scales investigated, D4-D7 (entropy is calculated for scales D2-D7), which correspond to frequency bands within the region of 0.01–0.10 Hz, typically studied in fMRI. Noise level was determined from the D1 scale corresponding to the frequency band 0.5 – 1.0 Hz. Posterior brain regions exhibit an elevated entropy values at frequencies as high as 0.20 Hz (D3). Regional differences are shown in figure 4b. The largest values occur in the precuneus, posterior cingulate cortex, angular cortex, and medial prefrontal cortex as well as regions of the primary visual network including the cuneus. The lowest values within the gray matter occur in the caudate, thalamus, hippocampus, and insular cortex. White matter exhibits the lowest values overall, showing little increase with increasing scale.
Figure 4.
The average regional entropy of five (N=5) healthy young volunteers across several time scales. a) Entropy maps for three selected slices (MNI z-coordinate: 12, 22, 32) at four wavelet scales: D4 (0.094 Hz) - D7 (0.012 Hz). Frequencies correspond to center of respective subband. b) Regional entropy differences. The mean entropies at wavelet scales D2(0.375 Hz) - D7 (0.012 Hz) for several brain regions. Solid red symbols indicate regions located in resting state networks. Solid dark blue symbols correspond to cortical regions exhibiting the lowest entropies across all scales (insula, caudate, thalamus, hippocampus). White matter (open black symbols) exhibits the lowest entropy values of a brain region.
Cognitive Data
We calculate the regularity of the rs-fMRI signal for a cognitively normal group (n = 25, CDR = 0) and compare with a mild cognitively impaired group (n = 25, CDR = 0.5) using two measures: Wavelet-based regularity, and MSE analysis. In wavelet-based regularity analysis, entropy maps were obtained for each of the scales D2-D5 (four maps per subject) that correspond to frequency bands within the region of 0.007–0.11 Hz. Each voxel’s noise level is estimated from the D1 scale corresponding to the frequency band 0.11 – 0.22 Hz. In MSE analysis, entropy maps were obtained for coarse-grained scales s = 2, 3, and 4 (three maps per subject).
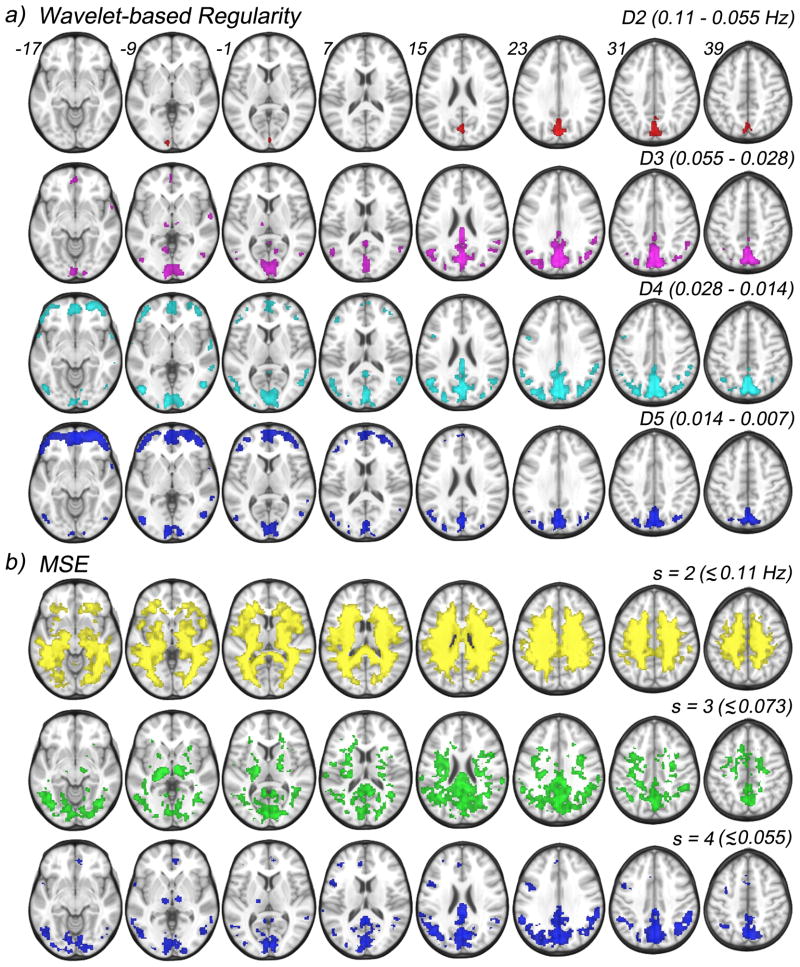
Figure 5 shows results of one sample t-tests performed voxelwise and scalewise across the wavelet-based regularity maps (Fig. 5a) and across the MSE maps (Fig. 5b) of both groups under the null hypothesis that entropy values in each scale are randomly scattered around the global (within scale) mean. Displayed regions exhibit significantly higher means (p < 0.001, cluster corrected for p<0.05 with a minimum cluster size of 60). Wavelet-based regularity results are entirely confined to gray matter regions across all scales. A single large cluster spanning regions of the precuneus and cuneus show elevated means within the D2 scale (0.11 – 0.055 Hz). Within the D3 scale (0.055 – 0.028 Hz), this cluster grows and new large clusters in the calcarine and posterior cingulate form. Further, distinct clusters appear bilaterally in the several posterior regions: angular, supramarginal, middle occipital, middle temporal, and lingual gyri as well as the thalamus. A single anterior cluster appears in the medial orbital frontal gyrus. We note that a majority of the observed clusters largely overlap with nodes of DMN (see SI).
Figure 5.
One sample t-tests results performed against the global mean, scalewise, across both CDR 0 and CDR 0.5 groups of the wavelet-based regularity maps, and MSE maps. a) Four scales and their corresponding frequency ranges are shown for wavelet-based regularity: D2 (0.11–0.055 Hz), D3 (0.055–0.028 Hz), D4 (0.028–0.014 Hz), and D5 (0.014–0.007 Hz). b) Three scales and approximate frequency sensitivity range are shown for MSE analysis: s = 2 (< 0.11 Hz), s=3 (< 0.055 Hz), and s=4 (< 0.028 Hz).
The entire set of posterior clusters persists, and grows, in the D4 scale (0.028–0.014 Hz) with the exception of the clusters in the thalamus, which disappear completely, indicating frequency specific activity. The anterior cluster in the medial orbital frontal gyrus grows in addition to new bilateral clusters appearing in the middle orbital and inferior orbital gyri. Bilateral clusters also appear in the middle and inferior frontal gyri as well as the superior temporal gyrus. Posterior activity at the coarsest temporal scale, D5 (0.014–0.007 Hz), is greatly reduced with clusters persisting in the precuneus, cuneus, and calcarine. Bilateral activation also persists in the angular, middle occipital, and middle temporal gyri. Activity in the supramarginal gyrus, and posterior cingulate drop below the significance threshold. The opposite is observed for anterior regions where coverage is greatly increased across orbitofrontal cortex as well as the middle and inferior frontal gyri.
Multiscale Entropy Results
MSE results of the cognitive data show high entropy at the lower scales, s = 2 and 3, where the noise dominates the entropy and gray matter regions are not distinguishable from white matter. The highest coarse-grained scale (s = 4) shows posterior activity patterns similar to those seen across the D2-D5 wavelet scales. Namely, clusters in the precuneus, cuneus, calcarine and posterior cingulate form (Fig. 5b). Further, extended bilateral clusters span the angular, supramarginal, and middle occipital gyri. Separate clusters also bilaterally occupy the middle temporal gyrus as well as the thalamus. However, very little anterior activity is seen with MSE analysis with a small cluster in the medial orbital frontal gyrus, and unilateral (left) clusters in the inferior frontal gyrus.
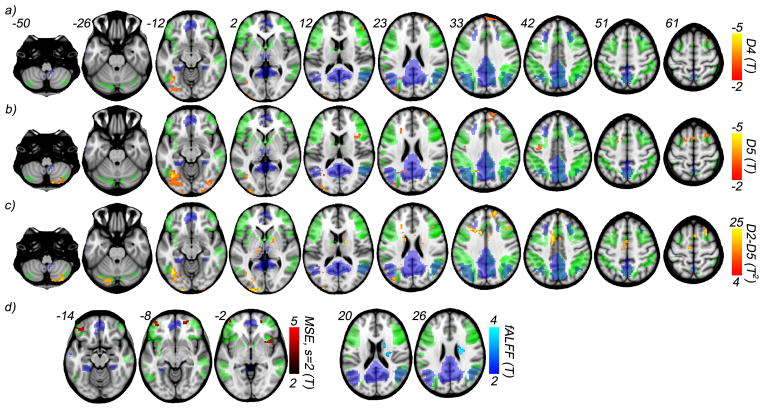
Figure 6 shows the maps of the group comparisons done using two sample t-tests between CDR 0 and CDR 0.5 groups. These maps are overlapped with two resting state network masks: the default mode network (posterior) and the executive control network (a composite of the left and right). Networks are identified using group ICA (see Methods), and the masks of RSNs indicate significant regions (p < 0.0001, familywise error corrected) from a one sample t-test performed across both groups. Table II lists the center and volume of each observed cluster for all measures. All group comparison results reported below are significant to p < 0.005, and cluster corrected for p < 0.05 with a minimum cluster size of 60 (Forman, 1995). The univariate entropy distributions at each scale and voxel were compared with Student’s two sample t-test for both wavelet-based regularity (Fig. 6a,b) and MSE (Fig. 6d). In the former case, regions of significant difference only appear in the low frequency scales D4 and D5 scales, with the CDR 0.5 group showing higher entropy. Regions are largely similar across the two scales except for differences in the cerebellum (crus II) and the inferior frontal gyri/insula. Contrariwise, MSE differences were only found at the lowest scale s = 2 (Fig. 6d), with the CDR 0 group showing the higher entropy. This reversal of direction is consistent with the wavelet-based regularity results. MSE is designed to suppress ‘noisy’ fluctuations, including those intrinsic to the signal. The lack of measurable group effect for MSE(s=4) highlights yet another difficulty in employing MSE analysis for short noisy time series. Namely, the tradeoff between greater noise filtering and reduced statistical power as the scale increases.
Figure 6.
Voxelwise comparison between healthy (CDR 0) and impaired (CDR 0.5) cognitive function groups from Healthy Aging and Senile Dementia (HASD) cohort using wavelet-based regularity analysis, MSE analysis, and fALFF. Results from two sample t-tests show decreased regularity in the CDR=0.5 group at scales a) D4, corresponding to the frequency range 0.028–0.014 Hz, and b) D5, corresponding to the frequency range 0.014–0.007 Hz. c) Two sample multivariate t-tests performed voxelwise across scales D2-D5 show an extended number of regions affected. d) MSE and fALFF two sample t-test (univariate) results are shown. MSE differences are observed only for s=2 and appear over a far narrower range of slices. Similarly, fALFF differences occur within a single cluster. All results are significant to p<0.005, and further cluster corrected for p<0.05, with a cluster size minimum of 60. Two resting state network masks, defined using group ICA across both groups, are shown for comparison: posterior default mode (blue), and a composite of the left and right executive control (green).
Table II.
Group differences between CDR-0 and CDR-0.5, using Wavelet-based Regularity analysis, Multiscale Entropy analysis, and Fractional Amplitude of Low Frequency Fluctuation (ALFF). Region, cluster center (MNI coordinates), and cluster size of two sample t-tests results are shown (p<0.005, cluster corrected for p<0.05).
| Location | MNI (x, y, z) | Size | MNI (x, y, z) | Size | MNI (x, y, z) | Size |
|---|---|---|---|---|---|---|
| Wavelet-based Regularity | D2-D5 | D5 | D4 | |||
| L. Fusiform | −38, −66, −12 | 490 | −36, −67, −12 | 1300 | −38, −62, −12 | 162 |
| R. Sup. Frontal | 18, 54, 33 | 215 | 18, 57, 31 | 274 | 17, 59, 32 | 179 |
| 25, 15, 59 | 66 | 27, 15, 63 | 69 | 24, 13, 65 | 61 | |
| Supp. Motor Area | 3, 12, 63 | 82 | 1, 12, 64 | 153 | −2, 10, 66 | 86 |
| −7, −12, 63 | 70 | |||||
| R. Caudate | 10, 8, 7 | 74 | ||||
| L. Thalamus | −10, −22, 1 | 61 | ||||
| L. Mid. Cingulate | −8, 4, 43 | 548 | ||||
| L. Cerebellum (crus I) | −18, −80, −24 | 140 | ||||
| R. Cerebellum (crus II) | 30, −76, −44 | 262 | 25, −81, −46 | 197 | ||
| L. Mid. Frontal | −29, 21, 37 | 172 | −24, 29, 21 | 76 | ||
| R. Mid. Frontal | 47, 25, 34 | 68 | 45, 44, 19 | 62 | ||
| L. Mid Occipital | −35, −81, 23 | 69 | −34, −84, 22 | 63 | ||
| R. Inf. Occipital | 38, −81, −13 | 130 | ||||
| R. Inf. Oper. Frontal | 41, 13, 12 | 88 | ||||
| L. Precuneus | −14, −58, 30 | 67 | ||||
| L. Sup. Frontal | −19, 7, 60 | 93 | ||||
| L. Postcentral | −42, −12, 41 | 66 | ||||
| L. Inf. Occipital | −31, −81, −11 | 219 | ||||
| Multiscale Entropy | s = 2 | |||||
| R. Insula | 40, 13, −2 | 72 | ||||
| R. Sup. Orb. Frontal | 20, 55, −6 | 101 | ||||
| L. Inf. Orb. Frontal | −37, 41, −16 | 140 | ||||
| Fractional ALFF | 0.11 – 0.01 Hz | |||||
| R. Caudate | 20, −11, 23 | 144 |
In addition to the scalewise comparisons, the difference in the multivariate entropy distributions defined across all scales is evaluated voxelwise with Hotelling’s T2-test (see Methods section). The results for wavelet-based regularity (Fig. 6c) overlap with those seen in scales D4 and D5, but with several additional clusters appearing. The largest of which occurs in the anterior region of the middle cingulate cortex. Direct comparison of the multivariate differences with the D4 and D5 univariate results indicate the CDR 0.5 exhibits higher irregularity in the overlapping clusters. For new clusters, simultaneous confidence intervals are used which also show the CDR 0.5 group having increased irregularity. Comparison of the multivariate entropy distributions defined across the MSE coarse-grained scales revealed no significant differences between the groups.
Effects of SNR, Delay Time, and Motion
Comparisons of both the SNR and delay time distributions are also performed, both within each wavelet scale, and across scales to determine whether the above wavelet-based regularity results can be explained by differences in signal strength and/or serial correlation between the two groups. SNR maps are obtained for each subject at each wavelet scale using equations 11 and 19. The univariate SNR and delay time distributions within each scale and the multivariate distributions defined across scales are compared with both Student’s t-test and Hotelling’s T2 test. No significant difference in SNR or delay time is found between the groups up to p < 0.01, uncorrected (see SI for average gray matter differences). Further we test for changes in relative signal strength across the frequency band 0.11–0.007 Hz using fractional amplitude of low-frequency fluctuation (fALFF) (Zou et al. 2008). We observe a single cluster in the caudate where the CDR 0 group exhibits an increased fALFF, opposite to the direction of wavelet-based regularity results (Fig. 6d). These results strongly indicate the observed wavelet-based regularity results, namely the increase in the irregularity of rs-fMRI fluctuations across several areas of the brain, are not accounted for by changes in signal strength.
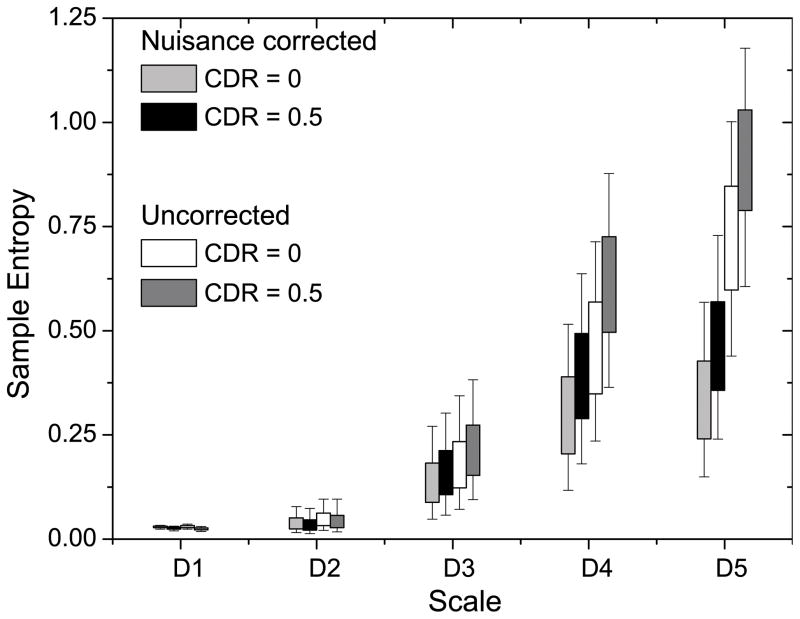
We used wavelet-based regularity analysis to investigate the dynamic effects of head motion and imaging parameters on the average gray matter entropy difference between the CDR 0 and CDR 0.5 groups (Fig. 7). Effects of head motion are evaluated by including motion parameters (e.g. rms head displacement) as a covariate in the regression of the bold time series. Physiological noise effects were evaluated by regressing out the average white matter and CSF times series (see Methods). Similar to existing metrics of rs-fMRI, the wavelet-based regularity analysis is susceptible to confounding factors of head motion. Head motion has been shown to affect the observed pattern of short and long-range connectivity in rs-fMRI studies. Noise caused by motion is often described by six parameters: translational motion in three orthogonal directions, and three rotation parameters (i.e. pitch, roll, and yaw). Motion can be highly non-stationary with persistent drifts or localized shifts/spikes being added to the signal. Entropy calculations were performed at two stages: 1) After linear registration, and 2) after motion parameter (including derivatives), white matter time series and linear trend regression. A significant drop in entropy was observed across both groups after regression of nuisance variables. Motion is known to introduce colored noise in the rs-fMRI signal (Power et al. 2012) and the entropy drop across scales reflects the removal of this noise. Our results demonstrate that nuisance variable dynamics do not contribute significantly to group differences in signal regularity.
Figure 7.
Comparison of nuisance variable effects between CDR 0 and CDR 0.5 groups. Entropy calculations were performed at two stages: after linear registration, and after motion parameter (including derivatives), white matter and cerebrospinal fluid time series, and linear trend regression.
Discussion
The proposed method aims to detect intrinsic signal regularity in short, noisy signals by maximizing the number of subsequence comparisons (sample size), while minimizing effects of serial correlations and random fluctuations from external noise. Preserving local temporal structures with high fidelity is essential in the decomposition of nonstationary signals. This is accomplished using a SWT, but at the cost of perpetuating any correlated structure. Correlated structure reduces the amount of new information contained in nearby time points. This weighting can be mitigated by reducing correlations between coordinates, as evidenced by the DWT method (Fig. 2a (DWT)).
However, poor statistics arising from the DWT subsampling gives rise to a large variation in entropy values that increases with increasing wavelet scale. The SWT τ-delay effectively reduces the serial correlation within subsequences, comparable to a DWT subsampling, while providing better statistics by significantly increasing the number subsequence comparisons.
Random fluctuations introduced by external uncorrelated noise tend to scatter signal patterns away from each other. Because of this scattering, the level of noise presents a sensitivity limitation to regularity measures such as approximate and sample entropy (Pincus, 1991; Richman and Moorman, 2000). In this report we estimate the noise level, and measure the likelihood of the intrinsic temporal patterns to repeat within the threshold set by the noise. This has the desired benefit of yielding low entropy values for both noisy signals, and highly regular signals, and high entropy for intrinsically irregular signals.
We employ this method to investigate the regularity with which the brain reconstructs temporal activity patterns by measuring the stability of recurring subsequences in the rs-fMRI signal. We find the most ‘active’ areas of the brain at rest exhibit a diverse array of strong temporal patterns. The movement through these patterns results in highly irregular, f−1-like, signal fluctuations across multiple time scales. The largest increases in sample entropy occur in the default mode network (precuneus, posterior cingulate cortex, angular cortex, and medial prefrontal cortex) and the primary visual network (cuneus, and occipital cortex). These regions correlate with findings showing increased signal intensity variation and perfusion (Luca et al. 2006), whereas other reports have shown the default mode network to exhibit increased connectivity during rest (Raichle et al. 2001; Beckmann et al. 2005; Damoiseaux et al. 2006). This complex trajectory through a diverse array of patterns is mirrored at finer temporal scales by the scale-free behavior of EEG microstates (Ville et al. 2010). EEG microstates (Lehman et al. 1987) are whole brain neural activity patterns persisting for ~100 ms and reported to be electrophysiological correlates of spontaneous rs-fMRI fluctuations within RSNs (Musso et al. 2010; Britz et al. 2010). Recent computational model of recurrent neural networks show that forming a diverse array of patterns increases the brains ability to distinguish small changes in synaptic input (Ostojic, 2014). Conversely, white matter exhibits low entropy across all scales indicating a dominance of external noise. This is unsurprising since the vast majority of neuronal bodies, and dendritic trees (i.e. the structures that generate local field potential which is the candidate signal associated with rs-fMRI signal changes (logothetis 2001)) are located in the gray matter.
However, emerging evidence indicates neural activity is a combination of both complex and recurrent behaviors. A mix of feedforward and feedback connections typifying these behaviors is evidenced in the visual processing networks (Lamme and Roelfsema, 2000; Kravitz et al. 2013). The interplay of these behaviors is speculated to govern neural processes in other systems. Considerable computational work on recurrent neural networks has shown dynamic neural behavior to consist of both highly irregular (chaotic) and recurrent (locally stable) behaviors (Mauk and Buonomano, 2004; Rabinovich et al. 2008; Buonomano and Maass, 2009; Laje and Buonomano, 2013; Ostojic, 2014), but with little supporting experimental evidence. We report, in an age matched comparison of two cognitive groups (healthy vs. impaired), evidence that recurrent temporal patterns destabilize, i.e. fail to persist, in mild cognitively impaired individuals in regions strongly correlating with several RSNs: the posterior default mode network, and the left and right executive-control networks. These networks are known to play an integral role in healthy cognition. The default mode network is reported to be a central hub of the brain that interconnects with several other networks (Bullmore and Sporns, 2009) and is thought to play a role in episodic memory (Greicius et al. 2004; Buckner et al. 2009). These networks are amongst those shown to be targets of neurodegenerative disease (Seeley et al. 2009). The observed decrease of stable, recurrent behavior implicates the disruption of information feedback as an agent of cognitive impairment. Similar decreases in the stability of EEG microstates, the duration they subsist, are observed with decreasing cognitive function (Strik et al. 1997). These results contribute to a growing body of evidence that points to the brain balancing the development of complex spatiotemporal patterns with an intrinsic tendency to revisit patterns of activity (Plenz and Thiagarajan, 2007; Ikegaya et al. 2004). We note that studies using MSE show a decrease in entropy (ROI based) with decreasing cognitive function (Yang et al. 2013). These results are in agreement with those reported here when it is considered that MSE is designed to filter out highly irregular fluctuations, regardless of their origin. This will suppress the noisier fluctuations observed in the CDR 0.5 group. A thorough evaluation of wavelet based regularity and MSE analysis needs to be performed in future studies.
Conclusion
We present a new regularity analysis that measures the stability of recurrent temporal activity patterns in the presence of significant noise levels. We adapt the multiresolution and noise estimation capabilities of wavelet analysis into a highly sensitive regularity analysis. Significant differences in recurrent temporal pattern stability are observed between healthy normal, and cognitively impaired groups in several resting-state networks involved in higher level cognitive processing. The findings in the paper suggest that wavelet based regularity analysis is a promising technique to characterize the dynamic temporal structure of rs-fMRI as well as other biological signals.
Supplementary Material
Acknowledgments
The authors wish to acknowledge the following funding sources: R01 EB014922, R01 MH080892, R01 NS081077, P50 HD055784. Healthy Aging and Senile Dementia cohort funding sources: P01 AG003991, P50 AG005681. KJ has a fellowship by SNSF/SFGMB grant no. 142743.
Appendix A
The following steps were used to generate time series with 1/fα power spectrum [Kasdin, 1995]:
- Recursively generate the impulse response values using a Runge-Kutta method [Kasdin, 1995b]:
Generate independent and identically distributed (iid) white noise, N(0,1).
Pad sequences from steps 1 and 2 with zeros to guarantee linear (and not circular) convolution, which assures causality (outputs are not dependent on future inputs).
Perform a discrete Fourier transform (DFT) of impulse response function in step 1 to obtain the discrete transfer function, H(z).
Perform a DFT of the white noise sequence in step 2.
Multiply H(z) together with the complex spectra from step 5.
Take the inverse DFT of the result in step 6.
References
- Ainsworth M, Lee S, Cunningham M, Traub R, Kopell N, Whittington M. Rates and rhythms: A synergistic view of frequency and temporal coding in neuronal networks. Neuron. 2012;75:572–583. doi: 10.1016/j.neuron.2012.08.004. [DOI] [PubMed] [Google Scholar]
- Andersson J, Jenkinson M, Smith S. Nonlinear registration, aka spatial normalisation. FMRIB technical report TR07JA2 2010 [Google Scholar]
- Antonini M, Barlaud M, Mathieu P, Daubechies I. Image coding using wavelet transform. IEEE Trans Image Processing. 1992;1:205–220. doi: 10.1109/83.136597. [DOI] [PubMed] [Google Scholar]
- Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of 1/f noise. Phys Rev Let. 1987;59:381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- Beckmann C, DeLuca M, Devlin J, Smith S. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin F, Haughton V, Hyde J. Functional connectivity in the motor cortex of resting human brain using echo-planar mri. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Britz J, Ville DD, Michel C. Bold correlates of eeg topography reveal rapid resting-state network dynamics. Neuroimage. 2010;52:1162–1170. doi: 10.1016/j.neuroimage.2010.02.052. [DOI] [PubMed] [Google Scholar]
- Buckheit J, Chen S, Donoho D, Johnstone I, Scargle J. Wavelab toolkit. 2005 http://www-stat.stanford.edu:80/wavelab/
- Buckner R, Sepulcre J, Talukdar T, Krienen F, Liu H, Hedden T, Andrews-Hanna J, Sperling R, Johnson K. Cortical hubs revealed by intrinsic functional connectivity: Mapping, assessment of stability, and relation to alzheimer’s disease. J Neurosci. 2009;29:1860–1873. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Buonomano D, Maass W. State-dependent computations: spatiotemporal processing in cortical networks. Nat Rev Neurosci. 2009;10:113–125. doi: 10.1038/nrn2558. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Adali T. Group ica of fmri toolbox (gift) 2013 http://mialab.mrn.org/software/gift/
- Catarino A, Churches O, Baron-Cohen S, Andrade A, Ring H. Atypical eeg complexity in autism spectrum conditions: A multiscale entropy analysis. Clin Neurophysiol. 2011;122:2375–2383. doi: 10.1016/j.clinph.2011.05.004. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover G. Effects of model-based physiological noise correction on default mode network anti-correlations and correlations. NeuroImage. 2009;47:1448–1459. doi: 10.1016/j.neuroimage.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover G. Time-frequency dynamics of resting-state brain connectivity measured with fmri. NeuroImage. 2010;50:81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang S, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans Image Processing. 2000;9:1532–1546. doi: 10.1109/83.862633. [DOI] [PubMed] [Google Scholar]
- Chialvo D. Emergent complex neural dynamics. Nat Phys Rev. 2010;6:744–750. [Google Scholar]
- Costa M, Goldberger A, Peng CK. Multiscale entropy analysis of complex physiologic time series. Phys Rev Let. 2002;89:068102–068102. doi: 10.1103/PhysRevLett.89.068102. [DOI] [PubMed] [Google Scholar]
- Costa M, Healey J. Multiscale entropy analysis of complex heart rate dynamics: discrimination of age and heart failure effects. Comput Cardiol. 2003;29:705–708. [Google Scholar]
- Costa M, Peng C, Goldberger A, Hausdorff J. Multiscale entropy analysis of human gait dynamics. Physica A. 2003;330:53–60. doi: 10.1016/j.physa.2003.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costa M, Goldberger A, Peng C. Multiscale entropy analysis of biological signals. Phys Rev E. 2005;71:021906–021923. doi: 10.1103/PhysRevE.71.021906. [DOI] [PubMed] [Google Scholar]
- Costa M, Peng C, Goldberger A. Multiscale analysis of heart rate dynamics: entropy and time irreversibility measures. Cardiovasc Eng. 2008;8:88–93. doi: 10.1007/s10558-007-9049-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux J, Rombouts S, Barkhof F, Scheltens P, Stams C, Smith S, Beckmann C. Consistent resting-state networks across healthy subjects. Proc Natl Acad Sci USA. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoho D, Johnstone I. Ideal spatial adaptation via wavelet shrinkage. Biometrika. 1994;81:425–455. [Google Scholar]
- Donoho D. De-noising by soft-thresholding. IEEE Trans Inform Theory. 1995;41:613–627. [Google Scholar]
- Eckmann JP, Ruelle D. Ergodic theory of chaos and strange attractors. Rev Mod Phys. 1985;57:617–656. [Google Scholar]
- Forman S, Cohen J, Fitzgerald M, Eddy W, Mintun M, Noll D. Improved assessment of significant activation in functional magnetic resonance imaging (fmri) Use of a clustersize threshold. Magn Reson Med. 1995;33:636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Fraser A, Swinney H. Independent coordinates for strange attractors from mutual information. Phys Rev A. 1986;33:1134–1140. doi: 10.1103/physreva.33.1134. [DOI] [PubMed] [Google Scholar]
- Friston K, Josephs O, Zarahn E, Holmes A, Rouquette S, Poline JB. To smooth or not to smooth? bias and efficency in fmri time-series analysis. NeuroImage. 2000;12:196–208. doi: 10.1006/nimg.2000.0609. [DOI] [PubMed] [Google Scholar]
- Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Let. 1983;50:346–349. [Google Scholar]
- Greicius M, Srivastava G, Reiss A, Menon V. Default-mode network activity distinguishes alzheimers disease from healthy aging: Evidence from functional mri. Proc Natl Acad Sci USA. 2004;101:4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan D, Anbarjafari G. Image resolution enhancement by using discrete and stationary wavelet decomposition. IEEE T Image Process. 2011;20:1458–1460. doi: 10.1109/TIP.2010.2087767. [DOI] [PubMed] [Google Scholar]
- He B, Zempel J, Snyder A, Raichle M. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010;66:353–369. doi: 10.1016/j.neuron.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikegaya Y, Aaron G, Cossart R, Aronov D, Lampl I, Ferster D, Yuste R. Synre chains and cortical songs: Temporal modules of cortical activity. Science. 2004;304:559–564. doi: 10.1126/science.1093173. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady J, Smith S. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Kasdin NJ. Discrete simulation of colored noise and stochastic processes and f-α power law noise generation. Proc IEEE. 1995;83:802. [Google Scholar]
- Kasdin NJ. Runge-Kutta algorithm for the numerical integration of stochastic differential equations. AIAA J Guidance, Control, and Dynamics. 1995;18:114–120. [Google Scholar]
- Kravitz D, Saleem K, Baker C, Ungerleider L, Mishkin M. The ventral visual pathway: an expanded neural frame-work for the processing of object quality. Trends Cogn Sci. 2013;17:26–49. doi: 10.1016/j.tics.2012.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laje R, Buonomano D. Robust timing and motor patterns by taming chaos in recurrent neural networks. Nat Neurosci. 2013;16:925–933. doi: 10.1038/nn.3405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamme V, Roelfsema P. The distinct modes of vision offered by feedforward and recurrent processing. Trends Neurosci. 2000;23:571–579. doi: 10.1016/s0166-2236(00)01657-x. [DOI] [PubMed] [Google Scholar]
- Lehmann D, Ozaki H, Pal I. Eeg alpha map series: Brain micro-states by space-oriented adaptive segmentation. Electroencephalogr Clin Neurophysiol. 1987;67:271–288. doi: 10.1016/0013-4694(87)90025-3. [DOI] [PubMed] [Google Scholar]
- Liu C, Krishnan A, Yan L, Smith RX, Kilroy E, Alger J, Ringman J, Wang D. Complexity and synchronicity of resting state blood oxygenation level-dependent (bold) functional mri in normal aging and cognitive decline. J Magn Reson Im. 2012;38:36–45. doi: 10.1002/jmri.23961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis N, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fmri signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Logothetis N, Pauls J, Poggio T. Shape representation in the inferior temporal cortex of monkeys. Curr Biol. 1995;5:552–563. doi: 10.1016/s0960-9822(95)00108-4. [DOI] [PubMed] [Google Scholar]
- Lowe M, Mock B, Sorenson J. Functional connectivity in single and multislice echoplanar imaging using resting-state fluctuations. NeuroImage. 1998;7:119–132. doi: 10.1006/nimg.1997.0315. [DOI] [PubMed] [Google Scholar]
- Luca MD, Beckmann C, Stefano ND, Smith PMS. Fmri resting state networks define distinct modes of long-distance interactions in the human brain. NeuroImage. 2006;29:1359–1367. doi: 10.1016/j.neuroimage.2005.08.035. [DOI] [PubMed] [Google Scholar]
- Luders E, Steinmetz H, Jancke L. Brain size and grey matter volume in the healthy human brain. Neuroreport. 2002;13:2371–2374. doi: 10.1097/01.wnr.0000049603.85580.da. [DOI] [PubMed] [Google Scholar]
- Mallat S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans Pattern Anal Machine Intell. 1989;11:674–693. [Google Scholar]
- Mandelbrot BB, Van Ness JW. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968;10:422–437. [Google Scholar]
- Marwan N, Romano M, Thiel M, Kurths J. Recurrence plots for the analysis of complex systems. Physics Reports. 2007;438:237–329. [Google Scholar]
- Mauk M, Buonomano D. The neural basis of temporal processing. Annu Rev Neurosci. 2004;27:307–340. doi: 10.1146/annurev.neuro.27.070203.144247. [DOI] [PubMed] [Google Scholar]
- Musso F, Brinkmeyer J, Mobascher A, Warbrick T, Winterer G. Spontaneous brain activity and eeg microstates. a novel eeg/fmri analysis approach to explore resting-state networks. Neuroimage. 2010;52:1149–1161. doi: 10.1016/j.neuroimage.2010.01.093. [DOI] [PubMed] [Google Scholar]
- Nason G, Silverman B. The Stationary Wavelet Transform and some Statistical Applications. Springer; New York: 1995. [Google Scholar]
- Nikulin V, Brismar T. Comment on “multiscale entropy analysis of complex physiologic time series. Phys Rev Let. 2004;92:089803. doi: 10.1103/PhysRevLett.92.089803. [DOI] [PubMed] [Google Scholar]
- Ostojic S. Two types of asynchronous activity in networks of excitatory and inhibitory spiking neurons. Nat Neurosci. 2014;17:594–602. doi: 10.1038/nn.3658. [DOI] [PubMed] [Google Scholar]
- Olivo-Marin JC. Extraction of spots in biological images using multiscale products. Pattern Recogn. 2002;35:1989–1996. [Google Scholar]
- Papoulis A. Probability, Random Variables, and Stochastic Processes. New York: McGraw-Hill; 1984. [Google Scholar]
- Pincus S. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci USA. 1991;88:2297–2301. doi: 10.1073/pnas.88.6.2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plenz D, Thiagarajan T. The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends in Neurosciences. 2007;30:101–110. doi: 10.1016/j.tins.2007.01.005. [DOI] [PubMed] [Google Scholar]
- Power J, Barnes K, Snyder A, Schlaggar B, Petersen S. Spurious but systematic correlations in functional connectivity mri networks arise from sub ject motion. NeuroImage. 2012;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinovich M, Huerta R, Laurent G. Transient dynamics for neural processing. Science. 2008;321:48–50. doi: 10.1126/science.1155564. [DOI] [PubMed] [Google Scholar]
- Raichle M, MacLeod A, Snyder A, Powers W, Gusnard D, Shulman G. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richman J, Moorman J. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000;278:2039–2049. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- Roulston M. Estimating the errors on measured entropy and mutual information. Physica D. 1999;125:285–294. [Google Scholar]
- Seeley W, Menon V, Schatzberg A, Keller J, Glover G, Kenna H, Reiss A, Greicius M. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci. 2007;27:2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley W, Crawford R, Zhou J, Miller B, Greicius M. Neurodegenerative diseases target large-scale human brain networks. Neuron. 2009;62:42–52. doi: 10.1016/j.neuron.2009.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith RX, Yan L, Wang D. Multiple time scale complexity analysis of resting state fmri. BrainImag and Behav. 2014;8:284–291. doi: 10.1007/s11682-013-9276-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strickland RN, Hahn HI. Wavelet Transform Methods for Object Detection and Recovery. IEEE T Image Process. 1997;6:724–735. doi: 10.1109/83.568929. [DOI] [PubMed] [Google Scholar]
- Strik W, Chiaramonti R, Muscas G, Paganini M, Mueller T, Fallgatter A, Versari A, Zappoli R. Decreased eeg microstate duration and anteriorisation of the brain electrical fields in mild and moderate dementia of the alzheimer type. Psychiatry Res. 1997;75:183–191. doi: 10.1016/s0925-4927(97)00054-1. [DOI] [PubMed] [Google Scholar]
- Starck JL, Fadili J, Murtagh F. The Undecimated Wavelet Decomposition and its Reconstruction. IEEE T Image Process. 2007;16:297–309. doi: 10.1109/tip.2006.887733. [DOI] [PubMed] [Google Scholar]
- Takahashi T, Cho R, Mizuno T, Kikuchic M, Takahashi TMK, Wada Y. Antipsychotics reverse abnormal eeg complexity in drug-naive schizophrenia: A multiscale entropy analysis. NeuroImage. 2010;51:173–182. doi: 10.1016/j.neuroimage.2010.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van De Ville D, Britz J, Michel C. Eeg microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc Natl Acad Sci USA. 2010;107:18179–18184. doi: 10.1073/pnas.1007841107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Li Y, Childress A, Detre J. Brain entropy mapping using fmri. PLOS One. 2014;9:e89948, 1–8. doi: 10.1371/journal.pone.0089948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward DB. AlphaSim. 2000 http://afni.nimh.nih.gov/pub/dist/doc/manual/AlphaSim.pdf.
- Woolrich M, Ripley B, Brady M, Smith S. Temporal autocorrelation in univariate linear modeling of fmri data. NeuroImage. 2001;14:1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- Wornell G. Wavelet-based representations for the 1/f family of fractal processes. Proc IEEE. 1993;81:1428–1450. [Google Scholar]
- Song Xiao-Wei, Dong Zhang-Ye, Long Xiang-Yu, Li Su-Fang, Zuo Xi-Nian, Zhu Chao-Zhe, He Yong, Yan Chao-Gan, Zang Yu-Feng. REST: A Toolkit for Resting-State Functional Magnetic Resonance Imaging Data Processing. PLoS ONE. 2011;6(9):e25031. doi: 10.1371/journal.pone.0025031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AC, Huang CC, Yeh HL, Liu ME, Hong CJ, Tu PC, Chen JF, Huang NE, Peng CK, Lin CP, Tsai SJ. Complexity of spontaneous BOLD activity in default mode network is correlated to cognitive Function in normal male elderly: a multiscale entropy analysis. Neurobiology of Aging. 2013;34(2):428–438. doi: 10.1016/j.neurobiolaging.2012.05.004. [DOI] [PubMed] [Google Scholar]
- Zou QH, Zhu CZ, Yang Y, Zuo XN, Long XY, Cao QJ, Wang YF, Zang YF. An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: Fractional ALFF. J Neurosci Methods. 2008;172:137–141. doi: 10.1016/j.jneumeth.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.