Abstract
Machine learning or MVPA (Multi Voxel Pattern Analysis) studies have shown that the neural representation of quantities of objects can be decoded from fMRI patterns, in cases where the quantities were visually displayed. Here we apply these techniques to investigate whether neural representations of quantities depicted in one modality (say, visual) can be decoded from brain activation patterns evoked by quantities depicted in the other modality (say, auditory). The main finding demonstrated, for the first time, that quantities of dots were decodable by a classifier that was trained on the neural patterns evoked by quantities of auditory tones, and vice-versa. The representations that were common across modalities were mainly right-lateralized in frontal and parietal regions. A second finding was that the neural patterns in parietal cortex that represent quantities were common across participants. These findings demonstrate a common neuronal foundation for the representation of quantities across sensory modalities and participants and provide insight into the role of parietal cortex in the representation of quantity information.
Keywords: Number representation, Cross-modality, fMRI, multivoxel pattern analysis
Introduction
An understanding of how numbers are mentally represented has fueled the work of psychologists for decades due to its educational significance (Varma & Schwartz, 2008) as well as its fundamental role in cognition. Many different approaches have attempted to illuminate the nature of number representation. After decades of behavioral studies on numerical cognition (Barth et al., 2003; Dehaene & Akhavein, 1995; Moyer & Landauer, 1967; Naccache & Dehaene, 2001b), both human functional imaging studies (Cohen Kadosh & Walsh, 2009; Dehaene, 1996; Eger et al., 2003; Libertus et al., 2007; Nacache & Dehaene, 2001a; Pinel et al., 2001) and animal studies (Neider et al., 2002) have increasingly delineated some of the brain mechanisms that represent numerical information, particularly converging on parietal and frontal brain regions. Now, with advancements in machine learning methods and its applications to fMRI data, research on this topic is uniquely positioned to decipher cortical representation of numbers.
Numbers can be expressed in different notational forms (e.g., the digit 3, the number word three in spoken or written form, or a non-symbolic set of three dots) and in different modalities (e.g. auditory or visual). Whether there is an abstract or common cognitive and neural representation of numbers across these notations and modalities is a topic of considerable debate (Cohen Kadosh, 2009; Dehaene et al., 1998). Recent behavioral studies have shown inconsistent findings regarding whether there is truly an abstract code for numbers in different modalities. A study using a psychophysical adaptation technique showed commonality of representations of numbers across different formats and modalities (Arrighi et al., 2014), whereas another study demonstrated that approximate numerical judgments of sequentially presented stimuli depend on sensory modality, calling into question the claim of modality independence (Tokita et al., 2013). Additionally, while a few previous neuroimaging studies indicating common neural representations across notation and modalities have implicated mainly bilateral parietal regions to be associated with these abstract representations (Dehane, 1996; Eger et al., 2003; Libertus et al., 2007; Naccache, & Dehaene, 2001b), others including an electrophysiological study have provided evidence against the abstract view of number representation (Ansari, 2007; Bulthe et al., 2014; Bulthe et al., 2015; Cohen Kadosh et al., 2007; Lyons et al., 2015; Notebaert et al., 2011; Piazza et al., 2007; Spitzer et al., 2014). So far, there is no conclusive evidence concerning a common neural representation of numbers across different input forms and modalities.
The increasing growth of machine learning fMRI techniques have enabled decoding stimulus features represented in primary or mid-level sensory cortices (Formisano et al., 2008; Haynes and Rees, 2005; Kamitani and Tong, 2006), identifying the cognitive states associated with object categories, such as houses (Cox & Savoy, 2003; Hanson et al., 2004; Haxby et al., 2001; Haynes & Rees, 2006; O'Toole et al., 2007), tools and dwellings (Shinkareva et al., 2008), nouns with pictures (Mitchell et al., 2008), nouns (Just et al., 2010), words and pictures (Shinkareva et al., 2011), emotions (Kassam et al., 2013), episodic memory retrieval (Chadwick et al., 2010; Rissman et al, 2010), mental states during algebra equation solving (Anderson et al., 2011) and decoding images of remembered scenes (Naselaris et al., 2015). More recently, these multivariate fMRI techniques have also been applied to the number domain to investigate neural coding of individual quantities and to determine whether there is indeed a common representation for quantities across different input forms (Damarla & Just, 2013; Eger et al., 2009).
Previous studies have demonstrated that individual numbers expressed as dots and digits (Eger et al., 2009) and quantities of objects (Damarla & Just, 2013) can be accurately decoded from neural patterns. Additionally, these studies have provided converging evidence for better individual number identification for non-symbolically presented quantities than symbolic digits in the visual domain. Furthermore, the findings demonstrated only partial or asymmetric generalization of neural patterns across the different input modes of presentation, questioning whether there is a truly abstract number representation. Finally, Damarla & Just (2013) showed that neural patterns underlying numbers were common across people only for the non-symbolic mode.
While earlier studies on number representations have provided important insights into how visually-depicted numbers are fundamentally represented in the brain, there is scarcity of evidence concerning the neural representation underlying auditorily presented numbers (Eger et al., 2003; Piazza et al., 2006). More importantly, given the findings of previous studies in the visual domain suggesting a shared representation for numbers presented non-symbolically, the current study was designed to test whether these neural representations for non-symbolically presented quantities were common across different input modalities as well. To our knowledge, the question of a neural representation of quantity that is common across modalities has not been previously investigated using machine learning (multi-voxel) methods. Furthermore, the study aimed to explore the commonality of neural representations of quantities across people in either modality.
Methods
Participants
Nine right-handed adults from the Carnegie Mellon community (one male), mean age 24.9 years (SD = 2.15; range = 21-28 years) participated and gave written informed consent. This study was approved by the University of Pittsburgh and Carnegie Mellon University Institutional Review Boards. All participants were financially compensated for the practice session and the fMRI data collection.
Experimental Paradigm
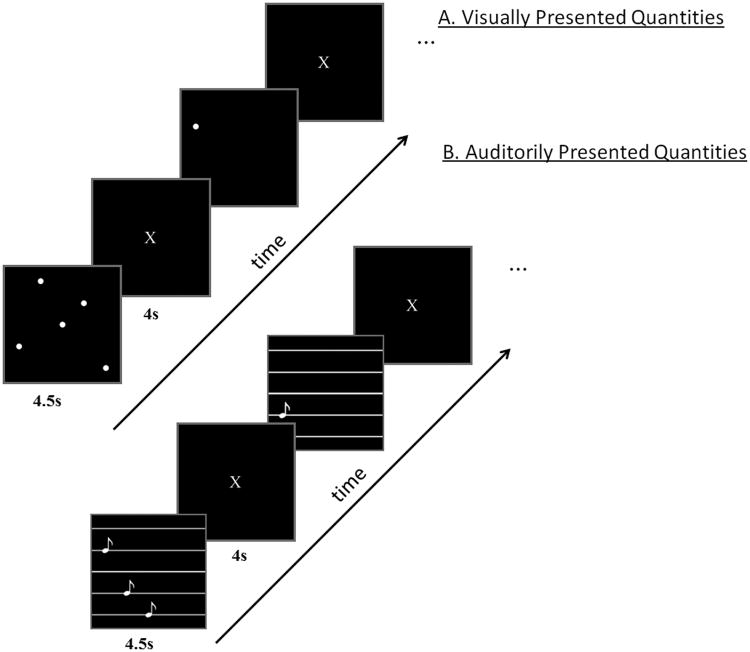
Stimuli were presented in the visual or auditory modality. In both modalities, participants were asked to determine the number of dots or tones presented, i.e. 1, 3 or 5, but no overt response was required. The visual stimuli were white dots on a black background and the auditory stimuli were pure tones. There were 3 possible quantities (1, 3, and 5), and two exemplars of each quantity. The alternate visual exemplars depicted dots indifferent locations and the auditory exemplars consisted of different tone frequencies (200-600Hz). The resulting six stimuli per modality (3 quantities and 2 exemplars per quantity) were presented eight times in separate blocks of trials, each time in a different random order. The presentations in the two modalities were made as similar as possible in terms of temporal sequence of presentation and duration. That is, the presentation of both the dots and the tones was sequential and started at the beginning of a 4.5s window with an interstimulus interval of 300ms. All three visually-depicted quantities remained on the screen until the end of 4.5s window. Each stimulus presentation was followed by a 4 s rest period (to accommodate for the hemodynamic response), during which the participants were instructed to fixate on an X displayed in the center of the screen. There were five presentations of a fixation period, 31 s each, distributed across the session, to provide a baseline measure of activation. A schematic diagram of the paradigm is shown in Figure 1.
Figure 1.
A schematic diagram of the experimental paradigm. A. Visually presented quantities (dots). B. Auditorily presented quantities (tones).
The study used a single event related design with the treatment of the hemodynamic response being different from those of conventional event related designs. The fMRI data from each trial consisted of the mean of 4 images (1 per sec) starting at 5 sec after stimulus onset and ending 4 sec later, capturing the peak of the activation response in this paradigm. This experimental paradigm and the 4-sec interval were chosen based on previous neurosemantic fMRI studies (e.g. Damarla & Just, 2013; Just et al., 2010; Mitchell et al., 2008; Shinkareva et al., 2012) that attempted to optimize classification accuracy. Since the stimuli were presented in a different random order in each block, there should be no systematic sequential dependencies that the classifier can learn from the negligible overlap between consecutive trials. Thus the results should be unbiased and, at worst, the classification accuracies should be, at least, as accurate as our results indicate below. It is possible that longer intervals between successive stimuli would have completely eliminated any overlap between the activation responses to successive stimuli (which were in different random orders in the different blocks of trials) and thereby increased the classification accuracies, so our results could be underestimates of how accurately these neural representation can be classified.
fMRI Procedure
Functional images were acquired on a Siemens Allegra 3.0T scanner (Siemens, Erlangen, Germany) at the Brain Imaging Research Center of Carnegie Mellon University and the University of Pittsburgh, using a gradient echo EPI pulse sequence with TR = 1000 ms, TE = 30 ms, and a 60° flip angle. Seventeen 5-mm thick oblique-axial slices were imaged with a gap of 1 mm between slices. The acquisition matrix was 64 × 64 with 3.125 × 3.125 × 5 mm voxels. The voxel dimensions used in the current study are asymmetric. However, to our knowledge there is no evidence that asymmetrical voxel dimensions cause any bias in classification. The success of the classification in this study and in other previous studies with asymmetrical voxel dimensions indicates the adequacy of the spatial resolution and voxel size and shape that was used (Abrams et al., 2011; Just et al., 2010; Mitchell et al., 2008; Rissman et al., 2010; Shinkareva et al., 2012).
fMRI Data Processing for Machine Learning
Initial signal processing was performed with Statistical Parametric Mapping software (SPM2, Wellcome Department of Imaging Neuroscience, London, UK). The data were corrected for slice timing, motion, and linear trend, and were temporally smoothed with a high-pass filter using a 190 s cutoff. The data were normalized to the Montreal Neurological Institute (MNI) template brain image without changing voxel size. The acquired brain images were parcellated using regional definitions derived from the Anatomical Automatic Labeling (AAL) system (Tzourio-Mazoyer et al., 2002).
The percent signal change (PSC) relative to the fixation condition was computed at each voxel for each item presentation. To compute the mean PSC for individual items or trials, the mean of 4 images acquired once per sec within the 4s window from 5s to 8s after stimulus onset was used. This value served as the main input measure for the classifiers' training and testing. Because each trial or item presentation was 4.5 seconds long, the window for the preceding trial was part of the inter-item rest period (or empty inter stimulus interval) that followed it. These methods are similar to other machine learning fMRI studies (Damarla & Just, 2013; Just et al., 2010; Kassam et al., 2013; Mitchell et al., 2008). The brain images (consisting of mean PSC data for each voxel) for each item presentation were further normalized to have mean zero and variance one, to provide data that are better suited for classification.
Machine Learning Methods
Classifiers were trained to identify neural representations associated with each visually or auditorily presented quantity, using the evoked pattern of functional activity (mean PSC). Classifiers were functions f of the form: f: mean_PSC → Yj, j={1, …, m}, where Yj was one of the three quantities (1, 3, or 5), where m was 3 and where mean_PSC was a vector of mean PSC in voxel activations, as described above. To evaluate classification performance, trials were divided into training and test sets. To reduce the dimensionality of the data, relevant features (voxels) were extracted from the training set prior to classification (see Feature Selection, below). A classifier was built from the training set using the selected features and was evaluated on the left-out test set, to ensure unbiased estimation of the classification error. Our previous explorations indicated that several feature selection methods and classifiers produced comparable results.
Classification
We used the Gaussian Naïve Bayes (GNB) pooled variance classifier for classification purposes (Mitchell, 1997). It is a generative classifier that models the joint distribution of a class Y (e.g., quantities or modalities) and attributes (voxels), and assumes the attributes X1, …, Xn are conditionally independent given Y. The classification rule is:
In this study, all classes were equally frequent. Rank accuracy (the mean normalized rank of the correct response in the probability-ordered list generated by the classifier, where chance level is 0.5) was used to evaluate 3-class classification. Classification results were evaluated using k-fold cross-validation described below. To evaluate the significance of obtained rank accuracies, random permutation tests (10,000 permutations) were performed for each type of classification.
Feature Selection
Features (voxels) were selected from the training set (training presentations), computed separately for each fold of the data selecting the 120 parietal or 120 frontal voxels whose vectors of response intensities to the set of stimulus items were the most stable over the set of presentations in the training set. (Previous studies indicated that 120 voxels (3.125 × 3.125 × 6 mm) typically are sufficient to obtain accurate classification of semantic representations (Just et al., 2010)). Considering only the most stable voxels, i.e. the ones that respond similarly to the stimulus set each time the set is presented. Only the activation levels of relatively stable voxels were assumed to provide information about quantities. A voxel's stability was computed as the average pairwise correlation between its 6-item (3 quantities times 2 exemplars of each quantity) activation profile across presentations in the training set. The feature selection process does not introduce any statistical bias in the data as voxels were chosen based exclusively on their activation in the training set.
To determine the locations of stable voxels that were common across participants, group stability maps were computed by first creating masks for the stable voxels that were common in at least six cross-validation folds with a cluster size of 5 contiguous voxels within each participant. Then these masks were averaged across participants showing only those voxels that were common in at least two participants with a minimum cluster size of 12 contiguous voxels. Such maps were created for frontal and parietal regions within each presentation modality separately. These methods to compute stability maps are similar to previously used ones in machine learning fMRI studies (Damarla & Just, 2013).
Cross Validation
Cross-validation procedures were used to obtain mean rank accuracies of the classification within each participant. In each fold of the cross-validation, the classifier was trained on the labeled data from six of the eight presentations or blocks and then tested on the mean data of the remaining two left-out blocks. This N-2 cross-validation procedure resulted in 28 possible cross-validation folds, and the mean rank accuracy of the classification was obtained by averaging the accuracies across the 28 folds. The training and test sets were always independent.
Within Participant Analysis
Cross-validation procedures were used to obtain mean rank accuracies of the classification within each participant. In each fold of the cross-validation, the classifier was trained on the labeled fMRI data from one set of presentations and then tested on the mean of an independent set. For within-participant, within-modality classification, the training set consisted of the fMRI data from 6 of the 8 presentations for each fold, and the classifier was tested on the mean of the remaining 2 presentations, resulting in 28 cross-validation folds. There were 6 items per presentation (labelled in terms of the three possible quantities and 2 exemplars per quantity). For within-participant, cross-modality classification, the selection of the 120 diagnostic voxels was based on their stability across the 6 presentations of the training modality and 6 of the 8 presentations of the test modality (i.e. excluding the 2 presentations being tested in the fold). The classifier was trained on all 8 presentations of the training modality data, and then tested on the mean of 2 presentations of the test modality data (the 2 presentations not involved in stability assessment). The resulting classification accuracies were averaged across all items and folds.
Between Participant Analysis
A classier was trained on data from all but one participant and then tested on the data from the left-out participant. The mean of 8 presentations of each item (either auditory or visual modality) was computed for each participant separately. Feature selection identified the voxels whose responses were the most stable in the set of eight participants in the training set. The 120 most stable voxels were selected, where voxel stability across training participants was computed as an average pairwise correlation between the activation profiles of the 6 items' (3 quantities and 2 exemplars per quantity) across eight participants in the training set. The same 120 voxels obtained were used in the training set were also used in testing the left-out participant. This process was repeated 9 times so that it reiteratively left out each of the participants.
Results
Overview
The central findings of the study demonstrated that a classifier trained on activation patterns evoked by quantities in one modality was able to classify quantities in the other modality. Second, in either modality, it was possible to accurately classify quantities from a given participant's activation data even if the classifier was trained exclusively on the data from other people. Finally, classification errors tended to preserve numerical inter-item distance information.
Cross-modality quantity classification
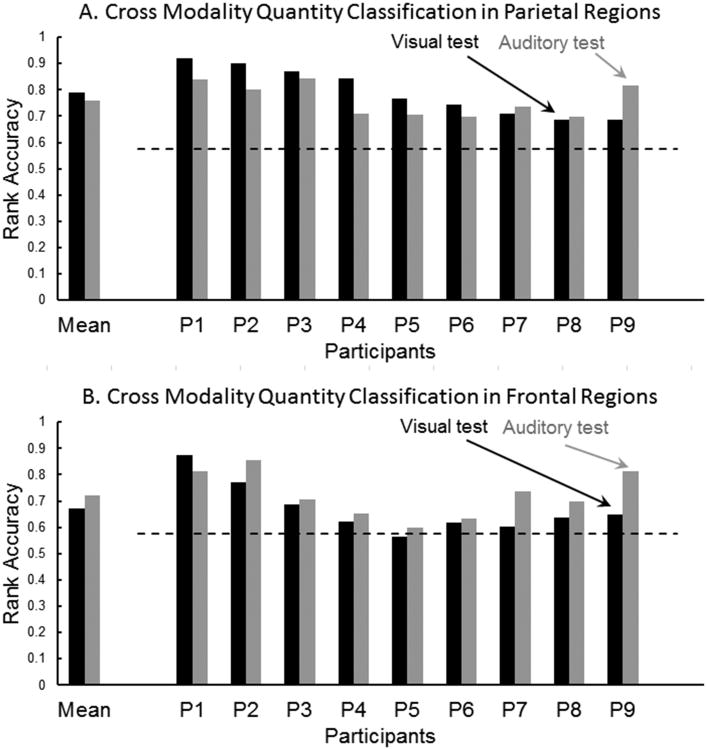
As a first step, cross-modality quantity classification accuracies (in both directions) were computed using voxels from only one of 40 AAL-based anatomical regions (Tzourio-Mazoyer et al., 2002) at a time. The mean accuracies (across 9 participants) were significant (at p < .05, Bonferroni-corrected) for 20 regions from bilateral parietal and frontal lobes, regardless of which modality was used as the training or test modality. The majority of the brain regions supporting quantity classification belongs to bilateral frontal and parietal lobes, although accurate quantity classification was also obtained for a few posterior temporal regions. For the parietal lobes, these regions included bilateral inferior and superior parietal lobules, intraparietal sulci, and postcentral regions. For the frontal lobes, the regions that supported accurate cross-modality quantity classification included bilateral precentral, superior frontal, and inferior frontal (opercularis) regions. Based on these initial analyses and on several previous neuroimaging studies implicating parietal and frontal regions in number representation (Cohen Kadosh et al., 2007; Cohen Kadosh & Walsh, 2009; Dehaene, 2003; Eger et al., 2003; 2009 Libertus et al., 2007; Nacache & Dehaene, 2001a; Pinel et al., 2001), the main analyses below focus on only parietal and frontal regions. When the classifier was trained on exemplars of quantities in one modality (using as features the stable voxels in the regions of the parietal lobe), it was possible to classify quantities in the other modality. When the classifier was trained on the neural patterns evoked by the auditory modality and tested on the visual modality, the mean within-participant classification rank accuracy was .79. When the classifier was trained on the visual modality and tested on the auditory modality, the mean within-participant rank accuracy was .76 (chance level of p<.01 is .58). For all 9 participants in both classifications, the accuracies were above thep <.01 level, as shown in Figure 2A. Thus there is reliable cross modal classification of small quantities based on parietal lobe representations.
Figure 2.
Cross-modality quantity classification. A. Parietal regions. B Frontal regions. Black and gray bars represent accuracy for testing visual and auditory modality respectively. The dashed line indicates the p < .01 chance level accuracy (0.58).
Accurate cross-modal classification was also obtained when the classifier's features were voxels from the frontal lobe. When the classifier was trained on the auditory modality activation and tested on the visual modality activation, the mean classification accuracy was .67, above the p < .01 level for 8 of 9 participants. When the classifier was trained on the visual modality and tested on the auditory modality, the mean classification accuracy was .72, above the p < .01 chance level for all participants, as shown in Figure 2B. Thus there is also reliable cross modal classification of small quantities based on frontal lobe representations.
Within-modality quantity classification
The classification accuracies were some what higher within a modality than across modalities. For example, using parietal lobe voxels as features, the mean accuracies were .84 and .86 for the auditory and visual modalities respectively, above the p < .01 chance level for all participants. When frontal lobe voxels were used as features, the mean accuracies were .80 and .74 for the auditory and visual modalities respectively, with all participants' accuracies falling above the p < .01 chance level. Although the main focus of this article is on cross-modality classification, the very high within-modality classification accuracy is also notable.
Commonality of quantity representations across participants
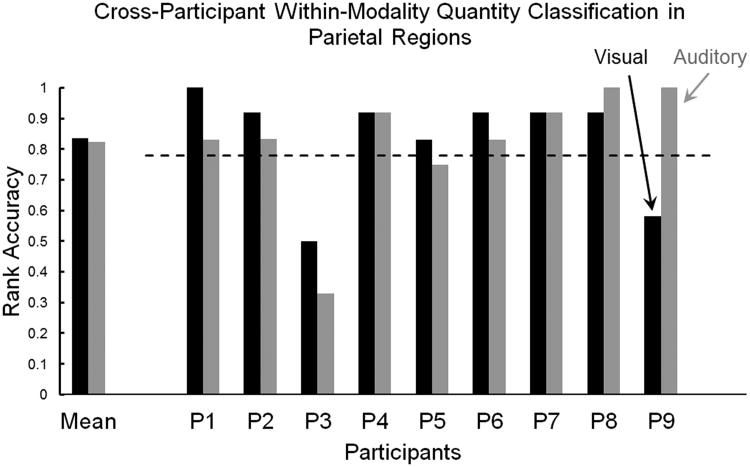
Classifiers were trained on data from eight of nine participants to determine if it was possible to identify each quantity (within each modality separately) in the held-out participant's data. When the classifier's features (voxels) were from the parietal lobe, the mean accuracies across participants in visual and auditory modalities were .83 (SD=.17) and .82 (SD=.20), respectively. Thus there is a great deal of commonality of the neural representation of quantities across participants in the parietal lobe. Reliable cross-participant classification accuracies (.78 represents a chance level of p <.05) were reached for seven out of nine participants in the visual modality (black bars in Figure 3) and the auditory modality (gray bars in Figure 3), using as features voxels from parietal regions.
Figure 3.
Cross-participant within-modality quantity classification in parietal regions. Gray bars represent auditory modality, black bars represent visual modality. The dashed line denotes the p < .05 chance level.
Unlike the parietal-based classification, when the features were voxels from the frontal lobe, the mean cross-participant quantity classification was below the p < .05 level of significance. Thus, there is a commonality of quantity representations across participants in the parietal lobe, but much less so in the frontal lobe.
Note that the substantial difference in the critical values of the rank accuracies for the within-participant (.58, p<.01) and between-participants (.78, p<.05) quantity classifications is a consequence of the differences in the number of entries contributing to the mean accuracy (168 entries for within- and 6 for between-participants analyses)(see footnote 2).
Quantity classification across lower-level stimulus properties
To assess the influence of lower-level stimulus properties on number representations, quantities of dots were presented in two different spatial configurations and quantities of tones were presented using two different sets of frequencies. The classifier trained on data from only one sample of dot configurations or tone frequencies was able to classify quantities in the other sample of dot configurations or tone frequencies based on activation in either parietal or frontal regions.
Within the parietal lobe, when the classifier was trained on data from one set of dot configurations (using as features parietal lobe voxels), the quantity classification accuracies for the same spatial configuration and for the other spatial configuration were .86 (SD =.06) and .80 (SD=.05) respectively (the p <.01 level is .61). Similarly, when the classifier was trained on tones of one set of frequencies, the classification accuracies for the same and different frequencies were .81 (SD = .05) and .76 (SD =.04) respectively.
Within the frontal lobe, the mean classification accuracies when trained and tested on the same and different spatial configuration of dots were .71 (SD = .06) and .66 (SD = .08) respectively (the p < .01 level is .61). Similarly, in the auditory modality, when the classification was based on frontal lobe voxels, the accuracies for the same and other set of tone frequencies were .79 (SD =.05) and .71 (SD = .06) respectively.
These results indicate that based on either parietal or frontal activation information, there is accurate classification of quantities arranged in a different perceptual configuration, although the accuracy is somewhat higher if the configural properties are the same. More generally, the neural representations of quantity have a very large degree of commonality across different perceptual configurations of the quantities.
Numerical distance effects
There was evidence of a distance-preserving representation of numerical values, indicated by the classifier's confusion errors for within-modality classifications. When the correct quantity label was one of the extreme values, 1 or 5, and the classifier's top ranked predicted label was incorrect, the incorrect guess was much more often the proximal number than the distal number (e.g. if the actual quantity was 5 and highest ranked predicted quantity was incorrect, the incorrect prediction was much more likely to be 3 than 1). A paired t-test for dot quantities revealed a significantly greater number of numerically proximal incorrect predictions than numerically distal incorrect predictions, both when the classification was based on parietal voxels (t(8) = 6.07, p < .001) and on frontal voxels (t(8) = 6.4, p < .001). Similarly, for tone quantities, a paired t-test revealed a significantly greater number of numerically proximal incorrect predictions than numerically distal incorrect predictions, based on parietal voxels (t(8) = 7.78, p < .001) and also on frontal voxels (t(8) = 7.07, p < .001). Thus the neural representations of quantities retain some of the monotonicity of the quantitative information in both parietal and frontal regions.
Very similar distance-preserving effects were also found in the cross-modality analyses, regardless of the direction of prediction. When the classifier was trained on the auditory quantities data and tested on visual quantities, similar t-tests for the parietal (t(8) = 5.35, p < .001) and frontal (t(8) = 5.34, p < .001) areas demonstrated that the proximal quantity was more frequently confused with the actual quantity than with the distal quantity. Similarly, when the classifier was trained on the visual quantities data and tested on auditory quantities, both the parietal (t(8) = 5.11, p < .001) and frontal (t(8) = 3.42, p < 0.01) voxels demonstrated similar significant distance-preserving effects.
Stability maps: Locations of the stable voxels for each modality in parietal and frontal regions
The stability maps were computed as a posthoc analysis only to visualize the exact location of some of the stable voxels in frontal and parietal lobes that determined quantity classification. Averaged stability maps were computed separately for parietal and frontal lobes, separately within each presentation modality. First, masks were created for each participant (a total of nine masks) that included stable voxels common across at least six folds with a minimum threshold of five contiguous voxels. Second, these individual masks were averaged across all participants resulting in one stability map for either frontal or parietal lobe within a modality. These maps show the locations of the voxels that were common in at least two participants with a threshold of twelve contiguous voxels.
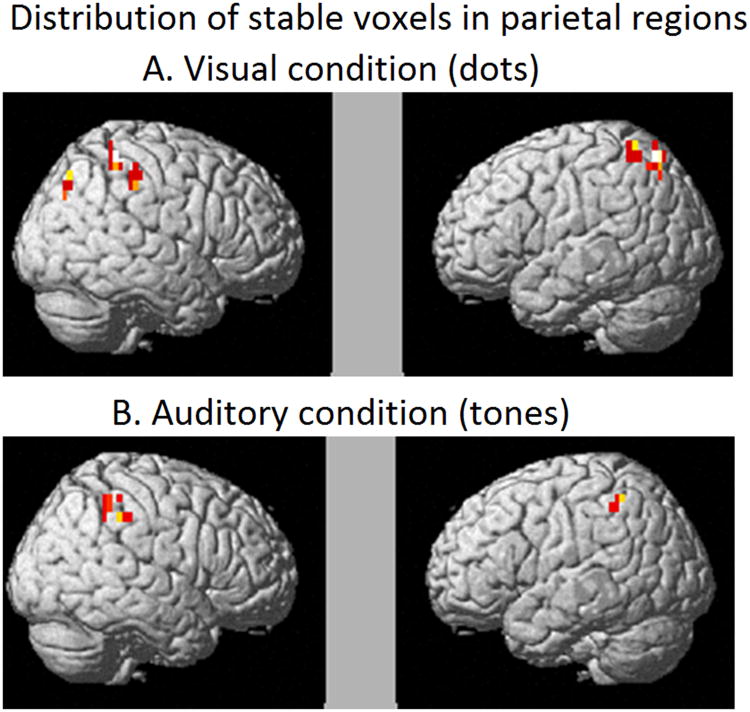
Although the locations of the most stable voxels were distributed bilaterally in the parietal regions in both the modalities, there was a greater number of stable voxels in the right hemisphere indicating some degree of hemispheric asymmetry in the representations of non-symbolic quantities (Damarla & Just, 2013). Additionally, some of the stable voxels in the right parietal region overlapped across the two modalities, as shown in Table 1 and Figure 4, suggesting common neuronal representations for symbolically presented quantities. Finally, the locations of the stable clusters primarily in right parietal and also some in left (IPS and SPL) are consistent with the coordinates that previously have been implicated in numerical processing (Cohen Kadosh et al., 2007; Dehaene et al., 2003).
Table 1. Distribution of stable voxels in parietal regions in quantity classification.
| A. Region labels and coordinates of cluster centroids in visual condition | |||||
|---|---|---|---|---|---|
|
| |||||
| Label | Voxels | Radius | x | y | z |
| IPS/Parietal_Sup_R | 17 | 9 | 24 | -68 | 45 |
| Intraparietal sulcus/IPL_R | 16 | 8 | 37 | -42 | 52 |
| SupraMarginal_R | 7 | 5 | 49 | -31 | 46 |
| IPS/Parietal_Sup_L | 13 | 6 | -21 | -67 | 57 |
| Parietal_Sup_L | 8 | 5 | -27 | -51 | 60 |
|
| |||||
| B. Region labels and coordinates of cluster centroids in auditory condition | |||||
|
| |||||
| Label | Voxels | Radius | x | y | z |
|
| |||||
| Intraparietal sulcus/IPL_R | 16 | 7 | 40 | -41 | 46 |
| Intraparietal sulcus/IPL_L | 5 | 4 | -40 | -48 | 52 |
Note: Minimum cluster size of five and inclusion of at least two participants
Figure 4.
Within participants stability maps (averaged across participants) indicating stable voxels in at least two participants in parietal regions. A. Visually presented quantities (dots). B. Auditorily presented quantities (tones).
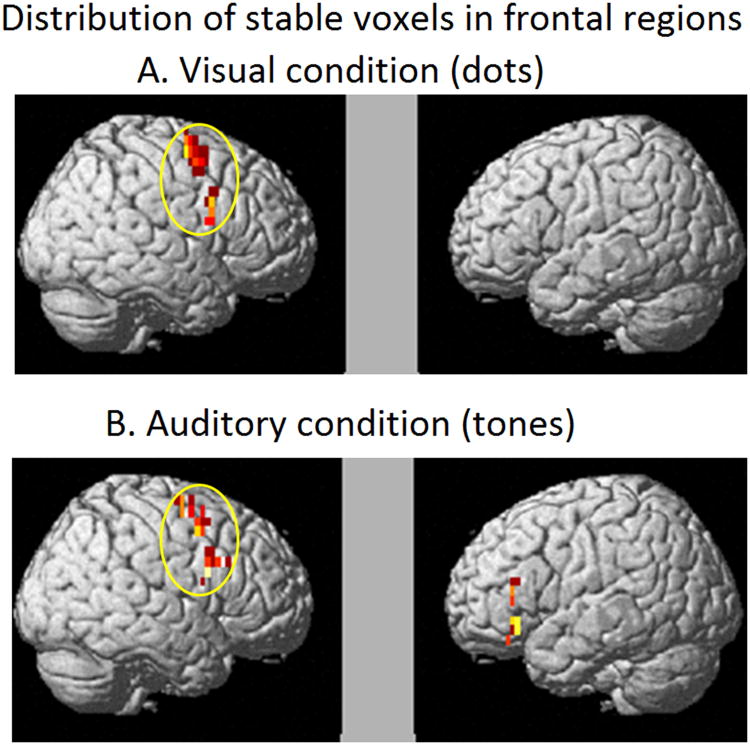
The stable voxels for the visually depicted quantities were found in right inferior and superior frontal regions, whereas for the auditorily-depicted quantities, they were bilaterally located in IFG and superior medial/precentral regions. As was the case for the parietal region, there was an overlap of stable voxels across the two modalities in frontal (right frontal) regions, as shown in Table 2 and Figure 5. And as was the case for the parietal region, there was right hemisphere dominance in the frontal lobe.
Table 2.
Distribution of stable voxels in frontal regions in quantity classification.
| A. Region labels and coordinates of cluster centroids in visual condition | |||||
|---|---|---|---|---|---|
|
| |||||
| Label | Voxels | Radius | x | y | z |
| Frontal_Inf_Oper_R | 16 | 8 | 52 | 9 | 26 |
| Frontal_Sup_R | 30 | 8 | 28 | -2 | 58 |
|
| |||||
| B. Region Labels and coordinates ofcluster centroids in auditory condition | |||||
|
| |||||
| Label | Voxels | Radius | x | y | z |
|
| |||||
| Frontal_Inf_Orb_L | 12 | 6 | -44 | 30 | -10 |
| Frontal_Inf_Tri_L | 6 | 5 | -44 | 31 | 12 |
| Frontal_Inf_Oper_R | 18 | 7 | 52 | 13 | 28 |
| Frontal_Sup_Medial_R | 8 | 4 | 3 | 31 | 43 |
| Supp_Motor_Area_R | 15 | 6 | 3 | 20 | 48 |
| Precentral_R | 6 | 4 | 41 | 4 | 49 |
| Frontal_Sup_R | 20 | 7 | 26 | -2 | 59 |
Note: Minimum cluster size of five and inclusion of at least two participants
Figure 5.
Within participants stability maps (averaged across participants) indicating stable voxels in at least two participants in frontal regions. A. Visually presented quantities (dots). B. Auditorily presented quantities (tones).
Thus, the common representations for non-symbolically presented quantities across the two modalities were mainly right lateralized in both parietal and frontal regions suggesting a dominant role of the right hemisphere in coding perceptually displayed non-symbolic quantities.
Discussion
This study showed, for the first time, that the neural representations of small quantities were common across different sensory modalities in both frontal and parietal regions. Moreover, the brain activation patterns evoked by individual quantities, in either modality, were general across people in parietal regions. Third, the neural patterns underlying individual quantities generalized across low-level perceptual properties (different spatial positioning of dots or different frequencies of tones). Finally, there was an indication of monotonicity in the neural representations of quantities, in both the modalities.
Neural Representations of Quantities across Modalities
The central finding of common neural patterns underlying individual quantities across modalities and across people signify the presence of stable and modality-general neural representations of perceptually depicted quantities.
This study involving perceptual representations is necessarily limited to relatively small quantities, so the conclusions may be limited to only relatively small quantities, but it is unclear whether the line is to be drawn at the subitizing threshold or somewhat above that, given previous findings of successful classification of quantities based on fMRI brain activation patterns both within and outside the subitizing range (e.g. 2, 4, 6 and 8) (Damarla & Just, 2013; Eger et al., 2009).
Many recent functional imaging studies on numerical cognition have suggested that visually-depicted non-symbolic quantities are represented more coarsely in the brain in comparison to symbolic quantities (Ansari, 2008; Piazza et al., 2007). A recent study by Damarla and Just (2013) showed that neural patterns underlying a given number were common across different objects (e.g. three-ness common across 3 tomatoes and 3 cars) only for non-symbolically presented quantities. The current study goes beyond the visual domain and provides evidence in favor of common neural representations of numbers across different perceptual modalities.
The neural representation of specific quantities of dots and tones were found to be largely overlapping and, hence classification was possible across the two perceptual modalities. Not only were the patterns of activation similar but also some of the locations of diagnostic (stable) voxels were similar across modalities. These modality-independent representations of non-symbolic quantities signify the presence of stable number-specific neural representations (Ansari, 2008; Piazza et al., 2007).
The finding of cross-participant commonality of neural representations of quantities in either modality contribute to the growing realization of how similarly human brains implement neural representations for shared concepts (Damarla & Just, 2013, Just et al., 2010; Shinkareva et al., 2008). Current theories suggest that quantities depicted as a number of discrete objects are developmentally fundamental, compared to symbolically conveyed quantities (Ansari, 2008; Dehaene, 1997; Piazza et al., 2007; Verguts & Fias, 2004). Perhaps it is due to this fundamental nature that the neuronal substrate coding for “three-ness” or “one-ness” was found to be common across participants. However, it is interesting to note that the generality of these representations over participants applied only to parietal regions and not frontal regions. One possible explanation for the poor cross-participant classification of quantities in frontal regions is that there may be greater variability in localization of function in frontal regions across individuals (Christoff et al., 2004; Duncan et al., 2000).
In the analyses that were performed within participants (namely classification across modalities and across perceptual configurations), the frontal regions did prove to contain common information, so the frontal lobes demonstrate other types of commonality. The commonality of neural patterns within parietal and frontal regions associated with a quantity (within a modality) generalized to the same number regardless of different spatial configuration or different auditory frequencies. These findings suggest that the representation of quantities within these regions is based on numerical magnitude rather than low-level perceptual features (different shapes or melodies for the same number). The findings of purely quantity-based representation are consistent with the findings of a previous study by Eger and colleagues (2009).
Interestingly, these modality-independent representations were found in both parietal and frontal regions. Although, most studies have indicated the importance of parietal regions in numerical processes (Dehaene, 1996; Eger et al., 2003; Libertus et al., 2007; Nacache & Dehaene, 2001a; Piazza et al., 2007; Pinel et al., 2001), there is growing evidence from human neuroimaging studies that have demonstrated the prefrontal cortex to be involved in numerical quantity representation as well (Venkatraman et al., 2005; Holloway et al., 2010). This study adds to the growing evidence of the presence of numerical representations, at least for non-symbolic quantities, in both frontal and parietal regions.
Furthermore, the findings of the current study also indicate that there is a bilateral representation for quantities but with more right hemispheric involvement as indicated by the greater number of stable voxels in right than left hemisphere areas. This hemispheric asymmetry was found in both frontal and parietal regions and in both modalities. This is consistent with findings in recent studies showing greater activation or greater numbers of participating voxels in the right parietal region for non-symbolic in comparison to symbolic quantities (Holloway et al., 2010; Damarla & Just, 2013). Additionally, a developmental study by Cantlon and colleagues (2006) reported that a common neural substrate for non-symbolic quantities in preschool children and in adults was found in right IPS, suggesting that right parietal regions may contain more primitive representations for non-symbolic quantities shared by both children and adults. Finally, a study using symbolic/non-symbolic arithmetic implicated both right frontal and parietal regions to be dominant for non-symbolic addition over symbolic ones (Venkatraman et al., 2005). Altogether, there seems to be converging evidence in favor of stronger representations of non-symbolic quantities in the right hemisphere.
Finally, in either modality, the neural activation patterns within both parietal regions and frontal regions were more confusable for the classifier for similar or numerically closer quantities, and the same was true for the cross-modality classifications, regardless of the direction. Previous macaque studies have shown that neurons in lateral prefrontal cortex have more similar firing rates for more proximal visually-presented non-symbolic numbers (Neider et al., 2002). Additionally, neuroimaging studies using both univariate (Pinel et al., 2001) and multivariate approaches (Eger et al., 2009; Damarla & Just, 2013) have demonstrated that parietal representations for numbers preserve some numerical distance information. Here we show that the neural patterns in both frontal and parietal regions for two proximal quantities are more similar than distal quantities regardless of the stimulus modality, and regardless of the training modality for the cross-modality classifications. This result provides evidence for a modality-independent neural representational similarity between numbers that are numerically close to each other and parallels the observations of numerical distance effects found in previous behavioral studies (Moyer &Landauer, 1967).
Another approach for comparing neural representations in addition to the MVPA cross-classification used in this article is fMRI adaptation (fMRIa) as a measure of similarity between two representations. Would fMRIa indicate the same degree of between-modality overlap in the neural representation of quantities as in the current study? Previous studies in domains other than number that used both approaches found that: (1) the fMRI MVPA approach was more sensitive than fMRIa in capturing neural differences between stimuli in a study of orientation (Sapountzis et al. 2009) and (2) the differences in spatial scale of neural representation underlying a cognitive process might also lead to different results (Drucker and Aguire, 2009). While fMRIa was found to be sensitive in capturing more focused coding of the entire shape space found in ventral LOC or lateral occipital complex (within a voxel), MVPA methods showed a strong correspondence of the distributed neural pattern and stimulus similarity in lateral LOC indicating a course spatial coding of shape features (Drucker and Aguire, 2009).
In the number domain, an fMRIa study found that adaptation for quantities generalized across notations in the same modality, indicating a notation-independent representation for visually presented approximate numbers (Piazza et al., 2007). Additionally, the current study using multivariate approach provides evidence of modality-independent representations for quantities. Given that both these two studies indicate some degree of abstraction in number representation, it is plausible that an fMRIa method applied to our question would find converging results. Direct comparison of the two methods within a single study to assess the cross-modality quantity representation similarities and differences might provide additional insights into the brain's coding schemes.
Conclusion
The novel findings of the current study were cross-modality representations of non-symbolic numbers in both frontal and parietal regions, indicating the presence of stable neural representations of numbers. Additionally, the findings demonstrate cross-participant commonalities of neural representations in parietal regions in either modality suggesting frontal regions to be more variable across people. Finally, the study provides further evidence for greater neural overlap between proximal than distalnon-symbolically presented quantities (Eger et al. 2009; Damarla &Just, 2013). The location of the voxels that were predictive of quantity indicate that there is hemispheric asymmetry with right frontal and right parietal having greater involvement in representation of quantities in either modality than their left hemisphere homologs. While the study provides several novel insights into the representation of small numbers, it will be important for future studies to investigate how these insights apply to the representation of a larger set of consecutive numbers and other types of quantitative concepts.
Acknowledgments
This research was supported by NIMH Grant MH029617. The authors thank Justin A. Abernethy for assistance with the data collection, and Sandesh Aryal for help with data analysis.
Footnotes
Rank accuracy is calculated as the normalized rank of the correct class in the classifier's rank-ordered list of all classes.
Significance levels were determined by random permutation testing. Our approach was to simulate the predictions of a classifier that has absolutely no information about the classes while keeping all of the classification parameters (the number of classes, data folds, and classifier predictions in each fold) exactly the same as in the actual classification procedures. After performing a large number (10000) of such simulations, the distribution of predicted rank accuracies was obtained, and the cutoff rank accuracy values corresponding to the p-values of .05 or .01 were estimated. These estimates were obtained and compared to the rank accuracies of real classifiers for each reported classification.
References
- Abrams DA, Bhatara A, Ryali S, Balaban E, Levitin DJ, Menon V. Decoding temporal structure in music and speech relies on shared brain resources but elicits different fine-scale spatial patterns. Cerebral Cortex. 2011;21(7):1507–1518. doi: 10.1093/cercor/bhq198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JR, Betts SA, Ferris JL, Fincham JM. Tracking children's mental states while solving algebra equations. Human Brain Mapping. 2011 doi: 10.1002/hbm.21391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansari D. Effects of development and enculturation on number representation in the brain. Nature Reviews Neuroscience. 2008;9:278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Ansari D, Dhital B. Age-related changes in the activation of the intraparietal sulcus during non-symbolic magnitude processing: An event-related fMRI study. Journal of Cognitive Neuroscience. 2006;18:1820–1828. doi: 10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ansari D. Does the parietal cortex distinguish between “10”, “Ten” and “Ten Dots”? Neuron. 2007;53:165–167. doi: 10.1016/j.neuron.2007.01.001. [DOI] [PubMed] [Google Scholar]
- Arrighi R, Togoli I, Burr DC. A generalized sense of number. Proceedings of the Royal Society B: Biological Sciences. 2014;281(1797) doi: 10.1098/rspb.2014.1791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth H, Kanwisher N, Spelke E. The construction of large number representations in adults. Cognition. 2003;86:201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
- Bulthé J, De Smedt B, Op de Beeck H. Visual number beats abstract numerosity: Format-dependent representations of Arabic digits and dot patterns in the human parietal cortex. Journal of Cognitive Neuroscience. 2015 doi: 10.1162/jocn_a_00787. [DOI] [PubMed] [Google Scholar]
- Bulthé J, De Smedt B, Op de Beeck HP. Format-dependent representations of symbolic and non-symbolic numbers in the human cortex as revealed by multi-voxel pattern analyses. Neuroimage. 2014;87:311–322. doi: 10.1016/j.neuroimage.2013.10.049. [DOI] [PubMed] [Google Scholar]
- Cantlon J, Brannon EM, Carter EJ, Pelphrey K. Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biology. 2006;4:e125. doi: 10.1371/journal.pbio.0040125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chadwick MJ, Hassabis D, Weiskopf N, Maguire EA. Decoding individual episodic memory traces in the human hippocampus. Current Biology. 2010;20:544–547. doi: 10.1016/j.cub.2010.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chochon F, Cohen L, van de Moortele PF, Dehaene S. Differential contributions of the left and right inferior parietal lobules to number processing. Journal Cognitive Neuroscience. 1999;11:617–630. doi: 10.1162/089892999563689. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh K, Kaas A, Henik A, Goebel R. Notation-dependent and -independent representations of numbers in the parietal lobes. Neuron. 2007;53:307–314. doi: 10.1016/j.neuron.2006.12.025. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Walsh V. Numerical representation in the parietal lobes: Abstract or not abstract? Behavioral and Brain Sciences. 2009;32:313–373. doi: 10.1017/S0140525X09990938. [DOI] [PubMed] [Google Scholar]
- Cox DD, Savoy RL. Functional magnetic resonance imaging (fMRI) “brain reading”: Detecting and classifying distributed patterns of fMRI activity in human visual cortex. Neuroimage. 2003;19:261–270. doi: 10.1016/s1053-8119(03)00049-1. [DOI] [PubMed] [Google Scholar]
- Christoff K, Prabhakaran V, Dorfman J, Zhao Z, Kroger JK, Holyoak KJ, Gabrieli JD. Rostrolateral prefrontal cortex involvement in relational integration during reasoning. Neuroimage. 2001;14:1136–1149. doi: 10.1006/nimg.2001.0922. [DOI] [PubMed] [Google Scholar]
- Damarla SR, Just MA. Decoding the representation of numerical values from brain activation patterns. Human Brain Mapping. 2013;34:2624–2634. doi: 10.1002/hbm.22087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cognitive Psychology. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Dehaene-Lambertz G, Cohen L. Abstract representations of numbers in the animal and human brain. Trends in Neurosciences. 1998;21:355–361. doi: 10.1016/s0166-2236(98)01263-6. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The number sense: How the mind creates mathematics. New York: Oxford University Press; 1997. [Google Scholar]
- Dehaene S. The organization of brain activations in number comparison: Event-related potentials and the additive-factors method. Journal of Cognitive Neuroscience. 1996;8:47–68. doi: 10.1162/jocn.1996.8.1.47. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Akhavein R. Attention, automaticity, and levels of representation in number processing. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:314–326. doi: 10.1037//0278-7393.21.2.314. [DOI] [PubMed] [Google Scholar]
- Duncan J, Seitz RJ, Kolodny J, Bor D, Herzog H, Ahmed A, Newell FN, Emslie H. A neural basis for general intelligence. Science. 2000;289:457–460. doi: 10.1126/science.289.5478.457. [DOI] [PubMed] [Google Scholar]
- Drucker DM, Aguirre GK. Different spatial scales of shape similarity representation in lateral and ventral LOC. Cerebral Cortex. 2009;19(10):2269–2280. doi: 10.1093/cercor/bhn244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eger E, Michel V, Thirion B, Amadon A, Dehaene S, Kleinschmidth A. Deciphering cortical number coding from human brain activity patterns. Current Biology. 2009;19:1608–1615. doi: 10.1016/j.cub.2009.08.047. [DOI] [PubMed] [Google Scholar]
- Eger E, Sterzer P, Russ MO, Giraud AL, Kleinschmidt A. A supramodal number representation in human intraparietal cortex. Neuron. 2003;37:719–725. doi: 10.1016/s0896-6273(03)00036-9. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Formisano E, De Martino F, Bonte M, Goebel R. “Who” is saying “what”? Brain-based decoding of human voice and speech”. Science. 2008;322:970–973. doi: 10.1126/science.1164318. [DOI] [PubMed] [Google Scholar]
- Hanson SJ, Matsuka T, Haxby JV. Combinatorial codes in ventral temporal lobe for object recognition: Haxby (2001). revisited: Is there a “face” area? NeuroImage. 2004;23:156–166. doi: 10.1016/j.neuroimage.2004.05.020. [DOI] [PubMed] [Google Scholar]
- Haxby JV, Gobbini MI, Furey ML, Ishai A, Schouten JL, Pietrini P. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science. 2001;293:2425–2430. doi: 10.1126/science.1063736. [DOI] [PubMed] [Google Scholar]
- Haynes JD, Rees G. Predicting the orientation of invisible stimuli from activity in human primary visual cortex. Nature Neuroscience. 2005;8:686–691. doi: 10.1038/nn1445. [DOI] [PubMed] [Google Scholar]
- Haynes JD, Rees G. Decoding mental states from brain activity in humans. Nature Review Neuroscience. 2006;7:523–534. doi: 10.1038/nrn1931. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Price GR, Ansari D. Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: an fMRI study. NeuroImage. 2010;49:1006–17. doi: 10.1016/j.neuroimage.2009.07.071. [DOI] [PubMed] [Google Scholar]
- Just MA, Cherkassky VL, Aryal S, Mitchell TM. A neurosemantic theory of concrete noun representation based on the underlying brain codes. PLoS ONE. 2010;5:e8622. doi: 10.1371/journal.pone.0008622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamitani Y, Tong F. Decoding seen and attended motion directions from activity in the human visual cortex. Current Biology. 2006;16:1096–1102. doi: 10.1016/j.cub.2006.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kassam KS, Markey AR, Cherkassky VL, Loewenstein G, Just MA. Identifying emotions on the basis of neural activation. PLoS ONE. 2013;8:e66032. doi: 10.1371/journal.pone.0066032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Woldorff MG, Brannon EM. Electrophysiological evidence for notation independence in numerical processing. Behavioral and Brain Function. 2007;3:1. doi: 10.1186/1744-9081-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell TM. Machine learning. Boston: McGraw-Hill; 1997. [Google Scholar]
- Lyons IM, Ansari D, Beilock SL. Qualitatively different coding of symbolic and nonsymbolic numbers in the human brain. Human Brain Mapping. 2015;36(2):475–488. doi: 10.1002/hbm.22641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell TM, Hutchinson R, Niculescu RS, Pereira F, Wang X, Just MA, Newman S. Learning to decode cognitive states from brain images. Machine Learning. 2004;57:145–175. [Google Scholar]
- Mitchell TM, Shinkareva SV, Carlson A, Chang KM, Malave VL, Mason RA, Just MA. Predicting human brain activity associated with the meanings of nouns. Science. 2008;320:1191–1195. doi: 10.1126/science.1152876. [DOI] [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. Time required for judgments of numerical inequality. Nature. 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Naccache L, Dehaene S. The priming method: Imaging unconscious repetition priming reveals an abstract representation of number in the parietal lobes. Cerebral Cortex. 2001a;11:966–974. doi: 10.1093/cercor/11.10.966. [DOI] [PubMed] [Google Scholar]
- Naccache L, Dehaene S. Unconscious semantic priming extends to novel unseen stimuli. Cognition. 2001b;80:223–237. doi: 10.1016/s0010-0277(00)00139-6. [DOI] [PubMed] [Google Scholar]
- Naselaris T, Olman CA, Stansbury DE, Ugurbil K, Gallant GL. A voxelwise encoding model for early visual areas decoded mental images of remembered scenes. Neuroimage. 2015;105:218–228. doi: 10.1016/j.neuroimage.2014.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieder A, Freedman DJ, Miller EK. Representation of the quantity of visual items in the primate prefrontal cortex. Science. 2002;297:1708–1711. doi: 10.1126/science.1072493. [DOI] [PubMed] [Google Scholar]
- Notebaert K, Nelis S, Reynvoet B. The Magnitude Representation of Small and Large Symbolic Numbers in the Left and Right Hemisphere: An Event-related fMRI Study. Journal of Cognitive Neuroscience. 2011;23:622–630. doi: 10.1162/jocn.2010.21445. [DOI] [PubMed] [Google Scholar]
- O'Toole A, Jiang F, Abdi H, Penard N, Dunlop JP, Parent M. Theoretical, statistical, and practical perspectives on pattern-based classification approaches to the analysis of functional neuroimaging data. Journal of Cognitive Neuroscience. 2007;18:1–19. doi: 10.1162/jocn.2007.19.11.1735. [DOI] [PubMed] [Google Scholar]
- Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage. 2009;45(1):S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M, Pinel P, Bihan DL, Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Piazza M, Mechelli A, Price CJ, Butterworth B. Exact and approximate judgements of visual and auditory numerosity: An fMRI study. Brain Research. 2006;1106:177–188. doi: 10.1016/j.brainres.2006.05.104. [DOI] [PubMed] [Google Scholar]
- Pinel P, Dehaene S, Rivière D, LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage. 2001;14:1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Rissman J, Greely HT, Wagner AD. Detecting individual memories through the neural decoding of memory states and past experience. Proceedings of the National Academy of Sciences, USA. 2010;107(21):9849–9854. doi: 10.1073/pnas.1001028107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sapountzis P, Schluppeck D, Bowtell R, Peirce JW. A comparison of fMRI adaptation and multivariate pattern classification analysis in visual cortex. Neuroimage. 2010;49:1632–1640. doi: 10.1016/j.neuroimage.2009.09.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinkareva SV, Malave VL, Just MA, Mitchell TM. Exploring commonalities across participants in the neural representation of objects. Human Brain Mapping. 2012;33:1375–1383. doi: 10.1002/hbm.21296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinkareva SV, Malave VL, Mason RA, Mitchell TM, Just MA. Commonality of neural representations of words and pictures. Neuroimage. 2011;54:2418–2425. doi: 10.1016/j.neuroimage.2010.10.042. [DOI] [PubMed] [Google Scholar]
- Shinkareva SV, Mason RA, Malave VL, Wang W, Mitchell TM, Just MA. Using fMRI brain activation to identify cognitive states associated with perception of tools and dwellings. PLoS ONE. 2008;3:e1394. doi: 10.1371/journal.pone.0001394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitzer B, Fleck S, Blankenburg F. Parametric alpha-and beta-band signatures of supramodal numerosity information in human working memory. The Journal of Neuroscience. 2014;34(12):4293–4302. doi: 10.1523/JNEUROSCI.4580-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokita M, Ashitani Y, Ishiguchi A. Is approximate numerical judgment truly modality-independent? Visual, auditory, and cross-modal comparisons. Attention, Perception, & Psychophysics. 2013;75(8):1852–1861. doi: 10.3758/s13414-013-0526-x. [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Venkatraman V, Ansari D, Chee MWL. Neural correlates of symbolic and non-symbolic arithmetic. Neuropsychologia. 2005;43:744–753. doi: 10.1016/j.neuropsychologia.2004.08.005. [DOI] [PubMed] [Google Scholar]
- Verguts T, Fias W. Representation of number in animals and humans: A neural model. Journal of Cognitive Neuroscience. 2004;16:1493–1504. doi: 10.1162/0898929042568497. [DOI] [PubMed] [Google Scholar]
- Varma S, Schwartz DL. How should educational neuroscience conceptualize the relation between cognition and brain function? Mathematical reasoning as a network process. Educational Research. 2008;50:149–161. [Google Scholar]