Quantitative Susceptibility Mapping: Contrast Mechanisms and Clinical Applications

Abstract

Quantitative susceptibility mapping (QSM) is a recently developed MRI technique for quantifying the spatial distribution of magnetic susceptibility within biological tissues. It first uses the frequency shift in the MRI signal to map the magnetic field profile within the tissue. The resulting field map is then used to determine the spatial distribution of the underlying magnetic susceptibility by solving an inverse problem. The solution is achieved by deconvolving the field map with a dipole field, under the assumption that the magnetic field is a result of the superposition of the dipole fields generated by all voxels and that each voxel has its unique magnetic susceptibility. QSM provides improved contrast to noise ratio for certain tissues and structures compared to its magnitude counterpart. More importantly, magnetic susceptibility is a direct reflection of the molecular composition and cellular architecture of the tissue. Consequently, by quantifying magnetic susceptibility, QSM is becoming a quantitative imaging approach for characterizing normal and pathological tissue properties. This article reviews the mechanism generating susceptibility contrast within tissues and some associated applications.

Introduction

Quantitative susceptibility mapping (QSM) is a non-invasive MRI technique that measures the spatial distribution of magnetic susceptibility within an object (1-15). In a most common practice, QSM computes the magnetic susceptibility from the phase images of gradient recalled echoes (GRE) with the assumption that the phase shift is mainly due to susceptibility induced field inhomogeneity. This tomographic capability is unique as no other imaging techniques provide such a 3D mapping of susceptibility in the interior of an object with the measurement equipment positioned exterior to the object. In imaging biological tissues and specimens, QSM has revealed a diverse range of tissue contrast in the brain and the body, reflecting the variations of tissue magnetic susceptibility (6, 8, 10, 16-24). As more tissues are being studied, the mechanisms of these contrasts are increasingly becoming more complex, which has simultaneously also allowed more potential applications in both research and clinical radiology. This article aims to review the basic mechanisms of the contrast generated by QSM and their associated applications.

How is QSM generated?

The field perturbations caused by inhomogeneous susceptibility within a volume of interest (VOI) may be measured from MRI phase data. GRE phase images can provide better contrast between grey and white matter in the brain than the corresponding magnitude image (25-27). However, the phase measured in GRE acquisitions is highly dependent on imaging parameters; moreover, phase values are non-local, i.e. the phase value measured in a voxel not only depends on local tissue properties, but also depends on the surrounding magnetic susceptibility distribution. If the susceptibility induced magnetization is treated as a magnetic dipole, then the field perturbation caused by a known distribution of isotropic susceptibility can be obtained by convolving the susceptibility distribution with a unit dipole kernel. This calculation may be performed simply and efficiently as a pointwise multiplication in k-space (2, 3), such that

$$\Delta B_z\left(\mathbf{k}\right)=B_0\left(\frac{1}{3}-\frac{k_z^2}{\mid {\mathbf{k}}^2\mid }\right)\chi \left(\mathbf{k}\right)$$ [1]

where k is the k-space vector and k_z is its z-component; B₀ is the applied magnetic field, taken to be in the z-direction; ΔB_z (k) is the Fourier transform of the z-component of the magnetic field perturbation; and χ(k) is the Fourier transform of the magnetic susceptibility distribution. QSM is achieved by inversion of this equation (Fig. 1). While this inversion resolves the non-local property of phase, QSM faces several challenges both in the measurement of ΔB_z and the ill-posed nature of the inversion itself.

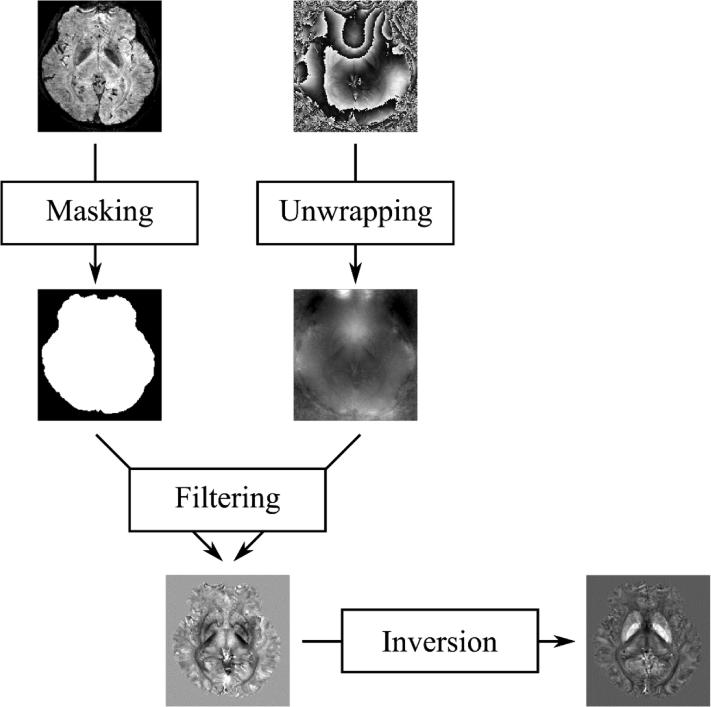
Fig. 1.

Flow chart of QSM. Magnitude and phase images are acquired with a GRE sequence. The magnitude image is used to create a mask of the brain providing the volume of interest. Phase image is first unwrapped followed by a background phase filtering in the masked region. Finally, susceptibility map is obtained by solving an inverse problem.

ΔB_z may be calculated from the GRE signal phase by scaling the measured phase by the gyromagnetic ratio and echo time to generate a field map. However, it must be first ensured that the phase is indeed caused by susceptibility and not by other effects such as chemical shift, receiver-coil phase (B₁ field) and flow-induced phase. For example, it is important to separate the phases induced by chemical shift when imaging regions of the body that have high fat content. Once susceptibility induced phase is isolated, the data must then be processed to remove phase wraps and background fields generated by sources outside of the VOI (Fig. 1). Phase unwrapping can be easily performed using path-based (28) or Laplacian-based (8, 29) unwrapping algorithms. Removal of background fields may be performed using a number of algorithms, including projection onto dipole fields (7, 30, 31), SHARP processing and its variants (10, 11) and HARPERELLA algorithm (13). High-pass spatial filtering can be used to simultaneously unwrap and filter the data, however this will also remove fields that are necessary for accurate QSM inversion. The filtered phase is then divided by the echo time (TE), yielding a map of frequency variation with respect to the reference frequency of the scanner. The local field perturbation is then given by ΔB_z = Δω/γ, where Δω is the local frequency perturbation and γ is the gyromagnetic ratio.

Recovery of a susceptibility map from a local tissue field map is a more complex task. The field map must be deconvolved with the unit dipole kernel, corresponding to a pointwise division in k-space. This deconvolution is ill-posed due to zeros in the k-space dipole kernel on two conical surfaces at approximately 54.7 degrees with respect to the direction of the main magnetic field. The inverse kernel is undefined at those surfaces and noise is greatly amplified in regions where the kernel is very small and the inverse kernel is very large, making a simple inversion of the forward calculation impossible. In general, QSM is achieved by conditioning of the ill-posed inverse calculation to measure the susceptibility distribution while excluding or minimizing noise and artefacts.

Susceptibility maps may be calculated from a single GRE acquisition using threshold-based masking or modification of the dipole kernel to remove or replace regions where the dipole kernel is small and the inverse kernel is very large or undefined (5, 7, 32). These algorithms are efficient and easy to implement, however they contain severe streaking artefacts due to the information lost through the masking process, and a compromise must be made between noise amplification and the reduction of streaking artefacts. Streaking in the focal areas of objects with large susceptibilities such as blood vessels may be reduced by estimating the missing data using iterative (33) or compressed sensing (11) algorithms.

In addition to the conditioning of the direct inverse calculation, iterative fitting algorithms have been proposed to create susceptibility maps by estimating the susceptibility distribution as a solution to a minimization problem. In addition to estimating the missing k-space data, various regularization-based optimization algorithms have been proposed using L1-norm (least absolute error) (9, 12, 20, 34) or L2-norm (least squares error) (31, 35) regularization to find a solution. Weighting based on spatial priors from the GRE magnitude (9, 36) or phase (20) may be included in the calculation to reduce streaking artefacts by enforcing smoothness in the solution in regions where the susceptibility distribution is assumed to be flat. While these algorithms can generate good quality susceptibility maps with minimal streaking artefacts, care must be taken on the assumptions made when selecting spatial priors to avoid reducing image contrast due to over-regularization (9, 35, 36).

The entirety of k-space may be sampled using the calculation of susceptibility through a multiple orientation sampling (COSMOS) algorithm (4). COSMOS combines data from images acquired with the ROI oriented at multiple (≥ 3) angles with respect to B₀. In the frame of reference of the ROI, the dipole kernel and its ill-defined surfaces are rotated at each orientation. Appropriate selection of object orientation allows the entirety of k-space to be sampled, with the exception of the origin of coordinates, and a direct inversion to be performed. The advantage of this algorithm is that the complete sampling of k-space in the inversion process allows the recovery of the susceptibility map free of streaking artefacts. However, COSMOS is often impractical, particularly for in vivo studies, due to the additional time and potential physical difficulty in acquiring images over a range of orientations.

While QSM has been shown by experiments to find the magnetic susceptibility distribution underlying the measured MR signal phase with good accuracy (4, 7), its accuracy is limited by its inherent assumption that the susceptibility is isotropic in nature. In reality, some molecules such as lipids in myelin, collagen and α-helix polypeptide (e.g. in myocardial filaments) have been shown to have an anisotropic susceptibility, characterized by a susceptibility tensor, creating an orientation-dependent magnetization when exposed to a magnetic field. Where such molecules form ordered structures such as myelin sheath in the brain, this can result in a measured susceptibility in QSM that varies with orientation with respect to B₀. The susceptibility anisotropy within a voxel can be measured with susceptibility tensor imaging (STI) (6). STI has been used to create high resolution fiber tracks in the mouse brain (37) and kidney (38).

Where does magnetic susceptibility come from?

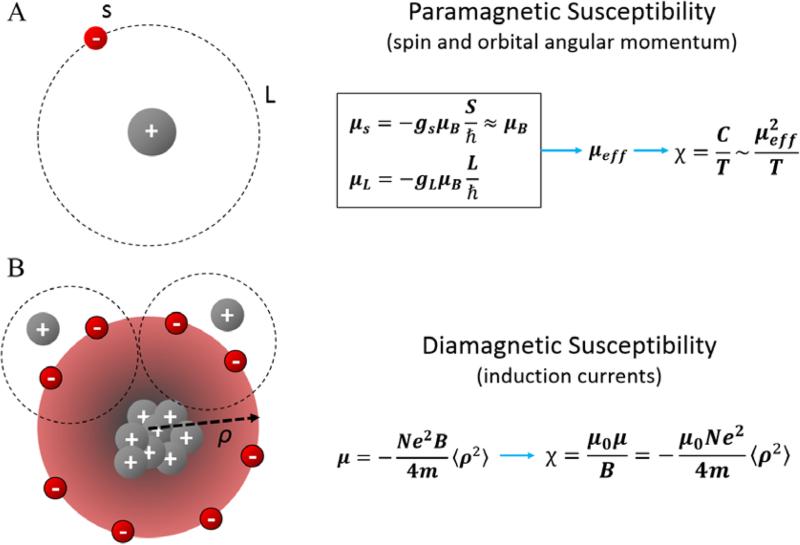
The general physical models of how materials become magnetized have grown to be very complex given the range of natural and manmade materials existing with diverse magnetic properties (39). While the theory of electromagnetics is described by the Maxell's equations, modeling magnetism of different materials remains a very active field of research. Much of the complexity results from the need to fully understand the collective behavior of a vast number of electrons in many different types of materials, as magnetism is believed to be predominantly contributed by the magnetic moments of electrons with the contribution of nuclear moments being negligibly small. A simple model of magnetism starting from non-interacting moments, though not complete (e.g. it does not explain the sharp transition of Curie temperature or ferromagnetism or superconductivity), has been useful for understanding the origins of paramagnetic and diamagnetic susceptibility.

In an atom or molecule, electrons are distributed into different energy levels with quantized spin and orbital angular momentum which gives rise to a set of quantized magnetic moments (39)

$${\mu }_s=-g_s{\mu }_B\frac{S}{\hslash }\approx {\mu }_B$$ [2]

$${\mu }_L=-g_L{\mu }_B\frac{L}{\hslash }$$ [3]

where μ_s and μ_L are the magnetic moment of an electron resulting from its spin and angular momentum respectively; g is the Landé g-factor; s and L are the spin and orbital angular momentum quantum number; h̷ is the reduced Planck constant; μ_B is the Bohr magneton (Fig. 2A). The probability of finding an electron with a given set of quantum numbers follows the Boltzmann's distribution, which in turn gives an effective magnetic moment μ_eff. As a rule of thumb, the more unpaired electrons, the larger the effective magnetic moment as paired electrons tend to cancel each other. For linear materials, magnetization (M) is proportional to the magnetic field (H), i.e. M = χH or in a differential from χ = ∂M/∂H. Therefore, $\chi \sim \frac{{\mu }_{eff}^2}{T}$ with the temperature coefficient being the Curie temperature C (Fig. 2A).

Fig. 2.

Atomic origin of paramagnetic and diamagnetic susceptibility. A. Paramagnetic susceptibility originates primarily from spin and orbital angular momentum induced magnetic moments (μ_s and μ_L respectively) of electrons. Electrons can be found in these quantized momentum levels following the Boltzmann distribution resulting in an expected magnetic moment μ_eff and an paramagnetic susceptibility inversely proportional to temperature. B. Diamagnetic susceptibility originates from the precession of orbital electrons about the applied external magnetic field. The precession of electrons is modeled as a circular current which generates secondly field opposing the applied magnetic field.

In addition to the aforementioned paramagnetism, the presence of an external field also causes the electrons to precess about the applied field, generating a secondary field that opposes the applied field thus giving rise to diamagnetism. According to the Langevin theory (a non-quantum mechanics classic model), the magnetic moment of this induced current is (39)

$$\mu =-\frac{N{e}^2{\mu }_{0}H}{4m_e}\langle {\rho }^2\rangle$$ [4]

where N is the number of electrons per unit volume; e is the electron charge; m_e is the electron mass; μ₀ is vacuum permeability; 〈ρ²〉 is the mean square distance of the electrons perpendicular to the H direction (Fig. 2B). Therefore, the diamagnetic susceptibility is $\chi =-\frac{N{e}^2{\mu }_0}{4m_e}\langle {\rho }^2\rangle$ which immediately indicates that 1) this susceptibility is negative; and 2) non-spherical molecules would have anisotropic magnetic susceptibility as the area of cross section is orientation dependent.

What are the factors influencing QSM measurements?

The susceptibility values measured by QSM are fundamentally determined by the molecular composition within an imaging voxel. They are also, however, affected by the nature of the MR imaging process. In bulk biological tissues as imaged by MRI, each voxel contains an ensemble of molecules of different kinds, all situated in a complex cellular environment. Given the finite resolution of MR images, susceptibility determined by QSM is only a sampled approximation of the true susceptibility distribution. This sampling process includes not only the digital sampling of the k-space but also the sensing of the local magnetic field based on a certain MR signal-generating nucleus, most often the proton. As a result, the susceptibility measured by QSM is influenced by the spatial variations of proton density as well as the relaxation properties of proton spins.

Molecular and cellular composition

Biological cells contain a myriad of molecules and ions. Each has its own magnetic susceptibility (40). The arrangement of cells within a tissue further complicates its magnetic property. It is thus nearly impossible to theoretically calculate the exact magnetic susceptibility of a cell or a volume of tissue. Nevertheless, within an imaged organ or body, all cells have some common features such as a lipid membrane, cytosol and organelles, while QSM only detects the magnetic susceptibility variations within the tissue rather than the absolute susceptibility. In other words, it is the relative portions of these molecules, especially those of strong susceptibility, that determine the contrast within a QSM image. For example, in white matter, lipids become the dominating sources due to the heavy myelination of axons which is not a feature of other cell types; in deep brain nuclei, iron-containing molecules are the main sources of its paramagnetism; in the kidney, the membranes of nephrons appear to be the leading source; in the myocardium, α-helixes of myofilaments are the major sources of anisotropy. In pathological tissues, focal depositions of minerals such as calcium, copper and iron have been found to be a major cause of susceptibility changes.

Tissue microstructure

Besides the molecular composition of a single cell, MRI-measured susceptibility is also highly dependent on the structure and arrangement of cells within a voxel. Thus, magnetic susceptibility can be used as a tool to probe tissue microstructure; for example, STI exploits the anisotropic susceptibility of certain tissues to determine the dominant orientation of the structures within a voxel and p-space multipole frequency mapping aims to infer the subvoxel magnetic field distribution (41, 42).

STI describes an anisotropic susceptibility tensor as opposed to the scalar quantity associated with isotropic QSM (41). Measuring the observed frequency offsets at multiple orientations with respect to the main field, B₀, enables the solution of the susceptibility tensor. The susceptibility tensor is related to frequency shift, in the subject frame of reference, according to the following (41):

$$f\left(\mathit{k}\right)=\gamma B_0\left(\frac{1}{3}\widehat{\mathit{H}}\chi \left(\mathit{k}\right)\widehat{\mathit{H}}-\widehat{\mathit{H}}\cdot \mathit{k}\frac{{\mathit{k}}^T\chi \left(\mathit{k}\right)\widehat{\mathit{H}}}{k^2}\right)$$ [5]

where χ is a second-order susceptibility tensor, Ĥ is the unit applied magnetic field vector, and B₀ is the magnitude of the magnetic flux density of the applied field. Assuming symmetry, there are six independent variables to be determined in the tensor. Thus, a minimum of six independent measurements are required, although fewer measurements are made possible through further assumptions and utilizing mutual information from diffusion tensor imaging (DTI) (19, 43). Rotation of the object of interest with respect to the main field allows acquisition of these independent measurements. Estimation of a susceptibility tensor is attained through inversion of the system of linear equations formed by Eq. (5). The estimated susceptibility tensor can be decomposed into three eigenvalues, representing principal susceptibilities, and the associated eigenvectors (Fig. 3). An orientation map can be formed for the principal susceptibility based on the direction of the associated eigenvector. Fiber tracks can then be reconstructed based on the STI (Fig. 3) in a process similar to DTI (21, 44).

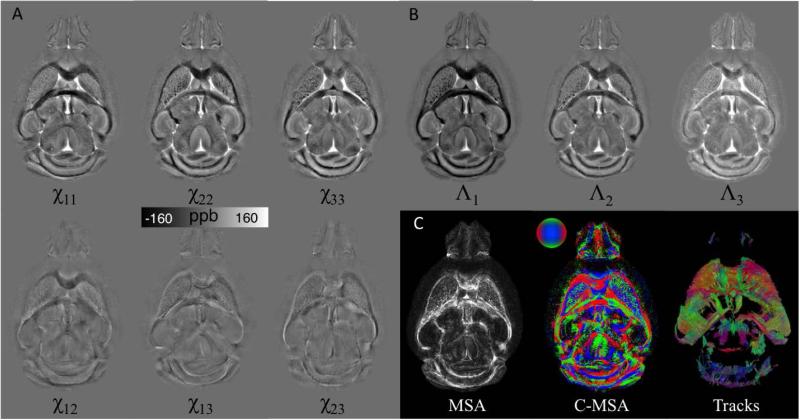
Fig. 3.

Illustration of STI on a mouse brain. Mouse brain was perfusion fixed with formalin and stained with Gd contrast agent. 3D Multi-echo GRE data were acquired in 12 specimen directions on a small-bore animal 7T scanner. A. The 6 independent tensor elements of a representative slice. B. Λ₁, Λ₂, and Λ₃ are the 3 eigenvalues representing the principal susceptibilities. C. Magnetic susceptibility anisotropy (MSA) and the color coded MSA were calculated based on the associated eigenvector orientations. Fiber tracking was performed using Diffusion Toolkit in a similar process to DTI and results were visualized using TrackVis. The track image shows the tracks intersecting 10 adjacent slices.

Applications of STI include but are not limited to characterization of white matter fiber tracks both in vivo and ex vivo, as well as mapping the renal tubule and cardiac myofiber architecture ex-vivo (21, 22, 41, 44).

STI of white matter is possible due to the presence of ordered bundles of axons forming fibers within the central nervous system. He and Yablonskiy originally predicted white matter frequency contrast dependent on the angle between axons and the applied magnetic field simply due to the elongated structure of the axons, but assuming isotropic susceptibility (45). Li et al provided both theoretical and experimental data demonstrating that the orientation dependent susceptibility observed in the white matter is due to anisotropic susceptibility of myelin lipids. Later, Wharton and Bowtell found that when modeling axons as hollow cylinders, the anisotropic susceptibility of myelin is necessary to fully explain the observed behavior of GRE phase (46). If sufficient multiple orientation GRE data is acquired, the fiber tracks can be reconstructed with comparable quality to DTI in the major white matter tracks (47).

Tubular structures in the nephron of the kidney exhibit similar susceptibility anisotropy as that of white matter fibers (21). The tubules are comprised of renal epithelia that also possess lipid bilayers composed of magnetically anisotropic lipid chains. The kidney is unique in that STI may provide more extensive tracking of the tubules in comparison to DTI as shown in a study on mouse kidneys (21). Whereas DTI is limited to the inner medulla, STI has the ability to track the tortuous tubules of the outer medulla and some of the cortex (21).

Significant susceptibility anisotropy is also present in the myocardium, arising from the composition and arrangement of myofilaments. A multi-filament model revealed that the arrangement of diamagnetically anisotropic peptide bonds comprising the myofibers produced the bulk susceptibility anisotropy of cardiac tissue (22). Thus STI enables mapping of the myofiber architecture, with complimentary results to DTI.

Unfortunately, STI has obvious limits in terms of clinical applicability due to the multiple-orientation requirements hindered by scan time limits and limited rotation within current transmit/receive coil arrays. Thus, non-rotational methods to investigate microstructure based on MRI-measured susceptibility are of great interest. If the structures within a voxel are heterogeneous, the magnetic field distribution within that voxel will also be heterogeneous. In principle, the field distribution for a single myelinated axon will be minimal in the parallel direction, but rapidly varying in the perpendicular direction. Unfortunately, the result of a standard GRE sequence is a single phase value for a given voxel that represents the summation of field offsets within that voxel. All spatial heterogeneity within the voxel is lost during the ensemble averaging. A spectral analysis technique in Fourier spectrum space, termed p-space, was proposed to recover the sub-voxel field distribution and infer the underlying microstructure (42). This method has been proven effective through extensive simulations, but its merit under practical imaging constraints is still under investigation (42, 48-50).

Imaging factors

As QSM relies on a signal-generating nucleus of an atom to sense the local field variations, the measured susceptibility is inherently influenced by the properties of these atoms. For example, are they uniformly distributed or compartmentalized? Do they have different relaxation properties? In the white matter, the myelin sheath possesses anisotropic and diamagnetic lipid chains, resulting in an increasingly more negative frequency shift in the myelin-water and axonal water (i.e. appearing more diamagnetic) as the fiber angle increases from 0 to 90 degrees. As the field inhomogeneity increases, the signal diphase more rapidly, which contributes to magnitude decay, characterized by varying T2* relaxation rate in GRE. The myelin-water component has short T2* compared to the axonal and extracellular space, and thus there is an absence of the myelin-water signal at later TEs. Thus, an appropriate echo time must be used to attain frequency contribution from the myelin-water component. Frequency shifts originating more locally can be attained by computing the difference between a short and long TE, allowing isolation of the myelin-water frequency in a method termed frequency difference mapping (FDM) (46, 51).

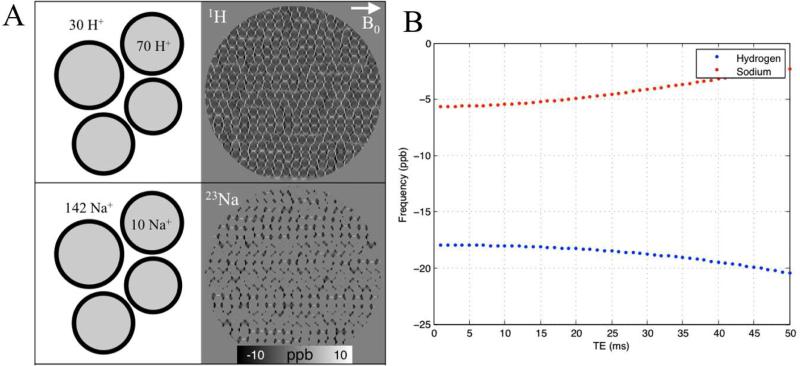
Cells also have elaborated mechanisms for maintaining the concentration gradients of many important ions and molecules across the cell membranes. For instance, ¹H protons are more abundant in the intracellular than extracellular space (intra:extra; ~70:30), whereas, ²³Na has much higher concentration in the extracellular space compared to the intracellular space (extra:intra;142:10) (34, 52). Phosphates, on the other hand, are mostly stored intracellularly (extra:intra; 2:149). Thus, in standard proton MRI, the phase values of the signal are weighted more heavily by intracellular protons, whereas in ²³Na MRI the phase highly reflects the field contribution from the extracellular space (Fig. 4).

Fig. 4.

Effect of compartmentalization on measured frequency shift. A. Simulated sub-voxel frequency distribution of ¹H and ²³Na for a WM fiber bundle, perpendicular to the main magnetic field at 3T. About 70% of water protons are intracellular while about 95% of ²³Na are extracellular. B. A single value for the voxel at each TE was attained through complex summation of all sub-voxel points. The weighting of intra-axonal and extracellular pools has significant impact on the resulting frequency values and temporal evolution.

The specific algorithmic steps taken to process the phase images and subsequently compute the susceptibility values also affect the quality of the resulting QSM maps. First, it is critical to generate a good mask of the VOI, excluding regions of unreliable phase values. Second, while different background phase removal algorithms produce generally similar looking phase maps, there are visually appreciable differences mainly in the low-frequency components. These differences may produce differences in the QSM maps, mostly around the edges. Third, the reproducibility and consistency within an inversion algorithm are generally found to be excellent (53, 54). There is still however a lack of data comparing different algorithms comprehensively such as truncated k-space division, LSQR and iLSQR, MEDI, L1 norm and L2 norm (5, 8-14, 20, 35, 36).

What are the clinical applications of QSM?

Magnetic susceptibility is influenced by a wide range of physiologically significant molecules. The state and concentration of these molecules may change in diseased tissues. Therefore, QSM is being evaluated in a growing number of clinical applications. The most readily translatable applications include among others: 1) the separation of diamagnetic calcium from paramagnetic iron; 2) the quantification of iron deposition and blood byproducts; and 3) the quantification of myelination in the white matter.

Hemorrhage

GRE is more sensitive than CT for detecting intracerebral hemorrhage (55, 56). However, T2* weighted hypointensity in GRE suffers from blooming artifacts that are highly dependent on imaging parameters. Conversely, QSM based on GRE phase data has become sufficiently accurate for measuring the strong susceptibilities of biomaterials including deoxyhemoglobin in the veins and blood degradation products. QSM can provide an accurate measurement of the hemorrhage volumes by removing blooming artifacts inherent in traditional T2* weighted imaging (57).

QSM can easily differentiate diamagnetic calcification from paramagnetic materials such as hemosiderin (58, 59) while both calcification and chronic hemorrhage appear hypointense on GRE magnitude images (Fig. 5). The study by Chen et al. demonstrated that QSM is superior to GRE imaging in differentiation of intracranial calcifications from hemorrhage (59). Thus, QSM may be used as a more accurate detection and measurement of microbleeds in GRE MRI (60, 61). It has also been reported that QSM can provide reliable measurement of hematoma volume (8, 9). Further, during blood degradation in hemorrhage, susceptibility progressively increases from oxyhemoglobin (diamagentic) to dexyhemoglobin (paramagentic), methemoglobin (strongly paramagnetic), and hemosiderin (super paramagentic) (58, 62). Therefore, QSM may be used to precisely quantify and spatially depict dynamically evolving changes in susceptibility over time due to evolution of blood product degradation thus may provide useful information allowing for a more precise management of hemorrhage patients.

Fig. 5.

Quantitative susceptibility mapping for measuring paramagnetic (microbleeds) and diamagnetic (calcifications) biomaterials on 45-yesr-old female patient. Note that calcification in the choroid plexus (yellow arrow) has a similar hyperintense appearance as a microbleed on the R2*. This ambiguity is removed on the QSM map. The scan parameters are: in plane resolution = 0.86 × 0.86 mm², matrix = 256 × 256, flip angle = 12°, TE of first echo = 3 msec, echo spacing = 3.08 msec, TR = 54 msec, and number of echoes = 8. Slice thickness is 1 mm.

Brain development

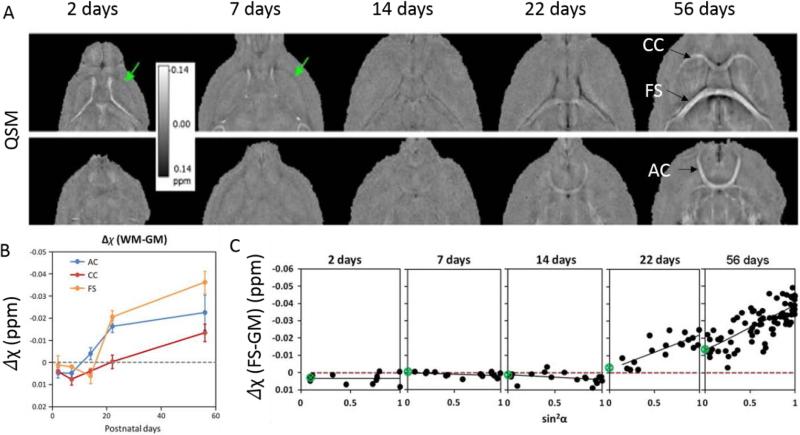
It is well known that the neonatal brain structure and myelination changes rapidly during early development leading to differences in brain tissue composition compared to the adult brain. Both human and mouse brains are poorly myelinated or un-myelinated at birth. Myelination occurs rapidly in the first few years of life for human and in the first few weeks for rodents. In human neonates, it was shown that phase difference between gray and white matter was greatly reduced compared to adults (63). In the developing mouse brain from postnatal day 4 (PND4) to PND40, it was shown that phase contrast between gray and white matter correlated with the optical intensity of myelin stained histological slides (64). However, these studies were based on phase contrast rather than the intrinsic tissue susceptibility. In the human brain, Li et al. reported that white matter became more diamagnetic as the brain developed from 1 to 83 years of age (65). In the mouse brain, Argyridis et al (66) evaluated the temporal evolution of magnetic susceptibility in the white matter of mouse brain from PND2 to PND56. They showed that, at PND2 and PND7, white matter appears paramagnetic compared to surrounding gray matter (Fig. 6). Its magnetic susceptibility then became increasingly diamagnetic as the brain developed. Furthermore, the increasing diamagnetism correlated well with the increasing myelin as depicted by myelin staining intensity.

Fig. 6.

A. Examples of magnetic susceptibility maps of the developing mouse brain. White matter largely appears paramagnetic relative to gray matter in PND2 and PND7 while contrast is weak at PND14. At PND22 and PND56, white matter appears diamagnetic. B. Magnetic susceptibility contrast of selected white matter regions relative to neighboring gray matter as a function of age. C. Apparent magnetic susceptibility of the fornix system as a function of sin²α where α is the fiber angle with respect to B0. The slope of the fitted trend line increases as the brain develops indicating increasing anisotropy. The scan parameters are: isotropic resolution = 59 × 59 × 59 μm³, matrix = 368 × 184 × 184, flip angle = 40°, TE = 20msec, TR = 200 msec. Figure was reproduced with permission from Argyridis et al (66).

Besides the diamagnetism, another important characteristic of white matter is that the magnetic susceptibility anisotropy (MSA) is directly proportional to myelin concentration (67). Argyridis et al. (66) also found that susceptibility anisotropy increased monotonically as a function of age from PND2 to PND56. It was further shown that MSA reached to 0.02 by PND22 compared to just −0.0028 at PND14 and continued to grow through PND56 reaching 0.026 (Fig. 6).

The sensitivity of QSM to myelination may therefore be useful for monitoring delayed myelination or loss of myelination during early brain development. For example, in a recent study of a mouse model of fetal alcohol spectral disorder (FASD), QSM revealed clear and significant abnormalities in anterior commissure, corpus callosum, and hippocampal commissure, which were likely due to reduced myelination (68). The study also suggested that QSM may be even more sensitive than DTI for examining changes due to prenatal alcohol exposure.

Aging

In white matter, the measured magnetic susceptibility has been related to diamagnetic myelin lipids and proteins of the myelin sheath. Li et al. has observed a biphasic pattern of susceptibility change in white matter tracts, such as the internal capsule, the splenium of corpus callosum and the optic radiation, with an initial decrease followed by an increase (65). This is consistent with known maturation and decay in the course of normal brain development and aging (69). The temporal characteristics, especially the time to reach minimum susceptibility, vary among different white-matter fiber bundles. For instance, susceptibilities of the internal capsule, the splenium of corpus callosum and the optic radiation reach their minimums at 45, 32 and 26 years, respectively.

In deep gray matter, iron accumulation throughout the lifespan has been well documented. Recently, there has been a growing interest in quantifying iron deposition in deep gray matter regions using QSM. Combined with X-ray fluorescence imaging, an ex vivo QSM study has established positive correlations between iron measurements and susceptibility values in deep gray matter regions (70). In two groups of extreme age (old group: age = 74.4±7.6 y/o, n = 11; young group: age = 24.0±2.5 y/o, n = 12), Bilgic et al. have demonstrated a strong significant correlation between susceptibility and postmortem iron measurements in deep gray matter regions (r = 0.881). Significantly higher susceptibility values in elderly group than young group have also been observed in regions such as putamen, globus pallidus, and red nucleus (16).

In a more comprehensive study of 191 subjects with consecutive age range (age = 7 - 87 y/o), non-linear increase of susceptibility with aging has been observed in globus pallidus, red nucleus, substantia nigra and dental nucleus. Relatively more linear increases with aging were found in putamen and caudate nucleus throughout the age investigated. Plateau of susceptibility in globus pallidus was found at the age of 20-30 years. One specific finding in globus pallidus is the inner and outer globus pallidus can be differentiated before the age of 27 years, which later become indistinguishable. One possible explanation is that medial medullary lamina grows thinner with aging. Higher susceptibility in the posterior putamen than the anterior has also been observed after the age of 27 years (65). Importantly, elevated iron in this healthy elderly group was found to be associated with motor function decline (71).

In a recent study focused on age-related susceptibility change after the age of 20 years, Gong et al. reported that regional susceptibility levels ranking from the highest to the lowest are: the globus pallidus, substantia nigra, red nucleus, caudate nucleus and putamen, and thalamus. In the age range investigated (25 ~ 78 years), linear age effects on susceptibility values were confirmed in regions other than globus pallidus and the rates varied, with the putamen exhibiting the highest rate of increase that was twice those in the substantia nigra and caudate nucleus. They further showed that hemisphere and gender-related differences existed in deep gray matter regions. Significant leftward asymmetries in iron content were observed in the substantia nigra and caudate nucleus. Gender difference was observed in the thalamus and red nucleus where men have higher iron level than women (72). These findings in deep gray matter regions may provide new clues for unveiling the underlying mechanisms of iron-related neurodegenerative diseases.

Parkinson's disease and pre-surgical planning

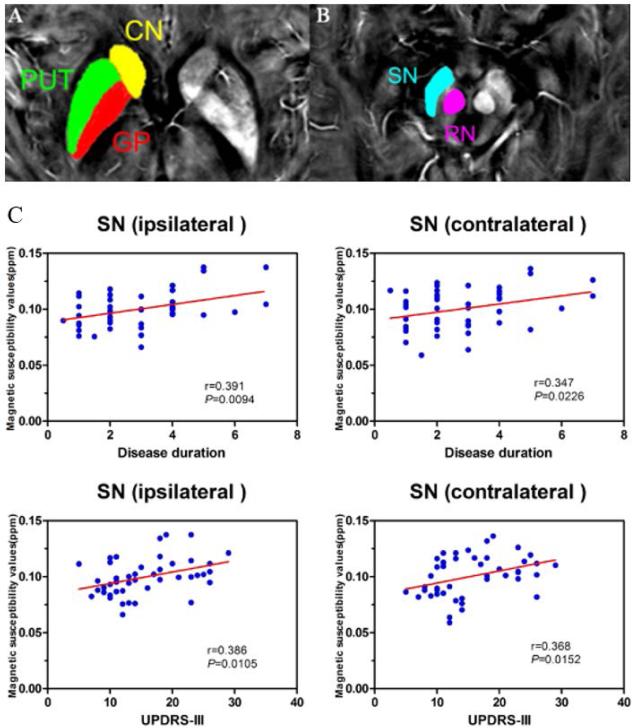
Development of Parkinson's disease (PD) is associated with dopaminergic cell loss and iron accumulation in the pars compacta (PC) within the substantia nigra (SN). Recent studies have shown QSM to be a potentially useful tool to assist the diagnosis and treatment of PD due to its sensitivity to variation in iron levels. In vivo studies have shown that QSM values are increased in the PC in PD patients relative to those measured in healthy controls (73-75), and that QSM is more sensitive than R₂ and R₂* measurements in discriminating between patients and healthy controls (74, 75). As such, QSM provides a useful, more quantitative means of assessing abnormal iron deposition in PD.

QSM has also been found to be sensitive enough to detect disturbed iron distribution in early idiopathic PD. In recent study by He et al (76), the inter-group differences of susceptibility and R2* value in deep grey matter nuclei, including the head of caudate nucleus, putamen, global pallidus, substantia nigra, and red nucleus, and the correlations between regional iron deposition and the clinical features were explored in 44 early PD patients and 35 gender and age-matched healthy controls. Susceptibility values were found to be elevated within bilateral substantia nigra (SNR) and red nucleus contralateral to the most affected limb in early PD compared with healthy controls. In comparison, increased R2* values were only seen within SN contralateral to the most affected limb in the PD group when compared with controls. Furthermore, it was found that bilateral SN magnetic susceptibility positively correlated with disease duration and the Unified Parkinson's Disease Rating Scale-III (UPDRS-III) scores in early PD. This finding further supports the potential value of QSM as a non-invasive quantitative biomarker of early PD.

Deep brain stimulation (DBS) is an effective treatment for the symptoms of PD (77, 78), involving the implantation of stimulating electrodes in the brain. Precise placement of these electrodes is essential to deliver the desired effects and to minimize side effects (79-82), and pre-surgical imaging is essential to determine patient suitability and to guide surgery (83-85). The dorsolateral portion subthalamic nucleus has been identified as the optimal stimulation site in the treatment of PD (86), while the medial globus pallidus may also be targeted (87). QSM has been shown to be superior to convential MRI protocols in the depiction of both the subthalamic nucleus (88) and medial globus pallidus (87), meaning that it may allow improved pre-surgical planning for DBS treatment of PD.

Multiple sclerosis

MRI is a well-established tool in the diagnosis and investigation of multiple sclerosis (MS), however common MR measurements such as lesion number or total lesion volume have not been shown to be predictive of disease progression (89). QSM has become increasingly prominent in the search for a quantitative biomarker to measure tissue changes occurring in MS, with a focus on quantifying iron levels in the deep grey matter, and identifying regions of demyelination and iron accumulation during the formation of MS lesions (Fig. 8) (17, 90-99).

Fig. 8.

Examples of QSM in the investigation of MS. A. QSM values can be used as a marker of iron deposition in the deep grey matter, which is characteristic of MS. The susceptibility map shows good delineation of the deep grey matter structures in closer agreement with the magnitude image then the non-local phase contrast. B. Some white matter lesions identified on GRE magnitude images appear in susceptibility maps, due to either reduced myelin content, increased iron content, or a combination of these factors. Here, the QSM data depicts the lesion with a clear hyperintense core, however the phase contrast is distorted, with a poorly defined lesion edge. The scan parameters are: 7T, 0.5 mm³ isotropic resolution, TE=20 ms, TR=150 ms, FOV=196×164×85 mm³, EPI factor = 3, SENSE factor = 2. Images courtesy of the Sir Peter Mansfield Imaging Centre, University of Nottingham, UK.

Langkammer et al (18) showed that susceptibility values in the deep grey matter measured using QSM correlate with increased iron levels measured using inductively coupled plasma mass spectrometry, suggesting that in this region QSM values may be assumed to mainly reflect local iron levels. Several studies have shown QSM values have been shown to be significantly raised in the deep grey matter in patients with clinically definite MS or clinically isolated syndrome suggestive of MS, relative to healthy controls (90, 91, 95), and these increases have been shown to correlate with expanded disability status scale (EDSS) measures of disability (95). It is thought that iron accumulation in the central nervous system may promote damage through oxidative stress, blocking repair mechanisms, activating microglia and macrophages, and/or facilitating mitochondrial changes leading to cellular degredation (100). Combining QSM and R₂* data has been shown to improve automated segmentation of deep grey matter structures in high (3T and higher) field strength MRI compared to segmentation based on T₁-weighted images.

Assessment of white matter changes in MS using QSM are more challenging due to the combination of demyelination, which causes a net increase in susceptibility due to the loss of diamagnetic myelin, and accumulation of paramagnetic iron in ferritin and presence of iron-bearing inclusions such as microglia and macrophages also causing an increase in susceptibility. Further, loss of iron-bearing oligodendrocytes during demyelinaton may offset some myelin loss by decreasing net susceptibility (99). While attempts have been made to separately quantify iron and myelin levels by combining QSM data with quantitative R₂* data (101), recent studies of white matter lesions in MS have inferred the definite presence of iron from QSM values greater than 0 ppm relative to the ventricular cerebrospinal fluid (CSF), as complete demyelination cannot raise the susceptibility beyond this value (97).

QSM is increasingly used in the study of MS lesions, where it has been shown to more accurately depict the heterogeneous distribution of magnetic susceptibility in such lesions more accurately than phase imaging (96). Li et al compared the appearance of MS lesions identified using MPFLAIR and T₁ MPRAGE magnitude images in R₂* and QSM images, and found that lesions may be either isointense or hyperintense in QSM, and are mostly diamagnetic relative to CSF, with QSM isointense lesions suggesting slightly higher myelin levels (99). A small number of lesions may have a positive susceptibility relative to CSF, suggesting increased iron levels and possibly complete demyelination (99). Wisnieff et al (97) compared QSM of white matter lesions with histological iron staining and suggested that in completely demyelinated lesions, iron levels may be directly quantified using QSM. Chen et al (94) compared the temporal evolution of QSM values in white matter lesions, finding that susceptibility increased from similar values to normal appearing white matter (NAWM) in acute enhancing lesions and retained significantly higher susceptibilities in early to intermediate non-enhancing lesions, but returned to similar values to NAWM in chronic non-enhancing lesions.

Alzheimer's disease

The basal ganglia are reported as the earliest and most intense accumulators of β-amyloid in subjects genetically predisposed to develop Alzheimer's disease (AD) in the future (102). Iron overload in basal ganglia is also a well-known feature of AD (103). Therefore accurately quantifying iron levels in vivo using QSM could possibly provide useful biomarkers for diagnosis of AD.

In a relatively small cohort (8 controls and 8 AD), Acosta-Cabronero et al. investigated susceptibility values using both region-based and whole brain analysis approaches. Abnormalities of susceptibility values were found in several gray and white matter regions. The most interesting finding was in the putamen, where higher susceptibility value was found in AD as compared against controls (104). Promising results has been reported in another study of 6 AD and 10 controls. Susceptibility of gray matter was found higher in β-amyloid-PET-positive AD patients as compared to β-amyloid-negative healthy controls (105).

Inconsistent results have also been reported by recent studies of subjects at early stage of the disease. A study of 18 mild cognitive impairment (MCI) subjects and 22 healthy controls observed no significant difference in basal ganglia and cortical gray matter between groups, suggesting that magnetic susceptibility may not be sufficient to serve as a biomarker for diagnosis at early stages of disease initiation (106). Another study of MCI subjects and healthy elderly controls investigated the relationship between magnetic susceptibility and Aβ measured by PiB-PET. While no correlation was found for healthy controls, strong positive correlations were observed in caudate nucleus, frontal, temporal, parietal and occipital lobes for MCI subjects. These findings suggested that cerebral iron accumulation might reflect Aβ associated brain dysfunction (107). One possible explanation for the discrepancy between these two studies could be the high heterogeneity of MCI subject group.

To date, QSM studies of AD are scarce yet the results are encouraging. Further studies dedicated to relating susceptibility with other established biomarkers for diagnosis of AD and especially MCI are needed to provide additional information for establishing the role of QSM for the diagnosis and management of AD patients.

Oxygenation

Oxygenation imaging could provide biomarkers for study cerebral physiology and improve understanding of disorders in which the oxygen supply is disturbed, such as stroke, tumor and Alzheimer's disease. In vessel segments that can be approximated as an infinite cylinder, the susceptibility difference between vein and tissue follows

$$\Delta {\mathrm{X}}_{\text{vein-tissue}}=\Delta {\mathrm{X}}_{\mathrm{do}}\times \mathrm{Hct}\times \mathrm{OEF}$$ [6]

whereΔX_do = 0.18 ppm is the susceptibility difference per unit hematocrit (Hct) between fully deoxygenated blood and fully oxygenated blood. Oxygen extraction fraction (OEF) can be calculated through measuring the susceptibility difference Δ X_vein-tissue. According to Fick principle, the cerebral metabolic rate for oxygen (CMRO₂) can be expressed as

$${\mathrm{CMRO}}_2=\mathrm{OEF}\times \mathrm{CBF}\times {\mathrm{C}}_a$$ [7]

where the carrying capacity of oxygen molecules per volume of blood (C_a) is a typical constant. By measuring cerebral blood flow (CBF) using other MRI protocol such as arterial spin labeling (ASL), local CMRO₂ could be also estimated.

Several QSM-based studies sought to measure OEF and CMRO₂ and compare the measurements to previously published results based on other MRI methods and PET imaging. In 12 healthy volunteers, Fan et al. reported a mean venous oxygen saturation of 59.7±2.4% and a mean CMRO₂ of 151±15 μmol/100g/min using QSM based method (108). Similarly assuming constant arterial oxygenation saturation level and total hemoglobin concentration, Zhang et al. generated quantitative maps of CMRO₂ and OEF before and after caffeine vasoconstriction in thirteen healthy volunteers. The reported CMRO₂ of 153±26.4 μmol/100g/min agreed well with previous MRI and PET literature (109). In 10 healthy subjects, Fan et al. also measured a strong reduction of local venous OEF during hypercapnia relative to baseline. For instance, OEF decreased by 40% in the straight sinus and in the internal cerebral veins draining the deep gray matter (110). In MS patients, they also observed a 3.4% absolute reduction of mean cortical OEF in MS relative to healthy controls. A weak correlation between OEF and cortical thickness was observed. Interestingly, OEF strongly correlated with cognitive performance, particularly information processing speed. A trend of progressive decrease in OEF with MS disease type was also reported (111).

More recent studies of patient populations focused on comparing QSM-derived OEF measurements directly with PET-based OEF measurements. In 27 patients with steno-occlusive cerebrovascular diseases, Uwano et al. reported a strong correlation between the OEF ratio on the QSM-OEF maps and that on the PET-OEF maps (r = 0.89, p < 0.001) (112). In another study of 26 patients with chronic cerebral ischemia, Kudo et al. reported a moderate correlation between QSM-OEF and PET-OEF measured by gold standard ¹⁵O PET (r = 0.60, p = 0.001) (113). These works demonstrated that QSM based noninvasive measurements of OEF and CMRO₂ can provide information regarding cerebral physiological changes, and raise the prospect of QSM as an alternative to ¹⁵O₂-PET for accessing patients with disruption in cerebral metabolism.

Practical matters of clinical translation

It is relatively straightforward to collect QSM data on a typical clinical MRI scanner as QSM uses the widely available 2D or 3D GRE sequence. In fact, many clinical protocols are already collecting 2D or 3D GRE data to obtain T2* or susceptibility weighting. A typical protocol for neural applications at 3T would be able to achieve a whole-brain coverage at around 0.8 mm in-plane resolution with a slice thickness around 2 mm in approximately 6 minutes of scan time. Faster scanning can be achieved with EPI, spiral trajectories or the recently proposed Wave-CAIPI technique (114-117). While 2D EPI is generally available, the other faster sequences are not yet widely available on clinical scanners. As susceptibility contrast and SNR improves with field strength, it is generally beneficial to use higher field strength when possible. Higher field strength shortens T2*, allowing shorter TE and TR thus faster scans. For a given TR, it is also beneficial to collect as many echoes as possible for improved efficiency and SNR through multi-echo averaging.

Currently, the main hurdle for broadly translating QSM into the clinics is that MRI vendors have yet to implement the necessary algorithms on their commercial scanners. First, most scanners do not store the phase images by default. Some susceptibility-weighted imaging (SWI) protocols output phase images that are high-pass filtered, which removes much of the useful phase information. Some scanners produce phase images containing discontinuities of singularity points or “open fringe lines” that usually caused by incorrect combination of images produced by multi-channel coils. Given that the manufacturers are still working out their preferred ways to generate phase images, at the present time, it still makes sense to store the unprocessed complex images of each coil and process them offline with in-house written or publically available software. If this is impractical for reasons such as increased storage space, at the minimum, it should be ensured that the phase images generated by the scanner are not filtered improperly. Second, MRI vendors have not implemented QSM algorithms to solve the phase-to-susceptibility inverse problem. However, there are shareware, for example, STI Suite (Duke University) available for research purposes (13). Nevertheless, to broadly evaluate and apply QSM in clinical radiology would require the scanners to generate QSM maps automatically.

While QSM of the brain has been most widely evaluated and is most readily translatable to the clinics, QSM of the body remains to be fully developed and optimized. The main challenge of body QSM is dealing with motion and water fat separation. However, early reports have shown promises in the kidney (23, 38), liver (24), heart (22) and cartilage (118, 119).

Conclusions

QSM has revealed extensive variations of magnetic susceptibility among biological tissues and between healthy and diseased tissues. Studies have shown that these variations are most often caused by their unique composition of molecules with distinctive magnetic properties and their microscopic tissue organization. Normal physiologic and abnormal disease processes can cause changes in the molecular and cellular level, resulting in measurable changes in magnetic susceptibility. QSM is thus becoming a valuable MRI tool for quantitatively assessing tissue property.

Fig. 7.

QSM of early-stage PD illustrates the regions of deep brain nuclei (A–B). CN, the head of caudate nucleus; PUT, putamen; GP, globus pallidus; SN, substantia nigra; RN, red nucleus. C. Scatter plots and regression lines show the significant relationship between susceptibility values in bilateral SN and clinical measures in early-stage PD. Correlations are partialed for age. The susceptibility value of ipsilateral SN is positively correlated with disease duration (upper-left: r = 0.391, P = 0.0094) and UPDRS-III score (bottom-left: r = 0.386, P = 0.0105) in PD. The susceptibility value in SN contralateral to the most affected side in PD patients is positively correlated with disease duration (upper-right: r = 0.347, P = 0.0226) and UPDRS-III score (bottom-right: r = 0.368, P = 0.0152). Figure reproduced from He et al. (76) with permission.